Electric field and strain tunable band gap and band alignments of MoSi₂N₄/MSe (M = In, Ga) van der Waals heterostructures

Abstract

Using van der Waals heterostructures (VDWHs) to engineer novel electronic properties of two-dimensional (2D) material systems has proven to be a viable strategy in recent years. Given the excellent mechanical and electronic properties of air-stable MoSi₂N₄ and the high electron mobility of air-sensitive wide band gap 2D monolayers of GaSe and InSe, we investigate the interaction of these materials using first-principles calculations. We find that the VDWHs have narrow type-II direct band gaps. We apply either vertical electric field, vertical strain or biaxial strain to MoSi₂N₄/GaSe and MoSi₂N₄/InSe for band gap modulation. We find that the band structure of MoSi₂N₄/GaSe and MoSi₂N₄/InSe is highly tunable, exhibiting a variety of behaviours such as type-II-to-type-H band alignment, large band gap changes and direct-to-indirect band gap transitions. Interestingly, we also find that both heterostructures have a large band gap modulation of 1.4 to 2.3 eV under 8% biaxial strain. We also find that we can reverse the direction of the electron transfer between the monolayers under external stimuli. These findings therefore reveal another viable path towards InSe and GaSe based electronics and optoelectronics by using MoSi₂N₄-based VDWHs.

---

1 Introduction

Since the isolation of graphene in 2004,¹ two-dimensional (2D) materials have generated intense research interest due to their vast potential applications ranging from transistors,² non-linear optics,³ magnetic random access memories (MRAM)⁴ and cooling⁵ to unconventional device architectures such as valleytronic⁶ and neuromorphic devices.⁷ Various other methods of obtaining 2D materials have since been developed^8,9 and their potential is further accentuated by the concept of van der Waals heterostructures (VDWHs) where 2D materials are stacked vertically. VDWHs have drawn keen research interest due to their ability to create hybrid materials with custom made properties depending on the constituent 2D materials, as well as the orientation and stacking order.¹⁰ VDWHs utilising different monolayers such as black phosphorus (BP) and MoS₂ to create BP/MoS₂ VDWH high performance transistors,¹¹ Moire superlattices where the individual h-BN monolayers are orientated at different angles which results in unique properties such as topological polarisation,¹² 2D VDWHs with multiple monolayers of graphene and h-BN,¹³ and multiferroic VDWHs¹⁴ composed of ferroelectric and ferromagnetic monolayers have all been demonstrated.

The recent computational discovery and experimental synthesis of the MA₂Z₄ (ref. 15) (M is transition metals, A is Si or Ge, and Z is N, P, or As) group of 2D materials have allowed for more variety of VDWHs that combine and possess excellent properties of MA₂Z₄ type materials, with the properties of the other monolayer(s) such as optical absorption in desired wavelengths of light.¹⁶ MoSi₂N₄ has no bulk 3D parent equivalent and is experimentally made by inserting MoN₂ with Si.¹⁵ This results in a septuple layered material consisting of MoN₂ sandwiched between two Si–N layers. This passivation of the surface means that MoSi₂N₄ is very air stable.¹⁷ This air stability possibly extends across the MA₂Z₄ group of materials. Density functional theory (DFT) has shown that the outer Si–N layers preserve the semiconducting characteristics of the inner Mo–N layer, protecting MoSi₂N₄ against Fermi level pinning.¹⁸ MoSi₂N₄ has also been experimentally verified to have high mechanical strength.¹⁷ Quantum transport calculations have shown that MoSi₂N₄ is a viable alternative to silicon for use in transistors,^19–21 with high carrier mobility demonstrated in experiments.¹⁷ These overall characteristics make it a suitable platform upon which 2D VDWHs can be built.^22,23 A recent variation has been experimentally created in which multiple MoN₂ layers are sandwiched by 2 Si–N layers,²⁴ presenting an interesting target for future studies due to their various predicted properties such as superconductivity and opening up the possibility for the creation of more MA₂Z₄(MoN)_n materials and heterostructures.²⁵ MoSi₂N₄ has been theoretically investigated to create VDWHs with WSi₂N₄ that exhibit ultra-fast transport,²⁶ enhanced electron mobility and optical absorption^16,27–29 with band gaps that are tunable under an external electric field^28,29 and strain.²⁹

2D InSe, part of a group together with InS and InTe, is derived from its bulk 3D parents and can be grown in various ways.³⁰ InSe has been found to be an n-type semiconductor with high electron mobility^31,32 that is retained down to small layer thickness³² and thus exhibits the quantum Hall effect.³² Back-gated InSe field emission transistors (FETs) have been fabricated and possess high on/off ratios of 10⁸ and a subthreshold swing (SS) of 300 mV dec⁻¹ at room temperature,³¹ comparable to that of TMDC FETs.³⁰ Multilayer InSe has a direct band gap³³ and thus is well suited for high speed electronics and optoelectronics, with a high responsivity of 10⁷ A W⁻¹ and detectivity of 10¹⁵ Jones.^34,35 Monolayer InSe is noted to have second-harmonic generation (SHG) stronger than MoS₂ or GaSe,³⁵ thus making it promising for optoelectronics. 2D GaSe, also part of a group with InS and InTe, is likewise also derived from its bulk 3D parents, with an atomic structure the same as that of InSe. Similarly, GaSe can also be grown in various ways³⁰ like InSe. Unlike InSe, GaSe is noted to be a p-type semiconductor with relatively poorer hole mobility due to the presence of heavy holes, but it must be noted that charge scattering at the interface can affect carrier mobility as in the case of InSe.³¹ DFT results³⁶ show that GaSe and InSe in general have high electron mobility but relatively poorer hole mobility, with the electron mobility of GaSe observed to be even higher than that of InSe. GaSe has been explored for use in single photon emitters,³⁷ high power terahertz sources,³⁸ ultraviolet emitters,³⁹ broadband ultrafast photonics⁴⁰ and SHG.⁴¹

2D InSe and GaSe degrade under exposure to air or ambient conditions,^32,35,42 thus various methods have been tried to encapsulate these materials to preserve their properties. One approach is to use other 2D materials that are air stable to create VDWHs. Encapsulation using h-BN (ref. 43) has been carried out, showing protection of the underlying InSe and GaSe layers. Graphene has also been used for InSe (ref. 44) and GaTe (ref. 45) encapsulation, with InSe encapsulation enhancing the underlying optoelectronic properties due to the charge transfer from InSe to graphene. DFT studies show that the electronic properties of GaTe/graphene are tunable by strain and an external electric field,⁴⁶ while experimentally, InSe/HBN/graphite VDWH FETs⁴⁷ have high electron mobility and high on/off ratios. The approach of encapsulation provides a relatively clean atomic interface, reducing the charge scattering that can adversely affect electron mobility and other performance characteristics.³¹

Motivated by the potential use of MA₂Z₄ to encapsulate GaSe and InSe, we carry out first-principles calculations on the electronic and mechanical properties of MoSi₂N₄/GaSe and MoSi₂N₄/InSe VDWHs by using DFT. We find that MoSi₂N₄/GaSe and MoSi₂N₄/InSe have direct type II band gaps. We subject both VDWHs to external electric fields, biaxial strain and vertical strain to explore the extent of tunability possible. Under external electric fields perpendicular to the plane of our VDWHs, we find that external electric fields can be used to drive transitions between direct and indirect bandgaps, as well as transitions between diverse band gap types, thus indicating the field-effect tunable optoelectronic properties of MoSi₂N₄/GaSe and MoSi₂N₄/InSe VDWHs. Additionally, the electronic properties, band alignment and the band gap nature of MoSi₂N₄/GaSe and MoSi₂N₄/InSe can also be controlled under mechanical compression and strain in both in plane and vertical directions. We find that biaxial strain is particularly effective in modulating band gaps of these VDWHs, with a 2.3 eV range (MoSi₂N₄/GaSe) and a 1.4 eV range (MoSi₂N₄/GaSe) of tunability, thus showing wide to narrow band gap modulation. We find that external stimuli can control the direction of the charge transfer and corresponding internal electric field between the monolayers. These results suggest that MoSi₂N₄/GaSe and MoSi₂N₄/InSe VDWHs are suitable for tunable electronic and optoelectronic device applications.

2 Computational methods

All simulations are completed using DFT as implemented in the Vienna ab initio simulation package.^48–51 PAW pseudopotentials⁵² are used for ion electron interaction, with GGA PBE⁵³ used to describe the exchange–correlation functional. While PBE is known to underestimate band gaps,^54–56 it does obtain structural parameters close to the experimental parameters.⁵⁷ This allows us to qualitatively capture general trends of the band structure and band alignment, especially when the atomic structures are strained, without the high computational costs imposed by HSE06. Grimme DFT-D3 corrections⁵⁸ are used to simulate VDW interactions between monolayers. Gamma-centred Brillouin zone sampling of 11 × 11 × 1 with a Monkhorst–Pack grid⁵⁹ is adopted. All materials are relaxed until ionic force converges to 0.01 V Å⁻¹. The electronic convergence is set at 10⁻⁸ eV. The energy cutoff is uniformly set to 500 eV to allow comparisons between the different converged simulations. A vacuum layer of 20 Å is applied to isolate periodic layers from interacting with each other. Dipole corrections are included in the calculations. GaSe and InSe both show important differences under spin orbit coupling (SOC).^60,61 However, SOC calculations are not considered due to the prohibitive computational costs of simulating 65 atoms with SOC. Experimental results have shown that MoSi₂N₄, GaSe and InSe are stable at temperatures elevated above room temperature.^17,62,63 Since van der Waals (vdW) forces are weak interactions, we expect that the monolayers will bind together while remaining structurally stable at room temperature.

3 Results and discussion

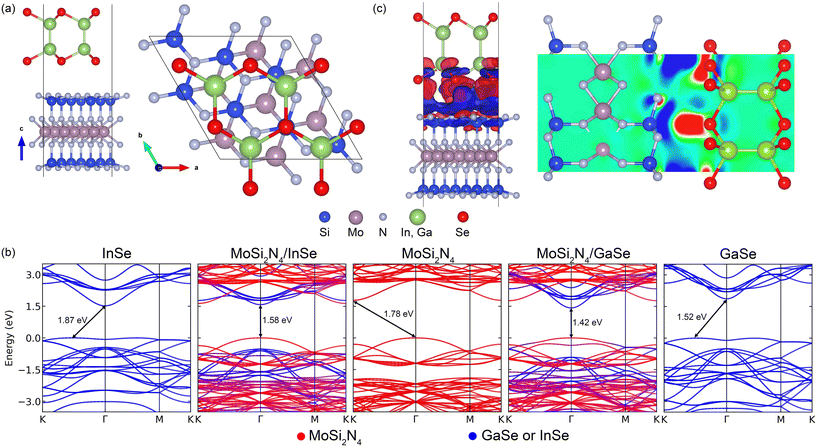
3.1 Structural properties and stacking configurations

MoSi₂N₄, GaSe and InSe are constructed and compared against previously reported experimental and computational lattice parameters.^{17,40,64–67} All freestanding unit cell monolayers are relaxed using previous simulation parameters to ensure accurate structural parameters. The calculated lattice constants are 3.82 Å (GaSe), 4.05 Å (InSe) and 2.91 Å (MoSi₂N₄). MoSi₂N₄ compared favorably against the aforementioned references. All VDWHs are initially constructed using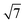 × 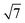unit cells of MoSi₂N₄ and 2 × 2 unit cells of GaSe or InSe, for a total number of 65 atoms per VDWH. Upon relaxation, it is found that the VDWHs have interlayer distances of 3.32 Å (MoSi₂N₄/GaSe) and 3.36 Å (MoSi₂N₄/InSe), which are reasonably close to the vdW radii of 1.55 Å (nitrogen)⁶⁸ and 1.90 Å (selenium).⁶⁸ Strain analysis shows that both MoSi₂N₄ monolayers are just under 1% strain, with 0.9% strain in GaSe and 4.7% compression in InSe. The binding energy between MoSi₂N₄ and GaSe (InSe) monolayers is calculated as E_b = (E_vdW − E_MoSi2N4 − E_μ)/65, where μ is GaSe or InSe. The values are −0.014 eV per atom (MoSi₂N₄/GaSe) and −0.0049 eV per atom (MoSi₂N₄/InSe), suggesting that the VDWHs are energetically stable and compare favorably against other bilayer materials.⁶⁹

3.2 Electronic structures

The band gaps and band gap types of the converged heterostructures are shown in Fig. 1(b). The VDWHs are type II direct band gap heterostructures with the GaSe (InSe) monolayer providing the conduction band minimum (CBM) at Γ. The MoSi₂N₄ valence band minimum (VBM) hybridises and interacts with the GaSe (InSe) VBM and therefore provides the majority contribution to the VDWH VBM through an avoided crossing through the GaSe (InSe) valence band. The MoSi₂N₄ VBM has a small contribution from the Si–N interface^70,71 and therefore the charge transfer from MoSi₂N₄ results in the hybridisation and interaction seen in the band structure. Overall, the band structures of the monolayers are superimposed onto each other, except that the VDWH band gaps are much narrower compared to freestanding monolayers. The differential charge density is calculated as Δρ = ρ_vdW − ρ_MoSi2N4 − ρ_μ, where μ is GaSe or InSe, ρ_vdW is the charge density of the VDWH and ρ_μ is the charge density of the individual monolayer. This reveals that charge transfers between the monolayers from MoSi₂N₄ to GaSe and InSe as seen in Fig. 1(c) narrow the band gaps, with charge transfers in both VDWHs similar to each other. We further observe charge depletion mainly from Si at the interface towards charge accumulation mainly on Se at the interface. With MoSi₂N₄/InSe, InSe compression plays an additional role in narrowing the band gap. GaSe and InSe transition from direct to indirect band gaps as the layer thickness is decreased.³³ We observe from Fig. 1(b) that all 2D InSe and GaSe monolayers are indirect band gaps with features as observed in other papers,³⁰ which is non-optimal for optoelectronics. On the other hand, our created VDWHs are direct band gaps, due to the replacement of the nearly flat VBM of InSe and GaSe with the more dispersive MoSi₂N₄ VBM as seen in Fig. 1(b). Thus, we expect overall carrier mobility of most of our VDWHs to improve, especially given the high elastic modulus and high carrier mobility of MoSi₂N₄.¹⁷ The creation of the internal electric field going from MoSi₂N₄ to GaSe and InSe creates a region where photogenerated charge carriers can be separated and thus improve optical absorption. These characteristics enhance the optoelectronic properties compared to freestanding InSe and GaSe.

Fig. 1 (a) Atomic structure of MoSi₂N₄/MSe (M = Ga, In). (b) Band structures of the individual monolayers and the VDWH. (c) Charge transfer between the monolayers in the VDWHs. The blue region shows electron depletion, and the red region shows electron accumulation. Hence electrons transfer from MoSi₂N₄ to GaSe (InSe).

3.3 Electric field and strain tuning

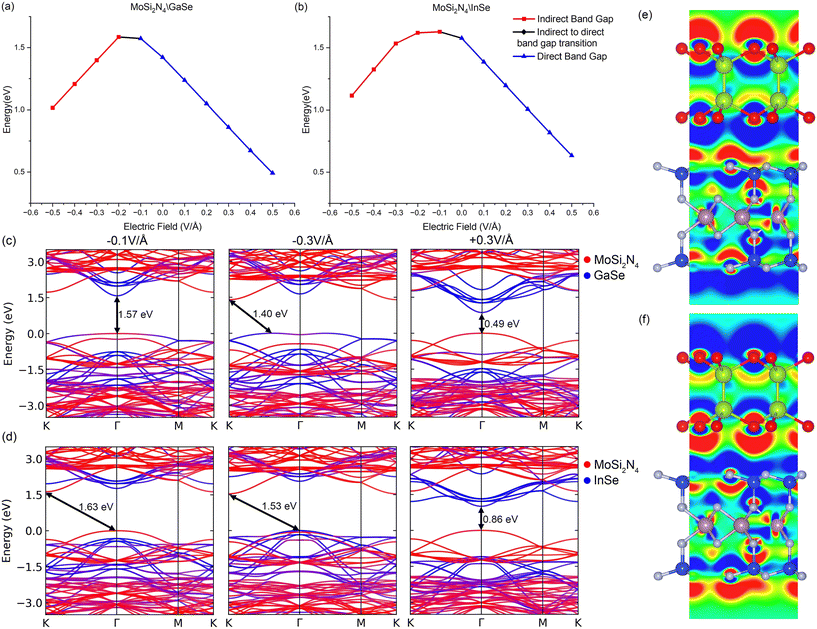
We explore the response of MoSi₂N₄/GaSe and MoSi₂N₄/InSe to external electric fields to better understand their properties. External electric fields are applied from −0.5 V Å⁻¹ to +0.5 V Å⁻¹ in increments of 0.1 V Å⁻¹, with the positive electric field going from GaSe (InSe) to MoSi₂N₄ and the negative electric field going from MoSi₂N₄ to GaSe and InSe. The effects of the external electric field on band gaps, band gap types and differential charge density difference are shown in Fig. 2, with the band structures shown in ESI†Fig. S1. The differential charge transfer is calculated as Δρ = ρ_electric −ρ_vdW, where ρ_vdW is the charge density of the original VDWH and ρ_electric is the charge density of the VDWH under an external electric field. The positive external electric field goes against the internal electric field, inducing electron accumulation on GaSe (InSe) and electron depletion on MoSi₂N₄. This lowers the GaSe (InSe) band structure and raises the MoSi₂N₄ band structure. For the positive electric field values tested, all band structures are direct band gap type II VDWHs. The decrease in the band gap, to 0.50 eV (+0.5 V Å⁻¹, MoSi₂N₄/GaSe) and to 0.63 eV (+0.5 V Å⁻¹, MoSi₂N₄/InSe), is largely linear.

Fig. 2 Band gap and band gap nature of (a) MoSi₂N₄/GaSe and (b) MoSi₂N₄/InSe under an external electric field. (c) Representative band structures of MoSi₂N₄/GaSe. VBM hybridisation ceases and CBM and VBM k points shift under a negative external electric field. Under a positive external electric field, the band gap narrows but remains a direct type II band gap. (d) Representative band structures of MoSi₂N₄/InSe. Under a negative external electric field, VBM hybridisation ceases and only the CBM k point shifts. Under a positive external electric field, the band gap narrows but with a smaller change compared to MoSi₂N₄/GaSe and remains a direct type II band gap. Differential charge density between the VDWH under (e) +0.4 V Å⁻¹ and (f) −0.4 V Å⁻¹ electric field with reference to the original VDWH. Red shows electron accumulation and blue shows electron depletion.

External negative electric fields induce electron accumulation on MoSi₂N₄ and electron depletion on GaSe and InSe, enhancing the internal electric field. The MoSi₂N₄ band lowers in energy, but the CBM of GaSe and InSe at Γ is lower than the CBM of MoSi₂N₄ between M and K, thus the CBM of GaSe and InSe is the VDWH CBM at values below −0.1 V Å⁻¹. The band gap change is therefore smaller to 1.57 eV (MoSi₂N₄/GaSe) and to 1.63 eV (MoSi₂N₄/InSe). Intermediate states between −0.1 V Å⁻¹ and −0.2 V Å⁻¹ (MoSi₂N₄/GaSe) and between −0.0 V Å⁻¹ and −0.1 V Å⁻¹ (MoSi₂N₄/InSe) exist, where MoSi₂N₄ at K and GaSe (InSe) at Γ both contribute to the CBM, with the VBM from MoSi₂N₄ at Γ. Stronger negative electric fields result in reducing hybridisation of the VDWH VBM at Γ as the MoSi₂N₄ VBM descends further in energy. The VDWH VBM switches over from MoSi₂N₄ to GaSe and InSe. In MoSi₂N₄/GaSe, the VDWH VBM shifts away from Γ and becomes an indirect type H VDWH for negative electric field values. Stronger negative electric field values at −0.2 V Å⁻¹ drive MoSi₂N₄/GaSe into indirect band gap type H, this time with the CBM contribution from MoSi₂N₄ at K as the MoSi₂N₄ band structure descends, with VBM contribution from both GaSe and MoSi₂N₄ between Γ and K. Hence, the band gap peaks at 1.59 eV and then decreases with more negative electric field values. Eventually the hybridisation of the VBM stops, turning the VDWH into indirect type II. In MoSi₂N₄/InSe, the switchover from the MoSi₂N₄ VBM to the InSe VBM is more gradual, as the MoSi₂N₄ CBM at K continues to descend. Thus, the band gap remains relatively constant while initially switching from direct type II to indirect type I as the VDWH VBM continues to be from MoSi₂N₄. Beyond −0.3 V Å⁻¹, the MoSi₂N₄ CBM continues to descend in energy, while the VDWH VBM switches over from the MoSi₂N₄ VBM to the InSe VBM at Γ, thus the heterostructure becomes a type II indirect band gap.

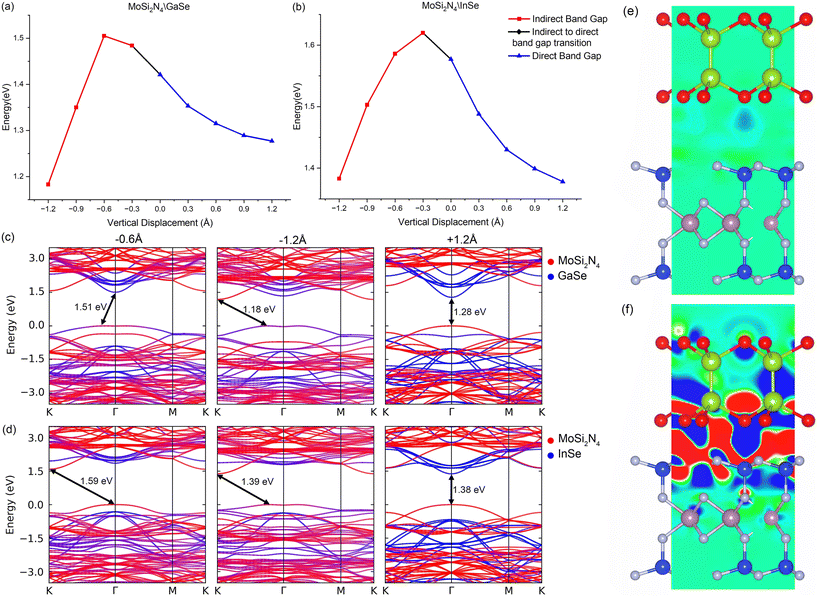
We also subject MoSi₂N₄/GaSe and MoSi₂N₄/InSe to vertical strain and compression by varying the interlayer distance in steps of 0.3 Å, with band gaps, charge transfers and the heterostructure type presented in Fig. 3, with the band structures shown in ESI† Fig. S2. The differential charge density this time is calculated as Δρ = ρ_vdW − ρ_MoSi2N4 − ρ_μ, where μ is GaSe or InSe, ρ_vdW is the charge density of the VDWH and ρ_μ is the charge density of the individual monolayer. The z coordinates for the interface atoms are kept fixed while allowing x and y coordinates to change, thus allowing biaxial strain to change. All other atoms are left unconstrained. Decreasing the interlayer distance reduces the width of the potential barrier between the monolayers, increasing the charge transfer from MoSi₂N₄ to GaSe (InSe). The band gap widens to 1.51 eV (0.6 Å compression, MoSi₂N₄/GaSe) and 1.86 eV (0.3 Å compression, MoSi₂N₄/InSe). The valence band flattens and both VDWHs change from a direct band gap type II to an indirect band gap type H VDWH. Upon additional vertical compression, GaSe (InSe) is forced to fit into the MoSi₂N₄ interface. Biaxial strain increases and becomes unevenly distributed. The net effect is that the electron transfer reverses direction, going from GaSe (InSe) to MoSi₂N₄, with corresponding electron depletion on the outer Se atoms. This results in MoSi₂N₄ bands descending compared to GaSe (InSe). The MoSi₂N₄ VBM lowers in energy and retracts away from the avoided crossing at Γ, changing the VDWH VBM from MoSi₂N₄ to GaSe (InSe) and shifting the VDWH VBM slightly away from Γ. The uneven strain on GaSe (InSe) results in the various bands having varying changes, as seen in the GaSe (InSe) bulk valence bands. Notably, the uneven strain raises the energy of the GaSe (InSe) CBM and retracts these into the bulk conduction bands, thus the MoSi₂N₄ CBM at K becomes a VDWH CBM. This band gap change is noted to be approximately linear from 1.51 eV (0.6 Å) to 1.18 eV (1.2 Å) compression for MoSi₂N₄/GaSe. Conversely, increasing the interlayer separation results in GaSe (InSe) having smaller biaxial strain. This effect is however small, as observed in the lack of strain effects in the band structures when compared to vertical compression. Instead, the more prominent effect in this case comes from increasing the width of the potential barrier between the monolayers as the interlayer distance increases. This reduces the interaction between the monolayers and limits the charge transfer between the monolayers, with only a slight electron depletion on GaSe (InSe) and slight electron accumulation on MoSi₂N₄. This results in the reduction of hybridisation in the VDWH valence band. Thus, the band gap becomes smaller at a decreasing rate as the interaction and charge transfer gradually cease, with the VDWH remaining direct band gap type II.

Fig. 3 Band gap and band gap nature of (a) MoSi₂N₄/GaSe and (b) MoSi₂N₄/InSe under vertical strain. (c) Representative band structures of MoSi₂N₄/GaSe. Under negative vertical strain (compression), the VBM flattens and hybridisation is reduced. CBM and VBM k points shift multiple times. Under positive vertical strain, the band gap narrows but remains a direct type II band gap. (d) Representative band structures of MoSi₂N₄/InSe. Under negative vertical strain, VBM hybridisation is reduced and both CBM and VBM k points shift multiple times. Under positive vertical strain, the band gap narrows but remains a direct type II band gap. Differential charge density between the monolayers under (e) +0.9 Å and (f) −0.9 Å vertical strain. Red shows electron accumulation and blue shows electron depletion.

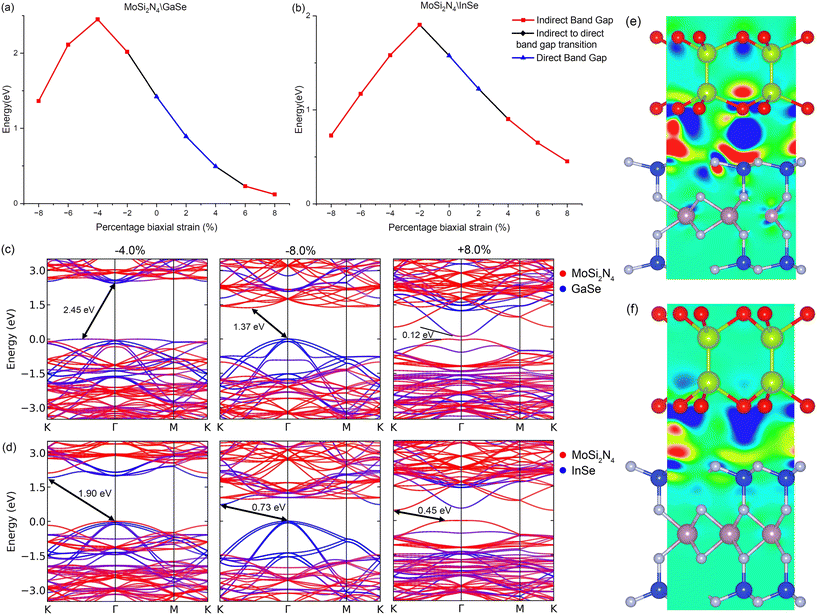
As MoSi₂N₄, GaSe and InSe are responsive to in-plane strain and VDWHs can be experimentally strained,^72–74 we also study the response of the VDWHs to biaxial strain engineering. The biaxial breaking strain of bilayer GaSe has been experimentally determined to be about 5%,⁷⁵ and that of octuple layered InSe to be about 8.57%.⁷⁶ The breaking strain for MoSi₂N₄ has been theoretically calculated to be about 19.5% (ref. 77) with experimental results verifying very high mechanical strength.¹⁷ We therefore expect our VDWHs to have a breaking strain between that of octuple layered InSe, bilayer GaSe and MoSi₂N₄ due to the high mechanical strength of MoSi₂N₄.¹⁷ The biaxial strain is thus calculated from −8% to 8% in increments of 2% with negative values representing compression and positive values representing strain. The band gaps, heterostructure type and differential charge transfers are plotted in Fig. 4, with the band structures shown in ESI† Fig. S3. Likewise, the differential charge density is also calculated as Δρ = ρ_vdW − ρ_MoSi2N4 − ρ_μ, where μ is GaSe or InSe, ρ_vdW is the charge density of the VDWH and ρ_μ is the charge density of the individual monolayer. When both VDWHs are strained, there is a net transfer of electrons from GaSe (InSe) to MoSi₂N₄, with additional electron depletion on the outer Se atoms. This net electron transfer and thus internal electric field are in the opposite direction from that of the original VDWH. The band gap narrows and both conduction bands of MoSi₂N₄ and GaSe (InSe) lower in energy. The conduction bands split and become less degenerate, with the CBM of both monolayers having a larger response than the bulk conduction bands, and lower in energy at a higher rate. The GaSe (InSe) bands just below the VBM which have a heavier Se contribution also decrease in energy at a higher rate with more strain compared to the bulk GaSe (InSe) bands, due to the stretching of Ga–Se (In–Se) bonds. The MoSi₂N₄ contribution to both VDWH valence bands becomes stronger with increasing strain. The band gap decreases mostly linearly to 0.49 eV (4% strain, MoSi₂N₄/GaSe) and to 0.90 eV (2% strain, MoSi₂N₄/InSe), with the VDWH remaining a direct band gap type II heterostructure throughout that range. The MoSi₂N₄/GaSe band gap narrows significantly to 0.23 eV (6% strain) and 0.12 eV (8% strain), resulting in the MoSi₂N₄ VBM and GaSe CBM strongly interacting and hybridising with each other. The interaction shifts the VBM away from Γ towards K, which changes the band gap into an indirect type H heterostructure. For MoSi₂N₄/InSe, with increasing strain, the MoSi₂N₄ CBM at K descends slightly lower in energy compared to the InSe CBM at Γ. The VDWH thus switches over to indirect band gap type I, with a smaller change in the band gap as compared to MoSi₂N₄/GaSe. The CBM of InSe is noted to also hybridise and interact with the MoSi₂N₄ VBM with increasing strain, though to a lesser extent than that of MoSi₂N₄/GaSe. In-plane compression also results in electron transfer from GaSe (InSe) to MoSi₂N₄, at a smaller rate than in plane strain and without electron depletion on the outer Se atoms. This charge transfer and the corresponding internal electric field are also reversed from that of the original VDWH. The net charge transfer results in MoSi₂N₄ bands descending relative to GaSe (InSe). This initially raises both the VDWH band gap mostly linearly to 2.45 eV (4% compression, MoSi₂N₄/GaSe) and to 1.98 eV (2% compression, MoSi₂N₄/InSe). The band gap slowly transitions from type II to type H as the MoSi₂N₄ VBM gradually retracts away from the VDWH VBM at Γ, reducing the hybridisation with GaSe (InSe), similar to the response with negative electric fields. The CBMs of the monolayers have a larger response and retract into the bulk conduction bands at a higher rate with more compression. The MoSi₂N₄ conduction band in the MoSi₂N₄/GaSe conduction band flattens and undergoes some level of hybridisation with GaSe, while the VDWH VBM also flattens significantly, becoming an indirect type H band gap. As seen previously with biaxial strain, the GaSe (InSe) bulk valence bands at Γ are more sensitive to compression, with these valence bands increasing with energy with more compression. With higher compression, these GaSe (InSe) bands emerge and contribute to the VDWH VBM and the MoSi₂N₄ conduction bands descend in energy. Thus, the band gap narrows from 2.45 eV to 1.37 eV and changes to an indirect band gap type II heterostructure, with the CBM initially between Γ and M (6% compression), before switching to between Γ and K (8% compression). In contrast, the MoSi₂N₄/InSe valence bands remain dispersive under compression. Under higher compression, the MoSi₂N₄ valence bands completely retract away from 0.0 to −1.5 eV. The InSe CBM at K descends lower than the MoSi₂N₄ CBM with higher compression, hence MoSi₂N₄/InSe becomes an indirect band gap type I heterostructure under compression.

Fig. 4 Band gap and band gap nature of (a) MoSi₂N₄/GaSe and (b) MoSi₂N₄/InSe under biaxial strain. The wide range of band gap modulation is shown. (c) Representative band structures of MoSi₂N₄/GaSe. Under negative biaxial strain (compression), the VBM initially flattens and hybridisation is reduced. The CBM also initially flattens. VBM hybridisation stops on further compression and both CBM and VBM k points shift multiple times. Under positive biaxial strain, the band gap almost closes but remains a direct type II band gap. (d) Representative band structures of MoSi₂N₄/InSe. Under negative biaxial strain, VBM hybridisation stops and both CBM and VBM k points shift multiple times. Under positive vertical strain, the band gap narrows but remains a direct type II band gap. Differential charge density between the monolayers under (e) 8% and (f) −8% biaxial strain. Red shows electron accumulation and blue shows electron depletion.

We note that the modulation of the band gap using biaxial strain appears to be more effective and higher than what is observed in most other materials and VDWHs, with 1 eV band gap change with just 4% biaxial strain (MoSi₂N₄/GaSe) and 6% biaxial strain (MoSi₂N₄/InSe). For our strain profiles, MoSi₂N₄/GaSe has 2.3 eV band change while MoSi₂N₄/InSe has 1.4 eV band gap change, much higher compared to other VDWHs that use GaSe (around 0.9 eV across entire biaxial strain profile in ref. 78), InS (around 0.5 eV across entire biaxial strain profile in ref. 79), InSe (around 1.0 eV across entire biaxial strain profile in ref. 80) or to monolayer MoS₂ (0.9 eV with 9% biaxial strain in ref. 81). Our VDWHs are therefore tunable all the way from wide to narrow band gaps with relatively smaller biaxial strain than normal.

4 Conclusions

Our DFT results show that MoSi₂N₄/GaSe and MoSi₂N₄/InSe form VDWHs of direct type II band gaps. We find that the strain is concentrated in the xy plane of GaSe and InSe bonds, leaving MoSi₂N₄ strain free. The substitution of the GaSe (InSe) valence band with MoSi₂N₄, combined with the high elastic modulus and carrier mobility of MoSi₂N₄, should improve the carrier mobility of the VDWHs compared to intrinsic GaSe (InSe). External electric fields and in plane and out of plane strain are applied to better understand the tunability of the VDWHs. The VDWHs can be driven between direct and indirect band gaps, as well as types I, II, and H and intermediate types, with adjustable band gaps. Biaxial strain is noted to be particularly effective in band gap modulation. We find that external stimuli can control the direction of the charge transfer and the corresponding internal electric field between the monolayers. Thus, encapsulating GaSe and InSe with MoSi₂N₄ enhances the underlying properties of GaSe and InSe, with properties amenable to engineering for versatile novel electronic and optoelectronic purposes.

Data availability

The data that support the findings of this study are available from the corresponding author upon reasonable request.

Author contributions

J. Q. N. performed the simulations and data analysis and writing of the paper. Q. W., L. K. A. and Y. S. A. supervised the project. Q. W., L. K. A. and Y. S. A. contributed to the revision of this work.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L. K. A. and Q. W. are supported by Singapore A*STAR IRG (M23M6c0102). Y. S. A. is supported by the SUTD-ZJU IDEA Visiting Professor Grant under the award number SUTD-ZJU (VP) 202001 and the SUTD Kickstarter Initiatives (SKI) under the award number SKI 2021_01_12. The calculations were carried out using the computational resources provided by the Athena supercomputing facility in SUTD and the National Supercomputing Centre (NSCC) Singapore.

Notes and references

1. K. S. Novoselov, A. K. Geim, S. V. Morozov, D.-E. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Science, 2004, 306, 666–669.
2. Y. Liu, X. Duan, H.-J. Shin, S. Park, Y. Huang and X. Duan, Nature, 2021, 591, 43–53.
3. B. Xu, Z. Jin, L. Shi, H. Zhang, Q. Liu, P. Qin, K. Jiang, J. Wang, W. Tang and W. Xia, Front. Optoelectron., 2023, 16, 1–10.
4. H. Yang, S. O. Valenzuela, M. Chshiev, S. Couet, B. Dieny, B. Dlubak, A. Fert, K. Garello, M. Jamet and D.-E. Jeong, et al. , Nature, 2022, 606, 663–673.
5. Y. Weng, S. Wu, L. Wang, W. Zhao, Y. Jiang and Y. Deng, J. Mater. Chem. C, 2022, 10, 13167–13173.
6. X. Feng, C. S. Lau, S.-J. Liang, C. H. Lee, S. A. Yang and Y. S. Ang, Adv. Funct. Mater., 2023, 2309848.
7. W. Huh, D. Lee and C.-H. Lee, Adv. Mater., 2020, 32, 2002092.
8. Z. Cai, B. Liu, X. Zou and H.-M. Cheng, Chem. Rev., 2018, 118, 6091–6133.
9. P. Kumar, A. Dey, J. Roques, L. Assaud, S. Franger, P. Parida and V. Biju, ACS Mater. Lett., 2022, 4, 263–270.
10. Y. Liu, N. O. Weiss, X. Duan, H.-C. Cheng, Y. Huang and X. Duan, Nat. Rev. Mater., 2016, 1, 16042.
11. M. Huang, S. Li, Z. Zhang, X. Xiong, X. Li and Y. Wu, Nat. Nanotechnol., 2017, 12, 1148–1154.
12. D. Bennett, G. Chaudhary, R.-J. Slager, E. Bousquet and P. Ghosez, Nat. Commun., 2023, 14, 1629.
13. L. Britnell, R. Gorbachev, R. Jalil, B. Belle, F. Schedin, A. Mishchenko, T. Georgiou, M. Katsnelson, L. Eaves and S. Morozov, et al. , Science, 2012, 335, 947–950.
14. L. Cao, X. Deng, G. Zhou, S.-J. Liang, C. V. Nguyen, L. Ang and Y. S. Ang, Phys. Rev. B, 2022, 105, 165302.
15. L. Wang, Y. Shi, M. Liu, A. Zhang, Y.-L. Hong, R. Li, Q. Gao, M. Chen, W. Ren and H.-M. Cheng, et al. , Nat. Commun., 2021, 12, 2361.
16. C. C. Tho, C. Yu, Q. Tang, Q. Wang, T. Su, Z. Feng, Q. Wu, C. Nguyen, W.-L. Ong and S.-J. Liang, et al. , Adv. Mater. Interfaces, 2023, 10, 2201856.
17. Y.-L. Hong, Z. Liu, L. Wang, T. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M.-L. Chen and D.-M. Sun, et al. , Science, 2020, 369, 670–674.
18. Q. Wang, L. Cao, S.-J. Liang, W. Wu, G. Wang, C. H. Lee, W. L. Ong, H. Y. Yang, L. K. Ang and S. A. Yang, et al. , npj 2D Mater. Appl., 2021, 5, 71.
19. B. Ye, X. Jiang, Y. Gu, G. Yang, Y. Liu, H. Zhao, X. Yang, C. Wei, X. Zhang and N. Lu, Phys. Chem. Chem. Phys., 2022, 24, 6616–6626.
20. X. Sun, Z. Song, N. Huo, S. Liu, C. Yang, J. Yang, W. Wang and J. Lu, J. Mater. Chem. C, 2021, 9, 14683–14698.
21. K. Nandan, B. Ghosh, A. Agarwal, S. Bhowmick and Y. S. Chauhan, IEEE Trans. Electron Devices, 2021, 69(1), 406–413.
22. L. Cao, G. Zhou, Q. Wang, L. Ang and Y. S. Ang, Appl. Phys. Lett., 2021, 118(1), 013106.
23. C. C. Tho, S.-D. Guo, S.-J. Liang, W. L. Ong, C. S. Lau, L. Cao, G. Wang and Y. S. Ang, Appl. Phys. Rev., 2023, 10(4), 041307.
24. Z. Liu, L. Wang, Y.-L. Hong, X.-Q. Chen, H.-M. Cheng and W. Ren, Natl. Sci. Rev., 2023, 10, nwac273.
25. C. C. Tho, X. Feng, Z. Jiang, L. Cao, C. S. Lau, S.-D. Guo and Y. S. Ang, Adv. Phys. Res., 2023, 3(7), 2300156.
26. P. Zhao, Z.-Y. Jiang, J.-M. Zheng, Y.-M. Lin and A. Du, J. Phys. Chem. C, 2022, 126, 11380–11388.
27. G. Yang and Y. Zhou, Comput. Mater. Sci., 2024, 231, 112617.
28. Z. Zhang, G. Chen, A. Song, X. Cai, W. Yu, X. Jia and Y. Jia, Phys. E, 2022, 144, 115429.
29. X. Cai, Z. Zhang, Y. Zhu, L. Lin, W. Yu, Q. Wang, X. Yang, X. Jia and Y. Jia, J. Mater. Chem. C, 2021, 9, 10073–10083.
30. H. Arora and A. Erbe, InfoMat, 2021, 3, 662–693.
31. W. Feng, W. Zheng, W. Cao and P. Hu, Adv. Mater., 2014, 26, 6587–6593.
32. D. A. Bandurin, A. V. Tyurnina, G. L. Yu, A. Mishchenko, V. Zólyomi, S. V. Morozov, R. K. Kumar, R. V. Gorbachev, Z. R. Kudrynskyi and S. Pezzini, et al. , Nat. Nanotechnol., 2017, 12, 223–227.
33. G. W. Mudd, S. A. Svatek, T. Ren, A. Patanè, O. Makarovsky, L. Eaves, P. H. Beton, Z. D. Kovalyuk, G. V. Lashkarev and Z. R. Kudrynskyi, et al. , Adv. Mater., 2013, 25, 5714–5718.
34. H.-W. Yang, H.-F. Hsieh, R.-S. Chen, C.-H. Ho, K.-Y. Lee and L.-C. Chao, ACS Appl. Mater. Interfaces, 2018, 10, 5740–5749.
35. S. A. Wells, A. Henning, J. T. Gish, V. K. Sangwan, L. J. Lauhon and M. C. Hersam, Nano Lett., 2018, 18, 7876–7882.
36. J. Chen, X. Tan, P. Lin, B. Sa, J. Zhou, Y. Zhang, C. Wen and Z. Sun, Phys. Chem. Chem. Phys., 2019, 21, 21898–21907.
37. P. Tonndorf, S. Schwarz, J. Kern, I. Niehues, O. Del Pozo-Zamudio, A. I. Dmitriev, A. P. Bakhtinov, D. N. Borisenko, N. N. Kolesnikov and A. I. Tartakovskii, et al. , 2D Mater., 2017, 4, 021010.
38. W. Shi and Y. J. Ding, Appl. Phys. Lett., 2004, 84, 1635–1637.
39. C. S. Jung, F. Shojaei, K. Park, J. Y. Oh, H. S. Im, D. M. Jang, J. Park and H. S. Kang, ACS Nano, 2015, 9, 9585–9593.
40. S. Ahmed, J. Qiao, P. K. Cheng, A. M. Saleque, M. N. A. S. Ivan, T. I. Alam and Y. H. Tsang, ACS Appl. Mater. Interfaces, 2021, 13, 61518–61527.
41. W. Jie, X. Chen, D. Li, L. Xie, Y. Y. Hui, S. P. Lau, X. Cui and J. Hao, Angew. Chem., Int. Ed., 2015, 54, 1185–1189.
42. A. Bergeron, J. Ibrahim, R. Leonelli and S. Francoeur, Appl. Phys. Lett., 2017, 110(24), 241901.
43. H. Arora, Y. Jung, T. Venanzi, K. Watanabe, T. Taniguchi, R. Hubner, H. Schneider, M. Helm, J. C. Hone and A. Erbe, ACS Appl. Mater. Interfaces, 2019, 11, 43480–43487.
44. Z. Chen, J. Biscaras and A. Shukla, Nanoscale, 2015, 7, 5981–5986.
45. E. Mercado, Y. Zhou, Y. Xie, Q. Zhao, H. Cai, B. Chen, W. Jie, S. Tongay, T. Wang and M. Kuball, ACS Omega, 2019, 4, 18002–18010.
46. H. Li, Z. Zhou, K. Zhang and H. Wang, Nanotechnology, 2019, 30, 405207.
47. L. Wu, J. Shi, Z. Zhou, J. Yan, A. Wang, C. Bian, J. Ma, R. Ma, H. Liu and J. Chen, et al. , Nano Res., 2020, 13, 1127–1132.
48. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558.
49. G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 14251.
50. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50.
51. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169.
52. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
53. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865.
54. L. J. Sham and M. Schlüter, Phys. Rev. Lett., 1983, 51, 1888.
55. J. P. Perdew and M. Levy, Phys. Rev. Lett., 1983, 51, 1884.
56. A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53, 3764.
57. G.-X. Zhang, A. M. Reilly, A. Tkatchenko and M. Scheffler, New J. Phys., 2018, 20, 063020.
58. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
59. H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188.
60. Z. Ben Aziza, V. Zólyomi, H. Henck, D. Pierucci, M. G. Silly, J. Avila, S. J. Magorrian, J. Chaste, C. Chen and M. Yoon, et al. , Phys. Rev. B, 2018, 98, 115405.
61. S. Magorrian, V. Zólyomi and V. Fal'Ko, Phys. Rev. B, 2017, 96, 195428.
62. Q. Zhao, R. Frisenda, P. Gant, D. Perez de Lara, C. Munuera, M. Garcia-Hernandez, Y. Niu, T. Wang, W. Jie and A. Castellanos-Gomez, Adv. Funct. Mater., 2018, 28, 1805304.
63. N. Balakrishnan, Z. R. Kudrynskyi, E. F. Smith, M. W. Fay, O. Makarovsky, Z. D. Kovalyuk, L. Eaves, P. H. Beton and A. Patanè, 2D Mater., 2017, 4, 025043.
64. A. Ray, S. Tyagi, N. Singh and U. Schwingenschlogl, ACS Omega, 2021, 6, 30371–30375.
65. V. Zólyomi, N. Drummond and V. Fal'Ko, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 205416.
66. M.-W. Chen, H. Kim, D. Ovchinnikov, A. Kuc, T. Heine, O. Renault and A. Kis, npj 2D Mater. Appl., 2018, 2, 2.
67. Q. Zhao, T. Wang, Y. Miao, F. Ma, Y. Xie, X. Ma, Y. Gu, J. Li, J. He and B. Chen, et al. , Phys. Chem. Chem. Phys., 2016, 18, 18719–18726.
68. S. S. Batsanov, Inorg. Mater., 2001, 37, 871–885.
69. J. E. Padilha, A. Fazzio and A. J. da Silva, Phys. Rev. Lett., 2015, 114, 066803.
70. Y. Wu, Z. Tang, W. Xia, W. Gao, F. Jia, Y. Zhang, W. Zhu, W. Zhang and P. Zhang, arXiv, 2021, preprint, arXiv:2107.10126,  DOI:10.1038/s41524-022-00815-6.
71. A. Bafekry, M. Faraji, D. M. Hoat, M. Shahrokhi, M. Fadlallah, F. Shojaei, S. Feghhi, M. Ghergherehchi and D. Gogova, J. Phys. D: Appl. Phys., 2021, 54, 155303.
72. W. Hou, A. Azizimanesh, A. Dey, Y. Yang, W. Wang, C. Shao, H. Wu, H. Askari, S. Singh and S. M. Wu, Nat. Electron., 2024, 7, 8–16.
73. A. Dey, A. Azizimanesh, S. M. Wu and H. Askari, ACS Appl. Mater. Interfaces, 2024, 16, 8169–8183.
74. A. Azizimanesh, A. Dey, S. A. Chowdhury, E. Wenner, W. Hou, T. Peña, H. Askari and S. M. Wu, Appl. Phys. Lett., 2023, 123, 043504.
75. B. Chitara and A. Ya'Akobovitz, Nanoscale, 2018, 10, 13022–13027.
76. Y. Li, C. Yu, Y. Gan, Y. Kong, P. Jiang, D.-F. Zou, P. Li, X.-F. Yu, R. Wu and H. Zhao, et al. , Nanotechnology, 2019, 30, 335703.
77. Q. Li, W. Zhou, X. Wan and J. Zhou, Phys. E, 2021, 131, 114753.
78. L. Zeng, S. Zhang, L. Yao, Z. Bi, Y. Zhang, P. Kang, J. Yan, Z. Zhang and J. Yun, Nanotechnology, 2022, 34, 065702.
79. H. Yao, C. Zhang, Q. Wang, J. Li, Y. Yu, F. Xu, B. Wang and Y. Wei, New J. Chem., 2021, 45, 2508–2519.
80. Y. Guo, J. Wang, G. Hu, X. Yuan and J. Ren, Phys. Lett. A, 2021, 404, 127395.
81. A. Chaves, J. G. Azadani, H. Alsalman, D. Da Costa, R. Frisenda, A. Chaves, S. H. Song, Y. D. Kim, D. He and J. Zhou, et al. , npj 2D Mater. Appl., 2020, 4, 29.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4lf00239c

---