Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Oxide ion dynamics in hexagonal perovskite mixed conductor Ba7Nb4MoO20: a comprehensive ab initio molecular dynamics study†
Bettina
Schwaighofer
 ab,
Markus
Appel
ab,
Markus
Appel
 a,
Miguel Angel
Gonzalez
a,
Miguel Angel
Gonzalez
 *a and
Ivana Radosavljevic
Evans
*a and
Ivana Radosavljevic
Evans
 *b
*b
aInstitut Laue Langevin, 71 Avenue de Martyrs, 38042, Grenoble Cedex 9, France. E-mail: gonzalezm@ill.fr
bDepartment of Chemistry, Durham University, Science Site, South Road, Durham, DH1 3LE, UK. E-mail: ivana.radosavljevic@durham.ac.uk
First published on 9th January 2024
Abstract
Hexagonal perovskite Ba7Nb4MoO20-related materials are very promising solid electrolytes with high oxide ion conductivity and redox stability, making them potentially applicable in solid oxide fuel cells. Optimizing the properties of this family of materials necessitates atomic-level understanding of the oxide ion dynamics leading to high conductivity. Here we report extensive ab initio molecular dynamics simulations of Ba7Nb4MoO20 investigating oxide ion motions, which allowed the observation of a continuous diffusion pathway for oxide ions in the (ab) plane, but also revealed significant contribution of the oxygen atoms from crystallographic sites located outside this plane, to the long-range dynamics. To probe the timescale of oxide ion diffusion, complementary quasielastic neutron scattering experiments were carried out, and showed that oxide ion dynamics in Ba7Nb4MoO20, even at 950 °C, are too slow to be observable on a nanosecond timescale. Based on the atomic-level understanding of structure–property relationships afforded by this detailed computational study, we propose new materials design strategies with potential to significantly increase oxide ion conductivity in Ba7Nb4MoO20-related hexagonal perovskites, which target the simultaneous increase of the number of oxide ion charge carriers and rotational flexibility of the (Nb/Mo)Ox polyhedra.
Introduction
Materials with high oxide ion conductivity are of considerable research interest owing to their applications in oxygen sensors, oxygen-permeable membranes and as electrolytes in solid oxide fuel cells (SOFCs), devices for green electricity generation. However, the high temperatures required to achieve significant conductivities in current electrolytes limit the more widespread use of SOFCs.1–3 This limitation can be overcome with new materials with excellent oxide ion conductivity in the temperature range between 300–500 °C.The perovskite-type materials with general formula ABO3 have long been known to support oxide ion conductivity, with Na0.5Bi0.5TiO3−δ and Sr- or Mg-doped LaGaO3 as the most notable examples.4,5 Modifications of chemical composition by substitution of A or B cations in ABO3 phases can lead to more complex layered or intergrowth perovskite-related structures. Several such classes of oxide ion conductors have been identified, including brownmillerites,6–14 Dion–Jacobson15,16 and A3OhTd2O7.5 (Oh = octahedrally and Td = tetrahedrally coordinated metal ion) phases.17–20 Among the currently most topical oxide ion conducting materials are hexagonal perovskites. Ba3NbMoO8.5 was the first such material reported,21 and a significant volume of research has since been carried out to understand the relationship of the conductivity of this and related materials to the crystal structure, local structure, composition and defect chemistry.22–27
Hexagonal perovskite Ba7Nb4MoO20 has recently been reported to be an excellent mixed proton and oxide ion conductor (σo = 0.5 × 10−3 S cm−1 at 525 °C).28 A small number of chemical modifications of Ba7Nb4MoO20 by aliovalent doping which increased the oxygen content above 20 per formula unit have been found to increase oxide ion conductivity while decreasing proton conduction. For example, in Ba7Nb3.9Mo1.1O20.05, oxide ion conductivity at 525 °C increased to 1.4 × 10−3 S cm−1 with the proton transport number decreasing from 0.81 to 0.04.28,29 Cr6+-doping resulted in a similar suppression of proton conductivity and increased total conductivity to 2 × 10−3 S cm−1 at 525 °C in Ba7Nb3.8Cr0.2MoO20.1.30 The total conductivity of Ba7Nb3.85W0.15MoO20.075 and Ba7Ta3.7Mo1.3O20.15 at 525 °C is 2.5 × 10−3 S cm−1 and 3.6 × 10−3 S cm−1, respectively.31,32 The increases in oxide ion conductivity in Ba7Nb4MoO20-derived materials have been ascribed to the introduction of additional charge carriers.29–32 However, the relatively modest improvements reported so far highlight the need to understand the oxide ion conduction mechanism in Ba7Nb4MoO20 at an atomic level in order to fully realize the potential for the optimization of its properties.
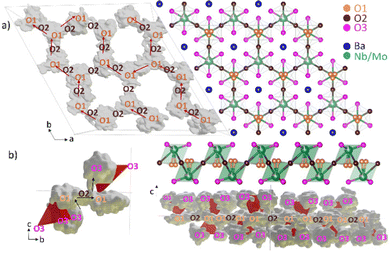
The structure of Ba7Nb4MoO20 can be described as an ordered intergrowth of palmierite Ba3M2O8 units and 12R perovskite Ba4M3O12 units (where M = Nb or Mo), forming a 7H hexagonal perovskite (Fig. 1).28,33 At room temperature (Fig. 1a), there are four crystallographically independent metal (M) sites modelled as jointly occupied by Mo and Nb (due to very similar scattering power for both X-rays and neutrons not allowing refinement of the Mo/Nb occupancies). The intrinsic cation vacancies are located on M1 and M2 sites, with fractional occupancies at 50 °C of 0.899(3) and 0.101(3), respectively.28 With increasing temperature, the occupancy of the M1 site increases while that of M2 decreases, resulting in occupancies of 0.931(3) and 0.069(3) at 530 °C.28 M3 and M4 sites, located in the 12R perovskite layers, as well as the four unique Ba sites are fully occupied at all temperatures.28 Three of the five unique oxygen sites are fully occupied at all temperatures – the O3 site located in the palmierite layer, as well as O4 and O5 sites in the 12R perovskite Ba4M3O12 units.28 By contrast, O1 and O2 sites, located in the (ab) plane of the palmierite Ba3M2O8 units are both partially occupied below 530 °C; above this temperature the O2 site is essentially unoccupied,28 resulting in a tetrahedral coordination environment for the M1 Nb/Mo site (Fig. 1b).
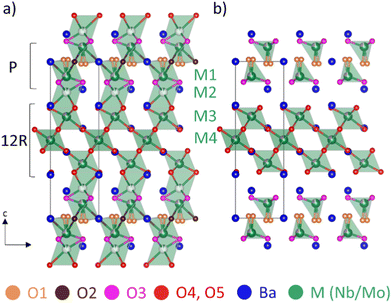 | ||
| Fig. 1 Crystal structure of Ba7Nb4MoO20 obtained from neutron diffraction data: (a) at 50 °C and (b) at 530 °C.28 | ||
Possible pathways of oxide ion diffusion in Ba7Nb3.9Mo1.1O20.05, Ba7Nb3.85W0.15MoO20.075 and Ba7Nb3.8Cr0.2MoO20.1 were investigated by the maximum entropy method (MEM). This suggests that diffusion occurs in two-dimensions, via O1 and O2 sites.29–31 Similarly, bond-valence energy landscape calculations for Ba7Nb4MoO20 suggest the presence of diffusion pathways via empty O2 sites.34 In the same study, a brief (20 ps) ab initio molecular dynamics (AIMD) simulation, performed only at one temperature (1000 K), was used to investigate the proton conductivity mechanism and confirm the O1–O2–O1 in-plane oxide ion dynamics.34 While this short simulation gave robust results with regard to the proton diffusion pathways, no long-range oxide ion diffusion could be simulated, with only a single O1–O2–O1 oxide ion jump observed.
Here we report an extensive AIMD computational study of oxide ion dynamics in Ba7Nb4MoO20. Performing simulations at three temperatures for up to 200 ps allowed the observation of a continuous diffusion pathway for oxide ions in the (ab) plane, but also revealed significant contribution of O3 oxygen atoms, located outside this plane, to the long-range dynamics. To complement this comprehensive computational study, neutron scattering experiments were used to probe the timescale of oxide ion diffusion in Ba7Nb4MoO20. Based on the atomic-level understanding of structure–property relationships afforded by this study, we propose new doping strategies with potential to result in a significant increase in oxide ion conductivity of Ba7Nb4MoO20-related hexagonal perovskite materials.
Experimental
Synthesis
For neutron scattering experiments, two large (7 g) polycrystalline samples of Ba7Nb4MoO20 were prepared using stoichiometric amounts of BaCO3 (Merck 99%), Nb2O5 (Fisher Sci 99.5%) and MoO3 (Fisher Sci 99.5%).29 The reagents were ball-milled under ethanol for 30 min at 300 rpm. The samples were left to dry and then heated at 900 °C for 12 h. The powder was ground thoroughly using an agate mortar and pestle, pressed into a rod using a hydraulic press and approximately 70 MPa, and heated at 1100 °C for 24 h. The progress of the solid state reaction and product purity were monitored using powder X-ray diffraction (PXRD), performed on a Bruker D8 ADVANCE diffractometer using Cu Kα radiation. The collected patterns were analyzed using the Rietveld method35 implemented in Topas Academic,36 using the structural data obtained from neutron diffraction data for Ba7Nb4MoO20 reported by Fop et al.28 as a starting model. The refinement parameters included cell parameters, zero-point, one global temperature factor, and pseudo-Voigt peak shape parameters. The background was modelled using a 9 parameter Chebyshev polynomial. The final product was found to be 92(1) % pure, with Ba5Nb4O15 (2.3(3) %) and Ba3NbMoO8.5 (5(1) %) identified as the impurities present. The final Rietveld fit obtained is shown in Fig. S1 (ESI†).Quasielastic neutron scattering
Neutron scattering data were collected on the backscattering spectrometer IN16b at the Institut Laue-Langevin (ILL) in Grenoble,37 using an incident neutron wavelength of 6.271 Å and instrument resolution of ∼0.8 μeV (FWHM). This gives access to dynamics on a nanosecond timescale. The Q-range accessible on IN16b is 0.1–1.8 Å−1, but due to the weak signal the Q-integrated data were used. Measurements were performed using a furnace,38 and to attempt a separation of the dynamics occurring due to two different charge carriers, oxide ions and protons, we performed measurements in vacuum, probing oxide ion diffusion, and in humid N2, probing proton diffusion. The energy transfer window used for all QENS measurements was ± 7 μeV. In both atmospheres, elastic (E = 0 μeV) and inelastic (E = 2 μeV) scattered intensities were measured in steps of 25 K, so called elastic and inelastic fixed window scans (EFWS, IFWS).39For the measurements performed under vacuum, 5.3 g of sample were placed in a Nb sample holder (diameter ∼ 8 mm, sample height ∼ 4 cm). During heating to 950 °C, EFWS (2 min) and IFWS (10 min) were collected, and at 950 °C a QENS measurement was performed with a total data collection time of 5 h. The sample was then cooled to 50 °C while again collecting EFWS (1 min) and IFWS (5 min). At 50 °C, QENS data were collected for 3 h.
For the measurement in humid atmosphere, approximately 8 g of sample were placed in a stainless-steel sample holder (diameter ∼ 10 mm). N2 gas was bubbled through distilled water and blown on the sample via a thin metal capillary in the steel tube. A first QENS spectrum (5 h) was measured at room temperature (RT). The sample was then heated to 500 °C during which EFWS (2 min) and IFWS (10 min) were collected. During heating, QENS measurements were also performed at 350 °C, 425 °C and 500 °C for 6 h per temperature. The sample was then cooled to 225 °C, measuring EFWS (2 min) and IFWS (10 min), to collect QENS data at 225 °C for 6 h, and after further cooling at 175 °C for 4 h. Data were also collected at RT on the empty tube (QENS: 4 h; EFWS: 2 min; IFWS 10 min) and on a vanadium standard (QENS: 30 min) for data reduction and analysis, which was carried out using the Mantid40 software.
Computational methods
Density functional theory (DFT) simulations were performed with the Vienna ab initio simulation package (VASP).41 The projector augmented wave (PAW) method42 with the GGA-PBE (Perdew–Burke–Ernzerhof generalized-gradient-approximation) exchange–correlation functional43 were used for all simulations. A structural model in space group P1 and containing 288 atoms, consisting of a near-isotropic 3 × 3 × 1 supercell (17.84 × 17.84 × 16.74 Å) of the high-temperature (530 °C) structure of Ba7Nb4MoO20 determined from neutron diffraction28 was used as a starting point for the simulations. As the occupancy of the M2 site at this temperature is very low (0.069), it was assumed to be empty, resulting in full occupancy of the M1 site. Distribution of Mo atoms as well as the selection of one out of three partially occupied symmetry-equivalent O1 positions for each M1O4 tetrahedron was performed using a random number generator. The atomic content of the final simulation box was Ba63Nb36Mo9O180. Before any ab initio molecular dynamics (AIMD) simulations were performed, a geometry optimization of this fixed supercell was carried out, allowing ions to relax until the residual forces on them were less than 0.01 eV Å−1. AIMD simulations were carried out with a cut-off energy of 300 eV and the k-space was sampled at the gamma-point only. AIMD simulations of 180 ps (1000 °C), 100 ps (1500 °C), and 200 ps (2000 °C) using the NVT ensemble and a time step of 2 fs were performed. The data analysis was carried out using the MDANSE code,44 and the space visited by oxide ions was visualized in cloud plots using LAMP.45Results and discussion
Timescale of ionic diffusion
To complement the extensive molecular dynamics study which is the main focus of this paper, quasielastic neutron scattering experiments were carried out. This section offers a brief discussion of the elastic (EFWS) and inelastic (IFWS) fixed window scans (Fig. S2, ESI†), collected on IN16b, aiming to provide an initial overview of the timescale of oxide ion and proton diffusion in Ba7Nb4MoO20. Generally, a gradual decrease of elastic intensity on heating is expected due to the Debye–Waller factor, which describes the loss of elastic intensity caused by an increase of thermal motions of atoms at higher temperatures. Any decrease of elastic intensity in addition to that is indicative of other effects, for example diffusion or dehydration. If the elastic intensity decreases due to diffusion processes, the IFWS is expected to increase at the same temperature. Dehydration, on the other hand, results in a loss of intensity in EFWS with no increase in inelastic intensity at the same temperature, due to the decrease of the total number of scattering atoms in the system; because hydrogen is a particularly strong neutron scatterer, this effect is very pronounced.A large (∼ 50 %) decrease in elastic intensity occurs between 210 °C and 360 °C on heating under vacuum (Fig. S2a, ESI†). There is no increase of inelastic intensity in the same temperature range (Fig. S2b, ESI†), which suggests that this is caused by dehydration, i.e. the loss of protons from the sample, and not an onset of dynamics. This observation is in excellent agreement with TGA data,28 showing the dehydration of the sample between approximately 200 and 400 °C (Fig. S3, ESI†). However, the IFWS in both atmospheres do not show an onset of significant dynamics in Ba7Nb4MoO20, and no broadening was observed in the QENS data collected at 950 °C under vacuum (Fig. S4, ESI†), or 225 °C in humid N2 (Fig. S5, ESI†). This suggests that ionic diffusion in Ba7Nb4MoO20 is slower than the nanosecond timescale probed here. The two impurities present at 7 wt% level do not have significant effect on the ion dynamics in the sample, which is dominated by the main phase, which constitutes 93% by weight.
Although QENS can be a powerful tool for the study of oxide ion diffusion,46–50 the small and predominantly coherent neutron scattering cross section of oxygen makes both observation and analysis of QENS difficult in many cases. Ab initio molecular dynamic (AIMD) simulations provide very similar information to QENS,10,11,47,49–53 and are well-suited for the study of atomistic diffusion. Consequently, computational results are the central emphasis of the investigation of oxide ion diffusion in Ba7Nb4MoO20 presented here.
Oxide ion dynamics investigated by ab initio molecular dynamics
Mean square displacement (MSD) plots for all oxygen atoms at 1000, 1500, and 2000 °C are shown in Fig. 2a. The flat MSD plot at 1000 °C is indicative of the absence of significant oxide ion dynamics, showing that higher temperatures are required to simulate diffusion of oxide ions. At 1500 °C, a slope in the MSD curve is apparent, suggesting the onset of long-range diffusion. The calculated diffusion coefficient (D) of 0.9 × 10−7 cm2 s−1 indicates that diffusion is slow. This is consistent with the absence of a QENS signal in the neutron scattering data collected on IN16b at 950 °C in Ba7Nb4MoO20. Using the diffusion coefficient reported by Yashima et al.29 for the related compound Ba7Nb3.9Mo1.1O20.05 at 700 and 800 °C, we can extrapolate D at 1500 °C to be 0.2 × 10−7 cm2 s−1, which compares well to our simulation result. For comparison, the diffusion coefficient determined from AIMD for the excellent oxide ion conductor Bi0.931V0.087O1.587, on which dynamics were clearly observed on IN16b,48 was approximately 5 × 10−7 cm2 s−1 at 600 °C (i.e. five times higher than that for Ba7Nb4MoO20 at 1500 °C).48 Further increase of the simulation temperature to 2000 °C leads to a more pronounced slope in the MSD curve caused by significant dynamics, with the diffusion coefficient increasing to 4 × 10−7 cm2 s−1. While this simulation temperature is very high, AIMD calculations often require higher temperatures than experiments to observe long-range diffusion. This is due to the intrinsic constraints of this computationally expensive method, which significantly limit both the size of the simulation cell as well as the achievable simulation time. By accelerating the diffusion process, the increased temperature reduces computational efforts while ensuring that an adequate number of jumps are observed. Hence, it allows a more efficient analysis of the long-range dynamics, which are often slow compared to the timescale accessible by AIMD. Elevated temperatures which deviate from experimental conditions are therefore commonly used in AIMD studies and have been shown to enable a comprehensive investigation of diffusion in many ionic conductors.11,52,54–66 This is also evident from the previous AIMD simulation on Ba7Nb4MoO20 at 1000 K,34 where only one oxide ion jump was observed, despite the high conductivity measured experimentally at this temperature. In the present work the simulation at 2000 °C was analyzed in detail to gain atomic-level insights into the oxide ion dynamics. The individual MSD curves for the oxide ions from different crystallographic sites occupied in the high-temperature structure (O1, O3, O4, O5) indicate that only those originally at O1 and O3 sites contribute to the dynamics in Ba7Nb4MoO20, while O4 and O5 oxygen atoms do not (Fig. 2b).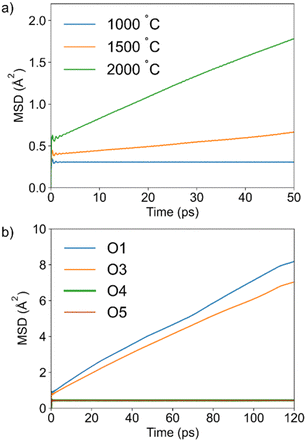 | ||
| Fig. 2 (a): MSD curves obtained from AIMD of all oxygen atoms at three simulation temperatures; (b): contribution of the individual oxygen sites to the MSD in the simulation performed at 2000 °C. | ||
Cloud plots can be used to visualize the simulated trajectories by highlighting the space visited by oxygen atoms over the course of the simulation. Fig. 3a shows the trajectories of all oxide ions originating on the O1 site in the simulation at 2000 °C, demonstrating a continuous pathway for oxide ion diffusion in the (ab) plane. This in-plane diffusion occurs by hopping of O1 oxygen atoms to neighboring O1 sites via the empty O2 sites, consistent with facile 2D migration suggested by bond valence considerations.29–31 However, our AIMD simulations reveal for the first time a significant contribution to the overall diffusion by the O3 oxygen atoms, located outside the plane of O1–O2–O1 hopping, as shown in the MSD curve and the cloud plots (Fig. 2b and 3b). The O3 oxygen atoms jump in the direction essentially perpendicular to the (ab) plane to the nearest O1 site and then diffuse via the O1–O2–O1 2D pathway (Fig. 3b). The mechanism of O3 involvement relies on rotational flexibility of the (Nb/Mo)Ox polyhedra and the ability of both Mo and Nb to adopt variable coordination environments, known to support fast dynamics in several other oxide ion conductors.21,47,67–72 Comparing the number of jumps shows that O3 dynamics become more significant with increasing temperatures (Table S1, ESI†), but are prevalent (accounting for at least two-thirds of all jumps) at both 1500 °C and 2000 °C, which can be explained by the activation energy for localized motions being generally lower than for long-range diffusion.48,73
Conclusions and implications on improvement of oxide ion conductivity of Ba7Nb4MoO20
We have investigated oxide ion dynamics in Ba7Nb4MoO20 using ab initio molecular dynamics and complementary neutron scattering. Our quasielastic neutron scattering experiments showed that oxide ion dynamics are not on the nanosecond timescale probed, indicating that long-range diffusion is slower and higher temperatures would be necessary to directly observe it. This finding is supported by the AIMD results, which do not show any oxide ion diffusion at 1000 °C on a timescale of hundred ps.Modelling of possible ionic migration pathways reported so far29–31 has revealed ionic hopping between the partially occupied O1 and O2 sites, suggesting that oxide ion conductivity could be improved by aliovalent doping of Ba7Nb4MoO20 to introduce extra oxygen in the structure and increase the number of charge carriers. The approach has been demonstrated in Ba7Nb3.9Mo1.1O20.05, Ba7Nb3.85W0.15MoO20.075, Ba7Ta3.7Mo1.3O20.15 and Ba7Nb4−xCrxMoO20+x/2 (x = 0.05–0.50); however, the improvements have been modest.29–32 Our extensive AIMD simulations reveal for the first time a significant contribution of the out-of-plane O3 dynamics to the conductivity mechanism, through a process which essentially amounts to the rotation of the (Nb/Mo)Ox polyhedra followed by injection of O3 atoms into the (ab) plane. The contribution of this process is very significant, as evidenced by the fact that these jumps outnumber those in the (ab) plane. Based on this, we propose strategies for new compositions related to Ba7Nb4MoO20, to facilitate and enhance (Nb/Mo)Ox polyhedral rotations, as well as introduce extra charge carriers. For example, a systematic exploratory synthesis strategy, targeting improvements of both in-plane and out-of-plane oxide ion dynamics, could be to substitute some Mo6+ with V5+ (thereby introducing rotationally flexible VOx)48,53,73,74 and charge-compensate by replacing Ba2+ with La3+ to create the Ba7−xLaxNb4Mo1−yVyO20 series; the best performers from this series could then be modified further to introduce extra oxide ion carriers, by varying the Nb5+:Mo6+ ratio. This two-pronged approach is likely to result in more significant improvements of oxide ion conductivity relative to Ba7Nb4MoO20.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Institut Laue-Langevin and EPSRC (grant EP/R513039/1)/Durham University for PhD funding for Bettina Schwaighofer. We also acknowledge Institut Laue-Langevin for the allocation of neutron beamtime which provided the experimental data underlying this study (available under doi:https://doi.org/10.5291/ILL-DATA.7-03-196) and allocation of computer resources through the C-lab.References
- B. C. H. Steele, J. Mater. Sci., 2001, 36, 1053–1068 CrossRef.
- C. Mendonça, A. Ferreira and D. M. F. Santos, Fuels, 2021, 2, 393–419 CrossRef.
- M. Singh, D. Zappa and E. Comini, Int. J. Hydrogen Energy, 2021, 46, 27643–27674 CrossRef CAS.
- M. Feng, J. B. Goodenough, K. Huang and C. Milliken, J. Power Sources, 1996, 63, 47–51 CrossRef CAS.
- M. Li, M. J. Pietrowski, R. A. De Souza, H. Zhang, I. M. Reaney, S. N. Cook, J. A. Kilner and D. C. Sinclair, Nat. Mater., 2014, 13, 31–35 CrossRef CAS PubMed.
- J. B. Goodenough, J. E. Ruiz-Diaz and Y. S. Zhen, Solid State Ionics, 1990, 44, 21–31 CrossRef CAS.
- S. B. Adler, J. A. Reimer, J. Baltisberger and U. Werner, J. Am. Chem. Soc., 1994, 116, 675–681 CrossRef CAS.
- V. Thangadurai, G. N. Subbanna, A. K. Shukla and J. Gopalakrishnan, Chem. Mater., 1996, 8, 1302–1306 CrossRef CAS.
- V. V. Kharton, I. P. Marozau, N. P. Vyshatko, A. L. Shaula, A. P. Viskup, E. N. Naumovich and F. M. B. Marques, Mater. Res. Bull., 2003, 38, 773–782 CrossRef CAS.
- W. Paulus, H. Schober, S. Eibl, M. Johnson, T. Berthier, O. Hernandez, M. Ceretti, M. Plazanet, K. Conder and C. Lamberti, J. Am. Chem. Soc., 2008, 130, 16080–16085 CrossRef CAS PubMed.
- J. E. Auckett, A. J. Studer, E. Pellegrini, J. Ollivier, M. R. Johnson, H. Schober, W. Miiller and C. D. Ling, Chem. Mater., 2013, 25, 3080–3087 CrossRef CAS.
- S. Corallini, M. Ceretti, A. Cousson, C. Ritter, M. Longhin, P. Papet and W. Paulus, Inorg. Chem., 2017, 56, 2977–2984 CrossRef PubMed.
- C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, S. J. Clark, J. S. O. Evans and I. R. Evans, Chem. Mater., 2019, 31, 7395–7404 CrossRef.
- C. A. Fuller, Q. Berrod, B. Frick, M. R. Johnson, M. Avdeev, J. S. O. Evans and I. R. Evans, Chem. Mater., 2020, 32, 4347–4357 CrossRef.
- W. Zhang, K. Fujii, T. Ishiyama, H. Kandabashi and M. Yashima, J. Mater. Chem. A, 2020, 8, 25085–25093 RSC.
- W. Zhang, K. Fujii, E. Niwa, M. Hagihala, T. Kamiyama and M. Yashima, Nat. Commun., 2020, 11, 1224 CrossRef PubMed.
- C. A. Fuller, D. A. Blom, T. Vogt, I. R. Evans and J. S. O. Evans, J. Am. Chem. Soc., 2022, 144, 615–624 CrossRef PubMed.
- C. A. Fuller, J. I. Murrell, D. A. Blom, T. Vogt, W. Zhang, P. S. Halasyamani, I. R. Evans and J. S. O. Evans, Chem. Mater., 2022, 34, 3185–3196 CrossRef PubMed.
- X. Kuang, M. Allix, R. M. Ibberson, J. B. Claridge, H. Niu and M. J. Rosseinsky, Chem. Mater., 2007, 11, 2884–2893 CrossRef.
- X. Yang, A. J. Fernández-Carrión and X. Kuang, Chem. Rev., 2023, 15, 9356–9396 CrossRef.
- S. Fop, J. M. Skakle, A. C. McLaughlin, P. A. Connor, J. T. S. Irvine, R. I. Smith and E. J. Wildman, J. Am. Chem. Soc., 2016, 138, 16764–16769 CrossRef.
- S. Fop, K. McCombie, R. I. Smith and A. C. McLaughlin, Chem. Mater., 2020, 32, 4724–4733 CrossRef.
- A. Bernasconi, C. Tealdi and L. Malavasi, Inorg. Chem., 2018, 57, 6746–6752 CrossRef.
- S. Fop, E. J. Wildman, J. T.S Irvine, P. A. Connor, J. M. Skakle, C. Ritter and A. C. Mclaughlin, Chem. Mater., 2017, 29, 4146–4152 CrossRef.
- M. S. Chambers, K. S. McCombie, J. E. Auckett, A. C. McLaughlin, J. T. S. Irvine, P. A. Chater, J. S. O. Evans and I. R. Evans, J. Mater. Chem. A, 2019, 7, 25503–25510 RSC.
- J. E. Auckett, K. L. Milton and I. R. Evans, Chem. Mater., 2019, 31, 1715–1719 CrossRef.
- J. E. Auckett, M. J. Gutmann and I. R. Evans, Inorg. Chem., 2020, 59, 14245–14250 CrossRef PubMed.
- S. Fop, K. S. McCombie, E. J. Wildman, J. M. S. Skakle, J. T. S. Irvine, P. A. Connor, C. Savaniu, C. Ritter and A. C. Mclaughlin, Nat. Mater., 2020, 19, 752–757 CrossRef.
- M. Yashima, T. Tsujiguchi, Y. Sakuda, Y. Yasui, Y. Zhou, K. Fujii, S. Torii, T. Kamiyama and S. J. Skinner, Nat. Commun., 2021, 12, 556 CrossRef.
- Y. Sakuda, J. R. Hester and M. Yashima, JCS-Japan., 2022, 130, 442–447 Search PubMed.
- Y. Suzuki, T. Murakami, K. Fujii, J. R. Hester, Y. Yasui and M. Yashima, Inorg. Chem., 2022, 61, 7537–7545 CrossRef.
- T. Murakami, T. Shibata, Y. Yasui, K. Fujii, J. R. Hester and M. Yashima, Small, 2022, 18, 2106785 CrossRef.
- M. Parras, E. Garcia-Gonzalez and J. M. Gonzalez-Calbet, Chem. Mater., 1999, 11, 433–437 CrossRef.
- S. Fop, J. A. Dawson, A. D. Fortes, C. Ritter and A. C. McLaughlin, Chem. Mater., 2021, 33, 4651–4660 CrossRef.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2, 65–71 CrossRef.
- A. A. Coelho, J. S. O. Evans, I. R. Evans, A. Kern and S. Parsons, Powder Diffr., 2011, 26, S22–S25 CrossRef.
- B. Schwaighofer, M. Appel, I. R. Evans, M. A. Gonzalez and M. M. Koza, Oxide ion and proton dynamics in Ba7Nb4MoO20 solid electrolyte, Institut Laue-Langevin (ILL), 2021 DOI:10.5291/ILL-DATA.7-03-196.
- C. Goodway, P. McIntyre, A. Sears, N. Belkhier, G. Burgess, O. Kirichek, E. Lelièvre-Berna, F. Marchal, S. Turc and S. Wakefield, J. Neutron Res, 2020, 21, 137–142 Search PubMed.
- B. Frick, J. Combet and L. Van Eijck, Nucl. Instrum. Methods Phys. Res., Sect. A, 2012, 669, 7–13 CrossRef.
- O. Arnold, J. C. Bilheux, J. M. Borreguero, A. Buts, S. I. Campbell, L. Chapon, M. Doucet, N. Draper, R. Ferraz Leal, M. A. Gigg, V. E. Lynch, A. Markvardsen, D. J. Mikkelson, R. L. Mikkelson, R. Miller, K. Palmen, R. Parker, G. Passos, T. G. Perring, P. F. Peterson, S. Ren, M. A. Reuter, A. T. Savici, J. W. Taylor, R. J. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef.
- G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- G. Goret, B. Aoun and E. Pellegrini, J. Chem. Inf. Model., 2017, 57, 1–5 CrossRef CAS PubMed.
- D. Richard, M. Ferrand and G. J. Kearley, J. Neutron Res, 1996, 4, 33–39 CrossRef.
- E. Mamontov, Solid State Ionics, 2016, 296, 158–162 CrossRef CAS.
- J. R. Peet, C. A. Fuller, B. Frick, M. Zbiri, A. Piovano, M. R. Johnson and I. R. Evans, Chem. Mater., 2017, 29, 3020–3028 CrossRef CAS.
- J. R. Peet, C. A. Fuller, B. Frick, M. M. Koza, M. R. Johnson, A. Piovano and I. R. Evans, J. Am. Chem. Soc., 2019, 141, 9989–9997 CrossRef CAS PubMed.
- J. Wind, R. A. Mole, D. Yu and C. D. Ling, Chem. Mater., 2017, 29, 7408–7415 CrossRef CAS.
- J. Wind, R. A. Mole and C. D. Ling, J. Phys. Chem. C, 2019, 123, 15877–15884 CrossRef CAS.
- X. Kuang, J. L. Payne, J. D. Farrell, M. R. Johnson and I. R. Evans, Chem. Mater., 2012, 24, 2162–2167 CrossRef CAS.
- R. Mittal, S. Kumar, M. K. Gupta, S. K. Mishra, S. Mukhopadhyay, M. D. Le, R. Shukla, S. N. Achary, A. K. Tyagi and S. L. Chaplot, Mater. Adv, 2022, 3, 2104–2116 RSC.
- B. Schwaighofer, M. A. Gonzalez, M. Appel, M. M. Koza and I. R. Evans, Chem. Mater., 2023, 35, 1125–1133 CrossRef CAS.
- J. R. Peet, M. S. Chambers, A. Piovano, M. R. Johnson and I. R. Evans, J. Mater. Chem. A, 2018, 6, 5129–5235 RSC.
- Y. Mo, S. P. Ong and G. Ceder, Chem. Mater., 2012, 24, 15–17 CrossRef CAS.
- Z. Deng, B. Radhakrishnan and S. P. Ong, Chem. Mater., 2015, 27, 3749–3755 CrossRef CAS.
- X. He, Y. Zhu, A. Epstein and Y. Mo, npj Comput. Mater., 2018, 4, 1–9 CrossRef CAS.
- J. Yang and J. S. Tse, J. Phys. Chem. A, 2011, 115, 13045–13049 CrossRef CAS.
- Y. Zhang, Y. Zhao and C. Chen, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 134303 CrossRef.
- A. Urban, D. H. Seo and G. Ceder, npj Comput. Mater., 2016, 2, 1–13 CrossRef.
- Y. Ma, Energy Environ. Mater., 2018, 1, 148–173 CrossRef CAS.
- S. C. Jung, H. J. Kim, J. W. Choi and Y. K. Han, Nano Lett., 2014, 14, 6559–6563 CrossRef CAS PubMed.
- K. Kaup, K. Bishop, A. Assoud, J. Liu and L. F. Nazar, J. Am. Chem. Soc., 2021, 143, 6952–6961 CrossRef CAS PubMed.
- W. D. Richards, T. Tsujimura, L. J. Miara, Y. Wang, J. C. Kim, S. P. Ong, I. Uechi, N. Suzuki and G. Ceder, Nat. Commun., 2016, 7, 11009 CrossRef CAS PubMed.
- F. Zhu, M. S. Islam, L. Zhou, Z. Gu, T. Liu, X. Wang, J. Luo, C. W. Nan, Y. Mo and C. Ma, Nat. Commun., 2020, 11, 1828 CrossRef CAS.
- Z. Gu, J. Ma, F. Zhu, T. Liu, K. Wang, C. W. Nan, Z. Li and C. Ma, Nat. Commun., 2023, 14, 1632 CrossRef CAS PubMed.
- I. R. Evans, J. A. K. Howard and J. S. O. Evans, Chem. Mater., 2005, 17, 4074–4077 CrossRef CAS.
- C. D. Ling, W. Miiller, M. R. Johnson, D. Richard, S. Rols, J. Madge and I. R. Evans, Chem. Mater., 2012, 24, 4607–4614 CrossRef CAS.
- M. L. Tate, J. Hack, X. Kuang, G. J. McIntyre, R. L. Withers, M. R. Johnson and I. R. Evans, J. Solid State Chem., 2015, 225, 383–390 CrossRef CAS.
- M. T. Dunstan, F. Blanc, M. Avdeev, G. J. McIntyre, C. P. Grey and C. D. Ling, Chem. Mater., 2013, 25, 3154–3161 CrossRef CAS.
- O. B. Lapina, D. F. Khabibulin, K. V. Romanenko, Z. Gan, M. G. Zuev, V. N. Krasil’nikov and V. E. Fedorov, Solid State Nucl. Magn. Reson., 2005, 28, 204–224 CrossRef CAS.
- O. B. Lapina, D. F. Khabibulin, A. A. Shubin and V. V. Terskikh, Prog. Nucl. Magn. Reson. Spectrosc., 2008, 53, 128–191 CrossRef CAS.
- M. T. Dunstan, D. M. Halat, M. L. Tate, I. R. Evans and C. P. Grey, Chem. Mater., 2019, 31, 1704–1714 CrossRef CAS.
- X. Kuang, J. L. Payne, M. R. Johnson and I. R. Evans, Angew. Chem., Int. Ed., 2012, 51, 690–694 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma00955f |
| This journal is © The Royal Society of Chemistry 2024 |