Detection of a Jahn–Teller mode as an ultrafast fingerprint of spin-transition-induced charge transfer in CoFe Prussian Blue Analogue

Abstract

Photoinduced spin transition is one of the fastest processes occurring in transition-metal-based molecules and materials, reaching down to tens of femtoseconds (1 fs = 10⁻¹⁵ s). The underlying dynamics have been well characterized for mononuclear Fe(II) spin-crossover (SCO) complexes, where it was shown that the spin transition can induce coherent activation of metal–ligand breathing and bending vibrational modes, identified as the main reaction coordinates. While precise characterization of the femtosecond nuclear wave packet brings rich information on photoinduced spin transitions, it is scarcely explored in bimetallic Prussian Blue Analogues (PBAs). In this work, we performed transient absorption spectroscopy with sub-20-fs time resolution on the [Cs_0.7Co(Fe(CN)₆)_0.9] PBA to unravel high-frequency coherent structural dynamics, which are interpreted as the activation of a low-symmetry CoN₆ Jahn–Teller mode at 12 THz. This coherent fingerprint shows that the photoexcitation initially drives motion along the Jahn–Teller coordinate before the spin transition occurs, i.e., over less than 50 fs. These results are in stark contrast with conventional activation of fully-symmetric breathing modes reported for several SCO compounds, thus providing new insights on the ultrafast spin-transition-induced charge transfer dynamics in PBAs.

---

Introduction

Light excitation with ultrashort laser pulses represents one of the most promising routes to control the physical properties of molecules and materials with contactless, ultrafast and highly efficient photoinduced processes.^1,2 In particular, transition-metals-based molecular materials have attracted lots of interest because their light-induced magnetic properties can be maintained, at low temperatures, once light irradiation is switched off. This is especially true for Laser-Induced Excited State Spin Trapping (LIESST) in Spin-Crossover (SCO) compounds,^3–6 photoinduced magnetic anisotropy in single-molecule magnets,^7–10 photoinduced magnetism in Prussian Blue Analogues (PBAs) resulting from a coupled charge-transfer and spin transition,^11,12 or synergetic LIESST-based single-molecule magnet properties.¹³ In many cases, photo-reversibility between different magnetic properties was even demonstrated.^14–16 With the objective of proposing new ways to control the photomagnetic properties, it is of prior importance to unravel the photoswitching mechanisms, that is to understand the coupling between photoexcited electronic degrees of freedom and structural reorganizations responsible for the consecutive structural trapping in the final, photoinduced, electronic state. These processes can be nowadays mapped on their intrinsic timescales using ultrafast technologies such as femtosecond optical or X-ray spectroscopies.^7,17–20

Recent investigations of LIESST dynamics in Fe(II) SCO compounds illustrate the detailed level of understanding and control that can be reached when transformation from low-spin (LS, S = 0, t⁶_2g) to high-spin (HS, S = 2, t⁴_2ge²_g) electronic configurations is triggered by ultrashort laser pulses. The direct LS-to-HS conversion being forbidden by selection rules, LIESST phenomenon involves intermediate states such as ^1,3MLCT (metal-to-ligand charge transfer) or ³T-like (triplet) states. The intersystem crossing sequence leads to the HS state, structurally trapped by metal–ligand bond elongation. This was observed in ultrafast experiments through the detection of vibrational coherences, which revealed the activation of the coupled breathing and bending modes, therefore identified as the main reaction coordinates connecting the LS and HS potential energy surfaces on the femtosecond timescale.^4,19,21–31 Compared to the conventional photoexcitation of MLCT states, the coherence of such structural dynamics is enhanced when d–d transitions are involved in photoexcitation, indicating a faster decay of the intermediates towards the final photoinduced state.^27,32 While the observation of photoinduced vibrational wave packets in the LIESST process contains rich information on the ongoing dynamics,³³ the identification of the coherently-activated reaction coordinates is nonetheless non-trivial. Indeed, the organic ligands surrounding the metal centre are usually complex and thus possess many vibrational modes that can be involved in the dynamics.^22,24,34,35

In the case of PBAs (of general formula AM[M′(CN)₆], A = alkali ion), the emergence of photomagnetic properties results from a charge transfer (CT) between the two cyanide-bridged metallic centres MN₆ and M′C₆, forming the three-dimensional cubic network.¹¹ This intermetallic CT is coupled to a spin transition (ST) on the MN₆ site, trapping the electronic state.^11,14,36 Time-resolved experiments^37–39 and theoretical calculations⁴⁰ have shown that CT occurs on ultrafast timescales, e.g., 200 fs in MnFe(CN)₆ PBA⁴¹ and CoFe(CN)₆ PBA,¹⁸ and that it relies on strong coupling between the electronic, spin, and structural degrees of freedom. In this paper, we are interested in the ultrafast photoinduced dynamics in [Cs_0.7Co(Fe(CN)₆)_0.9] PBA nanocrystals (A = Cs, M = Co, M′ = Fe), recently reported.^18,42,43 The nanocrystals are made of CoFe(CN)₆ active units, exhibiting photoinduced conversion from the Co^III(S = 0)Fe^II(S = 0) low-spin state to the Co^II(S = 3/2)Fe^III(S = 1/2) high-spin state, which is long-lived at low temperature. As for many other Co–NC–Fe systems, the Fe-to-Co CT and the ST on the Co site are coupled (Fig. 1a).^11,36,44,45 Since the discovery of photo-magnetism in PBAs, a key question arose: is the photoinduced charge-transfer driving the spin-transition or vice versa? Describing the switching pathway in PBAs is therefore more complex than for SCO compounds as it involves two different coordinated metal centres and two electronic processes. Recent works on CoFe(CN)₆ PBA nanocrystals using femtosecond X-ray absorption and transient optical absorption spectroscopies have revealed that optical excitation at 540 nm drives the ST on the Co site within 50 fs, prior to the Fe-to-Co CT.^18,43 Such a Spin-Transition-Induced Charge Transfer (STICT) process is also accompanied by an overall increase of Co–N bond distances due to the Co-centred ST (from Co^III(S = 0) to Co^II(S = 3/2)), as in the LIESST process. However, only vibrational coherence in low frequency torsion modes (of 650 fs period) was observed in these seminal reports.^18,43 This was due to the limited time resolution (50–100 fs), that did not allow to track the possible activation of CoN₆ stretching modes (∼75 fs period) and therefore to understand how instantaneous ST and delayed CT affect the structural dynamics during the STICT process.

Fig. 1 (a) Principle of sub-20-fs transient absorption spectroscopy in the CoFe PBA. Once excited by a 15-fs pump pulse, the spin-transition-induced charge transfer occurs from the Co^III(S = 0)Fe^II(S = 0) to the Co^II(S = 3/2)Fe^III(S = 1/2) state, trapped by the elongation of the Co–N bonds. (b) Absorption spectrum of the CoFe colloidal solution in a 1-mm-thick cuvette (blue line), together with the pump 560 nm excitation spectrum (green area). (c) Transient absorption changes of the CoFe solution, measured 220 fs after 560 nm excitation (orange line). The green area corresponds to pump scattering.

In the present work, we used transient absorption (TA) spectroscopy with sub-20-fs resolution to unravel coherent signatures of the structural dynamics during the STICT process of the CoFe(CN)₆ PBA nanocrystals (thereafter called CoFe). Our results reveal high-frequency vibrational coherence, and shed new light on the STICT mechanism.

Experimental

Synthesis of CoFe nanoparticles

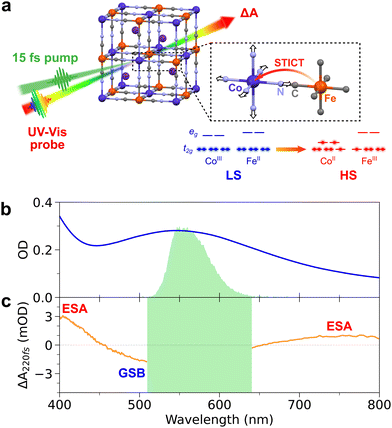
Colloidal solutions of CoFe PBA nanoparticles (of general formula Cs_0.7Co(Fe(CN)₆)_0.9) were prepared according to the procedure already reported in previous works.⁴² Briefly, it consists of 11 nm nanocrystals with photo-active Co^IIIFe^II sites in low-spin configuration, embedded in polyvinylpyrrolidone (PVP) and dispersed in water with a typical concentration of [Co] = [Fe] = 5 mM. The Cs⁺ counter-ions in the cubic structure (Fig. 1a) stabilize the LS state above room temperature. After STICT, its structure remains cubic in the photoinduced HS state. The absorption spectrum of the CoFe nanoparticles in a 1 mm cuvette is shown in Fig. 1b. It corresponds to a molar extinction coefficient of ∼600 M⁻¹ cm⁻¹ for the main absorption band centred at 545 nm. A small fraction of passive Co^IIFe^II sites is also present on the surface of the nanocrystals. Nanocrystals of 70 nm were also prepared and studied. Because of their higher core-to-shell ratio,⁴³ any spectroscopic signature of the protective PVP polymer or passive Co^IIFe^II shell would appear significantly weaker compared to the signatures of Co^IIIFe^II core.

Sub-20-fs transient absorption spectroscopy

Transient absorption (TA) spectroscopy was performed on the prepared CoFe solutions in a 1-mm-thick fused silica cuvette. CoFe nanoparticles were excited by 15-fs, 100-nJ laser pulses centred at 560 nm, generated using a home-built non-colinear optical parametric amplifier (NOPA), pumped by the second harmonic of a 1-kHz, 30-fs Ti:Sapphire chirped-pulse amplifier. The typical excitation spectrum is shown in Fig. 1b (green spectrum), and has a full width at half maximum of about 35 nm.

TA data were recorded using an acquisition set-up described in detail elsewhere.⁴⁶ In short, a white-light supercontinuum generated in CaF₂ is used as a probe pulse. Half of the probe intensity is used as a reference beam, and both probe and reference spectra are acquired with a prism spectrometer operated at a 1-kHz acquisition frequency (commercial acquisition system by Entwicklungsbüro G. Stresing, Berlin). The NOPA beam is chopped at 500 Hz, such that two successive probe spectra are used to compute the pump-induced absorption changes of the sample, ΔA(t,λ). A 500-μm travel piezoelectric transducer on the pump beam optical path is continuously oscillating at a 0.5-Hz period to implement a “fast” scan of the pump–probe delay. Relative linear polarization of pump and probe beams was controlled using a half-waveplate on the pump path, and it was set either with parallel or perpendicular pump–probe polarizations. The overall time resolution of the experiment was below 20 fs in the present measurements, which in principle enables the detection of photo-activated vibrational modes up to oscillation frequencies of ca. 1500 cm⁻¹.

Following chirp correction, TA data were analysed as follows. Pump–probe delays below 200 fs were not considered for the analysis, as they mostly correspond to cross-phase modulation (CPM) between pump and probe beams. Given the low extinction coefficient of CoFe, light scattering from the intense pump beam was predominant between 510 nm and 640 nm in the TA data. Therefore, this wavelength range was also discarded in the analysis. In a first approach, global fitting of TA data was performed between 400 nm and 800 nm, followed by Fast Fourier Transform (FFT) of the residuals of the fit. In a second approach, chirp-corrected TA data was integrated over specific wavelength ranges, and fitted in the time domain with appropriate decay and oscillatory contributions, with and without implementation of linear prediction with single value decomposition (LPSVD).^47–49 Both time-domain fitting procedures gave identical results (see ESI† for more details).

Computational methods

Density Functional Theory (DFT) calculations were performed to further support the observed dynamics. Given the complexity of PBA crystals, computations were performed on a single monomeric unit, (CN)₅Co–N–C–Fe(CN)₅⁶⁻, chosen as a model like in previous studies on CoFe¹⁸ and other PBAs.³⁸ Geometry optimization of the monomer and derivation of the associated vibrational frequencies were performed for both Co^III(S = 0)Fe^II(S = 0) and Co^II(S = 3/2)Fe^III(S = 1/2) configurations, corresponding to LS and HS states respectively. For both configurations, B3LYP functional was used at the 3–21g level, in its restricted version for the Co^III(S = 0)Fe^II(S = 0) monomer and unrestricted (UB3LYP) for the Co^II(S = 3/2)Fe^III(S = 1/2) monomer, and computations were carried out using Gaussian 09.⁵⁰ The geometries and vibrational distributions of both monomers are given in ESI.†

Results

Fig. 1b shows that 560 nm pump pulses excite the main visible band of the CoFe nanocrystals. Following 560 nm excitation, changes in the absorption of CoFe are observed, and Fig. 1c shows the pump-induced changes at a delay of 220 fs after excitation. Negative ΔA between 450 nm and 650 nm corresponds to the bleaching of the initial LS state (Ground State Bleaching, GSB), while positive ΔA centred at 400 nm and 750 nm respectively arise from Excited State Absorption (ESA), as observed in previous studies.^18,43

Fig. 2a shows the TA spectra ΔA(t,λ) up to 1.6 ps for parallel pump and probe polarizations. An overall decrease of the 400 nm ESA band and an increase of the 750 nm ESA band are observed. Fig. 2c shows the oscillating part of ΔA(t,λ), obtained as the residuals after global fitting (see ESI†). This signal reveals two main oscillatory features, with ∼600 fs and ∼50 fs periods. This observation is complemented by the computed FFT of the oscillating signal, shown in Fig. 2e. The intense oscillation mode around 60 cm⁻¹ corresponds to the longest oscillation period seen in Fig. 2c. It remains visible and dominant along the whole spectrum, with a phase shift between the ESA and GSB bands. For fast periods, two frequencies are detected. While the frequency of 515 cm⁻¹ is attributed to the cuvette since it is also present in the blank data (nanoparticle-free measurement, shown in Fig. S2, ESI†), the feature around 800 cm⁻¹ is a clear signature of CoFe nanocrystals. Interestingly, this second frequency is mostly visible in the ESA band above 650 nm, i.e., not in the GSB region, and therefore corresponds to an oscillatory feature in the photoinduced state. Also, the TA data recorded with perpendicular pump and probe polarizations (Fig. 2b, d and f) are very similar to the one with parallel polarizations.

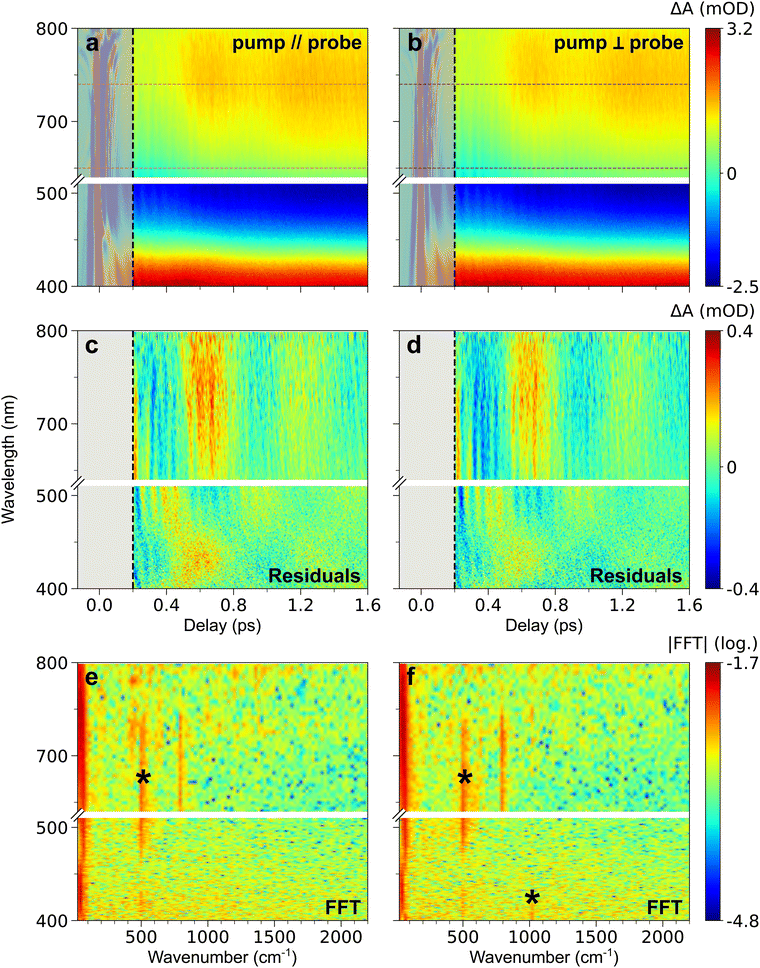Fig. 2 (a) and (b) TA map of CoFe for parallel (a) and perpendicular (b) pump and probe polarizations, representing the colour-coded variation of ΔA with delay and probe wavelength. (c) and (d) Time- and wavelength-dependent residuals of global fitting of TA data after 200 fs, in both parallel (c) and perpendicular (d) configurations. (e) and (f) 2D representation of the FFT of the residuals (in log scale), as a function of wavenumber and probe wavelength, for both parallel (e) and perpendicular (f) configurations. The oscillation frequencies indicated by a black asterisk are also observed in the blank (see ESI†). For all maps, grey-shaded area corresponds to the CPM contribution at delays below 200 fs, discarded in data analysis. The common colour scale for each row is shown on the right. It corresponds to the variations after 200 fs, therefore leading to saturation before this delay due to the CPM signal (see Fig. S1, ESI† for non-saturated CPM signal). The wavelength range chosen for ESA integration is shown by the magenta (parallel polarizations, panel a) and dark purple (perpendicular polarizations, panel b) dashed lines.

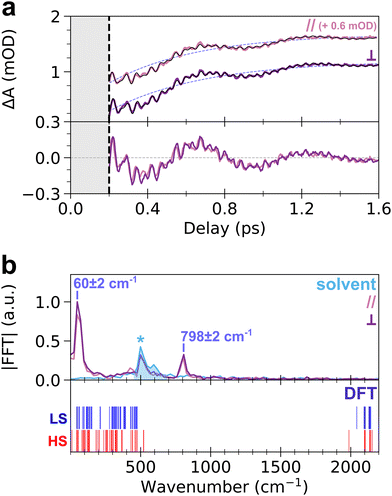
To get more insight into the observed oscillatory features, the TA signal was integrated over the ESA band from 650 nm to 740 nm, where both slow and fast oscillations are visible. The obtained transient signal, ΔA^ESA(t), is shown in the top panel of Fig. 3a, for both pump–probe polarization configurations. Both transient signals show similar dynamics, without any noticeable anisotropy. The fit of ΔA^ESA(t) was performed with a single exponential rise and three damped oscillatory features (Fig. 3a, see ESI† for details). The obtained rise time constant, 450 ± 40 fs (light purple dashed line in Fig. 3a), is in agreement with prior studies (450 ± 30 fs).¹⁸ The 60 ± 2 cm⁻¹ and 798 ± 2 cm⁻¹ oscillation frequencies obtained from the fit agree with the FFT spectrum of ΔA^ESA(t) shown in the top panel of Fig. 3b. The damping rates of these two modes are 690 ± 120 fs and 960 ± 180 fs, respectively. It is noteworthy that both frequencies are also observed for 70 nm CoFe particles, confirming that they are related to the photo-active Co^IIIFe^II pairs present in the core of the particles and not to, e.g., Resonant Impulsive-Stimulated Raman Scattering (RISRS)⁵¹ in the passive Co^IIFe^II + PVP shell (see Fig. S3 and ESI†). The bottom panel of Fig. 3a also displays the oscillatory part of ΔA^ESA(t) in parallel and perpendicular pump–probe polarization configurations. Given that chirp correction was performed independently on each dataset, the phase of the 60 cm⁻¹ mode was chosen as the time reference in each polarization configuration. Very good overlap between the two signals is observed. This shows that the oscillations at 798 cm⁻¹ observed in parallel and perpendicular configurations are in phase, within 8 fs accuracy over the 42 fs period (i.e., 0.4π accuracy, estimated from the standard deviation in least-square fits), although the absolute value of the phase cannot be extracted because of the intensity of the CPM contribution before 200 fs.

Fig. 3 (a) Top panel: time-dependent ESA-integrated transient absorption change, ΔA^ESA(t) (from 650 nm to 740 nm), for parallel (magenta) and perpendicular (dark purple) pump–probe polarizations. The least-square fit of ΔA^ESA(t) for each polarization configuration is also shown as a black curve, and the resulting exponential decay component is shown as a light purple dashed curve. For the sake of clarity, curves associated to parallel polarizations are shifted by +0.6 mOD. Bottom panel: oscillatory contribution of ΔA^ESA(t) in both polarization configurations, obtained by subtraction of the exponential decay component. (b) Top panel: FFT spectrum of the oscillatory contribution of ΔA^ESA(t), in parallel (magenta) and perpendicular (dark purple) configurations. The FFT spectrum for the blank is displayed as light blue curve, showing the spurious peak at 515 cm⁻¹ (marked by an asterisk, *, and the light-blue shaded area). Bottom panel: distribution of calculated vibrational modes of the CoFe monomer unit in LS (blue lines) and HS (red lines) states, where each mode is represented by a vertical line at its vibrational frequency.

While the oscillation at 60 cm⁻¹ and its observation in the ESA and GSB bands were previously reported for this compound as a signature of a lattice torsion mode,^18,43 the 798 cm⁻¹ oscillation revealed by the present data indicates that a higher-frequency mode also contributes to the dynamics. To understand the nature of this oscillating component, we conducted DFT calculations of the vibrational modes in the monomeric unit, (CN)₅Co–N–C–Fe(CN)₅⁶⁻. The bottom panel of Fig. 3b displays the calculated vibrational spectra of both LS and HS states (blue and red vertical lines, respectively). Despite the simplicity of the model, the obtained frequencies are in qualitative agreement with the general phonon structure of PBAs, obtained from experiments or advanced phonon calculations.^42,52–54 Lattice torsion modes are indeed observed below 150 cm⁻¹, including the torsion mode measured at 60 cm⁻¹. Metal-centred CoN₆ and FeC₆ modes, including e.g., breathing, Jahn–Teller or stretching modes are present between 150 cm⁻¹ and 530 cm⁻¹. The latter modes are very similar to those computed in the MnFe PBA, where the MnN₆ breathing and Jahn–Teller modes are found around 400 cm⁻¹.^41,52 Finally, CN stretching modes are found above 1980 cm⁻¹, up to 2200 cm⁻¹. The calculated vibrational spectrum of CoFe therefore displays a frequency gap between 530 cm⁻¹ and 1980 cm⁻¹ which is typical of PBA compounds, as revealed by more advanced phonon calculations in similar cyanide-bridged heterobimetallic networks.^42,52–54 This frequency gap is also observed in the infrared spectrum of the present compound, in agreement with the calculations (Fig. S7, ESI†). Consequently, the observed oscillation at 798 cm⁻¹ cannot be directly attributed to a specific phonon mode around this frequency. Hereafter we show that this observation of high-frequency oscillations allows a deeper understanding of the STICT process.

Discussion

The mechanism behind LS-to-HS photoswitching in the CoFe PBA was recently proposed using a combination of experimental and theoretical approaches,¹⁸ and is illustrated in Fig. 4a. It was shown that the main absorption at 545 nm corresponds to a Co^III-centred d–d transition, mainly transferring one electron from a t_2g-like orbital to an e_g-like one. This transition is usually forbidden in O_h symmetry by Laporte rule. Nonetheless, the thermal activation of low-energy torsion modes, transiently breaking O_h symmetry, results in a low but non-vanishing oscillator strength. The initially populated photo-excited (PE) state undergoes a rapid spin transition within 50 fs, therefore closing the t_2g–e_g energy gap (see the schematic electronic configurations in Fig. 4a). The resulting Co^III high-spin configuration (t⁴_2ge²_g, S = 2) only serves as a mediator (MED), as closing of the gap further drives the Fe-to-Co CT within 200 fs towards a Co^II HS state. This local CT results in the creation of a Co^IIFe^III small-polaron (SP), surrounded by Co^IIIFe^II units.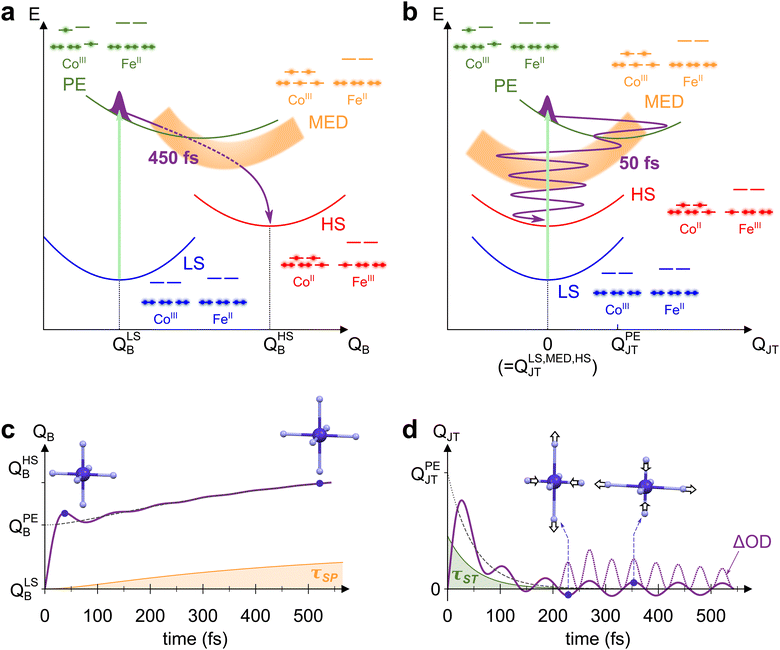

Fig. 4 (a) and (b) Schematic potential energy curves of CoFe electronic states involved in STICT, along the breathing mode Q_B (a) and the Jahn–Teller mode Q_JT (b). Photoexcitation of LS (blue curve) populates the PE state (green curve, with light-induced transition depicted as the light-green arrow). The PE state then decays to MED (orange curve) by the spin transition, and finally to the HS state (red curve) by charge transfer. The electronic configuration of each state is also represented, as well as the trajectory of the nuclear wave packet through the different states (purple line). (c) and (d) Corresponding evolution of Q_B (c) and Q_JT (d) with time, modelled by considering the changes occurring for both modes during the STICT process (see ESI† for details about the model). For each mode, the longest timescale influencing it is also shown (τ_SP for Q_B, in orange, and τ_ST for Q_JT, in green), as well as the average equilibrium position along the dynamics (dashed line). In the specific case of Q_JT, time evolution of ΔOD ∝ Q_JT² is also displayed (dotted line, rescaled for clarity), showing oscillations at twice the fundamental frequency 2ω_JT.

Due to the electronic redistribution among the t_2g and e_g orbitals from Co^III(S = 0) to Co^II(S = 3/2) states, the transition from LS to HS is accompanied by a global and symmetric increase of Co–N bond lengths, of ca. 0.2 Å.⁴⁴ As measured by femtosecond X-ray spectroscopy,¹⁸ a two-step bond elongation occurs, with a fast elongation due to the ST (50 fs), and a slower one (450 fs) associated to the structural reorganizations around the photoinduced CT polaron. The latter timescale, τ_SP, corresponds to the rise time observed in the present measurements (450 ± 40 fs). It stems from the adaptation of the lattice to the new Co–N bond lengths, before global crystal expansion eventually releases the photoinduced strain.⁴³ The bond elongations in the CoN₆ octahedron are here again the main reaction coordinate of the spin transition. Accordingly, we displayed in Fig. 4a the potential energy curves of the different electronic states (LS, PE, MED, HS) along the totally symmetric CoN₆ breathing mode, Q_B. Along this mode, an increase from Q^LS_B to Q^HS_B therefore occurs as the STICT process takes place, following in particular the 450 fs Co–N bond relaxation. The observed increase of Q_B after photoexcitation is analogous to the LIESST effect in SCO compounds, for which LIESST is accompanied by an increase of the bond lengths of the MN₆ core upon the LS-to-HS transition.⁴ In these compounds, this results in the observation of ultrafast vibrational coherences along Q_B.^19,21–24 The presence of such coherences, attributed to molecular breathing in the final HS state, is a signature of the ultrafast spin transition (typically of ∼120 fs in Fe^II complexes), that is faster than the typical MN₆ breathing period (∼300 fs). Increased coherence in some SCO compounds even indicated faster spin transition (within ∼75 fs),^27,32 as a result of initial d–d photoexcitation instead of MLCT population.

However, energetical and structural properties differ in the case of PBAs. Compared to SCO compounds, the global bond elongation is slower (450 fs in the present case), while the associated MN₆ breathing frequency is higher (around 400 cm⁻¹ typically, i.e., T_B = 84 fs period). Thus, while Q_B is also the main reaction coordinate in the STICT process, its activation is intrinsically incoherent due to important dephasing during the 450-fs bond elongation. This precludes any coherent signature of Q_B in the TA data, as schematically represented in Fig. 4c. Nonetheless, coherence is observed along the slower lattice torsion mode whose period is 560 fs (60 cm⁻¹), as a result of SP relaxation in a globally unexpanded LS lattice.

The detection of vibrational coherence at 798 cm⁻¹ indicates that the involved high-frequency mode does not dephase quickly during the STICT process, contrary to Q_B. Observation of the present coherent signature in the ESA band from 650 nm to 740 nm suggests that this mode is a Co-centred vibrational mode, as this band corresponds to the Co d–d transitions in the final HS state.⁵⁵ Additionally, given the frequency gap between 530 cm⁻¹ and 1980 cm⁻¹ in the DFT calculations, the observed oscillations can only be explained by the activation of a low symmetry mode around 399 cm⁻¹, that modulates the signal at its doubled frequency (798 cm⁻¹) due to symmetry rules. Among the Co-centred modes around 399 cm⁻¹, DFT calculations reveal a low symmetry CoN₆ Jahn–Teller (JT) mode at 386 cm⁻¹ in the LS state (Fig. S7, ESI†), similar to JT modes around 400 cm⁻¹ in other PBAs.^41,52–54 This mode (called thereafter Q_JT) is an E_g mode in O_h symmetry around the CoN₆ octahedron. Since the absorption properties belong to the A_1g irreducible representation, they are modulated by this JT mode as Q_JT², any modulation as Q_JT being forbidden by symmetry considerations (since A_1g ⊂ E_g × E_g but A_1g ⊄ E_g, as detailed in the ESI†).

To rationalize the activation of this Jahn–Teller mode in the STICT process, one should consider the nature of the transient PE state. In this state, a single electron populates one of the two antibonding e_g orbitals of Co (electronic configuration in green on Fig. 4a and b). As shown in the literature, this state is stabilized by a Jahn–Teller elongation, as it redistributes electron density along a preferential direction imposed by the populated orbital.^41,56 Thus, the population of the PE state should result in structural dynamics along the CoN₆ Jahn–Teller mode Q_JT. In the O_h point group, Q_JT belongs to the 2-dimensional E_g irreducible representation and its two components are conveniently represented in polar coordinates, Q₁ = Q_JT·cos θ and Q₂ = Q_JT·sin θ.⁵⁷ The potential exhibits a 3-fold symmetry around θ with a triple-well energy surface, corresponding to the 3-fold cubic symmetry with equivalent directions x, y and z.⁵⁷ For the sake of clarity, Fig. 4b represents the PE potential only along Q_JT, which maps the amplitude of the Jahn–Teller distortion that may occur along x, y or z: while the LS equilibrium position is centred at Q^LS_JT = 0, it is shifted at Q^PE_JT > 0 for the PE state, which triggers motion along Q_JT. Upon the impulsive sub-20-fs excitation, this motion takes the form of a vibrational coherence.

Following coherent excitation of Q_JT, the population is transferred to the MED state. Contrary to the PE state, both e_g orbitals of Co are populated in the MED state. This results back in a homogeneous electron density around the CoN₆ site, and therefore no preferential direction is imposed. As a consequence, the potential energy curve of this state is centred on O_h symmetry, i.e., Q^MED_JT = 0. As the PE-to-MED transfer occurs in 50 fs, i.e., faster than the JT period of 84 fs and its dephasing, the coherent dynamics triggered in the PE state are maintained after the spin transition. The final HS state is also centred on O_h symmetry (Q^HS_JT = 0), and therefore the Jahn–Teller coordinate is not altered anymore after the MED state. Consequently, the Jahn–Teller mode is a spectator mode in the slower MED-to-HS relaxation, and the associated coherent dynamics are preserved in the final state. This gives rise to the modulation of absorption at 2ω_JT = 798 cm⁻¹, as schematically depicted in Fig. 4d. Considering previous studies related to ultrafast polarization anisotropy and vibrational coherence measurements,⁵⁸ we can also attribute the isotropy observed after 200 fs between measurements in both polarization configurations as a result of the ultrafast ST process and the associated electronic dephasing on the sub-50-fs timescale. Overall, such a vibrational activation within the lifetime of the PE state shows that high-frequency vibrational coherences are solely possible along displacive modes in the initial state. This hinders the coherent activation of any other low-symmetry modes such as Fe(III)-centred Jahn–Teller modes that could be activated by the CT step, as the slower CT dynamics (200 fs) would result in an incoherent motion of this high-frequency mode (T ∼ 80 fs).

Interestingly, the present evidence of Jahn–Teller activation is similar to recent investigations in SCO compounds, where couplings to low-symmetry vibrational modes in Fe(II) O_h complexes⁵⁹ and vibrational coherences along these modes in Ru(II) complexes were reported, as a consequence of a single electron activation process similar to the present work.⁶⁰ The activation of a JT mode in the present PBA, upon impulsive photoexcitation and ultrafast spin transition, results in a vibrational coherence that persists well along the subsequent relaxation towards the final HS state. We suggest that the long damping time of JT coherence (960 fs) is due to the weak coupling of Q_JT with Q_B (orthogonal modes). Considering that the STICT process involves the expansion of the CoN₆ cage, such an activation of a JT mode represents a first step of elongation along one of the three Co–N axes only, determined by the initial d–d transition. This is rapidly followed by the increase of the other bond lengths, bringing the CoN₆ cage back to O_h symmetry.

Conclusions

Using sub-20-fs resolution experiments, we observed the femtosecond absorption changes during the photoinduced transformation from the low-spin Co^III(S = 0)Fe^II(S = 0) state to the high-spin Co^II(S = 3/2)Fe^III(S = 1/2) state in CoFe PBA nanocrystals. While coherent signatures of breathing modes during spin transition processes are broadly observed in SCOs compounds, our results suggest that the slow electronic changes during the STICT process in PBAs preclude the detection of any coherent fingerprints of the breathing mode in the final HS state. Instead, our measurements reveal an ultrafast modulation of OD at 798 cm⁻¹, attributed to the activation of a low-symmetry Jahn–Teller mode coupled to the photoexcitation in the early stage of the process, whose signature persists after the spin transition. This high-frequency modulation of the OD is a fingerprint of the STICT process, highlighting the structure of the single-electron Co-centred states and their role in the initial photoinduced dynamics. The present study therefore sheds new light on the coupled photoinduced electronic and structural dynamics at play in Prussian Blue Analogues. It also opens new opportunities for controlling magnetic properties of Prussian Blue Analogues on demand, using for instance nonlinear phononics strategies.^61,62

Author contributions

E. C. and M. H. conceived the project. E. C. and M. C. funded the project. M. H., B. M., S. H., J. L. and E. C. performed the transient absorption measurements and analysed the data. S. M. and T. M. synthetized the sample. S. F. M. performed theoretical calculations. S. F. M., M. H and E. C. analysed the results of the calculations. E. C. and M. H., with B. M., M. C., S. H. and J. L., set the physical picture. M. H. and E. C. wrote the manuscript, with contributions from all the authors.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors gratefully acknowledge the Agence Nationale de la Recherche for financial support under grants ANR-19-CE29-0018 MULTICROSS and ANR-19-CE07-0027 SMAC, the Interdisciplinary Thematic Institute QMat as part of the ITI 2021-2028 program of the University of Strasbourg, CNRS and Inserm via the IdEx Unistra (ANR 10 IDEX 0002), SFRI STRAT’US (ANR 20 SFRI 0012), and Labex NIE (ANR-11-LABX-0058-NIE) projects of the French Investments for the Future Program. E. C. thanks the University Rennes and the Fondation Rennes 1 for funding. This work was done within the Network “Sources et Lignes Femto”, with financial support from the GDR UP.

Notes and references

1. S. L. Johnson, Faraday Discuss., 2022, 237, 9–26.
2. G. R. Fleming, Faraday Discuss., 2022, 237, 419–427.
3. O. Sato, Nat. Chem., 2016, 8, 644–656.
4. A. Hauser, in Spin Crossover in Transition Metal Compounds II, Springer Berlin Heidelberg, Berlin, Heidelberg, 2004, vol. 234, pp. 155–198.
5. M. A. Halcrow, Spin-Crossover Materials: Properties and Applications, John Wiley & Sons, 2013.
6. R. Díaz-Torres, G. Chastanet, E. Collet, E. Trzop, P. Harding and D. J. Harding, Chem. Sci., 2023, 14, 7185–7191.
7. F. Liedy, J. Eng, R. McNab, R. Inglis, T. J. Penfold, E. K. Brechin and J. O. Johansson, Nat. Chem., 2020, 12, 452–458.
8. R. Phelps, A. Etcheverry-Berrios, E. K. Brechin and J. O. Johansson, Chem. Sci., 2023, 14, 6621–6630.
9. T. J. Penfold, J. O. Johansson and J. Eng, Coord. Chem. Rev., 2023, 494, 215346.
10. M. Hojorat, H. Al Sabea, L. Norel, K. Bernot, T. Roisnel, F. Gendron, B. L. Guennic, E. Trzop, E. Collet, J. R. Long and S. Rigaut, J. Am. Chem. Soc., 2020, 142, 931–936.
11. O. Sato, T. Iyoda, A. Fujishima and K. Hashimoto, Science, 1996, 272, 704–705.
12. S. Ohkoshi and H. Tokoro, Acc. Chem. Res., 2012, 45, 1749–1758.
13. C. Mathonière, H.-J. Lin, D. Siretanu, R. Clérac and J. M. Smith, J. Am. Chem. Soc., 2013, 135, 19083–19086.
14. H. Tokoro, T. Matsuda, T. Nuida, Y. Moritomo, K. Ohoyama, E. D. L. Dangui, K. Boukheddaden and S. Ohkoshi, Chem. Mater., 2008, 20, 423–428.
15. G. Azzolina, E. Collet, C. Mariette, M. Cammarata, E. Trzop, M. Sander, M. Levantino, K. Nakagawa, H. Tokoro, S. Ohkoshi and R. Bertoni, Eur. J. Inorg. Chem., 2019, 3142–3147.
16. A. Marino, P. Chakraborty, M. Servol, M. Lorenc, E. Collet and A. Hauser, Angew. Chem., Int. Ed., 2014, 53, 3863–3867.
17. M. Chergui and E. Collet, Chem. Rev., 2017, 117, 11025–11065.
18. M. Cammarata, S. Zerdane, L. Balducci, G. Azzolina, S. Mazerat, C. Exertier, M. Trabuco, M. Levantino, R. Alonso-Mori, J. M. Glownia, S. Song, L. Catala, T. Mallah, S. F. Matar and E. Collet, Nat. Chem., 2021, 13, 10–14.
19. W. Zhang, R. Alonso-Mori, U. Bergmann, C. Bressler, M. Chollet, A. Galler, W. Gawelda, R. G. Hadt, R. W. Hartsock, T. Kroll, K. S. Kjær, K. Kubiček, H. T. Lemke, H. W. Liang, D. A. Meyer, M. M. Nielsen, C. Purser, J. S. Robinson, E. I. Solomon, Z. Sun, D. Sokaras, T. B. van Driel, G. Vankó, T.-C. Weng, D. Zhu and K. J. Gaffney, Nature, 2014, 509, 345–348.
20. K. J. Gaffney, Chem. Sci., 2021, 12, 8010–8025.
21. C. Consani, M. PrØmont-Schwarz, A. ElNahhas, C. Bressler, F. van Mourik, A. Cannizzo and M. Chergui, Angew. Chem., Int. Ed., 2009, 4.
22. G. Auböck and M. Chergui, Nat. Chem., 2015, 7, 629–633.
23. H. T. Lemke, K. S. Kjær, R. Hartsock, T. B. van Driel, M. Chollet, J. M. Glownia, S. Song, D. Zhu, E. Pace, S. F. Matar, M. M. Nielsen, M. Benfatto, K. J. Gaffney, E. Collet and M. Cammarata, Nat. Commun., 2017, 8, 15342.
24. M. Cammarata, R. Bertoni, M. Lorenc, H. Cailleau, S. Di Matteo, C. Mauriac, S. F. Matar, H. Lemke, M. Chollet, S. Ravy, C. Laulhé, J.-F. Létard and E. Collet, Phys. Rev. Lett., 2014, 113, 227402.
25. B. C. Paulus, S. L. Adelman, L. L. Jamula and J. K. McCusker, Nature, 2020, 582, 214–218.
26. E. Biasin, T. B. van Driel, K. S. Kjær, A. O. Dohn, M. Christensen, T. Harlang, P. Chabera, Y. Liu, J. Uhlig, M. Pápai, Z. Németh, R. Hartsock, W. Liang, J. Zhang, R. Alonso-Mori, M. Chollet, J. M. Glownia, S. Nelson, D. Sokaras, T. A. Assefa, A. Britz, A. Galler, W. Gawelda, C. Bressler, K. J. Gaffney, H. T. Lemke, K. B. Møller, M. M. Nielsen, V. Sundström, G. Vankó, K. Wärnmark, S. E. Canton and K. Haldrup, Phys. Rev. Lett., 2016, 117, 013002.
27. S. Zerdane, L. Wilbraham, M. Cammarata, O. Iasco, E. Rivière, M.-L. Boillot, I. Ciofini and E. Collet, Chem. Sci., 2017, 8, 4978–4986.
28. J. N. Schrauben, K. L. Dillman, W. F. Beck and J. K. McCusker, Chem. Sci., 2010, 1, 405.
29. R. Bertoni, M. Cammarata, M. Lorenc, S. F. Matar, J.-F. Létard, H. T. Lemke and E. Collet, Acc. Chem. Res., 2015, 48, 774–781.
30. K. S. Kjær, T. B. Van Driel, T. C. B. Harlang, K. Kunnus, E. Biasin, K. Ledbetter, R. W. Hartsock, M. E. Reinhard, S. Koroidov, L. Li, M. G. Laursen, F. B. Hansen, P. Vester, M. Christensen, K. Haldrup, M. M. Nielsen, A. O. Dohn, M. I. Pápai, K. B. Møller, P. Chabera, Y. Liu, H. Tatsuno, C. Timm, M. Jarenmark, J. Uhlig, V. Sundstöm, K. Wärnmark, P. Persson, Z. Németh, D. S. Szemes, É. Bajnóczi, G. Vankó, R. Alonso-Mori, J. M. Glownia, S. Nelson, M. Sikorski, D. Sokaras, S. E. Canton, H. T. Lemke and K. J. Gaffney, Chem. Sci., 2019, 10, 5749–5760.
31. M. Alías-Rodríguez, S. Bhattacharyya and M. Huix-Rotllant, J. Phys. Chem. Lett., 2023, 14, 8571–8576.
32. S. Zerdane, M. Cammarata, O. Iasco, M.-L. Boillot and E. Collet, J. Chem. Phys., 2019, 151, 171101.
33. B. C. Paulus and J. K. McCusker, Faraday Discuss., 2022, 237, 274–299.
34. R. Field, L. C. Liu, W. Gawelda, C. Lu and R. J. D. Miller, Chem. – Eur. J., 2016, 22, 5118–5122.
35. G. Privault, J.-Y. Mevellec, M. Lorenc, B. Humbert, E. Janod, N. Daro, G. Chastanet, A. Subedi and E. Collet, Cryst. Growth Des., 2022, 22, 5100–5109.
36. D. Aguilà, Y. Prado, E. S. Koumousi, C. Mathonière and R. Clérac, Chem. Soc. Rev., 2016, 45, 203–224.
37. A. Asahara, M. Nakajima, R. Fukaya, H. Tokoro, S. Ohkoshi and T. Suemoto, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 86, 195138.
38. J. O. Johansson, J.-W. Kim, E. Allwright, D. M. Rogers, N. Robertson and J.-Y. Bigot, Chem. Sci., 2016, 7, 7061–7067.
39. K. Barlow and J. O. Johansson, Phys. Chem. Chem. Phys., 2021, 23, 8118–8131.
40. M. van Veenendaal, Sci. Rep., 2017, 7, 6672.
41. G. Azzolina, H. Tokoro, K. Imoto, M. Yoshikiyo, S. Ohkoshi and E. Collet, Angew. Chem., Int. Ed., 2021, 60, 23267–23273.
42. L. Trinh, S. Zerdane, S. Mazérat, N. Dia, D. Dragoe, C. Herrero, E. Rivière, L. Catala, M. Cammarata, E. Collet and T. Mallah, Inorg. Chem., 2020, 59, 13153–13161.
43. S. Zerdane, M. Hervé, S. Mazerat, L. Catala, R. Alonso-Mori, J. M. Glownia, S. Song, M. Levantino, T. Mallah, M. Cammarata and E. Collet, Faraday Discuss., 2022, 237, 224–236.
44. C. Cartier Dit Moulin, F. Villain, A. Bleuzen, M.-A. Arrio, P. Sainctavit, C. Lomenech, V. Escax, F. Baudelet, E. Dartyge, J.-J. Gallet and M. Verdaguer, J. Am. Chem. Soc., 2000, 122, 6653–6658.
45. J.-D. Cafun, J. Lejeune, F. Baudelet, P. Dumas, J.-P. Itié and A. Bleuzen, Angew. Chem., Int. Ed., 2012, 51, 9146–9148.
46. M. Gueye, J. Nillon, O. Crégut and J. Léonard, Rev. Sci. Instrum., 2016, 87, 093109.
47. H. Barkhuijsen, R. De Beer, W. M. M. J. Bovée and D. Van Ormondt, J. Magn. Reson., 1985, 61, 465–481.
48. H. Barkhuijsen, R. De Beer and D. Van Ormondt, J. Magn. Reson., 1987, 73, 553–557.
49. J. J. Helmus and C. P. Jaroniec, J. Biomol. NMR, 2013, 55, 355–367.
50. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, B. Mennucci, G. A. Petersson, H. Nakatsuji, M. Caricato, X. Li, H. P. Hratchian, A. F. Izmaylov, J. Bloino, G. Zheng, J. L. Sonnenberg, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. Bearpark, J. J. Heyd, E. Brothers, K. N. Kudin, V. N. Staroverov, R. Kobayashi, J. Normand, K. Raghavachari, A. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, N. Rega, J. M. Millam, M. Klene, J. E. Knox, J. B. Cross, V. Bakken, C. Adamo, J. Jaramillo, R. Gomperts, R. E. Stratmann, O. Yazyev, A. J. Austin, R. Cammi, C. Pomelli, J. W. Ochterski, R. L. Martin, K. Morokuma, V. G. Zakrzewski, G. A. Voth, P. Salvador, J. J. Dannenberg, S. Dapprich, A. D. Daniels, Ö. Farkas, J. B. Foresman, J. V. Ortiz, J. Cioslowski, and D. J. Fox, Gaussian 09, Gaussian, Inc., Wallingford CT, 2009.
51. S. L. Dexheimer, Q. Wang, L. A. Peteanu, W. T. Pollard, R. A. Mathies and C. V. Shank, Chem. Phys. Lett., 1992, 188, 61–66.
52. H. Tokoro, A. Namai, M. Yoshikiyo, R. Fujiwara, K. Chiba and S. Ohkoshi, Sci. Rep., 2018, 8, 63.
53. S. Ohkoshi, M. Yoshikiyo, A. Namai, K. Nakagawa, K. Chiba, R. Fujiwara and H. Tokoro, Sci. Rep., 2017, 7, 8088.
54. Y. Li, Q. Gao, D. Chang, P. Sun, J. Liu, Y. Jia, E. Liang and Q. Sun, J. Phys.: Condens. Matter, 2020, 32, 455703.
55. T. Kawamoto and S. Abe, Phase Transitions, 2001, 74, 209–233.
56. G. Azzolina, R. Bertoni, C. Mariette, M. Cammarata, E. Trzop, C. Ecolivet, M. Sander, M. Levantino, H. Tokoro, K. Imoto, M. Yoshikiyo, S. Ohkoshi and E. Collet, J. Mater. Chem. C, 2021, 9, 6773–6780.
57. J. D. Axe and Y. Yamada, Phys. Rev. B: Condens. Matter Mater. Phys., 1981, 24, 2567–2569.
58. D. A. Farrow, W. Qian, E. R. Smith, A. A. Ferro and D. M. Jonas, J. Chem. Phys., 2008, 128, 144510.
59. M. Oppermann, F. Zinna, J. Lacour and M. Chergui, Nat. Chem., 2022, 14, 739–745.
60. J. Kim, D. Kang, S. K. Kim and T. Joo, Phys. Chem. Chem. Phys., 2020, 22, 25811–25818.
61. R. Mankowsky, M. Först and A. Cavalleri, Rep. Prog. Phys., 2016, 79, 064503.
62. A. Subedi, C. R. Phys., 2021, 22, 161–184.

---

Footnotes

† Electronic supplementary information (ESI) available: Details on the analysis of transient absorption signal, DFT calculations, model of the temporal evolution along breathing and Jahn–Teller modes, detection of a Jahn–Teller mode in TA experiments and DFT structures. See DOI: https://doi.org/10.1039/d3ma01072d

‡ Present address: Laboratoire de Chimie de l’ENS de Lyon, French National Centre for Scientific Research (CNRS), 69364, Lyon, France.

---