Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Programming fibril alignment and mechanical response in reconstituted collagen fibers using reagent-free biomimetic energetic electron crosslinking†
Anastassiya
Bublikova‡
ab,
Friedrich
Schütte‡
 *ab and
Stefan G.
Mayr
*ab
*ab and
Stefan G.
Mayr
*ab
aDivision of Surface Physics, Department of Physics and Earth System Sciences, University of Leipzig, Linnéstr. 5, 04103 Leipzig, Germany. E-mail: friedrich.schuette@uni-leipzig.de; stefan.mayr@iom-leipzig.de
bLeibniz Institute of Surface Engineering (IOM), Permoserstr. 15, 04318 Leipzig, Germany
First published on 29th April 2024
Abstract
Due to its abundance in vertebrates, including humans, collagen is deemed to be a highly attractive bioderived material which bears large potential for cutting-edge applications in a variety of biomedical fields, including scaffolds, implantology, artificial organs, regenerative medicine and mechanobiology. Depending on structure, including hierarchical fibril alignment and crosslinking, in vivo collagen assemblies are characterized by Young's moduli ranging from some kPa to GPa. When heading for biomimicry of scaffolds and implants based on reconstituted collagen, control of mechanical response by fibril alignment and biomimetic crosslinking constitute central challenges. Within this work we demonstrate, that energetic electrons are a promising tool to permanently imprint prestrain-induced alignment of collagen fibrils within macroscopic collagen fibers by introduction of biomimetic crosslinks, resulting in elastic properties bridging orders of magnitude.
1 Introduction
Collagen is a versatile biomaterial that has tremendous potential in scientific, applied, and biomedical fields. It is biocompatible and biodegradable showing a high suitability for applications in areas of bio-engineering and regenerative medicine1 as tissue replacement and in cell culture.2–6 Collagen is a structural protein that is found in vertebrates, including connective tissues of mammals and humans, in the form of fibers.7,8 Up to date, 29 types of collagen have been identified, of which type I, II, III, IV, and IX are the most common in humans.9,10 Collagen type I is the most abundant protein in the human body and plays a critical role in providing structural support and strength to tissues such as skin, bone, cartilage, and tendons.7,11,12 In living organisms, collagen fibers are typically organized in different orientations depending on the tissue type, which plays an important role in the mechanical, physiological and biochemical functions.8 Collagen networks display highly nonlinear mechanics and stiffen significantly due to an internal and external strain increase.13–15 In addition, they are also viscoelastic: they partially store elastic energy and partially relax internal stress through dissipative processes.16 All of these properties are delicately influenced by the structure of the networks, by the molecular interactions between monomers, and by the addition of covalent cross-links.14As it is relatively easy to isolate from a variety of tissue sources, such as bovine,17 fish18 and rodent,19 and can be produced as a recombinant human protein,20 researchers are exploring the use of reconstituted collagen for a range of applications, including drug delivery21 and wound healing.18,22 Collagen-based drug delivery systems can protect drugs from degradation and the use of different cross-linking agents can also affect the release rate of drugs. Collagen-based dressings have been shown to promote wound healing by providing a moist wound environment and promoting the growth of new tissue. Collagen has been also extensively studied as a scaffold material for tissue engineering, with many examples of collagen-based biomaterials emerging in recent years.23,24 One major challenge is the development of biomaterials that can support the growth and function of cells. Collagen-based scaffolds have been shown to promote cell attachment, proliferation, and differentiation. Collagen fibers can be modified to improve their mechanical properties, stability and biological performance by adding cross-links.25,26 Chemical cross-linking using glutaraldehyde is common and widely used to tailor thermal and mechanical properties of a variety of biomaterials including collagen.27–29 However, it is often associated with cytotoxicity which interfere drastically with bio-compatibility.30,31 Treatment with energetic electrons, in contrast, is a reagent-free, biomimetic approach eliminating particularly the potential toxicity of chemical cross-linkers32 and allows for spatially resolved insertion of crosslinks.33 Previous studies have already demonstrated that electron treated hydrogels25,34 have been proven to have an influence on cellular morphology while also being non-cytotoxic which makes them even more suitable in the fields of mechanobiology and regenerative medicine.1
While there are numerous methods available for forming collagen scaffolds from isolated collagen, it can be difficult to control collagen fibril alignment. While various forms of physical manipulation including fluid shear35,36 and electromagnetic fields36,37 have been explored to improve collagen fibril alignment, exposure to strain38,39 before cross-linking is used in this work to produce reconstituted collagen type I fibers and increase fibril alignment. The collagen fibers are stretched using a tensile testing machine prior to being crosslinked with high energy electron irradiation at different doses in order to tailor and imprint their structural alignment and mechanical properties. This allows the mechanical properties to be simultaneously adjusted on two parameters, which means that a higher degree of accuracy in the mechanical response and mechanical anisotropy can be expected for custom-made scaffolds.
To establish structure–property relationships between fiber alignment and mechanics, polarized light microscopy (PLM)40 was found to be useful in analyzing changes in polymer structures parallel to mechanical tests. In this paper we use classical cross-polarized light microscopy to image the structure of prestrained and electron treated collagen fibers.
We present approaches to synthesize and cross-link prestrained collagen fibers extracted from rat tail tendons. We show that modification of the mechanical response can be achieved not only by using high-energy electrons, but also by aligning the internal fibril structure by prestraining and fixing it in the aforementioned electron beam treatment. The obtained elastic, viscoelastic and plastic properties of prepared non-prestrained collagen fibers are compared with those of irradiated fibers with respect to the electron irradiation dose as well as the degree of mechanical prestrain before application of energetic electrons. Afterwards, fibers were imaged using cross-polarized light microscopy to reveal and compare their modified structure.
2 Materials and methods
2.1 Collagen sample preparation
Collagen fiber samples were produced according to the work of Y. Kato et al.19 using chemicals listed in Table 1. Firstly, fiber formation buffer (FFB) is prepared before collagen fiber synthesis consisting of: distilled water (400 ml), 135 mM sodium chloride (2.75 g), 30 mM TES (3.16 g), 30 mM sodium phosphate dibasic (1.7 g).| Chemical name | Concentration/lab code |
|---|---|
| Collagen | Collagen Type I, Rat Tail, Cat. No.: 50205, pH 2–3 (ibidi GmbH, Germany) |
| Buffer | Sodium chloride NaCl, M = 58.44 g mol−1, S7653 (Sigma-Aldrich, Germany) |
| TES C6H15NO6S, M = 229.25 g mol−1, T1375 (Sigma-Aldrich, Germany) | |
| Sodium phosphate dibasic Na2HPO4, M = 141.96 g mol−1, S3264 (Sigma-Aldrich, Germany) | |
| Distilled water | dH 2 O, M = 18.02 g mol−1 |
| Isopropyl alcohol |
C
3
H
8
O, M = 60.10 g mol−1, 278![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 475 (Sigma-Aldrich, Germany) 475 (Sigma-Aldrich, Germany) |
| Sodium hydroxide | NaOH, M = 40.00 g mol−1, 72![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 068 (Sigma-Aldrich, Germany) 068 (Sigma-Aldrich, Germany) |
Using a hypodermic needle, collagen type I extracted from rat tail (5 ml) is slowly loaded into a syringe after centrifuging at 1000 rpm to extract air bubbles of collagen. The polytetrafluoroethylene (PTFE) connector tube is attached to this collagen-filled syringe and the syringe is loaded onto a syringe pump. The end of the connector tube has to be entirely submerged in the fiber formation buffer (FFB), outlined above. This FFB is poured into a large petri dish and placed onto a hot plate with a magnetic stirrer and heated to approximately 36 °C (see Fig. S1, ESI†). The pump infusion rate of the syringe pump is set to 0.2 ml min−1 and fibers start forming as soon as syringe pump is turned on and collagen is extruded into the FFB. This extruded collagen needs to be cut with clean sharp scissors every 20 seconds in order to obtain individual fibers of length of approximately 10 cm.
The fibers should remain in the FFB for at least 45 minutes in order to facilitate the polymerisation process. They are then washed in a series of 4 baths at room temperature, each bath lasting 60 minutes. Each subsequent bath decreases concentration of isopropyl alcohol, starting with 100% isopropyl alcohol and ending with 100% dH2O. After the last bath in distilled water, the fibers are hung to dry overnight at room temperature. The samples are stored dry at room temperature until use.
Collagen fibers are stretched in the Zwick-Roell tensile testing machine before irradiation with 0%, 25% or 60% of their original length. This process is referred to as “prestraining” throughout this paper. The fibers are glued onto a sample holder which is a frame of transparency paper and has a fixed gauge length (initial length of specimen), 3–4 dried fibers are glued at both ends by cyanoacrylate adhesive to a sample holder. The samples are then submerged in a bath with dH2O to swell for at least 30 minutes. The wet fibers attached to the sample holder are then clamped in the tensile testing machine and the sides of the sample are cut to allow the fibers to be stretched. The upper clamp then moves upwards at a steady speed until the samples reach the desired extension. When the clamp stops moving, without removing the sample holder from the clamp, a piece of Styrofoam is glued to either side of the sample holder in order to fix this new fiber length. These samples are then stored dry at room temperature until irradiation.
2.2 Electron irradiation
A 10 MeV linear accelerator (MB10-30MP; Mevex, Ontario, Canada) was used to irradiate collagen fibers. The precise device used is located in the Leibniz-Institute for Surface Modification e.V. Leipzig. The moving stage moves with a 180 HZ frequency rate, electron pulse of 8 μs long was used and the scanning horn scans the electron beam with a frequency of 3 Hz, similarly to Riedel et al.25 Irradiation is done in steps of 5 kGy in accordance to Wisotzki et al.,34 regardless of the final desired irradiation dose, with a rest period of 2–3 minutes between each step to prevent overheating and damaging of the samples. As a result, the total time to irradiate the samples takes approximately an hour, depending on the final irradiation dose. The irradiation doses are measured using graphite dosimeter having an uncertainty of 10%. The samples were irradiated up to 50 kGy in an inert plastic sample holder filled with distilled water.2.3 Tensile testing
A zwickiLine tensile testing machine (type Z0.5 TS, art. no. 058992, ZwickRoell GmbH & Co. KG, Germany) was used for prestraining and tensile testing of the collagen fibers. The built-in force sensor (type Xforce HP, art. no. 063924, ZwickRoell GmbH & Co. KG, Germany) is calibrated to 0.4% of the nominal force (i.e. max 0.02 N). The computer software testXpert III sets the parameters and collects the force data for the stress–strain curves at a sampling rate of 200 Hz. All tensile tests were performed strain controlled in fully hydrated conditions. Stress is obtained from the measured force acting in the direction parallel to the fiber (σ = F/A0 where A0 = πr02 and r0 is the initial radius) with a uniform loading rate of 1.5 mm min−1.For tensile testing, sample holders are prepared consisting of a frame of transparency paper which is cut with a fixed gauge length of 2 mm. This allowed a strain to be determined based on the standardized original sample length and the displacement measured with the calibrated ZwickRoell (type Z0.5 TS, art. no. 058992, ZwickRoell GmbH & Co. KG, Germany) force testing system. The fibers are glued with cyanoacrylate adhesive to a sample holder. The samples swell in a water bath for at least 2 hours before tensile testing. The sample is then clamped vertically inside a water bath in the tensile testing machine (shown in Fig. S2 and S3, ESI†). Each side of the sample holder is then cut to allow the collagen fiber to be stretched. The bottom clamp is stationary fixing the sample in place while the upper one moves, stretching the sample vertically. The light microscope set up behind the water bath allows real-time recording of the sample being measured.
2.4 Polarization microscopy
Polarized light microscopy was used to image the collagen fiber structure. The microscope Leica DM2700M (LeicaMicrosystems GmbH, Wetzlar, Germany) was configured to polarisation mode in accordance with the manual.41 The polariser and analyzer are initially set at 0° with respect to each other to obtain unpolarized images of the samples. Analyzer is then rotated 90° with respect to the polarizer, in this cross-orientation of the polarizers, the birefrigent sample appears bright on a dark background. The samples are imaged in a fully hydrated state by letting them swell in a water bath of dH2O for approximately 2 hours and more water being applied to the fiber during the measurement if needed. The light source used in the microscope is a white light high-power LED. Different objectives with increasing magnification are used to image the samples in greater detail (5×, 10×, 20×, 40×, 63×).2.5 Image and data analysis
The light microscope used during the tensile measurement is DinoLite AM7915MZT (AnMo Electronics Corporation, Taipei, Taiwan) with the DinoCapture 2.0 software. The images obtained from the polarization microscope were scaled to size using imageJ (version v1.53t) software. The data obtained from the tensile testing machine was analyzed using Python 3.6.15 code, analysis and fitting were done using the libraries NumPy, SciPy and Pandas, while the plotting is done using MatPlotLib.3 Results
3.1 Uniaxial mechanical characterization
Tensile tests were performed to determine viscoelastic behaviour of fully hydrated unirradiated non-prestrained (see Fig. S4, ESI†) and irradiated prestrained collagen fibers, respectively. In Fig. 1 for each electron dose D (5, 10, 25, 50 kGy, respectively) four stress–strain curves are shown, as-extruded, irradiated non-prestrained, irradiated prestrained 25% and irradiated prestrained 60%, respectively, employing the engineering stress and strain definitions. Regarding the qualitative shape of the curves, first it is interesting to note that by introduction of covalent crosslinks, energetic electron treatment prevents occurrence of ductile necking behavior, which is prevalent only in as-extruded samples. With both, higher dose and prestrain, fracture strain decreases while ultimate tensile strength (UTS) increases. The higher the dose, the stiffer the fiber becomes, thus the fracture strain decreases with each higher dose (see Table S1, ESI†). For as-extruded and samples exposed to doses of 10 kGy and higher, increases of UTS from 0.16 MPa to 0.77 MPa and higher, respectively can be observed. If prestrains εpre = 25% and εpre = 60% are applied, UTS at 50 kGy are 1.47 MPa and 3.50 MPa, respectively.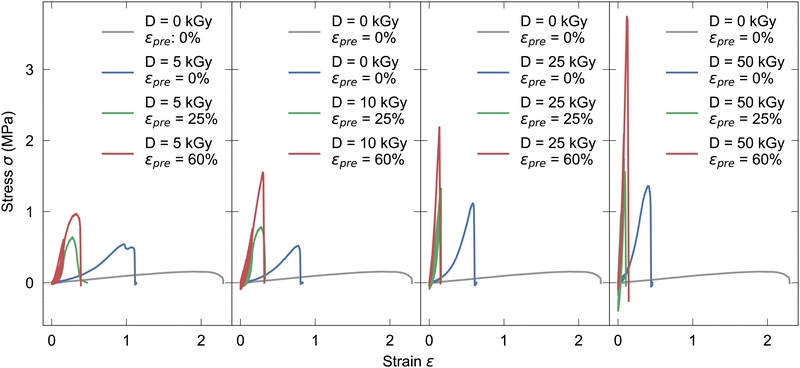 | ||
| Fig. 1 Exemplary tensile tests with 0%, 25%, 60% prestrain for increasing irradiation doses of 5, 10, 25 and 50 kGy from left to right, compared to unirradiated samples. | ||
The mechanical properties of cross-linked collagen fibers were determined by cyclically loading in loops of 10 cycles each, resulting in four loops with increasing maximum strains of 0.02, 0.04, 0.08, and 0.16, respectively. Cyclic stress–strain tests were mainly performed in the low-strain region, revealing a nonlinear elastic response indicating a central role of induced crosslinks for mechanical stability. For each loop the distribution of the differential Young's moduli K = dσ/dε42 was investigated at constant loading rate of 1.5 mm min−1 at frequencies of f2% = 0.313 Hz, f4% = 0.157 Hz, f8% = 0.078 Hz, f16% = 0.039 Hz, f32% = 0.020 Hz, respectively, as determined by the maximum deformation strains due to constant deformation rates (see Table S1, ESI†). The resulting stress–strain curves were smoothed with a spline fit in python,43 whereby K was defined as the stress gradient σ divided by the strain gradient ε. The differential moduli were calculated solely for extension, not for compressions in the respective loops. Depending on the prestrain, i.e. 0%, 25%, 60%, results are shown in Fig. 2 for the respective irradiation doses; they basically not only show an increasing Young's modulus with prestrain and dose, but also non-linearity, as reflected in the broadening of the distribution (see also Fig. S5–S7, ESI†).
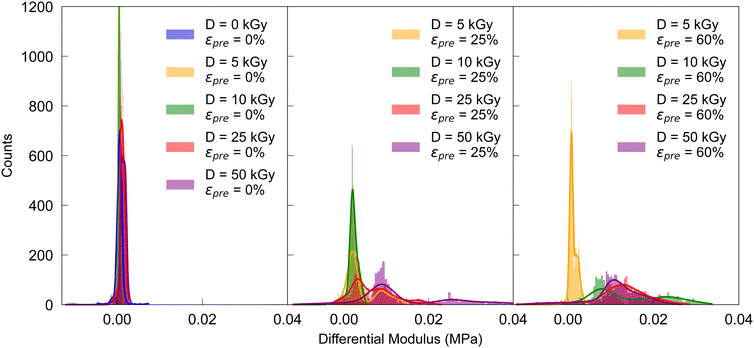 | ||
| Fig. 2 Distribution of differential moduli in the loop up to 4% peak strain for increasing prestrains in cyclic stress–strain curves. | ||
Since the cyclic force tests show a hysteretic response, energy dissipation is analyzed via
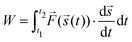 | (1) |
![[s with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0073_20d1.gif) (t). A higher irradiation dose does not have a particularly large effect on dissipation (also Fig. S8, ESI†). For a prestrain, however, it can be observed that the energy dissipation decreases dramatically. In fact, in Fig. 3, for cycles 20 and above, the energy dissipation is at least an order of magnitude higher for as-extruded samples when compared with prestrained samples. A distinction must be made between low-strain regions (up to cycle 20) in which almost no energy dissipation appears, and regions above this where the first relaxation effects can already be observed (cf.Fig. 3).
(t). A higher irradiation dose does not have a particularly large effect on dissipation (also Fig. S8, ESI†). For a prestrain, however, it can be observed that the energy dissipation decreases dramatically. In fact, in Fig. 3, for cycles 20 and above, the energy dissipation is at least an order of magnitude higher for as-extruded samples when compared with prestrained samples. A distinction must be made between low-strain regions (up to cycle 20) in which almost no energy dissipation appears, and regions above this where the first relaxation effects can already be observed (cf.Fig. 3).
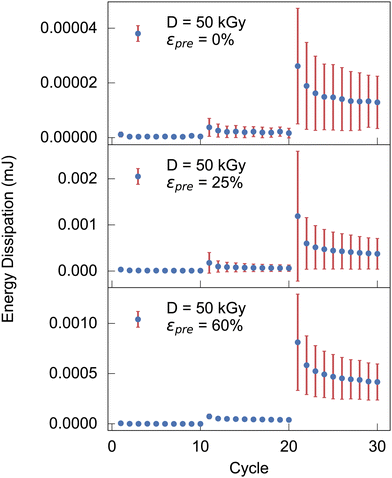 | ||
| Fig. 3 Energy dissipation during cyclic measurements with a peak strains of 0.02, 0.04, 0.08 for the cycle 1 to 10, 11 to 20, 21 to 30, respectively, for increasing prestrains. | ||
The relaxation behaviour of glassy complex systems can be modeled by introducing an additional stretch parameter44 to an exponentially decaying function. The stretched exponential is defined as
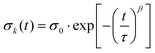 | (2) |
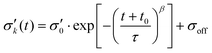 | (3) |
To reduce fit parameters and to include the offset σoff on the stress axis, 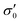 is written as
is written as
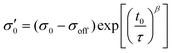 | (4) |
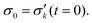 | (5) |
The fit parameters τ, β, σoff, t0 have been determined using as well eqn (3) as eqn (4) and constraints resulting from the data.
For the fitting procedure, the measurement data in the 4th loop from the cyclic stress–strain tests were averaged. The stretched exponential fit described above was then applied to the maximum mean values of the respective cycles. The values for the stretching exponent is in our study in the range of 0.2 < β < 1, whereby β decreases with increasing dose, viz. crosslinking density (see Fig. 4 0 kGy and 5 kGy). The results of the stretched exponential fits in the relaxation tests are approximately consistent with other studies.45
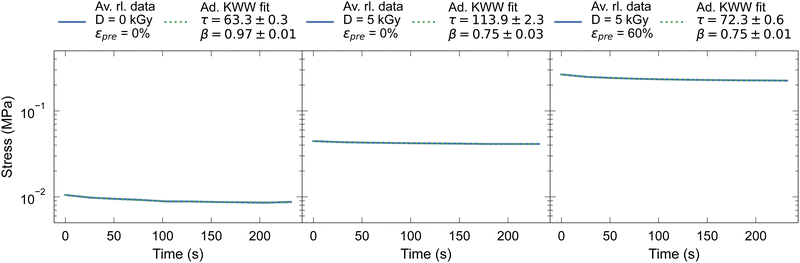 | ||
| Fig. 4 Averaged relaxation curves (Av. rl. data) with fitted data using an adapted KWW function (Ad. KWW fit) for prestrained crosslinked samples and unmodified reference samples. | ||
3.2 Characterization of fiber alignment using polarized light microscopy
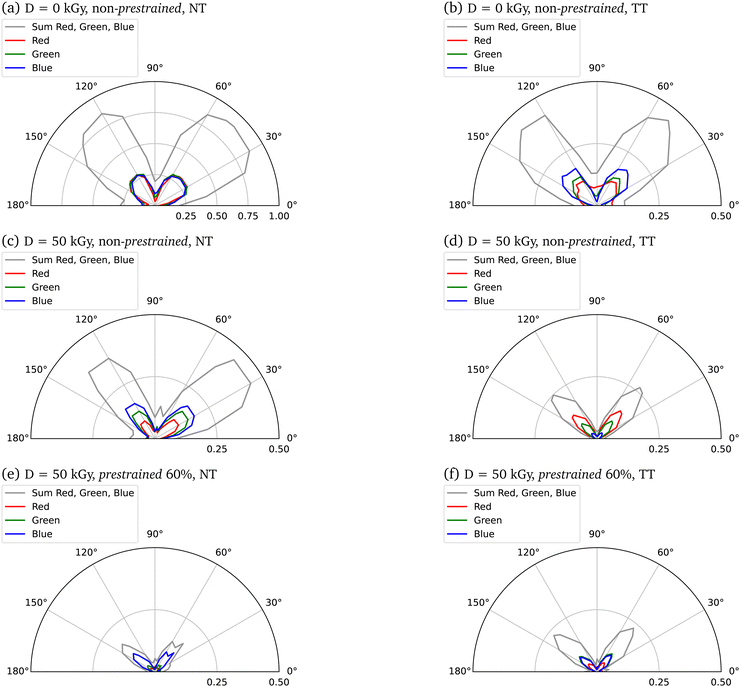
The samples were imaged under cross-polarized light and were rotated on the rotating plate 10° at a time (starting at 0° with sample being parallel to x-axis) in order to investigate further the inner alignment of the fibers. Brightness of the microscope's light source was lowered significantly for imaging as in the section above the samples were imaged at extinction (0°), as is clear from the images below. The same brightness as used in the imaging above results in samples being too bright when imaged at 45°. Only images at 0° and 45° are shown here because they provide the extinction and brightest position of the fibers, respectively.All samples in the images below appear brightest at 45° and dimmest at 0° and 90°. The non-prestrained and unirradiated sample is the brightest out of all samples at 45°, appearing mostly white. At 0° the sample appears blue and is still clearly visible. When unirradiated sample is stretched a portion of the light appears to be absorbed leaving the sample at extinction to appear orange on the outer edges at 0° and entirely at 45°.
When irradiated but still non-prestrained, the sample looks similar to the unirradiated non-prestrained sample, but dimmer at all angles. This is similar to what is seen for the unirradiated and irradiated non-prestrained samples shown in Fig. 5. When stretched, similar to the unirradiated sample, it appears orange but now at 45° while being completely extinct at 0°. Prestrained irradiated samples show similar colours to Fig. 5 at 45° and are completely extinct at 0°.
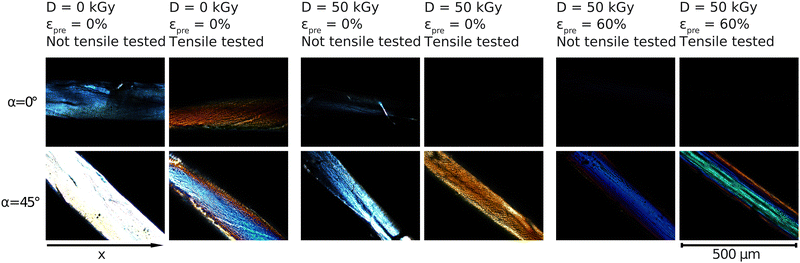 | ||
| Fig. 5 Crossed polarized light microscopy measurements for samples with prestrains of εpre = 0% and εpre = 60% with regard to radiation treatment before and after tensile tests. The angle of the rotating plate in the polarization microscope is α. The microscopy images in higher resolution are shown in the Fig. S9–S13 (ESI†). | ||
The image data from the polarization microscopy were evaluated via the intensity histograms (see Fig. S14, ESI†) of the individual red, green and blue channels (RGB) in order to assign potential effects of irradiation or induced stresses. Polar plots in Fig. 6 show intensity dependence for 0° ≤ α ≤ 180°.
4 Discussion
In the following, we aim to discuss the relation of collagen network properties and mechanical response. We start by first noting that our extruded collagen fibers largely consist of isotropic network structure, as confirmed by our present polarized light microscopy measurements (as-extruded fibers in absence of prestrain largely reveal zero transmittance when rotated between two crossed linear polarizers), as well as previous ESEM (environmental scanning electron microscopy) measurements.46 Energetic electron treatment of such isotropic networks results in dramatically increasing elastic moduli as e.g. reflected by the maximum Young's modulus, which increases e.g. by 1.5 orders of magnitude from 0.1 to 5 MPa upon exposure to an electron dose of 50 kGy. This is accompanied by a change of fracture mode from ductile to brittle; accordingly UTS and fracture strain increase (0.18 → 1.2 MPa) and decrease (2.4 → 0.5) by an order of magnitude and more, respectively. While our presently recorded uniaxial stress–strain curve until fracture thus constitute a comprehensive mechanical characterization, the finding on dramatically increasing Young's moduli are in accord with strongly increasing shear moduli determined in our previous shear rheology measurements on electron beam treated collagens of different source.25 Clearly energetic electron assisted introduction of covalent crosslinks constitutes the unerlying mechanism. The latter is accomplished by a hydrolysis-based mechanism, i.e. secondary electrons generated by the primary 10 MeV primary electrons, primarily split water (H2O → H+ + OH−) (beyond chain scission to some minor extends). The resulting H+ and OH− radicals successively attack collagen side groups, resulting - as demonstrated by us for porcine/rat-tail collagen blends - primarily in biomimetic crosslinking via tropocollagen lysine side groups, while the backbone chains are kept intact.32Clearly it is reasonable to assume, that the same energetic electron induced processes prevail also in presence of a prestress, i.e. crosslinks are expected to be introduced into the prestressed sample. However, the loci of the introduced crosslinks certainly will depend on the local network configuration, viz. local distances and displacement fields, which are related to global strains in a non-affine manner. Even though this relation certainly is expected to be complex, introduced covalent crosslinks certainly imprint (or, program) the local network configuration related to a global strain state - and then prevails even in absence of global stresses. Thus energetic electron treatment at increasing strains is expected to result in increasingly unisotropic, covalently crosslinked collagen networks with fibers increasingly aligned along the prestraining direction.
This picture is, in fact, confirmed by our polarized light microscopy measurements (Fig. 5), that demonstrate an increased degree of axial fiber alignment for increasing prestrains and electron doses. Selective absorption or transmission of different wavelengths or polarizations of light at different orientations of the sample suggests the presence of optical phenomena called dichroism (Fig. 6). In parallel, these measurements indicate Mie and Rayleigh scattering due to the small-scale structures in collagen.47–49 Several effects are to be expected that cause a change in the area under the curve due to a higher prestrain. Firstly, the geometric properties of the sample are changed by the prestrain. Secondly, the morphology of the samples changes as a result of the prestrain. By increasing the anisotropy with an alignment of the internal collagen fibrils measured with polarization microscopy, a change in intensity can be observed. Polarization microscopy shows in particular the angle dependence of the intensity, which means that certain wavelengths are less intense depending on the angle. All colors must be considered when analyzing the alignment, as on the one hand a white light source with a non-monochromatic spectrum was used, and on the other hand scattering effects can occur in the material, which means that a certain wavelength does not locally characterize the material property at a certain point. The analysis here is qualitative, with a laser setup spatial heterogeneity of the material could be analyzed even more precisely. Nevertheless, a higher angular dependence, i.e. a defined intensity maximum at a certain angle with a minimum curve width, can be used to interpret the measurements as a higher alignment of the collagen fibrils in the collagen fiber.
In a study by Cheung et al.,50 radioactively labeled tissue treated by glutaraldehyde and a diamine crosslinking process was subcutaneously implanted in rats, whereby the amount of radioactivity remaining in the tissue, indicative of resistance to biodegradation, was monitored over a period of one year. The breakdown of a biomaterial in vivo is caused by either a chemical degradation or a mechanical wear-and-tear induced or enhanced by host immune response, calcification, specific cellular or enzymatic degradative processes.50 In the case of a collagenous matrix, chemical degradation, namely proteolysis is the major cause of breakdown.50 Although native helical collagen molecules and fibers are very resistant to proteases (except collagenases), any damage on any of the polypeptide chains within a molecule will cause the whole molecule to unwind and degrade quickly.50 Mechanical stress or strain on the biopolymer in vivo may influence unwinding processes.50 Crosslinks stabilize collagen as well as other macromolecules by allowing the partially cleaved peptides to remain folded in their native state.50 Conversely, for long-term stability, the unwinding process of the collagen molecule, which in particular is (a) chemically or (b) mechanically induced, must be inhibited.
Concerning (a), native collagen generally has an isoelectric point near neutral pH, which means that it has poor water solubility under physiological conditions.51 The pH and ionic strength of the suspending medium clearly affect the collagen solubility and also affect the relaxation of isometric forces caused by heating.52 However, in collagenase solution the degree of enzymatic degradation of collagen hydrogels after immersion depends strongly on the crosslink density.53 The resistance to collagenase of the cross-linked collagen hydrogels is greater than that of the native hydrogel.53 This could be explained by the structural changes induced by cross-linking bonds.53,54 Brodsky et al.53,55 reported that the degradation was initiated by the cleavage of peptide bond at the site between residues 775 and 776 (Gly-Leu) in collagen triple helical domain due to collagenase. The fibrillar structure of collagen hydrogel became more compact via cross-linking and this steric hindrance decelerated the enzymatic degradation due to the inhibition of diffusion of collagenase to the cleavage sites.53,56,57 As demonstrated by us,32 at moderate doses crosslinks introduced into collagen due to application of energetic electrons are very much similar to crosslinks introduced biochemically under physiological conditions. Due to this biomimicry, we expect live expectancy of our crosslinks to be comparable to those introduced in vivo if not exposed to solubilizing enzymes or acidic conditions as mentionend above.
Regarding (b), a mechanically induced degradation of high-energy electron beam cross-linked collagen fibers, we refer to the relaxation analyses of the cyclic tests. Extrapolation of the fitted relaxation curves on more than 30 days using the optimised parameters from the adapted KWW function leads to stresses above 0.04 MPa and 0.22 MPa for 5 kGy without prestrain and for 5 kGy with 60% prestrain, respectively, being in the same order of magnitude and close to the stress of the first cycle in the respective loop of the measurement. Thus, the extrapolated data of the stretched exponential fit do not contradict long-term stability under repetitive load in an aqueous solution. However, the above-mentioned chemical effects can influence the morphology of the collagen fibres under permanent load in parallel to the mechanical degradation. Further experimental investigations under varying physiologically relevant conditions are required on the collagen system investigated here to monitor phenomena affecting the cross-link structure.
In terms of mechanics, it is noteworthy that our as-extruded collagen networks are largely isotropic subisostatic networks, whose mechanical response is established to be largely dominated by network topology and flexural moduli of fibers composing the network. With increased axial fiber alignment, uniaxial mechanical response is expected to be increasingly governed by axial Young's moduli of individual collagen fibers. In our mechanical measurement this scenario is, in fact, observed e.g. by an increase of the maximum Young's modulus by more than one order of magnitude when applying prestrain during exposure to an electron dose of 25 or 50 kGy (Fig. 1). Transition from a subisostatic random network to aligned fibers is also reflected by hysteresis, viz. energy dissipation. While it is established that subistostatic random networks (as the one obtained by our initial extrusion process) contain a large amount of floppy modes that dissipate energy during cycling, the latter are increasingly removed due to prestrain and electron induced crosslinking, viz. degeneracy regarding floppy modes is successively reduced. Within our cyclic mechanical tests this is reflected by a reduction of energy dissipation upon measuring cyclically, or, reduced broadness of hysteresis, or, equivalently, reduced imaginary part of the complex Young's modulus (Fig. 3).
Long-term swelling tests with collagen fibers were not carried out, although based on our previous work we expect a Flory–Rehner type of swelling behavior, in which osmotic pressure is balanced by network stresses, which, however, are genererated largely not entropically as in the original work, but by the more complex mechanical response of our electron beam crosslinked semiflexible collagen network, leading to reduced swelling with increasing mechanical stiffness. The collagen fibres were crosslinked in the fully hydraded state, whereby no instabilities were observed. Furthermore, the mechanical measurements of crosslinked fibers were also performed in the fully hydrated state after a swelling in distilled water, whereby no signs of disintegration were observed. However, studies have shown that collagen can denature in water at temperatures of around 80 °C, regardless of possible crosslinking techniques.58 Our experiments were carried out at room temperature; the temperature was only exceeded during synthesis in a buffer at 36 °C and during irradiation, where local temperature peaks can occur. It is known that high temperatures in particular can have an influence on the denaturation of collagen.59 It is therefore to be expected that at temperatures higher than body temperature and high hydration states, the material properties may change, which could be investigated in detail in further long-term studies.
Regarding cell tests, our research group has carried out comprehensive studies on collagen scaffolds crosslinked with high-energy electrons. High cell viability and exceptional biocompatibility were observed even after modification with electron beams.25 Compared to chemical crosslinking methods, no cytotoxic by-products are to be expected and thus an improvement in cell concerning properties. Further studies might provide a deeper understanding of collagen-cell interactions and thus future experiments need to be conducted.
Above, we have established a picture on how energetic electrons efficiently crosslink collagen and how this can be utilized to fixate fiber alignment with the help of prestrains. Despite preferential crosslinking sites via lysine side groups, energetic electron induced crosslinking remains a largely stochastic process regarding spatial distribution of the resulting crosslinks. These inherent spatial fluctuations in crosslink distributions will certainly lead to fluctuations in the energetics of activated processes, viz. increase temporal heterogeneity in thermally activated processes due to spatial heterogeneities. Generally, increasing presence of heterogeneities is reflected by increasing streched exponential relaxation behavior, i.e. increasing deviation of the Kohlrausch exponent β ≤ 1 from β = 1 (eqn (2)). In fact, upon increasing electron dose, decreasing Kohlrausch exponents β are observed, consistent with this interpretation (Fig. 4).
In short term, applications as suture in medical surgeries seem in reach. In the long term, the synthesis of artificial tendons or ligaments clearly is a vision. However, as the mechanical response in tendons and ligaments is governed by the complex hierarchical collagen structure, further structural tuning employing several steps in synthesis and radiation gradients will be key aspects to come closer to mimic biological response.
5 Conclusion
Within the present work we have demonstrated how application of mechanical strains during energetic electron assisted crosslinking of collagen can be employed to design anisotropic fibers with variable degree of axial network fiber alignment. While we have verified that programming of fiber alignment is feasible with this approach using polarized light microscopy, it allows for the design of highly customized collagen fibers with tailorable anisotropy and mechanical properties. Our presently reported finding thus paves the way for synthesizing advanced biomimetic scaffolds of highly variable anisotropy and mechanical response, potentially suitable for a broad range of applications in biomedicine.6 List of abbreviations
| PLM | Polarized light microscopy |
| FFB | Fiber formation buffer |
| PTFE | Polytetrafluoroethylene |
| LED | Light-emitting diode |
| UTS | Ultimate tensile strength |
| LED | Light-emitting diode |
| KWW | Kohlrausch–Williams–Watt function |
| RGB | RGB color model |
| ESEM | Environmental scanning electron microscope |
Availability of data and materials
The datasets used and/or analyzed during the current study are available from the corresponding authors on reasonable request.Authors’ contributions
Anastassiya Bublikova: investigation, conceptualization, data curation, methodology, visualization, writing – original draft, writing – review & editing. Friedrich Schütte: conceptualization, methodology, supervision, visualization, writing contribution to the original draft, writing – review & editing. Stefan G. Mayr: project idea, funding acquisition, supervision, project administration, writing – review & editing. Anastassiya Bublikova and Friedrich Schütte contributed equally to this work. All authors read and approved the final manuscript.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
Funding from the German Research Foundation (DFG), project MA 2432/6-3, and by the Open Access Publishing Fund of Leipzig University is gratefully acknowledged. We thank Prof. Dr Mareike Zink (University of Leipzig) for providing access to the ZwickRoell mechanical tester and laboratories for sample preparation and discussions. We thank Bernd Kohlstrunk (University of Leipzig) and the workshop of the Faculty of Physics (University of Leipzig) as well as Stefan Daum (IOM) and Florian Hager (IOM) for support in the development of the experimental setup. We acknowledge Robert Konieczny (IOM) for technical support by performing routine electron beam irradiation according to our previous protocols. We thank Prof. Dr Friedrich Kremer for fruitful discussions. This project was partially performed within the Leipzig Graduate School of Natural Sciences - Building with Molecules and Nano-objects (BuildMoNa).Notes and references
- M. C. Catoira, L. Fusaro, D. Di Francesco, M. Ramella and F. Boccafoschi, J. Mater. Sci.: Mater. Med., 2019, 30, 115 CrossRef PubMed.
- C. Frantz, K. M. Stewart and V. M. Weaver, J. Cell Sci., 2010, 123, 4195–4200 CrossRef CAS PubMed.
- J. A. Ramshaw, P. R. Vaughan and J. A. Werkmeister, Biomed. Eng., 2001, 13, 14–26 Search PubMed.
- T. Rozario and D. W. DeSimone, Dev. Biol., 2010, 341, 126–140 CrossRef CAS PubMed.
- M. Shoulders and R. Raines, Annu. Rev. Biochem., 2009, 78, 929–958 CrossRef CAS PubMed.
- S. A. Sell, P. S. Wolfe, K. Garg, J. M. McCool, I. A. Rodriguez and G. L. Bowlin, Polymers, 2010, 2, 522–553 CrossRef CAS.
- K. E. Kadler, C. Baldock, J. Bella and R. P. Boot-Handford, J. Cell Sci., 2007, 120, 1955–1958 CrossRef CAS PubMed.
- J. Lin, Y. Shi, Y. Men, X. Wang, J. Ye and C. Zhang, Tissue Eng., Part B, 2020, 26, 116–128 CrossRef CAS PubMed.
- K. Gelse, E. Pöschl and T. Aigner, Adv. Drug Delivery Rev., 2003, 55, 1531–1546 CrossRef CAS PubMed.
- C. Söderhäll, I. Marenholz, T. Kerscher, F. Rüschendorf, J. Esparza-Gordillo, M. Worm, C. Gruber, G. Mayr, M. Albrecht, K. Rohde, H. Schulz, U. Wahn, N. Hubner and Y.-A. Lee, PLoS Biol., 2007, 5, 1–10 CrossRef PubMed.
- S. H. Liu, R.-S. Yang, R. Al-Shaikh and J. M. Lane, Clin. Orthop. Relat. Res., 1995, 318, 265–278 Search PubMed.
- C. Lovell, K. Smolenski, V. Duance, N. Light, S. Young and M. Dyson, Br. J. Dermatol., 1987, 117, 419–428 CrossRef CAS PubMed.
- S. Münster, L. M. Jawerth, B. A. Leslie, J. I. Weitz, B. Fabry and D. A. Weitz, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 12197–12202 CrossRef PubMed.
- B. A. Roeder, K. Kokini, J. E. Sturgis, J. P. Robinson and S. L. Voytik-Harbin, J. Biomech. Eng., 2002, 124, 214–222 CrossRef PubMed.
- C. Storm, J. J. Pastore, F. C. MacKintosh, T. C. Lubensky and P. A. Janmey, Nature, 2005, 435, 191–194 CrossRef CAS PubMed.
- D. M. Knapp, V. H. Barocas, A. G. Moon, K. Yoo, L. R. Petzold and R. T. Tranquillo, J. Rheol., 1997, 41, 971–993 CrossRef CAS.
- S. Noorzai, C. J. R. Verbeek, M. C. Lay and J. Swan, Waste Biomass Valorization, 2020, 11, 5687–5698 CrossRef CAS.
- J. Chen, K. Gao, S. Liu, S. Wang, J. Elango, B. Bao, J. Dong, N. Liu and W. Wu, Mar. Drugs, 2019, 17, 33 CrossRef CAS PubMed.
- Y. Kato, D. L. Christiansen, R. A. Hahn, S.-J. Shieh, J. D. Goldstein and F. H. Silver, Biomaterials, 1989, 10, 38–42 CrossRef CAS PubMed.
- W. Liu, K. Merrett, M. Griffith, P. Fagerholm, S. Dravida, B. Heyne, J. C. Scaiano, M. A. Watsky, N. Shinozaki, N. Lagali, R. Munger and F. Li, Biomaterials, 2008, 29, 1147–1158 CrossRef CAS PubMed.
- V. Chak, D. Kumar and S. Visht, Int. J. Pharm. Teach. Pract., 2013, 4, 811–820 Search PubMed.
- Y. Zhang, Y. Wang, Y. Li, Y. Yang, M. Jin, X. Lin, Z. Zhuang, K. Guo, T. Zhang and W. Tan, Gels, 2023, 9, 185 CrossRef CAS PubMed.
- G. Liu, R. Agarwal, K. Ko, M. Ruthven, H. Sarhan and J. Frampton, Sci. Rep., 2017, 7, 9628 CrossRef CAS PubMed.
- L. Fan, Y. Ren, S. Emmert, I. Vučkovicć, S. Stojanovic, S. Najman, R. Schnettler, M. Barbeck, K. Schenke-Layland and X. Xiong, Int. J. Mol. Sci., 2023, 24, 3744 CrossRef CAS PubMed.
- S. Riedel, P. Hietschold, C. Krömmelbein, T. Kunschmann, R. Konieczny, W. Knolle, C. T. Mierke, M. Zink and S. G. Mayr, Mater. Des., 2019, 168, 107606 CrossRef CAS.
- N. E. Ben Ammar, T. Saied, M. Barbouche, F. Hosni, M. Adel and M. Sen, Polym. Bull., 2018, 75, 3825–3841 CrossRef CAS.
- I. Sallent, H. Capella and D. Zeugolis, Production and Characterization of Chemically Cross-Linked Collagen Scaffolds: Methods and Protocols, Springer, 2019, vol. 1944, pp. 23–38 Search PubMed.
- M. Nair, S. M. Best and R. E. Cameron, Appl. Sci., 2020, 10, 6911 CrossRef CAS.
- A. Bigi, G. Cojazzi, S. Panzavolta, K. Rubini and N. Roveri, Biomaterials, 2001, 22, 763–768 CrossRef CAS PubMed.
- D. P. Speer, M. Chvapil, C. D. Eskelson and J. B. Ulreich, J. Biomed. Mater. Res., 1980, 14(6), 753–764 CrossRef CAS PubMed.
- J. E. Gough, C. A. Scotchford and S. Downes, J. Biomed. Mater. Res., 2002, 61, 121–130 CrossRef CAS PubMed.
- N. Wilharm, M. Bertmer, W. Knolle, J. Griebel, C. Elsner and S. G. Mayr, Acta Biomater., 2022, 140, 219–232 CrossRef CAS PubMed.
- S. Riedel, K. Bela, E. I. Wisotzki, C. Suckfull, J. Zajadacz and S. G. Mayr, Mater. Design, 2018, 153, 80–85 CrossRef CAS.
- E. I. Wisotzki, M. Hennes, C. Schuldt, F. Engert, W. Knolle, U. Decker, J. A. Käs, M. Zink and S. G. Mayr, J. Mater. Chem. B, 2014, 2, 4297–4309 RSC.
- J. A. Paten, S. M. Siadat, M. E. Susilo, E. N. Ismail, J. L. Stoner, J. P. Rothstein and J. W. Ruberti, ACS Nano, 2016, 10, 5027–5040 CrossRef CAS PubMed.
- C. Guo and L. J. Kaufman, Biomaterials, 2007, 28, 1105–1114 CrossRef CAS PubMed.
- Y. Eguchi, S. Ohtori, M. Sekino and S. Ueno, Bioelectromagnetics, 2015, 36, 233–243 CrossRef CAS PubMed.
- C. Chaubaroux, F. Perrin-Schmitt, B. Senger, L. Vidal, J.-C. Voegel, P. Schaaf, Y. Haikel, F. Boulmedais, P. Lavalle and J. Hemmerlé, Tissue Eng., Part C, 2015, 21, 881–888 CrossRef CAS PubMed.
- D. Vader, A. Kabla, D. Weitz and L. Mahadevan, PLoS One, 2009, 4, e5902 CrossRef PubMed.
- R. Oldenbourg, Cold Spring Harbor Protocols, 2013, 2013, pdb.top078600 CrossRef PubMed.
- Leica DM2700 M Instructions.
- T. Golde, M. Glaser, C. Tutmarc, I. Elbalasy, C. Huster, G. Busteros, D. M. Smith, H. Herrmann, J. A. Käs and J. Schnauß, Soft Matter, 2019, 15, 4865–4872 RSC.
- G. Van Rossum and F. L. Drake, Python 3 Reference Manual, CreateSpace, Scotts, Valley, CA, 2009 Search PubMed.
- R. June, C. Neu, J. R. Barone and D. Fyhrie, Mater. Sci. Eng., C, 2011, 31, 781–788 CrossRef CAS PubMed.
- R. K. June and D. P. Fyhrie, Comput. Methods Biomech. Biomed. Eng., 2013, 16, 565–576 CrossRef PubMed.
- F. Schütte and S. Mayr, ACS Biomater. Sci. Eng., 2024, 10(2), 782–790 CrossRef PubMed.
- S. L. Jacques, Adv. Opt. Imaging Photon Migr., 1996, OPC364 Search PubMed.
- A. P. M. Michel, S. Liakat, K. Bors and C. F. Gmachl, Biomed. Opt. Express, 2013, 4, 520–530 CrossRef PubMed.
- Z. Gajinov, M. Matić, S. Prćić and V. Duran, Serbian J. Dermatology Venereol, 2013, 2, 131–136 Search PubMed.
- D. T. Cheung, D. Tong, N. Perelman, D. Ertl and M. E. Nimni, Connect. Tissue Res., 1990, 25, 27–34 CrossRef CAS PubMed.
- Y. Junhui, C. Ding, L. Tang, F. Deng, Y. Qili, H. Wu, L. Chen, Y. Ni, L. Huang and M. Zhang, ACS Omega, 2020, 5(11), 5772–5780 CrossRef PubMed.
- M. E. Latorre, A. L. Lifschitz and P. P. Purslow, Meat Sci., 2016, 118, 78–81 CrossRef CAS PubMed.
- Z. Tian, W. Liu and G. Li, Polym. Degrad. Stab., 2016, 130, 264–270 CrossRef CAS.
- S. Park, J. Park, H. Kim, M. Song and H. Suh, Biomaterials, 2002, 23, 1205–1212 CrossRef CAS PubMed.
- B. Brodsky and J. A. Ramshaw, Matrix Biol., 1997, 15, 545–554 CrossRef CAS PubMed.
- H. Saito, T. Taguchi, H. Kobayashi, K. Kataoka, J. Tanaka, S. Murabayashi and Y. Mitamura, Mater. Sci. Eng. C, 2004, 24, 781–785 CrossRef.
- D. P. Speer, M. Chvapil, C. D. Eskelson and J. B. Ulreich, J. Biomed. Mater. Res., 1980, 14(6), 753–764 CrossRef CAS PubMed.
- Y. Suwa, K. Nam, K. Ozeki, T. Kimura, A. Kishida and T. Masuzawa, J. Biomed. Mater. Res., Part B, 2016, 104, 538–545 CrossRef CAS PubMed.
- L. Bozec and M. Odlyha, Biophys. J., 2011, 101, 228–236 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma01111a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |