Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Thermally-induced charge carrier population control on graphene nanoribbons†
Tiago de Sousa Araújo
Cassiano
 a,
Geraldo Magela
e Silva
a,
Geraldo Magela
e Silva
 *a and
Pedro Henrique de Oliveira
Neto
*a and
Pedro Henrique de Oliveira
Neto
 ab
ab
aInstitute of Physics, University of Brasília, 70919-970, Brasília, Brazil. E-mail: magela@unb.br
bInternational Center of Physics, University of Brasília, 70919-970, Brasília, Brazil
First published on 26th February 2024
Abstract
Organic thermoelectric devices allow the conversion of heat into electricity in a sustainable way, making them strong candidates to solve the present energy crisis. In this context, integrating graphene nanoribbons (GNRs) into thermoelectrics holds great potential for addressing this challenge. The development of a physical description of charge carriers under thermal influence is a paramount step toward this objective. However, to this day, the effects of temperature on charged quasiparticles hosted on GNRs remain elusive. In this work, we propose an adaptation to the long-established Su–Schrieffer–Heeger (SSH) model Hamiltonian to accommodate thermal effects on GNRs. The results show that random lattice deformations can significantly alter polarons’ and bipolarons’ localization profiles. Moreover, we report a thermally-induced re-balance of carrier stability. As temperature increases, the probability of observing bipolarons decays in favor of the formation of two independent polarons. The results are especially relevant to Seeback-based thermoelectrics because they rely on temperature gradients. With the thermal stability of charge carriers, local thermal differences could regulate GNR-based currents with quasiparticle population control.
1 Introduction
The interest in thermoelectric devices has been revigorated in recent years. The potential of direct energy conversion from heat to electricity offers a promising avenue for addressing the current energy crisis.1 In this sense, organic-based apparatuses are particularly attractive due to their inherent flexibility, low weight, low cost, and sustainable production.2 With the recent rise of 2D materials, the idea of envisioning future organic thermoelectric applications with them is gaining momentum.Since the isolation of graphene about 20 years ago, 2D materials have been driving a revolution in materials science. Graphene derivatives play a special role in this development. Most of their appeal resorts to the emergence of unique quantum phenomena after simple structural/environmental changes.3–10 Nowadays, this attribute is the core of novel optoelectronic devices. Concerning semiconducting apparatuses, graphene nanoribbons (GNRs) stand out as the flagship choice in ultra-narrow applications. Among the many edge shapes,3,11 the armchair type (AGNR) has an encouraging prospect, already integrating novel devices.5,11,12 Given this scenario, using GNRs in next-generation thermoelectric devices is a natural path to proceed.13
Charge transport is fundamental for the description of the thermoelectric effect. In organic materials, the mechanism is driven by charged quasiparticles. They are polarized defects coupled with phonon clouds resulting from the collective response of the system.14,15 The polaron, a half-spin structure of charge e, is usually the main carrier during transport. Besides its importance, other high-order quasiparticles can emerge during the transport mechanism. In a highly doped configuration,16,17 two independent polarons can merge together, recombining into a new carrier known as a bipolaron.18 This bosonic quasiparticle has twice the polaron's charge. Naturally, it is an active carrier with its own transport and magnetic properties. Importantly, bipolarons also participate in photonic mechanisms19 because the scattering process may induce the formation of excitonic quasiparticles.16,18,20 Therefore, the stability of polarons and bipolarons reverberates in electronic and optical performance.
Importantly, due to the coupled nature of a charged quasiparticle, its shape and stability directly impact the mobility and effective mass. Therefore, characterizing charge carriers allows to predict performance capabilities and provides new insights into transport mechanisms. Such a strategy had previously led to important results for conjugated polymers,21–24 GNRs,6,25–27 and molecular crystals.28,29
However, describing the charge carriers is not enough to understand thermoelectric effects. A realistic physical description requires an explicit consideration of thermal response. Substantial effort was directed to developing adequate strategies.30 The lattice can be highly sensitive to thermal influence, making the use of hybrid Hamiltonians, with explicit electronic and lattice interactions, a desirable approach.30 The matter is especially relevant when considering systems with a strong electron–phonon coupling. In a hybrid Hamiltonian approach, one can model thermal effects as random distortions of the lattice bonds.31–33 In this context, the Su–Schrieffer–Heeger hybrid Hamiltonian15,34 is a robust framework to investigate thermal mechanisms in quantum systems, being the backbone of important studies.31,32,35–37
Progress was made through this route, which helped uncover the functioning of intricate phenomena in highly confined materials. For instance, with a mixed 1D Hamiltonian, Troisi recovered the long-established mobility power law dependence with temperature in rubrene crystals.28,29 Other studies reported a thermal-assisted reduction of electron–hole pair binding energy,32 the hampering of polaron stability,33,36 and shortening of quasiparticle recombination37 in conjugated polymers. These works demonstrate that the theoretical investigation of thermal properties holds a latent potential to elucidate and provide insights in nanoelectronics and photonics. However, besides the importance of GNRs, the impact of thermal influence over its charge carriers remains an open topic.
In this work, we simulate the formation of polarons and bipolarons on armchair graphene nanoribbons under several temperature regimes. The model consists of an adaptation of the SSH hybrid Hamiltonian. The proposed modification aims to consider thermal effects as bond distortions. We selected four armchair nanoribbons with different widths to implement the study. Bipolaron stability is determined. The results show that raising the temperature can progressively hamper bipolaron cohesion, favoring the formation of independent polaron pairs instead. Additionally, we report an increase of 25% of polarons for a temperature variation of 150 K. The results could benefit future thermoelectric applications based on the Seeback effect while providing a phyisically accurate description of charge carriers under thermal influence.
2 Methodology
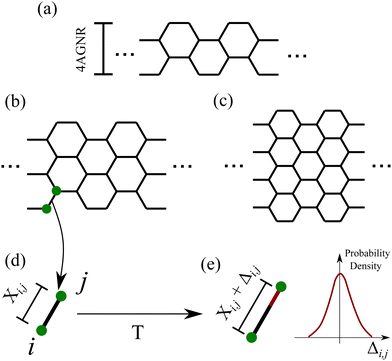
Four armchair nanoribbons were simulated. Three of them are illustrated in Fig. 1. Fig. 1(a), (b), and (c) present, respectively, the 4, 6, and 9AGNR structures. Their labels correspond to the number of carbon atoms along the width axis, as demonstrated in Fig. 1(a) for the 4AGNR. For each GNR, the SSH model Hamiltonian H consists of the sum of the lattice (Hlatt) and electronic (Helec) contributions:15,22,23,34| H = Hlatt + Helec | (1) |
The former is modeled under the Harmonic approximation, reading8,38,39
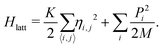 | (2) |
Here, K is the harmonic constant, M is the site mass, Pi is the conjugated momentum of the i-th site, and ηi,j is the deformation of the bond connecting sites i and j. The bracket at the lower sum index indicates a summation over neighboring bonds.
The electronic part is treated through a tight-binding formalism, which models the π-electron hopping as38
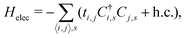 | (3) |
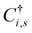 and Ci,s stand for the creation and annihilation operator of a π-electron with spin s at the i-th site. In addition, ti,j is the hopping integral linking sites i and j. Here, h.c. stands for the hermitian complex. Both the lattice and electronic interactions are subjected to periodic boundary conditions.
and Ci,s stand for the creation and annihilation operator of a π-electron with spin s at the i-th site. In addition, ti,j is the hopping integral linking sites i and j. Here, h.c. stands for the hermitian complex. Both the lattice and electronic interactions are subjected to periodic boundary conditions.
The electronic and lattice interactions are coupled through a first-order expansion of the hopping integral in the pristine configuration (t0):15,21,34
| ti,j = (t0 − αηi,j). | (4) |
The lattice coupling to the hopping integral is determined by the electron–phonon coupling α.
Following the Ehrenfest Theorem, the lattice solution can be obtained by solving the Euler–Lagrange equations of the expected value of the Lagrangian.8,21,38 In the case of stationary configurations, when no kinetic interaction is considered (Pi = 0), the minimization condition simplifies to:
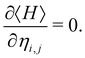 | (5) |
Here, 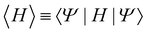 is the expected value of the potential energy. The state
is the expected value of the potential energy. The state 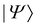 is a Slater determinant formed by the occupied π-electron orbitals. After explicit manipulation, this expression turns into38
is a Slater determinant formed by the occupied π-electron orbitals. After explicit manipulation, this expression turns into38
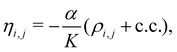 | (6) |
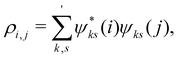 | (7) |
Since the Hamiltonian explicitly depends on the lattice configuration, a self-consistent algorithm is applied to solve the hybrid model.8 The procedure begins by choosing an appropriate guess for the bond distortion set {ηi,j} (which is usually taken as 0). Then, Helec can be numerically built and diagonalized, yielding the corresponding eigenvectors and eigenvalues. The new electronic solution is then applied to recalculate {ηi,j} according to eqn (6). Then, the newly calculated lattice configuration is compared with the previous set. This involves calculating the root mean squared error between the two solutions. If the difference is below a preset threshold, the algorithm stops. Otherwise, the procedure repeats by using the updated {ηi,j} in the initial step.
Charge states are obtained by removing the electrons from the material. This means extracting spin–orbitals from the neutral state Slater determinant. For instance, a positive polaron is created after removing an electron occupying the highest occupied molecular orbital (HOMO). In turn, a positive bipolaron emerges after removing two electrons from the HOMO. The corresponding carriers with a negative charge are obtainable by adding electrons to the unoccupied molecular orbital (LUMO). Importantly, the positive and negative quasiparticles are bound to exhibit the same properties due to the electron–hole symmetry.
The parameters of the model Hamiltonian are based on previous studies on AGNRs and similar conjugated systems. That is t0 = 2.7 eV,4,40K = 21 eV Å−2,34,41 and α = 5.2 eV Å−1.26,39,42,43
A. Thermal effects
Temperature effects can be modeled as noise distortions around the stationary lattice configuration.30–32 Suppose that the stationary algorithm yields a lattice configuration in which the sites i and j are linked by a bond with a length of Xi,j. The thermal-corrected bond length for a temperature T is the sum of a random disturbance (Δki,j(T)) to Xi,j:| Xki,j(T) = Xi,j + Δki,j(T), | (8) |
However, it is always possible to recognize ηi,j into Xi,j because they differ only by a constant. In other words,
| Xi,j = L0 + ηi,j, | (9) |
Because of that, the lattice changes due to thermal effects can be thought as corrections to the bond length distortion, turning each ηi,j into
| ηki,j(T) = ηi,j + Δki,j(T). | (10) |
The Δki,j(T) is sampled according to the Boltzmann probability distribution:30,32,33
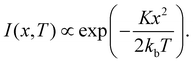 | (11) |
Here, kb is the Boltzmann constant and x is the distortion random variable. For each ensemble member, the sampling is done on all existing bonds. The process consists of two steps: (1) for each bond, an x value is sampled from the distribution in eqn (11) through the Box–Muller algorithm; (2) the distortions are implemented in the lattice, rendering a new set {η}. Then, Helec is diagonalized using the updated lattice, yielding the corrected eigenvalues and eigenvectors of this particular configuration. Finally, ensemble statistics will provide the physical description of the GNRs. As a side remark, we recall that the normalization of the distribution is irrelevant for the sampling because it is a common factor for all x at a fixed T.
Fig. 1(d) and (e) illustrate the sampling procedure. In Fig. 1(d), the converged bond length Xi,j connects the sites i and j. For a finite temperature T, Xi,j is corrected by a random distortion Δi,j that is sampled from the distribution in eqn (11). The result is a bond distorted from its equilibrium length, as shown in Fig. 1(e). This process is repeated for all unique bonds, giving one ensemble member as the end result. By repeating the procedure, an ensemble of GNR configurations is generated. Their collective response will translate into the physical description of the material under thermal effects.
All cases were simulated by constructing ensembles with 5000 members. This number was found to be adequate after verifying the statistical robustness of averaging processes. Fig. S1 (ESI†) illustrates this test. The variation of the total energy in the neutral, polaron and bipolaron states is presented in Fig. S1(a), (c) and (d) (ESI†). The solid lines represent the energy of a given ensemble element, while the dashed lines are the corresponding cumulative averages. As can be seen, the solid curves display an oscillating behavior. On the other hand, the dashed lines are stable, exhibiting no significant changes when the ensemble has more than 1000 elements. Therefore, any succeeding quantity that relies solely on the total energies should be equally stable.
We emphasize that a small ensemble can lead to an underrepresented thermal response. To see this, we present the zoomed versions of Fig. S1(a), (c) and (d) (ESI†), respectively, in Fig. S1(b), (d) and (e) (ESI†). As can be seen, the dashed curves are not straight lines anymore. For a small ensemble, the cumulative mean is not stable.
In the following discussion, the k index will be suppressed when its presence is not relevant. We emphasize that ordering the ensemble geometries has no physical meaning and is only important for the sake of clarity and practical reasons. Finally, all the simulated results obtained using the traditional model (with no explicit consideration of thermal effects) will be referred to as the “0 K” case.
In addition, we recall that in general, thermal effects influence the electrons through changes in the electronic occupation. Since electrons are fermionic particles, the Fermi–Dirac distribution determines the temperature dependence of the occupation. This effect was not included because all the simulated GNRs are intrinsic semiconductors, with a gap of ≈1–3 eV. In such cases, a significant modification in the electronic occupation is only visible for thermal baths at high temperatures ≈5000 K. Since we are concerned with near-ambient temperatures, the occupation change is negligible. Naturally, the situation can drastically change when dealing with semimetals, metals, and highly doped semiconductors. For those materials, even a low-temperature reservoir can thermally excite electrons to the conduction band. The impact of thermal effects on the electronic occupation depends on the actual density of charge carriers. In a high-density charge carrier regime, the system has many particles at the conductance (or valence) band. In such cases, occupation changes become relevant because there is a large number of particles to fill the vacant states. On the other hand, the intra-band excitation, although present, has a minimal impact. This is because it alters the occupation of only a few electrons (or holes).
Note that this does not mean that electrons are insensitive to thermal effects in the model. We recall that the electronic Hamiltonian has a contribution from the lattice through the electron–phonon coupling. Therefore, the thermal distortions in the sites’ positions reverberate due to the electronic eigenstates and eigenvalues.
B. Bipolaron stability
The bipolaron binding energy (BE) can be estimated as the energy difference between the bipolaron formation energy (FEbip) and two times the polaron formation energy (FEpol):44| BE = FEbip − 2FEpol, | (12) |
| FEbip = SCFbip − SCFneutr and |
| FEpol = SCFpol − SCFneutr. | (13) |
Here, SCFbip/pol is the self-consistent energy obtained from the stationary algorithm for the bipolaron/polaron state. In a similar manner, SCFneutr is the corresponding energy for the neutral configuration. If BE > 0, the formation of two independent polarons is energetically more favorable than a single bipolaron. In other words, bipolaron formation would occur only with the aid of an external agent. When BE < 0, the opposite becomes true: bipolarons are expected to form spontaneously.
It is important to note that SCFbip, SCFpol, and SCFneutr are distributions when considering thermal effects. Each state is represented by an ensemble of 5000 separate calculations. For this reason, eqn (12) needs to be adapted. First, it is important to realize that each ensemble member shares the same probability of being observable. In addition, BE should be a distribution that obeys eqn (12). Therefore, BE calculation is done by the sampling values obtained from FEbip and FEpol and applying them to eqn (12). However, although independent in principle, the polaron and bipolaron formation energies cannot be sampled separately for BE calculation. During each selection process, the same SCFneutr sampled energy was used to calculate both FEbip and FEpol. That way, we avoid the consideration of artificial recombinations involving ground-state lattice reorganization.
C. Dimerization ratio
An important feature of conjugated materials is the dimerization of neighboring bonds. Its presence is a sign of lattice cohesion and can be associated with optical/electronic properties.15,45 For this reason, tracking changes on this attribute can be a potential source for new insights. Here, we propose a simple calculation to estimate dimerization. For an ensemble of size Nens and a GNR with L bonds, the dimerization ratio (DR) is: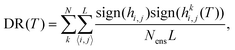 | (14) |
3 Results
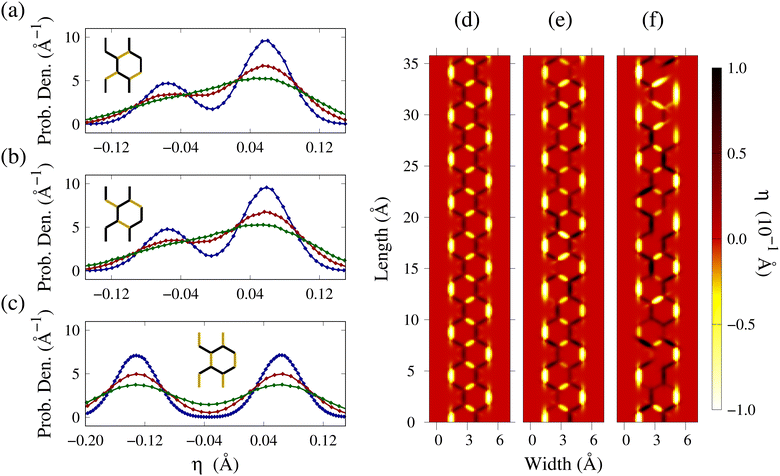
Our study begins by considering the effects of temperature in neutral AGNRs. The results will serve as a reference for the succeeding analysis on charged states. Fig. 2 displays the thermal influence on the 4AGNR's lattice. Fig. 2(a)–(c) exhibit the distortion distribution for the three types of bonds present in the hexagonal lattice: the trans (/), cis (\) and vertical (|), respectively. Near each distribution plot, a GNR slice is placed with the corresponding bond type highlighted in yellow. The colors of the curves indicate the temperature: 95 K (blue), 197 K (red), and 350 K (green). As can be seen, all three blue curves contain two distinguished peaks, one centralized in the η > 0 region and the other in the negative zone. The bond distortion length associated with each peak corresponds to the unique bonds at 0 K. As the temperature rises, the probability density drops around the peaks and the distribution begins to spread over. This is a direct result of sampling the bonds using eqn (11) because the standard deviation is proportional to the temperature.It is also suggested to look at the order parameter heatmap of ensemble members. Fig. 2(d)–(f) correspond to 0 K, 95 K and 350 K, respectively. For all cases, dark tones indicate a bond expansion, while light colors represent a contraction. Bonds in red display no distortion. When temperature is not considered, the 4AGNR bonds form an alternating pattern, intercalating between contraction and expansion along the width lines. This is the dimerization effect, which is widely reported for GNRs8,38 and other conjugated materials such as polymers.15,34 As the temperature increases, this pattern is progressively destroyed. Some bonds that were once contracting at 0 K start expanding now and vice versa. Another possibility is for the bond to display no distortion at all, indicated by the color red. The results show that thermal effects can significantly change the lattice. Therefore, any mechanism that rely, to some extent, on lattice properties is expected to be also influenced. This is especially relevant for quasiparticle formation that usually depends on the lattice symmetry for the generation of stable carriers. Therefore, it is expected that carriers created at high-temperature regimes are less stable than the 0 K case.
One may notice that the profile for 197 K is considerably closer to the 350 K configuration than it is from the 95 K configuration. In other words, the thermal response in a high T regime is expected to be less sensitive to temperature variations. This trend will be visible in all the following results.
Fig. S3–S5 (ESI†) present the same panel of Fig. 3 for the 6, 7, and 9AGNR. As in the 4AGNR case, these nanoribbon bonds display an increasing degree of expansion or shrinking as the temperature rises. Moreover, wider nanoribbons present bond length distributions with peaks closer to 0 Å. Because of that, thermal distortions in wider nanoribbons are more prone to change the bonding state (if it is expanding or shrinking). Therefore, the result foreshadows an enhanced sensitivity of wider nanoribbons to dimerization changes.
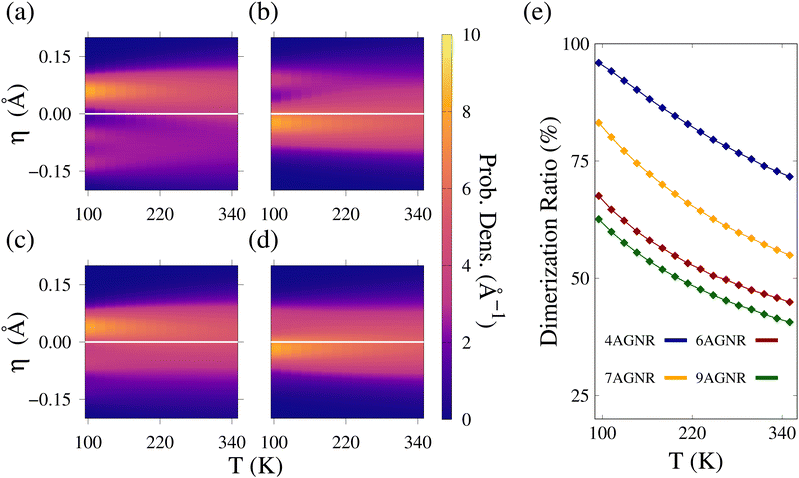
To further explore this indication, we proceed to analyze the bond distributions more systematically. Here, we present Fig. 3(a)–(d). They are the corresponding heatmaps of distortion distribution of all bond types combined for the 4, 6, 7, and 9AGNR. The yellow tones indicate a high probability of occurrence, while purple represents a low probability. A white line is drawn at η = 0 Å to serve as a guide. Each different nanoribbon has at least two high-probability regions. The first one corresponds to the expanded bonds (η > 0) and the other represents contraction (η < 0). The position of these zones along the η axis depends on the nanoribbon width. For instance, when T ≈ 95 K, the 4AGNR heatmap has an orange region near η = 0.06 Å, while the 6AGNR's corresponding peak is at η = 0.09 Å. In all cases, increasing the temperature seems to spread the high-probability regions over the η-axis, a response already observed in Fig. 2(a)–(c).
When T is high enough, the peaks that once were related to contracted bonds begin to overlap with the expansion peaks for all GNRs. As a result, the bond distortion sign begins to flip in some configurations. To better visualize the effect, we present DR as a function of the temperature for the 4 (blue), 6 (red), 7 (yellow), and 9AGNR (green) as shown in Fig. 3(e). Qualitatively, all curves share the same behavior: as T increases, DR decays monotonically. This is an expected outcome. It results from the growing overlap between the distributions’ peaks associated with contracted and expanded bonds.
Some nanoribbons are more prone to dimerization degradation than others. At 95 K, the 4AGNR has DR ≈ 96%, bearing almost no change compared with the 0 K solution. On the other hand, the 9AGNR has a DR of ≈62% for the same temperature. This is a result of the initial position of the η peaks shown in Fig. 2(a)–(d). The peaks closer to 0 Å will cross this value at lower temperatures, providing a non-zero probability to the flipping of the distortion sign of some bonds. The wider nanoribbons present bonds closer to this region. Therefore, the results suggest that width extension enhances the temperature changes in the nanoribbon structural stability. Since quasiparticle formation depends on lattice cohesion, charge carriers hosted on wider nanoribbons are expected to be less stable.
Although wider GNRs suffer more from temperature effects, the relation is not monotonic. For instance, the 6AGNR suffers a stronger dimerization degradation than the 7AGNR. That is due to the grouping of armchair families.10,46 Members belonging to the same family are expected to group together, making width effects to be non-monotonous. Because of that, the 4AGNR and 7AGNR have to display a similar response. The same applies to the 6AGNR and the 9AGNR. A clear example of such behavior is the dependence of the AGNR energy bandgap on the nanoribbon's width, as widely reported the in literature.10,46
Although temperature significantly impacts the dimerization of individual members of the ensemble, we observe no effects when considering the mean values of η. Fig. S1 (ESI†) displays this calculation for the 4AGNR at 300 K. Four ensemble individuals are displayed in Fig. S1(a) (ESI†). The average of them, along with the remaining 4996 units of the set, yields the heatmap shown in Fig. S1(b) (ESI†). This profile is equivalent to the one shown in Fig. 2(d). The explanation for this lies in the Gaussian form of the probability distribution used to sample the distortions. The average of Δki,j(T) is zero for any T because eqn (11) is symmetric. Therefore, summing out the contribution from each ensemble member will just set each bond distortion to its original value from the stationary algorithm, ηi,j.
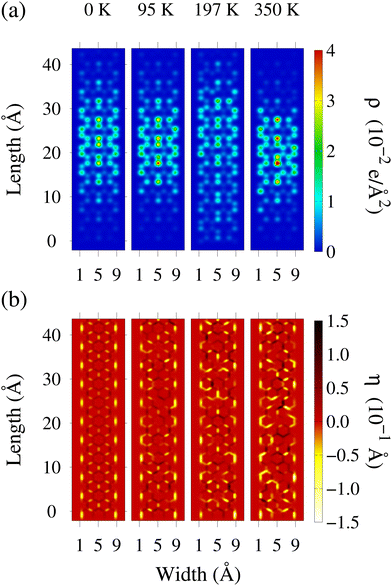
Provided the neutral state's general response, we proceed to analyze the effects on the charged states. Fig. 4(a) presents the charge density (ρ) for the 7AGNR. Four heatmaps are displayed, corresponding to individuals from ensembles of different temperatures. Hot colors signal high charge accumulation, while cold tones indicate a low local density. As can be seen, the carrier morphology suffers substantial changes due to temperature. The symmetry patterns present in the 0 K polaron are often eroded due to the random distortions. For instance, when T = 0 K, the amount of charge on the left side equals the right side. However, this symmetry is lost when considering the 197 K case. Here, the right side has slightly more charge. Changes in the quasiparticle size are observed too. The polarized region at 350 K extends over ≈30 Å, while the 0 K structure has a size of ≈25 Å. Similar asymmetries can be spotted for the other nanoribbons (not shown). These findings are consistent with previous studies on conjugated polymers, in which the polaronic picture of the carrier is challenged with increasing temperature.33
A complete overview of a charged quasiparticle requires examination of the nanoribbon lattice deformation profile. The order parameter heatmap is displayed in Fig. 4(b). At 0 K, a distinguishable local distortion is present at the center of the heatmap, representing the polaron local lattice deformation. Due to the coupling of carriers, the deformation size, shape, and magnitude directly impact the resulting charge accumulation.6,26,43,47 Importantly, the lattice disarray can induce asymmetries in the charge profile. Previous works regarding charge profiles on conjugated polymers indicate that cohesion loss can potentially hinder the transport capability.48 Here, we extend this reasoning by concluding that the thermally-induced random distortions may reduce the carrier's mobility. This is an expected outcome, corroborated by widely reported mobility degradation with increasing temperature in molecular crystals.28,31,49 Confirmation of this response is achievable through dynamical simulations.
We remark that the profiles displayed in Fig. 4 cannot be interpreted as the average behavior of the nanoribbon in that temperature regime. These profiles are snapshots of individual ensemble members. Therefore, a comparison between these structures holds no physical significance. Only the collective response of the ensemble set has this meaning. The heatmaps are presented to illustrate how distorted the 0 K polaron picture becomes when temperature effects emerge.
Now, we move to quantitative analysis. Fig. 5(a)–(d) display the formation energy distributions of the 4AGNR at 100, 150, 200, and 350 K. The curves in red refer to the polaron state, while the ones in blue represent the bipolaron response. Regardless of the temperature magnitude, each state distribution exhibits a Gaussian-like shape with a well-defined peak. Moreover, the peak position of the polaron case is always at a lower energy than that of the bipolaron. This is an expected outcome, reflecting that the system requires more energy to create a bipolaron than a polaron. That should be the case because the additional charge requires a more profound lattice reorganization to form a localized polarized structure. However, as the temperature rises, an interesting effect begins to unfold: the distributions overlap. In other words, certain polaron states, assisted by thermal effects, are energetically more costly to form than bipolaronic configurations. This nonintuitive setting suggests that quasiparticle stability can be widely affected by thermally-induced distortions. The overlapping feature is present in all simulated GNRs.
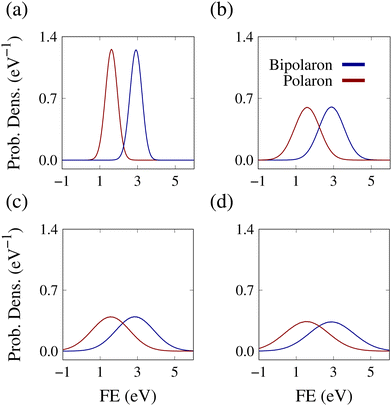 | ||
| Fig. 5 4AGNR probability density distribution of the polaron (red) and bipolaron (blue) formation energies. (a)–(d) Refer to, respectively, T = 95, 197, 299, and 350 cases. | ||
The variants shown in Fig. 5 for the 6, 7, and 9AGNR are presented in Fig. S6–S8 (ESI†). Qualitatively, all nanoribbons display the same behavior: the polaron and bipolaron distributions are monomodal curves that begin to overlap when increasing the temperature. However, close analysis shows that the overlap degree depends on the width. This can be verified by comparing Fig. 5(d) with Fig. S8(d) (ESI†). We recall that the dispersion of the distribution is associated with the material thermal response. The broader the curve, the more intense the change induced by the distortions. Therefore, the result evidences that wider nanoribbons are more sensitive to thermal influence.
For some configurations, EFbip < EFpol. Then, one should expect that the bipolaron stability distribution (see eqn (12)) may have a non-zero probability of being positive. In other words, a non-zero temperature favors the destabilization of bipolarons, effectively facilitating polaron formation. To verify this reasoning, we present the bipolaron stability heatmaps in Fig. 6(a)–(d) for the 4, 6, 7, and 9AGNR, respectively. The colors indicate the probability density magnitude: the zones in blue have a high probability density. In turn, the BE regions in yellow have a low probability density. For each heatmap, a red line is drawn at BE = 0 eV to serve as a reference. Near this line, all distributions display a single strong blue signal. Then, the density progressively drops for BE values away from the central region. This behavior is characteristic of a monomodal distribution. The FE curves shown in Fig. 5 display a similar response.
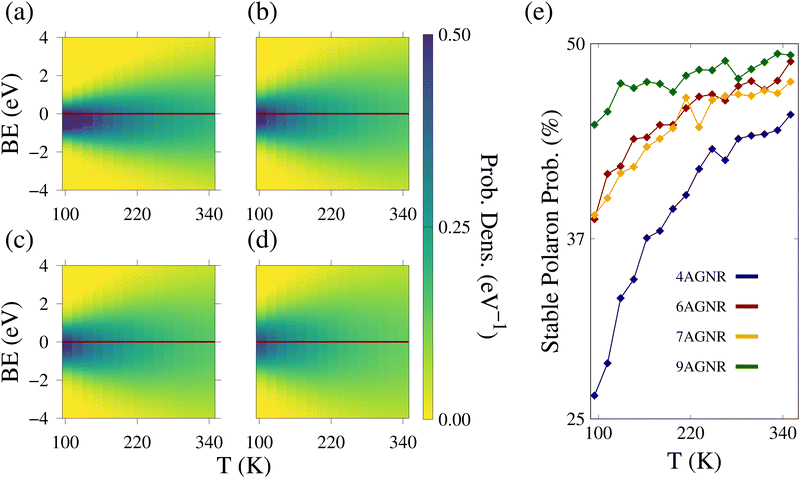 | ||
| Fig. 6 (a)–(d) depict the bipolaron binding energy distributions heatmaps for the 4, 6, 7, and 9AGNR, respectively. The regions in blue present high probability density, while those in yellow have a low probability. (e) displays the percentage of probability of stable polarons as a function of the temperature. This quantity is obtained by integrating each BE distribution in the region BE > 0 eV. The colors of the curves indicate the nanoribbon width, following the same convention shown in Fig. 3. | ||
Note that the center of the distributions is not at BE = 0 eV. In the absence of thermal effects, BE equals −0.36, −0.19, −0.23, and −0.10 eV for the 4, 6, 7, and 9AGNR, respectively. Therefore, bipolarons are more stable than two independent polarons when T = 0 K. As the temperature rises, the distribution expands along the y-axis, making high BE energy states accessible. A consequence of this feature is that the distributions begin to cross the red line, exhibiting a non-zero probability of occurring positive BE configurations.
That thermally-induced behavior has the potential to represent significant implications for GNR-based nanoelectronics. We recall that bipolarons are active agents in photonics. They are involved in excitonic formations, influencing the emission mechanism. Since temperature destabilizes bipolaron formation, thermal effects will reverberate due to the optical properties of GNRs. If bipolarons are prone to split into polarons, biexciton formation might be hampered. As a result, characteristic biexciton peaks at emission spectra are expected to drop with temperature increase. These findings could be explored in thermoelectric applications. Seeback-based gadgets make use of spatial temperature gradients to function. Then, the results suggest that the ratio of polaron/bipolaron populations will be different at the device's edges. Such configuration could be rationalized as a spin filter tool because polarons are fermionic carriers and bipolarons are bosons.
It is important to note that the current model does not include electron–electron repulsion terms. While these terms are pertinent in the context of collision-induced recombination50,51 and magnetic processes,52–54 their incorporation beyond these scenarios does not yield substantial enhancements for the model. The effect is to cause minor adjustments to the gap magnitude and quasiparticle profile. In the present case, the quasiparticles are isolated. Therefore, this addition can be avoided.
Moreover, the rising probability density for positive BE is bound to change charge transport efficiency. Bipolarons often present different transport properties compared with polarons.6,44,47 Our results show that temperature favors the formation of polarons. Therefore, the polaron population is expected to grow with T. As a result, the nanoribbon charge transport mechanism could be characterized by polarons and their properties even in regimes of strong doping. This feature can affect future thermoelectric applications in which transport efficiency (i.e. the current magnitude) is temperature-dependent.
The degree of bipolaron destabilization depends on the nanoribbon width. To investigate this in detail, Fig. 6(e) presents the probability of obtaining two stable polarons as a function of the temperature. The curves were obtained by integrating the probability density curve inside the positive BE region. The color of the curves indicates the nanoribbon width, following the same convention shown in Fig. 3(e). As expected, increasing the temperature raises the probability of positive BE for all AGNRs. However, the nanoribbon width has a profound impact on the probability value. For instance, the 4AGNR has a 26% chance of having a configuration with two stable polarons at 95 K. When T = 350 K, this probability goes to 45%. At the same temperature, in the case of the 9AGNR, the probability escalates from 45% to 49%. Another point worth mentioning is that due to the monomodal character of BE distribution, the probability of positive BE cannot be greater than 50%. The reason is that the probability density also spreads towards the negative BE region. Consequently, at least half of the distribution will still have BE < 0. This interesting result shows that one cannot indefinitely favor the bipolaron split through temperature increments.
4 Conclusion
In conclusion, we investigated the influence of thermal effects on the properties of armchair graphene nanoribbons. Four different width configurations are analyzed. The results show that temperature is an agent that erodes dimerization patterns. The degradation depends on the nanoribbon width. In general, it is shown that wider GNRs are more prone to lose this lattice cohesion.When it comes to charged states, thermal effects induce significant changes in the formation energies of polarons and bipolarons. As an outcome of ensemble statistics, these quantities become distributions. Their dispersion increases with rising temperature. As a result, an interesting result emerges for high T: bipolaron and polaron FE probability density distributions overlap. This means that certain configurations display a lower bipolaron formation energy compared with a single polaron. Further investigation of these cases led to the calculation of bipolaron binding energy distribution. The results show that temperature promotes the occurrence of states with BE > 0 eV, effectively favoring the formation of polarons instead of bipolarons. In contrast to 0 K simulations in which bipolarons are stable, here we report that almost 50% of the ensemble states contain stable polarons for high T. These unexpected results paint an encouraging prospect to envision thermoelectric devices that control the population of charge carriers. Moreover, the results illustrate the importance of including thermal effects to represent realistic scenarios.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author contributions
T. S. A. C. – conceptualization, data curation, formal analysis, methodology, validation, and writing – original draft preparation. G. M. S. – and P. H. O. N. – conceptualization, funding acquisition, formal analysis, visualization, validation, supervision, and writing – reviewing. All authors reviewed the manuscript.Conflicts of interest
The authors declare no competing financial or non-financial interests.Acknowledgements
The authors gratefully acknowledge the financial support from Brazilian Research Councils DC, (grant number 304637/2018-1) CAPES, and FAPDF. P. H. O. N. and G. M. S. gratefully acknowledge the financial support provided by FAPDF grants 00193-00001853/2023-15 and 00193-00001831/2023-47. G. M. S. and P. H. O. N. gratefully acknowledge the financial support provided by CNPq grants 304637/2018-1 and 306080/2022-2, respectively.References
- X.-L. Shi, J. Zou and Z.-G. Chen, Advanced thermoelectric design: from materials and structures to devices, Chem. Rev., 2020, 120(15), 7399–7515, DOI:10.1021/acs.chemrev.0c00026.
- S. Lee, S. Kim, A. Pathak, A. Tripathi, T. Qiao, Y. Lee, H. Lee and H. Y. Woo, Recent progress in organic thermoelectric materials and devices, Macromol. Res., 2020, 28(6), 531–552, DOI:10.1007/s13233-020-8116-y.
- Y. Yano, N. Mitoma, H. Ito and K. Itami, A quest for structurally uniform graphene nanoribbons: synthesis, properties, and applications, J. Org. Chem., 2019, 85(1), 4–33, DOI:10.1021/acs.joc.9b02814.
- A. C. Neto, F. Guinea, N. M. Peres, K. S. Novoselov and A. K. Geim, The electronic properties of graphene, Rev. Mod. Phys., 2009, 81(1), 109, DOI:10.1103/RevModPhys.81.109.
- D. J. Rizzo, G. Veber, T. Cao, C. Bronner, T. Chen, F. Zhao, H. Rodriguez, S. G. Louie, M. F. Crommie and F. R. Fischer, Topological band engineering of graphene nanoribbons, Nature, 2018, 560(7717), 204–208, DOI:10.1038/s41586-018-0376-8.
- W. F. da Cunha, P. H. Acioli, P. H. D. oliveira Neto, R. Gargano and G. M. e Silva, Polaron properties in armchair graphene nanoribbons, J. Phys. Chem. A, 2016, 120(27), 4893–4900, DOI:10.1021/acs.jpca.5b12491.
- E. McCann and M. Koshino, The electronic properties of bilayer graphene, Rep. Prog. Phys., 2013, 76(5), 056503, DOI:10.1088/0034-4885/76/5/056503.
- T. D. S. A. Cassiano, F. F. Monteiro, L. E. De Sousa, G. M. E. Silva and P. H. D. Oliveira Neto, Smooth gap tuning strategy for cove-type graphene nanoribbons, RSC Adv., 2020, 10(45), 26937–26943, 10.1039/D0RA02997A.
- M. Yankowitz, S. Chen, H. Polshyn, Y. Zhang, K. Watanabe, T. Taniguchi, D. Graf, A. F. Young and C. R. Dean, Tuning superconductivity in twisted bilayer graphene, Science, 2019, 363(6431), 1059–1064, DOI:10.1126/science.aav1910.
- Y.-W. Son, M. L. Cohen and S. G. Louie, Energy gaps in graphene nanoribbons, Phys. Rev. Lett., 2006, 97(21), 216803, DOI:10.1103/PhysRevLett.97.216803.
- A. Narita, X.-Y. Wang, X. Feng and K. Mullen, New advances in nanographene chemistry, Chem. Soc. Rev., 2015, 44, 6616–6643, 10.1039/C5CS00183H.
- J. Cai, C. A. Pignedoli, L. Talirz, P. Ruffieux, H. Söde, L. Liang, V. Meunier, R. Berger, R. Li and X. Feng, et al., Graphene nanoribbon heterojunctions, Nat. Nanotechnol., 2014, 9(11), 896–900, DOI:10.1038/nnano.2014.184.
- J. Oh, Y. Kim, S. Chung, H. Kim and J. G. Son, Fabrication of a MoS2/Graphene nanoribbon heterojunction network for improved thermoelectric properties, Adv. Mater. Interfaces, 2019, 6(23), 1901333, DOI:10.1002/admi.201901333.
- J. Bredas, J. Scott, K. Yakushi and G. Street, Polarons and bipolarons in polypyrrole: Evolution of the band structure and optical spectrum upon doing, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 30(2), 1023, DOI:10.1103/PhysRevB.30.1023.
- A. J. Heeger, S. Kivelson, J. Schrieffer and W.-P. Su, Solitons in conducting polymers, Rev. Mod. Phys., 1988, 60(3), 781, DOI:10.1103/RevModPhys.60.781.
- Z. Sun, Y. Li, S. Xie, Z. An and D. Liu, Scattering processes between bipolaron and exciton in conjugated polymers, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 79(20), 201310, DOI:10.1103/PhysRevB.79.201310.
- Y. Liu, S. Gao, X. Zhang, J. H. Xin and C. Zhang, Probing the nature of charge carriers in one-dimensional conjugated polymers: a review of the theoretical models, experimental trends, and thermoelectric applications, J. Mater. Chem. C, 2023, 11, 12–47, 10.1039/D2TC03574J.
- B. Di, Y. Meng, Y. Wang, X. Liu and Z. An, Formation and evolution dynamics of bipolarons in conjugated polymers, J. Phys. Chem. B, 2011, 115(5), 964–971, DOI:10.1021/jp110875b.
- D. Braun and A. J. Heeger, Visible light emission from semiconducting polymer diodes, Appl. Phys. Lett., 1991, 58(18), 1982–1984, DOI:10.1103/PhysRevB.44.8652.
- Z. Sun and S. Stafström, Bipolaron recombination in conjugated polymers, J. Chem. Phys., 2011, 135(7), 074902, DOI:10.1063/1.3624730.
- G. M. e Silva, Electric-field effects on the competition between polarons and bipolarons in conjugated polymers, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 61(16), 10777, DOI:10.1103/PhysRevB.61.10777.
- T. Astakhova and G. Vinogradov, New aspects of polaron dynamics in electric field, Eur. Phys. J. B, 2019, 92(11), 1–9, DOI:10.1140/epjb/e2019-100339-y.
- A. A. Johansson and S. Stafström, Nonadiabatic simulations of polaron dynamics, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69(23), 235205, DOI:10.1103/PhysRevB.69.235205.
- M. B. Falleiros and G. M. e Silva, Same charge polaron and bipolaron scattering on conducting polymers, J. Phys. Chem. A, 2019, 123(7), 1319–1327, DOI:10.1021/acs.jpca.8b11725.
- T. D. S. A. Cassiano, L. A. R. Júnior, G. M. e Silva and P. H. d O. Neto, Regulating Polaron Transport Regime via Heterojunction Engineering in Cove-Type Graphene Nanoribbons, Adv. Theory Simul., 2023, 2200877, DOI:10.1002/adts.202200877.
- P. H. D. oliveira Neto and T. Van Voorhis, Dynamics of charge quasiparticles generation in armchair graphene nanoribbons, Carbon, 2018, 132, 352–358, DOI:10.1016/j.carbon.2018.02.062.
- Y. Sakai and A. Terai, Dynamics of Quasiparticles Generation, Transport and Relaxation in Armchair-edge Graphene Nanoribbons, J. Phys. Soc. Jpn., 2019, 88(5), 054718, DOI:10.7566/JPSJ.88.054718.
- A. Troisi and G. Orlandi, Charge-transport regime of crystalline organic semiconductors: Diffusion limited by thermal off-diagonal electronic disorder, Phys. Rev. Lett., 2006, 96(8), 086601, DOI:10.1103/PhysRevLett.96.086601.
- A. Troisi, Prediction of the absolute charge mobility of molecular semiconductors: the case of rubrene, Adv. Mater., 2007, 19(15), 2000–2004, DOI:10.1002/adma.200700550.
- L. Wang, O. V. Prezhdo and D. Beljonne, Mixed quantum-classical dynamics for charge transport in organics, Phys. Chem. Chem. Phys., 2015, 17(19), 12395–12406, 10.1039/C5CP00485C.
- L. Wang, A. V. Akimov, L. Chen and O. V. Prezhdo, Quantized Hamiltonian dynamics captures the low-temperature regime of charge transport in molecular crystals, J. Chem. Phys., 2013, 139(17), 174109, DOI:10.1063/1.4828863.
- T. Gao, Q. Lu, C. Li, K. Gao and S. Xie, Thermally Induced Exciton Diffusion and Dissociation in Organic Semiconductors, J. Phys. Chem. C, 2019, 123(47), 28527–28532, DOI:10.1021/acs.jpcc.9b06789.
- L. Yang, D. Yi, S. Han and S. Xie, Theoretical investigation on thermal effect in organic semiconductors, Org. Electron., 2015, 23, 39–43, DOI:10.1016/j.orgel.2015.04.008.
- W. P. Su, J. R. Schrieffer and A. J. Heeger, Solitons in polyacetylene, Phys. Rev. Lett., 1979, 42(25), 1698, DOI:10.1103/PhysRevLett.42.1698.
- M. G. D. Amaral and C. A. D. Carvalho, A Hybrid Monte Carlo Study of the Su-Schrieffer-Heeger Model, Int. J. Mod. Phys. C, 1994, 5(03), 459–481, DOI:10.1142/S0129183194000659.
- W. F. da Cunha, P. H. D. oliveira Neto, R. Gargano and G. Magela e Silva, Temperature effects on polaron stability in polyacetylene, Int. J. Quantum Chem., 2008, 108(13), 2448–2453, DOI:10.1002/qua.21798.
- Y. Meng, G.-j Guo, Y.-d Wang, Y.-f Li and Z. An, The effects of temperature on the formation and stability of bipolarons in conjugated polymers, Eur. Phys. J. B, 2017, 90, 1–7, DOI:10.1140/epjb/e2017-80018-7.
- P. D. oliveira Neto, J. Teixeira, W. Da Cunha, R. Gargano and G. e Silva, Electron-lattice coupling in armchair graphene nanoribbons, J. Phys. Chem. Lett., 2012, 3(20), 3039–3042, DOI:10.1021/jz301247u.
- L. A. Ribeiro Jr, W. F. da Cunha, A. L. D. A. Fonseca, G. M. e Silva and S. Stafstrom, Transport of polarons in graphene nanoribbons, J. Phys. Chem. Lett., 2015, 6(3), 510–514, DOI:10.1021/jz502460g.
- V. N. Kotov, B. Uchoa, V. M. Pereira, F. Guinea and A. C. Neto, Electron-electron interactions in graphene: Current status and perspectives, Rev. Mod. Phys., 2012, 84(3), 1067, DOI:10.1103/RevModPhys.84.1067.
- J. Williams, T. Low, M. Lundstrom and C. Marcus, Gate-controlled guiding of electrons in graphene, Nat. Nanotechnol., 2011, 6(4), 222–225, DOI:10.1038/nnano.2011.3.
- M. M. Fischer, L. A. R. Junior, W. F. da Cunha, L. E. de Sousa, G. M. e Silva and P. H. D. oliveira Neto, Ultrafast direct generation of quasiparticles in graphene nanoribbons, Carbon, 2020, 158, 553–558, DOI:10.1016/j.carbon.2019.11.025.
- T. d S. A. Cassiano, G. M. e Silva and P. H. d oliveira Neto, Phase transition of polarons in bilayer graphene nanoribbons, Phys. Scr., 2023, 98(9), 095922, DOI:10.1088/1402-4896/acecc2.
- G. G. Silva, L. A. Ribeiro Junior, M. L. Pereira Junior, A. L. D. A. Fonseca and R. T. de Sousa Júnior, et al., Bipolaron dynamics in graphene nanoribbons, Sci. Rep., 2019, 9(1), 1–8, DOI:10.1038/s41598-019-39774-2.
- F. J. Martn-Martnez, S. Fias, G. Van Lier, F. De Proft and P. Geerlings, Electronic structure and aromaticity of graphene nanoribbons, Chem. – Eur. J., 2012, 18(20), 6183–6194, DOI:10.1002/chem.201103977.
- L. Yang, C.-H. Park, Y.-W. Son, M. L. Cohen and S. G. Louie, Quasiparticle energies and band gaps in graphene nanoribbons, Phys. Rev. Lett., 2007, 99(18), 186801, DOI:10.1103/PhysRevLett.99.186801.
- T. d S. A. Cassiano, L. E. de Sousa, L. A. R. Junior, G. M. e Silva and P. H. d oliveira Neto, Charge transport in cove-type graphene nanoribbons: The role of quasiparticles, Synth. Met., 2022, 287, 117056, DOI:10.1016/j.synthmet.2022.117056.
- L. A. Ribeiro, W. F. da Cunha, P. H. de Oliveria Neto, R. Gargano and G. M. e Silva, Effects of temperature and electric field induced phase transitions on the dynamics of polarons and bipolarons, New J. Chem., 2013, 37(9), 2829–2836, 10.1039/C3NJ00602F.
- V. Cataudella, G. De Filippis and C. A. Perroni, Transport properties and optical conductivity of the adiabatic Su-Schrieffer-Heeger model: A showcase study for rubrene-based field effect transistors, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83(16), 165203, DOI:10.1103/PhysRevB.83.165203.
- L. A. Ribeiro, W. F. da Cunha, P. H. d oliveira Neto, R. Gargano and G. M. e Silva, Dynamical study of impurity effects on bipolaron-bipolaron and bipolaron-polaron scattering in conjugated polymers, J. Phys. Chem. B, 2013, 117(39), 11801–11811, DOI:10.1021/jp402963k.
- A. Terai and Y. Ono, Dynamics of photogenerated soliton pairs in polyacetylene, Synth. Met., 1992, 50(1–3), 603–609, DOI:10.1016/0379-6779(92)90217-7.
- O. V. Yazyev, Magnetism in disordered graphene and irradiated graphite, Phys. Rev. Lett., 2008, 101(3), 037203, DOI:10.1103/PhysRevLett.101.037203.
- H. Lee, K. Wakabayashi, Y.-W. Son and Y. Miyamoto, A single particle Hamiltonian for electro-magnetic properties of graphene nanoribbons, Carbon, 2012, 50(10), 3454–3458, DOI:10.1016/j.carbon.2012.03.009.
- D. G. de Oteyza and T. Frederiksen, Carbon-based nanostructures as a versatile platform for tunable π-magnetism, J. Phys.: Condens. Matter, 2022, 34(44), 443001, DOI:10.1088/1361-648X/ac8a7f.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ma01181j |
| This journal is © The Royal Society of Chemistry 2024 |