Open Access Article
Open Access ArticleA new thermoelectric Ag8SiSe6 argyrodite for room temperature application: sensitivity of thermoelectric performance to cooling conditions
Bo
Wang
a,
Suwei
Li
a,
Yubo
Luo
 a,
Junyou
Yang
a,
Junyou
Yang
 a,
Haitao
Ye
a,
Haitao
Ye
 *b,
Yong
Liu
*c and
Qinghui
Jiang
*b,
Yong
Liu
*c and
Qinghui
Jiang
 *a
*a
aState Key Laboratory of Materials Processing and Die and Mould Technology, and School of Materials Science and Engineering, Huazhong University of Science and Technology, Wuhan 430074, Hubei Province, China. E-mail: qhjiang@hust.edu.cn
bSchool of Engineering, University of Leicester, University Road, Leicester, LE1 7RH, UK. E-mail: haitao.ye@leicester.ac.uk
cFoshan (Southern China) Institute for New Materials, Foshan 528220, Guangdong Province, P. R. China. E-mail: liuy08@qq.com
First published on 7th March 2024
Abstract
Current commercial thermoelectrics, like Bi2Te3-based compounds, generally include the expensive and toxic Te element, which hampers their large-scale thermoelectric applications in near room temperature conditions. In this work, a Ag8SiSe6 argyrodite compound, a new thermoelectric material as a potential candidate for Bi2Te3-based compounds, was fabricated by several synthesis processes. All the Ag8SiSe6-based thermoelectric bulks, exhibiting a density surpassing 95%, were successfully synthesized. The study investigated the impact of varying the quenching rate and techniques on Ag8SiSe6's thermoelectric performance. Our results revealed a pronounced relationship between the quenching parameters and pivotal thermoelectric metrics, including the Seebeck coefficient, electrical conductivity, and thermal conductivity. By optimizing the quenching conditions, we achieved a notable enhancement in ZT values, peaking over 0.7. This paves the way for Ag8SiSe6 to be considered as a competitive substitute for traditional n-type Bi2Te3-based compounds in thermoelectric applications under proximate room temperature conditions.
1 Introduction
Thermoelectric (TE) materials enable the conversion between thermal and electrical energy, a process of substantial importance for green energy harvesting and environmental protection.1,2 The figure of merit ZT, a dimensionless constant, dictates the conversion efficiency of TE devices and is expressed as ZT = S2σT/(κE + κL), where σ represents the conductivity, S is the Seebeck coefficient, κE is the electronic thermal conductivity, κL is the lattice thermal conductivity, T is the absolute temperature, and S2σ is defined as the power factor (PF). Total thermal conductivity (κ) can be written as κ = κE + κL. Clearly, an enhancement in the power factor coupled with a reduction in thermal conductivity is essential for improving the value of ZT.3In recent years, several strategies, including modulation doping, inducing resonant levels, and band convergence, have been adopted to obtain higher electrical properties and power factors for relevant materials. These enhancements have been verified in SnSe,4 PbTe,5–7 Bi2Te3,8 and BiCuSeO.9 To optimize the thermal conductivity, strategies such as the incorporation of nano-inclusions, secondary phase recombination, and lattice anharmonicity have been introduced, and have been successfully applied to reduce the thermal conductivity of thermoelectric materials such as Bi2Te3,10 CoSb3,11 Cu3SbSe4,12 AgSbTe2,13 SnTe,14 and Ag8SnSe6.15
At present, the commercial applications of thermoelectric materials are mainly focused on energy harvesting from the environment and solid-state cooling near room temperature.16 For a long time, Bi2Te3-based alloys were the only material used in industrial thermoelectric modules for thermoelectric cooling in electronic equipment, large instrument cooling, and household cooling appliances.17
Research on superionic compounds revealed that these substances possess ultralow thermal conductivity and narrow band gaps.18 These characteristics render superionic compounds as promising compounds to investigate for creating advanced thermoelectric materials with potential high ZT values.19 Argyrodite compounds, recognized as promising thermoelectrics, have attracted considerable attention due to their significantly low lattice thermal conductivity.20 This can be attributed to factors such as low sound velocity, complex crystal structure, liquid-like ions, and lattice anharmonicity. Pei et al. identified that the extremely low phonon velocity and small proportion of acoustic phonons in Ag9AlSe6 result in reduced thermal conductivity.21Yang et al. observed that the highly random ion occupancy in Ag8SnSe6 leads to soft bonding within the silver sub-lattice and phonon modes.22
Tremel et al. suggested that the thermal conductivity in Ag8SiSe6 is ameliorated by the high mobility and disorder of silver ions, thereby enhancing the thermoelectric properties of the material.23 Our group reported that the nanoprecipitation of Ag2Se and Si could further optimize the transport properties of Ag2Se-Si-Ag8SiSe6 composite.24 These two studies illuminated the potential of Ag8SiSe6 as a viable n-type candidate for the development of next-generation thermoelectric materials. Compounds from various groups have demonstrated a range of ZT values from 0.5 to 0.9.23,24 However, there are scant details on the experimental processes for obtaining Ag8SiSe6 or related discussions about its purity. This raises a pertinent question: is the purity and stability of Ag8SiSe6 highly sensitive to the fabrication or cooling processing parameters? Such sensitivity could complicate the understanding of the material's intrinsic physical properties.
In this study, we thoroughly investigated the synthesis of Ag8SiSe6 compounds and successfully fabricated Ag8SiSe6-based thermoelectric bulks with a density exceeding 95%. We then delved deeper into the crystal structure, microstructure, and thermoelectric properties of these materials. A relationship was revealed between the cooling conditions, phase, microstructure, and their respective thermoelectric properties. After optimization of the fabrication processing parameters, the Ag8SiSe6 compounds, which exhibited a low thermal conductivity of 0.7 W m−1 K−1 and a high power factor surpassing 1200 μW m-1 K-2, achieved a peak ZT of approximately 0.7 at 398 K.
2 Experimental
Synthesis of Ag8SiSe6
Polycrystalline Ag8SiSe6 ingots were synthesized using a high-temperature melting method with stoichiometric amounts of high-purity elements (> 99.99%) at 1223 K for 10 hours on quartz crucibles, which were subsequently cooled using different methods: cooling in a furnace (CF), quenching in air (QA), and quenching in water (QW). The resulting ingots were ground into powders and annealed at 773 K for 72 hours. Some quenched powders were additionally milled for 2 hours (QW&M). The final powders were hot-pressed under 60 MPa for 30 minutes to form pellets, achieving densities above 95% of the theoretical value.Characterization
Pellet samples were ground into fine powder for X-ray diffraction (XRD) analysis (data collected on an XRD 7000 from Shimadzu Instrument at room temperature, using Cu Kα radiation with λ = 0.15418 nm). The fracture morphologies and compositional analyses of the bulk samples were conducted using field-emission scanning electron microscopy (FESEM, GeminiSEM300, Carl Zeiss), accompanied by energy-dispersive spectrometry.Thermoelectric property measurements
The electrical resistivity (ρ = 1/σ) and Seebeck coefficient of the bulk samples were measured using a commercial Namicro III thermoelectric system, fabricated in the laboratory, with an uncertainty of 5%. The thermal conductivity (κ) was determined by the formula κ = CpDλ, where the relative densities (D) were calculated using the Archimedes method, the specific heat capacity (Cp) was determined using the Dulong-Petit model, and the thermal diffusivity (λ) was assessed using the laser flash diffusivity method with LFA-427 (NETZSCH) equipment, with an uncertainty of 4%. Differential scanning calorimetry (DSC) measurements were performed using STA449F3 (NETZSCH) equipment at a heating rate of 5 K min−1, and Hall measurements were conducted using an HMS 5500 Hall Effect measurement system under a 0.55 T magnetic field, employing the van der Pauw method.3 Results and discussion
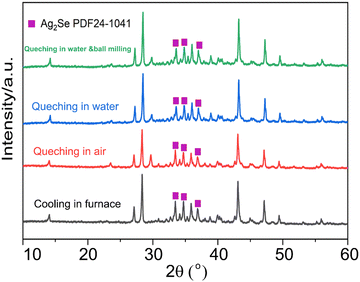
Fig. 1 presents the X-ray diffraction (XRD) patterns of the Ag8SiSe6 samples synthesized under various cooling conditions. The densities of these samples consistently exceed 95% of the theoretical value, a factor essential for optimizing the thermoelectric (TE) properties. The predominant diffraction peaks from the hot-pressed samples aligned with the Pmn21 space group, corroborating an earlier study by Aversive et al.25 Additionally, certain diffraction peaks could be attributed to a secondary phase of Ag2Se (PDF# 24-1041) characterized by the P212121 space group.26 Notably, as the cooling rate escalated, the intensity of the secondary phase (Ag2Se) peaks diminished. This observation implies that high-temperature quenching facilitates the synthesis of Ag8SiSe6 and that rapid cooling can inhibit the generation of impurities, thus streamlining the subsequent annealing process to yield a more refined phase. However, the aforementioned results indicate that a pure Ag8SiSe6 phase cannot be prepared using the current methods.Fig. 2 illustrates the fracture morphologies of Ag8SiSe6 bulk samples as revealed by scanning electron microscopy (SEM). The surface of the hot-pressed Ag8SiSe6, despite some discernible holes, appeared notably compact, corroborating the high density referred to earlier. As observed in the low-magnification SEM image in Fig. 2a, the grain diameter of Ag8SiSe6 (cooled in the furnace) varied between 2 and 3 μm. The medium-magnification SEM fracture image in Fig. 2b reveals complex grain boundaries and even some holes, potentially leading to increased material resistivity. Fig. 2c depicts the fracture morphologies of the Ag8SiSe6 samples quenched in water, exposing a cladding structure in which small grains enveloped larger ones. As shown in the high-magnification image in Fig. 2d, these small grains measured less than 500 nm and were nano-precipitates formed during quenching because the sample did not undergo ball milling.27 This figure also reveals there was a reduction in porosity compared with previous samples. Fig. 2e shows a typical low-magnification SEM image of Ag8SiSe6 (quenched in water) following the ball-milling process, with grain sizes generally under 1 μm. Moreover, the high-resolution image in Fig. 2f's reveals a highly dense and uniform microstructure, conducive to lower resistivity. Nevertheless, ball milling may create additional defects and grain boundary surfaces, potentially impairing the electronic transport properties.28 Therefore, optimal performance might be achieved through a judicious combination of these factors.
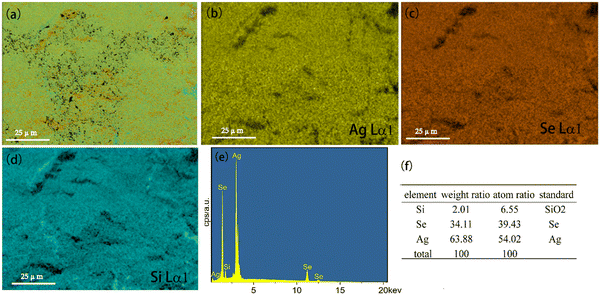
The microstructure of Ag8SiSe6 sample was evaluated using energy-dispersive spectrometry (EDS) for elemental analysis. Fig. 3a displays a hierarchical image of Ag8SiSe6, which encompasses all three constituent elements. The element distribution maps for Ag, Se, and Si are illustrated in Fig. 3b–d. Notably, the elements Ag, Se, and Si exhibited uniform distributions throughout the sample, devoid of any elemental clustering, a characteristic often observed in samples that undergo ball-milling treatment. To provide a deeper insight into the composition of the sample, a comprehensive analysis of the entire surface was performed. Fig. 3f presents the resultant data, delineating the weight ratio, atomic ratio, and standard sample measurements for all three elements. Through straightforward calculations, the actual atomic ratio for Ag, Si, and Se was determined to be approximately 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1:6, affirming the successful synthesis of the primary Ag8SiSe6 phase.
1:6, affirming the successful synthesis of the primary Ag8SiSe6 phase.
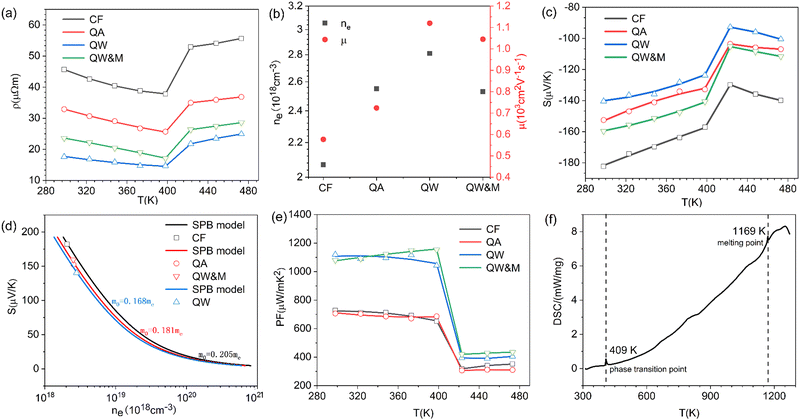
Fig. 4a illustrates the temperature-dependent electrical resistivity of Ag8SiSe6 samples prepared under various conditions. The electrical resistivity of the samples cooled in the furnace (CF) and quenched in air (QA) exceeded that of the samples quenched in water (QW). In Fig. 4b, the Hall coefficient measurement revealed that the observed variations in resistivity mainly stemmed from a simultaneous increase in carrier concentration and mobility. This interesting phenomenon can be explained as a reduction of the second phase in the Ag-Si-Se alloy; whereby, according to the equation 8Ag + Si + 6Se ⇒ Ag8SiSe6 ⇔ 4Ag2Se1+δ + (2 − 4δ)Se + Si, a reduction in the second phase would lead to decreased contents of Si and Se elements (although their low content and low crystalline mean they cannot be detected by XRD, as shown in Fig. 1). Since Si and Se have low a carrier concentration and mobility, their content reduction as second phases leads to low resistivity. After subjecting the samples to ball-milling treatment (QW&M), the electrical resistivity was slightly increased. Elemental analysis of the sample shown in Fig. 2f suggested that the milling process led to the creation of additional surfaces, defects, and stress, significantly contributing to the decrease in carrier concentration and mobility.
Fig. 4c illustrates the temperature dependence of the Seebeck coefficients of the Ag8SiSe6 samples, demonstrating that the room temperature Seebeck coefficients decreased with increasing the cooling rate. A corresponding downward trend in the measured carrier concentration was also noticeable. Fig. 4d depicts the relationship between the room temperature Seebeck coefficient and carrier concentration in accordance with Pisarenko's theory, further indicating a decrease in the effective mass m*. Herein, the single parabolic band (SPB) model was used to calculate the Pisarenko plot related to the Seebeck coefficient and carrier concentration according to the following equations:29
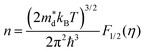 | (1) |
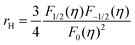 | (2) |
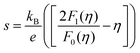 | (3) |
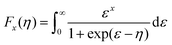 | (4) |
Regarding the calculated power factor (PF = (1/ρ)S2), the data were assembled and a graph plotted, as shown in Fig. 4e. All four samples exhibited similar trends, with their power factors remaining relatively stable until the phase-transition temperature. Notably, the PF of the QW sample was sharply augmented across the entire measurement temperature range. Upon the introduction of ball milling, the power factor escalated with increasing the temperature before 400 K, reaching a maximum value of approximately 1200 μW m−1 K−2 at 398 K in the QW&M sample.
The results from the differential scanning calorimetry (DSC) analysis of Ag8SiSe6 powder are presented in Fig. 4f. The peak value of 409 K is considered indicative of a phase-transition temperature during the first-order structural transition. For Ag–Si–Se compounds, this peak can only be attributed to the contribution of the phase transition of Ag2Se and Ag8SiSe6. Wang et al.30 and Mi et al.,31 respectively, reported there is a peak near 400 K consistent with the phase-transition temperature of Ag2Se compounds. Meanwhile, Tremel et al.23 identified that this peak was consistent with the phase transition occurring near 400 K in Ag8SiSe6, a representative of the argyrodite compounds. Above this temperature, Ag8SiSe6 exhibits a face-centered cubic structure in which Ag+ cations are fully disordered in the [SiSe6]8− anion sublattice, comprising Se2− anions and [SiSe4]4− units. Below this temperature, Ag8SiSe6 exhibits an orthorhombic structure with a space group Pmn21, transforming to a cubic structure with the space group F![[4 with combining macron]](https://www.rsc.org/images/entities/char_0034_0304.gif)
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at elevated temperatures.32,33 As a result, Ag+ cations are partially localized, leading to a reduction in electrical conductivity and an increase in Seebeck coefficients.
m at elevated temperatures.32,33 As a result, Ag+ cations are partially localized, leading to a reduction in electrical conductivity and an increase in Seebeck coefficients.
Similar semiconductor-superionic conductor phase transitions were reported in the Ag2Se system by Xie et al.34 These insights suggest a novel and effective approach to enhancing the thermoelectric power factor is by capitalizing on the abnormal electrical transport characteristics near the phase-transition temperature.
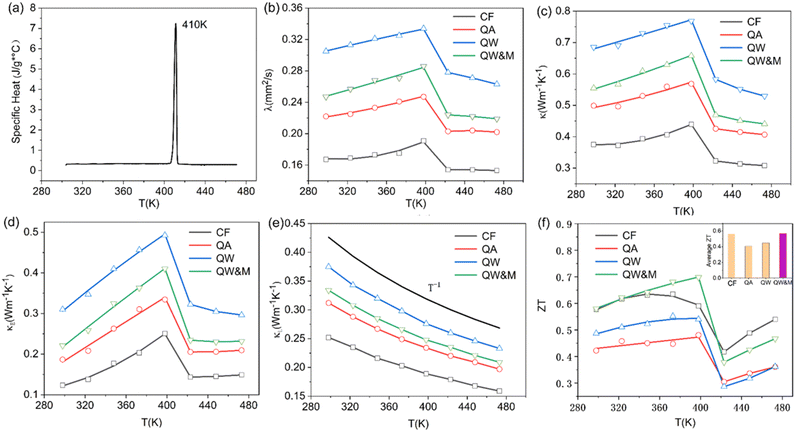
The thermal diffusivity coefficient λ and specific heat Cp are illustrated in Fig. 5a and b, respectively. The thermal conductivity κ was derived using the equation κ = DCpλ, and is presented in Fig. 5c (in order to avoid the argued abnormal behaviour in ZT like Cu2Se,35 the sharp peak near 400 K was ignored in the specific heat curve during the calculation of the thermal conductivity). With the increase in temperature, the thermal conductivity first exhibited a slight rise followed by a notable decline. Data points for κ across all the samples predominantly ranged between 0.3 and 0.8 W m−1 K−1 throughout the temperature spectrum. Such exceptionally low thermal conductivity36 has also been observed in other argyrodite compounds and can be attributed to factors such as low sound velocity, intricate crystal structures, liquid-like ions, and lattice anharmonicity.37
The electronic thermal conductivity, calculated using the Wiedemann–Franz law (κE = LT/ρ), is depicted in Fig. 5d. Here, L represents the Lorenz factor as determined by the single parabolic band (SPB) model in conjunction with acoustic scattering.38,39 The lattice thermal conductivity can then be deduced by subtracting the electronic thermal conductivity from the total thermal conductivity, as shown in Fig. 5e. A discernible linear relationship existed between κL and T−1, indicating that Umklapp scattering was the primary phonon mechanism. Furthermore, the lattice thermal conductivity reached a low of around 0.17 W m−1 K−1, a phenomenon likely resulting from the high disordering of soft bonding, Ag ions, and the low cut-off frequency of acoustic phonons.40 This value was consistent with the values for Ag8SiSe6 compounds published by other reports in literatures23,24 and is also one of the lowest values of lattice thermal conductivities (for example, see 0.12 W m−1 K−1 at 300 K for Ag9GaSe6,41 and 0.13 W m−1 K−1 for Ag8SnSe642). However, it is counterintuitive that the phase transition does not affect κL. The lack of a proper explanation for this phenomenon makes it an open question that requires further exploration.
ZT values are plotted in Fig. 5f, with the average ZT values featured in the inset. The combination of quenching and ball-milling treatment optimized the temperature-dependent ZT and average ZT values across the entire temperature range. A peak ZT value of approximately 0.71 was attained at 398 K in the QW&M sample, primarily stemming from the combined effect of a high power factor exceeding 1200 μW m−1 K−2 and a reduced lattice thermal conductivity. This value is similar to those reported in literature.23,24 The highest average ZT, around 0.57, was observed in the QW&M sample at 398 K (inset of Fig. 5f).
4 Conclusions
Thermoelectric bulks based on Ag8SiSe6 were synthesized through a traditional melting process combined with a hot pressing method, marking the first systematic investigation of their thermoelectric properties linked to different post-treatments. By varying the cooling rates of the ingots, a substantial improvement in the power factor was attained, particularly in the sample quenched in water, due to a marked reduction in resistivity. Although a pure Ag8SiSe6 phase could not be prepared using the current methods, a high-performance thermoelectric material was fabricated through the integration of ball-milling treatment with the quenched ingot, achieving a peak ZT value of approximately 0.71 at 398 K. Further research is warranted to understand the underlying mechanisms and optimize the material for commercial applications.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China (52273293, 52172187, 51772019, and 51572098).References
- S. Y. Tee, D. Ponsford, C. L. Lay, X. Wang, X. Wang, D. C. J. Neo, T. Wu, W. Thitsartarn, J. C. C. Yeo, G. Guan, T.-C. Lee and M.-Y. Han, Adv. Sci., 2022, 9, 2204624 CrossRef CAS PubMed.
- Q. Jiang, J. Yang, P. Hing and H. Ye, Mater. Adv., 2020, 1, 1038–1054 RSC.
- B. Cai, H. Hu, H.-L. Zhuang and J.-F. Li, J. Alloys Compd., 2019, 806, 471–486 CrossRef CAS.
- X. Zhang, J. Cai, X. Tan, S. Zhuang, W. Huang, Z. Zhang, H. Hu, J. Wu, G.-Q. Liu and J. Jiang, Mater. Adv., 2023, 4, 1372–1377 RSC.
- K. Zhang, H. Wang, W. Su, T. Wang, X. Wang, T. Chen, T. Huo, F. Dang, M. Dong, C. Wang, B. Dong and Z. Guo, J. Phys. D: Appl. Phys., 2020, 53, 245501 CrossRef CAS.
- T. Chen, K. Zhang, H. Wang, W. Su, F. Mehmood, T. Wang, J. Zhai, X. Wang, T. Huo and C. Wang, J. Mater. Chem. C, 2020, 8, 1679–1685 RSC.
- M. Huang, P. Zhai, S. I. Morozov, W. A. Goddard, G. Li and Q. Zhang, J. Alloys Compd., 2023, 959, 170429 CrossRef CAS.
- Y. Cheng, J. Yang, Y. Luo, W. Li, A. Vtyurin, Q. Jiang, S. Dunn and H. Yan, ACS Appl. Mater. Interfaces, 2022, 14, 37204–37212 CrossRef CAS PubMed.
- W. Tang, W. Ma, P. Yu, Z. Zhou, J. Lan, Y.-H. Lin and X. Yang, Mater. Today Phys., 2022, 28, 100898 CrossRef CAS.
- Q. Jiang, J. Yang, J. Xin, Z. Zhou, D. Zhang and H. Yan, J. Alloys Compd., 2017, 694, 864–868 CrossRef CAS.
- B. Popescu, M. Galatanu, M. Enculescu and A. Galatanu, J. Alloys Compd., 2022, 893, 162400 CrossRef CAS.
- D. Xie, B. Zhang, A. Zhang, Y. Chen, Y. Yan, H. Yang, G. Wang, G. Wang, X. Han, G. Han, X. Lu and X. Zhou, Nanoscale, 2018, 10, 14546–14553 RSC.
- M. Yan, X. Tan, Z. Huang, G. Liu, P. Jiang and X. Bao, J. Mater. Chem. A, 2018, 6, 8215–8220 RSC.
- X. Liu, B. Zhang, Y. Chen, H. Wu, H. Wang, M. Yang, G. Wang, J. Xu, X. Zhou and G. Han, ACS Appl. Mater. Interfaces, 2020, 12, 44805–44814 CrossRef CAS PubMed.
- W. Li, S. Lin, B. Ge, J. Yang, W. Zhang and Y. Pei, Adv. Sci., 2016, 3, 1600196 CrossRef PubMed.
- Z. Han, J.-W. Li, F. Jiang, J. Xia, B.-P. Zhang, J.-F. Li and W. Liu, J. Materiomics, 2022, 8, 427–436 CrossRef.
- Q. Jiang, D. Pan, Y. Wang, Y. Liu, Y. Luo, J. Yang, B. Li, S. Dunn and H. Yan, Small, 2024, 20, 2306786 Search PubMed.
- T. P. Bailey and C. Uher, Curr. Opin. Green Sustainable Chem., 2017, 4, 58–63 CrossRef.
- H. Hu, K. Xia, T. Zhu and X. Zhao, Chin. J. Rare Met., 2021, 45, 513–529 Search PubMed.
- C. Yang, Y. Xia, L. Xu, Y. Luo, X. Li, Z. Han and J. Cui, Chem. Eng. J., 2021, 426, 131752 CrossRef CAS.
- W. Li, S. Lin, M. Weiss, Z. Chen, J. Li, Y. Xu, W. G. Zeier and Y. Pei, Adv. Energy Mater., 2018, 8, 1800030 CrossRef.
- C. Yang, Y. Luo, X. Li and J. Cui, RSC Adv., 2021, 11, 3732–3739 RSC.
- B. K. Heep, K. S. Weldert, Y. Krysiak, T. W. Day, W. G. Zeier, U. Kolb, G. J. Snyder and W. Tremel, Chem. Mater., 2017, 29, 4833–4839 CrossRef CAS.
- Q. Jiang, S. Li, Y. Luo, J. Xin, S. Li, W. Li, G. Zhao and J. Yang, ACS Appl. Mater. Interfaces, 2020, 12, 54653–54661 CrossRef CAS PubMed.
- I. J. Alverdiev, S. M. Bagheri, Z. M. Aliyeva, Y. A. Yusibov and M. B. Babanly, Inorg. Mater., 2017, 53, 786–796 CrossRef CAS.
- C. Xiao, J. Xu, K. Li, J. Feng, J. Yang and Y. Xie, J. Am. Chem. Soc., 2012, 134, 4287–4293 CrossRef CAS PubMed.
- L. L. Zhao, X. L. Wang, J. Y. Wang, Z. X. Cheng, S. X. Dou, J. Wang and L. Q. Liu, Sci. Rep., 2015, 5, 7671 CrossRef CAS PubMed.
- L. Hu, T. Zhu, X. Liu and X. Zhao, Adv. Funct. Mater., 2014, 24, 5211–5218 CrossRef CAS.
- D. Zhang, J. Yang, Q. Jiang, Z. Zhou, X. Li, J. Xin, A. Basit, Y. Ren, X. He, W. Chu and J. Hou, ACS Appl. Mater. Interfaces, 2017, 9, 28558–28565 CrossRef CAS PubMed.
- J. L. Wang, W. L. Fan, J. Yang, Z. L. Da, X. F. Yang, K. M. Chen, H. Yu and X. N. Cheng, Chem. Mater., 2014, 26, 5647–5653 CrossRef CAS.
- W. Mi, P. Qiu, T. Zhang, Y. Lv, X. Shi and L. Chen, Appl. Phys. Lett., 2014, 104, 133903 CrossRef.
- X. Shen, C.-C. Yang, Y. Liu, G. Wang, H. Tan, Y.-H. Tung, G. Wang, X. Lu, J. He and X. Zhou, ACS Appl. Mater. Interfaces, 2018, 11, 2168–2176 CrossRef PubMed.
- E. Gaudin, F. Boucher, M. Evain and F. Taulelle, Chem. Mater., 2000, 12, 1715–1720 CrossRef CAS.
- C. Xiao, J. Xu, K. Li, J. Peng, J. Yang and Y. Xie, J. Am. Chem. Soc., 2012, 134, 4287–4293 CrossRef CAS PubMed.
- D. Byeon, R. Sobota, K. Delime-Codrin, S. Choi, K. Hirata, M. Adachi, M. Kiyama, T. Matsuura, Y. Yamamoto, M. Matsunami and T. Takeuchi, Nat. Commun., 2019, 10, 72 CrossRef CAS PubMed.
- E. Deligoz, H. Ozisik and E. Bolen, Inorg. Chem. Commun., 2022, 142, 109689 CrossRef CAS.
- C. Chang and L. D. Zhao, Mater. Today Phys., 2018, 4, 50–57 CrossRef.
- K. S. Weldert, W. G. Zeier, T. W. Day, M. Panthofer, G. J. Snyder and W. Tremel, J. Am. Chem. Soc., 2014, 136, 12035–12040 CrossRef CAS PubMed.
- J. Xin, J. Yang, S. Li, A. Basit, B. Sun, S. Li, Q. Long, X. Li, Y. Chen and Q. Jiang, Chem. Mater., 2019, 31, 2421–2430 CrossRef CAS.
- S. Lin, W. Li, S. Li, X. Zhang, Z. Chen, Y. Xu, Y. Chen and Y. Pei, Joule, 2017, 1, 816–830 CrossRef CAS.
- B. Jiang, P. Qiu, H. Chen, J. Huang, T. Mao, Y. Wang, Q. Song, D. Ren, X. Shi and L. Chen, Mater. Today Phys., 2018, 5, 20–28 CrossRef.
- Z. H. Yu, X. X. Wang, C. Y. Liu, Y. R. Cheng, Z. W. Zhang, R. F. Si, X. B. Bai, X. K. Hu, J. Gao, Y. Peng and L. Miao, J. Adv. Ceram., 2022, 11, 1144–1152 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |