Open Access Article
Open Access ArticleInvestigation of the intermolecular origins of high and low heats of fusion in azolium salt phase change materials for thermal energy storage†
Saliha
Saher
 a,
Samantha L.
Piper
a,
Samantha L.
Piper
 a,
Craig M.
Forsyth
a,
Craig M.
Forsyth
 a,
Mega
Kar
a,
Mega
Kar
 b,
Douglas R.
MacFarlane
b,
Douglas R.
MacFarlane
 *a,
Jennifer M.
Pringle
*a,
Jennifer M.
Pringle
 b and
Karolina
Matuszek
b and
Karolina
Matuszek
 *a
*a
aSchool of Chemistry, Monash University, Clayton, VIC 3800, Australia. E-mail: Karolina.Matuszek@monash.edu
bInstitute for Frontier Materials, Deakin University, 221 Burwood Highway, Burwood, VIC 3125, Australia
First published on 20th February 2024
Abstract
Renewable energy sources remain largely underutilised due to their intermittent nature. One potential solution is to store renewable thermal energy in phase change materials (PCMs), which absorb and release energy in a reversible phase transition. A clear understanding of the molecular origins of heat of fusion (ΔHf) is required to design efficient PCMs. In the present work, the thermal energy storage potential of imidazolium and 1,2,4-triazolium organic salts is investigated and compared with analogous pyrazolium salts. The studied azolium salts have melting points in the intermediate temperature range, which is ideal for renewable energy storage. To probe the origins of the heat of fusion, comparative single crystal X-ray diffraction and Hirshfeld surface analysis with pyrazolium salts showed that a mix of canonical and bifurcated H-bonds exist in the solid state structures of the azolium salts. The H-bonds play a crucial role in driving high ΔHf, as shown by 1,2,4-triazolium benzenesulfonate [Tri][C6H5SO3] and 1,2,4-triazolium trifluoromethansulfonate [Tri][CF3SO3] which have strong canonical H-bonds and high ΔHf (28 kJ mol−1). Conversely, all chloride salts (imidazolium chloride, pyrazolium chloride and 1,2,4-triazolium chloride) display the lowest values of ΔHf due to very weak H-bonding. Interestingly, strong H-bonding in the bisulfate salts has not resulted in high ΔHf. This is probably due to relatively little disruption of the H-bonds during melting and highlights the need for studies of the molten states to determine the whole picture. Additional factors including efficient crystal packing, solid–solid phase transitions, and repulsive interactions between anions also significantly influence ΔHf. This study thereby shows that azolium salts can be used to design intermediate temperature PCMs for renewable thermal energy storage.
Introduction
With the continuous rise of energy demand and the climate crisis, the need to efficiently utilise renewable energy sources is becoming increasingly urgent. Solar and wind energy have immense potential to fulfil global energy needs, but their intermittency necessitates the development of energy storage systems. Since nearly 90% of global energy consumption entails the production and manipulation of thermal energy in domestic, agricultural and industrial settings, the development of low-cost thermal energy storage technologies would be most impactful solution to the energy crisis.1 Thermal energy technologies are based on the change in internal energy of storage media by the reversible uptake of heat (e.g. from solar thermal, solar PV or wind driven electrical heating, or waste industrial heat). The change in internal energy can occur as a sensible, latent, thermochemical or a combination of these processes.2,3 Sensible heat storage (SHS) is simply a rise and fall in temperature as the material is heated or cooled and is based on its heat capacity. SHS has the lowest energy storage capacity and involves a wide temperature range for storage. Thermochemical energy storage (TCS) systems, on the other hand, can have enormously high energy storage densities, but often involve complex chemical reactions that are only sluggishly reversible; these are in an early stage of research and development.4 Latent heat storage (LHS), in which the energy is stored in a phase change of a material, is becoming a more popular thermal energy storage technique due to its ease of operation and high energy storage and release capacity over a narrow temperature range.5Phase change materials (PCMs) are materials that absorb and release latent heat during a reversible phase transition over a specified temperature range. The most common PCMs are solid to liquid PCMs, which involve energy intake (charging) during melting of the solid and release of the energy when the liquid crystallises into a solid. The melting points of useful PCMs vary from sub-ambient to 1000 °C,6 which means they can be used in diverse scenarios from cold chain transport (<20 °C)7 to solar energy storage (>200 °C).8 The PCMs with melting points of 100–220 °C (“intermediate temperature PCMs”) have recently been identified as valuable for solar and wind energy storage.9,10 This temperature is regularly achieved in vacuum tube solar thermal collectors and well-matched for diverse applications including domestic and industrial heat supply,11 hot water production, space heating, electricity generation in organic Rankine cycle (ORC) engines12 and for surplus electricity storage as thermal energy in a Carnot battery.13 While a plethora of PCMs have been reported, there is a scarcity of efficient intermediate temperature PCMs.
Among inorganic PCMs, metals and metal alloys often have high enthalpies of fusion but also have high melting points [e.g. Al (Tm = 661 °C, ΔHf = 388 J g−1), 88Al–12Si alloy (Tm = 576 °C, ΔHf = 560 J g−1)].14–16 Salt hydrates such as Na2CO3·10H2O (Tm = 33 °C, ΔHf = 247 J g−1) and MgCl2·6H2O (Tm = 111 °C, ΔHf = 155 J g−1) have high ΔHf values due to extensive H-bonding networks, however, they remain in a liquid state well below their melting point (i.e., supercool) and undergo incongruent melting, phase separation and sedimentation in storage containers.2,17–19 Organic PCMs including paraffins [e.g. n-tetradecane (Tm = 6 °C, ΔHf = 227 J g−1)],19,20 fatty acids [e.g. palmitic acid (Tm = 62 °C, ΔHf = 212 J g−1)],21 polyols [e.g. galactitol (Tm = 187 °C, ΔHf = 357 J g−1)],22 esters, and small organic compounds, may have a set of desired properties like congruent melting, high ΔHf values, and minimal corrosivity, but they collectively suffer from flammability, significant volatility and low thermal conductivity which leads to slower heat transfer rate and slower charging/discharging.23,24
Recently, the solid-state analogues of ionic liquids, i.e., organic salts, have been identified as promising PCMs.25–27 The inherent properties of ionic liquids such as non-flammability, non-volatility, high thermal and chemical stability, and higher energy storage density can circumvent some of the issues with traditional organic PCMs.26 Additionally, the thermal behaviour of organic salts can be adjusted by subtle alterations to the structure of the cation or anion.26 However, achieving the tunability of properties in organic salts is challenging as there is a lack of sufficient fundamental understanding of the origins of high ΔHf and how it relates to the structure of the ions.
Preliminary reports on organic salt-based PCMs used imidazolium,25 pyrazolium,27,28 thiazolium,29 guanidinium,30,31 formamidinium and acetamidinium32 cations. The melting point of many of these salts is in the intermediate temperature range, with promising enthalpies, for example up to 190 J g−1 for guanidinium mesylate, which is stable up to 400 heating–cooling cycles.31 A family of pyrazolium salts also showed great potential to be used as PCMs for intermediate temperature application; the pyrazolium mesylate (Tm = 168 °C, ΔHf = 160 J g−1) is stable up to 130 cycles and is estimated to potentially provide over ten times cheaper energy storage than lithium batteries.27 A recent study of guanidinium, acetamidinium and formamidinium salts highlights that the presence of linear and short H-bonds increases the enthalpy of fusion and it is suggested that matching the number of H-bond donor and acceptor sites can lead to strong and effective H-bonds.32,33
Herein we describe imidazolium and 1,2,4-triazolium salts as potential phase-change materials. The molecular level origins of the high and low melting enthalpies are investigated by studying the intermolecular interactions in the solid state via the use of single crystal X-ray crystallography and Hirshfeld surface analysis. The imidazolium and 1,2,4-triazolium salts are compared with previously reported, structurally similar, pyrazolium salts.
Experimental
Synthesis of azolium salts
Azolium salts were synthesised by dissolving 10 mmol of imidazole/1,2,4-triazole in 20 mL methanol followed by equimolar addition of the acid corresponding to the anion of the target salt. The reaction mixture was stirred at room temperature for two hours to ensure the reaction completion. The subsequent solution was concentrated by rotary evaporation followed by drying under vacuum (0.2 mbar, 40 °C–50 °C) for 24–48 hours. For triazolium salts, the temperature during vacuum drying should not exceed 50 °C to prevent the sublimation of the product. All salts were obtained as white solids and stored in a nitrogen glove box. Synthesis of the product was confirmed by 1H and 13C nuclear magnetic resonance spectroscopy (NMR, SI).Single crystal growth
Thermal analysis
Melting points (Tm), solid–solid transitions (Ts–s), crystallisation points (Tc), enthalpy of fusion (ΔHf), and enthalpy of crystallization (ΔHc) were recorded using a TA Q600 differential scanning calorimeter. The equipment was calibrated using indium (Tm = 156.6 °C, ΔHf = 28.45 J g−1) and cyclohexane (Tm = 6.47 °C) standards. Measurements were performed in triplicate under nitrogen atmosphere (N2 flow rate of 50 mL min−1) using 5–10 mg of sample sealed in an aluminium pan with heating and cooling rate of 10 °C min−1 and 1 minute isothermal at both temperatures ends. Thermal data was recorded from the second heating/cooling cycle. Tm was determined by the peak maxima (recognising that this represents a slight overestimate) and ΔHf was calculated by integrating the area under the endothermic transition curve, with Universal Analysis software.Thermal stability was ascertained by thermogravimetric analysis using a PerkinElmer Pyris 1 TGA with Pyris Software over a range of 25–550 °C under N2 (30 mL min−1), at a heating rate of 10 °C min−1. Decomposition temperatures, Td, were estimated from the onset of weight loss.
X-ray crystallography
Data for pyrazolium salts, two imidazolium salts ([Im][CH3SO3] and [Im][C2H5SO3]),34 and two triazolium salts ([Tri]Cl35 and [Tri][CH3SO3]36) was obtained from the Cambridge Crystallographic Data Centre. Data for all other salts was collected on a Rigaku Xtalab Synergy Dualflex using a monochromator equipped with Cu-Kα (λ = 1.5418 Å) radiation, at 123 K. All structures were solved and refined by the SHELX software suite37 and refined against F2 using Olex238 as a graphical user interface. Crystal and refinement data are listed in the ESI.†Results and discussion
Comparative analysis of imidazolium, pyrazolium and triazolium salts
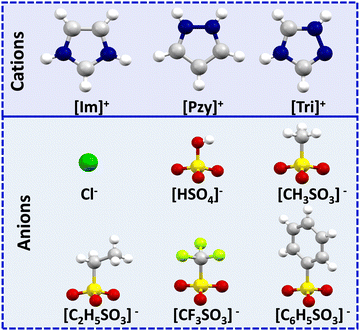
Organic salts of imidazolium [Im]+, pyrazolium [Pzy]+ and 1,2,4-triazolium [Tri]+ with anions chloride (Cl−), bisulfate [HSO4]−, methanesulfonate [CH3SO3]−, ethanesulfonate [C2H5SO3]−, trifluoromethanesulfonate [CF3SO3]−, and benzenesulfonate [C6H5SO3]− are studied here as potential intermediate temperature PCMs. The chemical structures and abbreviations of the cations and anions are given in Fig. 1. While three triazolium salts, ([Tri][C2H5SO3], [Tri][CF3SO3], [Tri][C6H5SO3]) are novel, the remainder of the salts have been reported in the literature,27,35,39,40 but only the pyrazolium salts have been investigated as thermal energy storage materials.27 These are revisited here with analogous imidazolium and triazolium salts to investigate the trends in their thermal properties, specifically enthalpies of fusion (ΔHf). This comparison will provide guidelines to inform future PCM design for thermal energy storage.The thermal properties of the salts, including melting points (Tm) and melting enthalpies (ΔHf), any solid–solid transitions (Ts–s) and associated enthalpy (ΔHs–s), the total entropy of phase transition (ΔSf) and decomposition onset temperature (Td) are detailed in Table 1. The melting enthalpy is often reported in J g−1, which is useful to compare energy storage capacity per unit mass of PCMs. However, while looking at the molecular level correlations, enthalpy in kJ mol−1 is more useful, hence it is these values that are discussed here. The thermal data is tabulated as groups of salts with a common anion to closely examine their properties with respect to cation structure. The imidazolium series contains the lowest melting point (Tm = 76 °C for [Im][HSO4]) as well as highest melting point salt (Tm = 195 °C for [Im][CH3SO3]). On the other hand, the pyrazolium series contains salts of the lowest transition enthalpy (ΔHf = 6 kJ mol−1 for [Pzy][CF3SO3]) and salts with enthalpies as high as 26 kJ mol−1 for [Pzy][CH3SO3]. Some of the salts in each cation series show single or multiple solid–solid transitions, which lowers the ultimate melting enthalpy as reported for some pyridinium salts.41 Studied salts showed supercooling between 14 °C (for [Im][CF3SO3]) to 63 °C (for [Tri][HSO4]), however, this is a stochastic phenomenon that depends on the volume of the sample, which is very small in the present studies. In application, the volume of material will be many orders of magnitude larger, which will minimise supercooling. Classically, this can also be improved by the addition of nucleators. It is obvious that both cation and anion influence the thermal behaviour of the salt. However, understanding inter-ionic interactions and their consequent effects on crystal packing in the solid state and on melting enthalpy is crucial. Herein we use single crystal X-ray crystallography and Hirshfeld surface analysis to visualise and quantify various intermolecular interactions in the solid state and investigate their subsequent effects on the thermal properties of the salts under investigation. Organic salts/ionic liquids have a unique combination of Coulombic forces, H-bonding, van der Waals and dispersion interactions. Subtle differences in interionic interactions due to changes in the chemical structure of constituent ions account for their diverse properties.42,43 Previous studies of the intermolecular interactions in imidazolium salts showed that about 70% of the interaction energy originates from Coulombic forces and rest of the interaction energy comes from H-bond and dispersion interactions.44 These Coulombic forces play a crucial role in determining the different properties of organic salts. For instance, weaker Coulombic forces in ionic liquids are responsible for their lower melting point compared to conventional inorganic salts.45 However, since we are investigating the energy changes involved during phase transitions (melting), it is important to consider that these long-range, non-directional Coulombic interactions are not greatly disrupted during the melting of an organic salt and continue to exist in liquid phase. On the other hand, short-range, directional interactions like H-bonding are expected to be significantly disrupted due to the loss of directionality of H-bonding and the enhanced movement of ions.46
| Anion | Cation | T m, °C ± 2 °C | T S–S, °C ± 2 °C | ΔHf, J g−1 ± 5% | ΔHs-s, J g−1 ± 5% | ΔHtotal, J g−1 ± 5% | ΔHtotal, kJ mol−1 ± 5% | ΔStotal (J mol−1 K−1) | T d onset, °C ± 2 °C |
|---|---|---|---|---|---|---|---|---|---|
| T m – melting point, Ts–s – solid–solid transition point, ΔHf – melting enthalpy, ΔHs–s – enthalpy of solid–solid transition, ΔHtotal – total enthalpy of melting and solid–solid transition, ΔStotal = total entropy change during melting and solid–solid transition and Td = decomposition onset determined from TGA. | |||||||||
| Cl | [Im] | 160 | — | 96 | — | 96 | 10 | 23 | 246 |
| [Pzy]27 | 112 | — | 80 | — | 80 | 8 | 22 | 91 | |
| [Tri] | 173 | 156 | 88 | 21 | 101 | 11 | 26 | 197 | |
| [HSO4] | [Im] | 76 | 44 | 37 | 13 | 50 | 6 | 24 | 266 |
| [Pzy]27 | 122 | — | 115 | — | 115 | 19 | 48 | 183 | |
| [Tri] | 97 | — | 95 | — | 95 | 16 | 43 | 272 | |
| [CH3SO3] | [Im] | 195 | 177 | 71 | 82 | 153 | 25 | 55 | 300 |
| [Pzy]27 | 168 | — | 160 | — | 160 | 26 | 59 | 206 | |
| [Tri] | 137 | — | 133 | — | 133 | 22 | 53 | 286 | |
| [C2H5SO3] | [Im] | 158 | 77, 130 | 97 | 8, 25 | 130 | 23 | 55 | 306 |
| [Pzy]27 | 113 | — | 108 | — | 108 | 19 | 50 | 156 | |
| [Tri] | 93 | — | 113 | — | 113 | 20 | 55 | 294 | |
| [CF3SO3] | [Im] | 195 | 32, 103, 162 | 36 | 25, 5, 5 | 71 | 15 | 40 | 370 |
| [Pzy]27 | 147 | 59, 95 | 27 | 17, 24 | 68 | 15 | 40 | 258 | |
| [Tri] | 168 | — | 129 | — | 129 | 28 | 64 | 356 | |
| [C6H5SO3] | [Im] | 113 | — | 108 | — | 108 | 24 | 63 | 364 |
| [Pzy]27 | 137 | — | 105 | — | 105 | 24 | 57 | 184 | |
| [Tri] | 144 | — | 123 | — | 123 | 28 | 67 | 323 | |
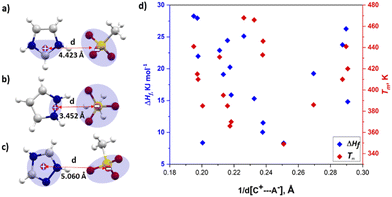
To investigate the correlation between thermal properties and interionic distance in azolium salts, the inter-centroid distance between the closest oppositely charged ions [d(C+⋯A−)] was taken as a measure of the strength of Coulombic ion pair binding energy. The positive charge was assumed to be spread over two nitrogen atoms and the central carbon (N–C–N) in imidazolium, two adjacent nitrogen atoms in pyrazolium and all five atoms in the 1,2,4-triazolium ring. The centroid of the three oxygen atoms in the sulfonate was taken as the position of negative charge in the sulfonate anion, as shown in Fig. 2a–c. According to Coulomb's law, the electrostatic force is inversely proportional (1/r) to the distance between pairs of ions. We hypothesised that a shorter interionic distance [d(C+⋯A−)] would result in higher melting enthalpy, due to the stronger interactions, if changes in these forces are significant in ΔHf. Fig. 2d shows a plot of ΔHfversus inverse of interionic distance (1/d(C+⋯A−), Å); there is no obvious correlation in the data, and the correlation did not improve when excluding data points for salts with solid–solid transitions (see Fig. S1, ESI†). Although the reciprocal of distance only varies over a narrow range of 0.19 Å–0.25 Å, indicating that the electrostatic forces do not vary widely in the studied azolium salts.
Therefore, it appears that changes in electrostatic forces do not play a decisive role in generating differences in the melting enthalpies of salts.
Hydrogen-bonding
Despite their ionic nature, H-bonds are a distinctive feature in many ionic liquids/organic salts and their influence on various properties is recognised to be important but not clearly understood.47In the present work, we investigate any possible relationship between the strength of H-bonds in these organic salts and their melting enthalpies. Estimating the strength of an H-bond by geometric parameters is well established in the literature, with shorter and more linear H-bonds being recognized as stronger interactions than those with longer and less linear H-bonds.48,49 Due to uncertainty in the position of H-atoms in the crystallographically determined structures, we relied on distances between non-hydrogen heavy atoms, i.e. the H-bond donor (D) and H-bond acceptor (A), as an indicator of an H-bond strength, along with the H-bond angle [∠(D-H⋯A)]. In the azolium salts, canonical H-bonds (one H-bond donor interacts with only one H-bond acceptor) and bifurcated H-bonds (H-bond donor interacts with two H-bond acceptors or vice versa) were also observed. Bifurcated H-bonds are known to be weaker than canonical H-bonds.50 Beyond these observations, various unique trends were observed across individual salt series, which are discussed in detail in the following sections.
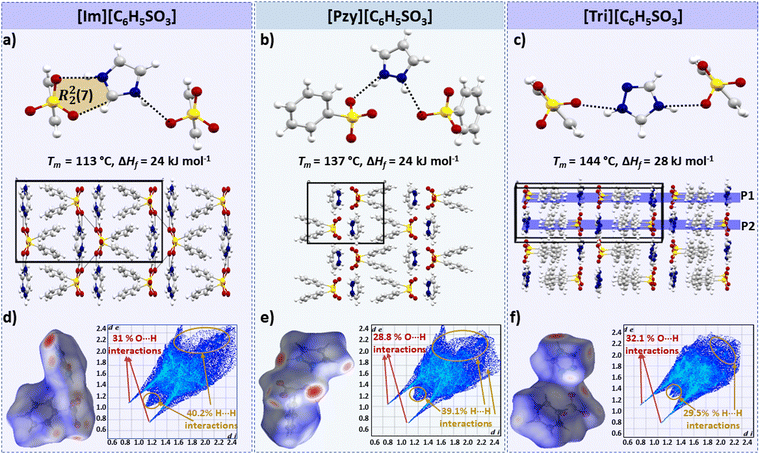
Benzenesulfonate salts
In this series [Tri][C6H5SO3] has the highest enthalpy of fusion (ΔHf = 28 kJ mol−1) followed by [Im][C6H5SO3] and [Pzy][C6H5SO3], which both melt with an ΔHf of 24 kJ mol−1 (the errors in these data are +/− 1 kJ mol−1, hence we believe this difference to be significant). All three salts have two H-bonds (N–H⋯O) per cation (Fig. 3). The H-bonds in imidazolium [(d(N1⋯O1) = 2.776 Å, ∠(N1–H1⋯O1) = 162.6°) and (d(N2⋯O2) = 2.843 Å, ∠(N2–H2⋯O2) = 167.2°)] and pyrazolium [(d(N1⋯O1) = 2.720 Å, ∠(N1–H1⋯O1) = 168.5°) and (d(N1⋯O1) = 2.776 Å, ∠(N2–H2⋯O2) = 160.5°)] are quite similar, which is consistent with their similar enthalpies of fusion. The imidazolium cation is acidic and interacts with the benzenesulfonate anion forming an R22(7) motif (Fig. 3a); the R22(7) motif is a graph-theory-based systematic presentation of unique H-bond motifs.51 Here this interaction is presumably weak due to its non-linearity (∠(C–H⋯O) = 114.83°, d(C⋯O) = 2.979 Å). Therefore, this H-bond may not significantly contribute towards ΔHf.On the other hand, the H-bonds in [Tri][C6H5SO3] are significantly less linear [(d(N2⋯O1) = 2.697 Å, ∠(N2–H2⋯O1) = 141.5°) and (d(N3⋯O3) = 2.720 Å, ∠(N3–H3⋯O3) = 157.2°)] compared to the imidazolium and pyrazolium salts, which indicates that other parameters such as crystal packing also have a strong influence on ΔHf.
The benzenesulfonate series demonstrates the influence of crystal packing on the enthalpy of fusion. The crystal density can be used as an indicator of the compact packing in benzene sulfonate salts. [Tri][C6H5SO3] has a more ordered and compact packing, having adjacent benzene sulfonate anions in parallel planes. [Tri][C6H5SO3] has slightly higher density at −150 °C (1.575 g cm−3), compared to 1.503 g cm−3 and 1.509 g cm−3 for [Im][C6H5SO3] and [Pyz][C6H5SO3] respectively. [Im][C6H5SO3] and [Pyz][C6H5SO3] have adjacent benzene sulfonate rings in non-parallel planes, like a butterfly's open wings, as shown in Fig. 3a and b. Moreover, the distance between the two parallel planes in the triazolium salts is the outcome of a slightly longer H-bond in the imidazolium salt as can be seen in its lower Tm = 113 °C. Moreover, the distance between the two parallel planes in [Tri][C6H5SO3] is 4.074 Å, and there may be π–π stacking indicating more efficient crystal packing that can therefore contribute to the higher melting enthalpy of this salt.
It should be noted that despite the disorder in the crystal structure of [Tri][C6H5SO3], no solid–solid transition was observed in the tested temperature range (−150 °C to 160 °C). Also, a significantly high observed entropy of fusion (ΔSf = 67 J mol−1 K−1) decreases the likelihood of there being any solid–solid transition below −150 °C. It is likely that the bulky benzenesulfonate anions restrict the rotations and prevent any significant thermal movement (i.e. solid–solid phase transitions) prior to the melting transition.
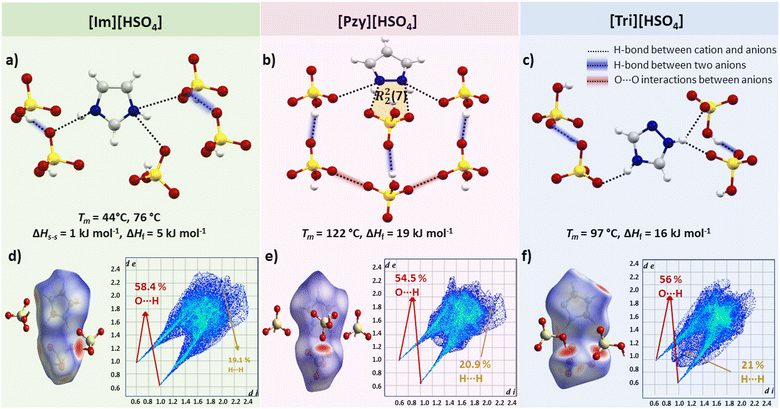
Another approach for comparative analysis of interactions in similar compounds using the Hirshfeld surface analysis, which is a unique way to visualize and quantify the intermolecular interactions at the whole molecule level in a crystal lattice with the possibility of quantifying individual atom⋯atom contacts.52,53 The Hirshfeld surface is the region of space in a crystal where the sum of electron density of the molecules within the surface is equal to the sum of the electron density contribution from the rest of the crystal. The distance of nuclei inside the surface (di) and external (de) to the Hirshfeld surface is shown in a colour-coded 3D image, where red regions indicate the short interactions (the distance between the outer and inner nuclei is less than the sum of their van der Waals radii), blue colouration shows weaker/distant interactions with internuclear distances greater than the sum of the radii of the interacting atoms (white areas show interactions with internuclear distance approximately equal to the sum of the van der Waals radii).52 Hirshfeld surfaces can also be presented as a 2D histogram, referred to as a fingerprint plot, of the surface obtained by putting (di, de pairs) in bins at 0.01 Å intervals and colour coding each bin according to the fraction of the surface points falling in that bin from blue (few points) through green to red (many points).52
Hirshfeld surface plots for the three benzenesulfonate salts are shown in Fig. 3(d–f). The fingerprint plot of [Tri][C6H5SO3] has a slightly different shape to the other two plots, with two sharp spikes corresponding to short O–H interactions (32% of total Hirshfeld surface) and has di and de distances <2.4 Å. The [Im][C6H5SO3] and [Pzy][C6H5SO3] salts have Hirshfeld fingerprint plots with two sharp spikes corresponding to O–H interactions and one relatively broad spike for H–H interactions. The significant difference in the Hirshfeld surface of these two salts compared to [Tri][C6H5SO3] indicates that the C–H interactions are elongated (di–de exceeding 2.4 Å), potentially leading to slightly lower ΔHf and Tm than in [Tri][C6H5SO3].
Overall, benzenesulfonate salts show that efficient crystal packing and the presence of strong H-bonding interactions may significantly contribute towards high ΔHf.
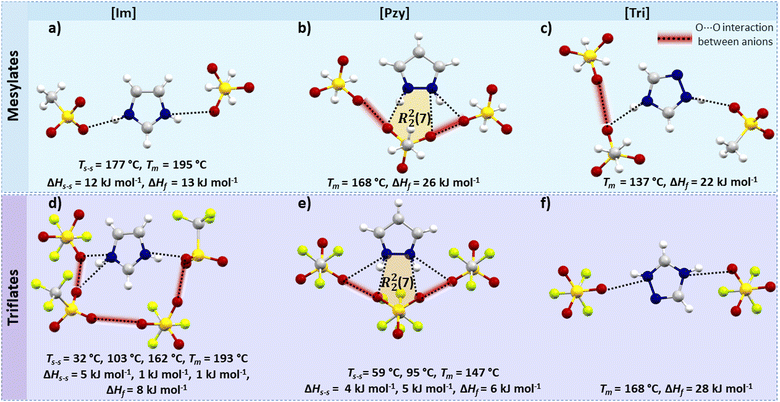
Mesylate salts
A trend of increasing melting enthalpy with increase in H-bond strength in mesylate salts of guanidinium, formamidinium and acetamidinium was reported earlier by Piper et al.32 The azolium mesylate salts studied here partly support this observation, as [Pzy][CH3SO3] and [Tri][CH3SO3] have stronger H-bonds than [Im][CH3SO3] and have higher melting enthalpy. The H-bonding pattern in all mesylate salts is shown in Fig. 4(a–c). There are two canonical H-bonds per cation in both [Im][CH3SO3] (Tm = 195 °C, ΔHf = 13 kJ mol−1) and [Tri][CH3SO3] (Tm = 137 °C, ΔHf = 22 kJ mol−1), however, the average length of the H-bonds in the latter is shorter by 0.135 Å and more linear by almost 9°. This could explain the lower enthalpy of [Im][CH3SO3], but the presence of a high energy solid–solid transition prior to melting (ΔHs–s = 12 kJ mol−1, Ts–s = 177 °C) in [Im][CH3SO3] complicates the situation. Goward et al.,54 studied [Im][CH3SO3] as a proton-conducting material and showed that the solid–solid transition in imidazolium mesylate originates from the reorientation of the imidazolium ring around the C2-axis, as indicated by solid state NMR. Further, Luo et al.,36 verified the thermal transition before melting in [Im][CH3SO3] with the help of variable temperature powder XRD and DSC. Similar thermal motions of imidazolium cations are expected to be responsible for the multiple solid–solid phase transitions in most of the tested imidazolium salts.[Pzy][CH3SO3] has the highest enthalpy among the three mesylate salts (Tm = 168 °C, ΔHf = 26 kJ mol−1). In comparison to two strong canonical H-bonds (avg. d(N⋯O) = 2.731 Å, ∠(N–H⋯O) = 168.18°) in [Tri][CH3SO3], the pyrazolium salt has one canonical (d(N⋯O) = 2.723 Å, ∠(N–H⋯O) = 169.06°) and two bifurcated H-bonds of varying strength. The bifurcated H-bonds are weaker than the canonical H-bond, but collectively the three H-bonds in [Pzy][CH3SO3] and the formation of H-bond ring motif R22(7) may be responsible for the higher melting enthalpy of this compound.
It is interesting that a mesylate anion in the [Pzy][CH3SO3] interacts with two neighbouring mesylate anions, with interatomic distances d(O1⋯O1) = 2.829 Å and d(O2⋯O2) = 2.991 Å. Similarly, mesylate anions in [Tri][CH3SO3] interact with one neighbouring mesylate [d(O⋯O) = 2.960 Å]. We hypothesise that these anionic interactions may be repulsive and lead to destabilization of the crystal structure, but the effect is not yet fully understood.
The Hirshfeld surface (Fig. S55, ESI†) shows that [Pzy][CH3SO3] and [Tri][CH3SO3] have relatively sharp spikes towards short distances, corresponding to strong O⋯H, H-bonds, constituting 42% and 41% of total Hirshfeld surface. The [Pzy][CH3SO3] have higher fraction of H⋯H interactions (36% of surface) than [Tri][CH3SO3] (26%), which may be correlated with a higher ΔHf in [Pzy][CH3SO3]. In comparison, [Im][CH3SO3], despite having higher fraction of O⋯H interactions (46%) has lower ΔHf, mainly due to the material undergoing solid–solid phase transitions.
Overall, this analysis of intermolecular interactions in mesylate salts showed that a higher number of bifurcated H-bonds, forming a ring motif, may lead to higher ΔHf than a lower number of canonical H-bonds.
Triflate salts
The triflate salts show interesting variations in the thermal properties with small changes in the chemical structure of the cation. The triflate anion, which has an electron withdrawing CF3 group, was anticipated to have reduced H-bond forming ability due to lower electron density on the O atoms. The H-bond distance in the salts was not greatly altered in comparison to the mesylate salts, but the linearity was significantly affected. Surprisingly, [Tri][CF3SO3] showed a high melting enthalpy (Tm = 168 °C, ΔHf = 28 kJ mol−1), comparable to the best reported organic salt PCMs i.e. guanidinium mesylate (Tm = 208 °C, ΔHf = 29 kJ mol−1).31 In contrast, [Im][CF3SO3] and [Pzy][CF3SO3] show multiple solid–solid transitions and low melting enthalpies, features unfit for application as a PCM but potentially useful for solid electrolytes.55,56 [Im][CF3SO3] has three solid–solid transitions at 32 °C (ΔHs–s = 5 kJ mol−1, ΔSs–s = 17 J mol−1 K−1), 103 °C (ΔHs–s = 1 kJ mol−1, ΔSs–s = 3 J mol−1 K−1), and 162 °C (ΔHs–s = 5 kJ mol−1, ΔSs–s = 17 J mol−1 K−1) before melting (Tm = 193 °C, ΔHf = 8 kJ mol−1). The solid–solid phase transitions are thought to originate from local conformational or rotational motions in the otherwise long-range ordered crystal lattice.57 [Pzy][CF3SO3] undergoes two solid–solid transitions at 59 °C (ΔHs–s = 4 kJ mol−1, ΔSs–s = 11 J mol−1 K−1) and 95 °C (ΔHs–s = 4 kJ mol−1, ΔS = 14 J mol−1 K−1) before melting (Tm = 147 °C, ΔHf = 6 kJ mol−1) and also shows plastic crystal behaviour.27The crystallographic analysis showed that [Im][CF3SO3] has three H-bonds per cation with three neighbouring triflate anions (Fig. 4(d and e)); one canonical [d(N–H⋯O) = 2.843 Å, ∠(N–H⋯O) = 173.78° and two unique bifurcated H-bonds [d(N–H⋯O) = 2.969 Å, ∠(N–H⋯O) = 136.05° and d(N–H⋯O = 2.846 Å, ∠(N–H⋯O) = 137.98°]. In [Pzy][CF3SO3], the pyrazolium cation is interacting with three triflate anions by four bifurcated H-bonds. Two equivalent H-bonds (d(N–H⋯O = 2.888 Å, ∠(N–H⋯O) = 154.06° with one triflate anion form a ring R22 (7) motif and two outer H-bonds (d(N–H⋯O = 2.949 Å, ∠(N–H⋯O) = 124.91° are formed with separate triflate anions.
[Tri][CF3SO3] has two canonical and shorter H-bonds [d(N2⋯O1 = 2.747 Å, ∠(N2–H2⋯O1) = 143.64° and (d(N1⋯O2 = 2.768 Å, ∠(N1–H1⋯O2) = 158.54°], and consequently has the highest ΔHf among three azolium salts. Additionally, [Tri][CF3SO3] has higher calculated density 1.915 g cm−3 (at −150 °C), than [Pzy][CF3SO3] (ρ = 1.778 g cm−3 at −100 °C) and [Im][CF3SO3] (ρ = 1.769 g cm−3 at −150 °C). Given their similar molecular weights this higher density indicates greater crystal packing efficiency in [Tri][CF3SO3] and this may contribute to higher ΔHf.
An interesting structural feature that may contribute towards multiple solid–solid transitions and lower enthalpy of fusion in [Im][CF3SO3] and [Pzy][CF3SO3] is the possible repulsive interactions between triflate anions. The O⋯O contacts in [Im][CF3SO3] (d(O⋯O) = 2.925 Å to 2.965 Å) and [Pzy][CF3SO3] (d(O⋯O) = 2.870 Å) are shorter than the sum of van der Waals radii of two oxygen atoms, (3.02 Å) and therefore repulsive forces may develop, which destabilise the crystals. Such a system would be prone to rearrangements, as suggested by multiple solid–solid transitions. Such repulsive interactions were not observed for [Tri][CF3SO3], which has four anions around one triazolium cation sitting at a sufficient distance to avoid possible repulsive interactions in two parallel planes.
The Hirshfeld surfaces of the three salts differ significantly (Fig. S57, ESI†). [Im][CF3SO3] and [Tri][CF3SO3] have two sharp spikes of O⋯H interactions showing short distance H-bonds contributing to 39% and 32% of the Hirshfeld surface respectively. However, the imidazolium salt shows a spread of interactions toward longer internuclear distances, indicating weaker interactions and likely lower ΔHf than in [Tri][CF3SO3]. The [Pzy][CF3SO3] Hirshfeld surface plot shows much more compact and shorter spikes corresponding to O–H interactions (29%).
In summary, the crystallographic analysis of these triflate salts showed that a higher number of bifurcated H-bonds, even when forming a ring motif, are not always beneficial for higher enthalpy and factors like solid–solid transitions and the presence of repulsive interactions may lead to a lower enthalpy of fusion.
Bisulfate salts
Salts containing the bisulfate anion present a special case where H-bonds are found not only between adjacent cation–anion pairs but also between neighbouring anions. Interestingly, this salt series does not demonstrate high heats of fusion. For instance, in [Im][HSO4] each bisulfate anion is interacting with two neighbouring bisulfate anions by very linear [∠(O3–H3⋯O1) = 173.29°] and short [d(O3⋯O1) = 2.586 Å] H-bonds, in addition to one canonical [∠(N1–H1⋯O1) = 170.44°, d(N3⋯O2) = 2.861 Å] and two bifurcated H-bonds [∠(N2–H2⋯O2) = 137.02°, d(N2⋯O1) = 2.869 Å] and [(∠(N2–H2⋯O4) = 130.13°, d(N2⋯O3)= 2.895 Å] between the imidazolium cation and bisulfate anion, but the ΔHf is only 5 kJ mol−1. It is possible that strong H-bonds between bisulfate anions and one strong H-bond between the cation–anion remain unbroken or not greatly disrupted during melting therefore not much energy is absorbed. Another reason for these unusually low ΔHf could be the very hygroscopic nature of [Im][HSO4]. We faced difficulty reproducing the thermal behaviour due to quick moisture absorption. Its melting point also varies in the literature from 78 °C58 to 85 °C.59 [Im][HSO4] undergoes a solid–solid transition prior to melting (Ts–s = 44 °C, ΔHs–s = 1 kJ mol−1) with low entropy change ΔSs–s = 7 J mol−1 K−1. The enthalpy of melting is also low in [Im][HSO4] (Tm = 76 °C, ΔHf = 5 kJ mol−1, ΔSf = 18 J mol−1 K−1). This shows that [Im][HSO4] has too low ΔHf to be a potential PCM but may be useful in other applications.52,59 The H-bonding pattern in [Tri][HSO4] is similar to [Im][HSO4] i.e., a strong H-bond between two neighbouring bisulfate anions [∠(O4–H4⋯O1) = 176.07°, d(O4⋯O1) = 2.611 Å] and three H-bonds between a triazolium and bisulfate ion pair. However, [Tri][HSO4] has higher ΔHf probably due to two less linear but shorter H-bonds (one canonical [∠(N3–H3⋯O2) = 156.3°, d(N3⋯O2) = 2.783 Å] and one bifurcated H-bond [∠(N2–H2⋯O1) = 140.23°, d(N2⋯O1) = 2.756 Å]. The other bifurcated H-bond is longer with a less linear H-bond angle [(∠(N2–H2⋯O3) = 129.67°, (d(N2⋯O3) = 2.992 Å]). [Pzy][HSO4] has an even higher ΔHf of 19 kJ mol−1 and has four unique bifurcated H-bonds arranged around the cations (Fig. 5) in a similar way as in [Pzy][CH3SO3] and [Pzy][CF3SO3]. One H-bond is strong (d(N⋯O) = 2.780 Å and ∠(N–H⋯O) = 167.2°) and other three expected to be relatively weak due to poor geometry. In addition to cation–anion interactions, H-bonds between hydroxyl and oxygen of neighbouring anions were also found. The H-bond between two neighbouring anions in [Pzy][HSO4] appears to be quite strong (d(O⋯O) = 2.621 Å, ∠(O–H⋯O) = 178.52°) and likely contributes towards higher ΔHf.Hirshfeld surfaces of all three bisulfate salts, presented in Fig. 5, is particularly useful in visualising the H-bond among sulfate anions. The strong H-bond between bisulfate anions appear as red spots, and fingerprint plots show sharp spikes of O⋯H interactions which correspond to strong H-bonds constituting 58%, 54% and 56% of all interactions in [Im][HSO4], [Pzy][HSO4] and [Tri][HSO4] respectively. The second most frequent interaction, as indicated by Hirshfeld surface analysis, is the H⋯H interaction, contributing around 20% of all interactions in the bisulfate salts.
Conclusions
We have investigated the thermal properties of azolium salts and looked for probable relationships between the intermolecular interactions in the crystal structure and the melting enthalpy. A detailed comparative analysis of imidazolium, pyrazolium and triazolium salts showed that H-bonding is a pertinent intermolecular interaction, but no explicit trend could be observed. This may be due to the lesser density of hydrogen bonds in these structures, therefore other dominant interactions play a more significant role in determining ΔHf. Chloride salts, having the weakest H-bonds among the tested salts, have low enthalpies but bisulfate salts, having the strongest H-bonds, do not show high melting enthalpy. The presence of a H-bonding ring motif R22(7) seemed to be responsible for the higher ΔHf in [Pzy][CH3SO3] and [Pzy][HSO4] than in analogous salts. The plot of average H-bond distance and average H-bond length against ΔHf (azolium salts showing solid-solid transitions are excluded in this dataset) shows poor correlation between H-bond strength and melting enthalpy (Fig. 6). This poor correlation shows that other factors like anion–anion repulsive interactions, crystal packing tendencies and the presence of solid–solid phase transitions also influence ΔHf. Most of the salts have a combination of canonical and bifurcated H-bonds with different geometries, making it difficult to accurately estimate the individual strength of H-bonds and hence their influence on ΔHf. A further key factor is important to determine the intermolecular interactions in the liquid state of salts as the extent of their disruption during melting is the origin of high or low ΔHf.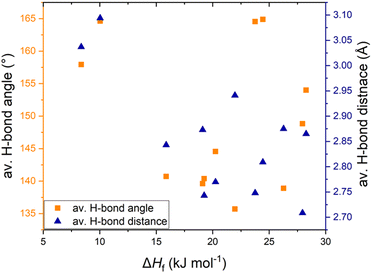 | ||
| Fig. 6 Relationship of ΔHf with average H-bond distance and average H-bond angle in studies salts (excluding salts with solid–solid transitions). | ||
In conclusion, the tested azolium salts have appropriate melting points (76 °C to 195 °C) and promising melting enthalpies (8–28 kJ mol−1) for application as intermediate PCMs. Further studies about the interactions in liquids may help to develop a clearer picture of the origins of higher ΔHf, enabling its further optimization in organic salt PCMs.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge funding from Australian Research Council (LP19010522) and Higher Education Commission Pakistan.Notes and references
- A. Henry, R. Prasher and A. Majumdar, Nat. Energy, 2020, 5, 635–637 CrossRef CAS.
- A. Sharma, V. V. Tyagi, C. Chen and D. Buddhi, Renewable Sustainable Energy Rev., 2009, 13, 318–345 CrossRef CAS.
- M. Haider and A. Werner, e+i Elektrotech. Informationstech., 2013, 130, 153–160 CrossRef.
- C. Prieto, P. Cooper, A. I. Fernández and L. F. Cabeza, Renewable Sustainable Energy Rev., 2016, 60, 909–929 CrossRef CAS.
- S. Saha, A. R. M. Ruslan, A. Monjur Morshed and M. Hasanuzzaman, Clean Technol. Environ. Policy, 2021, 23, 531–559 CrossRef.
- H. Mehling and L. F. Cabeza, Heat Mass Transfer, 2008, 11–55 Search PubMed.
- Y. Zhao, X. Zhang and X. Xu, J. Therm. Anal. Calorim., 2020, 139, 1419–1434 CrossRef CAS.
- C. Zhou and S. Wu, Int. J. Energy Res., 2019, 43, 621–661 CrossRef CAS.
- T. Okazaki, Y. Shirai and T. Nakamura, Renewable Energy, 2015, 83, 332–338 CrossRef.
- K. Matuszek, M. Kar, J. M. Pringle and D. R. MacFarlane, Chem. Rev., 2022, 123, 491–514 CrossRef PubMed.
- R. Tamme, T. Bauer, J. Buschle, D. Laing, H. Müller-Steinhagen and W. D. Steinmann, Int. J. Energy Res., 2008, 32, 264–271 CrossRef CAS.
- J. Z. Alvi, Y. Feng, Q. Wang, M. Imran and J. Alvi, Appl. Therm. Eng., 2020, 170, 114780 CrossRef CAS.
- O. Dumont, G. F. Frate, A. Pillai, S. Lecompte and V. Lemort, J. Energy Storage, 2020, 32, 101756 CrossRef.
- S. Khare, M. Dell’Amico, C. Knight and S. McGarry, Sol. Energy Mater. Sol. Cells, 2012, 107, 20–27 CrossRef CAS.
- X. Wang, J. Liu, Y. Zhang, H. Di and Y. Jiang, Energy Convers. Manage., 2006, 47, 2211–2222 CrossRef.
- D. Farkas and C. Birchenall, Metall. Trans. A, 1985, 16, 323–328 CrossRef.
- Z. Khan, Z. Khan and A. Ghafoor, Energy Convers. Manage., 2016, 115, 132–158 CrossRef CAS.
- Y. M. Choo and W. Wei, Energy Sci. Eng., 2022, 10, 1630–1642 CrossRef CAS.
- K. Nagano, T. Mochida, S. Takeda, R. Domański and M. Rebow, Appl. Therm. Eng., 2003, 23, 229–241 CrossRef CAS.
- H. Bo, E. M. Gustafsson and F. Setterwall, Energy, 1999, 24, 1015–1028 CrossRef CAS.
- D. Feldman, M. Shapiro, D. Banu and C. Fuks, Sol. Energy Mater., 1989, 18, 201–216 CrossRef CAS.
- G. Barone, G. Della Gatta, D. Ferro and V. Piacente, J. Chem. Soc., Faraday Trans., 1990, 86, 75–79 RSC.
- F. Kuznik, K. Johannes and D. David, Advances in Thermal Energy Storage Systems, Elsevier, 2015, pp. 325–353 Search PubMed.
- V. Chinnasamy and S. Appukuttan, Energy Storage, 2019, 1, e80 CrossRef CAS.
- J. Zhu, L. Bai, B. Chen and W. Fei, Chem. Eng. J., 2009, 147, 58–62 CrossRef CAS.
- S. L. Piper, M. Kar, D. R. MacFarlane, K. Matuszek and J. M. Pringle, Green Chem., 2022, 24, 102–117 RSC.
- K. Matuszek, R. Vijayaraghavan, C. M. Forsyth, S. Mahadevan, M. Kar and D. R. MacFarlane, ChemSusChem, 2020, 13, 159–164 CrossRef CAS.
- K. Matuszek, R. Vijayaraghavan, C. M. Forsyth, S. Mahadevan, M. Kar and D. R. MacFarlane, ChemSusChem, 2020, 13, 159–164 CrossRef CAS PubMed.
- C. Castillo, E. Chenard, M. Zeller, N. Hatab, P. F. Fulvio and P. C. Hillesheim, J. Mol. Liq., 2021, 327, 114800 CrossRef CAS.
- R. Vijayraghavan, U. A. Rana, G. D. Elliott and D. R. MacFarlane, Energy Technol., 2013, 1, 609–612 CrossRef CAS.
- K. Matuszek, R. Vijayaraghavan, M. Kar, S. Mahadevan and D. R. MacFarlane, ChemSusChem, 2021, 14, 2757–2762 CrossRef CAS.
- S. L. Piper, C. M. Forsyth, M. Kar, D. R. MacFarlane, K. Matuszek and J. M. Pringle, Mater. Adv., 2021, 2, 7650–7661 RSC.
- K. Matuszek, R. Vijayaraghavan, M. Kar and D. R. MacFarlane, Cryst. Growth Des., 2019, 20, 1285–1291 CrossRef.
- L. Xu, X. Mu, X.-G. Chen, H.-Y. Zhang and R.-G. Xiong, Chem. Mater., 2021, 33, 5769–5779 CrossRef CAS.
- M. Bujak and J. Zaleski, Z. Naturforsch. B, 2002, 57, 157–164 CrossRef CAS.
- J. Luo, J. Hu, W. Saak, R. Beckhaus, G. Wittstock, I. F. Vankelecom, C. Agert and O. Conrad, J. Mater. Chem., 2011, 21, 10426–10436 RSC.
- G. Sheldrick, Acta Crystallogr., Sect. C: Struct. Chem., 2015, 71, 3–8 Search PubMed.
- O. V. Dolomanov, L. J. Bourhis, R. J. Gildea, J. A. K. Howard and H. Puschmann, J. Appl. Crystallogr., 2009, 42, 339–341 CrossRef CAS.
- B. Vestergaard, N. Bjerrum, I. Petrushina, H. Hjuler, R. W. Berg and M. Begtrup, J. Electrochem. Soc., 1993, 140, 3108 CrossRef CAS.
- J. Hao, X. Li, S. Yu, Y. Jiang, J. Luo, Z. Shao and B. Yi, J. Energy Chem., 2015, 24, 199–206 CrossRef.
- K. Matuszek, C. Hatton, M. Kar, J. M. Pringle and D. R. MacFarlane, J. Non-Cryst. Solids: X, 2022, 15, 100108 CAS.
- K. Fumino and R. Ludwig, J. Mol. Liq., 2014, 192, 94–102 CrossRef CAS.
- K. Fumino, S. Reimann and R. Ludwig, Phys. Chem. Chem. Phys., 2014, 16, 21903–21929 RSC.
- K. Dong, Y. Song, X. Liu, W. Cheng, X. Yao and S. Zhang, J. Phys. Chem. B, 2012, 116, 1007–1017 CrossRef CAS PubMed.
- J. H. Davis Jr, C. M. Gordon, C. Hilgers and P. Wasserscheid, Ionic Liq. Synth., 2002, 7–40 Search PubMed.
- P. M. Dean, J. M. Pringle and D. R. MacFarlane, Phys. Chem. Chem. Phys., 2010, 12, 9144–9153 RSC.
- R. Hayes, S. Imberti, G. G. Warr and R. Atkin, Angew. Chem., 2013, 125, 4721–4725 CrossRef.
- T. Steiner, Angew. Chem., Int. Ed., 2002, 41, 48–76 CrossRef CAS.
- W. W. Cleland, P. A. Frey and J. A. Gerlt, J. Biol. Chem., 1998, 273, 25529–25532 CrossRef CAS PubMed.
- E. S. Feldblum and I. T. Arkin, Proc. Natl. Acad. Sci. U. S. A., 2014, 111, 4085–4090 CrossRef CAS PubMed.
- M. C. Etter, J. C. MacDonald and J. Bernstein, Acta Crystallogr., Sect. B: Struct. Sci., 1990, 46, 256–262 CrossRef.
- J. J. McKinnon, D. Jayatilaka and M. A. Spackman, Chem. Commun., 2007, 3814–3816 RSC.
- M. A. Spackman and D. Jayatilaka, CrystEngComm, 2009, 11, 19–32 RSC.
- G. R. Goward, K. Saalwächter, I. Fischbach and H. W. Spiess, Solid State Nucl. Magn. Reson., 2003, 24, 150–162 CrossRef CAS PubMed.
- H. Zhu, X. Wang, R. Vijayaraghava, Y. Zhou, D. R. MacFarlane and M. Forsyth, J. Phys. Chem. Lett., 2018, 9, 3904–3909 CrossRef CAS.
- V. Tricoli, G. Orsini and M. Anselmi, Phys. Chem. Chem. Phys., 2012, 14, 10979–10986 RSC.
- J. Timmermans, J. Phys. Chem. Solids, 1961, 18, 1–8 CrossRef CAS.
- M. Bielejewski, M. Ghorbani, M. A. Zolfigol, J. Tritt-Goc, S. Noura, M. Narimani and M. Oftadeh, RSC Adv., 2016, 6, 108896–108907 RSC.
- S. Ketabi, B. Decker and K. Lian, Solid State Ionics, 2016, 298, 73–79 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. CCDC 2312261, 2312262, 2313263–2313267 and 2313285. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4ma00002a |
| This journal is © The Royal Society of Chemistry 2024 |