Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Hydrophobized lignin nanoparticle-stabilized Pickering foams: building blocks for sustainable lightweight porous materials†
Tao
Zou‡
 ab,
Erfan
Kimiaei‡
ab,
Erfan
Kimiaei‡
 a,
Zahra
Madani
c,
Muzaffer A.
Karaaslan
a,
Zahra
Madani
c,
Muzaffer A.
Karaaslan
 b,
Jaana
Vapaavuori
b,
Jaana
Vapaavuori
 c,
Johan
Foster
c,
Johan
Foster
 d,
Scott
Renneckar
d,
Scott
Renneckar
 b and
Monika
Österberg
b and
Monika
Österberg
 *a
*a
aDepartment of Bioproducts and Biosystems, School of Chemical Engineering, Aalto University, Espoo, Finland. E-mail: monika.osterberg@aalto.fi
bDepartment of Wood Science, University of British Columbia, 2424 Main Mall, Vancouver, British Columbia V6T 1Z4, Canada
cDepartment of Chemistry and Materials Science, School of Chemical Engineering, Aalto University, Espoo, Finland
dDepartment of Chemical and Biological Engineering, University of British Columbia, CHBE 421, 2360 East Mall, Vancouver V6T 1Z3, British Columbia, Canada
First published on 10th June 2024
Abstract
Pickering particles play an essential role in stabilizing Pickering foams that can be utilized as templates for making lightweight porous materials for thermal insulation purposes. With the shift from petroleum to renewable-source-derived materials, particles synthesized from biomass are emerging but are typically too hydrophilic to function as Pickering particles in foams. Here, we report the hydrophobization of lignin nanoparticles (LNPs) by adsorption of an oppositely charged surfactant for air-in-water Pickering foam stabilization. The surface tension and complex viscoelasticity of the aqueous dispersions were tunable by varying the concentration of LNPs and the adsorption ratio of hexadecyltrimethylammonium bromide (CTAB) onto LNPs, which were systematically studied with the pendant drop technique (DPT). Under the optimum conditions, the achieved air-in-water Pickering foams were remarkably stable against coalescence and coarsening, i.e., the bubble size distribution remained unchanged over 30 days. We further utilized the Pickering foams as templates for making dry lightweight composite foams with the introduction of cellulose nanofibrils (CNFs). The closed-cell composite foams, with lignin as the major component, exhibited good thermal insulation properties and mechanical properties that were comparable to commercial rigid polyurethane (PU) foams. We envision that the renewable Pickering particles could find applications in many other areas beyond the templates for porous materials such as enhanced oil recovery.
Introduction
Pickering foams are biphasic wet foams stabilized by particles.1 Pickering foams are stable against coalescence (film rupture) and coarsening (diffusion of gas molecules from small bubbles to large bubbles due to differences in Laplace pressure, also known as Ostwald ripening) as the particles can strongly adsorb at the gas–liquid interface. The energy needed to remove the particles from the interface can reach thousands of κBT (κB and T denote Boltzmann constant and temperature, respectively), which is three orders of magnitude higher than for conventional surfactants.1,2 As a consequence, Pickering foams have been widely used in various applications such as food,3 froth flotation of minerals,4 enhanced oil recovery,5 and as precursors for the production of low-density and porous materials.6,7Traditionally, inorganic and synthetic polymeric particles such as silica nanoparticles,8 alumina particles,9 and polystyrene particles,10 have been mainly studied for Pickering foam stabilization. These particles normally undergo partial hydrophobization to function as Pickering particles. In recent years, there has been growing interest in particles derived from biological origin for Pickering foam stabilization.11 Compared with inorganic or synthetic polymeric particles, biomass-derived particles offer the advantages of renewability, biodegradability, and biocompatibility, making them favorable for circular economy and a sustainable society. Among these particles, cellulosic particles made from cellulose or cellulose derivatives have been mostly reported.11 Alike inorganic and synthetic polymeric particles, partial hydrophobization of cellulosic particles is required for them to function as Pickering particles. This has been achieved either by etherification or esterification of cellulose and further conversion into spherical particles,12,13 or by physical adsorption of oppositely charged surfactant or hydrophobic cellulose onto cellulose nanofibrils (CNFs) or cellulose nanocrystals (CNCs).7,14
Compared with cellulosic particles, lignin nanoparticles (LNPs), an emerging biomass-derived particle made of lignin,15,16 have not been studied for Pickering foam stabilization. LNPs are typically spherical in shape,17 which gives them a lower aspect ratio compared to CNFs or CNCs.18 The aspect ratio also plays a relevant role in Pickering foam stabilization with higher aspect ratio leading to higher foam stability.19 Lignin, the second most abundant biomass photosynthesized in nature right after cellulose, has been treated as a side stream in the pulp and paper industry.20,21 Annually, approximately 98% out of 100 million tons of lignin are burnt for energy purposes, causing premature CO2 emission.22 Nevertheless, lignin valorization for materials applications has triggered tremendous interest in recent years, not only because of its abundance, and non-competition with food sources, but also due to its attractive properties such as antioxidant and UV blocking properties.22,23 Over the years, the underutilization of lignin for materials applications has been mainly hindered by the heterogeneous molar mass, molecular structure, and functional groups arising from different plant species and isolation processes.23 To address this issue, one promising approach is converting lignin to LNPs.17 Unlike raw lignin, LNPs have a well-defined surface chemistry, large surface area per mass unit, and good dispersibility in water from pH 3 to 10.17,24 These improved properties enable value-added applications of lignin,17 including Pickering emulsion stabilization.25–29 However, to our best knowledge, no efforts have been conducted to utilize LNPs as emulsifiers for Pickering foam stabilization. The underlying reason is that LNPs are too hydrophilic to be used for Pickering foam stabilization, similar to other biomass-derived particles.30 Besides, generating Pickering foams is more challenging than producing Pickering emulsions due to the former (gas/liquid) exhibiting a higher interfacial energy compared to the latter (liquid/liquid), hence more hydrophobic LNPs are needed. One study reported the combination of LNPs and alpha olefin sulfonate (AOS) for wet foam stabilization and found that the foam exhibited 10 times longer half-life time than the foam stabilized solely by AOS.31 However, the enhanced stability was not a result of the Pickering effect, but due to the particle congestion in the Plateau borders that slowed down the drainage and bubble coalescence.32
In this work, we systematically studied the surface tension and complex viscoelasticity of the aqueous LNP dispersion across a broad range of LNP concentrations (0–5 wt%) and varying the adsorption ratios of Hexadecyltrimethylammonium bromide (CTAB) to achieve optimum conditions for generating Pickering foams. CTAB, a quaternary ammonium cationic surfactant, has been successfully utilized to hydrophobize anionic LAPONITE® and silica particles for Pickering foam stabilization.33,34 One recent study furthermore showed that CTAB meets the criteria for ready biodegradability without sorbent, and its toxicity can be mitigated when particle sorbents are used.35 On top of the Pickering foam stabilization, we further demonstrate that the Pickering foam system can be utilized as a template for making lightweight, strong, closed-cell foams with the introduction of cellulose nanofibrils (CNFs).
Experimental
Materials
Softwood kraft lignin (SKL) (Brand name: Biopiva 100) used in this study was isolated from black liquor using LignoBoost technology (UPM, Finland).36 SKL was well characterized in previous studies,37,38 it has a sugar content of 0.05 mmol g−1, nominal number-average molecular weight (Mn) and weight-average molecular weight (Mw) of 693 and 4630 g mol−1 (determined with gel permeation chromatography using polystyrene sulfonates as standards), respectively. The aliphatic OH, phenolic OH, and carboxyl groups contents were 1.89, 4.05, and 0.38 mmol g−1 (determined with 31P NMR), respectively. The cellulose nanofibrils (CNFs) were prepared according to Österberg et al.39 In brief, never dried bleached hardwood kraft pulp fibers were washed into sodium form and then subjected to mechanical disintegration. The mechanical disintegration was performed using an M-110P microfluidizer (Microfluidics, Newton, Massachusetts, USA) by six passes through a series of 400 and 100 μm chambers at 2000 bar. The final obtained CNF suspension had a solid content of 2.1 wt%, which was stored at 4 °C before use. Hexadecyltrimethylammonium bromide (CTAB) (purity ≥98%) was purchased from Sigma-Aldrich. Deionized water was used throughout the experiments. A commercial rigid polyurethane (PU) foam with the brand name FF-PIR PLK was purchased from Finnfoam (Finland).Preparation of lignin nanoparticles
LNPs were prepared following previously reported method with slight modifications.26,40 In brief, 15 g of wet SKL (∼33 wt% moisture) was dissolved in 500 g of aqueous acetone (75 wt%) under stirring for 4 hours, followed by vacuum filtration through a paper filter (Whatman GF/F, pore size 0.7 μm) to remove the undissolved solids. Afterward, lignin solution was quickly poured into deionized water (1500 g) under vortex-stirring to form LNPs instantly. The LNP dispersion was then subjected to rotary evaporation at 45 °C under reduced pressure to remove acetone and further concentrated to 5–7 wt%. The final aqueous LNP dispersion consisted solely of LNPs dispersed in water.Hydrodynamic diameter (Dh) and ζ potential analysis
The hydrodynamic diameter (Dh) and ζ potential of the LNPs were determined using a Zetasizer Nano ZS90 instrument (Malvern Instruments Ltd, United Kingdom). Prior to measurement, the LNP dispersion was diluted to 0.01 wt% with deionized water and subjected to bath ultrasonication for 10 minutes. The Dh was obtained at the scattering angle of 90°. The ζ potential measurement were conducted with a dip cell probe using automatic voltage and the ζ potential was calculated using Helmholtz–Smoluchowski equation.41 Three measurements were recorded for Dh and ζ potential and the average values were used for reporting. The LNPs prepared in this work had the average hydrodynamic diameter Dh (intensity-based) around 140 nm and the ζ potential around −37 mV at pH 5.Atomic force microscopy (AFM)
The AFM images of LNPs and CNFs were taken with a MultiMode 8 AFM equipped with a NanoScope V controller (Bruker Corporation) in tapping mode in ambient air using NCHV-A probes (Bruker). The LNP sample was prepared by dropping 5 μL LNP dispersion (0.01 wt%) on a mica surface followed by ambient drying, while the CNF sample was prepared by spin-coating of CNF dispersion (0.1 wt%) on a silica surface. Image processing (third order plane fit) was performed using Nanoscope Analysis (version 1.5, Bruker).Surface tension and dilational viscoelasticity
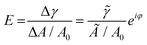 | (1) |
![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) ei(2πν+φ) (
ei(2πν+φ) (![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) is the amplitude and φ is the phase shift), A0 is the surface area at equilibrium state of the droplet.
is the amplitude and φ is the phase shift), A0 is the surface area at equilibrium state of the droplet. ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) /(Ã/A0) is usually reported in the term of complex viscoelastic modulus |E|.
/(Ã/A0) is usually reported in the term of complex viscoelastic modulus |E|.
At a relative low oscillation frequency, e.g., at 0.1 Hz, ![[small gamma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0dd.gif) is low for a droplet containing conventional surfactant, as the surfactant can diffuse to/away from the interface that dampens the external area perturbation, thus a relatively low |E| is expected. In contrast, a relatively high |E| is expected for a droplet containing particles at the interface due to strong adsorption, since a high energy is required for the desorption of particles from the interface.1,45φ on the other hand reflects how viscoelastic the interface is.
is low for a droplet containing conventional surfactant, as the surfactant can diffuse to/away from the interface that dampens the external area perturbation, thus a relatively low |E| is expected. In contrast, a relatively high |E| is expected for a droplet containing particles at the interface due to strong adsorption, since a high energy is required for the desorption of particles from the interface.1,45φ on the other hand reflects how viscoelastic the interface is.
Wet and dry foam preparation
Wet foams stabilized by CTAB–LNPs were prepared by first mixing an aqueous CTAB solution (1 wt%) with a LNP dispersion (5–7 wt%) at different ratios (e.g., 0 to 15 mg g−1 CTAB to LNP) by gentle-stirring for 3 hours, followed by foaming using an Ultra-turrax T18 (basic IKA homogenizer) for 3 min at 14 k rpm. Wet foams containing CTAB–LNPs and CNFs were prepared similarly as above with the only difference that CNFs were added into the LNP dispersions right after adding CTAB with a final concentration at 0.7–0.9 wt%. The detailed foam formulations can be found in the ESI† (Table S1 and S2).The dry foams were prepared by freeze-drying (Labconco, freezone 2.5). Prior to freeze-drying, the wet foams were transferred into a round-shape poly(tetrafluoroethylene) (PTFE) mold (80 mm in diameter and 28 mm in height), followed by freezing at −20 °C in a freezer.
Wet foam characterization
The foamability was illustrated using the foaming index that was calculated according to the following equation:| Foaming index (%) = 100% × (Foam volume/initial liquid volume) | (2) |
The foam stability was estimated from the change of foaming index over time.
The microstructure of the wet foams was observed with an optical microscope (Leica Zeiss DM750) equipped with Leica imaging software. The captured images were analyzed by ImageJ.
The bubble size distribution and uniformity of the wet foams were determined with a Mastersizer 2000 (Malvern, UK). The refractive indices of the dispersed and continuous phases were set at 1.6 and 1.33, respectively. The wet foams were diluted with deionized water to reach the laser obscuration of 5–10% prior to starting the measurement. The mean droplet diameter was calculated according to volume-based size distribution (d43, De Brouckere Mean Diameter). The uniformity of the size distribution was calculated according to the following equation:
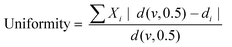 | (3) |
Dry foam characterization
The cellular structure of the dry foams was determined using scanning electron microscopy (SEM) (Zeiss Sigma VP, Germany) at an acceleration voltage of 2 kV. Prior to imaging, the samples were deposited with a 4 nm-thick layer of gold–palladium alloy. The images were taken from the cryo-fractured cross-section areas and the top surfaces of the samples. ImageJ was used to analyze the SEM images. About 50 cells per sample were measured to determine the cell size distribution.The closed-cell content was measured by determining the actual density using gas pycnometer (Quantachrome, USA) according to the ASTM D6226 standard and the following equations.46
| Closed cells (%) = 100% − Open cell (%) | (4) |
| Open cell (%) = (actual density − apparent density)/apparent density × 100% | (5) |
The thermal conductivity measurement was performed on a Hot Disk TPS 2500 S (Sweden). A Kapton sensor (model 5465) was adapted for determining the thermal conductivity. The sensor was placed in between two identical foam slabs (∼30 mm × 30 mm × 5 mm) and an extra force (2–3 N) was applied to the foams to ensure good contact. The measurement was performed at a heating power of 7 mW for 5 s at 22 °C. Data points between 1 s and 4 s were selected for the thermal conductivity calculation. Two parallel measurements were conducted, and the average values were used for data reporting. The thermal insulation behavior of the foams (∼10 mm thick for LNP-CNF foams, and 5 mm thick for the PU foam) was further analyzed by placing them on a hot copper plate at 120 °C for 1 hour (see the setup in the ESI†). The copper plate (155 mm × 155 mm ×1 mm) was placed on the hot plate to ensure thermal uniformity. An infrared camera (PIR uc 605, 640 × 480 pixels) was used to monitor the temperature change at 1 frame per second. ThermaCAM™ Researcher Pro v2.10 was used for data analysis. For data reporting, a colormap was used to indicate the temperature change between 30 °C and 120 °C. The thermal stability of the foams was analyzed via thermogravimetric analysis using a TGA Q500 instrument (TA Instruments, USA). The samples were heated at a heating rate of 10 °C min−1 up to 800 °C under a nitrogen atmosphere. The temperature corresponding to the highest rate of degradation was determined by plotting the first derivative of the thermogravimetric curves (DTG).
Compression tests were performed on a universal testing machine (Instron 5944). The samples (∼30 mm × 30 mm × 10 mm) were first conditioned for 48 h at 23 °C with a relative humidity of 55%. Next, they were compressed up to 80% strain at a tensile speed of 1 mm min−1 under a 2 kN load cell. The compressive strength at 10% and 50% strain was used to compare the samples. The toughness was calculated over the strain from 0 to 80%. At least three samples were measured, and the mean values were used for reporting.
Results and discussion
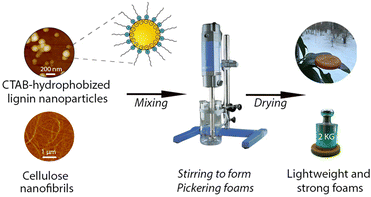
This work aimed to tune the wetting properties of LNPs by adsorbing oppositely charged surfactants onto their surfaces for creating durable Pickering foams. The Pickering foams were further used as templates for lightweight porous materials aiming at future use for thermal insulation and cushioning applications. A general view of this work is shown in Scheme 1.To obtain optimal performance in foams, the first step was to fundamentally understand how the surface tension and complex viscoelasticity of the aqueous LNP dispersions were affected by the particle concentrations and adsorption ratios of oppositely charged surfactants.
Hydrophobization of LNPs by adsorption of CTABs for durable Pickering foams
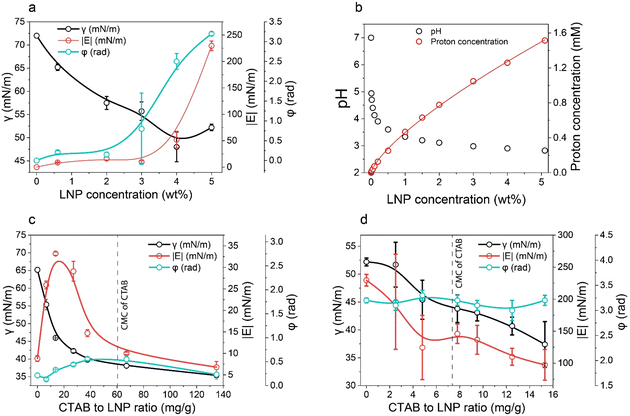 | ||
| Fig. 1 Wettability of LNPs at different concentrations and adsorption ratios of CTAB. (a) Surface tension (γ), complex viscoelastic modulus (|E|), and phase shift (φ) of LNP aqueous dispersions plotted against LNP concentration. (b) pH and proton concentration of LNP aqueous dispersions as a function of LNP concentration. Proton concentration was calculated based on the pH data. Fitting function for proton concentration follows y = 0.46 × 0.74. (c) and (d) γ, |E|, and φ of CTAB–LNP aqueous dispersions at the LNP concentrations of 0.6 wt% and 5 wt%, respectively (eqn (1)). The dashed lines denote the critical micelle concentration (CMC) of CTAB in water. Note that the lines in a, c, and d are only added as guides for the eyes. | ||
Unlike the results observed with 0.6 wt% LNPs, at 5 wt% LNPs, an increase in the CTAB to LNP ratio resulted in a decrease in both γ and |E|, and no obvious change in φ around π (Fig. 1d). The decrease in γ was expected and the reason could be similarly explained as for the CTAB adsorption onto LNPs at a low LNP concentration (0.6 wt%). However, in contrast to the situation for 0.6 wt% LNPs, the maximum |E| corresponding to the highest hydrophobicity and IEP was not observed at 5 wt% of LNPs. The relatively high |E| and the φ around π reflected closely-packed particles at the air–water interface, regardless of the CTAB amount. This might hinder the observation of the maximum |E|. Nevertheless, we could estimate that the IEP for 5 wt% LNPs should be less than 14 mg g−1 since a higher LNP concentration corresponded to a lower number of dissociated carboxyl groups per particle due to the protonation effect. In fact, the foaming results discussed in the next paragraph indirectly suggested an IEP of 5 mg g−1 for CTAB–LNPs at 5 wt% LNPs.
Therefore, we focused on the Pickering foam formation at 5 wt% LNPs. We found that the initial foaming index increased from 207% to 327% with an increased CTAB–LNP ratio from 0 to 15 mg g−1 (Fig. 2a and b), indicating improved foamability. Interestingly, the foam stability first improved and then decreased, and the most stable foam was stabilized by 5 mg g−1 CTAB–LNPs, as indicated by the smallest change in the foaming index over 30 days (Fig. 2b). Note that the decrease in the foaming index during the first half hour was caused by creaming effect. In contrast, the foams stabilized by the neat LNPs, 12.5 or 15 mg g−1 CTAB–LNPs were significantly weaker and completely vanished after 24 hours (Fig. 2a, b and Fig. S4, ESI†). In case of the neat LNPs, the particles were not sufficiently hydrophobic to make the foam durable. For the 12.5 or 15 mg g−1 CTAB–LNPs, we speculate that only the free CTAB molecules adsorbed to the air–water interfaces. Since CTAB reached its CMC at 7.2 mg g−1 CTAB–LNPs (Fig. 1d), there was likely excess CTAB in the aqueous phase after forming micelles on the LNP surfaces. The assumption was supported by comparing to the foams solely stabilized by CTAB at 27.4 mM, which showed similar foam stability (Fig. 2a and b). For the durable foams stabilized by 2.5 to 10 mg g−1 CTAB–LNPs, we further observed the bubble profiles with an optical microscope (OM) and measured the bubble size distributions with dynamic light scatting. The OM images displaced spherical “cells” with ruptured shells upon drying of the wet foams, suggesting that the CTAB–LNPs adsorbed at the air–water interface and provided air bubbles with high stability (Fig. S5, ESI†). The average bubble size, along with the uniformity of these bubbles, are summarized in Table 1. We found that the foam stabilized by 5 mg g−1 CTAB–LNPs exhibited the narrowest bubble size distribution, ranging from 9 to 80 μm, with an average bubble size of 28 μm and a uniformity of 0.4. At 2.5 mg g−1 CTAB–LNPs, the LNPs were likely not sufficiently hydrophobized, while at a CTAB–LNP ratio beyond 5 mg g−1, the LNPs became slightly positively charged and hydrophilic again due to CTAB micelle formation. As a result, the foams stabilized by these particles exhibited a broader bubble size distribution compared to the ones at 5 mg g−1 (Fig. 2c). This result is consistent with the foam stability indicated by the change in foaming index over time (Fig. 2b).
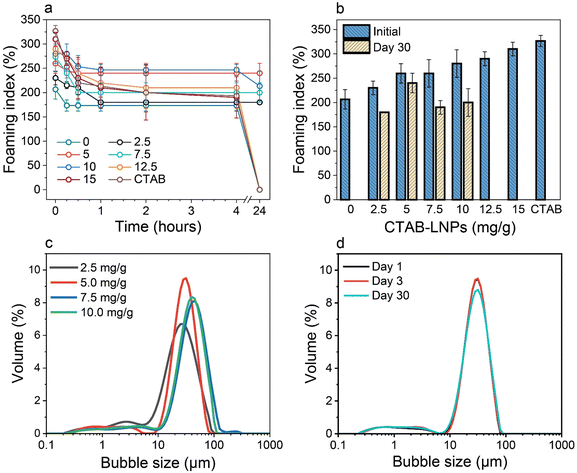 | ||
| Fig. 2 Effect of CTAB to LNP ratio on foamability (eqn (2)) and foam stability at the fixed LNP concentration of 5 wt%. (a) Foaming index over 24 hours for the foams stabilized by the CTAB–LNPs (0–15 mg g−1) and the neat CTAB. (b) Initial foaming indices (right after foaming) and foaming indices after 30 days. (c) Bubble size distributions of the Pickering foams stabilized by CTAB–LNPs (2.5–10 mg g−1), measured 3 days after foaming. (d) Bubble size distributions of the 5 mg g−1 CTAB–LNP-stabilized foam on day 1, 3, and 30 after foaming. | ||
| CTAB to LNP ratio (mg g−1) | Mean bubble size (μm) | Uniformity |
|---|---|---|
| 2.5 | 25 ± 3 | 0.6 |
| 5 | 28 ± 1 | 0.4 |
| 7.5 | 42 ± 1 | 0.5 |
| 10 | 37 ± 2 | 0.5 |
Choosing the foam stabilized by 5 mg g−1 CTAB–LNPs, we monitored the bubble size distribution for 30 days to evaluate its long-lasting foam stability. It was found that the bubble size did not change over this period (Fig. 2d). This result suggested that the foam was surprisingly stable, with no coalescence or coarsening occurring. Inspired by this excellent foam stability, we selected the same CTAB–LNPs ratio of 5 mg g−1 and investigated if these modified LNPs could be used to produce lightweight dry composite foams in combination with CNFs in the next step.
Wet Pickering foams as templates for lightweight composite foams
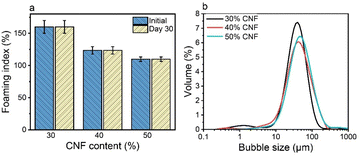
Direct drying of CTAB–LNP-stabilized Pickering foams led to a collapsed foam structure due to the brittle nature of lignin and the absence of a strong percolation network structure. Our previous study showed that a composite film made of CNFs and LNPs significantly improved the mechanical properties compared to a neat CNF film, due to the synergistic effect of the two nanomaterials.46 Furthermore, it has been reported that the addition of CNFs to the hydrophobized silica nanoparticles or LNP dispersions significantly improved the Pickering foam/emulsion stability, attributed to the formation of a CNF percolation network structure.26,49 We thus employed CNFs in our Pickering foam system to enhance both the stability of the wet Pickering foams upon drying and the mechanical properties of the solid foams after drying.To further improve the mechanical properties of the foams after drying, we increased the CNF fraction up to 30 wt%, 40 wt%, and 50 wt% at a fixed CTAB–LNP ratio of 5 mg g−1. The CTAB–LNP concentration was reduced to 1.7 wt%, 1.2 wt% and 0.9 wt%, respectively. The increase in CNF fraction resulted in a reduced foaming index (Fig. 3a), primarily due to both increased viscosity and decreased CTAB–LNP concentration. Nevertheless, all the CNF-containing wet foams exhibited an unchanged foaming index for 30 days. In contrast, the foams stabilized solely with CTAB–LNPs (5 mg g−1) at the concentrations of 1.7 wt%, 1.2 wt% and 0.9 wt% experienced a significant drop in the foaming index after 30 days (Fig. S8, ESI†). Meanwhile, the bubble size distribution of the foams became slightly but not significantly broader with increased CNF fractions (Fig. 3b). Overall, all the wet foams displayed a good distribution of bubble size ranging roughly between 10 and 200 μm.
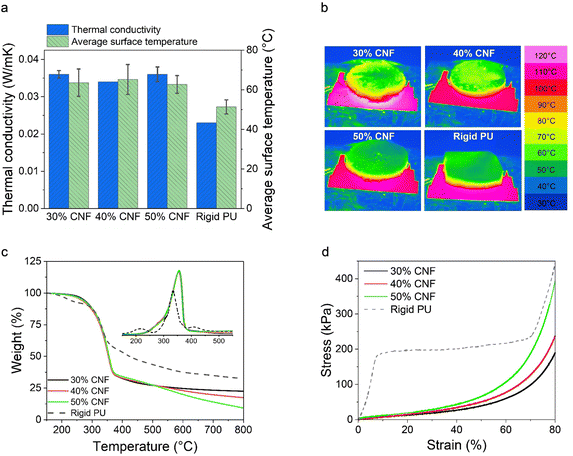
To validate the SEM observations, we further analyzed the closed-cell contents of the LNP-CNF foams and a commercial rigid PU foam (as comparison) using a pycnometer. The results are listed in Table 2. As anticipated, the closed-cell contents of the LNP-CNF foams dominated the cell structure, and increased from 78.1% to 88.6% with the increased CNF content. This result confirmed that the pore structure could be better preserved upon drying with increased CNF content due to increased viscosity of the system. While comparing the closed-cell contents of the LNP-CNF foams to the rigid PU (97.6%), the highest closed-cell content of the LNP-CNF foam was 9% lower than for PU. This explains partially the better thermal insulation behaviour of the PU foam discussed in the following section. Unfortunately, we could not find the closed/open-cell contents of cellulose/lignin-based foams in the literature for comparison.
| Foam | Apparent density (kg m−3) | Actual density (kg m−3) | Closed-cell content (%) |
|---|---|---|---|
| 30 wt% CNFs | 32 ± 3 | 57 | 78.1 |
| 40 wt% CNFs | 34 ± 4 | 64 | 85.3 |
| 50 wt% CNFs | 35 ± 2 | 66 | 88.6 |
| Rigid PU | 43 | 85 | 97.6 |
We further compared the decomposition temperatures of the LNP-CNF foams to the PU foam in a N2 atmosphere. Overall, the LNP-CNF foams showed similar maximum decomposition temperature at 354 °C, regardless of the CNF content. This value was higher than for the PU foam (335 °C), indicating higher thermal stability of the LNP-CNF foams (Fig. 5c). Interestingly, the LNP-CNF foams yielded less carbon content compared to the PU foam, as indicated by the lower residue weight percentage at 800 °C. Comparing among the LNP-CNF foams with various CNF contents, the more CNF that was added, the lower the carbon content of the foam. This is reasonable, since lignin typically exhibits a higher carbon content compared to cellulose.57
| Foam | Compressive stress at 10% strain (kPa) | Compressive stress at 50% strain (kPa) | Toughness (kJ m−3) | Specific compressive stress at 10% strain (kPa × m3 kg−1) | Specific compressive stress at 50% strain (kPa × m3 kg−1) | Specific toughness (kJ kg−1) |
|---|---|---|---|---|---|---|
| 30 wt% CNFs | 6.1 ± 3.1 | 31.3 ± 7.9 | 28.0 ± 6.5 | 0.19 ± 0.10 | 0.98 ± 0.25 | 0.88 ± 0.20 |
| 40 wt% CNFs | 5.4 ± 1.3 | 40.0 ± 8.7 | 35.4 ± 6.2 | 0.16 ± 0.04 | 1.18 ± 0.26 | 1.04 ± 0.18 |
| 50 wt% CNFs | 7.6 ± 3.7 | 43.1 ± 20.0 | 39.3 ± 21.1 | 0.22 ± 0.11 | 1.23 ± 0.57 | 1.12 ± 0.60 |
| Rigid PU | 166.9 ± 45.1 | 191.2 ± 49.9 | 155.4 ± 35.4 | 3.88 ± 1.05 | 4.44 ± 1.16 | 3.61 ± 0.82 |
Conclusions
In this work, the wettability of LNPs was systematically analyzed over a broad range of concentrations (0–5 wt%) and adsorption ratios of CTAB using DPT. The hydrophobicity of LNPs increased with the LNP concentration due to the protonation of the carboxyl groups. Moreover, the adsorption of CTAB on LNPs could further enhance the hydrophobicity of LNPs. The highest hydrophobicity was achieved when the CTAB–LNPs reached the IEP, as revealed by the highest |E| and the most stable foam stabilized by CTAB–LNPs. At a high LNP concentration (5 wt%) and an adsorption ratio of 5 mg g−1 CTAB to LNPs, the achieved Pickering foams were remarkably stable as indicated by the unchanged bubble size distribution over 30 days. The Pickering foams were successfully utilized as templates for making lightweight, strong, and mostly closed-cell foams with the introduction of CNFs. The obtained LNP-CNF foams showed comparable thermal insulation behaviours and better thermal stability compared to a commercial rigid PU foam. The mechanical properties of the dry foams improved with increasing CNF content. The specific toughness of the best LNP-CNF foam (50 wt% CNFs) was about 30% of the value obtained for the rigid PU foam. Overall, our study emphasizes the critical role of interfacial design in leveraging the distinctive properties of lignocellulosic materials for Pickering stabilization in foam applications. By carefully tailoring the interface between the lignocellulosic particles and the surrounding medium, we were able to optimize the stability and performance of the foams. These insights contribute not only to the fundamental understanding of colloidal systems but also offer practical implications for the development of eco-friendly and high-performing foams for applications such as thermal insulation and cushioning.Author contributions
T. Z. and E. K. designed the experiments with the input from M. Ö. T. Z. performed the particle preparation, surface tension and dilatational viscoelasticity analysis and analyzed the data. E. K. conducted the wet foam and dry foam preparation, characterization, and data analysis. Z. M. and M. A. K. were responsible for the compressive test and the thermal conductivity measurement, respectively. T. Z. and E. K. co-wrote the manuscript with the input from all authors. All authors have given approval to the final version of the manuscript.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
T. Z. acknowledges funding from the MEC Global Program. E. K. acknowledges funding from the Finnish Natural Resources Research Foundation organization in the chemistry – forest product sector under grant number 20210035. We are grateful to Prof. Robin Ras for granting access to the tensiometer at the Department of Applied Physics, Aalto University, and the valuable technical assistance offered by Dr Kai Liu. M.Sc. Senni Heimala was thanked for performing the dynamic foaming analysis (DFA) experiments. This work was mostly performed at Aalto University Bioeconomy Facilities. The authors would also like to acknowledge the OtaNano Nanomicroscopic Center at Aalto University. The authors are also grateful for the support from the FinnCERES Materials Bioeconomy Ecosystem.References
- B. P. Binks, Curr. Opin. Colloid Interface Sci., 2002, 7, 21–41 CrossRef CAS.
- U. T. Gonzenbach, A. R. Studart, E. Tervoort and L. J. Gauckler, Langmuir, 2007, 23, 1025–1032 CrossRef CAS PubMed.
- E. Dickinson, Curr. Opin. Colloid Interface Sci., 2010, 15, 40–49 CrossRef CAS.
- G. Bournival, S. Ata and G. J. Jameson, Miner. Process. Extr. Metall. Rev., 2017, 38, 366–387 CrossRef CAS.
- N. Yekeen, M. A. Manan, A. K. Idris, E. Padmanabhan, R. Junin, A. M. Samin, A. O. Gbadamosi and I. Oguamah, J. Pet. Sci. Eng., 2018, 164, 43–74 CrossRef CAS.
- U. T. Gonzenbach, A. R. Studart, E. Tervoort and L. J. Gauckler, J. Am. Ceram. Soc., 2007, 90, 16–22 CrossRef CAS.
- N. T. Cervin, L. Andersson, J. B. S. Ng, P. Olin, L. Bergström and L. Wågberg, Biomacromolecules, 2013, 14, 503–511 CrossRef CAS PubMed.
- B. P. Binks and T. S. Horozov, Angew. Chem., Int. Ed., 2005, 44, 3722–3725 CrossRef CAS PubMed.
- U. T. Gonzenbach, A. R. Studart, E. Tervoort and L. J. Gauckler, Angew. Chem., Int. Ed., 2006, 45, 3526–3530 CrossRef CAS PubMed.
- S. Fujii, P. D. Iddon, A. J. Ryan and S. P. Armes, Langmuir, 2006, 22, 7512–7520 CrossRef CAS PubMed.
- S. Lam, K. P. Velikov and O. D. Velev, Curr. Opin. Colloid Interface Sci., 2014, 19, 490–500 CrossRef CAS.
- H. A. Wege, S. Kim, V. N. Paunov, Q. Zhong and O. D. Velev, Langmuir, 2008, 24, 9245–9253 CrossRef CAS PubMed.
- H. Jin, W. Zhou, J. Cao, S. D. Stoyanov, T. B. J. Blijdenstein, P. W. N. de Groot, L. N. Arnaudov and E. G. Pelan, Soft Matter, 2012, 8, 2194–2205 RSC.
- Z. Hu, R. Xu, E. D. Cranston and R. H. Pelton, Biomacromolecules, 2016, 17, 4095–4099 CrossRef CAS PubMed.
- P. Figueiredo, K. Lintinen, J. T. Hirvonen, M. A. Kostiainen and H. A. Santos, Prog. Mater. Sci., 2018, 93, 233–269 CrossRef CAS.
- M. H. Sipponen, H. Lange, C. Crestini, A. Henn and M. Österberg, ChemSusChem, 2019, 12, 2039–2054 CrossRef CAS PubMed.
- M. Österberg, M. H. Sipponen, B. D. Mattos and O. J. Rojas, Green Chem., 2020, 22, 2712–2733 RSC.
- N. Lavoine and L. Bergström, J. Mater. Chem. A, 2017, 5, 16105–16117 RSC.
- N. T. Cervin, E. Johansson, J.-W. Benjamins and L. Wågberg, Biomacromolecules, 2015, 16, 822–831 CrossRef CAS PubMed.
- W. G. Glasser, Front. Chem., 2019, 7, 565 CrossRef CAS PubMed.
- T. Li and S. Takkellapati, Biofuels, Bioprod. Biorefin., 2018, 12, 756–787 CrossRef CAS PubMed.
- D. S. Bajwa, G. Pourhashem, A. H. Ullah and S. G. Bajwa, Ind. Crops Prod., 2019, 139, 111526 CrossRef CAS.
- D. Kai, M. J. Tan, P. L. Chee, Y. K. Chua, Y. L. Yap and X. J. Loh, Green Chem., 2016, 18, 1175–1200 RSC.
- M. Österberg, K. A. Henn, M. Farooq and J. J. Valle-Delgado, Chem. Rev., 2023, 123, 2200–2241 CrossRef PubMed.
- A. Moreno and M. H. Sipponen, Nat. Commun., 2020, 11, 5599 CrossRef CAS PubMed.
- E. Kimiaei, M. Farooq, R. Grande, K. Meinander and M. Österberg, Adv. Mater. Interfaces, 2022, 9, 2200988 CrossRef CAS.
- M. H. Sipponen, M. Smyth, T. Leskinen, L.-S. Johansson and M. Österberg, Green Chem., 2017, 19, 5831–5840 RSC.
- T. Zou, M. H. Sipponen and M. Österberg, Front. Chem., 2019, 7, 370 CrossRef CAS PubMed.
- M. Ago, S. Huan, M. Borghei, J. Raula, E. I. Kauppinen and O. J. Rojas, ACS Appl. Mater. Interfaces, 2016, 8, 23302–23310 CrossRef CAS PubMed.
- M. Farooq, Z. Tao, J. J. Valle-Delgado, M. H. Sipponen, M. Morits and M. Österberg, Langmuir, 2020, 36, 15592–15602 CrossRef CAS PubMed.
- X. Fan, X. Guan, M. Zhang, Y. Liu and Y. Li, Colloids Surf., A, 2022, 643, 128727 CrossRef CAS.
- P. Amani, R. Miller, A. Javadi and M. Firouzi, Adv. Colloid Interface Sci., 2022, 301, 102606 CrossRef CAS PubMed.
- S. Zhang, Q. Lan, Q. Liu, J. Xu and D. Sun, Colloids Surf., A, 2008, 317, 406–413 CrossRef CAS.
- X. Sun, Y. Chen and J. Zhao, RSC Adv., 2016, 6, 38913–38918 RSC.
- N. Timmer, D. Gore, D. Sanders, T. Gouin and S. T. J. Droge, Chemosphere, 2019, 222, 461–468 CrossRef CAS PubMed.
- P. Tomani, Cellul. Chem. Technol., 2010, 44, 53–58 CAS.
- T. Zou, M. H. Sipponen, A. Henn and M. Österberg, ACS Nano, 2021, 15, 4811–4823 CrossRef CAS PubMed.
- M. H. Sipponen, M. Farooq, J. Koivisto, A. Pellis, J. Seitsonen and M. Österberg, Nat. Commun., 2018, 9, 2300 CrossRef PubMed.
- M. Österberg, J. Vartiainen, J. Lucenius, U. Hippi, J. Seppälä, R. Serimaa and J. Laine, ACS Appl. Mater. Interfaces, 2013, 5, 4640–4647 CrossRef PubMed.
- T. Zou, N. Nonappa, M. Khavani, M. Vuorte, P. Penttilä, A. Zitting, J. J. Valle-Delgado, A. M. Elert, D. Silbernagl, M. Balakshin, M. Sammalkorpi and M. Österberg, J. Phys. Chem. B, 2021, 125, 12315–12328 CrossRef CAS PubMed.
- S. Bhattacharjee, J. Controlled Release, 2016, 235, 337–351 CrossRef CAS PubMed.
- F. Ravera, G. Loglio and V. I. Kovalchuk, Curr. Opin. Colloid Interface Sci., 2010, 15, 217–228 CrossRef CAS.
- C. E. Stauffer, J. Phys. Chem., 1965, 69, 1933–1938 CrossRef CAS.
- J. Yang, J. Wu and S. Bi, J. Chem. Eng. Data, 2021, 66, 2615–2628 CrossRef CAS.
- A. Stocco, W. Drenckhan, E. Rio, D. Langevin and B. P. Binks, Soft Matter, 2009, 5, 2215–2222 RSC.
- S. Estravís Sastre, Universidad de Valladolid. Facultad de Ciencias, 2014.
- B. Kronberg, K. Holmberg and B. Lindman, Surface Chemistry of Surfactants and Polymers, John Wiley & Sons, Ltd, 2014, pp. 153–173 Search PubMed.
- S. A. Kedzior, H. S. Marway and E. D. Cranston, Macromolecules, 2017, 50, 2645–2655 CrossRef CAS.
- R. Abidnejad, M. Beaumont, B. L. Tardy, B. D. Mattos and O. J. Rojas, ACS Nano, 2021, 15, 19712–19721 CrossRef CAS PubMed.
- R. Mort, K. Vorst, G. Curtzwiler and S. Jiang, RSC Adv., 2021, 11, 4375–4394 RSC.
- B. Doğan and H. Tan, Int. J. Polym. Sci., 2019, 2019, e6350326 CrossRef.
- I. Gnip, S. Vėjelis and S. Vaitkus, Energy Build., 2012, 52, 107–111 CrossRef.
- V. Apostolopoulou-Kalkavoura, P. Munier and L. Bergström, Adv. Mater., 2021, 33, 2001839 CrossRef CAS PubMed.
- J. König, A. Lopez-Gil, P. Cimavilla-Roman, M. A. Rodriguez-Perez, R. R. Petersen, M. B. Østergaard, N. Iversen, Y. Yue and M. Spreitzer, Constr. Build. Mater., 2020, 247, 118574 CrossRef.
- R. Hasanzadeh, T. Azdast, A. Doniavi and R. E. Lee, Therm. Sci. Eng. Prog., 2019, 9, 21–29 CrossRef.
- T. Lohtander, R. Herrala, P. Laaksonen, S. Franssila and M. Österberg, Cellulose, 2022, 29, 1855–1871 CrossRef CAS.
- T. Haensel, A. Comouth, P. Lorenz, S. I.-U. Ahmed, S. Krischok, N. Zydziak, A. Kauffmann and J. A. Schaefer, Appl. Surf. Sci., 2009, 255, 8183–8189 CrossRef CAS.
- S. Y. Park, S. Goo, H. Shin, J. Kim and H. J. Youn, Cellulose, 2021, 28, 10291–10304 CrossRef CAS.
- J. Liao, P. Luan, Y. Zhang, L. Chen, L. Huang, L. Mo, J. Li and Q. Xiong, J. Environ. Chem. Eng., 2022, 10, 107788 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00295d |
| ‡ These authors have contributed equally to this work and are co-first authors. |
| This journal is © The Royal Society of Chemistry 2024 |