DOI:
10.1039/D4MA00306C
(Paper)
Mater. Adv., 2024,
5, 4480-4490
A truncated octahedron NaCe(MoO4)2 nanostructure: a potential material for blue emission and acetone sensing†
Received
22nd March 2024
, Accepted 5th April 2024
First published on 9th April 2024
Abstract
Scheelite-type NaCe(MoO4)2, a promising nanostructure for optoelectronic applications, has been synthesized using a typical hydrothermal technique, and its structural and microstructural properties have been characterized using several microscopic and spectroscopic techniques. We observed intense blue emission from the 5d–4f transitions of Ce3+ within CeO8, while the presence of mono-(CeO7) and divacancies (CeO6) of oxygen cause relatively weak emissions at 488 nm, 462 nm and 531 nm. Our study reveals that the use of trisodium citrate during synthesis plays a significant role to tune the formation of CeO7 and CeO6, which in consequence also modify the band edges of the system. The Commission Internationale de l'Eclairage (CIE) coordinates are found to be within the blue region with a correlated color temperature (CCT) of ∼7854 K, indicating the potential of NaCe(MoO4)2 nanostructures for cold solid-state lighting applications. Moreover, the oxygen deficiencies are found to act as active sites for the selective adsorption of acetone, leading to acetone sensing. Hence, NaCe(MoO4)2 nanostructures may be potential smart materials for blue-lighting and acetone sensors. Ab initio calculations have been carried out to obtain theoretical insights into the electronic structure of the bare and oxygen-deficient NaCe(MoO4)2 and to understand the guiding parameters for acetone sensing. Our calculations also demonstrate that acetone adsorption occurs mostly through the (112) plane.
1. Introduction
Recently, rare-earth (RE)-based scheelite micro/nanostructures have attracted considerable interest from researchers for various optoelectronic applications, including solid-state lasers, fluorescent lamps, optical sensors, scintillators, light-emitting diodes, fiber optic communications, and biological labeling due to their unique features of tuneable emission, narrow bandgap, high quantum yield and high opto-electric conversion, and excellent thermal and chemical stability.1–3 Among them are the alkali RE binary molybdates with the generic formula AILnIII(MoO4)2 (A = alkali metal, Ln = RE lanthanide), in which the Ln3+ embedded in the A+ lattice exhibits a strong 5d–4f transition depending on the symmetry of the unit cell.4,5 Extensive research work has been carried out by various researchers, including us, to understand the parameters influencing the emission. As an example, Cheng et al. have investigated the influence of Li/Ag on the luminescence properties of Li1−xAgxLu(MoO4)2:Eu3+,6 while Song et al. have explored red emission from Eu3+-doped AgGd(MoO4)2.7 The strong integrated emission and higher color purity observed for LiEu(MoO4)2 among the AEu(MoO4)2 materials (A = Li+, Na+ and K+) have been ascribed to its higher, faster charge transfer due to the shortened and more covalent Li–O bond in comparison with those of its Na or K counterpart.8 Most of the conventional techniques (e.g., the Czochralski method, solid-state reaction, etc.) lead to agglomeration with high grain size and irregular morphology;9 however, recent studies reveal a remarkable correlation between the morphology and emission as the selection rules of optical transition significantly depend on shape, size, exposure facets, dimensionality, hierarchy, etc. To date, abundant efforts have been devoted to generating various scheelite micro/nanostructures using hydrothermal and other techniques to gain an intuitive understanding of optical emissions. As a reference, Liu et al. reported the preparation of uniform tetragonal microspindles and nanoplates using the surfactant ethylenediaminetetraacetic acid (EDTA-2Na),10 while microrods, microcuboids and microflowers have been obtained via a synthesis technique based on the ligand polyvinylpyrrolidone.11 Zheng et al. synthesized a cotton-shaped 3D flower-like morphology using a trisodium citrate assisted method,12 whilst uniform spherical nanoparticles have been achieved via a cetyltrimethyl ammonium bromide (CTAB) assisted hydrothermal method.13 A triclinic → tetragonal phase transition was observed by our group during the CTAB-assisted hydrothermal synthesis of NaCe(WO4)2.14,15
In this manuscript, we report for the first time a NaCe(MoO4)2 truncated octahedral nanostructure with inherent oxygen mono- and divacancy (VO and 2VO) defects and describe the role of these defects in its photoluminescence. In addition, VO and 2VO often accumulate at the surface of nanostructures and trap electrons that facilitate gas-sensing properties.16–19 Although optical studies have been reported in the literature, reports on the gas-sensing of scheelite nano/microstructures are very rare. As an example, Lin et al. reported the VO-induced gas sensing activity of NaBi(MoO4)2 nanomaterials,20 while our recent study demonstrated the NH3-sensing ability of NaCe(WO4)2.14 We herein also identify acetone-sensing ability in NaCe(MoO4)2 nanostructures, with VO and 2VO playing crucial roles in determining the sensitivity. To the best of our knowledge, this is the first report on the acetone-sensing ability of NaCe(MoO4)2. Additionally, as there have been no in-depth theoretical calculations on the electronic structure of NaCe(MoO4)2, to achieve a better understanding, we have also calculated the ab initio band structure of NaCe(MoO4)2. The calculations reveal that the Ce 5dz2, dx2–y2, and dyz orbitals result in blue and green emissions in the presence of VO and 2VO, respectively. We have demonstrated that the electronic excitation involved the MoO4 tetrahedra and that emission takes place within the CeO8 polyhedra, while MoO4 → CeO8 charge transfer is mediated through the ν4(F2) phonon mode. Overall, it may be inferred that the truncated octahedron NaCe(MoO4)2 nanostructures have strong potential in violet emission and sensing applications.
2. Experimental section
2.1 Materials and synthesis
To prepare NaCe(MoO4)2 nanomaterials through the typical hydrothermal method, 1.00 mmol (0.434 g) of cerium nitrate [Ce(NO3)3·6H2O, Merck, Germany] and trisodium citrate [Na3Cit·2H2O, Merck, Germany] were mixed with 60 ml DI water, followed by stirring for 2 h at room temperature. Another aqueous solution of 2.00 mmol (0.484 g) sodium molybdate [Na2MoO4·H2O, Merck, Germany] in 20 ml DI water was added dropwise to the above solution. After 30 minutes of vigorous stirring, the resulting solution turned a pale yellow colour; the solution was then transferred to a Teflon autoclave for hydrothermal reaction at 180 °C for 24 h. The final product was collected by centrifugation, followed by simultaneous washing with DI water and ethanol, overnight drying at 70 °C and calcination at 800 °C for 5 h in a muffle furnace. The synthesis was repeated using different concentrations of Na3Cit·2H2O (0.00, 0.50, 0.78, and 1.00 mmol, i.e., 0.00, 0.147, 0.229, and 0.294 g) to examine its effect on the final product, and the resulting samples were labelled as NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively. The reaction procedure is presented schematically in Fig. S1 of the ESI.†
2.2 Characterization and gas-sensing properties
X-Ray diffraction (XRD) patterns were obtained using a Rigaku Ultima III powder diffractometer equipped with CuKα radiation (λ = 1.54056 Å) and utilized to examine the phase purity and other crystallographic information through the Rietveld refinement method using the FullProf program suite. Experimental profiles were fitted with a suitable pseudo-Voigt analytical asymmetric function, while the background was fitted with a fourth-order polynomial function. Field emission scanning electron microscopy (FESEM: Hitachi S – 4800, operated at 5 kV) was used to inspect the morphology of the samples, while a transmission electron microscope (TEM-2100 Plus Electronmicroscope, 200 kV) was used to obtain high-resolution microscopic images and selected area electron diffraction (SAED). Raman spectra obtained using an alpha 300 Witec with a 530 nm laser (power: 3 mW; spot size: 2 μm) and Fourier transform infrared (IR) spectra recorded using an IR Prestige were utilized to examine the short-range structural distortion. X-Ray photoelectron spectra (XPS) were collected using a PHI Versa Probe III Scanning XPS Microprobe with an Al K source. The optical properties of the as-prepared samples were investigated at room temperature using UV-Vis spectroscopy (JASCO V650) and photoluminescence spectroscopy (FP-8300, JASCO, 100 W Xe lamp).
Gas-sensing properties were examined using Taguchi-type sensor module, in which a hollow cylindrical Al2O3 substrate having Pt electrodes was coated with a thick slurry of the nanostructured NCMO materials through the drop-casting method. The slurry was prepared by mixing the as-prepared samples with isopropyl alcohol as a binder, and the coated substrates were heated at 100 °C for 12 h to remove residual solvents. Ni–Cr wire was inserted through the hole of the substrate as a heating element to provide the required temperature by adjusting the applied voltage across the wire. Gases supplied from cylinders, balanced with air, were used during measurement of the sensing performance with an Agilent 34461A digital multimeter interfaced with data logger software.
2.3 Calculation of band structure and investigation of gas-sensing mechanism using ab initio density functional theory
It is well-known that the electronic band structure provides theoretical insight into the opto-electronic properties of any material; hence, we computed the spin-polarized band structure, density of states (DOS), partial DOS (pDOS), total DOS (TDOS) and projected DOS (PDOS) using VASP.21 Here, the plane-wave pseudo-potential (PAW) was used, while the Perdew–Burke–Ernzerhof (PBE) exchange correlation and ultra-soft potential as basis set were considered.22 We employed the valence electrons of the respective atoms as follows: Na atom (1s2 2s2 2p6 3s1), Ce atom (5s2 5p6 4f1 5d1 6s2), Mo atom (4p6 5s2 4d10), and O atom (2s2 2p4). For this calculation, 5 × 5 × 7 Monkhorst–Pack k points were used, as this allowed an accurate representation of the Brillouin zone and the electronic properties of the material. Prior to calculating the band structure along Γ → X → H1 → C → H → Y → Γ, the structure was optimized with the lowest single-point ground state energy by fixing the cut-off energy at 520 eV, while the convergence was tested between 220 and 620 eV. A maximum atomic displacement of ∼5 × 10−4 Å and stress of ∼0.02 GPa were considered for this calculation. Each atom was exposed to a 0.01 eV Hellmann–Feynman force to ensure stable convergence, while the EDIFF and force EDIFG parameters were adjusted to 10−6 eV and 10−3 eV, respectively, to ensure high-precision computational convergence.14
In order obtain theoretical insight into the influence of the defects on the gas-sensing performance, we calculated the adsorption energies of acetone on the NCMO surface as shown in Table S2 (ESI†). Herein, we have modelled the tetragonal NCMO (112) plane with supercell dimension of 7.573 Å × 17.823 Å × 32.422 Å. The k-point mesh for this calculation was optimized at 3 × 3 × 1, while the thickness of the slab and the vacuum level were ∼3 nm and 15 Å, respectively. In these calculations, the bottom half of the layers were frozen, whereas the top half of the layers with acetone as the adsorbent were set to relax. The adsorption energy was then calculated using eqn (1):
| | | Eads = ENCMO+acetone − ENCMO − Eacetone | (1) |
where
ENCMO+acetone,
ENCMO and
Eacetone represent the total ground state energies of NCMO in combination with the acetone molecule, bare NCMO and acetone gas, respectively. In order to examine the influence of defects on the gas-sensing activity, we carried out the above calculations by removing one or two oxygen atoms from the (112) plane of NCMO, as shown in Fig. S2 (ESI
†).
3. Results and discussion
3.1 Structural and morphological studies using XRD, FESEM and TEM
The XRD patterns of all the samples (Fig. 1) closely match with that of scheelite-type tetragonal NCMO with the space group I41/a (C4h6, ICDD Database No. 04-007-5489). The absence of any peak other than those of NCMO confirms the phase purity of the synthesized nanostructures, while the sharp diffraction peaks indicate good crystallinity. The unit cell is represented in Fig. S3, and Table S1 in the ESI† summarizes the structural parameters as obtained from Rietveld refinement, which was carried out until satisfactory convergence of χ2, Rp and Rwp were achieved.23 As shown in Fig. S3 (ESI†), the unit cell of NCMO comprises Na and Ce atoms at the 4b sites and is coordinated to eight O atoms at 16f site via two different bond lengths to produce (Na/Ce)O8 polyhedra; in turn, these polyhedrons are connected to MoO4 tetrahedra with Mo at the 4a site. The unit cell volume, c value, c/a ratio, Na/Ce–O bond lengths, and the Na/Ce–O–Mo and O–Mo–O bond angles (but not the Mo–O bond lengths) decrease monotonically from NCMO0.00 to NCMO1.00, indicating an enhancement in the distortion of the unit cells. The (Na/Ce)O8 polyhedral (N) and MoO4 tetrahedral (K) distortions were calculated using the expressions 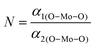 ,24 where α1(O–Mo–O) and α2(O–Mo–O) denote the two different bond angles, and
,24 where α1(O–Mo–O) and α2(O–Mo–O) denote the two different bond angles, and 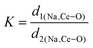 , where d1(Na,Ce–O) and d2(Na,Ce–O) represent the two different bond lengths and were found to be N = 1.011, 1.029, 1.043, 1.052 and K = 1.0587, 1.0827, 1.0838, 1.0842 for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively.25,26 According to previous studies, a decrease in the c/a ratio is associated with the partial substitution of Na+ by Ce3+,27,28 while the perquisite charge neutrality is balanced by O vacancies (VO), causing increases in K and N.
, where d1(Na,Ce–O) and d2(Na,Ce–O) represent the two different bond lengths and were found to be N = 1.011, 1.029, 1.043, 1.052 and K = 1.0587, 1.0827, 1.0838, 1.0842 for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively.25,26 According to previous studies, a decrease in the c/a ratio is associated with the partial substitution of Na+ by Ce3+,27,28 while the perquisite charge neutrality is balanced by O vacancies (VO), causing increases in K and N.
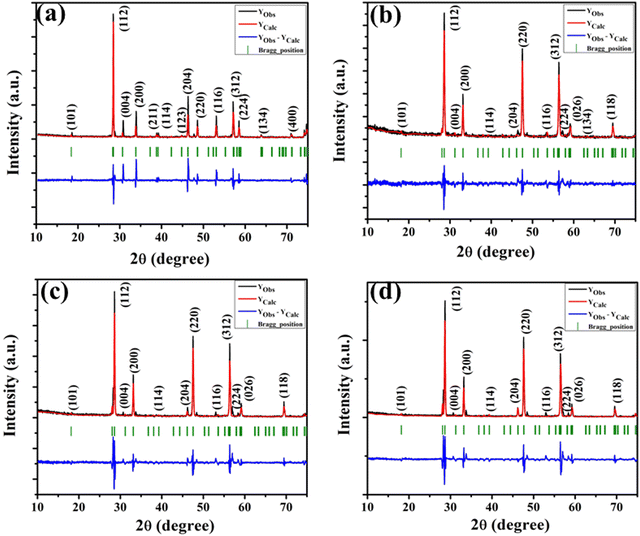 |
| | Fig. 1 XRD patterns of the NaCe(MoO4)2 samples (a) NCMO0.00, (b) NCMO0.50, (c) NCMO0.78 and (d) NCMO1.00, respectively. | |
It can be noted from the FESEM image that NCMO0.00 possesses an irregular shape (Fig. 2(a)), while a gradual transformation from an irregular to a truncated octahedral shape was observed for NCMO0.50, NCMO0.78 and NCMO1.00 (Fig. 2(b)–(d)) suggesting that Na3Cit has significant role during hydrothermal reaction to tune morphology. Mapping of the samples (Fig. S4, ESI†) clearly reveals even distribution of elements. For a better understanding of the shape of these microstructures, transmission electron microscopy (TEM) was further employed. Fig. 2(e) depicts a typical TEM image of NCMO1.00, which corroborates the truncated octahedral shape, while the selected area diffraction pattern (Fig. 2(f)) consists of five diffraction spots corresponding to the (112), (211), (123), (222) and (224) planes of tetragonal NCMO, denoting its crystalline character.
 |
| | Fig. 2 FESEM images of NCMO samples (a) NCMO0.00, (b) NCMO0.50, (c) NCMO0.78 and (d) NCMO1.00, (e) and (f) TEM image and SAED pattern of NCMO1.00. | |
3.2 Investigations of local structure using FTIR, Raman and X-ray photoelectron spectroscopies
To understand the influence of VO on the short-range structural distortions of (Na/Ce)O8 polyhedra and MoO4 tetrahedra, we obtained the FTIR and Raman spectra of our synthesized samples. The various peaks in the absorption band (shown in Fig. S5 of the (ESI†)) between 500 and 1000 cm−1 are attributed to the various active internal vibrations of MoO4 tetrahedra. Commonly, MoO4 tetrahedra crystallize in either regular (MoRO4) or distorted form (MoDO4) due to VO, while the vibration (ΓTd) of the isolated MoRO4 is represented by:29However, the symmetry of the tetrahedra changes to S4 in NCMO, for which the IR active modes include ν1(A1), ν2(E1), ν3(F2), ν4(F2), one free rotation νf.r.(F1) and one translation F2. In contrast to MoRO4, MoDO4, which has the C2h6 space group, exhibits four formula units per crystallographic unit cell with 2Mo(C2), 4Mo(C1), 4Ce(C1) and 24O(C1) symmetries of the atoms, indicating splitting of the vibrational modes (i.e., O → Mo(C1) → O and O → Mo(C2) → O) within MoDO4 due to lower site symmetry.30 The two bands at 650–749 and 750–1000 cm−1 are ascribed to ν3(F2) and ν4(F2), while the peak at 670 cm−1 is assigned to ν2(E1). Careful deconvolution (Fig. S6, ESI†) of the ν3(F2) and ν4(F2) modes yields three peaks (i.e., 693, 705, 722 cm−1 and 813, 858, 909 cm−1). As per the bond length–stretching frequency correlation described by Hardcastle et al., an increase in the bond length decreases the vibrational frequency.31 Hence, the vibrational mode with lower energy corresponds to MoDO4, while the high-energy peaks are ascribed to MoRO4. Therefore, the peaks at 722 and 909 cm−1 are attributed to the ν3(F2) and ν4(F2) modes of MoRO4, respectively, while the peaks at 693/705 cm−1 and 813/858 cm−1 correspond to the ν3(F2) and ν4(F2) mode of vibration within MoDO4.30 The MoDO4/MoRO4 ratio, which was calculated from the areas under the curve, was found to be 0.8, 1.0, 1.6 and 2.9 for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively, indicating an increase in tetrahedral distortion with increasing Na3Cit concentration, which corroborates the previous structural studies using XRD.
The Raman spectra, which were obtained up to the range of 1000 cm−1 at ambient temperature (Fig. S7, ESI†), consist of a peak at 463 cm−1 and three bands at 64–231, 255–425 and 681–966 cm−1. In general, Raman spectra of scheelite materials at the Γ-point is expressed as:
where the non-degenerate A
g and B
g modes and the doubly degenerate E
g mode correspond to the various external and internal vibrations of MoO
4 and CeO
8.
29 The peak at 64–231 cm
−1 corresponds to the rotation and translation of the MoO
4 tetrahedra and Na
+ and Ce
3+, respectively. The sharp peak is attributed to the external vibration of CeO
8, which is in good agreement with previous results,
32 while the bands are ascribed to the internal bending of the MoO
4 tetrahedra. After thorough examination, the two peaks at 318 and 380 cm
−1 were assigned to the symmetric A
g bending and antisymmetric B
g bending vibrational modes of MoO
4, respectively.
33 While the peak at 463 cm
−1 is assigned to antisymmetric A
g bending mode of MoO
4. The other two Raman peaks at 823 and 889 cm
−1 are assigned to (O → Mo → O) antisymmetric stretching B
g and (O ← Mo → O) symmetric A
g mode of vibration.
29,34,35 The decrease in Raman intensity with increasing Na
3Cit concentration is believed to be related to the increase of V
O and antisite defects, in agreement with the XRD and FTIR studies.
36,37
X-Ray photoelectron spectroscopy (XPS), a well-known technique to investigate the chemical state of elements, was adopted here to examine VO-associated changes in the valence states of Na, Ce, Mo and O, as they are highly sensitive to the local electronic environment. The binding energy data of all elements were adjusted with respect to the binding energy (∼284.6 eV) of surface-adsorbed atmospheric C 1s.14 The survey scans for all the synthesized samples are presented in Fig. S8 of the ESI,† while the high-resolution spectra of Mo, Ce, and O are illustrated in Fig. S9–S11 of the ESI.† Two peaks (i.e., 232.7 and 236.0 eV) of Mo can be readily ascribed to the spin–orbit splitting of the 3d5/2 and 3d3/2 orbitals of Mo6+, while careful deconvolution (Fig. S9(a)–(d), ESI†) reveals the presence of two peaks for the two orbitals (i.e., 232.5 and 232.9 eV for 3d5/2 and 235.7 and 236.2 eV for 3d3/2), which were assigned as Mo3d5/2(I), Mo3d5/2(II) and Mo3d3/2(I), Mo3d3/2(II), respectively. Accordingly, we ascribed Mo3d5/2(II) and Mo3d3/2(II) to MoRO4, while Mo3d5/2(I) and Mo3d3/2(I) corresponded to MoDO4; their difference can be assigned to the VO-induced changes in electronic repulsion. In brief, electrons are located on O due to its strong electronegativity, which makes the Mo–O bond significantly ionic, while VO increases the effective charge on Mo. Hence, the electron–electron repulsion on Mo reduces the binding energies of the Mo 3d5/2 and 3d3/2 orbitals in MoDO4. In this context, the smaller energy difference between 3d5/2 and 3d3/2 in MoDO4 with respect to MoRO4 (i.e., 3.23 and 3.19 eV) again indicates the influence of the local field generated from VO on spin–orbit splitting. The weighted percentage of MoDO4 calculated from the area under the curve was found to be ∼26, 32, 35 and 42% for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively, which agrees well with the previous finding of increasing MoDO4 content. As illustrated in Fig. S10(a)–(d) (ESI†), the two asymmetric peaks observed at 877–891 and 894–912 eV are attributed to the spin–orbit splitting of the 3d5/2 and 3d3/2 orbitals of Ce3+. Similar to the Mo orbitals, careful deconvolution of the asymmetric d5/2 peak yields three peaks at 882.0, 884.6, and 886.9 eV, which were designated as Ce3d5/2(I), Ce3d5/2(II) and Ce3d5/2(III), indicating the presence of Ce with three different oxidation states. Ce3d5/2(III) was assigned to the Ce of the regular CeO8 polyhedra, while Ce3d5/2(II) and Ce3d5/2(I) correspond to Ce belonging to the CeO8 polyhedra with one or two oxygen vacancies (ca. VO and 2VO) and with the nomenclature CeO7 and CeO6, respectively. In this context, it may be stated that CeO7 and CeO6 represent deformed CeO8 polyhedra with one or two nearby MoDO4 and MoDO4 subunits (shown schematically in Fig. 3). Due to smaller difference in electronegativity between Ce and O, the Ce–O bond is supposed to be more covalent; therefore, VO plays the predominant role in terms of this covalence and the binding energy. We observed from the Rietveld analysis that VO shortens Ce–O bond lengths, which in consequence increases electron–electron repulsion at Ce site; thus, the binding energy of the 3d orbitals is decreased in the distorted polyhedra.38 The analysis showed that the weighted percentage of Cea increases (∼19, 23, 37, 41%), while there is a significant decrease in the weighted percentage of Ceb (∼48, 46, 37, 26%) from NCMO0.00 to NCMO1.00. On the other hand, Cec remains almost unchanged for all samples (∼30%). Therefore, the analysis indicates greater generation of 2VO at the cost of VO; hence, the tendency for VO cluster formation increases. The XPS of O 1s displays asymmetry, indicating the presence of two different O species. A careful analysis reveals two O 1s peaks (Fig. S11, ESI†) at 530.6 and 532.4 eV, corresponding to lattice O and the O atom of the MoDO4 tetrahedra.39 The increasing ratio of the area under the fitted curves illustrates the monotonic increase in MoDO4 tetrahedra from NCMO0.00 to NCMO1.00.
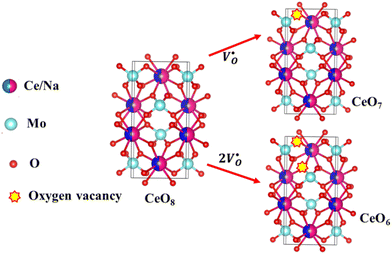 |
| | Fig. 3 Schematic diagram of oxygen vacancies of the CeO8 polyhedral unit. | |
3.3 Optical properties of the as-prepared NCMO samples using UV-Vis and photoluminescence spectroscopy
The optical band gap (Eg) was calculated to be ∼3.07, 3.05, 3.02 and 2.99 eV for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00 based on the UV-Vis absorption spectra (shown in Fig. S12, ESI†). This variation can be understood as follows: our band structure calculations (discussed later) reveal that the valence band (VB) is made up of O 2p–Mo 4d hybridization, while the conduction band (CB) comprises Mo 4d, Ce 4f and a minute contribution from O 2p orbitals. The decrease of Mo–O bond length in the presence of VO and 2VO reduces the O 2p–Mo 4d overlap, which causes a blue-shift of the VB, and subsequently, Eg is reduced. All the samples exhibit a broad peak at 380 nm in their photoluminescence excitation (PLE) spectra, which were obtained using an emission wavelength λem of 531 nm (Fig. S13, ESI†), while the emission spectra recorded in the visible region using an excitation wavelength of λex = 380 nm are depicted in Fig. 4(a)–(d). The PLE peak was assigned to O 2p–Mo 4d charge transfer absorption within MoO4 tetrahedra.40,41 The emission spectra have four distinct peaks in the blue (i.e. blue I, blue II, blue III) and green regions, with an intense blue I peak being observed at 440 nm (22![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 cm−1), while relatively weaker blue II, blue III peaks and a prominent green peak are observed at 462 nm (21
727 cm−1), while relatively weaker blue II, blue III peaks and a prominent green peak are observed at 462 nm (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 cm−1), 488 nm (20
645 cm−1), 488 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 492 cm−1) and 531 nm (18
492 cm−1) and 531 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 cm−1), respectively. The Stokes shift of the excitation and emission spectra were noted to be ∼3588 cm−1, suggesting the absence of reabsorption and interference among the various emissions.42 Although understanding the emission spectra of lanthanides is difficult for several reasons, including symmetry, the crystal field surrounding the host crystal, anion polarizability, and covalence of the host crystal, the present emissions are believed to be 5d–4f transitions within Ce3+
832 cm−1), respectively. The Stokes shift of the excitation and emission spectra were noted to be ∼3588 cm−1, suggesting the absence of reabsorption and interference among the various emissions.42 Although understanding the emission spectra of lanthanides is difficult for several reasons, including symmetry, the crystal field surrounding the host crystal, anion polarizability, and covalence of the host crystal, the present emissions are believed to be 5d–4f transitions within Ce3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 and can be validated as follows. The emission wavelength (λ in nm) for intra-5d–4f transitions can be calculated using eqn (4):44,45
43 and can be validated as follows. The emission wavelength (λ in nm) for intra-5d–4f transitions can be calculated using eqn (4):44,45| | 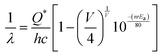 | (4) |
where, Q*, V, ‘n’, Ea and ‘r’ represent the energy of the 5d band edge of a free Ce3+ ion (= 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1), the valence of the Ce3+, the number of anions in the immediate shell around the Ce3+, the electron affinity of the atoms forming the anions (∼2.16 eV) and the difference between the average bond length and radius of Ce3+ within the CeO8 polyhedra (1.03 Å). Very careful calculation yields λ ∼ 449 nm, which corresponds to blue I emission. Previous studies indicate that VO and 2VO can significantly modify the 5d–4f transitions of lanthanide atoms, resulting in different emissions. As an example, Sokolenko et al.46 assigned green–red emission to
000 cm−1), the valence of the Ce3+, the number of anions in the immediate shell around the Ce3+, the electron affinity of the atoms forming the anions (∼2.16 eV) and the difference between the average bond length and radius of Ce3+ within the CeO8 polyhedra (1.03 Å). Very careful calculation yields λ ∼ 449 nm, which corresponds to blue I emission. Previous studies indicate that VO and 2VO can significantly modify the 5d–4f transitions of lanthanide atoms, resulting in different emissions. As an example, Sokolenko et al.46 assigned green–red emission to 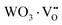 oxygen-deficient complexes, while Korzhik et al. ascribed green emission to WO3 centres.47 Considering CeO7 and CeO6 to be VO- and 2VO-containing distorted CeO8 polyhedra, we have calculated λ values of 487 and 537 nm for intra-Ce3+ 5d–4f transitions using eqn (4), which are in good agreement with the blue III and green emissions (schematically represented in Fig. S14, ESI†).
oxygen-deficient complexes, while Korzhik et al. ascribed green emission to WO3 centres.47 Considering CeO7 and CeO6 to be VO- and 2VO-containing distorted CeO8 polyhedra, we have calculated λ values of 487 and 537 nm for intra-Ce3+ 5d–4f transitions using eqn (4), which are in good agreement with the blue III and green emissions (schematically represented in Fig. S14, ESI†).
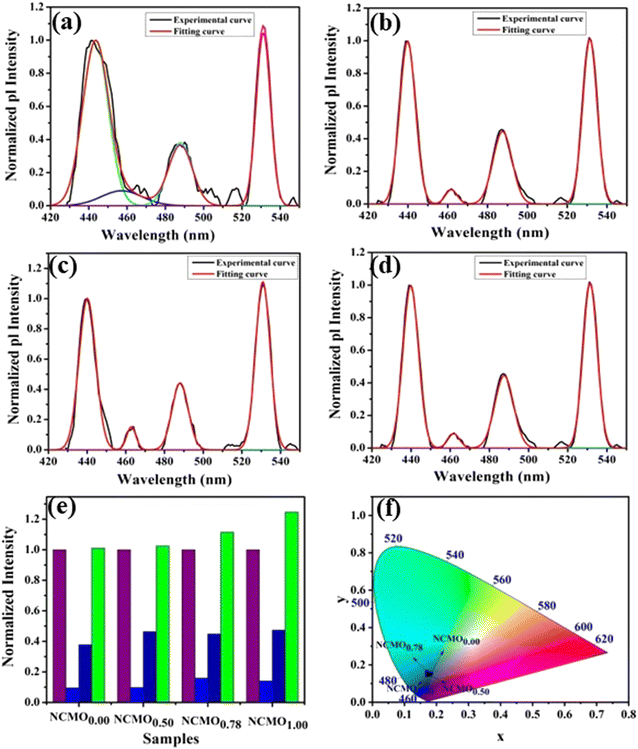 |
| | Fig. 4 Photoluminescence spectra of (a) NCMO0.00, (b) NCMO0.50, (c) NCMO0.78 and (d) NCMO1.00. (e) Normalized PL intensity ratio of emission wavelengths. (f) CIE chromaticity diagram of the NCMO phosphors. | |
The shift of the centroids of the d-orbitals (in eV) of Ce3+, εc(1,3+,Ce3+) in CeO7 and CeO6 are believed to tune the 5d–4f transition, giving various emissions (see discussion in the ESI†). Careful monitoring of the green emission reveals the presence of a phonon side band (PSB) at 516 nm with a phonon energy of 930 cm−1, which exactly matches the energy of the ν4(F2) phonon mode, indicating that MoO4 → CeO6 charge transfer is mediated by the ν4(F2) phonon mode. In this context, the Huang–Rhys (S) factor, an indicator of electron–phonon coupling, was calculated using eqn (5) and (6):48,49
| | 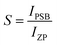 | (5) |
| | 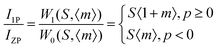 | (6) |
where,
IPSB,
IZP and
I1P are the integrated intensities of the PSB, zero-phonon line and one-phonon line. As this emission includes a single phonon (
p ≥ 0 in
eqn (6)), and considering the
5D
0–
2F
5/2 transition to be purely dipolar, we may write
IPSB =
I1P. In addition, 〈1 +
m〉 can also be considered to be 1 due to the higher phonon energy at room temperature. The decrease in the
S-factor (0.098, 0.077, 0.032 and 0.039 for the four respective samples) is ascribed to increasing distortion in the lattice structure due to V
O and 2V
O.
The Commission International De l'Eclairage (CIE) coordinates (Fig. 4(f)), which were calculated to be (0.180, 0.149), (0.180, 0.147), (0.170, 158) and (0.172, 0.148) for the NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00 samples, are well spread throughout the blue region of the visible spectrum, indicating the color purity (CP) of the NCMO samples.50 We also validated the CP using eqn (7):51,52
| | 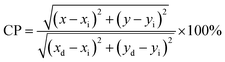 | (7) |
where (
x,
y) denotes the color coordinates of the phosphor; (
xi,
yi) is the 1931 CIE Standard Source's illuminant point, with color coordinates of (0.3101, 0.3162); and (
xd,
yd) is the color coordinates of the dominant wavelength. Outstanding CP values of ∼90–94% were observed for the samples, indicating that NCMO could be a good candidate for blue-light-emitting applications. The correlated colour temperature (CCT) was calculated using McCamy's relation:
53| | | CCT = 449n3 + 3525n2 + 6823.3n + 5520.3 | (8) |
where
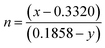
and (
x,
y) represent the chromaticity co-ordinates. The CCT values were ∼7819 K, 7630 K, 7715 K and 7854 K for the samples NCMO
0.00, NCMO
0.50, NCMO
0.78 and NCMO
1.00, respectively. The high CCT indicates that NCMO can be used for cold blue lighting.
3.4 Investigations of gas-sensing properties of NCMO nanostructures
The gas-sensing abilities of metal oxide nanostructures involve a solid–gas interfacial reaction mechanism in which the adsorption/desorption of the targeted gas molecules on the surface of the nanostructure leads to significant changes in resistance. A careful literature survey indicates that the following redox reactions between the nanostructure and acetone (CH3COCH3), ethanol (C2H5OH), ammonia (NH3), methanol (CH3OH), formaldehyde (HCHO) take place in the presence of O2−(ads).| | | CH3COCH3(gas) + 8O2−(ads) ↔ 3H2O(gas) + 3CO2(gas) + 8e− | (9) |
| | | CH3CH2OH(gas) + O2−(ads) ↔ 2H2O(gas) + C2H2O + 2e− | (10) |
| | | 4NH3(gas) + 3O2−(ads) ↔ 6H2O(gas) + 2N2(gas) + 3e− | (11) |
| | | CH3OH(gas) + O2−(ads) ↔ 2H2O(gas) + CO(gas) + 2e− | (12) |
| | | HCHO(gas) + O2−(ads) ↔ H2O(gas) + CO2(gas) + 2e− | (13) |
Our previous investigations indicate that VO and 2VO defects are often ionized (e.g., 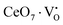 ,
, 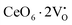 ) and act as electron donors ([CeO8]′ and [CeO8]′′), which can be understood from Kröger–Vink notation:
) and act as electron donors ([CeO8]′ and [CeO8]′′), which can be understood from Kröger–Vink notation:
| | 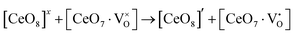 | (14) |
| | 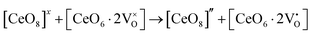 | (15) |
These [CeO8]′ and [CeO8]′′ facilitate electron transfer from the host materials to the chemisorbed oxygen molecule to generate O2−(ads), as described by the reaction: O2(gas) + e− ↔ O2−(ads).54–57 In order to validate the gas-sensing ability of our synthesized NCMO nanostructures as a proof of concept, we carried out a series of sensing measurements using NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00 as a resistive sensor probe against NH3, CH3COCH3, C2H5OH, CH3OH and HCHO at different operating temperatures (200–450 °C) at intervals of 50 °C. An optimum operating temperature of ∼300 °C was observed for all the samples (shown in Fig. 5(a)), and they are highly selective toward CH3COCH3 (Fig. 5(b), 5.0 ppm concentration) in comparison with C2H5OH, NH3, CH3OH, and HCHO 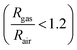 . The sensitivity monotonically increases from NCMO0.00 to NCMO1.00, with the highest sensitivity being observed for NCMO1.00. To understand the role of VO, 2VO in CH3COCH3 adsorption/desorption, we fitted the response data using the Freundlich adsorption isotherm as given in eqn (16) and (17).
. The sensitivity monotonically increases from NCMO0.00 to NCMO1.00, with the highest sensitivity being observed for NCMO1.00. To understand the role of VO, 2VO in CH3COCH3 adsorption/desorption, we fitted the response data using the Freundlich adsorption isotherm as given in eqn (16) and (17).
i.e.,
| | log(Sg − 1) = a + b![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log(Cg) log(Cg) | (17) |
where
Sg and
Cg represent sensitivity and concentration respectively, while ‘
a’ and ‘
b’ are constants that depend on the electrical charge of the species and stoichiometry of the reactions on the surface of the sensing probe. In the literature, ‘
b’ is noted to be dependent on the adsorbed O species, with
b ≤ 0.5 for O
2− adsorption and ≈1.0 for O
− adsorption.
58 From slope of the linear regressions (
Fig. 5(c)) curves obtained using
eqn (17), we calculated
b values of ∼0.423, 0.279, 0.088, 0.053 for NCMO
1.00, NCMO
0.78, NCMO
0.50 and NCMO
0.00, respectively, suggesting that 2V
O acts as a more-active site for O
2− generation, facilitating CH
3COCH
3 adsorption. The dynamic sensing responses ofNCMO
1.00 (
Fig. 5(d)) measured at 300 °C demonstrate sensitivity values of ∼1.86, 2.81, 4.95, 6.21 and 6.89 in the presence of 1.0, 5.0, 10.0, 50.0 and 100.0 ppm of CH
3COCH
3, while the response and recovery (at 5.0 ppm of CH
3COCH
3, see Fig. S15(b) of the ESI
†) remain the same for six consecutive cycles (error ≤ 2%), indicating the excellent reproducibility and reliability of NCMO
1.00 as a sensor probe in comparison with the other samples (Fig. S15(c–e), ESI
†). In addition, the very low response and recovery time of ∼1.5 s/33.8 s (
Fig. 5(e), measured at 10.0 ppm) indicate the fast response of NCMO
1.00, while its long-term stability was checked and verified over 90 days at intervals of 10 days (
Fig. 5(f)).
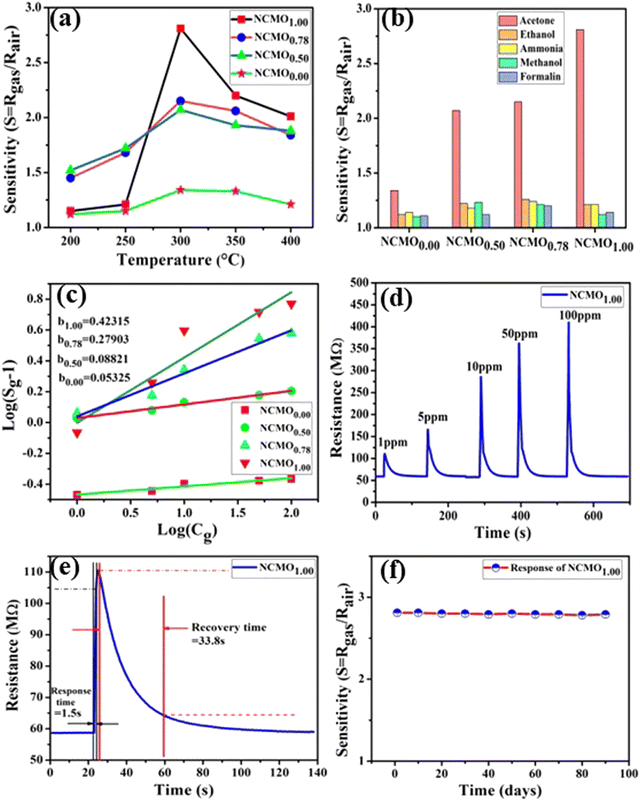 |
| | Fig. 5 (a) Temperature calibration curves of NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively. (b) Selectivity ofNCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00 sensors measured at an operating temperature of 300 °C. (c) Linear fitting of the logarithm of sensitivity and logarithm of acetone concentration data of all samples. (d) Dynamic acetone response curves of the NCMO1.00 sensor to acetone concentrations from 1–100 ppm at 300 °C. (e) Response and recovery time of the NCMO1.00-based sensor for 1 ppm acetone at 300 °C. (f) Long-term stability of the NCMO1.00-based sensor in sensing 1 ppm acetone measured over 90 days. | |
3.5 Density functional theory (DFT) calculations of NCMO
In order to validate the VO- and 2VO-associated optical emissions and sensing activity, we calculated the electronic band structure, total density of states (TDOS), and angular momentum projected partial density of states (PDOS) using ab initio density functional theory (DFT), which provides valuable insights to explain the luminescence and gas sensing behaviour. For this, we calculated band structure along several high symmetry k-points within the Brillouin zone. In this calculation, we removed one or two O atoms from the NCMO unit cell to mimic CeO7 (VO) and CeO6 (2VO). Prior to calculating the electronic band structure, we optimized the unit cell of pure NCMO and obtained lattice parameters a = b = 5.355 and c = 11.611 Å and Na/Ce–O and Mo–O lengths of ∼2.453 and 1.806 Å, respectively. These were in good agreement with the experimental results, proving the accuracy of our calculations, specifically, the choice of exchange correlation and pseudopotential. The top of the valence band maxima (VBM) was set to zero as a reference for other calculations. As shown in Fig. 6(a), NCMO appears to be an indirect bandgap material (Eg ∼ 3.23 eV) with a spin-unpolarized VBM and spin-polarized conduction band minima (CBM) at Γ- and X-points, respectively. The curvature of the VBM is observed to be low, indicating a comparatively high effective hole mass, while the CBM has a high curvature suggesting a low effective electron mass. The TDOS (shown in Fig. 6(b)) and PDOS contributions of O, Mo, Ce and Na (shown in Fig. S16(c)–(f), ESI†) demonstrate that the upper part of the VB is primarily composed of the O 2px, 2py, and 2pz orbitals with very small contributions from Mo 2px, 2py, and 2pz, giving a low curvature. The lower part of the VB originates from predominant hybridization between Mo 4dxy, 4dxz, 4dz2 and O 2px, 2py, and 2pz orbitals, whereas 4dx2 and 4dyz make insignificant contributions. We noted almost no contribution to the VB from the Ce 4f and Na 3s orbitals. The CBM comprises spin-polarized (i.e., up-spin) Ce 4fz3, 4fxz2 and 4fy3x2 orbitals, among which the most predominant contribution comes from 4fxz2, hybridized with O 2px, 2py, and 2pz orbitals, giving a higher curvature in comparison with the VBM, while the upper portion of the CB is made up of Mo–4dz2 and 4dx2. Thus, it may be stated that the MoO4 tetrahedra mostly construct the VB, while the CB is predominantly contributed by the CeO8 polyhedra, and the band-to-band transition includes a Mo ↔ Ce charge transfer process.
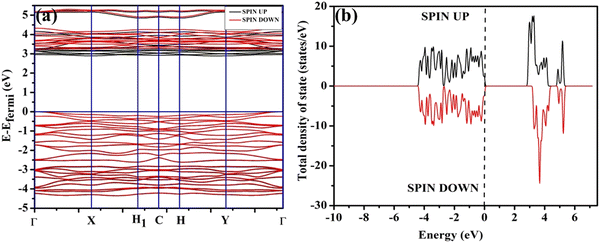 |
| | Fig. 6 (a) Band structure and (b) spin-polarised TDOS of NCMO. | |
The band structures, TDOS and PDOS of the 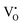 - and
- and 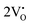 -containing NCMO samples, designated as
-containing NCMO samples, designated as 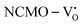 and
and 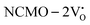 , are represented in Fig. S17 and S18 (ESI†), respectively. Notably, both the VBM and CBM (shown in Fig. S17(a), ESI†) of
, are represented in Fig. S17 and S18 (ESI†), respectively. Notably, both the VBM and CBM (shown in Fig. S17(a), ESI†) of 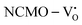 remain unchanged, while in case of
remain unchanged, while in case of 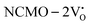 , the CBM band has shifted into the Γ-point (shown in Fig. S17(a), ESI†), indicating the transformation from an indirect to a direct Eg nature for NCMO. We observed an Eg of 3.01 and 2.95 eV for
, the CBM band has shifted into the Γ-point (shown in Fig. S17(a), ESI†), indicating the transformation from an indirect to a direct Eg nature for NCMO. We observed an Eg of 3.01 and 2.95 eV for 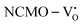 and
and 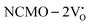 , suggesting a decrease in Eg due to
, suggesting a decrease in Eg due to 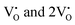 . Thus, the monotonic decrease in the experimentally measured Eg from NCMO0.00 to NCMO1.00 is believed to be due to increasing VO and 2VO, corroborating previous studies. The reduction of Eg can be understood as follows: TDOS (Fig. S17(b) and S18(b), ESI†) and PDOS (Fig. S17(c)–(f) and S18(c)–(f), ESI†) calculations show that the VB width decreases in
. Thus, the monotonic decrease in the experimentally measured Eg from NCMO0.00 to NCMO1.00 is believed to be due to increasing VO and 2VO, corroborating previous studies. The reduction of Eg can be understood as follows: TDOS (Fig. S17(b) and S18(b), ESI†) and PDOS (Fig. S17(c)–(f) and S18(c)–(f), ESI†) calculations show that the VB width decreases in 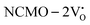 due to the greater localization of the O 2p orbitals, while the curvature increases in
due to the greater localization of the O 2p orbitals, while the curvature increases in 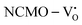 and
and 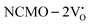 , which is attributed to the enhanced overlap between the Ce 4fzx2, 4fxz2, 4fyz, and 4fxyz and O 2px, 2py, and 2pz orbitals due to the decrease in the Ce–O bond length in the CeO8 polyhedra, indicating higher carrier mobility. Further analysis of the TDOS and PDOS reveals that the contributions from Ce 5dxy and 5dxz to the CB increase in
, which is attributed to the enhanced overlap between the Ce 4fzx2, 4fxz2, 4fyz, and 4fxyz and O 2px, 2py, and 2pz orbitals due to the decrease in the Ce–O bond length in the CeO8 polyhedra, indicating higher carrier mobility. Further analysis of the TDOS and PDOS reveals that the contributions from Ce 5dxy and 5dxz to the CB increase in 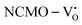 and
and 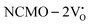 . The defect state at 2.44 eV above the valence band in
. The defect state at 2.44 eV above the valence band in 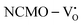 was assigned to Ce 5dz2, whilst these defects are found at 2.26 and 2.40 eV above in
was assigned to Ce 5dz2, whilst these defects are found at 2.26 and 2.40 eV above in 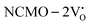 due to Ce 5dz2 and Ce 5dx2, respectively. Therefore, it can be stated that the blue III emission originates from Ce 5dz2 → 4f transitions in the CeO7 polyhedra, while the blue II and green emissions are attributed to Ce 5dz2 → 4f and Ce 5dx2 → 4f transitions in the CeO6 polyhedra, respectively, as schematically presented in Fig. 7.
due to Ce 5dz2 and Ce 5dx2, respectively. Therefore, it can be stated that the blue III emission originates from Ce 5dz2 → 4f transitions in the CeO7 polyhedra, while the blue II and green emissions are attributed to Ce 5dz2 → 4f and Ce 5dx2 → 4f transitions in the CeO6 polyhedra, respectively, as schematically presented in Fig. 7.
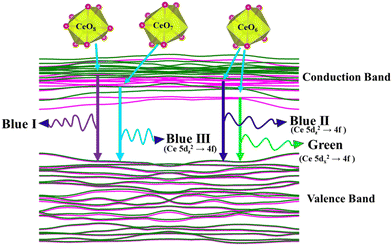 |
| | Fig. 7 Schematic picture of luminescent transitions within different CeO8 polyhedra involving different orbitals. | |
From the calculation of the adsorption energies on the (112) plane with the lowest energy for the NCMO, 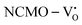 and
and 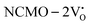 systems using eqn (1), we found the energies listed in Table S2 (ESI†). The Eads (eV) values represent the adsorption energies of the pristine NCMO,
systems using eqn (1), we found the energies listed in Table S2 (ESI†). The Eads (eV) values represent the adsorption energies of the pristine NCMO, 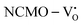 ,
, 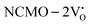 systems, and it was found that Eads < 0, indicating that the adsorption processes involved in these systems are thermodynamically stable and exothermic, meaning that they release energy during the adsorption process. Additionally, the increasingly negative values of
systems, and it was found that Eads < 0, indicating that the adsorption processes involved in these systems are thermodynamically stable and exothermic, meaning that they release energy during the adsorption process. Additionally, the increasingly negative values of 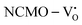 and
and 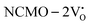 suggest the presence of active sites (oxygen vacancies) on the NCMO surface, which create localized electron-rich sites enabling strong interactions to occur between the CH3COCH3 and NCMO surfaces.59 Hence, the highest sensitivity of NCMO1.00 (Fig. 5) can purely be assigned to the presence of the highest 2VO content, which is in good agreement with the experimental results and theoretical calculations.
suggest the presence of active sites (oxygen vacancies) on the NCMO surface, which create localized electron-rich sites enabling strong interactions to occur between the CH3COCH3 and NCMO surfaces.59 Hence, the highest sensitivity of NCMO1.00 (Fig. 5) can purely be assigned to the presence of the highest 2VO content, which is in good agreement with the experimental results and theoretical calculations.
4. Conclusion
In summary, this study reports the synthesis and characterization of oxygen-deficient NCMO-truncated octahedral nanostructures, which exhibit intense blue I and green emissions and comparatively low-intensity blue II and blue III emissions. Excitation involves MoO4 tetrahedra, while emissions are attributed to the 5d → 4f transitions of Ce in different CeO8 polyhedral configurations. This study also identified the acetone-sensing ability of NCMO, which has been attributed to CeO6. The valence and conduction bands of NCMO comprise O 2p and O 2p and Ce 5d orbitals, respectively; hence, they are highly sensitive to oxygen vacancies and have a potential role in luminescence and gas sensing. Our study suggests that NCMO may be a promising material for blue-light-emitting and acetone-sensing applications.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
One of the authors (NH) thanks UGC, Govt. of India, and TM thanks CSIR, Govt. of India, for financial support during execution of their work. NH and TM made equal contributions to this manuscript. The authors would also like to acknowledge Researchers Supporting Project (RSP2024R373), King Saud University, Riyadh, Saudi Arabia.
References
- B. Glorieux, V. Jubera, A. Apheceixborde and A. Garcia, Sol. State. Sci., 2011, 13, 460–467 CrossRef.
- H. Yang, F. Peng, Q. Zhang, W. Liu, D. Sun, Y. Zhao and X. Wei, Opt. Mater., 2013, 35, 2338–2342 CrossRef CAS.
- J. R. de Moraes, S. L. Baldochi, L. D. R. L. Soares, V. L. Mazzocchi, C. B. R. Parente and L. C. Courrol, Mater. Res. Bull., 2012, 47, 744–749 CrossRef CAS.
- Z. Xu, S. Li, Q. Meng, X. Wang, Q. Zhu and J. G. Li, J. Alloys Compd., 2020, 830, 154676 CrossRef CAS.
- J. Kim, Inorg. Chem., 2017, 56, 8078–8086 CrossRef CAS PubMed.
- F. Cheng, Z. Xia, M. S. Molokeev and X. Jing, Dalton Trans., 2015, 44, 18078–18089 RSC.
- J. Song, Y. Du, L. Xu, H. Wei, D. He and H. Jiao, J. Am. Ceram. Soc., 2014, 97, 1442–1449 CrossRef CAS.
- A. Sarapulova, D. Mikhailova, A. Senyshyn and H. Ehrenberg, J. Solid State Chem., 2009, 182, 3262–3268 CrossRef CAS.
- L. S. Cavalcante, J. C. Sczancoski, R. L. Tranquilin, M. R. Joya, P. S. Pizani, J. A. Varela and E. Longo, J. Phys. Chem. Solids, 2008, 69, 2674–2680 CrossRef CAS.
- X. Liu, W. Hou, X. Yang and J. Liang, CrystEngComm, 2014, 16, 1268–1276 RSC.
- S. Huang, D. Wang, C. Li, L. Wang, X. Zhang, Y. Wan and P. Yang, CrystEngComm, 2012, 14, 2235–2244 RSC.
- Y. Tian, B. Chen, R. Hua, N. Yu, B. Liu, J. Sun, L. Cheng, H. Zhong, X. Li, J. Zhang and B. Tian, CrystEngComm, 2012, 14, 1760–1769 RSC.
- Z. Wang, Y. Li, Q. Jiang, H. Zeng, Z. Ci and L. Sun, J. Mater. Chem. C, 2014, 2, 4495–4501 RSC.
- N. Haldar, T. Mondal, T. Das, D. Sarkar, M. Pal and C. K. Ghosh, CrystEngComm, 2023, 25, 3514–3527 RSC.
- N. Haldar, T. Mondal, A. Dutta, D. Sarkar, U. K. Ghorai and C. K. Ghosh, Appl. Phys. A: Mater. Sci. Process., 2023, 129, 708 CrossRef CAS.
- S. Das, U. K. Ghorai, R. Dey, C. K. Ghosh and M. Pal, New J. Chem., 2022, 46, 17585–17595 RSC.
- S. Das, U. K. Ghorai, R. Dey, C. K. Ghosh and M. Pal, Phys. Chem. Chem. Phys., 2017, 19, 22995–23006 RSC.
- B. Ding, H. Qian, C. Han, J. Zhang, S. E. Lindquist, B. Wei and Z. Tang, J. Phys. Chem. C, 2014, 118, 25633–25642 CrossRef CAS.
- R. Fernández-Climent, S. Giménez and M. García-Tecedor, Sustainable Energy Fuels, 2020, 4, 5916–5926 RSC.
- Z. Lin, M. Xu, Y. Hong, X. Wang and P. Fu, Mater. Lett., 2016, 168, 72–75 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- W. R. Liu, C. W. Yeh, C. H. Huang, C. C. Lin, Y. C. Chiu, Y. T. Yeh and R. S. Liu, J. Mater. Chem., 2011, 21, 3740–3744 RSC.
- L. S. Cavalcante, F. M. C. Batista, M. A. P. Almeida, A. C. Rabelo, I. C. Nogueira, N. C. Batista, J. A. Varela, M. R. M. C. Santos, E. Longo and E. M. S. Li, RSC Adv., 2012, 2, 6438–6454 RSC.
- G. M. Kuzmicheva, A. V. Eremin, V. B. Rybakov, K. A. Subbotin and E. V. Zharikov, Russ. J. Inorg. Chem., 2009, 54, 854–863 CrossRef.
- R. L. Andrews, A. M. Heyns and P. M. Woodward, Dalton Trans., 2015, 44, 10700–10707 RSC.
- L. Li, Y. Su and G. Li, Appl. Phys. Lett., 2007, 90, 054105 CrossRef.
- G. M. Kuz'Micheva, I. A. Kaurova, V. B. Rybakov, P. A. Eistrikh-Geller, E. V. Zharikov, D. A. Lis and K. A. Subbotin, CrystEngComm, 2016, 18, 2921–2928 RSC.
- J. V. B. Moura, G. S. Pinheiro, J. V. Silveira, P. T. C. Freire, B. C. Viana and C. Luz-Lima, J. Phys. Chem. Solids, 2017, 111, 258–265 CrossRef CAS.
- Z. Xu, P. Du, Q. Zhu, X. Li, X. Sun and J. G. Li, Dalton Trans., 2021, 50, 17703–17715 RSC.
- J. A. Horsley, I. E. Wachs, J. M. Brown, G. H. Via and F. D. Hardcastle, J. Phys. Chem., 1987, 91, 4014–4020 CrossRef CAS.
- B. P. Singh and R. A. Singh, New J. Chem., 2015, 39, 4494–4507 RSC.
- F. F. Wu, D. Zhou, C. Du, S. K. Sun, L. X. Pang, B. B. Jin, Z. M. Qi, J. Varghese, Q. Li and X. Q. Zhang, J. Mater. Chem. C, 2021, 9, 9962–9971 RSC.
- Z. Zhao, Z. Sui, X. Wei, J. Zuo, X. Zhang, R. Dai, Z. Zhang and Z. Ding, CrystEngComm, 2015, 17, 7905–7914 RSC.
- J. Victor-Barbosa-Moura, A. Amison-Gomes-de Souza, P. de Tarso-Cavalcante-Freire, C. da Luz-Lima and T. Mielle-Brito-Ferreira-Oliveira, Int. J. Appl. Ceram. Technol., 2021, 18, 615–621 CrossRef CAS.
- Y. Xiong, B. Wang, H. Zhuang, X. Jiang, G. Ma, Y. Yi, W. Hu and Y. Zhou, RSC Adv., 2014, 4, 36738–36741 RSC.
- N. Dirany, E. McRae and M. Arab, CrystEngComm, 2017, 19, 5008–5021 RSC.
- S. Mandal, C. K. Ghosh, D. Sarkar, U. N. Maiti and K. K. Chattopadhyay, Solid State Sci., 2010, 12, 1803–1808 CrossRef CAS.
- T. Thomas, N. Jayababu, J. Shruthi, A. Mathew, A. Cerdán-Pasarán, J. A. Hernández-Magallanes, K. C. Sanal and R. Reshmi, Thin Solid Films, 2021, 722, 138575 CrossRef CAS.
- A. I. Becerro, M. Allix, M. Laguna, D. González-Mancebo, C. Genevois, A. Caballero, G. Lozano, N. O. Núñez and M. Ocaña, J. Mater. Chem. C, 2018, 6, 12830–12840 RSC.
- L. Xu, G. Liu, H. Xiang, R. Wang, Q. Shan, S. Yuan, B. Cai, Z. Li, W. Li, S. Zhang and H. Zeng, Appl. Phys. Rev., 2022, 9, 021308 CAS.
- R. Xiao, N. Guo, X. Lv, Q. Ma, B. Shao and R. Ouyang, Dalton Trans., 2022, 51, 15484–15495 RSC.
- G. Li, Y. Tian, Y. Zhao and J. Lin, Chem. Soc. Rev., 2015, 44, 8688–8713 RSC.
- Y. Zhu, Y. Liang, M. Zhang, M. Tong, G. Li and S. Wang, RSC Adv., 2015, 5, 98350–98360 RSC.
- L. G. Van Uitert, J. Lumin., 1984, 29, 1–9 CrossRef CAS.
- E. V. Sokolenko, V. M. Zhukovskii, E. S. Buyanova and Y. A. Krasnobaev, Inorg. Mater., 1998, 34, 499–502 CAS.
- M. V. Korzhik, V. B. Pavlenko, T. N. Timoschenko, V. A. Katchanov, A. V. Singovskii, A. N. Annenkov, V. A. Ligun, I. M. Solskii and J. P. Peigneux, Phys. Status Solidi A, 1996, 154, 779–788 CrossRef CAS.
- A. Lecointre, A. Bessière, A. J. J. Bos, P. Dorenbos, B. Viana and S. Jacquart, J. Phys. Chem. C, 2011, 115, 4217–4227 CrossRef CAS.
- J. Raha, N. Haldar and C. K. Ghosh, Appl. Phys. A: Mater. Sci. Process., 2021, 127, 1–8 CrossRef.
- S. Das, C. K. Ghosh, R. Dey and M. Pal, RSC Adv., 2016, 6, 236–244 RSC.
- Y. Shi, Y. Wen, M. Que, G. Zhu and Y. Wang, Dalton Trans., 2014, 43, 2418–2423 RSC.
- Q. Wang, G. Zhu, Y. Li and Y. Wang, Opt. Mater., 2015, 42, 385–389 CrossRef CAS.
- M. Rai, G. Kaur, S. K. Singh and S. B. Rai, Dalton Trans., 2015, 44, 6184 RSC.
- Z. Wang, X. Qiu, W. Xi, M. Tang, J. Liu, H. Jiang and L. Sun, Sens. Actuators, B, 2021, 345, 130417 CrossRef CAS.
- Z. Wang, X. Qiu, W. Xi, M. Tang, J. Liu, H. Jiang and L. Sun, Sens. Actuators, B, 2023, 376, 132936 CrossRef CAS.
- T. Das, S. Das, M. Karmakar, S. Chakraborty, D. Saha and M. Pal, Sens. Actuators, B, 2020, 325, 128765 CrossRef CAS.
- T. Das, S. Mojumder, S. Chakraborty, D. Saha and M. Pal, Appl. Surf. Sci., 2022, 602, 154340 CrossRef CAS.
- Z. Wang, J. Xue, D. Han and F. Gu, ACS Appl. Mater. Interfaces, 2015, 7, 308–317 CrossRef CAS PubMed.
- M. Ali, N. Amrane and N. Tit, Results Phys., 2020, 16, 102907 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00306c |
| ‡ At present: University of Engineering and Management, New Town, Kolkata-700160, India. |
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
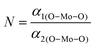 ,24 where α1(O–Mo–O) and α2(O–Mo–O) denote the two different bond angles, and
,24 where α1(O–Mo–O) and α2(O–Mo–O) denote the two different bond angles, and 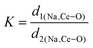 , where d1(Na,Ce–O) and d2(Na,Ce–O) represent the two different bond lengths and were found to be N = 1.011, 1.029, 1.043, 1.052 and K = 1.0587, 1.0827, 1.0838, 1.0842 for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively.25,26 According to previous studies, a decrease in the c/a ratio is associated with the partial substitution of Na+ by Ce3+,27,28 while the perquisite charge neutrality is balanced by O vacancies (VO), causing increases in K and N.
, where d1(Na,Ce–O) and d2(Na,Ce–O) represent the two different bond lengths and were found to be N = 1.011, 1.029, 1.043, 1.052 and K = 1.0587, 1.0827, 1.0838, 1.0842 for NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively.25,26 According to previous studies, a decrease in the c/a ratio is associated with the partial substitution of Na+ by Ce3+,27,28 while the perquisite charge neutrality is balanced by O vacancies (VO), causing increases in K and N.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 727 cm−1), while relatively weaker blue II, blue III peaks and a prominent green peak are observed at 462 nm (21
727 cm−1), while relatively weaker blue II, blue III peaks and a prominent green peak are observed at 462 nm (21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 645 cm−1), 488 nm (20
645 cm−1), 488 nm (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 492 cm−1) and 531 nm (18
492 cm−1) and 531 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 832 cm−1), respectively. The Stokes shift of the excitation and emission spectra were noted to be ∼3588 cm−1, suggesting the absence of reabsorption and interference among the various emissions.42 Although understanding the emission spectra of lanthanides is difficult for several reasons, including symmetry, the crystal field surrounding the host crystal, anion polarizability, and covalence of the host crystal, the present emissions are believed to be 5d–4f transitions within Ce3+
832 cm−1), respectively. The Stokes shift of the excitation and emission spectra were noted to be ∼3588 cm−1, suggesting the absence of reabsorption and interference among the various emissions.42 Although understanding the emission spectra of lanthanides is difficult for several reasons, including symmetry, the crystal field surrounding the host crystal, anion polarizability, and covalence of the host crystal, the present emissions are believed to be 5d–4f transitions within Ce3+![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 43 and can be validated as follows. The emission wavelength (λ in nm) for intra-5d–4f transitions can be calculated using eqn (4):44,45
43 and can be validated as follows. The emission wavelength (λ in nm) for intra-5d–4f transitions can be calculated using eqn (4):44,45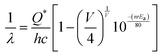
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1), the valence of the Ce3+, the number of anions in the immediate shell around the Ce3+, the electron affinity of the atoms forming the anions (∼2.16 eV) and the difference between the average bond length and radius of Ce3+ within the CeO8 polyhedra (1.03 Å). Very careful calculation yields λ ∼ 449 nm, which corresponds to blue I emission. Previous studies indicate that VO and 2VO can significantly modify the 5d–4f transitions of lanthanide atoms, resulting in different emissions. As an example, Sokolenko et al.46 assigned green–red emission to
000 cm−1), the valence of the Ce3+, the number of anions in the immediate shell around the Ce3+, the electron affinity of the atoms forming the anions (∼2.16 eV) and the difference between the average bond length and radius of Ce3+ within the CeO8 polyhedra (1.03 Å). Very careful calculation yields λ ∼ 449 nm, which corresponds to blue I emission. Previous studies indicate that VO and 2VO can significantly modify the 5d–4f transitions of lanthanide atoms, resulting in different emissions. As an example, Sokolenko et al.46 assigned green–red emission to 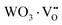 oxygen-deficient complexes, while Korzhik et al. ascribed green emission to WO3 centres.47 Considering CeO7 and CeO6 to be VO- and 2VO-containing distorted CeO8 polyhedra, we have calculated λ values of 487 and 537 nm for intra-Ce3+ 5d–4f transitions using eqn (4), which are in good agreement with the blue III and green emissions (schematically represented in Fig. S14, ESI†).
oxygen-deficient complexes, while Korzhik et al. ascribed green emission to WO3 centres.47 Considering CeO7 and CeO6 to be VO- and 2VO-containing distorted CeO8 polyhedra, we have calculated λ values of 487 and 537 nm for intra-Ce3+ 5d–4f transitions using eqn (4), which are in good agreement with the blue III and green emissions (schematically represented in Fig. S14, ESI†).
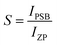
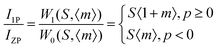
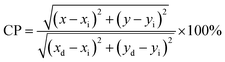
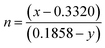 and (x, y) represent the chromaticity co-ordinates. The CCT values were ∼7819 K, 7630 K, 7715 K and 7854 K for the samples NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively. The high CCT indicates that NCMO can be used for cold blue lighting.
and (x, y) represent the chromaticity co-ordinates. The CCT values were ∼7819 K, 7630 K, 7715 K and 7854 K for the samples NCMO0.00, NCMO0.50, NCMO0.78 and NCMO1.00, respectively. The high CCT indicates that NCMO can be used for cold blue lighting.
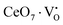 ,
, 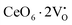 ) and act as electron donors ([CeO8]′ and [CeO8]′′), which can be understood from Kröger–Vink notation:
) and act as electron donors ([CeO8]′ and [CeO8]′′), which can be understood from Kröger–Vink notation: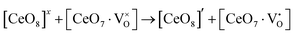
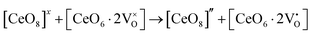
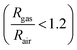 . The sensitivity monotonically increases from NCMO0.00 to NCMO1.00, with the highest sensitivity being observed for NCMO1.00. To understand the role of VO, 2VO in CH3COCH3 adsorption/desorption, we fitted the response data using the Freundlich adsorption isotherm as given in eqn (16) and (17).
. The sensitivity monotonically increases from NCMO0.00 to NCMO1.00, with the highest sensitivity being observed for NCMO1.00. To understand the role of VO, 2VO in CH3COCH3 adsorption/desorption, we fitted the response data using the Freundlich adsorption isotherm as given in eqn (16) and (17).![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) log(Cg)
log(Cg)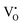 - and
- and 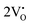 -containing NCMO samples, designated as
-containing NCMO samples, designated as 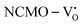 and
and 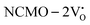 , are represented in Fig. S17 and S18 (ESI†), respectively. Notably, both the VBM and CBM (shown in Fig. S17(a), ESI†) of
, are represented in Fig. S17 and S18 (ESI†), respectively. Notably, both the VBM and CBM (shown in Fig. S17(a), ESI†) of 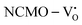 remain unchanged, while in case of
remain unchanged, while in case of 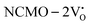 , the CBM band has shifted into the Γ-point (shown in Fig. S17(a), ESI†), indicating the transformation from an indirect to a direct Eg nature for NCMO. We observed an Eg of 3.01 and 2.95 eV for
, the CBM band has shifted into the Γ-point (shown in Fig. S17(a), ESI†), indicating the transformation from an indirect to a direct Eg nature for NCMO. We observed an Eg of 3.01 and 2.95 eV for 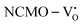 and
and 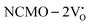 , suggesting a decrease in Eg due to
, suggesting a decrease in Eg due to 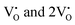 . Thus, the monotonic decrease in the experimentally measured Eg from NCMO0.00 to NCMO1.00 is believed to be due to increasing VO and 2VO, corroborating previous studies. The reduction of Eg can be understood as follows: TDOS (Fig. S17(b) and S18(b), ESI†) and PDOS (Fig. S17(c)–(f) and S18(c)–(f), ESI†) calculations show that the VB width decreases in
. Thus, the monotonic decrease in the experimentally measured Eg from NCMO0.00 to NCMO1.00 is believed to be due to increasing VO and 2VO, corroborating previous studies. The reduction of Eg can be understood as follows: TDOS (Fig. S17(b) and S18(b), ESI†) and PDOS (Fig. S17(c)–(f) and S18(c)–(f), ESI†) calculations show that the VB width decreases in 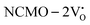 due to the greater localization of the O 2p orbitals, while the curvature increases in
due to the greater localization of the O 2p orbitals, while the curvature increases in 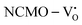 and
and 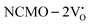 , which is attributed to the enhanced overlap between the Ce 4fzx2, 4fxz2, 4fyz, and 4fxyz and O 2px, 2py, and 2pz orbitals due to the decrease in the Ce–O bond length in the CeO8 polyhedra, indicating higher carrier mobility. Further analysis of the TDOS and PDOS reveals that the contributions from Ce 5dxy and 5dxz to the CB increase in
, which is attributed to the enhanced overlap between the Ce 4fzx2, 4fxz2, 4fyz, and 4fxyz and O 2px, 2py, and 2pz orbitals due to the decrease in the Ce–O bond length in the CeO8 polyhedra, indicating higher carrier mobility. Further analysis of the TDOS and PDOS reveals that the contributions from Ce 5dxy and 5dxz to the CB increase in 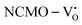 and
and 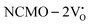 . The defect state at 2.44 eV above the valence band in
. The defect state at 2.44 eV above the valence band in 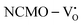 was assigned to Ce 5dz2, whilst these defects are found at 2.26 and 2.40 eV above in
was assigned to Ce 5dz2, whilst these defects are found at 2.26 and 2.40 eV above in 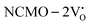 due to Ce 5dz2 and Ce 5dx2, respectively. Therefore, it can be stated that the blue III emission originates from Ce 5dz2 → 4f transitions in the CeO7 polyhedra, while the blue II and green emissions are attributed to Ce 5dz2 → 4f and Ce 5dx2 → 4f transitions in the CeO6 polyhedra, respectively, as schematically presented in Fig. 7.
due to Ce 5dz2 and Ce 5dx2, respectively. Therefore, it can be stated that the blue III emission originates from Ce 5dz2 → 4f transitions in the CeO7 polyhedra, while the blue II and green emissions are attributed to Ce 5dz2 → 4f and Ce 5dx2 → 4f transitions in the CeO6 polyhedra, respectively, as schematically presented in Fig. 7.
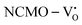 and
and 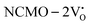 systems using eqn (1), we found the energies listed in Table S2 (ESI†). The Eads (eV) values represent the adsorption energies of the pristine NCMO,
systems using eqn (1), we found the energies listed in Table S2 (ESI†). The Eads (eV) values represent the adsorption energies of the pristine NCMO, 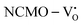 ,
, 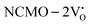 systems, and it was found that Eads < 0, indicating that the adsorption processes involved in these systems are thermodynamically stable and exothermic, meaning that they release energy during the adsorption process. Additionally, the increasingly negative values of
systems, and it was found that Eads < 0, indicating that the adsorption processes involved in these systems are thermodynamically stable and exothermic, meaning that they release energy during the adsorption process. Additionally, the increasingly negative values of 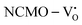 and
and 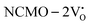 suggest the presence of active sites (oxygen vacancies) on the NCMO surface, which create localized electron-rich sites enabling strong interactions to occur between the CH3COCH3 and NCMO surfaces.59 Hence, the highest sensitivity of NCMO1.00 (Fig. 5) can purely be assigned to the presence of the highest 2VO content, which is in good agreement with the experimental results and theoretical calculations.
suggest the presence of active sites (oxygen vacancies) on the NCMO surface, which create localized electron-rich sites enabling strong interactions to occur between the CH3COCH3 and NCMO surfaces.59 Hence, the highest sensitivity of NCMO1.00 (Fig. 5) can purely be assigned to the presence of the highest 2VO content, which is in good agreement with the experimental results and theoretical calculations.



