Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Molecular adsorption–desorption of carbon monoxide on ferroelectric BaTiO3(001)†
Alexandru-Cristi
Iancu
ab,
Nicoleta G.
Apostol
a,
Adela
Nicolaev
a,
Laura E.
Abramiuc
 a,
Cristina F.
Chirilă
a,
Dana G.
Popescu
a and
Cristian M.
Teodorescu
a,
Cristina F.
Chirilă
a,
Dana G.
Popescu
a and
Cristian M.
Teodorescu
 *a
*a
aNational Institute of Materials Physics, Atomiştilor 405A, 077125 Măgurele, Ilfov, Romania. E-mail: teodorescu@infim.ro
bUniversity of Bucharest, Faculty of Physics, Atomiştilor 405, 077125 Măgurele, Ilfov, Romania
First published on 11th June 2024
Abstract
Carbon monoxide (CO) is reversibly adsorbed on and desorbed from ferroelectric (001) oriented, BaO-terminated barium titanate. All processes are characterized in real time via photoelectron spectroscopy. Adsorption proceeds on different sites/geometries as a function of substrate temperature. Below room temperature, CO is adsorbed on surface Ba. At room temperature, adsorption proceeds on surface oxygen, whereas at high temperatures, “hollow” site adsorption occurs with carbon coordinated with three oxygens, one oxygen initially belonging to CO and two oxygens from the substrate. The amount of CO adsorbed is about one molecule for 10 surface unit cells, which is slightly increased at low temperatures. CO is desorbed if the substrate is heated above the Curie temperature, which is a sign of the definitory role of ferroelectric polarization. The BaTiO3(001) surface is unaffected by repeated cycles of adsorption–desorption.
1. Introduction
Carbon monoxide is widely used in a wealth of chemical reactions, such as hydrogenation to form alcohols, Fischer–Tropsch reactions to produce hydrocarbons, and water gas shift for hydrogen production.1,2 There are a myriad of reports on these subjects and on catalytic systems, allowing one to understand these reactions. However, the use of ferroelectric systems, i.e. those providing permanent polarization enabling molecular fixation and bond weakening or breaking, is still at an incipient stage,3–5 although controllable substrate polarization might be used to overcome the Sabatier principle between the high adsorption binding strength needed to fix and activate reactants and low strengths needed for subsequent desorption.6 One difficulty arises from the lack of understanding of the ferroelectric order. Only recently, a microscopic model for ferroelectricity in thin films with a single domain structure was proposed, highlighting the definitory role of charges accumulated at surfaces and interfaces.7–9 The second difficulty is related mainly to the possibility of working on atomically clean model systems, such as ferroelectric single crystals, in order to quantitatively assess surface adhesion and dissociation. Moreover, such results were lacking until recently, when carbon monoxide adsorption and dissociation on a strong ferroelectric single crystalline thin film, lead zirconate titanate (PZT), were followed-up using photoelectron spectroscopic techniques.10,11It should be noted that carbon dioxide sequestration based on barium titanate was patented one decade ago and probably industrially implemented to date but without any known reference to the ferroelectric properties of this material.12 More connexions to the ferroelectricity of barium titanate are discussed in ref. 13 and 14. Regarding carbon monoxide adsorption on barium titanate, there is no relevant previous reference to the best of our knowledge.
This work investigates the process of carbon monoxide adsorption and desorption on a ferroelectric substrate, BaTiO3(001) or BTO(001). The main reason for choosing this substrate stems from its non-toxicity, wide availability and affordable price, which are beneficial if one intends to develop catalysts at the industrial level. At the same time, before designing an industrial catalyst, the detailed processes leading to molecular fixation and possible surface reactions need to be investigated on model systems, such as ultraclean single crystal films. Another reason for choosing BTO(001) will be revealed in the following brief evaluation.
The basic idea of this study stems from the external field, E = P/ε0, that a ferroelectric material can provide outside the material after a suitable cleaning procedure, where P is polarization and ε0 is vacuum permittivity. This field induces a dipole moment p = αE = 4πε0αvE, in the molecule, where α is the molecular polarizability in F m2 and αv is the polarizability in volumetric units (e.g., in Å3). If one supposes that the molecule progressively approaches the ferroelectric substrate, the field experienced by the molecule increases progressively from 0 to E, and the molecule progressively acquires a dipole moment. The interaction energy of the external field with the induced dipole may be obtained by the simple integration 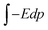 as:
as:
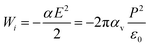 | (1) |
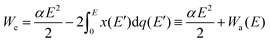 | (2) |
For dissociating the molecule, it suffices to have We > D, where D is the dissociation energy. The first term, which is numerically equal to |Wi|, can be estimated in practical units as:
| |Wi| [eV] ≈ 4.45αv [Å3]P2 [C m−2](>D) | (3) |
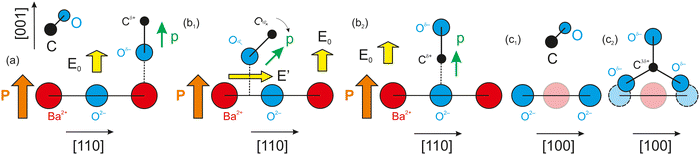
As mentioned above, CO dissociation on ultraclean PZT(001) with strong out-of-plane polarization was reported in ref. 10 and 11. For a ferroelectric thin film with weaker out-of-plane polarization, such as BaTiO3(001), CO is expected to be adsorbed only in molecular form and to be released immediately when the surface loses its polarization, by heating above the Curie temperature. The main ideas yielding to the adsorption mechanisms and possible dissociation are shown in Fig. 1 below. It should be mentioned that in ref. 10, after CO dissociation following adsorption at room temperature (RT), the whole amount of carbon left the surface upon progressively increasing the substrate temperature above the Curie temperature. It was argued that the reduced carbon left the surface in the form of CO2 by taking up oxygen from the PZT. Therefore, the substrate is affected after a cycle of CO adsorption/desorption. Consequently, finding a ferroelectric substrate that is not affected by the adsorption/desorption mechanism is a valuable effort in view of determining new reversible molecular sequestration mechanisms.
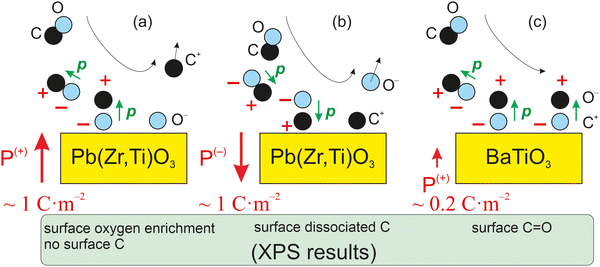 | ||
| Fig. 1 Mechanism for the progressive polarization of CO as it approaches a ferroelectric material in the case of a ferroelectric substrate with a strong out-of-plane polarization, such as PZT (a) and (b),10,11 and in the case of a ferroelectric substrate with a weaker out-of-plane polarization (c), such as barium titanate (right), analyzed in this study. | ||
Therefore, another reason for choosing BTO was its considerably lower polarization (about 0.2–0.3 C m−2). According to the above evaluations, its lower polarization would not suffice to dissociate carbon monoxide. If CO is adsorbed non-dissociatively on ferroelectric BTO, this would at the same time reinforce the conclusions from ref. 10 and 11, where CO was adsorbed on PZT(001). At the same point, this offers the possibility to ‘gently’ manipulate CO molecules by reversible trapping and release them for subsequent chemical reactions, which might find applications in reactions such as the ones mentioned above.
One could also imagine a drawback of working with a ferroelectric material with lower polarization. Since the interaction energy with the polarized molecule is weaker, this also implies that the adsorption energy on the surface is lower (in absolute value) and this might imply a lower number of molecules stabilized on the surface. The final coverage depends in fact on which process is the dominant one leading to molecular adsorption: it could be a dynamical equilibrium between the adsorbed and desorbed species governed by the adsorption energy and the substrate temperature, but there could also be other effects related to changes in the surface electronic density of states, leading to a lower adsorption affinity of the surface once a certain number of molecules are adsorbed. Such effects might be assessed by ab initio molecular dynamics computations, but nevertheless have to be experimentally checked at different temperatures. This was another motivation for this work.
CO adsorption on the incipient ferroelectric KTaO3(001) was reported at low temperature (below 200 K) mainly on TaO2-terminated areas.6 However, for practical applications, one needs to identify adsorption processes near RT. For simplicity reasons, it is also desirable to work on substrates with a well-defined termination. Hence, in this work, we shall investigate adsorption processes on BTO(001) with a single termination (BaO) near RT (RT and slightly above or below), while desorption will be investigated up to temperatures exceeding the Curie temperature of BTO (about 123 °C18 for the bulk, probably higher by 25–50 °C in thin films).
X-Ray photoelectron spectroscopy (XPS) is the ideal tool to characterize these processes, especially when using a powerful light source (synchrotron radiation), enabling one to visualize adsorption and desorption processes in real time. Apart for its chemical characterization possibility and the extreme surface sensitivity, XPS was recently proven as a valuable tool to quantify band bending at surfaces and interfaces, which is a direct method to assess the orientation of polarization in free ferroelectric surfaces.19,20 A visualization of the concomitant loss of the surface C 1s signal and of the progressive loss of the surface polarization by investigating core levels from the ferroelectric substrate allowed one to unambiguously connect the adsorbed molecules with the out-of-plane ferroelectric polarization.10,11 In addition, the method allows a precise quantification of the number of adsorbed molecules. Other surface science methods, such as low energy electron diffraction (LEED), are used to characterize the surface crystallinity. The same strategy will be adopted in this work. The main goals of this study are as follows: (i) derive the composition of BTO at each stage; (ii) derive the BTO termination, if possible; (iii) derive the polarization orientation; (iv) characterize the stability of BTO, i.e., the ability to recover the same surface state after desorption; (v) derivation of the amount of CO adsorbed; (vi) derivation of the state (adsorption geometry?) of CO adsorbed; (vii) determine if there is any polarization change upon CO adsorption; (viii) follow-up of CO desorption, correlated with the BTO polarization.
2. Experimental
Experiments were performed in the CoSMoS (combined spectroscopy and microscopy on surfaces) end station connected to the SuperESCA beamline at the Elettra (Trieste) synchrotron radiation facility, using horizontal linearly polarized soft X-rays. The station comprises a preparation (molecular beam epitaxy, MBE) chamber, a scanning tunneling microscopy (STM) chamber, a photoemission analysis chamber, a storage chamber and a load-lock, the former four ones operating in a base pressure of low 10−10 to 10−11 hPa. XPS was performed by using a Phoibos (Specs) 150 analyzer with angular acceptance of ±7°. Pass energies were 5 eV for C 1s and Ba 4d, measured with 390 eV photon energy, and 10 eV for the survey spectra, Ti 2p and O 1s, all measured with 650 eV photon energy. The photoelectron take-off angle was 24°, and the angle between the direction of incoming X-rays and the detected photoelectrons was 90°. Hence, the detected electrons are in a direction parallel to the polarization of incoming soft X-rays. The estimated resolving power (combined broadening due to the beamline and of the analyzer) was better than 500, related to the photoelectron kinetic energy (≤0.2 eV instrumental broadening for ∼100 eV electron kinetic energy). LEED was performed by using a Specs rear view optics ErLEED 150.BaTiO3(001) thin films were grown on 0.5% Nb-doped SrTiO3(001) (STON) by pulsed laser deposition (PLD) in a surface setup, using a KrF laser (248 nm wavelength) with a repetition rate of 5 Hz and laser fluence of 1.5 J cm−2. The substrate was heated at 700 °C and the partial O2 pressure was 14 Pa. After deposition, the sample was cooled down in a rich O2 atmosphere, 0.1 MPa, with a rate of 10 °C min−1. X-ray diffraction revealed the tetragonal crystal structure of BTO(001) with lattice parameters a = 3.905 Å (in plane) and c = 4.121 Å (out-of-plane, i.e., along the [001] direction; see the ESI,† Fig. S1). Hence, BTO is grown epitaxially on SrTiO3(001) with the same in-plane lattice constant. X-Ray reflectivity (XRR) measurements allowed one to determine the BTO(001) film thickness, which is close to 12.5 nm (see Fig. S2, ESI†). BTO was grown on STON since it is expected that ultrathin films will present a polarization oriented outwards.21
BTO(001) experienced air exposure between its synthesis by PLD and its introduction. Therefore, a cleaning procedure was defined well in advance before the synchrotron radiation experiments. It consists of heating the BTO up to about 1150 K for 2000 s in an oxygen pressure of 5 × 10−7 hPa, then cooling down in an oxygen pressure of 2 × 10−6 hPa. XPS spectra revealed a low amount of reduced carbon on the surface, and trials to eliminate it were unsuccessful. After cleaning, samples were characterized by core level XPS, then CO was adsorbed at different temperatures: RT (20 °C), high temperature, i.e., +48 °C and low temperature, i.e., −46 °C. The CO dose was similar in all cases: 5 × 10−6 hPa for a duration of 15 min, i.e., about 3.4 kL. Before each dose, the CO gas line was flushed in order to avoid the formation of Ni carbonyls by taking up Ni from the stainless steel pipes, which was confirmed by the absence of Ni 3p and 3s lines from survey scans (Fig. S3, ESI†). After each dose, the surface was characterized by core level XPS. Subsequently, it was heated by following the signals from different core levels (Ba 4d, C 1s, Ti 2p, O 1s) using ultrafast XPS. At the end of the thermally-induced desorption process, the surface was again characterized to confirm its cleanness.
In a separate experiment, LEED was performed on clean BTO(001) in the MBE chamber and after dosing CO in a similar amount at RT.
3. Results and discussions
3.1. Low energy electron diffraction (LEED)
Fig. 2 presents the LEED patterns obtained at two energies on clean BTO(001) and after dosing 3.4 kL CO at RT. There was no sizable modification in the broad LEED pattern observed, nor in the relatively high background, after CO dosing. This is the first sign that the surface structure is not strongly affected by CO adsorption. | ||
| Fig. 2 Low energy electron diffraction (LEED) images on clean BaTiO3(001) and after CO dosing. The electron energies are indicated on each photograph. | ||
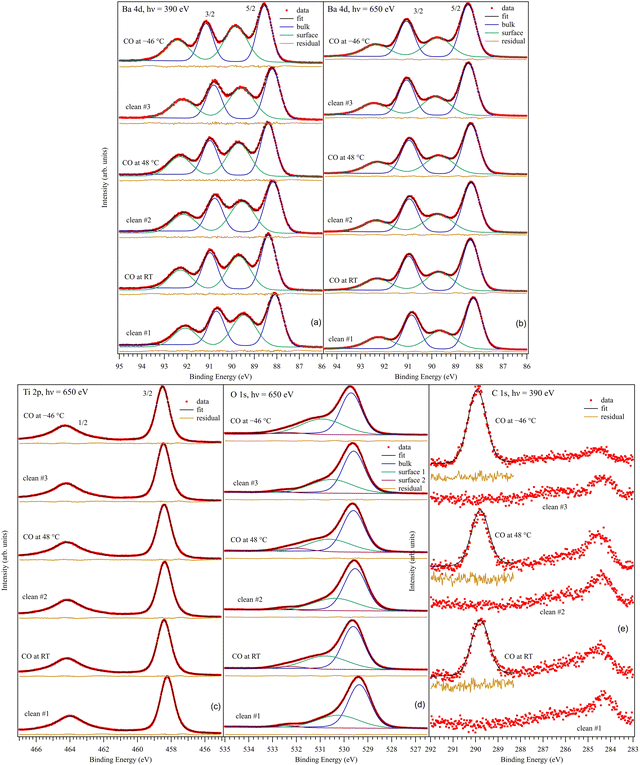
3.2. Core level X-ray photoelectron spectroscopy. General aspects
Fig. 3 presents the XPS core level investigations for clean BTO(001), several clean samples, and for CO/BTO(001) upon dosing at different substrate temperatures. The spectra are analyzed (‘deconvoluted’) as follows:(i) For the Ba 4d spectra (Fig. 3(a) and (b)), two Gaussian doublets were used, with the ratio between the line integrals equal to the branching ratio (theoretically, Ba 4d5/2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4d3/2 should be 1.5) and the difference in binding energy (BE) being the spin–orbit splitting. The use of Gaussian line-shapes comes from the fact that it is estimated that the core level width (which might manifest as a Lorentzian lineshape) of Ba 4d should be much lower than the estimated experimental broadening, of Gaussian nature, of at least 0.2 eV at 390 eV22 and at least 0.5 eV at 650 eV. One doublet will be named in the following as a ‘component’. Each ‘component’ has its own associated inelastic background. A low background is a sign that the ‘component’ in question belongs to surface atoms, since there are no inelastic losses to be expected in the photoelectron yield for those atoms.23 This is the case for the high BE ‘component’ of Ba 4d. Additionally, the ratio between this ‘component’ and the lower BE one decreases for the series recorded at 650 eV photon energy (Fig. 3(b)) with respect to that recorded at 390 eV photon energy (Fig. 3(a)). In the latter case, the kinetic energy and inelastic mean free path of the recorded photoelectron are both lower. Therefore, the relative amplitude of the surface ‘component’ increases for lower photon energy. These are then two facts suggesting that the higher BE component (denoted as ‘Ba2’) belong to surface Ba atoms, and ‘Ba1’ (the lower BE component) belongs to bulk Ba. It is reasonable to suppose that the surface Ba atoms have higher BE since their coordination with oxygen is lower, and then the crystal field experienced by surface Ba atoms has a lower value (neighboring O2− anions give a repulsive term, rising the core levels). SrO termination was also reported for SrTiO3(001) single crystals upon annealing in oxygen (2 × 10−6 hPa) and flashing in ultrahigh vacuum at about 1000 K,24 with a similar attribution of the higher BE component. The same situation was reported for a BaTiO3(001) single crystal.25 In addition, as will be demonstrated below, surface Ba atoms are more strongly affected by the near surface band bending owing to the outwards polarization of the BTO(001). The average binding energies for Ba 4d5/2 are 88.33 ± 0.13 eV for ‘Ba1’ and 89.67 ± 0.11 eV for ‘Ba2’. The tiny differences between the clean and CO-dosed samples will be discussed in the following. The spin–orbit splitting values are 2.600 ± 0.004 eV and 2.602 ± 0.003 eV for the two doublets used. The branching ratio for ‘Ba1’ is close to its theoretical value of 1.5, whereas it is close to 1.6 for ‘Ba2’. The line full widths at half maximum (FWHM) are 0.80 ± 0.02 eV and 1.29 ± 0.06 eV for ‘Ba1’ and ‘Ba2’, respectively, which points to a larger disorder for the surface atoms.
4d3/2 should be 1.5) and the difference in binding energy (BE) being the spin–orbit splitting. The use of Gaussian line-shapes comes from the fact that it is estimated that the core level width (which might manifest as a Lorentzian lineshape) of Ba 4d should be much lower than the estimated experimental broadening, of Gaussian nature, of at least 0.2 eV at 390 eV22 and at least 0.5 eV at 650 eV. One doublet will be named in the following as a ‘component’. Each ‘component’ has its own associated inelastic background. A low background is a sign that the ‘component’ in question belongs to surface atoms, since there are no inelastic losses to be expected in the photoelectron yield for those atoms.23 This is the case for the high BE ‘component’ of Ba 4d. Additionally, the ratio between this ‘component’ and the lower BE one decreases for the series recorded at 650 eV photon energy (Fig. 3(b)) with respect to that recorded at 390 eV photon energy (Fig. 3(a)). In the latter case, the kinetic energy and inelastic mean free path of the recorded photoelectron are both lower. Therefore, the relative amplitude of the surface ‘component’ increases for lower photon energy. These are then two facts suggesting that the higher BE component (denoted as ‘Ba2’) belong to surface Ba atoms, and ‘Ba1’ (the lower BE component) belongs to bulk Ba. It is reasonable to suppose that the surface Ba atoms have higher BE since their coordination with oxygen is lower, and then the crystal field experienced by surface Ba atoms has a lower value (neighboring O2− anions give a repulsive term, rising the core levels). SrO termination was also reported for SrTiO3(001) single crystals upon annealing in oxygen (2 × 10−6 hPa) and flashing in ultrahigh vacuum at about 1000 K,24 with a similar attribution of the higher BE component. The same situation was reported for a BaTiO3(001) single crystal.25 In addition, as will be demonstrated below, surface Ba atoms are more strongly affected by the near surface band bending owing to the outwards polarization of the BTO(001). The average binding energies for Ba 4d5/2 are 88.33 ± 0.13 eV for ‘Ba1’ and 89.67 ± 0.11 eV for ‘Ba2’. The tiny differences between the clean and CO-dosed samples will be discussed in the following. The spin–orbit splitting values are 2.600 ± 0.004 eV and 2.602 ± 0.003 eV for the two doublets used. The branching ratio for ‘Ba1’ is close to its theoretical value of 1.5, whereas it is close to 1.6 for ‘Ba2’. The line full widths at half maximum (FWHM) are 0.80 ± 0.02 eV and 1.29 ± 0.06 eV for ‘Ba1’ and ‘Ba2’, respectively, which points to a larger disorder for the surface atoms.
(ii) For the Ti 2p spectra (Fig. 3(c)), a spin–orbit split doublet using Voigt lines26 was sufficient to ‘deconvolute’ the spectra. This implies a single ‘component’ for Ti 2p. Therefore, all Ti atoms are in similar chemical environments, corresponding to Ti in bulk BTO. Again, this suggests that the surface is BaO-terminated. A more in-depth analysis of the amplitude ratios presented in the following confirms this hypothesis. The need for Voigt profiles comes from the relatively larger core level widths, approaching the experimental Gaussian broadening.27 Furthermore, the Lorentzian width of the 2p1/2 is considerably higher than that of the 2p3/2 line. This is because the Coster–Kronig decay channels yield a reduced lifetime of the 2p1/2 core hole,28 as well as the occurrence of more subtle many-body effects yielding a mixture of configurations with a 2p3/2 core hole and those with a 2p1/2 core hole in the spectral region of the latter level.29 The Ti 2p3/2 binding energy is 458.40 ± 0.09 eV, the spin–orbit splitting is 5.746 ± 0.003 eV, the Gaussian width (FWHM) is 0.71 ± 0.01 eV, the Lorentzian FWHMs are 0.44 ± 0.01 eV for 2p3/2 and 1.86 ± 0.03 eV for 2p1/2, and the branching ratio result is 1.435 ± 0.012, while it should be theoretically 2. Further discussion on this latter fitting parameter can be found in the next subsection.
(iii) For the O 1s spectra (Fig. 3(d)), three ‘components’, denoted by O1, O2 and O3 in order of increasing BE, have to be considered. Each ‘component’ is simulated by a Voigt line, since it is expected that the core hole width of O 1s exceeds 0.1 eV. O2 and O3 have low backgrounds; hence, they belong to surface atoms. O2 will be associated with Ba2 and belong to the first surface BaO layer, while O3 will be associated with carbon in COx compounds formed at the surface. It is clear that O3 increases considerably after each CO dosing. The presence of O3 in clean samples could be attributed to O being close to a region with a relative oxygen deficit, promoting its core levels to higher energies (lower BEs), or to surface hydroxyls adsorbed from the residual gas,25 owing to the high affinity for polar molecules or radicals of areas with outwards polarization.20 The same remark regarding a possible effect of the outwards polarization for surface oxygen, as for the case of surface barium, will be evidenced by the temperature dependence of the XPS data, which will be described in a later subsection. Numerically, the O 1s binding energies yielded 529.57 ± 0.12 eV for ‘O1’, 530.58 ± 0.25 eV for ‘O2’ and 532.24 ± 0.16 eV for ‘O3’. The Lorentzian FWHM was kept the same at 0.128 ± 0.004 eV, while the Gaussian FWHMs are 1.02 ± 0.03 eV for ‘O1’, 2.06 ± 0.04 eV for ‘O2’ and 1.43 ± 0.07 eV for ‘O3’. This suggests a possible multiple origin of the ‘O2’ component or a larger degree of disorder for surface oxygens.
(iv) The C 1s spectra were analyzed only in the region where COx lines show up after CO dosing by a single Gaussian component. The statistics of these data did not allow a more refined ‘deconvolution’. The background coefficient is also negligible for C 1s. The average binding energy is 289.85 ± 0.07 eV and the FWHM is 0.92 ± 0.03 eV.
It is then clear that after each CO dosing, a distinct component shows up in the C 1s spectra. This is accompanied by an increase of the O3 component. This suggests that CO is adsorbed in molecular form on BTO. Also, after each desorption experiment, the core levels of the substrate are quite similar. In the following, we will discuss the findings from these spectra in more detail.
3.3. Composition analysis
For the composition analysis, one needs first to normalize the spectra. This was performed with respect to cross-sections σ and with the asymmetry factor 1 + βP2(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ), where γ is the angle between the polarization of the incoming X-rays and the detection direction of the photoelectron (γ = 0 for the experimental geometry used), P2 is the Legendre polynomial of second order (P2(1) = 1 in the actual setup), and β is the asymmetry parameter. For each level and employed photon energy, σ and β are taken from ref. 30. The cross-sections for Ba 4d, Ti 2p and O 1s at 650 eV are 0.4604 Mb, 0.9937 Mb and 0.3383 Mb, respectively. The asymmetry parameters are 1.206, 1.353 and 2.0. We first analyzed the survey spectra taken at 650 eV with a pass energy of 10 eV, which are represented in the ESI,† Fig. S3. The experimentally derived composition ratios, after normalization with respect to the cross-section and with the asymmetry parameters, were an average of Ba
γ), where γ is the angle between the polarization of the incoming X-rays and the detection direction of the photoelectron (γ = 0 for the experimental geometry used), P2 is the Legendre polynomial of second order (P2(1) = 1 in the actual setup), and β is the asymmetry parameter. For each level and employed photon energy, σ and β are taken from ref. 30. The cross-sections for Ba 4d, Ti 2p and O 1s at 650 eV are 0.4604 Mb, 0.9937 Mb and 0.3383 Mb, respectively. The asymmetry parameters are 1.206, 1.353 and 2.0. We first analyzed the survey spectra taken at 650 eV with a pass energy of 10 eV, which are represented in the ESI,† Fig. S3. The experimentally derived composition ratios, after normalization with respect to the cross-section and with the asymmetry parameters, were an average of Ba![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti ≈ 3.61 and O
Ti ≈ 3.61 and O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba ≈ 1.45 (the O
Ba ≈ 1.45 (the O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ti ratio can be derived from the above two, and will not be discussed in the following). It can be readily observed that the Ti content seems to be too low. We will argue below that some intensity in the Ti 2p3/2 peak seems to be lost, and this manifests in a much lower experimental branching ratio (of the integral intensities of the 2p3/2 and the 2p1/2 peak) rexp. ≈ 1.44. Therefore, a correction factor for the Ti intensity (1 + rth.)/(1 + rexp.) ≈ 3/2.44 ≈ 1.23 will be employed. With this correction, Ba:Ti ≈ 2.94.
Ti ratio can be derived from the above two, and will not be discussed in the following). It can be readily observed that the Ti content seems to be too low. We will argue below that some intensity in the Ti 2p3/2 peak seems to be lost, and this manifests in a much lower experimental branching ratio (of the integral intensities of the 2p3/2 and the 2p1/2 peak) rexp. ≈ 1.44. Therefore, a correction factor for the Ti intensity (1 + rth.)/(1 + rexp.) ≈ 3/2.44 ≈ 1.23 will be employed. With this correction, Ba:Ti ≈ 2.94.
Clearly, the high Ba content can be explained by the BaO termination of the sample. The deviations from the ‘ideal’ composition, Ba:Ti = 1, O:Ba = 3, can be modeled by introducing different inelastic mean free paths (IMFP) for Ba, Ti and O λO, λTi, λBa since their kinetic energies are O 1s: 120.4 eV; Ti 2p3/2: 191.7 eV; Ba 4d5/2: 561.7 eV. Assuming a BaO termination, the intensities result by summing the contribution of all involved layers as follows:
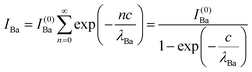 | (4) |
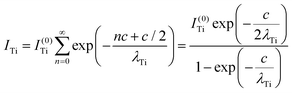 | (5) |
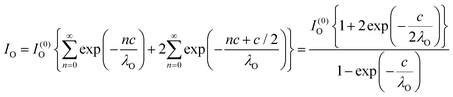 | (6) |
The intensity ratios are given by:
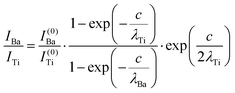 | (7) |
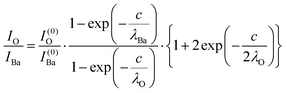 | (8) |
The next step in composition analysis is to use the ‘deconvolution’ of the spectra. As commented above, Ti 2p can be fitted with a single component. However, the branching ratio of 1.44 ± 0.01 is quite low, while it should theoretically be 2. Deviations from the theoretical value of the branching ratio can be attributed to photoelectron diffraction effects31 or to many body effects, as described by Bagus et al.29 Other empirical arguments will be presented below. Since the kinetic energy of electrons originating from Ti 2p3/2 is quite close to the ionization energy of Ba 4p1/2, one could suspect an increasing loss in the yield of these photoelectrons due to inelastic interactions with Ba atoms sitting on top. For that reason, we investigated the Ti 2p branching ratio by measuring the same samples (as introduced and after cleaning) in another setup with monochromatic Al Kα radiation (1496.7 eV). The result was a quite similar branching ratio of 1.43, irrespective of the cleanliness of the sample (Fig. S4 from ESI†). At the same time, the Ti 2p spectra from Pb(Zr,Ti)O3 excited with 600 eV in a different setup, but using a similar electron energy analyzer, yielded a branching ratio of 1.83.10 Meanwhile, for SrTiO3(001) measured in exactly the same setup as the one used for the actual experiments, a branching ratio of 2.2 for Ti 2p was obtained.24 Therefore, the low branching ratio obtained in the case of BaTiO3(001) seems to be really connected to this specific material and/or structure. We then conjectured that there is some inelastic loss of unknown nature from the Ti 2p3/2 intensity. Therefore, we re-calibrated the total areas corresponding to the Ti 2p doublet by a factor, taking into account this possible loss (1 + rth.)/(1 + rexp.) ≈ 3/2.44 ≈ 1.23, as mentioned above.
The Ba 4d spectra present two components (Ba1 and Ba2 in order of increasing binding energy), and the attribution suggested above is that Ba2 represents Ba from the surface BaO layer. Owing to the reduced oxygen coordination, the average crystal field potential energy is higher. The same is valid for oxygen, which presents three lines (O1, O2, and O3 in order of increasing binding energy). Now, O3 is negligible for clean BaTiO3(001) and will not be discussed in relation with the clean samples. Thus, O2 will be attributed to the surface BaO layer, as for Ba2. The chemical shifts are rather similar, 1.34 eV between Ba2 and Ba1 and 1.01 eV between O2 and O1. Then, the ‘bulk’ signals are Ba1, O1 and Ti; the surface BaO yields Ba2 and O2. The integral amplitude ratios resulting from ‘deconvolutions’, normalized with respect to the cross-sections and taking into account the asymmetry parameters, are O1:Ba1 ≈ 1.42 instead of 3, O2:Ba2 ≈ 1.50 instead of 1, Ba1:Ti (corrected) ≈ 1.47 instead of 1. One can observe that the ratio O2:Ba2 deviates seriously from 1, which is the ‘theoretical’ value for the surface BaO layer. At the same time, the O1:Ba1 intensity ratio, attributed to bulk components, is considerably lower than 3. This suggests that some part from O2 still belongs to the bulk, e.g., it is due to oxygen from the second layer (TiO2) influenced by the surface band bending due to the ferroelectric polarization. We anticipate here a result that will become evident in the next subsection by analyzing the spectra while heating the BTO, in which the BTO has a polarization oriented outwards. (It should be noted that there is no such influence on the Ti 2p signal.) In order to obtain the average value of O2:Ba2 ≈ 1, about f ≈ 0.335 is ‘translated’ into O1 from the contribution of O2. The resulting ratios are (O1 + f·O2):Ba1 ≈ 1.72, (1 − f)·O2:Ba2 ≈ 1, Ba1:Ti(corrected) ≈ 1.47 (the same value as above). Still, the bulk composition is not derived.
The relative Ba ‘excess’ is then attributed, as in the case of the analysis of survey spectra, to the considerably larger IMFP of Ba 4d with respect to the other two core levels. More precisely, for the bulk (excluding the surface BaO layer), one obtains the following intensities:
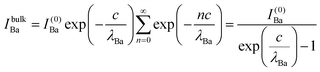 | (9) |
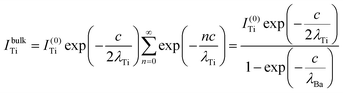 | (10) |
 | (11) |
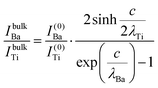 | (12) |
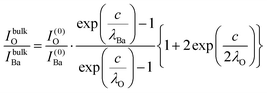 | (13) |
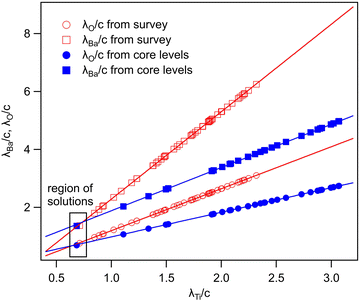
In summary, Fig. 4 presents the dependencies λO(λTi) and λBa(λTi) (in c units) obtained from the analysis of survey spectra (total integrated intensities of all Ba 3d, Ti 2p and O 1s signals), and from the components attributed to ‘bulk’ resulting from the deconvolution of the spectra (still, with some fraction of O2, the ‘surface’ BaO, translated towards O1, the bulk component). It may easily be seen that these dependencies intersect themselves at about a similar value of λTi/c. This may be interpreted as a proof that the procedure is self-consistent; in particular, the correction factor for Ti 2p and the ‘translated’ intensity from O2 to O1 have real support. As a consequence, the following IMFPs are derived: λTi/c = 0.69 ± 0.05, λO/c = 0.72 ± 0.04, λBa/c = 1.42 ± 0.05. By introducing c ≈ 4.12 Å, one obtains λTi ≈ 2.8 Å, λO ≈ 3.0 Å and λBa ≈ 5.9 Å. It should be noted that the sample is tilted off-normal by β = 24°. Therefore, one has to multiply by the above IMFPs by (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) β)−1 ≈ 1.1. With these IMFPs, the composition ratios obtained using eqn (7), (8), (12) and (13) are as follows:
β)−1 ≈ 1.1. With these IMFPs, the composition ratios obtained using eqn (7), (8), (12) and (13) are as follows:
(1) (Ba:Ti) from survey, total intensity = 3.12 vs. 2.94 experimentally.
(2) (Ba:Ti) from bulk components resulting from deconvolutions = 1.55 vs. 1.47 experimentally.
(3) (O:Ba) from survey, total intensity = 1.35 vs. 1.45 experimentally.
(4) (O:Ba) from bulk components resulting from deconvolutions = 1.70 vs. 1.72 experimentally.
If the Ti 2p intensity is not corrected, a similar analysis is presented in the ESI,† Fig. S5. As expected from the larger ratios IBa/ITi (total intensities) or from IbulkBa/IbulkTi, the derived IMFP for Ti 2p is too low, and lies in the range of 2.2 to 2.5 Å. Also, the coincidence of the λTi solutions from the two procedures is worse than that presented in Fig. 4.
To date, we have no clear explanation for the intensity quenching of the Ti 2p3/2 photoemission line for BTO(001). In the following section, we proceed with a first attempt. According to the previous determinations, the specificity of this material/sample is as follows: (i) the sample is BaO terminated. This is clear from the invariance of the Ti 2p spectrum with surface modification (CO adsorption or even for a ‘dirty’, as-introduced sample, see Fig. S4, ESI†), the lack of any ‘surface’ titanium peak, and the clear evidence of Ba 4d and O 1s surface peaks. (ii) The Ba–O bond has a more prominent ionic character, as compared with Pb–O (in PZT) or with Sr–O (in SrTiO3) owing to the lower Pauling electronegativity of barium (0.89, to be compared with 1.87 for Pb or 0.95 for Sr32). Hence, valence electrons in the topmost BaO layer are more concentrated on the oxygen anions. On the other hand, in all geometries employed so far, the detection of the outgoing photoelectrons was close to normal emission. This means that electrons emitted from Ti can be scattered by the oxygen anion sitting on top to a larger extent in BTO(001) with pure BaO termination than in other samples (although in the SrTiO3(001) analyzed in ref. 24, the single crystal was SrO terminated). It seems that some of the electron excitation channels are attenuated. Fig. S6 (ESI†) shows drawn diagrams reporting all of the possible excitations towards continuum states, starting from the 2p1/2 and 2p3/2 states. For each excitation, the squared Clebsch–Gordan coefficient 〈jimji1q|jfmjj〉 is represented, where ji = 1/2 or 3/2 is the initial total angular moment, mji is its projection, 1 is the photon angular moment, q = 0, ±1 indexes the components of the complex polarization vector of the incoming radiation, and (jf,mjj) indexes the final angular state of the outgoing photoelectrons. It may be easily seen that
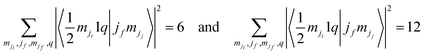 | (14) |
As a consequence, one may infer a nearly perfect stoichiometry of BTO(001). Most deviations from ideal composition ratios are due mainly to IMFP effects, but also occur due to (i) some band bending manifesting just in the O 1s component, shifting artificially some of the ‘bulk’ intensity towards the ‘surface’ (first monolayer) component, and to (ii) some missing intensity in the Ti 2p3/2 line, which is clearly related to BaO-terminated BaTiO3(001), since it does not occur in Pb(Zr,Ti)O3 and SrTiO3 measured under similar conditions.
3.4. Carbon coverage and coordination
The next question concerns the CO coverage of the BTO(001) for dosing at different temperatures. From the Ba 4d and C 1s measured at 390 eV, one may derive the ratio C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ba2, knowing that Ba2 is attributed to the first monolayer. We use the cross-sections of 0.4929 Mb and 0.8775 for C 1s and Ba 4d excited with 390 eV photon energy, and the asymmetry parameters 2 and 0.8268, respectively.30 It should be noted again here that we attributed the change in component O3, which shifted at about 2.8 eV higher binding energies with respect to the main component (oxygen from bulk BTO), to the adsorbed CO. Then, from the ratio Ba2
Ba2, knowing that Ba2 is attributed to the first monolayer. We use the cross-sections of 0.4929 Mb and 0.8775 for C 1s and Ba 4d excited with 390 eV photon energy, and the asymmetry parameters 2 and 0.8268, respectively.30 It should be noted again here that we attributed the change in component O3, which shifted at about 2.8 eV higher binding energies with respect to the main component (oxygen from bulk BTO), to the adsorbed CO. Then, from the ratio Ba2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O3 obtained from measurements at 650 eV, one may finally obtain the ratio C
O3 obtained from measurements at 650 eV, one may finally obtain the ratio C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O3, i.e., also the molecular state of carbon-containing molecules. The results are represented in Table 1.
O3, i.e., also the molecular state of carbon-containing molecules. The results are represented in Table 1.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O ratios derived from XPS data from Fig. 3 for dosing BTO(001) with 3.4 kL CO at different temperatures
O ratios derived from XPS data from Fig. 3 for dosing BTO(001) with 3.4 kL CO at different temperatures
| CO dosing temperature | C:Ba2 | Ba2:O3 | C:O3 | Approximate composition |
|---|---|---|---|---|
| RT (20 °C) | 0.089 | 4.97 | 0.44 | CO2 |
| 48 °C | 0.088 | 3.38 | 0.30 | CO3 |
| −46 °C | 0.118 | 6.25 | 0.74 | C3O4 (2CO + CO2) |
As a consequence, the ratio C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Basurf. is about 9% for adsorptions at RT and at 48 °C, and increases up to about 12% for adsorption at −46 °C. The interesting aspect comes when one associates the intensities of the O3 component, which increased each time after dosing, with the intensity of C 1s. It seems that by adsorption at low temperatures, the stoichiometry of CO is approximately retrieved (slightly enriched in oxygen). However, the surface molecules have an approximate stoichiometry of CO2 by adsorption at RT, and this evolved towards CO3 at high temperature.
Basurf. is about 9% for adsorptions at RT and at 48 °C, and increases up to about 12% for adsorption at −46 °C. The interesting aspect comes when one associates the intensities of the O3 component, which increased each time after dosing, with the intensity of C 1s. It seems that by adsorption at low temperatures, the stoichiometry of CO is approximately retrieved (slightly enriched in oxygen). However, the surface molecules have an approximate stoichiometry of CO2 by adsorption at RT, and this evolved towards CO3 at high temperature.
A mechanical hypothesis is that by applying the surface electric field and elongating the C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O molecule, the triple bond is broken and surface reactions occur, such as:
O molecule, the triple bond is broken and surface reactions occur, such as:
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O + (BaO)surf. → C O + (BaO)surf. → C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O–[Ba(–O)]surf. O–[Ba(–O)]surf. | (15) |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O + (BaO)surf. → O O + (BaO)surf. → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C–[O(–Ba)]surf. C–[O(–Ba)]surf. | (16) |
C![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O + 2(BaO)surf. → O O + 2(BaO)surf. → O![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C[(–O–Ba)2]surf. C[(–O–Ba)2]surf. | (17) |
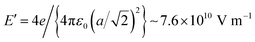 , where a ≈ 3.905 Å is the in-plane lattice constant. The factor 4 in front comes from the charge 2 of barium and oxygen, and from the need to consider both contributions of the field generated by Ba2+ and O2−. If the molecule reaches the BaO surface layer close to the middle of the Ba2+–O2− bond, this in-plane field tilts the molecule to bring it with Cδ+ towards the surface O2−. A local CO2-like coordination is thus formed, and its dipole moment probably will be oriented outwards in the final state (Fig. 5(b2)). This seems to happen at RT adsorption, and also partially for low temperature adsorption. Finally, more complicated surface interactions are probably involved for high temperature adsorption, yielding C bound to three oxygen atoms, one from the initial CO molecule and two oxygens from the substrate, in a ‘hollow’ site, as represented in Fig. 5(c2), suggesting a reaction such as that from eqn (17). These hypotheses can be taken as a possible input for molecular dynamics or density functional calculations.
, where a ≈ 3.905 Å is the in-plane lattice constant. The factor 4 in front comes from the charge 2 of barium and oxygen, and from the need to consider both contributions of the field generated by Ba2+ and O2−. If the molecule reaches the BaO surface layer close to the middle of the Ba2+–O2− bond, this in-plane field tilts the molecule to bring it with Cδ+ towards the surface O2−. A local CO2-like coordination is thus formed, and its dipole moment probably will be oriented outwards in the final state (Fig. 5(b2)). This seems to happen at RT adsorption, and also partially for low temperature adsorption. Finally, more complicated surface interactions are probably involved for high temperature adsorption, yielding C bound to three oxygen atoms, one from the initial CO molecule and two oxygens from the substrate, in a ‘hollow’ site, as represented in Fig. 5(c2), suggesting a reaction such as that from eqn (17). These hypotheses can be taken as a possible input for molecular dynamics or density functional calculations.
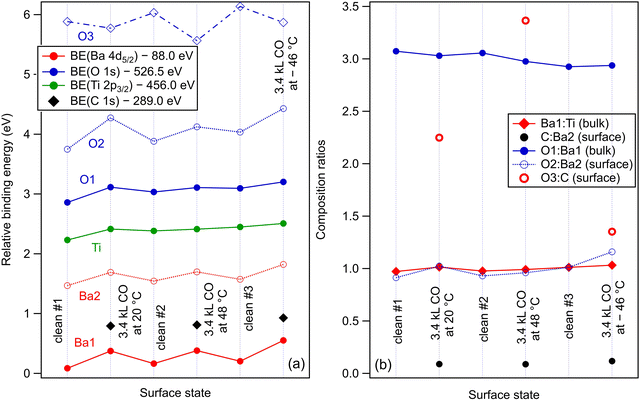
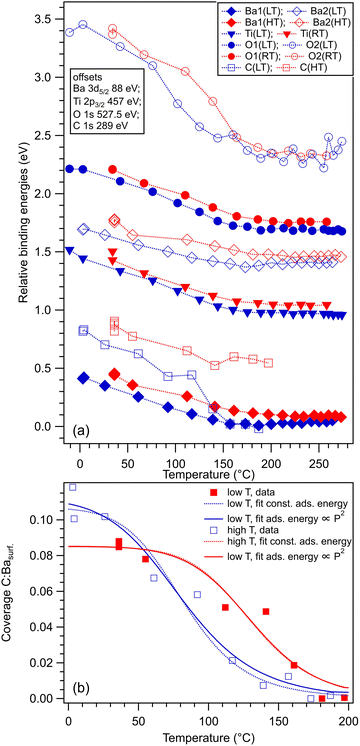
Within the actual data, some tests can already be performed by looking at the XPS results, as represented in Fig. 6. Firstly, we note that the Ba1 and Ba2 BEs increase slightly by CO adsorption, which suggest some charge transfer from Ba towards the molecule (BTO(001) is supposed to have a polarization oriented outwards). A more striking influence is on the O2 BE, which also comes from the surface BaO layer (Fig. 6(a)). This is in line with the reductive properties of a ferroelectric thin film with outwards polarization.20 As for the proposed geometries, a first examination will be to see if the situation with CO adsorbed on-top on Ba yields a decrease of the Ba2 (surface) signal. Indeed, this seems to be the case for the adsorption at low temperature, Fig. 6(b), where the O2:Ba2 is shown to increase. This effect is less prominent for the data obtained from the other two adsorptions. At the same time, the C 1s BE shows a noticeable increase by about 0.13 eV for the adsorption at low temperature. This is probably due to a less negative environment owing to the proximity of Ba2+.
3.5. Thermally induced CO desorption
Fig. 7 presents the XP spectra (temperature programmed desorption TPD) of Ba 4d, Ti 2p, O 1s and C 1s obtained while heating the substrate, following dosing at temperatures below RT. For similar TPD data obtained after dosing CO at higher temperature, see the ESI,† Fig. S7. One may firstly notice a constant shift of all core levels towards lower binding energies as the substrate is heated above the Curie temperature. This means that at the beginning of the experiment, the sample was in a state with polarization oriented outwards,19,20,34 as we supposed initially. The C 1s signal vanishes after heating at about 160 °C, which is the same result as in ref. 10 and 11 for CO adsorbed on PZT. As soon as the polarization of the substrate is lost, the molecules are desorbed. Therefore, the basic electrostatic mechanism sketched in Fig. 1 is confirmed.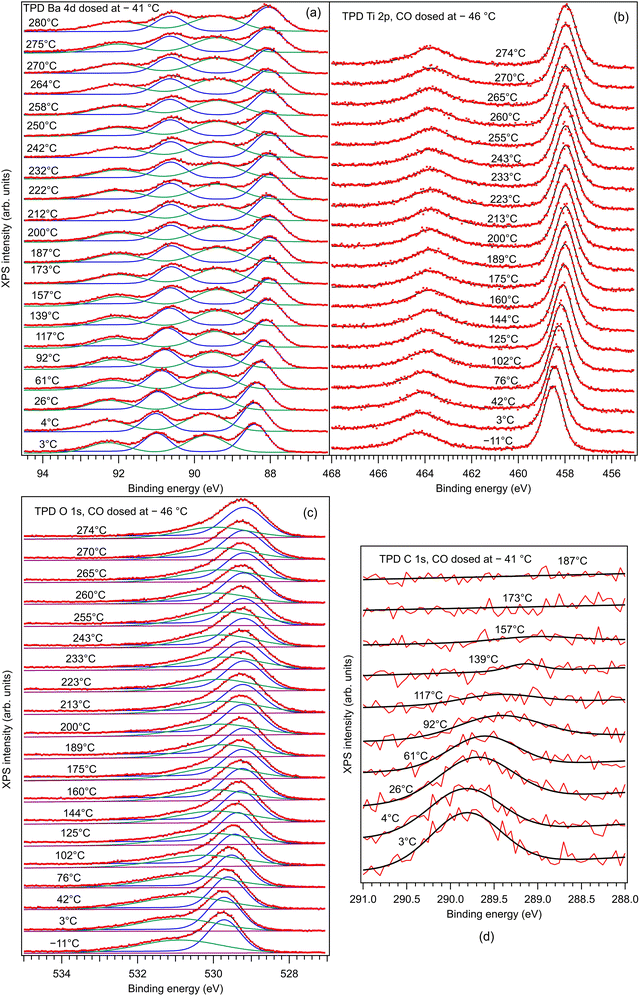 | ||
| Fig. 7 Temperature-programmed desorption of CO initially adsorbed at low temperature (3.5 kL), and follow-up using all core levels: (a) Ba 4d; (b) Ti 2p; (c) O 1s; (d) C 1s. Dots are experimental data (red lines for C 1s). Full lines are fitting functions (black for the total fit) and the separate contribution of two ‘components’ (for Ba 4d and O 1s). For fits, similar functions as for the basic XPS analysis from Fig. 3 are used. For O 1s, only two Voigt singlets were employed, instead of three. | ||
Fig. 8 analyzes the fitting parameters obtained from ‘deconvolutions’ of all spectra in more detail (including for that presented in Fig. S7 from the ESI†). It should be noted that for O 1s, owing to the worse statistics of the TPD data, no fit with physical insight could be obtained by using three ‘components’. Conversely, the fit with two ‘components’ gives reasonable and reproducible results. Therefore, in the discussion of the O 1s spectra from TPD, we will neglect the weak O3 ‘component’. No noticeable variations were detected for Lorentzian or Gaussian widths, spin–orbit splittings, and branching ratios for Ba 4d and Ti 2p, nor for the amplitudes from the substrate. Hence, the substrate composition seems rather unaffected by CO adsorption or desorption. The shifts in binding energies are on the order of 0.48 ± 0.05 eV, which are higher by a factor of more than two compared to 0.2 eV, as reported in ref. 35. This difference is most probably due to a different degree of cleanliness of the substrate, and also to the fact that the thickness of BTO was considerably lower in the actual case, granting the single domain structure. However, it should be noted that the relative shift of the O2 ‘component’ towards lower binding energies (about 1.1 eV) is about twice the shift recorded for all other ‘components’ and core levels. On the one hand, this reassures us that the progressive shift observed by heating is not due to, e.g., changes in the surface conductivity yielding a better neutralization of the photoemitted charges (i.e., all shifts would be just a charging effect). On the other hand, this suggests that the potential energy due to the ferroelectric-induced band bending is ‘felt’ to a larger extent by the oxygen anions than by the barium cations from the surface.
The C 1s signal decreases steadily with the increase of temperature. Although the initial CO coverage was higher for adsorption at low temperature, the decrease of the C 1s signal is significantly faster for that adsorption than for the adsorption at RT. In line with the considerations when we analyzed the C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O3 surface ratios (see Table 1 and Fig. 5), it seems that when CO is adsorbed mostly on Ba atop sites at low temperature, the desorption is faster than when there is a significant part of CO forming other bonds with surface oxygen, as schematized in Fig. 5(b2) and (c2). However, in both cases, the whole amount of CO is desorbed from BTO(001) at about 180 °C. In ref. 10, a sizable decrease in the C 1s signal was detected in a short time when starting the core level measurements after dosing, i.e., after beginning the sample irradiation with soft X-rays. For all dosing experiments, we investigated if such decrease is present in the case of CO/BTO(001), and concluded that no clear radiation-induced desorption occurs in this case (Fig. S8, ESI†). This can imply that the irradiation-induced desorption is in fact due to hot electrons released by Auger cascades following core level excitation, where these hot electrons essentially originate from the Pb 5d shallow levels in the case of PZT, as proposed in ref. 36.
O3 surface ratios (see Table 1 and Fig. 5), it seems that when CO is adsorbed mostly on Ba atop sites at low temperature, the desorption is faster than when there is a significant part of CO forming other bonds with surface oxygen, as schematized in Fig. 5(b2) and (c2). However, in both cases, the whole amount of CO is desorbed from BTO(001) at about 180 °C. In ref. 10, a sizable decrease in the C 1s signal was detected in a short time when starting the core level measurements after dosing, i.e., after beginning the sample irradiation with soft X-rays. For all dosing experiments, we investigated if such decrease is present in the case of CO/BTO(001), and concluded that no clear radiation-induced desorption occurs in this case (Fig. S8, ESI†). This can imply that the irradiation-induced desorption is in fact due to hot electrons released by Auger cascades following core level excitation, where these hot electrons essentially originate from the Pb 5d shallow levels in the case of PZT, as proposed in ref. 36.
More refinements can be made by supposing a simple Langmuir model for molecular adsorption, as in ref. 10. The relative molecular coverage is written as:
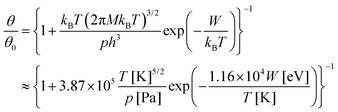 | (18) |
Another hypothesis would be to suppose that the adsorption energy is (in absolute value) proportional to the square of the substrate polarization, i.e., to suppose that the leading factor yielding the molecular adsorption is the dipolar interaction. Thus, one has to introduce an interaction energy on the form given by eqn (1) and (3), and also take into account the decrease of the polarization with temperature. By using the Langevin summation over states and an approximation of the inverse Langevin function,37 a simple mean field model developed in ref. 7 yields the dependence of the remnant polarization of the ferroelectric material, such as:
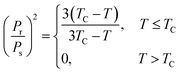 | (19) |
A more accurate analysis of the desorption curves, by taking into account the rate of temperature increase, might be performed using the Redheed formalism.6,38 This analysis actually implies the analysis of desorption rates, i.e., differentiating dependences, such as the ones represented in Fig. 8(b). Owing to the noise present in the data, this cannot be achieved on the bare data, but on some empirical simulations of them. The induced errors by such simulations are unacceptable for a decent analysis with reliable results.
We end this attempt of analyzing the coverage dependence on temperature by noting that both hypotheses, with constant adsorption energy or with adsorption energy proportional to the squared remnant polarization of the substrate, give reasonable results; the pressure parameters obtained alone have no immediate meaning in terms of dosing or desorption pressures. This problem needs a more accurate statistical mechanics evaluation.
4. Conclusion
The main conclusions are that CO is adsorbed on BTO(001) in a non-dissociated form. It is desorbed when the substrate is heated above the Curie temperature, and the substrate is unaffected by repeated CO adsorption and desorption. The adsorption geometries suggested by the C: (surface oxygen) atomic ratio seem to be different at different adsorption temperatures, and this suggestion might stimulate a deeper theoretical investigation.We are then able to respond to all queries formulated in the Introduction: (i) the BTO composition is nearly perfect, provided that one takes into account the effect of the different inelastic mean free path and the ‘loss’ in Ti 2p3/2 intensity of yet undecided nature. Also, one needs to assess a part of the ‘surface’ oxygen to bulk BTO that is probably affected by the surface band bending, which manifests to a higher extent in the relative shift of the surface oxygen core level. (ii) The BTO(001) termination is BaO. (iii) The BTO(001) is polarized outwards. (iv) BTO(001) is stable against repeated adsorption/desorption processes. (v) The amount of CO adsorbed is in the range of one molecule for ten surface unit cells, increasing by about 30% for adsorption below RT (around −40 °C). (vi) A majority of CO is adsorbed at low temperature atop sites on barium from the surface, with oxygen towards barium. Meanwhile, CO is adsorbed on surface oxygen at higher temperature, forming a “CO2-like” configuration, or even on hollow sites on surface BaO, mimicking a “CO3-like” configuration. (vii) There is a readable reinforcement of the band bending towards lower energies (higher binding energies) upon CO adsorption, manifested especially in the surface Ba and O components. The dipolar adsorbed CO is probably reinforcing the surface polarization of BTO. (viii) CO is completely desorbed upon heating above the Curie temperature.
As briefly discussed in the Introduction, indeed in the case of CO/BTO(001), we detect lower carbon coverage (a factor of 2–3) as compared with CO/PZT(001).10 The effects relying on changes of the electronic structure can be taken into account. However, according to Fig. 6(a), the binding energies of most levels and components increase slightly after CO adsorption, which could be interpreted as an enhancement of the surface band bending. This is possibly due to an increase of the polarization. Thus, a lower driving field towards the surface when there are already adsorbed molecules could possibly be ruled out. Another effect that might be taken into account is the reduction of the spatial range, where the electric field produced by the ferroelectric material polarizes the molecules in the gas phase and succeeds to attract them towards the surface. In ref. 39, there is a computation of the electrostatic potential generated by the surface dipole at a surface of a clean ferroelectric material in vacuum, outside the sample. This potential energy distribution could be integrated into a statistical mechanics treatment of polarizable molecules, ending with the adsorption dynamics in a modified Langmuir model. In our opinion, this can be an interesting theoretical work to be undertaken.
The relatively low amount of CO adsorbed near RT is not a major drawback from the possible utilization of this material for controlled CO removal from the atmosphere. In ref. 6, CO was adsorbed on KTaO3 only at low temperature. In ref. 10 and 11, a maximum amount of 0.3 monolayers was derived for a ferroelectric material with much stronger polarization, PZT. We can briefly sketch a possible application in the sequestration of carbon monoxide. If the absorber is in the form of small cuboidal nanoparticles, the surface/volume ratio scales with the inverse of the nanoparticle size. Under these conditions, 1 m2 of BTO(001) surface may accommodate about 31 μg of CO. A finely dispersed powder with 50 nm particles exhibits a maximal specific surface area of about 20 m2 g−1 (the density of BTO is 6020 kg m−3). Thus, 1 g of this material may accommodate up to 611 μg of CO. If adsorption–desorption cycles can be imagined (with the collection of CO during the desorption) taking about ten minutes per cycle, then 1 g of BTO will be able to store and achieve controlled release about 32 times its weight in carbon monoxide in one year. This stimulates the use of ferroelectric absorbers or supports for controlled adsorption for other molecules, such as CO2, NOxetc. The fact that the molecule in its free form does not have a dipole moment is not a drawback: it is only necessary for the molecule to have a polarizability exceeding a few Å3. We end with the conviction that this field will be explored further, both theoretically and experimentally.
Open questions from this study are related to the low branching ratio derived for Ti 2p, which was ascribed to some loss in the intensity of the 2p3/2 line of unknown nature, but clearly related to BaTiO3(001) being terminated by BaO, and the high value of the p parameter that has to be introduced in the simulation of the coverage dependence on temperature using a simple Langmuir model.
Author contributions
Alexandru-Cristi Iancu: XPS and LEED experiments, data analysis. Nicoleta G. Apostol: XPS and LEED experiments, data analysis. Adela Nicolaev: XPS and LEED experiments, data analysis. Laura E. Abramiuc: XPS data analysis. Cristina F. Chirilă: BTO preparation by PLD. Dana G. Popescu: XRD experiments and data analysis, funding management. Cristian M. Teodorescu: conceptualization, XPS and LEED experiments and data analysis, drawing conclusions, modelling, manuscript writing, funding management.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was funded by the Core Program of the National Institute of Materials Physics, under the project PC1–PN23080101. All experiments were performed using the National Interest Setup “System of complex XPS/ESCA installations and research using synchrotron radiation”. DGP acknowledges the financial support of the Ministry of Research, Innovation and Digitization, CNCS – UEFISCDI, project number PN-III-P1-1.1-TE-2021-0136.References
- E. de Smit and B. M. Weckhuysen, The renaissance of iron-based Fischer–Tropsch synthesis: on the multifaceted catalyst deactivation behaviour, Chem. Soc. Rev., 2008, 37, 2758–2781 RSC.
- J. Bao, G. H. Yang, Y. Yoneyama and N. Tsubaki, Significant advances in C1 catalysis: Highly efficient catalysts and catalytic reactions, ACS Catal., 2019, 9, 3026–3053 CrossRef CAS.
- K. Garrity, A. M. Kolpak, S. Ismail-Beigi and E. I. Altman, Chemistry of ferroelectric surfaces, Adv. Mater., 2010, 22, 2969–2973 CrossRef CAS PubMed.
- A. Kakekhani and S. Ismail-Beigi, Ferroelectric-based catalysis: Switchable surface chemistry, ACS Catal., 2015, 5, 4537–4545 CrossRef CAS.
- A. Kakekhani, S. Ismail-Beigi and E. I. Altman, Ferroelectrics: A pathway to switchable surface chemistry and catalysis, Surf. Sci., 2016, 650, 302–316 CrossRef CAS.
- Z. C. Wang, M. Reticcioli, Z. Jakub, I. Sokolović, M. Meier, L. A. Boatner, M. Schmid, G. S. Parkinson, U. Diebold, C. Franchini and M. Stevin, Surface chemistry on a polarizable surface: Coupling of CO with KTaO3(001), Sci. Adv., 2022, 8, eabq1433 CrossRef CAS PubMed.
- C. M. Teodorescu, Ferroelectricity in thin films driven by charges accumulated at interfaces, Phys. Chem. Chem. Phys., 2021, 23, 4085–4093 RSC.
- C. M. Teodorescu, Self-consistently derived sample permittivity in stabilization of ferroelectricity due to charge accumulated at interfaces, Phys. Chem. Chem. Phys., 2022, 24, 5419–5430 RSC.
- L. E. Abramiuc, L. C. Tănase, M. J. Prieto, L. de Souza Caldas, A. Tiwari, N. G. Apostol, M. A. Huşanu, C. F. Chirilă, T. Schmidt, L. Pintilie and C. M. Teodorescu, Surface charge dynamics on air-exposed ferroelectric Pb(Zr,Ti)O3(001) thin films, Nanoscale, 2023, 15, 13062–13075 RSC.
- L. C. Tănase, N. G. Apostol, L. E. Abramiuc, C. A. Tache, L. Hrib, L. Trupină, L. Pintilie and C. M. Teodorescu, Ferroelectric triggering of carbon monoxide adsorption on lead zirco-titanate (001) surfaces, Sci. Rep., 2016, 6, 35301 CrossRef PubMed.
- N. G. Apostol, M. A. Huşanu, D. Lizzit, I. A. Hristea, C. F. Chirilă, L. Trupină and C. M. Teodorescu, CO adsorption, reduction and oxidation on Pb(Zr,Ti)O3(001) surfaces associated with negatively charged gold nanoparticles, Catal. Today, 2021, 366, 141–154 CrossRef CAS.
- S. C. Kwon, J. H. Park, H. J. Kwon, Y. J. Park, H. C. Lee and Y.-K. Choi, Carbon dioxide adsorbent including barium titanate, carbon dioxide capure module including the same, and methods for separating carbon dioxide using the same, US Pat., US 2014/0174292 A1, 2016 Search PubMed.
- A. L. Cabrera, F. Vargas and R. A. Zarate, Adsorption of carbon dioxide by barium titanate: Evidence of adsorption process mediated by dipole-dipole interaction, J. Phys. Chem. Solids, 1994, 55, 1303–1307 CrossRef CAS.
- T. Watanabe, S. Md Khan, H. Kanoh and T. Ohba, Significant CO2 adsorption ability of nanoscale BaTiO3 ceramics fabricated by carbon-template-solvothermal reactions, Phys. Chem.: Indian J., 2017, S1, 101 Search PubMed.
- S. Sowlati-Hashjin and C. F. Matta, The chemical bond in external electric fields: Energies, geometries, and vibrational Stark shifts of diatomic molecules, J. Chem. Phys., 2013, 139, 144101 CrossRef PubMed.
- T. M. Miller, Atomic and molecular polarizabilities, in CRC Handbook of Chemistry and Physics, Internet Version 2005, ed. D. R. Lide, CRC Press, Boca Raton, FL, USA, 2005, pp. 10–167/10–182, https://www.hbcpnetbase.com Search PubMed.
- J. Alistair Kerr, Strengths of chemical bonds, in CRC Handbook of Chemistry and Physics, Internet Version 2005, ed. D. R. Lide, CRC Press, Boca Raton, FL, USA, 2005, pp. 9–52/9–75, https://www.hbcpnetbase.com. See also https://en.wikipedia.org/wiki/Bond-dissociation_energy Search PubMed.
- K. Sakayori, Y. Matsui, H. Abe, E. Nakamura, M. Kenmoku, T. Hara, D. Ishikawa, A. Kokubu, K. Hirota and T. Ikeda, Curie temperature of BaTiO3, Jap. J. Appl. Phys., 1995, 34, 5443–5445 CrossRef CAS.
- N. G. Apostol, L. E. Stoflea, G. A. Lungu, C. A. Tache, D. G. Popescu, L. Pintilie and C. M. Teodorescu, Band bending at free Pb(Zr,Ti)O3 surfaces analyzed by X-ray photoelectron spectroscopy, Mater. Sci. Eng. B, 2013, 178, 1317–1322 CrossRef CAS.
- L. E. Ştoflea, N. G. Apostol, L. Trupină and C. M. Teodorescu, Selective adsorption of contaminants on Pb(Zr,Ti)O3 surfaces shown by X-ray photoelectron spectroscopy, J. Mater. Chem. A, 2014, 2, 14386–14392 RSC.
- L. C. Tănase, L. E. Abramiuc, D. G. Popescu, A.-M. Trandafir, N. G. Apostol, I. C. Bucur, L. Hrib, L. Pintilie, I. Pasuk, L. Trupină and C. M. Teodorescu, Polarization orientation in lead zirco-titanate (001) thin films driven by the interface with the substrate, Phys. Rev. Appl., 2018, 10, 034020 CrossRef.
- N. G. Apostol, I. C. Bucur, G. A. Lungu, C. A. Tache and C. M. Teodorescu, CO adsorption and oxidation at room temperature on graphene synthesized on atomically clean Pt(001), Catal. Today, 2021, 366, 155–163 CrossRef CAS.
- D. Luca, D. Mardare, F. Iacomi and C. M. Teodorescu, Increased surface hydrophilicity of titania thin films by doping, Appl. Surf. Sci., 2006, 252, 6122–6126 CrossRef CAS.
- D. G. Popescu, A. Nicolaev, R. M. Costescu, L. E. Borcan, G. A. Lungu, C. A. Tache, M. A. Huşanu and C. M. Teodorescu, Spin asymmetry of O 2p – related states in SrTiO3(001), Phys. Scripta, 2024 Search PubMed , under review.
- A. Pancotti, J. Wang, P. Chen, L. Tortech, C. M. Teodorescu, E. Frantzeskakis and N. Barrett, X-ray photoelectron diffraction study of relaxation and rumpling of ferroelectric domains in BaTiO3(001), Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 184116 CrossRef.
- C. M. Teodorescu, J. M. Esteva, R. C. Karnatak and A. El Afif, An approximation of the Voigt I profile for the fitting of experimental X-ray absorption data, Nucl. Instrum. Methods Phys. Res., 1994, 345, 141–147 CrossRef CAS.
- M. O. Krause and J. H. Oliver, Natural widths of atomic K and L levels, Ka X-ray lines and several KLL Auger lines, J. Phys. Chem. Ref. Data, 1979, 8, 329–338 CrossRef CAS.
- D. Luca, C. M. Teodorescu, R. Apetrei, D. Macovei and D. Mardare, Preparation and characterization of increased-efficiency photocatalytic TiO2–2xNx thin films, Thin Solid Films, 2007, 515, 8605–8610 CrossRef CAS.
- P. S. Bagus, C. J. Nelin, C. R. Brundle and S. A. Chambers, A new mechanism for XPS line broadening: The 2p-XPS of Ti(IV), J. Phys. Chem. C, 2019, 123, 7705–7716 CrossRef CAS.
- https://vuo.elettra.eu/services/elements/WebElements.html, Z, At. Data Nucl. Data Tables 32, 1–55, 1985.
- H. W. Yeom, T. Abukawa, Y. Takakuwa, S. Fujimori, T. Okane, Y. Ogura, T. Miura, S. Sato, A. Kakizaki and S. Kono, Anisotropy of the spin-orbit branching ratio in angle-resolved photoemission from adsorbate layers, Surf. Sci., 1998, 395, L236–L241 CrossRef CAS.
- See ref. 17, pp. 9–74 and also https://en.wikipedia.org/wiki/Electronegativities_of_the_elements_(data_page).
- B. H. Bransden and C. J. Joachain, Physics of atoms and molecules, Longman, Harlow, 1983, p. 357. See also https://en.wikipedia.org/wiki/Table_of_Clebsch_Gordan_coefficients Search PubMed.
- N. G. Apostol, L. E. Stoflea, G. A. Lungu, C. Chirila, L. Trupina, R. F. Negrea, C. Ghica, L. Pintilie and C. M. Teodorescu, Charge transfer and band bending at Au/Pb(Zr,Ti)O3 interfaces investigated by photoelectron spectroscopy, Appl. Surf. Sci., 2013, 273, 415–425 CrossRef CAS.
- D. G. Popescu, M. A. Husanu, C. Chirila, L. Pintilie and C. M. Teodorescu, The interplay of work function and polarization state at the Schottky barriers height for Cu/BaTiO3 interface, Appl. Surf. Sci., 2020, 502, 144101 CrossRef CAS.
- L. E. Abramiuc, L. C. Tănase, A. Barinov, N. G. Apostol, C. Chirilă, L. Trupină, L. Pintilie and C. M. Teodorescu, Polarization landscape effects in soft X-ray-induced surface chemical decomposition of lead zirco-titanate, evidenced by photoelectron spectromicroscopy, Nanoscale, 2017, 9, 11055–11067 RSC.
- A. Cohen, A Padé approximant to the inverse Langevin function, Rheol. Acta, 1991, 30, 270–273 CrossRef CAS.
- P. A. Redhead, Thermal desorption of gases, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- C. M. Teodorescu, L. Pintilie, N. G. Apostol, R. M. Costescu, G. A. Lungu, L. Hrib, L. Trupină, L. C. Tănase, I. C. Bucur and A. E. Bocîrnea, Low energy electron diffraction from ferroelectric surfaces. Dead layers and surface dipoles in clean Pb(Zr,Ti)O3(001), Phys. Rev. B, 2017, 96, 115438 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: (i) X-Ray diffraction and X-ray reflectivity. (ii) Survey XPS spectra; (iii) Ti 2p XPS spectra obtained with monochromatic Al Kα radiation: (iv) derivation of inelastic mean free paths by using uncorrected Ti 2p intensity; (v) transitions from Ti 2p1/2 and Ti 2p3/2 core levels, together with their relative weight: (vi) TPD data after CO adsorption at room temperature and high temperature. See DOI: https://doi.org/10.1039/d4ma00389f |
| This journal is © The Royal Society of Chemistry 2024 |