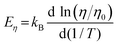Open Access Article
Open Access ArticleCrystallization kinetics of stacked phase-change films for multi-level storage
Yimin
Chen
 *abc,
Ce
Fan
ab,
Nan
Han
ab,
Kexing
Peng
ac,
Chenjie
Gu
*abc,
Ce
Fan
ab,
Nan
Han
ab,
Kexing
Peng
ac,
Chenjie
Gu
 abc,
Zijun
Liu
abc,
Zijun
Liu
 ac,
Guoxiang
Wang
ac,
Tiefeng
Xu
ac,
Junqiang
Wang
ac,
Guoxiang
Wang
ac,
Tiefeng
Xu
ac,
Junqiang
Wang
 d and
Xiang
Shen
d and
Xiang
Shen
 *ac
*ac
aLaboratory of Infrared Material and Devices & Key Laboratory of Photoelectric Materials and Devices of Zhejiang Province, Advanced Technology Research Institute, Ningbo University, Ningbo, 315211, China. E-mail: chenyimin@nbu.edu.cn; shenxiang@nbu.edu.cn
bDepartment of Microelectronic Science and Engineering, School of Physical Science and Technology, Ningbo University, Ningbo, 315211, China
cEngineering Research Center for Advanced Infrared Photoelectric Materials and Devices of Zhejiang Province, Ningbo University, Ningbo 315211, China
dCAS Key Laboratory of Magnetic Materials and Devices & Zhejiang Province Key Laboratory of Magnetic Materials and Application Technology, Ningbo Institute of Materials Technology & Engineering, Chinese Academy of Sciences, Ningbo, 315201, China
First published on 5th July 2024
Abstract
Good thermal stability, fast operation speed, high-level storage density, and low power consumption are increasingly required for neuro-inspired phase-change random access memory. Herein, we designed a multi-level storage phase-change film with three Sb–GeO2 components that are stacked and separated by SiO2 dielectric layers. The fragile-to-strong (F–S) kinetics feature, which is desirable in phase-change supercooled liquids for alleviating the contradictory relation between good thermal stability near the glass transition temperature and fast crystallization speed around the melting temperature, is revealed in some of the Sb–GeO2 components. Moreover, we found that the introduction of stacked structures and adjacent phase-change layers can significantly weaken the F–S kinetics feature of the low thermally stable Sb–GeO2 film but has no influence on the high thermally stable Sb–GeO2 film. It is confirmed that the residual stresses arise from the expansion of stacked films are the origins for the influence on the crystallization kinetics. These findings open opportunities for the design of high-density storage devices with multilayer phase-change films to large-scale neuro-inspired computing.
1. Introduction
The increased need for data storage and information processing drives the urgent search for new computing devices. Phase-change random access memory (PCRAM) is an emerging technology, which, unlike flash memory, does not suffer from problems associated with the storage of charge. In comparison with other memories such as dynamic random access memory (DRAM), PCRAM offers a wider range of advantages including superb scalability,1 faster write/read speed,2 lower energy consumption,3 longer data retention time and non-volatility.4 The above-mentioned advantages of PCRAM are determined by the properties of phase-change materials (PCMs), which show the rapid transition capacity of amorphous to crystalline state with the significant changes in their electrical and/or optical contrast.5Several studies have focused on the improvement of the above-mentioned properties; however, another important characteristic of memory, the storage density, is less investigated. As we noted, both the dimensional down-scaling and the way more akin to “high-rise building” may be supposed eventually to reach the physical limit.6 Therefore, the concept of multistage PCMs, which can realize multiple storage states that provides engineers with an alternative solution to enhance the storage density of monolithic hardware, is proposed. Actually, the flagship Ge–Sb–Te (GST) material undergoes two transitions from amorphous to fcc crystalline structure and fcc to hcp crystalline structure and across three states from high, intermediate, and low resistance, respectively, upon annealing, implying a multistage property.7 Nevertheless, the narrow temperature span of the intermediate state and high changeable rate of resistance make the control of intermediate resistance state difficult, and the resolution for the data collection is rather low. It was reported that nitrogen doping induces a wide quasi-platform of the intermediate resistance state and simultaneously increases the crystallization temperature due to changes in the electrical structures.8 Although such a doping method is a universal means to realize multistage function in PCRAM, it easily results in phase separation, which would deteriorate the duration of the memory. Recently, the concept of superlattice method was employed to realize multistage PCMs, such as the GaSb/Ge2Te,9 GeTe/Sb2Te3,10 SnSb4–GeTe,11 GeTe/Ge8Sb92,12 and SbSe/Ga3Sb7.13 However, two phase-change layers in such superlattice-like PCMs are easy to penetrate, resulting in the functional instability of the multilayer interface.14
There are numerous studies on the basic physical characteristics of multilevel storage materials and the fundamental test performance of devices,15,16 and it suggests that the introduction of dielectric layer (like the SiO2) to separate the two phase-change layers is helpful to improve the stability of the multilayer interface and the durability of multi-storage PCRAM. Nevertheless, the introduction of a dielectric layer that results in the stacked structure would affect the crystallization kinetics of multilayer PCMs. Especially, the effect of an adjacent PCM layer is rarely mentioned, and there is no systematic investigation to discuss such a significant issue. In this work, we design three nanocomposite Sb–GeO2 films, which have no phase separation before crystallization and stack them to form a multilayer PCMs that can be used to realize two-bit function in one storage cell with a wide temperature span and stable resistance of each intermediate state. Moreover, together with flash differential scanning calorimetry (FDSC) and generalized Mauro–Yue–Ellison–Gupta–Allan (g-MYEGA) viscosity model, the fragile-to-strong transition (FST) behaviors in Sb–GeO2 materials were revealed, and the effects of the adjacent phase-change layer on the crystallization kinetics of multilayer PCMs were quantitatively studied.
2. Experimental methods
2.1 Film depositions and characterizations
The single and multilayer Sb–GeO2 films were deposited on Si(100) and NaCl(100) substrates by magnetron sputtering at room temperature. The high purity Sb (99.95 at%) and GeO2 (99.95 at%) targets were used to deposit the phase-change layer of Sb–GeO2, and high purity SiO2 (99.999 at%) target was employed to deposit the dielectric layer (non-phase-change layer) of SiO2. The sputtering atmosphere was Ar with a gas flow of 15 sccm. The base pressure was 6 × 10−6 Pa and the working pressure was 3 mT. The compositions of three single Sb–GeO2 films were in situ controlled by the sputtering power of Sb and GeO2 targets and ex situ examined by energy dispersive spectroscopy (EDS, Tescan Vega 3SBH), such as Sb89.2(GeO2)10.8 (the abbreviation is SGO1), Sb72.6(GeO2)27.4 (SGO2), and Sb61.8(GeO2)38.2 (SGO3). Noteworthily, 5 nm-thick SiO2 layers were also deposited on the two sides of these single Sb–GeO2 films. With the same sputtering parameters, multilayer Sb–GeO2 film, which consists of three single film layers and four 5 nm thick SiO2 layers, were deposited, and its abbreviation is SGO multilayer film. The thickness of each SGO-X (X = 1, 2, 3) layer in the SGO multilayer were in situ controlled by the deposition time and ex situ examined by scanning electron microscopy (SEM). We designed three thickness of 20, 100, and 200 nm for each SGO layer, and the SEM pattern of the typical 100 nm-thick SGO film is shown in Fig. 1. The sheet resistance–temperature (or resistance–time) curves were characterized via a homemade heating platform with an accuracy of ±0.1 °C. Three SGO single films and SGO multilayer film were all annealed in a rapid annealing furnace that was filled with high purity N2 atmosphere at different temperatures for a holding time of 3 min. The micro-structures of crystalline SGO films were examined by X-ray diffraction (XRD, Bruker D2 PHASER diffractometer, Cu Kα radiation with a wavelength of 0.15405 nm). It should be noted that the XRD patterns of SGO-1, SGO-2, and SGO-3 layer were measured via the 170 °C-annealed, 220 °C-annealed, and 270 °C-annealed stacked SGO films, respectively.2.2 Crystallization kinetics analyses
The peak temperature (Tp) values for crystallization were measured by flash differential scanning calorimetry (FDSC, Mettler Toledo Flash DSC1) at varying heating rates in the range of 20–40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K s−1. In order to obtain the reproducible results, all the FDSC measurements were repeated more than 3–5 times at each heating rate both for multilayer and single SGO films. The measurement details are similar to our previous report.17 Temperature calibration was performed and thermal lag was evaluated before the FDSC measurements in this work. Depending on the measured Tp values and combined with the g-MYEGA viscosity model18 and Johnson–Mehl–Avrami (JMA) crystallization kinetics model,19–22 we then studied the crystallization kinetics of single and multilayer SGO films.
000 K s−1. In order to obtain the reproducible results, all the FDSC measurements were repeated more than 3–5 times at each heating rate both for multilayer and single SGO films. The measurement details are similar to our previous report.17 Temperature calibration was performed and thermal lag was evaluated before the FDSC measurements in this work. Depending on the measured Tp values and combined with the g-MYEGA viscosity model18 and Johnson–Mehl–Avrami (JMA) crystallization kinetics model,19–22 we then studied the crystallization kinetics of single and multilayer SGO films.
3. Results
3.1 Thermal stability and crystallization behavior
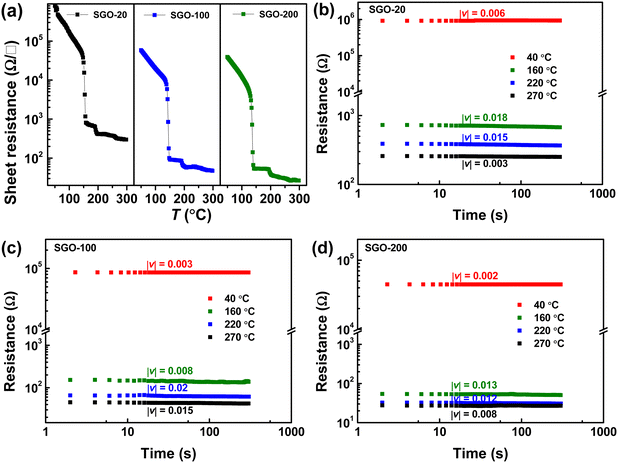
Fig. 2(a) shows the resistance–temperature curves of the SGO multilayer phase-change films with different layer thickness of 20 (SGO-20), 100 (SGO-100), and 200 nm (SGO-200). It was found that the sheet resistance suffers from abrupt drops with the boosted temperature, which corresponds to the phase transitions. These multilayer SGO films all undergo three-step phase transition, and this transition seems to become more obvious with the decrease in thickness. By testing the time-dependent resistance of the film at a specific temperature over a period of time, another important parameter, the resistance drift coefficient, can be evaluated by the following formula23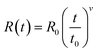 | (1) |
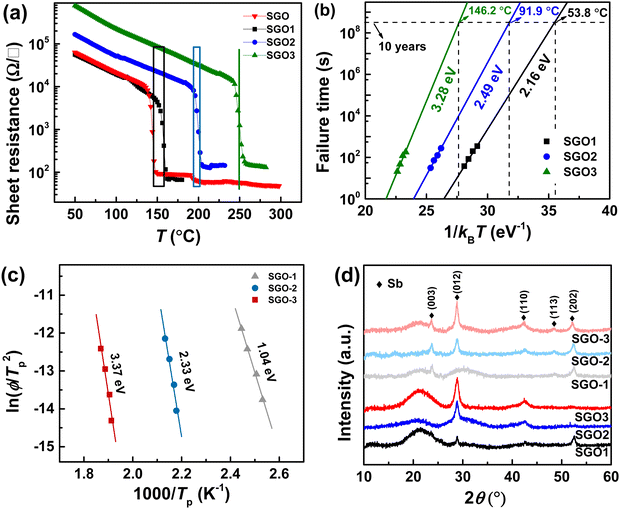
Fig. 3(a) shows the temperature-dependent sheet resistance of single SGO films and multilayer SGO (SGO-100) film with a heating rate of 60 K min−1. As we can see, only one phase transition occurs in these SGO single films, and the crystallization temperatures of SGO1, SGO2, and SGO3 are 156, 198, and 250 °C, respectively. For the multilayer SGO film, the three-step phase transition temperatures are 144, 192, and 251 °C. It indicates that the thermal stability of the SGO layer with lower crystallization temperature is more easily influenced by the adjacent phase-change layer in the multilayer SGO film. We further estimated the activation energy for crystallization (Ea) and extrapolated the temperature that data can be stored safely for 10 years (T10yr) using the Arrhenius plot, which is described as:24
t = τ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(Ea/kBT) exp(Ea/kBT) | (2) |
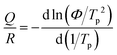 | (3) |
Fig. 3(d) shows the XRD patterns for the determination of the crystalline phases in SGO films. They are all belong to the Sb crystalline phase (JCPDS no. 1-802) in these SGO films. Besides a weak crystallographic plane (003) that was found, there is no divergence between the crystalline SGO2 and SGO-2 as well as SGO3 and SGO-3. Compared with the crystalline SGO1 and SGO-1, nevertheless, a preferential orientation of crystallographic plane has been detected, i.e., the obvious (012) plane in SGO1 is replaced by the (003) plane in the SGO-1 film. It implies that the amorphous thermal stability and corresponding crystallization behavior of SGO-1 phase-change layer are really influenced by the adjacent layer in the multilayer SGO film.
3.2 Crystallization kinetics features
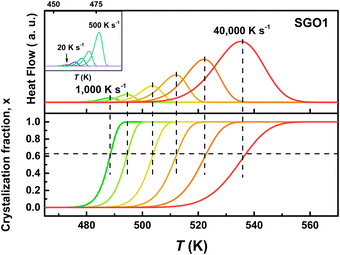
As we reported in previous studies,27,28 the SGO film with crystallization temperature of ∼200 °C (the SGO2 in this work) exhibits distinct fragility to strong (F–S) crystallization kinetics feature, which is beneficial to balance the contradictory requirement between good amorphous thermal stability (low crystallization rate) around the glass transition temperature (Tg) and fast crystallization rate nearby melting temperature (Tm) in one material. It encourages us to clarify whether F–S crystallization kinetics exists in SGO1 and SGO3 film, and would the adjacent layers influence the crystallization kinetics in multilayer SGO phase-change film? Using the FDSC measurements, we performed the investigations of crystallization kinetics to reveal the above questions. Fig. 4 shows the representative FDSC traces of single and multilayer SGO films. The Tp values of all SGO films increases with the increase in the heating rate. Similar to the results obtained from sheet resistance measurements, only one exothermic peak occurs in the single SGO films but there are three exothermic peaks corresponding to the three-step crystallization, which can be found in the multilayer SGO film.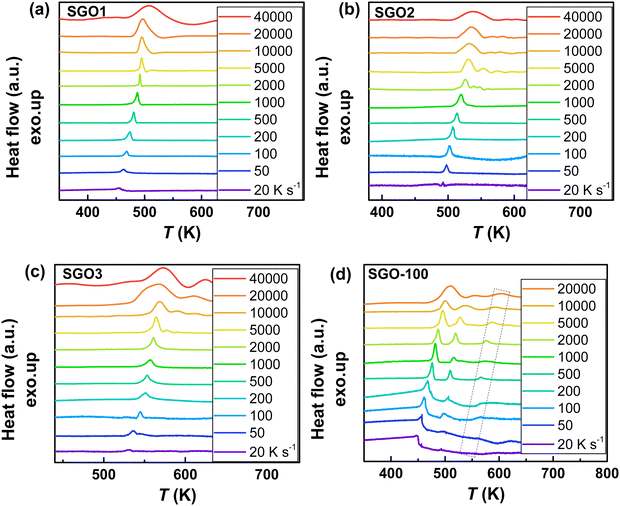 | ||
Fig. 4 The representative FDSC traces after background subtraction for (a) SGO1, (b) SGO2, (c) SGO3 single film, and (d) SGO multilayer film. The heating rate is in the range from 20 to 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K s−1 for single SGO films, and it is in the range from 20 to 20 000 K s−1 for single SGO films, and it is in the range from 20 to 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 K s−1 for SGO multilayer films. The black dotted zone in Fig. 4(d) represents the relative weak third-order exothermic peak in the SGO multilayer. 000 K s−1 for SGO multilayer films. The black dotted zone in Fig. 4(d) represents the relative weak third-order exothermic peak in the SGO multilayer. | ||
For discussing the crystallization kinetics quantitatively and more clearly, the above FDSC data are portrayed in the Kissinger plots. The gradient of Kissinger plot indicates the activation energy for crystallization, which can be used for the extrapolation of the crystal growth rate.29Fig. 5(a) and (b) is the Kissinger plots of single SGO films and multilayer SGO film, respectively. All these plots obey a strict Arrhenius behavior in the low-temperature region, which is similar to the results in Fig. 3(c). However, the non-Arrhenius behaviors are found in these SGO films more or less at the high-temperature region.
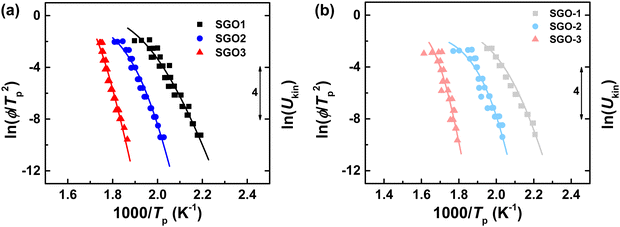 | ||
| Fig. 5 (a) The Kissinger plots of three single SGO films. (b) The Kissinger plots of each phase-change layer in multilayer SGO film. The related Ukin of these SGO films are extrapolated as curved lines using eqn (3). | ||
Henderson suggested that the Kissinger method could be valid for crystallization kinetics study if the Tp is equal to T0.63 (the temperature at which the crystallized fraction is 63%).30 Due to the unpredictable noise signal in FDSC measurements, the FDSC traces could not be used directly. Before the confirmation, we thus did the JMA numerical simulation, which depends on the Tp values obtained from FDSC traces and combines with the g-MYEGA viscosity model. As we can see in Fig. 6, the Tp values of SGO1 measured by the FDSC traces are perfectly replicated by the JMA numerical simulations. Such numerical simulations of other five SGO films were also performed but are not shown here. There is no obvious divergence between Tp and T0.63 that can be found even at an ultrahigh heating rate, indicating that the Kissinger method is valid to study the crystallization kinetics in these films. Together with the g-MYEGA viscosity model and Stokes–Einstein relation of Ukin ∝ η−ξ (Ukin is the temperature-dependent crystallization kinetics coefficient, η is the temperature-dependent viscosity, ξ is the decoupling coefficient), we then fitted these Tp data and obtained the relative Ukin that are the curved lines shown in Fig. 5(a) and (b) using the transposed formula:
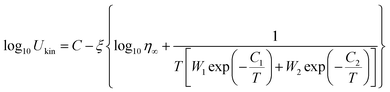 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ukin and −log10
Ukin and −log10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) η, η∞ is the viscosity at infinite high temperature, W1 and W2 are the weight coefficients for the description of brittle phase and the strong phase, and C1 and C2 are the two constants corresponding to the two mechanisms of brittleness and strength, respectively.24 The main fitting parameters are listed in Table 1.
η, η∞ is the viscosity at infinite high temperature, W1 and W2 are the weight coefficients for the description of brittle phase and the strong phase, and C1 and C2 are the two constants corresponding to the two mechanisms of brittleness and strength, respectively.24 The main fitting parameters are listed in Table 1.
| PCM | W 1 | C 1 | W 2 | C 2 | ξ | T fs (K) |
|---|---|---|---|---|---|---|
| SGO1 | 11062.1 | 8309.0 | 0.0099 | 1524.2 | 0.79 | 487 |
| SGO-1 | 4106.4 | 7505.7 | 0.0083 | 1472.0 | 0.71 | 460 |
| SGO2 | 75123.0 | 9660.9 | 0.0038 | 1374.7 | 0.81 | 493 |
| SGO-2 | 7046.2 | 8235.5 | 0.0020 | 1153.5 | 0.78 | 470 |
| SGO3 | 2.4 × 108 | 15473.2 | 0.0622 | 2911.2 | 0.73 | 569 |
| SGO-3 | 3.3 × 108 | 15795.3 | 0.0265 | 2501.3 | 0.74 | 572 |
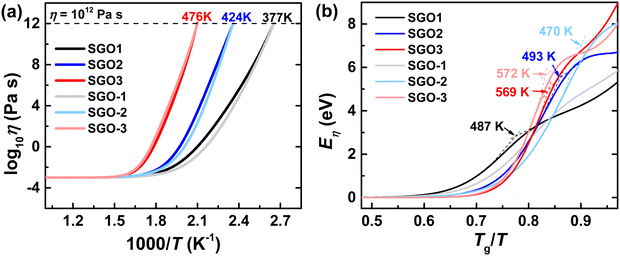
In order to further study the specific impact of the adjacent phase-change layer in stacked multilayer films, we are thus encouraged to further study the temperature-dependent viscosity of these films with the results from the Kissinger plots. The Angell plots, which indicate the change trend of the temperature-dependent viscosity of SGO supercooled liquids, are depicted in Fig. 7(a). Noteworthily, the Tg is determined as the temperature where the η reaches 1012 Pa s with the suitable decoupling coefficient ξ used. The Tg is 377, 424, and 476 K for SGO1 (or SGO-1), SGO2 (or SGO-2), and SGO3 (or SGO-3), respectively. As noted here, there is a distinct divergence in the Angell plots of SGO1 and SGO-1, and less divergence in the Angell plots of SGO2 and SGO-2, but almost no divergence in the Angell plots of SGO3 and SGO-3.
The viscosity activation energies of SGO films are estimated in Fig. 7(b). It shows that the Eη of SGO-1 (the gray curve in Fig. 7(b)) increases monotonically as the temperature decrease to Tg, but that of SGO1 increases non-monotonically and reach a plateau at a specific temperature, which is the F–S transition temperature (Tfs) and can be calculated by the equation as 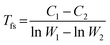 .31 Such a plateau is also found in other SGO films, indicating the existence of the F–S kinetics feature. However, the introduction of an additional phase-change layer brings an apparent effect on the F–S crystallization kinetics of SGO films. For the low thermal stable SGO1 film, the introduction of additional layers makes the F–S behavior vanish. For the SGO2 film, the F–S temperature Tfs decreases from 493 to 470 K as additional layers are introduced. However, for the SGO3 film, the value of Tfs is maintained at ∼570 K with the introduction of additional layers. Similar to the above obtained results, it is implied that the F–S crystallization kinetics could be influenced significantly when the additional layers capped on the SGO1 film.
.31 Such a plateau is also found in other SGO films, indicating the existence of the F–S kinetics feature. However, the introduction of an additional phase-change layer brings an apparent effect on the F–S crystallization kinetics of SGO films. For the low thermal stable SGO1 film, the introduction of additional layers makes the F–S behavior vanish. For the SGO2 film, the F–S temperature Tfs decreases from 493 to 470 K as additional layers are introduced. However, for the SGO3 film, the value of Tfs is maintained at ∼570 K with the introduction of additional layers. Similar to the above obtained results, it is implied that the F–S crystallization kinetics could be influenced significantly when the additional layers capped on the SGO1 film.
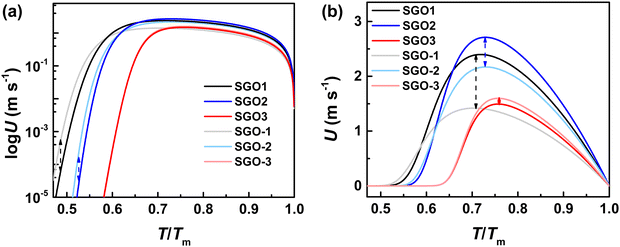
3.3 Crystal growth rates
We further estimated the crystal growth rate (U) for these SGO films via the formula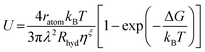 | (5) |
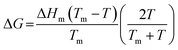 | (6) |
4. Discussion
It was reported in previous works that the crystallization process of the PCMs would be influenced by the neighboring dielectric layers.34–37 For instance, Ruitenberg et al. found that the nucleation of GST occurs at the interface between the phase-change layer and the dielectric Si3N4 layer.34 Pandian et al. found that the nucleation and growth parameters of Sb–Te films were influenced by the dielectric capping layers, such as the activation energy for crystal growth increases 40% as the GeCrN or ZnS–SiO2 capping layers are added.35 The above variations observed in the crystallization are attributed to variations in the interface energy between the phase-change layer and the capping layers. However, the decrease of Tp in these SGO films cannot be explained by the interface effect because the 5 nm-thick SiO2, which is the dielectric layer in the multilayer SGO film, is also capped on the single SGO film. Moreover, the interface effect model based on the amorphous dielectric layer (like the SiO2 used here) predicts that the introduction of the dielectric layer would hinder crystallization with increased crystallization temperature.38We here consider another reason, which is the stress effect, to deduce the mechanism of the depressed thermal stability in stacked multilayer SGO film. It is well reported that the stress induced can enhance the nucleation or reduce the crystallization temperature.39 The capping layers would suffer the stresses as high as 1.7 GPa from the GST phase change layer as the shrinkage crystallization happens.40 Devasia et al. analyzed the residual stress in bilayer chalcogenide Ge2Se3/SnTe film and found that the amorphous Ge2Se3 could also bring continuous stress to impact the crystalline SnTe layer when the temperature increases. The residual stress from the amorphous Ge2Se3 layer is more than 1.2 GPa, which results in the SnTe XRD peak shifting significantly.41
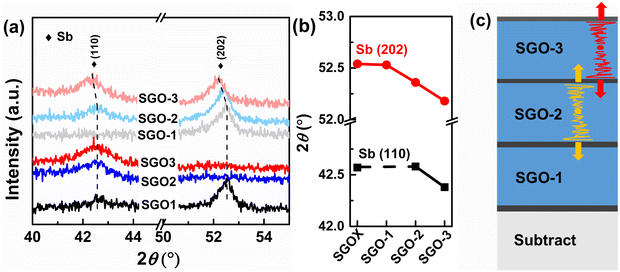
As shown in Fig. 9(a), which is the enlarged XRD patterns from Fig. 3(d), however, the Sb diffraction peaks can be found to shift significantly with the increase in the annealing temperature. We figured out the diffraction peak shifts of Sb (110) and Sb (202) in Fig. 9(b). As we noted, the Sb (202) plane is present in the crystalline SGO1 film but does not exist in crystalline SGO2 and SGO3. When the stacked multilayer film is annealed at 170 °C (slightly larger than the crystallization temperature of the SGO-1 layer), the Sb (202) plane is also present in the SGO-1 layer. Nevertheless, the corresponding diffraction peak persistently shifts to a low 2θ when the annealing temperature increases to 220 and 270 °C (slightly larger than the crystallization temperature of the SGO-2 and SGO-3 layer, respectively). This implies the large and continuous residual stresses from the SGO2 and SGO3 layer present in the stacked film with the increase in the annealed temperature, and this would be the key factor to affect the crystallization of the SGO1 layer. The Sb (110) plane is present in the SGO2 and SGO3 film but is not apparent in the SGO1 film. This plane is also not found in the SGO-1 layer but detected in the SGO-2 and SGO-3 layer. The corresponding diffraction peak maintains the same position even when the annealing temperature increases to 220 °C, but it shifts to low 2θ as the annealing temperature further increases to 270 °C, indicating that the residual stress from SGO-3 is the essential factor influencing SGO2 crystallization. The schematic to illustrate how the residual stress affects the crystallization behavior of each SGO layer in the stacked films is described in Fig. 9(c). Although there is no evidence to directly confirm where the residual stress comes from this stacked film, we believe the thermal expansion of the SGO layers is the origin.
It is confirmed that the lattice distortions, which are attributed to the residual stress, lead to the above XRD diffraction peak shifts. Together with the XRD results and Bragg's law, we estimated the lattice distortions in the stacked films. The lattice constants (a and c) for rhombohedral Sb were calculated. We chose the stable (003) plane to estimate the value of c as 11.311 Å and then chose the changeable (202) plane to estimate the variational a, which is 3.659, 3.660, 3.670. and 3.683 Å for SGO1, SGO-1, SGO-2, and SGO-3, respectively. In this work, the residual stresses from the SGO phase-change layers are difficult to directly estimate. However, this residual stress from the above lattice distortions can be determined indirectly from a set of interplanar spacings as a function of sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ,42 where Ψ can be the angle difference between the unstressed and stressed film of the diffracting plane. The slope of linear fitting between the interplanar spacing and sin2
Ψ,42 where Ψ can be the angle difference between the unstressed and stressed film of the diffracting plane. The slope of linear fitting between the interplanar spacing and sin2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Ψ is calculated as 0.084. The residual stress σ can be determined by σ = mEf/[a0(1 + vf)], where m is the above slope of linear fitting, a0 is the lattice spacing under the unstressed condition (it is 1.740 Å), and Ef and vf are Young's modulus and Poisson's ratio, respectively.42 The Ef and vf of the Sb phase were reported as 6.17 × 1011 dyn cm−2 and 0.27, respectively.43 Taking these parameters in the above equation, the residual stress of the stacked SGO film can be estimated as 2.34 GPa, which is reasonably higher than that of the GST material (1.7 GPa). It implies that the residual stress significantly affects the crystallization behavior of SGO stacked films.
Ψ is calculated as 0.084. The residual stress σ can be determined by σ = mEf/[a0(1 + vf)], where m is the above slope of linear fitting, a0 is the lattice spacing under the unstressed condition (it is 1.740 Å), and Ef and vf are Young's modulus and Poisson's ratio, respectively.42 The Ef and vf of the Sb phase were reported as 6.17 × 1011 dyn cm−2 and 0.27, respectively.43 Taking these parameters in the above equation, the residual stress of the stacked SGO film can be estimated as 2.34 GPa, which is reasonably higher than that of the GST material (1.7 GPa). It implies that the residual stress significantly affects the crystallization behavior of SGO stacked films.
5. Conclusion
We designed a stacked PCM with multistage phase transition. The specific 5 nm thick SiO2 dielectric layers were introduced into three optimal 100 nm-thick Sb–GeO2 phase-change layers with the different components of Sb89.2(GeO2)10.8, Sb72.6(GeO2)27.4, and Sb61.8(GeO2)38.2. The multi-level storage with three phase transitions at the temperatures of 144, 192, and 251 °C, is realized. However, the crystallization temperature, activation energy for crystallization, and crystalline phases of each SGO layer in the multilayer film are changed compared with that of the corresponding single SGO film. Such changes are also observed in their F–S kinetics features, especially in the low thermal stable SGO film, with the introduction of an additional phase-change layers in multilayer films. Based on the analyses from the FDSC data and g-MYEGA viscosity model, it was found that compared with SGO1, the F–S transition temperature Tfs and crystal growth rate U of SGO-1 are greatly reduced and that of SGO-2 are slightly changed compared with SGO2, but that of SGO-3 are almost unchanged compared with SGO3. According to the shifts in the crystalline Sb diffraction peaks for these SGO films, we believe that the residual stress comes from the expansion of the additional layers introduced in the stacked multilayer films, which is the natural origin for the changes in the crystallization behaviors and F–S kinetics features. This reveals the influences of additional layers introduced into multilayer films for high-density storage, enabling a systematic optimization of large-scale neuro-inspired computing.Data availability
The data that support the findings of this study are available from the corresponding authors upon reasonable request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This Project is supported by the National Natural Science Foundation of China (grant no. 62374096, 62075110, 62074089), the Major Program of Zhejiang Provincial Natural Science Foundation of China (LDT23F05012F05), Zhejiang Provincial Natural Science Foundation of China (LY21F040003), the Fundamental Research Funds for the Provincial Universities of Zhejiang (SJLZ2023002), and sponsored by K. C. Wong Magna Fund in Ningbo University, China.References
- H. S. P. Wong, S. Raoux, S. Kim, J. Liang, J. P. Reifenberg, B. Rajendran, M. Asheghi and K. E. Goodson, Phase Change Memory, Proc. IEEE, 2010, 98, 2201–2227 Search PubMed.
- G. W. Burr, M. J. Breitwisch, M. Franceschini, D. Garetto, K. Gopalakrishnan, B. Jackson, B. Kurdi, C. Lam, L. A. Lastras, A. Padilla, B. Rajendran, S. Raoux and R. S. Shenoy, Phase change memory technology, J. Vac. Sci. Technol., B, 2010, 28, 223–262 CrossRef CAS.
- D. Loke, T. H. Lee, W. J. Wang, L. P. Shi, R. Zhao, Y. C. Yeo, T. C. Chong and S. R. Elliott, Breaking the Speed Limits of Phase-Change Memory, Science, 2012, 336, 1566–1569 CrossRef CAS.
- F. Rao, K. Ding, Y. Zhou, Y. Zheng, M. Xia, S. Lv, Z. Song, S. Feng, I. Ronneberger, R. Mazzarello, W. Zhang and E. Ma, Reducing the stochasticity of crystal nucleation to enable subnanosecond memory writing, Science, 2017, 358, 1423–1426 CrossRef CAS PubMed.
- S. Raoux, W. Welnic and D. Ielmini, Phase Change Materials and Their Application to Nonvolatile Memories, Chem. Rev., 2010, 110, 240–267 CrossRef CAS.
- B. Liu, K. Li, W. Liu, J. Zhou, L. Wu, Z. Song, S. R. Elliott and Z. Sun, Multi-level phase-change memory with ultralow power consumption and resistance drift, Sci. Bull., 2021, 66, 2217–2224 CrossRef CAS.
- K.-K. Du, Q. Li, Y.-B. Lyu, J.-C. Ding, Y. Lu, Z.-Y. Cheng and M. Qiu, Control over emissivity of zero-static-power thermal emitters based on phase-changing material GST, Light: Sci. Appl., 2016, 6, e16194 CrossRef PubMed.
- X. Yu, Y. Zhao, C. Li, C. Hu, L. Ma, S. Fan, Y. Zhao, N. Min, S. Tao and Y. Wang, Improved multi-level data storage properties of germanium-antimony-tellurium films by nitrogen doping, Scr. Mater., 2017, 141, 120–124 CrossRef.
- Z. Li, Y. Lu, M. Wang, X. Shen, X. Zhang, S. Song and Z. Song, Controllable multilevel resistance state of superlattice-like GaSb/Ge2Te films for ultralong retention phase-change memory, J. Non-Cryst. Solids, 2018, 481, 110–115 CrossRef CAS.
- A. I. Khan, H. Kwon, M. E. Chen, M. Asheghi, H. S. P. Wong, K. E. Goodson and E. Pop, Electro-Thermal Confinement Enables Improved Superlattice Phase Change Memory, IEEE Electron Device Lett., 2022, 43, 204–207 CAS.
- R. Liu, P. Wu, Z. He, J. Zhai, X. Liu and T. Lai, Study of crystallization and thermal stability of superlattice-like SnSb4-GeTe thin films, Thin Solid Films, 2017, 625, 11–16 CrossRef CAS.
- W. Wu, S. Chen, J. Zhai, X. Liu, T. Lai, S. Song and Z. Song, Multi-level storage and ultra-high speed of superlattice-like Ge50Te50/Ge8Sb92 thin film for phase-change memory application, Nanotechnology, 2017, 28, 405206 CrossRef PubMed.
- Y. Hu, X. Feng, S. Li, T. Lai, S. Song, Z. Song and J. Zhai, Superlattice-like Sb50Se50/Ga30Sb70 thin films for high-speed and high density phase change memory application, Appl. Phys. Lett., 2013, 103, 152107 CrossRef.
- K. Jiang, Y. Lu, Z. Li, M. Wang, X. Shen, G. Wang, S. Song and Z. Song, GeTe/Sb4Te films: A candidate for multilevel phase change memory, Mater. Sci. Eng., B, 2018, 231, 81–85 CrossRef CAS.
- Y. G. Liu, Y. F. Chen, D. L. Cai, Y. Y. Lu, L. Wu, S. Yan, Y. Li, J. J. Lu, L. Yu and Z. T. Song, High performance of multilevel-cell phase change memory device with good endurance reliability, Semicond. Sci. Technol., 2019, 34, 105019 CrossRef CAS.
- M. S. Arjunan, A. Mondal, S. Durai, K. V. Adarsh and A. Manivannan, Impact of crystallization process in multilevel optical switching in Ge2Sb2Te5 and Ag5In5Sb60Te30 phase-change materials, J. Phys. D: Appl. Phys., 2020, 53, 495303 CrossRef.
- Y. Chen, H. Pan, S. Mu, G. Wang, R. Wang, X. Shen, J. Wang, S. Dai and T. Xu, Intermediate crystallization kinetics in Germanium-Tellurides, Acta Mater., 2019, 164, 473–480 CrossRef CAS.
- C. Zhang, L. Hu, Y. Yue and J. C. Mauro, Fragile-to-strong transition in metallic glass-forming liquids, J. Chem. Phys., 2010, 133, 014508 CrossRef PubMed.
- W. A. Johnson and R. F. Mehl, Reaction kinetics in processes of nucleation and growth, Trans. AIME, 1939, 135, 396–415 Search PubMed.
- M. Avrami, Kinetics of Phase Change. I General Theory, J. Chem. Phys., 1939, 122, 064901 Search PubMed.
- M. Avrami, Kinetics of phase change. II transformation-time relations for random distribution of nuclei, J. Chem. Phys., 1940, 122, 064901 Search PubMed.
- M. Avrami, Granulation, phase change, and microstructure kinetics of phase change. III, J. Chem. Phys., 1941, 122, 064901 Search PubMed.
- W. Zhang and E. Ma, Unveiling the structural origin to control resistance drift in phase-change memory materials, Mater. Today, 2020, 41, 156–176 CrossRef CAS.
- Y. Chen, J. Gu, Q. Zhang, Y. Mao, G. Wang, R. Wang, X. Shen, J.-Q. Wang and T. Xu, Fragile-to-strong crossover in optimized In-Sb-Te phase-change supercooled liquids, Phys. Rev. Mater., 2020, 4(3), 033403 CrossRef CAS.
- B. Chen, G. H. ten Brink, G. Palasantzas and B. J. Kooi, Crystallization kinetics of GeSbTe phase-change nanoparticles resolved by ultrafast calorimetry, J. Phys. Chem. C, 2017, 121, 8569–8578 CrossRef CAS.
- G. Wang, F. Liu, Y. Lu, Y. Chen and X. Shen, Crystallization mechanism and switching behavior of In-S-Sb phase change thin films, Appl. Phys. Lett., 2021, 119, 011601 CrossRef CAS.
- K. Peng, Y. Chen, W. Leng, G. Wang, C. Gu, Y. Gao, J.-Q. Wang and X. Shen, Tailorable fragile-to-strong kinetics features of metal oxides nanocomposite phase-change antimony films, Acta Mater., 2022, 234, 118013 CrossRef CAS.
- K. Peng, Y. Chen, Y. Meng, J.-Q. Wang, C. Gu, Y. Gao, G. Wang and X. Shen, Revealing the influence of oxygen doping on the crystallization kinetics of Sb–GeO2, Cryst. Growth Des., 2022, 22, 4970–4976 CrossRef CAS.
- J. Orava, D. W. Hewak and A. L. Greer, Fragile-to-strong crossover in supercooled liquid Ag–In–Sb–Te studied by ultrafast calorimetry, Adv. Funct. Mater., 2015, 25, 4851–4858 CrossRef CAS.
- D. W. Henderson, Thermal analysis of non-isothermal crystallization kinetics in glass forming liquids.pdf, J. Non-Cryst. Solids, 1979, 30, 301–315 CrossRef CAS.
- C. Zhou, L. N. Hu, Q. J. Sun, H. J. Zheng, C. Z. Zhang and Y. Z. Yue, Structural evolution during fragile-to-strong transition in CuZr(Al) glass-forming liquids, J. Chem. Phys., 2015, 142, 064508 CrossRef PubMed.
- M. Salinga, E. Carria, A. Kaldenbach, M. Bornhofft, J. Benke, J. Mayer and M. Wuttig, Measurement of crystal growth velocity in a melt-quenched phase-change material, Nat. Commun., 2013, 4, 2371 CrossRef PubMed.
- C. A. Angell, Glass formation and glass transition in supercooled liquids, with insights from study of related phenomena in crystals, J. Non-Cryst. Solids, 2008, 354, 4703–4712 CrossRef CAS.
- G. Ruitenberg, A. K. Petford-Long and R. C. Doole, Determination of the isothermal nucleation and growth parameters for the crystallization of thin Ge2Sb2Te5 films, J. Appl. Phys., 2002, 92, 3116–3123 CrossRef CAS.
- R. Pandian, B. J. Kooi, J. T. M. De Hosson and A. Pauza, Influence of capping layers on the crystallization of doped SbxTe fast-growth phase-change films, J. Appl. Phys., 2006, 100, 123511 CrossRef.
- W. K. Njoroge, H. Dieker and M. Wuttig, Influence of dielectric capping layers on the crystallization kinetics of Ag5In6Sb59Te30 films, J. Appl. Phys., 2004, 96, 2624–2627 CrossRef CAS.
- R. Berthier, N. Bernier, D. Cooper, C. Sabbione, F. Hippert and P. Noe, In situ observation of the impact of surface oxidation on the crystallization mechanism of GeTe phase-change thin films by scanning transmission electron microscopy, J. Appl. Phys., 2017, 122, 115304 CrossRef.
- M. Zacharias and P. Streitenberger, Crystallization of amorphous superlattices in the limit of ultrathin films with oxide interfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 8391–8396 CrossRef CAS.
- Y. P. Mitrofanov, M. Peterlechner, I. Binkowski, M. Y. Zadorozhnyy, I. S. Golovin, S. V. Divinski and G. Wilde, The impact of elastic and plastic strain on relaxation and crystallization of Pd–Ni–P-based bulk metallic glasses, Acta Mater., 2015, 90, 318–329 CrossRef CAS.
- T. P. L. Pedersen, J. Kalb, W. K. Njoroge, D. Wamwangi, M. Wuttig and F. Spaepen, Mechanical stresses upon crystallization in phase change materials, Appl. Phys. Lett., 2001, 79, 3597–3599 CrossRef CAS.
- A. Devasia, F. Bai, M. Davis, K. A. Campbell, S. Gupta and S. Kurinec, Analyzing residual stress in bilayer chalcogenide Ge2Se3/SnTe films, Thin Solid Films, 2009, 517, 6516–6519 CrossRef CAS.
- R. Wang, S. Pan and Y. Zhou, Stress reduction by ion bombardment in CeO2 films, Solid State Commun., 2000, 114, 613–616 CrossRef CAS.
- D. J. Gunton and G. A. Saunders, The Young's modulus and Poisson's ratio of arsenic, antimony and bismuth, J. Mater. Sci., 1972, 7, 1061–1068 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |