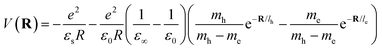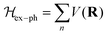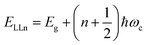DOI:
10.1039/D4MA00454J
(Review Article)
Mater. Adv., 2024, Advance Article
Exciton binding energies and polaron interplay in the optically excited state of organic–inorganic lead halide perovskites
Received
1st May 2024
, Accepted 14th October 2024
First published on 16th October 2024
Abstract
Organic–inorganic lead halide perovskites (OILHPs) have been spotlighted by many researchers due to their unique features and potential for high-performance devices. One of the major obstacles with perovskites is determining the universal value for the exciton binding energy. Numerous contradictory reports in previous studies reveal a wide range of values for the exciton binding energy, spanning from a few meV to several hundred meV. Here we review different experimental and theoretical methodologies carried out to measure the exciton binding energy of OILHPs. Some of the recently explored parameters in the literature that influence exciton binding energy, like exciton dynamics and recombination, are also discussed. Besides this, prospective research initiatives in the field of exciton binding energies, with an emphasis on improving measurement precision and understanding exciton–polaron dynamics, are also highlighted. This critical understanding of exciton and polaron physics is a significant resource for researchers working on exciton-related phenomena, allowing for future breakthroughs in the design and development of efficient, high-performance devices.
1 Introduction
Organic–inorganic lead halide perovskites (OILHPs) are characterized by the general chemical expression of APbX3, where A represents cation groups such as methylammonium (MA; CH3NH3), formamidinium (FA; CH(NH2)2), cesium (Cs) or their mixtures, and X represents a halide like iodide (I), bromide (Br), chloride (Cl), or their mixed composition. Such materials have proven remarkable electronic and optical properties, making them promising for high-efficiency, low-cost devices. Some of the notable features of these materials that render them exceptional are their band gap tailoring for optimum solar absorption,1–7 enhanced carrier lifetimes,1,8,9 long charge carrier diffusion length,9–11 high charge carrier mobility,10,12–14 and abnormally high defect tolerance.15–17 Research on amplified spontaneous emission (ASE) or lasers,18–22 light-emitting diodes (LEDs),23–25 and photodetectors26–34 has attracted significant interest in the aftermath of OILHPs’ success in photovoltaics35–43 thereby replacing the traditional III–V compound semiconductors. Meanwhile, the rapid advancement of OILHPs across various applications has led to a growing interest in understanding their photophysical properties to explain the origins of their exceptional device performance and the nature of the photoexcitation species that are widely discussed.38,44–48
In most of the studies, it has been shown that in OILHPs, the optical excitation close to the bandgap impacts the main factors, like hampering the bound state of e–h pairs and their transport behavior, which in turn affects the performance of photovoltaic and optoelectronic devices. The consideration of e–h coulombic interactions usually refers to excitons during excitation. The amount of energy required to hold or break up such bound states of photoexcited e–h pairs is known as exciton binding energy (Exb), which is helpful in explaining the fundamentals of photophysics and their connection to device performances. Understanding the exciton binding energy offers insights for optimizing OILHP-based devices, leading to enhanced performance. In a typical direct bandgap semiconducting material, two types of optically excited states occur near the band edge: free charge carriers and excitons. Generally, inorganic semiconductors, like GaAs, GaN, and InP, are usually considered free carrier materials, with their excited levels mainly dominated by free carriers as excitons known as Wannier–Mott excitons, which dissociate instantaneously into free carriers upon photoexcitation. Such materials have small effective masses and high permittivity, and their exciton binding energy is lower (less than 10 meV) in comparison to thermal energy (kBT) at room temperature (RT).49,50 On the other hand, bulk organic semiconductors, such as molecular crystals, are excitonic materials because their excited states are primarily populated by excitons, specifically referred to as Frenkel excitons. These materials have large effective masses and low permittivity and their value for exciton binding energy at RT ranges from 40 to 700 meV.51–54 In addition to Wannier–Mott and Frenkel excitons, a third type, known as charge transfer (CT) excitons, is worth considering. These are formed when an electron or hole is transferred across a material interface.55,56 OILHPs, which consist of both organic and inorganic components, form a unique class of materials that combine the properties of both types. The exciton binding energy measured through experiments lies approximately between 7.457 and 16258 meV for MAPbI3 with different structural morphologies. Such a large difference in the measured value for the exciton binding energy, compared to the small differences in bandgap values, leads to the unexplained phenomenon of free carrier or exciton generation in the optically excited state. It remains unclear which of the two species plays an active role in optical excitation, thereby influencing the photophysical properties of the material. Many reported measurements revealed that excitons being generated at RT will dissociate spontaneously into free carriers upon photoexcitation during the duration of the sub-ps range, resulting in free carrier dominance in the subsequent optically excited processes.59–61 Beyond the dielectric and quantum confinement effects in these materials, recent discussions on quasiparticles dressed by lattice phonons known as polarons have prompted researchers to consider their impact when studying exciton transport properties in OILHPs. Large polaron formation significantly influences the effective masses and mobility of excitons, affecting their optical transport mechanisms.62–64 Along with the excitonic features, the formation of polarons plays a significant role in realizing the excited-state optical characteristics of OILHPs due to the existence of high exciton resonances in their transient absorption spectra and band edge absorption onsets. Therefore, despite significant progress in exciton and polaron physics in recent years, the fundamental understanding and determination of exact reliable values for exciton binding energies of OILHPs still need to be revealed.
In this article, our focus is centered on commonly studied OILHPs, thereby explaining their underlying photophysical processes and illustrating the disparities in the outcomes of various relevant experiments and theoretical approaches. This review article aims to provide an up-to-date analysis of exciton binding energy and exciton/polaron physics in OILHPs, with implications for both fundamental research and practical applications.
2. Techniques for determining exciton binding energies
Perovskite systems are commonly described using the Wannier–Mott model65–67 due to the significantly larger effective Bohr radii of excitons compared to the lattice constant in these materials. This model relies on the assumption of effective masses of the carriers and the inclusion of the dielectric constant. Within this framework, the nth state excitonic energy can be determined by| |
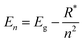 | (1) |
where Eg is the bandgap energy and R* is the effective Rydberg excitonic energy. Generally, for semiconductors, the carrier effective mass tends to be smaller as compared to that of free electrons. It is also known that the interaction between carriers is effectively screened by the lattice. This leads to the concept of the effective Rydberg energy, which can be applied to Wannier excitons by renormalizing the hydrogenic Rydberg energy (RH = 13.6 eV) and is given by| |
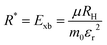 | (2) |
where 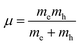 is the reduced exciton mass with effective masses me,h for the electron and hole and εr is the relative dielectric constant, which describes the carrier screening by the crystal lattice. In large-bandgap materials such as LiF and Ar, Frenkel excitons are highly localized and tightly bound within a single crystal unit due to their effective Bohr radii being smaller than the lattice constant. Consequently, the Wannier–Mott model is inadequate for accurately describing Frenkel excitons. However, from the perspective of first-principles electronic structure theory, Wannier and Frenkel excitons are conceptually equivalent as they both represent excitations within a many-body system. The distinguishing feature of excitons is their collective nature, arising from superpositions of many single-particle excitations. For 3D OILHP systems, the Wannier–Mott model yields fairly accurate results, but it leads to the controversial estimation of exciton binding energy due to the large difference between static and high frequency dielectric constants (e.g. ε0 ≈ 33–20 and ε∞ ≈ 4.5–6.75 [see Table 2]). Moreover, due to the anisotropic nature of the dielectric constant (ε∞), the calculations of exciton binding energy may be problematic as both temperature68,69 and frequency70,71 affect the dielectric function for OILHPs. However, for OILHPs, the static value (ε0) may not always be a reliable estimate of the effective dielectric constant (εeff), because it is likely valid only when the exciton binding energy appears to be lower than the longitudinal optical phonon energy (ELO = ħωLO).72
is the reduced exciton mass with effective masses me,h for the electron and hole and εr is the relative dielectric constant, which describes the carrier screening by the crystal lattice. In large-bandgap materials such as LiF and Ar, Frenkel excitons are highly localized and tightly bound within a single crystal unit due to their effective Bohr radii being smaller than the lattice constant. Consequently, the Wannier–Mott model is inadequate for accurately describing Frenkel excitons. However, from the perspective of first-principles electronic structure theory, Wannier and Frenkel excitons are conceptually equivalent as they both represent excitations within a many-body system. The distinguishing feature of excitons is their collective nature, arising from superpositions of many single-particle excitations. For 3D OILHP systems, the Wannier–Mott model yields fairly accurate results, but it leads to the controversial estimation of exciton binding energy due to the large difference between static and high frequency dielectric constants (e.g. ε0 ≈ 33–20 and ε∞ ≈ 4.5–6.75 [see Table 2]). Moreover, due to the anisotropic nature of the dielectric constant (ε∞), the calculations of exciton binding energy may be problematic as both temperature68,69 and frequency70,71 affect the dielectric function for OILHPs. However, for OILHPs, the static value (ε0) may not always be a reliable estimate of the effective dielectric constant (εeff), because it is likely valid only when the exciton binding energy appears to be lower than the longitudinal optical phonon energy (ELO = ħωLO).72
Several experimental and theoretical approaches were deployed to reliably measure the exciton binding energies in OILHPs as shown in detail in Table 1. Experimental techniques mostly involved magneto-absorption, optical absorption, and photoluminescence (PL) spectroscopy which have both merits and demerits. Theoretical methods, such as many-body perturbation theory (MBPT) within the framework of density functional theory (DFT) and time-dependent density functional theory (TD-DFT), were also used to precisely estimate the universal values for exciton binding energies. In this section, we will discuss these techniques in detail.
Table 1 Available data for measured exciton binding energy of OILHPs for different morphologies and temperatures/phases. Experimental and theoretical techniques are also mentioned for each case. The data are arranged in order from early 1994 to the latest measurements for each material
| Material |
Morphology/geometry |
Temperature (K)/phase |
Exciton binding energy (meV) |
Measurement setup |
Authors |
| MAPbI3 |
3D |
4.2 |
37 |
Magneto-absorption and Wannier–Mott model |
Hirasawa et al.73 |
| |
3D |
78 |
45 |
Optical absorption |
Ishihara et al.74 |
| |
3D |
80–300 (tetragonal) |
32 |
Temperature dependent PL spectra (Arrhenius fitting) |
Saveniji et al.75 |
| |
3D |
Cubic |
29 |
Reflectance spectra and Wannier–Mott model |
Koutselas et al.76 |
| |
Thin film (<100 nm) |
10–300 |
19 ± 3 |
Temperature dependent PL spectra (Arrhenius fitting) |
Sun et al.77 |
| |
Thin film |
4.2 |
50 |
Magneto-absorption and Wannier–Mott model |
Tanaka et al.78 |
| |
Thin film (800 nm) |
170–300 |
25 ± 3 |
UV-vis absorption spectra (Elliott's fitting) |
Saba et al.79 |
| |
Thin film |
RT |
45 |
Optical absorption and Wannier–Mott model |
Grancini et al.80 |
| |
3D bulk |
RT |
12.3 |
UV-vis absorption spectra (Elliott's fitting) |
Green et al.81 |
| |
Thin film |
RT |
41 |
UV-vis absorption spectra (Elliott's fitting) |
Kumar et al.82 |
| |
Thin film |
13 |
30 |
Optical absorption spectra (Elliott's fitting) |
Yamada et al.83 |
| |
300 |
6 |
| |
Thin film (332 ± 38 nm) |
RT |
13 |
Transmission absorption spectroscopy (Elliott's fitting) |
Yang et al.84 |
| |
Thin film (150 nm) |
RT |
7.4 ± 2 |
Electro-absorption (EA) spectroscopy (Elliott's fitting) |
Ziffer et al.57 |
| |
3D |
Cubic |
12 ± 9 |
TD-DFT |
Hakamata et al.85 |
| |
3D unit cell |
Cubic |
45 |
DFT and SOC-GW-BSE (with dielectric constant derived from SOC-DFPT) |
Bokdam et al.86 |
| |
Thin film |
10 |
13 (for defect free) |
Time-integrated four-wave mixing (TIFWM) spectroscopy |
March et al.87 |
| |
29 (for defect-bound) |
| |
Thin films (≈350 nm thick) |
2 (orthorhombic) |
16 |
High field magneto-absorption and Wannier–Mott model |
Galkowski et al.88 |
| |
|
High temperature (tetragonal) |
12 |
| |
Nanostructures |
10–300 |
44 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zheng et al.89 |
| |
Thin film |
77–340 |
∼43 |
Temperature dependent UV-vis absorption spectra |
Ye et al.90 |
| |
Thin film |
RT (tetragonal) |
19 |
Temperature dependent electro-absorption spectroscopy |
Ruf et al.91 |
| |
162 (orthorhombic) |
26 |
| |
Thin film (single crystal) |
RT (tetragonal) |
17 |
Temperature dependent photoluminescence |
Shi et al.92 |
| |
Thin film |
0–160 (orthorhombic) |
20 ± 2 |
Optical absorption (Elliott's fitting) |
Davies et al.93 |
| |
Quantum dots |
Cubic |
540 |
TD-DFT |
Athanasios et al.94 |
| |
3D unit cell |
Tetragonal |
15 |
DFT and SOC-GW-BSE (with dielectric constant derived from SOC-DFPT) |
Umari et al.95 |
| |
Thin film |
200–360 |
11.7 |
Temperature and density-resolved optical spectroscopy |
Liu et al.96 |
| |
Thin film ∼340–450 nm thick |
10 |
24 |
Optical absorption (Elliott's fitting) |
Ruf et al.97 |
| |
150 |
29 |
| |
>150 |
32 |
f-Sum rule |
| |
3D unit cells |
Cubic |
58 |
DFT and Wannier–Mott model |
Xu et al.98 |
| |
Tetragonal |
64 |
| |
Orthorhombic |
66 |
| |
Quantum dots |
250–300 |
162.1 ± 22.2 |
Temperature dependent PL spectra (Arrhenius fitting) |
Parveen et al.58 |
| |
3D unit cell |
Cubic |
50–110 (with ε∞ varying from 5.45 to 5.65) |
DFT and Wannier–Mott model |
Xu et al.99 |
| |
2D mica/perovskite (6 nm) interface |
RT |
10 |
Time-resolved photoluminescence spectra |
Bai et al.100 |
| |
Polycrystalline thin film |
Tetragonal |
12.6 |
Temperature dependent photoluminescence spectra |
Hamada et al.101 |
| |
Orthorhombic |
30 |
| |
160–290 |
85 ± 30 |
Temperature dependent photoluminescence spectra |
| |
290 (tetragonal) |
11.6 |
Electro-absorption spectra (Elliott's fitting) |
| |
60 (orthorhombic) |
24.2 |
| |
3D unit cell |
Tetragonal |
9.85 |
DFT and Wannier–Mott model |
Ali et al.102 |
| |
Single crystal |
RT |
15 |
Modeling dispersion relations |
Xiong et al.103 |
| |
3D unit cell |
Cubic |
43 |
DFT and Wannier–Mott model |
Li et al.104 |
| |
Film deposited on a glass slide |
300 |
26 |
UV-vis absorption spectroscopy and differential transmission (DT) |
Simbula et al.105 |
| |
3D unit cell |
Cubic |
4.88 |
TD-DFT and interfragment charge transfer method (IFCT) |
Gao et al.106 |
| |
Thin film |
Pseudo-cubic |
16.9 |
Edward's model and Hang-Schmitt-Rink's (HSR) model. Mott densities extracted from the carrier-density-dependent hot carrier experimental graph |
Chan et al.107 |
| |
3D unit cell |
Cubic |
16.13 |
DFT and Wannier–Mott model |
Basera et al.108 |
| |
|
— |
40.6 (without polaron inclusion) |
Path integral molecular dynamics simulations |
Park et al.63 |
| |
27.0 (with polaron inclusion) |
| |
3D unit cell |
Cubic |
37 |
DFT and Wannier–Mott model |
Biffi et al.109 |
| |
Thin film |
RT |
10 |
Optical pump THz probe |
Ulatowski et al.110 |
| |
| MAPbBr3 |
Single crystal 5 × 5 × 3 mm3 |
4.2 |
76 |
Magneto-absorption and Wannier–Mott model |
Tanaka et al.78 |
| |
Thin film |
RT |
37 |
UV-vis absorption spectra (Elliott's fitting) |
Kumar et al.82 |
| |
3D bulk |
RT |
36.3 |
UV-vis absorption spectra (Elliott's fitting) |
Green et al.81 |
| |
Quantum dots (average diameter of 3.3 nm) |
5–300 |
42 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zhang et al.111 |
| |
300–400 |
375 |
| |
Microsized bulk particles 2–8 μm |
5–300 |
65 |
| |
Nanoparticles |
240–350 |
320 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zheng et al.112 |
| |
3D bulk |
|
84 |
|
|
| |
Thin film (86 ± 11 nm) |
RT |
40 |
Transmission absorption spectroscopy |
Yang et al.84 |
| |
Single crystal (4 × 4 × 2 mm3) |
4 |
80–100 |
Temperature dependent reflectance spectra |
Kunugita et al.113 |
| |
Thin films (≈350 nm thick) |
2 (orthorhombic) |
25 |
High field magneto-absorption and Wannier–Mott model |
Galkowski et al.88 |
| |
3D unit cell |
Cubic |
71 |
DFT and SOC-GW-BSE |
Bokdam et al.86 |
| |
Rectangular microstructures with length 1–3 μm |
10–300 |
53.35 ± 2.60 |
Temperature dependent PL spectra (Arrhenius fitting) |
Dai et al.114 |
| |
Single crystal (with dimensions of 3 × 3 × 3 mm) |
10 |
15.33 |
Temperature dependent PL spectra |
Tilchin et al.115 |
| |
Single crystal |
5 |
20–40 |
Photoluminescence spectra at low temperature |
Kunugita et al.116 |
| |
Single crystal |
10–230 |
21 ± 3 |
Temperature dependent reflectance spectra (Lorentz model) |
Thu Ha Do et al.117 |
| |
Quantum dots |
Cubic |
610 |
TD-DFT |
Athanasios et al.94 |
| |
Polycrystalline film (∼200 nm) |
RT (tetragonal) |
20 |
Optical absorption spectra |
Shi et al.92 |
| |
2D mica/perovskite (8 nm) interface |
RT |
30 |
Time-resolved photoluminescence spectra |
Bai et al.100 |
| |
Thin film ∼340–450 nm thick |
10 |
30 |
Optical absorption (Elliott's fitting) |
Ruf et al.97 |
| |
150 |
38 |
| |
>150 |
41 |
f-Sum rule |
| |
Thin film |
280–380 |
25.9 |
Temperature and density-resolved optical spectroscopy |
Liu et al.96 |
| |
Quantum dots |
250–300 |
271.1 ± 34.1 |
Temperature dependent PL spectra (Arrhenius fitting) |
Parveen et al.58 |
| |
Single crystal platelets (5.9–28.2 nm) |
77–300 |
70 –150 |
Temperature dependent PL spectra (Arrhenius fitting) |
Liu et al.118 |
| |
Single crystal |
RT |
15 |
Modeling of dispersion relations |
Xiong et al.103 |
| |
Polycrystalline |
RT |
40 |
Temperature dependent PL spectra |
Shi et al.119 |
| |
Thin film |
RT |
34.8 |
Optical absorption (Elliott's fitting) |
Ulatowski et al.120 |
| |
3D unit cell |
Cubic |
27.33 |
DFT + Wannier–Mott model |
Jain et al.121 |
| |
Film deposited on a glass slide |
77–300 |
64 |
UV-vis absorption spectroscopy and differential transmission (DT) |
Simbula et al.105 |
| |
3D unit cell |
Cubic |
5.43 |
TD-DFT and interfragment charge transfer method (IFCT) |
Gao et al.106 |
| |
Microwires with a length of 343.5 μm |
80–300 |
75 |
Temperature dependent photoluminescence spectra |
Yan et al.122 |
| |
Thin film |
RT (cubic) |
36 |
Using Edward's model and Hang-Schmitt-Rink's (HSR) model. Mott densities extracted from the carrier-density-dependent hot carrier (HC) experimental graph |
Chan et al.107 |
| |
| FAPbI3 |
3D bulk |
RT |
8.4 |
UV-vis absorption spectra (Elliott's fitting) |
Green et al.81 |
| |
Thin films (≈350 nm thick) |
2 (orthorhombic) |
14 |
High field magneto-absorption and Wannier–Mott model |
Galkowski et al.88 |
| |
High temperature (tetragonal) |
10 |
| |
3D unit cell |
Cubic |
35 |
DFT and SOC-GW-BSE |
Bokdam et al.86 |
| |
Thin film |
150–295 (α-phase) |
8.1 |
Temperature dependent PL spectra (Arrhenius fitting) |
Fang et al.123 |
| |
5–110 (β-Phase) |
18 |
| |
Thin film |
80–340 |
29 |
Temperature dependent PL spectra |
Yuan et al.124 |
| |
Single crystal |
α-Phase (trigonal) |
43.5 |
UV-vis absorption spectra |
Sachenko et al.125 |
| |
Nanostructures |
10–300 |
8.4 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zheng et al.89 |
| |
Thin single crystal nanoplates |
RT |
∼10 |
Time-resolved photoluminescence (TRPL) |
Fu et al.126 |
| |
3D unit cell |
Tetragonal |
17 |
SR-DFT and SOC-GW |
Umari et al.95 |
| |
Thin film |
10 |
5.3 |
THz photoconductivity spectra |
Davies et al.127 |
| |
3D unit cell |
Cubic |
50–85 (with ε∞ varying from 5.45 to 5.65) |
DFT and Wannier–Mott model |
Xu et al.99 |
| |
Thin film |
200–360 |
9.95 |
Temperature and density-resolved optical spectroscopy |
Liu et al.96 |
| |
Single crystal |
20–240 |
∼2–5 |
Temperature dependent absorption spectra (Elliott's fitting) |
Johnston et al.128 |
| |
3D unit cell |
Cubic |
13.30 |
DFT and Wannier–Mott model |
Basera et al.108 |
| |
3D unit cell |
Cubic |
4.93 |
TD-DFT and interfragment charge transfer method (IFCT) |
Gao et al.106 |
| |
3D bulk |
Tetragonal |
93 |
DFT and SOC-GW-BSE (with dielectric constant derived from SOC-GW) |
Muhammad et al.129 |
| |
Hexagonal |
567 |
| |
Thin film (with a thickness of 400 nm) |
RT |
11 |
Optical absorption (Elliott's fitting) |
Jeon et al.130 |
| |
Quantum dots |
80–390 |
69.2 |
Temperature dependent PL spectra (Arrhenius fitting) |
Wang et al.131 |
| |
Bulk |
91 |
| |
Thin film |
0–300 |
20–3 |
Optical absorption (Elliott's fitting) |
Elmestekawy et al.132 |
| |
| FAPbBr3 |
3D bulk |
RT |
31.8 |
UV-vis absorption spectra (Elliott's fitting) |
Green et al.81 |
| |
Thin films (≈350 nm thick) |
2 (orthorhombic) |
22 |
High field magneto-absorption and Wannier–Mott model |
Galkowski et al.88 |
| |
High temperature (tetragonal) |
24 |
| |
3D unit cell |
Cubic |
60 |
DFT and SOC-GW-BSE |
Bokdam et al.86 |
| |
Rectangular microstructures with length 1–3 μm |
10–300 |
21.67 ± 1.62 |
Temperature dependent PL spectra (Arrhenius fitting) |
Dai et al.114 |
| |
Nanocrystals (12–14 nm) |
180–360 |
170 |
Time-resolved PL spectra (Arrhenius fitting) |
Perumal et al.133 |
| |
Nanocrystals |
90–350 |
160 |
Time-resolved PL spectra (Arrhenius fitting) |
Yang et al.134 |
| |
Nanocrystals (5–20 nm) |
0–300 |
∼57.5 |
Time-resolved PL spectra (Arrhenius fitting) |
Han et al.135 |
| |
2D nanoplatelet thin films |
120–300 |
287.5 |
Temperature dependent PL spectra |
Fang et al.136 |
| |
Nanocrystals |
100–380 |
∼68.4 |
Temperature dependent PL spectra (Arrhenius fitting) |
Liu et al.137 |
| |
Thin film |
280–380 |
9.95 |
Temperature and density-resolved optical spectroscopy |
Liu et al.96 |
| |
Quasi-2D co-interlayer |
78–290 |
228 |
Temperature dependent PL spectra |
Meng et al.138 |
| |
Nanocrystals encapsulated by siliceous nanosphere |
RT |
5 |
Optical absorption spectra |
Sui et al.139 |
| |
Nanocrystals with an average length of ∼12 nm |
4 |
∼17 |
Temperature dependent PL spectra |
Liu et al.140 |
| |
Nanoplatelets (n = 2) |
RT |
112 |
Temperature dependent PL spectra (Arrhenius fitting) |
Peng et al.141 |
| |
Nanocrystals (6–8 nm) |
80–175 |
42.3 |
Temperature dependent steady state PL spectra (Arrhenius fitting) |
Wang et al.142 |
| |
175–400 |
80.2 |
| |
Square and quasi-circular microdisks having typical edge lengths/diameters ranging from a few to tens of micrometers with thicknesses ranging from 200 nm to a few micrometers |
75–300 |
24.6 |
Temperature dependent PL spectra |
Li et al.143 |
| |
Nanocrystals |
80–300 |
51 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zhang et al.144 |
| |
3D unit cell |
Cubic |
22.06 |
DFT + Wannier–Mott model |
Jain et al.121 |
| |
Thin film |
Cubic |
9.3 |
Edward's model and Hang-Schmitt-Rink's (HSR) model. Mott densities extracted from the carrier-density-dependent hot carrier experimental graph |
Chan et al.107 |
| |
3D unit cell |
Cubic |
5.29 |
TD-DFT and interfragment charge transfer method (IFCT) |
Gao et al.106 |
| |
Thin film with 350 nm thickness |
Cubic |
53 |
Optical absorption (Elliott's fitting) |
Qaid et al.145 |
| |
Nanocrystals |
— |
69.668 |
Temperature dependent PL spectra |
Zhang et al.146 |
| |
| MAPbBr3−xClx (0 ≤ x ≤ 3) |
Thin films |
Cubic |
21 ± 1–52 ± 6 |
Optical absorption spectra |
Comin et al.147 |
| MAPbI3−xClx |
Polycrystalline film |
150–290 |
55 ± 21 |
Temperature dependent PL spectra |
D’Innocenzo et al.148 |
| FA0.81MA0.15Pb(I0.836Br0.15)3 |
Thin film |
77–340 |
∼13 |
Temperature dependent UV-vis absorption spectra |
Ye et al.90 |
| Csx(FA0.4MA0.6)1−xPbI2.8Br0.2 (0 ≤ x ≤ 0.2) |
Film |
303.15–833.15 |
8.0–10.1 |
UV-vis absorption spectra (Elliott's fitting) |
Liu et al.149 |
| FAxMA1−xPbI3 (0.2 ≤ x ≤ 0.8) |
Nanostructures |
10–300 |
20.8 ± 3.9–28 ± 3.9 |
Temperature dependent PL spectra (Arrhenius fitting) |
Zheng et al.89 |
| MAPbI3−xBrx (0 ≤ x ≤ 3) |
Nanocrystalline solid films |
RT |
9–15 |
Electro-absorption spectra |
Awasthi et al.150 |
| FA0.85Cs0.15PbI2.9Br0.1 |
Thin film |
77–250 |
5.9 ± 2.0 |
Temperature dependent spectroscopic ellipsometry |
Whitcher et al.151 |
| (MA0.13FA0.87)PbI3 |
Single crystal |
400 |
40 |
Optical absorption spectra (Elliott's fitting) |
Chen et al.152 |
| 4.4 |
16 |
| FAPbBr3−xClx |
Nanocrystals |
75–270 |
137 (for Br-ligand) |
Temperature dependent PL spectra (Arrhenius fitting) |
Zhang et al.153 |
| Br-ligand → 14.6 nm |
|
| Br-ligand → 12.1 nm |
223 (for Cl-ligand) |
| MAPbBr3−xClx (0 ≤ x ≤ 25 mol%) |
3D bulk (2 × 2 × 1 supercell) |
Cubic |
67–66 |
DFT and Wannier–Mott model |
Rybin et al.154 |
| FAPb(I1−xBrx)3 (0 ≤ x ≤ 1) |
3D bulk (1 × 1 × 2 supercell) |
Cubic |
74–112 |
DFT and SOC-GW-BSE |
Muhammad et al.155 |
| CsxFA1−xPbI3 (0.25 ≤ x ≤ 0.75) |
Quantum dots |
80–390 |
53.1–36.4 |
Temperature dependent PL spectra |
Wang et al.131 |
| FA0.85Cs0.15Pb(I0.97Br0.03)3 |
Thin film |
RT |
38 ± 4 |
Steady-state and transient absorption spectra (Elliott's fitting) |
Bao et al.64 |
2.1 Magneto-absorption studies
In magneto-absorption studies, the exciton binding energy measurement is based on the combined contributions arising from the Zeeman effect and the diamagnetic shift of excitons. In the region of a low magnetic field, when the cyclotron energy of carriers (ħBe/μ) is significantly less than the electrostatic energy arising from interacting carriers, the excitonic energy shift becomes156| |
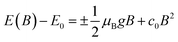 | (3) |
Here E0 represents the exciton ground state energy, μB is the Bohr magneton, g is the Landé g-factor, and c0 is the diamagnetic coefficient that can be expressed as| |
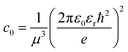 | (4) |
The value of c0 is helpful in determining the exciton radius rE and reduced mass μ provided that the relative dielectric constant εr is known78| |
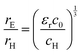 | (5) |
| |
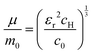 | (6) |
| |
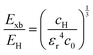 | (7) |
where rH, cH, m0, and EH are the hydrogen atom (Bohr) radius, diamagnetic coefficient, the rest mass of the electron, and binding energy.
The magneto-absorption method was first adopted to determine the exciton binding energy for MAPbI3 microcrystals at low temperatures. The magneto-absorption spectra of MAPbI3 using a magnetic field of ∼40 T at a lower temperature (4.2 K) were investigated by Hirasawa et al.73 They first measured the value for c0 which is 2.7 μeV T−2. Next, they found an Exb of 37 meV with rB = 28 Å and μ = 0.12 using ε∞ = 6.5. Later Tanaka and coworkers78 used the same procedure of Hirasawa with magnetic field B = 50 T which yielded a smaller value of c0 which is 1.35 μeV T−2 for MAPbI3 and 1.28 μeV T−2 for MAPbBr3. Opting the value of ε∞ calculated by Hirasawa et al., an Exb of 50 meV with rB = 22 Å and μ = 0.15 and similarly an Exb of 76 meV with rB = 20 Å and μ = 0.13 were obtained for MAPbI3 and MAPbBr3 thin films, respectively.
In comparison to other methods, analyzing the shift in high field excitonic absorption is quite simple, that is, the considerably widened excitonic transition shift can be monitored easily thereby improving the accuracy of data analysis. However, there are three main issues with the early studies on perovskites in magnetic fields. The first is the arbitrary selection of the dielectric constant and the second is considering the field strength of 50 T as the minimum field limit. According to Lin et al., there is some controversy about whether ε∞ should be included in the measurement of Exb.70 An exciton binding energy Exb = 1.7–2.1 meV may be obtained by analyzing Tanaka et al.'s data using the static dielectric constant of 70.70 Finally, the third issue is that the measurements were based on the exciton diamagnetic coefficient in MA spectra and thus the calculated exciton binding energy was purely based on approximating the hydrogenic (Wannier–Mott) model which may not be valid or least valid for OILHPs.
Recently, with advanced techniques, a much stronger magnetic field of more than 200 T can be used to study both exciton absorption (1s and 2s) and the intraband free carrier absorption84,88,157–159 as shown in Fig. 1(a)–(d) for MAPbI3−xClx and FAPbI3. With extreme magnetic fields, band-to-band multiple transitions of free carriers are observed at higher energies larger than the free exciton transition energies. Such transitions are observed between van Hove singularities of the Landau states with energies described by
| |
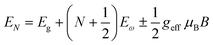 | (8) |
where
N = 1, 2, 3… and so on is the orbital quantum number of the Landau state,
Eω =
ħωc is the exciton cyclotron energy, and
geff is the effective
g-factor. The energy fluctuation of the Landau states as a function of the magnetic field imposes a substantial limit on the bandgap energy and exciton's reduced mass. Makado and McGill
160 developed a numerical model that was used to investigate the exciton diamagnetic shift in the hydrogen atom in the presence of a magnetic field. This model can be used across all magnetic field strengths. It solely relies on the exciton reduced mass and exciton binding energy as input data, making it unnecessary to assume a specific value for the dielectric constant prior. Due to the high field measurements, two of the three limitations that were included in the earlier magneto-absorption investigations are no longer valid.
Fig. 1(e) and (f) shows the field-dependent 1s and 2s excitonic states along with Landau energy states that are concurrently plotted on the fan chart layout. The reduced mass is unaffected by free carrier transitions, leaving the exciton binding energy as the sole parameter in the simulated hydrogen model. This enables the accurate and consistent measurement of the exciton binding energy, bandgap, reduced exciton mass, and effective dielectric while keeping carriers' effective mass constant.
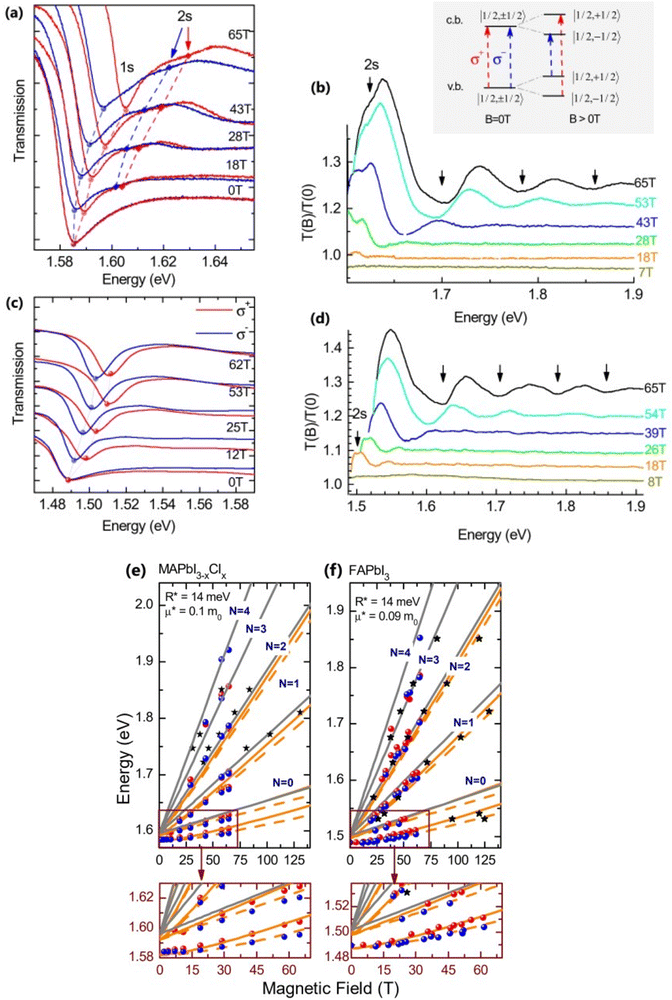 |
| | Fig. 1 (a)–(d) Transmission data at low temperatures for MAPb3−xClx and FAPbI3 respectively. The red and blue lines in panels (a) and (c) show σ+ and σ− polarized light, respectively. The inset displays the selection criteria for each of the two polarizations. The data collected at various magnetic field strengths are represented by different colors in panels (b) and (d). (e) and (f) The transition energies for MAPbI3−xClx and FAPbI3 respectively derived from the experimental data and the results of the fit. The orange and gray lines indicate the fitting data of theoretical results. The interband transitions between Landau states are shown by grey lines. The strongly bound levels of the hydrogen-like exciton are depicted by the orange lines. The solid and dashed lines in (e) and (f) indicate the Zeeman split transitions. Here R* denotes exciton binding energy. The low field and low energy portion of the whole fan chart diagram is magnified below each graph. Reprinted with permission,88 Copyright 2019, Royal Society of Chemistry. | |
Using the high field magneto-absorption, Galkowski et al.88 estimated Exb of 14 meV and 16 meV at 2 K and μ of 0.09 and 0.104 for FAPbI3 and MAPbI3 respectively. Similarly, at 161 K, they also found Exb of 10 meV and 12 meV for FAPbI3 and MAPbI3 respectively. In this scenario, the 1s–2s splitting (Δ1–2) in the hydrogen model can be deployed to directly determine Exb. Although thin films have a lower Exb, their transition strength is significantly higher compared to that observed in single crystals. Remarkably, the effective mass and Exb derived from magneto-optical thin film experiments differ from those obtained from single crystals. This finding shows that some features of the excitonic behavior are not fully interpreted from the data of high-field magneto-optical experiments. Notably, the shift in band dispersion to non-parabolic cannot account for the observed decrease in reduced mass at elevated fields. The magneto-optical studies still describe accurately the excitonic transitions and upper bound exciton binding energy. However, they fail to explain band-to-band excitonic absorption at room or higher temperatures. Meanwhile, the decrease in Exb observed in magneto-optical studies at temperatures slightly above the phase transition, along with data from electroabsorption57,150 and other absorption studies,83,161 strongly supports the hypothesis that Exb is reduced at RT by a few meV.
2.2 Absorption studies
The absorption methods are probably the most classical approach for estimating Exb in semiconductors having direct bandgap. For high quality samples, the measurement of the energy gap between the Wannier type excitonic energy levels, which can be seen individually as peaks in the absorption spectrum at the band edge, can be described through Elliott's equation.162| |
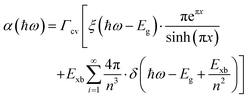 | (9) |
where the frequency dependent Γcv represents the proportionality constant that considers the intraband electric dipole transition matrix element. ξ is the Heaviside step function, δ represents the delta function, and 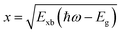 . In this model the first part represents a comprehensive intrinsic absorption continuum state in the presence of Coulomb interactions. Within this framework, the photon-to-exciton conversion rate completely determines the energy dissipation rate from the photon field, thereby establishing a direct link between the two processes.162,163 Such correlation will increase the absorption relative to vanishing excitonic effects which is often referred to as Sommerfeld amplification. The latter term describes the series of optically allowed excitonic transitions near the bandedge with discrete energy levels as in the hydrogen atom. Fig. 2(a) shows a typical absorption spectrum near the bandedge produced by arbitrary line broadening and changing the constants in eqn (9). The first three exciton peaks (designated as 1S, 2S, and 3S) in this hypothetical scenario are resolved below the continuum state. However, with increasing n the amplitude of the excitonic peaks diminishes, and the spectra across a small energy range approach a constant thereby merging into the continuum at the bandedge. The density of states close to the bandgap would vanish when no excitonic effects are considered [red curve, Fig. 2(a)].
. In this model the first part represents a comprehensive intrinsic absorption continuum state in the presence of Coulomb interactions. Within this framework, the photon-to-exciton conversion rate completely determines the energy dissipation rate from the photon field, thereby establishing a direct link between the two processes.162,163 Such correlation will increase the absorption relative to vanishing excitonic effects which is often referred to as Sommerfeld amplification. The latter term describes the series of optically allowed excitonic transitions near the bandedge with discrete energy levels as in the hydrogen atom. Fig. 2(a) shows a typical absorption spectrum near the bandedge produced by arbitrary line broadening and changing the constants in eqn (9). The first three exciton peaks (designated as 1S, 2S, and 3S) in this hypothetical scenario are resolved below the continuum state. However, with increasing n the amplitude of the excitonic peaks diminishes, and the spectra across a small energy range approach a constant thereby merging into the continuum at the bandedge. The density of states close to the bandgap would vanish when no excitonic effects are considered [red curve, Fig. 2(a)].
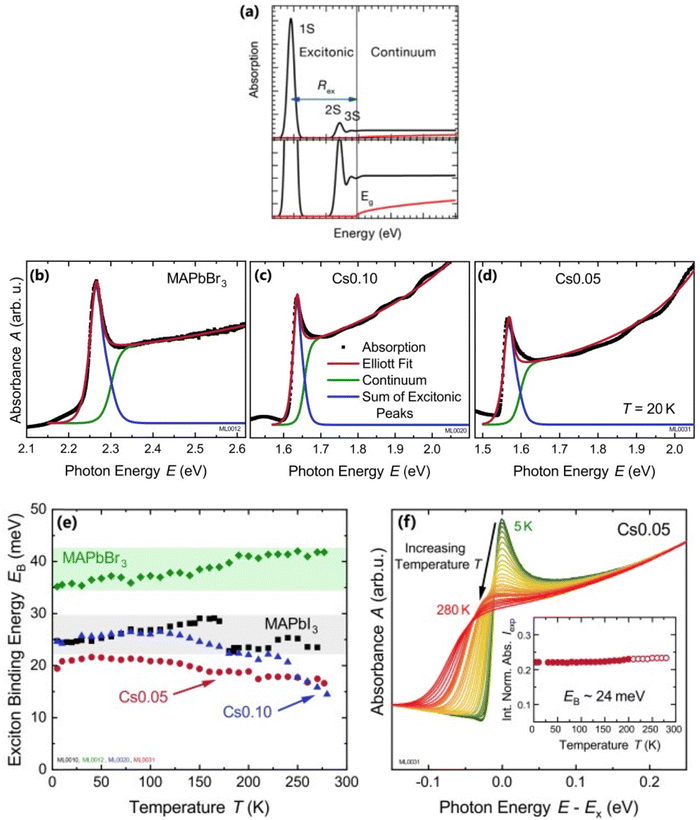 |
| | Fig. 2 (a) An example of bandedge absorption spectrum based on eqn (9). The lowest first, second, and third exciton states are approximated with arbitrary broadening which saturates into the continuum near the bandedge. The exciton binding energy is the difference in energy between the free carrier absorption edge and the first exciton peak. The red curve represents the absorption spectrum of free carriers while neglecting the excitonic effects. A magnified image is shown below the main graph. Reprinted with permission,164 Copyright 2018, American Chemical Society. (b)–(d) Absorption spectra at 20 K as a function of photon energy for MAPbBr3, Cs0.01FA0.765MA0.135Pb(I0.765Br0.235)3 (depicted as Cs0.10), and Cs0.05(FA0.83MA0.17)0.95Pb(I0.83Br0.17)3 (depicted as Cs0.05) respectively. The red line represents Elliot's fit while the green and blue lines correspond to excitons and continuum contribution. (e) Estimation of exciton binding energy Exb for MAPbI3, MAPbBr3, Cs0.01, and Cs0.05 according to the absorption spectra of (b, c, d). (f) Normalized spectra for Cs0.05 from 5 K to 280 K with respect to energy shift by excitonic peak Ex whereas the inset represents the integrated normalized spectra Iexp. Adapted from ref. 97, Copyright 2019, American Institute of Physics. | |
For example, Ruf et al.97 obtained Elliott fitted spectra (red curve) comprised of continuum states (green curve) due to free carrier resonances and discrete excitonic peaks (blue curve) at 20 K for MAPbBr3 and Cs-containing mixed perovskites Cs0.10[(FAMA)Pb(IBr)3] (designated as Cs0.10) and Cs0.05[FAMAPb(IBr)3] (designated as Cs0.05) as depicted in Fig. 2(b)–(d) respectively. These spectra clearly illustrate that Elliott fitting purely relies on the relevant bandgap energy Eg and exciton binding energy Exb as outlined in the summary provided in Fig. 2(f). Since the excitonic peak energy is lower than Eg by the magnitude of Exb, a thorough understanding of Exb is crucial for accurate measuring Eg as excitonic effects play a vital role in analyzing absorption spectra at RT. With increasing temperature, the discrete excitonic feature is difficult to distinguish due to the significant increase in excitonic absorption broadening as shown in Fig. 2(e) for Cs0.05. In such circumstances, Exb cannot reliably be measured. Logically, this is true for Eg, although it is considerably less significant as Eg ≫ Exb. The inverse correlation between excitonic absorption broadening and Exb affects the prominent position of the excitonic peak in the spectrum which can become more challenging for compounds with lower Exb. Consequently, the absorption spectra are usually unclear with some parameters that approximate transition broadening to evaluate Exb through the Elliott formula.83,161,165 The band nonparabolic behavior is also frequently taken into consideration to match the results with the experimental data.97,147 However, with a high uncertainty in the extracted Exb, such observations lead to doubtful results due to the involvement of a large number of fitting parameters. The same scenario can be noticed from large variations in the measured value of Exb using this method for OILHPs (Table 1). Furthermore, there is disagreement about the temperature dependence of Exb. Some studies show a constant Exb79,97,165 in the temperature range 10–300 K, whereas others report strong evidence of temperature-dependent Exb.83,166 These conflicting findings raise serious concerns about the scientific reliability of the Exb derived from the Elliott theory. For example, Saba et al. extracted an identical Exb of 25 meV for two different temperatures 300 and 170 K, by using the absorption onsets for MAPbI3.79 Kumar et al. obtained an Exb of 41 meV for MAPbI3 at RT.82 According to Even et al., the Exb of MAPbI3 increases sharply to 15 meV in the low temperature 0–160 K range (orthorhombic phase) but remains relatively constant at 5 meV in the high temperature 160–330 K range (tetragonal phase).166 Yamada et al. showed that when the temperature drops from 300 to 13 K, Exb gradually increases from 6 meV up to 30 meV.83 In an attempt to eliminate the temperature dependence issue, Sestu et al. applied an alternative method called the f-sum rule, which normalizes the variation in integrated absorption due to temperature to a certain energy. This enables for the explicit determination of the independent influence of linewidth broadening and Exb on the shape of the absorption line.165 Using this method, the authors deduced an Exb of 29 meV for MAPbBr3 which is nearly independent of temperature across the range of 80–300 K. However, for MAPbI3 an Exb of 34 meV in the low temperature range (80–140 K) and 29 meV in the high temperature range (170–300 K) was obtained.
Alternatively, Exb can be deduced by analyzing the full width at half maximum (FWHM) of the temperature-dependent excitonic absorption.148 The broadening of the excitonic transition can be described as
| |
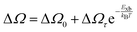 | (10) |
where Δ
Ω0 denotes the broadening parameter independent of temperature and the term Δ
Ωτ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
exp(−
Exb/
kBT) represents the thermally dissociated exciton broadening. Using this approach for MAPbI
3−xCl
x,
Exb was found to be 55 ± 10 meV. Due to the band-to-band absorption and the overlap of excitons, accurate experimental determination of the FWHM might pose challenges.
2.3 Temperature-dependent photoluminescence studies
Temperature-dependent photoluminescence (PL) is another technique that experimentally determines Exb which is based on fitting of integrated PL intensity I(T) as a function of temperature using the Arrhenius formula,| |
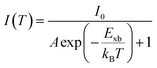 | (11) |
In general, the PL intensity diminishes with increasing temperature, which is associated with thermally induced exciton dissociation, and the process is usually known as PL quenching.75 Fig. 3(a) and (b) demonstrate an example of extracting Exb from the temperature-dependent PL spectra analysis.137 However, using this method a large variation in the values of Exb was observed. For instance, Exb = 10 meV (RT)110 and 162 meV (250–300 K)58 for MAPbI3, 42 meV (5–300 K)111 and 320 meV (240–360 K)112 for MAPbBr3, 8.1 meV (150–295 K)123 and 91 meV (80–390 K)131 for FAPbI3, and 22 meV (10–300 K)114 and 170 meV (180–360 K)133 for FAPbBr3. Significantly, these values are much larger than those reported in absorption studies. It is perhaps insufficient to attribute thermal quenching solely to thermally induced exciton dissociation. Furthermore, the origin of large deviations in Exb evaluated by this technique may be partially attributed to shallow trap states and the complex time dependence of the radiative recombination rate in OILHP.46,167,168
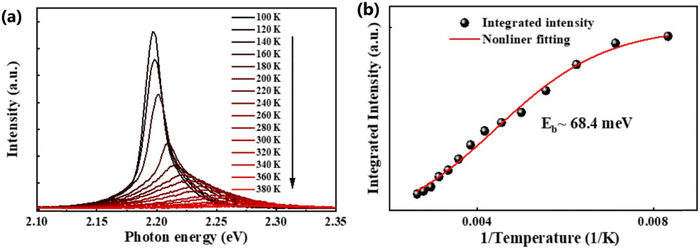 |
| | Fig. 3 (a) Temperature-dependent PL spectra of the FAPbBr3 NCs from 100 K to 380 K. (b) The integrated PL intensity with respect to temperature; the red line corresponds to nonlinear fitting. Adapted from ref. 137, Copyright 2019, American Chemical Society. | |
2.4 Theoretical methods
Different theoretical techniques have been implemented to extract the exciton binding energy for OILHPs. Such approaches that are based on density functional theory (DFT) and the hydrogenic model have nevertheless yielded much higher values for Exb as compared to experiments (Table 1). Some of the commonly used techniques are described in the following.
2.4.1 Many body perturbation theory method. The many body perturbation theory (MBPT)169 method derived from first principles is a useful tool to accurately describe the quasiparticle excitations and excitonic features in materials. It is based on electronic self-energy, which incorporates many-body exchange and correlation effects in addition to the Hartree potential. Such a framework allows for consideration of quasiparticles, which behave like single particles due to the coulombic screening. Adopting the MBPT approach, the exciton binding energies are estimated using the GW-BSE (Green's function and Bethe–Salpeter equation) method, which considers electron–hole (e–h) and electron–electron (e–e) interactions beyond the ground state of DFT. Fig. 4 depicts the schematic performances of DFT, GW, and GW-BSE approaches for bandgap energy Eg calculations. The GW approach enhances DFT-bandgap, whereas GW-BSE accounts for excitonic effects in optical spectra, allowing the optical bandgap and thus exciton binding energy to be determined. The screening and excitonic properties can be determined by solving BSE incorporating the quasi-particle energies (EQP) from GW calculations as described by ref. 170–173| |
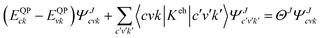 | (12) |
where ΨJcvk is the Jth order exciton wave function, Keh is the interacting e–h kernel and ΘJ corresponds to excitation energies of the Jth state. The subscripts c, v, and k represent indices for conduction bands, valence bands, and k-points. Since the GW-BSE approach involves a large number of basis sets, achieving well-converged optical spectra and exciton binding energies at higher k-mesh values is challenging due to the high computational cost. Therefore, an alternative approach termed model BSE (mBSE) suggested by Liu et al.174 can be adopted in which the GW based dielectric function is approximated within the diagonal matrix using an analytical model dielectric function for the diagonal elements.| | |
ε−1(|W|) = 1 − (1 − ε∞−1)exp(−|W|2/4xr2)
| (13) |
where ε∞, xr, and |W| are the ion-clamped or high-frequency dielectric constant, range-separation parameter, and plane-wave vector, respectively. Such method directly interprets the optical spectra and exciton binding energies for OILHPs from first-principles. Using the GW and mBSE approach, Bokdam et al.86 calculated the exciton binding energy as the difference of fundamental bandgap Eg and optical bandgap Eopt for various organic–inorganic metal halide perovskites with lattice vibrations fixed. The calculated Exb ranges from 29 meV to 257 meV with an increasing GW bandgap following the halogen's ionic size reduction from I → Br → Cl as shown in Fig. 4(b). However, they elaborated that ionic screening that influences the exciton binding energy is almost temperature independent but causes a substantial increase in static dielectric constant ε0 using the density functional perturbation theory (DFPT)175–177 method compared to molecular dynamics (MD) calculations as shown in Fig. 4(c). They further stated that the formation of polarons (as discussed in Section 4) is responsible for lowering the fundamental bandgap in halide perovskites at RT upon optical excitation. Similarly, Muhammad et al.155 measured Exb for various compositions of the FAPb(I1−xBrx)3 alloy. They showed that Exb increases (from 74 meV to 112 meV) with increasing Br content, which also follows the increasing trend in bandgap energy. From their GW-BSE based optical analysis, they found that the calculated excitonic spectra align well with the experimental data and an overall blue shift is observed with increasing Br concentration as shown in Fig. 4(d). Such optical behavior as well as the increase in exciton binding energy was attributed to a decrease in transition oscillator strengths near the first peak of the corresponding spectra and a decrease in high frequency dielectric constant ε∞. In another study, the same authors also evaluated Exb for temperature-dependent different phases of FAPbI3.129 They showed that Exb is much higher in the low-temperature hexagonal phase (567 meV) as compared to the high-temperature cubic (74 meV) and tetragonal (93 meV) phases of FAPbI3. These findings suggest a clear relationship between the dynamics of the PbI3 sublattice and the rotational entropy of the FA molecule that is closely correlated with variations in Exb. The GW and mBSE methods can generate excitonic optical spectra and converged values for Exb; however, they require heavier k-meshing, resulting in significant computational cost.
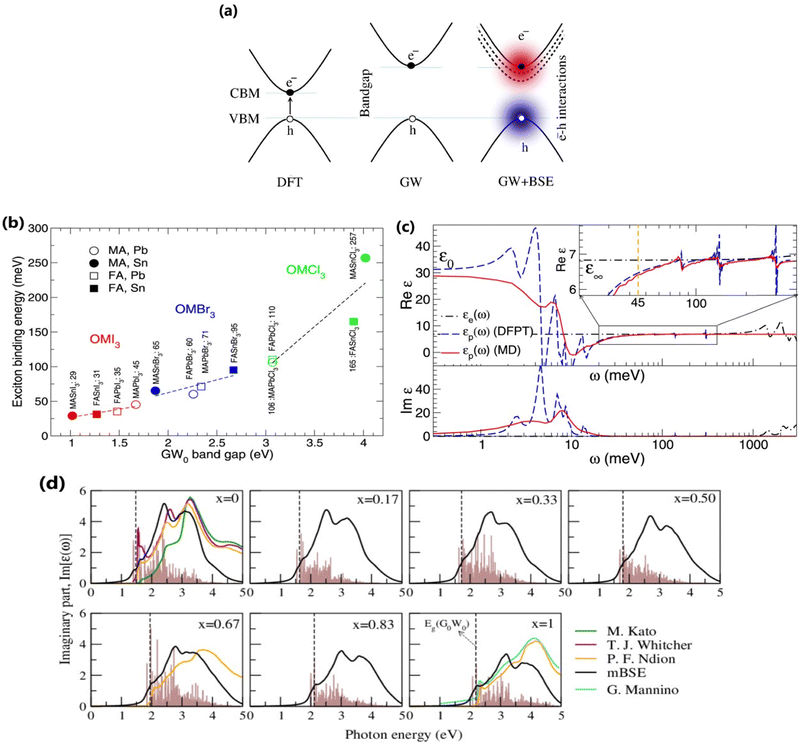 |
| | Fig. 4 (a) Schematic representations of DFT, GW, and GW+BSE approaches for bandgap Eg calculations. (b) Electronic [εe(ω)] and ionic [εp(ω)] contribution to the dielectric function of MAPbI3. The dashed blue and solid red lines correspond to the data collected from the MD (T = 300 K) and DFPT (T = 0 K) methods respectively. The inset shows an enlarged image of Re[εp(ω)] near Exb = 45 meV. (c) Calculated Exb with respect to GW bandgaps for various OILHPs using the DFT based mBSE method. Adapted from ref. 86, Copyright 2016, Springer Nature. (d) Calculated excitonic imaginary part of the dielectric function for the FAPb(I1−xBrx)3 alloy along with comparison to different experimental data.151,178–180 The dashed line indicates the corresponding GW bandgap. The brown histogram represents the calculated optical transition oscillator strengths. Reprinted with permission,155 Copyright 2020, Springer Royal Society of Chemistry. | |
To deal with the experimental overestimation in Exb, Umari et al.95 introduced the frequency dependent effective dielectric constant εeff−1 in which the dielectric function ε(ω) includes phonon induced screening that can be formulated as
| |
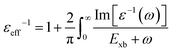 | (14) |
where Im[
ε−1(
ω)] represents the usual energy loss function which can be obtained within the framework of DFPT. Now clearly
εeff is
Exb dependent; therefore the function
εeff(
Exb) can be defined effectively by using
eqn (14), which accounts for frequency integration. Replacing
ε∞−1 by
εeff−1 in
eqn (13), the condition for self-consistent fully relativistic BSE based
Exb can be described as
| |
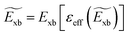 | (15) |
Using this approximation with
εeff = 12 (
εeff = 9.5), an
Exb of 15 meV (19 meV) is obtained for MAPbI
3 derived from SOC-DFT (scalar relativistic DFT) calculations. The authors also inferred that exciton screening is not caused by the rotational dynamics or by its steric effects. Such screening strongly depends on the vibrational response of the lattice induced by phonons.
Although the MBPT approach may provide enough information about excitonic effects in OILHPs, it will be more interesting when applied to layer type morphologies including exciton–phonon coupling. Hopefully, such simulations will further elaborate the excitonic features with advanced computational methods and machine learning techniques.
2.4.2 Time-dependent density functional theory (TD-DFT) method. Time-dependent density functional theory (TD-DFT)181–183 is an extended version of DFT. It is specifically designed to describe the excited state properties of materials derived from the frequency dependent linear response function which is helpful in extracting optical spectra and exciton binding energies.184–186 Based on TD-DFT calculations, Hakamata et al. calculated Exb between the photogenerated electron and hole in a 3D cubic 2 × 2 × 2 supercell of MAPbI3. By comparing the electronic excitation energy with the energy difference between the dominant electron and hole states, they found that these values were nearly identical, indicating very weak values for Exb as depicted in Fig. 5(a). The time-averaged Exb was estimated to be 12 ± 9 meV, suggesting that such weakly bound excitons can easily dissociate by thermal energy at RT, leading to freely moving electrons and holes. Fig. 5(b) shows the time evolution of Kohn–Sham eigen energies in non-adiabatic quantum molecular dynamics simulation, with the red and blue curves representing KS energy levels that mainly influence the quasi-electron and quasi-hole, respectively. Here a large number of electronic level crossings can be observed due to atomic thermal motion, which results in frequent electronic transitions that occur between excited electron and hole states. This ab initio study supports the experimental observations and highlights the presence of charge carriers rather than strongly bound excitons in MAPbI3.187,188
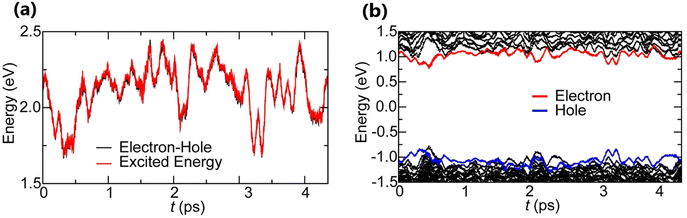 |
| | Fig. 5 (a) Time evolution of the many-body electronic excitation energy, including excitonic binding (red), in a 2 × 2 × 2 supercell nonadiabatic quantum molecular dynamics (NAQMD) simulation, along with compared energy difference between the electron and hole (black). (b) Time evolution of KS eigen energies, with the KS states that mostly contribute to the quasi-electron and quasi-hole shown in red and blue, respectively. Adapted from ref. 85, Copyright 2016, Springer Nature. | |
Similarly, Ganesh et al. determined an Exb of 1790 meV for the MAPbI3 cubic structure, which is way too high compared to other theoretical and experimental data. Such a large value can be attributed to using the CAM-B3LYP functional with the LanL2DZ basis set189 rather than the traditional Perdew–Burke–Ernzerhof (PBE) method involving the plane-wave basis set.190–192 Gao et al.106 evaluated Exb of 4.88 meV, 5.43 meV, 4.95 meV, and 5.29 meV for 3D MAPI3, MAPbBr3, FAPbI3, and FAPbBr3 respectively. Since Exb defines the amount of separation between electrons and holes, the coulombic interaction between electrons and holes can be calculated as
| |
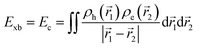 | (16) |
where
ρh and
ρe are hole and electron densities with their coordinates
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1
1 and
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2
2 respectively. Using the inter-fragment charge transfer method (IFCT),
193,194 the number of electrons transferred can be calculated from the ground state to the first singlet state between each species of perovskites. However,
eqn (16) neglects the kinetic energy term associated with electron–hole confinement that highly affects the dielectric behavior.
In addition to bulk OILHPs, Athanasios et al. using the simplified TD-DFT method studied the excitonic optical properties of quantum dot (QD) nanostructures. They modeled cuboid QD structures of MAPbI3 and MAPbBr3 each having the size of approximately 1.0–1.5 nm, revealing Exb of 540 meV and 610 meV. These values were significantly larger in the QD regime compared to their bulk counterparts, showcasing the quantum confinement effect. However, these calculations did not account for temperature variations and optical phonon modes which could influence Exb, exciton dynamics and photocarrier lifetimes.
3. Exciton generation, dynamics and recombination
Some researchers also revealed the generation of photoinduced free charge carriers in OILHPs.187,188,195 The tera-hertz (THz) spectroscopy technique is used to investigate the photoinduced carrier dynamics and its interactions with phonons, which directly affect the exciton population in OILHPs.196–198 When examining the kinetics of photoinduced charge carriers, Cooke and coworkers,59 through the analysis of frequency-dependent THz complex conductivity, found that excitons in the form of free charge carriers vanish in perovskite single crystals within 1 ps. This results in a short-lived intra-excitonic transition accompanied by an Exb of 17 meV at RT under high pump fluence. Therefore, in comparison to the recombination process and charge transport, the generation rate of carriers in perovskites is substantially higher. A similar study by Douhal et al.60 found that, a large number of excitons will instantly dissociate into free carriers for the FAPbI3 film. Major findings from their THz analysis revealed that most of the mobile charge carrier population was formed within ∼1 ps comparable to the resolution in the THz spectroscopy setup. Jha et al.61 used ultrafast 2D electronic spectroscopy to provide a more direct observation of ultrafast exciton dissociation. The authors demonstrated that excitons spontaneously turn into free carriers in less than 50 fs for the MAPbI3 thin film, which was one of the key reasons for the high efficiency of perovskite photovoltaics.
The correlation between free charge carriers and exciton population after photoinduction under certain equilibrium conditions was also studied.148,199,200 The coexistence of mobile charge carriers and exciton population at equilibrium can be described by the Saha–Langmuir expression (also known as mass law for excitons and free charges).201 According to this model, the branching ratio ϕ of the exciton population to free charge carriers can be formulated as
| |
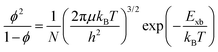 | (17) |
where
N represents the total number of excitons and free charge carriers. D'Innocenzo
et al. applied this relationship for the first time in perovskites to investigate the equilibrium branching ratio between excitons and free carriers.
148 Using the Saha–Langmuir model Geng
et al.202 estimated the
Exb of the FAPbBr
3 thin film for various excitation densities at RT [
Fig. 6(a)]. For higher values of
Exb, the dissociation of excitons into free carriers becomes less efficient in perovskites which strongly agrees with the simulations. Furthermore, in the low excitation regions, the fraction of free carriers falls rapidly with increasing exciton population. The exciton to free carrier transition becomes more prevalent for higher excitation regions due to the presence of excited carriers that instantly screen the electrostatic interaction between e–h pairs. Using the data from
Fig. 6(a), it is possible to calculate exciton and free carrier densities as a function of fluence [
Fig. 6(b)]. According to the Saha-Langmuir relation, the ratio of free charge carriers to excitons increases with temperature; however, it decreases due to the free e–h capture events that are more likely to occur at higher excitation densities.
148
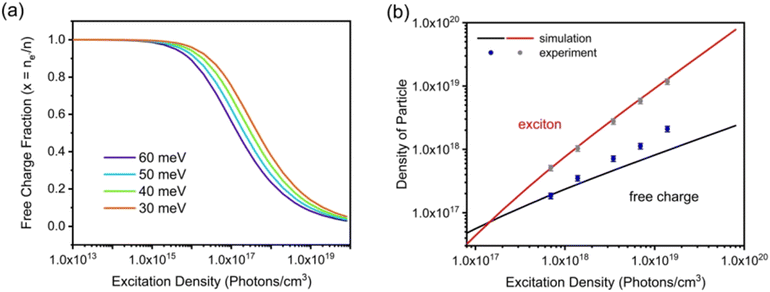 |
| | Fig. 6 (a) Modeling of photoexcited free charge carriers in the FAPbBr3 film using different excitation densities according to the Saha–Langmuir equation. Exb = 60, 50, 40, and 30 meV were used with a reduced mass of exciton μ = 0.15m0. (b) Simulation data were obtained by multiplying the fractions of free charge carriers by the excitation density, and experimental data for free charge carrier and exciton densities were obtained from PLmax. Reprinted with permission,202 Copyright 2023, Springer Royal Society of Chemistry. | |
At certain excitation density (known as critical excitation) at which excitons are completely transformed into free carriers, the Saha–Langmuir relation becomes less relevant. Therefore, the recombination mechanism and excitonic transport are significantly important to evaluate the exciton binding energy. For such a situation, Ulatowski et al.110 investigated charge carrier transport and recombination in various temperature-dependent compositions for OILHPs using a combination of microwave conductivity (at high-frequency) and PL measurements as shown in Fig. 7(a). To simulate the photogenerated conductivity and transient luminescence, a set of rate equations was was used to describe the transport properties of photoinduced charge carriers. Many other authors have also used this method to reveal the behavior of trapping and recombination processes in OILHPs, as shown schematically in Fig. 7(b).167,203–206
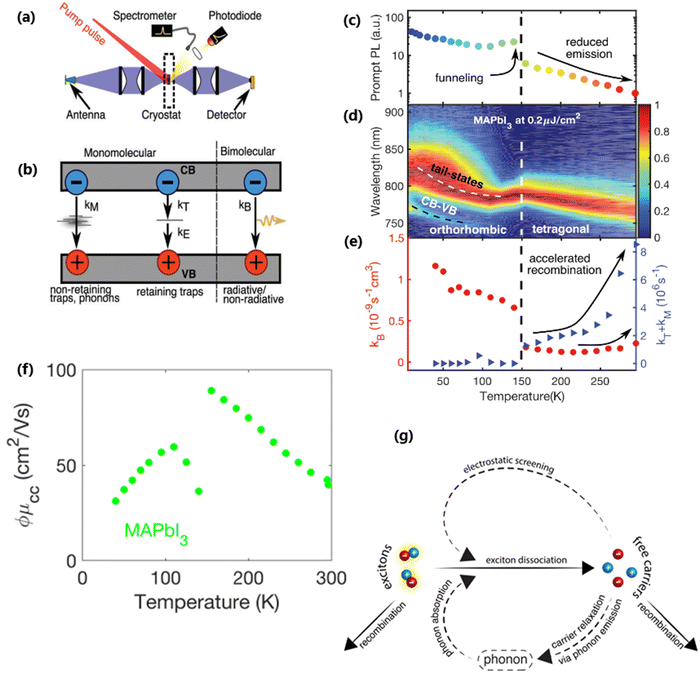 |
| | Fig. 7 (a) A schematic experimental setup to obtain data for TRPL and PL spectra. The microwave radiation is launched through the feed horn antenna. The data for PL measurements are obtained through a spectrometer and photodiode. Microwave radiation is detected using a Schottky diode. (b) A simplified model illustrating the mechanism of charge carrier recombination in OILHPs that defines the pathways for both single molecular and bimolecular recombination and distinguishes between charge non-retaining (phonons) and retaining traps. kM, kT and kE represent single molecular, trap-mediated, and carrier mediated recombination rate constants respectively. (c) Prompt PL intensity, (d) emission spectrum, and (e) rates of dynamic decay as a function of temperature, with the dashed line at 150 K representing the phase transition for the MAPbI3 thin film. (f) Temperature-dependent effective charge carrier mobility for the MAPbI3 thin film. Adapted from ref. 110, Copyright 2023, John Wiley & Sons, Inc. (g) Schematic representation of exciton dissociation via free carriers, Coulomb screening, and phonons ensuring an enhanced lifetime of free-carrier population. Reprinted with permission,196 Copyright 2019, American Chemical Society. | |
To study the recombination mechanism, the time evolution of conduction band electron density (n) and trapped electron density (nT) in a photoinduced pure semiconductor can be described by the following pair of differential equations:
| |
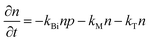 | (18a) |
| |
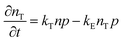 | (18b) |
where
kBi,
kM,
kT, and
kE are the band-to-band bimolecular, single molecular, trap-mediated, and carrier mediated recombination rate constants respectively.
p is the free hole density in the valence band which is the sum of
n and
nT. In terms of temperature dependence, the overall patterns of the prompt PL and bimolecular recombination rate for MAPbI
3 are shown in
Fig. 7(c)–(e) after ref.
110. The bimolecular band-to-band recombination increases for the MAPbI
3 thin film as the temperature decreases, showing a narrowing of the thermal distributions of electrons and holes in the valence and conduction bands. The structural phase transition in MAPbI
3 instantly affects the behavior of photoinduced charge carriers. At lower temperatures, a funneling of charge carriers will enhance the radiative recombination due to the rise in local charge carrier density. This will rapidly increase both the prompt photoluminescence and the bimolecular recombination rate constant as the temperature is reduced below 150 K [
Fig. 7(c)]. At extremely low excitation density and low temperatures, most of the emission takes place at the bandedge due to charge carrier recombination, which was previously believed to be a direct transition from the conduction band to the valence band.
168,207 As obvious in time-integrated PL spectra [
Fig. 7(d)], traps with a wide energetic distribution appeared just below the band states. High energy recombination between the conduction band and the valence band dominates the emission spectra at high excitation densities, causing the band tail states to become saturated. With the increase in temperature, the bimolecular recombination rate constant between the bands slightly increases [
Fig. 7(e)]. This increase is accompanied by a much notable increase in the total single molecular trap-mediated recombination constant. This indicates the presence of non-radiative trap-assisted Auger recombination. Moreover, for the low fluence, long wavelength, sub-bandgap emission dominates the spectra below 150 K. The reduced charge carrier mobility in the lower temperature range as shown in
Fig. 7(f) indicates that charge carriers localize in energetic traps just below the bandedge which reduces the total charge carrier conductivity of the photoexcited material. At this stage, the exciton generation becomes more prominent as the branching ratio
ϕ of photon-to-free-carrier decreases thus reducing the overall charge carrier mobility
ϕμcc. However, for high excitation fluence, the higher energy band-to-band transition becomes the main radiative recombination pathway which produces narrow emission linewidths due to the suppression of electron–phonon coupling.
In the context of exciton–phonon correlation, Fig. 7(g) illustrates the interacting excitons, free carriers, and phonons. Upon photoexcitation, excitons and free carriers are generated, gaining enough kinetic energy to produce a large number of hot phonons as the carriers cool down. The reabsorption of these hot phonons causes excitons to split up into free charge carriers. Meanwhile, the photoinduced free charge carriers enhance the Coulomb screening, thereby reducing the exciton binding energy which results in even more generation of free charge carriers by exciton dissociation. Such regeneration of free charge carriers due to exciton–phonon interaction and enhanced Coulomb screening are responsible for an extended lifetime of the free charge carrier population in OILHPs.
4. Interplay of polarons
The inclusion of polaronic effects in exciton binding energy measurements is presently an area of active development. Polarons are quasiparticles coupled with the polarization field of the local lattice due to the electron–phonon Coulomb interaction. Such electron–phonon interaction is usually found in polar and ionic semiconductors resulting from the coupling of electronic and longitudinal optical phonon modes. The strength of electron–phonon interaction is higher for systems with larger ionicity. In a perovskite lattice, an injected charge carrier can cause structural distortion of the soft nature of the metal-halide sublattice and reorientation of the polar organic cations to minimize the local lattice's Gibbs free energy. This results in the formation of a spatially extended polarized charge distribution that follows the carrier as it propagates. Depending on the spatial size of the polarized charge distribution, polarons are characterized as small or large polarons. The formation of large polarons results from the long-range electrostatic interactions of the ionic lattice with the free carrier, whereas small polarons are associated with modifications in local bonding. Small polarons are approximately close to one single lattice constant, whereas large polarons are close to numerous unit cells.208 The phenomena of exciton self-trapping and the resulting low carrier mobility are typically linked to electron–phonon Coulomb interactions that are considered to be primary components governing the carrier transport nature.62 Moreover, the large polaron formation in the OILHP layer yields higher dielectric constants and screens e–h Coulomb interactions leading to a low recombination rate.71 Such polaron generation also reduces exciton binding energy and enhances the lifetime and effective masses of the carriers.63,64 Owing to the formation of large polarons in OILHPs, many attempts have already been made to address some of the unclear optically excited carrier dynamics in these materials. For instance, the discrepancy between long diffusion lengths and relatively moderate carrier mobility can somehow be explained based on large polaron formation despite having small carrier effective mass.209–211 In the context of exciton binding energy measurement, polaronic effects play a significant role while analyzing the exciton spectrum.158
Since in polar systems the majority of carrier interactions take place in the direction of the polarizing field of electrons, the longitudinal optical (LO) phonons produced strongly contribute to the bandedge states than the transverse optical (TO) phonons.212 The strength of such interactions can be described by a dimensionless quantity known as the Fröhlich coupling constant α213 given by
| |
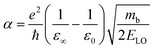 | (19) |
Here
e is the elementary charge,
ħ is the reduced Plank's constant,
mb is the bare effective mass of the electron or hole, and
ELO is the LO phonon energy. The terms
ε∞ and
ε0 are the high-frequency dielectric and static dielectric constants respectively and their difference describes ionic screening parameter 1/
ε*. In fact, the different values for
ε∞ and
ε0 indicate the electric polarization due to the electron–phonon and optical phonon interactions. In polar semiconductors, the large difference between
ε∞ and
ε0 provides clear evidence for large polaron formation in perovskites, thus renormalizing the carrier effective mass and bandgap energy along with nonhydrogenic exciton states. In a weak coupling regime, the polaron effective mass
mp (in units of
m0) and radius
lp can be approximated as
| |
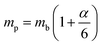 | (20) |
| |
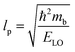 | (21) |
The results obtained for the above polaron parameters using various experimental and theoretical techniques are summarized in
Table 2. The polaronic effects increase the effective mass of the carriers, which results in a decrease in their mobility. According to Evan
214 the increased localizability of the heavy atom causes a more complete screening of its charge by the lattice, which increases the reduced mass. The parameters for polaron effective mass must be treated in terms of the kinetic energy of the Hamiltonian.
Table 2 Parameters for the polaron model using different techniques
| Material |
Sample morphology |
α |
mb ( 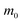
) |
mp ( 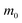
) |
ε0 |
ε∞ |
ELO (meV) |
Technique |
Ref. |
| Frequencies are converted to energy (meV). Cube root result. These values are extracted using eqn (20). Ref. 88. Ref. 215. Ref. 216. Ref. 159. |
| MAPbI3 |
3D cubic |
2.3 |
0.19 |
0.263c |
30 |
6 |
8 |
DFPT(T = 0 K)/MD(T = 300 K) method |
Bokdam et al.86 |
| Polycrystalline grains |
∼2.64–2.46 |
0.1 |
0.144–0.141 |
30 |
5.5 |
4.84–4.91a |
Time resolved THz spectroscopy |
Jin et al.217 |
| 3D cubic |
2.39 |
0.12 |
0.168 |
24.1 |
4.5 |
9.3a |
DFT + Feynman polaron model |
Frost211 |
| Thin films (266 nm) |
1.71 |
0.104d |
0.134c |
33.5 |
5.0 |
4.96a |
Far-infrared spectroscopy |
Sendner et al.209 |
| 3D orthorhombic phase |
1.18 |
0.190 |
0.228 |
22.54e |
5.32f |
3.38b |
DFT + Pollmann–Büttner model |
Proupin et al.158 |
| 3D orthorhombic phase |
1.4 |
0.22 |
0.27 |
— |
— |
13 |
DFT+GW and multiphonon Fröhlich model |
Schlipf et al.218 |
| Thin film |
1.91 |
0.211 |
0.47 |
22.6 |
5.9 |
12.6 |
DFPT+GW calculations |
Poncé et al.219 |
| 3D cubic |
1.49 |
0.21 |
1.20 |
30.42 |
6.75 |
8.76a |
DFT and Fröhlich's mesoscopic model |
Basera et al.108 |
| — |
1.41 |
0.23g |
0.284c |
19.6g |
5g |
19.42 |
Elliott's band fluctuation (EBF) model |
Lizárraga et al.220 |
| Single crystal |
1.12 |
0.102 |
0.114 |
15 |
7 |
12 |
Magneto-optical spectroscopy and Bajaj exciton-polaron model |
Baranowski et al.221 |
| |
| MAPbBr3 |
Thin films (287 nm) |
1.69 |
0.117d |
1.35 |
32.3 |
4.7 |
6.32a |
Far-infrared spectroscopy |
Sendner et al.209 |
| — |
1.90 |
0.29 |
0.382c |
25.5 |
4.4 |
19.97 |
Elliott's band fluctuation (EBF) model |
Lizárraga et al.220 |
| 3D tetragonal |
1.54 |
0.13 |
0.16c |
21.36 |
4.4 |
4.10a |
Time-resolved optical Kerr effect (TR-OKE) spectroscopy and DFT |
Miyata et al.222 |
| Single crystal |
1.75 |
0.151 |
0.137 |
16 |
5.2 |
15 |
Magneto-optical spectroscopy and Bajaj exciton-polaron model |
Baranowski et al.221 |
| |
| FAPbI3 |
3D cubic |
1.37 |
0.195 |
1.19 |
37.91 |
7.02 |
9.94a |
DFT and Fröhlich's mesoscopic model |
Basera et al.108 |
| |
| FA0.85Cs0.15Pb(I0.97Br0.03)3 |
Thin film |
3.8 |
— |
0.2 |
— |
— |
14.3a |
Time-resolved terahertz spectroscopy and transient absorption spectroscopy |
Bao et al.64 |
4.1 Polaron–exciton models
Various models have been suggested in the literature to explain the role of polarons in exciton binding energy calculations.223–225 The effective Hamiltonian for a system of excitons interacting with the LO phonon can be expressed as| |
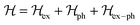 | (22) |
The first term includes kinetic energies of carriers and Coulomb interaction given by| |
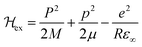 | (23) |
where P and M refer to momentum and mass of the center-of-mass system, while p and μ represent their relative quantities. R is the position coordinate. Similarly the Hamiltonian due to phonons can be described as| |
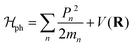 | (24) |
Here Pn and mn are the momentum and mass of the nth system. V(R) is the interacting potential as a function of position R. According to the Haken model223 the effective interacting potential due to electron–hole Coulomb interaction can be expressed as follows:| |
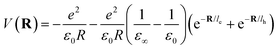 | (25) |
where le,h represents electron– and hole–polaron radii as defined according to eqn (21). This theory describes two polaron interactions, each of which has a radius substantially less than the effective radius of excitons. Later, Bajaj224 proposed a phenomenological modification to the Haken potential to address the overestimation of exciton binding energy in polar crystals:| |
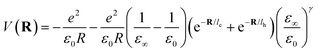 | (26) |
where 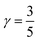 represents the optimal choice for polar crystals having large α values.224 Pollman and Büttner225 introduced the electron–polaron and hole–polaron correlations in the Haken potential and the resulting potential can be expressed as
represents the optimal choice for polar crystals having large α values.224 Pollman and Büttner225 introduced the electron–polaron and hole–polaron correlations in the Haken potential and the resulting potential can be expressed as| |
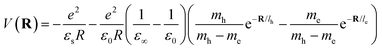 | (27) |
To approximate this potential, it was assumed that the polaron lengths were much smaller than the effective radius of the exciton. This effective radius can be used as an initial input parameter in the variational calculations. Similarly, the exciton–phonon Hamiltonian is given by| |
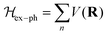 | (28) |
For a two-particle system, a path integral approach can be followed to study the effects arising due to exciton–phonon interaction. According to these approximations, Park et al.226 evaluated the exciton binding energy of MAPbI3 using static (50.4 meV), dynamic (36.9 meV), and non-local (38.1 meV) screening models. The smaller values of Exb under dynamic and non-local screenings indicate the polaronic effects and the results are consistent with the computed carrier lifetimes and trap-assisted bimolecular e–h recombination rates. Moreover, for a low temperature regime, an Exb of 20.8 meV is obtained for MAPbI3 showing good agreement with experiments.88,148
4.2 Polaron formation time
Polaron formation time in OILHPs is highly influenced by both the size of organic cations and vibrational modes of the PbX3 sublattice.222,227,228 Such factors affect the energetics of the relevant coupling between organic and inorganic lattices that can provide information about polaron photoexcitation in OILHPs.229–231 For example, for MAPbBr3 single crystals, Miyata et al.222 using the tight-binding (TB) model reported that the deformation of the PbBr3 sublattice is dominantly responsible for large polaron formation based on the computed small polaron formation time of 0.3 ps for MAPbBr3 in comparison to 0.7 ps for CsPbBr3. The dynamic disorders produced by fluctuations of cations and anions lead to a complex potential energy surface that screens the e–h pair into their corresponding polarons, resulting in a considerable reduction in charge carrier recombination as well as reduced carrier mobility.
A recent study conducted by Bao et al.64 showed strong evidence of polaron formation in FA0.85Cs0.15Pb(I0.97Br0.03)3 using the data from their transient absorption spectroscopy (TAS) and time-resolved terahertz spectroscopy (TRTS). The carrier effective mass was calculated with respect to pump–probe delay τ as shown in Fig. 8. After 1 ps, the value of m* rapidly increased after photoexcitation, indicating that the electron is strongly dressed by its surroundings, and m* reached a maximum at about 200 ps [Fig. 8(a)]. The persistence of m* for such a long time can be associated with polaron formation. Here the calculation of m* was tested using different fitting models to validate m* estimation [Fig. 8(b)]. However, using the same approach for MAPbI3, m* peaks were found at 20 ps.
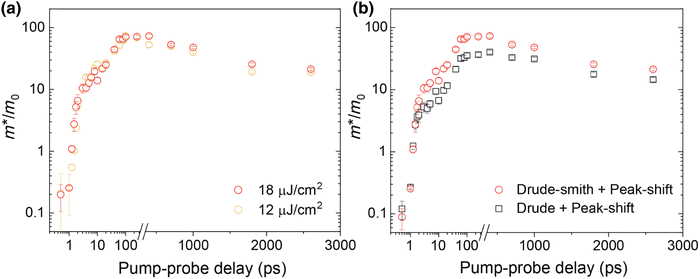 |
| | Fig. 8 (a) Effective mass of electrons as a function of pump–probe delay using the Drude-Smith + peak-shift formulation for various fluence intensities. (b) Comparison of the Drude-Smith + peak-shift and Drude + peak-shift formulation for calculation of the effective mass of electrons. Adapted from ref. 64, Copyright 2023, American Physical Society. | |
4.3 Polaronic effects from magneto-optical studies
The concept of polaronic effects successfully explains the discrepancies in the optical response, e.g., the rare observation of excited excitonic states, which deviate from the Wannier–Mott exciton model.115,232,233 It also unveils the considerable differences in the values of the carrier mass reported from magneto-optical studies conducted in high88,234 and low235 magnetic field regimes. Baranowski et al.221 employed magneto-optical spectroscopy combined with exciton–polaron modeling to probe carrier–phonon interactions. High-quality perovskite single crystals, including MAPbI3, MAPbBr3, and CsPbBr3, were investigated using ∼90 T pulsed magnetic fields. Spectral analysis revealed notable differences in excitonic transition behaviors and effective masses under varying magnetic field strengths. Fig. 9(a) presents the reflection spectrum of MAPbBr3 at 2 K (blue line) alongside its derivative (yellow line), where the minima indicate the energies of excitonic transitions. The optical response is predominantly characterized by a strong 1s excitonic transition at 2.249 eV. A weaker 2s exciton state follows this on the higher energy side at 2.262 eV. The 2s transition strength is significantly smaller than 1/8 of the 1s transition strength, suggesting the polaronic nature of the observed excitonic transition. The reduced effective mass was probed by analyzing the evolution of exciton and Landau level transitions under high magnetic fields. Fig. 9(b) shows the evolution of the reflection spectrum of MAPbBr3. The excitonic states exhibit Zeeman splitting at higher magnetic fields, and both excitonic transitions show a blue shift. The transitions between interband Landau levels are shown in Fig. 9(c) by dividing the spectra measured at nonzero magnetic fields by the spectrum obtained at zero magnetic field. Fig. 9(d)–(f) describes the evolution of the interband Landau level transitions, which are characterized by evenly spaced patterns in the high energy region of the spectrum. This behavior can be well described by the parabolic band dispersion relation:156| |
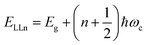 | (29) |
This formula provides direct measurement of the reduced mass of the carriers, yielding values of 0.096m0, 0.106m0, and 0.117m0 for MAPbI3, MAPbBr3, and CsPbBr3 respectively. Such findings reveal that the effective mass of charge carriers, as inferred from Landau level transitions at high fields, was consistently lower compared to the values derived from exciton spectroscopy at low fields, indicating a significant polaronic enhancement. For determining the reduced mass of the carriers in the low field, 1s and 2s excitonic transitions can be used which are detectable irrespective of the field strength. Fig. 9(g)–(i) represents the evolution in the magnetic field shown by diamond points. Observing 1s and 2s excitonic states simultaneously constrains the exciton binding energy, leaving just the reduced effective mass, μ, as a fitting parameter. The dashed red lines show that the Wannier–Mott model reasonably describes the shifts of the 1s and 2s states due to the applied magnetic field, as well as their energy separation. However, the data fitting requires significantly higher μ values than those obtained from Landau level observations at high magnetic fields. This shows that excitons act differently than those predicted by Landau level analysis, which depends on bare carrier mass. This finding strongly indicates polaronic mass enhancement in OILHPs. The use of bare carrier masses, as predicted by the Wannier–Mott-exciton model, fails to fit the data, as illustrated by the short-dashed red lines.
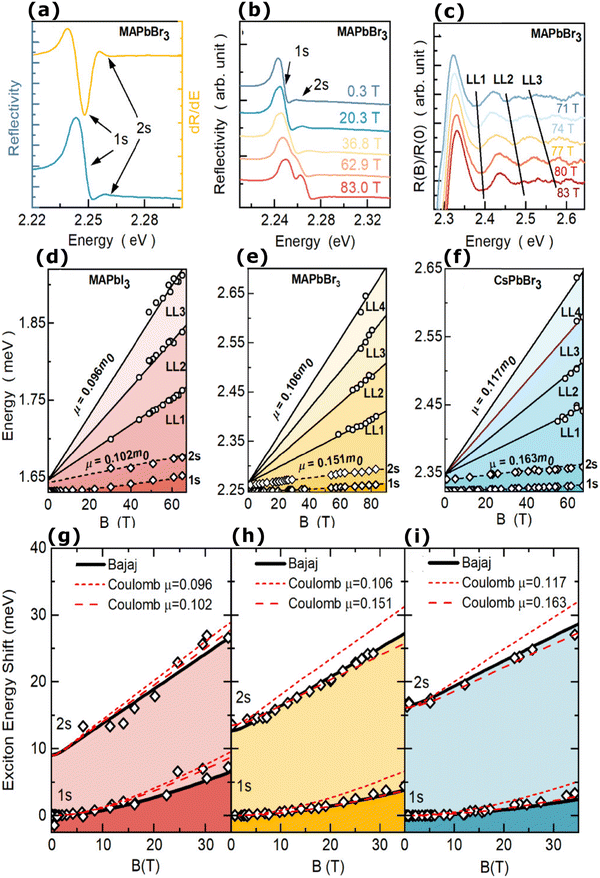 |
| | Fig. 9 (a) The reflectance spectrum of MAPbBr3 with the corresponding derivative (yellow) displaying resonance characteristics of the excitonic transitions 1s and 2s. (b) The evolution of the reflectance spectrum in the magnetic field. (c) Rationed reflectance spectra for various values of the magnetic field strengths; the black lines correspond to transitions of the Landau level (LL). (d)–(f) Fan charts illustrating the energies for Landau level interband transition for MAPbI3, MAPbBr3, and CsPbBr3 with respect to magnetic field strength. Effective reduced mass μ was evaluated using eqn (29). (g)–(i) Energies of 1s and 2s excitonic transitions for MAPbI3, MAPbBr3, and CsPbBr3 with respect to magnetic field strength (open points). The red dashed line represents the Wannier–Mott theory, while the red short-dashed line represents a prediction of the Wannier–Mott theory with μ obtained from the spectroscopy of the Landau level. The black line corresponds to the Bajaj potential. Adapted from ref. 221, Copyright 2024, American Chemical Society. | |
Shin et al.236 explored the magneto-photoluminescence transitions in single crystals of MAPbX3 (X = Cl, Br, and I) subjected to strong magnetic fields of ∼60 T at 4.2 K. Photoluminescence spectra were recorded under varying magnetic field strengths, revealing a power-law dependence of shifts in transition energy for both σ+ and σ− directions in MAPbI3. Their study showed that the combination of polaronic effects and Rashba splitting can explain the photoluminescence transitions generated by the various halogens under magnetic fields, which are difficult to describe by a single unified model. Such findings underscore the need to incorporate polaronic effects into models of perovskite materials to accurately predict their optical and electronic properties, thereby advancing their application in optoelectronic devices.
Here we have discussed some aspects of polaron formation and its impact on optical response and carrier effective masses in OILHPs, but it still lacks which method can surely be universally suitable for thin films as well as bulk cube-like structures. The theories of Haken and Pollman–Büttner satisfactorily explain the excitons and polarons in OILHPs at low temperatures where excitonic effects are much more prominent but will be more challenging for higher temperature phases where such effects practically disappear due to the increase in static dielectric associated with the rotational motion and steric effects of organic cations.128,237 Understanding polarons in such systems requires improved experimental and theoretical techniques capable of exploring both excitonic and polaronic properties at the bulk and nanoscale. More emphasis should be placed on polaron formation, dynamics, dielectric and quantum confinement effects, and their relation to carrier scattering, and dielectric properties, for different morphologies. Therefore, a careful analysis of these factors needs to be undertaken to conclude the universal method for evaluating the exciton binding energy along with the polaron formation mechanism in OILHPs which is critical for the designing and fabrication of photovoltaic as well as optoelectronic devices.
5. Summary and outlook
In this article, an adequate understanding of excitonic and polaronic physics in OILHPs is presented. The exciton binding energy (Exb) of various OILHPs with different morphologies and compositions has been measured at different temperatures using both experimental and theoretical techniques. Some of the factors that lead to conflicting values for exciton binding energy by different authors in OILHPs can be summarized as follows. Most of the calculated exciton binding energy is based on the Wannier–Mott model which raises serious concerns about the accuracy of whether to use the static or high frequency dielectric constant. In the previous literature, it was assumed that Exb is independent of the magnetic field and that the use of the high frequency dielectric constant may yield results with high uncertainties. The Exb in OILHPs is evaluated using the static dielectric constant, which replaces the effective dielectric constant during calculations. While this method is useful, it is only applicable when the exciton binding energy is lower than the longitudinal optical phonon energy.72 Ambient conditions, such as temperature and pressure, greatly influence absorption and photoluminescence spectra, affecting the vibrational modes of atoms and lattice dynamics. This, in turn, leads to different recombination and coupling mechanisms of photogenerated carriers, resulting in a wide range of Exb. Crystal quality, morphology and trap states also influence the screening behavior of the photogenerated charge carriers, which alters the bimolecular and trap-assisted recombination processes, which in turn affects the excitonic properties in OILHPs. It is also evident that complexities arise in low dimensional OILHPs like 2D thin films, nanostructures, or quantum dots stemming from quantum confinement and modified dielectric confinement, which demand distinct approaches.
The role of large polaron formation in OILHPs is presently under intense debate. Considering polaron formation and its correlation to carrier recombination mechanisms, carrier effective mass and mobility can somewhat explain the discrepancies in calculating the exciton binding energy. However, it will be interesting to explore the polaron dynamics and carrier scattering upon photoexcitation in bulk and layered form of OILHPs using single experimental or theoretical techniques to provide a universal image for excitonic and polaronic physics (beyond the dielectric and quantum confinement effects). This will address the existing discrepancies in the excitonic and polaronic behavior of OILHPs in their optically excited state, and provide a clearer understanding of their impact on photovoltaic and optoelectronic properties.
Author contributions
Zeeshan Muhammad: investigation and writing – original draft, Arooj Rashid: writing – original draft.
Data availability
There are no raw data related to this review paper.
Conflicts of interest
The authors affirm that they have no known financial or interpersonal issues that would have appeared to have an impact on the research described in this publication.
References
- J. H. Noh, S. H. Im, J. H. Heo, T. N. Mandal and S. I. Seok, Nano Lett., 2013, 13, 1764–1769 CrossRef CAS.
- F. Hao, C. C. Stoumpos, R. P. H. Chang and M. G. Kanatzidis, J. Am. Chem. Soc., 2014, 136, 8094–8099 CrossRef CAS.
- W. Rehman, R. L. Milot, G. E. Eperon, C. Wehrenfennig, J. L. Boland, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Mater., 2015, 27, 7938–7944 CrossRef CAS PubMed.
- D. Bi, W. Tress, M. I. Dar, P. Gao, J. Luo, C. Renevier, K. Schenk, A. Abate, F. Giordano, J. P. Correa Baena, J. D. Decoppet, S. M. Zakeeruddin, M. K. Nazeeruddin, M. Grätzel and A. Hagfeldt, Sci. Adv., 2016, 2, e1501170 CrossRef.
- L. Li, N. Liu, Z. Xu, Q. Chen, X. Wang and H. Zhou, ACS Nano, 2017, 11, 8804–8813 CrossRef CAS PubMed.
- K. A. Bush, K. Frohna, R. Prasanna, R. E. Beal, T. Leijtens, S. A. Swifter and M. D. McGehee, ACS Energy Lett., 2018, 3, 428–435 CrossRef CAS.
- E. S. Parrott, T. Green, R. L. Milot, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Funct. Mater., 2018, 28, 1802803 CrossRef.
- Y. Chen, H. T. Yi, X. Wu, R. Haroldson, Y. N. Gartstein, Y. I. Rodionov, K. S. Tikhonov, A. Zakhidov, X. Y. Zhu and V. Podzorov, Nat. Commun., 2016, 7, 12253 CrossRef CAS.
- A. A. Zhumekenov, M. I. Saidaminov, M. A. Haque, E. Alarousu, S. P. Sarmah, B. Murali, I. Dursun, X.-H. Miao, A. L. Abdelhady, T. Wu, O. F. Mohammed and O. M. Bakr, ACS Energy Lett., 2016, 1, 32–37 CrossRef CAS.
- G. Xing, N. Mathews, S. Sun, S. S. Lim, Y. M. Lam, M. Gratzel, S. Mhaisalkar and T. C. Sum, Science, 2013, 342, 344–347 CrossRef CAS.
- G. W. P. P. Adhyaksa, L. W. Veldhuizen, Y. Kuang, S. Brittman, R. E. I. I. Schropp and E. C. Garnett, Chem. Mater., 2016, 28, 5259–5263 CrossRef CAS.
- C. Wehrenfennig, G. E. Eperon, M. B. Johnston, H. J. Snaith and L. M. Herz, Adv. Mater., 2014, 26, 1584–1589 CrossRef CAS.
- J. Lim, M. T. Hörantner, N. Sakai, J. M. Ball, S. Mahesh, N. K. Noel, Y. H. Lin, J. B. Patel, D. P. McMeekin, M. B. Johnston, B. Wenger and H. J. Snaith, Energy Environ. Sci., 2019, 12, 169–176 RSC.
- N. T. P. Hartono, S. Sun, M. C. Gélvez-Rueda, P. J. Pierone, M. P. Erodici, J. Yoo, F. Wei, M. Bawendi, F. C. Grozema, M. J. Sher, T. Buonassisi and J.-P. P. Correa-Baena, J. Mater. Chem. A, 2019, 7, 23949–23957 RSC.
- T. M. Brenner, D. A. Egger, L. Kronik, G. Hodes and D. Cahen, Nat. Rev. Mater., 2016, 1, 15007 CrossRef CAS.
- T. Leijtens, G. E. Eperon, A. J. Barker, G. Grancini, W. Zhang, J. M. Ball, A. R. S. Kandada, H. J. Snaith and A. Petrozza, Energy Environ. Sci., 2016, 9, 3472–3481 RSC.
- H. T. Yi, X. Wu, X. Zhu and V. Podzorov, Adv. Mater., 2016, 28, 6509–6514 CrossRef CAS PubMed.
- N. Arora, M. I. Dar, M. Hezam, W. Tress, G. Jacopin, T. Moehl, P. Gao, A. S. Aldwayyan, B. Deveaud, M. Grätzel and M. K. Nazeeruddin, Adv. Funct. Mater., 2016, 26, 2846–2854 CrossRef CAS.
- J. Shi, Y. Li, J. Wu, H. Wu, Y. Luo, D. Li, J. J. Jasieniak and Q. Meng, Appl. Phys., arXiv.
- P. Brenner, O. Bar-On, M. Jakoby, I. Allegro, B. S. Richards, U. W. Paetzold, I. A. Howard, J. Scheuer and U. Lemmer, Nat. Commun., 2019, 10, 988 CrossRef.
- P. Liu, C. Gu and Q. Liao, ACS Omega, 2021, 6, 34021–34026 CrossRef CAS PubMed.
- T. Shen, J. Qin, Y. Bai, J. Zhang, L. Shi, X. Hou, J. Zi and B. Hu, Opto-Electron. Adv., 2022, 5, 200051 CAS.
- H. Kim, L. Zhao, J. S. Price, A. J. Grede, K. Roh, A. N. Brigeman, M. Lopez, B. P. Rand and N. C. Giebink, Nat. Commun., 2018, 9, 4893 CrossRef.
- Y. Shang, Y. Liao, Q. Wei, Z. Wang, B. Xiang, Y. Ke, W. Liu and Z. Ning, Sci. Adv., 2019, 5, eaaw8072 CrossRef CAS PubMed.
- A. S. Pannu, S. Sen, X. (Tony) Wang, R. Jones, K. (Ken) Ostrikov and P. Sonar, Nanoscale, 2023, 15, 2659–2666 RSC.
- L. Dou, Y. Yang, J. You, Z. Hong, W.-H. Chang, G. Li and Y. Yang, Nat. Commun., 2014, 5, 5404 CrossRef CAS.
- C. Xie, C. Liu, H. Loi and F. Yan, Adv. Funct. Mater., 2020, 30, 1903907 CrossRef CAS.
- Y. Yang, H. Dai, F. Yang, Y. Zhang, D. Luo, X. Zhang, K. Wang, X. W. Sun and J. Yao, Nanoscale Res. Lett., 2019, 14, 291 CrossRef.
- R. Ray, N. Nakka and S. K. Pal, Nanotechnology, 2021, 32, 085201 CrossRef CAS.
- I.-H. Park, K. C. Kwon, Z. Zhu, X. Wu, R. Li, Q.-H. Xu and K. P. Loh, J. Am. Chem. Soc., 2020, 142, 18592–18598 CrossRef CAS.
- L. Mei, R. Huang, C. Shen, J. Hu, P. Wang, Z. Xu, Z. Huang and L. Zhu, Adv. Opt. Mater., 2022, 10, 2102656 CrossRef CAS.
- A. Moeini, L. Martínez-Sarti, K. P. S. Zanoni, M. Sessolo, D. Tordera and H. J. Bolink, J. Mater. Chem. C, 2022, 10, 13878–13885 RSC.
- M. B. Mohammadzadeh Shamloo, S. Darbari and Y. Abdi, in 2021 Iranian International Conference on Microelectronics (IICM), IEEE, 2021, pp. 1–4.
- Y. Xu, F. Wang, J. Xu, X. Lv, G. Zhao, Z. Sun, Z. Xie and S. Zhu, Opt. Express, 2023, 31, 8428 CrossRef CAS PubMed.
- J. Fan, B. Jia and M. Gu, Photonics Res., 2014, 2, 111 CrossRef.
- M. Szafrański and A. Katrusiak, J. Phys. Chem. Lett., 2017, 8, 2496–2506 CrossRef.
- L. K. Jagadamma, O. Blaszczyk, M. T. Sajjad, A. Ruseckas and I. D. W. Samuel, Sol. Energy Mater. Sol. Cells, 2019, 201, 110071 CrossRef CAS.
- G. Grancini and M. K. Nazeeruddin, Nat. Rev. Mater., 2018, 4, 4–22 CrossRef.
- Y. Furukawa, S. Ikawa, H. Kiyohara, Y. Sendai and A. Bahtiar, Key Eng. Mater., 2020, 860, 3–8 Search PubMed.
- A.-B. Mekky, Ann. Chim. - Sci. des Matériaux, 2020, 44, 179–184 CrossRef.
- M. L. Ball, J. V. Milić and Y.-L. Loo, Chem. Mater., 2022, 34, 2495–2502 CrossRef CAS.
- A. Olaleru, E. Maluta, J. Kirui and O. Adekoya, Thin Films Photovoltaics, IntechOpen, 2022 Search PubMed.
- A. Bulloch, S. Wang, P. Ghosh and L. K. Jagadamma, Philos. Trans. R. Soc., A., 2022, 380, 20210144 CrossRef CAS PubMed.
- M. Saba, F. Quochi, A. Mura and G. Bongiovanni, Acc. Chem. Res., 2016, 49, 166–173 CrossRef CAS PubMed.
- S. A. Kulkarni, S. G. Mhaisalkar, N. Mathews and P. P. Boix, Small Methods, 2019, 3, 1–16 CrossRef.
- N. Droseros, D. Tsokkou and N. Banerji, Adv. Energy Mater., 2020, 10, 1903258 CrossRef CAS.
- W. Gao, J. Ding, Z. Bai, Y. Qi, Y. Wang and Z. Lv, Nanophotonics, 2021, 10, 3945–3955 CrossRef CAS.
- M. Li, P. Huang and H. Zhong, J. Phys. Chem. Lett., 2023, 14, 1592–1603 CrossRef CAS.
- D. E. Hill, Solid State Commun., 1972, 11, 1187–1191 CrossRef CAS.
- W. J. Turner, W. E. Reese and G. D. Pettit, Phys. Rev., 1964, 136, A1467–A1470 CrossRef.
- A. Sugie, K. Nakano, K. Tajima, I. Osaka and H. Yoshida, J. Phys. Chem. Lett., 2023, 14, 11412–11420 CrossRef CAS.
- Y. Zhu, F. Zhao, W. Wang, Y. Li, S. Zhang and Y. Lin, Adv. Energy Sustainability Res., 2022, 3, 2100184 CrossRef CAS.
- B. Schweitzer and H. Bässler, Synth. Met., 2000, 109, 1–6 CrossRef CAS.
- M. Liess, S. Jeglinski, Z. V. Vardeny, M. Ozaki, K. Yoshino, Y. Ding and T. Barton, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 15712–15724 CrossRef CAS.
- J.-L. Brédas, D. Beljonne, V. Coropceanu and J. Cornil, Chem. Rev., 2004, 104, 4971–5004 CrossRef.
- A. Bian, D. He, S. Hao, Y. Fu, L. Zhang, J. He, Y. Wang and H. Zhao, Nanoscale, 2020, 12, 8485–8492 RSC.
- M. E. Ziffer, J. C. Mohammed and D. S. Ginger, ACS Photonics, 2016, 3, 1060–1068 CrossRef CAS.
- S. Parveen, K. K. Paul, R. Das and P. K. Giri, J. Colloid Interface Sci., 2019, 539, 619–633 CrossRef CAS PubMed.
- D. A. Valverde-Chávez, C. S. Ponseca, C. C. Stoumpos, A. Yartsev, M. G. Kanatzidis, V. Sundström and D. G. Cooke, Energy Environ. Sci., 2015, 8, 3700–3707 RSC.
- P. Piatkowski, B. Cohen, C. S. Ponseca, M. Salado, S. Kazim, S. Ahmad, V. Sundström and A. Douhal, J. Phys. Chem. Lett., 2016, 7, 204–210 CrossRef CAS.
- A. Jha, H.-G. Duan, V. Tiwari, P. K. Nayak, H. J. Snaith, M. Thorwart and R. J. D. Miller, ACS Photonics, 2018, 5, 852–860 CrossRef CAS.
- W. P. D. Wong, J. Yin, B. Chaudhary, X. Y. Chin, D. Cortecchia, S.-Z. A. Lo, A. C. Grimsdale, O. F. Mohammed, G. Lanzani and C. Soci, ACS Mater. Lett., 2020, 2, 20–27 CrossRef CAS.
- Y. Park and D. T. Limmer, J. Chem. Phys., 2022, 157, 11780 Search PubMed.
- D. Bao, Q. Chang, B. Chen, X. Chen, H. Sun, Y. M. Lam, D. Zhao, J.-X. Zhu and E. E. M. Chia, PRX Energy, 2023, 2, 013001 CrossRef.
- H. Haug and S. W. Koch, Quantum Theory of the Optical and Electronic Properties of Semiconductors, World Scientific, 5th edn, 2009 Search PubMed.
- G. H. Wannier, Phys. Rev., 1937, 52, 191–197 CrossRef CAS.
- G. Dresselhaus, J. Phys. Chem. Solids, 1956, 1, 14–22 CrossRef.
- A. Poglitsch and D. Weber, J. Chem. Phys., 1987, 87, 6373–6378 CrossRef CAS.
- N. Onoda-Yamamuro, T. Matsuo and H. Suga, J. Phys. Chem. Solids, 1992, 53, 935–939 CrossRef CAS.
- Q. Lin, A. Armin, R. C. R. Nagiri, P. L. Burn and P. Meredith, Nat. Photonics, 2015, 9, 106–112 CrossRef CAS.
- E. J. Juarez-Perez, R. S. Sanchez, L. Badia, G. Garcia-Belmonte, Y. S. Kang, I. Mora-Sero and J. Bisquert, J. Phys. Chem. Lett., 2014, 5, 2390–2394 CrossRef CAS PubMed.
- H. Kalt and C. F. Klingshirn, Semiconductor Optics 1, Springer International Publishing, Cham, 5th edn, 2019 Search PubMed.
- M. Hirasawa, T. Ishihara, T. Goto, K. Uchida and N. Miura, Phys. B, 1994, 201, 427–430 CrossRef CAS.
- T. Ishihara, J. Lumin., 1994, 60–61, 269–274 CrossRef CAS.
- T. J. Savenije, C. S. Ponseca, L. Kunneman, M. Abdellah, K. Zheng, Y. Tian, Q. Zhu, S. E. Canton, I. G. Scheblykin, T. Pullerits, A. Yartsev and V. Sundström, J. Phys. Chem. Lett., 2014, 5, 2189–2194 CrossRef CAS PubMed.
- I. B. Koutselas, L. Ducasse and G. C. Papavassiliou, J. Phys.: Condens. Matter, 1996, 8, 1217–1227 CrossRef CAS.
- S. Sun, T. Salim, N. Mathews, M. Duchamp, C. Boothroyd, G. Xing, T. C. Sum and Y. M. Lam, Energy Environ. Sci., 2014, 7, 399–407 RSC.
- K. Tanaka, T. Takahashi, T. Ban, T. Kondo, K. Uchida and N. Miura, Solid State Commun., 2003, 127, 619–623 CrossRef CAS.
- M. Saba, M. Cadelano, D. Marongiu, F. Chen, V. Sarritzu, N. Sestu, C. Figus, M. Aresti, R. Piras, A. Geddo Lehmann, C. Cannas, A. Musinu, F. Quochi, A. Mura and G. Bongiovanni, Nat. Commun., 2014, 5, 5049 CrossRef CAS.
- G. Grancini, A. R. Srimath Kandada, J. M. Frost, A. J. Barker, M. De Bastiani, M. Gandini, S. Marras, G. Lanzani, A. Walsh and A. Petrozza, Nat. Photonics, 2015, 9, 695–701 CrossRef CAS.
- M. A. Green, Y. Jiang, A. M. Soufiani and A. Ho-Baillie, J. Phys. Chem. Lett., 2015, 6, 4774–4785 CrossRef CAS.
- A. Kumar, N. K. Kumawat, P. Maheshwari and D. Kabra, in 2015 IEEE 42nd Photovoltaic Specialist Conference (PVSC), IEEE, 2015, pp. 1–4.
- Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, IEEE J. Photovoltaics, 2015, 5, 401–405 Search PubMed.
- Y. Yang, M. Yang, Z. Li, R. Crisp, K. Zhu and M. C. Beard, J. Phys. Chem. Lett., 2015, 6, 4688–4692 CrossRef CAS.
- T. Hakamata, K. Shimamura, F. Shimojo, R. K. Kalia, A. Nakano and P. Vashishta, Sci. Rep., 2016, 6, 19599 CrossRef CAS PubMed.
- M. Bokdam, T. Sander, A. Stroppa, S. Picozzi, D. D. Sarma, C. Franchini and G. Kresse, Sci. Rep., 2016, 6, 28618 CrossRef CAS PubMed.
- S. A. March, C. Clegg, D. B. Riley, D. Webber, I. G. Hill and K. C. Hall, Sci. Rep., 2016, 6, 1–7 CrossRef PubMed.
- K. Galkowski, A. Mitioglu, A. Miyata, P. Plochocka, O. Portugall, G. E. Eperon, J. T.-W. W. Wang, T. Stergiopoulos, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Energy Environ. Sci., 2016, 9, 962–970 RSC.
- H. Zheng, J. Dai, J. Duan, F. Chen, G. Zhu, F. Wang and C. Xu, J. Mater. Chem. C, 2017, 5, 12057–12061 RSC.
- T. Ye, M. Petrovic, S. Peng, J. L. K. Yoong, C. Vijila and S. Ramakrishna, ACS Appl. Mater. Interfaces, 2017, 9, 2358–2368 CrossRef CAS.
- F. Ruf, A. Magin, M. Schultes, E. Ahlswede, H. Kalt and M. Hetterich, Appl. Phys. Lett., 2018, 112, 083902 CrossRef.
- J. Shi, H. Zhang, Y. Li, J. J. Jasieniak, Y. Li, H. Wu, Y. Luo, D. Li and Q. Meng, Energy Environ. Sci., 2018, 11, 1460–1469 RSC.
- C.
L. Davies, M. R. Filip, J. B. Patel, T. W. Crothers, C. Verdi, A. D. Wright, R. L. Milot, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2018, 9, 1–9 CrossRef CAS.
- A. Koliogiorgos, C. S. Garoufalis, I. Galanakis and S. Baskoutas, ACS Omega, 2018, 3, 18917–18924 CrossRef CAS.
- P. Umari, E. Mosconi and F. De Angelis, J. Phys. Chem. Lett., 2018, 9, 620–627 CrossRef CAS PubMed.
- Y. Liu, J. Wang, N. Zhu, W. Liu, C. Wu, C. Liu, L. Xiao, Z. Chen and S. Wang, Opt. Lett., 2019, 44, 3474 CrossRef CAS.
- F. Ruf, M. F. Aygüler, N. Giesbrecht, B. Rendenbach, A. Magin, P. Docampo, H. Kalt and M. Hetterich, APL Mater., 2019, 7, 031113 CrossRef.
- Z. W. Xu, C. R. Zhang, Y. Z. Wu, J. J. Gong, W. Wang, Z. J. Liu and H. S. Chen, Results Phys., 2019, 15, 102709 CrossRef.
- Q. Xu, A. Stroppa, J. Lv, X. Zhao, D. Yang, K. Biswas and L. Zhang, Phys. Rev. Mater., 2019, 3, 125401 CrossRef CAS.
- Y. Bai, H. Zhang, M. Zhang, D. Wang, H. Zeng, J. Zhao, H. Xue, G. Wu, J. Su, Y. Xie, Y. Zhang, H. Jing, H. Yu, Z. Hu, R. Peng, M. Wang and Y. Wu, Nanoscale, 2020, 12, 1100–1108 RSC.
- M. Hamada, S. Rana, E. Jokar, K. Awasthi, E. W. G. Diau and N. Ohta, ACS Appl. Energy Mater., 2020, 3, 11830–11840 CrossRef CAS.
- R. Ali, Z. G. Zhu, Q. B. Yan, Q. R. Zheng, G. Su, A. Laref, C. S. Saraj and C. Guo, ACS Appl. Mater. Interfaces, 2020, 12, 49636–49647 CrossRef CAS PubMed.
- C. Xiong, J. Sun, C. Cai, W. Caiyang and Y. Zhu, Sol. Energy, 2020, 204, 155–160 CrossRef CAS.
- D. Li, D. Li, H. Zhang, A. Yang and C. Liang, J. Phys. Chem. Lett., 2020, 11, 5282–5294 CrossRef CAS PubMed.
- A. Simbula, R. Pau, Q. Wang, F. Liu, V. Sarritzu, S. Lai, M. Lodde, F. Mattana, G. Mula, A. Geddo Lehmann, I. D. Spanopoulos, M. G. Kanatzidis, D. Marongiu, F. Quochi, M. Saba, A. Mura and G. Bongiovanni, Adv. Opt. Mater., 2021, 9, 2100295 CrossRef CAS.
- Z. Gao, S. Chen, Y. Bai, M. Wang, X. Liu, W. Yang, W. Li, X. Ding and J. Yao, Phys. Chem. Chem. Phys., 2021, 23, 11548–11556 RSC.
- C. C. S. Chan, K. Fan, H. Wang, Z. Huang, D. Novko, K. Yan, J. Xu, W. C. H. Choy, I. Lončarić and K. S. Wong, Adv. Energy Mater., 2021, 11, 2003071 CrossRef CAS.
- P. Basera, A. Singh, D. Gill and S. Bhattacharya, J. Mater. Chem. C, 2021, 9, 17113–17123 RSC.
- G. Biffi, Y. Cho, R. Krahne and T. C. Berkelbach, J. Phys. Chem. C, 2023, 127, 1891–1898 CrossRef CAS.
- A. M. Ulatowski, K. A. Elmestekawy, J. B. Patel, N. K. Noel, S. Yan, H. Kraus, P. G. Huggard, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2023, 2305283 CrossRef CAS.
- F. Zhang, H. Zhong, C. Chen, X. G. Wu, X. Hu, H. Huang, J. Han, B. Zou and Y. Dong, ACS Nano, 2015, 9, 4533–4542 CrossRef CAS PubMed.
- K. Zheng, Q. Zhu, M. Abdellah, M. E. Messing, W. Zhang, A. Generalov, Y. Niu, L. Ribaud, S. E. Canton and T. Pullerits, J. Phys. Chem. Lett., 2015, 6, 2969–2975 CrossRef CAS PubMed.
- H. Kunugita, T. Hashimoto, Y. Kiyota, Y. Udagawa, Y. Takeoka, Y. Nakamura, J. Sano, T. Matsushita, T. Kondo, T. Miyasaka and K. Ema, Chem. Lett., 2015, 44, 852–854 CrossRef CAS.
- J. Dai, H. Zheng, C. Zhu, J. Lu and C. Xu, J. Mater. Chem. C, 2016, 4, 4408–4413 RSC.
- J. Tilchin, D. N. Dirin, G. I. Maikov, A. Sashchiuk, M. V. Kovalenko and E. Lifshitz, ACS Nano, 2016, 10, 6363–6371 CrossRef CAS PubMed.
- H. Kunugita, Y. Kiyota, Y. Udagawa, Y. Takeoka, Y. Nakamura, J. Sano, T. Matsushita, T. Kondo and K. Ema, Jpn. J. Appl. Phys., 2016, 55, 060304 CrossRef.
- T. Thu Ha Do, A. Granados Del Águila, C. Cui, J. Xing, Z. Ning and Q. Xiong, Phys. Rev. B, 2017, 96, 1–9 CrossRef.
- Z. Liu, Y. Li, X. Guan, Y. Mi, A. Al-Hussain, S. T. Ha, M. H. Chiu, C. Ma, M. R. Amer, L. J. Li, J. Liu, Q. Xiong, J. Wang, X. Liu and T. Wu, J. Phys. Chem. Lett., 2019, 10, 2363–2371 CrossRef CAS.
- J. Shi, Y. Li, J. Wu, H. Wu, Y. Luo, D. Li, J. J. Jasieniak and Q. Meng, Adv. Opt. Mater., 2020, 8, 1–11 Search PubMed.
- A. M. Ulatowski, A. D. Wright, B. Wenger, L. R. V. Buizza, S. G. Motti, H. J. Eggimann, K. J. Savill, J. Borchert, H. J. Snaith, M. B. Johnston and L. M. Herz, J. Phys. Chem. Lett., 2020, 11, 3681–3688 CrossRef CAS PubMed.
- M. Jain, D. Gill, P. Bhumla, P. Basera and S. Bhattacharya, Appl. Phys. Lett., 2021, 118, 192103 CrossRef CAS.
- S. Yan, K. Wang, G. Xing, J. Xu, S. Su, Z. Tang, S. Wang and K. W. Ng, ACS Appl. Mater.
Interfaces, 2021, 13, 38458–38466 CrossRef CAS.
- H.-H. Fang, F. Wang, S. Adjokatse, N. Zhao, J. Even and M. Antonietta Loi, Light: Sci. Appl., 2016, 5, e16056 CrossRef CAS.
- F. Yuan, Z. Wu, H. Dong, J. Xi, K. Xi, G. Divitini, B. Jiao, X. Hou, S. Wang and Q. Gong, J. Phys. Chem. C, 2017, 121, 15318–15325 CrossRef CAS.
- A. V. Sachenko, V. P. Kostylyov, A. V. Bobyl, V. M. Vlasyuk, I. O. Sokolovskyi, E. I. Terukov and M. A. Evstigneev, Tech. Phys. Lett., 2017, 43, 678–680 CrossRef CAS.
- Y. Fu, T. Wu, J. Wang, J. Zhai, M. J. Shearer, Y. Zhao, R. J. Hamers, E. Kan, K. Deng, X. Y. Zhu and S. Jin, Nano Lett., 2017, 17, 4405–4414 CrossRef CAS PubMed.
- C. L. Davies, J. Borchert, C. Q. Xia, R. L. Milot, H. Kraus, M. B. Johnston and L. M. Herz, J. Phys. Chem. Lett., 2018, 9, 4502–4511 CrossRef CAS.
- A. Johnston, G. Walters, M. I. Saidaminov, Z. Huang, K. Bertens, N. Jalarvo and E. H. Sargent, ACS Nano, 2020, 14, 15107–15118 CrossRef CAS.
- Z. Muhammad, P. Liu, R. Ahmad, S. Jalali-Asadabadi, C. Franchini and I. Ahmad, AIP Adv., 2022, 12, 025330 CrossRef CAS.
- N. J. Jeon, J. Seo, S. Nah and J.-K. Lee, Adv. Chem. Eng. Sci., 2022, 12, 54–64 CrossRef CAS.
- S. Wang, Q. Zhao, A. Hazarika, S. Li, Y. Wu, Y. Zhai, X. Chen, J. M. Luther and G. Li, Nat. Commun., 2023, 14, 2216 CrossRef CAS PubMed.
- K. A. Elmestekawy, B. M. Gallant, A. D. Wright, P. Holzhey, N. K. Noel, M. B. Johnston, H. J. Snaith and L. M. Herz, ACS Energy Lett., 2023, 2543–2551 CrossRef CAS.
- A. Perumal, S. Shendre, M. Li, Y. K. E. Tay, V. K. Sharma, S. Chen, Z. Wei, Q. Liu, Y. Gao, P. J. S. Buenconsejo, S. T. Tan, C. L. Gan, Q. Xiong, T. C. Sum and H. V. Demir, Sci. Rep., 2016, 6, 36733 CrossRef CAS.
- L. Yang, K. Wei, Z. Xu, F. Li, R. Chen, X. Zheng, X. Cheng and T. Jiang, Opt. Lett., 2018, 43, 122 CrossRef CAS PubMed.
- D. Han, M. Imran, M. Zhang, S. Chang, X. G. Wu, X. Zhang, J. Tang, M. Wang, S. Ali, X. Li, G. Yu, J. Han, L. Wang, B. Zou and H. Zhong, ACS Nano, 2018, 12, 8808–8816 CrossRef CAS PubMed.
- H. Fang, W. Deng, X. Zhang, X. Xu, M. Zhang, J. Jie and X. Zhang, Nano Res., 2019, 12, 171–176 CrossRef CAS.
- Z. Liu, Z. Hu, Z. Zhang, J. Du, J. Yang, X. Tang, W. Liu and Y. Leng, ACS Photonics, 2019, 6, 3150–3158 CrossRef CAS.
- F. Meng, X. Liu, Y. Chen, X. Cai, M. Li, T. Shi, Z. Chen, D. Chen, H. L. Yip, C. Ramanan, P. W. M. Blom and S. J. Su, Adv. Funct. Mater., 2020, 30, 1–9 Search PubMed.
- L. Sui, G. Niu, J. Jiang, Q. Li, Y. Zhang, G. Wu, F. Li and K. Yuan, J. Phys. Chem. C, 2020, 124, 14390–14399 CrossRef CAS.
- J. Liu, F. Hu, Y. Zhou, C. Zhang, X. Wang and M. Xiao, J. Lumin., 2020, 221, 117032 CrossRef CAS.
- S. Peng, Z. Wen, T. Ye, X. Xiao, K. Wang, J. Xia, J. Sun, T. Zhang, G. Mei, H. Liu, B. Xu, X. Li, R. Chen, G. Xing, K. Wang and Z. Tang, ACS Appl. Mater. Interfaces, 2020, 12, 31863–31874 CrossRef CAS.
- X. Wang, Q. Wang, Z. Chai and W. Wu, RSC Adv., 2020, 10, 44373–44381 RSC.
- X. Li, K. Wang, M. Chen, S. Wang, Y. Fan, T. Liang, Q. Song, G. Xing and Z. Tang, Adv. Opt. Mater., 2020, 8, 1–7 CAS.
- C. Zhang, S. Wang, X. Li, M. Yuan, L. Turyanska and X. Yang, Adv. Funct. Mater., 2020, 30, 1910582 CrossRef CAS.
- S. M. H. Qaid, H. M. Ghaithan, K. K. AlHarbi, A. F. Bin Ajaj, B. A. Al-Asbahi and A. S. Aldwayyan, Photonics, 2021, 9, 4 CrossRef.
- X. Zhang, S. Xiao, X. Wang, T. He and R. Chen, Chin. Phys. B, 2023, 32, 064212 CrossRef.
- R. Comin, G. Walters, E. S. Thibau, O. Voznyy, Z. H. Lu and E. H. Sargent, J. Mater. Chem. C, 2015, 3, 8839–8843 RSC.
- V. D. Innocenzo, G. Grancini, M. J. P. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith, A. Petrozza, V. D’Innocenzo, G. Grancini, M. J. P. P. Alcocer, A. R. S. Kandada, S. D. Stranks, M. M. Lee, G. Lanzani, H. J. Snaith and A. Petrozza, Nat. Commun., 2014, 5, 3586 CrossRef.
- S. Liu, W. Huang, P. Liao, N. Pootrakulchote, H. Li, J. Lu, J. Li, F. Huang, X. Shai, X. Zhao, Y. Shen, Y. B. Cheng and M. Wang, J. Mater. Chem. A, 2017, 5, 22952–22958 RSC.
- K. Awasthi, K.-B. B. Du, C.-Y. Y. Wang, C.-L. L. Tsai, M. Hamada, S. Narra, E. W.-G. G. Diau and N. Ohta, ACS Photonics, 2018, 5, 2408–2417 CrossRef CAS.
- T. J. Whitcher, J. X. Zhu, X. Chi, H. Hu, D. Zhao, T. C. Asmara, X. Yu, M. B. H. Breese, A. H. Castro Neto, Y. M. Lam, A. T. S. Wee, E. E. M. Chia and A. Rusydi, Phys. Rev. X, 2018, 8, 1–10 Search PubMed.
- H. W. Chen, D. P. Gulo, Y. C. Chao and H. L. Liu, Sci. Rep., 2019, 9, 1–9 CrossRef PubMed.
- L. D. F. Zhang, X. Zhang, C. Wang, M. Sun, X. Luo, Y. Yang, S. Chang and D. Zhang, Nano Energy, 2021, 79, 105486 CrossRef.
- N. Rybin, D. Ghosh, J. Tisdale, S. Shrestha, M. Yoho, D. Vo, J. Even, C. Katan, W. Nie, A. J. Neukirch and S. Tretiak, Chem. Mater., 2020, 32, 1854–1863 CrossRef CAS.
- Z. Muhammad, P. Liu, R. Ahmad, S. Jalali Asadabadi, C. Franchini and I. Ahmad, Phys. Chem. Chem. Phys., 2020, 22, 11943–11955 RSC.
- N. Miura, Physics of Semiconductors in High Magnetic Fields, Oxford University Press, Oxford, 2007 Search PubMed.
- A. Miyata, A. Mitioglu, P. Plochocka, O. Portugall, J. T.-W. Wang, S. D. Stranks, H. J. Snaith and R. J. Nicholas, Nat. Phys., 2015, 11, 582–587 Search PubMed.
- E. Menéndez-Proupin, C. L. Beltrán Ríos and P. Wahnón, Phys. Status Solidi RRL, 2015, 9, 559–563 Search PubMed.
- A. M. Soufiani, F. Huang, P. Reece, R. Sheng, A. Ho-Baillie and M. A. Green, Appl. Phys. Lett., 2015, 107, 231902 CrossRef.
- P. C. Makado and N. C. McGill, J. Phys. C: Solid State Phys., 1986, 19, 873–885 CrossRef CAS.
- Y. Yang, D. P. Ostrowski, R. M. France, K. Zhu, J. Van De Lagemaat, J. M. Luther and M. C. Beard, Nat. Photonics, 2016, 10, 53–59 CrossRef CAS.
- R. J. Elliott, Phys. Rev., 1957, 108, 1384–1389 CrossRef CAS.
- P. Y. Yu and M. Cardona, Fundamentals of Semiconductors, Springer Berlin Heidelberg, Berlin, Heidelberg, 3rd edn, 2005 Search PubMed.
- X. Chen, H. Lu, Y. Yang and M. C. Beard, J. Phys. Chem. Lett., 2018, 9, 2595–2603 CrossRef CAS PubMed.
- N. Sestu, M. Cadelano, V. Sarritzu, F. Chen, D. Marongiu, R. Piras, M. Mainas, F. Quochi, M. Saba, A. Mura and G. Bongiovanni, J. Phys. Chem. Lett., 2015, 6, 4566–4572 CrossRef CAS.
- J. Even, L. Pedesseau and C. Katan, J. Phys. Chem. C, 2014, 118, 11566–11572 CrossRef CAS.
- S. D. Stranks, V. M. Burlakov, T. Leijtens, J. M. Ball, A. Goriely and H. J. Snaith, Phys. Rev. Appl., 2014, 2, 034007 CrossRef CAS.
- A. D. Wright, R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2017, 27, 1700860 CrossRef.
- F. Bruneval, F. Sottile, V. Olevano, R. Del Sole and L. Reining, Phys. Rev. Lett., 2005, 94, 186402 CrossRef.
- G. Strinati, Phys. Rev. B: Condens. Matter Mater. Phys., 1984, 29, 5718–5726 CrossRef CAS.
- M. Rohlfing and S. G. Louie, Phys. Rev. B: Condens. Matter Mater. Phys., 2000, 62, 4927–4944 CrossRef CAS.
- F. Fuchs, C. Rödl, A. Schleife and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 085103 CrossRef.
- F. Ferreira and R. M. Ribeiro, Phys. Rev. B, 2017, 96, 115431 CrossRef.
- P. Liu, B. Kim, X. Q. Chen, D. D. Sarma, G. Kresse and C. Franchini, Phys. Rev. Mater., 2018, 2, 75003 CrossRef CAS.
- X. Wu, D. Vanderbilt and D. R. Hamann, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 72, 035105 CrossRef.
- M. Gajdoš, K. Hummer, G. Kresse, J. Furthmüller and F. Bechstedt, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 045112 CrossRef.
- M. A. Pérez-Osorio, R. L. Milot, M. R. Filip, J. B. Patel, L. M. Herz, M. B. Johnston and F. Giustino, J. Phys. Chem. C, 2015, 119, 25703–25718 CrossRef.
- M. Kato, T. Fujiseki, T. Miyadera, T. Sugita, S. Fujimoto, M. Tamakoshi, M. Chikamatsu and H. Fujiwara, J. Appl. Phys., 2017, 121, 115501 CrossRef.
- P. F. Ndione, Z. Li and K. Zhu, J. Mater. Chem. C, 2016, 4, 7775–7782 RSC.
- G. Mannino, I. Deretzis, E. Smecca, A. La Magna, A. Alberti, D. Ceratti and D. Cahen, J. Phys. Chem. Lett., 2020, 11, 2490–2496 CrossRef CAS PubMed.
- E. Runge and E. K. U. Gross, Phys. Rev. Lett., 1984, 52, 997–1000 CrossRef CAS.
- M. Petersilka, U. J. Gossmann and E. K. U. Gross, Phys. Rev. Lett., 1996, 76, 1212–1215 CrossRef CAS PubMed.
- C. A. Ullrich, Time-Dependent Density-Functional Theory: Concepts and Applications, Oxford University Press, 2012 Search PubMed.
- S. Botti, F. Sottile, N. Vast, V. Olevano, L. Reining, H.-C. Weissker, A. Rubio, G. Onida, R. Del Sole and R. W. Godby, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 155112 CrossRef.
- Z. Yang and C. A. Ullrich, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 195204 CrossRef.
- Y.-M. Byun and C. A. Ullrich, Phys. Rev. B, 2017, 95, 205136 CrossRef.
- J. S. Manser and P. V. Kamat, Nat. Photonics, 2014, 8, 737–743 CrossRef CAS.
- Y. Yamada, T. Nakamura, M. Endo, A. Wakamiya and Y. Kanemitsu, J. Am. Chem. Soc., 2014, 136, 11610–11613 CrossRef CAS.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- J. P. Perdew, J. A. Chevary, S. H. Vosko, K. A. Jackson, M. R. Pederson, D. J. Singh and C. Fiolhais, Phys. Rev. B: Condens. Matter Mater. Phys., 1992, 46, 6671–6687 CrossRef CAS PubMed.
- D. M. Ceperley and B. J. Alder, Phys. Rev. Lett., 1980, 45, 566–569 CrossRef CAS.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- P. Bultinck, C. Van Alsenoy, P. W. Ayers and R. Carbó-Dorca, J. Chem. Phys., 2007, 126, 144111 CrossRef PubMed.
- Y. Jiang, X. Wang and A. Pan, Adv. Mater., 2019, 31, 1–47 Search PubMed.
- D. Zhao, H. Hu, R. Haselsberger, R. A. Marcus, M.-E. Michel-Beyerle, Y. M. Lam, J.-X. Zhu, C. La-o-vorakiat, M. C. Beard and E. E. M. Chia, ACS Nano, 2019, 13, 8826–8835 CrossRef CAS.
- D. Zhao and E. E. M. Chia, Adv. Opt. Mater., 2020, 8, 1900783 CrossRef CAS.
- R. L. Milot, G. E. Eperon, H. J. Snaith, M. B. Johnston and L. M. Herz, Adv. Funct. Mater., 2015, 25, 6218–6227 CrossRef CAS.
- C. Sheng, C. Zhang, Y. Zhai, K. Mielczarek, W. Wang, W. Ma, A. Zakhidov and Z. V. Vardeny, Phys. Rev. Lett., 2015, 114, 116601 CrossRef.
- Y.-C. Hsiao, T. Wu, M. Li, Q. Liu, W. Qin and B. Hu, J. Mater. Chem. A, 2015, 3, 15372–15385 RSC.
- M. N. Saha, Proceedings of the Royal Society of London. Series A, Containing Papers of a Mathematical and Physical Character, 1921, vol. 99, pp. 135–153 Search PubMed.
- X. Geng, Y. Liu, X. Zou, E. M. J. Johansson and J. Sá, Phys. Chem. Chem. Phys., 2023, 25, 22607–22613 RSC.
- E. M. Hutter, G. E. Eperon, S. D. Stranks and T. J. Savenije, J. Phys. Chem. Lett., 2015, 6, 3082–3090 CrossRef CAS PubMed.
- M. J. Trimpl, A. D. Wright, K. Schutt, L. R. V. Buizza, Z. Wang, M. B. Johnston, H. J. Snaith, P. Müller-Buschbaum and L. M. Herz, Adv. Funct. Mater., 2020, 30, 2004312 CrossRef CAS.
- A. Kiligaridis, P. A. Frantsuzov, A. Yangui, S. Seth, J. Li, Q. An, Y. Vaynzof and I. G. Scheblykin, Nat. Commun., 2021, 12, 3329 CrossRef CAS.
- E. M. H. Tom, J. Savenije, D. Guo and V. M. Caselli, Adv. Energy Mater., 2020, 10, 1903788 CrossRef.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Pérez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Herz, Nat. Commun., 2016, 7, 11755 CrossRef.
- W. Nie, J.-C. Blancon, A. J. Neukirch, K. Appavoo, H. Tsai, M. Chhowalla, M. A. Alam, M. Y. Sfeir, C. Katan, J. Even, S. Tretiak, J. J. Crochet, G. Gupta and A. D. Mohite, Nat. Commun., 2016, 7, 11574 CrossRef CAS PubMed.
- M. Sendner, P. K. Nayak, D. A. Egger, S. Beck, C. Müller, B. Epding, W. Kowalsky, L. Kronik, H. J. Snaith, A. Pucci and R. Lovrinčić, Mater. Horiz., 2016, 3, 613–620 RSC.
- X.-Y. Zhu and V. Podzorov, J. Phys. Chem. Lett., 2015, 6, 4758–4761 CrossRef CAS.
- J. M. Frost, Phys. Rev. B, 2017, 96, 195202 CrossRef.
- A. M. Fox, Optical Properties of Solids, Oxford University Press, 2001 Search PubMed.
- H. Fröhlich, Adv. Phys., 1954, 3, 325–361 CrossRef.
- E. O. Kane, Phys. Rev. B: Solid State, 1978, 18, 6849–6855 CrossRef CAS.
- F. Brivio, A. B. Walker and A. Walsh, APL Mater., 2013, 1, 042111 CrossRef.
- E. Menéndez-Proupin, P. Palacios, P. Wahnón and J. C. Conesa, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 90, 045207 CrossRef.
- Z. Jin, Y. Peng, Y. Fang, Z. Ye, Z. Fan, Z. Liu, X. Bao, H. Gao, W. Ren, J. Wu, G. Ma, Q. Chen, C. Zhang, A. V. Balakin, A. P. Shkurinov, Y. Zhu and S. Zhuang, Light: Sci. Appl., 2022, 11, 209 CrossRef CAS.
- M. Schlipf, S. Poncé and F. Giustino, Phys. Rev. Lett., 2018, 121, 086402 CrossRef CAS.
- S. Poncé, M. Schlipf and F. Giustino, ACS Energy Lett., 2019, 4, 456–463 CrossRef.
- K. Lizárraga, P. Llontop, L. A. Enrique-Morán, M. Piñeiro, E. Perez, E. Serquen, A. Tejada, F. Ruske, L. Korte and J. A. Guerra, arXiv, 2023, preprint, arXiv:2306.17314 DOI:10.48550/arXiv.2306.17314.
- M. Baranowski, A. Nowok, K. Galkowski, M. Dyksik, A. Surrente, D. Maude, M. Zacharias, G. Volonakis, S. D. Stranks, J. Even, M. Maczka, R. Nicholas and P. Plochocka, ACS Energy Lett., 2024, 9, 2696–2702 CrossRef CAS PubMed.
- K. Miyata, D. Meggiolaro, M. T. Trinh, P. P. Joshi, E. Mosconi, S. C. Jones, F. De Angelis and X.-Y. Zhu, Sci. Adv., 2017, 3, e1701217 CrossRef PubMed.
- H. Haken, Fortschr. Phys., 1958, 6, 271–334 CrossRef CAS.
- K. K. Bajaj, Solid State Commun., 1974, 15, 1221–1224 CrossRef CAS.
- J. Pollmann and H. Büttner, Phys. Rev. B: Solid State, 1977, 16, 4480–4490 CrossRef CAS.
- Y. Park, A. Obliger and D. T. Limmer, Nano Lett., 2022, 22, 2398–2404 CrossRef CAS PubMed.
- H. Uratani and H. Nakai, J. Phys. Chem. Lett., 2020, 11, 4448–4455 CrossRef CAS PubMed.
- H. Zhu, K. Miyata, Y. Fu, J. Wang, P. P. Joshi, D. Niesner, K. W. Williams, S. Jin and X.-Y. Zhu, Science, 2016, 353, 1409–1413 CrossRef CAS PubMed.
- J. Yang, X. Wen, H. Xia, R. Sheng, Q. Ma, J. Kim, P. Tapping, T. Harada, T. W. Kee, F. Huang, Y.-B. Cheng, M. Green, A. Ho-Baillie, S. Huang, S. Shrestha, R. Patterson and G. Conibeer, Nat. Commun., 2017, 8, 14120 CrossRef CAS PubMed.
- V. Carpenella, C. Fasolato, D. Di Girolamo, J. Barichello, F. Matteocci, C. Petrillo, D. Dini and A. Nucara, J. Phys. Chem. C, 2023, 127, 22097–22104 CrossRef CAS PubMed.
- D. Meggiolaro, F. Ambrosio, E. Mosconi, A. Mahata and F. De Angelis, Adv. Energy Mater., 2020, 10, 1902748 CrossRef CAS.
- M. Baranowski, K. Galkowski, A. Surrente, J. Urban, Ł. Kłopotowski, S. Maćkowski, D. K. Maude, R. Ben Aich, K. Boujdaria, M. Chamarro, C. Testelin, P. K. Nayak, M. Dollmann, H. J. Snaith, R. J. Nicholas and P. Plochocka, Nano Lett., 2019, 19, 7054–7061 CrossRef CAS.
- Z. Yang, A. Surrente, K. Galkowski, N. Bruyant, D. K. Maude, A. A. Haghighirad, H. J. Snaith, P. Plochocka and R. J. Nicholas, J. Phys. Chem. Lett., 2017, 8, 1851–1855 CrossRef CAS PubMed.
- Z. Yang, A. Surrente, K. Galkowski, A. Miyata, O. Portugall, R. J. Sutton, A. A. Haghighirad, H. J. Snaith, D. K. Maude, P. Plochocka and R. J. Nicholas, ACS Energy Lett., 2017, 2, 1621–1627 CrossRef CAS.
- Y. Yamada, H. Mino, T. Kawahara, K. Oto, H. Suzuura and Y. Kanemitsu, Phys. Rev. Lett., 2021, 126, 237401 CrossRef CAS PubMed.
- Y. H. Shin, H. Choi, C. Park, D. Park, M. S. Jeong, H. Nojiri, Z. Yang, Y. Kohama and Y. Kim, Phys. Rev. B, 2021, 104, 035205 CrossRef CAS.
- J. M. Frost, K. T. Butler and A. Walsh, APL Mater., 2014, 2, 081506 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Arooj Rashidb
*a and
Arooj Rashidb
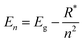
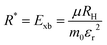
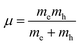 is the reduced exciton mass with effective masses me,h for the electron and hole and εr is the relative dielectric constant, which describes the carrier screening by the crystal lattice. In large-bandgap materials such as LiF and Ar, Frenkel excitons are highly localized and tightly bound within a single crystal unit due to their effective Bohr radii being smaller than the lattice constant. Consequently, the Wannier–Mott model is inadequate for accurately describing Frenkel excitons. However, from the perspective of first-principles electronic structure theory, Wannier and Frenkel excitons are conceptually equivalent as they both represent excitations within a many-body system. The distinguishing feature of excitons is their collective nature, arising from superpositions of many single-particle excitations. For 3D OILHP systems, the Wannier–Mott model yields fairly accurate results, but it leads to the controversial estimation of exciton binding energy due to the large difference between static and high frequency dielectric constants (e.g. ε0 ≈ 33–20 and ε∞ ≈ 4.5–6.75 [see Table 2]). Moreover, due to the anisotropic nature of the dielectric constant (ε∞), the calculations of exciton binding energy may be problematic as both temperature68,69 and frequency70,71 affect the dielectric function for OILHPs. However, for OILHPs, the static value (ε0) may not always be a reliable estimate of the effective dielectric constant (εeff), because it is likely valid only when the exciton binding energy appears to be lower than the longitudinal optical phonon energy (ELO = ħωLO).72
is the reduced exciton mass with effective masses me,h for the electron and hole and εr is the relative dielectric constant, which describes the carrier screening by the crystal lattice. In large-bandgap materials such as LiF and Ar, Frenkel excitons are highly localized and tightly bound within a single crystal unit due to their effective Bohr radii being smaller than the lattice constant. Consequently, the Wannier–Mott model is inadequate for accurately describing Frenkel excitons. However, from the perspective of first-principles electronic structure theory, Wannier and Frenkel excitons are conceptually equivalent as they both represent excitations within a many-body system. The distinguishing feature of excitons is their collective nature, arising from superpositions of many single-particle excitations. For 3D OILHP systems, the Wannier–Mott model yields fairly accurate results, but it leads to the controversial estimation of exciton binding energy due to the large difference between static and high frequency dielectric constants (e.g. ε0 ≈ 33–20 and ε∞ ≈ 4.5–6.75 [see Table 2]). Moreover, due to the anisotropic nature of the dielectric constant (ε∞), the calculations of exciton binding energy may be problematic as both temperature68,69 and frequency70,71 affect the dielectric function for OILHPs. However, for OILHPs, the static value (ε0) may not always be a reliable estimate of the effective dielectric constant (εeff), because it is likely valid only when the exciton binding energy appears to be lower than the longitudinal optical phonon energy (ELO = ħωLO).72
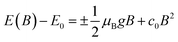
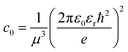
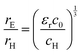
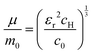
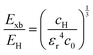
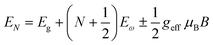

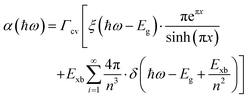
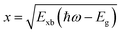 . In this model the first part represents a comprehensive intrinsic absorption continuum state in the presence of Coulomb interactions. Within this framework, the photon-to-exciton conversion rate completely determines the energy dissipation rate from the photon field, thereby establishing a direct link between the two processes.162,163 Such correlation will increase the absorption relative to vanishing excitonic effects which is often referred to as Sommerfeld amplification. The latter term describes the series of optically allowed excitonic transitions near the bandedge with discrete energy levels as in the hydrogen atom. Fig. 2(a) shows a typical absorption spectrum near the bandedge produced by arbitrary line broadening and changing the constants in eqn (9). The first three exciton peaks (designated as 1S, 2S, and 3S) in this hypothetical scenario are resolved below the continuum state. However, with increasing n the amplitude of the excitonic peaks diminishes, and the spectra across a small energy range approach a constant thereby merging into the continuum at the bandedge. The density of states close to the bandgap would vanish when no excitonic effects are considered [red curve, Fig. 2(a)].
. In this model the first part represents a comprehensive intrinsic absorption continuum state in the presence of Coulomb interactions. Within this framework, the photon-to-exciton conversion rate completely determines the energy dissipation rate from the photon field, thereby establishing a direct link between the two processes.162,163 Such correlation will increase the absorption relative to vanishing excitonic effects which is often referred to as Sommerfeld amplification. The latter term describes the series of optically allowed excitonic transitions near the bandedge with discrete energy levels as in the hydrogen atom. Fig. 2(a) shows a typical absorption spectrum near the bandedge produced by arbitrary line broadening and changing the constants in eqn (9). The first three exciton peaks (designated as 1S, 2S, and 3S) in this hypothetical scenario are resolved below the continuum state. However, with increasing n the amplitude of the excitonic peaks diminishes, and the spectra across a small energy range approach a constant thereby merging into the continuum at the bandedge. The density of states close to the bandgap would vanish when no excitonic effects are considered [red curve, Fig. 2(a)].

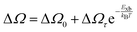
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Exb/kBT) represents the thermally dissociated exciton broadening. Using this approach for MAPbI3−xClx, Exb was found to be 55 ± 10 meV. Due to the band-to-band absorption and the overlap of excitons, accurate experimental determination of the FWHM might pose challenges.
exp(−Exb/kBT) represents the thermally dissociated exciton broadening. Using this approach for MAPbI3−xClx, Exb was found to be 55 ± 10 meV. Due to the band-to-band absorption and the overlap of excitons, accurate experimental determination of the FWHM might pose challenges.
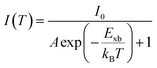

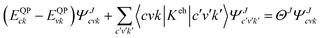

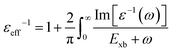
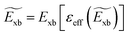

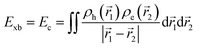
![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 1 and
1 and ![[r with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_0072_20d1.gif) 2 respectively. Using the inter-fragment charge transfer method (IFCT),193,194 the number of electrons transferred can be calculated from the ground state to the first singlet state between each species of perovskites. However, eqn (16) neglects the kinetic energy term associated with electron–hole confinement that highly affects the dielectric behavior.
2 respectively. Using the inter-fragment charge transfer method (IFCT),193,194 the number of electrons transferred can be calculated from the ground state to the first singlet state between each species of perovskites. However, eqn (16) neglects the kinetic energy term associated with electron–hole confinement that highly affects the dielectric behavior.
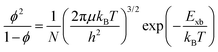


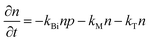
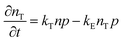
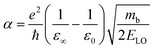
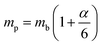
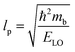
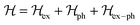
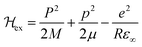
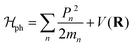
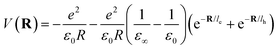
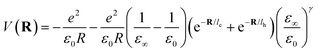
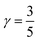 represents the optimal choice for polar crystals having large α values.224 Pollman and Büttner225 introduced the electron–polaron and hole–polaron correlations in the Haken potential and the resulting potential can be expressed as
represents the optimal choice for polar crystals having large α values.224 Pollman and Büttner225 introduced the electron–polaron and hole–polaron correlations in the Haken potential and the resulting potential can be expressed as