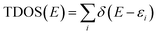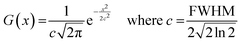Open Access Article
Open Access ArticleToward tuning the bandgap in meta-substituted Fe-MOFs†
Kyle I.
Williamson
,
Daniel J. C.
Herr
* and
Yirong
Mo
 *
*
Department of Nanoscience, Joint School of Nanoscience and Nanoengineering, University of North Carolina at Greensboro, Greensboro, NC 27401, USA. E-mail: djherr@uncg.edu; y_mo3@uncg.edu
First published on 5th August 2024
Abstract
Semiconductor materials are crucial components in current and upcoming green industrial sectors, such as electric vehicles. As supply chain issues loom with sources of semiconductor materials, there is an emerging need for alternative and environmentally friendly semiconducting materials. One of the potential candidates is iron metal–organic frameworks (Fe-MOFs) which have been used as photocatalysts. Studying the bandgap modulation trends in Fe-MOFs thus will be beneficial for future applications in semiconductor technologies. With a response surface method, here we examine the bandgap, HOMO, and LUMO energy level trends in MOF-5 fully transmetalated with iron (i.e., Fe-MOF-5), as a function of the substituent effect (in the term of Hammett constant σm) and solvent effect (in the term of dielectric constant ε). The bandgap, HOMO, and LUMO energy levels all decrease with decreasing ε and increasing σm. However, the dominating influence for the bandgap switches from σm and ε to just ε as the value of ε increases. This result along with the polynomial equations of fit from statistical analysis suggest that the bandgap in these transmetalated models is significantly influenced by the dipole–induced dipole interactions. These results provide insight into the impact of shifting interactions of σm and ε on the bandgap of Fe-MOF-5.
Introduction
Metal–organic frameworks (MOFs) have been studied extensively for various applications, such as gas absorption/storage, chemical sensing, and catalysis.1–9 In recent years, transmetalation reaction has been applied to MOFs to enhance and control their various applications.10–17 Transmetalation is a fundamental reaction in organometallic chemistry in which organic ligands are transferred between metal groups.18 This reaction has long been used in the photocatalysis research community as a facile avenue to control reduction oxidation reactions.12,19–29 As a result, transmetalated MOFs have been of keen interest in the search for new photocatalysts that are environmentally stable and friendly. This has progressed into photocatalytic MOF research focusing on the reduction of CO2, solar powered water splitting, and environmental remediation within the range of visible light.30–37 Photocatalytic performance of MOFs can be tuned with the ligand via modifications to the ligand functional group or using a ligand with an active site.31 Additionally, the metal node can be modified with the specific interest in mixed valence metals that can increase the efficiency of photocatalytic reduction reations.33 Iron based MOFs (Fe-MOFs) show great promise as environmentally friendly photocatalysts due to their thermal stability, chemical stability, water stability, and low toxicity.30,37 These advances suggest that Fe-MOFs may also be used as environmentally friendly semiconductor materials.MOFs have only recently been studied as potential semiconductor materials, but their design space is promising for new materials in fields ranging from electronics to electrochemistry.38–41 This expansion has included computational studies to assess the roles of the metal nodes and ligands in relation to the bandgaps of MOFs.10,11,42–48 Both experimental and computational reports of large changes in the bandgap resulting from ligand modifications have stimulated more studies in this direction. For instance, Gascon et al. reported an inverse linear relationship between band gap values and the Hammett σ values of the different substituents of the linker.26 From the foundational physical organic chemistry, the Hammett plot is a scale in which negative Hammett σ meta (σm) values indicate electron donation, and positive Hammett σm values correspond to electron withdrawal.49,50 The role of electron donating and withdrawing groups on bandgap has been studied on several MOFs, including MOF-5 and UiO-66.22,26,51,52 In contrast, the role of metal centers on the bandgap of MOFs has been little addressed.
In terms of bandgap, cobalt transmetalation of MOF-5 was reported in a previous computational study by Choi et al.53 Varying the amount of cobalt from 0–100% resulted in the bandgap decreasing, reaching zero, then increasing again. Yasin et al. modeled the electronic structure properties of MOFs while varying the metal atoms down the same column in the periodic table.54 A major finding from this study was that the smallest bandgap occurred for the metal at the top of the same group. While insightful, these previous works do not include solvents in the computational models. Considering the porosity of MOFs, the environmental effect may considerably influence bandgaps. Thus, this work focuses on the impacts of both substituent groups and solvents on the bandgap of MOF-5 fully transmetalated with iron (Fe-MOF-5).
We seek to understand potential interaction trends between ligand modification via substituent groups and solvent environment on the bandgap of Fe-MOF-5. We achieved this by using a quadratic response surface experimental design to create various Fe-MOF-5 models that were fully transmetalated with iron. Previously we used a similar strategy to study the Zn-MOFs.55 Modelling the full transmetalation was chosen to ensure there would be a bandgap to monitor, given the results of previous studies.53 Likewise, iron was chosen as the transmetalated metal due to the promising properties and potential of Fe-MOFs as a green semiconductor.30,36 The input responses in the statistical analysis were substituent groups (in the term of Hammett constant σm) and solvents (in the term of dielectric constant ε), and the output responses were bandgap, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) energy levels. The impact of solvents on MOFs is usually detrimental, leading to structural degradation.56–58 However, as MOFs are porous materials likely to come into contact with solvents in the environment, it is prudent to study solvent effects on the bandgap in Fe-MOF-5 models. From literature results, the expectation is that the lowest bandgap value will result from the combination of the lowest dielectric solvent and an electron donating substituent group such as NH2.
Methods
This work utilizes a response surface method (RSM) design to study changes in the bandgap, HOMO energy level, and LUMO energy level of Fe-MOF-5 models that vary based on the ligand substituents and solvent. Generally, RSM methods are used to estimate interactions and quadratic effects, which inform the local shape of the response surface.59 While RSM methods have several applications, including finding optimal process settings, our goal in using a RSM design is to generate fitted curves from the simulated results to find trends in bandgap modulation of Fe-MOF-5. For our numerical inputs, we utilized Hammet's σm values to represents the electron donating and electron withdrawing capability of the substituent groups on the ligands and solvent dielectric (ε) values to represent the solvent polarity from the environment in the MOF pore. Doing so allows us to interpret the resulting response surface trends using fundamental physical chemistry principles.The response surfaces were created and analyzed using the standard quadratic response design in the EChip software.60 In experimental design, a minimal number of trials under different conditions are performed to generate data to fit a response surface. A certain number of replicates, or repeats of trials under the same conditions, is always needed to verify the fit, or lack of fit, of the response surface to the resulting data. Determining fit is usually accomplished using the replicate standard deviation from the data from the initial trials.60 The total number of trials is listed in Table 1 in the Results and discussion section, and goes beyond the original number 11 for trials and 5 for replicates suggested by the software. Note that the replicate trials (Trial 1–5) resulted in the same values due to the accuracy of the computational chemistry program. While this would not result in sufficient variability for the EChip software to account for replicate variations, the residual variations reported are low. Residual standard deviation, or the residual variation, is the root mean squared values between the reported data points and the fitted curve.60 While a poorer estimate of true error than replicate standard deviation, residual standard deviation can still be used to determine significance of effects of the substituent groups and solvent on the response factors (bandgap, HOMO, and LUMO). This lowers the statistical rigor of this analysis, but extra trials beyond the initially suggested number of trials bolsters the reliability of our results.
| Trial | σ m | Substituent | ε | Solvent | Bandgap (eV) | HOMO (eV) | LUMO (eV) |
|---|---|---|---|---|---|---|---|
| 10 | 0.71 | NO2 | 47.2 | DMSO | 0.23 | −4.61 | −4.38 |
| 4 | 0.71 | NO2 | 80.4 | Water | 0.23 | −4.59 | −4.37 |
| 1 | −0.16 | NH2 | 80.4 | Water | 0.23 | −4.26 | −4.03 |
| 3 | 0.25 | SH | 80.4 | Water | 0.23 | −4.39 | −4.16 |
| 9 | 0.71 | NO2 | 24.3 | Ethanol | 0.23 | −4.61 | −4.38 |
| 11 | 0.12 | OH | 47.2 | DMSO | 0.23 | −4.33 | −4.09 |
| 4 | 0.71 | NO2 | 80.4 | Water | 0.23 | −4.59 | −4.37 |
| 5 | 0.71 | NO2 | 1.89 | Hexane | 0.22 | −4.78 | −4.56 |
| 8 | 0.12 | OH | 1.89 | Hexane | 0.22 | −4.01 | −3.79 |
| 3 | 0.25 | SH | 80.4 | Water | 0.23 | −4.39 | −4.16 |
| 1 | −0.16 | NH2 | 80.4 | Water | 0.23 | −4.26 | −4.03 |
| 7 | 0.43 | CF3 | 1.89 | Hexane | 0.22 | −4.55 | −4.33 |
| 5 | 0.71 | NO2 | 1.89 | Hexane | 0.22 | −4.78 | −4.56 |
| 22 | −0.07 | CH3 | 80.4 | Water | 0.23 | −4.3 | −4.07 |
| 2 | −0.07 | CH3 | 38.3 | DMF | 0.23 | −4.29 | −4.06 |
| 23 | 0.35 | CHO | 80.4 | Water | 0.23 | −4.49 | −4.26 |
| 24 | 0.62 | NO | 80.4 | Water | 0.23 | −4.58 | −4.36 |
| 25 | 0.62 | NO | 1.89 | Hexane | 0.22 | −4.73 | −4.51 |
| 2 | −0.07 | CH3 | 38.3 | DMF | 0.23 | −4.29 | −4.06 |
| 12 | 0.71 | NO2 | 47.2 | DMSO | 0.23 | −4.6 | −4.37 |
| 13 | 0.56 | CN | 1.89 | Hexane | 0.22 | −4.77 | −4.55 |
| 14 | 0.25 | SH | 47.2 | DMSO | 0.23 | −4.37 | −4.14 |
| 15 | 0.35 | CHO | 47.2 | DMSO | 0.23 | −4.49 | −4.27 |
| 16 | 0.25 | SH | 1.89 | Hexane | 0.23 | −4.18 | −3.95 |
| 17 | 0.35 | CHO | 1.89 | Hexane | 0.22 | −4.54 | −4.31 |
| 18 | 0 | H | 80.4 | Water | 0.23 | −4.33 | −4.1 |
| 19 | 0 | H | 38.3 | DMF | 0.23 | −4.33 | −4.09 |
| 20 | 0 | H | 1.89 | Hexane | 0.23 | −4.1 | −3.88 |
| 6 | −0.07 | CH3 | 47.2 | DMSO | 0.23 | −4.29 | −4.06 |
| 21 | 0.62 | NO | 2.4 | Toluene | 0.22 | −4.7 | −4.48 |
| 22 | −0.07 | CH3 | 80.4 | Water | 0.23 | −4.3 | −4.07 |
| 23 | 0.35 | CHO | 80.4 | Water | 0.23 | −4.49 | −4.26 |
| 24 | 0.62 | NO | 80.4 | Water | 0.23 | −4.58 | −4.36 |
| 25 | 0.62 | NO | 1.89 | Hexane | 0.22 | −4.73 | −4.51 |
GaussView was utilized to build the cluster model structures, which include the metal node of MOF-5 with zinc replaced with iron and connected to the six ligands with substituent groups based on Hammett σm values.62 Given the large number of atoms in MOF structures, many studies, including those using periodic DFT methods, treat the metal nodes and ligands separately.21,22,53,63 The rationale behind choosing a cluster model for the Fe-MOF-5 systems was to holistically represent the main building block of the MOF-5 structure.10,64 As can be seen in Table 1, each Hammett σm value corresponds to one substituent group and each ε value corresponds to a solvent. Each trial has a unique combination of σm and ε values. The substituent group indicated by the σm value was placed at the meta position on each cyclic ring on the six ligands. Thus, the values are not summed for the Fe-MOF-5 systems, but are numerical stand ins for substituent groups that can be processed by the EChip program. In this way, Fe-MOF-5 models with the same substituent group were optimized under different implicit solvent conditions. There was no mixing of substituent groups on the six ligands in the cluster model so the results would align with the experimental design discussed previously.
The quantum chemistry program ORCA 5.0 was used to run simulations in parallel due to the large size of the models.61,65 For each trial both geometry optimization and frequency calculation were run using Grimme's B97-3C composite density functional theory (DFT) method and the CPCM implicit solvation method with the appropriate solvent from the experimental design.66,67 Once each geometry optimization and frequency calculation were completed the final structures were reviewed to ensure no irregular bending in the metal nodes or ligands. As we did not restrict the ligands during geometry optimization, this process ensured that the final geometries aligned with the assumption that MOF-5 transmetalated with iron maintains the same lattice structure of MOF-5. Following this criteria, three simulation results were thrown out of the data set for being unphysical. These results are not included in Table 1, but the representative final geometries of the models in this study and of the three results excluded are in the Fig. S4 and S5 (ESI†).
The B97-3C composite method was chosen because the bandgap value for MOF-5 after the geometry optimization and frequency calculation was 4.23 eV, which is between the values determined experimentally (3.4–4.0 eV) and computationally (∼4.6 eV).24,26,39,68 The bandgap value discussed was calculated by subtracting the LUMO energy level value by the HOMO energy level value. Note the computing the transition energies from the ground state to the excited state with TD-DFT calculations would provide a more accurate representation of this energy difference.64,69 Unfortunately, performing TD-DFT calculations on these Fe-MOF-5 cluster models was beyond the capabilities of the available computational resources, even when the calculations were parallelized.
Based off our previous work, we determined that adding solvent molecules in the calculation was feasible, but did not result in a major change in bandgap, HOMO energy level, or LUMO energy level when compared with the implicit solvent models.55 With this knowledge, we chose to use implicit CPCM solvent models to study the influence of solvent polarity on the bandgap of Fe-MOF-5. A caveat of adding solvent molecules or using implicit solvent models is that a limited number of solvent molecules would enter the pores of Fe-MOF-5. This means that some of the solvents applied in this study with the CPCM model are unlikely to enter the pores of a MOF with the structure of MOF-5. However, design of pore size is a major strength of MOF materials, and many MOFs with larger pores than MOF-5 exist.47,52,54,70,71 Therefore, we believe that interactions between environmental solvent polarity and the bandgap of Fe-MOF-5 in this study might inform future studies of bandgaps in MOFs with larger pore sizes. Table 1 lists the solvents used corresponding to their respective solvent dielectric (ε) values and substituent group identities corresponding to the Hammett σm values. The specific values of ε were pulled from the ORCA handbook and the σm values were taken from tables in the classic work of Hansch et al.50,65
All molecular orbital diagrams were generated using the orca_plot function in ORCA 5.0 and VMD for visualization.65,72 In addition, the MultiWFN program73 was used to generate ORCA input files from the Protein Data Bank (PDB) structural files outputted by GaussView. The total density of state (TDOS) and partial density of state (PDOS) data sets were generated using the Becke atomic space method and density of state approximation methods in the MultiWFN program.73–75 The TDOS, PDOS, and discrete energy levels of the data sets were plotted using Excel. It is important to discuss the caveats of using this method in MultiWFN. From the stand point of solid-state physics, density of state (DOS) represents the number of energy states or levels as contiguous, and thus is plotted as a curve.76 For isolated systems such as molecules and the cluster models used in this study, energy levels are discrete.69 The MultiWFN program replacing the Dirac delta function (δ) in the following equation with a broadening function F(x) dependent on the full width half maximum (FWHM).73–75
This artificially broadens the discrete energy levels to a curve, allowing analysis of the electron structure across the different Fe-MOF-5 models. We understand that this method is debated among the computational chemistry community due to the inherent limitations and assumptions of the broadening function in the above equation. However, we make no claim that the approximated DOS plots in this work are quantitative at the scale of larger periodic structures, which is the domain of periodic DFT calculations. Rather, we use these approximated DOS plots to inform changes in the nature of the electron structure across the various Fe-MOF-5 models in this study. In doing so, our work attempts intimate why the trends, or lack thereof, between bandgap, substituent group, and solvent occur in Fe-MOF-5.
Results and discussion
Following previous work,49,50,55 the Hammett σm and solvent dielectric ε values were used as the variables in the quadratic response surface design as these have been empirically determined. An issue with the original set of trials was the presence of three outlying outcomes, as shown in the chart in Fig. 1 and Fig. S5 (ESI†). Note that two of the trials had the same values, resulting in only two stars being visible in the chart. Also, this chart was generated with the EChip program from bandgap results.60 These three outcomes had geometries with twisted metal nodes, which would be unlikely in the actual extended MOF structure. Following the criteria discussed in the Methods section, these three trials were excluded from Table 1 and further analysis in this design due to being unphysical. Note that this limits the boundaries of the response as seen in Fig. 2 and 3, meaning that any interpretation of results in these regions is an extrapolation.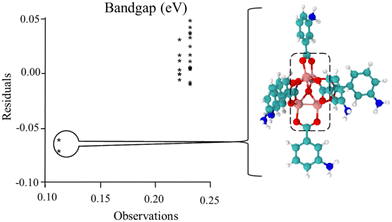 | ||
| Fig. 1 Comparison of observations to residuals in the original set of trials. For the structures of the bandgap observations at 0.11 eV, there was significant twisting of the metal node as shown. This occurred for the original trial 6, shown in this figure, and trial 2 and trial 2 replicate, in the Fig. S5 (ESI†). As this twisting is expected not to exist in the fully extended MOF, these results were determined as unphysical and excluded from the data set for subsequent analyses. | ||
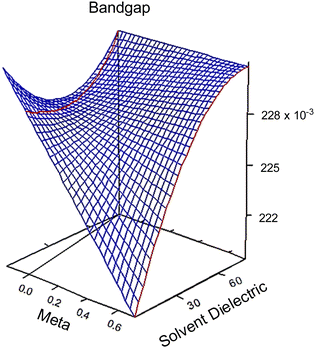 | ||
| Fig. 2 3D response surfaces of bandgap behaviors in regards to meta (σm) and solvent dielectric (ε). The 3D response surfaces for the HOMO and LUMO response are in the ESI,† Fig. S6. Note the red and black lines on the left side of each graph. These intersections with the surfaces indicate that anything plotted to the left of that line is an extrapolation and no conclusion should be drawn based on this portion of the surface. | ||
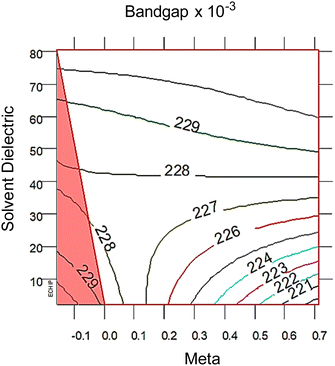 | ||
| Fig. 3 2D response surfaces of bandgap, with the red triangle correlates with the red and black intersecting lines in the 3D response surfaces in Fig. 2 The 2D response surfaces for HOMO and LUMO are in the ESI,† Fig. S7. Note that lower solvent dielectric (ε) leads to meta (σm) having a larger impact on bandgap, whereas at higher ε values the σm term is not important. The distance between each colored line is 2σ significance. | ||
It also should be noted that we did not use the nearest neighbor substituent group method used in our previous work55 to approximate replicate standard deviations. The statistical analysis software used in this study assumes variability from performing the same experiment twice, which is not the case for computational modelling. The decision to change the method of analysis was reached due to the lower residual standard deviation of the bandgap (0.002), HOMO energy level (0.06), and LUMO energy level (0.06). Further discussion of this can be found in ESI.† The takeaway from this information is that the following trends follow the data closely, but any relationship like eqn (1)–(3) are not statistically significant.
A result of this analysis is that substituent groups and solvent molecules interact to impact the three response factors, albeit in a minor way. This can be seen in the following polynomial equations that describe the response surfaces seen in Fig. 2.
| Bandgap = 0.23 − 4.16 × 10−6σm + 7.09 × 10−5ε + 0.0002σm × ε − 4.34 × 10−6σmε2 | (1) |
| HOMO = −4.39 − 0.37σm − 0.001ε + 0.009σm × ε − 0.0002σm × ε2 | (2) |
| LUMO = −4.17 − 0.39σm − 0.001ε − 0.009σm × ε − 0.0002σm × ε2 | (3) |
Note that these equations are reported to demonstrate the varying model coefficients and the influence on the response surface. Additionally, all the statistical significance and error information from the software is not present in these equations. Thus, these equations cannot be used simply to extrapolate beyond the dataset.60 The significance levels between bandgap and the variables are: ε (0.01%), σmε (0.01%), and σmε2 (5%). For the HOMO and LUMO energy levels, the significance levels are the same: σm (0.01%), ε (1%), σmε (0.01%), and σmε2 (0.01%). While these significance levels are not statistical due to the design, these values quantify the relationships seen in Fig. 2.
At high dielectric values, the slope of the bandgap response surface barely changes as the Hammett σm goes from 0 to 0.71. As the solvent dielectric decreases, the bandgap also decreases, especially as the Hammett σm value increases. This curvature at high σm values along the solvent dielectric axis for bandgap appears to be due to the HOMO and LUMO. As seen in Fig. S6 (ESI†), the response surfaces for both HOMO and LUMO are dominated by σm until at high σm values the solvent dielectric curves down. The 2D topographies in Fig. S7 (ESI†) further supports a shifting relationship between σm and ε. The 2D topography graphs for HOMO and LUMO in Fig. S7 (ESI†) show both values bulge outward as the ε value increases. The first conclusion of this bulging is that the substituent group is more impactful in modulating HOMO and LUMO at lower ε values. As ε values increase, the substituent groups diminish their influence over HOMO and LUMO energy levels drastically. This is seen in the bandgap trend, where the substituent group becomes unimportant in changing the bandgap value as ε values increase. This leads to the second, unexpected conclusion in the bandgap trend, which is the switching of modulation method as ε decreases. At and above the ε value of ∼45, bandgap is controlled by ε alone. Below the ε value of ∼45, bandgap is controlled by both ε and σm.
From the polynomial equation used to generate the response surface for bandgap, eqn (1), there is a second order effect in ε that interacts with σm in the last term. This is likely why the 2D response surface for bandgap in Fig. 3 shifts from curved lines to horizontal lines as ε increases. In terms of explaining the nature of the interaction behind this phenomenon, we believe that there is a dipole–induced dipole interaction between solvent (with a permanent dipole moment μ) and the modeled MOF molecule (with a polarizability α).77 The rationale comes from the fundamental equation of the average interaction energy V for the dipole–induced dipole interaction (eqn (4)) where α′ is the polarizability volume proportional to the polarizability α of the MOF molecule (eqn (5)).
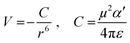 | (4) |
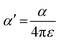 | (5) |
Experimentally, polarizability volume α′ increases as the difference between LUMO and HOMO energy levels (the bandgap) decreases.77 This suggest that polarizability volume of the MOF increases as the substituent become more electron withdrawing (σm value increases from 0 to 0.71 along Meta axis on bandgap graph in Fig. 2). Ostensibly, this shift in α′ appears to be due to the electron withdrawing group increasing the polarizability α of the MOF. The second order effect for ε seen in eqn (1) may be explained by the ε term appearing in both eqn (4) and (5). Thus, even if the substituent group increases α′, increasing the value of ε from 1.89 to 80.4 lowers both α′ and V.
This aligns with the bandgap trend seen in Fig. 3 where the ε term solely controls bandgap at high values, but interacts with the σm term at low values. While the models used in this study are approximations, these results have interesting physical implications. When the solvent is non-polar, or low ε value, the increasing polarizability due to increasing electron withdrawing ability of the substituent groups causes a stronger average interaction between the solvent and MOF. As the solvent become polar protic, or high ε value, the shifting polarizability becomes an unimportant term. This interpretation reveals that engineering bandgap in metal–organic frameworks may be feasible through interactions of electron structure changes (substituent groups) and environmental factors (polarity of the solvent).
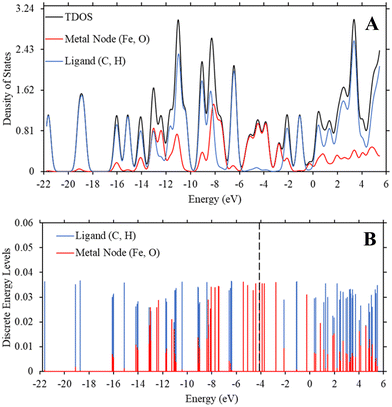
While interesting, the relationship we draw above between the trend in Fe-MOF-5 bandgap and the fundamental equations for dipole-induced dipole interactions is based on a minimal change in bandgap between 0.22 eV to 0.23 eV. This is surprising, as our previous study using a similar method revealed that changing substituent groups on the ligand was statistically significant to modulating bandgap in MOF-5.55 To further understand why substituent groups and solvents had such a minimal impact on Fe-MOF-5 compared to MOF-5, we generated density of state graphs and discrete energy level graphs as described in Methods. These graphs reveal the role of iron in controlling the bandgap and keeping changes minimal.
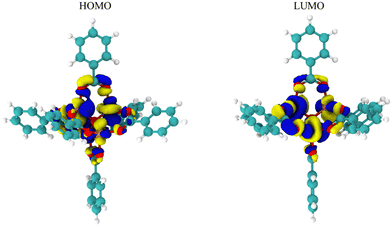
While Fig. 2 and 3 show this shifting relationship, the preceding approximate density of state and discrete energy level graphs suggest why the bandgap shifts by a small degree (Fig. 4 and Fig. S8, S9, ESI†). With iron completely replacing the zinc in the MOF-5 structure, the bandgap barely shifts as the substituent groups are changed in hexane. While the total density of state changes, the HOMO and LUMO energy levels are dominated by the metal node, as seen by the red spectrum and discrete energy levels in Fig. 4. The orbital plots (Fig. 5 and Fig. S10, S11, ESI†) also show a high concentration around the metal node, agreeing with the graphs in Fig. 4. This stabilization in bandgap due to switching zinc with iron in the MOF-5 structure is expected, but it is unclear if this is solely governed by the iron atom.
To determine if the iron atom is directly responsible for the bandgap, we generated the density of state and discrete energy level graphs focusing solely on the iron and oxygen atoms (Fig. 6). In Fig. 6, the HOMO energy level (vertical dashed line at −4.104 eV) and LUMO energy level are firmly in the energy levels of the iron atoms, as seen in the approximated PDOS spectrum and the red discrete energy levels. Therefore, the bandgap in Trial 20 is determined by the energy levels of iron atoms in the model. To see if this trend holds across the study, we generated approximate density of state graphs and discrete energy level graphs at different substituent and solvent conditions in this study. In Fig. S12–S14 (ESI†), the substituent groups vary from σm values of 0 to 0.71 while keeping the solvent the, hexane (ε = 1.89), the same. In Fig. S14–S16 (ESI†), the ε values vary from 80.4 to 1.89 while the substituent group, NO2 (σm = 0.71), is kept the same. Across all these conditions, the bandgap, or HOMO–LUMO energy difference, is within the energy levels of the iron atoms.
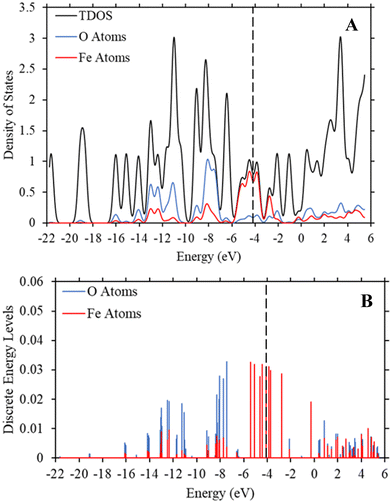 | ||
| Fig. 6 (A) TDOS and PDOS maps of the iron and oxygen atoms in Trial 20 of Fe-MOF-5 with a ε value of 1.89 (hexane). (B) The discrete energy levels of the iron (red) and oxygen (blue) atoms in the Fe-MOF-5 model. These graphs, along with those in the ESI,† show that the HOMO and LUMO energy levels are within the energy levels of the iron atoms. The vertical dashed line is the HOMO energy level at −4.104 eV. The y-axis represents the strength of the density of states and discrete energy levels and are unitless. | ||
These figures show that the tight control of bandgap across different substituent groups and solvents appears to be due to the minimal shifting in the electron density in iron in the Fe-MOF-5 frameworks. As seen in Table 1, the bandgap for these models varies between 0.22–0.23 eV, which is why the approximated density of state graphs appear to have no bandgap in the HOMO–LUMO region. As explained in the Methods section, this is a limitation of the approximation method used to generate the density of state graphs. The important take aways from these results is that the energy levels of the iron atoms determine the bandgap in the Fe-MOF-5 models and that these iron energy levels are not drastically impacted by changing substituent groups or solvents. Another result supported by literature, but not captured in this response surface design alone, is that changing the metal in MOFs, i.e. changing the d-shell valency in the structure, drastically impacts bandgap.11,16 This suggest that the bandgap stabilization see in this study may be related to iron atoms having more open energy levels in the valent d-shell as compared to zinc atoms.
The behavior seen in the approximate density of state graphs above reveals a sharp difference between the electron structure of Fe-MOF-5 and MOF-5. From the electron structure of MOF-5 in our previous study revealed the HOMO–LUMO transition was focused around the ligands and substituent groups.55 Given the dominant impact of the substituent group in modulating bandgap in MOF-5, we were unable to determine the dipole–induced dipole relationship. Using eqn (4) and (5) as a frame of reference, the previous behavior of MOF-5 bandgap may be explained by the zinc atoms creating an environment for the electron structure of MOF-5 to shift drastically across different substituents. This drastic change in electron structure due to the substituent groups resulted in larger changes in polarizability of MOF-5 that overtook the influence of solvent polarity.
Thus, this set of data suggests the following as a guiding principle in modulating bandgap in MOFs. Decreasing the d-shell vacancy of the metal atoms in the MOF node decreases the polarizability shift from substituent groups, allowing the solvent dielectric, or solvent polarity, to influence the bandgap. This solvent influence on bandgap seems to occur via a dipole–induced dipole interaction between the solvent and Fe-MOF-5 models. Again, the bandgap shifts seen in the Fe-MOF-5 models in this work are very small, indicating that MOF-5 fully transmetalated with iron has a very stable electron structure. This is supported by other work in iron MOFs, which have shown that iron MOFs are incredibly stable in the environment.36,37 While studying the stability of the Fe-MOF-5 models was outside the scope of this work, these results suggest that stabilizing MOFs via transmetalation with iron may decrease the efficacy of bandgap modulation strategies. From these results, the solvent in pore environment of MOFs need to be further studied to determine tradeoffs between environmental stability and bandgap modulation in MOFs via transmetalation.
Conclusion
This work used a quadratic response surface experimental design to computationally map out the influences of substituent groups and solvents on the bandgap, HOMO, and LUMO energy levels in MOF-5 fully transmetalated with iron atoms. While the resulting models are qualitative, the low residual standard deviation values suggest that the trends in this study are still informative. The results indicate that the substituent group (in σm) and solvent (in ε) interact to change the bandgap, HOMO, and LUMO energy levels. For the bandgap, the interaction between substituent group and solvent decreases as the ε increases until the solvent alone influences the bandgap value. For the HOMO and LUMO energy levels, the substituent is the most impactful variable at low values of ε. However, when ε increases, the influence of the substituent on HOMO and LUMO energy levels decreases (Fig. 3). Given the second order effect of ε seen in eqn (1)–(3), the likely physical or molecular interaction is a dipole–induced dipole electrostatic interaction. The interaction between σm and ε seemingly originates from the full transmetalation of MOF-5 from zinc to iron. From the molecular orbital diagrams of the HOMO and LUMO energy levels, the electron density centers around the metal node. Specifically, the density of state graphs in Fig. 5 and 6 shows that HOMO and LUMO both lie in the electron density of the iron atoms in the models. Ostensibly, this is all due to the lower d-shell valency of the iron atoms as compared to the full d-shell valency of the zinc atoms.In conclusion, this study reveals a few guiding principles for bandgap modulation in MOF-5 fully transmetalated with iron. First, in solvents with high ε values, changing the substituent group have little to no impact on bandgap values. As the solvent ε values decrease to low values, the substituent interacts with the solvent to lower bandgap as the substituent becomes more electron withdrawing. Second, while the above results are shown in this study, the actual changes to bandgap, HOMO, and LUMO energy levels is small. This is due the HOMO and LUMO energy level being in the electron density of the iron atoms, which are not strongly influenced by the substituent groups or solvents. This suggest that using a metal between iron and zinc (cobalt, nickel, and copper) may allow for shifting substituent groups and solvents to more significantly influence the response factors through a dipole–induced dipole interaction.
While this work focused specifically on engineering bandgap in MOFs, these results have implications for using MOFs as photo-catalyst.13,26,28,70 In terms of future work, this method and results indicate fruitful ground to explore in terms of other stable metal ions (such as Al, Ti, and Zr), mixed metal system (bimetallic and trimetallic), and ligand systems capable of capturing metal ions.30,37,78,79 Another area for future investigations is Fe-MOF-5 systems where the substituent groups were mixed across the ligands. The expectation is that such systems will align with the results of this study, however uncaptured influences like steric and inductive interactions may influence such systems. Lastly, further computational and experimental investigations of the tradeoffs between environmental stability and bandgap modulation in MOFs is critical as the field continues to develop MOFs as components in applied sensor technologies.78,80–84
Data availability
The data that support the findings of this study are available in the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was performed at the Joint School of Nanoscience and Nanoengineering, a member of the Southeastern Nanotechnology Infrastructure Corridor (SENIC) and National Nanotechnology Coordinated Infrastructure (NNCI), supported by the NSF (Grant ECCS-2025462). This work was partly supported by Department of Defense (Contract #W911QY2220006).References
- O. M. Yaghi, M. O’Keeffe, N. W. Ockwig, H. K. Chae, M. Eddaoudi and J. Kim, Reticular Synthesis and the Design of New Materials, Nature, 2003, 423(6941), 705–714, DOI:10.1038/nature01650.
- M. Wang, L. Guo and D. Cao, Metal–Organic Framework as Luminescence Turn-on Sensor for Selective Detection of Metal Ions: Absorbance Caused Enhancement Mechanism, Sens. Actuators, B, 2018, 256, 839–845, DOI:10.1016/j.snb.2017.10.016.
- M. Eddaoudi, J. Kim, N. Rosi, D. Vodak, J. Wachter, M. O’Keeffe and O. M. Yaghi, Systematic Design of Pore Size and Functionality in Isoreticular MOFs and Their Application in Methane Storage, Science, 2002, 295(5554), 469–472 CrossRef CAS.
- E. J. García, D. Bahamon and L. F. Vega, Systematic Search of Suitable Metal–Organic Frameworks for Thermal Energy-Storage Applications with Low Global Warming Potential Refrigerants, ACS Sustainable Chem. Eng., 2021, 9(8), 3157–3171, DOI:10.1021/acssuschemeng.0c07797.
- C. A. Bauer, T. V. Timofeeva, T. B. Settersten, B. D. Patterson, V. H. Liu, B. A. Simmons and M. D. Allendorf, Influence of Connectivity and Porosity on Ligand-Based Luminescence in Zinc Metal−Organic Frameworks, J. Am. Chem. Soc., 2007, 129(22), 7136–7144, DOI:10.1021/ja0700395.
- S. Bauer, C. Serre, T. Devic, P. Horcajada, J. Marrot, G. Férey and N. Stock, High-Throughput Assisted Rationalization of the Formation of Metal Organic Frameworks in the Iron(III) Aminoterephthalate Solvothermal System, Inorg. Chem., 2008, 47(17), 7568–7576, DOI:10.1021/ic800538r.
- H. Li, M. Eddaoudi, M. O’Keeffe and O. M. Yaghi, Design and Synthesis of an Exceptionally Stable and Highly Porous Metal–Organic Framework, Nature, 1999, 402(6759), 276–279, DOI:10.1038/46248.
- H. Kim, S. Das, M. G. Kim, D. N. Dybtsev, Y. Kim and K. Kim, Synthesis of Phase-Pure Interpenetrated MOF-5 and Its Gas Sorption Properties, Inorg. Chem., 2011, 50(8), 3691–3696, DOI:10.1021/ic200054b.
- N. Stock and S. Biswas, Synthesis of Metal–Organic Frameworks (MOFs): Routes to Various MOF Topologies, Morphologies, and Composites, Chem. Rev., 2012, 112(2), 933–969, DOI:10.1021/cr200304e.
- J. L. Mancuso, A. M. Mroz, K. N. Le and C. H. Hendon, Electronic Structure Modeling of Metal–Organic Frameworks, Chem. Rev., 2020, 120(16), 8641–8715, DOI:10.1021/acs.chemrev.0c00148.
- J. A. Botas, G. Calleja, M. Sánchez-Sánchez and M. G. Orcajo, Cobalt Doping of the MOF-5 Framework and Its Effect on Gas-Adsorption Properties, Langmuir, 2010, 26(8), 5300–5303, DOI:10.1021/la100423a.
- M. A. Syzgantseva, C. P. Ireland, F. M. Ebrahim, B. Smit and O. A. Syzgantseva, Metal Substitution as the Method of Modifying Electronic Structure of Metal–Organic Frameworks, J. Am. Chem. Soc., 2019, 141(15), 6271–6278, DOI:10.1021/jacs.8b13667.
- J. L. Mancuso and C. H. Hendon, Titanium(IV) Inclusion as a Versatile Route to Photoactivity in Metal–Organic Frameworks, Adv. Theory Simul., 2019, 2(11), 1900126, DOI:10.1002/adts.201900126.
- P. Deria, J. E. Mondloch, O. Karagiaridi, W. Bury, J. T. Hupp and O. K. Farha, Beyond Post-Synthesis Modification: Evolution of Metal–Organic Frameworks via Building Block Replacement, Chem. Soc. Rev., 2014, 43(16), 5896–5912, 10.1039/C4CS00067F.
- S. Hausdorf, F. Baitalow, T. Böhle, D. Rafaja and F. O. R. L. Mertens, Main-Group and Transition-Element IRMOF Homologues, J. Am. Chem. Soc., 2010, 132(32), 10978–10981, DOI:10.1021/ja1028777.
- C. K. Brozek, V. K. Michaelis, T.-C. Ong, L. Bellarosa, N. López, R. G. Griffin and M. Dincă, Dynamic DMF Binding in MOF-5 Enables the Formation of Metastable Cobalt-Substituted MOF-5 Analogues, ACS Cent. Sci., 2015, 1(5), 252–260, DOI:10.1021/acscentsci.5b00247.
- M. Fuentes-Cabrera, D. M. Nicholson, B. G. Sumpter and M. Widom, Electronic Structure and Properties of Isoreticular Metal–Organic Frameworks: The Case of M-IRMOF1 (M = Zn, Cd, Be, Mg, and Ca), J. Chem. Phys., 2005, 123(12), 124713, DOI:10.1063/1.2037587.
- S. C. Rasmussen, Transmetalation: A Fundamental Organometallic Reaction Critical to Synthesis and Catalysis, ChemTexts, 2021, 7(1), 1, DOI:10.1007/s40828-020-00124-9.
- H. Khajavi, J. Gascon, J. M. Schins, L. D. A. Siebbeles and F. Kapteijn, Unraveling the Optoelectronic and Photochemical Behavior of Zn4O-Based Metal Organic Frameworks, J. Phys. Chem. C, 2011, 115(25), 12487–12493, DOI:10.1021/jp201760s.
- I. I. Vrubel, N. Yu Senkevich, E. V. Khramenkova, R. G. Polozkov and I. A. Shelykh, Electronic Structure and Optical Response of Zn-Based Metal–Organic Frameworks, Adv. Theory Simul., 2018, 1(9), 1800049, DOI:10.1002/adts.201800049.
- T. Musho and N. Wu, Ab Initio Calculation of Electronic Charge Mobility in Metal–Organic Frameworks, Phys. Chem. Chem. Phys., 2015, 17(39), 26160–26165, 10.1039/C5CP03920G.
- T. Musho, J. Li and N. Wu, Band Gap Modulation of Functionalized Metal–Organic Frameworks, Phys. Chem. Chem. Phys., 2014, 16(43), 23646–23653, 10.1039/C4CP03110E.
- G. D. Degaga, R. Pandey, C. Gupta and L. Bharadwaj, Tailoring of the Electronic Property of Zn-BTC Metal–Organic Framework via Ligand Functionalization: An Ab Initio Investigation, RSC Adv., 2019, 9(25), 14260–14267, 10.1039/C9RA00687G.
- K. T. Butler, C. H. Hendon and A. Walsh, Electronic Chemical Potentials of Porous Metal–Organic Frameworks, J. Am. Chem. Soc., 2014, 136(7), 2703–2706, DOI:10.1021/ja4110073.
- L.-M. Yang, P. Vajeeston, P. Ravindran, H. Fjellvåg and M. Tilset, Theoretical Investigations on the Chemical Bonding, Electronic Structure, And Optical Properties of the Metal−Organic Framework MOF-5, Inorg. Chem., 2010, 49(22), 10283–10290, DOI:10.1021/ic100694w.
- J. Gascon, M. D. Hernández-Alonso, A. R. Almeida, G. P. M. van Klink, F. Kapteijn and G. Mul, Isoreticular MOFs as Efficient Photocatalysts with Tunable Band Gap: An Operando FTIR Study of the Photoinduced Oxidation of Propylene, ChemSusChem, 2008, 1(12), 981–983, DOI:10.1002/cssc.200800203.
- S. Hamad, N. C. Hernandez, A. Aziz, A. R. Ruiz-Salvador, S. Calero and R. Grau-Crespo, Electronic Structure of Porphyrin-Based Metal–Organic Frameworks and Their Suitability for Solar Fuel Production Photocatalysis, J. Mater. Chem. A, 2015, 3(46), 23458–23465, 10.1039/C5TA06982C.
- A. Aziz, A. R. Ruiz-Salvador, N. C. Hernández, S. Calero, S. Hamad and R. Grau-Crespo, Porphyrin-Based Metal–Organic Frameworks for Solar Fuel Synthesis Photocatalysis: Band Gap Tuning via Iron Substitutions, J. Mater. Chem. A, 2017, 5(23), 11894–11904, 10.1039/C7TA01278K.
- C. H. Hendon, D. Tiana, M. Fontecave, C. Sanchez, L. D’arras, C. Sassoye, L. Rozes, C. Mellot-Draznieks and A. Walsh, Engineering the Optical Response of the Titanium-MIL-125 Metal–Organic Framework through Ligand Functionalization, J. Am. Chem. Soc., 2013, 135(30), 10942–10945, DOI:10.1021/ja405350u.
- M. Tahir, B. Ajiwokewu, A. A. Bankole, O. Ismail, H. Al-Amodi and N. Kumar, MOF Based Composites with Engineering Aspects and Morphological Developments for Photocatalytic CO2 Reduction and Hydrogen Production: A Comprehensive Review, J. Environ. Chem. Eng., 2023, 11(2), 109408, DOI:10.1016/j.jece.2023.109408.
- L. Jiao, Y. Wang, H.-L. Jiang and Q. Xu, Metal–Organic Frameworks as Platforms for Catalytic Applications, Adv. Mater., 2018, 30(37), 1703663, DOI:10.1002/adma.201703663.
- J. Liu, L. Chen, H. Cui, J. Zhang, L. Zhang and C.-Y. Su, Applications of Metal–Organic Frameworks in Heterogeneous Supramolecular Catalysis, Chem. Soc. Rev., 2014, 43(16), 6011–6061, 10.1039/C4CS00094C.
- R. Li, W. Zhang and K. Zhou, Metal–Organic-Framework-Based Catalysts for Photoreduction of CO2, Adv. Mater., 2018, 30(35), 1705512, DOI:10.1002/adma.201705512.
- X. Li, Z. Wang and L. Wang, Metal–Organic Framework-Based Materials for Solar Water Splitting, Small Sci., 2021, 1(5), 2000074, DOI:10.1002/smsc.202000074.
- S. Varangane, C. S. Vennapoosa, A. Tiwari, S. K. Nataraj, T. P. Yendrapati and U. Pal, In Situ Synthesis of Cu-Doped ZIF-8 for Efficient Photocatalytic Water Splitting, Appl. Organomet. Chem., 2022, 36(9), e6815, DOI:10.1002/aoc.6815.
- Q. Wang, Q. Gao, A. M. Al-Enizi, A. Nafady and S. Ma, Recent Advances in MOF-Based Photocatalysis: Environmental Remediation under Visible Light, Inorg. Chem. Front., 2020, 7(2), 300–339, 10.1039/C9QI01120J.
- S. Li, P. Luo, H. Wu, C. Wei, Y. Hu and G. Qiu, Strategies for Improving the Performance and Application of MOFs Photocatalysts, ChemCatChem, 2019, 11(13), 2978–2993, DOI:10.1002/cctc.201900199.
- J. Li, T. Musho, J. Bright and N. Wu, Functionalization of a Metal–Organic Framework Semiconductor for Tuned Band Structure and Catalytic Activity, J. Electrochem. Soc., 2018, 166(5), H3029, DOI:10.1149/2.0051905jes.
- S. Bordiga, C. Lamberti, G. Ricchiardi, L. Regli, F. Bonino, A. Damin, K.-P. Lillerud, M. Bjorgen and A. Zecchina, Electronic and Vibrational Properties of a MOF-5 Metal–Organic Framework: ZnO Quantum Dot Behaviour, Chem. Commun., 2004,(20), 2300–2301, 10.1039/B407246D.
- H. C. Streit, M. Adlung, O. Shekhah, X. Stammer, H. K. Arslan, O. Zybaylo, T. Ladnorg, H. Gliemann, M. Franzreb, C. Wöll and C. Wickleder, Surface-Anchored MOF-Based Photonic Antennae, ChemPhysChem, 2012, 13(11), 2699–2702, DOI:10.1002/cphc.201200262.
- C. Muschielok and H. Oberhofer, Aspects of Semiconductivity in Soft, Porous Metal–Organic Framework Crystals, J. Chem. Phys., 2019, 151(1), 015102, DOI:10.1063/1.5108995.
- S. S. Han, S.-H. Choi and A. C. T. van Duin, Molecular Dynamics Simulations of Stability of Metal–Organic Frameworks against H2O Using the ReaxFF Reactive Force Field, Chem. Commun., 2010, 46(31), 5713–5715, 10.1039/C0CC01132K.
- M. Tafipolsky, S. Amirjalayer and R. Schmid, Ab Initio Parametrized MM3 Force Field for the Metal–Organic Framework MOF-5, J. Comput. Chem., 2007, 28(7), 1169–1176, DOI:10.1002/jcc.20648.
- Q. Yang, D. Liu, C. Zhong and J.-R. Li, Development of Computational Methodologies for Metal–Organic Frameworks and Their Application in Gas Separations, Chem. Rev., 2013, 113(10), 8261–8323, DOI:10.1021/cr400005f.
- K. C. Stylianou, J. Rabone, S. Y. Chong, R. Heck, J. Armstrong, P. V. Wiper, K. E. Jelfs, S. Zlatogorsky, J. Bacsa, A. G. McLennan, C. P. Ireland, Y. Z. Khimyak, K. M. Thomas, D. Bradshaw and M. J. Rosseinsky, Dimensionality Transformation through Paddlewheel Reconfiguration in a Flexible and Porous Zn-Based Metal–Organic Framework, J. Am. Chem. Soc., 2012, 134(50), 20466–20478, DOI:10.1021/ja308995t.
- J. Witte, J. B. Neaton and M. Head-Gordon, Assessing Electronic Structure Approaches for Gas-Ligand Interactions in Metal–Organic Frameworks: The CO2-Benzene Complex, J. Chem. Phys., 2014, 140(10), 104707, DOI:10.1063/1.4867698.
- M. Taddei, D. Tiana, N. Casati, J. A. Bokhoven, B. van Smit and M. Ranocchiari, Mixed-Linker UiO-66: Structure–Property Relationships Revealed by a Combination of High-Resolution Powder X-Ray Diffraction and Density Functional Theory Calculations, Phys. Chem. Chem. Phys., 2017, 19(2), 1551–1559, 10.1039/C6CP07801J.
- S. S. Han, J. L. Mendoza-Cortés and W. A. G. Iii, Recent Advances on Simulation and Theory of Hydrogen Storage in Metal–Organic Frameworks and Covalent Organic Frameworks, Chem. Soc. Rev., 2009, 38(5), 1460–1476, 10.1039/B802430H.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University Science Books, 2006 Search PubMed.
- Corwin Hansch, A. Leo and R. W. Taft, A Survey of Hammett Substituent Constants and Resonance and Field Parameters, Chem. Rev., 1991, 91(2), 165–195, DOI:10.1021/cr00002a004.
- H. Q. Pham, T. Mai, N.-N. Pham-Tran, Y. Kawazoe, H. Mizuseki and D. Nguyen-Manh, Engineering of Band Gap in Metal–Organic Frameworks by Functionalizing Organic Linker: A Systematic Density Functional Theory Investigation, J. Phys. Chem. C, 2014, 118(9), 4567–4577, DOI:10.1021/jp405997r.
- K. Hendrickx, D. E. P. Vanpoucke, K. Leus, K. Lejaeghere, A. Van Yperen-De Deyne, V. Van Speybroeck, P. Van Der Voort and K. Hemelsoet, Understanding Intrinsic Light Absorption Properties of UiO-66 Frameworks: A Combined Theoretical and Experimental Study, Inorg. Chem., 2015, 54(22), 10701–10710, DOI:10.1021/acs.inorgchem.5b01593.
- J. H. Choi, Y. J. Choi, J. W. Lee, W. H. Shin and J. K. Kang, Tunability of Electronic Band Gaps from Semiconducting to Metallic States via Tailoring Zn Ions in MOFs with Co Ions, Phys. Chem. Chem. Phys., 2009, 11(4), 628–631, 10.1039/B816668D.
- A. S. Yasin, J. Li, N. Wu and T. Musho, Study of the Inorganic Substitution in a Functionalized UiO-66 Metal–Organic Framework, Phys. Chem. Chem. Phys., 2016, 18(18), 12748–12754, 10.1039/C5CP08070C.
- K. I. Williamson, D. J. C. Herr and Y. Mo, Mapping the Correlations Between Bandgap, HOMO, and LUMO Trends for Meta Substituted Zn-MOFs, J. Comput. Chem., 2024, 45(25), 2119–2127, DOI:10.1002/jcc.27432.
- C. Chen, Z. Yu, D. S. Sholl and K. S. Walton, Effect of Loading on the Water Stability of the Metal–Organic Framework DMOF-1 [Zn(Bdc)(Dabco)0.5], J. Phys. Chem. Lett., 2022, 13(22), 4891–4896, DOI:10.1021/acs.jpclett.2c00693.
- K. Schröck, F. Schröder, M. Heyden, R. A. Fischer and M. Havenith, Characterization of Interfacial Water in MOF-5 (Zn4(O)(BDC)3)—a Combined Spectroscopic and Theoretical Study, Phys. Chem. Chem. Phys., 2008, 10(32), 4732–4739, 10.1039/B807458P.
- M. Edgar, R. Mitchell, A. M. Z. Slawin, P. Lightfoot and P. A. Wright, Solid-State Transformations of Zinc 1,4-Benzenedicarboxylates Mediated by Hydrogen-Bond-Forming Molecules, Chem. – Eur. J., 2001, 7(23), 5168–5175, DOI:10.1002/1521-3765(20011203)7:23
![[double bond splayed right]](https://www.rsc.org/images/entities/char_e00a.gif) 5168::AID-CHEM5168
5168::AID-CHEM5168![[double bond splayed left]](https://www.rsc.org/images/entities/char_e009.gif) 3.0.CO;2-S.
3.0.CO;2-S. - NIST/SEMATECH e-Handbook of Statistical Methods DOI:10.18434/M32189 (accessed 2023-07-08).
- ECHIP (Computer Software), Experimentation By Design LLC, Wilmington, DE, Retrieved from https://www.Experimentationbydesign.Com (https://www.Experimentationbydesign.Com) Search PubMed.
- F. Neese, The ORCA Program System, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2(1), 73–78, DOI:10.1002/wcms.81.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian∼16 Revision C.01, 2016 Search PubMed.
- J. H. Choi, H. J. Jeon, K. M. Choi and J. K. Kang, Metal–Organic Frameworks for Visible Light Absorption via Anion Substitution, J. Mater. Chem., 2012, 22(20), 10144, 10.1039/c2jm16245h.
- S. O. Odoh, C. J. Cramer, D. G. Truhlar and L. Gagliardi, Quantum-Chemical Characterization of the Properties and Reactivities of Metal–Organic Frameworks, Chem. Rev., 2015, 115(12), 6051–6111, DOI:10.1021/cr500551h.
- F. Neese, Software Update: The ORCA Program System—Version 5.0, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2022, 12(5), e1606, DOI:10.1002/wcms.1606.
- J. G. Brandenburg, C. Bannwarth, A. Hansen and S. Grimme, B97-3c: A Revised Low-Cost Variant of the B97-D Density Functional Method, J. Chem. Phys., 2018, 148(6), 064104, DOI:10.1063/1.5012601.
- S. Chopra, Performance Study of the Electronic and Optical Parameters of Thermally Activated Delayed Fluorescence Nanosized Emitters (CCX-I and CCX-II) via DFT, SCC-DFTB and B97-3c Approaches, J. Nanostruct. Chem., 2020, 10(2), 115–124, DOI:10.1007/s40097-020-00334-0.
- M. Alvaro, E. Carbonell, B. Ferrer, F. X. Llabrés i Xamena and H. Garcia, Semiconductor Behavior of a Metal–Organic Framework (MOF), Chem. – Eur. J., 2007, 13(18), 5106–5112, DOI:10.1002/chem.200601003.
- C. J. Cramer, Essentials of Computational Chemistry: Theories and Models, Wiley, Chichester, West Sussex, England; Hoboken, NJ, 2nd edn, 2004 Search PubMed.
- X. Mu, J. Jiang, F. Chao, Y. Lou and J. Chen, Ligand Modification of UiO-66 with an Unusual Visible Light Photocatalytic Behavior for RhB Degradation, Dalton Trans., 2018, 47(6), 1895–1902, 10.1039/C7DT04477A.
- E. Flage−Larsen, A. Røyset, J. H. Cavka and K. Thorshaug, Band Gap Modulations in UiO Metal–Organic Frameworks, J. Phys. Chem. C, 2013, 117(40), 20610–20616, DOI:10.1021/jp405335q.
- W. Humphrey, A. Dalke and K. Schulten, VMD: Visual Molecular Dynamics, J. Mol. Graphics, 1996, 14(1), 33–38, DOI:10.1016/0263-7855(96)00018-5.
- T. Lu and F. Chen, Multiwfn: A Multifunctional Wavefunction Analyzer, J. Comput. Chem., 2012, 33(5), 580–592, DOI:10.1002/jcc.22885.
- A. D. Becke, A Multicenter Numerical Integration Scheme for Polyatomic Molecules, J. Chem. Phys., 1988, 88(4), 2547–2553, DOI:10.1063/1.454033.
- Z. Liu, T. Lu and Q. Chen, An Sp-Hybridized All-Carboatomic Ring, Cyclo[18]Carbon: Electronic Structure, Electronic Spectrum, and Optical Nonlinearity, Carbon, 2020, 165, 461–467, DOI:10.1016/j.carbon.2020.05.023.
- S. H. Simon, The Oxford Solid State Basics, Oxford University Press, Oxford, 1st edn, 2013 Search PubMed.
- P. J. Atkins, J. D. Paula and J. Keeler, Atkins Physical Chemistry, Oxford Univ. Press, Oxford, 2017 Search PubMed.
- S. Abednatanzi, P. G. Derakhshandeh, H. Depauw, F.-X. Coudert, H. Vrielinck, P. V. D. Voort and K. Leus, Mixed-Metal Metal–Organic Frameworks, Chem. Soc. Rev., 2019, 48(9), 2535–2565, 10.1039/C8CS00337H.
- J. D. Evans, C. J. Sumby and C. J. Doonan, Post-Synthetic Metalation of Metal–Organic Frameworks, Chem. Soc. Rev., 2014, 43(16), 5933–5951, 10.1039/C4CS00076E.
- J. P. Dürholt, B. F. Jahromi and R. Schmid, Tuning the Electric Field Response of MOFs by Rotatable Dipolar Linkers, ACS Cent. Sci., 2019, 5(8), 1440–1448, DOI:10.1021/acscentsci.9b00497.
- I. Stassen, N. Burtch, A. Talin, P. Falcaro, M. Allendorf and R. Ameloot, An Updated Roadmap for the Integration of Metal–Organic Frameworks with Electronic Devices and Chemical Sensors, Chem. Soc. Rev., 2017, 46(11), 3185–3241, 10.1039/C7CS00122C.
- D. K. Singha, P. Majee, S. K. Mondal and P. Mahata, A Eu-Doped Y-Based Luminescent Metal–Organic Framework as a Highly Efficient Sensor for Nitroaromatic Explosives, Eur. J. Inorg. Chem., 2015,(8), 1390–1397, DOI:10.1002/ejic.201403097.
- D. K. Singha, S. Bhattacharya, P. Majee, S. K. Mondal, M. Kumar and P. Mahata, Optical Detection of Submicromolar Levels of Nitro Explosives by a Submicron Sized Metal–Organic Phosphor Material, J. Mater. Chem. A, 2014, 2(48), 20908–20915, 10.1039/C4TA05014B.
- L. E. Kreno, K. Leong, O. K. Farha, M. Allendorf, R. P. Van Duyne and J. T. Hupp, Metal–Organic Framework Materials as Chemical Sensors, Chem. Rev., 2012, 112(2), 1105–1125, DOI:10.1021/cr200324t.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00512k |
| This journal is © The Royal Society of Chemistry 2024 |