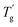Open Access Article
Open Access ArticlePhase separation-induced glass transition under critical miscible conditions†
Mayu
Watanabe
a,
Dong
Shi
b,
Ryuji
Kiyama
bc,
Kagari
Maruyama
a,
Yuichiro
Nishizawa
 d,
Takayuki
Uchihashi
d,
Takayuki
Uchihashi
 d,
Jian Ping
Gong
d,
Jian Ping
Gong
 be and
Takayuki
Nonoyama
be and
Takayuki
Nonoyama
 *b
*b
aGraduate School of Life Science, Hokkaido University, North 21 West 11, Kita-ku, Sapporo, 001-0021, Japan
bFaculty of Advanced Life Science, Hokkaido University, North 21 West 11, Kita-ku, Sapporo, 001-0021, Japan. E-mail: nonoyama@sci.hokudai.ac.jp
cLaboratoire de Sciences et Ingénierie de la Matière Molle, CNRS, ESPCI Paris, PSL Research University, 10 rue Vauquelin, 75005 Paris, France
dGraduate School of Science, Nagoya University, Furo-cho, Chikusa-ku, Nagoya, 464-8601, Japan
eInstitute for Chemical Reaction Design and Discovery (WPI-ICReDD), Hokkaido University, North 21 West 11, Kita-ku, Sapporo, 001-0021, Japan
First published on 2nd September 2024
Abstract
Plasticizers have been widely utilized to adjust the glass transition temperature (Tg) of glassy polymeric materials. To optimize performance while minimizing volume, plasticizers with a strong affinity for the target polymer are typically chosen. If we consider a combination of a glassy polymer and a plasticizer with a critical miscibility condition, where the miscible/immiscible states are altered by changing the temperature, phase separation induced by temperature variations will trigger the glass transition. In this study, we report on a polymeric material synthesized from a blend of a high Tg polymer and a plasticizer, exhibiting a phase separation-induced glass transition around the upper critical solution temperature (UCST). It is expected from a crossover point of the Tg curve and the demixing curve in a thermodynamic phase diagram, corresponding to the Berghmann point. Poly(isobornyl acrylate) (PIBXA) with an original Tg of ∼100 °C and triethyl phosphate (TEP) were employed as the glassy polymer and plasticizer, respectively. When the TEP fraction was relatively small (∼10 wt%), the sample showed no phase separation and a decrease in Tg compared to that of the pristine PIBXA, following the conventional trend of plasticizer addition. Conversely, at 20 wt% or higher fractions, the samples displayed UCST-type phase separation and an abnormal increase in Tg with increasing plasticizer content. Furthermore, this miscible/immiscible transition can be predicted through an analysis of the temperature-corrected Hansen solubility parameter (HSP). This report proposes a novel role for plasticizers in adjusting Tg and prediction of objective combinations that satisfy the critical miscible condition.
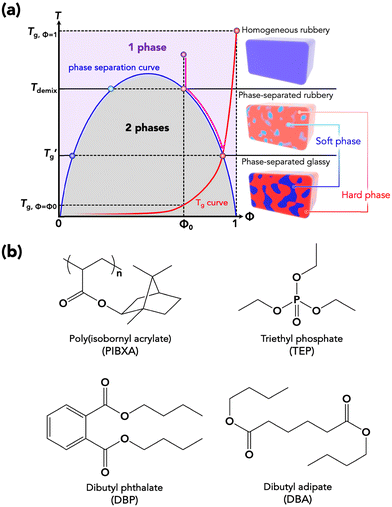
In present-day societies, polymeric materials have become as essential as metals and ceramics. To adjust the mechanical properties, thermal stability, and flame resistance of glassy polymers, the addition of plasticizers has been widely utilized.1–5 The principle behind how conventional plasticizers soften polymeric materials involves inserting themselves between polymer chains and weakening the intermolecular forces. The interactions between polymer chains primarily include van der Waals forces comprising dispersion forces, induction forces, and orientation forces as well as hydrogen bond and ionic bond interactions. Although each individual interaction is weak, numerous interactions within polymers significantly influence the material properties, leading to rigid crystalline or glassy states. Small molecular compounds exhibiting similar interactions can effectively penetrate between polymer chains, weakening these interactions and thereby tuning the properties of the polymer materials. Therefore, plasticizers with a small molecular structure should be carefully selected to interact effectively with the target polymer.
Usually, a plasticizer, which is highly compatible with the objective glassy polymer, is selected so that a minimal amount of the plasticizer is sufficient to achieve the desirable effect. Furthermore, the polymer and the plasticizer should exhibit stable compatibility over a wide temperature range. In contrast to the above conventional use of plasticizers adjusting the mechanical properties, we here consider a critical case between a glassy polymer and a plasticizer whose miscibility dramatically changes with temperature. Specifically, they are miscible at high temperatures but not below a critical temperature in this study. We refer to this as the “critical miscible condition.” If polymer–plasticizer mixtures satisfy this condition, they will have a demixing temperature corresponding to the upper critical solution temperature (UCST).6,7Fig. 1a depicts a thermodynamic phase diagram of glassy polymer–plasticizer materials, where Φ represents the polymer volume fraction. The blue line represents the demixing curve separating the upper miscible and lower immiscible regions, obtained from the Flory–Huggins theory.8,9 When a material with a certain Φ0 is in the miscible state and is cooled down, it exhibits demixing temperature (Tdemix) on the demixing curve. Below this temperature, the composition separates into polymer-dense (reddish circle) and dilute phases (bluish circle) following the demixing curve. Considering the glass transition of a glassy polymer, the red curve of the glass transition temperature (Tg) can be drawn on the same diagram. Generally, the Tg of a glassy polymer remains almost constant when the plasticizer concentration is high enough, but it dramatically increases with decreasing plasticizer concentration at relatively high Φ.10 Taking these two curves into account, the growth of the phase separation structure during the cooling process increases the polymer fraction of the dense phase. Ultimately, the dense phase transits to a glassy state at the crossover point of the two curves 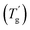 . Therefore, the glass transition is induced by strong phase separation forming a two-phase composite state. This crossover point is also referred to as the Berghmann point in the literature.11,12 In a broader sense, this phenomenon can also find an analogy with the liquid glass transition of metals.13 The phase separation-induced glass transition can be realized in the heating process like a low critical solution temperature (LCST)-type phase separation. Similar to this study, we previously reported that an extremely strong phase separation in a hydrogel induces rubbery-to-glassy transition with elevating temperature.14
. Therefore, the glass transition is induced by strong phase separation forming a two-phase composite state. This crossover point is also referred to as the Berghmann point in the literature.11,12 In a broader sense, this phenomenon can also find an analogy with the liquid glass transition of metals.13 The phase separation-induced glass transition can be realized in the heating process like a low critical solution temperature (LCST)-type phase separation. Similar to this study, we previously reported that an extremely strong phase separation in a hydrogel induces rubbery-to-glassy transition with elevating temperature.14
In this study, a polymeric material exhibiting a UCST-type phase separation-induced glass transition is synthesized satisfying the critical miscible condition. To explore the desired combination of a glassy polymer and a plasticizer, an analysis of Hansen solubility parameters (HSPs) was carried out.15 The Hildebrand solubility parameter (δ) at ambient temperature and pressure is defined using eqn (1),16 utilizing the molar potential energy of the liquid (−e0) and its molar volume (Vm).
| δ = (−e0/Vm)0.5 | (1) |
Here, the potential energy can be replaced by the evaporation energy of the solvent, ΔE, and the solubility parameter is calculated as the square root of the cohesive energy density for all liquids where the vapor can be considered ideal.
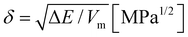 | (2) |
In the HSP, δ is divided into three terms; a dispersion force term (δd) corresponding to the van der Waals force, a polar force term (δp) corresponding to the dipole moment, and a hydrogen bond term (δh) corresponding to the hydrogen bonding contribution. δ is related to δd, δp, and δh as follows,
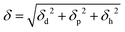 | (3) |
Therefore, the HSP of substances can be described as a coordinate in three-dimensional Hansen's space with axes of δd, δp and δh. The miscibility of two different substances can be evaluated from the distance between the coordinates in the Hansen's space. The closer the distance, the higher the miscibility. This distance (Ra) is written as,
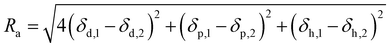 | (4) |
Substances with closely matched HSPs are more likely to be miscible with each other, while perfect HSP congruence is not necessary for miscibility. For this reason, the Hansen solubility sphere model, which represents a spatial region where miscibility is possible, can be considered. For instance, the sphere of a polymer is often determined through a solubility test. The solubility of the target polymer in various solvents with known HSPs is assessed. Subsequently, the sphere is defined by including only the coordinates of the miscible solvents. The radius of the sphere is referred to as the interaction radius (R0).
Often, the HSP analysis is carried out at room temperature (25 °C). But when temperature is varied, the values of HSPs must be corrected from the reference temperature. Williams et al. suggested the temperature effect on δd, δp and δh by considering the thermal expansion coefficient in volume, α (K−1), as follows:17
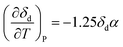 | (5-1) |
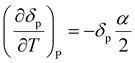 | (5-2) |
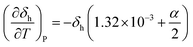 | (5-3) |
Here, α can be described as a derivative form of volume V or density ρ,
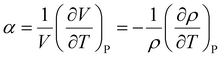 | (6) |
Dissolving these differential equations under constant pressure, the HSP equations are obtained as the volume change,
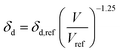 | (7-1) |
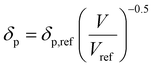 | (7-2) |
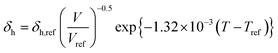 | (7-3) |
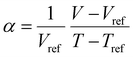 | (8) |
Finally, the temperature-corrected equations of HSPs can be obtained as a function of temperature,
| δd = δd,ref{α(T − Tref) + 1}−1.25 | (9-1) |
| δp = δp,ref{α(T − Tref) + 1}−0.5 | (9-2) |
δh = δh,ref{α(T − Tref) + 1}−0.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp{−1.32 × 10−3(T − Tref)} exp{−1.32 × 10−3(T − Tref)} | (9-3) |
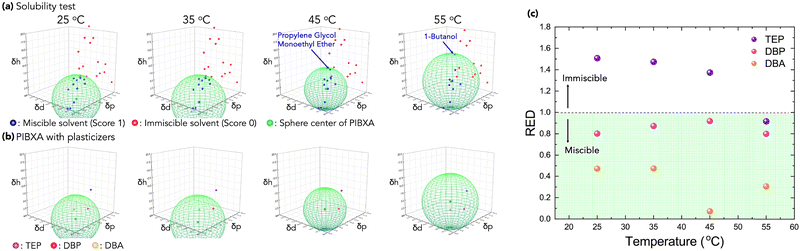
In this study, poly(isobornyl acrylate) (PIBXA) was chosen as the glassy polymer,18,19 and three plasticizers, triethyl phosphate (TEP), dibutyl phthalate (DBP), and dibutyl adipate (DBP) were selected (Fig. 1b). Firstly, to predict the miscibility of PIBXA and the plasticizers, HSP analysis was conducted at various temperatures. In material synthesis, pristine PIBXA was obtained through UV-irradiated radical polymerization from a solution of the liquid IBXA monomer (4.7 M) containing 0.1 mol% benzophenone initiator (referred to as the IBXA concentration, detailed procedures are described in the ESI†). Fig. 2a and Table 1 depict the determination of PIBXA's HSPs through solubility tests using 28 different solvents with known HSPs (Table S1, ESI†). Their HSPs at the reference temperature were referred from the database of HSPiP® software. These solvents, selected to ensure HSP diversity, were categorized as miscible (blue, score 1) or immiscible (red, score 0). Experimentally, the state of PIBXA swelling or dissolving in a solvent was score 1, and other states were score 0. The miscible sphere, representing pure PIBXA's HSP, was calculated through least-squares fitting of the sphere including the miscible solvents by HSPiP®.20,21 The coordinates and radius corresponded to the HSP of PIBXA (δd, δp, and δh) and the interaction radius (R0), respectively. When determining HSPs at different temperatures from the reference state (25 °C), the HSPs of the 28 solvents were adjusted using eqn (9). The thermal expansion coefficient (α) of each solvent was measured using a density meter at various temperatures with eqn (6). The density versus temperature curve showed good linear relation for all solvents within the measured temperature range (Fig. S1 and Table S1, ESI†) so that α can be considered constant in this study. Additionally, a test with an evaporating solvent was excluded from the HSP evaluation. Since PIBXA became miscible with several solvents such as 1-butanol and propylene glycol monoethyl ether at high temperatures, δd, δp, δh, and R0 were shifted. Especially, it is found that the δh contribution and R0 were increased with increasing temperature. Next, the resulting miscible sphere was then overlaid with three plasticizers, TEP, DBP, and DBA (Fig. 2b). Similar to the test solvents, the HSPs of plasticizers were also adjusted for temperature variations (Table 1). DBP and DBA were included in the PIBXA sphere at every temperature, while TEP altered from sphere-out to -in with elevating temperature. Additionally, the distance between the coordinates of PIBXA and the plasticizer (Ra) was calculated. Since both PIBXA and the plasticizer shift with changing temperature in this analysis, the relative energy density (RED), defined as Ra/R0, serves as a useful index for easily predicting miscibility (Fig. 2c). The REDs of DBP and DBA were consistently less than 1 (included in the PIBXA's sphere) at every test temperature, indicating that PIBXA will be miscible with DBP and DBA within this temperature range. On the other hand, the RED of TEP was larger than 1 from 25 to 45 °C and then eventually became less than 1 at 55 °C. This suggests that PIBXA–TEP is not miscible at low temperatures but becomes miscible around 55 °C. Thus, the PIBXA–TEP mixture would be an upper critical solution temperature (UCST)-type elastomer displaying a phase-separation structure at the critical temperature.
| Chemical | Temp. (°C) | HSP (MPa1/2) | R 0 (MPa1/2) | RED | ||
|---|---|---|---|---|---|---|
| δ d | δ p | δ h | ||||
| PIBXA | 25 | 17.35 | 3.24 | 2.30 | 7.14 | — |
| 35 | 16.65 | 2.42 | 1.41 | 7.97 | — | |
| 45 | 16.09 | 3.53 | 5.04 | 6.31 | — | |
| 55 | 15.55 | 3.88 | 7.14 | 8.29 | — | |
| TEP | 25 | 16.70 | 11.40 | 9.20 | — | 1.51 |
| 35 | 16.50 | 11.35 | 9.04 | — | 1.47 | |
| 45 | 16.30 | 11.29 | 8.87 | — | 1.37 | |
| 55 | 16.11 | 11.24 | 8.72 | — | 0.92 | |
| DBP | 25 | 17.80 | 8.60 | 4.10 | — | 0.80 |
| 35 | 17.62 | 8.57 | 4.03 | — | 0.87 | |
| 45 | 17.45 | 8.53 | 3.96 | — | 0.92 | |
| 55 | 17.28 | 8.50 | 3.89 | — | 0.80 | |
| DBA | 25 | 16.30 | 3.70 | 4.90 | — | 0.47 |
| 35 | 16.12 | 3.68 | 4.81 | — | 0.47 | |
| 45 | 15.94 | 3.67 | 4.73 | — | 0.07 | |
| 55 | 15.76 | 3.65 | 4.65 | — | 0.31 | |
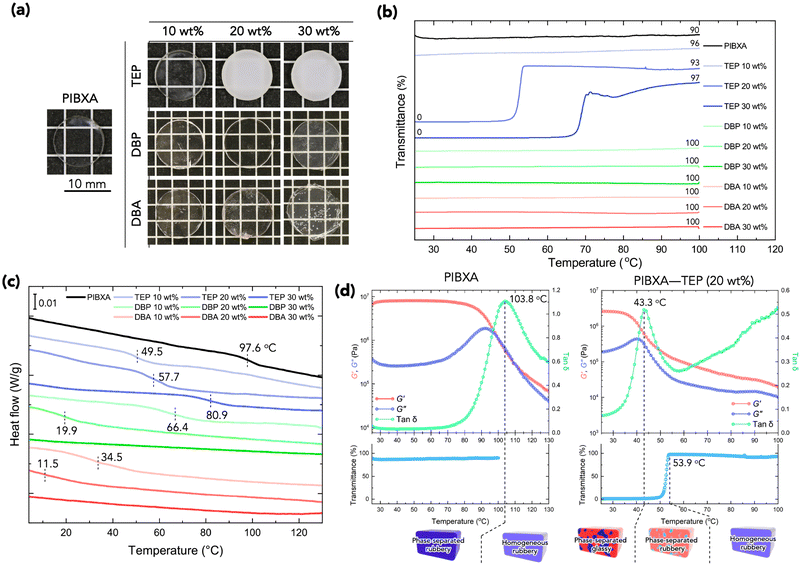
Next, PIBXA containing plasticizer was synthesized from a pre-mixing solution of the IBXA liquid monomer and plasticizer. Fig. 3a displays the appearances of PIBXA with TEP, DBP, and DBA at the reference temperature. The weight fraction of plasticizers varied from 10 to 30 wt%. PIBXA–DBP and PIBXA–DBA were transparent at every plasticizer fraction. PIBXA with 10 wt% TEP was transparent, while samples with 20 and 30 wt% TEP concentrations became turbid after polymerization due to the formation of phase separation. Transmittance with temperature variations was measured using a UV-vis spectrometer (Fig. 3b). The DBP and DBA remained transparent at every fraction, as did 10 wt% TEP, across the temperature range from 25 to 100 °C. However, samples with 20 and 30 wt% TEP exhibited very low transmittance at low temperatures and became dramatically transparent around 50 and 65 °C, respectively, indicating the presence of an upper critical solution temperature (UCST). This observation was consistent with the HSP analysis, except for very low fractions of TEP. HSP analysis proves to be highly beneficial in material development, enabling the prediction not only of miscibility at reference temperature but also of the critical miscible condition of multiple components. Purposely ideal candidates from infinite combinations can be found based on the parameters.
The Tg of samples affected by mixing the plasticizer was evaluated using modulated differential scanning calorimetry (MDSC) measurement.22,23Fig. 3c illustrates the reversing heat flow separated from the total heat flow. Pure PIBXA exhibited a Tg at 97.6 °C. The Tgs of both PIBXA–DBP and PIBXA–DBA decreased with increasing plasticizer concentration, consistent with the common trend of plasticizer addition to glassy polymers. However, PIBXA–TEP showed that Tg decreased to 49.5 °C initially at 10 wt%, while increasing at 20 wt% (57.7 °C) and 30 wt% (80.9 °C). The two abnormal Tgs observed at higher TEP fractions were not consistent but approximately 10 °C lower than the temperatures at which transmittance changes occurred in the UV-Vis profiles. Supporting this observation, the Tg of the 20 wt% TEP sample, as determined viscoelastically from the peak of the tangent delta in the rheogram, was 43.3 °C, almost consistent with the Tg observed in MDSC (Fig. 3d). These results can be explained from the thermodynamic phase diagram in Fig. 1. With decreasing temperature, the homogeneous and rubbery PIBXA–TEP firstly shows phase separation with starting of turbidity detected by UV-vis measurement that corresponds to Tdemix while still keeping the rubbery state. With further decreasing of temperature, the modulus increases dramatically, and the PIBXA–TEP finally becomes glassy state with the peak of tan![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) δ shifting in MDSC that corresponds to
δ shifting in MDSC that corresponds to 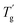 in the diagram. Therefore, both Tdemix and
in the diagram. Therefore, both Tdemix and 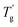 come from the phase separation while they are not consistent because of the degree of phase separation. Approaching this point from higher temperatures, the PIBXA polymer chains begin to demix from the TEP plasticizer at Tdemix, eventually losing mobility and transitioning to a glassy state. Contrary to the normal role of plasticizers, the addition of TEP exceeding 20 wt% to PIBXA increased Tg because this glass transition was driven by the formation of UCST-type phase separation.
come from the phase separation while they are not consistent because of the degree of phase separation. Approaching this point from higher temperatures, the PIBXA polymer chains begin to demix from the TEP plasticizer at Tdemix, eventually losing mobility and transitioning to a glassy state. Contrary to the normal role of plasticizers, the addition of TEP exceeding 20 wt% to PIBXA increased Tg because this glass transition was driven by the formation of UCST-type phase separation.
The plateau of storage modulus G′ of PIBXA–TEP (20 wt%) around 25 °C was slightly small when compared to that of pristine PIBXA at the same temperature, indicating that the locally dense structure of PIBXA formed by phase separation exhibits similar dynamics to that of the conventionally global glassy state. The reason for the modulus slightly lower than that of the pristine PIBXA might be the difference in the polymer volume fraction. If the glass transition originates from the Berghmann point, the Tg should remain the same regardless of the initial fraction of the polymer–plasticizer mixture. The difference in Tg observed for 20 and 30 wt% TEP would be attributed to the phase separation and the Tg curve changes due to the primary structure of PIBXA. TEP, acting as a solvent, would influence the stereoregularity of PIBXA during polymerization. It is known that polymers with different stereoregularities exhibit different interaction parameters in solvents and Tg.24 On the other hand, when the molecular weight is sufficiently high, the contribution from the difference in the polymer molecular weight becomes almost negligible. TEP slightly reduces the efficiency of polymerization, but the weight-average molar masses (Mw) of PIBXA polymerized with 20 and 30 wt% TEP were 288.9 k and 173.7 k, respectively, both of which are sufficiently high values.
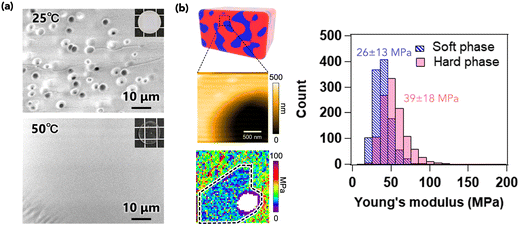
To elucidate the stiffening effect caused by the formation of phase separation, the local microscale structure was evaluated using microscopy techniques. Fig. 4a presents scanning electron microscopy (SEM) images of the cross-section of PIBXA–TEP (20 wt%) annealed at 25 and 50 °C. No specific structure was observed at 50 °C, while a pore structure with an approximate diameter of 3 μm was evident at 25 °C. Considering the loading weight fractions of PIBXA and TEP, the pore likely corresponds to the PIBXA-dilute and TEP-dense region, which are softer than the surrounding area. Next, the local modulus was analyzed by force mapping with atomic force microscopy (AFM)25,26 (Fig. 4b). Young's modulus (E) of the hard phase, indicated by the yellowish region, was measured to be 39 ± 18 MPa, almost comparable to G′ (=E/3) in Fig. 3d. Conversely, the modulus in the pore region (soft phase) was determined to be 26 ± 13 MPa. Considering the unmeasurable whitish region at the center of the pore, the true average modulus in the pore region might be smaller than the calculated value. The modulus mapping results indicate that the global modulus of the phase-separated PIBXA–TEP at the macroscale is governed by the continuous hard phase at the microscale. Phase separation can induce a glass transition by reducing the plasticizer content from the glassy polymer.
In conclusion, we have successfully developed a UCST-type material with a phase separation-induced glass transition by combining the glassy polymer PIBXA and the plasticizer TEP under “critical miscible conditions.” Based on the thermodynamic phase diagram featuring phase separation and glass transition curves, the Tg arises from the growth of the phase separation structure, corresponding to the Berghmann point. While the Tg of polymeric materials typically decreases with increasing plasticizer content, the trend is reversed in the PIBXA–TEP system. This abnormal trend extends the role of plasticizers. In the material design process, this critical miscible condition can be predicted using temperature-corrected Hansen solubility parameters. This is a simple prediction based solely on whether the relative energy density is above or below 1. The HSP method offers industrial benefits as it allows for the selection of the optimal combination based on these parameters. By utilizing this concept, materials exhibiting LCST-type phase separation can also be developed in the future, demonstrating vitrification at high temperatures, which will represent an inverse glass transition.
Data availability
Data for this article, including density, AFM, SEM, rheometer, DSC, and UV-vis spectra are available at https://doi.org/DOI/10.5281/zenodo.12772861. The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge the supply of IBXA monomer by Mr Yoshiyuki Saruwatari, Osaka Organic Chemical Industry Co., Ltd. This work was financially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (grant number JP22K21342, JP22H04968, JP21H01990), Japan Science and Technology Agency (JST) FOREST (grant number JPMJFR201Q), SPRING (grant number JPMJSP2119), and ALCA-NEXT (grant number JPMJAN23C3). We thank the Open Facility, Global Facility Center, Creative Research Institution, Hokkaido University.References
-
A. S. Wilson, Plasticisers: Principles and Practice, Institute of Materials, London, 1995 Search PubMed
.
-
G. Wypych, Handbook of Plasticizers, ChemTec Publishing, Toronto, Canada, 3rd edn, 2017 Search PubMed
.
- S. H. Brandsma, J. de Boer, P. E. G. Leonards, W. P. Cofino, A. Covaci and P. E. G. Leonards, Organophosphorus flame-retardant and plasticizer analysis, including recommendations from the first worldwide interlaboratory study, Trends Anal. Chem., 2013, 43, 217–228 CrossRef CAS
.
- M. Bocqué, C. Voirin, V. Lapinte, S. Caillol and J. J. Robin, Petro-based and bio-based plasticizers: Chemical structures to plasticizing properties, J. Polym. Sci., Part A: Polym. Chem., 2016, 54, 11–33 CrossRef
.
- S. Kumar, Recent Developments of Biobased Plasticizers and Their Effect on Mechanical and Thermal Properties of Poly(vinyl chloride): A Review, Ind. Eng. Chem. Res., 2019, 58, 11659–11672 CrossRef CAS
.
- A. Sehlinger, O. Kreye and M. A. R. Meier, Tunable Polymers Obtained from Passerini Multicomponent Reaction Derived Acrylate Monomers, Macromolecules, 2013, 46, 6031–6037 CrossRef CAS
.
- J. Seuring and S. Agarwal, Polymers with Upper Critical Solution Temperature in Aqueous Solution: Unexpected Properties from Known Building Blocks, ACS Macro Lett., 2013, 2, 597–600 CrossRef CAS PubMed
.
- P. J. Flory, Thermodynamics of High Polymer Solutions, J. Chem. Phys., 1942, 10, 51–61 CrossRef CAS
.
- M. L. Huggins, Some Properties of Solutions of Long-chain Compounds, J. Phys. Chem., 1942, 46, 151–158 CrossRef CAS
.
- O. Fridman, Structural-relaxation Mechanism of Glassy-like Polymers Plasticization, Am. J. Polym. Sci., 2013, 2013, 7–12 Search PubMed
.
- S. Callister, A. Keller and R. M. Hikmet, On thermoreversible gels: Their classification, relation to phase transitions and vitrification, their morphology and properties, Makromol. Chem., Macromol. Symp., 1990, 39, 19–54 CrossRef CAS
.
- V. Aseyev, H. Tenhu and F. Winnik, Non-ionic Thermoresponsive Polymers in Water, Adv. Polym. Sci., 2010, 242, 29–89 CrossRef
.
- R. F. Tournier and M. I. Ojovan, NiTi2, a New Liquid Glass, Materials, 2023, 16, 6681 CrossRef CAS PubMed
.
- T. Nonoyama, Y. W. Lee, K. Ota, K. Fujioka, W. Hong and J. P. Gong, Instant Thermal Switching from Soft Hydrogel to Rigid Plastics Inspired by Thermophile Proteins, Adv. Mater., 2020, 32, 1905878 CrossRef CAS PubMed
.
-
C. M. Hansen, Hansen Solubility Parameters: A User's Handbook, CRC Press, 2nd edn, 2007 Search PubMed
.
-
J. H. Hildebrand and R. L. Scott, Solubility of Nonelectrolytes, Reinhold, New York, 3rd edn, 1958 Search PubMed
.
- L. L. Williams, J. B. Rubin and H. W. Edwards, Calculation of Hansen Solubility Parameter Values for a Range of Pressure and Temperature Conditions, Including the Supercritical Fluid Region, Ind. Eng. Chem. Res., 2004, 43, 4967–4972 CrossRef CAS
.
- O. Jaehoon and S. Myungeun, Photoinitiated Polymerization-Induced Microphase Separation for the Preparation of Nanoporous Polymer Films, ACS Macro Lett., 2015, 4, 1244–1248 CrossRef PubMed
.
- T. Jianbo, H. Chundong, L. Dongdong, Z. Xuechao, B. Yuhao and Z. Li, Alcoholic Photoinitiated Polymerization-Induced Self-Assembly (Photo-PISA): A Fast Route toward Poly(isobornyl acrylate)-Based Diblock Copolymer Nano-Objects, ACS Macro Lett., 2016, 5, 894–899 CrossRef PubMed
.
- J. V. Mark, S. S. Craig, B. T. Chase, A. M. Brent, W. P. Gregory and P. P. Thomas, Solvent Selection Guided by Self-Consistent Field Theory for Improved Dispersion of Metal–Organic Frameworks in Polymers, ACS Appl. Polym. Mater., 2024, 6, 888–895 CrossRef
.
- M. D. D. L. Ríos, E. H. Ramos, V. G. Canavaciolo, R. V. Murillo, K. P. Carrión and L. Z. D. Cárdenas, Obtaining a Fraction of Sugarcane Wax Rich in Policosanol by Using Ethanol as Solvent: Results Interpretation through Hansen's Solubility Theory, ACS Omega, 2022, 7, 27324–27333 CrossRef PubMed
.
- A. Boller, C. Schick and B. Wunderlich, Modulated differential scanning calorimetry in the glass transition region, Thermochim. Acta, 1995, 266, 97–111 CrossRef CAS
.
- Z. Jiang, C. T. Imrie and J. M. Hutchinson, An introduction to temperature modulated differential scanning calorimetry (TMDSC): a relatively non-mathematical approach, Thermochim. Acta, 2002, 387, 75–93 CrossRef CAS
.
- G. Beaucage and R. S. Stein, Tacticity effects on polymer blend miscibility. 3. Neutron scattering analysis, Macromolecules, 1993, 26, 1617–1626 CrossRef CAS
.
- T. Ando, T. Uchihashi and T. Fukuma, High-speed atomic force microscopy for nano-visualization of dynamic biomolecular processes, Prog. Surf. Sci., 2008, 83, 337–437 CrossRef CAS
.
- C. Ganser and T. Uchihashi, Microtubule self-healing and defect creation investigated by in-line force measurements during high-speed atomic force microscopy imaging, Nanoscale, 2019, 11, 125–135 RSC
.
Footnote |
| † Electronic supplementary information (ESI) available: Detailed experimental procedures, Fig. S1, S2 and Table S1. See DOI: https://doi.org/10.1039/d4ma00737a |
| This journal is © The Royal Society of Chemistry 2024 |