Open Access Article
Open Access ArticleA cost-effective strategy to design and fabricate absorption dominant flexible multilayer laminates by rationally tailoring their layers†
Vaishnavi
Khade
a,
Avanish Babu
Thirumalasetty
 a,
Yogesh Kumar
Choukiker
b and
Madhuri
Wuppulluri
a,
Yogesh Kumar
Choukiker
b and
Madhuri
Wuppulluri
 *c
*c
aDepartment of Physics, School of Advanced Sciences, Vellore Institute of Technology, Vellore, Tamil Nadu, India
bSchool of Electronics Engineering, Vellore Institute of Technolog, Vellore, Tamil Nadu, India
cCeramic Composites Laboratory, Centre for Functional Materials, Vellore Institute of Technology, Vellore, Tamil Nadu 632014, India. E-mail: madhuriw12@gmail.com
First published on 21st October 2024
Abstract
Owing to the ever-increasing complexity of the electromagnetic environment, the market for electromagnetic interference (EMI) shielding is expanding at a rapid rate. Recently, there has been a focus on developing new methods that can be used to fine-tune and forecast the shielding qualities of buildings without using up all of the raw materials. Additionally, methods that are economical and need a short duration of time for optimization have been prioritized. The purpose of this article is to demonstrate an efficient and accurate method for predicting the EMI shielding effectiveness (EMI SE) of materials. This is accomplished by simulating the performance of composites that contain alternate layers of conducting and magnetic materials within a virtual waveguide measurement environment. Using CST Studio Suite software, the EMI shielding effectiveness of multilayered structures is simulated in the X-band range. The strategic arrangement of electromagnetic (EM) energy-trapping layers within impedance-matching layers in the multilayered structures is found to significantly contribute to the enhancement of absorption-dominated EMI shielding, as demonstrated through a simulation carried out by varying the order and number of the conducting and magnetic layers. Among the multilayered structures, the PC/PM/PC (PVDF-CNF/PVDF-MWCNTs/PVDF-CNF) systems showed the best shielding efficiency, with a value of 96.47 dB. Poly(vinylidene fluoride)-based composites comprising low-cost MWCNTs are used to construct the multilayered structures for testing purposes. After completing this research, we came up with the hypothesis that it is not required to use materials that have a high manufacturing cost and need laborious fabrication processes in order to create extremely effective shielding materials.
1. Introduction
EM radiation-based products and gadgets have grown increasingly essential in our daily lives ever since EM frequencies were first commercialized in the late 1800s. The amount of EM radiation surrounding us has unquestionably increased with the introduction of the internet of things (IoT) and advancements in technology, leaving us vulnerable to a complicated electromagnetic environment.1–3 Furthermore, it is apparent in the current available literature that electromagnetic interferences have a disruptive effect on the optimal operation of sophisticated precision electronic devices utilized for advanced applications across diverse domains, including medicine, aerospace, and military sectors.4–7 Moreover, numerous data indicate the detrimental effects of EM radiation on the overall health and welfare of humans and other living organisms.8,9 Thus, there has been an increasing demand for the development of EMI shielding materials that are capable of efficiently mitigating electromagnetic waves. This demand arouses primarily as a result of the implementation of fifth-generation networks, which utilize higher-frequency electromagnetic radiation. Therefore, innovation in the development of technically improved EMI shielding materials and reinforcement of engineering strategies for shielding structures are urgently required.Two basic mechanisms that are engaged in electromagnetic interference shielding are reflection and absorption. Therefore, electromagnetic interference shielding materials can be roughly categorized into two types: reflection-dominant shielding materials and absorption-dominant shielding materials. Despite the fact that metals, conductive polymers, and low-dimensional materials such as reduced graphene oxide and MXenes can achieve high EMI SE, the inherent reflection of electromagnetic waves due to the conductivity of these materials can have adverse effects on the environment and electronic devices utilized in an enclosure for aerospace and military purposes.10–13 The attainment of such material combinations can be accomplished through the appropriate integration of magnetic and conducting materials in order to facilitate impedance matching and consequently minimize the reflection of electromagnetic waves.14 Additionally, it has been reported that the utilization of a multilayered configuration consisting of magnetic and conductive structures can effectively enhance the shielding capabilities of the composites. This is achieved by capitalizing on the phenomenon of multiple internal reflections that occur due to the impedance mismatch between the several layers with differing properties.14,15
The utilization of multilayered composites presents a compelling approach to mitigate reflection-based shielding by strategically arranging the conducting and magnetic layers in a certain order. Enormous research has been conducted to investigate the EMI SE of various arrangements of multilayered composite structures.15–18 The method is further validated by recent review articles that explore the possibility of multilayered structures made of polymers for EMI shielding.19–21 When using multilayer structures, the EMI shielding efficiency can be tuned by adjusting the concentration of the fillers, layer order, layer thickness, and layer number, as well as by choosing the conducting and magnetic fillers for each layer. A prevalent myth is that producing high-performance EMI shielding materials is too expensive, time-consuming, and labor-intensive for industrial integration because of the optimization step alone. Therefore, it is critical to innovate methods by implementing strategies that can yield good outcomes in a reasonable amount of time without wasting resources.
An intriguing and underexplored approach to predicting a material's EMI SE from its electrical conductivity and electromagnetic parameters is the use of simulation in the design of EMI shielding materials and then comparing and measuring the EMI shielding parameters as well. According to the literature, many studies have focused on fabricating and testing various microwave-absorbing and EMI shielding materials with different properties. However, very few have attempted to design EMI shielding materials using robust simulation tools and then validate the simulated results with the experimental results obtained after fabrication. For X-band applications, Liu et al. and Kashi et al. utilized CST Studio Suite in 2020 to investigate and optimize the EMI shielding characteristics of textiles modified with Ag nanowires and poly- (butylene adipate-co-terephthalate) and poly-lactide nanocomposites incorporating graphene, respectively.22 Phan et al. also investigated the use of the high frequency structure simulator (HFSS) to conduct simulation-based EMI shielding investigations on transparent shielding applications involving multilayered salt-water in planar acrylic and glass within the frequency range of 7.5–8.5 GHz.23 Subsequently in 2022, Hu et al. conducted simulations within the 1.0–1.5 GHz frequency range on the optimized textile model in order to optimize a multitude of parameters for shielding applications based on textiles.24
This study details a novel systematic simulation analysis of multilayered composites made of conducting and magnetic filler-reinforced polymers along with experimental evidence for the purpose of mitigating electromagnetic radiation. Co0.9Ni0.1Fe2O4 (CNF) is used as a magnetic filler, multiwalled carbon nanotubes (MWCNTs) are used as the conductive filler and poly(vinylidene fluoride) (PVDF) is the selected polymer matrix because of its exceptional mechanical qualities. The multilayer structures are created by stacking the single-layers that are produced using the doctor blade process and then hot-pressing these individual layers. This paper further dives into measuring EMI shielding efficiency and understanding the EMI shielding mechanism of multilayer structures with different layered configurations and numbers of layers by modelling the electromagnetic characteristics of the individual layers using CST Studio Suite software along with visualization of electric and magnetic field propagations through individual layers as well as multilayer structures. This work primarily focused on three arrangements: (1) PC/PM (PVDF-CNF/PVDF-MWCNTs), (2) PC/PM/PC (PVDF-CNF/PVDF-MWCNTs/PVDF-CNF), and (3) PM/PC/PM (PVDF-MWCNTs/PVDF-CNF/PVDF- MWCNTs). We take a close look at the underlying mechanisms that increase the shielding efficiency of multilayer structures, highlighting the importance of choosing the correct sequence and number of layers. In conclusion, this paper mainly delves into the function of simulation in engineering, design, and prediction of laminated structures, as well as their capacity to protect against electromagnetic radiation, with enough supporting experimental evidence.
2. Materials and methods
2.1. Simulation
All of the EMI shielding structures that are addressed in this study have been constructed and simulated in the X-band region by utilizing the finite element method using CST Studio Suite software. This involves developing a virtual EMI shielding measurement setup (see ESI,† Section S1 for details of the virtual wave guide environment). This is accomplished by designing a rectangular waveguide and placing the material under test (MUT) between port-1 and port-2 of the waveguide. The multilayer structures are constructed by assigning the electromagnetic parameters and electrical conductivity to individual layers, which will contribute to the total EMI shielding efficiency (SET) of multilayer structures.The simulated structures are shown in Fig. 1(a)–(c). Shielding effectiveness is evaluated based on absorption (SEA), reflection (SER), and total shielding (SET) using the reflection (S11, S22) and transmission scattering characteristics (S12, S21) derived from the following equations:
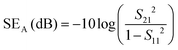 | (1) |
SER (dB) = −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log (1 − S112) = −10 log (1 − S112) = −10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log (1 − S222) log (1 − S222) | (2) |
| SET = SEA + SER + SE | (3) |
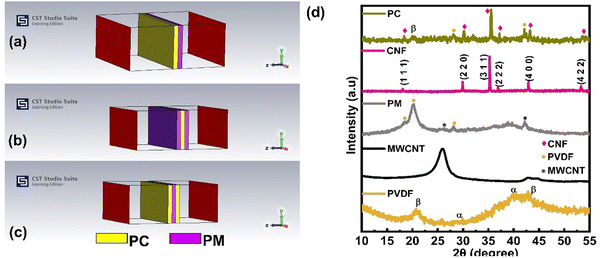 | ||
| Fig. 1 (a)–(c) Model of simulated multilayer structures in CST Studio Suite software and (d) XRD pattern for pure PVDF, PM, and PC layers. | ||
2.2. Fabrication of multilayer structures
The multilayer structures consisting of conductive MWCNTs (AdNano Technologies Pvt. Ltd., 99% purity) and magnetic CNF layers are prepared through a solvent casting and hot-pressing method. The synthesis of CNF is outlined in Section S2 (ESI†). In order to create separate conducting and magnetic layers, 1 g of PVDF powder is dissolved in 5 ml of N,N-dimethylformamide (DMF). 15 wt% MWCNTs is added to the fully dissolved uniform PVDF-DMF mixture and stirred overnight using a magnetic stirrer set at a speed of 300 rpm. The solution is subjected to sonication for a duration of 30 minutes using a bath sonicator maintained at room temperature. Ultimately, using the doctor blade technique the film is produced and maintained at ambient temperature for 24 h in order to achieve a consistent and even PC layer. A similar method is employed to manufacture the PM magnetic layer. The CNF layer is fabricated with 15 wt% of CNF.The multilayered structures PM/PC, PM/PC/PM, and PC/PM/PC are created by stacking alternating layers of PM and PC (see Fig. 1(a)–(c)). The composites are subsequently exposed to hot-pressing at a temperature of 220 °C for a duration of 15 minutes, with minimal applied pressure. The PM/PC is a combination of a conducting and magnetic layer. PM/PC/PM and PC/PM/PC composites consist of a conducting layer sandwiched between two magnetic layers, and vice versa, respectively. The PM/PC, PM/PC/PM, and PC/PM/PC composites consist of a sequential arrangement of conducting and magnetic layers. There is a total of 2- and 3-layers, each with a uniform thickness of 3.8 mm (see ESI,† Fig. S1(a) for the schematic of preparation of multilayer structures).
2.3. Characterization
The degree of crystallinity and identification of phases in CNF and individual layers of multilayer structures are examined using X-ray diffraction (XRD) (BRUKER D8 advanced X-ray diffractometer) with Cu Kα radiation (λ = 1.5406 Å). The scanning range is set from 2θ = 10° to 80°. The individual composite layers are analyzed for their microstructure using a field emission scanning electron microscope (FESEM) (Thermo Fisher Scientific FEI Quanta 250 FEG). The electromagnetic properties of the individual layers in the X-band range are also determined using the waveguide approach. The conductivity of the individual layers of multilayer structures is determined based on the complex permittivity of the composites. The SET of the individual layers as well as multilayer structures in the X-band region is determined by analyzing the reflection and transmission scattering parameters. These parameters are assessed using a vector network analyzer (VNA) (Anritsu) through the transmission-line method.3. Results and discussion
3.1. Characterization of individual PM and PC layers
Before moving to the characterization of individual layers, the characteristics of synthesized CNF are presented and discussed elsewhere.26 The XRD patterns of individual PM and PC layers are graphically represented in Fig. 1(d). Confirmation of the cubic structure of CNF is provided by the data presented in Fig. 1(d), which is indexed at 2θ = 18° (1 1 1), 29.9° (2 2 0), 36.9° (3 1 1), 42.9° (2 2 2), 53.3° (4 2 2), 56.8° (5 1 1), and 62.4° (4 4 0). Upon examination of the X-ray diffraction pattern for PM, it is evident that the diffraction peaks that correspond to the (3 1 1) crystal planes of CNF and the β-phase peak of PVDF are present. In a similar manner, it is observed for the PC film. No secondary peaks are noticed, confirming the formation of the PM and PC composite films.The morphology studies of the individual PC and PM layer are shown in Fig. 2(a) and (b). Fig. 2(a) depicts the distribution of CNF throughout the PVDF matrix, and the morphology reveals that PVDF granules have been created in a clear and distinct manner. It has also been observed that the PM layer has a higher degree of porosity in comparison to the rigid CNF discussed in the article.26 Therefore, with reference to EMI shielding, the porous layer of the PC contributes to the enhancement of the effectiveness of absorption shielding. An SEM image of the PM layer (see Fig. 2(b)) clearly demonstrates the presence of MWCNTs, which indicates that they are distributed uniformly throughout the PVDF matrix. The FTIR absorption spectra of a pure PVDF film, the individual PC and PM layer are shown in Fig. 2(c). In the FTIR spectrum of PVDF, absorption bands are observed at 614, and 763, and 795 cm−1 (as shown in Fig. 2(c)). These bands are associated with the mixed CF2 bending, and C–C–C skeletal vibration, respectively, for the α-phase.27 Furthermore, a distinct low- intensity band at 1275 cm−1 is noted, indicating the existence of the β-phase. It may be deduced that the pure PVDF material does not contain the γ-phase because there is no band at 1234 cm−1. So, it's reasonable to assume that the α-phase makes up the majority of the pure PVDF film, while the β-phase is indicated by bands at 1275 cm−1, 841 cm−1, and 510 cm−1. Fig. 2(c) shows the FTIR spectrum of the PC and PM layer. The spectra show a pattern similar to that of PVDF, as previously noted. The PC layer additionally shows a band at a frequency of 560 cm−1, which corresponds to the stretching vibrations of the metal–oxide groups that are situated in the tetrahedral sites of ferrite.28 The Fe–Co bond is responsible for the band found at 1155 cm−1.29
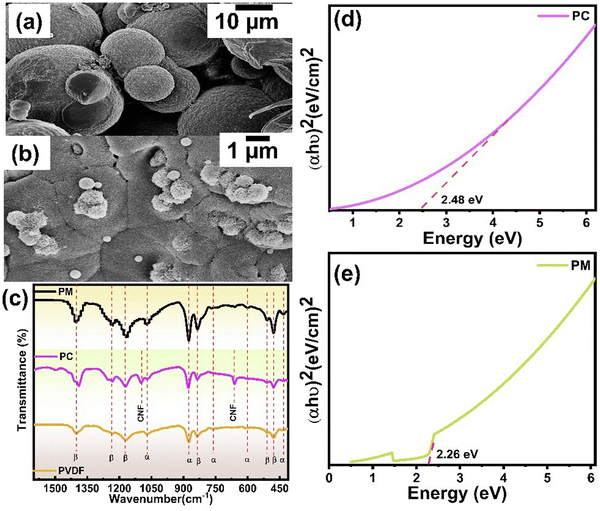 | ||
| Fig. 2 (a) and (b) SEM images for PC and PM layers, respectively, (c) FT-IR studies of pure PVDF, PM, and PC layers and (d) and (e) band gap studies for PC and PM layers. | ||
The band gap energy is the amount of energy that is required to excite an electron from the valence band to the conduction band. The calculation of the band gap energy with precision is very necessary in order to accurately predict the electromagnetic absorption characteristics of the multilayer structure, it is essential to ensure that the band gap energy of individual layers of the multilayer structure is calculated. The Eg is obtained by analyzing the tangent that is extrapolated to the X-axis of the ‘Tauc’ plots (see Fig. 2(e) and (f)) and the formula used to find the band gap is discussed in Section S3 (ESI†).30 The Eg values for PC and PM layers are 2.48 eV and 2.26 eV, respectively. It has been demonstrated that the band gap decreases with the addition of CNF and MWCNT when compared to pure PVDF (see Fig. S2(a), ESI†). Thus, it may enhance EMI shielding efficiency by forming a conductive network.
Electrical conductivity (σ) is an essential factor that plays a significant role in determining the EMI shielding ability of a material. This is because σ is directly related to both SER and SEA.21,31 In addition, it is a well-established fact that an increase in electrical conductivity leads to an increase in reflection. As a result, the amount of conductive filler in the matrix and the arrangement of the system that involves the conducting layers may be adjusted to achieve the desired level of shielding. Fig. 3(a) shows the electrical conductivity of the individual PM and PC layers. In the case of the PM and PC layers, they exhibited an electrical conductivity of 3.5 and 2.79 S m−1, respectively. A minor increase in conductivity is shown for the multilayer structures as the number of layers increases. In addition, it is important to understand that the sequence in which the layers are arranged is a significant factor in determining the conductivity of the composites. Due to the absence of a conductive upper and lower layer, the conductivity of the PC/PM/PC structure is seen to decrease by a significant amount. This is in accordance with the findings of Guo et al.25
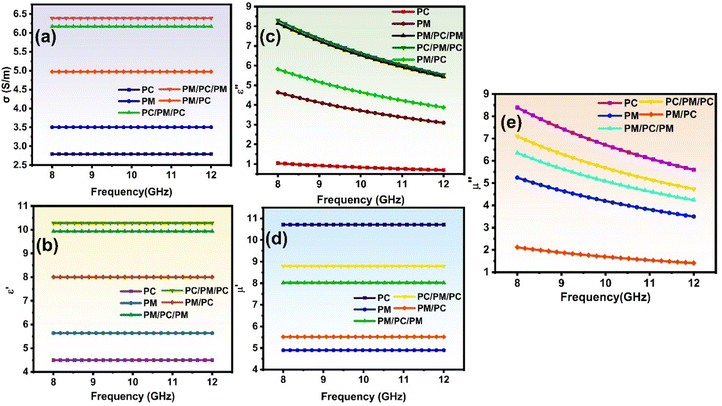 | ||
| Fig. 3 (a) Electrical conductivity versus frequency for individual and multilayer structures and (b)–(e) electromagnetic characteristics for individual and multilayer structures. | ||
The electromagnetic properties of a shielding material have a significant impact on the EMI shielding performance. Complex permittivity (εr = ε′ − jε′′) and complex permeability (μr = μ′ − jμ′′) are the parameters that characterize the electromagnetic (EM) properties of a material, where the imaginary parts of permittivity and permeability correlate with the EM energy losses (ε′′ and μ′′), and the real component of permittivity and permeability (ε′ and μ′) is assigned to the electromagnetic energy retention potential when it comes to electromagnetic energy. Fig. 3(b) and (c) illustrates the dielectric constant and loss of the PM and PC layer in the 8–12 GHz frequency range. In comparison to the PC, the PM layer has the highest permittivity. This can be due to the high electrical conductivity of the MWCNTs present in the matrix, as well as the added Maxwell–Wagner–Sillars (MWS) polarization. Due to the discrepancy in their electrical conductivity, the free charge carriers will be trapped at the filler–matrix interfaces in heterogeneous systems. This will result in the formation of MWS polarization, which is a result of the contribution of both the migrating and the hopping electrons.32,33 It can be observed from Fig. 3(b) that the PC layer has the lowest permittivity, in accordance with the lowest conductivity of the layer. In the case of the multilayer structures, the PC/PM/PC exhibits a higher permittivity than PM/PC/PM and PM/PC, which agrees with the trend in electrical conductivity of the multilayer structures. The analysis of the dielectric loss (see Fig. 3(c)) revealed that the PM layer presents more dielectric loss than the PC layer, which might be attributed to the conduction losses associated with percolative composite systems. In the case of PM/PC (see Fig. 3(c)), the high dielectric loss stems from the ohmic losses contributed by the well-connected conductive network formed by MWCNTs and the polarization losses arising from the increased interfaces in the composite.33 The PC layer exhibited a dielectric loss of 0.725 (see Fig. 3(c)). The dielectric loss of the multilayer structures PC/PM/PC and PM/PC/PM followed the same trend as observed in the case of real permittivity (see Fig. 3(c)). The curve in Fig. 3(d) and (e) depicts the magnetic permeability and losses of the PM, PC/PM, PM/PC/PM and PC/PM/PC structures as a function of frequency. It is possible to ascribe the magnetic permeability of ferrites to the domain wall motion that is common in low-frequency regions as well as the gyromagnetic spin rotation that is predominant in high-frequency regions.34 The μ′ values of all the structures followed a steady a pattern with an increase in frequency. This trend is in line with the observations made on ferrite-based composites that have been documented in the literature.35,36 As can be seen in Fig. 3(d) and (e), the magnetic permeability and loss of the multilayer structures are lower than those of the individual magnetic PC layer. One possible explanation for this is that the inclusion of nonmagnetic MWCNTs results in a decrease in the magnetic characteristics of the material. Over the X-band, the electromagnetic properties of each of the composites are tabulated in Table 1. It is clear that the conducting PM layer and the magnetic PC layer each provide a unique contribution to the improved shielding behaviour of the multilayered structures. This is demonstrated by the high dielectric loss of the PM layer and the superior magnetic characteristics of the PM layer.
| Composite | ε′ | ε′′ | μ′ | μ′′ | σ (S m−1) |
|---|---|---|---|---|---|
| PM | 5.64 | 3.34 | — | — | 3.50 |
| PC | 4.49 | 0.73 | 10.71 | 5.86 | 2.79 |
| PM/PC | 8.0 | 4.06 | 5.52 | 1.48 | 4.97 |
| PM/PC/PM | 9.93 | 5.8 | 8.02 | 4.44 | 6.39 |
| PC/PM/PC | 10.28 | 5.69 | 8.79 | 4.96 | 6.17 |
3.2. Simulation
The capability of a material to provide protection against electromagnetic radiation is referred to as the EMI shielding effectiveness. Three mechanisms—reflection, absorption, and multiple internal reflections—are responsible for determining the overall EMI shielding performance of any material. It is therefore possible to express the entire shielding efficiency as the sum of SER, SEA, and SEM, as shown in eqn (5). SER is highly dependent on the electrical conductivity of the shielding material since the shielding that is induced by reflection occurs as a result of the interaction between the charge carriers and the electromagnetic field. It is possible to express it in decibels by using the following equation: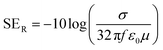 | (4) |
Similarly, shielding due to absorption can be given as
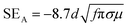 | (5) |
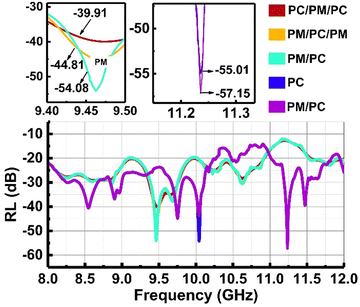
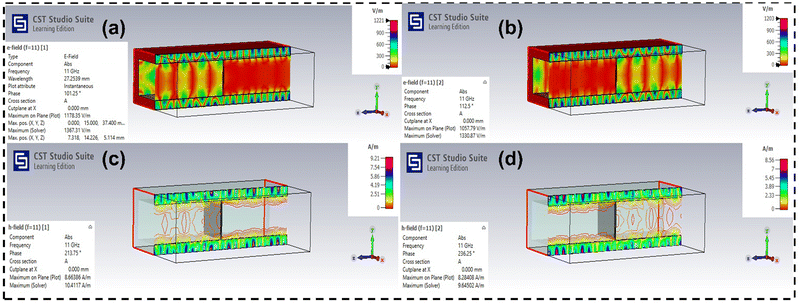
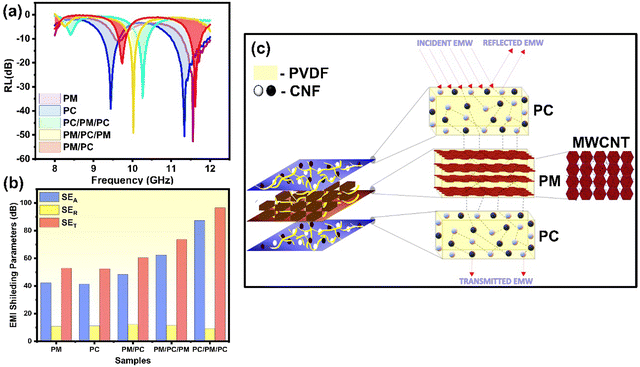
The simulated RL curves of the individual layers PM and PC and multilayer structures PM/PC, PM/PC/PM, and PC/PM/PC are presented in Fig. 4. The predicted RL of the composites from the simulation is in the order of PC/PM/PC > PM/PC/PM > PM/PC > PC > PM. Fig. 5(a)–(d) and animated videos in Supporting information V1(a)–(d) (ESI†) show the electric field and magnetic field propagation in the waveguide with PC/PM/PC and without the material (see the animated videos in Supporting information V2(a)–(d), ESI†). For PM/PC, and PM/PC/PM the electric and magnetic field propagation through the material in the waveguide is presented in Fig. S2(b) (ESI†). It is noteworthy to observe that the RL of PM/PC, PM/PC/PM, and PC/PM/PC multilayer structures is superior to that of the individual PM and PC layers. Furthermore, the PM/PC/PM structure displayed a RL that is greater than that of the PM/PC and PC/PM/PC, while having a conductivity that is significantly higher. From the results it is understood that when it comes to multilayer structures, the sequence in which the layers are arranged is a significant factor. Additional mechanisms that are involved are the conduction losses that occur from the PM, the polarization losses that occur from the PM, the magnetic losses, and the many internal reflections that occur at the interface between the PM and PC.33
3.3. Testing the EMI shielding properties of multi-layered structures
Fig. 6(a) illustrates the frequency response curves of the composites, with respect to reflection loss (RL) characteristics for PM, PC, PM/PC/PM, and PC/PM/PC. It is evident from the illustration that the maximum difference between the simulated and measured RL values does not exceed 5 dB. The reflection losses are found to rise with the number of layers and the arrangement of individual layers, which has an effect on the absorption properties of multilayer structures. When compared to other structures, the PC/PM/PC exhibits a larger reflection loss of −34.49 dB (see Table 2), which indicates that 99.99% of electromagnetic waves are absorbed, hence increasing the number of electromagnetic waves that are absorbed. This topic will be covered in greater depth in subsequent Section 3.3.1.| Sample | RL simulated (dB) | RL (dB) | SEA (dB) | SER (dB) | SET (dB) |
|---|---|---|---|---|---|
| PM | −52.66 | −57.15 | 42.14 | 10.66 | 52.79 |
| PC | −50.50 | −53.72 | 41.33 | 11.03 | 52.36 |
| PM/PC | −49.18 | −54.08 | 48.28 | 12.04 | 60.32 |
| PM/PC/PM | −38.2 | −44.81 | 62.21 | 11.35 | 73.55 |
| PC/PM/PC | −34.49 | −39.91 | 87.37 | 9.10 | 96.47 |
The SEA, SER, and SET as a function of frequency are displayed in Fig. 6(b) for PM, PC, PM/PC, PM/PC/PM, and PC/PM/PC structures. The measurements demonstrate that PC/PM/PC has the highest SET value with a large increase in SEA without a corresponding rise in SER compared to other developed structures (see Table 2). Furthermore, the SET of the manufactured structures clearly demonstrates an impact of the arrangement of the conducting and magnetic layers. The experimental data indicate that the arrangement of layers is a crucial factor in regulating the reflection-based shielding and electromagnetic energy trapping in the multilayer structures. This finding aligns with the outcomes derived from the simulation. The reason behind the larger SET value of PC/PM/PC structures than other structures is discussed in Sections 3.3.2. and 3.3.3.
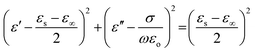 | (6) |
In the cases of PM/PC and PM/PC/PM structures, electromagnetic radiation will be incident on the conducting PM layer, which will then reflect the electromagnetic waves back to the source. It is expected that the electromagnetic waves that are transmitted from the PM layer in the case of the PM/PC structure will be absorbed at the PC layer due to impedance matching, whereas for PM/PC/PM these are caught between the conducting PM layer and the magnetic PC layer (see Fig. 6(c)). With the distinct contributions of the conducting and magnetic layers, as well as the various back-and-forth reflections of electromagnetic waves that occur within the energy-trapping layers, the electromagnetic energy will be greatly reduced.
For the PC/PM/PC composite, the impedance matching provided by the first magnetic layer PC (see Fig. S4(a) (ESI†) for impedance matching degree of PC and PM) makes it possible for electromagnetic waves to penetrate the sample in an effective manner; hence, the reflection is minimum, thus justifying the low SER value of PC/PM/PC (see Fig. 6(b)). Due to magnetic losses associated with the magnetic layer, the conduction losses associated with the conductive layer, and the dielectric losses, the electromagnetic wave that is introduced will be reduced in intensity. On the other hand, the waves that travel through the second conductive layer will come to interact with an impedance matching-magnetic layer. Despite experiencing attenuation because of magnetic and polarization losses, in contrast to the PM/PC/PM structure, some electromagnetic waves that remain unattenuated will traverse the last boundary of the composite material. The effectiveness of EM wave trapping is limited due to the arrangement of impedance-matching layers on both the front and back. Nevertheless, the utilization of PC/PM/PC ordering offers benefits in terms of reducing SER. To enhance the shielding efficiency of the multilayer structure, it is advisable to carefully choose a highly conductive layer as the intermediate layer. The results obtained from studying the EMI shielding mechanism of the PC/PM/PC and PM/PC/PM structures suggest that the specific arrangement of the layers significantly improves the efficiency of shielding in multilayer structures. Further, to justify the obtained SET values for multilayer structures attenuation constant studies are carried out, which agrees well with SET values (see Fig. S4(b), ESI†).
4. Conclusion
This study focuses on a simulation-based methodology to fabricate multilayered structures that exhibit enhanced electromagnetic interference shielding performance. The study primarily involves simulating several layered structures with varying layer patterns and number of layers. It is observed that the efficiency of shielding in multilayered structures is directly influenced by the order and number of layers. Moreover, thorough examinations of the impact of layer order on SE have shown that the careful selection of an appropriate configuration of the conducting and magnetic layers is crucial in improving the shielding effectiveness of the multilayered structures. The simulation of multilayered structures demonstrates that the strategic placement of the impedance matching layers in PC/PM/PC structures significantly improves absorption-dominated shielding by enhancing numerous internal reflections. PC/PM/PC structures provide a superior shielding efficiency of 96.47 dB compared to PM/PC/PM structures, with about 99% of the EM radiation attenuation being attributed to absorption. The EMI SE tests conducted on 2-layer (PM/PC) and 3-layer (PM/PC/PM and PC/PM/PC) structures show that the shielding characteristics of all the developed composites closely match the simulation results. This suggests that electromagnetic modelling is a highly effective method for forecasting the shielding characteristics of different structures with low requirements, and it can be used for all frequency ranges within the microwave spectrum. The findings of this study indicate that it is feasible to build microwave-absorbing structures with great efficiency by strategically arranging layers in magnetic-conducting topologies, without the need for expensive raw materials. Moreover, this study highlights a significant concept that electromagnetic simulation has great potential to design and optimize the EMI shielding characteristics of materials before the manufacturing stage of the systems. This enables the development of shielding structures with exceptional properties without depleting resources and capital.Author contributions
V. K.: synthesis, data collection, draft preparation; A. B.: synthesis, data collection, draft preparation; Y. C.: EMI data curation and discussions; W. M.: conceptualization, methodology, final drafting and supervising the project.Data availability
Data will be made available on request.Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
The authors would like to thank the SAS, VIT University, for XRD, UV-vis, FTIR facilities. Thanks to Hyderabad Central University for FESEM facilities.References
- J. C. Shu, W. Q. Cao and M. S. Cao, Diverse Metal–Organic Framework Architectures for Electromagnetic Absorbers and Shielding, Adv. Funct. Mater., 2021, 31(23), 1–20, DOI:10.1002/adfm.202100470.
- Y. Wan, P. Xiong, J. Liu, F. Feng, X. Xun, F. M. Gama, Q. Zhang, F. Yao, Z. Yang, H. Luo and Y. Xu, Ultrathin, Strong, and Highly Flexible Ti3C2Tx MXene/Bacterial Cellulose Composite Films for High-Performance Electromagnetic Interference Shielding, ACS Nano, 2021, 15(5), 8439–8449, DOI:10.1021/acsnano.0c10666.
- H. Zhao, X. Xu, D. Fan, P. Xu, F. Wang, L. Cui, X. Han and Y. Du, Anchoring Porous Carbon Nanoparticles on Carbon Nanotubes as a High-Performance Composite with a Unique Core-Sheath Structure for Electromagnetic Pollution Precaution, J. Mater. Chem. A, 2021, 9(39), 22489–22500, 10.1039/D1TA06147J.
- S. Satyamurthy, S. Savithri, R. Nirmala, A. Devarpiran and A. Ravichandran, A Case History of EMI Problems of an Optoelectronic Stabilized Sight, Proceedings of the International Conference on Electromagnetic Interference and Compatibility ’99 (IEEE Cat. No. 99TH 8487), 1997, pp. 321–327 DOI:10.1109/ICEMIC.1997.669822.
- W. A. Radasky and M. Bäckström, Brief Historical Review and Bibliography for Intentional Electromagnetic Interference (IEMI), 2014 XXXIth URSI General Assembly and Scientific Symposium (URSI GASS), 2014, pp. 1–4 DOI:10.1109/URSIGASS.2014.6929517.
- K.-S. Tan and I. Hinberg, 62 - Electromagnetic Interference with Medical Devices: In Vitro Laboratory Studies and Electromagnetic Compatibility Standards. Clinical Engineering Handbook, ed J. F. Dyro, Biomedical Engineering, Academic Press, Burlington, 2004, pp. 254–262 DOI:10.1016/B978-012226570-9/50068-5.
- R. D. Leach, Failures and Anomalies Attributed to Electromagnetic Interference, InSpace Programs and Technologies Conference, 1995, pp. 1–11 DOI:10.2514/6.1995-3654.
- A. Ahlbom, J. Bridges, R. De Seze, L. Hillert, J. Juutilainen, M.-O. Mattsson, G. Neubauer, J. Schüz, M. Simko and K. Bromen, Possible Effects of Electromagnetic Fields (EMF) on Human Health - Opinion of the Scientific Committee on Emerging and Newly Identified Health Risks (SCENIHR), Toxicology, 2008, 246(2), 248–250, DOI:10.1016/j.tox.2008.02.004.
- E. Kivrak, K. Yurt, A. Kaplan, I. Alkan and G. Altun, Effects of Electromagnetic Fields Exposure on the Antioxidant Defense System, J. Microsc. Ultrastruct., 2017, 5(4), 167, DOI:10.1016/j.jmau.2017.07.003.
- V. Lalan and S. Ganesanpotti, The Smallest Anions{,} Induced Porosity and Graphene Interfaces in C12A7:E− Electrides: A Paradigm Shift in Electromagnetic Absorbers and Shielding Materials, J. Mater. Chem. C, 2022, 10(3), 969–982, 10.1039/D1TC03762E.
- Z. Guo, P. Ren, Z. Lu, K. Hui, J. Yang, Z. Zhang, Z. Chen, Y. Jin and F. Ren, Multifunctional CoFe2O4@MXene-AgNWs/Cellulose Nanofiber Composite Films with Asymmetric Layered Architecture for High-Efficiency Electromagnetic Interference Shielding and Remarkable Thermal Management Capability, ACS Appl. Mater. Interfaces, 2022, 14(36), 41468–41480, DOI:10.1021/acsami.2c12555.
- M. Amini, M. Kamkar, F. Rahmani, A. Ghaffarkhah, F. Ahmadijokani and M. Arjmand, Multilayer Structures of a Zn0.5Ni0.5Fe2O4-Reduced Graphene Oxide/PVDF Nanocomposite for Tunable and Highly Efficient Microwave Absorbers, ACS Appl. Electron. Mater., 2021, 3(12), 5514–5527, DOI:10.1021/acsaelm.1c00940.
- J. B. Anooja, K. S. Dijith, K. P. Surendran and G. Subodh, A Simple Strategy for Flexible Electromagnetic Interference Shielding: Hybrid RGO@CB-Reinforced Polydimethylsiloxane, J. Alloys Compd., 2019, 807, 151678, DOI:10.1016/j.jallcom.2019.151678.
- I. R. Ibrahim, K. A. Matori, I. Ismail, Z. Awang, S. N. A. Rusly, R. Nazlan, F. Mohd Idris, M. M. Muhammad Zulkimi, N. H. Abdullah, M. S. Mustaffa, F. N. Shafiee and M. Ertugrul, A Study on Microwave Absorption Properties of Carbon Black and Ni0.6Zn0.4Fe2O4 Nanocomposites by Tuning the Matching-Absorbing Layer Structures, Sci. Rep., 2020, 10(1), 1–14, DOI:10.1038/s41598-020-60107-1.
- Q. Qi, L. Ma, B. Zhao, S. Wang, X. Liu, Y. Lei and C. B. Park, An Effective Design Strategy for the Sandwich Structure of PVDF/GNP-Ni-CNT Composites with Remarkable Electromagnetic Interference Shielding Effectiveness, ACS Appl. Mater. Interfaces, 2020, 12(32), 36568–36577, DOI:10.1021/acsami.0c10600.
- A. Sheng, W. Ren, Y. Yang, D. X. Yan, H. Duan, G. Zhao, Y. Liu and Z. M. Li, Multilayer WPU Conductive Composites with Controllable Electro-Magnetic Gradient for Absorption-Dominated Electromagnetic Interference Shielding, Composites, Part A, 2020, 129, 105692, DOI:10.1016/j.compositesa.2019.105692.
- D. J. Kwon, I. J. Kwon, J. A. Milam-Guerrero, S. B. Yang, J. H. Yeum and H. H. Choi, Aramid Nanofiber-Reinforced Multilayer Electromagnetic-Interference (EMI) Shielding Composites with High Interfacial Durability, Mater. Des., 2022, 215, 110452, DOI:10.1016/j.matdes.2022.110452.
- D. D. L. Chung, Materials for Electromagnetic Interference Shielding, Mater. Chem. Phys., 2020, 255, 123587, DOI:10.1016/j.matchemphys.2020.123587.
- C. Liang, Z. Gu, Y. Zhang, Z. Ma, H. Qiu and J. Gu, Structural Design Strategies of Polymer Matrix Composites for Electromagnetic Interference Shielding: A Review, Nano-Micro Lett., 2021, 13(1), 1–29, DOI:10.1007/s40820-021-00707-2.
- L. Xu, S. Wan, Y. Heng, S. Wang, J. Yang, Y. Dong, Y. Fu and Q. Ni, Double Layered Design for Electromagnetic Interference Shielding with Ultra-Low Reflection Features: PDMS Including Carbon Fibre on Top and Graphene on Bottom, Compos. Sci. Technol., 2023, 231, 109797, DOI:10.1016/j.compscitech.2022.109797.
- M. Kamkar, A. Ghaffarkhah, E. Hosseini, M. Amini, S. Ghaderi and M. Arjmand, Multilayer Polymeric Nanocomposites for Electromagnetic Interference Shielding: Fabrication{,} Mechanisms{,} and Prospects, New J. Chem., 2021, 45(46), 21488–21507, 10.1039/D1NJ04626H.
- J. Liu, S. Lin, K. Huang, C. Jia, Q. Wang, Z. Li, J. Song, Z. Liu, H. Wang, M. Lei and H. Wu, A Large-Area AgNW-Modified Textile with High-Performance Electromagnetic Interference Shielding, npj Flex. Electron., 2020, 4(1), 1–7, DOI:10.1038/s41528-020-0074-0.
- D. T. Phan and C. W. Jung, Multilayered Salt Water with High Optical Transparency for EMI Shielding Applications, Sci. Rep., 2020, 10(1), 1–9, DOI:10.1038/s41598-020-78717-0.
- S. Hu, D. Wang, Y. Kyosev, D. Kremenakova and J. Militky, The Novel Approach of EMI Shielding Simulation for Metal Coated Nonwoven Textiles with Optimized Textile Module, Polym. Test., 2022, 114(July), 107706, DOI:10.1016/j.polymertesting.2022.107706.
- Z. Guo, P. Ren, B. Fu, F. Ren, Y. Jin and Z. Sun, Multi-Layered Graphene-Fe3O4/Poly (Vinylidene Fluoride) Hybrid Composite Films for High-Efficient Electromagnetic Shielding, Polym. Test., 2020, 89, 106652, DOI:10.1016/j.polymertesting.2020.106652.
- V. Khade, A. B. Thirumalasetty, A. A. Rathod, Y. K. Chaoukiker and M. Wuppulluri, Flexible and Rigid Spinel Ferrite Carboneous Composite as a Future of Tunable Absorption Dominant CmWave Shielding Materials, J. Mater. Chem. A, 2024, 2(15), 8914–8926, 10.1039/D3TA07624E.
- K. Cai, X. Han, Y. Zhao, R. Zong, F. Zeng and D. Guo, A Green Route to a Low Cost Anisotropic MoS2/Poly(Vinylidene Fluoride) Nanocomposite with Ultrahigh Electroactive Phase and Improved Electrical and Mechanical Properties, ACS Sustainable Chem. Eng., 2018, 6(4), 5043–5052, DOI:10.1021/acssuschemeng.7b04697.
- C. Singh, A. Goyal and S. Singhal, Nickel-Doped Cobalt Ferrite Nanoparticles: Efficient Catalysts for the Reduction of Nitroaromatic Compounds and Photo-Oxidative Degradation of Toxic Dyes, Nanoscale, 2014, 6(14), 7959–7970, 10.1039/c4nr01730g.
- D. Karthickraja, S. Karthi, G. A. Kumar, D. K. Sardar, G. C. Dannangoda, K. S. Martirosyan and E. K. Girija, Fabrication of Core-Shell CoFe2O4@HAp Nanoparticles: A Novel Magnetic Platform for Biomedical Applications, New J. Chem., 2019, 43(34), 13584–13593, 10.1039/c9nj02510c.
- P. Makuła, M. Pacia and W. Macyk, How To Correctly Determine the Band Gap Energy of Modified Semiconductor Photocatalysts Based on UV-Vis Spectra. J. Phys, Chem. Lett., 2018, 9(23), 6814–6817, DOI:10.1021/acs.jpclett.8b02892.
- P. Saini and M. Arora, Microwave Absorption and EMI Shielding Behavior of Nanocomposites Based on Intrinsically Conducting Polymers, Graphene and Carbon Nanotubes, New Polymers for Special Applications, ed. A. D. S. Gomes, IntechOpen, Rijeka, 2012 DOI:10.5772/48779.
- X. Li, S. Zeng, S. E, L. Liang, Z. Bai, Y. Zhou, B. Zhao and R. Zhang, Quick Heat Dissipation in Absorption-Dominated Microwave Shielding Properties of Flexible Poly(Vinylidene Fluoride)/Carbon Nanotube/Co Composite Films with Anisotropy-Shaped Co (Flowers or Chains), ACS Appl. Mater. Interfaces, 2018, 10(47), 40789–40799, DOI:10.1021/acsami.8b14733.
- V. Lalan, A. Puthiyedath Narayanan, K. P. Surendran and S. Ganesanpotti, Room-Temperature Ferromagnetic Sr3YCo4O10 + δ and Carbon Black-Reinforced Polyvinylidenefluoride Composites toward High-Performance Electromagnetic Interference Shielding, ACS Omega, 2019, 4(5), 8196–8206, DOI:10.1021/acsomega.9b00454.
- K. Sun, Z. Zhang, R. Fan, M. Chen, C. Cheng, Q. Hou, X. Zhang and Y. Liu, Random Copper/Yttrium Iron Garnet Composites with Tunable Negative Electromagnetic Parameters Prepared by in Situ Synthesis, RSC Adv., 2015, 5(75), 61155–61160, 10.1039/C5RA09882C.
- L. Sun, L. Liang, Z. Shi, H. Wang, P. Xie, D. Dastan, K. Sun and R. Fan, Optimizing Strategy for the Dielectric Performance of Topological-Structured Polymer Nanocomposites by Rationally Tailoring the Spatial Distribution of Nanofillers, Eng. Sci., 2020, 12(16), 95–105 Search PubMed.
- A. Rajan, K. Solaman and S. Ganesanpotti, Design and Fabrication of Layered Electromagnetic Interference Shielding Materials: A Cost-Effective Strategy for Performance Prediction and Efficiency Tuning, ACS Appl. Mater. Interfaces, 2023, 15(4), 5822–5835, DOI:10.1021/acsami.2c19016.
- M.-S. Cao, J.-C. Shu, X.-X. Wang, X. Wang, M. Zhang, H.-J. Yang, X.-Y. Fang and J. Yuan, Electronic Structure and Electromagnetic Properties for 2D Electromagnetic Functional Materials in Gigahertz Frequency, Ann. Phys., 2019, 531(4), 1800390, DOI:10.1002/andp.201800390.
- Z. Guo, P. Ren, Z. Lu, K. Hui, J. Yang, Z. Zhang, Z. Chen, Y. Jin and F. Ren, Multifunctional CoFe(2)O(4)@MXene-AgNWs/Cellulose Nanofiber Composite Films with Asymmetric Layered Architecture for High-Efficiency Electromagnetic Interference Shielding and Remarkable Thermal Management Capability, ACS Appl. Mater. Interfaces, 2022, 14(36), 41468–41480, DOI:10.1021/acsami.2c12555.
- S. A. Oliver, M. L. Chen, I. Kozulin and C. Vittoria, Structure and Magnetic Properties of Barium Hexaferrite Films Deposited at Low Oxygen Pressures, J. Magn. Magn. Mater., 2000, 213(3), 326–334, DOI:10.1016/S0304-8853(00)00004-4.
- M.-S. Cao, X.-X. Wang, M. Zhang, J.-C. Shu, W.-Q. Cao, H.-J. Yang, X.-Y. Fang and J. Yuan, Electromagnetic Response and Energy Conversion for Functions and Devices in Low-Dimensional Materials, Adv. Funct. Mater., 2019, 29(25), 1807398, DOI:10.1002/adfm.201807398.
- Z. Wang, R. Wei and X. Liu, Fluffy and Ordered Graphene Multilayer Films with Improved Electromagnetic Interference Shielding over X-Band, ACS Appl. Mater. Interfaces, 2017, 9(27), 22408–22419, DOI:10.1021/acsami.7b04008.
- S.-H. Lee, D. Kang and I.-K. Oh, Multilayered Graphene-Carbon Nanotube-Iron Oxide Three-Dimensional Heterostructure for Flexible Electromagnetic Interference Shielding Film, Carbon, 2017, 111, 248–257 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ma00741g |
| This journal is © The Royal Society of Chemistry 2024 |