Open Access Article
Open Access ArticleOn the use of modelling antagonistic enzymes to aid in temporal programming of pH and PVA–borate gelation†
Nadeem
Bashir
 ab,
Anna S.
Leathard
ab,
Anna S.
Leathard
 d,
Madeline
McHugh
a,
Imogen
Hoffman
a,
Fahima
Shaon
a,
Jorge A.
Belgodere
d,
Madeline
McHugh
a,
Imogen
Hoffman
a,
Fahima
Shaon
a,
Jorge A.
Belgodere
 ac,
Annette F.
Taylor
ac,
Annette F.
Taylor
 *d and
John A.
Pojman
Sr
*d and
John A.
Pojman
Sr
 *a
*a
aDepartment of Chemistry & The Macromolecular Studies Group, Louisiana State University, Baton Rouge, Louisiana 70803, USA. E-mail: john@pojman.com
bPostgraduate Department of Chemistry, Government College for Women, Nawakadal, Srinagar, 190002, India
cTulane Departments of Medicine, Section of Hematology & Medical Oncology, Tulane University Health Science Center, New Orleans, LA 70112, USA
dChemical and Biological Engineering, University of Sheffield, Sheffield S1 3JD, UK. E-mail: a.f.taylor@sheffield.ac.uk
First published on 4th January 2024
Abstract
Feedback through enzyme reactions creates new possibilities for the temporal programming of material properties in bioinspired applications, such as transient adhesives; however, there have been limited attempts to model such behavior. Here, we used two antagonistic enzymes, urease in watermelon seed powder and esterase, to temporally control the gelation of a poly(vinyl alcohol)–borate hydrogel in a one-pot formulation. Urease produces base (ammonia), and esterase produces acid (acetic acid), generating a pH pulse, which was coupled with reversible complexation of PVA. For improved understanding of the pulse properties and gel lifetime, the pH profile was investigated by comparison of the experiments with kinetic simulations of the enzyme reactions and relevant equilibria. The model reproduced the general trends with the initial concentrations and was used to help identify conditions for pulse-like behaviour as the substrate concentrations were varied.
Design, System, ApplicationEnzyme reactions with pH-driven feedback provide a convenient route for programming gelation and motion of polymers in applications such as soft robotics. There is a need to develop models to improve our understanding and control of such systems. Here, we investigated the transient formation of PVA–borate hydrogels driven by a combination of acid- and base-producing enzymes and compared experiments to kinetic simulations of the reactions and equilibria. The model reproduced the general trends and enabled a rapid search of parameters to find optimal conditions for the desired pulse-like behavior. |
1. Introduction
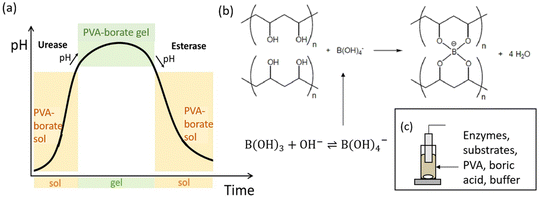
There is increasing interest in the exploitation of feedback in the programming of smart materials, such as hydrogels or polymers that undergo conformational transitions (volume phase or gel-to-solution phase) in response to environmental signals.1–3 Feedback arises through the pH when acidic or basic products catalyze the reaction; leading to rate acceleration and phenomena such as a pH clock (sharp switch in pH after a time lapse), pulse (transient increase/decrease in pH) or oscillations.4,5 Transient changes in pH may be exploited as a convenient method to control the lifetime of pH-sensitive hydrogels in bioinspired applications, such as temporary adhesives or soft robotics.6,7 Proposed mechanisms for temporary adhesion include secretion of an adhesive and de-adhesive substance in aquatic organisms such as starfish8 and slime moulds achieve motion using periodic contraction of actin fibrils.9 These organisms have long been studied for their ability to perform seemingly complex spatial tasks, such as maze-solving.10 A better understanding of pH-driven feedback in soft matter is still required to achieve the level of self-organization obtained in biological systems.Examples of using chemical feedback to trigger polymerization or chemomechanical responses mainly involve inorganic or toxic reactants. Hu et al. demonstrated a proof of concept of time-lapse curing of polymerization driven by a formaldehyde–sulfite pH clock.11 This reaction exhibits base-catalyzed feedback that results in an increase in pH after a controllable time lag, or clock time, and the sharp changes in state can be temporally programmed through the initial concentrations. The reaction has also been used for production of zeolites and chitosan particles.12,13 Yoshida and collaborators achieved chemomechanical oscillations by coupling a pH-sensitive hydrogel with the iodate–sulfite pH oscillating reaction in a flow reactor, and this was subsequently developed into a synthetic muscle.14,15 The feedback in these systems involves acid autocatalysis and hydrogels with ionisable groups that change state according the pH of the environment. Novakovic and Isakova created a pH oscillating chitosan gel for pulsatile drug release using a palladium-catalyzed carbonylation reaction.16 In closed systems, only the Belousov–Zhabotinsky (BZ) reaction, which is autocatalytic in bromous acid, has been exploited for periodic changes. A self-oscillating gel was obtained with a ruthenium catalyst covalently bonded to the gel matrix and periodic polymerization was observed using the BZ reaction with acrylonitrile.17,18 The major disadvantage of the BZ reaction, as well as most pH oscillators, is the harsh oxidizing environment.
Enzymes offer sustainable and benign approaches to controlling material formation in a closed system.19,20 Compared to traditional methods that rely on harsh chemicals, enzymatic approaches can be coupled with sensitive biomolecules and bioactive components, expanding the potential for diverse applications including pacemakers, drug delivery systems, self-healing polymers, self-walking actuators and transducers.21,22 Only a small number of enzymes with feedback have been used to date for materials applications. Siegel et al. used glucose oxidase to create chemomechanical oscillations in a hydrogel system.23,24 Acid production from glucose modulated the swelling of a hydrogel and periodically delivered a hormone across a membrane. A trypsin-based system was used to drive periodic assembly of complex coacervates.25 Urease catalyzes the formation of ammonia from urea and has been widely used to control the timing of base-driven gelation, supramolecular polymerization and peptide self-assembly.7,19 Spatial pH patterns have also been produced, for example, the base produced by the reaction was used to catalyze a thiol–acrylate Michael addition reaction resulting in propagating hydrogel fronts and urease was combined with glucose oxidase to generate spatial gradients in pH in a hydrogel that were perpetuated in the presence of nanoparticles.26,27 For a more complex temporal response, the coupling of pH clocks from opposing enzyme reactions with pH-responsive DNA hydrogels was demonstrated by Heinen et al.28 The system utilized urease and esterase, which catalyzed the hydrolysis of ethyl acetate into acetic acid. Together, these enzymatic reactions generated a pH pulse, characterized by an initial increase followed by a decrease in pH, and the lifetime of the DNA gel was controlled.
There have been few attempts to model enzyme reactions with feedback for the temporal control of hydrogel properties. Mostly these focused on glucose oxidase-based reactions coupled to changes in hydrogel permeability, however a model was proposed for antagonistic enzymes involving bond formation and destruction in which it was demonstrated that transient gelation could occur.20,23 Models have been developed for the feedback-driven increase or decrease in pH with the urease or esterase reactions, but questions remain regarding their ability to predict pH pulses in a multiphase system. Therefore, we combined experiments with modelling to show that these enzymes can be used to temporally control the gelation of polyvinyl alcohol (PVA) with borate. PVA–borate gels are non-toxic, biodegradable and inexpensive hydrogels that undergo pH responsive, reversible transitions that may be exploited in applications.29–31 Formulations have been developed for topical drug release, although in recent years some concerns over boric acid toxicity have been raised.32,33 Other applications include cleaning of painted surfaces in art conservation and PVA–borate gels are also widely used as model systems for studying physical gelation properties.34,35 Inorganic reactions have also been used for control of PVA gelation including autocatalytic iodate systems to form PVA–iodine gels, where it was demonstrated that the mechanical properties of the gel could be tuned through the changes in the reaction time.36,37
Herein, we obtained transient gelation of PVA–borate in a one-pot formulation containing the urease and esterase enzymes, buffer, boric acid and PVA solution. In order to determine the conditions for a pH pulse and transient gelation, a kinetic model was developed incorporating the enzyme reactions and equilibria with data obtained from the literature and our previous work.38 The model reproduced the general trends with initial concentrations and was used to find optimal substrate concentrations for a pH pulse. However, a quantitative match between experiments and simulations was lacking in some cases, suggesting additional factors are required to fully explain the behavior.
2. Experimental section
2.1. Materials
Sodium acetate (3 M, pH 5.2) was purchased from VWR Chemicals. Poly(vinyl alcohol) (LMW, Mw = 31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–50
000–50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, 98–99% hydrolysed), boric acid (ACS reagent, 99.5%), acetic acid (glacial), urea and ethyl acetate (ρ = 0.902 g ml−1) were purchased from Sigma Aldrich. The enzyme esterase was from porcine liver (Sigma, E3019-100KU) with an activity of 18 U mg−1. All chemicals were used as purchased without further purification.
000, 98–99% hydrolysed), boric acid (ACS reagent, 99.5%), acetic acid (glacial), urea and ethyl acetate (ρ = 0.902 g ml−1) were purchased from Sigma Aldrich. The enzyme esterase was from porcine liver (Sigma, E3019-100KU) with an activity of 18 U mg−1. All chemicals were used as purchased without further purification.
The watermelon seed powder (WMSP) containing the enzyme urease was prepared as described in our earlier work.39 To summarize, Jubilee improved seeds were obtained from Eden brothers (Arden, USA) and were ground to a fine powder in a flour mill, ensuring that the mixture doesn't overheat. Acetone, in a ratio 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 of acetone to seed powder by volume, was used to de-lipidate the seeds and this mixture was left overnight. The seed mixture was filtered, and the cake washed again with acetone. The cake was allowed to dry out in a fume hood overnight. The activity of the urease in the batch of watermelon seed powder used in experiments was determined using Nessler's reagent and was 347.8 mg NH3 per g WMSP per 5 minutes or 4084 U g−1.40
1 of acetone to seed powder by volume, was used to de-lipidate the seeds and this mixture was left overnight. The seed mixture was filtered, and the cake washed again with acetone. The cake was allowed to dry out in a fume hood overnight. The activity of the urease in the batch of watermelon seed powder used in experiments was determined using Nessler's reagent and was 347.8 mg NH3 per g WMSP per 5 minutes or 4084 U g−1.40
2.2. Production of the PVA–borate hydrogels
Stock solutions were prepared of poly(vinyl alcohol) (PVA, 4–10 wt%), boric acid (5 wt%, 0.8 M), urea (1 or 0.5 g ml−1 prepared by ultrasonication) and sodium acetate/acetic acid buffer (pH 4.05). The acetate buffer solution was prepared by adding 7.5 ml of acetic acid (glacial. 17.5 M) to 20 ml of 3 M sodium acetate and then acid added dropwise to obtain a final pH of 4.05. The buffer concentration was [acetate] + [acetic acid] = 6.9 M.For the formation of PVA–borate hydrogels, typically 10 ml of PVA solution was added to a 25 ml round bottom flask and then boric acid solution (5 wt%) was added dropwise with swirling. The watermelon seed powder (WMSP) was added to the flask, and the solution was vortexed for 5 minutes. The esterase powder was then added to the flask, and the mixture vortexed again for 5 minutes. Then the buffer solution was added with a micropipette. The flask was placed on an Anzeser magnetic stirrer hotplate. A Vernier pH probe was inserted into the mixture, and the pH was monitored until it stabilized. The reaction was initiated by simultaneous addition of the urea solution and ethyl acetate and the mixture was constantly stirred using a magnetic flea at a stirring rate of 800 rpm. Complete gelation was recorded when the motion of the flea stopped. The flask was covered with foil while the reaction proceeded to reduce loss of ammonia. Experiments were performed at room temperature (25 °C).
Unless otherwise stated, the mixture composition for a pulse was: 10 mL PVA (4 wt%) solution, 50 μL of boric acid solution (5 wt%), 0.45 g of WMSP, 0.15 g of esterase, 100 μL acetate buffer (6.9 M), 400 μL of urea (1 g ml−1), and 1050 μL of ethyl acetate. Thus, the standard concentrations were: urease activity = 184 U ml−1, esterase activity = 270 U ml−1, [PVA] = 40 g L−1, [boric acid] = 4 mM, [acetate buffer] = 0.0693 M, [urea] = 0.667 M and [ethyl acetate] = 1.08 M. The effect of buffer concentration on the pH pulse was investigated by varying the volume of acetate buffer from 100 to 800 μL in separate experimental runs. The effect of urease concentration on the pH pulse was investigated by varying the mass of the watermelon seed powder from 0.15 g to 0.90 g and the effect of urea concentration was investigated by varying the volume of urea solution added from 100 to 800 μL. Variations in esterase, PVA and boric acid concentrations were also investigated in some experiments. Repeated pulses were obtained by simultaneous additions of the urea solution and ethyl acetate after each pulse. The viscosity of the mixture in time was determined using a Brookfield DV-II+ viscometer with a LV2-62 spindle at 50 RPM with a 10% PVA solution and the other concentrations as above.
3. Modelling of the coupled urease–esterase reaction
The system was modelled using a set of coupled ordinary differential equations (ODEs) that describe the rate of change of species within the solution. The main processes in the model were (3.1) the urease-catalyzed reaction, (3.2) the esterase-catalyzed reaction, and (3.3) the equilibria that govern the pH (3.3). We used a bell-shaped dependence of the rate on pH for urease (in WMSP) and esterase with a maximum rate at pH ∼ 8.3.1. Urease-catalyzed reaction
Urease-catalyzed hydrolysis of urea yields ammonia and carbon dioxide: | (1) |
 | (2) |
The turnover number (kcat (s−1)) of urease varies depending on the source, purity and conditions of the assay.41 In our previous work with urease type III from jack bean (Sigma), we defined k1a = kcat/p/Mr × (1000 ml dm−3), where p = specific activity, Mr is molecular mass and with [E]T given as activity in U ml−1 so that the product k1[E]T gives the maximum rate, Vmax in M s−1.38 There is limited experimental data for urease contained in WMSP (which is not pure), so we took a value of kcat = 5500 s−1 in line with our previous work and used p = 3750 U mg−1, Mr = 470 kDa and KM = 8 mM for urease extracted from WMSP to give a value of k1a = 3.12 × 10−6 M U−1 ml s−1. For WMS urease, the pH optimum was ∼8,39,43 so here we used values of Kes1 and Kes2 to give that optimum (Fig. S1†), and the values of Ks and KI within ranges given the literature. We adjusted the value Kp to give a better match to experiments (see discussion). The rate constants are listed in Table 1.
| Equilibria rate constants | k 2 s−1 | k 2r M−1 s−1 | k 3 s−1 | k 3r M−1 s−1 | k 4 M s−1 | k 4r M−1 s−1 | k 5 s−1 | k 5r M−1 s−1 |
| 7.3 × 105 | 4.2 × 1010 | 1.25 × 10−6 | 1 × 1010 | 1 × 10−4 | 1 × 1010 | 24 | 4.3 × 1010 | |
| k 6 s−1 | k 6r M−1 s−1 | k 7 s−1 | k 7r M−1 s−1 | k 8 s−1 | k 8r M−1 s−1 | k 9 M−1 s−1 | k 9r s−1 | |
| 0.037 | 7.9 × 104 | 2.8 | 5 × 1010 | 5.794 | 1 × 10−10 | 200 | 1 | |
| Urease enzyme constants | k 1a M U−1 ml s−1 | K Ma M | K es1a | K es2a | K s M | K p M | K I M | |
| 3.12 × 10−6 | 8 × 10−3 | 8 × 10−7 | 2 × 10−11 | 3 | 2 | 1 × 10−4 | ||
| Esterase enzyme constants | k 1b M U−1 ml s−1 | K Mb M | K es1b | K es2b | ||||
| 1.17 × 10−6 | 3 × 10−3 | 2 × 10−6 | 2 × 10−11 | |||||
3.2. Esterase-catalyzed reaction
Esterase-catalyzed hydrolysis of ethyl acetate yields acetic acid and ethanol: | (3) |
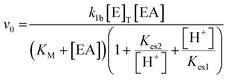 | (4) |
The form of the rate equation for esterase depends on the source and heterogeneity of enzyme, and nature of the substrate. There was limited experimental data on the rate for pig's liver esterase with ethyl acetate, however, early work suggested a small deviation from Michaelis–Menten kinetics and the value of kcat = 3.55 s−1 and KM = 1 mM (pH 8, 25 °C).44 With the molecular weight of 168 kDa and specific activity of 18 U mg−1 for esterase purchased from Sigma, we took a value of k1b = 1.17 × 10−6 M U−1 ml s−1 and with [E]T recorded in U ml−1 so that the product k1[E]T gives the maximum rate, Vmax in M s−1. The pH–rate curve in earlier work also varied with the enzyme source and substrate and the maximum rate was between 6.5 and 8, with a high activity maintained up to pH = 10, so here we used values of Kes1 and Kes2 to give that broad optimum (Fig. S1†).28,45,46
3.3. pH equilibria
When both the urease and esterase reactions are considered together, the pH is determined by the following reversible reactions:| R2 | CH3COOH ⇌ H+ + CH3COO− | pKa = 4.79 | Rate = k2[CH3COOH] − k2r[CH3COO−][H+] |
| R3 | CH3CH2OH ⇌ H+ + CH3CH2O− | pKa = 15.9 | Rate = k3[CH3CH2OH] − k3r[CH3CH2O−][H+] |
| R4 | H2O ⇌ H+ + OH− | pKa = 14 | Rate = k4 − k4r[OH−][H+] |
| R5 | NH4+ ⇌ NH3 + H+ | pKa = 9.25 | Rate = k5[NH4+] − k5r[NH3][H+] |
| R6 | CO2 + H2O ⇌ H+ + HCO3− | pKa = 6.35 | Rate = k6[CO2] − k6r[HC3−][H+] |
| R7 | HCO3− ⇌ H+ + CO32− | pKa = 10.25 | Rate = k7[HCO3−] − k7r[CO32−][H+] |
| R8 | B(OH)3 + H2O ⇌ B(OH)4− + H+ | pKa = 9.24 | Rate = k8[B(OH)3] − k8r[B(OH)4−][H+] |
| R9 | B(OH)4− + diol ⇌ (B(OH)4–diol) | K = 200 | Rate = k9[B(OH)3][diol] − k9r[(B(OH)4−–diol)] |
The acid equilibria rate constants are well established.47–49 The equilibrium constant, K, for the boric acid–PVA complex was taken from the literature50 where [diol] is the concentration of the diol subunit of PVA, calculated from the mass of PVA in experiments and Mr = 88 g mol−1. We used only the monodiol complexation reaction here, assuming the didiol complex is not significant at these borate concentrations.
3.4. Model equations and parameters
Reactions 1 and 3 and R2–R9 produce 17 coupled rate equations, including the pH determining equilibria and the two enzyme rates which are of a modified Michaelis–Menten form. The values of all the rate constants taken in this work are shown in Table 1. The rate equations were solved using XPPAUT with integration method CVODE (model file included in ESI†).51 The phase diagram was produced by incrementally increasing the values of one substrate with the other fixed and recording the data for a total of 1000 minutes to determine the magnitude of the pulse from the difference between the maximum pH and final pH at 1000 minutes.A typical mixture composition for the simulations of the pH pulse was [urease] = 184 U ml−1, [esterase] = 267 U ml−1, [acetate buffer] = 0.0693 M, [ethyl acetate] = 1.08 M, [urea] = 0.667 M, [boric acid] = 4 mM, [diol] = 0.45 M.
4. Results
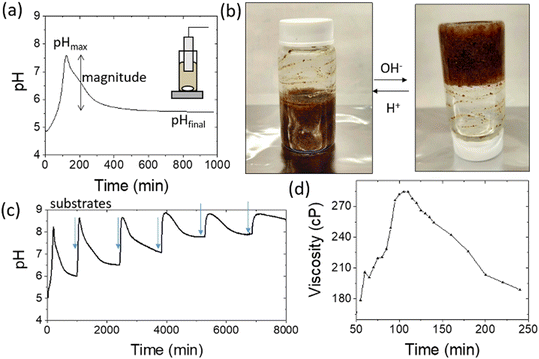
A schematic representation of the proposed system can be seen in Fig. 1. The coupling of the urease and esterase reactions leads to a pH pulse, i.e., a rise then fall in pH, for certain initial concentrations (Fig. 1a). The urease reaction is slow initially as the solution is at low pH. The ammonia produced from hydrolysis of urea results in an increase in pH and a shift of the boric acid equilibrium to borate anion which is used to cross-link the PVA gel (Fig. 1b). However, the rate of the esterase reaction also increases, producing acetic acid, which then lowers the pH, and the de-gelation of PVA–borate occurs. For autonomous control, we employed a one-pot formulation containing enzymes and substrates, PVA, boric acid and buffer (Fig. 1c). Watermelon seed powder (WMSP) served as a cheap, easily accessible source of urease in this system.A typical pH pulse during the experiment is shown in Fig. 2(a). The maximum pH and the steady state pH at 1000 minutes (pHfinal), are indicated on the plot as well as the pulse magnitude, defined here as the difference between pHmax and pHfinal. In general, with sufficient boric acid and PVA, for a pHmax greater than ∼7.5 gelation of the mixture was observed, as illustrated in Fig. 2(b). If the final pH fell below ∼6, then de-gelation of the mixture was obtained. In theory, gelation is completely reversible, and it was found that with repeated addition of the substrates, urea and ethyl acetate, multiple pulses could be obtained (Fig. 2(c)). However, the minimum pH failed to fall below 7 after several additions, likely because of deactivation of the esterase enzyme, and de-gelation was not obtained on this timescale. The transient increase in viscosity observed during a pH pulse was followed using a viscometer and is shown in Fig. 2(d) with max value of 270 cP. A range of states at pHmax was obtained, from a highly viscous solution to a gel, as the concentrations of PVA and boric acid were increased. The properties of borax-hydrogels are known to depend on the concentration of the PVA and boric acid, as well as the pH,29,35 and addition of co-solvents such as propanol also influence the rheological properties.34
In this paper we focus on the kinetics of the pH changes. The characteristic features of the pH pulse, pHmax and pHfinal, and hence the temporal properties of the gel can be controlled by varying the initial concentrations and the kinetic balance between the base producing and acid producing reactions. We determined the general trends and compared them to kinetic simulations for different experimental conditions: varying the boric acid or buffer concentration, varying the substrate concentration and varying the watermelon seed powder (WMSP) or esterase concentration. The comparison between the experimental observations and the simulated results allows us to better understand the mechanism and the potential additional factors that may influence the pH–time pulse.
4.1. Effect of boric acid and acetate buffer concentration on the pH pulse
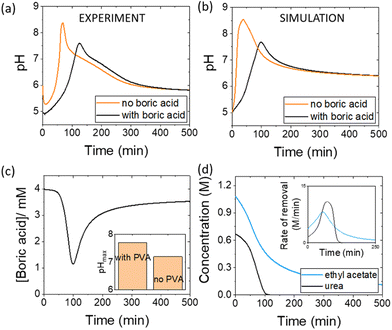
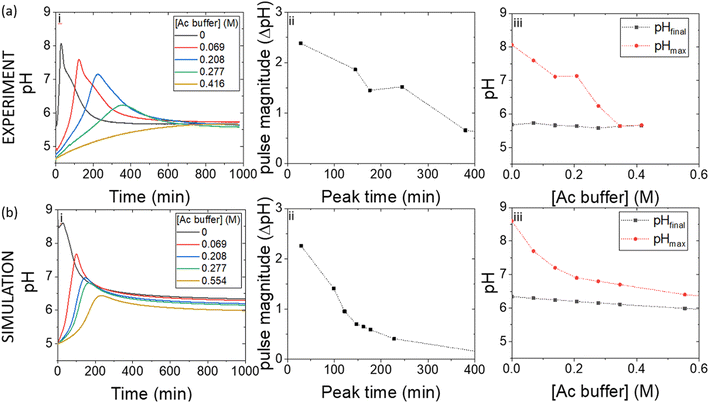
Pulses obtained in experiments with and without boric acid are shown in Fig. 3(a). The addition of boric acid decreases the maximum pH and increases the peak time. These results are qualitatively reproduced in the simulations with the inclusion of inhibition of urease by boric acid (Fig. 3(b)). Boric acid is removed by complexation with PVA during the pulse (Fig. 3(c)), and the pHmax is higher compared to reaction without PVA (Fig. 3(c) inset). In the simulation, urea is also completely removed during a pulse and the rate of removal of both substrates is observed to increase during the reaction, indicative of feedback (Fig. 3(d) inset). Feedback arises in the urease reaction as a result of the increase in rate of the enzyme reaction with an increase in pH.38The acetic acid buffer can be used to increase the peak time (time to pHmax). The watermelon seed powder raised the initial pH of the solution to ∼6.5 in the absence of buffer and the time to pHmax was 27 minutes (Fig. 4(a)i). With a buffer concentration = 0.069 M, the pH increased from ∼4.5 to pHmax ∼7.5 after 100 minutes. However, the magnitude of the pulse, defined here as pHmax–pHfinal, decreased with the increase in peak time (Fig. 4(a)ii). The buffer kept the pH low, suppressing the urease reaction and reducing the pH maximum (Fig. 4(a)iii). The simulated profile also showed a pronounced pH pulse for [Ac buffer] <0.1 M (Fig. 4(b)i), and the same general trends were obtained as in the experiments with increasing acetate buffer concentration (Fig. 3(b)ii and iii).
4.2. Effect of varying enzyme concentration on the pH pulse
In experiments with increasing mass of WMSP (Fig. 5), and hence urease activity, the magnitude of the pulse increased along with a decrease in the peak time (Fig. 5(a)ii). The faster rate of production of ammonia by urease raised the pHmax higher before the esterase could take effect (Fig. 5(a)iii). These general trends were qualitatively reproduced in the simulations with increasing activity of urease (Fig. 5(b)), however, the effect of urease on the maximum pH was more pronounced than in the experiments. Increasing the concentration of esterase had the reverse effect to urease, which was also reproduced qualitatively in the model (Fig. S2†).4.3. Effect of varying substrate concentration on the pH pulse
The simulations can be used to rapidly map out parameter space to find the optimal conditions for a pH pulse. A phase diagram of pulse magnitude, is shown in Fig. 6(a) as a function of the two substrates, urea and ethyl acetate. The colour map indicates the pH change, in which dark blue shows the largest magnitude of pulse. For a given value of ethyl acetate concentration, there is an optimal range of urea concentrations for which pulse behaviour is obtained, and this expands as the concentration of ethyl acetate is increased.The magnitude of the pulse increased then decreased with an increase in urea concentration and with [EA] = 1.08 M, the maximum magnitude was obtained at [U] = 0.67 M (Fig. 6(b)). The concentration of urea had a relatively small effect on the peak times compared to other parameters. The relationship between pulse magnitude and peak time is shown in Fig. 6(c) for two different concentrations of ethyl acetate. A decrease in [EA] to 0.6 M resulted in a larger maximum magnitude, but the peak times were also reduced.
Illustrative experiments at two different EA concentrations are shown in Fig. 6(d). As the [EA] was increased, the final pH was lower, as expected from the faster rate of production of acid. With [EA] = 1.08 M in experiments, a broad range of [U] gave pulse-like behaviour and the maximum pulse magnitude was obtained for [U] = 0.67 M, in good agreement with the simulations. No pulse-like behaviour was observed for [U] < 0.5 M and the process was dominated by esterase.
5. Discussion
It has been established in previous work that combining a base producing enzyme reaction and acid producing enzyme reaction can result in a pH pulse for temporal control of physical processes such as gelation.28 Herein, we investigated the widely-used urease and esterase reactions coupled to PVA–borate gelation in order to determine how simulations may be used to aid in finding optimal conditions for a pulse. The rate of change of pH will influence both the properties and lifetime of the gel state37 and the nature of the optimum will depend on the application. We focused on how the pH–time profile depends on the initial composition of the reaction mixture with comparison of the characteristic features of the pulse magnitude (pHmax–pHfinal) and peak time in the experiments and simulations.Overall, the model captured the general trends of pulse magnitude and peak time with initial concentrations. The simulations illustrated the switch from the urease rate to the esterase rate dominating as the reaction proceeds and the rate acceleration associated with the increase in pH (Fig. 3(d)). An increase in urease concentration (or decrease in esterase) resulted in a higher pHmax and there was an optimal substrate concentration for the largest pulse magnitude (Fig 6(a)). In general, there is a trade-off between pulse magnitude and peak time, as an increase in the magnitude arises from faster urease reaction relative to esterase, and hence shorter time to pHmax.
The model was less effective at producing a quantitative match to the experimental data and the results were found to be particularly sensitive to some of the enzyme parameters. The effect of halving or doubling k1 or Kes1 (the low pH binding site) on peak time and pHmax are shown in Table 2. Changing these parameters for urease results in ∼60–500% change in the peak time and ∼10–15% change in pHmax. We found that changing KM or Kes2 had no effect on the pH–time profile under the conditions explored here. We mainly used values from the literature for the enzyme constants, with some minor adjustments to improve the fit to the experiments. However, we note that for urease contained in WMSP, and for esterase with ethyl acetate specifically, there was limited data available.43,52,53 For urease from jack bean, a more complex dependence of the rate on pH has been proposed.42 Additionally, features associated with heterogeneous forms of the esterase enzyme were not taken into account.44 Earlier work suggests that there are multiple binding sites possible, with activities depending on the substrate chain length and concentration, and the different isoforms have different optimal pH's.53 A more complex expression rather than the modified MM used here would likely improve the fit to the data; however this would result in more fitting parameters and hence we chose the simpler form here.
| Esterase | % change in peak time | % change in pHmax | Urease | % change in T | % change in pHmax |
|---|---|---|---|---|---|
| 0.5 × Kes1b | −54 | 9.1 | 0.5 × Kes1a | 477 | −14.3 |
| 2 × Kes1b | 115 | −11.7 | 2 × Kes1a | −61 | 9.1 |
| 0.5 × k1b | −65.7 | 14.3 | 0.5 × k1a | 588 | −15.6 |
| 2 × k1b | 250 | −15.6 | 2 × k1a | −83.5 | 14.3 |
The importance of including the inhibition of urease by boric acid was also demonstrated, with an inhibition constant, KI, similar to that of jack bean urease giving a reasonable match between simulations and experiments.42 The substrate inhibition term Ks was found to play a small role in the dynamics, however the product inhibition Kp was found to completely suppress activity with the typical literature value of 0.002 used in our earlier work.38 It is possible that product inhibition is different for urease contained in WMSP; this requires further investigation. However, the value of KI was also previously determined for jack bean urease under conditions of much lower substrate, and hence product, compared to the conditions used here.41
Factors that were not included in the model include mixing effects caused by inhomogeneity in the distribution of watermelon seed powder and the influence of the increase in viscosity on the reaction rate. In experiments with no boric acid, the increase in viscosity with PVA from 1–12% was found to have a small effect on the peak time and value of pHmax (Fig. S2(a)†). However, with boric acid included, the change in peak time was greater, suggesting the dynamic change in viscosity may affect the rate of the urease reaction relative to the esterase reaction (Fig. S2(b)†). The diffusive restriction in the watermelon seed particles may also have influenced the effective enzyme rate compared to the simulations. For a better quantitative match to experiments, these features may be incorporated into the model in the future.
6. Conclusions
In conclusion, we have demonstrated the use of antagonistic enzymes, urease in WMSP and esterase, to obtain a pH pulse and coupled it to reversible gelation of PVA in a one-pot formulation. Our findings highlight the ability to modulate the pH–time pulse profile by manipulating experimentally controllable parameters. By varying the concentrations of substrate, buffer, and WMSP, we observed distinct changes in the pH dynamics. Repeated addition of substrates gave rise to multiple pulses, demonstrating the possibility of multiple gel cycles. The simulations reproduced the experimental trends qualitatively but there was a quantitative shift in the behavior compared to the experiments. These findings suggest that additional factors may be important, such as the more complex dependence of enzyme rate on pH or influence of increased viscosity and mixing effects on enzyme rate. Further investigation is needed to understand these issues and refine the model to better capture the experimental trends and to obtain control of the temporal programming of pH and gel properties. Overall, these results contribute to our understanding of coupled enzyme-catalyzed reactions and aid in the optimization of enzyme systems for various material applications.Author contributions
JAP conceived of the idea, NB provided lab supervision and performed experiments; MM, IH, FS performed experiments; JB performed the viscosity measurements; AL and AFT wrote the model script and performed the simulations; AL and AFT wrote the original manuscript and all authors contributed to final version of the paper.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work is supported by the US National Science Foundation under grant number OIA-1946231 and the Louisiana Board of Regents for the Louisiana Materials Design Alliance (LAMDA) and National Science Foundation under grant number 2051050 (REU SMART Polymers). We acknowledge the SIRE Award to Nadeem Bashir from Science and Engineering Research Board, Government of India with award number SIR/2022/000314. AL and AFT thank the Leverhulme Trust grant: RPG-2020-143 for funding.References
- A. Walther, Adv. Mater., 2020, 32, 1905111 CrossRef CAS PubMed.
- G. Panzarasa, T. Sai, A. L. Torzynski, K. Smith-Mannschott and E. R. Dufresne, Mol. Syst. Des. Eng., 2020, 5, 445–448 RSC.
- E. Tóth-Szeles, J. Horváth, G. Holló, R. Szűcs, H. Nakanishi and I. Lagzi, Mol. Syst. Des. Eng., 2017, 2, 274–282 RSC.
- B. Dúzs, I. Lagzi and I. Szalai, ChemSystemsChem, 2023, 5, e202200032 CrossRef.
- V. K. Vanag, D. G. Míguez and I. R. Epstein, J. Chem. Phys., 2006, 125, 194515 CrossRef PubMed.
- B. Lengerer and P. Ladurner, J. Exp. Biol., 2018, 221 Search PubMed.
- C. Sharma, I. Maity and A. Walther, Chem. Commun., 2023, 59, 1125–1144 RSC.
- P. Flammang, A. Michel, A. Van Cauwenberge, H. Alexandre and M. Jangoux, J. Exp. Biol., 1998, 201, 2383–2395 CrossRef PubMed.
- J. P. Rieu, H. Delano-Ayari, S. Takagi, Y. Tanaka and T. Nakagaki, J. R. Soc., Interface, 2015, 12 Search PubMed.
- T. Nakagaki, H. Yamada and Á. Tóth, Nature, 2000, 407, 470–470 CrossRef CAS PubMed.
- G. Hu, C. Bounds, J. A. Pojman and A. F. Taylor, J. Polym. Sci., Part A: Polym. Chem., 2010, 48, 2955–2959 CrossRef CAS.
- N. Német, G. Holló, G. Schuszter, D. Horváth, Á. Tóth, F. Rossi and I. Lagzi, Chem. Commun., 2022, 58, 5777–5780 RSC.
- G. Panzarasa, A. Osypova, A. Sicher, A. Bruinink and E. R. Dufresne, Soft Matter, 2018, 14, 6415–6418 RSC.
- J. R. Howse, P. Topham, C. J. Crook, A. J. Gleeson, W. Bras, R. A. L. Jones and A. J. Ryan, Nano Lett., 2006, 6, 73–77 CrossRef CAS PubMed.
- R. Yoshida, H. Ichijo, T. Hakuta and T. Yamaguchi, Macromol. Rapid Commun., 1995, 16, 305–310 CrossRef CAS.
- A. Isakova and K. Novakovic, J. Mater. Chem. B, 2018, 6, 5003–5010 RSC.
- R. Yoshida, T. Takahashi, T. Yamaguchi and H. Ichijo, J. Am. Chem. Soc., 1996, 118, 5134–5135 CrossRef CAS.
- R. P. Washington, W. W. West, G. P. Misra and J. A. Pojman, J. Am. Chem. Soc., 1999, 121, 7373–7380 CrossRef CAS.
- S. Panja and D. J. Adams, Chem. – Eur. J., 2021, 27, 8928–8939 CrossRef CAS PubMed.
- S. Giraudier and V. Larreta-Garde, Biophys. J., 2007, 93, 629–636 CrossRef CAS PubMed.
- P. Li, Y. Zhong, X. Wang and J. Hao, ACS Cent. Sci., 2020, 6, 1507–1522 CrossRef CAS PubMed.
- A. Isakova and K. Novakovic, Eur. Polym. J., 2017, 95, 430–439 CrossRef CAS.
- J. C. Leroux and R. A. Siegel, Chaos, 1999, 9, 267–275 CrossRef CAS PubMed.
- G. P. Misra and R. A. Siegel, J. Controlled Release, 2002, 81, 1–6 CrossRef CAS PubMed.
- S. N. Semenov, A. S. Y. Wong, R. M. van der Made, S. G. J. Postma, J. Groen, H. W. H. van Roekel, T. F. A. de Greef and W. T. S. Huck, Nat. Chem., 2015, 7, 160–165 CrossRef CAS PubMed.
- E. Jee, T. Bánsági, Jr., A. F. Taylor and J. A. Pojman, Angew. Chem., Int. Ed., 2016, 55, 2127–2131 CrossRef CAS PubMed.
- R. R. Mahato, E. Shandilya Priyanka and S. Maiti, Chem. Sci., 2022, 13, 8557–8566 RSC.
- L. Heinen, T. Heuser, A. Steinschulte and A. Walther, Nano Lett., 2017, 17, 4989–4995 CrossRef CAS PubMed.
- C. Wang, Z. Shen, P. Hu, T. Wang, X. Zhang, L. Liang, J. Bai, L. Qiu, X. Lai, X. Yang and K. Zhang, J. Sol-Gel Sci. Technol., 2022, 101, 103–113 CrossRef CAS.
- C. Zhang, H. Lu and X. Wang, Chin. J. Chem., 2022, 40, 2794–2800 CrossRef CAS.
- B. Lu, F. Lin, X. Jiang, J. Cheng, Q. Lu, J. Song, C. Chen and B. Huang, ACS Sustainable Chem. Eng., 2017, 5, 948–956 CrossRef CAS.
- N. Hadrup, M. Frederiksen and A. K. Sharma, Regul. Toxicol. Pharmacol., 2021, 121, 104873 CrossRef CAS PubMed.
- D. H. Abdelkader, M. A. Osman, S. A. El-Gizawy, A. M. Faheem and P. A. McCarron, Int. J. Pharm., 2016, 500, 326–335 CrossRef CAS PubMed.
- E. Carretti, S. Grassi, M. Cossalter, I. Natali, G. Caminati, R. G. Weiss, P. Baglioni and L. Dei, Langmuir, 2009, 25, 8656–8662 CrossRef CAS PubMed.
- G. Huang, H. Zhang, Y. Liu, H. Chang, H. Zhang, H. Song, D. Xu and T. Shi, Macromolecules, 2017, 50, 2124–2135 CrossRef CAS.
- S. Riedel and G. Panzarasa, Mol. Syst. Des. Eng., 2021, 6, 883–887 RSC.
- S. Riedel, T. Schweizer, K. Smith-Mannschott, E. R. Dufresne and G. Panzarasa, Soft Matter, 2021, 17, 1189–1193 RSC.
- G. Hu, J. A. Pojman, S. K. Scott, M. M. Wrobel and A. F. Taylor, J. Phys. Chem. B, 2010, 114, 14059–14063 CrossRef CAS PubMed.
- A. Q. Q. Mai, Characterization, Immobilization, and Polymer Related Applications of Watermelon Seed Powder, a Practical Source of Urease Enzyme, Doctoral Dissertations, LSU, 2021, p. 5464 Search PubMed.
- J. F. Thompson and G. R. Morrison, Anal. Chem., 1951, 23, 1153–1157 CrossRef CAS.
- B. Krajewska, J. Mol. Catal. B: Enzym., 2009, 59, 9–21 CrossRef CAS.
- B. Krajewska and S. Ciurli, Plant Physiol. Biochem., 2005, 43, 651–658 CrossRef CAS PubMed.
- O. Prakash, S. Puliga and L. S. Bachan Upadhyay, Biotechnol. Bioprocess Eng., 2007, 12, 131–135 CrossRef CAS.
- P. R. Ocken and M. Levy, Biochim. Biophys. Acta, 1970, 212, 450–457 CrossRef CAS PubMed.
- W. Junge and E. Heymann, Eur. J. Biochem., 1979, 95, 519–525 CrossRef CAS PubMed.
- S. Lange, A. Musidlowska, C. Schmidt-Dannert, J. Schmitt and U. T. Bornscheuer, ChemBioChem, 2001, 2, 576–582 CrossRef CAS PubMed.
- X. Wang, W. Conway, R. Burns, N. McCann and M. Maeder, J. Phys. Chem. A, 2010, 114, 1734–1740 CrossRef CAS PubMed.
- M. Eigen, Angew. Chem., Int. Ed. Engl., 1964, 3, 1–19 CrossRef.
- H. Ghanizadeh, F. Kiani, F. Koohyar and B. Khanlarzadeh, Turk. J. Pharm. Sci., 2020, 17, 177–181 CrossRef CAS PubMed.
- H. F. Mahjoub, M. Zammali, C. Abbes and T. Othman, J. Mol. Liq., 2019, 291, 111272 CrossRef.
- B. Ermentrout, Simulating, Analyzing, and Animating Dynamical Systems, Society for Industrial and Applied Mathematics, 2002 Search PubMed.
- A. A. Wani, D. S. Sogi, P. Singh and U. S. Shivhare, Food Sci. Biotechnol., 2011, 20, 877–887 CrossRef CAS.
- W. Junge and E. Heymann, Eur. J. Biochem., 1979, 95, 519–525 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3me00138e |
| This journal is © The Royal Society of Chemistry 2024 |