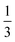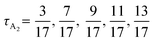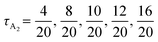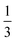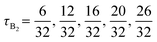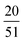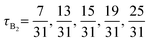Open Access Article
Open Access ArticleSelf-consistent field theory and coarse-grained molecular dynamics simulations of pentablock copolymer melt phase behavior†
So Jung
Park‡
 a,
Tristan
Myers‡
a,
Tristan
Myers‡
 a,
Vinson
Liao
a,
Vinson
Liao
 a and
Arthi
Jayaraman
a and
Arthi
Jayaraman
 *abc
*abc
aDepartment of Chemical and Biomolecular Engineering, University of Delaware, Colburn Lab, 150 Academy Street, Newark, DE 19716, USA. E-mail: arthij@udel.edu
bDepartment of Materials Science and Engineering, University of Delaware, Newark, DE, USA
cData Science Institute, University of Delaware, Newark, DE, USA
First published on 24th September 2024
Abstract
Block copolymer (BCP) self-assembly leads to nanostructured materials with diverse ordered morphologies, some of which are attractive for transport applications. Multiblock AB copolymers are of interest as they offer a larger design parameter space than diblock copolymers allowing researchers to tailor their self-assembly to achieve target morphologies. In this study, we investigate the phase behavior of symmetric AxByAzByAx and BxAyBzAyBx pentablock copolymers (pentaBCPs) where A and B monomers have the same statistical segment length. We use a combination of self-consistent field theory (SCFT) calculations and molecular dynamics (MD) simulations to link the polymer design parameters, namely the fraction of middle block volume to the volume of all blocks of same type, τ, overall volume fraction of A block, fA, and segregation strength, χN, to the equilibrium morphologies and the distributions of chain conformations in these morphologies. In the phase diagrams calculated using SCFT, we observe broader double gyroid windows and the existence of lamellar morphologies even at small values fA in contrast to what has been seen for diblock copolymers. We also see a reentrant phase sequence of double gyroid → cylinder → lamellae → cylinder → double gyroid with increasing τ at fixed fA. The chain conformations adopted in these morphologies are sampled in coarse-grained MD simulations and quantified with distributions of the chain end-to-end distance and fractions of chains whose middle (A or B) and end (A or B) blocks remain within domains of same chemistry (A or B). These analyses show that the pentaBCP chains adopt “looping”, “bridging”, and “hybrid” (both looping and bridging) conformations, with a majority of the chains adopting the hybrid conformation. The spatial distributions for each of the blocks in the pentaBCPs show that blocks of the same type in a chain locally segregate within the same domains, with shorter blocks segregating towards the domain boundaries and longer blocks filling the domain interior. This combined SCFT-MD approach enables us to rapidly screen the extensive pentaBCP design space to identify design rules for transport-favorable morphologies as well as verify the chain conformations and spatial arrangements associated with the theory predicted reentrant phase behavior.
Design, System, ApplicationBlock copolymers (BCPs) self-assemble into a variety of nanostructures, such as lamellae, hexagonal-packed cylinders, and double gyroid, which in turn enable engineering of materials with desired transport and mechanical properties. The morphology formed by a given BCP is highly dependent on its design in terms of the monomer chemistry, number of blocks (diblock to multiblock), block lengths, and block sequence. As compared to diblock copolymers, multiblock copolymers have been studied to a smaller extent due to their larger design parameter space. However, it is noteworthy that a handful of computational studies of multiBCPs have uncovered novel nanostructures and phase behavior not seen in the well-studied diblock copolymers. In this study, we focus on linking the design of pentablock copolymers (pentaBCPs) to their morphology in the melt state using self-consistent field theory (SCFT) and molecular dynamics (MD) simulations. Our goal is to identify design rules for experimentalists looking to broaden phase windows of transport-friendly morphologies, such as double gyroid. The combination of theory and simulation allows for faster screening of design parameter space using SCFT as compared to MD simulations and quantification of chain conformations using MD simulations especially when getting distribution of chain conformations from SCFT is non-trivial. |
I. Introduction
Block copolymers (BCPs) self-assemble into ordered periodic nanostructures through microphase separation arising from the chemical incompatibility and connectivity between the blocks.1,2 The rich phase diagram makes BCPs ideal to use as materials for applications in next-generation memory devices, membranes, sensors, photonic crystals, and solar cells.3–8 For the simplest case of linear AB diblock copolymer (in short, diBCP), the equilibrium morphology depends on three parameters – χN, fA, and ε, where χ is Flory–Huggins parameter quantifying the segregation strength between A and B monomers, N is degree of polymerization, fA is A block composition, and ε is the conformational asymmetry between two blocks.1,2,9 According to mean field theory, the order-to-disorder transition (ODT) for a linear AB diBCP occurs at a critical value of (χN)ODT = 10.5 with the volume fractions of A and B component equal (fA = 0.5).10 Above the ODT, the ordered (canonical) morphologies including lamellae (L), hexagonal-packed cylinders (C6), double gyroid (DG), and body-centered cubic (BCC) spheres are accessed in order of increasing asymmetry in copolymer composition. The chains self-assemble into these morphologies to minimize free energy by minimizing entropy loss associated with chain stretching and maximizing energetically favorable A–A and B–B contacts (enthalpic gain). The curvature of the A domain–B domain interface is determined by balance between stretching energies of two blocks, under the constraints associated with filling space at uniform density and minimizing packing frustration.11,12While the simplest case of linear diBCP has been studied extensively with experiments, theory, and simulations, there is a need to establish the above concepts – ODT, assembled equilibrium morphologies, order-to-order transition (OOT), adopted chain conformations within these morphologies – for other copolymer designs. With significant advances in polymer synthesis in the past couple of decades, researchers have been able to go beyond the simple linear diBCPs to complex multi-block and tapered sequences13,14 as well as non-linear polymer architectures (e.g., star, cyclic, coil-brush, bottlebrush).15–19 As these new polymers are created, it has also motivated researchers to understand how changing sequence and architecture impacts the assembled morphologies at equilibrium or during processing. Depending on the number of blocks (e.g., triblock, tetrablock, pentablock) and the sequence of A and B monomers (e.g., BAB vs. ABA for triblock), the phase diagrams for linear multiblock copolymers (in short multiBCPs) exhibit subtle or major differences from the linear AB diBCP phase diagram. For example, for symmetric ABA triBCPs, the overall topology of phase diagram remains similar to AB diBCP because an ABA triBCP if snipped in the middle forms two diBCPs.20,21 There are, however, some clear differences between the ABA triBCP and AB diBCP: (i) at the same composition, fA, the ODT is shifted to lower temperatures for ABA triBCPs as compared to AB diBCPs with a higher critical value of (χN)ODT ≈ 18 compared to that of diBCPs, (χN)ODT = 10.5,22 and (ii) while the morphologies accessed by ABA triBCPs are same as those of AB diBCPs, unlike the AB diBCPs, the ABA triBCPs adopt either looping (both end A blocks in the same A domains) or bridging (each A block in different A domains) conformations. Two different shifts of ODT to lower temperatures were found via predictions from self-consistent field theory (SCFT)23 and experiments where a relatively short A end block, when synthetically added to the B block of the AB diBCP, causes the ODT to be lower than the parent AB diBCP.24 For asymmetric (A)N1(B)NB(A)N2 copolymers, an interesting phase behavior was predicted based on the SCFT calculations by Matsen;23 he found that with varying parameter τ = N1/(N1 + N2), where N1 and N2 is degree of polymerization of A1 block and A2 block, the OOT phase boundary shifts nonmonotonically. This nonmonotonic shift of phase boundaries results in reentrant morphological transitions (e.g., lamella → double gyroid → cylinder → double gyroid → lamella) with decreasing τ at fixed fA. This reentrant morphological change (cylinder → lamella → cylinder) was also experimentally observed with asymmetric polystyrene-block-polybutadiene-block-polystyrene triBCP.25
In the case of ABAB tetraBCPs, specifically styrene-b-isoprene-b-styrene-b-isoprene tetraBCPs, experiments showed that the ODT temperature is considerably lower than that of comparable AB diBCPs.26 The phase diagrams of ABAB tetraBCPs constructed by SCFT theory27,28 and molecular dynamics (MD) simulation29 include canonical morphologies (spheres, cylinders, and lamellae) as observed in simpler AB diBCPs. However, compared to ABA triBCPs, existence of an additional tail B block in ABAB tetraBCP leads to the emergence of morphologies not seen with ABA triBCPs. For example, a hybrid lamella-sphere structure phase, where lamellar and spherical domains of the same component are separated by domains of the other component,27 and Frank–Kasper (FK) phases, a group of complex spherical packing phases,28 are predicted by the SCFT. The OOT phase behavior of ABAB tetraBCPs is also significantly different from that of ABA triBCPs. The reentrant phase transition (lamellae → double gyroid → hexagonal-packed cylinders → lamellae) was predicted by SCFT calculations of ABAB tetraBCPs with increasing ratio of the end A block length to total length of both A blocks, at a symmetric A–B volume fraction (fA = fB = 0.5).27 The same reentrant morphological transition was experimentally observed with polystyrene-b-polyisoprene-b-polystyrene-b-polyisoprene (SISI) tetraBCPs.30 It is notable that in these tetraBCPs, the cylinder and double gyroid phases are stable even at symmetric composition (A volume fraction = B volume fraction) of the copolymer unlike the simpler AB linear BCPs which only form lamellar phases at symmetric A and B volume fraction. In another experiment of SISI tetraBCPs,31 an unusual transition from cylindrical to lamellar morphology was observed upon increasing temperature; this is opposite to the OOT from lamella to cylinder morphology observed in AB diBCPs or ABA triBCPs. All of the above work demonstrates that presence of an additional B block in ABAB tetraBCP as compared to the ABA triBCP produces different phase behavior.
Compared to the ABA triBCPs and the ABAB tetraBCPs, experimental and computational studies of A and B containing pentaBCPs are sparse. For example, Zhao et al. calculated the SCFT phase diagrams of symmetric BABAB pentaBCPs, where the lengths of the two end B blocks are the same and the lengths of two A blocks are the same.32 The phase diagram with respect to χN and fA exhibits (χN)ODT > 30, at symmetric composition, fA = 0.5, in contrast to diBCP which has an (χN)ODT = 10.5, and symmetric triBCP, (χN)ODT ≈ 18. For these BABAB pentaBCPs, the same order of canonical morphologies (L → DG → C6 → BCC) was observed with decreasing fA as in the AB diBCPs and ABA triBCPs. Interestingly, for these symmetric BABAB pentaBCPs, the phase diagram with respect to fA and τ (where τ is the volume fraction of two end B blocks among all B blocks) exhibits, with decreasing τ, a reentrant phase behavior of body-centered cubic (BCC) and face-centered cubic (FCC) spherical phases (BCC → FCC → BCC → FCC → BCC).32 The reentrant phase behavior was supported by the SCFT density distributions of blocks, but the explicit chain conformations responsible for the reentrant phase behavior have not been verified yet.
In another recent SCFT study, it was shown that by optimizing design parameters in pentaBCP, i.e. individual length ratios of constituent blocks, one can achieve nontraditional phases that are difficult to access through simpler multiBCPs.33,34 SCFT calculations from Xie et al. proposed a strategy to stabilize single gyroid in BABAB pentaBCPs where the gyroid network structure is formed by the two A blocks.33 The constituent block lengths in pentaBCP was precisely tuned in the way that the stability of single gyroid is induced by the synergetic effect of lowered packing frustration and stretching energy of the bridging B blocks. The packing frustration in B domains of single gyroid is relieved through the local segregation of the two tail B blocks of asymmetric length, filling near and far space from the A–B interface. Further, the double gyroid which competes thermodynamically with single gyroid is destabilized by the stretched bridging B block connecting the two networks. Moreover, the equilibrium phase diagram of the BABAB pentaBCP with respect to the two design parameters – degree of asymmetry in length of two tail B blocks and length ratio of bridging B block to total B blocks – shows a stable phase of a square array of cylinders as compared to the canonical hexagonal-packed cylinders.33,34
Morphologies where the domains have a lower coordination number (e.g., square vs. hexagonal-packed cylinders or single gyroid vs. double gyroid) have attracted attention due to potential applications in photonic crystals5 and next-generation integrated circuits,3 and have been attempted to be accessed using more complex branched BCPs16,35,36 or blending different types of linear BCPs.3,37 The prior pentaBCP studies suggest that linear AB-type multiBCP designs have the potential of offering noncanonical structures with fewer molecular design parameters to consider, i.e. block sequence and relative length ratios between blocks, as compared to the branched BCP or the multicomponent BCP systems. Moreover, with experimentally tractable design parameters, systematic analysis of pentaBCP systems can give us insight into how BCP self-assembly behavior evolves from AB diBCP, ABA triBCP to AB-type multiBCP. Experimentally, symmetric pentaBCPs are considered easier to synthesize than tetraBCPs because symmetric pentaBCPs grown via difunctional initiators require fewer chain extensions than tetraBCPs grown from monofunctional initiators.38 As a result, study of pentaBCPs offers a more practical approach to understanding BCP self-assembly behavior.
In this paper, we investigate the equilibrium phase behavior of symmetric linear pentaBCPs with alternating sequences of A and B blocks – AxByAzByAx and BxAyBzAyBx – using a combined approach of SCFT calculation and MD simulation. We first present the SCFT calculations that lead to phase diagrams of the AxByAzByAx and BxAyBzAyBx pentaBCPs at different χN and various end vs. middle block volume fractions. Using a coarse-grained model for the pentaBCPs in MD simulations with chains of finite lengths and analogous design parameters as used in SCFT, we quantify distributions of chain conformations and spatial organization of the blocks within the A and B domains to explain the observed phase behavior in the SCFT phase diagram.
II. Approach
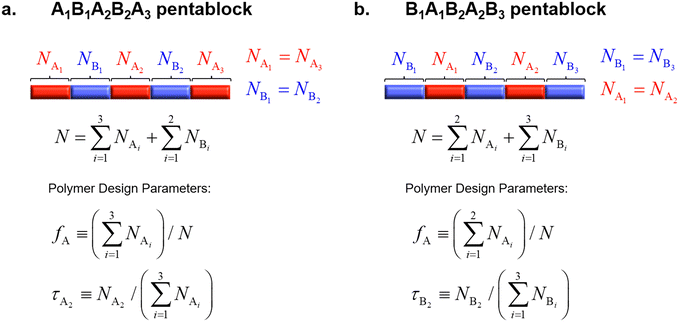
A. Pentablock copolymer (pentaBCP) design
We consider melts of linear AxByAzByAx and BxAyBzAyBx pentaBCPs with the design space shown in Fig. 1. For the remainder of this paper, we will denote these two cases of pentaBCPs as A1B1A2B2A3 and B1A1B2A2B3 pentaBCPs, identifying the order of the blocks in the subscript rather than the degree of polymerization of the block.We only consider the case where the degree of polymerization of the two end blocks are equal and the degree of polymerization of the second and forth blocks are equal. In other words, NA1 = NA3 and NB1 = NB2 for the A1B1A2B2A3 pentaBCPs, and NB1 = NB3 and NA1 = NA2 for the B1A1B2A2B3 pentaBCPs, where Nγ is defined as degree of polymerization of γ type block in the polymer chain. We also assume that the A and B monomers have the same statistical segment length, bA = bB; the analogous cases where bA ≠ bB will be the focus of a future publication.
Our chosen designs reduce the number of parameters for the block compositions to two independent parameters, the overall volume fraction of A block, fA, and the fraction of the middle A2 (or B2) block to the total A (or B) blocks for the A1B1A2B2A3 block (for the B1A1B2A2B3) copolymers, denoted as τA2 and τB2 as shown in Fig. 1.
In short, we study the phase behavior of linear A1B1A2B2A3 and B1A1B2A2B3 pentaBCP melts by varying the polymer design parameters, fA, τA2, τB2, and segregation strength between A and B monomers, χN.
B. SCFT formalism for pentaBCP melt
We use SCFT formalism39 to predict equilibrium phase behavior of pentaBCP melts in a system volume V. The polymers are modeled as flexible Gaussian chains with a total degree of polymerization N and A and B monomers with equal statistical segment length b and segment volume ν. With this model, the polymer design parameter τA2 (or τB2) is interpreted as the number ratio of statistical segments in the middle bridging blocks, A2 (or B2), to the total A (or B) blocks for A1B1A2B2A3 (or B1A1B2A2B3) pentaBCPs.As we are considering single-component melts, we use canonical ensemble SCFT for calculating Helmholtz free energies of the pentaBCP melts. In the SCFT formalism, the partial partition function q(r, s) of the chain fragment is calculated by solving the following modified diffusion equation (eqn (1)). The parameter s is a continuous parameter s ∈ [0, N] indicating the specific segment along the chain contour with the free first segment denoted as s = 0 and the last segment as s at position r in q(r, s). The modified diffusion equation is written as follows:
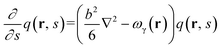 | (1) |
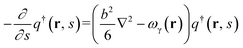 | (2) |
From the computed partial partition functions, the density of monomers belonging to type γ blocks is determined by
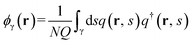 | (3) |
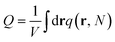 . The incompressibility condition requires the total density of monomers at position r satisfies
. The incompressibility condition requires the total density of monomers at position r satisfies 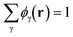 .
.
In SCFT, the mean field solutions for the densities and chemical potential fields satisfy the following equations,
| ωA(r) = χϕB(r) + ξ(r) | (4) |
| ωB(r) = χϕA(r) + ξ(r) | (5) |
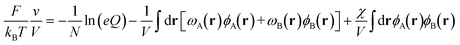 | (6) |
C. SCFT calculations
The calculations of the above SCFT formalism for pentaBCPs are performed using the open-source polymer self-consistent field (PSCF) software.39 The diffusion equations (eqn (1) and (2)) are numerically solved using the pseudo-spectral method40 with periodic boundary conditions. For the integration, we use the integration step of ds ≈ 0.005 and a large number of spatial grid points (Table 1) to keep accuracy of numerical solutions as high as possible while keeping computational costs reasonable. To find the self-consistent mean field solutions, the diffusion equations are iteratively solved with chemical potential fields ωA(r) and ωB(r), which are updated by the self-consistent mean field equations (eqn (4) and (5)) for the next iteration cycle. The Anderson mixing iteration scheme is implemented when updating the fields iteratively to accelerate the convergence to the self-consistent mean field solutions.41 The iterative computation stops when the errors in the self-consistent mean field equations (eqn (4) and (5)) are less than the specified error tolerance. The SCFT simulation details implemented in PSCF software are provided in ref. 39.To determine the equilibrium phase at given polymer design parameters, the Helmholtz free energies for the ordered phases, lamellae (L), double gyroid (DG), Fddd orthorhombic network (O70), hexagonal-packed cylinders (C6), and body-centered cubic spheres (BCC), and homogeneous disordered phase (Dis), are compared (ESI† Fig. S2). The morphologies of the candidate phases we consider in SCFT calculations are provided in Table 1. We did not consider non-classical phases such as single gyroid and square array of cylinders; those phases have been predicted by SCFT to be stable in AB-type pentaBCP melts with highly asymmetric end blocks.33,34 For the pentablock copolymer designs we consider in this work, the two end blocks have the same length where such non-classical phases are not favored.
D. Coarse-grained (CG) model used in molecular dynamics (MD) simulations
To complement SCFT morphological predictions with quantitative information of chain conformations in the observed equilibrium morphologies, we use CG MD simulations.We model pentaBCPs as CG bead-spring chains composed of two types of beads, A and B, where each bead represents a Kuhn segment of the copolymer.42 Such models have been used extensively in past studies of MD simulations of copolymers as well as polymer blends to predict melt morphology as a function of polymer composition, architecture, and total chain length.42–50 To match the SCFT design space, we maintain both bead types to be of the same statistical segment size 1d; all other simulation lengths are normalized to this 1d.
Pairs of bonded beads in each chain have a harmonic bond potential of the form
| Ubond = kbond(r − r0)2 | (7) |
Pairs of non-bonded beads interact with each other via the cut-and-shifted Lennard-Jones (LJ) potential51 which has the form
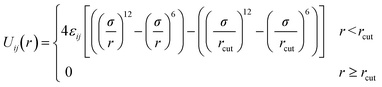 | (8) |
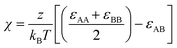 | (9) |
E. MD simulation
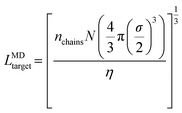
In the first system, we simulate 400 chains of each polymer design at χN = 60 within a cubic simulation box with side length LMDtarget calculated as
 | (10) |
In the second system, the chain end-to-end distance RMDee sampled at χN = 60 from the first system is used to specify the target cube side length LMDtarget. We take inspiration from the SCFT calculations in which the length of the unit cell LSCFTuc is expressed as
| LSCFTuc = CSCFTucRSCFTee | (11) |
The third system size is a cube of size LMDtarget which is a multiple of Lq* = 2π/q*, corresponding to the position of the major peak of the A domain structure factor SAA(q*) sampled at χN = 120 for each chain design in the second system. We found that the LMDuc from the second system was often mismatched with Lq*, indicating that the simulation box size was incommensurate with the morphology periodicity. We quantify this discrepancy between the unit cell size found in SCFT and MD by comparing CSCFTuc with the MD unit cell parameter CMDuc, found as the quotient of Lq*, from the second system, and RMDee from the first system. We found that CMDuc corresponded to the CSCFTuc for chain designs SCFT predicted would form the lamella (L) morphology, but often disagreed for those predicted to form C6 and DG (cylinders and double gyroid) morphologies; this prompted us to use the third system with LMDuc = 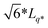 for chain designs which are predicted by SCFT calculations to form DG at χN = 60, and with LMDuc = Lq* if any other morphology is predicted. We set the integer ratio between LMDtarget and LMDuc such that nchains ≥ 1000 to reduce the impact of finite-size effects. We simulate increasing χN from 40 to 120 in increments of 10 to sample the pentaBCP morphology and chain conformations.
for chain designs which are predicted by SCFT calculations to form DG at χN = 60, and with LMDuc = Lq* if any other morphology is predicted. We set the integer ratio between LMDtarget and LMDuc such that nchains ≥ 1000 to reduce the impact of finite-size effects. We simulate increasing χN from 40 to 120 in increments of 10 to sample the pentaBCP morphology and chain conformations.
For readers interested in the values of CSCFTuc used for the second system size, the RMDee and Lq* sampled from the first and second system sizes, and CMDuc calculated from the results of the first and second system sizes, we provide this information in Table S1 in the ESI.†
We then simulate the melts at each segregation strength χN in the NPT ensemble (with T* = 1, P* = 1) using the Nosé–Hoover thermostat and barostat. We maintain a cubic simulation box by coupling all three side lengths. We set εAA and εBB equal to 1kBT and select εAB so as to achieve our target χ using eqn (9). We first equilibrate the melt for 1.5 × 107 timesteps, which we verify to be sufficient by ensuring the convergence of the profile of mean-squared internal distances:
 | (12) |
Lastly, we also conduct tests of stability of the MD simulation and SCFT predicted morphologies using a new computational approach – rapid analysis of polymer structure and inverse design strategy (RAPSIDY) – that we describe in a separate publication.61 Briefly, in this new approach we begin MD simulations using initial configurations where we pre-place chains directly into a desired morphologies (e.g., lamellae or double gyroid or others) to rapidly test the stability or metastability of that morphology for the specific polymer design. We describe this method in detail in the ESI.†
We identify ordered microphase-separated morphologies of pentaBCP melts visually using isosurface snapshots and via the emergence of the microphase peak (q* peak) in the A domain structure factor SAA(q). We employ a procedure derived from that described by Brisard and Levitz63 to efficiently calculate the structure factor while accounting for finite simulation volume. We treat each bead as a point scatterer and calculate the scattering amplitude as
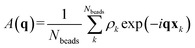 | (13) |
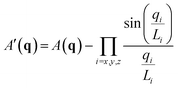 | (14) |
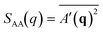 | (15) |
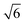
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and
1 and 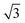
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 for the DG and O70 morphologies, respectively.65–67
1 for the DG and O70 morphologies, respectively.65–67
To analyze the conformations of simulated chains, we identify the A and B domains of the simulated melts using isosurfaces drawn with a Gaussian density mesh method68 implemented in the OVITO software.69 We identify A domains by generating isosurfaces around beads of type A with a resolution of 30, radius scaling of 100%, and iso value of 10; this combination of parameters correctly yields the fraction of the simulation volume occupied by A domains to be equal to fA. We then quantify the fraction of each type of block (e.g., the end A blocks, B blocks, and middle A block for the A1B1A2B2A3 pentaBCP) in A domains. For comparison, we also quantify the distribution of each block type in each domain using a particle mesh Ewald (PME) method developed by Essmann et al.,70 and we present the results of both methods in the ESI.† This PME calculation is used to distribute bead charges onto a voxel grid for the efficient calculation of electrostatic interactions; as in previous simulation work on BCPs,71 we use this method to distribute the mass of each bead onto a voxel grid and then assign each voxel to the domain type (A or B) corresponding to the majority of the bead mass in that voxel. This allows us to confirm that our conclusions about the chain conformations are consistent and independent of the type of calculation. We also use these bead mass grids to create 1D and 2D distributions of each block type within A and B domains for comparison with SCFT data.
We further distinguish chain conformations by using the chain end-to-end distance Ree to estimate the number of domains accessed by each chain. We analyze the Ree distribution of simulated melts to determine the proportion of each conformation.
F. Simulated pentaBCP designs
The advantage of combining SCFT and MD simulations is that SCFT accelerates the design parameter sweep as compared to MD simulations. Thus, running MD simulations at every point in the design space defeats the purpose of this accelerated exploration with SCFT. Instead, using the results from SCFT (discussed in Section III.A), we select a few pentaBCP designs to simulate and analyze their chain conformations. The design parameters for the twenty simulated pentaBCP designs are listed in Table 2. Each simulated system is comprised of identical chains of specified N, fraction of A-type beads fA, and the fraction τi represented by the chain's middle block of the total beads of its type. The composition of pentaBCPs of sequence A1B1A2B2A3 and B1A1B2A2B3 are specified by the parameters τA2 and τB2, respectively.III. Results
A. SCFT phase diagrams of ABABA and BABAB pentaBCPs
In Fig. 2 we show the SCFT phase diagrams of the A1B1A2B2A3 pentaBCPs at different χN values with respect to the design parameters, τA2 and fA. We observe disordered phases (Dis) only in the phase diagrams calculated at χN = 35 and 40. Between χN = 40 and 60, all design parameters forming the disordered phases at χN = 40 undergo a transition from disorder to order and the phase diagram at χN = 60 only shows ordered morphologies. | ||
| Fig. 2 The SCFT phase diagrams with respect to the polymer design parameters τA2 and fA (as defined in Fig. 1) for the A1B1A2B2A3 pentaBCPs at (a) χN = 35, (b) χN = 40, and (c) χN = 60. The legend on top of the figure shows which symbols represent the different equilibrium phases identified by SCFT free energy calculations: homogeneous disorder (Dis), body-centered cubic spheres (BCC), hexagonal-packed cylinders (C6), double gyroid (DG), Fddd (O70), and lamellae (L) phases. The conventional presentation of SCFT phase diagrams with the continuous phase boundaries are presented in ESI† Fig. S4. | ||
The values of τA2 = 0 and τA2 = 1 correspond to the symmetric ABA and BAB triBCPs, respectively. At these extreme values of τA2, for all three values of χN, as fA increases, we observe this sequence of ordered phases: C6 → DG → L. At intermediate values of τA2 and χN values of 35 and 40 (Fig. 2a and b), we observe the transition from Dis → BCC → C6 → DG or O70 → L. This order of sequences is similar to that observed with the AB diBCP phase diagram because as A/B block composition becomes more symmetric, the polymers assemble into morphologies with less curved A–B interfaces. While this order of sequences C6 → DG → L with increasing fA remains consistent at all values of τA2, the value of fA where the OOT occurs depends on the value of τA2. At χN = 60 (Fig. 2c) we observe no disordered phase, and all the chain designs exhibit ordered phases (BCC, C6, DG, and L).
The phase behavior A1B1A2B2A3 pentaBCPs at the three values of χN varies the most between 0.3 ≤ τA2 ≤ 0.5. At χN = 35 (Fig. 2a), a wide window of disordered phase is observed around 0.3 ≤ τA2 ≤ 0.5. The ordered phases next to the disordered region of the phase diagram are weakly segregated with a broader A–B interface compared to the ordered phases in τA2 = 0 and τA2 = 1 at the same fA (ESI† Fig. S6). In this weakly segregated regime, the DG phase stability is outcompeted by the O70 phase stability, which is a characteristic feature of AB diBCP phase behavior near ODTs. At χN of 60 (Fig. 2c) and 0.3 ≤ τA2 ≤ 0.5, all phases are ordered over the fA range we present, and the L stability region extends to low fA values (fA ≈ 0.38) with well segregated A and B domains (ESI† Fig. S7). In contrast, the width and position of the phase stability windows for the τA2 ≈ 0 and τA2 ≈ 1 are insensitive to χN, indicating that (χN)ODT from SCFT calculations is well below 35. This suggests that among A1B1A2B2A3 pentaBCP designs with the same amount A monomers, the pentaBCP designs with relatively evenly distributed A monomers among the three A blocks (0.3 ≤ τA2 ≤ 0.5) have lower ODT temperatures and higher (χN)ODT than the designs where A monomers are predominantly distributed to either the end or the middle blocks (τA2 ≈ 0 and τA2 ≈ 1). Considering that τA2 = 0 and τA2 = 1 correspond to the ABA and BAB triBCPs, respectively, this finding indicates that the A1B1A2B2A3 pentaBCPs have higher (χN)ODT (or lower ODT temperature) than the triBCPs. The higher (χN)ODT in A1B1A2B2A3 pentaBCPs is likely because there are more available configurations in the pentaBCPs than the triBCPs when A and B blocks are microphase-separated by looping or bridging the intermediate blocks, which results in higher degree of A–B mixing for the pentaBCPs than the triBCPs at the same χN.
At all three values of χN for a fixed fA value as we increase τA2, we observe a reentrant phase sequence; e.g., at fA = 0.45, going from τA2 = 0 to 1 at χN = 60 (Fig. 2c), the equilibrium phase goes from L → DG → L → DG → L (see ESI† Fig. S8 for the fA = 0.45 line overlaid on Fig. 2c; along this line the reentrant phase sequence is observed). Similar reentrant phase behavior has been observed in ABA triBCPs,23,25 and ABAB tetraBCPs,27,28,30 but not in simple AB diBCPs. In the case of ABA triBCPs,23 the SCFT phase diagram of the ABA triBCPs is plotted with respect to τ and fA, where the asymmetry parameter τ is the volume fraction of one A block to all A blocks; τ = 0 corresponds to the AB diBCP and τ = 0.5 corresponds to a symmetric ABA triBCP. For the ABA triBCPs, the reentrant phase transition (L → DG → C6 → DG → L) and phase boundary shape with decreasing τ from 0.5 to 0 is similar to the shape of the phase boundaries and the ordered phase transitions observed in the half portion of our A1B1A2B2A3 pentaBCP phase diagram (0 ≤ τA2 ≤ 0.5) in Fig. 2. For the ABA triBCP, the reentrant phase transition was explained by the tendency of asymmetric ABA triBCP to form curved A–B interfaces found in DG and C6 while the AB diBCP (τ = 0) and the symmetric ABA triBCP (τ = 0.5) prefer the zero A–B interface curvature found in the L phase. The authors of that SCFT study23 suggested that at the intermediate values of τ between 0 and 0.5, the A blocks of different lengths spatially organize both near and far from the A–B interfaces, increasing the tendency to curve the A–B interface toward the inner parts of the A domains to reduce the overall stretching penalty. This discussion of the triBCP is relevant because one could consider the A1B1A2B2A3 pentaBCP design as two identical triBCPs connected in series. We assume that there is higher tendency to form curved geometry phases for the pentaBCP designs (0 < τA2 < 0.5 and 0.5 < τA2 < 1) equivalent to the two asymmetric triBCPs connected, caused by spatial organization of A blocks of different lengths, than for the symmetric ABA triBCP (τA2 = 0), symmetric BAB triBCP (τA2 = 1), and A1B1A2B2A3 pentaBCP of τA2 = 0.5 which is equivalent to the two symmetric ABA triBCP connected in serial. For the case of A1B1A2B2A3 pentaBCP of τA2 = 0.5, the middle A2 block has twice the length of the end A blocks, but the looped or bridged A2 block conformations make the stretched chain length similar between the middle A2 block and the two end A blocks, making it less efficient to spatially organize for forming the curved A domains. The nonmonotonic trend in interfacial curvature due to different spatial organizations of blocks at different τA2 values likely cause the reentrant phase behavior. We discuss this effect of τA2 on the adopted chain conformations and spatial organization of the A and B blocks in Section III.B.
Fig. 3 shows the B1A1B2A2B3 pentaBCP phase diagrams at three different χN. Similar to the A1B1A2B2A3 phase diagrams in Fig. 2, B1A1B2A2B3 pentaBCPs also exhibit reentrant phase behavior at fixed fA values, and with decreasing χN, the ordered phases are destabilized exhibiting disordered phases at the intermediate τB2 values. In fact, if the identities of A and B blocks are interchanged, the B1A1B2A2B3 pentaBCP phase diagrams correspond to those of the A1B1A2B2A3 pentaBCP phase diagrams over the range 0.55 < fA < 0.85. The combined phase diagrams of Fig. 2 and 3 are provided in ESI† Fig. S9. One key difference between Fig. 2 and 3 is that the ordered phase stability windows for the curved structures (BCC, C6, DG, and O70) are mostly located in fA < 0.40 for the B1A1B2A2B3 pentaBCPs while a larger stability window of those phases is observed in fA > 0.40 for the A1B1A2B2A3 pentaBCPs (Fig. 2). For example, the DG stability windows of B1A1B2A2B3 pentaBCPs at χN = 60 (Fig. 3c) are located in fA ≤ 0.38 while a large portion of DG stability windows of A1B1A2B2A3 pentaBCPs at the same χN = 60 (Fig. 2c) is located over fA = 0.38, especially with DG windows at the highest fA for τA2 = 0.2 and τA2 = 0.8.
 | ||
| Fig. 3 Same figure caption as Fig. 2 but for B1A1B2A2B3 pentaBCPs at (a) χN = 35, (b) χN = 40, and (c) χN = 60. | ||
The differences in the position of the phase stability windows between A1B1A2B2A3 and B1A1B2A2B3 pentaBCPs implies that A1B1A2B2A3 pentaBCPs have a higher tendency to form curved A–B interfaces than B1A1B2A2B3 pentaBCPs at the same fA and χN. For the A1B1A2B2A3 pentaBCPs, the A domains are formed by the two free end blocks (A1 and A3 blocks) and the one looped or bridged middle block (A2 block), while for the B1A1B2A2B3 pentaBCPs the A domains are formed by looped or bridged A1 and A2 blocks of equal length. Local segregation of same component blocks within same domains has been well known as an important mechanism for accommodating interfacial curvatures of complex spherical phases.28,72,73 We use MD simulations to calculate the spatial distributions of the A and B blocks in both A and B domains and present those results in Section III.C.
B. Density profiles of A and B blocks for ABABA pentaBCPs
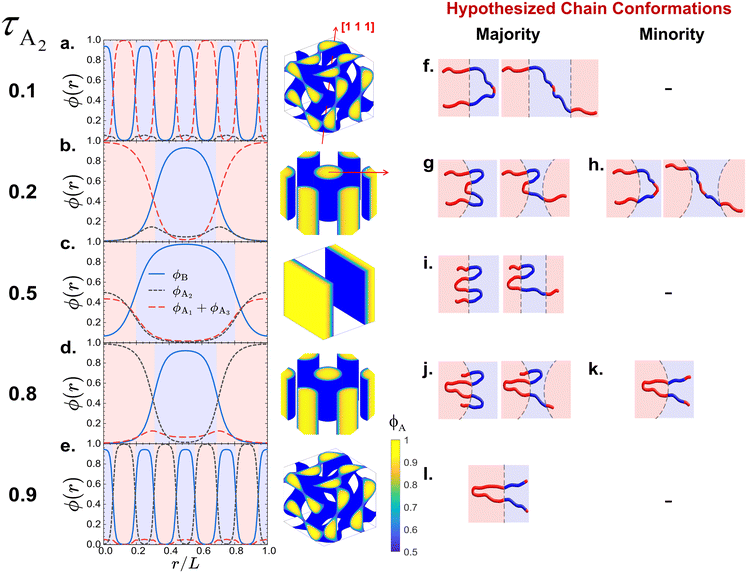 | ||
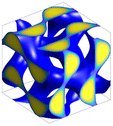
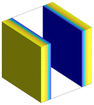
| Fig. 4 (a–e) The spatial SCFT density distributions for all B blocks (ϕB = ϕB1 + ϕB2, blue lines), the middle A blocks (ϕA2, black short-dashed lines), and the end A blocks (ϕA1 + ϕA3, red long-dashed lines) for the equilibrium phases at fA = 0.4 and (a) τA2 = 0.1 (DG), (b) τA2 = 0.2 (C6), (c) τA2 = 0.5 (L), (d) τA2 = 0.8 (C6) and (e) τA2 = 0.9 (DG), identified on the A1B1A2B2A3 pentaBCP phase diagram at χN = 60 (Fig. 2c). The A domain (ϕA > 0.5) and B domain (ϕB > 0.5) are represented with the shaded red and blue regions, respectively. The SCFT equilibrium morphologies (DG → C6 → L → C6 → DG) are presented next to the density profiles. The red lines on the DG and C6 morphologies depict the directions along which the densities are plotted. For the DG phases, the densities are plotted along the [111] direction of the unit cells, which passes though the four three-fold connectors of DG network domains. For the C6 phases, the densities are plotted along the center-to-center direction of the cylinders. (f–l) Our hypothesized majority and minority chain conformations forming the A/B domain interfaces, corresponding to from τA2 = 0.1 to 0.9. The A/B domain interfaces in the DG phases are depicted as flat to exaggerate the interfacial curvature change in the reentrant phase behavior. | ||
The density distributions at τA2 = 0.2 (Fig. 4b) show the spatial segregation of A blocks within the A domains of the C6 morphology. The long A end blocks form the core of the cylinder domains and the short middle A2 blocks form the shell of the cylinder domains with their highest concentration being near the A–B interface. Some amount of middle A2 block density (ϕA2 = 0.048) remains at the center of the B domains; this suggests that while majority of the chains prefer A and B blocks to be segregated in their respective domains by looping or bridging the B blocks (see hypothesized chain conformations in Fig. 4g), a small fraction of chains adopt configurations where middle A2 blocks is solubilized within the B domains (see hypothesized chain conformations in Fig. 4h).
The density distributions at τA2 = 0.5 (Fig. 4c) show all end and middle A blocks exhibit similar spatial density distributions in the A lamellar domains; this is because the volume of two end A blocks is equal to that of the one middle A2 block. We assume that at τA2 = 0.5, the degree of stretching in the end A blocks and middle A block are relatively comparable than the case where the length ratio between the two types of A blocks is highly asymmetric (e.g. τA2 = 0.1 or 0.2), as indicated in the similar spatial density distributions within the A domains. The spatial segregation of A blocks within the A domains of the C6 morphology becomes stable again at τA2 = 0.8, where the long middle A2 block and short end A blocks are preferentially localized into core and shell regions within the A cylindrical domains (Fig. 4d). We hypothesize that in a majority of cases, the A and B blocks segregate in the different domains (as shown in our schematic in Fig. 4j), and for a small fraction of chain conformations the short end A blocks are solubilized in the B domains (schematic in Fig. 4k). We also hypothesize that at extremely strong segregation regime (χN → ∞), the minority chain conformations (Fig. 4h and k) would disappear for both τA2 = 0.2 and τA2 = 0.8 due to significant enthalpic A–B contact penalty.
The density distributions at τA2 = 0.9 (Fig. 4e) show that the A domains in the DG phase are mostly formed by the middle A2 blocks and the short end A blocks are solubilized in the B domains. As in the τA2 = 0.1 case, the enthalpic loss from the unfavorable A–B mixing is compensated by the configurational entropy gain from the relaxed B blocks (see our hypothesized conformation in Fig. 4l).
C. Chain conformations adopted by pentaBCPs in various morphologies
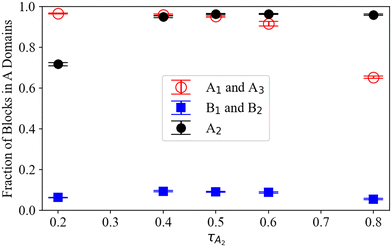
We find that smaller blocks are more likely to solubilize, leading to the lowest average A block solubilization when the end and middle A block sizes are balanced at τA2 = 0.5, as predicted in Fig. 4i. The end A blocks (A1 and A3) are increasingly solubilized in B domains as τA2 increases and, therefore, the end block size relative to the middle A2 block shrinks. In contrast, middle A2 blocks are less likely to reside in B domains as τA2 increases. The fraction of B blocks (B1 and B2) found in A domains is greatest when τA2 ∼ 0.5 and decreases at extreme values of τA2. We speculate that this is because the greater solubilization of the small A blocks at either extreme (i.e., τA2 = 0.2 and τA2 = 0.8) permits the B blocks to reside further away from the A–B interface on average and therefore decreases their solubilization in A domains. Conversely, the B blocks become more solubilized in A domains on average when the end and middle A blocks are both sufficiently large to remain in the A domains (at τA2 ∼ 0.5).
Using the preferred domain location of each block type, we can now evaluate the hypothesized proportions of each A1B1A2B2A3 pentaBCP chain conformation in Fig. 4. For all τA2, the B blocks of the A1B1A2B2A3 pentaBCPs mostly remain in B domains (see blue symbols in Fig. 5) which supports the hypothesized B block arrangement in chain conformations in Fig. 4. For all τA2 besides 0.2 and 0.8, more than 90% of the end and middle A blocks in A domains, which is also in accordance with the hypothesized chain conformations for τA2 = 0.5 (Fig. 4i). For τA2 of 0.2, the middle A2 block for ∼30% of the chains (i.e., minority) resides in the B domain; this also supports the hypothesized “majority” and “minority” conformations in Fig. 4g and h. For τA2 of 0.8, the majority of end A blocks reside in A domains but chains have at least one “solubilized” end block; as each pentaBCP has two end blocks, it has a ∼ (70%)2 = 49% chance of having at least one end A block in an A domain. This means that the most frequent conformation for chains with τA2 of 0.8 would be a combination of the hypothesized conformations in Fig. 4j and k, with one end A block in a B domain.
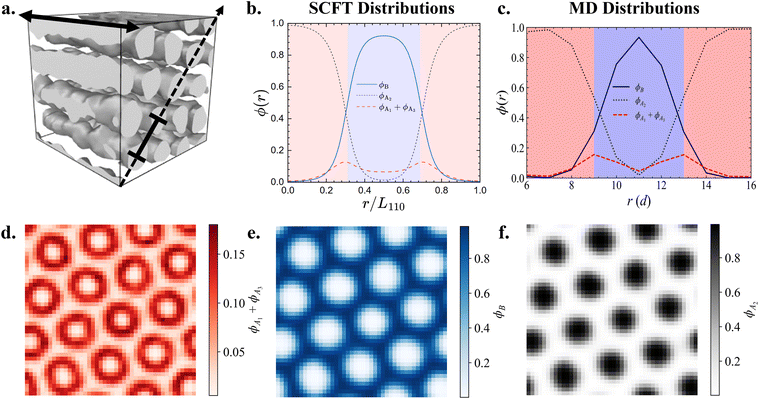
To further compare the distribution of each block type between SCFT and MD, we present one- and two-dimensional volume fraction distributions of the end A blocks, B blocks, and middle A2 blocks of the A1B1A2B2A3 pentaBCP with fA = 0.4 and τA2 = 0.8 in Fig. 6; this polymer design assembles into the C6 morphology at χN = 120 (Fig. 6a). We calculate one-dimensional distributions of each block, analogous to those derived from the SCFT calculations in Fig. 4, by sampling the volume fractions in a plane parallel to (one of) the periodic axis of the morphology; this periodic axis is indicated with a dashed line in Fig. 6a. We present the distributions derived from the SCFT calculations for the same chain designs, originally given in Fig. 4d, in Fig. 6b for comparison. We present the same data in ESI† Fig. S19 for a simulated melt of the A1B1A2B2A3 pentaBCP with fA = 0.4 and τA2 = 0.5, which forms the L phase.
We observe that the one-dimensional MD volume fraction distributions exhibit many of the same characteristics as the SCFT-derived distributions, including those which we took as evidence of the chain conformations hypothesized in Fig. 4. For the SCFT and MD distributions for the cylinder-forming melt (Fig. 6b and c respectively), the volume fraction of the end A blocks (ϕA1 + ϕA3) is highest near the A–B interface (ϕA1 + ϕA3 ∼ 0.16), declines towards the center of the B domains, and becomes nearly zero at the middle of the A domains. This suggests that the end A blocks segregate towards the outside of the A domains and can also be present in B domains in simulated melts of this chain design, as predicted by SCFT calculations and reflected in the chain conformations in Fig. 4j and k. The volume fraction of B blocks ϕB reaches a maximum in the middle of the B domains and a minimum in the A domains. Conversely, ϕA2 is highest at the middle of each A domain and lowest, but not zero, at the middle of the B domains. We note that ϕA2 ∼0.05 in the MD data and ∼0.01 in the SCFT data in the B domains.
The two-dimensional spatial distributions of the blocks provide further evidence that the spatial segregation of A blocks in A domains in simulation agrees with SCFT predictions. The two-dimensional distributions of end A blocks (ϕA1 + ϕA3) in Fig. 6d show that end A blocks (A1 and A3) preferentially segregate towards the outside of each cylindrical A domain near the A–B interface and have a sparse presence towards the center of each A domain and in the B domain between them. Fig. 6e and f show that the B blocks (B1 and B2) and middle A blocks (A2) reside primarily in the B domains and the interior of A domains, respectively.
We find that the one-dimensional block volume fraction distributions for the L-forming melt in ESI† Fig. S19c are also consistent with SCFT results. The volume fractions of the end A blocks (ϕA1 + ϕA3) and middle A blocks (ϕA2) both reach a maximum of ∼0.45 at the middle of A domains and decline to nearly zero towards the center of B domains. These volume fraction distributions suggest that both end and middle A blocks distribute relatively evenly throughout A domains as reflected in the hypothesized conformations in Fig. 4i and do not exhibit the segregated distribution as observed in Fig. 6. Conversely, the volume fraction of B blocks (ϕB) is highest at the middle of B domains and declines to ∼0.08 at the middle of A domains. These distributions demonstrate that each block type mostly resides in domains of the same type in simulation, as reflected in Fig. 5, which also supports the conformations in Fig. 4i. The two-dimensional block distributions for the end and middle A blocks (ESI† Fig. S19d and f) further suggest that both block types distribute evenly throughout A domains.
The correspondence between the 1D block distributions from SCFT and MD and the local segregation present in the 2D distributions from MD both support the hypothesized chain conformations in Fig. 4. However, these data are insufficient to determine which A domains each A block resides in; the majority and minority chain conformations in Fig. 4 are further distinguished by whether or not the end blocks of a pentaBCP are in the same domain.
D. Determining the population of each chain conformation in MD simulations
We use the chain end-to-end distance Ree to understand if both end blocks are located in the same domain or not. We define “looping” chains as chains where both second and fourth “connecting” blocks (e.g., B1 and B2 for A1B1A2B2A3 and A1 and A2 for B1A1B2A2B3) adopt looping configurations in domains of the same type, such that the end and middle A blocks all reside in A domains. Chains with the looping conformation often have a “bundled” appearance and, therefore, low Ree. We define “bridging” chains as chains where both connecting blocks (e.g., B1 and B2 for A1B1A2B2A3) adopt bridging configurations to stretch across distinct domains and therefore allow each of the chain's end and middle blocks to occupy separate domains as well (i.e., all five blocks located in their own domains), leading to relatively high Ree. In contrast, the connecting blocks of chains with the “hairpin” conformation (described in the ESI†) occupy the same domain, leading to a much lower Ree; we found this conformation was rare for all chain designs and we therefore do not systematically distinguish it. PentaBCPs may also have a connecting block in either configuration, which leads to a “hybrid” conformation with one looping and one bridging block and an intermediate chain Ree.In Fig. 7a, we present a snapshot of a L morphology formed by a melt of A1B1A2B2A3 pentaBCP chains with fA = 0.4 and τA2 = 0.5 with several example chains adopting looping, hybrid, and bridging conformations within the A and B domains of the L phase. We include the distribution of end-to-end distance Ree in Fig. 7b for the same pentaBCP design (also examined in Fig. 7e) to show the low, medium, and high Ree modes, separated at Ree = 7d and 16d. The proportion of chains with Ree < 7d, 7d ≤ Ree < 16d, and 16d ≤ Ree at several τA2 are shown in Fig. 7c–g, along with snapshots of representative chains and their Ree in parenthesis from each population.
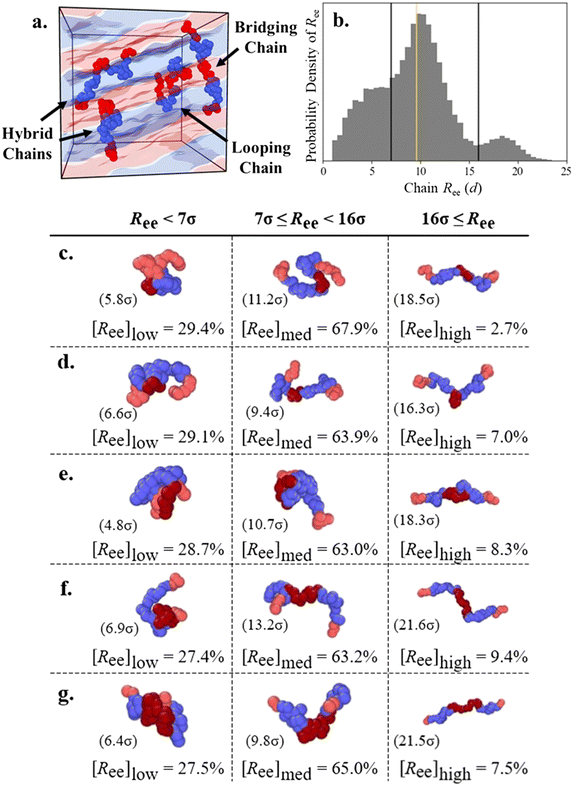 | ||
| Fig. 7 (a) Representative snapshot of A1B1A2B2A3 chains adopting looping, hybrid, and bridging conformations in a lamellar melt. (b) Example probability density histogram of chain end-to-end distance Ree for the A1B1A2B2A3 pentaBCP at χN = 120 with fA = 0.4 and τA2 = 0.5, which is also represented in Fig. 7e. Black vertical lines mark the boundaries at Ree = 7d and 16d between the low, medium, and high Ree chain populations, and the gold vertical line marks the real-space distance Lq* sampled from SAA(q). The Ree distributions for each design are presented in ESI† Fig. S20. (c–g) The percentages of chains within a specific range of Ree is denoted as [Ree] for Ree < 7d, 7d ≤ Ree < 16d, and 16d ≤ Ree for A1B1A2B2A3 pentaBCP at χN = 120 with fA = 0.4 and (c) τA2 = 0.2, (d) τA2 = 0.4, (e) τA2 = 0.5, (f) τA2 = 0.6, and (g) τA2 = 0.8. Representative chains are presented along with their Ree for each population; the end A blocks of the chains (light red) are highlighted against the middle A blocks (dark red). The morphologies observed with MD simulation for these values of τA2 (0.2 to 0.8) are DG, L, L, L, and C6, respectively (ESI† Fig. S14). | ||
We use a gold line to mark the characteristic domain size of each melt on the distributions in Fig. 7b and S20,† which we identify as the real-space length corresponding to the major peak in the melt structure factor (Lq*). We observe that the low, medium, and high Ree populations have peaks at ∼0.5, 1, and 2 times Lq*, which corresponds to the expected relationship between Lq* and Ree for looping, hybrid, and bridging chains. Looping chains have small Ree as their end blocks occupy the same domain, although it is possible for their Ree ∼ Lq*. The ends of hybrid and bridging chains are separated by one and two morphology periods, respectively, which suggests that chains of these conformations form the medium and high Ree populations. Inspection of the example chains also suggests that these low, medium, and high Ree populations mostly consist of chains with the looping, hybrid, and bridging conformations, respectively.
The proportion of each population is broadly consistent for each given chain design: high Ree chains are always the smallest fraction, ranging from ∼3–10% of all chains; small Ree chains are the next largest population at ∼27–30%; and medium Ree chains constitute ∼63–68% of all chains. The small proportion of high Ree chains for each chain design support the assumption that the conformations with two B blocks bridging are rare and can be neglected in the hypothesized conformations in Fig. 4f–l. Further, the relative proportions of low and medium Ree chains suggest that the hybrid conformation, the right-side conformation in Fig. 4g, i, and j, is most prevalent in melts of each chain design.
Although the size of each population is insensitive to τA2, we observe some trends that relate the domain fraction results presented in Fig. 5 to the prevalence of looping, hybrid, and bridging conformations. The bridging conformation, which has the highest average Ree, relies on both end blocks remaining in separate domains and the middle block bridging to opposite sides of its domain. Accordingly, this conformation is suppressed in the melt of pentaBCP chains with τA2 = 0.2, for which the middle A block is the smallest among the simulated chain designs and therefore has a high stretching energy penalty in the bridging configuration; the high Ree peak for the corresponding distribution in ESI† Fig. S20a is subtle. The distributions for the L-forming melts with τA2 = 0.4, 0.5, and 0.6 (Fig. S20b–d†) appear relatively similar; for all three systems, the low Ree population decreases and the high Ree population increases as τA2 increases, in tandem with the increase and decrease in solubilization of the end and middle A blocks, respectively. These data demonstrate that the bridging conformation is promoted as the size of the middle block increases and the looping conformation is suppressed as the size of the end blocks decreases, even within the same morphology. The proportions of each Ree population do not continue these trends monotonically for the pentaBCP melt with τA2 = 0.8, as the low and high Ree populations are instead larger and smaller, respectively, as compared to the τA2 = 0.6 melt.
IV. Discussions
A. Design rules for stabilizing DG and observing L morphologies
If one is targeting transport-favorable morphologies such as DG or L, the phase diagrams on Fig. 2 and 3 give valuable insights to experimentalists for the choice of polymer designs that gives high propensity for forming DG and L phases. Here, we discuss the design parameters that give the widest DG window and the stable L phase formation at the low fA based on the phase diagrams (Fig. 2 and 3).The maximum DG window width (ΔfA ≈ 0.06) is found around τA2 = 0.8 for the A1B1A2B2A3 pentaBCPs for all three χN, which is slightly wider than that of diblock copolymers (ΔfA = 0.03–0.04). The higher stability of DG in the A1B1A2B2A3 pentaBCPs can be explained as follows. In AB diBCPs, only one block per polymer chain forms the gyroid structure (e.g., A block if A is the minority composition block) while in the A1B1A2B2A3 pentaBCP, the three A blocks form the gyroid structure. In the case of τA2 = 0.8, where the DG window width is the widest, the middle A block is eight times longer than the end A block. It has been shown in prior literature that dispersity in block lengths relieves the packing frustration in the complex network phases.12,82 Packing frustration is high in the three-fold connectors of DG which have high variations in domain thickness and curvature compared to the classical L, C6, and BCC phases. We speculate that the differences in the block length of the end and middle A blocks helps to efficiently organize the A blocks within A domains to relieve packing frustration and widen the DG stability window.
Moreover, compared to the AB diBCP design, the A1B1A2B2A3 pentaBCP design introduces one additional free end of A blocks at the expense of one free end loss of B blocks. Due to the two free A ends in A1B1A2B2A3 pentaBCP design, A blocks are more flexible in adopting various configurations than the B blocks tethered to the A blocks. The configurational entropy of A blocks helps to enhance the stability of curved phases (BCC, C6, and DG) versus L phase because the total stretching energy of pentaBCPs is minimized by curving the A–B interface toward A domains at expense of stretching A blocks in order to relax the B blocks. The stability of curved phases over L phase is supported by our observation that in the A1B1A2B2A3 pentaBCP phase diagram (Fig. 2), the DG windows are located around 0.45 < fA < 0.5, which are relatively high values compared to those of the diBCPs and symmetric triBCPs (0.3 < fA < 0.35).20,21 We speculate that the along with the dispersity in the A blocks, the enhanced tendency to curve the A–B interface contributes to the stabilization of DG phase, and thus widening DG stability windows.
In contrast, among the polymer designs in the B1A1B2A2B3 pentaBCPs, a comparably wide DG window width (ΔfA ≈ 0.04) is only found for χN = 60 around τA2 = 0.5 at low fA values (0.34 < fA < 0.38). The results suggest that for stabilizing DG phases in pentaBCPs, A1B1A2B2A3 pentaBCPs around τA2 = 0.8 is the best design choice, but the B1A1B2A2B3 pentaBCP with τB2 = 0.5 at higher χN is better if lower volume fraction DG structures are preferred.
In diBCP melt systems, the L phase has wide stability windows spanning over symmetric A/B compositional fractions (e.g., fA ∼ 0.5). Generally, using a symmetric composition of A and B monomers is a reliable strategy for achieving L phase in AB-type BCP melts. However, in case one of the A and B type monomers have higher costs or are environmentally less favorable, it may be desired to find polymer design rules which provides stable L phases at highly asymmetric compositional fractions, where BCC or C6 phases are usually preferred. The phase diagrams in Fig. 3 show that the L phase windows for the B1A1B2A2B3 pentaBCPs at τB2 = 0.1 and 0.9 extends to the lowest fA values among all the pentaBCP and triBCP designs we investigated. We note that the L phase is stable in B1A1B2A2B3 pentaBCPs with highly asymmetric compositional fraction (fA = 0.25) at τB2 = 0.1 and χN = 60 (Fig. 3c). Therefore, among all the pentaBCP designs we investigated, including the ABA/BAB triblocks, A1B1A2B2A3 pentaBCPs, and B1A1B2A2B3 pentaBCPs, the B1A1B2A2B3 pentaBCPs at τB2 = 0.1 and 0.9 are the best design choice to stabilize L with the lowest content of the A monomer.
B. Underlying mechanism for the reentrant phase behavior
In Section III, we hypothesize that the spatial segregation of A blocks in A domains promotes the A–B interfacial curvature at intermediate τA2 values (0 < τA2 < 0.5 and 0.5 < τA2 < 1), which leads to the reentrant phase behavior. The MD simulation results for the spatial distributions of each block in Fig. 6c and S19c† confirm that the partitioning of A blocks within A domains is governed by their relative size and qualitatively consistent with SCFT density profiles in Fig. 4. It is notable that even with the different chain models (Gaussian thread model in SCFT and bead-spring model in MD simulation) and the field-based versus particle-based approach, we observe the similar reentrant phase behavior and the consistent spatial distributions of blocks within the various domains in both SCFT calculations and MD simulations.The consistent distribution of Ree across τA2 in ESI† Fig. S20 and the corresponding chain conformations in Fig. 7 suggest that Ree is mainly determined by the configuration of B blocks (bridge, loop, or hybrid) but less correlated with τA2, which quantifies the relative size of the end and middle A blocks. The similar shape of probability density histograms of Ree across τA2 in ESI† Fig. S20 indicates that the population of chain conformations is robust to the change of τA2 and morphology. Thus, it is likely that the spatial segregations of end A block and middle A blocks within A domains is mostly responsible for the reentrant phase behavior. Assuming that the configurations of B blocks are insensitive to the change of τA2, the overall stretching energy of polymer chains are affected by spatial organization of A blocks. At intermediate τA2 values (0 < τA2 < 0.5 and 0.5 < τA2 < 1), the spatial segregation of end and middle A blocks of different length within the same domains makes it easier to reduce the overall stretching energy of the blocks and relieves the packing frustration in the curved domains than the similar spatial distributions of A blocks at τA2 = 0.5, which we think is the driving factor for the reentrant phase behavior.
V. Conclusions
We employed a combined approach of SCFT calculations and MD simulations to study the equilibrium phase behavior of symmetric pentablock copolymer (pentaBCP) melts, with A1B1A2B2A3 and B1A1B2A2B3 sequence, where the first and last block have same volume fraction and second and fourth block have same volume fraction. We construct the SCFT phase diagrams for the self-assembled morphologies to identify the ideal pentaBCP designs for targeting the widest DG windows and the L phase stabilization at the lowest fA. We also performed CG MD simulations with a set of pentaBCP designs selected from the SCFT phase diagrams and analyzed the SCFT and MD chain conformations in several morphologies. Our work leverages the chain-level detail provided by MD simulations to evaluate the underlying mechanisms of complex reentrant phase behavior observed in pentaBCP morphology predictions made with SCFT. This study establishes several design rules that may aid researchers in synthesizing pentaBCPs with transport-favorable morphologies and demonstrates the utility of complementary computational methods in the study of multiBCPs.Data availability
The input and output files of the PSCF program for the SCFT calculations and the final configurations of one trial of unbiased MD simulation for each pentablock copolymer design are available in a Zenodo repository at https://doi.org/10.5281/zenodo.13307547.Author contributions
So Jung Park conceptualization, data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft, writing – review & editing; Tristan Myers data curation, formal analysis, investigation, methodology, software, visualization, writing – original draft, writing – review & editing; Vinson Liao formal analysis, investigation, software, visualization, writing – review & editing; Arthi Jayaraman conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – review & editing.Conflicts of interest
The authors declare that there is no known conflict of interests.Acknowledgements
The authors acknowledge financial support from Multi University Research Initiative (MURI) grant from the Army Research Office, Award Number W911NF2310260. The SCFT calculations and CG MD simulations were run on Caviness supercomputing cluster at University of Delaware (UD). Authors also thank Brent Sumerlin and Kaden Stevens at University of Florida for useful discussions about the limitations of various multiblock polymer synthesis techniques.References
- F. S. Bates and G. H. Fredrickson, Phys. Today, 1999, 52, 32–38 CrossRef CAS.
- H. Feng, X. Lu, W. Wang, N.-G. Kang and J. W. Mays, Polymers, 2017, 9, 494 CrossRef PubMed.
- C. Tang, E. M. Lennon, G. H. Fredrickson, E. J. Kramer and C. J. Hawker, Science, 2008, 322, 429–432 CrossRef CAS PubMed.
- E. J. W. Crossland, M. Kamperman, M. Nedelcu, C. Ducati, U. Wiesner, D. M. Smilgies, G. E. S. Toombes, M. A. Hillmyer, S. Ludwigs, U. Steiner and H. J. Snaith, Nano Lett., 2009, 9, 2807–2812 CrossRef CAS PubMed.
- M. Stefik, S. Guldin, S. Vignolini, U. Wiesner and U. Steiner, Chem. Soc. Rev., 2015, 44, 5076–5091 RSC.
- A. C. Chang, T. Mulia, Y. S. Wu, Y. H. Weng, Y. C. Lin and W. C. Chen, J. Polym. Sci., 2023, 61, 2633–2654 CrossRef CAS.
- L. Li, L. Schulte, L. D. Clausen, K. M. Hansen, G. E. Jonsson and S. Ndoni, ACS Nano, 2011, 5, 7754–7766 CrossRef CAS PubMed.
- H. S. Kang, S. W. Han, C. Park, S. W. Lee, H. Eoh, J. Baek, D. G. Shin, T. H. Park, J. Huh, H. Lee, D. E. Kim, D. Y. Ryu, E. L. Thomas, W. G. Koh and C. Park, Sci. Adv., 2020, 6, eabb5769 CrossRef PubMed.
- M. W. Matsen and F. S. Bates, J. Polym. Sci., Part B: Polym. Phys., 1997, 35, 945–952 CrossRef CAS.
- L. Ludwik, Macromolecules, 1980, 13, 1602–1617 CrossRef.
- M. W. Matsen, J. Phys.: Condens. Matter, 2002, 14, R21–R47 CrossRef CAS.
- M. W. Matsen and F. S. Bates, Macromolecules, 1996, 29, 7641–7644 CrossRef CAS.
- M. Iijima, D. Ulkoski, S. Sakuma, D. Matsukuma, N. Nishiyama, H. Otsuka and C. Scholz, Polym. Int., 2016, 65, 1132–1141 CrossRef CAS.
- N. Singh, M. v. S. Tureau and T. H. Epps, Soft Matter, 2009, 5, 4757–4762 RSC.
- M. W. Bates, S. M. Barbon, A. E. Levi, R. M. Lewis, H. K. Beech, K. M. Vonk, C. Zhang, G. H. Fredrickson, C. J. Hawker and C. M. Bates, ACS Macro Lett., 2020, 9, 396–403 CrossRef CAS PubMed.
- S. J. Park, F. S. Bates and K. D. Dorfman, Phys. Rev. Mater., 2023, 7, 105601 CrossRef CAS.
- S. J. Park, G. K. Cheong, F. S. Bates and K. D. Dorfman, Macromolecules, 2021, 54, 9063–9070 CrossRef CAS.
- S. Mekcham and K. Nomura, J. Am. Chem. Soc., 2023, 145, 17001–17006 CrossRef CAS PubMed.
- M. B. Koo, S. W. Lee, J. M. Lee and K. T. Kim, J. Am. Chem. Soc., 2020, 142, 14028–14032 CrossRef CAS PubMed.
- M. W. Matsen and R. B. Thompson, J. Chem. Phys., 1999, 111, 7139–7146 CrossRef CAS.
- M. W. Matsen, Macromolecules, 2012, 45, 2161–2165 CrossRef CAS.
- A. M. Mayes and M. Olvera De La Cruz, J. Chem. Phys., 1989, 91, 7228–7235 CrossRef CAS.
- M. W. Matsen, J. Chem. Phys., 2000, 113, 5539–5544 CrossRef CAS.
- M. W. Hamersky, S. D. Smith, A. O. Gozen and R. J. Spontak, Phys. Rev. Lett., 2005, 95, 168306 CrossRef PubMed.
- S. Sakurai, K. Shirouchi, S. Munakata, H. Kurimura, S. Suzuki, J. Watanabe, T. Oda, N. Shimizu, K. Tanida and K. Yamamoto, Macromolecules, 2017, 50, 8647–8657 CrossRef CAS.
- B. R. Chapman, M. W. Hamersky, J. M. Milhaupt, C. Kostelecky, T. P. Lodge, E. D. Von Meerwall and S. D. Smith, Macromolecules, 1998, 31, 4562–4573 CrossRef CAS.
- B. Zhao, W. Jiang, L. Chen, W. Li, F. Qiu and A. C. Shi, ACS Macro Lett., 2018, 7, 95–99 CrossRef CAS PubMed.
- B. Zhao, C. Wang, Y. Chen and M. Liu, Langmuir, 2021, 37, 5642–5650 CrossRef CAS PubMed.
- S. Li, W. Tao, K. Gao, N. Athir, F. Li, Y. Chen, J. Liu, L. Zhang and M. Tsige, RSC Adv., 2019, 9, 42029–42042 RSC.
- S. Ahn, J. K. Kim, B. Zhao, C. Duan and W. Li, Macromolecules, 2018, 51, 4415–4421 CrossRef CAS.
- S. Ahn, Y. Seo, J. K. Kim, C. Duan, L. Zhang and W. Li, Macromolecules, 2019, 52, 9039–9044 CrossRef CAS.
- B. Zhao, Q. Dong, Y. Wei and Y. Xu, Molecules, 2023, 28, 3536 CrossRef CAS PubMed.
- Q. Xie, Y. Qiang and W. Li, ACS Macro Lett., 2022, 11, 205–209 CrossRef CAS PubMed.
- K. Yuan, Z. Xu, X. Huang and W. Li, Chem. – Eur. J., 2023, 29, e202301043 CrossRef CAS PubMed.
- Q. Dong and W. Li, Macromolecules, 2021, 54, 203–213 CrossRef CAS.
- L. Li and W. Li, Giant, 2021, 7, 100065 CrossRef CAS.
- S. J. Park, F. S. Bates and K. D. Dorfman, ACS Macro Lett., 2022, 11, 643–650 CrossRef CAS PubMed.
- M. E. Lott, L. Trachsel, E. Schué, C. L. G. Davidson, R. A. Olson S, D. I. Pedro, F. Chang, Y. Hong, W. G. Sawyer and B. S. Sumerlin, Macromolecules, 2024, 57, 4007–4015 CrossRef CAS.
- A. Arora, J. Qin, D. C. Morse, K. T. Delaney, G. H. Fredrickson, F. S. Bates and K. D. Dorfman, Macromolecules, 2016, 49, 4675–4690 CrossRef CAS.
- A. Ranjan, J. Qin and D. C. Morse, Macromolecules, 2008, 41, 942–954 CrossRef CAS.
- M. W. Matsen, Eur. Phys. J. E: Soft Matter Biol. Phys., 2009, 30, 361–369 CrossRef CAS PubMed.
- G. S. Grest, M.-D. Lacasse, K. Kremer and A. M. Gupta, J. Chem. Phys., 1996, 105, 10583–10594 CrossRef CAS.
- G. Fredrickson, The Equilibrium Theory of Inhomogeneous Polymers, 2005 Search PubMed.
- A. Kulshreshtha, R. C. Hayward and A. Jayaraman, Macromolecules, 2022, 55, 2675–2690 CrossRef CAS.
- J. H. Ryu, H. S. Wee and W. B. Lee, Phys. Rev. E, 2016, 94, 032501 CrossRef PubMed.
- B. Steinmüller, M. Müller, K. R. Hambrecht, G. D. Smith and D. Bedrov, Macromolecules, 2011, 45, 1107–1117 CrossRef.
- M. A. Horsch, Z. Zhang, C. R. Iacovella and S. C. Glotzer, J. Chem. Phys., 2004, 121, 11455–11462 CrossRef CAS PubMed.
- J. R. Brown, Y. Seo, S. W. Sides and L. M. Hall, Macromolecules, 2017, 50, 5619–5626 CrossRef CAS.
- H. Guo and K. Kremer, J. Chem. Phys., 2003, 119, 9308–9320 CrossRef CAS.
- L. A. Moreira, G. Zhang, F. Müller, T. Stuehn and K. Kremer, Macromol. Theory Simul., 2015, 24, 419–431 CrossRef CAS.
- J. E. Jones, Proc. R. Soc. London, Ser. A, 1924, 106, 463–477 CAS.
- M. Murat, G. S. Grest and K. Kremer, Macromolecules, 1999, 32, 595–609 CrossRef CAS.
- A. Arora, D. C. Morse, F. S. Bates and K. D. Dorfman, Soft Matter, 2015, 11, 4862–4867 RSC.
- J. Huh, C. Park and Y. K. Kwon, J. Chem. Phys., 2010, 133, 114903 CrossRef PubMed.
- F. J. Martinez-Veracoechea and F. A. Escobedo, J. Chem. Phys., 2006, 125, 104907 CrossRef PubMed.
- J. Škvor and Z. Posel, Macromol. Theory Simul., 2014, 24, 141–151 CrossRef.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J. E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- S. Nosé, Mol. Phys., 2006, 52, 255–268 CrossRef.
- W. G. Hoover, Phys. Rev. A: At., Mol., Opt. Phys., 1985, 31, 1695–1697 CrossRef PubMed.
- V. Liao, T. Myers and A. Jayaraman, Soft Matter, 2024 10.1039/D4SM01037J.
- K. Kim, A. Arora, R. M. Lewis, 3rd, M. Liu, W. Li, A. C. Shi, K. D. Dorfman and F. S. Bates, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, 847–854 CrossRef CAS PubMed.
- S. Brisard and P. Levitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 013305 CrossRef PubMed.
- Á. González, Math. Geosci., 2009, 42, 49–64 CrossRef.
- D. A. Hajduk, P. E. Harper, S. M. Gruner, C. C. Honeker, G. Kim, E. L. Thomas and L. J. Fetters, Macromolecules, 2002, 27, 4063–4075 CrossRef.
- T. H. Epps, E. W. Cochran, C. M. Hardy, T. S. Bailey, R. S. Waletzko and F. S. Bates, Macromolecules, 2004, 37, 7085–7088 CrossRef CAS.
- H. Lee, S. Kwon, J. Min, S. M. Jin, J. H. Hwang, E. Lee, W. B. Lee and M. J. Park, Science, 2024, 383, 70–76 CrossRef CAS PubMed.
- M. Krone, J. E. Stone, T. Ertl and K. Schulten, Eurographics Conference on Visualization, 2012 Search PubMed.
- A. Stukowski, Modell. Simul. Mater. Sci. Eng., 2010, 18, 015012 CrossRef.
- U. Essmann, L. Perera, M. L. Berkowitz, T. Darden, H. Lee and L. G. Pedersen, J. Chem. Phys., 1995, 103, 8577–8593 CrossRef CAS.
- F. A. Detcheverry, H. Kang, K. C. Daoulas, M. Müller, P. F. Nealey and J. J. de Pablo, Macromolecules, 2008, 41, 4989–5001 CrossRef CAS.
- M. Liu, Y. Qiang, W. Li, F. Qiu and A. C. Shi, ACS Macro Lett., 2016, 5, 1167–1171 CrossRef CAS PubMed.
- A. J. Mueller, A. P. Lindsay, A. Jayaraman, T. P. Lodge, M. K. Mahanthappa and F. S. Bates, ACS Macro Lett., 2020, 9, 576–582 CrossRef CAS PubMed.
- Z. Xu and W. Li, Chin. J. Chem., 2022, 40, 1083–1090 CrossRef CAS.
- F. Drolet and G. H. Fredrickson, Macromolecules, 2001, 34, 5317–5324 CrossRef CAS.
- R. K. W. Spencer and M. W. Matsen, Macromolecules, 2017, 50, 1681–1687 CrossRef CAS.
- F. S. Bates, M. F. Schulz, A. K. Khandpur, S. Förster, J. H. Rosedale, K. Almdal and K. Mortensen, Faraday Discuss., 1994, 98, 7–18 RSC.
- T. M. Beardsley and M. W. Matsen, J. Chem. Phys., 2021, 154, 124902 CrossRef CAS PubMed.
- M. W. Matsen, T. M. Beardsley and J. D. Willis, Phys. Rev. Lett., 2023, 130, 248101 CrossRef CAS PubMed.
- M. W. Matsen, T. M. Beardsley and J. D. Willis, Phys. Rev. Mater., 2023, 7, 105605 CrossRef CAS.
- O. N. Vassiliev and M. W. Matsen, J. Chem. Phys., 2003, 118, 7700–7713 CrossRef CAS.
- C. To Lai and A.-C. Shi, Macromol. Theory Simul., 2021, 30, 2100019 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4me00138a |
| ‡ S. J. P. and T. M. contributed equally to the article. |
| This journal is © The Royal Society of Chemistry 2024 |

![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif)