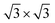Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Atomic scale quantum anomalous hall effect in monolayer graphene/MnBi2Te4 heterostructure†
Yueh-Ting
Yao
a,
Su-Yang
Xu
*b and
Tay-Rong
Chang
 *acd
*acd
aDepartment of Physics, National Cheng Kung University, Tainan 70101, Taiwan. E-mail: u32trc00@phys.ncku.edu.tw
bDepartment of Chemistry and Chemical Biology, Harvard University, Cambridge, MA 02138, USA. E-mail: suyangxu@fas.harvard.edu
cCenter for Quantum Frontiers of Research and Technology (QFort), Tainan 701, Taiwan
dPhysics Division, National Center for Theoretical Sciences, Taipei 10617, Taiwan
First published on 19th April 2024
Abstract
The two-dimensional quantum anomalous Hall (QAH) effect is direct evidence of non-trivial Berry curvature topology in condensed matter physics. Searching for QAH in 2D materials, particularly with simplified fabrication methods, poses a significant challenge in future applications. Despite numerous theoretical works proposed for the QAH effect with C = 2 in graphene, neglecting magnetism sources such as proper substrate effects lacks experimental evidence. In this work, we propose the QAH effect in graphene/MnBi2Te4 (MBT) heterostructure based on density-functional theory (DFT) calculations. The monolayer MBT introduces spin-orbital coupling, Zeeman exchange field, and Kekulé distortion as a substrate effect into graphene, resulting in QAH with C = 1 in the heterostructure. Our effective Hamiltonian further presents a rich phase diagram that has not been studied previously. Our work provides a new and practical way to explore the QAH effect in monolayer graphene and the magnetic topological phases by the flexibility of MBT family materials.
New conceptsIntroduced by 2016 Nobel Prize Winner Prof. F. D. M. Haldane in 1988, the quantum anomalous Hall effect (QAHE) proposes a quantized Hall conductivity in the graphene lattice, even in the absence of an external magnetic field. Despite successful QAHE realization in 3D topological insulators, achieving QAHE in the original Haldane model within 2D graphene remains challenging. Recent theoretical works reported QAHE in freestanding graphene, yet experimental evidence is lacking possibly due to oversight regarding magnetic sources such as substrate effects. In this study, we present QAHE in a graphene/MnBi2Te4 heterostructure through first-principles calculations. This finding starkly contrasts with previous investigations. Additionally, our effective Hamiltonian unveils a comprehensive topological phase diagram not explored before. Leveraging the established experimental benefits of graphene/Bi2Te3 and the structural similarity between graphene/Bi2Te3 and graphene/MnBi2Te4 interfaces, we confidently predict the experimental realization of the graphene/MnBi2Te4 heterostructure. Our work not only introduces a new pathway for achieving QAHE in graphene but also investigates magnetic topological phase transitions within 2D heterostructures, capitalizing on the flexibility of MnBi2Te4 families and graphene systems. |
1. Introduction
Searching the non-trivial topological states in real material is a primary goal in modern condensed matter physics.1,2 The quantum anomalous Hall (QAH) effect, which is the experimental observation of the Chern insulator, shows promising potential in electronic devices with low power consumption.3–5 Until now, the QAH effect has been observed in magnetically-doped topological insulators,6–8 the intrinsic magnetic topological insulator MnBi2Te4 families,9,10 and twisted multilayer moiré systems.11,12 The exploration of QAH materials continues to attract considerable attention in applications.Graphene, as the prototypical 2D material, boasts numerous advantages, including remarkable robustness, high electronic mobility, and a massless Dirac band structure. In particular, the massless Dirac band structure can be viewed as a critical point adjacent to various topological phases. For instance, the introduction of spin–orbit coupling (SOC) transforms monolayer graphene into a quantum spin Hall (QSH) insulator.13,14 Moreover, with the incorporation of both SOC and Zeeman exchange fields, monolayer graphene can evolve into a quantum anomalous Hall insulator.15,16 Despite numerous theoretical works that proposed the QAH effect in graphene,15–21 experimental evidence remains absent. This discrepancy may stem from prior investigations neglecting magnetism sources such as proper substrate effects. In recent years, the intrinsic topological insulator MnBi2Te4 (MBT) families have emerged as a promising platform for exploring magnetic topological phases.22 The monolayer MBT can be viewed as intercalating a Mn–Te bilayer into the center of a Bi2Te3 quintuple layer, forming a Te–Bi–Te–Mn–Te–Bi–Te septuple layer. Notably, the MBT lattice exhibits an almost perfect lattice match with the 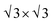 supercell of monolayer graphene. Indeed, researchers have investigated the potential use of the Bi2Te3 families23 (which have the same lattice constant as MBT but lacking magnetism) to introduce SOC in graphene, both theoretically and experimentally.24–26 Drawing inspiration from these findings and preceding studies, our present work explores the innovative prospect of utilizing MBT as a substrate for monolayer graphene. This approach aims to concurrently introduce SOC, Kekulé distortion, and Zeeman exchange field, thereby inducing the QAH effect in monolayer graphene.
supercell of monolayer graphene. Indeed, researchers have investigated the potential use of the Bi2Te3 families23 (which have the same lattice constant as MBT but lacking magnetism) to introduce SOC in graphene, both theoretically and experimentally.24–26 Drawing inspiration from these findings and preceding studies, our present work explores the innovative prospect of utilizing MBT as a substrate for monolayer graphene. This approach aims to concurrently introduce SOC, Kekulé distortion, and Zeeman exchange field, thereby inducing the QAH effect in monolayer graphene.
In this work, we analyze the electronic structure and present a comprehensive topological phase diagram for the monolayer graphene/MBT heterostructure. Our results reveal that the proximity to monolayer MBT opens a band gap in graphene by introducing SOC and/or Kekulé distortion. Specifically, SOC causes graphene to transition from a Dirac semimetal to the QSH state,13,14 while the Kekulé distortion introduces a superlattice potential, mixing different valley states and transforming graphene into a normal insulator (NI).25–27 The interplay of these gap-opening mechanisms and the Zeeman exchange field from the monolayer MBT significantly enriches the topological phase diagram, giving rise to spin Chern insulator (observed QSH effect), Chern insulator (observed QAH effect), two-fold/four-fold/eight-fold degenerate Dirac semimetal, and NI phases. The conventional understanding for inducing the QAH effect in graphene posits that each valley contributes a unit conductance e2/h, leading to a quantized Hall conductivity at σxy = 2e2/h, without considering the source of Zeeman exchange field.15,16,19,20 In contrast, incorporating the Zeeman exchange field from the MBT substrate, coupled with valley mixing from Kekulé distortion, results in a quantized Hall conductivity at σxy = e2/h, representing the ground state of Chern insulator with C = 1. Our first-principles calculations substantiate the existence of the C = 1 ground state with σxy = e2/h in graphene/MBT heterostructure. The emergence of Kekulé distortion at the graphene/MBT interface presents a unique opportunity for achieving tunable Chern numbers in the heterostructure system.
2. Results
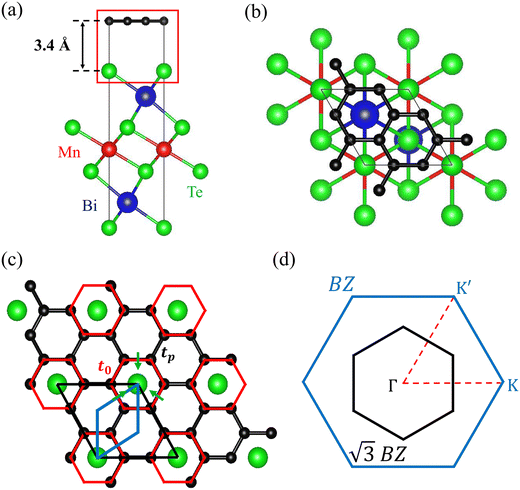
The graphene/MBT heterostructure consists of monolayer graphene and one septuple-layer MBT, as illustrated in Fig. 1(a) for the side view and Fig. 1(b) for the top view. The in-plane lattice constant of MBT is approximately 4.33 Å, while the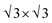 supercell constant of graphene is around 4.27 Å. Consequently, a 1.4% lattice mismatch exists between MBT and
supercell constant of graphene is around 4.27 Å. Consequently, a 1.4% lattice mismatch exists between MBT and 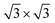 graphene. Due to the mechanical flexibility of graphene, the lattice mismatch, along with the topmost Te layer, locally stretches the graphene lattice, leading to Kekulé distortion. The Kekulé distortion breaks the bond symmetry in graphene, forming equivalent C–C bonding into two distinct red and black bonds in Fig. 1(c) with different hopping strengths.26,27 To describe the electronic properties of the graphene/MBT heterostructure, we employ an effective graphene supercell Hamiltonian by introducing SOC, Kekulé distortion, and Zeeman exchange field in graphene:
graphene. Due to the mechanical flexibility of graphene, the lattice mismatch, along with the topmost Te layer, locally stretches the graphene lattice, leading to Kekulé distortion. The Kekulé distortion breaks the bond symmetry in graphene, forming equivalent C–C bonding into two distinct red and black bonds in Fig. 1(c) with different hopping strengths.26,27 To describe the electronic properties of the graphene/MBT heterostructure, we employ an effective graphene supercell Hamiltonian by introducing SOC, Kekulé distortion, and Zeeman exchange field in graphene: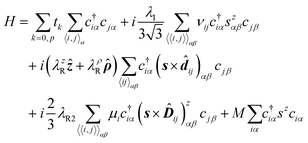 | (1) |
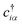 is the creation operator and cjα is the annihilation operator of an electron with spin polarization α at site i. 〈i, j〉 and 〈〈i, j〉〉 run over the nearest neighbor and next-nearest neighbor hopping sites with unit vector
is the creation operator and cjα is the annihilation operator of an electron with spin polarization α at site i. 〈i, j〉 and 〈〈i, j〉〉 run over the nearest neighbor and next-nearest neighbor hopping sites with unit vector ![[d with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0064_0302.gif) ij and
ij and ![[D with combining circumflex]](https://www.rsc.org/images/entities/b_i_char_0044_0302.gif) ij, respectively. The first term describes the nearest neighbor hopping of graphene with two different hopping strengths: the t0 with red-bonding carbon rings surrounding the top Te atoms and tp connecting the rings (Fig. 1(c)). The hopping difference reflects the Kekulé distortion in graphene supercell, opening a band gap of 2|t0 − tp|. The second term represents the intrinsic SOC, which opens a non-trivial band gap of 2 λI, where s = (sx, sy, sz) is the Pauli matrix in the spin degree of freedom. The parameter νij describes the next-nearest neighbor hopping in a clockwise/counterclockwise direction to the positive z-axis with +1/−1 values. The third and fourth terms account for the Rashba SOC. The third term λzR, associated with the nearest neighbor hopping, is induced by the external electric field perpendicular to the graphene sheet from the MBT substrate, breaking the out-of-plane inversion symmetry. The fourth term λρR arises from the nonuniform in-plane electric field, represented by the green arrow in Fig. 1(c), breaking the in-plane inversion symmetry. The fifth term is the second-order Rashba SOC λR2, associated with next-nearest-neighbor hopping, with μi = +1(−1) for the A(B) site. The sixth term represents the Zeeman exchange field magnetization originating from the Mn atoms in the MBT substrate.
ij, respectively. The first term describes the nearest neighbor hopping of graphene with two different hopping strengths: the t0 with red-bonding carbon rings surrounding the top Te atoms and tp connecting the rings (Fig. 1(c)). The hopping difference reflects the Kekulé distortion in graphene supercell, opening a band gap of 2|t0 − tp|. The second term represents the intrinsic SOC, which opens a non-trivial band gap of 2 λI, where s = (sx, sy, sz) is the Pauli matrix in the spin degree of freedom. The parameter νij describes the next-nearest neighbor hopping in a clockwise/counterclockwise direction to the positive z-axis with +1/−1 values. The third and fourth terms account for the Rashba SOC. The third term λzR, associated with the nearest neighbor hopping, is induced by the external electric field perpendicular to the graphene sheet from the MBT substrate, breaking the out-of-plane inversion symmetry. The fourth term λρR arises from the nonuniform in-plane electric field, represented by the green arrow in Fig. 1(c), breaking the in-plane inversion symmetry. The fifth term is the second-order Rashba SOC λR2, associated with next-nearest-neighbor hopping, with μi = +1(−1) for the A(B) site. The sixth term represents the Zeeman exchange field magnetization originating from the Mn atoms in the MBT substrate.
We explore the topological phase diagram in eqn (1) through the utilization of two fundamental topological invariants, Chern number C and spin Chern number Cs. For the Chern insulator, as observed in the QAH effect, the quantized charge Hall conductivity σxy = C × e2/h is directly proportional to an integer denoted as Chern number C. The Chern number can be calculated from the integral of Berry curvature in the momentum space and sum over all occupied bands below the bulk band gap, which is directly related to the number of chiral edge states in the two-dimensional topological system.3,28 In a sz conserved system, the spin Chern number Cs is identical to ![[Doublestruck Z]](https://www.rsc.org/images/entities/char_e17d.gif) 2 index owing to the good quantum number sz. The Cs is expressed as
2 index owing to the good quantum number sz. The Cs is expressed as 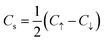 , where C↑/C↓ is computed similarly to the Chern number, but the occupied states are separated by spin-up/spin-down electrons.13,14 This configuration characterizes the system as a spin Chern insulator, observed in the QSH effect. Recent studies show that even in scenarios where sz is not a good quantum number, the Cs remains well-defined through the introduction of Rashba SOC.29–32 By calculating these two critical invariants, we identify the topological phase at each point within the parameter space of the phase diagram.
, where C↑/C↓ is computed similarly to the Chern number, but the occupied states are separated by spin-up/spin-down electrons.13,14 This configuration characterizes the system as a spin Chern insulator, observed in the QSH effect. Recent studies show that even in scenarios where sz is not a good quantum number, the Cs remains well-defined through the introduction of Rashba SOC.29–32 By calculating these two critical invariants, we identify the topological phase at each point within the parameter space of the phase diagram.
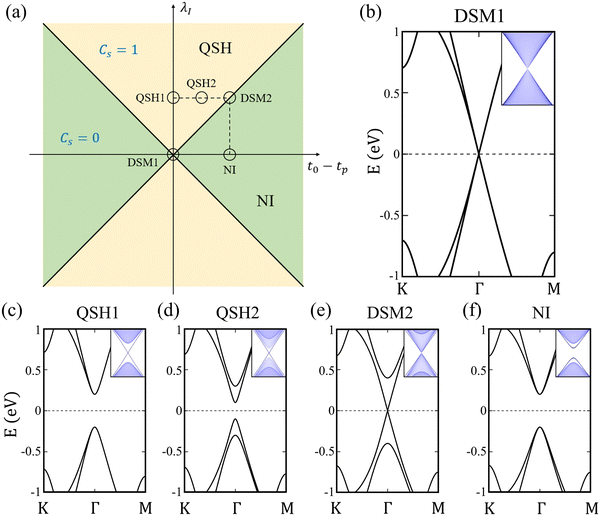
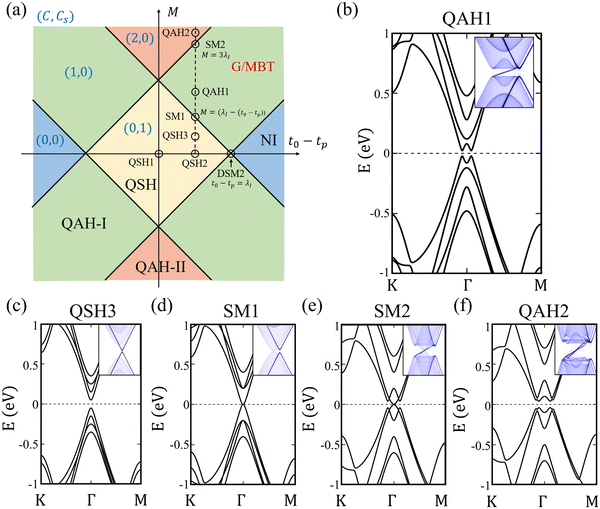
We initially present the topological phase diagram, delineating the interplay between the two band gap opening mechanisms, Kekulé distortion and intrinsic SOC, in the absence of exchange field M (Fig. 2(a)). The two Dirac cones within the graphene unit cell distinctly segregate into two valleys, K and K′, positioned at the corner of the Brillouin zone (BZ). Considering the periodicity with the MBT substrate, the unit cell of the heterostructure aligns with a commensurate 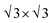 graphene supercell. This alignment folds both Dirac cones from the corner of the original BZ of graphene to Γ point in the momentum space of the supercell (Fig. 1(d)). This folding effect gives rise to the Dirac semimetal DSM1 phase, illustrating an eight-fold degenerate Dirac point at the Γ point (Fig. 2(b)). Upon the introduction of intrinsic SOC λI, this highly degenerate Dirac state undergoes band gap opening (Fig. 2(c)). Due to the spin and valley degeneracy, the valence and conduction bands that separate by a gap become four-fold degenerate at the Γ point. In this scenario, graphene transforms from DSM1 to a spin Chern insulator with Cs = 1 (labeled QSH1). The boundary state with the armchair edge showcases a non-trivial edge state connecting the valence and conduction bands, characteristic of the QSH effect (inset of Fig. 2(c)). In contrast to the intrinsic SOC, Kekulé distortion introduces a superlattice potential in the graphene supercell, resulting in the opening of a band gap for the Dirac cones with Cs = 0. The edge state calculations reveal a gapped edge state, as depicted in the inset of Fig. 2(f). Due to the competing mechanisms of the intrinsic SOC and Kekulé distortion, the ground state of the graphene supercell will lie between QSH1 and NI. For instance, Fig. 2(d) illustrates a spin Chern insulator induced by the cooperative action of intrinsic SOC and Kekulé distortion (labeled QSH2). The doubly degenerated band dispersion arises from the PT-symmetry, wherein the opposite spin states degenerate in different valleys. In this case, λI > |t0 − tp|, thus the stronger intrinsic SOC results in the spin Chern insulator phase with the non-trivial edge state (inset of Fig. 2(d)). When λI = |t0 − tp|, a topological phase transition critical point, a Dirac semimetal phase with a four-fold degenerate Dirac point (DSM2) emerging between QSH2 and NI, as presented in Fig. 2(e).
graphene supercell. This alignment folds both Dirac cones from the corner of the original BZ of graphene to Γ point in the momentum space of the supercell (Fig. 1(d)). This folding effect gives rise to the Dirac semimetal DSM1 phase, illustrating an eight-fold degenerate Dirac point at the Γ point (Fig. 2(b)). Upon the introduction of intrinsic SOC λI, this highly degenerate Dirac state undergoes band gap opening (Fig. 2(c)). Due to the spin and valley degeneracy, the valence and conduction bands that separate by a gap become four-fold degenerate at the Γ point. In this scenario, graphene transforms from DSM1 to a spin Chern insulator with Cs = 1 (labeled QSH1). The boundary state with the armchair edge showcases a non-trivial edge state connecting the valence and conduction bands, characteristic of the QSH effect (inset of Fig. 2(c)). In contrast to the intrinsic SOC, Kekulé distortion introduces a superlattice potential in the graphene supercell, resulting in the opening of a band gap for the Dirac cones with Cs = 0. The edge state calculations reveal a gapped edge state, as depicted in the inset of Fig. 2(f). Due to the competing mechanisms of the intrinsic SOC and Kekulé distortion, the ground state of the graphene supercell will lie between QSH1 and NI. For instance, Fig. 2(d) illustrates a spin Chern insulator induced by the cooperative action of intrinsic SOC and Kekulé distortion (labeled QSH2). The doubly degenerated band dispersion arises from the PT-symmetry, wherein the opposite spin states degenerate in different valleys. In this case, λI > |t0 − tp|, thus the stronger intrinsic SOC results in the spin Chern insulator phase with the non-trivial edge state (inset of Fig. 2(d)). When λI = |t0 − tp|, a topological phase transition critical point, a Dirac semimetal phase with a four-fold degenerate Dirac point (DSM2) emerging between QSH2 and NI, as presented in Fig. 2(e).
Subsequently, we extend our analysis to include the Zeeman exchange field M in the graphene supercell, simulating the graphene/MBT heterostructure. The intricate interplay among SOC, Kekulé distortion, and the Zeeman effect give rise to a comprehensive phase diagram. For example, commencing with the QSH2 characterized by a band gap Eg(QSH2) = λI – (t0 – tp) (Fig. 2(d)), the introduction of the exchange field M induces a time-reversal breaking spin Chern insulator (labeled QSH3) when M < Eg(QSH2). The topological edge state of QSH3 shifts away from the Γ point due to the breaking of time-reversal symmetry. Simultaneously, this edge state opens a gap when further considering the effect of Rashba SOC.29 At a critical point, M = Eg(QSH2), a two-fold degenerated quadratic band dispersion emerges (labeled SM1, Fig. 3(d)). Subsequently, a band inversion occurs in the parameter region of Eg(QSH2) < M < 3Eg(QSH2), leading the system into a Chern insulator with C = 1 (labeled QAH1, Fig. 3(b)). The inset of Fig. 3(b) displays a chiral edge state of QAH1. With a further increase in the strength of the Zeeman exchange field, the evolution of the band structure progresses through another two-fold quadratic semimetal phase SM2 (Fig. 3(e)), and then a second band inversion transpires, resulting in a Chern insulator with C = 2 (labeled QAH2, Fig. 3(f)). The inset of Fig. 3(f) exhibits two chiral edge states within the bulk gap of QAH2.
To pinpoint the ground state of graphene/MBT heterostructure within the presented parameter space of the phase diagram (Fig. 3(a)), we conducted the first-principles calculations using DFT. The graphene/MBT first-principle calculations are presented by DFT with the projector augmented wave method implemented in the Vienna ab initio simulation package (VASP).33–35 The top and bottom vacuum space is 10 Å to avoid the interaction between two adjacent heterostructures. The structure in Fig. 1(a) is fully relaxed until the force on each atom is smaller than 0.01 eV Å−1. The interlayer distance between graphene and MBT is 3.4 Å. We used the Monkhorst–pack grides with 11 × 11 × 1 mesh. The exchange–correlation method with GGA+U is adopted with Hubbard U is 4 eV. The Heyd–Scuseria–Ernzerhof (HSE) hybrid function36 is used to correct the band gap of monolayer MBT. The van der Waals interaction correction using the Grimme (DFT-D2) method37 was considered. Our calculations demonstrate that the hollow site stacking with an out-of-plane ferromagnetic spin configuration exhibits the lowest energy. The energy differences for alternative stacking and spin configurations are provided in Tables S1 and S2 in the ESI,† respectively.
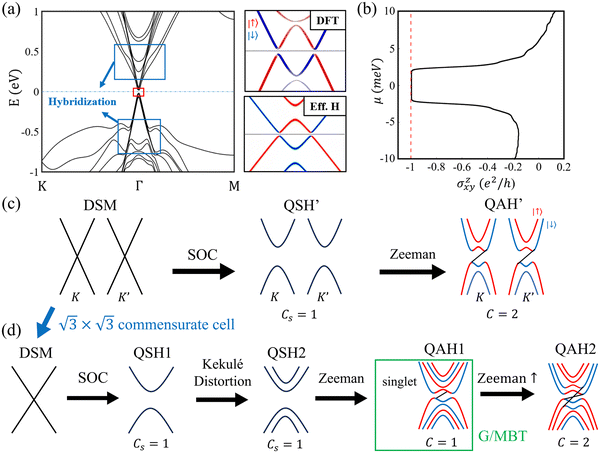
The calculated band structure of the graphene/MBT heterostructure is depicted in Fig. 4(a). We find the band structure exhibits pronounced hybridization at higher binding energies, typically around ±0.5 eV. At binding energies proximate to the Fermi level, graphene predominantly governs the band structure, while MBT acts as a Zeeman exchange field upon graphene, notably influencing the four bands surrounding the Fermi level. It is noteworthy that each band exhibits single degeneration with a band gap of 3.5 meV. Additionally, the zoom-in band structure reveals a resemblance to the band dispersion observed in QAH1 (Fig. 3(b)). The Hall conductivity calculated using the Kubo formula showcases a quantized value of e2/h, indicative of Chern insulator with C = 1 (Fig. 4(b)). This finding starkly contrasts with previous investigations where the Chern number was identified as C = 2 (labeled QAH′ in Fig. 4(c)). The QAH state in earlier studies results from the band inversion at both valleys, induced by the interplay of SOC and Zeeman exchange field. This mechanism, though conceptually straightforward, lacks consideration for substrate effects, making experimental realization challenging. Fig. 4(d) provides a schematic representation systematically illustrating the formation of the Chern insulating state with C = 1 in the graphene/MBT heterostructure. The original unit cell of graphene harbors two Dirac cones at K/K′ valleys. These Dirac cones fold to a Γ point, forming the DSM phase within the context of a 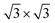 commensurate supercell of graphene. The introduction of SOC opens the band gap at both K/K′ valleys, giving rise to the QSH1. Upon further consideration of the substrate effect, specifically Kekulé distortion, QSH1 transitions into QSH2. In this phase, two valleys at the original BZ of graphene become intertwined exhibiting distinct energy eigenvalues. Consequently, the Zeeman exchange field selectively inverts the topmost valence band and the bottommost conduction band, leading to the emergence of QAH1 with C = 1. How the Zeeman exchange field of MBT affects the evolution of graphene band structure from QSH2 to QAH1 is explained in more detail in the ESI.†
commensurate supercell of graphene. The introduction of SOC opens the band gap at both K/K′ valleys, giving rise to the QSH1. Upon further consideration of the substrate effect, specifically Kekulé distortion, QSH1 transitions into QSH2. In this phase, two valleys at the original BZ of graphene become intertwined exhibiting distinct energy eigenvalues. Consequently, the Zeeman exchange field selectively inverts the topmost valence band and the bottommost conduction band, leading to the emergence of QAH1 with C = 1. How the Zeeman exchange field of MBT affects the evolution of graphene band structure from QSH2 to QAH1 is explained in more detail in the ESI.†
3. Discussion and conclusions
Our systematic study unveils the capability of the graphene/MBT heterostructure to control topological phase transitions, offering avenues for manipulation through methods, such as doping or stacking additional van der Waals layers to adjust the Fermi level and/or the strength of exchange coupling.38–40 For instance, the Zeeman exchange field can be enhanced by increasing the stack of MBT layers and MnTe layers38 to produce the QAH2 C = 2 phase, as shown in Fig. 3(f). These advantages present a tunable platform for quantum Hall devices and advancing spintronics.In summary, we systematically investigated the realization of the QAH effect on monolayer graphene through an effective model Hamiltonian and first-principle calculations. We discern that the graphene/MBT heterostructure manifests a Chern insulating phase with C = 1, considering the interplay of the SOC, Kekulé distortion, and Zeeman exchange interaction within a fruitful topological phase diagram. Leveraging the flexibility inherent in both MBT families and graphene systems, coupled with the previously established experimental advantage of graphene/Bi2Te3 systems,24 our work not only introduces a novel avenue for achieving the QAH effect in monolayer graphene but also delves into magnetic topological phase transition within 2D heterostructures.
Author contributions
S.-Y. X. and T.-R. C. conceived and designed the research. Y.-T. Y. conducted theoretical calculations; Y.-T. Y., S.-Y. X., and T.-R. C. analyzed the data; Y.-T. Y., S.-Y. X., and T.-R. C. wrote the manuscript; T.-R. C. supervised the project.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
T.-R. C. was supported by the 2030 Cross-Generation Young Scholars Program from the National Science and Technology Council (NSTC) in Taiwan (Program No. MOST111-2628-M-006-003-MY3), National Cheng Kung University (NCKU), Taiwan, and National Center for Theoretical Sciences, Taiwan. This research was supported, in part by the Higher Education Sprout Project, Ministry of Education to the Headquarters of University Advancement at NCKU. T. R. C thank to National Center for High-performance Computing (NCHC) of National Applied Research Laboratories (NARLabs) in Taiwan for providing computational and storage resources. Work in the SYX group was partly supported by the U.S. Department of Energy (DOE) Office of Science through the Ames National Laboratory under contract DE-AC0207CH11358, and partly through Air Force Office of Scientific Research (AFOSR) grant FA9550-23-1-0040.References
- A. Bansil, H. Lin and T. Das, Colloquium: Topological band theory, Rev. Mod. Phys., 2016, 88, 021004 CrossRef.
- M. Z. Hasan and C. L. Kane, Colloquium: Topological insulators, Rev. Mod. Phys., 2010, 82, 3045–3067 CrossRef CAS.
- C.-Z. Chang, C.-X. Liu and A. H. MacDonald, Colloquium: Quantum anomalous Hall effect, Rev. Mod. Phys., 2023, 95, 011002 CrossRef CAS.
- Y. Liang, et al., High-temperature quantum anomalous Hall insulator in two-dimensional Bi2ON, Appl. Phys. Lett., 2020, 116, 162402 CrossRef CAS.
- R. Peng, Z. He, Y. Dai, B. Huang and Y. Ma, Intrinsic valley-related multiple Hall effect in the two-dimensional organometallic lattice of NbTa-benzene, Phys. Rev. B, 2022, 106, 035403 CrossRef CAS.
- J. Zhang, et al., Topology-driven magnetic quantum phase transition in topological insulators, Science, 2013, 339, 1582–1586 CrossRef CAS PubMed.
- C.-Z. Chang, et al., Experimental Observation of the Quantum Anomalous Hall Effect in a Magnetic Topological Insulator, Science, 2013, 340, 167–170 CrossRef CAS PubMed.
- C.-Z. Chang, et al., High-precision realization of robust quantum anomalous Hall state in a hard ferromagnetic topological insulator, Nat. Mater., 2015, 14, 473–477 CrossRef CAS PubMed.
- Y. Deng, et al., Quantum anomalous Hall effect in intrinsic magnetic topological insulator MnBi2Te4, Science, 2020, 367, 895–900 CrossRef CAS PubMed.
- C. Hu, et al., Realization of an intrinsic ferromagnetic topological state in MnBi8Te13, Sci. Adv., 2020, 6, eaba4275 CrossRef CAS PubMed.
- M. Serlin, et al., Intrinsic quantized anomalous Hall effect in a moiré heterostructure, Science, 2020, 367, 900–903 CrossRef CAS PubMed.
- G. Chen, et al., Tunable correlated Chern insulator and ferromagnetism in a moiré superlattice, Nature, 2020, 579, 56–61 CrossRef CAS PubMed.
- C. L. Kane and E. J. Mele, Quantum Spin Hall Effect in Graphene, Phys. Rev. Lett., 2005, 95, 226801 CrossRef CAS PubMed.
- C. L. Kane and E. J. Mele, Topological Order and the Quantum Spin Hall Effect, Phys. Rev. Lett., 2005, 95, 146802 CrossRef CAS PubMed.
- W.-K. Tse, Z. Qiao, Y. Yao, A. H. MacDonald and Q. Niu, Quantum anomalous Hall effect in single-layer and bilayer graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 155447 CrossRef.
- M. Ezawa, Valley-Polarized Metals and Quantum Anomalous Hall Effect in Silicene, Phys. Rev. Lett., 2012, 109, 055502 CrossRef PubMed.
- Z. Qiao, et al., Quantum Anomalous Hall Effect in Graphene Proximity Coupled to an Antiferromagnetic Insulator, Phys. Rev. Lett., 2014, 112, 116404 CrossRef PubMed.
- J. Zhang, B. Zhao, Y. Yao and Z. Yang, Robust quantum anomalous Hall effect in graphene-based van der Waals heterostructures, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 165418 CrossRef.
- Z. Qiao, et al., Quantum anomalous Hall effect in graphene from Rashba and exchange effects, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 161414 CrossRef.
- Z. Qiao, H. Jiang, X. Li, Y. Yao and Q. Niu, Microscopic theory of quantum anomalous Hall effect in graphene, Phys. Rev. B: Condens. Matter Mater. Phys., 2012, 85, 115439 CrossRef.
- J. Zhang, B. Zhao, Y. Yao and Z. Yang, Quantum Anomalous Hall Effect in Graphene-based Heterostructure, Sci. Rep., 2015, 5, 10629 CrossRef PubMed.
- J. Li, et al., Intrinsic magnetic topological insulators in van der Waals layered MnBi2Te4-family materials, Sci. Adv., 2019, 5, eaaw5685 CrossRef CAS PubMed.
- H. Zhang, et al., Topological insulators in Bi2Se3, Bi2Te3 and Sb2Te3 with a single Dirac cone on the surface, Nature Phys., 2009, 5, 438–442 CrossRef CAS.
- D. Khokhriakov, et al., Tailoring emergent spin phenomena in Dirac material heterostructures, Sci. Adv., 2018, 4, eaat9349 CrossRef PubMed.
- K. Song, et al., Spin Proximity Effects in Graphene/Topological Insulator Heterostructures, Nano Lett., 2018, 18, 2033–2039 CrossRef CAS PubMed.
- Z. Lin, et al., Competing Gap Opening Mechanisms of Monolayer Graphene and Graphene Nanoribbons on Strong Topological Insulators, Nano Lett., 2017, 17, 4013–4018 CrossRef CAS PubMed.
- C. Gutiérrez, et al., Imaging chiral symmetry breaking from Kekulé bond order in graphene, Nat. Phys., 2016, 12, 950–958 Search PubMed.
- F. D. M. Haldane, Model for a Quantum Hall Effect without Landau Levels: Condensed-Matter Realization of the ‘Parity Anomaly’, Phys. Rev. Lett., 1988, 61, 2015–2018 CrossRef CAS PubMed.
- Y.-T. Yao et al. Feature-energy duality of topological boundary states in multilayer quantum spin Hall insulator. https://arxiv.org/abs/2312.11794v1 ( 2023).
- D. N. Sheng, Z. Y. Weng, L. Sheng and F. D. M. Haldane, Quantum Spin-Hall Effect and Topologically Invariant Chern Numbers, Phys. Rev. Lett., 2006, 97, 036808 CrossRef CAS PubMed.
- E. Prodan, Robustness of the spin-Chern number, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 125327 CrossRef.
- Y. Yang, et al., Time-Reversal-Symmetry-Broken Quantum Spin Hall Effect, Phys. Rev. Lett., 2011, 107, 066602 CrossRef PubMed.
- P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set, Comput. Mater. Sci., 1996, 6, 15–50 CrossRef CAS.
- A. D. Becke and E. R. Johnson, A simple effective potential for exchange, J. Chem. Phys., 2006, 124, 221101 CrossRef PubMed.
- S. Grimme, Semiempirical GGA-type density functional constructed with a long-range dispersion correction, J. Comput. Chem., 2006, 27, 1787–1799 CrossRef CAS PubMed.
- P. Chen, et al., Tailoring the magnetic exchange interaction in MnBi2Te4 superlattices via the intercalation of ferromagnetic layers, Nat. Electron, 2023, 6, 18–27 CAS.
- Y. Gao, K. Liu and Z.-Y. Lu, Intrinsic ferromagnetic and antiferromagnetic axion insulators in van der Waals materials MnX2B2T6 family, Phys. Rev. Res., 2022, 4, 023030 CrossRef CAS.
- T. Qian, et al., Magnetic dilution effect and topological phase transitions in Mn1-xPbxBi2Te4, Phys. Rev. B, 2022, 106, 045121 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00165f |
| This journal is © The Royal Society of Chemistry 2024 |