DOI:
10.1039/D4MH00302K
(Communication)
Mater. Horiz., 2024,
11, 2615-2627
Inverse design of Bézier curve-based mechanical metamaterials with programmable negative thermal expansion and negative Poisson's ratio via a data augmented deep autoencoder†
Received
16th March 2024
, Accepted 25th April 2024
First published on 30th April 2024
Abstract
Controlling stress and deformation induced by thermo-mechanical stimulation in high-precision mechanical systems can be achieved by mechanical metamaterials (MM) exhibiting negative thermal expansion (NTE) and negative Poisson's ratio (NPR). However, the inverse design of MM exhibiting a wide range of arbitrary target NTEs and NPRs is a challenging task due to the low design flexibility of analytical methods and parametric studies based on numerical simulation. In this study, we propose Bézier curve-based programmable chiral mechanical metamaterials (BPCMs) and a deep autoencoder-based inverse design model (DAIM) for the inverse design of BPCMs. Through iterative transfer learning with data augmentation, DAIM can generate BPCMs with a curved rib shape inaccessible with the Bézier curve, which improves the inverse design performance of the DAIM in the data sparse domain. This approach decreases the mean absolute error of NTE and NPR between the inverse design target and the numerical simulation results of inverse designed BPCMs on the data-sparse domain by 79.25% and 83.33% on average, respectively. A 3D-printed BPCM is validated experimentally and exhibits good coincidence with the target NTE and NPR. Our proposed BPCM and the corresponding inverse design framework enable the inverse design of BPCMs with NTE in the range of −1100 to 0 ppm K−1 and NPR in the range of −0.6 to −0.1. Furthermore, programmable thermal deformation modes with a fixed Poisson's ratio are realized by combining various inverse designed BPCM unit cells. BPCMs and the DAIM for their inverse design are expected to improve the mechanical robustness of high-precision mechanical systems through tunable modulation of thermo-mechanical stimulation.
New concepts
Previous studies on mechanical metamaterials (MMs) implementing negative thermal expansion (NTE) and negative Poisson's ratio (NPR) rely on structures tractable with analytical methods or parametric study based on numerical simulation, which leads to low design flexibility. To address this issue, we demonstrate a deep learning-based inverse design framework for Bézier curve-based programmable chiral mechanical metamaterials (BPCMs) to realize a wide range of NTE and NPR. To enable the inverse design of BPCMs implementing target NTE and NPR, a deep autoencoder-based inverse design model (DAIM) is proposed. To improve the inverse design performance of the DAIM at data-sparse domains, iterative transfer learning with data augmentation is conducted, which dramatically increases the accuracy of the inverse design at the data-sparse domain. Furthermore, data augmentation enabled DAIM to design MMs with outstanding NTE and NPR by generating the shape of a curved rib, which cannot be defined with the cubic Bézier curve. Moreover, by combining the inverse-designed unit cell of BPCMs, programmable thermal deformation modes with fixed Poisson's ratio, are realized. Thus, BPCMs and DAIM for their inverse design pave the way for innovative approaches in the design of mechanical systems robust to thermal-mechanical loading.
|
1. Introduction
Mechanical metamaterials (MMs) are artificially architected materials that can realize distinct and exotic mechanical properties that cannot be observed in natural materials, such as ultra-stiffness, quasi-zero stiffness, negative response to external stimuli, and programmable response by designing periodic unit cells constituting the entire MM structure.1–3 In particular, MMs exhibit unusual thermal shrinkage under heating, which is referred to as negative thermal expansion (NTE). Given that most natural materials possess positive thermal expansion, high-precision mechanical systems, which are exposed to high-temperature environments such as space structures, solar cells, and semiconductor substrates, suffer from thermal stress induced by the thermal expansion of materials, which causes serious damage to the sensitive components within the mechanical system.4–6 However, MMs exhibiting NTE could dramatically reduce the thermal stress by being integrated into base materials with positive thermal expansion. NTE can be achieved through deformation induced by the difference in coefficient of thermal expansion (CTE) between the two materials, and this exotic behavior can be realized through various mechanisms such as bending deformation of the bi-material rib, stretching behavior of the triangular unit, and an origami structure with bi-layer plates.7–9 Furthermore, engineered MMs can achieve negative Poisson's ratio (NPR), which has excellent energy absorption capacity, compressive strength, and impact resistance to external mechanical stimuli.10–12 NPR can be implemented by auxetic structures such as re-entrant honeycombs, chiral, origami, kirigami, and lattice structures.10,13–18
The integration of such mechanisms for NTE and NPR has enabled MMs with simultaneous NTE and NPR such as chiral structures with bi-material curved ribs, structures composed of trapezoidal units exhibiting stretching behavior, and bi-material topology optimization with a multi-objective function.19–22 Analytical approaches have been proposed to design MMs simultaneously exhibiting NTE and NPR, but the MMs tractable with analytical approaches have limited structural shapes and low design flexibility, which leads to a narrow range of NTE and NPR.23,24 To widen the range of NTE and NPR with increased design flexibility, more complex structures such as hybrid design of bending and stretching behaviors, and patterned bi-material strips have been introduced.25–27 However, such structures were designed through a parametric study based on the iteration of numerical simulation, which roughly infers the design parameters within the range. Studies on utilizing topology optimization for the design of MMs exhibiting arbitrary NTE and NPR have also been proposed, but topology optimization requires an iterative optimization process for each inverse design of MM, which entails a large computational cost.21,22
Deep learning is a field of machine learning that utilizes an artificial neural network that mimics a human neural network to perform various high-level tasks such as image recognition, natural language processing, active control, signal processing, and manufacturing process optimization that are difficult to solve with conventional methods.28–33 Recently, the deep learning-based inverse design method has risen as an alternative to address the challenges of structure inverse design. Several studies have been conducted to utilize deep learning for the efficient inverse design of various structures with complex and nonlinear mechanisms, such as thermal metamaterials, acoustic metamaterials, electromagnetic metamaterials, composites, and airfoils.34–39 Such innovations in structural inverse design with deep learning have enabled various attempts in MM design, such as lattice structures with superior elastic modulus, controllable auxeticity, and the inverse design of MMs exhibiting target stress–strain curves.40–45 However, a deep learning-based inverse design framework for MMs with target NTE and NPR has not yet been proposed.
In this study, we present Bézier curve-based programmable chiral mechanical metamaterials (BPCMs) to implement arbitrary target NTE and NPR. BPCMs consist of a bi-material curved rib described by Bézier curves, enabling a wide range of NTE and NPR. However, due to the structural complexity of the Bézier curve-shaped rib constituting a BPCM unit cell, the inverse design of BPCMs with analytical approaches is a challenging task. A deep autoencoder-based inverse design model (DAIM) is introduced to enable the inverse design and property prediction of BPCMs. To train the DAIM with the geometric features of the BPCM and increase the design flexibility of BPCMs, we utilize the 1-D shape data of the curved rib as the input data for the DAIM instead of the control point data of the Bézier curve. Given that the inverse design accuracy of the DAIM deteriorated in data-sparse domains, we perform iterative transfer learning with data augmentation on the data-sparse domain to improve the inverse design performance of the DAIM. The inverse designed BPCM is fabricated through 3D printing. Experimental validation is performed to confirm the inverse design performance of the DAIM. In addition, programmable thermal deformation with fixed Poisson's ratio (PR) is achieved by combining pre-defined BPCM unit cells inverse designed through DAIM.
2. Bézier curve-based programmable chiral mechanical metamaterials
2.1. Design of the BPCM
The structure of BPCM proposed in this study is shown in Fig. 1. To realize the high design flexibility of the BPCM, we define the geometric shape of the bi-material curved rib of the BPCM unit cell as a cubic Bézier curve, as shown in Fig. 1b. The Bézier curve is a parametric curve defined by the control points and can be expressed as follows:12,46| | 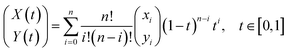 | (1) |
xi, yi, X(t), Y(t), and n represent the x-coordinate and y-coordinate of the ith control point, the x-coordinate, and y-coordinate of the Bézier curve, and order of the Bézier curve, respectively. While various curves can be employed to define curve-shaped ribs, Bézier curves can facilitate the generation of curves that satisfy the constraints through the manipulation of control points, which plays a significant role in dataset generation. In addition, Bézier curves ensure relatively smooth curvature, which is essential for manufacturing. The number of control points is one higher than the order of the Bézier curve. Since we apply a cubic Bézier curve, n and the number of control points are set to 3 and 4, respectively. The control points at both ends of the cubic Bézier curve are fixed, and the distance (R) between the fixed control points P1 and P4 is set to 20 mm. By manipulating the remaining two control points P2 and P3, we define various shapes of the Bézier curve-shaped rib, and the range of the Bézier curve control points is shown in Table 1. A chiral structure composed of a Bézier curve-shaped rib is defined as the unit cell of BPCM. The 2D cross-section image of the BPCM unit cell is shown in Fig. 1a and the 3D structure of the BPCM unit cell is shown in Fig. 1c. The width (w) of the Bézier curve-shaped rib is a factor that can potentially affect the mechanical properties of the BPCM. As an overly thick width can lead to a small amplitude of NTE, while an excessively thin width can pose challenges in the manufacturing and tensile test of the BPCM, the width of the Bézier curve-shaped rib is set to 2 mm, with the width of the inner and outer layers set to 1 mm equally (Fig. S1 and Table S1, ESI†). The out-of-plane thickness (t) of the Bézier curve-shaped rib is set to 2 mm. Nylon and PVA are used as the outer and inner layer material of the Bézier curve-shaped ribs, respectively. By combining the unit cells in a 5 by 5 array, the BPCM is configured, which is shown in Fig. 1d. The BPCM is fabricated using a dual-nozzle fused deposition modeling (FDM) 3D printer (UltiMaker S5, UltiMaker, USA). Commercially available UltiMaker 2.85 mm NFC Nylon filaments and UltiMaker 2.85 mm NFC PVA filaments are used for the fabrication. The representative structure of the fabricated BPCM is shown in Fig. 2.
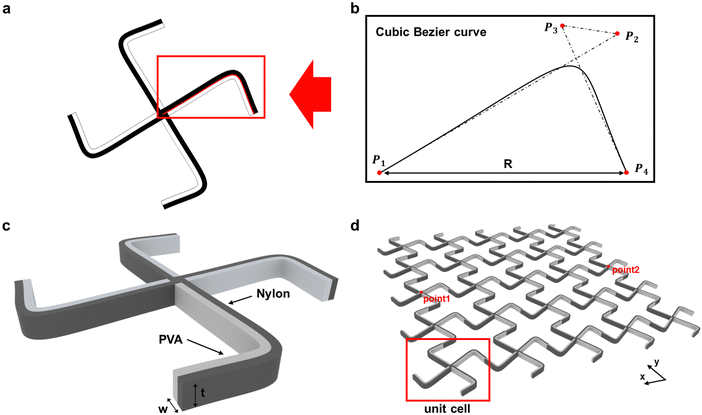 |
| | Fig. 1 Structure of the BPCM: (a) 2D cross-section of the BPCM unit cell, (b) Bézier curve depicting the curved rib of the BPCM unit cell, (c) 3D structure of the BPCM unit cell, and (d) overall structure of the BPCM. | |
Table 1 Control point range of the Bézier curve
| Bézier curve control point coordinate range |
| 0 mm ≤ Px1 ≤ 20 mm |
| 0 mm ≤ Py1 ≤ 20 mm |
| 0 mm ≤ Px2 ≤ 20 mm |
| 0 mm ≤ Py2 ≤ 20 mm |
 |
| | Fig. 2 (a) 2D cross-section image of a representative BPCM and (b)–(d) the fabricated BPCMs via dual nozzle 3D printing. | |
2.2. Mechanical properties of the BPCM
The BPCM can achieve both NPR and NTE. The equivalent PR of the BPCM is defined as follows:| | 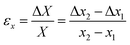 | (2) |
| | 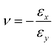 | (3) |
x1, x2, Δx1, and Δx2, represent the x-direction positions and displacements at point 1 and point 2 in Fig. 1d, respectively. εx and εy denote the x- and y-direction strains, respectively, and εy is fixed to 0.1. Since the BPCM exhibits identical mechanical behavior along the x- and y-directions, only the x-direction strain under elongation in the y-direction is considered. The equivalent CTE of the BPCM is defined as follows:| | 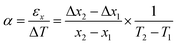 | (4) |
The temperature is assumed to increase from T1 = 303 K to T2 = 333 K. Considering that the BPCM exhibits identical mechanical behavior along the x and y-direction, the CTE is defined only by the x-direction strain. To determine the mechanical properties of the BPCM corresponding to different Bézier curve-shaped ribs, numerical simulation is performed using COMSOL Multiphysics software. The material properties of the nylon and PVA constituting the BPCM in the simulation are listed in Table 2.19 We could confirm various BPCM structures exhibiting distinct NPR and NTE, as shown in Fig. 3.
Table 2 Material properties of PVA and nylon
|
|
PVA |
Nylon |
| Thermal expansion coefficient |
47 ppm K−1 |
121 ppm K−1 |
| Young's modulus (303 K) |
439.4 Mpa |
233.9 Mpa |
| Young's modulus (333 K) |
14.8 Mpa |
78.1 Mpa |
 |
| | Fig. 3 Numerical simulation results of the BPCM for PR and CTE, scale factor = 4.5: (a) CTE = −237.356 ppm K−1, PR = −0.1327, (b) CTE = −844.864 ppm K−1, PR = −0.0989 and (c) CTE = −31.5737 ppm K−1, PR = −0.5655 (all the scale bars are 40 mm). | |
3. Inverse design of the BPCM
3.1. Deep autoencoder-based inverse design model
Analytical methods to obtain the CTE of MMs with arc-shaped rib chiral structures have been proposed.7,47 However, designing MMs with a complex unit cell structure is still limited to parametric studies based on numerical simulations.19,25,27,48 Since a parametric study based on the numerical simulation can only determine the CTE and PR within limited combinations of design parameters, such a design approach exhibits a low design flexibility and requires cumbersome iterations of numerical simulation for the inverse design of an MM with the target NTE and NPR. To overcome the limitations of the analytical method and parametric study based on numerical simulations, the deep learning-based inverse design method has attracted attention as an alternative for the inverse design of MMs with a complex unit cell structure.13,42,44 In this study, the inverse design of a BPCM with the target NTE and NPR is achieved by introducing the DAIM. The autoencoder composed of a bottleneck-shape neural network has demonstrated superior performance compared with the existing simple deep neural network in structural inverse design.39,49,50 It is also feasible to simultaneously train a prediction model for predicting the physical properties of the structure while training the inverse design model.51 The overall structure of the DAIM is shown in Fig. 4, and the training of the DAIM proceeds by minimizing the following loss function:| | 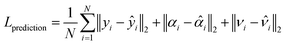 | (5) |
yi, αi, and νi represent the normalized y-coordinate data of the Bézier curve constituting the curved rib of the BPCM unit cell, the normalized equivalent CTE of the BPCM, and the normalized equivalent PR of the BPCM, respectively, and ŷi, ![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/char_e101.gif) i, and
i, and  represent predicted data by the DAIM. The control points of the Bézier curve determine the shape of the Bézier curve, which implies that a deep-learning model, which utilizes the control points as the input and output data, would generate only Bézier curves, while the Bézier curve cannot generate all types of curved rib. To obtain more diverse curved rib structures beyond the Bézier curve, the 1-D shape data of the curved rib are used as the input data of the DAIM instead of the control points of the Bézier curve. The utilization of such 1-D shape data can potentially expand the structure of the curve-shaped ribs to other parametric curves such as polynomials and trigonometric functions (Fig. S2, ESI†). The 1-D shape data of the curved rib are defined by the y-coordinate data of the Bézier curve calculated through that corresponding to the 32 evenly spaced x-coordinate points. The 1-D shape data of the curved rib are normalized by dividing by 20 mm considering the size of the unit cell of the BPCM. The PR and CTE values, which are used for the label data of DAIM, are Min–Max normalized to resolve the scale differences between the mechanical properties. The geometric features of the Bézier curve-shaped rib of the BPCM are extracted from the 1-D shape data of the curved rib by inputting into the 1-D convolution layer of the encoder. The extracted geometric features of the curved rib of the BPCM are reduced to a two-dimensional latent space by passing through a dense layer of the encoder. A deeper neural network is required for effective matching between the Bézier curve shape and the mechanical properties. However, as deeper neural networks often induce gradient vanishing problems, ResNet, which achieves a deeper neural network without gradient vanishing problems by exploiting skip connections is employed for both the convolution layer and the dense layer.52 To constrain the mechanical properties of the BPCM to the DAIM, the mean-squared error (MSE) between each node of the latent space and the mechanical properties of the BPCM is added to the loss function as represented in eqn (5). The variables of the 2-D latent space are input into the dense layer and the convolution transpose layer of the decoder to generate the 1-D shape data of the curved rib. The encoder of DAIM is constructed by ResNet including 16 1-D convolution layers and 11 dense layers. The decoder of DAIM is composed of ResNet with 11 dense layers and 4 transposed convolution layers. To achieve stable convergence without overfitting during the training process, a batch normalization layer and dropout layer with a dropout rate of 0.2 are added. The detailed network structure of the DAIM including the depth of layers, specific activation function, number of convolution filters, and nodes is shown in Fig. S3 and S4 (ESI†). The MSE between the generated 1-D shape data of the curved rib and the input 1-D shape data of the curved rib is added to the loss function, as shown in eqn (5).
represent predicted data by the DAIM. The control points of the Bézier curve determine the shape of the Bézier curve, which implies that a deep-learning model, which utilizes the control points as the input and output data, would generate only Bézier curves, while the Bézier curve cannot generate all types of curved rib. To obtain more diverse curved rib structures beyond the Bézier curve, the 1-D shape data of the curved rib are used as the input data of the DAIM instead of the control points of the Bézier curve. The utilization of such 1-D shape data can potentially expand the structure of the curve-shaped ribs to other parametric curves such as polynomials and trigonometric functions (Fig. S2, ESI†). The 1-D shape data of the curved rib are defined by the y-coordinate data of the Bézier curve calculated through that corresponding to the 32 evenly spaced x-coordinate points. The 1-D shape data of the curved rib are normalized by dividing by 20 mm considering the size of the unit cell of the BPCM. The PR and CTE values, which are used for the label data of DAIM, are Min–Max normalized to resolve the scale differences between the mechanical properties. The geometric features of the Bézier curve-shaped rib of the BPCM are extracted from the 1-D shape data of the curved rib by inputting into the 1-D convolution layer of the encoder. The extracted geometric features of the curved rib of the BPCM are reduced to a two-dimensional latent space by passing through a dense layer of the encoder. A deeper neural network is required for effective matching between the Bézier curve shape and the mechanical properties. However, as deeper neural networks often induce gradient vanishing problems, ResNet, which achieves a deeper neural network without gradient vanishing problems by exploiting skip connections is employed for both the convolution layer and the dense layer.52 To constrain the mechanical properties of the BPCM to the DAIM, the mean-squared error (MSE) between each node of the latent space and the mechanical properties of the BPCM is added to the loss function as represented in eqn (5). The variables of the 2-D latent space are input into the dense layer and the convolution transpose layer of the decoder to generate the 1-D shape data of the curved rib. The encoder of DAIM is constructed by ResNet including 16 1-D convolution layers and 11 dense layers. The decoder of DAIM is composed of ResNet with 11 dense layers and 4 transposed convolution layers. To achieve stable convergence without overfitting during the training process, a batch normalization layer and dropout layer with a dropout rate of 0.2 are added. The detailed network structure of the DAIM including the depth of layers, specific activation function, number of convolution filters, and nodes is shown in Fig. S3 and S4 (ESI†). The MSE between the generated 1-D shape data of the curved rib and the input 1-D shape data of the curved rib is added to the loss function, as shown in eqn (5).
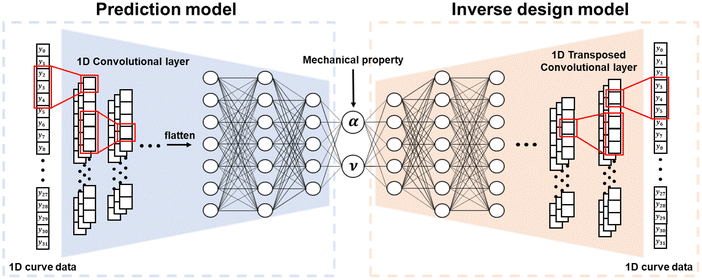 |
| | Fig. 4 An overall architecture of the DAIM. | |
3.2. Model training
A total of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 distinct Bézier curves are defined through random Bézier control point sampling. For the DAIM training, such Bézier curves are transformed into 1-D shape data of the curved rib, which consists of 32 y-coordinate data of the Bézier curve. By performing numerical simulations on the BPCM structures configured by the generated 1-D shape data of the curved rib, 10
927 distinct Bézier curves are defined through random Bézier control point sampling. For the DAIM training, such Bézier curves are transformed into 1-D shape data of the curved rib, which consists of 32 y-coordinate data of the Bézier curve. By performing numerical simulations on the BPCM structures configured by the generated 1-D shape data of the curved rib, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 data of CTE and PR are generated. The dataset for training and validation consisted of 1-D shape data of the curved rib with the size of 32 × 1 and the CTE and PR data corresponding to each 1-D shape data. The training and test dataset contains 9834 and 1093 data samples, which is 90% and 10% of the total data, respectively. As a high learning rate induces unstable convergence and, a low learning rate results in slow convergence, we employed the decaying learning rate starting with an initial learning rate of 1 × 10−4 and multiplied by 0.1 every 100 epochs until 300 epochs. The batch size is set to 512, and the training is conducted up to 500 epochs through the adaptive moment estimation optimizer. The training is conducted using NVIDIA GeForce GTX 1660 GPU and Intel® Core™ i5-9400F CPU @ 2.90GHz 2.90 GHz. By examining the learning curve, we confirm the stable convergence of the loss without overfitting (Fig. S5, ESI†). After sufficient training of the DAIM, the prediction model, the encoder part of the DAIM, can predict the CTE and PR of the BPCM by inputting the 1-D shape data of the curved rib, and the inverse design model, the decoder part of the DAIM, can generate the corresponding 1-D shape data of the curved rib by receiving the target CTE and PR.
927 data of CTE and PR are generated. The dataset for training and validation consisted of 1-D shape data of the curved rib with the size of 32 × 1 and the CTE and PR data corresponding to each 1-D shape data. The training and test dataset contains 9834 and 1093 data samples, which is 90% and 10% of the total data, respectively. As a high learning rate induces unstable convergence and, a low learning rate results in slow convergence, we employed the decaying learning rate starting with an initial learning rate of 1 × 10−4 and multiplied by 0.1 every 100 epochs until 300 epochs. The batch size is set to 512, and the training is conducted up to 500 epochs through the adaptive moment estimation optimizer. The training is conducted using NVIDIA GeForce GTX 1660 GPU and Intel® Core™ i5-9400F CPU @ 2.90GHz 2.90 GHz. By examining the learning curve, we confirm the stable convergence of the loss without overfitting (Fig. S5, ESI†). After sufficient training of the DAIM, the prediction model, the encoder part of the DAIM, can predict the CTE and PR of the BPCM by inputting the 1-D shape data of the curved rib, and the inverse design model, the decoder part of the DAIM, can generate the corresponding 1-D shape data of the curved rib by receiving the target CTE and PR.
The coefficient of determination for the CTE and PR prediction are 0.9957 and 0.9964, respectively, as shown in Fig. 5a and b, which guarantees high accuracy for the mechanical property prediction performance of the prediction model. The inverse designed BPCMs are represented in the mechanical property space with the CTE as the x-axis and PR as the y-axis, as shown in Fig. 5c. The yellow dots represent the training dataset, the red dots represent the target input of the CTE and PR, and the blue dots represent the CTE and PR of the inverse designed BPCM generated by the inverse design model of the DAIM with the input of the target CTE and PR.
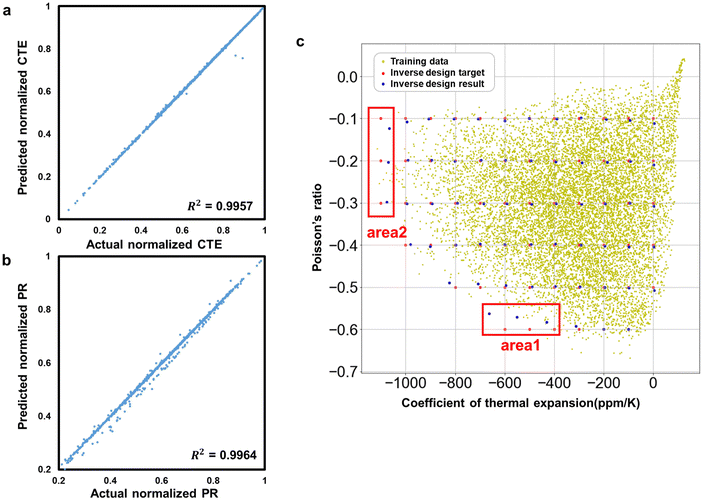 |
| | Fig. 5 (a) CTE prediction performance of the DAIM prediction model, (b) PR prediction performance of the DAIM prediction model and (c) inverse design result of the DAIM inverse design model (blue dot), target input (red), and training dataset (yellow dot) represented on the mechanical property. | |
3.3. Data augmentation
In Fig. 5c, the considerable gap between the CTE and PR of the inverse designed BPCM calculated by numerical simulation and the target CTE and PR can be confirmed in the data-sparse domain, which indicates deterioration of the inverse design accuracy. The underlying cause of the deterioration of the inverse design can be elucidated from the data dependencies of deep learning, which shows excellent performances in domains with abundant training datasets but poor performance in unseen domains. To address this issue, iterative transfer learning on DAIM through data augmentation was performed to improve the inverse design performance for the data-sparse domain of the mechanical property space.41,53,54 Transfer learning is a machine learning method that trains a pre-trained model with additional data. Iterative transfer learning on a pre-trained model with an augmented training dataset gradually improves the model performance in the data-sparse domain of the mechanical property space.55,56 In the mechanical property space represented in Fig. 5c, two areas exhibiting low inverse design performance due to data sparsity are marked as area 1 and area 2. We perform iterative transfer learning with data augmentation for area 1 and area 2, respectively, and the overall flow chart of the iterative transfer learning is shown in Fig. 6. The schematic of the transfer learning process with data augmentation for each iteration is shown in Fig. 7. The data augmentation candidates are generated by grid sampling of 220 and 341 data for area 1 and 2 in the ranges shown in Table 3 with 10 ppm K−1 intervals for CTE and 0.01 intervals for PR. The data augmentation candidates are input into the inverse design model of the DAIM to generate 1-D shape data of the curved rib. The CTE and PR data are obtained by performing the numerical simulation on the generated 1-D shape data of the curved rib, and data that significantly deviated from the corresponding data augmentation area are excluded. The numbers of augmented data for each iteration are shown in Table 4. For each iteration, transfer learning is performed on the pre-trained DAIM with the training dataset augmented with the generated data. The above process is repeated until all of the mean absolute error (MAE) of CTE and PR between the inverse design target and result in the corresponding data-sparse domain of the mechanical property space converges to less than 20 and 0.01, which is 2.5% of the average CTE and PR of the inverse design target in the data-sparse domain for more than 3 iterations, respectively (Fig. S6 and S7, ESI†).
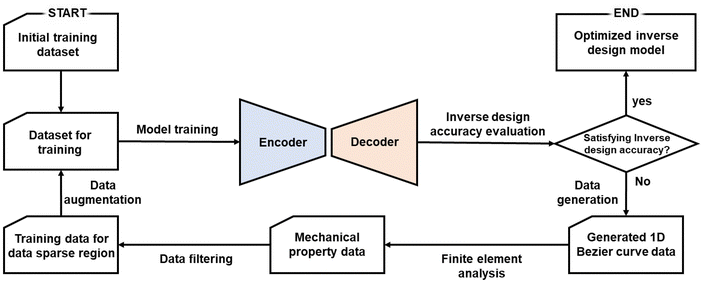 |
| | Fig. 6 Overall flow chart of iterative transfer learning with data augmentation. | |
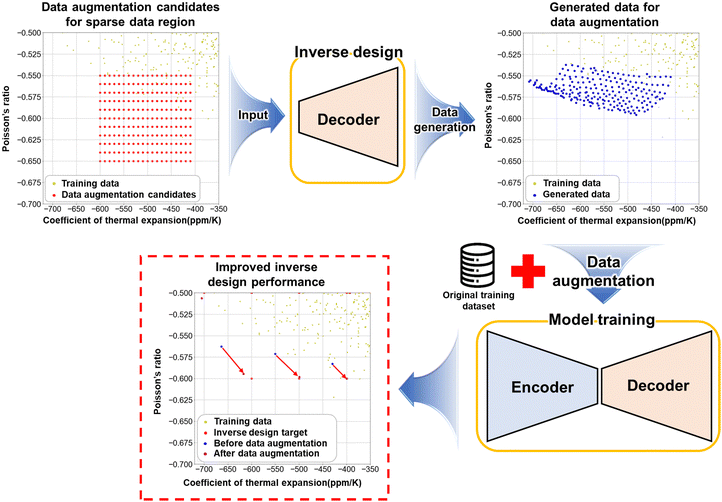 |
| | Fig. 7 Details of the transfer learning process with data augmentation for the data-sparse domain. | |
Table 3 The sampling range and number of data augmentation candidates
|
|
PR |
CTE |
Number of data |
| Min |
Max |
Min |
Max |
| Area 1 |
−0.55 |
−0.65 |
−410 ppm K−1 |
−600 ppm K−1 |
220 |
| Area 2 |
−0.1 |
−0.4 |
−1000 ppm K−1 |
−1100 ppm K−1 |
341 |
Table 4 The number of augmented data according to iterations
|
|
Iterations |
| 0 |
1 |
2 |
3 |
4 |
5 |
| Area 1 |
Number of augmented data |
— |
218 |
219 |
216 |
218 |
158 |
| Number of total data |
9834 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052 052 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271 271 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487 487 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705 705 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863 863 |
| Area 2 |
Number of augmented data |
— |
340 |
338 |
339 |
341 |
339 |
| Number of total data |
9834 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174 174 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512 512 |
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851 851 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192 192 |
11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531 531 |
4. Results & discussion
4.1. Inverse design model performance improvement
Through iterative transfer learning, we confirm an improvement of the BPCM inverse design performance of the inverse design model in the data spare domain. In Fig. 8, as the transfer learning iteration is repeated, the MAE of CTE and PR between the inverse design target and the numerical simulation result of the inverse designed BPCM decreased and converged below the stopping criteria. The MAE of CTE and PR for area 1 decreased by 87.49% and 91.33% on average, respectively, and the MAE of CTE and PR for area 2 decreased by 71.01% and 75.32% on average, respectively, compared between the DAIM before and after iterative transfer learning with data augmentation. In addition, iterative transfer learning with data augmentation extends the design domain of the mechanical property space of the BPCM, as shown in Fig. 9a. In the extended design domain, a curved rib shape, which cannot be defined with the cubic Bézier curve, is designed to realize a BPCM with the inverse design target of CTE and PR in the data-sparse domain. Utilizing 1-D shape data of the curved rib rather than the control point coordinates of the Bézier curve enhances the design flexibility, which leads to the generation of diverse curved rib shapes. Based on the enhanced design flexibility, the DAIM could design the BPCM, realizing the inverse design target beyond the design domain defined with the Bézier curve-shaped rib. Through the design domain extension, the inverse design of the BPCM with NTE in the range of −1100 to 0 ppm K−1 and NPR in the range of −0.6 to −0.1 is achieved.
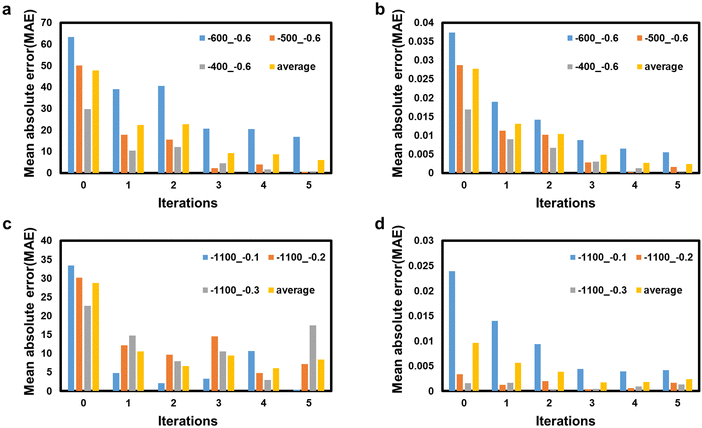 |
| | Fig. 8 Inverse design error according to data augmentation progress: (a) MAE of CTE for area 1, (b) MAE of PR for area 1, (c) MAE of CTE for area 2 and (d) MAE of PR for area 2. | |
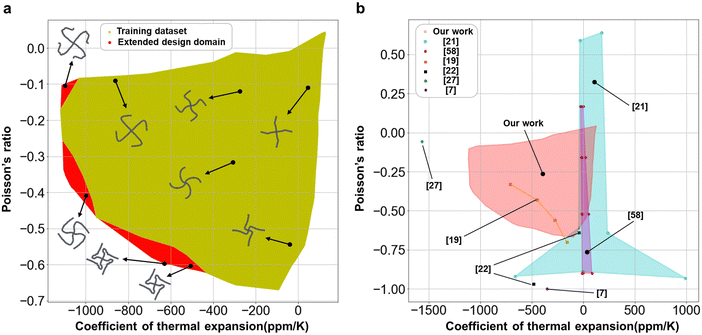 |
| | Fig. 9 (a) Design domain of the training dataset (yellow) and extended design domain (red) represented on the mechanical property space; (b) comparison results with other literature with respect to a range of CTEs and PRs. | |
4.2. Experimental validation
To verify the performance of the inverse designed BPCM, we conducted experimental validation with the 3D-printed BPCM. Since measuring the CTE of BPCM is difficult with commercial CTE measurement equipment, such as a dilatometer, due to the large area of BPCM, we devise the custom-made thermal expansion coefficient experiment equipment based on the digital image correlation method (DICM).8,57 A heating bed is installed to heat the BPCM to the target temperature, and an acrylic cover is installed for thermal insulation. The thermal deformation of BPCM is observed through a CCD camera (VR2308C, Viewrun, South Korea) with the temperature increasing from 303 K to 333 K, and CTE is calculated through eqn (4). We conducted a tensile test to confirm the PR of the BPCM. The BPCM is elongated using a universal testing machine (RB 301 UNITECH-T, R&B South Korea), and the PR is calculated through the vertical and horizontal strains of the BPCM measured using the DICM system (VIC-2D, Correlated Solutions, USA). The inverse design targets, corresponding to numerical simulation results, and experiment results of the BPCM are shown in Table 5 (Fig. S8 and S9, ESI†). We confirm that the inverse design target, the numerical simulation results of the inverse designed BPCM through DAIM, and the experimental results coincide with high accuracy.
Table 5 Numerical simulation and experiment results for a representative inverse designed BPCM
| Target |
Numerical simulation |
Experiment |
| PR |
CTE |
PR |
CTE |
PR |
Numerical |
| −0.4 |
0 |
−0.403 |
0.898084 |
−0.395 |
3.857 |
| −0.1 |
−200 |
−0.102 |
−194.476 |
−0.0932 |
−196.395 |
| −0.6 |
−500 |
−0.598 |
−499.397 |
−0.588 |
−484.799 |
| −0.2 |
−1100 |
−0.202 |
−1092.86 |
−0.204 |
−904.678 |
4.3. Programmable thermal deformation mode with fixed PR
The realization of programmable thermal deformation modes with a fixed PR is a challenging task for MM with a conventional arc-shaped bi-material rib, which exhibits narrow ranges of NTE and NPR due to the low design flexibility.19 In contrast, the high design flexibility of the BPCM enables pre-defined BPCM unit cells with a wide range of different NTEs with identical NPR. The combination of such pre-defined BPCM unit cells exhibiting distinct NTE with identical NPR can achieve programmable thermal deformation modes with a fixed PR. As listed in Table 6, pre-defined BPCM unit cells with NPR of −0.2 are generated through the DAIM from NTE ranging from 0 to −1000 with 200 ppm K−1 intervals and symbolized as 0 to 5. The arbitrary target thermal deformation mode can be defined by a code matrix representing the arrangement of the pre-defined BPCM unit cells symbolized as 0 to 5. As the temperature increases from 303 K to 333 K, the trapezoidal and rhombic thermal deformation mode with NPR of −0.196 and −0.18 is achieved by the combination of various pre-defined BPCM unit cells with NPR of −0.2 represented through the code matrix, as shown in Fig. 10. This result demonstrates that the combination of the pre-defined BPCM unit cells enables an arbitrary anisotropic deformation with fixed target NPR. For the demonstration of a more complex thermal deformation mode, a sine wave-shaped thermal deformation mode and corresponding code matrix are introduced, as shown in Fig. 11 (Fig. S10, ESI†).
Table 6 Pre-defined BPCM unit cells with PR −0.2 inverse designed through DAIM
|
|
PR |
CTE |
| 0 |
−0.208 |
0.789 |
| 1 |
−0.206 |
−186.235 |
| 2 |
−0.203 |
−391.941 |
| 3 |
−0.2 |
−593.747 |
| 4 |
−0.2 |
−796.586 |
| 5 |
−0.199 |
−1001.43 |
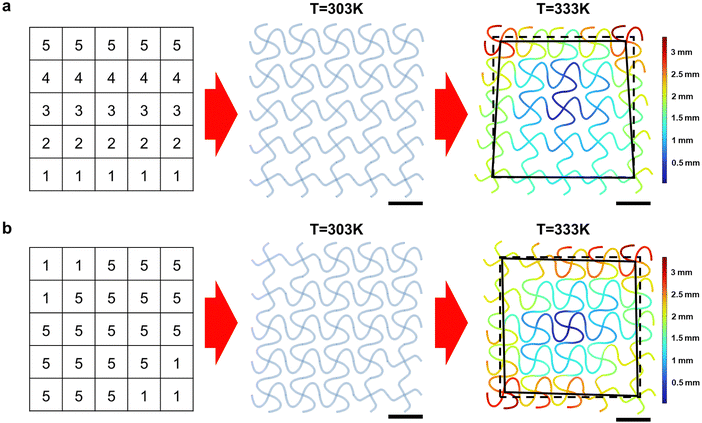 |
| | Fig. 10 Programmable thermal deformation mode with fixed PR, scale factor = 4.5: (a) trapezoidal thermal deformation mode with PR = −0.196 and (b) rhombic thermal deformation mode with PR = −0.18 (all the scale bars are 40 mm). | |
 |
| | Fig. 11 Sine wave-shaped thermal deformation mode (all the scale bars are 40 mm). | |
4.4. Comparison and discussion
To compare the BPCM with the MM introduced in other papers, the CTE and PR of the BPCM and those in other papers are represented in the mechanical property space, as shown in Fig. 9b. In general, the design of MM has been mainly accomplished by iterative searching of the diverse combination of design parameters such as rotation angle, width, and thickness of the ribs through an analytical approach or numerical simulation. Because the MM characterized by the combination of such design parameters has a limited number of design options, such MM exhibited a narrow range of NTE and NPR. In the literature,19 MM consisting of arc-shaped ribs realized the limited range of NPR and NTE. Other studies suggested various types of MM exhibiting simultaneous NTE and NPR but the unit cells of such MMs depend on the combination of design parameters, which leads to a narrow range of NTE and NPR.7,27,58 A wide range of CTE and PR is implemented by introducing topology optimization.21,22 However, topology optimization involves a cumbersome optimization process for each design of MM with arbitrary target CTE and PR. In addition, the corresponding method exhibited a narrower range of NTE compared with our study. Our proposed BPCM and inverse design framework with the DAIM can accomplish a wide range of arbitrary NTEs and NPRs without an additional optimization process.
5. Conclusions
In this study, we propose a BPCM that enables a wide range of programmable NTEs and NPRs. For efficient BPCM inverse design, a data-driven inverse design method of DAIM is introduced. In addition, we improve the inverse design performance of the DAIM for the data-sparse domains of the mechanical property space through iterative transfer learning with data augmentation. Experimental validation is conducted to confirm the coincidence between the inverse design target and the 3D-printed BPCMs. Furthermore, programmable thermal deformation modes with a fixed PR are realized by combining pre-defined BPCM unit cells which are inverse designed through the DAIM. Our proposed BPCM inverse design framework with the DAIM enables the inverse design of BPCMs with a wide range of arbitrary target NTEs and NPRs. The BPCM and inverse design of the corresponding structure with the DAIM are expected to improve the robustness of high-precision mechanical systems under simultaneous thermo-mechanical stimuli, such as circuit boards and flexible solar cells.
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work is supported by a National Research Foundation of Korea (NRF) grant funded by the Korean government (MSIT) (No. RS-2023-00209094). This research was supported by the Ministry of Trade, Industry, and Energy (MOTIE), Korea, under “Innovative Digital Manufacturing Platform” (No. P0022331) supervised by the Korea Institute for Advancement of Technology (KIAT). This study was supported by the fundamental Research Program of the Korea Institute of Materials Science [grant numbers PNK9940]. This study has been conducted with the support of the Korea Institute of Industrial Technology as “Development of intelligent root technology with add-on modules (KITECH EO-24-0005)”.
References
- P. Jiao, J. Mueller, J. R. Raney, X. R. Zheng and A. H. Alavi, Nat. Commun., 2023, 14, 6004 CrossRef CAS PubMed.
- A. A. Zadpoor, Mater. Horiz., 2016, 3, 371–381 RSC.
- J. U. Surjadi, L. Gao, H. Du, X. Li, X. Xiong, N. X. Fang and Y. Lu, Adv. Eng. Mater., 2019, 21, 1800864 CrossRef CAS.
- D. Zhengchun, Z. Mengrui, W. Zhiguo and Y. Jianguo, Compos. Struct., 2016, 152, 693–703 CrossRef.
- W. Zhang, L. He, Y. Zhou, D. Tang, B. Ding, C. Zhou, P. J. Dyson, M. K. Nazeeruddin and X. Li, Chem. Eng. J., 2023, 457, 141216 CrossRef CAS.
- H. Liu, J. Chen, X. Jiang, Z. Pan, L. Zhang, Y. Rong, Z. Lin and X. Xing, J. Mater. Chem. C, 2017, 5, 931–936 RSC.
- C. S. Ha, E. Hestekin, J. Li, M. E. Plesha and R. S. Lakes, Phys. Status Solidi B, 2015, 252, 1431–1434 CrossRef CAS.
- K. Wei, X. Xiao, W. Xu, Z. Han, Y. Wu and Z. Wang, Virtual Phys. Prototyping, 2021, 16, S53–S65 CrossRef.
- E. Boatti, N. Vasios and K. Bertoldi, Adv. Mater., 2017, 29, 1700360 CrossRef PubMed.
- X. Xue, C. Lin, F. Wu, Z. Li and J. Liao, Mater. Today Commun., 2023, 34, 105132 CrossRef CAS.
- W. Wu, Mater. Des., 2019, 180, 107950 CrossRef.
- J. Dong, C. Hu, J. Holmes, Q.-H. Qin and Y. Xiao, Compos. Struct., 2022, 282, 115035 CrossRef CAS.
- G. Felsch, N. Ghavidelnia, D. Schwarz and V. Slesarenko, Comput. Methods Appl. Mech. Eng., 2023, 410, 116032 CrossRef.
- L. Mizzi, K. M. Azzopardi, D. Attard, J. N. Grima and R. Gatt, Phys. Status Solidi RRL, 2015, 9, 425–430 CrossRef CAS.
- L. Mizzi, Mater. Des., 2018, 146, 28–37 CrossRef.
- F. Meng, S. Chen, W. Zhang, P. Ou, J. Zhang, C. Chen and J. Song, Mech. Mater., 2021, 155, 103774 CrossRef.
- K. K. Saxena, R. Das and E. P. Calius, Adv. Eng. Mater., 2016, 18, 1847–1870 CrossRef CAS.
- C. Du, Y. Wang and Z. Kang, ACS Appl. Mater. Interfaces, 2023, 15, 19190–19198 CrossRef CAS PubMed.
- Y. Bai, C. Liu, Y. Li, J. Li, L. Qiao, J. Zhou and Y. Bai, ACS Appl. Mater. Interfaces, 2022, 14, 35905–35916 CrossRef CAS PubMed.
- Q. Zhang and Y. Sun, Int. J. Mech. Sci., 2024, 261, 108692 CrossRef.
- Z. Han, X. Xiao, J. Chen, K. Wei, Z. Wang, X. Yang and D. Fang, ACS Appl. Mater. Interfaces, 2022, 50068–50078 CrossRef CAS PubMed.
- Z. Han and K. Wei, Addit. Manuf., 2022, 54, 102742 Search PubMed.
- J. Li, Q. Yang, Y. Wei, N. Huang and R. Tao, Compos. Struct., 2021, 275, 114446 CrossRef.
- J. Chen, W. Xu, Z. Wei, K. Wei and X. Yang, Int. J. Mech. Sci., 2021, 202–203 CAS.
- Y. Zhang, Y. Pan, D. Han, W. Z. Jiang, W. Jiang, X. G. Zhang, X. C. Teng, X. H. Ni and X. Ren, Compos. Struct., 2023, 323, 117474 CrossRef CAS.
- S. Liu and Y. Li, Adv. Eng. Mater., 2023, 25, 2201527 CrossRef CAS.
- J. S. Raminhos, J. P. Borges and A. Velhinho, Smart Mater. Struct., 2019, 28, 045010 CrossRef CAS.
- S. Kuutti, R. Bowden, Y. Jin, P. Barber and S. Fallah, IEEE Trans. Intell. Transp. Syst., 2021, 22, 712–733 Search PubMed.
- I. Lauriola, A. Lavelli and F. Aiolli, Neurocomputing, 2022, 470, 443–456 CrossRef.
- J. Chai, H. Zeng, A. Li and E. W. T. Ngai, Mach. Learn. Appl., 2021, 6, 100134 Search PubMed.
- M. J. Kim, J. Y. Song, S. H. Hwang, D. Y. Park and S. M. Park, Sci. Rep., 2022, 12, 16281 CrossRef CAS PubMed.
- S. H. Hwang, J. Y. Song, H. I. Ryu, J. H. Oh, S. Lee, D. Lee, D. Y. Park and S. M. Park, Adv. Fiber Mater., 2023, 5, 617–631 CrossRef.
- B. Kim, J. Y. Song, D. Y. Kim, M. W. Cho, J. G. Park, D. Choi, C. Lee and S. M. Park, Small, 2024, e2400484, DOI:10.1002/smll.202400484.
- Y. Wang, W. Sha, M. Xiao, C. W. Qiu and L. Gao, Adv. Mater., 2023, 35, e2302387 CrossRef PubMed.
- K. Donda, Y. Zhu, A. Merkel, S. Wan and B. Assouar, Extreme Mech. Lett., 2022, 56, 101879 CrossRef.
- W. Ma, F. Cheng, Y. Xu, Q. Wen and Y. Liu, Adv. Mater., 2019, 31, e1901111 CrossRef PubMed.
- F. Sui, R. Guo, Z. Zhang, G. X. Gu and L. Lin, ACS Mater. Lett., 2021, 3, 1433–1439 CrossRef CAS.
- X. Du, J. Ren and L. Leifsson, Aerosp. Sci. Technol., 2019, 85, 371–385 CrossRef.
- K. Mahesh, S. K. Ranjith and R. Mini, Eng. Comput., 2023, 1–22 Search PubMed.
- X. Zheng, T. T. Chen, X. Guo, S. Samitsu and I. Watanabe, Mater. Des., 2021, 211, 110178 CrossRef.
- S. Lee, Z. Zhang and G. X. Gu, Mater. Horiz., 2022, 9, 952–960 RSC.
- D. Wang, L. Dong and G. Gu, Adv. Funct. Mater., 2023, 33, 2208849 CrossRef CAS.
- Q. Zeng, Z. Zhao, H. Lei and P. Wang, Int. J. Mech. Sci., 2023, 240, 107920 CrossRef.
- B. Deng, A. Zareei, X. Ding, J. C. Weaver, C. H. Rycroft and K. Bertoldi, Adv. Mater., 2022, 34, e2206238 CrossRef PubMed.
- J.-H. Bastek and D. M. Kochmann, Nat. Mach. Intell., 2023, 5, 1466–1475 CrossRef.
- A. Álvarez-Trejo, E. Cuan-Urquizo, A. Roman-Flores, L. G. Trapaga-Martinez and J. M. Alvarado-Orozco, Mater. Des., 2021, 199, 109412 CrossRef.
- R. Lakes, J. Mater. Sci. Lett., 1996, 15, 475–477 CrossRef CAS.
- L. Wu, B. Li and J. Zhou, ACS Appl. Mater. Interfaces, 2016, 8, 17721–17727 CrossRef CAS PubMed.
- L. Wang, Y.-C. Chan, F. Ahmed, Z. Liu, P. Zhu and W. Chen, Comput. Methods Appl. Mech. Eng., 2020, 372, 113377 CrossRef.
- M. Lee and K. Min, J. Chem. Inf. Model., 2022, 62, 2943–2950 CrossRef CAS PubMed.
- S. So, J. Mun and J. Rho, ACS Appl. Mater. Interfaces, 2019, 11, 24264–24268 CrossRef CAS PubMed.
- K. He, X. Zhang, S. Ren and J. Sun, Proc. IEEE Comput. Soc. Conf. Comput. Vis. Pattern Recognit., 2016, 770–778 Search PubMed.
- Y. Kim, Y. Kim, C. Yang, K. Park, G. X. Gu and S. Ryu, npj Comput. Mater., 2021, 7, 140 CrossRef.
- S. Lee, W. Choi, J. W. Park, D.-S. Kim, S. Nahm, W. Jeon, G. X. Gu, M. Kim and S. Ryu, Nano Energy, 2022, 103, 107846 CrossRef CAS.
- J. Hu, X. Li, G. Hu, Y. Lyu, K. Susztak and M. Li, Nat. Mach. Intell., 2020, 2, 607–618 CrossRef PubMed.
- Y. Xu, X. Lu, Y. Fei and Y. Huang, J. Comput. Des. Eng., 2022, 9, 2089–2102 Search PubMed.
- T.-I. Lee, M. S. Kim and T.-S. Kim, Polym. Test., 2016, 51, 181–189 CrossRef CAS.
- K.-J. Liu, H.-T. Liu and J. Li, Int. J. Mech. Sci., 2023, 242, 108015 CrossRef.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a
*a
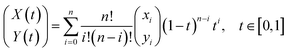

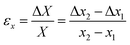
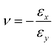
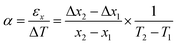
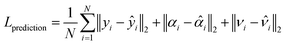
![[small alpha, Greek, circumflex]](https://www.rsc.org/images/entities/char_e101.gif) i, and
i, and 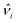 represent predicted data by the DAIM. The control points of the Bézier curve determine the shape of the Bézier curve, which implies that a deep-learning model, which utilizes the control points as the input and output data, would generate only Bézier curves, while the Bézier curve cannot generate all types of curved rib. To obtain more diverse curved rib structures beyond the Bézier curve, the 1-D shape data of the curved rib are used as the input data of the DAIM instead of the control points of the Bézier curve. The utilization of such 1-D shape data can potentially expand the structure of the curve-shaped ribs to other parametric curves such as polynomials and trigonometric functions (Fig. S2, ESI†). The 1-D shape data of the curved rib are defined by the y-coordinate data of the Bézier curve calculated through that corresponding to the 32 evenly spaced x-coordinate points. The 1-D shape data of the curved rib are normalized by dividing by 20 mm considering the size of the unit cell of the BPCM. The PR and CTE values, which are used for the label data of DAIM, are Min–Max normalized to resolve the scale differences between the mechanical properties. The geometric features of the Bézier curve-shaped rib of the BPCM are extracted from the 1-D shape data of the curved rib by inputting into the 1-D convolution layer of the encoder. The extracted geometric features of the curved rib of the BPCM are reduced to a two-dimensional latent space by passing through a dense layer of the encoder. A deeper neural network is required for effective matching between the Bézier curve shape and the mechanical properties. However, as deeper neural networks often induce gradient vanishing problems, ResNet, which achieves a deeper neural network without gradient vanishing problems by exploiting skip connections is employed for both the convolution layer and the dense layer.52 To constrain the mechanical properties of the BPCM to the DAIM, the mean-squared error (MSE) between each node of the latent space and the mechanical properties of the BPCM is added to the loss function as represented in eqn (5). The variables of the 2-D latent space are input into the dense layer and the convolution transpose layer of the decoder to generate the 1-D shape data of the curved rib. The encoder of DAIM is constructed by ResNet including 16 1-D convolution layers and 11 dense layers. The decoder of DAIM is composed of ResNet with 11 dense layers and 4 transposed convolution layers. To achieve stable convergence without overfitting during the training process, a batch normalization layer and dropout layer with a dropout rate of 0.2 are added. The detailed network structure of the DAIM including the depth of layers, specific activation function, number of convolution filters, and nodes is shown in Fig. S3 and S4 (ESI†). The MSE between the generated 1-D shape data of the curved rib and the input 1-D shape data of the curved rib is added to the loss function, as shown in eqn (5).
represent predicted data by the DAIM. The control points of the Bézier curve determine the shape of the Bézier curve, which implies that a deep-learning model, which utilizes the control points as the input and output data, would generate only Bézier curves, while the Bézier curve cannot generate all types of curved rib. To obtain more diverse curved rib structures beyond the Bézier curve, the 1-D shape data of the curved rib are used as the input data of the DAIM instead of the control points of the Bézier curve. The utilization of such 1-D shape data can potentially expand the structure of the curve-shaped ribs to other parametric curves such as polynomials and trigonometric functions (Fig. S2, ESI†). The 1-D shape data of the curved rib are defined by the y-coordinate data of the Bézier curve calculated through that corresponding to the 32 evenly spaced x-coordinate points. The 1-D shape data of the curved rib are normalized by dividing by 20 mm considering the size of the unit cell of the BPCM. The PR and CTE values, which are used for the label data of DAIM, are Min–Max normalized to resolve the scale differences between the mechanical properties. The geometric features of the Bézier curve-shaped rib of the BPCM are extracted from the 1-D shape data of the curved rib by inputting into the 1-D convolution layer of the encoder. The extracted geometric features of the curved rib of the BPCM are reduced to a two-dimensional latent space by passing through a dense layer of the encoder. A deeper neural network is required for effective matching between the Bézier curve shape and the mechanical properties. However, as deeper neural networks often induce gradient vanishing problems, ResNet, which achieves a deeper neural network without gradient vanishing problems by exploiting skip connections is employed for both the convolution layer and the dense layer.52 To constrain the mechanical properties of the BPCM to the DAIM, the mean-squared error (MSE) between each node of the latent space and the mechanical properties of the BPCM is added to the loss function as represented in eqn (5). The variables of the 2-D latent space are input into the dense layer and the convolution transpose layer of the decoder to generate the 1-D shape data of the curved rib. The encoder of DAIM is constructed by ResNet including 16 1-D convolution layers and 11 dense layers. The decoder of DAIM is composed of ResNet with 11 dense layers and 4 transposed convolution layers. To achieve stable convergence without overfitting during the training process, a batch normalization layer and dropout layer with a dropout rate of 0.2 are added. The detailed network structure of the DAIM including the depth of layers, specific activation function, number of convolution filters, and nodes is shown in Fig. S3 and S4 (ESI†). The MSE between the generated 1-D shape data of the curved rib and the input 1-D shape data of the curved rib is added to the loss function, as shown in eqn (5).
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 distinct Bézier curves are defined through random Bézier control point sampling. For the DAIM training, such Bézier curves are transformed into 1-D shape data of the curved rib, which consists of 32 y-coordinate data of the Bézier curve. By performing numerical simulations on the BPCM structures configured by the generated 1-D shape data of the curved rib, 10
927 distinct Bézier curves are defined through random Bézier control point sampling. For the DAIM training, such Bézier curves are transformed into 1-D shape data of the curved rib, which consists of 32 y-coordinate data of the Bézier curve. By performing numerical simulations on the BPCM structures configured by the generated 1-D shape data of the curved rib, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 927 data of CTE and PR are generated. The dataset for training and validation consisted of 1-D shape data of the curved rib with the size of 32 × 1 and the CTE and PR data corresponding to each 1-D shape data. The training and test dataset contains 9834 and 1093 data samples, which is 90% and 10% of the total data, respectively. As a high learning rate induces unstable convergence and, a low learning rate results in slow convergence, we employed the decaying learning rate starting with an initial learning rate of 1 × 10−4 and multiplied by 0.1 every 100 epochs until 300 epochs. The batch size is set to 512, and the training is conducted up to 500 epochs through the adaptive moment estimation optimizer. The training is conducted using NVIDIA GeForce GTX 1660 GPU and Intel® Core™ i5-9400F CPU @ 2.90GHz 2.90 GHz. By examining the learning curve, we confirm the stable convergence of the loss without overfitting (Fig. S5, ESI†). After sufficient training of the DAIM, the prediction model, the encoder part of the DAIM, can predict the CTE and PR of the BPCM by inputting the 1-D shape data of the curved rib, and the inverse design model, the decoder part of the DAIM, can generate the corresponding 1-D shape data of the curved rib by receiving the target CTE and PR.
927 data of CTE and PR are generated. The dataset for training and validation consisted of 1-D shape data of the curved rib with the size of 32 × 1 and the CTE and PR data corresponding to each 1-D shape data. The training and test dataset contains 9834 and 1093 data samples, which is 90% and 10% of the total data, respectively. As a high learning rate induces unstable convergence and, a low learning rate results in slow convergence, we employed the decaying learning rate starting with an initial learning rate of 1 × 10−4 and multiplied by 0.1 every 100 epochs until 300 epochs. The batch size is set to 512, and the training is conducted up to 500 epochs through the adaptive moment estimation optimizer. The training is conducted using NVIDIA GeForce GTX 1660 GPU and Intel® Core™ i5-9400F CPU @ 2.90GHz 2.90 GHz. By examining the learning curve, we confirm the stable convergence of the loss without overfitting (Fig. S5, ESI†). After sufficient training of the DAIM, the prediction model, the encoder part of the DAIM, can predict the CTE and PR of the BPCM by inputting the 1-D shape data of the curved rib, and the inverse design model, the decoder part of the DAIM, can generate the corresponding 1-D shape data of the curved rib by receiving the target CTE and PR.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 052
052![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 271
271![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 487
487![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 705
705![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 863
863![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 174
174![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 512
512![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 851
851![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 192
192![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 531
531









