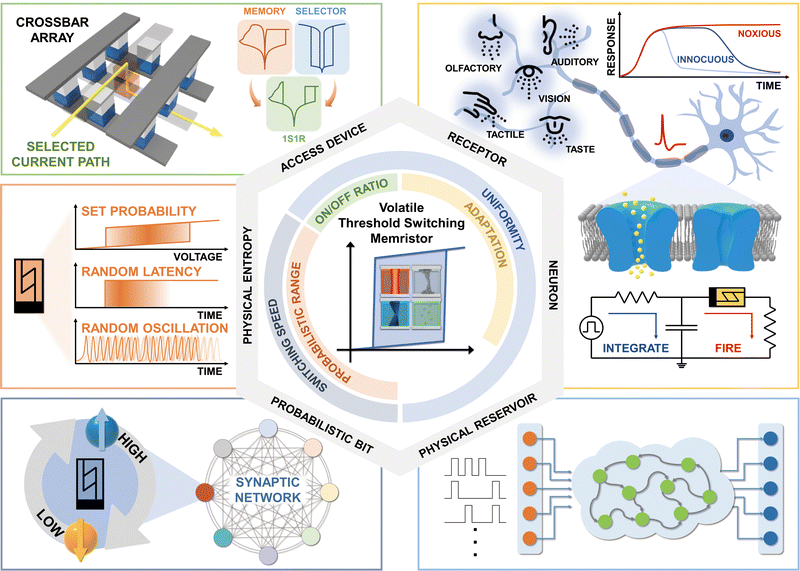
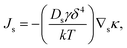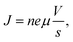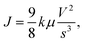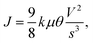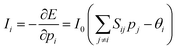Leveraging volatile memristors in neuromorphic computing: from materials to system implementation

Abstract

Inspired by the functions of biological neural networks, volatile memristors are essential for implementing neuromorphic computing. These devices enable large-scale and energy-efficient data processing by emulating neural functionalities through dynamic resistance changes. The threshold switching characteristics of volatile memristors, which are driven by various mechanisms in materials ranging from oxides to chalcogenides, make them versatile and suitable for neuromorphic computing systems. Understanding these mechanisms and selecting appropriate devices for specific applications are crucial for optimizing the performance. However, the existing literature lacks a comprehensive review of switching mechanisms, their compatibility with different applications, and a deeper exploration of the spatiotemporal processing capabilities and inherent stochasticity of volatile memristors. This review begins with a detailed analysis of the operational principles and material characteristics of volatile memristors. Their diverse applications are then explored, emphasizing their role in crossbar arrays, artificial receptors, and neurons. Furthermore, the potential of volatile memristors in artificial inference systems and reservoir computing is discussed, due to their spatiotemporal processing capabilities. Hardware security applications and probabilistic computing are also examined, where the inherent stochasticity of the devices can improve the system robustness and adaptability. To conclude, the suitability of different switching mechanisms for various applications is evaluated, and future perspectives for the development and implementation of volatile memristors are presented. This review aims to fill the gaps in existing research and highlight the potential of volatile memristors to drive innovation in neuromorphic computing, paving the way for more efficient and powerful computational paradigms.

---

Taehwan Moon

Taehwan Moon is an Assistant Professor in the Department of Intelligence Semiconductor Engineering at Ajou University. He was a Postdoctoral Researcher at the University of Southern California (2022–2024) and a Staff Researcher at Samsung Advanced Institute of Technology (2019–2022). He received his PhD in Materials Science and Engineering from Seoul National University (2013–2019) and his BS in Materials Science and Engineering from Seoul National University (2009–2013). His research seeks emerging memory technology, neuromorphic computing and Post-CMOS hardware accelerator for AI.

Keunho Soh

Keunho Soh received his BS degree in the department of Electronic and IT Media Engineering from Seoul National University of Science and Technology in 2022. Since then, he has studied as a MS candidate under the co-guidance of Prof. Jung Ho Yoon in Sungkyunkwan University, Dr Ji-Soo Jang in KIST, and Prof. Soo Young Kim in Korea University. His current research interest is the security and probabilistic computing applications using volatile memristor device.

Jong Sung Kim

Jong Sung Kim received his BS degree in the department of Materials Science and Engineering from Inha University in 2023. Since then, he has studied as a PhD candidate under the co-guidance of Dr Kyungjune Cho in Korea Institute of Science and Technology (KIST) and Prof. SoongJu Oh in Korea University. His current research interest is the bio-mimicking device for neuromorphic computing.

J. Joshua Yang

J. Joshua Yang is the Arthur B. Freeman Chair Professor in the Department of Electrical and Computer Engineering at the University of Southern California. He was a professor of the ECE department at the University of Massachusetts Amherst between 2015 and 2020. He spent about 8 years at HP Labs between 2007 and 2015, leading an emerging materials and devices team for memory and computing. His current research interest is Post-CMOS hardware for in-memory computing, near-sensor computing, neuromorphic computing, machine learning and artificial intelligence.

Jung Ho Yoon

Jung Ho Yoon is an assistant professor at the Advanced Materials Science and Engineering Department of Sungkyunkwan University (SKKU). He received his PhD from Seoul National University in 2015. After gaining initial postdoctoral experience at SNU and the University of Massachusetts, he also served as a Visiting Research Scholar at the Nanoscience and Technology division of Argonne National Laboratory, USA. In 2018, he returned to Korea and joined SNU's Inter-university Semiconductor Research Center, followed by a stint as a Staff Researcher at Samsung Advanced Institute of Technology's Inorganic Material Lab. He was a senior researcher at the Center for Electronic Materials of the Korea Institute of Science and Technology (KIST) between 2020 and 2024. Since 2024, He has been contributing to the field as an assistant professor at SKKU. His research fields include neuromorphic computing applications, bio-mimicking emulators for humanoid robots, and emerging memory devices.

---

Wider impact

Volatile memristors exhibit various operating voltages and current ranges based on their switching mechanisms, rendering them versatile for various neuromorphic applications. Therefore, it is essential to consider both mechanisms and applications simultaneously to explore new areas using innovative approaches. Moreover, investigating the spatiotemporal signal processing and inherent stochasticity of volatile memristors beyond their traditional applications can significantly accelerate research in this field. These insights could lead to advancements in volatile memristors and their applications, ultimately advancing the field of neuromorphic computing and its applications. Thus, it is essential to gain insights into emerging fields, such as hardware security applications and probabilistic computing, which have recently received increased attention. This review provides insights into volatile memristor applications and integrates hardware implementation approaches for neuromorphic computing. Combining these aspects paves the way for the future development of more sophisticated and efficient neuromorphic systems.

1. Introduction

The current era of big data is driven by the rapid expansion of data technologies, such as artificial intelligence (AI), the Internet of Things (IoT), and advancements in scientific research. Within AI, generative AI¹ and autonomous driving² technologies are prominent focal points; both rely heavily on vast datasets for deep learning processes. Generative AI generates images and videos, whereas autonomous driving systems recognize and navigate their surroundings. Additionally, the integration of IoT with AI enhances interaction with the physical environment. Numerous devices capture environmental data, generating substantial datasets that enable decisions such as smart home lighting adjustments³ or smart farm irrigation scheduling.⁴ In academia, AI simulates complex experiments such as heat transfer⁵ and protein structure synthesis.⁶ These data-intensive applications require large-scale storage solutions and efficient computing systems capable of swift processing and high energy efficiency. Neuromorphic computing has emerged as a promising candidate for meeting these demands.

Neuromorphic computing, inspired by the intricate functionalities of biological neural networks, has emerged as a promising paradigm to overcome the limitations of conventional computing architectures.⁷ Unlike traditional, complementary metal-oxide semiconductor (CMOS) based computing, which relies on Von Neumann architecture and requires significant data movement between separate memory and processor units, neuromorphic computing emulates the brain's information processing capabilities. The Von Neumann architecture, which is the foundation of modern computing, has several limitations that have become more pronounced with technological advancements. The most prominent limitation is the “Von Neumann bottleneck,” arising from the architecture design, where the data path between the central processing unit (CPU) and memory is a single bus. This constriction in data flow creates a bottleneck, impeding the system performance, as the CPU must often wait for data retrieval or storage in memory, thereby hindering the execution speed. In addition, the sequential execution model of the architecture does not inherently support parallel processing, posing challenges as applications demand larger computational power. These limitations hinder the computational speed and energy efficiency, consequently affecting the efficacy of AI applications. Conversely, neuromorphic computing aims to develop hardware systems that emulate the efficient, scalable, low-power, and adaptable information-processing capabilities of the brain. Among various emerging technologies, volatile memristors have garnered considerable attention as pivotal components for implementing dynamic synaptic behaviors, which are crucial for cognitive processes.

The human brain and its neural system, with its intricate network of neurons, synapses, and receptors, serve as blueprints for the emerging field of neuromorphic computing. Unlike traditional computing architectures that rely on sequential data processing, the brain operates on a highly parallel and distributed model, efficiently facilitating complex cognitive functions such as signal sensing, learning, and adaptation through its dynamic network.^8,9 This biological mechanism has inspired the development of computing systems that aim to mimic these processes to enhance computational efficiency and capability. Among the innovations in this field, memristors (memory resistors) have gained prominence as potential keystones for building neuromorphic computing architectures. Introduced by Leon Chua in 1971, memristors are recognized as the fourth fundamental circuit element, complementing resistors, capacitors, and inductors.¹⁰ These devices possess unique electrical properties, particularly nonlinear resistance, influenced by the applied voltage or current history. This feature enables memristors to mimic the synaptic functionalities of the human brain, offering a promising avenue for developing computing systems capable of adaptation and learning.¹¹ Memristors offer several advantages, including a simple structure, compatibility with existing CMOS fabrication technologies, and low power consumption. These advantages have positioned memristors as leading candidates for revolutionizing future computing paradigms.

A memristor possesses a unique property: it changes its resistive state between a low-resistance state (LRS) and a high-resistance state (HRS) in response to external stimuli, such as voltage or current. This change in resistance is crucial for replicating the synaptic functions found in biological neural networks. The retention time of the altered state can vary, leading to classifications such as volatile and non-volatile memristors. Non-volatile memristors are particularly notable for retaining their LRS even after the stimulus is removed, emulating the long-term synaptic plasticity in the human brain.¹² This feature makes them ideal for integration into artificial neural networks to simulate synaptic functionalities, providing a durable and energy-efficient foundation for memory storage and processing.¹³ Particularly when integrated with non-volatile memristors, the crossbar array structure accelerates the application of neuromorphic computing in various fields such as data storage,^14–16 bio-inspired computing,^17–21 and graph analysis.²² This is achieved by storing the weight matrix as the conductance level of each element and performing vector–matrix multiplication in a space-efficient and effective manner. In contrast, volatile memristors revert to their original HRS once the external stimulus is removed.^23,24 The temporal and dynamic behavior of the resistive state can be applied in diverse applications, such as access device in crossbar array structures,^25–28 artificial receptors,^29,30 and neurons^31–35 in neuromorphic computing systems. However, recent efforts have predominantly focused on non-volatile memristors, which are used to simulate artificial synapses in advanced memory technologies.^36,37 Thus, further research on volatile memristors is necessary to achieve a closer simulation of the human brain, as they are crucial for developing artificial receptors and neurons. In addition, their versatility makes them suitable for probabilistic computing,^38,39 where they can contribute to the development of systems capable of complex decision-making processes. Given the current gaps in the literature regarding the dynamics, materials, and applications of volatile memristors, this review aims to offer detailed insights into their operational principles, material characteristics, and potential applications.

In this review, the latest advancements, challenges, and prospects in this burgeoning field are systematically examined as depicted in Fig. 1. First, the fundamental characteristics of volatile threshold-switching memristors are meticulously analyzed, and the various materials and mechanisms governing their operation are determined. This foundational understanding serves as a cornerstone for evaluating the electrical performance and potential applications of volatile memristors. Subsequently, the use of volatile memristors as integral elements in crossbar array structures, artificial receptors, and neurons is discussed. Finally, the key insights into volatile memristor-based neuromorphic computing applications and probabilistic computing are synthesized. This review aims to stimulate further research and development, fostering a deeper understanding and broader implementation of volatile memristors in neuromorphic computing systems.

Fig. 1 Schematic illustration of the volatile threshold switching memristor with various applications such as an access device, receptor, neuron, physical reservoir, probabilistic bit, and physical entropy device.

2. Volatile threshold switching memristor

2.1. Metal cation-based memristor

Volatile threshold switching (TS) of the resistance, based on metal cations, is achieved through the formation of conductive metallic filaments within the switching layer. Memristors operating via this mechanism are also known as diffusive memristors because metal cations, such as Ag or Cu ions, exhibit rapid diffusive characteristics.⁴⁰ Metal-cation-based memristors typically employ a metal–insulator–metal (MIM) structure, with one electrode, termed the active electrode, composed of an active metal, such as Ag, Cu, or Ni, and another electrode, known as the inert electrode, made of an inert metal, such as Pt, Ir, or W. An insulating layer, referred to as the switching layer, is sandwiched between the two electrodes, where resistive switching occurs. The formation of conductive metallic filaments involves a series of steps:

• An external electric field oxidizes the active electrode into metal cations:

X → Xⁿ⁺ + ne⁻

• Metal cations drift across the insulating layer under an external electric field.

• Metal cations are reduced to metal atoms on the surface of the inert metal electrode:

Xⁿ⁺ + ne⁻ → X

Metal atoms accumulate successively on the inert electrode, forming conductive filaments that grow towards the active metal electrode. When the two electrodes are connected, the memristor transitions into the LRS, also known as the ON state, via the SET process.

The dynamics of conductive filament growth in the insulator layer are governed by kinetic parameters such as mobility and redox rates.⁴¹ When ion mobility and redox rates are high, the metal cations reach the inert electrode without agglomeration. In this scenario, conductive filaments can form from an inert electrode and grow towards the active electrode without nucleation within the insulator layer. These filaments adopt an inverted cone shape owing to the substantial ion supply from the high redox rates. Conversely, when ion mobility and redox rates are limited, metal cations accumulate within the insulating layer, reaching critical nucleation conditions. Subsequent filament growth occurs through cluster displacement, which involves repeated splitting and merging processes. This repetitive process occurs because of the bipolar electrode behavior of the metal clusters formed in the insulating layer. The metal cluster facing the active electrode reduces the number of incoming metal cations, whereas the metal is oxidized to metal cations on the side facing the inert electrode. When the ion mobility is low, along with high redox rates, metal nucleation is initiated within the insulating layer. The nuclei, characterized by bipolar electrode features, deposit a substantial number of atoms onto the facet directed towards the active electrode. Upon establishing a connection between the nuclei and the active electrode, growth continues on the side facing the inert electrode, progressing until it reaches its endpoint. Conversely, the nucleation occurs at the inert electrode if ion mobility is high and the redox rates are low. Owing to the low redox rates, the availability of metal cations at the periphery of the nuclei is constrained, leading to filamentous growth with a branched configuration towards the active electrode.

Typically, an opposing external electric field must be applied to non-volatile memristors to switch the device to the HRS, which is also known as the OFF state. However, if a weak or thin conductive metallic filament is formed, self-rupturing occurs, causing the device to revert to the HRS when the applied external electric field decreases below a certain voltage or is completely removed. The voltage at which the device switches to the OFF state is known as the hold voltage (V_hold). The driving forces behind the self-rupture of conductive filaments are primarily the surface energy minimization effect^42,43 and steric repulsion effects.^44,45

First, surface energy minimization is achieved through atomic surface diffusion, leading to the spontaneous rupture of the conductive filaments. According to the Gibbs–Thomson effect, the surface atomic flux can be expressed as:⁴⁶

where D_s represents the surface diffusion coefficient, γ denotes the surface energy, δ signifies the inter-atomic distance, k is Boltzmann's constant, T is the temperature, and κ is the surface curvature. Given that the surface atomic flux corresponds to the surface curvature gradient, surface diffusion results in the segmentation of conductive filaments and the formation of one or more intermediary clusters comprising metal atoms. Surface energy minimization can also be explained by the classical nucleation theory.⁴³ The relation to the conductive filament size expresses the Gibbs free energy change:

ΔG = −πr²L|G_V| + πr²(γ_T + γ_B) + 2πrLγ_D,

where r and L are the radius and length of the conductive filament, respectively; |G_V| is the difference in the Gibbs bulk free energy per unit volume; γ_T, γ_B, and γ_D are the surface energy per unit area of the conductive filament contacting with the top electrode, bottom electrode, and insulating layer, respectively. The critical radius can be calculated by differentiating the above formula with respect to the radius. The energy required to overcome the nucleation barrier increases when the voltage is removed. This implies that the conductive filament must be larger than the critical size to achieve thermodynamic stability. Consequently, if the conductive filament (r) size is below the critical radius, self-rupture occurs, facilitating the formation of smaller clusters. The second explanation for the driving force behind the self-rupture of conductive filaments is the steric repulsion effect. According to a previous study,⁴⁴ the self-breaking tendency of Ag-based conductive filaments during growth within the TiO₂ switching layer is attributed to efforts to mitigate the steric repulsion between the Ag metal atoms and the TiO₂ insulating layer. This phenomenon occurs because of the transfer of the Ag 5s valence electron to the vacant Ti 3d state, leading to the formation of localized Ti³⁺ and the ionization of Ag atoms. Moreover, another explanation has been proposed regarding the mechanism of self-rupturing of the conductive filament, with a particular focus on the interaction between the conductive filament and the switching layer. It has been reported that, after the formation of a conductive filament, the mechanical stress exerted by the switching layer can lower the energy barrier for ion migration, contributing to self-rupture and retraction in the direction of the electrode.⁴⁷ Other methods, such as controlling the compliance current^48,49 and duration of the applied voltage,⁵⁰ have been employed to affect the strength of the conductive filament and transition the device to a volatile memristor.

2.2. Ovonic threshold switching-based memristor

Ovonic threshold switching (OTS) was first identified by Ovshinsky in the 1960s.⁵¹ This phenomenon occurs in various disordered materials, specifically in amorphous chalcogenides with a band gap ranging from 0.6 to 1.4 eV, including sulfides, selenides, and tellurides. Memristors based on OTS typically exhibit TS behavior. This implies that the device switches to the ON state when the applied voltage surpasses the threshold voltage (V_th) and switches to the OFF state when the applied voltage drops below V_hold. Joule heating can induce crystallization in amorphous materials if the ON state is maintained for a certain duration. Consequently, the device persists in the ON state even if the voltage falls below V_hold, displaying memory-switching behavior. Numerous theories have been proposed to explain the OTS mechanism. However, no single model has been able to fully explain the physical switching of OTS, and a unified model that captures this physical switching remains elusive. Nonetheless, most models agree that the OTS operates primarily via an electronic phenomenon with a secondary thermal effect that does not involve an atomic arrangement.

Adler et al. proposed a model based on carrier generation and trap filling under an applied electric field.^52,53 According to this model, the application of a critical field initiates carrier generation near an electrode, leading to field redistribution. When the area near the cathode reaches the critical field, the generated charge carriers occupy all trap states, enhancing mobility and conductance. This enhanced conductance area then propagates through the chalcogenide layer, leading to a sharp increase in the current.

Karpov et al. proposed another model based on a field-induced nucleation mechanism.^54,55 This model explains that the switching from the HRS amorphous state to the LRS crystalline state is initiated when the applied voltage surpasses V_th. The LRS crystalline state forms through the HRS amorphous layer in a filamentary form. Highly conductive crystalline particles emerge under sufficient biased conditions. Their dipole momentum interacts with the electric field, reducing the energy of the system and facilitating nucleation. If a device exhibits strong bias, it plays a crucial role in promoting the nucleation of additional conductive particles, which leads to a subsequent increase in the electric field. Consequently, a conductive crystalline filament is established throughout the entire amorphous region, resulting in the TS of the resistance.

Finally, Ielmini and Zhang proposed a model based on trap-limited TS using the Poole–Frenkel effect.^56,57 The unique behavior of TS arises from the non-equilibrium state of carriers residing in shallow traps with enhanced mobility, especially under stronger electric fields. This behavior is also influenced by the nonuniform distribution of the electric field throughout the thickness of the amorphous material. When subjected to a relatively weak electric field, electrons occupy trap sites below the Fermi level. However, as the electric field increases, the energy of the electrons within these trap states increases. Consequently, electrons transition from lower-energy trap states to higher-energy states, which is facilitated by processes such as thermal emission, tunneling, or the energy gained from the applied electric field. This transition shifts the charge carries from an equilibrium distribution to a distinct non-equilibrium state. During the relaxation process, the kinetic energy acquired by a trapped electron may be transferred to other excited electrons, causing a significant change in conductivity. An alternative explanation for TS involves the use of a thermally assisted hopping transport model. In this scenario, the presence of a strong electric field introduces instability in the transport process, leading to a sudden surge in conductivity.

2.3. Metal–insulator transition-based memristor

Among volatile memristors, those based on the metal–insulator transition (MIT) utilize Mott materials, such as VO₂, NbO₂, NiO₂, and TiO_x, as insulating switching layers. The conductance of these materials undergoes significant changes by several orders of magnitude during the MIT. An MIT-based memristor remains in the HRS when the switching layer is an insulator. Upon the application of external stimulation to the device, the switching layer transitions into a metal state, thereby switching the device to the LRS. Upon removing the applied stimulation, the switching layer returns to the insulating state, causing the device to revert to the HRS. The MIT phenomenon may be induced by external factors, such as electric fields, temperature, light, pressure, and chemical doping. Among these external influences, recent research has focused on electric-field-triggered MIT in memristors, as the ability to control the bias facilitates more convenient conductance programming. Although the exact mechanism underlying the MIT process remains undefined, two primary theoretical explanations for the phase transition are currently under debate: lattice–electron interactions, known as the Peierls phase transition, and electron–electron correlation, referred to as the Mott phase transition.

The Peierls phase transition occurs when the energy required to open the bandgap exceeds the elasticity of the lattice strain. This reduction in the energy of the entire electronic lattice system caused the system to shift from a conductor to an insulator. For example, in VO₂, the V atoms change from their original linear isometric form to a V–V zigzag configuration during the transition from the tetragonal to the monoclinic phase. This V–V zigzag configuration leads to overlapping V-orbitals and the creation of a bandgap, resulting in the material becoming an insulator.

The Mott phase transition occurs in Mott–Hubbard insulators, where the Coulomb repulsion within the 3d orbitals divides the energy band into upper and lower Hubbard bands. External conditions that alter the bandwidth of these Hubbard bands lead to overlapping of inter-atomic orbitals. The primary external factors driving the Mott transition are temperature and voltage. When a high voltage is applied to Mott–Hubbard insulators, a Joule heating effect occurs, resulting in a temperature-driven Mott transition. Additionally, the voltage can introduce extra carriers, which may alter the carrier density. These effects can lead to Fowler–Nordheim tunneling, Poole–Frenkel emission, and band-to-band tunneling.

Current research has actively explored the utilization of MIT characteristics in neuromorphic devices because they exhibit a rapid MIT process on the nanosecond scale owing to atomic rearrangement. This feature renders MIT-based memristors suitable for high-frequency spike generators. Compared to other alternative mechanisms, MIT-based memristors display lower off-state resistance and faster discharge speeds. However, a notable consideration is the requirement for substantial operating currents in the milliampere (mA) range to attain the phase-transition temperature, leading to higher energy consumption.

2.4. Electron trapping/de-trapping-based memristor

Electron trapping and de-trapping in the dielectric layer or near the electrode–dielectric interface leads to changes in the resistance.^58–65 Specifically, sudden resistance shifts occurring beyond a certain V_th owing to electron trapping and de-trapping processes are typically associated with bulk trap-related space-charge-limited conduction (SCLC).^66,67 This carrier transport mechanism assumes that the electrode and dielectric layer interface form an Ohmic contact. At low voltages, the current through the film is primarily driven by the drift of thermally generated carriers in the dielectric layer, according to Ohm's law:
Here, J represents the current density, n is the carrier density in the film, e is the elementary charge, μ is the carrier mobility, V is the external bias, and s is the film thickness. Therefore, the current–voltage relationship follows Ohm's law. At high voltages (above the transition voltage), the carrier density injected from the cathode exceeds the equilibrium carrier density, forming a space charge. Accordingly, carrier transport is affected by both the drift and diffusion processes. Mott and Gurney's law explains the corresponding voltage–current relationship in this regime as:
where k denotes the dielectric constant of the layer. The current increases more rapidly with increasing voltage. Conversely, traps capture the injected electrons in materials with bulk trap sites. Thus, the trapped charge density must be considered. Mott and Gurney's law is slightly modified as follows:
where θ is the ratio of free carriers to trapped charges. This trap-limited SCLC regime is readily switched to the trap-free SCLC regime above the trap-free level voltage (V_TFL) because the carriers fully occupy the traps with increasing voltage. Therefore, an abrupt current jump occurs at V_TFL, resulting in the threshold resistance switching from the off to the on state. Conversely, as the voltage decreases, the carrier injection rate decreases, and unoccupied traps occur because of the escape of carriers from the traps, leading to switching from the on to the off state. This threshold-type resistance switching occurs for both bias polarities because the phenomenon originates from the bulk effect rather than the interfacial effect. In practical cases, although the interface between the electrode and dielectric layer often does not form an ideal ohmic contact,^62–64 the basic principle is similar. In addition, this threshold resistance-switching mechanism is more likely to be uniform over the entire electrode area, although it can sometimes exhibit local conduction behavior.⁶¹ In short, the transition between trap-limited and trap-free SCLC at V_TFL is responsible for the volatile TS based on electron trapping and de-trapping.

2.5. Electrical performance comparison

The preceding subsections have discussed the diverse switching mechanisms of volatile memristors, each exhibiting distinct performance characteristics. Fig. 2 illustrates the DC current–voltage (IV) curves for each mechanism. Given the pivotal role of volatile memristors in neuromorphic computing, understanding these performance indicators is crucial for selecting the appropriate mechanism before proceeding with a detailed implementation.

Fig. 2 Schematic illustrations of the switching mechanisms (top) and IV curves (bottom) of the volatile memristors. (a) Metal-cation-based memristors. (b) OTS-based memristors. (c) MIT-based memristors. (d) Electron trapping/de-trapping-based memristors.

Metal-cation-based memristors have a remarkably low off-current level in the HRS, yielding a substantial on/off current ratio. In addition, they feature an exceptionally low V_th, making them ideal for applications requiring high selectivity and a narrow operating voltage range. However, their switching speed may lag behind other mechanisms owing to the formation of conductive filaments, leading to endurance degradation as the defects penetrate the device interior. In addition, the nanometer-scale diameter of the conductive filament imposes constraints on the maximum allowable current, raising concerns about the fracture risk due to Joule heating. These considerations are pivotal for constructing a neuromorphic system. Nonetheless, the unpredictable dynamics of conductive filament formation can be harnessed in hardware security applications or probabilistic computing, in which memristors serve as sources of physical entropy.

OTS-based memristors exhibit a relatively low V_th and an appropriate V_hold level, making them suitable for selection devices, artificial receptors, and neuron implementations. Moreover, they offer excellent switching variability and speed, with early integration attempts in memory cells. Their high maximum permissible current widens their applicability. However, complex compositional engineering of chalcogenide materials presents a challenge. Moreover, significant voids and defects in the switching layer can result in a less rigid structure, inducing learning phenomena in high-aspect-ratio stacked structures. Operational interference owing to the heat generated during the transition between the amorphous and crystalline phases should also be considered.

MIT-based memristors typically feature high V_th and V_hold, accompanied by a relatively high off-current level, which may not be suitable for low-power operations or applications requiring a large on/off ratio. Nonetheless, their excellent switching variability facilitates reliable signal generation, which is particularly advantageous for implementing artificial neurons and robust signal processing, such as spike generation and spatiotemporal operations in neuromorphic computing. Moreover, their excellent endurance and nanosecond-scale high-speed switching offer significant potential for a wide range of applications.

Furthermore, electron trapping/de-trapping based memristors, which are not as prevalent in neuromorphic computing as ion-motion-mediated memristors, offer less destructive switching behavior but a relatively slow switching speed owing to the time delay for trap filling. Furthermore, their compatibility with CMOS-compatible materials suggests their promising applicability, albeit requiring further research and development. However, careful adjustment of the compliance current is necessary for TS operation, and there are limitations to non-volatile switching when operating at high currents.

Table 1 provides a summary of the electrical performance of volatile memristors by mechanism, and based on the characteristics of these mechanisms, various examples of neuromorphic computing implementations are detailed in Section 3:

Table 1 Summary of the electrical performance of volatile memristors by mechanism

Mechanism	Structure	Applications	V th	V hold	Latency	Endurance	Ref.
NDR: negative differential resistance.
Metal cation-based	Pt/Ag/SiO2 NRs/Ag/Pt	Receptor	−0.72 V/0.78 V	—	20 μs	100 cycles	29
	Pt/SiOx:Ag/Ag/Pt	Receptor	±0.25 V	±0.15 V	—	—	68
	Ag/ZrOx/Pt	Receptor/neuron	0.4 V	0.02 V	—	220 cycles	69
	Pt/Ag/SiO2 NRs/Ag/Pt (UVO treated)	Neuron	−0.467 V/0.465 V	−0.03 V	0.64 μs	500 cycles	70
	Pt/Ag/Ag:SiO2/Pt	TRNG	0.5 V	0.3 V	50–300 μs	10^7 cycles	71
	Cu0.1Te0.9/HfO2/Pt	P-bit	1.5–2.5 V	—	85 ps	>10^6 cycles	72
OTS-based	Ag/PMMA/Bi2Se3/ITO	Receptor	0.86 V	0.2 V	—	100 cycles	73
	W/GeTex/W	TRNG	1.3 V	0.35 V	100 ns	10^9 cycles	74
	Pt/CuS/GeSe/Pt	P-bit	0.3–0.7 V	0–0.2 V	200 ns	1.8 × 10^6 cycles	75
	W/GeTe9/Ge/GeTe9/SiO2/W	Selector	1.28–1.44 V	1–1.15 V	8.2 ns	1.3 × 10^10 cycles	28
	W/BTeN/W	Selector	∼1.15 V	0.9 V	—	>10^11 cycles	76
	W/N-doped SiTe/W	Neuron	1.12 V	0.69 V	∼15 ns	10^7 cycles	77
MIT-based	Pt/VO2/Pt	Receptor	0.6 V	0.22 V	—	>10^8 cycles	78
	Au/Ti/VO2/Ti/Au	Receptor	1.6 V	0.95 V	120 ns	10^6 cycles	79
	Au/VO2/c-Al2O3	Neuron	±1.33 V	±0.87 V	200 ns	1000 cycles	80
	Pt/VO2/Pt	Neuron	1.2 V	0.4 V	18 μs	10^7 cycles	81
	Pt/NbOx/Pt	Neuron	±2.2 V (NDR)	±1.8 V (NDR)	60 ns	10^5 cycles	82
	Pt/Ti/NbOx/Pt	TRNG	1 V (NDR)	0.8 V (NDR)	15–21.5 μs	4 × 10^8 cycles	83
	TiN/NbOx/TiN	P-bit	0.9 V (NDR)	0.6 V (NDR)	—	—	84
Electron trapping/de-trapping-based	TiN/CeOx/ZnO/ITO/mica	Optoelectronic	6.5 V	—	—	—	85
	Pt/HfO2/TiN	TRNG	5 V	—	30–80 μs	—	63

---

3. Volatile memristor-based elements for neuromorphic computing

3.1. Implementation of an access device within a crossbar array structure

3.1.1. Sneak-path current issue. The advantages of resistive switching devices lie in their simple structure, comprising a two-terminal bottom electrode-switching layer-top electrode configuration, and their reduced dependency on the device area, which is particularly evident in filamentary switching devices. These features enable the implementation of dense memory blocks with a cell footprint of 4F².⁸⁶ The row and column transmission lines are arranged perpendicular to each other, with memory cells formed at each crossing point, thus forming a crossbar array structure. To verify the resistance state, representing the data of resistive switching memory, a read voltage is applied to the selected row while grounding the selected column, as shown in Fig. 3(a). Red arrows indicate the desired current path for the selected memory cell to be read. However, undesired current, known as “sneak-path current,” can flow through the parallel resistor circuit depicted by the dotted arrows. For example, considering three major sneak-paths, as shown in Fig. 3(a), the parallel resistance is R_HRS + 2/3R_LRS, comparable to the high resistance of a single memory cell. The total current is influenced by the sneak-path current and not solely by the selected-path current. This issue is exacerbated by a larger array. Therefore, implementing appropriate operation schemes and access devices is crucial for mitigating sneak-path issues in the crossbar array structure.

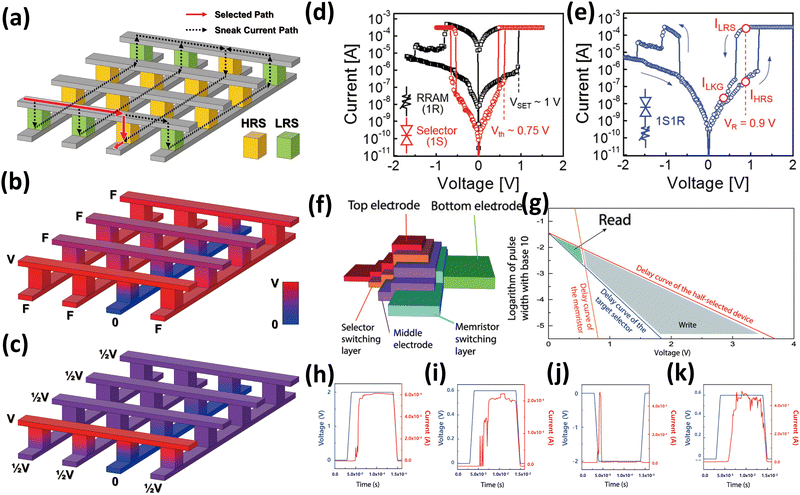Fig. 3 Schematic illustrations of (a) selected and sneak path currents, (b) floating bias scheme, and (c) half-voltage bias scheme. (d) Overlapped IV curve of the selector (red dot) and resistive switching memory (black dot). (e) IV curve of the implemented one-selector-one-resistive switching memory device.⁸⁷ Reproduced with permission from ref. 87. Copyright 2019 John Wiley and Sons. (f) Schematic illustration of a series-connected one-selector-one-resistor memory cell. (g) Time domain examination of the proper region of read operation under a half-voltage scheme. Demonstrated basic (h) set, (i) read for LRS, (j) reset, and (k) read for HRS operations for a one-timing selector-one non-volatile memristor.⁸⁸ Reproduced with permission from ref. 88. Copyright 2021 John Wiley and Sons.

Conversely, the crossbar array structure is advantageous for high-density non-volatile memory and memristive computing, expediting tasks such as vector–matrix multiplication during neural network operation.^20,89,90 The synaptic weight is mapped onto the conductance of the memristors in the crossbar array (G_ij), whereas the input vector for the neuronal input is transformed into a vector of the input voltage on the rows (V_j). Therefore, the output current through the columns (I_i) corresponds to the output vector and the result of the vector–matrix multiplication. To ensure that the sneak-path current does not interfere, all the rows and columns are biased to the desired voltage and grounded during the calculation. However, during the programming of the memristor array, efforts must be made to suppress the sneak-path current issue because the conductance of individual memristors needs verification to confirm that the desired conductance is programmed correctly (neglecting the voltage drop on the serial parasitic resistance).

3.1.2. Operation schemes and corresponding access device. The individual memory cells of the array are accessed randomly by applying a bias and grounding on the selected row and column transmission lines. Bias conditions for the unselected lines determine the array operating scheme. The basic approach, called a floating scheme, is illustrated in Fig. 3(b). This method involves leaving the unselected line floating and minimizing peripheral circuit overhead and total power consumption. However, the floating scheme is vulnerable to sneak-path currents during the reading operations. Moreover, unselected cells may experience uncontrolled voltage drops, potentially disrupting the data for these cells. For example, the unselected cells in the first row and third column can undergo a significant voltage drop comparable to that of the selected cell. Consequently, the data of the unselected cell can be disturbed during the programming of the selected cell. To address this issue, a half-voltage scheme has been proposed to mitigate programming disturbances.⁹¹ The unselected rows and columns are biased to half the voltage on the selected row, as shown in Fig. 3(c). This setup ensures a zero-voltage drop across the unselected cells, thus minimizing data disturbances. Conversely, half-selected cells require a sufficiently high nonlinearity in the programming voltage. Therefore, the memory cell should exhibit sufficiently high nonlinearity in the programming voltage. Furthermore, the one-third-voltage scheme minimizes programming disturbance on the half-selected cell by adjusting bias voltages.⁹¹ With this arrangement, the voltage drop across the half-selected and unselected cells becomes 1/3 V and −1/3 V, respectively, resulting in less programming disturbances. By contrast, a nonlinear programming voltage is unnecessary when the nonlinear selector is serially connected to a non-volatile memristor.

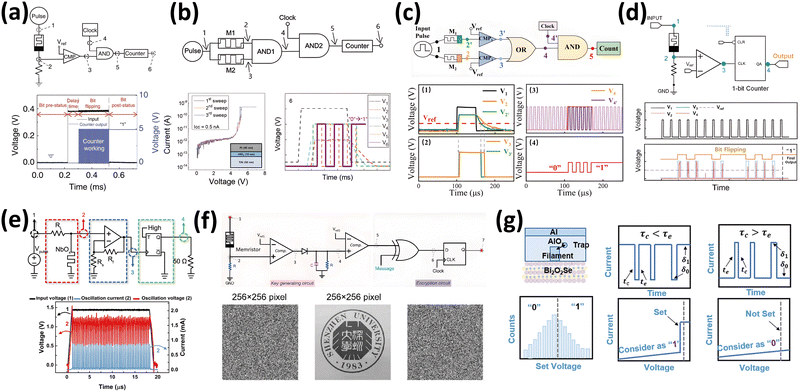
The selection device enables selective access to the target cell, preventing sneak-path currents and programming disturbance on unselected cells. Integrating a transistor with a memory cell is a well-established and effective method for implementing random access, akin to the one-transistor-one-capacitor cell structure in dynamic random access memory (DRAM).^92–95 However, the transistor requires additional transmission lines to control the gate, thereby increasing the design and circuit complexity. Consequently, two-terminal selection devices in series with resistive switching memory or non-volatile memristors are preferred for dense crossbar arrays. The diode suppresses the sneak-path current by regulating the reverse current because the sneak-path current always involves the reverse path. However, the suppressed reverse current limits the device type of the resistive switching memory or memristor to a unipolar device. Bidirectional two-terminal selectors should be employed in crossbar arrays to fully leverage the versatile resistive switching memory and memristors. Volatile threshold-switching memristors exhibit suitable behavior as bidirectional selectors.^93–103 As previously discussed, the resistance of a volatile memristor abruptly drops beyond V_th, demonstrating sufficiently high nonlinearity.

The specific operational principle of a volatile memristor as a selector is illustrated using examples. Yoo et al. demonstrated a threshold-switching selector based on OTS from B-Te materials.⁸⁷ As depicted in Fig. 3(d), the selector (red dot) exhibited a lower off-state current (V < V_th) compared to resistive switching memory (black dot) and a sufficiently high on-state current reaching the compliance current (V > V_th). To ensure that the memory state remains undisturbed, most of the voltage must drop across the selector in series, necessitating the off-resistance of the selector to be greater than that of the resistive switching memory. Conversely, the on-state resistance of the selector should be lower than that of the memory to allow a sufficiently high current to flow through the memory, thereby inducing a set or reset operation. The DC-IV curve of a series-connected one-selector-one-resistor memory cell is shown in Fig. 3(e), and an overall schematic is depicted in Fig. 3(f). The hysteresis in the low voltage range of the memory cell disappears because the I–V behavior is dominated by the selector before it is turned on. Once the selector is turned on, the memory can switch from a high-resistance state to a low-resistance state and vice versa. The read voltage, V_R, is slightly higher than V_th because the memory state cannot be verified until the selector is turned on. Consequently, V_th should not be excessively high, or a higher read voltage would be required. Conversely, a low V_th results in a loss of selectivity. Based on these behavioral characteristics, it is possible to determine the appropriate electrical characteristics to act as selectors: (1) high off-state resistance, (2) low on-state resistance, and (3) moderate V_th. Moreover, other characteristics are required for reliable memory-cell operation, including fast switching, high endurance, and low variation. Considering the high off-state resistance, the metal-cation-based memristor is the most promising among other volatile memristors. Except for the electron-trapping/de-trapping-based memristors, all volatile memristors demonstrate sufficiently low on-state resistance owing to their localized conduction paths. Localized switching events in volatile memristors trigger feedback effects, resulting in relatively fast switching. For instance, the switching speed of metal-cation-based memristors correlates strongly with ion diffusivity. As the current density increases with the applied voltage, heat is generated at the local conduction path, enhancing the ion diffusivity. Consequently, enhanced ion motion accelerates filament growth, and prolonged filaments decrease resistance, leading to a higher current flow and more heat generation. MIT-based memristors generally exhibit superior endurance compared to other memristors; however, the endurance of other memristors can also be improved through material engineering or program schemes.⁹⁶ Unfortunately, from a variation perspective, most volatile threshold-switching memristors demonstrate poor variation characteristics. Nevertheless, various approaches have been proposed to mitigate this variation.^103,104 Furthermore, the stochastic switching property offers another application opportunity, which will be discussed later.

Rao et al. proposed an alternative approach for cell selection based on the time domain rather than the voltage domain.⁸⁸ The switching speed, or delay time, of memristors strongly depends on the bias voltage, as it affects the particular current density or injected carrier density that triggers the switching. For instance, if the V_th of the selector is 0.5 V, a DC 2 V target bias will not operate the crossbar array with the half-voltage scheme. This is because the half-selected cells would undergo a 1 V bias, which is higher than V_th, resulting in program disturbance or additional current through the half-selected cells. In contrast, the delay time of the selected cell is less than 1% of that for the half-selected cell, as shown in Fig. 3(g). When the pulse duration of a 2 V amplitude pulse is shorter than 300 μs, the selector on the target cell successfully turns on, while that on the half-selected cell does not. Therefore, the half-voltage scheme is valid for an appropriate pulse width-voltage space. The read-and-write pulse conditions can be determined by considering the transient dynamics of the selector and the non-volatile memristor. Fig. 3(h)–(k) illustrate the basic operations for a one-timing selector (Pt/Ag-doped SiO₂/Pt)-one non-volatile memristor (Pt/HfO₂/Ta/Pt): (h) set operation, (i) read for LRS, (j) reset operation, and (k) read for HRS. Although metal-cation-based memristors were used as selectors, the timing selection approach also applies to other threshold-switching memristors.

3.2. Implementation of an artificial receptor

3.2.1. Working principle of sensory signal detection. Biological receptors play crucial roles in enabling humans to perceive external stimuli and respond to potentially hazardous situations. These receptors convert external stimuli into biological electrical signals, which are interpreted by the nervous system. They are distributed throughout the body, particularly in the epidermal, dermal, and hypodermal skin layers.

Sensory receptors can be classified into three categories: mechanoreceptors, thermoreceptors, and nociceptors. Mechanoreceptors detect mechanical stimuli, such as pressure and vibration, with some adapting quickly and others adapting slowly, based on their location and function. For instance, those responsible for detecting spatial deformation and sustained pressure display slow adaptation, whereas those responsible for detecting temporal changes in skin deformation exhibit fast adaption.¹⁰⁵ Thermoreceptors sense temperature changes in response to external stimuli, whether the change is a cooling or warming effect. Nociceptors specialize in detecting external stimuli that can inflict permanent damage to the human body. They are known as non-adaptive pain receptors because they do not adapt to noxious or painful stimuli, a mechanism designed to prevent further damage.

Receptors serve as the cornerstone of the sensory nervous system, making the development of artificial receptors crucial for creating and implementing artificial sensory systems.

Emulating sensory receptors involves integrating features such as threshold, relaxation, sensitivity, adaptation, and sensitization. Threshold behavior renders the receptor unresponsive to stimuli below a certain threshold but highly responsive to stimuli surpassing that threshold. Discriminating between different stimulus levels is crucial for accurate sensory perception. After removing stimuli that surpass the threshold, the receptors enter a relaxation period during which they gradually deactivate. Due to their volatile nature, receptors deactivate when external stimuli cease. Sensitivity refers to the manner in which a response varies with external stimuli. It directly affects receptor efficiency, with low sensitivity diminishing the overall effectiveness of the sensory system by reacting similarly to innocuous and noxious stimuli. Adaptation behavior refers to the phenomenon wherein the signal of the receptor diminishes with the repeated application of innocuous stimuli. Initially, receptors respond to innocuous stimuli surpassing the threshold value; however, over time, their sensitivity decreases until they fully adapt to the stimuli and cease to emit signals. Similar to sensitivity, adaptation enhances the receptor efficiency by disregarding repetitive innocuous stimuli. This sensitization leads to hypersensitive receptor reactions due to damage or injury, which are typically observed in maladaptive receptors or nociceptors. There are two types of hypersensitivity reactions, allodynia and hyperalgesia. Allodynia occurs when signals are emitted in response to external stimuli below a threshold value, whereas hyperalgesia involves stronger signals than usual in response to stimuli that surpass a threshold value. Despite the advantages of adapting to external stimuli, sensitization enables the body to react promptly to harmful stimuli, thereby preventing further injury.

Volatile switching memristors effectively emulate the characteristics of sensory receptors. Their relaxation properties, are key features that allow receptors to revert to an inactive state after activation, which is crucial for responding to new stimuli. Moreover, the intrinsic threshold behavior of volatile switching memristors closely resembles that of biological receptors. Numerous studies have investigated adaptive and maladaptive features exhibited by volatile memristors. The following subsection discusses recent research on adaptive receptors and sensitized nociceptors.

3.2.2. Adaptation & maladaptation. As highlighted earlier, the adaptation and maladaptation features observed in sensory receptors play a crucial role in protecting humans from injury caused by noxious stimuli and in optimizing the efficiency of the sensory system. Therefore, mimicking these features in artificial receptors is important for the comprehensive imitation of biological sensory receptors. This subsection presents recent studies that aimed to mimic the adaptation and maladaptation of biological sensory receptors using volatile memristors.

Song et al. utilized metal cation-based volatile memristors to emulate fast, slow, and non-adapting receptors, as depicted in Fig. 4(a).²⁹ By employing Ag as the active material and SiO₂ as the switching layer, the Ag deposition level determined the adaptability of the device. A series of electrical pulses were applied to devices with varying amounts of Ag to assess the adaptation rates of the different devices. Those with only 1 nm of Ag deposited in the active layer exhibited adaptive behavior, wherein their output current pulses ceased after a certain number of pulses. Thin and weakly conductive filaments formed by Ag within the SiO₂ switching layer would ruptured because of Joule heating when high-amplitude voltage pulses were applied. Conversely, memristors featuring 3 nm of Ag deposited in the active layer demonstrated non-adaptive behavior to a series of electrical pulses by sustaining their output currents. Thick and robust conductive filaments were formed, resisting self-rupture even under high-amplitude voltage pulses, thus rendering the device non-adaptive. Rapid, slow, and maladaptive receptors were successfully simulated using 1 nm, 2 nm, and 3 nm Ag as the active layer. Using these devices, Song et al. constructed an artificial thermoreceptor. They connected rapid, slow, and maladaptive receptors to a thermoelectric module, as shown in Fig. 4(b), designated as Ch. 2, Ch. 3, and Ch. 4, respectively. Temperature settings of 40 °C, 70 °C, and 90 °C represented innocuous, noxious, and very noxious temperatures, respectively. Upon application of a 40 °C temperature stimulus, Ch. 2 exhibited a fast-adapting behavior, whereas Ch. 3 demonstrated a slow-adapting behavior. Ch. 4 did not respond because of the voltage distribution to the series-connected resistors. At 70 °C, Ch. 2 and Ch. 3 displayed a fast-adapting behavior induced by Joule heating, while Ch.4 maintained output currents owing to the robust conductive filaments. At 90 °C, only Ch. 4 exhibited a response by generating output currents. This artificial thermoreceptive system exhibited a selective response to a specific temperature range. Only the adaptive receptor responded and adapted to innocuous thermal stimuli. In contrast, when a noxious temperature was applied, only the maladaptive receptor responded and continuously emitted signals without interruption.

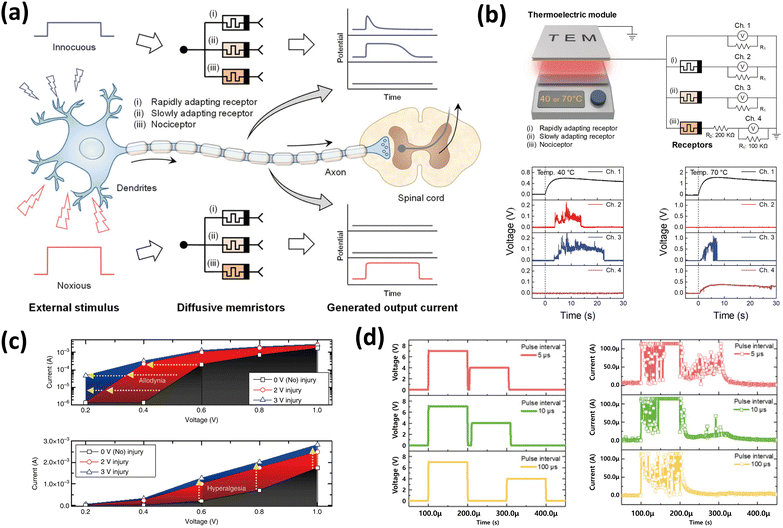Fig. 4 (a) Schematic illustration of the artificial receptors based on a memristor showing adapting and maladapting behavior under different stimuli. (b) Schematic diagram of the artificial thermoreceptor: (top) the voltage generated by different channels under 40 °C (bottom-left) and 70 °C (bottom-right) temperatures²⁹ Reproduced with permission from ref. 29. Copyright 2021 John Wiley and Sons. (c) Corresponding output currents: allodynia (top) and hyperalgesia (bottom) behaviors.⁶⁸ Reproduced with permission from ref. 68. Copyright 2018 Springer Nature. (d) The input voltages and the output current responses of 7 V and 4 V pulses with intervals of 5, 10, and 100 μs.⁶⁹ Reproduced with permission from ref. 69. Copyright 2022 John Wiley and Sons.

Yoon et al. employed a diffusive memristor to fabricate a maladaptive receptor, also referred to as a nociceptor.⁶⁸ This device comprises a 1 nm thick Ag active layer serving as a reservoir for Ag atoms and an Ag-doped SiO_x switching layer. As the essential characteristics of the nociceptor include ‘threshold,’ ‘no adaptation,’ and ‘relaxation,’ the device was subjected to electrical pulses of varying amplitudes, widths, and numbers. To examine the threshold features, a single electrical pulse with a width of 1 ms was applied at different amplitudes. The device exhibited threshold-switching behavior by transitioning to the LRS, or ON state, at 0.6 V. Testing different pulse widths revealed that a pulse width of at least 1 ms was required to switch the device to the ON state when a pulse with a 0.6 V amplitude was applied. For the ‘no adaptation’ feature, the device underwent multiple 100 μs pulse trains at amplitudes of 0.6 V, 0.8 V, and 1.0 V. Regardless of the amplitude, the device maintained its current level without degradation or inclination, indicating its ability to manifest maladaptation. The time required to switch the device to the ON state decreased as the amplitude increased. Finally, the ‘relaxation’ feature was tested by applying sub-V_th pulses (0.4 V) following the noxious voltage (0.6 V) at intervals of 100 μs, 1 ms, and 10 ms. A 10 ms interval proved sufficient for the device to relax completely, rendering it unresponsive to sub-V_th. However, with intervals of 100 μs and 1 ms, the device was still in the relaxation process, causing it to react to sub-V_th. This phenomenon is significant for nociceptors because the heightened sensitivity following a noxious voltage protects against further damage.

As discussed in the previous subsection, sensitization is crucial for safeguarding an injured area against further harm, as it manifests as hyperalgesia and allodynia. Yoon et al. illustrated the sensitization feature of the device by initially ‘injuring’ it with noxious voltage pulses of 2 and 3 V, each with a 1 ms width. Subsequently, the device underwent a series of pulses ranging from 0.2 V to 1.0 V with a 1 ms width. As shown in Fig. 4(c), the device exhibited allodynia upon transitioning to the ON state at sub-V_ths. The V_th shifted to a lower level, with a more pronounced shift observed after a 3 V ‘injury’ than a 2 V ‘injury.’ Additionally, the device demonstrated hyperalgesia behavior, manifesting higher output current at the same input voltage when the device was ‘injured.’ These sensitization behaviors stem from the residual conductive filaments that persist in the switching layer. These electroformed residuals play a bridging role in the leakage current, thereby enhancing the sensitivity of the memristor.

Yang et al. replicated a maladaptive receptor by using a ZrO_x-based volatile TS memristor. The device comprised an Ag active layer and a ZrO_x switching layer, demonstrating a switching mechanism typical of a metal cation-based memristor.⁶⁹ Conductive Ag filaments were formed within the ZrO_x switching layer. The device as assessed by applying pulse trains with varying amplitudes, widths, and numbers to validate the fundamental features of the nociceptive receptors, as shown in Fig. 4(d). Threshold behavior was identified by applying pulse trains with different amplitudes and widths, revealing that a 6 V pulse with a duration of 100 μs served as the threshold value for this device. The relaxation feature was confirmed by administering a sub-V_th (4 V) after a noxious, above-V_th (7 V), with 5, 10, and 100 μs intervals. The results indicated that a 100 μs interval was necessary for complete relaxation. Otherwise, shorter intervals resulted in a reaction to the sub-V_th owing to incomplete relaxation. Maladaptation was tested by applying prolonged successive stimuli to the device. With each application of pulse trains of a width of 50 μs at amplitudes of 3.5 V, 4 V, and 4.5 V, the device maintained its output current without exhibiting degradation. Through these experiments, Yang et al. effectively replicated the biological maladaptive receptor, encompassing all essential features required for full functionality.

3.2.3. External stimulus-mediated receptors. The five primary external stimuli are visual, olfactory, gustatory, auditory, and tactile stimuli. Each sensory receptor operates within an intricate and distinct system, posing a challenge for emulation using memristor-based artificial receptors.^106,107 Significant efforts have been made to replicate these sensory receptors. Various approaches have been used to engineer artificial receptors. In one method, the sensor modules are connected to memristors.^108–112 The sensor modules detect external stimuli and translate them into electrical signals. A memristor responds to a threshold, adaptation, or sensitization reaction based on the received electrical signals. Alternatively, some studies have constructed artificial receptors using a standalone memristor-based device without sensor modules attached. In this scenario, the memristor simultaneously senses and processes the external stimuli as electrical signals. Fabricated with materials that can detect stimuli such as pressure, temperature, and light, memristors have become a key player in this context. This subsection explores studies that have focused explicitly on single-device artificial receptors.

Zhou et al. fabricated an optoelectronic memristor based on CeO_x/ZnO featuring a two-terminal structure composed of TiN/CeO_x/ZnO/ITO/mica, as shown in Fig. 5(a).⁸⁵ The device is responsive to visible light at a wavelength of 405 nm. Due to electron trapping and de-trapping at the CeO_x/ZnO interface, the barrier height was modulated, leading to photoelectric characteristics. Under the different light intensity stimulations of 0, 1.4, 2.8, and 5.5 μW cm⁻², the device can switch from HRS to LRS when the light is switched off just before measuring begins. However, when the device was measured under continuous lighting, it failed to return to the HRS owing to the lingering vacancies resulting from the generation of electron–hole pairs. This distinctive property enables optoelectronic memristors to respond to light pulses without significant degradation of their output current in dark environments. The device demonstrates volatile and non-volatile switching characteristics under different environmental conditions, allowing it to recognize and process light stimuli. It also possesses memory features, as shown in Fig. 5(b).

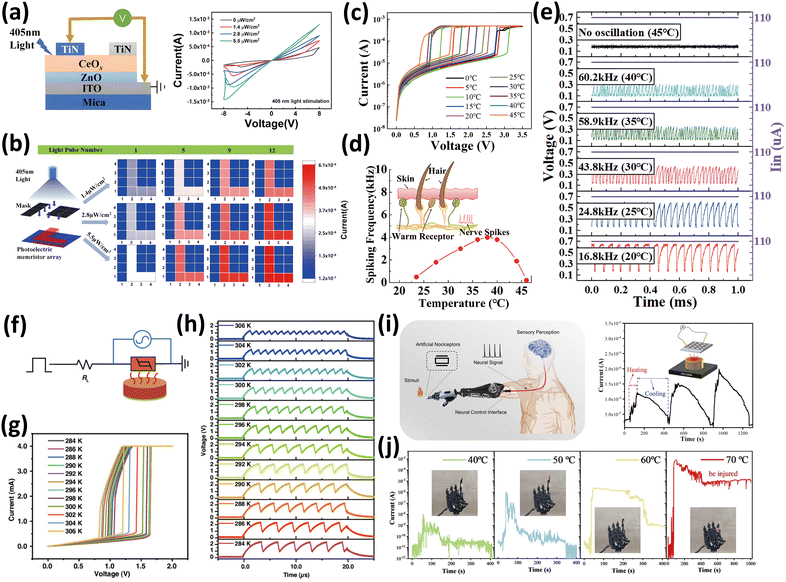Fig. 5 (a) Schematic diagram of the optoelectronic memristor composed of TiN/CeO_x/ZnO/ITO/mica. (b) The current responses of the photoelectric memristors under different light intensities and numbers of light pulses.⁸⁵ Reproduced with permission from ref. 85. Copyright 2021 AIP Publishing. (c) IV curves of the VO₂ Mott memristor under different temperatures. (d) Spiking frequency in response to different temperatures, the inset is the schematic illustration of the warm receptors under the skin. (e) Output voltage spikes of the VO₂ memristor under different temperatures.⁷⁸ Reproduced with permission from ref. 78. Copyright 2022 John Wiley and Sons. (f) Schematic diagram of the circuit of the artificial warm receptor. (g) IV curves of the VO₂ volatile memristors under different temperatures. (h) Self-oscillating spike frequencies as the temperature increased from 284 to 306 K.⁷⁹ Reproduced with permission from ref. 79. Copyright 2022 John Wiley and Sons. (i) Schematic illustration of the artificial electronic receptor implementing a thermal nociceptor (left), Output current of the device during heating and cooling process (right). (j) The neural reflex movement at different temperatures.⁷³ Reproduced with permission from ref. 73. Copyright 2023 Elsevier.

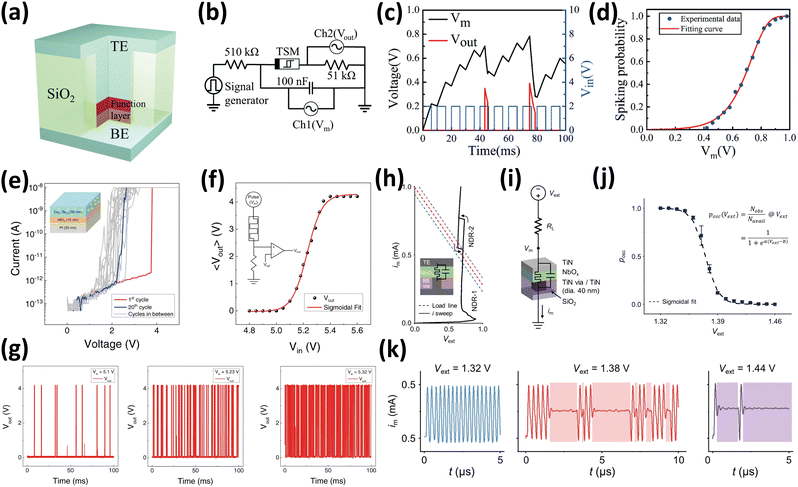
Many researchers have studied the use of VO₂ as a warm receptor, owing to its MIT characteristics at low temperatures. Han et al. developed an artificial warm receptor employing VO₂-based Mott memristors.⁷⁸ The device exhibits a Pt/VO₂/Pt structure. As VO₂ is well known for its low insulator-to-metal transition temperature of 68 °C, it plays a pivotal role in these warm receptors. The stand-alone functionality of the VO₂ memristor as a thermal sensor was demonstrated, showing a decrease in V_th with increasing temperature, as shown in Fig. 5(c), enabling it to sense and respond effectively to temperature fluctuations. Furthermore, the VO₂ memristor exhibits oscillations solely through a driven current source, which is attributed to parasitic capacitance. This unique characteristic allows the device to respond to temperature stimuli with spiked outputs similar to those of actual warm receptors, as shown in Fig. 5(d). The Mott memristor demonstrated an escalating spiking frequency up to 40 °C, beyond which the device ceased oscillation, indicating exposure to noxious temperatures as shown in Fig. 5(e). The primary focus of the study is the development of a single-device artificial thermoreceptor. Han et al. successfully replicated human skin properties by crafting a device on a flexible Kapton polyimide (PI) substrate and successfully retained the functionality of the device after 1000 bending cycles. Similarly, Duan et al. engineered a warm receptor using a VO₂ Mott memristor, as shown in Fig. 5(f).⁷⁹ They successfully demonstrated varying V_th and V_hold values at temperatures ranging from 284 to 306 K, as shown in Fig. 5(g). Taking advantage of the self-oscillating nature of VO₂ arising from parasitic capacitance, the device exhibited a heightened frequency of output spikes, escalating from 0.3 to 0.8 MHz as the temperature increased within the 284 K to 306 K range, as shown in Fig. 5(h). Therefore, VO₂-based memristors can sense and respond to external temperature stimuli when used as artificial warm receptors.

Materials other than VO₂ have also been investigated to imitate thermal sensory receptors. Shi et al. presented an artificial thermal nociceptor system utilizing bismuth selenide (Bi₂Se₃), a thermoelectric film designed for in situ temperature sensing.⁷³ The device was fabricated using Ag/polymethyl methacrylate (PMMA)/Bi₂Se₃/ITO. Through temperature-dependent experiments, as shown in Fig. 5(i), and leveraging the impressive thermoelectric conversion capabilities of Bi₂Se₃, the study successfully replicated the neural responses of human heat receptors to elevated temperatures. In the HRS or normal condition, the device underwent heating from 40 °C to 70 °C in 10 °C increments. During the application of 40 °C and 50 °C thermal stimuli, the device exhibited an increase in output current throughout the heating period, followed by a decrease as the cooling phase started. At 60 °C, the device transitioned to an intermediate resistive state after the heating phase, subsequently switching to a slightly lower resistance state than the initial HRS state, indicating a minor level of damage. Ultimately, when subjected to 70 °C, the device shifted to the LRS and failed to recover after the heating process ended, indicating that the device was severely damaged. This thermal sensing capability relies on the Seebeck voltage, where charges accumulate at the two ends owing to the temperature difference, forming a self-generated electric field inside the material that induces carrier drift. As shown in Fig. 5(j), the system effectively simulated nerve reflex actions in response to thermal stimulation when integrated with a robotic manipulator.

3.3. Implementation of an artificial neuron

Biological neurons, the foundational units of the human nervous system, integrate stimuli transmitted through synapses and generate spike-like signals when the received stimuli exceed a certain threshold. Volatile memristors, on the other hand, are well suited for artificial neuron implementation because of their characteristics of resistive switching from the HRS to the LRS when electrical stimuli surpass a threshold. Moreover, they can convert continuous analog signals into spike-like electrical signals without the need for complex conversion circuits such as analog-to-digital converters. This capability positions them as central to implementing neuromorphic computing platforms and bioinspired applications. This section explores techniques that utilize volatile memristors to generate spike-like signals corresponding to the action potentials of biological neurons and their potential applications in various sensory systems.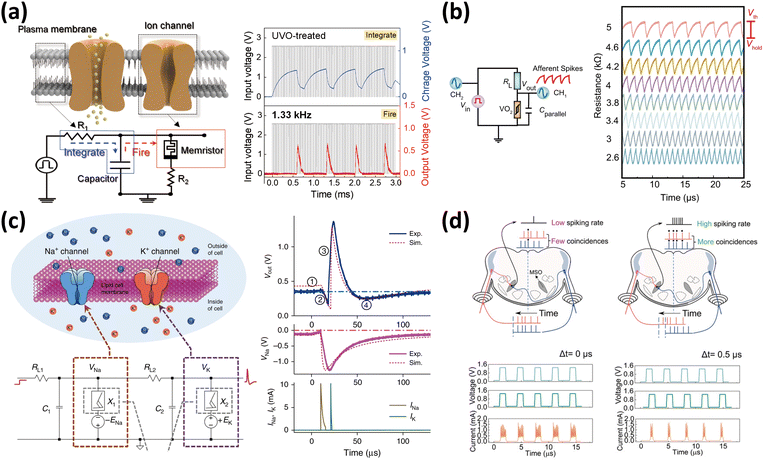

3.3.1. Spike generation and frequency modulation. Action potentials in biological neurons begin with the influx of ions, primarily sodium, through voltage-gated channels upon depolarization of the cell membrane. This influx triggers a rapid increase in membrane potential, known as the depolarization phase. Subsequently, potassium channels open, allowing potassium ions to exit the cell and repolarize the membrane potential. Finally, the cell undergoes a brief hyperpolarization phase before returning to its resting membrane potential. These fluctuations in membrane potential occur owing to the dynamic opening and closing of ion channels in response to voltage changes. To emulate the behavior of biological neurons using memristors, it is crucial to replicate these dynamic changes in the membrane potential and the opening and closing of ion channels. The leaky integrate-and-fire (LIF) model approximates neuronal behavior by integrating incoming signals and firing an action potential when the membrane potential reaches a threshold. It has a relatively simple structure, which makes it widely applicable for volatile memristor-based artificial neuron implementations. Song et al. constructed an LIF circuit incorporating a Ag/SiO₂/Ag layered memristor and successfully generated spike signals, as shown in Fig. 6(a).⁷⁰ When external signals are applied in the form of a voltage, charging occurs through R₁ in the capacitor. The potential of the integrating capacitor corresponds to the membrane potential of biological neurons. When this potential exceeds the threshold, the memristor switches to the LRS, causing the stored charge in the capacitor to flow through the memristor and R₂, producing spike-like signals during firing. As the generation of spike signals in the LIF model relies on the charging and discharging of resistors and capacitors, the firing frequency of such spikes can be adjusted by manipulating the circuit parameters. Yuan et al. constructed an LIF neuron based on memristors with VO₂ as the channel layer and demonstrated a wide-range frequency modulation ranging from tens of hertz to MHz by adjusting the parameters of the resistors and capacitors, as shown in Fig. 6(b).⁸⁰ Notably, they showed that variations between individual devices, known as device-to-device variations, could be mitigated by adding serial resistors, enabling them to form firing frequencies within the same range. This highlights the flexibility of the LIF model in reliably converting external stimuli into spike signals and its suitability for accommodating various stimuli.

Fig. 6 (a) Schematic illustration of a biological neuron alongside its corresponding electrical LIF circuit model (left); the response of the LIF circuit to ongoing input pulses in the UVO-treated device (right).⁷⁰ Reproduced with permission from ref. 70. Copyright 2023 American Chemical Society. (b) Schematic illustration of the LIF neuron circuit based on the VO₂ memristor (left); various output spikes under different series resistances (right).⁸⁰ Reproduced with permission from ref. 80. Copyright 2022 Springer Nature. (c) Schematic illustration of the Na⁺ channel and K⁺ channel in the biological neuron and the corresponding circuit of the two-channel active memristor-based neuron (left); the experimental and simulated action potentials, Na⁺ channel membrane potential, and simulated Na⁺ and K⁺ channel currents (right).⁸¹ Reproduced with permission from ref. 81. Copyright 2018 Springer Nature. (d) Schematic diagram of the sound localization by the oscillation neuron (top); the spike response of the oscillation neuron is due to an identical pulse train with different time differences (bottom).⁸² Reproduced with permission from ref. 82. Copyright 2022 John Wiley and Sons.

However, this LIF neuronal model oversimplifies the complex dynamics of biological neurons. In contrast, the Hodgkin–Huxley (HH) model offers a more detailed representation by considering the dynamics of individual ion channels and their conductivity. Yi et al. introduced a HH neuron comprising opposite DC-biased memristors with VO₂ as the channel layer, along with load resistors and capacitors separately configured for voltage-gated Na⁺ and K⁺ membrane protein ion channels, as shown in Fig. 6(c).⁸¹ This neuron model successfully reproduces signals corresponding to resting, hyperpolarization, depolarization, and the refractory undershoots observed in the action potentials of biological neurons. Furthermore, by simply replacing load resistor R_L1 with capacitor C_in, the model implements a phasically active neuron capable of generating single spikes in response to stable inputs and a tonically active neuron that generates spikes at regular intervals. Moreover, 23 types of known biological neuron spiking behaviors were implemented using three different neuron circuit topologies (tonically active, phasically active with R_L1 replaced by C_in, and mixed-mode neurons with R_L1 and C_in in parallel).

Another important reason for neuron spike generation and frequency modulation is that they enable the spatiotemporal processing of external information. Essentially, spike encoding of signals coming through different channels in the human sensory system functions as a key element in direction selectivity and sound localization. In the case of direction selectivity, the output can be determined based on the order in which the signals reach two volatile memristors that play excitatory and inhibitory roles, as an object moves in the preferred or opposite direction.¹¹³ In the case of sound localization, neurons in the medial superior olive (MSO) detect interaural time differences (ITD) in signals coming through the two ears and adjust their output firing frequency. Zhong et al. implemented this approach using a neuron circuit incorporating memristors with a Pt/NbO_x/Pt structure.⁸² They constructed a system where when two identical synaptic inputs are delivered synchronously (Δt = 0), a high firing frequency occurs, whereas if they are delivered asynchronously (Δt ≠ 0), the firing frequency decreases according to the magnitude of the time difference as shown in Fig. 6(d). This setup validated the spatiotemporal processing capabilities of artificial neurons. These findings indicate that volatile memristors enables the emulation of biological neuronal behavior and are suitable for implementation in neuromorphic computing.

3.3.2. Artificial neuron-based inference system. In neuromorphic computing, the efficient processing of complex data relies on the reliable encoding of external signals into spikes and the accuracy of inference. Therefore, verifying the reliability of spike encoding and the accuracy of inference in systems that transform biological signals or perform spatiotemporal processing is crucial. In addition, the development of inference systems based on these principles is imperative.

Yuan et al. successfully encoded electrocardiogram (ECG) and electroencephalography (EEG) signals without information loss using symmetric volatile switching of VO₂-based memristors, exhibiting highly uniform device characteristics.¹¹⁴ They achieved arrhythmia classification and epileptic seizure detection through learning using long short-term memory-spiking neural networks (LSNN), as shown in Fig. 7(a). The temporal processing capability of artificial neurons included in an LSNN is crucial for the processing and inference of biological signals. To enhance this capability, they incorporated an adaptive component in which the RC discharge operation acted as a primary factor in the LIF neuron, as shown in Fig. 7(b), thus forming an adaptive LIF (ALIF) neuron. Consequently, LSNNs constructed with ALIF neurons demonstrated improved accuracy compared to those constructed with LIF neurons, as shown in Fig. 7(c), indicating the potential for the efficient processing of biological signals. Therefore, the development of sophisticated strategies for collecting spike signals and implementing inference systems is imperative for sensory signal processing. For instance, the human auditory system is complex and encompasses various processes, such as frequency selectivity, phase locking, intensity coding, tonotopy, ITD, and frequency mixing. As the intensity of sound increases, the basilar membrane in the human auditory system vibrates more significantly, stimulating the depolarization of hair cells and subsequently increasing the firing frequency of action potentials. Yu et al. established a coding strategy for sound information using a memristor with a Pd/Nb/NbO_x/Nb/Pd structure by applying a bias corresponding to the near-threshold potential and adding sinusoidal perturbations.¹¹⁵ This allowed for the modulation of the spike firing frequency of artificial neurons depending on the amplitude and frequency of the sinusoidal perturbations and the series resistor composing the artificial neuron, as shown in Fig. 7(d) and (e). Therefore, it is possible to perform spike coding, which was previously confined to frequency, to encompass a greater amount of information, as shown in Fig. 7(f) and (g).

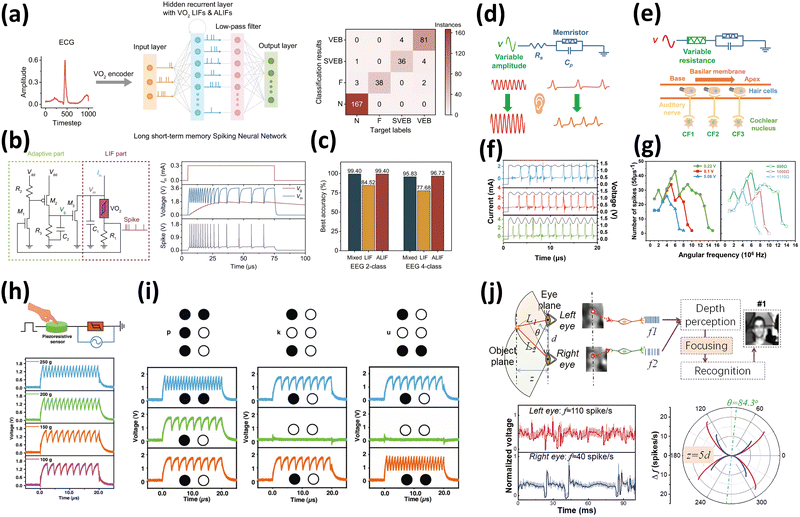Fig. 7 (a) Schematic illustration of the VO₂ memristor-based long short-term memory spiking neural network for ECG heartbeat classification. (b) Circuit diagram of the ALIF neuron. (c) The accuracy comparison of the mixed LSNN, LIF-only LSNN, and the ALIF-only LSNN in ECG 2-class and 4-class.¹¹⁴ Reproduced with permission from ref. 114. Copyright 2023 Springer Nature. (d) Schematic illustration of the intensity coding with the variation of the amplitude. (e) Schematic illustration of the tonotopy with variable resistance. (f) Obtained spikes under different amplitudes. (g) The number of spikes with variable amplitudes and series resistances.¹¹⁵ Reproduced with permission from ref. 115. Copyright 2023 John Wiley and Sons. (h) Schematic diagram of the haptic perception neuron circuit (top); different neuronal responses under different weights (bottom). (i) Output frequencies of Braille characters ‘p’, ‘k’, and ‘u’ using tactile sensing.⁷⁹ Reproduced with permission from ref. 79. Copyright 2022 John Wiley and Sons. (j) Schematic illustration of the binocular vision process in the human brain (top); the firing rate of the left and the right eyes (bottom left); the difference in firing rate between the left and the right eye as a function of the visual angle (bottom right).¹¹⁶ Reproduced with permission from ref. 116. Copyright 2022 John Wiley and Sons.

Inference systems based on artificial neurons demonstrate robustness in integrating spatially correlated sensory stimuli received through multiple channels and in performing recognition and inference based on those stimuli. Duan et al. constructed a haptic perception system by combining a neural circuit containing VO₂-based memristors with a piezoresistive sensor connected in series, as shown in Fig. 7(h).⁷⁹ This system modulates the firing frequency of artificial neurons based on the pressure detected by a sensor. In addition, they combined a neuron circuit with two piezoresistive sensors connected in parallel, setting the firing frequency to 0, 0.4, and 1.1 MHz, depending on the number of sensors detecting pressure. This parallel arrangement of haptic perception units enabled the recognition of braille characters composed of multiple convex patterns, as shown in Fig. 7(i). Similarly, Chen et al. constructed photoelectric artificial neurons symbolizing the two eyes using Ag/TaO_x/ITO structured memristors, as shown in Fig. 7(j), inspired by human visual perception originating from binocular operations.¹¹⁶ The firing frequency of the two neurons is determined by the distance from each eye to the object (L₁ and L₂), the distance between the two eyes (d), and the distance between the eye plane and the object plane (z), which are related to the visual angle (θ). If the object is not precisely centered between the two eyes, the incident light intensity differs, resulting in distinct firing frequencies of the artificial neurons. This disparity forms the basis of depth perception, thereby increasing the accuracy of visual inference.

4. Innovative approach to neuromorphic computing

4.1. Implementation of the physical reservoir

Artificial neural networks have achieved significant success in AI tasks such as classification and recognition.^117,118 Furthermore, recurrent neural networks have been developed to handle temporal data.¹¹⁹ Among these, reservoir computing, a type of recurrent neural network, has gained considerable attention because of its low computing cost during training. The reservoir computing system consists of a reservoir and readout layer, as shown in Fig. 8(a).¹²⁰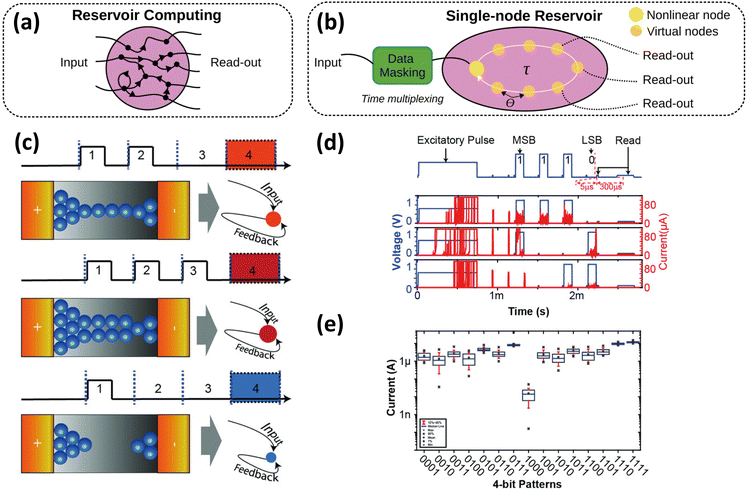

Fig. 8 Schematic illustration of (a) reservoir computing, (b) a single-node reservoir with nonlinear nodes and virtual nodes.¹²⁰ Reproduced with permission from ref. 120. Copyright 2022 IOP Publishing Ltd. (c) Different reservoir states depending on external pulses and time intervals. (d) Pulse applying scheme (top) and examples of output current depends on bit patterns (bottom). (e) Provided multiple reservoir states by applied pulse patterns.¹²¹ Reproduced with permission from ref. 121. Copyright 2019 John Wiley and Sons.

A reservoir is a nonlinear dynamic system with high dimensionality, such as an echo state network or a liquid state machine.^122,123 The readout layer is a fully connected network where the input is the output of the reservoir. The only trainable parameters are the synaptic weights in the readout layer, making the reservoir computable at a low cost. The concept and structure of reservoir computing have evolved from software to physical hardware.^124–127 Among the physical implementations of reservoir computing, memristor-based approaches are advantageous because of their compact structure and fading memory characteristics. The memristor-based physical reservoir maps the input into a high-dimensional space using delayed feedback rather than physically separating the nodes. A single-node reservoir generates multiple virtual nodes through temporal multiplexing, as shown in Fig. 8(b). Therefore, the memristor should exhibit a history-dependent response that represents the reservoir state. The nonlinear dynamic response of the threshold-switching memristors can also be exploited as a physical reservoir. However, the temporal multiplexing of a physical reservoir requires a sufficiently low cycle-to-cycle distribution for reliable operation, which is a drawback of threshold-switching memristors. Consequently, there have been limited studies on this topic.

Midya et al. developed a physical reservoir based on a metal-cation-based threshold-switching memristor.¹²¹ An Ag-doped SiO_x-based memristor exhibited rich dynamics owing to the migration of Ag ions, which is suitable for a physical reservoir. As discussed in Section 2, Ag-ion-based memristors form a conductive filament under bias and dissolve the filament via diffusion. Therefore, alternating the growth and dissolution of the filament using external pulses and time intervals results in different conductance values, which represent the reservoir state of a memristor-based physical reservoir. Fig. 8(c) shows the temporal dynamics of the formation and dissolution of the silver filament. In the top panel, electric pulses are applied in two consecutive time slots, resulting in continuous filament formation and high conductance upon verification. As shown in the middle panel, three consecutive pulses induce a thicker filament and higher conductance. As shown in the bottom panel, an electric pulse applied in the first time slot leads to filament rupture because of diffusion. Fig. 8(d) presents an example of an experiment exploring the effect of waveforms on filament evolution. The excitatory pulse presets the memristor to a similar state before applying a designated bit pattern (waveform). Consequently, different bit patterns generate different conductance values, as shown in Fig. 8(e), implying that the rich dynamics of the memristor provided multiple reservoir states.

4.2. Volatile memristor as a physical entropy source

4.2.1. Inherent stochasticity. The previous section focused on achieving highly reliable switching characteristics in memristors. Although the deterministic characteristics of memristors play a vital role in implementing the precise operations of crossbar arrays and emulating biological neurons, it is essential to explore the potential applications arising from the inherently probabilistic behavior of volatile memristors. Neural cells, which are known for their probabilistic nature, often exhibit complex and stochastic behaviors that can be effectively captured by volatile memristors.

The properties of volatile memristors that spontaneously return to the HRS without a dedicated reset process by removing the external bias make them well suited for exploiting the stochasticity that occurs in each switching cycle. Several studies have reported the origin of the stochastic behavior in volatile memristors, which is attributed to the random growth of the conductive filament driven by ion diffusion dynamics or the different shapes of the amorphous and crystalline regions in each cycle. Leveraging this stochasticity, extracting high-quality random numbers for hardware security applications, and providing noise elements for neuromorphic computing, such as generative adversarial networks, are promising directions.

4.2.2. True random number generator. In recent years, memristor-based true random number generators (TRNGs) have emerged as promising hardware security devices. Unlike pseudorandom number generators (PRNGs), which generate random numbers from a predetermined seed, TRNGs generate random numbers from physical entropy sources. Their inherent unpredictability and true randomness render them invaluable for security applications. Owing to their CMOS compatibility and excellent scalability, memristors have compelling potential as entropy sources for TRNGs.

Jiang et al. introduced a diffusive memristor-based TRNG using a Pt/Ag/Ag:SiO₂/Pt structure, demonstrating successful random number generation without postprocessing (Fig. 9(a)).⁷¹ Woo et al. reduced the required number of transistors in a TRNG system by incorporating Pt/HfO₂/TiN electron trapping/de-trapping-based memristors, showing sustained random number generation even in the presence of a hard breakdown in one of the memristors (Fig. 9(b)).⁶³ Bian et al.'s Au/Ag:I-car/Pt-based TRNG differentiated itself by acquiring randomness from two memristors with distinct relaxation times (Fig. 9(c)).¹²⁸ Lu et al. utilized a metal cation-based device that includes a TiN barrier and trilayer-hafnia to obtain a random number generation sequence through integration-and-fire characteristics (Fig. 9(d)).¹²⁹

Fig. 9 Circuit diagram of a TRNG and its random bit generation mechanism achieved by (a) random delay time of a Pt/Ag/Ag:SiO₂/Pt memristor⁷¹ Reproduced with permission from ref. 71. Copyright 2017 Springer Nature; (b) random delay and relaxation time of two Pt/HfO₂/TiN memristors⁶³ Reproduced with permission from ref. 63. Copyright 2018 John Wiley and Sons; (c) random relaxation time of two Au/Ag:I-car/Pt memristors¹²⁸ Reproduced with permission from ref. 128. Copyright 2023 AIP Publishing; (d) integrate-and-fire characteristic of a trilayer-hafnia-based memristor¹²⁹ Reproduced with permission from ref. 129. Copyright 2022 John Wiley and Sons; (e) self-clocking property of Pt/Ti/NbO_x/Pt memristor.⁸³ Reproduced with permission from ref. 83. Copyright 2021 Springer Nature. (f) Circuit diagram of key generating TRNG and encryption circuit (top); encryption key, image to use as message, and encrypted image (bottom).¹³⁰ Reproduced with permission from ref. 130. Copyright 2023 Elsevier. (g) Schematic illustration of the Al/AlO_x/Bi₂O₂Se device and its random number generation mechanism.¹³¹ Reproduced with permission from ref. 131. Copyright 2022 American Chemical Society.

Despite the diverse materials and circuit configurations used in memristor-based TRNGs, challenges remain in simplifying circuit structures and realizing practical applications for generated random numbers. Kim et al. introduced a TRNG with a Pt/Ti/NbO_x/Pt memristor structure, as shown in Fig. 9(e), eliminating the need for a conventional high-speed clock source by leveraging the self-oscillation signals from the NbO_x-based volatile memristor's negative differential resistance (NDR) characteristics.⁸³ Xing et al. implemented a TRNG using an Ag/phenylalanine dipeptide microrod/Ag memristor and a separate comparator, demonstrating easy encryption through exclusive OR (XOR) operations on the message and encryption key sequences, as shown in Fig. 9(f).¹³⁰ Finally, Liu et al.'s Al/AlO_x/Bi₂O₂Se with a Pd contact-based TRNG utilized a bias-induced set probability for generating binary random numbers, as shown in Fig. 9(g) while also exploring Random Telegraph Noise (RTN) between the ruptured filament and Al electrode for additional entropy.¹³¹ Encryption techniques were proposed by synthesizing the RTN noise using a human voice and securely transmitting the sequence using a key exchange protocol based on binary random numbers.

4.3. Probabilistic computing

Conventional computers with the Von Neumann architecture face a significant limitation when solving combinatorial optimization problems, such as the Traveling Salesman Problem and the Satisfiability Problem. The processing time increases exponentially with a slight increase in the number of variables. Quantum annealing machines have been proposed as efficient problem-solving methods. However, their practical implementation is hindered by the requirements of cryogenic environments. To address these challenges and improve the efficiency, a novel approach called probabilistic computing has been proposed, which exploits the probabilistic behavior of memristors. This innovative approach aims to overcome the limitations of conventional computing architectures and provides a promising method for solving combinatorial optimization problems within a reasonable timeframe. Memristors introduces a probabilistic element that offers potential improvements in computational speed and versatility, making them a compelling alternative for solving complex optimization problems.

4.3.1. p-Bit with bias-dependent output. Probabilistic computing relies on a fundamental unit known as the probabilistic bit (p-bit), which oscillates between zero and one states. The occurrence frequencies of 0 and 1 are determined probabilistically, and each p-bit functions as a binary stochastic neuron. The connections between p-bits are interpreted as synaptic weights that contribute to the overall energy of the network. The energy of the entire network is expressed as a Hamiltonian, with the output of each p-bit and synaptic weights factored into the computation as follows:

where E is the energy of the entire network, p_i is the ith p-bit output, S_ij is the connection weight between ith and jth p-bit, θ_i is the applied bias, I_i is the input for ith p-bit, and I₀ is a scaling factor to keep the input within the range that p-bit produces probabilistic output.

The Hamiltonian formulation resembles the Ising model, which describes the ferromagnetic phases and formulations for stochastic Hopfield networks and Boltzmann machines. Additionally, the frequency of binary output occurrences varies probabilistically depending on the external inputs. The next input is determined by minimizing the overall network energy, which is calculated using the Hamiltonian formulation. An essential aspect of implementing p-bits is the prioritization of features that provide a controllable output probability and inherent stochasticity. The ability to control the output probability of the p-bits, coupled with their stochastic behavior, plays a critical role in steering the entire network towards solutions and exploring multiple possibilities. This functionality is particularly evident when examining the output probabilities of individual p-bits in response to unit inputs, where the fitting of the sigmoidal curves reveals their controllable stochastic nature. Until recently, stochastic magnetic tunnel junctions (MTJs) have been the predominant components used to implement p-bits. Borders et al. successfully demonstrated p-bits, including MTJs with millisecond-scale retention times, that generate sigmoid functions under an external bias.¹³² These p-bits exhibited commendable performance and demonstrated capabilities such as successfully performing integer factorization, which is difficult for conventional computing with the von Neumann architecture. However, the complex stack structure of the device and the inclusion of NMOS transistors in MTJ-based p-bits require further improvement.

Wang et al. implemented a probabilistic unit with a bias-dependent output using an LIF neuron, which included a Pt/CuS/GeSe/Pt structure volatile memristor, as shown in Fig. 10(a) and (b).⁷⁵ They verified that the constructed neuron circuit properly generated the spike output, as shown in Fig. 10(c). Although not explicitly called a p-bit, the LIF neuron can efficiently adjust the spiking frequency as the input signal amplitude increases, as shown in Fig. 10(d), because of the reduced time required for the membrane voltage to reach the threshold of the volatile memristor. In addition, the LIF neuron model consists only of resistors and capacitors, making its structure remarkably simple without the need for elements such as comparators or transistors.

Fig. 10 (a) Schematic illustration of a Pt/CuS/GeSe/Pt structure volatile memristor. (b) Circuit diagram of LIF neuron and the parameters for each circuit elements. (c) Generated spike output through leaky integrate-and-fire process. (d) Sigmoid-fitted output characteristic of LIF neuron.⁷⁵ (e) IV curves of Cu_0.1Te_0.9/HfO₂/Pt memristor under multiple cycles (inset schematic illustration provides the structure of device). (f) Sigmoid-fitted output characteristic achieved by p-bit with Cu_0.1Te_0.9/HfO₂/Pt memristor (inset circuit diagram shows constructed p-bit). (g) Input bias dependent output generation probability of p-bit⁷² Reproduced with permission from ref. 72. Copyright 2022 Springer Nature. (h) Current sweep curve of TiN/NbO_x/TiN memristor and accompanying load lines (inset schematic illustration provides the cross-sectional structure of device). (i) Circuit diagram of self-oscillating p-bit. (j) Sigmoid-fitted output characteristic achieved by p-bit with TiN/NbO_x/TiN memristor. (k) Input bias dependent oscillation output frequency of p-bit⁸⁴ Reproduced with permission from ref. 84. Copyright 2023 Springer Nature.

Woo et al. implemented p-bits using a diffusive Cu_0.1Te_0.9/HfO₂/Pt memristor, as shown in Fig. 10(e).⁷² By applying pulses to the memristor and a series-connected resistor, the memristor stochastically transitions to the LRS, with the transition frequency increasing with higher input pulse amplitudes. This implementation also successfully achieved a sigmoid-fitted bias-dependent output, as shown in Fig. 10(f) and (g).

Rhee et al. demonstrated a self-oscillating p-bit using an MIT-based TiN/NbO_x/TiN structure and a series-connected resistor, as shown in Fig. 10(h) and (i).⁸⁴ While previous reports showed a tendency for the firing probability to increase with higher input bias. In this case, the oscillation frequency decreased with increasing input bias, as shown in Fig. 10(j) and (k). However, if the p-bit provides a bias-dependent output in either direction, it can be seamlessly used for probabilistic computations. Detailed information on the problem-solving aspects is discussed in the following subsections.

4.3.2. p-bit-based network construction and problem solving. Wang et al. demonstrated the application of probabilistic computing in tumor diagnosis tasks using a Spiking Neural Network (SNN) built on stochastic neurons, as shown in Fig. 11(a).⁷⁵ The SNN processes benign/malignant tumor data from input neurons and performs classification at the output neuron. The output spikes, characterized by stochastic behavior, are approximate samples from the posterior distribution over the hidden causes. The activities of the output neurons quantitatively represent the diagnostic results for benign or malignant tumors using Bayesian inference. This probabilistic SNN exhibits improved accuracy in diagnosing tumors compared to conventional artificial neural networks (ANNs) with deterministic neurons, which are often misclassified. The diagnostic accuracy is enhanced compared to that of ANN systems based solely on deterministic neurons. These findings suggest that incorporating stochastic neurons into SNNs results in superior diagnostic capabilities for more accurate tumor diagnosis compared with traditional deterministic approaches.

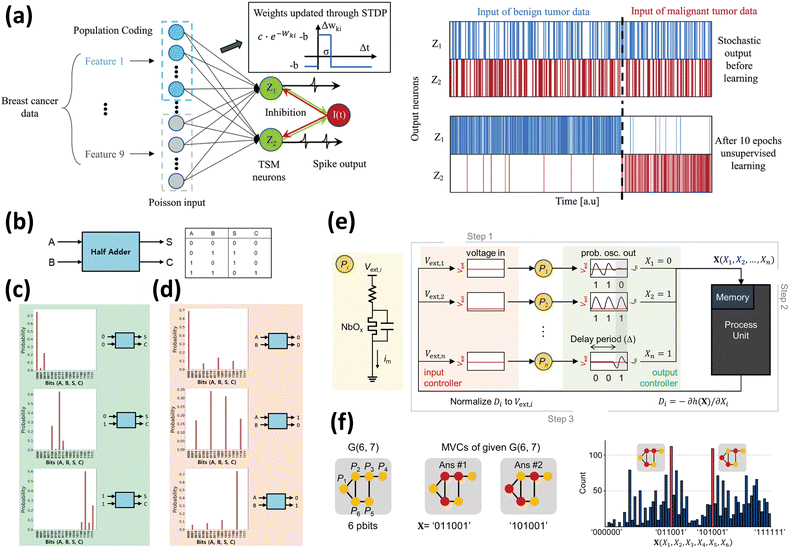Fig. 11 (a) Schematic illustration of Bayesian inference system for tumor diagnosis based on LIF neuron (left) and benign/malignant diagnosis result (right).⁷⁵ (b) Schematic illustration of half adder and accompanying truth table. Probabilistic computing results in (c) forward operation and (d) inverse operation of half adder.⁷² Reproduced with permission from ref. 72. Copyright 2022 Springer Nature. (e) Constructed memristive Boltzmann machine includes self-oscillating p-bits and its signal transmission flow. (f) Schematic illustration of minimum vertex covering example (left) and corresponding probabilistic computing result (right).⁸⁴ Reproduced with permission from ref. 84. Copyright 2023 Springer Nature.

Woo et al. described a methodology for probabilistic computing using CMOS-based sequential logic.⁷² While logic gates typically have one-way operations where inputs determine outputs, probabilistic computing treats the output as a combinatorial optimization problem, yielding possible input scenarios for a given output. To achieve this, each input and output terminal is designated as a p-bit, and synaptic weights are set for logic gates or sequential logic operations, thereby enabling the simultaneous completion of forward and inverse operations. A truth table is constructed to implement the desired logic function, and the corresponding equations for each input variable are formulated, as shown in Fig. 11(b). The error term for the computational results is obtained by squaring the input and output differences. When the logic functions correctly, the error is minimized and approaches zero. Therefore, when implementing logic in a p-bit-based network, the error can serve as a Hamiltonian or cost function. The cost function of each p-bit is obtained by partial differentiation with respect to each input variable and is iteratively fed back as the input for the next iteration. This iterative process ensures that the network converges to the lowest energy level, producing results that indicate proper functioning of the logic, including forward and inverse operations, as shown in Fig. 11(c) and (d). This methodology provides a framework for implementing probabilistic computing in CMOS-based sequential logic and offers a new approach to logic operations with potential applications in various computing scenarios.

Rhee et al. showcased the construction of a memristive Boltzmann machine based on the probabilistic self-oscillating p-bits introduced in the previous subsection, demonstrating the resolution of the NP-hard problem known as minimum vertex covering.⁸⁴ Each vertex is represented as a p-bit in this setup, and the connections between the vertices are quantified using a Hamiltonian. The iterative process involves inputting the numerical values of the Hamiltonian partial derivatives back into each p-bit, as illustrated in Fig. 11(e). Remarkably, using this approach, they successfully solved a covering problem with six vertices within 2000 iterations, as depicted in Fig. 11(f). The input voltages provided to each p-bit during this process are computed in the processing unit, facilitating smooth operation of the memristive Boltzmann machine, even when utilizing the inverse sigmoid function. This highlights the versatility and efficiency of the proposed approach and opens up possibilities for addressing complex NP-hard problems using memristor-based computing paradigms.

5. Conclusions and perspective

In this review, various origins of threshold-switching memristors have been discussed in detail, highlighting materials such as metal cation-based, OTS-based, MIT-based, and electron trapping/de-trapping-based memristors. Section 2.5 compared the characteristics of these different types of memristors. The inherent distinctions among memristors result in various advantages and disadvantages, rendering them suitable for various applications. Representative applications of volatile TS memristors were introduced, including their use as access devices within crossbar arrays, artificial receptors, artificial neurons, physical reservoirs, and physical entropy sources. Fig. 12 summarizes the general characteristics of threshold-switching memristors.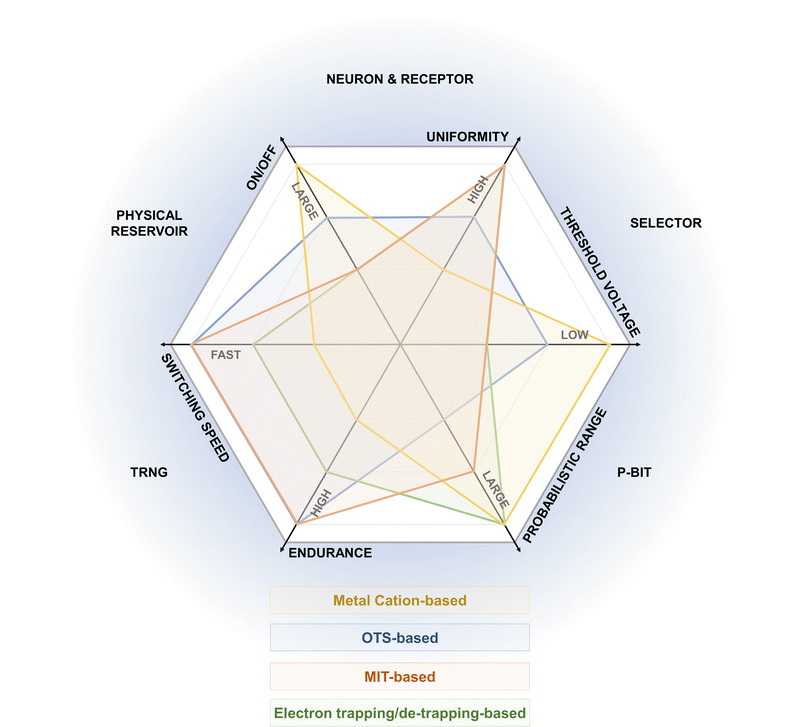

Fig. 12 Schematic illustration of summarized general characteristics of TS memristors corresponding to each switching mechanism.^{28,63,71,72,77,82,83} Parameters for metal cation-based memristor from ref. 71,72, OTS-based memristor from ref. 28,77, MIT-based memristor from ref. 82,83, and electron trapping/de-trapping-based memristor from ref. 63.

Metal-cation-based memristors typically exhibit low off-currents and V_th but suffer from poor variability. Although these characteristics ensure high selectivity and an optimal operating voltage, they may not be suitable for electronic circuits because of their undesirable variability and endurance. This variability and endurance arise from the spatial randomness in filament. To address these limitations, various methods have been proposed to localize filament formation. These attempts can be categorized into two approaches such as local ion pathway generation and local active electrode formation. The grain boundaries of the dielectric layer¹³³ or the residual filaments in the dielectric layer with low ion mobility after the forming¹²⁹ provide predefined pathways for active metal ions. Meanwhile, defective sites in the graphene between the active electrode and the dielectric layer¹³⁴ or nanodots of active ions¹³⁵ serve as local active electrodes. Conversely, poor variability can serve as a source of physical entropy, making it suitable for implementing true random number generators and probabilistic computing. However, the CMOS compatibility of highly diffusive species is a concern for this type of memristor. Metal cations may diffuse from the memristor to the front end, potentially causing chip damage.¹³⁶ Appropriate diffusion barrier materials and sealed structures must be employed to mitigate this issue. Fortunately, copper, which is an active material for metal cation-based memristor as well as a metallization material, diffusion barrier has been comprehensively explored for decades due to their importance in the reliability of CMOS integration.¹³⁷ Additionally, metal nitrides successfully impede the diffusion of silver, similar to the copper case.¹³⁸

OTS-based memristors are highly successful selectors for crossbar arrays in mass-production lines because of their bidirectional TS, high speed, and high on/off ratio. The local conductive filament offers sufficient current density in scaled devices, enabling a high on-current and fast operation through positive feedback from Joule heating. However, these devices face challenges owing to heat generation, leading to the crystallization of chalcogenides, which disrupts reversible switching between the on and off states. Simultaneously, improvements in uniformity and reduction of the off-current are still necessary. Consequently, research has focused on compositional engineering with dopants to address this issue. Doping with elements such as Si^139,140 or In¹⁴¹ into the chalcogenide matrix reinforces the atomic bonding between chalcogen atoms, resulting in more stable operation during switching. Additionally, N doping is expected to increase the optical bandgap, thereby reducing the off-current.⁷⁶

Despite their diverse working principles, threshold-switching memristors effectively realize leaky integrate-and-fire functionality for artificial receptors or neurons, as detailed in Sections 3.2 and 3.3. However, MIT-based memristors have emerged as the most promising candidates owing to their superior endurance. Conversely, their on/off ratios are relatively poor compared to those of metal-cation- or OTS-based memristors, which hinders their utilization as selectors. Fortunately, the inclusion of a thin insulating layer helps achieve a high resistance in the off state, thereby enhancing the on/off ratio.¹⁴²

Electron-trapping/de-trapping-based memristors may not offer electrical performances comparable to those of other memristors. However, integrating this type of memristor into a CMOS chip is relatively straightforward because of the unlimited material choices available, unlike the requirements for mobile metal ions, chalcogenides, and Mott materials in other memristors. Therefore, it is crucial to optimized the process to create appropriate defects in the switching layer. For instance, oxygen vacancies in oxide layers serve as active trap sites, and their concentration can be adjusted through oxidation during deposition or subsequent plasma treatment.^143–146

Non-volatile memristors, derived from resistive switching memory or phase change memory technology, have garnered considerable attention compared to volatile memristors. Volatile threshold-switching memristors are emerging as crucial components in neuromorphic computing. While non-volatile memristors are necessary for storing synaptic weights within memristive neural networks, the construction of ultra-dense crossbar arrays requires a two-terminal selector with a substantial on–off ratio to prevent programming interference. This requirement makes volatile threshold-switching memristors promising selector candidates. Furthermore, artificial nervous systems, including neurons and receptors, have been successfully developed using volatile threshold-switching memristors. In addition, their dynamic behavior and inherent stochasticity, which have been overlooked or considered minimal, can be leveraged as physical reservoirs and physical entropy sources, respectively. For instance, the p-bit, the key component of probabilistic computing, should be capable of generating probabilistic outputs and should be adjustable based on external stimuli. The dynamic and stochastic behaviors of volatile threshold-switching memristors are functions of the preceding pulse amplitude and width. Different applications require different key characteristics, and volatile TS memristors exhibit various traits based on their principles. Therefore, selecting an appropriate memristor and enhancing its characteristics to meet system requirements are vital for future computing technologies.

Author contributions

T. Moon, K. Soh, and J. S. Kim conceived the review and wrote the manuscript. J. E. Kim and S. Y. Chun reviewed the manuscript. J. H. Yoon and J. J. Yang supervised the review and finalized the manuscript. All authors have given approval to the final version of the article.

Data availability

No primary research results, software or code have been included and no new data were generated or analysed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This research was supported by the National R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (RS-2024-00406418 and NRF-2022R1C1C1004176).

References

1. Z. Epstein, A. Hertzmann, Investigators of Human Creativity, M. Akten, H. Farid, J. Fjeld, M. R. Frank, M. Groh, L. Herman, N. Leach, R. Mahari, A. S. Pentland, O. Russakovsky, H. Schroeder and A. Smith, Science, 2023, 380, 1110–1111.
2. E. Yurtsever, J. Lambert, A. Carballo and K. Takeda, IEEE Access, 2020, 8, 58443–58469.
3. B. L. Risteska Stojkoska and K. V. Trivodaliev, J. Cleaner Prod., 2017, 140, 1454–1464.
4. J. Muangprathub, N. Boonnam, S. Kajornkasirat, N. Lekbangpong, A. Wanichsombat and P. Nillaor, Comput. Electron. Agric., 2019, 156, 467–474.
5. J. Kim and C. Lee, J. Fluid Mech., 2020, 882, A18.
6. M. Schauperl and R. A. Denny, J. Chem. Inf. Model., 2022, 62, 3142–3156.
7. C. Wan, P. Cai, M. Wang, Y. Qian, W. Huang and X. Chen, Adv. Mater., 2020, 32, e1902434.
8. T. Wang, X.-X. Wang, J. Wen, Z.-Y. Shao, H.-M. Huang and X. Guo, Adv. Intell. Syst., 2022, 4, 2200047.
9. J. Q. Yang, R. Wang, Y. Ren, J. Y. Mao, Z. P. Wang, Y. Zhou and S. T. Han, Adv. Mater., 2020, 32, 2003610.
10. L. Chua, IEEE Trans. Circuit Theory, 1971, 18, 507–519.
11. S. H. Jo, T. Chang, I. Ebong, B. B. Bhadviya, P. Mazumder and W. Lu, Nano Lett., 2010, 10, 1297–1301.
12. J. U. Kwon, Y. G. Song, J. E. Kim, S. Y. Chun, G. H. Kim, G. Noh, J. Y. Kwak, S. Hur, C. Y. Kang, D. S. Jeong, S. J. Oh and J. H. Yoon, ACS Appl. Mater. Interfaces, 2022, 14, 44550–44560.
13. S. Y. Chun, Y. G. Song, J. E. Kim, J. U. Kwon, K. Soh, J. Y. Kwon, C. Y. Kang and J. H. Yoon, Adv. Mater., 2023, 35, e2302219.
14. Y. Feng, Y. Zhang, Z. Zhou, P. Huang, L. Liu, X. Liu and J. Kang, Nat. Commun., 2024, 15, 1132.
15. K.-H. Kim, S. Gaba, D. Wheeler, J. M. Cruz-Albrecht, T. Hussain, N. Srinivasa and W. Lu, Nano Lett., 2012, 12, 389–395.
16. T.-Y. Wang, J.-L. Meng, L. Chen, H. Zhu, Q.-Q. Sun, S.-J. Ding, W.-Z. Bao and D. W. Zhang, InfoMat, 2021, 3, 212–221.
17. X. Duan, Z. Cao, K. Gao, W. Yan, S. Sun, G. Zhou, Z. Wu, F. Ren and B. Sun, Adv. Mater., 2024, 36, 2310704.
18. B. Sun, T. Guo, G. Zhou, S. Ranjan, Y. Jiao, L. Wei, Y. N. Zhou and Y. A. Wu, Mater. Today Phys., 2021, 18, 100393.
19. B. Sun, G. Zhou, L. Sun, H. Zhao, Y. Chen, F. Yang, Y. Zhao and Q. Song, Nanoscale Horiz., 2021, 6, 939–970.
20. Q. Xia and J. J. Yang, Nat. Mater., 2019, 18, 309–323.
21. S.-O. Park, H. Jeong, J. Park, J. Bae and S. Choi, Nat. Commun., 2022, 13, 2888.
22. Y. H. Jang, J. Han, J. Kim, W. Kim, K. S. Woo, J. Kim and C. S. Hwang, Adv. Mater., 2023, 35, 2209503.
23. Z. Wang, S. Joshi, S. E. Savel’ev, H. Jiang, R. Midya, P. Lin, M. Hu, N. Ge, J. P. Strachan, Z. Li, Q. Wu, M. Barnell, G.-L. Li, H. L. Xin, R. S. Williams, Q. Xia and J. J. Yang, Nat. Mater., 2017, 16, 101–108.
24. S. Kumar, J. P. Strachan and R. S. Williams, Nature, 2017, 548, 318–321.
25. R. Midya, Z. Wang, J. Zhang, S. E. Savel’ev, C. Li, M. Rao, M. H. Jang, S. Joshi, H. Jiang, P. Lin, K. Norris, N. Ge, Q. Wu, M. Barnell, Z. Li, H. L. Xin, R. S. Williams, Q. Xia and J. J. Yang, Adv. Mater., 2017, 29, 1604457.
26. X. Li, Z. Yuan, Y. Xue, Y. Zhu, S. Song and Z. Song, ACS Appl. Electron. Mater., 2023, 5, 3499–3506.
27. J. Chen, L. Wang, Z. Liu, J. Wen, H. Tong and X. Miao, IEEE Electron Device Lett., 2024, 45, 44–47.
28. L. Wang, J. Wen, Z. Liu, J. Chen, H. Tong and X. Miao, IEEE Electron Device Lett., 2023, 44, 1096–1099.
29. Y. G. Song, J. M. Suh, J. Y. Park, J. E. Kim, S. Y. Chun, J. U. Kwon, H. Lee, H. W. Jang, S. Kim, C. Y. Kang and J. H. Yoon, Adv. Sci., 2022, 9, e2103484.
30. R. Khan, N. U. Rehman, N. Ilyas, N. Sfina, M. Barhoumi, A. Khan, K. Althubeiti, S. A. Otaibi, S. Iqbal, N. Rahman, M. Sohail, A. Ullah, T. Del Rosso, Q. Zaman, A. Ali Khan, S. S. Abdullaev and A. Khan, Nanoscale, 2023, 15, 1900–1913.
31. S. Kumar, X. Wang, J. P. Strachan, Y. Yang and W. D. Lu, Nat. Rev. Mater., 2022, 7, 575–591.
32. L. Song, P. Liu, J. Pei, F. Bai, Y. Liu, S. Liu, Y. Wen, L. W. T. Ng, K.-P. Pun, S. Gao, M. Q.-H. Meng, T. Hasan and G. Hu, Adv. Electron. Mater., 2024, 10, 2300564.
33. Y. Jiang, D. Wang, N. Lin, S. Shi, Y. Zhang, S. Wang, X. Chen, H. Chen, Y. Lin, K. C. Loong, J. Chen, Y. Li, R. Fang, D. Shang, Q. Wang, H. Yu and Z. Wang, Adv. Sci., 2023, 10, 2301323.
34. X. Li, Y. Zhong, H. Chen, J. Tang, X. Zheng, W. Sun, Y. Li, D. Wu, B. Gao, X. Hu, H. Qian and H. Wu, Adv. Mater., 2023, 35, 2203684.
35. G. Kim, J. H. In, Y. Lee, H. Rhee, W. Park, H. Song, J. Park, J. B. Jeon, T. D. Brown, A. A. Talin, S. Kumar and K. M. Kim, Nat. Mater., 2024 DOI:10.1038/s41563-024-01913-0.
36. W. Huh, D. Lee and C. H. Lee, Adv. Mater., 2020, 32, e2002092.
37. H. Zhang, R. Liu, H. Zhao, Z. Sun, Z. Liu, L. He and Y. Li, Coatings, 2021, 12, 21.
38. S. Chowdhury, A. Grimaldi, N. A. Aadit, S. Niazi, M. Mohseni, S. Kanai, H. Ohno, S. Fukami, L. Theogarajan, G. Finocchio, S. Datta and K. Y. Camsari, IEEE J. Explor. Solid-State Comput. Devices Circuits, 2023, 9, 1–11.
39. Y. Seo, Y. Park, P. Hur, M. Jo, J. Heo, B. J. Choi and J. Son, Adv. Mater., 2024, 36, 2402490.
40. I. Valov, R. Waser, J. R. Jameson and M. N. Kozicki, Nanotechnology, 2011, 22, 289502.
41. Y. Yang, P. Gao, L. Li, X. Pan, S. Tappertzhofen, S. Choi, R. Waser, I. Valov and W. D. Lu, Nat. Commun., 2014, 5, 4232.
42. W. Wang, M. Wang, E. Ambrosi, A. Bricalli, M. Laudato, Z. Sun, X. Chen and D. Ielmini, Nat. Commun., 2019, 10, 81.
43. Z. Xiong, Z. Cui, Z. Wen, Z. Hu, S. Mei, J. Wang, W. Zhang, F. Xie and R. Guo, IEEE Trans. Electron Devices, 2022, 69, 1107–1114.
44. S. Jeonghwan, W. Jiyong, A. Prakash, L. Daeseok and H. Hyunsang, IEEE Electron Device Lett., 2015, 36, 681–683.
45. S. Prada, M. Rosa, L. Giordano, C. Di Valentin and G. Pacchioni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 245314.
46. W. W. Mullins, J. Appl. Phys., 1957, 28, 333–339.
47. S. Ambrogio, S. Balatti, S. Choi and D. Ielmini, Adv. Mater., 2014, 26, 3885–3892.
48. S. Munjal and N. Khare, Nanotechnology, 2021, 32, 185204.
49. M. K. Rahmani, B.-D. Yang, H. Kim, H. Kim and M. H. Kang, Semicond. Sci. Technol., 2021, 36, 095031.
50. S. A. Chekol, S. Menzel, R. W. Ahmad, R. Waser and S. Hoffmann-Eifert, Adv. Funct. Mater., 2021, 32, 2111242.
51. S. R. Ovshinsky, Phys. Rev. Lett., 1968, 21, 1450–1453.
52. D. Adler, M. S. Shur, M. Silver and S. R. Ovshinsky, J. Appl. Phys., 1980, 51, 3289–3309.
53. D. Adler, H. K. Henisch and S. N. Mott, Rev. Mod. Phys., 1978, 50, 209–220.
54. V. G. Karpov, Y. A. Kryukov, S. D. Savransky and I. V. Karpov, Appl. Phys. Lett., 2007, 90, 123504.
55. I. V. Karpov, M. Mitra, D. Kau, G. Spadini, Y. A. Kryukov and V. G. Karpov, Appl. Phys. Lett., 2008, 92, 173501.
56. D. Ielmini and Y. Zhang, J. Appl. Phys., 2007, 102, 054517.
57. D. Ielmini and Y. Zhang, Appl. Phys. Lett., 2007, 90, 192102.
58. L. Völkel, D. Braun, M. Belete, S. Kataria, T. Wahlbrink, K. Ran, K. Kistermann, J. Mayer, S. Menzel, A. Daus and M. C. Lemme, Adv. Funct. Mater., 2023, 34, 2300428.
59. M. Park, B. Jeon, J. Park and S. Kim, Nanomaterials, 2022, 12, 4206.
60. L. Wu, H. Liu, J. Lin and S. Wang, IEEE Trans. Electron Devices, 2021, 68, 1622–1626.
61. S. Saitoh and K. Kinoshita, Appl. Phys. Lett., 2020, 116, 112101.
62. K. S. Woo, Y. Wang, Y. Kim, J. Kim, W. Kim and C. S. Hwang, Adv. Electron. Mater., 2020, 6, 1901117.
63. K. S. Woo, Y. Wang, J. Kim, Y. Kim, Y. J. Kwon, J. H. Yoon, W. Kim and C. S. Hwang, Adv. Electron. Mater., 2018, 5, 1800543.
64. Y. Kim, Y. J. Kwon, D. E. Kwon, K. J. Yoon, J. H. Yoon, S. Yoo, H. J. Kim, T. H. Park, J. W. Han, K. M. Kim and C. S. Hwang, Adv. Mater., 2018, 30, 1704320.
65. X. Li, Z. Feng, J. Zou, X. Wang, G. Hu, F. Wang, C. Ding, Y. Zhu, F. Yang, Z. Wu and Y. Dai, J. Appl. Phys., 2022, 132, 064904.
66. A. Rose, Phys. Rev., 1955, 97, 1538–1544.
67. A. A. Grinberg, S. Luryi, M. R. Pinto and N. L. Schryer, IEEE Trans. Electron Devices, 1989, 36, 1162–1170.
68. J. H. Yoon, Z. Wang, K. M. Kim, H. Wu, V. Ravichandran, Q. Xia, C. S. Hwang and J. J. Yang, Nat. Commun., 2018, 9, 417.
69. J. H. Yang, S. C. Mao, K. T. Chen and J. S. Chen, Adv. Electron. Mater., 2022, 9, 2201006.
70. Y. G. Song, J. E. Kim, J. U. Kwon, S. Y. Chun, K. Soh, S. Nahm, C. Y. Kang and J. H. Yoon, ACS Appl. Mater. Interfaces, 2023, 15, 5495–5503.
71. H. Jiang, D. Belkin, S. E. Savel’ev, S. Lin, Z. Wang, Y. Li, S. Joshi, R. Midya, C. Li, M. Rao, M. Barnell, Q. Wu, J. J. Yang and Q. Xia, Nat. Commun., 2017, 8, 882.
72. K. S. Woo, J. Kim, J. Han, W. Kim, Y. H. Jang and C. S. Hwang, Nat. Commun., 2022, 13, 5762.
73. Y. Shi, Q. Hua, Z. Dong, B. Wang, X. Dai, J. Niu, Z. Cui, T. Huang, Z. L. Wang and W. Hu, Nano Energy, 2023, 113, 108549.
74. Y. Fu, J. Wen, L. Wang, L. Yang, Q. Zhu, W. Zuo, P. Zhang, Y. Li, H. Tong, G. Ma, H. Wang and X. Miao, IEEE Electron Device Lett., 2023, 44, 853–856.
75. K. Wang, Q. Hu, B. Gao, Q. Lin, F. W. Zhuge, D. Y. Zhang, L. Wang, Y. H. He, R. H. Scheicher, H. Tong and X. S. Miao, Mater. Horiz., 2021, 8, 619–629.
76. J. Lee, S. Ban, T. H. Lee and H. Hwang, IEEE Electron Device Lett., 2023, 44, 1468–1471.
77. K. Li, J. Yao, P. Zhao, Y. Luo, X. Ge, R. Yang, X. Cheng and X. Miao, Mater. Horiz., 2024, 11, 2106–2114.
78. C. Y. Han, Z. R. Han, S. L. Fang, S. Q. Fan, J. Q. Yin, W. H. Liu, X. Li, S. Q. Yang, G. H. Zhang, X. L. Wang and L. Geng, Adv. Mater. Interfaces, 2022, 9, 2200394.
79. Q. Duan, T. Zhang, C. Liu, R. Yuan, G. Li, P. Jun Tiw, K. Yang, C. Ge, Y. Yang and R. Huang, Adv. Intell. Syst., 2022, 4, 2200039.
80. R. Yuan, Q. Duan, P. J. Tiw, G. Li, Z. Xiao, Z. Jing, K. Yang, C. Liu, C. Ge, R. Huang and Y. Yang, Nat. Commun., 2022, 13, 3973.
81. W. Yi, K. K. Tsang, S. K. Lam, X. Bai, J. A. Crowell and E. A. Flores, Nat. Commun., 2018, 9, 4661.
82. S. Zhong, Y. Zhang, H. Zheng, F. Yu and R. Zhao, Adv. Intell. Syst., 2022, 4, 2200076.
83. G. Kim, J. H. In, Y. S. Kim, H. Rhee, W. Park, H. Song, J. Park and K. M. Kim, Nat. Commun., 2021, 12, 2906.
84. H. Rhee, G. Kim, H. Song, W. Park, D. H. Kim, J. H. In, Y. Lee and K. M. Kim, Nat. Commun., 2023, 14, 7199.
85. Z. Zhou, Y. Pei, J. Zhao, G. Fu and X. Yan, Appl. Phys. Lett., 2021, 118, 191103.
86. M. J. Kang, T. J. Park, Y. W. Kwon, D. H. Ahn, Y. S. Kang, H. Jeong, S. J. Ahn, Y. J. Song, B. C. Kim, S. W. Nam, H. K. Kang, G. T. Jeong and C. H. Chung, 2011.
87. J. Yoo, S. H. Kim, S. A. Chekol, J. Park, C. Sung, J. Song, D. Lee and H. Hwang, Adv. Electron. Mater., 2019, 5, 1900196.
88. M. Rao, W. Song, F. Kiani, S. Asapu, Y. Zhuo, R. Midya, N. Upadhyay, Q. Wu, M. Barnell, P. Lin, C. Li, Z. Wang, Q. Xia and J. Joshua Yang, Small Sci., 2021, 2, 2100072.
89. C. Li, M. Hu, Y. Li, H. Jiang, N. Ge, E. Montgomery, J. Zhang, W. Song, N. Dávila, C. E. Graves, Z. Li, J. P. Strachan, P. Lin, Z. Wang, M. Barnell, Q. Wu, R. S. Williams, J. J. Yang and Q. Xia, Nat. Electron., 2017, 1, 52–59.
90. Z. Wang, S. Joshi, S. Savel’ev, W. Song, R. Midya, Y. Li, M. Rao, P. Yan, S. Asapu, Y. Zhuo, H. Jiang, P. Lin, C. Li, J. H. Yoon, N. K. Upadhyay, J. Zhang, M. Hu, J. P. Strachan, M. Barnell, Q. Wu, H. Wu, R. S. Williams, Q. Xia and J. J. Yang, Nat. Electron., 2018, 1, 137–145.
91. A. Chen, IEEE Trans. Electron Devices, 2015, 62, 2845–2849.
92. A. Spessot and H. Oh, IEEE Trans. Electron Devices, 2020, 67, 1382–1393.
93. D. Garbin, W. Devulder, R. Degraeve, G. L. Donadio, S. Clima, K. Opsomer, A. Fantini, D. Cellier, W. G. Kim, M. Pakala, A. Cockburn, C. Detavernier, R. Delhougne, L. Goux and G. S. Kar, 2019.
94. A. Verdy, G. Navarro, M. Bernard, S. Chevalliez, N. Castellani, E. Nolot, J. Garrione, P. Noé, G. Bourgeois, V. Sousa, M. C. Cyrille and E. Nowak, 2018.
95. F. Hatem, Z. Chai, W. Zhang, A. Fantini, R. Degraeve, S. Clima, D. Garbin, J. Robertson, Y. Guo, J. F. Zhang, J. Marsland, P. Freitas, L. Goux and G. S. Kar, 2019.
96. X. Li, Z. Yuan, S. Lv, S. Song and Z. Song, Thin Solid Films, 2021, 734, 138837.
97. S. Lee, J. Lee, M. Kwak, O. Mosendz and H. Hwang, Appl. Phys. Lett., 2021, 118, 212103.
98. M. Song, S. Lee, S. S. T. Nibhanupudi, J. V. Singh, M. Disiena, C. J. Luth, S. Wu, M. J. Coupin, J. H. Warner and S. K. Banerjee, Nano Lett., 2023, 23, 2952–2957.
99. D. Kim, J. H. Park, D. S. Jeon, T. D. Dongale and T. G. Kim, J. Alloys Compd., 2021, 854, 157261.
100. J. H. Park, D. Kim, D. Y. Kang, D. S. Jeon and T. G. Kim, ACS Appl. Mater. Interfaces, 2019, 11, 29408–29415.
101. Q. Hua, H. Wu, B. Gao, M. Zhao, Y. Li, X. Li, X. Hou, M. F. Marvin Chang, P. Zhou and H. Qian, Adv. Sci., 2019, 6, 1900024.
102. T. D. Dongale, G. U. Kamble, D. Y. Kang, S. S. Kundale, H.-M. An and T. G. Kim, Phys. Status Solidi RRL, 2021, 15, 2100199.
103. Y. Cho, J. Heo, S. Kim and S. Kim, Surf. Interfaces, 2023, 41, 103273.
104. Y. Song, X. Wang, Q. Wu, C. Wang, S. Du, L. Zhang and X. Miao, Appl. Phys. Lett., 2021, 118, 223501.
105. M. Wang, Y. Luo, T. Wang, C. Wan, L. Pan, S. Pan, K. He, A. Neo and X. Chen, Adv. Mater., 2021, 33, e2003014.
106. Y. H. Jung, B. Park, J. U. Kim and T. I. Kim, Adv. Mater., 2019, 31, e1803637.
107. K. Xiao, C. Wan, L. Jiang, X. Chen and M. Antonietti, Adv. Mater., 2020, 32, 2000218.
108. F. Li, R. Wang, C. Song, M. Zhao, H. Ren, S. Wang, K. Liang, D. Li, X. Ma, B. Zhu, H. Wang and Y. Hao, ACS Nano, 2021, 15, 16422–16431.
109. K. He, Y. Liu, M. Wang, G. Chen, Y. Jiang, J. Yu, C. Wan, D. Qi, M. Xiao, W. R. Leow, H. Yang, M. Antonietti and X. Chen, Adv. Mater., 2020, 32, e1905399.
110. W. Ye, J. Lin, X. Zhang, Q. Lian, Y. Liu, H. Wang, S. Wu, H. Chen and T. Guo, Nano Energy, 2022, 100, 107525.
111. G. Ding, R. S. Chen, P. Xie, B. Yang, G. Shang, Y. Liu, L. Gao, W. A. Mo, K. Zhou, S. T. Han and Y. Zhou, Small, 2022, 18, e2200185.
112. X. Zhang, Y. Zhuo, Q. Luo, Z. Wu, R. Midya, Z. Wang, W. Song, R. Wang, N. K. Upadhyay, Y. Fang, F. Kiani, M. Rao, Y. Yang, Q. Xia, Q. Liu, M. Liu and J. J. Yang, Nat. Commun., 2020, 11, 51.
113. W. Wang, E. Covi, A. Milozzi, M. Farronato, S. Ricci, C. Sbandati, G. Pedretti and D. Ielmini, Adv. Intell. Syst., 2021, 3, 2000224.
114. R. Yuan, P. J. Tiw, L. Cai, Z. Yang, C. Liu, T. Zhang, C. Ge, R. Huang and Y. Yang, Nat. Commun., 2023, 14, 3695.
115. J. Yu, F. Zeng, Q. Wan, Z. Lu and F. Pan, InfoMat, 2023, 5, e12458.
116. C. Chen, Y. He, H. Mao, L. Zhu, X. Wang, Y. Zhu, Y. Zhu, Y. Shi, C. Wan and Q. Wan, Adv. Mater., 2022, 34, e2201895.
117. O. I. Abiodun, M. U. Kiru, A. Jantan, A. E. Omolara, K. V. Dada, A. M. Umar, O. U. Linus, H. Arshad, A. A. Kazaure and U. Gana, IEEE Access, 2019, 7, 158820.
118. S. H. S. Basha, S. R. Dubey, V. Pulabaigari and S. Mukherjee, Neurocomputing, 2020, 378, 112–119.
119. A. Sherstinsky, Phys. D, 2020, 404, 132306.
120. M. Cucchi, S. Abreu, G. Ciccone, D. Brunner and H. Kleemann, Neuromorphic Comput. Eng., 2022, 2, 032002.
121. R. Midya, Z. Wang, S. Asapu, X. Zhang, M. Rao, W. Song, Y. Zhuo, N. Upadhyay, Q. Xia and J. J. Yang, Adv. Intell. Syst., 2019, 1, 1900084.
122. H. Jaeger, GMD-Report 148, German National Research Institute for Computer Science, 2001.
123. W. Maass, T. Natschläger and H. Markram, Neural Comput., 2002, 14, 2531–2560.
124. S. Choi, J. Shin, G. Park, J. S. Eo, J. Jang, J. J. Yang and G. Wang, Nat. Commun., 2024, 15, 2044.
125. R. Li, H. Yang, Y. Zhang, N. Tang, R. Chen, Z. Zhou, L. Liu, J. Kang and P. Huang, Nanotechnology, 2023, 34, 505207.
126. Y. Zhong, J. Tang, X. Li, X. Liang, Z. Liu, Y. Li, Y. Xi, P. Yao, Z. Hao, B. Gao, H. Qian and H. Wu, Nat. Electron., 2022, 5, 672–681.
127. L. Sun, Z. Wang, J. Jiang, Y. Kim, B. Joo, S. Zheng, S. Lee, W. J. Yu, B.-S. Kong and H. Yang, Sci. Adv., 2021, 7, eabg1455.
128. J. Bian, Y. Tao, Z. Wang, Y. Dong, Z. Li, X. Zhao, Y. Lin, H. Xu and Y. Liu, Appl. Phys. Lett., 2023, 122, 193502.
129. Y. F. Lu, H. Y. Li, Y. Li, L. H. Li, T. Q. Wan, L. Yang, W. B. Zuo, K. H. Xue and X. S. Miao, Adv. Electron. Mater., 2022, 8, 2200202.
130. X. Xing, S. Huang, Y. Gong, J. Wang, Z. Lv, Y. Zhou, X. Zhao, J. Hao and S. T. Han, Mater. Today Nano, 2023, 22, 100315.
131. B. Liu, Y. F. Chang, J. Li, X. Liu, L. A. Wang, D. Verma, H. Liang, H. Zhu, Y. Zhao, L. J. Li, T. H. Hou and C. S. Lai, ACS Nano, 2022, 16, 6847–6857.
132. W. A. Borders, A. Z. Pervaiz, S. Fukami, K. Y. Camsari, H. Ohno and S. Datta, Nature, 2019, 573, 390–393.
133. O. Kapur, D. Guo, J. Reynolds, D. Newbrook, Y. Han, R. Beanland, L. Jiang, C. H. K. de Groot and R. Huang, Sci. Rep., 2024, 14, 14008.
134. X. Zhao, J. Ma, X. Xiao, Q. Liu, L. Shao, D. Chen, S. Liu, J. Niu, X. Zhang, Y. Wang, R. Cao, W. Wang, Z. Di, H. Lv, S. Long and M. Liu, Adv. Mater., 2018, 30, e1705193.
135. Y. Li, J. Tang, B. Gao, W. Sun, Q. Hua, W. Zhang, X. Li, W. Zhang, H. Qian and H. Wu, Adv. Sci., 2020, 7, 2002251.
136. A. A. Istratov and E. R. Weber, J. Electrochem. Soc., 2002, 149, G21.
137. A. E. Kaloyeros and E. Eisenbraun, Annu. Rev. Mater. Res., 2000, 30, 363–385.
138. L. Gao, J. Gstöttner, R. Emling, M. Balden, C. Linsmeier, A. Wiltner, W. Hansch and D. Schmitt-Landsiedel, Microelectron. Eng., 2004, 76, 76–81.
139. S. Ban, S. Lee, J. Lee and H. Hwang, IEEE Electron Device Lett., 2022, 43, 643–646.
140. Z. Lin, J. Su, Y. Wang, H. Wan, G. Ma, Y. Rao and H. Wang, Vacuum, 2023, 213, 112127.
141. H. Y. Cheng, W. C. Chien, I. T. Kuo, C. H. Yang, Y. C. Chou, R. L. Bruce, E. K. Lai, D. Daudelin, C. W. Yeh, L. Gignac, C. W. Cheng, A. Grun, C. Lavoie, N. Gong, L. Buzi, H. Y. Ho, A. Ray, H. Utomo, M. BrightSky and H. L. Lung, presented in part at the 2021 IEEE International Electron Devices Meeting (IEDM), 2021.
142. Q. Luo, J. Yu, X. Zhang, K. H. Xue, J. H. Yuan, Y. Cheng, T. Gong, H. Lv, X. Xu, P. Yuan, J. Yin, L. Tai, S. Long, Q. Liu, X. Miao, J. Li and M. Liu, 2019.
143. S.-J. Park, J.-P. Lee, J. S. Jang, H. Rhu, H. Yu, B. Y. You, C. S. Kim, K. J. Kim, Y. J. Cho, S. Baik and W. Lee, Nanotechnology, 2013, 24, 295202.
144. K. V. Egorov, D. S. Kuzmichev, P. S. Chizhov, Y. Y. Lebedinskii, C. S. Hwang and A. M. Markeev, ACS Appl. Mater. Interfaces, 2017, 9, 13286–13292.
145. F. V. Hensling, C. Xu, F. Gunkel and R. Dittmann, Sci. Rep., 2017, 7, 39953.
146. A. A. Gismatulin, V. A. Voronkovskii, G. N. Kamaev, Y. N. Novikov, V. N. Kruchinin, G. K. Krivyakin, V. A. Gritsenko, I. P. Prosvirin and A. Chin, Nanotechnology, 2020, 31, 505704.

---

Footnote

† Contributed equally to this work.

---