Open Access Article
Open Access ArticleEncapsulated stretchable amphibious strain sensors†
Shuang
Wu
 a,
Doyun
Kim
a,
Xiaoqi
Tang
b,
Martin W.
King
b and
Yong
Zhu
a,
Doyun
Kim
a,
Xiaoqi
Tang
b,
Martin W.
King
b and
Yong
Zhu
 *a
*a
aDepartment of Mechanical and Aerospace Engineering, North Carolina State University, Raleigh, NC 27695, USA. E-mail: yzhu7@ncsu.edu
bWilson College of Textiles, North Carolina State University, Raleigh, NC 27695, USA
First published on 1st August 2024
Abstract
Soft and stretchable strain sensors have found wide applications in health monitoring, motion tracking, and robotic sensing. There is a growing demand for strain sensors in amphibious environments, such as implantable sensors, wearable sensors for swimmers/divers, and underwater robotic sensors. However, developing a sensitive, stretchable, and robust amphibious strain sensor remains challenging. This work presents an encapsulated stretchable amphibious strain sensor. The conductive layer, made of silver nanowires embedded below the surface of polydimethylsiloxane, was sandwiched by two layers of thermoplastic polyurethane. Periodic sharp cuts were introduced to change the direction of flow from across the sensor to along the conductive path defined by the opening cracks. The crack advancing and opening is controlled by a unique combination of weak/strong interfaces within the sandwich structure. The cut design and the interfacial interactions between the layers were investigated. The strain sensor exhibited a high gauge factor up to 289, a linear sensing response, a fast response time (53 ms), excellent robustness against over-strain, and stability after 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loading cycles and 20 days in an aqueous saline solution. The functionality of this amphibious strain sensor was demonstrated by tracking the motion of a robotic fish, undertaking language recognition underwater, and monitoring the blood pressure of a porcine aorta. This illustrates the promising potential for this strain sensor for both underwater use and surgically implantable applications.
000 loading cycles and 20 days in an aqueous saline solution. The functionality of this amphibious strain sensor was demonstrated by tracking the motion of a robotic fish, undertaking language recognition underwater, and monitoring the blood pressure of a porcine aorta. This illustrates the promising potential for this strain sensor for both underwater use and surgically implantable applications.
New conceptsThis work has demonstrated a novel structural design that features a robust and reversible interface between the functional layer and the encapsulating layer. Many stretchable devices, beyond stretchable sensors in this work, require encapsulation to enhance environmental stability, water/saline impermeability, and abrasion resistance. However, the encapsulation generally limits the device stretching range and functions. The interface design presented in this work can be broadly applicable to such stretchable devices. We introduced the periodic cut patterns to achieve the strain sensing with an unusual combination of sensitivity, strain range, and robustness. We conducted both experiments and finite element analysis to investigate how the strain sensor responds with the constraint of the encapsulation. |
Introduction
Stretchable strain sensors have demonstrated extensive utility across a variety of applications, including health monitoring,1–9 motion tracking,10–20 human–machine interfaces,21–29 and soft robotics.30–36 Notably, there is a growing demand for amphibious strain monitoring. In healthcare, amphibious strain sensors can be used for implantable sensing, aquatic therapy, and rehabilitation exercises. In sports science, understanding the strain on athletes’ bodies during water-based activities like diving, swimming, or rowing is essential for improving training outcomes and preventing injuries. In ecological research, amphibious strain sensors can be used to study the movement and behavior of aquatic animals without disturbing them. Amphibious wearable strain sensors are also valuable for military applications, where soldiers may need to operate in diverse environments including underwater. While stretchable strain sensors have been extensively reported in the literature, design, fabrication and evaluation of durable, stretchable, and amphibious strain sensors has not been reported previously.There are three types of sensors that can perform amphibious strain sensing: gel-based strain sensors, superhydrophobic strain sensors, and encapsulated strain sensors. Gel-based materials, such as ionogel hydrogels, have emerged as outstanding materials for underwater applications. Xu et al. reported a transparent, stretchable, and self-healing ionogel strain sensor for wearable underwater motion tracking.37 A conductive polymer hydrogel with an anisotropic structure was developed to monitor the real-time movement of underwater robotics.38 The gel-based strain sensors exhibited remarkable stretchability and water-compatibility. However, gels typically suffer from swelling, contraction and degradation when exposed to changes in temperature and humidity, which greatly limits the lifespan of gel-based devices.39 Furthermore, some hydrogels undergo dehydration when exposed to air, leading to substantial changes in mechanical properties.40 Other sensing devices rely on a layer of superhydrophobic coating or surface modification to survive the aquatic environment. For example, a paper-based strain sensor inspired by the papilla-like structure of the lotus leaf's superhydrophobic surface was developed for underwater strain sensing.41 However, damage to the surface features, such as scratches or excessive strains, poses limitations to the resilience of the sensor and leads to mechanical failure.42 In pursuit of an amphibious and resilient strain sensor, a few designs incorporating a series of encapsulated layers have been reported.43–45 For example, a MXene/cotton yarn encapsulated by polydimethylsiloxane (PDMS) has shown good performance in monitoring human physiology when moving in air or underwater.45 While the resistance to water and external damage is improved, the encapsulated layer can severely limit the sensitivity, the range of stretch, and the robustness of the strain sensor due to the mechanical constraints imposed by the bonding between the functional layers.46
This work reports on the design, fabrication and evaluation of an encapsulated stretchable strain sensor that can achieve highly sensitive, linear, and robust amphibious strain sensing. The superior sensing performance is attributed to the unique crack pattern and interface between the encapsulated layers and the functional layers. This is a resistance-based encapsulated strain sensor with the resistor being a silver nanowire (AgNW) network embedded below the surface of a sheet of PDMS. Periodic sharp cuts were made in the AgNW/PDMS composite, changing the direction of current flow from across the sensor to a conducting path guided by the cuts. The AgNW/PDMS composite layer was encapsulated on both sides by layers of thermoplastic polyurethane (TPU), which provided the following attractive features of high elasticity, ease of thermal processing, good biocompatibility, strong chemical resistance, and low water permeability.47–49 Upon stretching, the resistance increases, as the crack propagates and increases the length of the conductive pathway, but remains constant once the crack reaches the cut length. Both the sensing region and the plateau region are fully reversible without any hysteresis. The effect of the cut length and distance between the cuts was studied, highlighting an unusual combination of GF and electrical signals during the cyclic extension and recovery phases of strain. The interface between the encapsulated layers and the functional layers provided excellent durability against excessive strain and cyclic loading, and superior resistance against the aqueous saline solution. The stretchable strain sensor was incorporated into both a robotic fish and a glove so as to demonstrate underwater strain monitoring. In another demonstration, the strain sensor was wrapped around a porcine aorta and used to continuously monitor the systolic and diastolic blood pressure with a cyclic fatigue tester. This supports the claim that that this strain sensor has potential for monitoring implantable devices.
Results and discussion
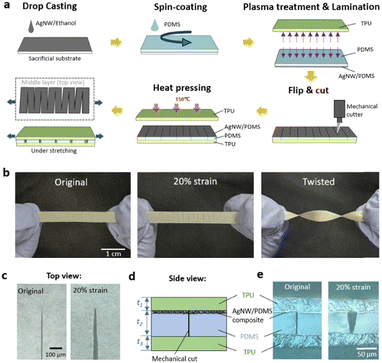
Fig. 1a shows the fabrication process of the amphibious strain sensor with the periodic cut design. First, AgNW solution was drop-cast on a sacrificial substrate. The AgNWs (chemically synthesized with an average diameter of 90 nm and length of 30 μm) form a percolation network (Fig. S1a, ESI†).50,51 Then, liquid PDMS precursor was mixed thoroughly and spin-coated on top of the AgNW network. The AgNW/PDMS composite was cured at 70 °C and then peeled from the substrate with the AgNW network embedded below the surface of the PDMS matrix.52 The AgNW/PDMS film was then laminated onto a thin layer of spin-coated TPU following plasma treatment of the laminating surfaces of the PDMS and TPU layers. Then the AgNW/PDMS composite film was slowly cut with a zigzag-shaped pattern using a standard mechanical cutter to achieve highly sensitive, linear, and robust amphibious strain sensing. The superior sensing performance is attributed to the unique crack pattern and interface between the encapsulated layers and the functional layers. This is a resistance-based encapsulated strain sensor with the resistor being the AgNW network embedded below the surface of a sheet of PDMS. Periodic sharp cuts were made in the AgNW/PDMS composite, changing the direction of current flow from across the sensor to a conducting path guided by the cuts. The AgNW/PDMS composite layer was encapsulated on both sides by layers of TPU, which provided the following attractive features of high elasticity, ease of thermal processing, good biocompatibility, strong chemical resistance, and low water permeability.47–49 The mechanical straight blade was programmed to cut through the AgNW/PDMS layer and stop at the top surface of the TPU layer. The top encapsulating TPU layer was designed slightly larger in size than the AgNW/PDMS/TPU film so as to cover the edges and fuse to the bottom TPU layer, making the AgNW network completely isolated from the aqueous saline solution.Fig. 1b shows the fabricated sensor after stretching and twisting. The cracks were visible through the transparent TPU layers. Fig. 1c shows microscopic images of the crack tip at zero strain and 20% strain. When the sensor was stretched, the cracks opened, reaching the predetermined cut length, before eventually breaking.53Fig. 1d illustrates the side view of the 3-layer structure consisting of a cut AgNW/PDMS layer sandwiched between two TPU layers. The thickness of the AgNW/PDMS composite was ∼3 μm, while the total thickness of PDMS network, t2 was 60 μm; the thickness of the two TPU layers, t1 and t3 were each 30 μm. Fig. 1e shows the side view of the 3-layer structure at both zero and 20% strain. When 20% strain is applied the AgNW/PDMS film separates at the cut interface, causing a local disconnection of the AgNW network.
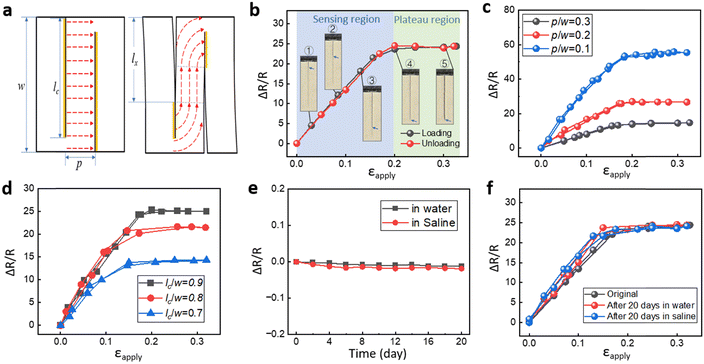
Fig. 2a shows a schematic diagram of the electric current pathway through the AgNW conductor when the predefined cuts gradually open while the strain sensor is stretched. Initially, the current runs horizontally from left to right across the cuts. The closed cuts (regions marked in yellow) maintain the electrical contact, while the opened cuts lose the electrical contact. A scanning electron microscope image shows the top view of the crack front, opened cut, and closed cut during the crack propagation and opening process (Fig. S1b, ESI†). Our previous study suggested an AgNW density of over 0.5 mg cm−1 to guarantee good electrical contact at the cut surfaces.53Fig. 2b shows the resistance change as a function of the applied cyclic strain during loading and unloading. The resistance change upon stretching can be divided into two regions, a sensing region where the resistance increases linearly with increasing strain (R2 = 0.998), and a plateau region. The crack propagation and opening process was observed in situ under an optical microscope (Fig. 2b), while the resistance was measured simultaneously. The optical images in the sensing range (Fig. 2b) show the crack propagation and opening along the predefined cut. Fig. S1c (ESI†) shows the side view of the strain sensor under the scanning electron microscope (SEM). In the sensing range, the current flow follows the crack-guided paths. As a result, the resistance of the sensor increases with the advancing crack front. The resistance reaches a plateau and remains constant when the crack front reaches the pre-defined cut length as shown in the magnified optical image (Fig. 1c and e). The sensor can be further stretched without any resistance change, as shown in the plateau region (Fig. 2b). In this region, the crack front remains stationary and does not advance beyond the predefined cut length. The crack propagation along the cut length with respect to applied strain is shown in Fig. S2a (ESI†). The plateau region is important as it informs the user that the sensor has reached the limit of its linear working range and that it should not be stretched further to protect it from breaking under exceedingly large strains. The sensor's performance is reversible within the sensing region and the plateau region. With increasing strain beyond the plateau region, the local strain in front of the crack tip would exceed the failure strain of the AgNW/PDMS composite and cause irreversible structural damage to the AgNW network, leading to an irreversible change in resistance (Fig. S3, ESI†). The periodic cut design slightly reduces the effective Young's modulus of the structure (with 10 cuts), e.g., by 5% compared to the one without cuts (Fig. S2b, ESI†).
The electrical performance of the encapsulated strain sensors is tuneable due to the periodic cut design. Two critical parameters are defined in Fig. 2a: the distance between the cuts normalized by the specimen width p/w, and the cut length normalized by the specimen width lc/w. Fig. 2c illustrates the effect of p/w on the relative change in resistance while lc/w is kept constant at 0.9. With a decreasing distance between the cuts, the contour length of the electrical path increases, leading to an increase in resistance and GF at the same applied strain. For example, when p/w decreases from 0.3 to 0.1, GF increases from 83 to 289. Fig. 2d shows an increase in the resistance change with increasing lc/w while keeping p/w constant at 0.2. The maximum increase in resistance is related to the cut length. With an increasing cut length, the contour length of the electrical path also increases. And because the sensing range is smaller for the samples with a smaller lc, the cracks reach the cut length at a lower strain level. These results, based on the two parameters p/w and lc/w, demonstrated the excellent tunability of the sensor, both in terms of the GF and the sensing range.
The response time of the strain sensor was captured by attaching the sensor around a pressurized thin rubber tube which was 1 mm thick (Fig. S4a, ESI†). The rubber tube was connected to a hydraulic pump. The applied pressure in the tube and the change in resistance of the strain sensor were synchronized. The inset of Fig. S4a (ESI†) shows a response time of 53 ms for the resistance to increase from the baseline to 90% of the maximum resistance change. Fatigue testing involved 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 loading/unloading cycles at a strain rate of 0.6 s−1 and maximum strain of 30%. This demonstrated the excellent repeatability of the sensor for long-term use (Fig. S4b, ESI†).
000 loading/unloading cycles at a strain rate of 0.6 s−1 and maximum strain of 30%. This demonstrated the excellent repeatability of the sensor for long-term use (Fig. S4b, ESI†).
The sensors were immersed in water and saline solution for 20 days to test their durability in aqueous and biological fluid environments. The resistance of the sensors changed by 1.1% in water and 1.2% in saline solution after 20 days (Fig. 2e). We also tested the durability of the sensors by measuring the resistance vs. strain before and after 20 days of exposure to water and saline solution. After immersing in water and saline solution for 20 days, the sensor was taken out and tested with 30% tensile testing. The sensing performance remained stable in terms of the GF and the strain measurements during the cyclic extension and recovery phases (Fig. 2f).
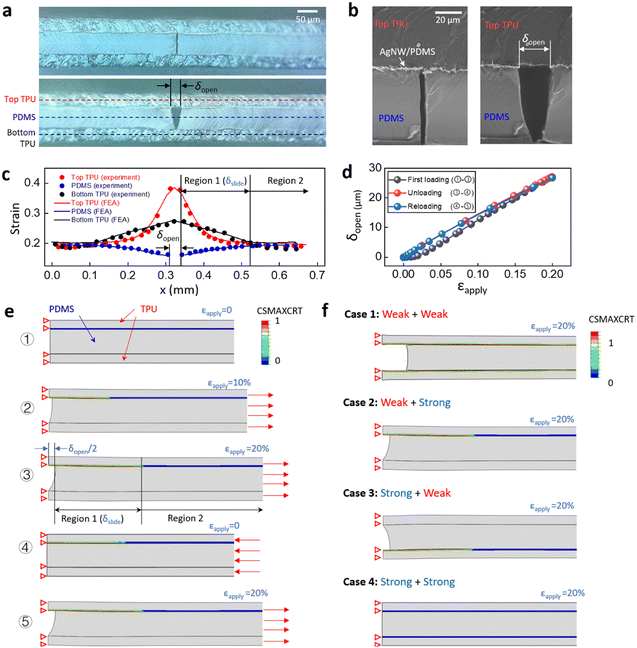
To better understand the underlying mechanism of crack propagation and opening, we measured the strain distributions in the three layers; namely the top TPU layer, the middle PDMS layer, and the bottom TPU layer, and conducted finite element analysis (FEA) to predict the forces acting on the sensor. Fig. 3a shows the optical images of the side view of the strain sensor under zero and 20% strain. Fig. 3b shows the SEM images of the side view of the sensor under zero and 10% strain. Fig. 3c plots the strain distribution in the three layers. The strains in the different layers are measured by the relative displacement of selected feature points (markers) under the microscope. The strain in the top TPU layer (red dots) shows a significant level of strain in the central region where the cut opens, while the strain in the bottom TPU layer (black dots) shows a limited response. However, in Region 2 at some distance from the cut, the strains in all three layers, including the PDMS layer (blue dots), are almost identical. At locations closer to the cut, we observed a larger mismatch in strain between the three layers. So based on this observation, we defined two regions in the length direction: namely Region 1 and Region 2. These two regions divide at the point where the strain in the top TPU layer and the PDMS layer diverge. In Region 1, the large mismatch of strains between the two layers is due to sliding at the interface because of relatively weak adhesion between the layers as a result of heat pressing. Fig. S1d (ESI†) shows the SEM images of the interfacial sliding between the top TPU layer and the AgNW/PDMS layer. The strain distribution measured from the SEM image agrees with the results measured by optical microscope (Fig. S1e, ESI†). The interface between the PDMS layer and the bottom TPU layer was plasma treated before lamination, which generated strong adhesion and prevented sliding between the layers (Fig. S1c, ESI†). When exposed to increasing levels of strain the crack propagates and opens along the predefined cut direction, and because of the different bonding strengths at the upper and lower interfaces, the crack surfaces form a V shape (Fig. 3a and b).
FEA of the three-layer structure with predefined cuts was conducted to understand the effect of interfacial bonding strength on the crack opening behaviour. Fig. 3d shows the simulated crack opening δopen during initial loading, unloading, and reloading at 20% strain for the sample with p/w = 0.2, lc/w = 0.9, t1 = t3 = 30 μm, and t2 = 60 μm. The corresponding images of the structure at different stages are shown in Fig. 3e. The contour plots in Fig. 3e show the maximum traction damage criteria for cohesive surfaces (CSMAXCRT), which evaluates the sliding damage at the interface on a scale of 0–1, where 1 represents a completely separated interface. During the initial loading cycle, δopen shows a slightly nonlinear response at 0–5% strain, followed by a linear response between 5–20% strain. This nonlinear response is due to the critical interfacial stress σc, beyond which the contact surfaces start to slide. Fig. S5 (ESI†) shows a nonlinear traction-separation law that is applied to the upper interface which involves a linear increase of stress followed by a constant critical stress of 0.02 MPa.54,55 During the unloading and reloading cycles, the sliding surfaces, which are considered damaged cohesive elements in FEA, remain in constant friction. As a result, in subsequent loading and unloading cycles, δopen shows a highly repeatable and linear applied strain response. At 20% strain, the simulated crack propagates to the predefined cut length, resulting in a predicted strain distribution in the three layers (Fig. 3c), which agrees well with the observed experimental results. Image ③ of Fig. 3e shows the simulation results for the maximum cut opening δopen (27.5 μm) and maximum sliding length δslide (162.7 μm) at 20% applied strain. This predicted value is in excellent agreement with the observed experimental results (δopen = 26.9 μm, δslide = 161.2 μm). With an increasing interfacial strength between the top and middle layers, the nonlinear response of the initial loading becomes more significant (Fig. S6a, ESI†). Conversely, with a decrease in the interfacial strength, sliding can occur at a lower applied strain (Fig. S6b, ESI†).
To further illustrate the importance of the interface design, we have compared four different combinations of interfacial strengths (Fig. 3f). Case 1 represents a sensor with weak bonding (σc = 0.02 MPa) at both the upper and lower interfaces. In this case, the strain mismatch induced simultaneous sliding at both interfaces, causing a cut opening of 94.78 μm. In comparison, Case 2 has weak bonding at the upper interface and strong bonding at the lower interface. Compared with Case 2, Case 1 yields a significantly larger δopen at 20% applied strain, which introduces a large local strain of 8.9% to the AgNW/PDMS composite in front of the crack tip and causes irreversible damage (Fig. S7a, ESI†).
In contrast, Case 2 with a value of δopen = 26.9 μm generates a totally reversible maximum strain of 4.9% in front of the crack tip on the top surface and 4.5% on the bottom surface. Fig. S3 (ESI†) shows the strain range for the AgNW/PDMS composite to be 5%. Case 3 is essentially the inverse of Case 2. For Case 4, with both interfaces strongly bonded, the local strain in the AgNW/PDMS layer reaches the reversible limit of 5% at the crack front with an applied strain of only 2.7%. In this case, the strain sensor has a limited stretchability. In conclusion, only the design with a weak upper interface, where the conductive materials are located, and a strong lower interface provides a relatively large linear and reversible sensing range. In general, many stretchable devices require encapsulation to enhance their environmental stability, their water and saline impermeability as well as their abrasion resistance. The interface design presented in this work can provide a valuable guide for a wide range of different applications.
Table 1 lists representative examples of gel-based, superhydrophobic, and encapsulated underwater strain sensors. The hydrogel and ionogel based underwater strain sensors respond to a large range of strains, but the GFs are small and provide a non-linear response in a wide range of different strains.37,38,56 The durability of gel-based sensors is limited when exposed to water, saline and air.40 A carbon black nanoparticle-based strain sensor with superhydrophobic surface modification achieved a good combination of both a wide range of strains and GFs, but the changes in resistance were nonlinear with GFs ranging from 1.5 to 354.57 Similarly, the AgNW/Mxene based sensor with PDMS coating showed a wide range of strains at 160%, but the GFs ranged from 255 to 948.45 A strain sensor exhibiting a highly nonlinear response complicates the interpretation of the sensing results. One reported sensor; namely the AgNPs based strain sensor with a superhydrophobic coating, exhibited a linear response with a constant GF.41 However, the sensing range of 0.1% strain was extremely narrow. In comparison, the strain sensor reported here exhibits both high linearity throughout the sensing range and a large GF of 289.
| Materials | Strain range (%) | GF | Linear sensing range | Safe range | Response time (ms) | Cyclic test | Water/saline durability (days) |
|---|---|---|---|---|---|---|---|
| Hydrogel56 | 300 | 1.4–3.4 | × | × | 130 | 1000 | 7 |
| Hydrogel38 | 300 | 0.6–3.9 | × | × | 125 | 3000 | n/a |
| Ionogel37 | 600 | 0.8–1.8 | × | × | 200 | 300 | n/a |
| AgNPs41 | 0.1 | 263.3 | √ | × | 75 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
n/a |
| Carbon Black NPs57 | 250 | 1.5–354 | × | × | n/a | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
14 |
| AgNW/Mxene45 | 160 | 255–948 | × | × | 71 | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
n/a |
| This work | 20 | 289 | √ | √ | 53 | 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
20 |
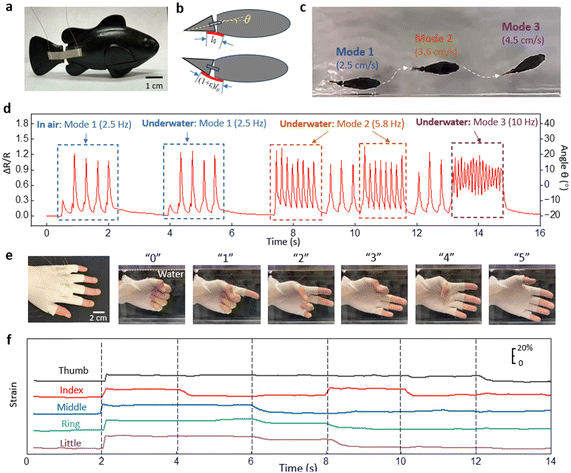
To demonstrate the strain sensor's suitability for amphibious applications, we mounted the strain sensor on a robotic fish. The two ends of the strain sensor were glued across the body and tail of the robotic fish (Fig. 4a). Fig. 4b shows the relative position of the sensor and the robotic fish from above. The strain sensor is at its initial length when the robotic tail is bent in the extreme clockwise direction and the angle between the body and the tail is denoted as θ = −20°. When the tail is parallel to the body, θ = 0. When the tail is bent in the extreme counterclockwise direction, the sensor undergoes maximum strain and the angle between the body and the tail is denoted as θ = 20°. Using a simple geometrical relationship, the strain on the sensor is considered linearly proportional to the change of angle Δθ. The robotic fish is programmed to swim with random motion. Fig. 4c shows the overlapped images of the robotic fish at different speeds and orientations. Fig. 4d shows the strain values of the sensor attached to the robotic fish which have been converted to the relative angle θ. The robotic fish was turned on in the air before dropped into the water tank. The first and second sets of motions in Fig. 4d are in the same mode (Mode 1), and the sensor shows an almost identical response for the motions in air and in water. After dropping the robotic fish in the tank, three different patterns of tail propulsion were observed with different amplitudes and frequencies. For example, Mode 1 and Mode 2 show the same sweeping angle of the tail between −20° and 20°, but with frequencies were different at 2.5 Hz and 5.8 Hz respectively. At the higher frequency the robotic fish swam faster (3.6 cm s−1) than at the lower frequency (2.5 cm s−1). In Mode 3, the signal showed an asymmetric sweeping range from −5° to 15°, which resulted in the robotic fish swimming in a curved motion (Fig. 4c).
Another demonstration involved an underwater glove used for sign language recognition. Fig. 4e shows five strain sensors heat pressed into the five finger joints of a latex glove. The calibration of the sensors attached to the finger joints is provided in ESI† (Fig. S8).
The images in Fig. 4e show how the numbers “0”, “1”, “2”, “3”, “4”, and “5” are signed in sign language. The corresponding strain signals from the sensors are shown in Fig. 4f. The strain on each finger joint is precisely captured during the flexion and extension of the fingers. This type of glove with integrated sensors can be used to monitor underwater communication between divers.
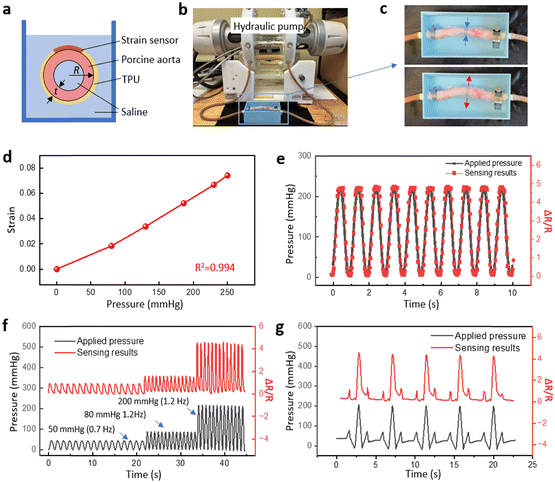
Measuring the strain on arterial vessels is crucial to assess the risk of arterial diseases such as aneurysms, stenosis and occlusion which can lead to heart attacks and strokes.58 Continuous monitoring of arterial strain can aid in early detection and management of potential complications, and hence avoid these life-threatening situations. Here we applied the strain sensor on a porcine aorta to demonstrate the performance of the strain sensor for blood pressure monitoring. Fig. 5a illustrates the cross-sectional view of the aorta surrounded by the ring-shaped strain sensor fabricated with an extended TPU substrate. The two ends of the TPU were heat-pressed to form a ring shape that fits the circumference of the aorta which was connected to a hydraulic pump and immersed in saline. The hydraulic pump in the fatigue tester was programmed to generate internal pressure inside the aorta (Fig. 5b). Fig. 5c shows the aorta under low and high internal pressure. The signal from the strain sensor was converted to pressure in mm Hg using the applied pressure calibration curve (Fig. 5d). While most mammals haves a linear stress–strain response within the normal blood pressure range, the slight nonlinearity in Fig. 5d is attributed to the nonlinear behavior of this ex vivo porcine aorta.59Fig. 5e shows the internal pressure and the sensing results when a sinusoidal pressure wave was applied. The response gave excellent agreement with the resistance change curve. Fig. 5f demonstrates a similar response but with changing frequency and an increasing applied systolic pressure. Finally, a unique pressure wave was created with small peaks before and after the main peak to mimic the blood pressure pulse in arteries.60 Details of the captured strain sensor readings are presented in Fig. 5g. Fig. 5e–g demonstrate the high precision and fast response of the strain sensor, indicating their potential for healthcare monitoring of blood vessels.
The amphibious strain sensor described in this study has shown a good combination of sensitivity and strain range, which is suitable for detecting the strain of robotic fish, a glove used underwater and the internal pressure of a porcine aorta. However, the local strain on human skin can reach 50% at some locations such as the back, elbows and knees.61 To make our strain sensor applicable to all wearable end-uses, several mechanical designs can be incorporated within our sensor to increase the sensing range. Fig. S9a (ESI†) shows an amphibious strain sensor with length l1, heat pressed onto athletic tape with length l2. Upon stretching, the athletic tape experiences a global strain of ε2 = 48%, while the local strain on the sensor is only ε1 = 20%. This is due to the larger Young's modulus of the sensor/tape composite compared to the athletic tape. On the other hand, the effective GF of the structure decreases to 120. Similarly, kirigami cuts can increase the stretching range. Fig. S9b (ESI†) shows an amphibious strain sensor with kirigami cuts on the extended TPU substrate. The region with kirigami patterns experiences larger strains compared to the sensor region, resulting in a global strain range of 52%, GF remain at 111 and only 20% strain on the amphibious sensor.
Experimental
Synthesis of the silver nanowire solution
Initially, a solution of polyvinylpyrrolidone (PVP) was prepared by combining 60 mL of 0.147 M PVP solution (MW ∼40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000, Sigma-Aldrich) with ethylene glycol (EG) in a flask and placing this mixture in an oil bath at 151.5 °C with continuous magnetic stirring at 150 rpm for 1 hour. Then 200 μL of 24 M CuCl2 solution in EG was added to the PVP solution followed by combining the PVP-CuCl2 mixture with 60 mL of 0.094 M AgNO3 solution in EG.50
000, Sigma-Aldrich) with ethylene glycol (EG) in a flask and placing this mixture in an oil bath at 151.5 °C with continuous magnetic stirring at 150 rpm for 1 hour. Then 200 μL of 24 M CuCl2 solution in EG was added to the PVP solution followed by combining the PVP-CuCl2 mixture with 60 mL of 0.094 M AgNO3 solution in EG.50
Fabrication and test of the strain sensors
In order to prepare a AgNW film, the synthesized AgNW solution was drop-cast on a plasma treated glass slide, which was placed on a hot plate at 60 °C to evaporate the solvent. After the solvent was evaporated, liquid PDMS (SYLGARD 184, DOW Inc.) with a weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 was mixed thoroughly and spin-coated on top of the AgNWs at 1000 rpm for 30 s. The AgNW/PDMS composite was cured at 70 °C for 1 hour and then peeled off from the sacrificial substrate.8,62 The cured sample was then attached to a spin-coated TPU film after plasma treatment on both surfaces. The AgNW/PDMS/TPU composite film was cut from the top surface using a mechanical cutter (silhouette CAMEO). The cut depth was programmed to penetrate through the AgNW/PDMS layers but stop at the surface of the TPU layer. Copper wires were attached to the two outer ends of the sample with silver epoxy (MG Chemicals), and another layer of TPU was applied and attached to the AgNW side of the AgNW/PDMS/TPU composite film by heat pressing at 150 °C for 3 min. For the sign language recognition test, the sensors were integrated on a latex glove by heat pressing at 150 °C for 3 min and tested on healthy human subject. Informed consent was obtained from the human participants involved in this experiment. The study protocol was approved by the Institutional Review Board at North Carolina State University. For the porcine aorta test, the aorta samples utilized in our study were kindly gifted by Dr Ke Cheng (Department of Molecular Biomedical Sciences at the College of Veterinary Medicine, North Carolina State University). This approach ensures that the samples we use are from healthy animals and allows for the ethical and efficient use of biological materials.
1 was mixed thoroughly and spin-coated on top of the AgNWs at 1000 rpm for 30 s. The AgNW/PDMS composite was cured at 70 °C for 1 hour and then peeled off from the sacrificial substrate.8,62 The cured sample was then attached to a spin-coated TPU film after plasma treatment on both surfaces. The AgNW/PDMS/TPU composite film was cut from the top surface using a mechanical cutter (silhouette CAMEO). The cut depth was programmed to penetrate through the AgNW/PDMS layers but stop at the surface of the TPU layer. Copper wires were attached to the two outer ends of the sample with silver epoxy (MG Chemicals), and another layer of TPU was applied and attached to the AgNW side of the AgNW/PDMS/TPU composite film by heat pressing at 150 °C for 3 min. For the sign language recognition test, the sensors were integrated on a latex glove by heat pressing at 150 °C for 3 min and tested on healthy human subject. Informed consent was obtained from the human participants involved in this experiment. The study protocol was approved by the Institutional Review Board at North Carolina State University. For the porcine aorta test, the aorta samples utilized in our study were kindly gifted by Dr Ke Cheng (Department of Molecular Biomedical Sciences at the College of Veterinary Medicine, North Carolina State University). This approach ensures that the samples we use are from healthy animals and allows for the ethical and efficient use of biological materials.
Numerical simulation of crack opening
FEA (ABAQUS CAE, Version 2017) was used to simulate crack opening and closing under applied strain. A symmetrical 3D model with a three-layer structure was built with the corresponding material properties for each of the different layers (Fig. S10, ESI†). The tip of the predefined cut was modeled with a curvature of ρ = 5 μm. The dimensions of the three layers were taken from experimental data and imported into Abaqus CAE and then meshed with solid quadratic tetrahedral elements (C3D10H). The Young's modulus of PDMS (2 MPa) was taken from the Dow Inc. datasheet. The Young's modulus of TPU (26 MPa) was taken from the TPU 95A datasheet. A cohesive zone model with a nonlinear traction-separation law was applied to the upper interface.54,55 The traction-separation law is composed of two phases: a period of linear relationship between traction σ and displacement δ with interfacial stiffness of K0, followed by a constant critical stress σc (Fig. S4, ESI†). The critical strength σc (0.02 MPa) and the interfacial stiffness K0 (60 MPa mm−1) between TPU and PDMS after heat pressing was estimated by performing a series of peel tests.63,64 Perfect bonding was applied to the lower interface to represent the strong bonding resulting from the plasma treatment. A symmetrical boundary condition was applied to the left edges of the two TPU layers and the uncut region with a length of w–lc in the AgNW/PDMS layer. A displacement boundary condition was applied to the opposite edges of the two TPU layers and the uncut region of AgNW/PDMS layer.Conclusions
We present an encapsulated stretchable amphibious strain sensor with a periodic cut pattern and a tailored interface design. The conductive layer of the resistance-based sensor is made of silver nanowires embedded below the surface of PDMS. The periodic cut design and the interfacial interactions between different layers have been studied to reveal the fundamental sensing mechanism. When stretched, the electrical resistance increases and the crack propagates. The sensor signal remains constant as the crack reaches the cut length and the tip opens. Both the sensing region and the plateau region are fully reversible without any hysteresis. The effect of the cut length and distance between the cuts have been studied, highlighting an unusual combination of sensitivity, sensing range, and sensor signal during the initial recovery phase. Experimental observations and finite element analysis have been conducted to study the effect of interfacial design on the crack advancing an opening. The strain sensor exhibits a GF up to 289, a high linear strain range (20%) together with an extra 10% additional safety range, a fast response time of 53 ms, excellent robustness for 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 repeated loading cycles, and resistance to water and saline solution degradation for over 20 days. We have demonstrated the amphibious strain sensor on a robotic fish in air and water, an underwater sign language recognition glove, and as a blood pressure sensor for monitoring arterial blood pressure, illustrating great potential for use in both underwater environments and for implantable medical devices. Of particular note is the interface design presented in this work, which can provide valuable guidance for many stretchable devices with encapsulated layers.
000 repeated loading cycles, and resistance to water and saline solution degradation for over 20 days. We have demonstrated the amphibious strain sensor on a robotic fish in air and water, an underwater sign language recognition glove, and as a blood pressure sensor for monitoring arterial blood pressure, illustrating great potential for use in both underwater environments and for implantable medical devices. Of particular note is the interface design presented in this work, which can provide valuable guidance for many stretchable devices with encapsulated layers.
Author contributions
S. W. and Y. Z. conceived the idea and designed the experiments and simulations. S. W. conducted the finite element analysis, S. W., D. K. and X. T. conducted the experiments and data analysis. S. W., M. W. K. and Y. Z. wrote the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
The authors gratefully acknowledge the financial support from NSF (award no. 2122841 and 2134664), NIH (award no. R01HD108473), and DOD (award no. W81XWH-21-1-0185).Notes and references
- S. Yao, P. Swetha and Y. Zhu, Adv. Healthcare Mater., 2018, 7, 1700889 CrossRef CAS PubMed.
- Y. Yang, Z. Cao, P. He, L. Shi, G. Ding, R. Wang and J. Sun, Nano Energy, 2019, 66, 104134 CrossRef CAS.
- Y. Luo, M. R. Abidian, J.-H. Ahn, D. Akinwande, A. M. Andrews, M. Antonietti, Z. Bao, M. Berggren, C. A. Berkey, C. J. Bettinger, J. Chen, P. Chen, W. Cheng, X. Cheng, S.-J. Choi, A. Chortos, C. Dagdeviren, R. H. Dauskardt, C.-a. Di, M. D. Dickey, X. Duan, A. Facchetti, Z. Fan, Y. Fang, J. Feng, X. Feng, H. Gao, W. Gao, X. Gong, C. F. Guo, X. Guo, M. C. Hartel, Z. He, J. S. Ho, Y. Hu, Q. Huang, Y. Huang, F. Huo, M. M. Hussain, A. Javey, U. Jeong, C. Jiang, X. Jiang, J. Kang, D. Karnaushenko, A. Khademhosseini, D.-H. Kim, I.-D. Kim, D. Kireev, L. Kong, C. Lee, N.-E. Lee, P. S. Lee, T.-W. Lee, F. Li, J. Li, C. Liang, C. T. Lim, Y. Lin, D. J. Lipomi, J. Liu, K. Liu, N. Liu, R. Liu, Y. Liu, Y. Liu, Z. Liu, Z. Liu, X. J. Loh, N. Lu, Z. Lv, S. Magdassi, G. G. Malliaras, N. Matsuhisa, A. Nathan, S. Niu, J. Pan, C. Pang, Q. Pei, H. Peng, D. Qi, H. Ren, J. A. Rogers, A. Rowe, O. G. Schmidt, T. Sekitani, D.-G. Seo, G. Shen, X. Sheng, Q. Shi, T. Someya, Y. Song, E. Stavrinidou, M. Su, X. Sun, K. Takei, X.-M. Tao, B. C. K. Tee, A. V.-Y. Thean, T. Q. Trung, C. Wan, H. Wang, J. Wang, M. Wang, S. Wang, T. Wang, Z. L. Wang, P. S. Weiss, H. Wen, S. Xu, T. Xu, H. Yan, X. Yan, H. Yang, L. Yang, S. Yang, L. Yin, C. Yu, G. Yu, J. Yu, S.-H. Yu, X. Yu, E. Zamburg, H. Zhang, X. Zhang, X. Zhang, X. Zhang, Y. Zhang, Y. Zhang, S. Zhao, X. Zhao, Y. Zheng, Y.-Q. Zheng, Z. Zheng, T. Zhou, B. Zhu, M. Zhu, R. Zhu, Y. Zhu, Y. Zhu, G. Zou and X. Chen, ACS Nano, 2023, 17, 5211–5295 CrossRef CAS PubMed.
- D. J. Lipomi, M. Vosgueritchian, B. C. Tee, S. L. Hellstrom, J. A. Lee, C. H. Fox and Z. Bao, Nat. Nanotechnol., 2011, 6, 788–792 CrossRef CAS PubMed.
- H. U. Chung, A. Y. Rwei, A. Hourlier-Fargette, S. Xu, K. Lee, E. C. Dunne, Z. Xie, C. Liu, A. Carlini, D. H. Kim, D. Ryu, E. Kulikova, J. Cao, I. C. Odland, K. B. Fields, B. Hopkins, A. Banks, C. Ogle, D. Grande, J. B. Park, J. Kim, M. Irie, H. Jang, J. Lee, Y. Park, J. Kim, H. H. Jo, H. Hahm, R. Avila, Y. Xu, M. Namkoong, J. W. Kwak, E. Suen, M. A. Paulus, R. J. Kim, B. V. Parsons, K. A. Human, S. S. Kim, M. Patel, W. Reuther, H. S. Kim, S. H. Lee, J. D. Leedle, Y. Yun, S. Rigali, T. Son, I. Jung, H. Arafa, V. R. Soundararajan, A. Ollech, A. Shukla, A. Bradley, M. Schau, C. M. Rand, L. E. Marsillio, Z. L. Harris, Y. Huang, A. Hamvas, A. S. Paller, D. E. Weese-Mayer, J. Y. Lee and J. A. Rogers, Nat. Med., 2020, 26, 418–429 CrossRef CAS PubMed.
- D.-H. Kim, N. Lu, R. Ma, Y.-S. Kim, R.-H. Kim, S. Wang, J. Wu, S. M. Won, H. Tao, A. Islam, K. J. Yu, T.-I. Kim, R. Chowdhury, M. Ying, L. Xu, M. Li, H.-J. Chung, H. Keum, M. Mccormick, P. Liu, Y. Zhang, F. G. Omenetto, Y. G. Huang, T. Coleman and J. A. Rogers, Science, 2011, 333, 838–843 CrossRef CAS PubMed.
- C. M. Boutry, Y. Kaizawa, B. C. Schroeder, A. Chortos, A. Legrand, Z. Wang, J. Chang, P. Fox and Z. Bao, Nat. Electron., 2018, 1, 314–321 CrossRef.
- S. Yao and Y. Zhu, Nanoscale, 2014, 6, 2345–2352 RSC.
- J. Zhang, B. Xu, K. Chen, Y. Li, G. Li and Z. Liu, SusMat, 2024, e207 CrossRef.
- M. Amjadi, K. U. Kyung, I. Park and M. Sitti, Adv. Funct. Mater., 2016, 26, 1678–1698 CrossRef CAS.
- A. Libanori, G. Chen, X. Zhao, Y. Zhou and J. Chen, Nat. Electron., 2022, 5, 142–156 CrossRef CAS.
- Z. Zhou, K. Chen, X. Li, S. Zhang, Y. Wu, Y. Zhou, K. Meng, C. Sun, Q. He, W. Fan, E. Fan, Z. Lin, X. Tan, W. Deng, J. Yang and J. Chen, Nat. Electron., 2020, 3, 571–578 CrossRef.
- M. Amjadi, A. Pichitpajongkit, S. Lee, S. Ryu and I. Park, ACS Nano, 2014, 8, 5154–5163 CrossRef CAS PubMed.
- S. Yao, L. Vargas, X. Hu and Y. Zhu, IEEE Sens. J., 2018, 18, 3010–3015 Search PubMed.
- S. Yao, P. Ren, R. Song, Y. Liu, Q. Huang, J. Dong, B. T. O'Connor and Y. Zhu, Adv. Mater., 2020, 32, 1902343 CrossRef CAS PubMed.
- C. Wang, M. Cai, Z. Hao, S. Nie, C. Liu, H. Du, J. Wang, W. Chen and J. Song, Adv. Intell. Syst., 2021, 3, 2100031 CrossRef.
- Y. Jiang, Z. Liu, N. Matsuhisa, D. Qi, W. R. Leow, H. Yang, J. Yu, G. Chen, Y. Liu, C. Wan, Z. Liu and X. Chen, Adv. Mater., 2018, 30, 1706589 CrossRef PubMed.
- Y. Wang, R. Shu and X. Zhang, Angew. Chem., Int. Ed., 2023, 62, e202303446 CrossRef CAS PubMed.
- R. Zhou, Y. Zhang, F. Xu, Z. Song, J. Huang, Z. Li, C. Gao, J. He, W. Gao and C. Pan, Small, 2023, 19, 2301544 CrossRef CAS PubMed.
- B. Liu, B. Lan, L. Shi, Y. Cheng, J. Sun and R. Wang, ACS Appl. Mater. Interfaces, 2024, 16, 35865–37338 CrossRef PubMed.
- Y. Yu, J. Nassar, C. Xu, J. Min, Y. Yang, A. Dai, R. Doshi, A. Huang, Y. Song, R. Gehlhar, A. D. Ames and W. Gao, Sci. Robot., 2020, eaaz7946 CrossRef PubMed.
- K. Wang, L. W. Yap, S. Gong, R. Wang, S. J. Wang and W. Cheng, Adv. Funct. Mater., 2021, 2008347 CrossRef CAS.
- J.-W. Jeong, W.-H. Yeo, A. Akhtar, J. J. S. Norton, Y.-J. Kwack, S. Li, S.-Y. Jung, Y. Su, W. Lee, J. Xia, H. Cheng, Y. Huang, W.-S. Choi, T. Bretl and J. A. Rogers, Adv. Mater., 2013, 25, 6839–6846 CrossRef CAS PubMed.
- W. Zhou, S. Yao, H. Wang, Q. Du, Y. Ma and Y. Zhu, ACS Nano, 2020, 14, 5798–5805 CrossRef CAS PubMed.
- Y. Liu, C. Yiu, Z. Song, Y. Huang, K. Yao, T. Wong, J. Zhou, L. Zhao, X. Huang, S. K. Nejad, M. Wu, D. Li, J. He, X. Guo, J. Yu, X. Feng, Z. Xie and X. Yu, Sci. Adv., 2022, 8, eabl6700 CrossRef PubMed.
- X. Guo, X. Wang, D. Ou, J. Ye, W. Pang, Y. Huang, J. A. Rogers and Y. Zhang, npj Flexible Electron., 2018, 2, 14 CrossRef.
- L. Veeramuthu, C.-J. Cho, F.-C. Liang, M. Venkatesan, R. Kumar G, H.-Y. Hsu, R.-J. Chung, C.-H. Lee, W.-Y. Lee and C.-C. Kuo, ACS Appl. Mater. Interfaces, 2022, 14, 30160–30173 CrossRef CAS PubMed.
- F.-C. Liang, H.-J. Ku, C.-J. Cho, W.-C. Chen, W.-Y. Lee, W.-C. Chen, S.-P. Rwei, R. Borsali and C.-C. Kuo, J. Mater. Chem. C, 2020, 8, 5361–5369 RSC.
- Y. Liu, M. Ahmad, R. A. Venditti, O. D. Velev and Y. Zhu, Adv. Electron. Mater., 2024, 2300792 CrossRef CAS.
- S. I. Rich, R. J. Wood and C. Majidi, Nat. Electron, 2018, 1, 102–112 CrossRef.
- T. G. Thuruthel, B. Shih, C. Laschi and M. T. Tolley, Sci. Robot., 2019, 4, eaav1488 CrossRef PubMed.
- O. A. Araromi, M. A. Graule, K. L. Dorsey, S. Castellanos, J. R. Foster, W.-H. Hsu, A. E. Passy, J. J. Vlassak, J. C. Weaver, C. J. Walsh and R. J. Wood, Nature, 2020, 587, 219–224 CrossRef CAS PubMed.
- S. Wu, G. L. Baker, J. Yin and Y. Zhu, Soft Robot., 2021, 9, 1031–1039 CrossRef PubMed.
- S. Wu, Y. Hong, Y. Zhao, J. Yin and Y. Zhu, Sci. Adv., 2023, 9, eadf8014 CrossRef CAS PubMed.
- D. Zhu, S. Duan, J. Liu, S. Diao, J. Hong, S. Xiang, X. Wei, P. Xiao, J. Xia, W. Lei, B. Wang, Q. Shi and J. Wu, Nanoscale, 2024, 16, 5409–5420 RSC.
- S. Wu, T. Zhao, Y. Zhu and G. H. Paulino, Proc. Natl. Acad. Sci. U. S. A., 2024, 121, e2322625121 CrossRef CAS PubMed.
- L. Xu, Z. Huang, Z. Deng, Z. Du, T. L. Sun, Z. H. Guo and K. Yue, Adv. Mater., 2021, 33, 2105306 CrossRef CAS PubMed.
- Z. Zhang, G. Chen, Y. Xue, Q. Duan, X. Liang, T. Lin, Z. Wu, Y. Tan, Q. Zhao and W. Zheng, Adv. Funct. Mater., 2023, 33, 2305705 CrossRef CAS.
- G. Li, C. Li, G. Li, D. Yu, Z. Song, H. Wang, X. Liu, H. Liu and W. Liu, Small, 2022, 18, 2101518 CrossRef CAS PubMed.
- K. Kudo, J. Ishida, G. Syuu, Y. Sekine and T. Ikeda-Fukazawa, J. Chem. Phys., 2014, 140, 044909 CrossRef PubMed.
- L. Liu, Z. Jiao, J. Zhang, Y. Wang, C. Zhang, X. Meng, X. Jiang, S. Niu, Z. Han and L. Ren, ACS Appl. Mater. Interfaces, 2020, 13, 1967–1978 CrossRef PubMed.
- B. P. Dyett, A. H. Wu and R. N. Lamb, ACS Appl. Mater. Interfaces, 2014, 6, 18380–18394 CrossRef CAS PubMed.
- M.-F. Lin, J. Xiong, J. Wang, K. Parida and P. S. Lee, Nano Energy, 2018, 44, 248–255 CrossRef CAS.
- J. Qu, Q. Yuan, Z. Li, Z. Wang, F. Xu, Q. Fan, M. Zhang, X. Qian, X. Wang and X. Wang, Nano Energy, 2023, 111, 108387 CrossRef CAS.
- W. Fan, C. Li, C. Wang, C. Huang, T. Ma, W. Zhou and Z. Wan, Carbon, 2024, 118918 CrossRef CAS.
- T. Kim, T. Lee, G. Lee, Y. W. Choi, S. M. Kim, D. Kang and M. Choi, Appl. Sci., 2018, 8, 367 CrossRef.
- H.-Y. Mi, X. Jing, B. N. Napiwocki, B. S. Hagerty, G. Chen and L.-S. Turng, J. Mater. Chem. B, 2017, 5, 4137–4151 RSC.
- N. Dolmaire, E. Espuche, F. Méchin and J. P. Pascault, J. Polym. Sci., Part B: Polym. Phys., 2004, 42, 473–492 CrossRef CAS.
- M. Dong, Q. Li, H. Liu, C. Liu, E. K. Wujcik, Q. Shao, T. Ding, X. Mai, C. Shen and Z. Guo, Polymer, 2018, 158, 381–390 CrossRef CAS.
- Y. Sun, B. Gates, B. Mayers and Y. Xia, Nano Lett., 2002, 2, 165–168 CrossRef CAS.
- S. Wu, S. Yao, Y. Liu, X. Hu, H. H. Huang and Y. Zhu, ACS Appl. Mater. Interfaces, 2020, 12, 41696–41703 CrossRef CAS PubMed.
- F. Xu and Y. Zhu, Adv. Mater., 2012, 24, 5117–5122 CrossRef CAS PubMed.
- S. Wu, K. Moody, A. Kollipara and Y. Zhu, ACS Appl. Mater. Interfaces, 2022, 15, 1798–1807 CrossRef PubMed.
- T. Jiang, R. Huang and Y. Zhu, Adv. Funct. Mater., 2014, 24, 396–402 CrossRef CAS.
- F. R. Poblete and Y. Zhu, J. Mech. Phys. Solids, 2019, 127, 191–207 CrossRef CAS.
- J. Ren, Y. Liu, Z. Wang, S. Chen, Y. Ma, H. Wei and S. Lü, Adv. Funct. Mater., 2022, 32, 2107404 CrossRef CAS.
- Z. Dai, S. Ding, M. Lei, S. Li, Y. Xu, Y. Zhou and B. Zhou, J. Mater. Chem. A, 2021, 9, 15282–15293 RSC.
- A. S. Shah, C. W. Chin, V. Vassiliou, S. J. Cowell, M. Doris, T. N. C. Kwok, S. Semple, V. Zamvar, A. C. White and G. McKillop, Circulation, 2014, 130, 1607–1616 CrossRef PubMed.
- R. S. Seymour and A. J. Blaylock, Physiol. Biochem. Zool., 2000, 73, 389–405 CrossRef CAS PubMed.
- J. K. Li, Dynamics of the vascular system, World Scientific, 2004 Search PubMed.
- A. J. Gallagher, A. Ní Annaidh, K. Bruyère, M. Otténio, H. Xie and M. Gilchrist, Dynamic tensile properties of human skin, in IRCOBI conference, International Research Council on the Biomechanics of Injury, Dublin Ireland, 2012, vol. 59, pp. 494–502 Search PubMed.
- S. Yao, J. Cui, Z. Cui and Y. Zhu, Nanoscale, 2017, 9, 3797–3805 RSC.
- K. Kendall, J. Phys. D: Appl. Phys., 1975, 8, 1449 CrossRef.
- K. Kendall, J. Phys. D: Appl. Phys., 1975, 8, 512 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00757c |
| This journal is © The Royal Society of Chemistry 2024 |