Principles for designing sustainable and high-strain rate stress wave dissipating materials

Abstract

Dynamic covalent networks serve as effective tools for dissipating high-strain rate mechanical energy throughout reversible bond exchange reactions. Despite their potential, a gap exists in understanding how polymer chain mobility and the kinetics of bond exchange reactions impact the energy dissipating capabilities of dynamic covalent networks. This study presents an optimal strategy to enhance energy dissipation by controlling the side chain structures and bond exchange rates of dynamic covalent networks. Lipoic acid-derived polymers are chosen as our model system due to their easily tunable side chains and disulfide-rich backbones. High-strain rate stress waves are subjected to the polymers using a laser-induced shock wave technique. A strong correlation is observed between the energy dissipation capability and the glass transition temperature of the poly(disulfide)s. Furthermore, the addition of a catalyst to accelerate the disulfide exchange reaction improves energy dissipation. Leveraging the inherent nature of cyclic disulfides, our polymers exhibit self-healing and chemical recycling to monomers. The principles observed in this study provide a rational framework for designing sustainable and efficient energy dissipating materials.

---

New concepts

This study introduces a novel approach to understanding and enhancing stress wave dissipation in polymer materials under high-strain rates by elucidating the interplay between polymer chain mobility and dynamic covalent bond exchange kinetics. While incorporating dynamic covalent bonds into polymer networks has been explored for strain energy dissipation, the effects of molecular architecture and bond dynamics in these systems remained poorly understood. By manipulating the side chain architecture of poly(disulfide)s and incorporating a catalyst that promotes exchange kinetics, we demonstrate that optimizing chain mobility and bond exchange rates leads to superior damping performance within a specific strain range. This concept provides unprecedented insights into the design principles for dynamic covalent polymers, revealing the complex relationship between molecular structure, bond dynamics, and stress wave dissipation. Moreover, the inherent self-healing and recycling abilities of these materials present a sustainable solution for protective materials against high-strain rate events.

1. Introduction

The dynamic response of materials to high-strain rate stress waves, generated by high-energy events such as high-speed impact and explosions, has gained significant attention in recent years across various engineering and industrial sectors. For instance, hypervelocity impacts caused by collisions with small space debris traveling at speeds exceeding 7 km s⁻¹ are becoming frequent due to the growing density of human activities in Earth's orbit.¹ The increased use of high-energy explosives and advanced weaponry also results in more frequent generation of high-strain rate stress waves. These high-strain rate stress waves accompanying high pressure can compromise structural integrity,² accelerate material fatigue,³ and threaten human health.⁴ As such, the ability to effectively dissipate the pressure of these waves is paramount in enhancing the durability and safety of critical machinery and human lives.

Traditional methods for dissipating low frequency stress waves, including vibrations and noises, utilize the viscoelastic behaviors and segmental chain motions of polymers. These properties can be enhanced by adjusting the glass transition temperature (T_g) and incorporating additional relaxational components like secondary bonds and entanglements.^5–7 However, these passive approaches often prove inadequate for extremely fast stress waves and high pressure, since their dynamics are limited at such short timescales. This limitation has stimulated interest in developing highly damping materials that can actively respond and adapt to high-strain rates and frequencies exceeding 10⁶ s⁻¹ and high pressure. Among the most promising advancements in this field is the leverage of dynamic chemistry and material microstructures. Dynamic chemistries, which offer reversible bond exchange mechanisms, can be employed to create materials with fast strain rate reactivity.^8,9 However, designing high-performance damping materials using dynamic bonds presents a significant challenge in balancing the reactivity and stability of the dynamic bonds. These bonds must be reversible enough to dissipate energy quickly, but stable enough to maintain structural integrity. Additionally, certain dynamic covalent polymers have demonstrated tunable nanophase-separated microstructures. These microstructures can be exploited to respond effectively to low-strain rate stress waves.^10,11 Nevertheless, research on their response to high-strain rate stress waves is still limited, except in the case of polymers with secondary bonding.¹²

Disulfide bonds are robust but undergo reversible exchange reactions triggered by heat,^13,14 light,^15–17 mechanical stress,^18,19 and chemical stimulus.^20,21 This dynamic nature of disulfides is utilized for creating autonomous polymers with self-healing, shape-morphing, and degrading capabilities.^22–24 Particularly, five-membered cyclic disulfides exhibit unique dynamicity due to their intermediate ring strain values that facilitate reversible ring-opening polymerization and ring-closing depolymerization.^25,26 Lipoic acid (LA), a naturally occurring five-membered cyclic disulfide (1,2-dithiolane) with a carboxylic acid end group, has been extensively investigated to construct sustainable poly(disulfide)s. These polymers can be accomplished either directly from LA or by using derivative monomers through modification of its carboxylic acid functionality. We hypothesize that adjusting the exchange rate of disulfide bonds in poly(disulfide)s can effectively attenuate the pressure of high-strain stress waves. Additionally, diverse nanoscale morphologies can be engineered by exploiting the chemical conjugation of phase-separation-inducing agents to the carboxylic acid groups.

In this study, we aim to explore how polymer architectures and the rates of reversible exchange reactions influence the dissipation of high-strain rate stress wave, particularly when subjected to a shock wave input. LA-derived polymers serve as our model system due to their easily tunable side chains and disulfide-rich main chains (Scheme 1). To control the aliphatic chain length and the presence of hydrogen bonding in LAs, we employ esterification or amidification of their carboxylic acid end groups. The exchange reaction of disulfides is accelerated at room temperature by adjusting the amount of a strong base, 1,8-diazabicyclo[5.4.0]undec-7-ene (DBU).²⁷ Utilizing a laser-induced shock wave technique,²⁸ we demonstrate superior energy dissipation in dynamic poly(disulfide)s with optimum side chain architecture and rapid disulfide exchange rate. Additionally, these polymers exhibit fast self-healing and efficient chemical recycling, which offers a promising route for designing sustainable energy-dissipating materials.

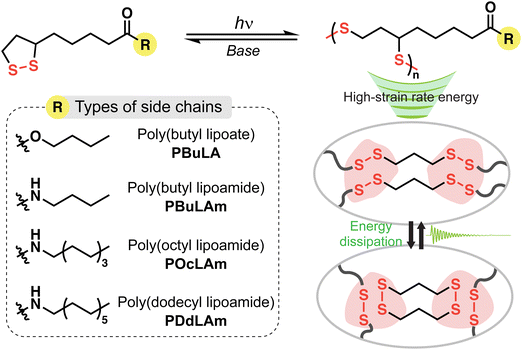Scheme 1 Chemically recyclable and high-strain rate stress wave dissipating poly(disulfide)s with engineered side chains.

2. Results and discussion

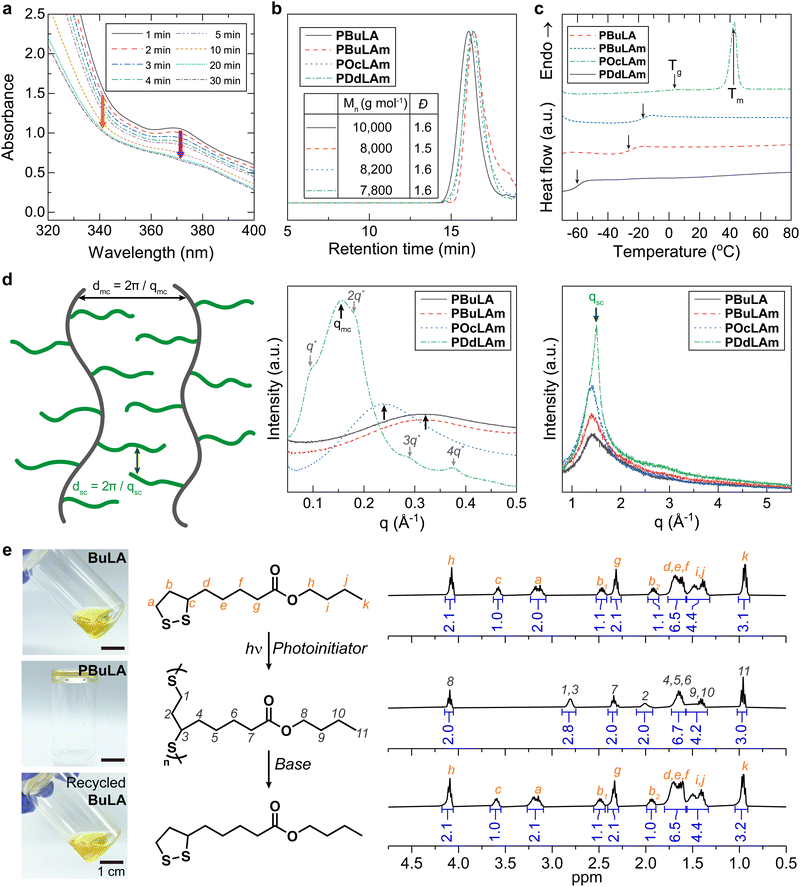
We synthesized four types of monomers by carbodiimide coupling reaction of LA with 1-butanol (BuLA), 1-butylamine (BuLAm), 1-octylamine (OcLAm), and dodecylamine (DdLAm) (Scheme S1, ESI†). While some of LA derivatives have been successfully polymerized under heat without any initiators, our synthesized monomers did not show high conversion to polymers above their melting temperatures for a long period. Instead, we decided to add small amounts of photo-initiators to accelerate the photo-initiated ring opening polymerization (ROP) process. The kinetics of photo-initiated ROP was monitored by UV-vis absorption spectroscopy (Fig. 1a and Fig. S1, ESI†). The distinctive absorption peak of the cyclic LA derivatives around 340 nm and the peak of the photo-initiators around 370 nm gradually diminished under a white lamp (70 mW cm⁻²) and reached equilibrium within 30 minutes, implying the completion of polymerization. With this optimized polymerization condition and further purification, linear poly(disulfide)s were successfully synthesized, confirmed by ¹H NMR analysis (Fig. S2–S5, ESI†). All LA derived polymers had a molecular weight of approximately 7800 to 10 000 g mol⁻¹ with a moderate dispersity (Đ ≈ 1.5) (Fig. 1b). Differential scanning calorimetry (DSC) results indicated that the thermal behaviors of linear polymers are greatly influenced by the chemical structure of their side chains (Fig. 1c). The additional intermolecular interactions induced by hydrogen bonding enhance the T_g of polymer with similar side chain length from −60 °C (PBuLA) to −26 °C (PBuLAm). We did not observe internal plasticization effect by increasing the aliphatic chain length from PBuLAm to PDdLAm.^29,30 Instead, the T_g of the linear polymers steadily increases with the length of side chain. A notable melting peak (T_m) was observed only in PDdLAm since comb-like polymers tend to be crystallized in the side chains with more than 10–12 alkyl carbons.^31,32 To further elucidate the structure of the synthesized polymers, we conducted wide-angle X-ray diffraction (WAXD) and small-angle X-ray scattering (SAXS) experiments (Fig. 1d). The peak observed in the SAXS region (indicated by black arrows, q_mc) represents the average distance between main chains (d_mc). Due to a better long-range order of the corresponding structure, the peak sharpens as increasing the number of aliphatic units. Additionally, the peak shifts systematically to the lower scattering vectors from 0.032 to 0.016 Å⁻¹. The slope of d_mc on the number of aliphatic units was calculated to be 2.6 Å, which is two-fold higher than one CH₂ unit (1.25 Å), implying end-on contact of the side chains.^33,34 Additionally, PDdLAm exhibited a lamellar phase due to the crystallization of long alkyl chains (indicated by gray arrows). The average distance between the side chains (d_sc) was estimated from the amorphous halo (q_sc = 1.5 Å⁻¹) observed in the XRD data (indicated by green arrows, q_sc), which is constant regardless of side chain length. Finally, the viscous polymer was completely depolymerized in a basic solution (0.02 M DBU in dichloromethane), and the recovered monomers exhibited identical NMR spectra with that of initial monomers (Fig. 1e and Fig. S6–S8, ESI†).

Fig. 1 Characterization of linear poly(disulfide)s. (a) The change in UV-vis absorption spectra of BuLA during a photo-polymerization process. The orange arrow indicates the distinctive peak of the cyclic LA derivatives, while the purple arrow marks the peak corresponding to the photo-initiators. (b) Molecular weights and dispersity (Đ), (c) heat flow thermograms, (d) schematic illustration (left), SAXS (middle), and XRD (right) results of poly(disulfide)s. The peak observed at the lower q range (q_mc) corresponds to the average distance between main chains (black arrows, d_mc) and the peak at the higher q range (q_sc) represents the average distance between aliphatic side chains (green arrows, d_sc). Only PDdLAm exhibited additional lamellar self-assembly. (e) Chemical recycling of PBuLA. ¹H NMR spectra indicate reversible polymerization and depolymerization of PBuLA.

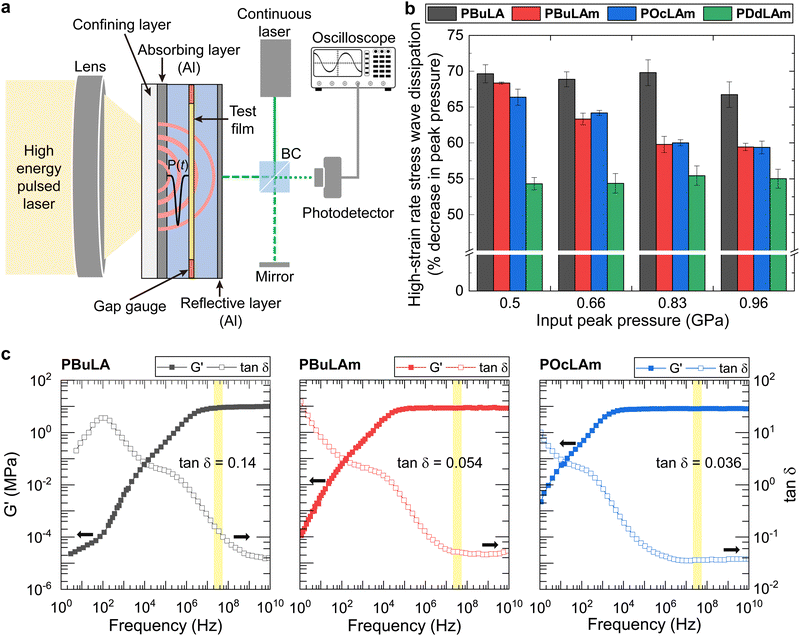
The effects of T_g and the morphology on high-strain rate stress wave dissipation under shock loading were investigated. The percentage of pressure dissipation for the linear poly(disulfide)s was investigated by applying laser-induced high-strain stress waves in a sandwich specimen configuration (Fig. 2a), and experimental detail was described in the ESI† (Section S4).³⁵ Increasing the length of side chains (PBuLAm, POcLAm, and PDdLAm) led to a deterioration in pressure attenuation ability (Fig. 2b). The observed pressure attenuation trend appears to be correlated with the T_g of linear polymers. Among the poly(disulfide)s, PBuLA with the lowest T_g demonstrates the most effective pressure dissipating performance, whereas PDdLAM with the highest T_g shows the least favorable pressure dissipating performance. Polymers with similar T_g values, such as PBuLAm and POcLAm, exhibit comparable pressure dissipating properties. Abrupt drop in pressure dissipation performance of PDdLAm compared to that of other polymers can be rationalized by restricted chain segmental motions of crystalline regions in the semi-crystalline structure.¹²

Fig. 2 High-strain stress wave dissipating properties of linear poly(disulfide)s. (a) Schematics of laser induced high-strain rate stress wave experimental setup and specimen structure. (b) The percentage of the stress wave dissipation of poly(disulfide)s as a function of input peak pressure. (c) The time–temperature superposition of storage modulus (G′, closed square) and loss factor (tan δ, open square) for poly(disulfide)s by horizontally shifting plots along the frequency scale with the reference temperature of 25 °C. The frequency ranges for high-strain rate stress waves are colored in yellow.

To elucidate the relationship between rheological properties and energy dissipation, we constructed master curves of storage modulus (G′) and loss factor (tan δ) at a reference temperature (T_ref) of 25 °C based on the time–temperature superposition principle (Fig. 2c and Fig. S9–S14, ESI†). The G′ is proportional to the stiffness of a material and measures its ability to store energy. Conversely, the G′′ measures the damping characteristics of the material, reflecting the amount of energy dissipated as heat due to molecular motions. The tan δ, defined as the ratio of G′′ to G′, quantifies the material's ability to dissipate energy relative to its ability to store it, thus serving as a measure of the material's damping capacity. Based on this understanding, we hypothesized that a sample with a higher tan δ at a corresponding frequency should exhibit superior stress wave dissipating capability. In laser-induced shock wave tests, the strain rate is approximated by the equation 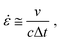where ν is the particle velocity generated by the pressure pulse over duration Δt, and c is the longitudinal wave velocity. This study uses nominal strain rates between 5.5–9.6 × 10⁶ s⁻¹. The corresponding frequencies, calculated as the reciprocal of twice the duration, ranged from 2.5–3.6 × 10⁷ Hz (Fig. S17, ESI†).³⁶ In the calculated frequency domain, PBuLA (tan δ = 0.14) is more than 2 times higher than that of PBuLAm (tan δ = 0.054) and POcLAm (tan δ = 0.036). As we hypothesized, PBuLA, which has a higher tan δ at that frequency, has a better ability to dissipate stress waves than PBuLAm and POcLAm. Although the tan δ of PBuLAm is only marginally higher than that of POcLAm, the stress wave dissipating capability is similar within the margin of error, which may be an additional effect of microstructure. Previous studies have shown that the primary peak that appears in the range of 0.2–0.5 Å⁻¹ in SAXS analysis is associated with phase separation, and that the intensity and position of the peak affects the stress wave dissipating capability.¹² Therefore, the microstructure of POcLAm provides an additional energy dissipation mechanism, improving the pressure dissipation ratio to a level comparable to PBuLAm.

To assess the impact of disulfide bonds on high-strain rate stress wave dissipation, we established a control system by excluding reversible covalent bonds in the polymer chain backbones. Poly(hexyl acrylate)s (PHA) were selected and synthesized through free-radical polymerization, resulting in a molecular weight of 8700 g mol⁻¹ with moderate dispersity (Đ ≈ 1.5) (Fig. S18, ESI†). Compared to PBuLA, PHA exhibited a similar T_g (about −60 °C) (Fig. S19, ESI†), and comparable G′ (around 9.8 MPa) and tan δ (around 0.1) values across the shock wave frequency range (Fig. S20–S22, ESI†). The only difference between these samples lies in the presence of reversible disulfide bonds. Unexpectedly, PHA demonstrated an equally effective dissipating capability as PBuLA (Fig. S23, ESI†). We suspect that the reversible disulfide exchange reactions may not occur at high frequency strain rates, particularly at room temperature. Therefore, we opted to introduce a specific catalyst to facilitate the disulfide exchange reactions even at room temperature.

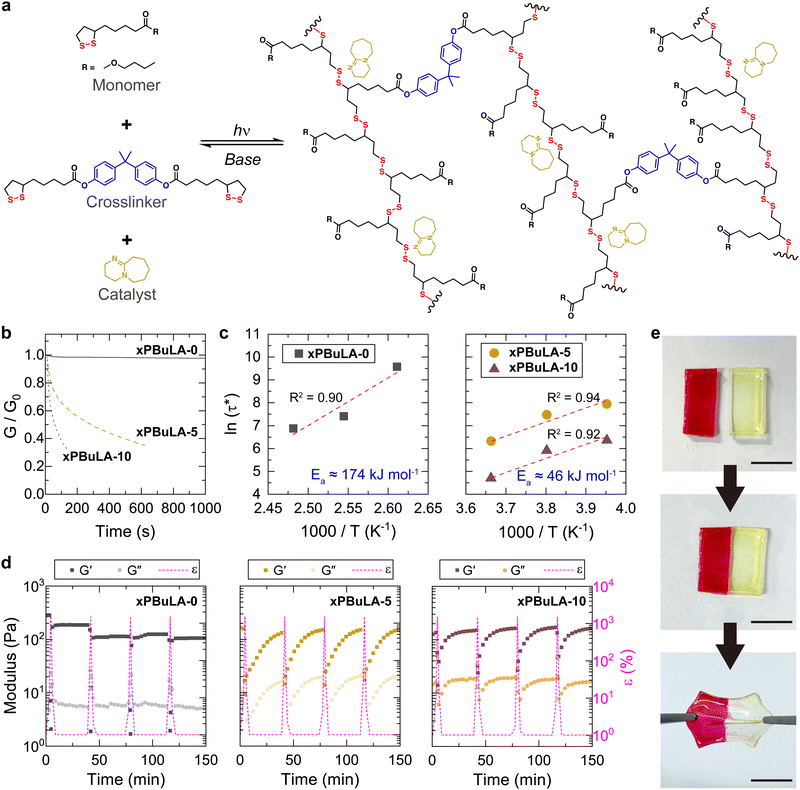
A strong base like DBU is recognized for accelerating disulfide exchange reactions under ambient conditions.^27,37 However, when DBU was incorporated into linear poly(disulfide)s, the high-strain rate wave pressure dissipation of polymer was unable to be evaluated since the excessively rapid reversible reaction led to depolymerization, transforming them into liquid-like materials. Instead, we decided to prepare crosslinked poly(disulfide)s using the most effective stress wave dissipating unit, BuLA, as a monomer, and 1,2-dithiolane substituted at both ends of bisphenol A (BPA-LA, Scheme S2, ESI†) as a crosslinker (Fig. 3a). Samples containing DBU were fabricated by dropping 5 wt% or 10 wt% DBU (xPBuLA-5 and xPBuLA-10) onto a crosslinked film (xPBuLA-0). The sample was left overnight until DBU was completely dispersed. Then, we examined the temperature dependence of the thermo-mechanical properties for the prepared polymers (Fig. S24, ESI†). Although DBU containing samples underwent depolymerization above 40 °C, all the polymers had similar T_g (the peak of tan δ) and moduli below 40 °C.

Fig. 3 Crosslinked poly(disulfide)s. (a) Reversible polymerization and depolymerization of BuLA based crosslinked poly(disulfide)s. DBU catalysts promote disulfide exchange reactions. (b) The change in normalized relaxation modulus for pristine (xPBuLA-0) and DBU incorporated crosslinked polymers (xPBuLA-5 and xPBuLA-10) at room temperature. (c) Arrhenius plots obtained from τ* (relaxation time, defined when G/G₀ is equal to 1/e) at different temperatures. The activation energy (E_a) for the disulfide exchange reaction was calculated from a linear fit. (d) Cyclic strain step test for evaluating self-healing characteristics. Strain (ε) ramped from 1% to 1500% (above flow point for all polymers). Each sample was recovered at 1% strain for 30 min. (e) Interfacial self-healing of xPBuLA-10. Two halves of samples were cut from films with or without Rhodamine B staining and rejoined those samples at room temperature.

A significant change in the kinetics of disulfide exchange reactions in polymeric networks was observed through stress relaxation behaviors of each sample at room temperature (Fig. 3b). xPBuLA-0 showed no substantial stress relaxation, whereas xPBuLA-5 and xPBuLA-10 exhibited rapid stress relaxation. The relaxation rate is often measured by the relaxation time (τ*), defined as the time for the modulus to reach 1/e of its initial relaxation modulus. The temperature dependence of τ* for each polymer was fitted to an Arrhenius relationship to determine the apparent activation energy (E_a) of uncatalyzed and catalyzed disulfide exchange reaction (Fig. 3c and Fig. S25, ESI†).^38,39 The E_a for uncatalyzed disulfide exchange reaction in xPBuLA-0 was calculated to be 174 kJ mol⁻¹, a relatively high value compared to other disulfide-containing polymeric networks.⁴⁰ However, the E_a for DBU catalyzed disulfide exchange reaction was approximately 46 kJ mol⁻¹, irrespective of the amount of catalyst, which is a comparable value for inducing the exchange reaction without heat.⁴¹

The DBU-catalyzed rapid disulfide exchange reactions were further confirmed through a cyclic strain sweep test, oscillating between 1% (non-deformative) and 1500% (highly deformative) of strain amplitudes (Fig. 3d). Under the application of a 1500% strain, all the samples exhibited liquid-like behavior (G′ < G′′), suggesting network rupture. Following the removal of the high strain, these samples spontaneously recovered and demonstrated solid-like behavior (G′ > G′′). In contrast to xPBuLA-5 and xPBuLA-10, which completely regained their initial G′ values within 30 minutes over four cycles of rupture and recovery, the G′ value of xPBuLA-0 consistently decreased during repeated strain sweep tests. The self-healing abilities of xPBuLA-10 were further confirmed by a macroscopic self-healing test (Fig. 3e). Two square-shaped xPBuLA-10 films (one of them stained with Rhodamine B) were halved using a knife and placed in direct contact with each other at the cut side. After 30 minutes of incubation at room temperature, the two differently colored pieces rejoined, and the healed polymer film regained the ability to withstand substantial strain. Although the addition of DBU led to a softening of the crosslinked polymers (Fig. S26a, ESI†), the self-healed xPBuLA-10 samples exhibited mechanical properties similar to the pristine samples (Fig. S26b, ESI†).

Closed-loop chemical recycling, which breaks down polymers and convert them back into their original monomers, is an ideal solution to reduce plastic waste and achieve a circular polymer economy.^42–44 By immersing the crosslinked poly(disulfide)s in a DBU solution, our polymers were depolymerized, and successful recovery of the monomers (BuLA) and crosslinkers (BPA-LA) was verified by ¹H NMR spectroscopy (Fig. S27, ESI†).

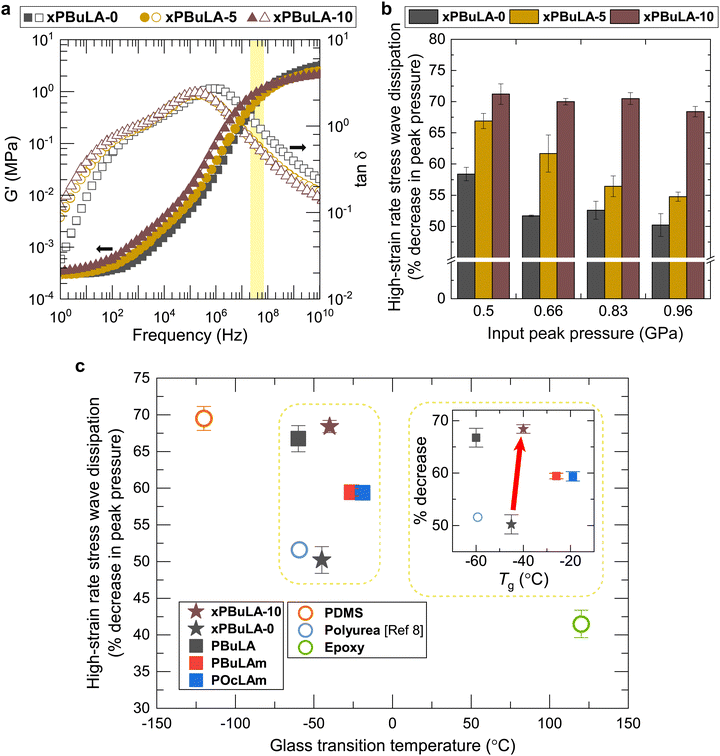
Inspired by the remarkable self-healing performance, we set out to examine the high-strain rate stress wave dissipating abilities of xPBuLA with varying amounts of DBU. Initially, the G′ and tan δ values for each sample were compared across the frequency ranges of shock waves (2.5–3.6 × 10⁷ Hz) (Fig. 4a and Fig. S28–S33, ESI†). The addition of DBU did not impact their rheological behaviors significantly, and all the samples exhibited similar G′ and tan δ values at all frequencies below 10⁸ Hz. Furthermore, X-ray scattering results showed no significant microstructural changes after DBU incorporation (Fig. S34, ESI†). Therefore, among the various properties of these samples that can influence the stress wave dissipating properties, the kinetics of disulfide exchange reactions in the polymeric networks is the sole factor. The high-strain rate stress wave dissipation performance in the disulfide network is correlated with the content of DBU (Fig. 4b). As the DBU content increased, the stress wave dissipation ability improved by up to 36% compared to that of xPBuLA-0. xPBuLA-10, which exhibits the fastest stress relaxation at room temperature, showed a remarkable pressure dissipation ability over 70% for all input peak pressures. In contrast, xPBuLA-0, which exhibits the slowest stress relaxation, revealed the percentage decrease in pressure around 50%. Interestingly, the inverse of the relaxation times obtained from Arrhenius plots displayed a positive linear correlation with stress energy dissipation ability (Fig. S35, ESI†). This result demonstrates that the kinetics of the disulfide exchange reaction plays a critical role in the stress wave dissipation ability of the dynamic polymers. We expect that enhanced stress wave damping capabilities can be achieved in other dynamic covalent network systems through catalytically accelerated exchange reactions, including transesterification, silyl ether metathesis, and vinylogous urethane–amine exchange reactions.^45–47

Fig. 4 Enhanced high-strain rate stress wave dissipating capabilities by accelerating disulfide exchange reactions in crosslinked poly(disulfide)s. (a) Storage modulus (G′) and loss factor (tan δ) for xPBuLA as a function of DBU amount. The frequency ranges for high-strain rate stress wave are colored in yellow. (b) The percentage decrease in peak pressure of xPBuLAs as a function of input peak pressure. (c) Correlation between the stress wave dissipation and glass transition temperature for our disulfide polymers and state-of-the-art alternative materials.

For optimal dissipation performance, the glass transition zone, where a rubbery polymer transitions from a rubbery to a glassy state, should correspond to the operating temperature or frequency.^48,49 Considering the frequency range of our experimental setup and the time–temperature superposition principle, low-T_g polymers are expected to excel in dissipating high-strain rate stress waves. To elucidate this relationship, we plotted high-strain stress wave dissipation performance against the T_g for our polymers and various representative materials (Fig. 4c). A strong inverse correlation was observed: lower T_g correlated with higher peak pressure reduction. While polydimethylsiloxane (PDMS) showed the highest dissipation (69.5%) at about 1 GPa of input peak pressure due to its extremely low T_g,⁵⁰xPBuLA-10 achieved comparable dissipation (68.4%) despite having a 60 °C higher T_g. Notably, xPBuLA-0 (50.2%) performed similarly to polyurea (51.6%), but its performance significantly improved after accelerating the disulfide exchange reaction using a catalyst without altering its T_g. To the best of our knowledge, this is the first demonstration of constructive effects of dynamic exchange reaction kinetics on high-strain rate stress wave damping. These findings elucidate the design principles for dynamic covalent polymers, facilitating the development of effective dampers across all frequency spectra.

3. Conclusion

We have reported an optimal strategy to enhance the high-strain rate stress wave dissipating capabilities in poly(disulfide)s by controlling the side chain structures and disulfide exchange rates. Four types of linear poly(disulfide)s were synthesized with varying aliphatic chain length and the presence of hydrogen bonding. Through laser-induced high-strain rate stress wave experiments, we confirmed a strong correlation between the glass transition temperatures (T_g) of linear poly(disulfide)s and their ability to dissipate the stress waves. Among these polymers, PBuLA, with the lowest T_g, exhibited the most effective stress wave dissipating performance. This performance was further improved by incorporating a strong base, DBU, as a catalyst into crosslinked PBuLA. Remarkably, xPBuLA-10, containing 10 wt% of DBU, demonstrated an exceptional high-strain stress wave dissipation capability, exceeding about 70% across all input shock pressures. This performance surpasses that of conventional materials like epoxy and polyurea, and is comparable to PDMS, despite xPBuLA-10 having a T_g that is 60 °C higher. Additionally, we leveraged the inherent nature of cyclic disulfides to achieve fast self-healing at room temperature and efficient chemical recyclability to monomers. We envision that the principles established in this study will provide a rational framework for designing sustainable and efficient stress wave dissipating materials across various fields, including aerospace, defense, and high-speed machinery, where protection against high-strain rate events is critical.

Author contributions

Juho Lee: investigation, visualization, validation, writing – original draft; Gyeongmin Park: formal analysis, investigation, visualization, validation, writing – original draft; Dongju Lee: investigation, visualization, validation, writing – original draft; Jiyun Shin: investigation, validation; Cheol-Hee Ahn: supervision; Jaejun Lee: conceptualization, supervision, project administration, funding acquisition, writing – review & editing; Tae Ann Kim: conceptualization, visualization, supervision, project administration, funding acquisition, writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

This work was supported by the National Research Council of Science & Technology (NST) grant from the Korea government (MSIT) (CRC22031-000) and the Nano & Material Technology Development Program through the National Research Foundation of Korea (NRF) funded by Ministry of Science and ICT (RS-2024-00448445). This work was also supported by National Research Foundation of Korea, the ICT (2021M3F6A1085855) with the title of the “Development of Shockwave Protective Composite Materials”.

References

1. A. Venkatesan, J. Lowenthal, P. Prem and M. Vidaurri, Nat. Astron., 2020, 4, 1043–1048.
2. J. Ekström, R. Rempling and M. Plos, Eng. Struct., 2016, 122, 72–82.
3. A. P. Mouritz, Composites, 1995, 26, 3–9.
4. S. Kabu, H. Jaffer, M. Petro, D. Dudzinski, D. Stewart, A. Courtney, M. Courtney and V. Labhasetwar, PLoS One, 2015, 10, e0127971.
5. M. A. Shaid Sujon, A. Islam and V. K. Nadimpalli, Polym. Test., 2021, 104, 107388.
6. J. Huang, Y. Xu, S. Qi, J. Zhou, W. Shi, T. Zhao and M. Liu, Nat. Commun., 2021, 12, 1–9.
7. J. Xiaolin, X. Min, W. Minhui, M. Yuanhao, Z. Wencong, Z. Yanan, R. Haoxiang and L. Xun, Eur. Polym. J., 2022, 162, 110893.
8. J. Lee, B. B. Jing, L. E. Porath, N. R. Sottos and C. M. Evans, Macromolecules, 2020, 53, 4741–4747.
9. N. Zheng, Y. Xu, Q. Zhao and T. Xie, Chem. Rev., 2021, 121, 1716–1745.
10. M. M. Obadia, A. Jourdain, P. Cassagnau, D. Montarnal, E. Drockenmuller, M. M. Obadia, A. Jourdain, P. Cassagnau, E. Drockenmuller and D. Montarnal, Adv. Funct. Mater., 2017, 27, 1703258.
11. Y. Spiesschaert, C. Taplan, L. Stricker, M. Guerre, J. M. Winne and F. E. Du Prez, Polym. Chem., 2020, 11, 5377–5385.
12. J. Lee, V. M. Lau, Y. Ren, C. M. Evans, J. S. Moore and N. R. Sottos, ACS Macro Lett., 2019, 8, 535–539.
13. J. Canadell, H. Goossens and B. Klumperman, Macromolecules, 2011, 44, 2536–2541.
14. A. Rekondo, R. Martin, A. Ruiz de Luzuriaga, G. Cabañero, H. J. Grande and I. Odriozola, Mater. Horiz., 2014, 1, 237–240.
15. H. Otsuka, S. Nagano, Y. Kobashi, T. Maeda and A. Takahara, Chem. Commun., 2010, 46, 1150–1152.
16. F. Fan, S. Ji, C. Sun, C. Liu, Y. Yu, Y. Fu and H. Xu, Angew. Chem., Int. Ed., 2018, 57, 16426–16430.
17. C. Choi, J. L. Self, Y. Okayama, A. E. Levi, M. Gerst, J. C. Speros, C. J. Hawker, J. Read De Alaniz and C. M. Bates, J. Am. Chem. Soc., 2021, 143, 9866–9871.
18. A. P. Wiita, S. R. K. Ainavarapu, H. H. Huang and J. M. Fernandez, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 7222–7227.
19. Z. Shi, Q. Song, R. Göstl and A. Herrmann, Chem. Sci., 2021, 12, 1668–1674.
20. Z. Q. Lei, H. P. Xiang, Y. J. Yuan, M. Z. Rong and M. Q. Zhang, Chem. Mater., 2014, 26, 2038–2046.
21. J. Wu, L. Zhao, X. Xu, N. Bertrand, W. I. Choi, B. Yameen, J. Shi, V. Shah, M. Mulvale, J. L. Maclean and O. C. FaroKhzad, Angew. Chem., Int. Ed., 2015, 54, 9218–9223.
22. S. Wang and M. W. Urban, Nat. Rev. Mater., 2020, 5, 562–583.
23. Y. Xia, Y. He, F. Zhang, Y. Liu and J. Leng, Adv. Mater., 2021, 33, 1–33.
24. Q. Zhang, N. Re Ko and J. Kwon Oh, Chem. Commun., 2012, 48, 7542.
25. Q. Zhang, D.-H. Qu, B. L. Feringa and H. Tian, J. Am. Chem. Soc., 2022, 144, 2022–2033.
26. B. Sen Wang, Q. Zhang, Z. Q. Wang, C. Y. Shi, X. Q. Gong, H. Tian and D. H. Qu, Angew. Chem., Int. Ed., 2023, 62, e202215329.
27. C. Choi, Y. Okayama, P. T. Morris, L. L. Robinson, M. Gerst, J. C. Speros, C. J. Hawker, J. Read de Alaniz and C. M. Bates, Adv. Funct. Mater., 2022, 32, 2200883.
28. J. Wang, R. L. Weaver and N. R. Sottos, J. Appl. Phys., 2003, 93, 9529–9536.
29. S. S. Rogers and L. Mandelkern, J. Phys. Chem., 1957, 61, 985–990.
30. H. K. Reimschuessel, J. Polym. Sci., Polym. Chem. Ed., 1979, 17, 2447–2457.
31. E. F. Jordan, D. W. Feldeisen and A. N. Wrigley, J. Polym. Sci., Part A-1: Polym. Chem., 1971, 9, 1835–1851.
32. E. Hempel, H. Huth and M. Beiner, Thermochim. Acta, 2003, 403, 105–114.
33. V. Arrighi, A. Triolo, I. J. McEwen, P. Holmes, R. Triolo and H. Amenitsch, Macromolecules, 2000, 33, 4989–4991.
34. S. Pankaj, E. Hempel and M. Beiner, Macromolecules, 2009, 42, 716–724.
35. K. Yang, J. Lee, N. R. Sottos and J. S. Moore, J. Am. Chem. Soc., 2015, 137, 16000–16003.
36. A. N. Pronin and V. Gupta, J. Mech. Phys. Solids, 1998, 46, 389–410.
37. A. M. Belenguer, T. Friščić, G. M. Day and J. K. M. Sanders, Chem. Sci., 2011, 2, 696–700.
38. S. Yoon, J. H. Choi, B. J. Sung, J. Bang and T. A. Kim, NPG Asia Mater., 2022, 14, 61.
39. S. Lee, J. Song, J. Cho, J. G. Son and T. A. Kim, ACS Appl. Polym. Mater., 2023, 5, 7433–7442.
40. J. Luo, X. Zhao, H. Ju, X. Chen, S. Zhao, Z. Demchuk, B. Li, V. Bocharova, J. M. Y. Carrillo, J. K. Keum, S. Xu, A. P. Sokolov, J. Chen and P. F. Cao, Angew. Chem., Int. Ed., 2023, 62, e202310989.
41. A. Ruiz De Luzuriaga, R. Martin, N. Markaide, A. Rekondo, G. Cabañero, J. Rodríguez and I. Odriozola, Mater. Horiz., 2016, 3, 241–247.
42. A. R. Rahimi and J. M. Garciá, Nat. Rev. Chem., 2017, 1, 0046.
43. G. W. Coates and Y. D. Y. L. Getzler, Nat. Rev. Mater., 2020, 5, 501–516.
44. J. Lee, D. Lee, C.-H. Ahn and T. A. Kim, Adv. Funct. Mater., 2024, 2414842.
45. M. Capelot, M. M. Unterlass, F. Tournilhac and L. Leibler, ACS Macro Lett., 2012, 1, 789–792.
46. C. A. Tretbar, J. A. Neal and Z. Guan, J. Am. Chem. Soc., 2019, 141, 16595–16599.
47. W. Denissen, M. Droesbeke, R. Nicola, L. Leibler, J. M. Winne and F. E. Du Prez, Nat. Commun., 2017, 8, 1–7.
48. R. B. Bogoslovov, C. M. Roland and R. M. Gamache, Appl. Phys. Lett., 2007, 90, 221910.
49. L. Cheng, J. Zhao, Z. Xiong, S. Liu, X. Yan and W. Yu, Angew. Chem., Int. Ed., 2024, 63, e202406937.
50. M. R. Armstrong, P. V. Grivickas, A. M. Sawvel, J. P. Lewicki, J. C. Crowhurst, J. M. Zaug, H. B. Radousky, E. Stavrou, C. T. Alviso, J. Hamilton and R. S. Maxwell, J. Polym. Sci., Part B: Polym. Phys., 2018, 56, 827–832.

---

Footnotes

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00868e

‡ J. Lee, G. Park, and D. Lee contributed equally to this work.

---