Hyperplane tree-based data mining with a multi-functional memristive crossbar array†
Sunwoo
Cheong‡
a,
Dong Hoon
Shin‡
a,
Soo Hyung
Lee
a,
Yoon Ho
Jang
a,
Janguk
Han
a,
Sung Keun
Shim
a,
Joon-Kyu
Han
ab,
Néstor
Ghenzi
*ac and
Cheol Seong
Hwang
 *a
*a
aDepartment of Materials Science and Engineering and Inter-university Semiconductor Research Center, College of Engineering, Seoul National University, Seoul, 08826, Republic of Korea. E-mail: cheolsh@snu.ac.kr
bSystem Semiconductor Engineering and the Department of Electronic Engineering, Sogang University, Seoul, Republic of Korea
cUniversidad de Avellaneda UNDAV and Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Mario Bravo 1460, Avellaneda, Buenos Aires 1872, Argentina. E-mail: nghenzi@snu.ac.kr
First published on 2nd October 2024
Abstract
This study explores the stochastic and binary switching behaviors of a Ta/HfO2/RuO2 memristor to implement a combined data mining approach for outlier detection and data clustering algorithms in a multi-functional memristive crossbar array. The memristor switches stochastically with high state dispersion in the stochastic mode and deterministically between two states with low dispersion in the binary mode, while they can be controlled by varying operating voltages. The stochastic mode facilitates the parallel generation of random hyperplanes in a tree structure, used to compress spatial information of the dataset in the Euclidian space into binary format, still retaining sufficient spatial features. The ensemble effect from multiple trees improved the classification performance. The binary mode facilitates parallel Hamming distance calculation of the binary codes containing spatial information, which measures similarity. These two modes enable efficient implementation of the newly proposed minority-based outlier detection method and modified K-means method on the same hardware. Array measurements and hardware simulations investigate various hyperparameters’ impact and validate the proposed methods with practical datasets. The proposed methods show linear O(n) time complexity and high energy efficiency, consuming <1% of the energy compared to digital computing with conventional algorithms while demonstrating software-comparable performance in both tasks.
New conceptsThe current memristor-based data mining studies have focused on analog in-memory computing, which encompasses a significant burden in analog conductance mapping to hardware due to the iterative write-and-verify process. It also lacked an algorithm more suitable for memristor-based systems. This study proposes a method to overcome these limitations using reconfigurable stochastic and binary modes of a given memristor (Ta/HfO2/RuO2) by controlling reset voltage. Unlike Euclidean distance-based data mining, this method can simultaneously perform data clustering and outlier detection with reduced computational cost through hyperplane and Hamming distance concepts. These two concepts are implemented in a memristive crossbar array by altering the pulse application method. The time complexity of data mining tasks was reduced to a linear level through efficient vector–matrix multiplication. This method can solve the biggest problem of the K-means method, vulnerability to noise, through prior outlier detection. It feasibly handled iris and synthetic datasets even with intentionally added noise. Energy consumption and latency were compared with complementary metal oxide semiconductor (CMOS) based digital computing hardware for quantitative indicators, and efficiency was demonstrated. This study paves the way for efficient data mining hardware in materials research, leaving a mark on the in-memory computing era. |
Introduction
In current data-driven computation for artificial intelligence, extracting meaningful insights from massive datasets is essential.1 This extraction process, or data mining, requires unsupervised learning, where knowledge is gleaned from data without labels or predefined answers, which is increasingly crucial in actual data mining techniques. Consequently, many algorithms for outlier detection (OD) and data clustering (DC), two pillar techniques of unsupervised learning, have been developed for various data formats.2–4OD is a task to detect outliers in the given dataset to protect the implication of normal data from contamination by outliers in fraud detection, security, and image anomaly detection fields.2 On the other hand, DC is a task that groups similar data into clusters based on their shared characteristics. It is widely used in text analysis, image classification, and customer segmentation.3–6 However, these tasks are performed based on the distance between data points. Therefore, as the size of the dataset increases, the number of calculations increases exponentially, making the conventional complementary-metal-oxide-semiconductor (CMOS) based computing system inefficient in these tasks. Also, sequentially operating the OD and DC increases the computational cost substantially. Therefore, a method that can process both tasks parallelly without additional cost is required to overcome these limitations.
Meanwhile, research aiming to implement massive computing algorithms directly to the hardware has seen significant progress with the emergence of memristive crossbar arrays (CBAs), where the parallel vector–matrix multiplication (VMM) can be performed efficiently using the Ohm's and Kirchhoff's laws.7–15 However, most previous studies usually use analog characteristics for the distance calculation, which often requires significantly iterative write-and-verify steps.8,13,14,16 This burden becomes even more severe when expanded to the CBA structure, as Fig. S1 of the ESI† explains.
This work presents an alternative method to address the abovementioned problems using the multi-functional CBA (mf-CBA), capable of exhibiting both stochastic and deterministic binary resistive switching in a reconfigurable manner. In this case, spatial information of all data points is simplified into binary digits when adopting the suggested method based on the hyperplanes and Hamming distance (HD) described below. This method does not require precise distance calculation, substantially decreasing the computational burden. For this method, the stochastic behavior of a memristor, usually regarded as an undesirable factor for most applications, can be a crucial ingredient in implementing the method in the mf-CBA. On the other hand, binary switching behavior with a large memory window and low state dispersion enables efficient HD calculation. Simulated hardware based on the suggested mf-CBA and hyperplane algorithm further verified the impact of various hyperparameters on OD and DC, compared performance with existing algorithms, and applied to high-dimensional datasets. These analyses confirmed that mf-CBA could accomplish the same tasks using less than 1% of the energy consumed by conventional CMOS-based technology.
Results and discussion
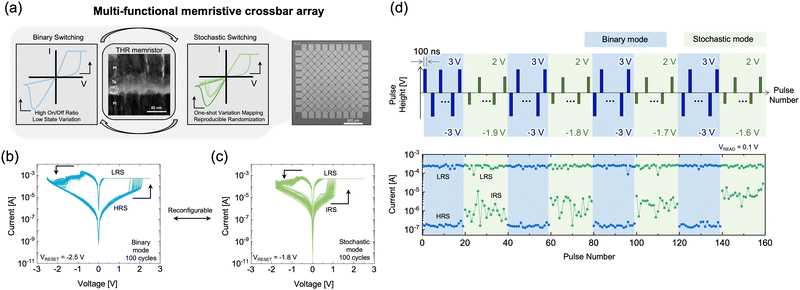
Multi-functional memristive crossbar array for stochastic and binary resistive switching
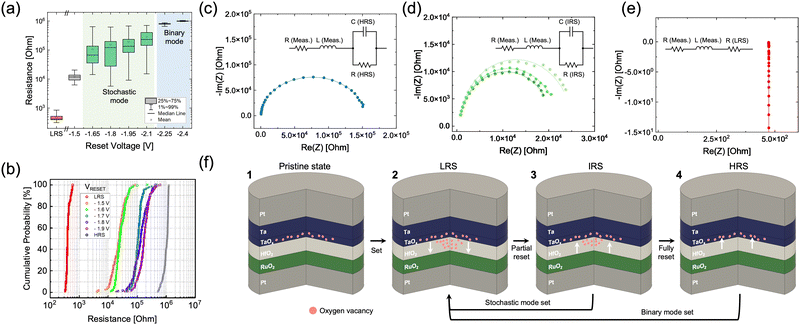
Fig. 1 summarizes the electrical characteristics of the two reconfigurable modes of the Ta/HfO2/RuO2 (THR) device for the mf-CBA to implement the proposed hyperplane-based data mining method. Fig. 1(a) shows the schematic of reconfigurable switching modes of the THR memristor, stacked film microstructure via cross-sectional transmission electron microscopy (TEM), and the top-view scanning electron microscopy (SEM) image of the fabricated 9 by 9 mf-CBA with the 4 μm line width. Additional details of the THR device fabrication process and structural analysis can be found in the Method Section and Fig. S2 and S3 of the (ESI†). Fig. 1(b) and (c) show the THR memristor's representative current–voltage (I–V) characteristics in the binary and stochastic modes, respectively, obtained through 100 consecutive I–V cycles. The pristine THR device exhibits electroforming-free switching beginning in the high resistance state (HRS), and it switches to the low resistance state (LRS) upon application of set voltages ranging from ∼1.5 V to ∼2.5 V. The compliance current of 500 μA was applied in the set operation to prevent the hard breakdown of the HfO2 resistive switching layer. By applying a negative reset voltage (VRESET) of −2.5 V to the top electrode (TE), the device resets to HRS. This transition is manifested in a discernible binary state, where each LRS and HRS exhibit minimal state dispersion, corresponding to the binary operation mode. The memory window in binary mode is ∼103, considering the HRS and LRS dispersion at the read voltage of 0.1 V. On the other hand, by applying an intermediate VRESET of −1.8 V to the TE, the device undergoes only a partial reset, reaching a resistance state with significant dispersion even with a given VRESET and resulting in the stochastic operation mode. In this stochastic operation mode, the resistance state falls between the HRS and LRS stochastically, designated as the intermediate resistance state (IRS). Fig. S4, ESI,† illustrates the I–V cycles with different VRESET values, showing that the IRS distribution is consistent regardless of VRESET in stochastic mode operation. Furthermore, Fig. 1(d) depicts the operation mode reconfiguration between two modes via pulse stream. The upper panel shows the applied pulse voltages (+3 and −3 V for set and reset in binary mode, blue bars, and +2 and –1.9 to −1.6 V for set and reset in stochastic mode, green bars, with a pulse length of 100 ns). The lower panel shows the corresponding output current obtained at a read voltage of 0.1 V. THR demonstrates reproducible transitions between binary mode with high and deterministic on/off ratio and stochastic mode with varying IRS current even for the given reset pulse condition. Still, the average reset current decreases with increasing reset pulse amplitude. Additional analysis related to the pulse amplitude-dependent mode reconfiguration is explained in Fig. S5, ESI.† The method section and Fig. S6, ESI,† show the additional pulse-driven mode reconfigurations (>105 cycles) with closed-loop pulse switching. Fig. S7 and S8, ESI,† show the switching endurance and state retention. Additionally, Fig. S9–S11, ESI,† show the intra- and inter-array device-to-device variations of mf-CBA, highlighting the high functionality and reproducibility of the THR memristor in the mf-CBA. Moreover, Fig. S12, ESI,† analyzes the uniformity and multi-functionality within a larger scale array.Fig. 2(a) shows the resistance distribution of the THR memristor over 50 cycles, where VRESET was varied from −1.5 V to −2.4 V with a decrement of −0.15 V, and the resistance values were read at 0.1 V (VREAD). Starting from LRS (red), the device exhibited binary mode's LRS and HRS with approximately three orders of magnitude resistance ratio and minimal resistance distribution for the VRESET values from −2.25 V to −2.4 V (blue). In contrast, the device showed stochastic IRS resistance values with approximately two orders of magnitude resistance ratio for the VRESET values from −1.65 V to −2.1 V (green). The cumulative resistance distribution curves in Fig. 2(b), representing the resistance over 200 switching cycles for the VRESET values between −1.5 V and −2.4 V, further illustrate the relationship between state dispersion and VRESET. The LRS (red open circle) and HRS (grey open circle) states in the binary mode exhibit minimal dispersion, whereas the stochastic switching region exhibits broad IRS resistance distributions (other color open circles) depending on the VRESET.
To identify the cause of these differences in resistance dispersion according to VRESET and to elucidate the device's operational mechanism, electrochemical impedance spectroscopy (EIS) analysis was conducted.17,18 Detailed methodologies for EIS measurements are provided in the Method section, and the configuration of the conducting filament (CF) in the memristor at HRS, IRS, and LRS was analyzed, as shown in Fig. 2(c)–(e). The equivalent circuit for each state at the device scale is depicted in the insets of each figure HRS and IRS were fitted with a model where the resistance and capacitance of the resistive switching layer are connected in parallel. In contrast, LRS was fitted as a single resistance due to the presence of the oxygen vacancy-based CF.19–21 Additionally, parasitic series resistance and inductance from the measurement setup were included in the EIS fitting. In the Nyquist plots of Fig. 2(c)–(e), the measured values for each state are shown as dots, and the fitting results are shown as solid lines. The fitted circuit parameters for each circuit element are listed in Table 1. For HRS, the relatively large R(HRS) of 151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 Ohms and the capacitance of 3.57 pF indicate that electrical conduction occurs through dielectric leakage without a major conduction path such as a CF. Notably, the fitted capacitance was similar to the capacitance of a planar capacitor with a 3.6-nm-thick HfO2 dielectric layer (dielectric constant approximately 2522) and an 8 × 8 μm2 area, further supporting the accuracy of the EIS measurement.
794 Ohms and the capacitance of 3.57 pF indicate that electrical conduction occurs through dielectric leakage without a major conduction path such as a CF. Notably, the fitted capacitance was similar to the capacitance of a planar capacitor with a 3.6-nm-thick HfO2 dielectric layer (dielectric constant approximately 2522) and an 8 × 8 μm2 area, further supporting the accuracy of the EIS measurement.
| Element | Parameter value |
|---|---|
| R (Meas.) | 358.4 Ohm |
| L (Meas.) | 17.44 μH |
| C (HRS) | 3.57 pF |
| C (IRS) | (4.75, 4.77, 4.79) pF |
| R (HRS) | 151![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 794 ohm 794 ohm |
| R (IRS) | (20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 343, 21 343, 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 545, 24 545, 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 739) Ohm 739) Ohm |
| R (LRS) | 115.9 Ohm |
Conversely, for LRS, the conduction is interpreted as metallic due to a metallic filament, with an R(LRS) of 115.9 Ohms and negligible capacitance influence. For the three IRS states at VRESET = −1.8 V, despite the variability in the fitting parameters, the EIS behavior was generally fitted with a smaller R(IRS) than HRS (∼20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 ohms) and a similar range of capacitance (∼4.7 pF). The intermediate R(IRS) indicated the partially ruptured filaments. The larger capacitance compared to HRS might indicate that the film thickness region containing the partially ruptured filaments behaves like a resistor, while the other thickness region without them worked as the capacitive layer.
000 ohms) and a similar range of capacitance (∼4.7 pF). The intermediate R(IRS) indicated the partially ruptured filaments. The larger capacitance compared to HRS might indicate that the film thickness region containing the partially ruptured filaments behaves like a resistor, while the other thickness region without them worked as the capacitive layer.
Based on these findings, the switching mechanism of the THR device and the corresponding nanostructural changes are illustrated in Fig. 2(f). In its pristine state (panel 1), THR has oxygen vacancies in the suboxide at the Ta/HfO2 interface. When a set voltage is applied, the device transitions to LRS, forming a metallic filament through the drift and diffusion of oxygen vacancies (panel 2). When a reset voltage is applied to operate in stochastic mode, filament rupture occurs due to Joule heating and vacancy drift, resulting in stochastic resistance states (panel 3).23–26 However, applying sufficient reset voltage fully dissolves the ruptured filament, restoring the device to HRS with conduction behavior identical to the pristine state. This finding is inferred from the electroforming-free characteristics facilitated by the roles of the RuO2 electrode and TaOx suboxide layer, as reported elsewhere.27–29 This characterization of the multi-functional (stochastic/deterministic) properties controlled by the reset voltage enables new data mining methodologies, described in the following section.
Hyperplane tree-based data mining method
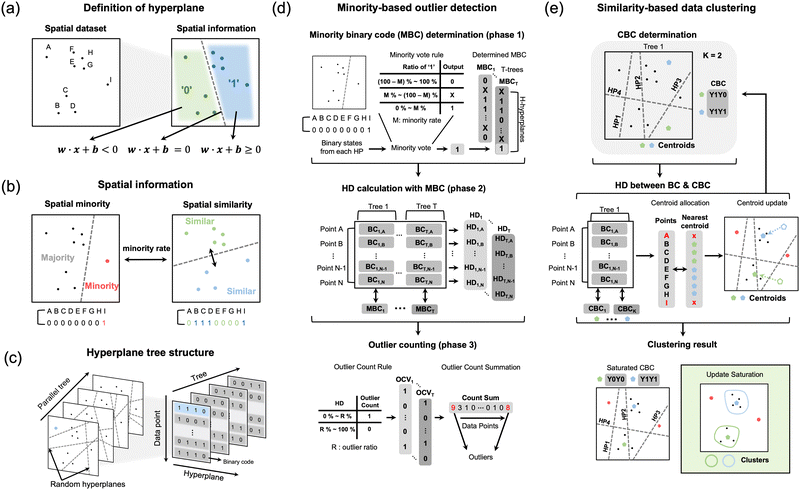
(Table S1 of the ESI† summarizes many abbreviations and their meanings in this section).Fig. 3(a)–(c) show the process flow for the spatial information compression using the hyperplane method. This method partitions the data points distributed within the Euclidean space according to their proximity. The Figures explain this method using an example 9-point dataset labeled A to I (left panel of Fig. 3(a)). The right panel of Fig. 3(a) shows that the hyperplane partitions the dataset into two regions. The formula for expressing a hyperplane to divide a specific m-dimensional space can be written as eqn (1):
| w·x + b = 0, | (1) |
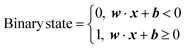 | (2) |
Although this simple calculation can efficiently compress analog spatial information into binary digits, not all hyperplanes are meaningful. Setting the effective hyperplane depends on the specific dataset, and thus, several methods were proposed using multiple randomly generated hyperplanes.16,32 However, multiple random sampling is required to generate the coefficients w and b of multiple hyperplanes, which is computationally expensive. Additionally, as the number of hyperplanes increases, the number of operations required for each data point increases. These problems are solved by parallel computing using the stochastic mode in the suggested mf-CBA, discussed later.
Meanwhile, partitioning has different implications in data structure analysis. Fig. 3(b) shows how a hyperplane extracts spatial minority and similarity measures. For the given 9-point dataset, the hyperplane in the left panel of Fig. 3(b) separates point I from all other points, and such a situation can be represented by setting one “1” for point I and eight “0” s for other points for encoding the binary spatial information to each point. It should be noted that assigning “1” to a specific data point does not imply that it belongs to the minority; it only follows the rule described by eqn (2). This spatial minority directly implies the spatial outlier for a given hyperplane, which is further utilized to OD. On the other hand, in the case of the right panel of Fig. 3(b) with a different hyperplane, the 9-point dataset is divided into 5 and 4 points by another hyperplane. In this case, the 5 points (with the binary state code of “0”) and the other 4 points (with the binary state code of “1”) belong to the different sections created by the given hyperplane. This bisecting is related to the spatial similarity of the data points, and the spatially similar points are grouped into the same section (with the same binary code) by a hyperplane.
The hyperparameter for deciding if a given hyperplane is related to a minority or similarity is “minority rate (M)”, which serves as a threshold for distinguishing them. If the ratio of “0” or “1” to the total number of data points in the compressed spatial information is less than M, the hyperplane indicates spatial minority; otherwise, spatial similarity. In spatial minority, the drawn information can be used efficiently to perform OD because it is possible to know the region where a small number of points are distributed in the dataset. Conversely, the drawn spatial similarity information can be used for DC because close-together points will likely share the same binary state code.
The spatial analytic capability of the hyperplanes described above is further improved by generating an ensemble of hyperplanes in a parallel tree structure, as shown in Fig. 3(c). Each tree has data points with binary code (BC) assigned by multiple random hyperplanes based on eqn (2). The left panel of Fig. 3(c) shows a parallel tree structure constructed equivalently and randomly. In this case, 16 hyperplanes were randomly generated by assigning random w and b values, and four were assigned to each tree. In this case, the spatial information of each point in the dataset in one tree is expressed as 4-bit BC, which offers a higher spatial resolution than the case with a 1-bit BC. For example, data point A (indicated by a light blue color) in tree #1 (the first plane in the left panel of Fig. 3(c)) has a BC of (1, 1, 1, 0) because the four (randomly) assigned hyperplanes in the same tree assigned the spatial state code of 1, 1, 1, and 0, respectively, as shown in the right panel of Fig. 3(c). Eventually, each data point in the given dataset will have four (equal to the number of trees) 4-bit-length (equal to the number of hyperplanes comprising a tree) BCs. Randomly generated multiple trees help mitigate overfitting and enhance generalization capabilities, enabling more adaptable performance to various data patterns and structures.
The BCs mentioned above of each data point, representing compressed spatial information, can be further utilized for OD and DC with appropriate BC processing methods. Fig. 3(d) shows the newly suggested OD method, denoted as “minority-based OD (MOD)”, consisting of three phases. The first phase is “minority binary code (MBC) determination” to find the outlier candidates in each tree. The second phase calculates the HD between the MBC and all data points’ BCs in each tree. The last phase, “outlier counting”, determines the outlier for each tree based on the calculated HD results. Then, the final set of outliers is established by combining the results from all trees (ensemble effect).
The following explains the three phases of the MOD method in detail. The first MBC determination begins by calculating the ratio of “1” s for each hyperplane. The upper middle panel of Fig. 3(d) shows the “minority vote rule”, which uses this ratio to determine the MBC. For the given hyperplane in the upper left panel, the only point I has a BC of “1”, so the ratio of “1” to the total cases is 0.11 (= 1/9). When the hyperparameter M is arbitrarily taken as 0.25, the rule states that the “minority bit” for this specific hyperplane is “1” because the ratio of 0.11 < 0.25. There could be another hyperplane, which produces the ratio > (1 − M), i.e., 0.75, of which the minority bit becomes “0” following the rule. When the ratio is between these two values, the minority bit for that hyperplane is assigned to be X (do not care bit). Therefore, the relationship between the tree and all the points in the given dataset can be represented by the MBC vector with H components when H hyperplanes are assigned for a given tree. It should be noted that each component in a given MBC vector represents the property of the hyperplane, not a data point. For the T numbers of trees, there are T H-long-MBC vectors, as shown in the upper right panel of Fig. 3(d). This approach prioritizes regions with fewer data points (“minority”) as potential outlier locations.
Assigning several specific hyperplanes with the minority bit of X implies a pruning process for those hyperplanes lacking spatial minority information. When a specific hyperplane yields the “X” minority bit, information related to that hyperplane is excluded from subsequent phases. This exclusion is necessary because such a hyperplane tends to indicate a near-equal distribution of “0” s and “1” s, and, thus, to judge almost half of the data points as outliers, degrading the OD performance eventually. However, these hyperplanes are useful for similarity identification, as discussed later.
The second phase calculates the HD between the MBC and all data points’ BCs, serving as an outlier score for each point because the MBC was designed to be close to outlier candidates. It should be noted that the HD counts the number of different components between two binary vectors, so the larger the HD the more different the two vectors.33 The middle panel of Fig. 3(d) shows this HD calculation process for each tree. In the case of a tree with an “X” state, the calculation discards it, and the HD is calculated with a code shorter than the original length. For example, if a tree with four hyperplanes has an MBC of (1, X, 0, 1), the second bits of BC and MBC vectors were excluded from the HD calculation. After the calculations, T HD vectors are acquired, each with a length of data point number.
Outliers are detected based on the calculated HD results in the last outlier counting phase. The lower panel of Fig. 3(d) shows how each tree's outlier candidates are determined, using a new hyper-parameter, “R”, representing the expected percentage of outliers within the dataset. The calculated HD vectors of each tree are converted to the outlier count vector (OCV), following the outlier counting rule, which assigns “1” or “0” to the components of OCV whether the HD of each data point is within 0 − R or R − 100, respectively, in ascending order. This assignment implies that the data points with high HD values, i.e., less similar to the MBC vector, tend to have the OCV component of “0”. After performing this process for all trees, achieving T OCVs, each component in the OCVs is component-wise added to calculate the final outlier count. Finally, several data points with the highest final outlier count are designated as outliers. This ensemble approach yields robust OD results by utilizing the summed outlier counts across all trees. For more explanations, Fig. S13 of the ESI† shows the results of applying these phases to the example 9-point dataset. To validate the feasibility of the method, Supporting Note 1 of ESI† analyzes the mathematical justification for this method.
Once the MOD determines the outliers, they are removed from the dataset, and DC is performed only on the remaining data points. At this stage, the DC process focuses on hyperplanes that reveal spatial similarity. Among the pre-generated hyperplanes, only hyperplanes representing spatial similarity, which were assigned to be X in the MOD, are now focused. Fig. 3(e) shows the modified K-means process, a representative DC algorithm, using the example 9-point dataset based on the HD and the hyperplane concepts. First, a predefined number of centroids (K) are created in the given Euclidean data space. Then, hyperplanes compress the spatial information of the centroids, producing a BC vector of the added centroids called the “centroid binary code (CBC)” vector, where each component is generated following eqn (2). The tree concept is not used in this process, so one CBC vector is produced per centroid, and a single BC vector is generated for each data point. In this case, in contrast to the MOD case, hyperplanes with spatial minority are invalid in CBC (marked as Y, do not care bit) and also excluded from the subsequent process. Therefore, all generated hyperplanes are used for OD or DC without waste. Afterward, CBCs are utilized to calculate the pairwise HD with the remaining normal data points. Then, K HD vectors are created, and the data points with the smallest HD values in the component-wise comparison between the K HD vectors are assigned to that specific centroid, grouping the data points.3,4,34 For the given hyperplanes in the upper panel of Fig. 3(e), hyperplanes 1 and 3 coincide with the minority cases and points A and I are classified as outliers. In the middle panel, points B–C and E–H are classified as closer to centroid 1 (green dot) and 2 (blue dot), respectively.
Once such a grouping is over, each centroid's coordinates are updated to the average position of its assigned data points. This process repeats iteratively until the centroid's coordinates stabilize. The lower panel of Fig. 3(e) shows the positions of the two saturated centroids after several iterations. Based on these positions, the seven normal data points are divided into two clusters.
Such a hyperplane-based approach can efficiently perform the two data mining tasks (OD and DC) for diverse datasets. However, it bears a severe computation burden in CMOS-based hardware for generating multiple random hyperplanes and subsequent HD calculations. The following sections describe the solution to these problems: how to utilize the THR device's stochasticity to efficiently generate random hyperplanes, how to utilize deterministic binary states for HD calculation, and how to extend these two characteristics to an array scale for parallelism.
Hardware implementation utilizing both switching modes in the mf-CBA
The methods described above can be processed efficiently through mf-CBA composed of stochastic and binary arrays with the software's help, as shown in Fig. 4(a), describing the overall OD and DC process using the mf-CBA. Fig. 4(b) shows the fundamental operations of the mf-CBA. In the stochastic-mode array (S-array), multiple hyperplane mapping is efficiently performed through one-shot mapping, which is explained below, and binary encoding for all hyperplanes for each data point is performed at once due to the parallelism of the mf-CBA (the left panel). In the binary-mode array (B-array), BCs obtained through the S-array are mapped, and parallel HD calculation is performed using them (the right panel). The method for determining MBC and CBC is shown in Fig. S14 of the ESI.† The MBC and CBC vectors are input to the mf-CBA with voltage form in hardware operation.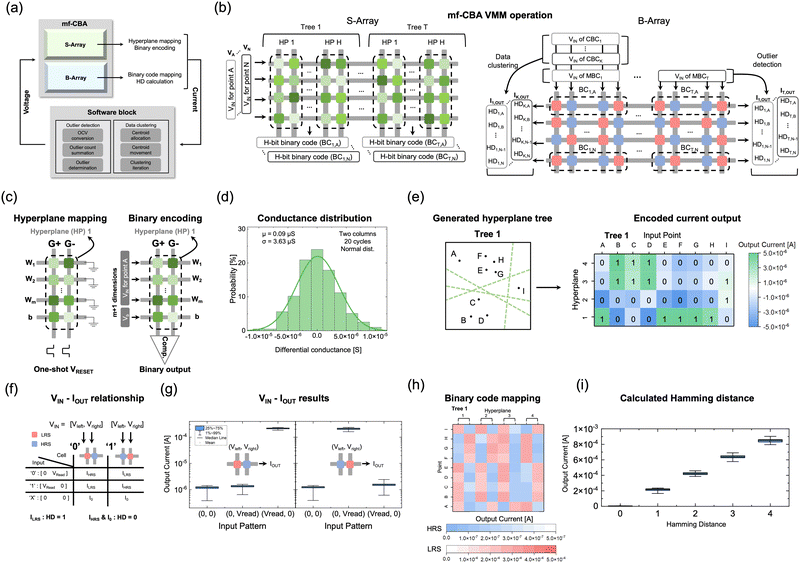 | ||
| Fig. 4 Hardware implementation of the proposed data mining methods with mf-CBA. (a) Data mining process flow of the proposed data mining methods with mf-CBA. (b) Schematic diagram of a spatially divided 9-point dataset with a single hyperplane. (c) The two-column induced S-array mapping and VMM method for single hyperplane generation and binary encoding of spatial relationship. (d) Experimental differential conductance distribution of two columns of the array. The distribution is fitted with normal distribution to 180 conductance pairs, showing near-zero mean-valued differential conductance distribution. (e) Spatial information compression of the 9-point dataset by one tree composed of four hyperplanes and output current results. These results are converted to BCs by comparators. (f) Mapping method of conductance and voltage for the HD calculation in the B-array. One hyperplane consisted of two columns containing a 1-bit binary state of each data in a row direction. The output current is directly related to the 1-bit HD between the input voltage and mapped state by applying input voltage in two columns. (g) Experimental results of all input combinations of HD calculation in Fig. 4(f). Each box contains 50 current results in a log scale plot. (h) Output current results of one 9 by 9 mf-CBA for one tree composed of four hyperplanes. Output currents from the S-array are mapped as binary conductance with the spatial relationship information of each point and hyperplane. (i) Applying random voltage inputs to this B-array produces output current results with different HD cases. Each box contains 50 current results, showing the linear and non-overlapping current results of different HD between mapped states and applied inputs. | ||
The S-array generates conductance-based random variables through parallel operations to create a hyperplane tree structure. The w and b, which define a specific hyperplane, are mapped to conductance values (Gw and Gb) of the cells in the S-array based on the relationship between conductance and voltage. Random generation of the hyperplanes corresponds to the random values of Gw and Gb, so the stochastically operating THR device can be a feasible hardware for this purpose. However, memristors can only have positive conductance values. Therefore, a differential conductance method is adopted by subtracting the conductance values of two cells to generate random real-numbered variables.35,36 Subsequently, the voltage corresponding to each point's coordinates x is applied, and the output current values represent the spatial relationships between the inputted points and the stored hyperplane, which eqn (3) describes.
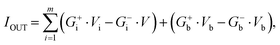 | (3) |
Fig. 4(c) illustrates the two crucial steps of the hyperplane mapping process. Two columns in S-array are adopted, with all THR memristors being in the uniform LRS. Then, they are switched to the stochastic IRS by applying a single VRESET to all cells, resulting in the random IRS, of which conductance is measured at VREAD of 0.1 V. Rows 1 to m encode the vector components of the hyperplane in the corresponding dimensions (w), while the last row stores the offset term b. Subsequently, when the voltage input of a specific data point (x) is applied in the row direction, the output currents from two columns are compared in a comparator to acquire a sign of the output current (eqn (3)). The current sign is then converted into binary data (0, 1), as shown in the right panel of Fig. 4(c), to obtain the spatial relationship between the selected data point and the corresponding hyperplane.
Fig. 4(d) shows the experimentally measured conductance distribution under VRESET = −1.8 V condition of 20 stochastic sampling cycles from two columns. Fig. S14 of the ESI† shows the conductance distribution from each column. Differential conductance between two columns showed a normal distribution with a near-zero mean value and a significant standard deviation. Fig. S15–S18 of the ESI† shows the differential conductance with different VRESET values and the array-level reproducibility. Therefore, the THR memristors in stochastic mode are suitable for representing the random hyperplane generation when they are arranged in S-array.
The suggested mapping method can be extended to the parallel generation of hyperplanes grouped into the S-array trees using the mf-CBA structure's parallelism, as shown in the left panel of Fig. 4(b). These tree-like structures can simultaneously output the BC values of a selected data point for all the hyperplanes. It can also incorporate the ensemble effect of a randomly generated tree structure, encompassing various hyperplanes within each tree.
Four trees with four hyperplanes in each tree were generated in the Euclidean space of the example 9-point dataset to validate the suggested method. The left panel of Fig. 4(e) depicts the generated hyperplanes of the one tree. The right panel shows the current results obtained by applying a voltage corresponding to the coordinates of points in the S-array corresponding to this tree. Here, the sign of the output current can identify the relative positional relationships of 9 points regarding a single hyperplane. Finally, these current output data are converted to BC, as shown in the binary numbers (0 and 1). Supporting Note 2 of the ESI† explains more details of the S-array operation. Fig. S19 and S20 of the ESI† show the array measurement setup and the results for the remaining trees, respectively.
The next step is to extract similarities using these BCs in the mf-CBA. Because the binary mode exhibits two well-distinguished states with low dispersion, the B-array is suitable for representing the BCs and operating the bit-wise calculations. Fig. 4(f) shows a 1-bit representation in conductance form, where two cells in the same row with (LRS/HRS) stands for ‘0’ and (HRS/LRS) does ‘1’, and in applying voltage form, where two columns with (VREAD, 0) for ‘1’ and (0, VREAD) for ‘0’. These cases result in different output current values (IHRS and ILRS) depending on whether the intersecting cell for VREAD is HRS or LRS. Additionally, the ‘X’, or ‘do not care’ term, needed for the subsequent BC processing, produces a negligible output current (I0) since the voltage is not applied to both columns, regardless of whether the mapped value is ‘0’ or ‘1’. Fig. 4(g) shows output current results in the corresponding six cases, with the mapped state and applied voltage configuration shown in the inset. Due to binary mode THR's significant on–off ratio and low state dispersion, the ratio of ILRS and IHRS exhibit a significant value of >∼200. Due to these differences, the HD between an input bit (in the form of voltage) and a mapped bit (in the form of conductance) can be calculated as output current; ILRS for HD = 1, and (IHRS, I0) for HD = 0, respectively.
Furthermore, the inherent parallel operation of the mf-CBA structure allows for the summation of currents from each row, enabling efficient and parallel HD calculations, as shown in the right panel of Fig. 4(b). In this case, the MBC and CBC vectors are inputted in voltage form to the bit lines (column lines), and the output currents through the BC-containing B-array at each word line (row lines) represent the HD for OD and DC. Supporting Note 2 of the ESI† explains more details of the B-array operation. The BC values of tree 1 in Fig. 4(e) are mapped onto the B-array, as shown in Fig. 4(h). The current values (read at 0.1 V) from cells corresponding to HRS were marked in blue, and cells corresponding to LRS were marked in red, respectively. Additional results of the remaining trees are depicted in Fig. S21 of the ESI.† This current map allows for calculating the output current results for the 4-bit HD values with randomized voltage inputs, shown in Fig. 4(i). They show well-separated values with a linear relationship with the HD values, demonstrating the feasibility of the suggested mf-CBA for HD calculations.
Evaluations of the mf-CBA-based data mining method
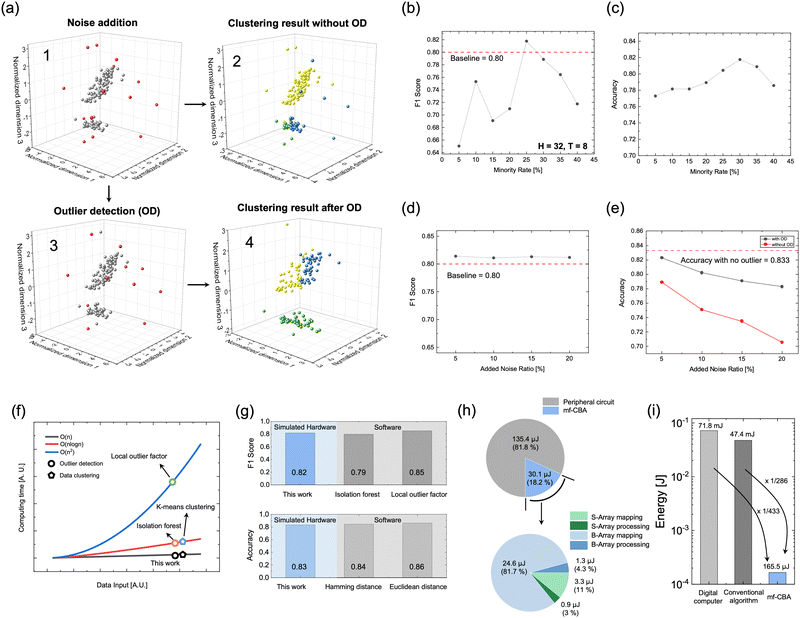
Based on efficient operations in S-array and B-array of the mf-CBA for the newly proposed data mining method, its performance was evaluated with a larger dataset that artificially added random outliers to the iris dataset, a representative DC dataset with three clusters. All subsequent evaluation results are average results from 100 trials that generate random noises and hyperplane tree structure based on the iris dataset to mitigate the potential overestimation of MOD and modified K-means performance utilizing the simulated hardware constructed with THR memristor's switching characteristics. (See Supporting Note 3 and Fig. S22 of the ESI†). The F1-score, suitable for evaluating unbalanced datasets, was used as an evaluation index for the MOD. Moreover, accuracy was chosen as an evaluation index for the modified K-means. To further demonstrate the versatility of the suggested MOD method, results from other datasets of various shapes are shown in Fig. S23 of the ESI.† In the modified K-means, the most critical problem, vulnerability to outliers, was solved by removing outliers through MOD in advance.Fig. 5(a) shows the results of the two data mining methods, revealing the vulnerability to outliers of conventional K-means. In the first case (sequence 1 → 2), the clustering is performed without OD, and the outliers distort the entire dataset, leading to inaccurate clustering results. The second case (sequence 1 → 3 → 4) shows the clustering results when initially performing the MOD method. The MOD method removes almost all outliers, resulting in clusters comparable to the original outlier-free iris dataset (Fig. S24 of the ESI†). Before evaluating the performance of these two cases, the MOD method was first evaluated using sequence 1 → 3. Fig. 5(b) shows the results of hyperparameter M tuning, where M ∼ 0.25 achieves optimal performance. When M is too small, many minority bits contributing to the MBC enter the “X” state, incorrectly excluding valid hyperplanes involved in the outlier score, and the total number of hyperplanes becomes insufficient for accurate outlier assessment. Conversely, when it becomes too large, too many hyperplanes, some with unreliable spatial information for OD, are included, compromising the outlier score's reliability. For the next step, the accuracy of the modified K-means method was evaluated using sequence 3 → 4. Fig. 5(c) shows the accuracy as a function of M. For reasons similar to the MOD, optimal performance was achieved when M ∼ 0.25. Also, Fig. S25 of the ESI† shows the influence of model parameters H and T on performance. Fig. 5(d) examines the impact of varying the number of artificially added outliers. The MOD maintains its performance even with increasing outlier counts, verifying its reliability. Finally, Fig. 5(e) quantifies the improvement produced by the MOD method when comparing the two cases mentioned above. Because the MOD method may not eliminate all outliers, a minor performance degradation occurs even after performing OD compared to the baseline result without outliers. The baseline was set through the average result from 100 trials using randomly generated hyperplane tree structures with a dataset without outliers. However, as the number of added outliers increases, the MOD implementation leads to significantly less performance degradation than without OD. This result highlights the high potential of the mf-CBA hardware capable of OD and DC for significantly improving the K-means algorithm implementation. To verify THR suitability in the above methods, performance results according to variation level and memory window are shown in Fig. S26 of the ESI.†
Furthermore, Fig. 5(f)–(i) compare performance with representative methods and energy consumption with conventional CMOS-based hardware. The circle symbols in Fig. 5(f) compare the time complexity of the MOD method with other representative methods (local outlier factor and isolation forest).37–39 The local outlier factor has a time complexity of O(n2) due to pairwise distance calculations for all data points, while the isolation forest has O(n![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n) time complexity due to decision trees with a limited depth of log
n) time complexity due to decision trees with a limited depth of log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n level.37,40 In contrast, the MOD achieves a linear time complexity O(n), enabled by its only similarity measure and parallel distance calculation. For the DC, the pentagram symbols in Fig. 5(f) show that the modified K-means method has reduced time complexity compared with the conventional K-means method. Next, the upper panel of Fig. 5(g) reveals that the MOD does not compromise on performance, reaching a comparable level to the other two methods. Also, the lower panel of Fig. 5(g) compares the accuracy using hardware- and software-calculated distances. The result of the simulated hardware is comparable to the results using the two software-calculated distances, highlighting the potential of mf-CBA hardware capable of calculating accurate similarities. Fig. S27 of the ESI† shows the results of calculated HDs and Euclidean distances between all data points in the iris dataset.
n level.37,40 In contrast, the MOD achieves a linear time complexity O(n), enabled by its only similarity measure and parallel distance calculation. For the DC, the pentagram symbols in Fig. 5(f) show that the modified K-means method has reduced time complexity compared with the conventional K-means method. Next, the upper panel of Fig. 5(g) reveals that the MOD does not compromise on performance, reaching a comparable level to the other two methods. Also, the lower panel of Fig. 5(g) compares the accuracy using hardware- and software-calculated distances. The result of the simulated hardware is comparable to the results using the two software-calculated distances, highlighting the potential of mf-CBA hardware capable of calculating accurate similarities. Fig. S27 of the ESI† shows the results of calculated HDs and Euclidean distances between all data points in the iris dataset.
Finally, Fig. 5(h) and (i) show the energy efficiency of the mf-CBA compared with CMOS-based digital computing hardware. Fig. 5(h) shows the composition of energy consumption. The energy consumed in the peripheral circuit is overwhelmingly larger than in the four parts of mf-CBA.41–44 However, a much larger energy consumption is necessary when assuming that all four parts are performed in a CMOS-based digital computing circuit, as shown in Fig. 5(i). Here, the results of calculations using software for the proposed data mining method (digital computer), OD using isolation forest, and DC using K-means (conventional algorithm) on the same IRIS dataset are presented, along with the results based on the power consumption of the mf-CBA and the peripheral circuit. Supporting Note 4 of the ESI† explains the energy calculation process in detail.
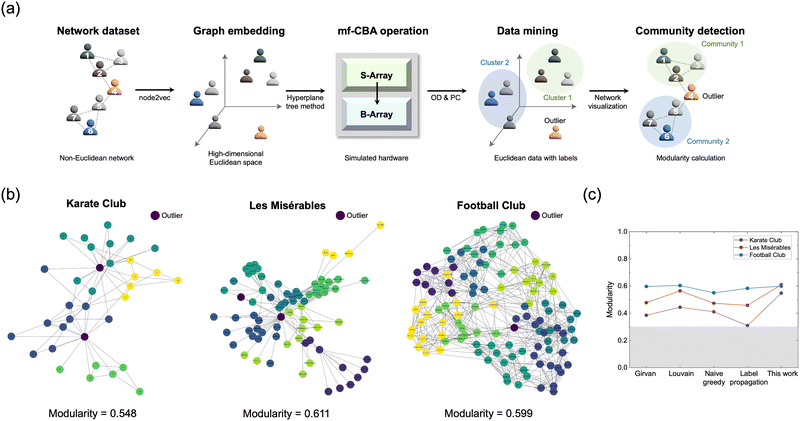
Application of the proposed methods to high-dimensional datasets
The suggested data mining method using mf-CBA was applied to the high-dimensional datasets, enabling dimension expansion in Euclidean space. Additionally, when processing such high-dimensional data, the mapping burden does not increase with dimension due to one-shot mapping in the S-array, making it advantageous for processing. Various network datasets were utilized with simulated hardware further to verify the proposed methods’ efficiency on high-dimensional datasets.45–47 Since network datasets are generally given with non-Euclidean graph structures with nodes and edges, they are usually embedded into Euclidean space for analysis. However, numerous operations in high-dimensional space after embedding posed a significant problem. Moreover, finding highly connected communities within the network or identifying outliers not strongly associated with any particular community is highly effective in network analysis.48 The mf-CBA in this study, with its inherent parallel VMM, can efficiently analyze the relationships between nodes in the embedded network by drawing out spatial minorities and similarities.Fig. 6(a) shows the process of processing the embedded network dataset through mf-CBA. In this process, the network dataset embedded through the node2vec algorithm is expressed in high-dimensional Euclidean space.49 Subsequently, the data in the Euclidean space undergo the suggested hyperplane tree-based data mining process to identify outliers and clusters. The results (cluster numbers and outliers) are then mapped back to the original network data to reveal communities and outliers. Fig. 6(b) shows community detection results with outliers using several well-known practical network datasets. The modularity index was used to evaluate the performance of community detection results.50 As outlier nodes (represented in purple circles) previously detected in each dataset are removed, all edges connected to them also disappear. As these outlier nodes were removed, the modularity increased compared to community detection results that did not previously perform OD. Fig. S28 of the ESI† shows the results without performing OD, demonstrating that outlier node detections improve modularity. Additionally, Fig. 6(c) compares the modularity of the three network datasets in Fig. 6(b) using widely utilized community detection algorithms, and comparable performance was found. These results confirmed that high-dimensional data mining can also be effectively performed on the mf-CBA.
Conclusions
This study demonstrated newly proposed data mining methods with high energy efficiency and reduced time complexity using THR memristor-based mf-CBA. The THR memristor could be reconfigured between stochastic mode and deterministic binary mode. Their behavior enabled the implementation of multiple hyperplanes through one-shot mapping and parallel HD calculation through vector–matrix multiplication. Newly proposed MOD and modified K-means methods were experimentally verified through four 9 by 9 mf-CBAs. In addition, robust results were obtained for various datasets through simulation based on device modeling in both tasks. Notably, OD and DC can be directly conducted with identical mapping and operation structures inside the given mf-CBA, thus contributing to direct in-memory computing for unsupervised learning. Also, vulnerability to outliers of conventional K-means algorithm was solved through MOD with the time complexity of O(n). The efficiency of high-dimensional processing was also verified through various network datasets. As a result, it could operate under 1% of the energy compared to CMOS-based hardware due to the in-memory computing structure and newly proposed methods. These results may overestimate the energy performance of the suggested method due to the lack of detailed peripheral circuit configuration. Nevertheless, its in-memory computing architecture will contribute to enhanced energy and computational efficiency once its hardware is fully settled.Experimental section/methods
Device fabrication and characterization
The fabrication process for the multi-functional Ta/HfO2/RuO2 memristors proceeded as follows (see Fig. S2 of the ESI†): initially, a 5 nm-thick Ti adhesion layer and a 20 nm-thick RuO2 layer were deposited on a SiO2/Si substrate using reactive sputtering (SNTEK, CDS 5000) to serve as the bottom electrode. Subsequently, conventional photolithography and lift-off processes were employed to define the width of the bottom electrode (ranging from 2- to 10-μm). The Ti deposition was carried out at a working pressure of 4.0 × 10−3 Torr and a sputtering power of 100 W, with an Ar gas flow rate of 20 standard cubic centimeters per minute (sccm). For the deposition of RuO2, a power of 60 W and a pressure of 1.6 × 10−2 Torr were utilized, along with an Ar/O2 flow rate of 30/3.5 sccm, respectively. Next, a 3.6-nm-thick HfO2 resistive switching layer was deposited via plasma-enhanced atomic layer deposition using Hf (NC2H5CH3)4 precursor and O2 plasma at a wafer temperature of 200 °C. The Ta top electrode and Pt passivation layer were then deposited using a sputtering method (SNTEK, CDS 5000), with power settings of 100 W and 60 W, and working pressures of 1.6 × 10−2 and 1.5 × 10−2 Torr for Ta and Pt, respectively (Ar gas flow rate of 30 sccm for both). Finally, the top electrode was patterned into lines with widths ranging from 2- to 10-μm using conventional photolithography and lift-off processes. Post-fabrication analysis of the THR device was performed using TEM and electrical dispersive spectroscopy (EDS, JEOL, JEM-ARM200F). Further chemical analysis was conducted using Auger electron spectroscopy (AES, ULVAC, PHI-710) and X-ray photoelectron spectroscopy (XPS, KRATOS, AXIS SUPRA). AES and XPS depth profiles were acquired by in situ Ar+ ion etching in the analysis chamber.Electrical measurements
The I–V sweep characteristics of the THR devices were evaluated using the semiconductor parameter analyzer (SPA) comprising HP4155A and HP4155B models. Biasing was applied to the top electrode, while the bottom electrode was grounded during the I–V sweep measurements. To measure 9 by 9 arrays, multi-probes consisting of 9 tips were used (see Fig. S14 of the ESI†). Closed-loop pulse switching was performed using a custom-built field-programmable gate array board, administering pulses until the device achieved the desired resistance. For the set operation, incremental pulses ranging from 0.3 V with a step of 0.05 V were applied to the top electrode, with the bottom electrode grounded, until the target LRS resistance was reached. Similarly, for the reset operation, decremental pulses ranging from −0.3 V with a step of −0.05 V were applied until the device reached the target HRS resistance value. All resistive states are measured at a read voltage of 0.1 V. EIS analysis was conducted using the impedance analyzer (HP4194) in the frequency range from 1 kHz to 10 MHz, with a 0.3 V DC bias and a 0.05 V oscillation. All EIS analyses were performed on cells with an 8-μm line width to minimize noise in the leakage current measurements of the memristor.Dataset preparation
(1) Iris dataset: artificial outliers were added to the iris dataset for outlier detection. The iris dataset is one of the most well-known datasets in data clustering. It contains measurements of the width and length of the petals and sepals of flowers.51(2) Zachary's karate club dataset: Zachary's karate club dataset illustrates the social connections among 34 members of a university karate club. Wayne Zachary gathered this dataset in 1977. The graph represents an undirected and unweighted social network.45
(3) Les miserables dataset: this dataset represents a social network where each node corresponds to a character from the novel, and each edge represents the co-occurrence of two characters within the same chapter. The graph depicts an undirected and unweighted social network.46
(4) American college football dataset: the American College Football dataset illustrates the network of American college football games between division IA colleges during the regular season of Fall 2000. This dataset represents a social network where each node corresponds to a football team, and each edge represents a game between two teams.47
Performance indexes
(1) Precision, Recall, and F1-score:Precision is a performance metric used to measure the performance of a classification model. It represents the proportion of true positive samples among the model's predicted positive samples.
 | (4) |
Recall is another performance metric used to evaluate the performance of a classification model. Recall represents the proportion of true positive samples among all actual positive samples.
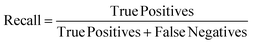 | (5) |
The F1-score is a performance metric for classification models, calculated as the harmonic mean of Precision and Recall. It represents a balanced measure between Precision and Recall, providing a harmonic adjustment between the two.
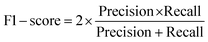 | (6) |
(2) Accuracy: accuracy is one of the performance metrics for classification models. It represents the proportion of total correct predictions made by the model. In other words, it measures the ratio of the number of correct predictions to the total number of predictions made by the model.
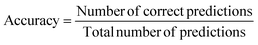 | (7) |
(3) Modularity: modularity is a performance metric that evaluates the quality of a network's division into communities or clusters. It measures the strength of the division of a network into modules (also called communities), where a module is a group of nodes that have dense connections internally but sparser connections with nodes in other modules. Higher modularity indicates a stronger community structure.
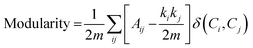 | (8) |
Community detection algorithms
The performance of the suggested method was compared with the representative software-level community detection algorithms (Girvan-Newmann,52 Louvain,53 Naïve greedy,54 and Label propagation55).System energy consumption estimation
The comprehensive energy consumption analysis for the mf-CBA and its associated peripheral circuit was divided into five distinct parts. The whole circuit's energy expenditure was estimated using switching energy (Eswitching) and static energy (Estatic) separately. For the S-array, energy consumption calculations were performed as follows for the mapping step: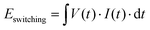 | (9) |
Analogously, the static energy was calculated for each iteration in the VMM operations as:
| Estatic = Istochastic·tread·(Vread,1·Ncell,1·Ndataset + Vin,1·Ncentroid) | (10) |
Similarly, energy consumption calculations for the B-array were determined with eqn (10) for the Eswitching during the mapping step, and the static energy was calculated for each iteration in the VMM operations as:
| Estatic = Ibinary·tread·Ndataset·(Vread,2·Ncell,2·(1 − RX) + Vread,2·Ncell,2·RX·Ncentroid) | (11) |
In addition, the energy consumption of the peripheral circuit on the mf-CBA was estimated based on 130 nm Si CMOS technology.41–44 Energy consumption for the comparative CPU-based digital computing system was estimated employing the thermal design power (TDP) of AMD Ryzen 5 4600H. The calculation method was implemented as:
CPU energy = TDP × CPU![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) utilization × computation utilization × computation![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Time Time | (12) |
Author contributions
S. C. and D. H. S. designed the study concept. D. H. S. fabricated the device. S. C., D. H. S., and N.G. performed electrical measurements. S. C. and N. G. contributed to the simulations. S. C., D. H. S., S. H. L., Y. H. J., J. H., S. K. S, and J.-K. H. Y. H. J contributed to the analysis and discussion. S. C., D. H. S., and N. G. wrote the manuscript. C. S. H. supervised the whole research and edited the manuscript.Data availability
All the relevant data are available from the corresponding authors upon request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Research Foundation of Korea (grant no. 2020R1A3B2079882).Notes and references
- M. S. Chen, J. Han and P. S. Yu, IEEE Trans. Knowl. Data Eng., 1996, 8(6), 866–883 CrossRef.
- V. J. Hodge and J. Austin, Artif. Intell. Rev., 2004, 22, 85–126 CrossRef.
- A. K. Jain, M. N. Murty and P. J. Flynn, Data Clustering: A Review, ACM Comput. Surv., 2000, 31(3), 264–323 CrossRef.
- A. K. Jain, Machine Learning and Knowledge Discovery in Databases, 2008 Search PubMed.
- J. A. Hartigan and M. A. Wong, Appl. Stat., 1979, 28(1), 100–108 Search PubMed.
- W. M. Rand, J. Am. Stat. Assoc., 1971, 66(336), 846–850 CrossRef.
- A. Sebastian, M. Le Gallo, R. Khaddam-Aljameh and E. Eleftheriou, Nat. Nanotechnol., 2020, 15, 529–544 CrossRef CAS PubMed.
- M. Hu, C. E. Graves, C. Li, Y. Li, N. Ge, E. Montgomery, N. Davila, H. Jiang, R. S. Williams, J. J. Yang, Q. Xia and J. P. Strachan, Adv. Mater., 2018, 30(9) DOI:10.1002/adma.201705914.
- M. Rao, H. Tang, J. Wu, W. Song, M. Zhang, W. Yin, Y. Zhuo, F. Kiani, B. Chen, X. Jiang, H. Liu, H. Y. Chen, R. Midya, F. Ye, H. Jiang, Z. Wang, M. Wu, M. Hu, H. Wang, Q. Xia, N. Ge, J. Li and J. J. Yang, Nature, 2023, 615, 823–829 CrossRef CAS PubMed.
- S. Choi, P. Sheridan and W. D. Lu, Sci. Rep., 2015, 5, 10492 CrossRef PubMed.
- P. Yao, H. Wu, B. Gao, J. Tang, Q. Zhang, W. Zhang, J. J. Yang and H. Qian, Nature, 2020, 577, 641–646 CrossRef CAS PubMed.
- X. Zhu, Q. Wang and W. D. Lu, Nat. Commun., 2020, 11, 2439 CrossRef CAS PubMed.
- C. Li, M. Hu, Y. Li, H. Jiang, N. Ge, E. Montgomery, J. Zhang, W. Song, N. Dávila, C. E. Graves, Z. Li, J. P. Strachan, P. Lin, Z. Wang, M. Barnell, Q. Wu, R. S. Williams, J. J. Yang and Q. Xia, Nat. Electron., 2018, 1, 52–59 CrossRef.
- S. Cheong, D. H. Shin, S. H. Lee, Y. H. Jang, T. Park, J. Han, S. K. Shim, Y. R. Kim, J. K. Han, N. Ghenzi and C. S. Hwang, Adv. Funct. Mater., 2023, 34(8) DOI:10.1002/adfm.202309108.
- D. H. Shin, S. Cheong, S. H. Lee, Y. H. Jang, T. Park, J. Han, S. K. Shim, Y. R. Kim, J. K. Han, I. K. Baek, N. Ghenzi and C. S. Hwang, Mater. Horiz., 2024, 11, 4493–4506 RSC.
- R. Wang, T. Shi, X. Zhang, J. Wei, J. Lu, J. Zhu, Z. Wu, Q. Liu and M. Liu, Nat. Commun., 2022, 13, 2289 CrossRef CAS PubMed.
- A. Bou and J. Bisquert, J. Phys. Chem. B, 2021, 125(35), 9934–9949 CrossRef CAS PubMed.
- A. R. C. Bredar, A. L. Chown, A. R. Burton and B. H. Farnum, ACS Appl. Energy Mater., 2020, 3(1), 66–98 CrossRef CAS.
- J. W. Yoon, J. H. Yoon, J. H. Lee and C. S. Hwang, Nanoscale, 2014, 6, 6668–6678 RSC.
- X. L. Jiang, Y. G. Zhao, Y. S. Chen, D. Li, Y. X. Luo, D. Y. Zhao, Z. Sun, J. R. Sun and H. W. Zhao, Appl. Phys. Lett., 2013, 102(25) DOI:10.1063/1.4812811.
- Y. H. You, B. S. So, J. H. Hwang, W. Cho, S. S. Lee, T. M. Chung, C. G. Kim and K. S. An, Appl. Phys. Lett., 2006, 89(22) DOI:10.1063/1.2392991.
- S. W. Jeong, H. J. Lee, K. S. Kim, M. T. You, Y. Roh, T. Noguchi, W. Xianyu and J. Jung, Thin Solid Films, 2006, 515(2), 526–530 CrossRef CAS.
- Y. Zhang, G. Q. Mao, X. Zhao, Y. Li, M. Zhang, Z. Wu, W. Wu, H. Sun, Y. Guo, L. Wang, X. Zhang, Q. Liu, H. Lv, K. H. Xue, G. Xu, X. Miao, S. Long and M. Liu, Nat. Commun., 2021, 12, 7232 CrossRef CAS PubMed.
- S. Dirkmann, J. Kaiser, C. Wenger and T. Mussenbrock, ACS Appl. Mater. Interfaces, 2018, 10(17), 14857–14868 CrossRef CAS PubMed.
- Y. Yang, P. Gao, S. Gaba, T. Chang, X. Pan and W. Lu, Nat. Commun., 2012, 3, 732 CrossRef PubMed.
- T. Wei, Y. Lu, F. Zhang, J. Tang, B. Gao, P. Yu, H. Qian and H. Wu, Adv. Mater., 2023, 35(10) DOI:10.1002/adma.202209925.
- G. S. Kim, H. Song, Y. K. Lee, J. H. Kim, W. Kim, T. H. Park, H. J. Kim, K. Min Kim and C. S. Hwang, ACS Appl. Mater. Interfaces, 2019, 11(50), 47063–47072 CrossRef CAS PubMed.
- T. H. Park, Y. J. Kwon, H. J. Kim, H. C. Woo, G. S. Kim, C. H. An, Y. Kim, D. E. Kwon and C. S. Hwang, ACS Appl. Mater. Interfaces, 2018, 10, 21445–21450 CrossRef CAS PubMed.
- D. H. Shin, H. Park, N. Ghenzi, Y. R. Kim, S. Cheong, S. K. Shim, S. Yim, T. W. Park, H. Song, J. K. Lee, B. S. Kim, T. Park and C. S. Hwang, ACS Appl. Mater. Interfaces, 2023, 16(13), 16462–16473 CrossRef PubMed.
- D. Che, Q. Liu, K. Rasheed and X. Tao, Adv. Exp. Med. Biol., 2011, 696, 191–199 CrossRef CAS PubMed.
- A. F. Veinott, Oper. Res., 1967, 15(1), 1–183 CrossRef.
- L. Yang, X. Huang, Y. Li, H. Zhou, Y. Yu, H. Bao, J. Li, S. Ren, F. Wang, L. Ye, Y. He, J. Chen, G. Pu, X. Li and X. Miao, InfoMat, 2023, 5(5) DOI:10.1002/inf2.12416.
- A. Bookstein, V. A. Kulyukin and T. Raita, Inf. Retr. Boston, 2002, 5, 353–375 CrossRef.
- Y. J. Jeong, J. Lee, J. Moon, J. H. Shin and W. D. Lu, Nano Lett., 2018, 18, 4447–4453 CrossRef CAS PubMed.
- F. Aguirre, A. Sebastian, M. Le Gallo, W. Song, T. Wang, J. J. Yang, W. Lu, M. F. Chang, D. Ielmini, Y. Yang, A. Mehonic, A. Kenyon, M. A. Villena, J. B. Roldán, Y. Wu, H. H. Hsu, N. Raghavan, J. Suñé, E. Miranda, A. Eltawil, G. Setti, K. Smagulova, K. N. Salama, O. Krestinskaya, X. Yan, K. W. Ang, S. Jain, S. Li, O. Alharbi, S. Pazos and M. Lanza, Nat. Commun., 2024, 15, 1974 CrossRef CAS PubMed.
- C. Liu, M. Hu, J. P. Strachan and H. H. Li, in Proceedings - Design Automation Conference, 2017, vol. Part 128280.
- M. M. Breuniq, H. P. Kriegel, R. T. Ng and J. Sander, SIGMOD Record (ACM Special Interest Group on Management of Data), 2000, 29 DOI:10.1145/335191.335388.
- H. Xu, L. Zhang, P. Li and F. Zhu, J. Algorithm. Comput. Technol., 2022, 16 DOI:10.1177/17483026221078111.
- F. T. Liu, K. M. Ting and Z. H. Zhou, in Proceedings - IEEE International Conference on Data Mining, ICDM, 2008.
- M. Tokovarov and P. Karczmarek, Inf. Sci., 2022, 584, 433–449 CrossRef.
- F. Solis, Á. Fernández Bocco, A. C. Galetto, L. Passetti, M. R. Hueda and B. T. Reyes, Int. J. Circuit Theory Appl., 2021, 49(10), 3171–3185 CrossRef.
- A. K. Adepu and K. K. Kolupuri, Int. J. Cybern. Inform., 2016, 5(4), 315 Search PubMed.
- F. Moradi, G. Panagopoulos, G. Karakonstantis, H. Farkhani, D. T. Wisland, J. K. Madsen, H. Mahmoodi and K. Roy, Microelectron. J., 2014, 45(1), 23–34 CrossRef.
- B. B. A. Fouzy, M. B. I. Reaz, M. A. S. Bhuiyan, M. T. I. Badal and F. H. Hashim, in 2016 International Conference on Advances in Electrical, Electronic and Systems Engineering, ICAEES 2016, 2016.
- W. W. Zachary, J. Anthropol. Res., 1977, 33(4), 452–473 CrossRef.
- D. E. Knuth, in Proceedings of the Fourth Annual ACM-SIAM Symposium on Discrete Algorithms, 1993.
- M. E. J. Newman, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74(3) CrossRef CAS PubMed.
- B. Kamiński, P. Prałat and F. Théberge, Appl. Netw. Sci., 2023, 8(1), 25 CrossRef.
- A. Grover and J. Leskovec, 2016.
- A. Clauset, M. E. J. Newman and C. Moore, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2004, 70(6) DOI:10.1103/PhysRevE.70.066111.
- R. A. Fisher, UCI Machine Learning Repository, 1988.
- M. Girvan and M. E. J. Newman, Proc. Natl. Acad. Sci. U. S. A., 2002, 99, 7821 CrossRef CAS PubMed.
- V. D. Blondel, J. L. Guilaume, R. Lambiotte and E. Lefebvre, J. Stat. Mech.: Theory Exp., 2008, 2008(10) Search PubMed.
- H. Shiokawa, Y. Fujiwara and M. Onizuka, Proceedings of the AAAI Conference on Artificial Intelligence, 2013, 27.
- G. Cordasco and L. Gargano, 2010 IEEE International Workshop, 2010.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh00942h |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |