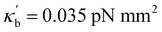Open Access Article
Open Access ArticleFluid mediated communication among flexible micro-posts in chemically reactive solutions†
Moslem
Moradi
 a,
Oleg E.
Shklyaev
a,
Oleg E.
Shklyaev
 a,
Wenzheng
Shi
b and
Anna C.
Balazs
a,
Wenzheng
Shi
b and
Anna C.
Balazs
 *a
*a
aDepartment of Chemical Engineering, University of Pittsburgh, Pittsburgh, PA 15261, USA. E-mail: balazs@pitt.edu
bCourant Institute, New York University, New York, NY 10012, USA
First published on 17th October 2024
Abstract
Communication in biological systems typically involves enzymatic reactions that occur within fluids confined between the soft, elastic walls of bio-channels and chambers. Through the inherent transformation of chemical to mechanical energy, the fluids can be driven to flow within the confined domains. Through fluid–structure interactions, the confining walls in turn are deformed by and affect this fluid flow. Imbuing synthetic materials with analogous feedback among chemo-mechanical, hydrodynamic and fluid–structure interactions could enable materials to perform self-driven communication and self-regulation. Herein, we develop computational models to determine how chemo-hydro-mechanical feedback affects interactions in biomimetic arrays of chemically active and passive micro-posts anchored in fluid-filled chambers. Once activated, the enzymatic reactions trigger the latter feedback, which generates a surprising variety of long-range, cooperative motion, including self-oscillations and non-reciprocal interactions, which are vital for propagating coherent, directional signals over net distances in fluids. In particular, the array propagates a distinct message; each post interprets the message; and the system responds with a specific mode of organized, collective behavior. This level of autonomous remote control is relatively rare in synthetic systems, particularly as this system operates without external electronics or power sources and only requires the addition of chemical reactants to function.
New conceptsBy modeling an array of surface-anchored micro-posts in solution, we find that the array undergoes autonomous communication involving continuous two-way feedback between the “sender” and “receiver”, unlike the one-way exchanges typical of stimuli-responsive material. Active posts in this array are coated with enzymes, while the remaining posts are passive. Enzymatic reactions at the active posts release chemical energy that is inherently transduced into mechanical forces, which propel the spontaneous motion of the fluid. Through fluid–structure interactions, the flowing fluid deforms the flexible posts, which in turn exert an opposing force on the fluid and modifies the fluid flow, leading to continuous feedback among chemical, hydrodynamic and mechanical interactions. This mode of self-sustained chemo-hydro-mechanical feedback is evident in biology, but rarely achieved in synthetic systems. This distinctive feedback enables the system to undergo unexpected self-oscillations and non-reciprocal interactions, which are vital for propagating coherent, directional signals over net distances in fluids. Additionally, the feedback allows the posts to achieve large-scale remote control, as one post regulates the motion of faraway structures. The observed range of dynamic behavior is activated solely by the simple addition of reactants and is vital for creating soft robotic materials undergoing sustained, autonomous motion. |
I. Introduction
Reactions in the body transform chemical energy into mechanical forces in a process called “chem-mechanical transduction”. The resultant mechanical forces act on the surrounding fluid and instigate its flow. In turn, the flowing fluid deforms the surrounding soft tissue (through fluid–structure interactions). To conserve momentum, the deformed tissue exerts an opposing force on the fluid and consequently modifies the velocity of the fluid flow. The change in fluid velocity ultimately affects the rate of the chemical reaction and thereby introduces feedback among chemistry, hydrodynamics and fluid–structure interactions. In biology, this feedback provides a vital mechanism to sense, communicate and respond to the inherent “messaging” in the body. Designing systems with analogous chemo-mechanical coupling could yield materials with remarkable autonomous communication and self-regulation.1 Herein, we develop computational models to design and simulate the behavior of fluidic chambers containing tethered micro-posts that exhibit this inherent feedback and undergo biomimetic communication, where components continually adapt to self-generated signals in the solution. In this system, some posts are coated with enzymes and become chemically active when dissolved chemicals instigate an enzymatic reaction at a specific post. The resulting interactions give rise to a surprising variety of long-range, cooperative motion even within sparse arrays of these posts. This level of autonomous communication is relatively rare in synthetic systems that operate without external electronics or power sources and only require the addition of chemical reactants to function.Examples of the distinctive behavior are detailed in the Results and Discussion, including cases where the array displays two-way biomimetic communication between “sender” and “receiver” posts. In this system, the receiver affects the subsequent signal from the sender, much like a two-way exchange in a conversation. The posts also communicate across the extent of the array, allowing one post to regulate the behavior of a distant one and thereby perform action at a distance. Consequently, this system can selectively drive movement in some part of the sample, but not in another, as occurs for instance with the selective movement of one finger within a hand. Similarly, the system can support multiple modes of motion occurring simultaneously in an array. Moreover, chemically active posts can trigger nearby passive posts to oscillate or display non-reciprocal interactions, even though the active sender post itself remains stationary. As described below, the feedback among chemistry, hydrodynamics and fluid–structure interactions causes the array to propagate a distinct message; each post to interpret the message; and the system to respond with a specific mode of organized, collective behavior.
To date, to the best of our knowledge, there are very few comparable experimental (or theoretical) studies on synthetic systems that: trigger a chemical signal, convey the signal throughout entire system (the array in solution), instigate specific motion at specific locations in the system and support multiple modes of motion occurring simultaneously in a given system. Hence, it is difficult to make a one-to-one comparison between findings from experiments and results from our computational modeling on the latter system. We have, however, validated our computational models through direct comparison with experiments on a broad class of synthetic systems that showed biomimetic chemo-mechanical. For example, we have modeled systems that encompass enzymatic reactions, chemically generated fluid flow and fluid–structure interactions with hard, non-deformable materials and found good agreement between the predictions from our simulations and the corresponding experiments.2–14 In addition, recent independent experimental studies showed qualitative agreement with our predictions14 for the behavior of flexible sheets in solution that were chemically driven by promotor–inhibitor reactions.15 Moreover, we performed collaborative studies on arrays of catalyst-coated micro-posts in aqueous solution16 showing that these posts displayed self-oscillatory behavior, and found excellent agreement between the modelling and experiments. We note that in the latter studies, the posts were not individually addressable, and every post exhibited the same motion; hence, the system did not display the complexity discussed here. Furthermore, we collaborated with experimentalists to validate our prediction that light can trigger biomimetic chemo-mechanical transduction in micro-posts of liquid crystalline elastomers.17,18 Finally, we note our collaborations with experimentalists on the behavior of self-oscillating Belousov–Zhabotinsky (BZ) gels,19–23 which undergo biomimetic chemo-mechanical transduction. The latter experiments validated our predictions on the factors that regulate the self-oscillations of the gels.19–23
Notably, solutal buoyancy has been detected in biological systems; it plays a critical role in the range expansion of yeast cells that are located at the air/water interface.24 As the yeast metabolizes nutrients, they introduce density variations in the underlying fluid that generates flow. Forces from the flow break up the large colonies into smaller, more dispersed aggregates. This breakup and dispersion enable the yeast cells to proliferate into new areas and thereby extend the range of their activity. In effect, the generated density gradients, the resulting hydrodynamics and subsequent forces at the fluid/colony interface serve as mode of communication, informing the colony to divide and then grow at the new sight. The effects of solutal buoyancy in biology have only recently been identified24 and have not been thoroughly explored. Further studies may reveal other examples where microscale bio-communication depends not only on complex biochemical machinery, but also on fundamental hydrodynamic and fluid–structure interactions.25,26
In previous studies focused on the dynamic behavior of complaint posts, researchers used a combination of external stimuli and the appropriate stimuli-responsive polymers to generate self-oscillation, self-regulation, and non-reciprocal interactions in gel microstructures. For example, researchers developed an array of uniformly oscillating, self-regulating posts by utilizing active, thermo-responsive hydrogels in solution.16 An exothermic reaction on the top of gel posts induced changes in the phase behavior of the thermo-responsive gels and ultimately led all the units to oscillate as they periodically bent up and down into the solution. More recently, scientists designed arrays of photo-responsive liquid crystalline elastomer (LCE) posts and used light to induce pronounced non-reciprocal motion in the posts, as well as other forms of movement.17 To exhibit this wealth of complex dynamics, the material had to be “preprogrammed”, using a magnetic field to set the orientation of the nematic director.27–31 Non-reciprocal motion in photo-active LCEs was also elicited by irradiating the sample with different wavelengths of light,32–34 or orthogonally aligned lasers,35 as well as selective focusing of the light to different positions of the sample.36 Polyelectrolyte gel filaments in a viscous environment can exhibit nonreciprocal motion in a steady, uniform the electric field.37
Distinct from the latter studies, we use just the addition of chemical reactants to generate rich dynamic behavior. In our previous studies, we developed computational models2 to show that even the stationary states produced by the chemically generated flows lead to an unexpected richness of stable designs, from Mandela figures to kaleidoscopic images. The arrays also produced unique “fingerprints” that characterize the system, reflecting the type of enzymes used, placement of the enzyme-coated posts, height of the chamber, and bending modulus of the elastic posts. This behavior can enable microfluidic devices to be spontaneously reconfigured for specific applications without construction of new chambers and the fabrication of standalone sensors that operate without extraneous power sources. Moreover, as shown in these studies, generated non-reciprocal movement is not limited to a single anchored post or confined between two such structures, but can be propagated among multiple posts in an array and hence, the system can promote extensive directional flow and broader propagation of “instructions” within microfluidic chambers.
To determine the different modes of induced dynamic motion and delineate the parameter range that produces this motion, we use our computational models to calculate phase maps for arrays containing both active and passive posts. We uncover a wealth of dynamic behavior, where each mode of chemically triggered motion can serve a distinct purpose, and the entire array can offer a range of utility. The system only requires low energy input to drive autonomous materials, including in soft robots.
Below, we describe our computational approach to capture the diversity of motion displayed in arrays containing chemically active and passive elastic posts. In the, we examine the posts and array. In Section IIIA of the Results and discussion, we show that intrinsic, chemo-mechanical interactions enable the posts to undergo two-way communication; Section IIIB, describes the position dependent self-oscillations and non-reciprocal motion displayed by domain. In Section IIIC, we compare the results obtained from two different modeling approaches to indicate the robustness of our predictions. The ability of active posts to control action at a distance and simultaneously generate different modes of motion in a single sample is described in Sections D–F. Section G details the influence of passive posts as active posts propagate a signal in the system. Using our modeling approach, we also designed systems that display and regulate these different activities all at once, showing a richness of dynamic behavior not commonly associated with synthetic materials.
II. Computational model
Previous studies of “chemical pumps”, showed that despite the exothermicity of the catalytic reactions, the convective flow was generated primarily by solutal buoyancy.38,39 Therefore, we couple the fluid motion to the chemical composition of the solution solely through the buoyancy mechanism. In our model, we explicitly model M reactants and the jth reagent of concentration Cj diffuses with the diffusion constant Dj (1 ≤ j ≤ M). The change in the local fluid density due to the chemical reaction is given as where ρ0 is the solvent density and
where ρ0 is the solvent density and  is the corresponding solutal expansion coefficient. The density variation in the solution gives rise to a buoyancy force per unit volume given by
is the corresponding solutal expansion coefficient. The density variation in the solution gives rise to a buoyancy force per unit volume given by  where g represents gravitational acceleration. This buoyancy force drives the spontaneous motion of the fluid and consequently, deforms the immersed post. If the products of the reactions are less dense than the reactants, the product-rich fluid flows upward and the reactant-rich fluid flows along the bottom surface toward the post. This motion is referred to as “inward flow”. Alternatively, if the products are denser than the reactants, then the product-rich fluid flows along the bottom surface and away from the post to produce an “outward” flow.
where g represents gravitational acceleration. This buoyancy force drives the spontaneous motion of the fluid and consequently, deforms the immersed post. If the products of the reactions are less dense than the reactants, the product-rich fluid flows upward and the reactant-rich fluid flows along the bottom surface toward the post. This motion is referred to as “inward flow”. Alternatively, if the products are denser than the reactants, then the product-rich fluid flows along the bottom surface and away from the post to produce an “outward” flow.
The simulation domain is a rectangular box Ω = {(x, y, z): 0 ≤ x ≤ Lx, 0 ≤ y ≤ Ly, 0 ≤ z ≤ H} with horizontal dimensions Lx and Ly, and height H. The elastic post is modeled as a linear chain of N beads, described by positions ri, that interconnected by elastic rods. The nodes of active posts are uniformly coated with a catalyst that generates the buoyancy force. The passive posts are uncoated, so the buoyancy forces originate solely from the reactions promoted by the surface-coated active posts. The movements of the spherical beads (nodes) are described as:
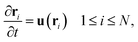 | (1) |
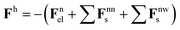 .
.
The fluid dynamics in the chamber are described by the respective continuity, Navier–Stokes equations (in Bossinesq approximation41), and reaction–diffusion equations
| ∇·u = 0, | (2) |
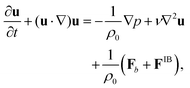 | (3) |
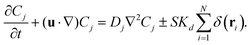 | (4) |
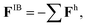 which is calculated via the immersed boundary method40 (IBM), providing fluid–structure interactions between the solution and the elastic posts.
which is calculated via the immersed boundary method40 (IBM), providing fluid–structure interactions between the solution and the elastic posts.
The chemicals are consumed or produced at the position of the enzyme-coated bead rk of the post with a reaction rate given by SKd where S is the area coated by catalyst. We assume that the catalytic reaction on the post follows the Michaelis–Menten kinetics,42 where the rate of consumption per unit area of the catalytic coverage is given by
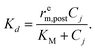 | (5) |
We prescribe no-slip boundary conditions at the confining solid walls and prohibit the penetration of chemical Cj through the boundaries of the container by specifying
| {x, y} = 0, L and z = 0, H: u = 0, n·∇Cj = 0, | (6) |
III. Results and discussion
A. Self-oscillating of a passive elastic post induced by a non-oscillating active one
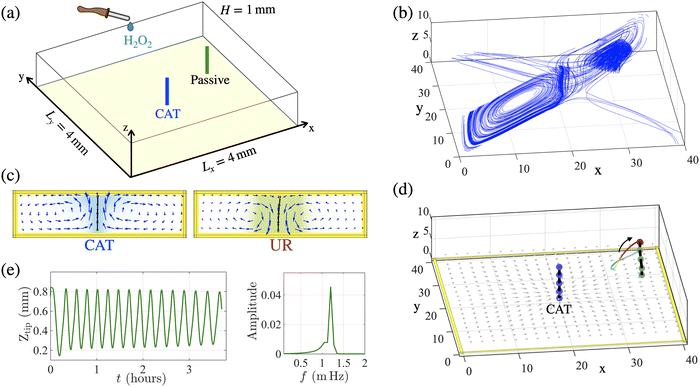
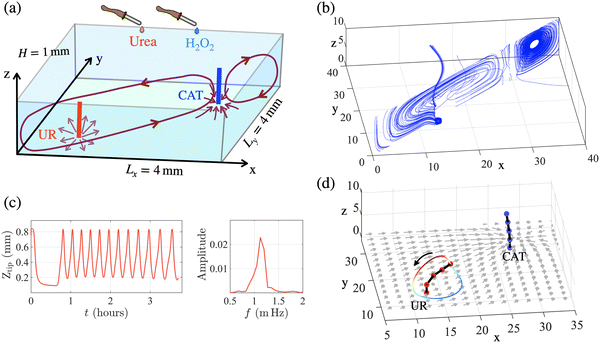
In biological communication, both the “sender” and “receiver” adapt to changes in the environment. In the case below, local asymmetries in the generated flow cause this adaptive behavior to simultaneously support two different modes of motion in one system. An active post (sender) generates a flow profile that causes that post to remain stationary, but simultaneously drives a distant passive post (receiver) to undergo regular oscillations. This example highlights the system's sensitivity to the local flow fields and ability to control movements at a distance from the sender.To start, we analyze the dynamics of a single, passive post in the convective flow generated by a single active post, which is coated with catalase (CAT). Both the passive and active posts are flexible and tethered to the bottom surface of a fluid-filled chamber. It might be anticipated that the active post would exhibit complex movements since the dynamic action in the system originates from this post and further, that the compliant passive post would simply mimic the motion of the active one. Here, however, we find that the active post remains stationary, and it is the passive post that displays oscillatory behavior. As explained below, this case highlights the importance of the relative locations of the posts in controlling the overall spatiotemporal behavior in the chamber.
The active post is tethered at the center of simulation box and the passive post is situated near a corner (Fig. 1a). The length and diameter of both posts are L = 0.8 mm and w = 0.26 mm, respectively. The dimensions of the enclosing chamber are 4 mm × 4 mm in the lateral directions and H = 1 mm for the chamber height. Initially, the tethered posts assume a vertical configuration. When hydrogen peroxide (H2O2) is added to the confined aqueous solution, catalase decomposes hydrogen peroxide into water, H2O, and oxygen, O2:
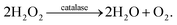 | (7) |
With the CAT-coated post located at the center of the box, the generated inward flow is symmetric about the post and hence, for all the parameter values considered here, the active post remains upright (Fig. 1c). Conversely, in the case of the passive post, with κb = 0.057 pN mm2, the circulating buoyancy-driven flow drags the free end of the passive post downwards and along the streamlines of the fluid (Fig. 1b). This passive post starts to oscillate (see Movie S1 in ESI,† Appendix) only when it is sufficiently flexible to interact with the different regions of fluid flow and is located at certain positions in the chamber, e.g., near the corners/sidewalls (see next section) so that the post feels both the push and pull of the circulating fluid.
Fig. 1e shows the tip height of the passive post as a function of time and the frequency spectrum of the resulting oscillatory behavior. The trajectory of this motion is shown in Fig. 1d. For the set of parameters used in the simulations, the frequency of oscillation is f = 1.2 mHz, which corresponds to a period of T ∼ 13.8 min. Note that systems based on gels43 and LCEs16 produce oscillations with frequencies 10 mHz and 16 mHz, respectively. These values are not substantially different from the frequencies produced by the oscillatory posts in our system, which is on order of 1 mHz.
The duration of the fluid motion and resulting dynamics of the posts largely depend on the initial concentration C0 of reactants (amount of fuel in the system) and rates SKd at which the chemicals are consumed during the reaction. The two quantities determine the duration of all dynamical processes that include the fluid motion and post behavior. When all reactants are converted to products all dynamical processes stop. In the simulations, we used experimentally-relevant values38 of C0 = 50 mM and Srem,post ∼ 10−10 mols−1 that enable fluid motion for hours (the time is shown on the horizontal axes in Fig. S5a, ESI†). For a one CAT-coated post at the center, with initial concentration of C0 = 50 mM, the average chemical concentration in the domain will drop to half of the initial concentration after 4 hours, and the average speed of the fluid in the domain reaches a maximum of |u| = 5 μm s−1 (see Fig. S9 in ESI,† Appendix) after 6 minutes and drop to |u| = 3.5 μm s−1 after 4 hours. The duration of the dynamic behavior decreases with the decrease of the initial concentration (less fuel in the system) as it is shown in Fig. S5a (ESI†).
The response speed can be characterized by the viscose H2/ν ∼ 1 s and diffusive H2/D ∼ 103 s time scales that control the dynamics of the system (we take domain height H = 1 mm, and typical values ν ∼ 10−6 m2 s−1, D ∼ 10−9 m2 s−1). Because the viscous time scale is much less than the diffusive one, the system is controlled by the slowest process, which is the speed ofdiffusion. The response time on the order of 10 min is typical response time observed in the relevant experiments.38
B. Passive posts exhibit position-dependent modes of motion
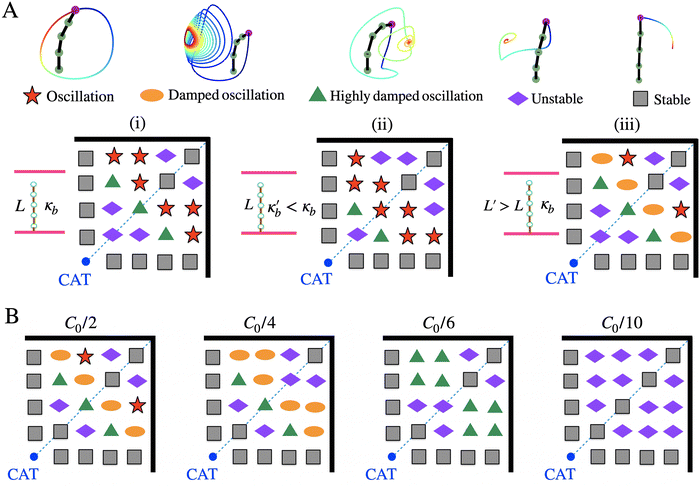
As noted above, with the CAT-coated post located in the middle of the square chamber, the radially symmetric forces generated about this active post cause it to maintain a steady, upright configuration. On the other hand, the motion of the passive post in the system is dependent on its location inside the chamber, length, and bending stiffness (as well as initial chemical concentration of the reactant). For example, near walls or corners, passive posts experience not only the flow generated at the active post, but also the flow reflected from the bounding, hard surfaces. Due to these position dependent fluid–structure interactions, the “message” transmitted through the array can be tuned by altering the location of the passive unit, as detailed below.To generate the state diagram (Fig. 2) that reveals the behavior of the passive post at various locations in the box, the passive post is placed in one of the 24 different positions in the computational domain and the simulations are performed to determine the post's dynamics at that specific site. The passive post was then moved to the next site where the computation was repeated. The position of the one CAT-coated post is held fixed at the center of the box. The x–y coordinates of 24 passive posts in Fig. 2 are constructed so that they are placed in a square array of 9 × 9 array, where the post spacing is δ = Lx/9 = 40/9 = 4.4Δx. The coordinates of the passive posts in the first quadrant of the domain can be written as (x0 + n1δ, y0 + n2δ), where (x0, y0) = (20, 20) is the position of active (CAT-coated) post at the center, and the coefficients n1, n2 ∈ {0, 1, 2, 3, 4}, and (n1, n2) ≠ (0, 0). The generated state map indicates different modes of motion exhibited by the one passive post and the range of parameters that lead to this behavior. Relative to values used in Fig. 2A(i), simulations are performed for a different bending stiffness (Fig. 2A(ii)) and at a different length (Fig. 2A(iii)) of the posts. In all these studies, we use the same values of κb and L for the passive and active posts; this allows us to focus on a sample that has homogeneous geometrical and mechanical properties. Local heterogeneities in κb and L can also give rise to striking behavior, which will be examined in later studies.
Certain features are common to all the cases in Fig. 2A(i)–(iii). For example, due to the four-fold symmetry of the flow field, we only consider the state diagram in the first quadrant of the simulation box. Points that lie at equivalent locations about the right and left of the diagonal line cutting through this quadrant show the same behavior. Along the lateral lines marking the four-fold symmetry of the box, the passive posts exhibit stable behavior (grey boxes); they initially bend away from the active post and then assume a stationary configuration. Far from the active post, the passive units also display stable behavior along the diagonal line.
Another common feature is the non-reciprocal nature of oscillatory motion, as needed for directed fluid flow over a net distance. The identical back and forth strokes in reciprocal oscillations just perturb the fluid, but do not lead to sustained directional motion. The asymmetric oscillatory behavior observed here is due to the extensive nature of the fluid–structure interactions. The widespread flows generated near the top surface (as detailed further below) bend the tops of posts so that they are no longer symmetric about their long axis (Fig. 2). The posts’ tips remain bent as flow contributes to the post's overall motion. In other words, the fundamental oscillating unit is the bend post.
In Fig. 2A(i), the bending stiffness is set to κb = 0.057 pN mm2 and the length of the box is set to L = 0.8 mm. A particularly striking feature of this plot is the oscillatory behavior (red stars) displayed by passive posts that are near the side walls, and yet at a distance from the active post. The fluid reflected from these boundaries flows back toward the passive posts; this forward and backward thrust promotes oscillatory behavior. Closer to the active post, but away from the side walls, the fluid flow cannot sustain regular oscillations, and the posts display highly damped oscillations.
Comparisons of Fig. 2A(i) and (ii) indicate the effects of decreasing the bending stiffness from κb = 0.057 pN mm2 to 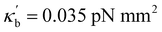 while fixing L = 0.8 mm. The number of sites that previously displayed highly damped oscillations (green triangles) in Fig. 2A(i), show stable oscillatory behavior (red stars) for the decreased bending stiffness in Fig. 2A(ii) (Movie S2 in ESI,† Appendix). The decrease in bending stiffness corresponds to an increase in the post's flexibility and enables the flexible posts to more closely follow the flow streamlines. The more flexible passive posts can more readily sense and respond to the oscillatory message produced by the extensive circulating flow centered about the active post. Relative to Fig. 2A(i), post sites that display oscillatory behavior are shifted closer toward the CAT-coated post (Fig. 2A(ii)), which triggers the circular fluid flow. Similarly, the decrease in bending stiffness enables the passive posts with unstable behavior (Fig. 2A(i)) to show damped oscillations near the central CAT post (Fig. 2A(ii)).
while fixing L = 0.8 mm. The number of sites that previously displayed highly damped oscillations (green triangles) in Fig. 2A(i), show stable oscillatory behavior (red stars) for the decreased bending stiffness in Fig. 2A(ii) (Movie S2 in ESI,† Appendix). The decrease in bending stiffness corresponds to an increase in the post's flexibility and enables the flexible posts to more closely follow the flow streamlines. The more flexible passive posts can more readily sense and respond to the oscillatory message produced by the extensive circulating flow centered about the active post. Relative to Fig. 2A(i), post sites that display oscillatory behavior are shifted closer toward the CAT-coated post (Fig. 2A(ii)), which triggers the circular fluid flow. Similarly, the decrease in bending stiffness enables the passive posts with unstable behavior (Fig. 2A(i)) to show damped oscillations near the central CAT post (Fig. 2A(ii)).
If the length of the post is increased from L = 0.8 mm to L = 0.875 mm (at κb = 0.057 pN mm2) the most pronounced difference is a change from the previously observed oscillatory behavior (Fig. 2A(i)) to damped oscillation (Fig. 2A(iii)). Increasing the length of the tethered post is analogous to decreasing stiffness since the tips now lie further away from the anchoring sites on the bottom and hence, their motion is less constrained. The posts in Fig. 2A(iii) are too “floppy” to follow the cyclic fluid flow and hence cannot execute oscillations shown in Fig. 2A(i) with shorter posts.
Finally, we examine the effect of changing the initial chemical concentration on the motion of passive post. In Fig. 2B, we plot the state diagram as we reduce the initial concentration from C0 = 50 mM (the value that we used in Fig. 2A) to C0/2, C0/4, C0/6 and C0/10. Reducing the initial concentration reduces the average velocity field in the domain and suppresses the oscillation of the passive post (see Fig. S5 in Appendix ESI†). By reducing the initial chemical concentration by half, we only observe two oscillating positions in the chamber and greater reductions in C0-lead to no more oscillating positions in the domain and introduce damped, highly damped and unstable points, respectively. We also increased the initial chemical concentration to 2C0, and the state diagram does not change compared to the state diagram with the initial C0 (Fig. 2A(i)).
C. Comparison of simulation with semi-analytical model
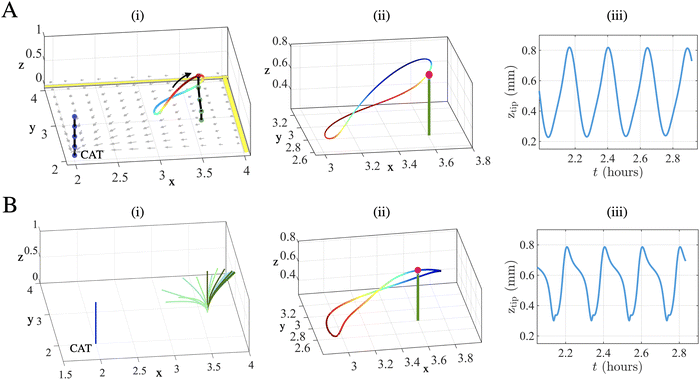
To validate the above results, we use elasto-hydrodynamic theory (detailed in the Methods section) to model a passive post near a wall that displays oscillatory behavior in the presence of one, central CAT-coated post. We use the background fluid flow obtained in the simulations as the input to the elasto-hydrodynamic theory. The results from the simulations (Fig. 3A) show: (i) the flow field, (ii), trajectory of the tip of passive post, and (iii), the tip height of the passive post. The plots in Fig. 3B(i)–(iii) show the corresponding data obtained with the elasto-hydrodynamic theory and show qualitatively similar behavior as the respective plots in Fig. 3A. The agreement between the two different approaches corroborates the findings from the simulations.D. Active post mediates communication between two passive ones and enables action at a distance
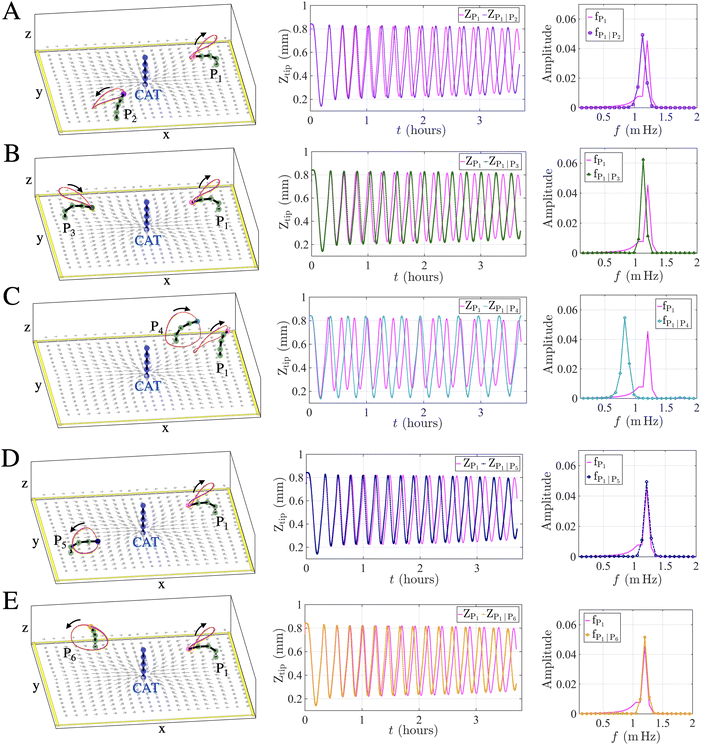
Having validated the results from the computational model and knowing the regions where a single passive post displays oscillatory behavior, we examine movements in a system that contains the centrally located CAT-coated post and two passive posts. These simulations allow us to determine how the active post mediates the communication between the two passive units and how the relative positions of the two passive posts affect their mutual behavior. Surprisingly, even in this sparse system (Fig. 4), the signal from an active post can mediate the interaction between two well-separated passive ones. Moreover, the two passive posts communicate with each other to establish the dynamic behavior in the entire domain.We specifically examine how the oscillation frequency of one passive post (post P1) is altered by the presence of a second passive one. The position of P1 is held fixed while the second post occupies five different sites denoted as Pi (i = 2, 3, 4, 5, 6). Following the state map in Fig. 2, the post positions were chosen to place both P1 and Pi (left panels) in the regime of oscillatory behavior. The middle panels in Fig. 4 indicate the oscillations of the tip for P1 in the absence (magenta) and presence (different colors) of the second passive post, (see also Movie S3 in ESI,† Appendix). The corresponding oscillation frequencies are shown in the right panels.
In all cases (A)–(E), the oscillation frequency at P1 is altered relative to that when P1 is the only passive post in the domain. In other words, the presence of the second passive post affects the oscillatory behavior at P1. As flow generated at the central active post impinges on Pi, it modifies the hydrodynamic and fluid–structure interactions that affect the streamlines in the entire chamber. Hence, P1 now experiences a flow field that is distinct from that generated by just one passive post in the presence of the CAT post.
The largest variation in this frequency occurs when the second post occupies the position at P4, where the separation between P1 and Pi is the smallest of the five scenarios (panel C); the proximity of the passive posts produces the greatest perturbations of the flow fields. In the other examples (A, B, D, E), the separation and symmetric placement of the two passive posts causes these two posts to produce similar oscillatory behavior.
Recall that the dynamic interactions in the system are instigated by fluid flow from the active post.
The behavior in Fig. 4 shows that the active post displays action at a distance, i.e., control over the behavior at remote parts of the domain. With the one central “antenna”, the prescribed placement of the passive units can be used to control the oscillation frequency in the chamber. Notably, without the chemo-mechanical interactions emanating from the active post, the two passive posts would remain in their initial upright position, with no inter-post communication.
E. Two active posts form fluidic “dipole”
To gain further insight into possible modes of signaling and communication between posts, we examine the system in Fig. 5a that encompasses two enzyme-coated posts, one of which is coated with CAT, and another with urease (UR). The CAT-coated post generates inward flow, and the UR-coated post generates outward flow. Together, the two active posts produce a “dipolar” flow pattern. This example illustrates how the local flow profiles combine in the region between the two posts and affect the global response of this sparse array. As shown below, variations in the posts’ bending stiffness enables the tip of one post to experience different flow regimes and thereby affect the system's dynamics.The UR-coated post catalyzes the transformation of urea ((NH2)2CO) into ammonium bicarbonate (NH4+ and HCO3− ions),
 | (8) |
When hydrogen peroxide and urea are added to the solution simultaneously, the CAT-coated post on the right generates inward flow while the UR-coated post on the left generates outward flow. Remarkably, even though the two active posts lie equidistant from the center of the diagonal that connects them and cuts through the center of the box, the combination of this inward and outward flow is not symmetric about this central point. This asymmetry leads to the behavior described below.
In the central region between the posts, the inward flow produced by CAT-coated post directed so that the fluid near the bottom wall moves from the UR-coated post toward the CAT-coated post, as shown schematically in Fig. 5a. The site can be said to act as a puller, pulling the flow toward the CAT. Simultaneously, in the same region, the outward flow produced around the UR-coated post pushes the fluid along the bottom surface away from the UR-coated post, and consequently, toward the CAT post. This site effectively acts as “pusher”, pushing fluid away from the UR. Hence, both the inward and outward flows generated by the respective active posts propel the fluid in the same direction, toward the CAT catalyst.
Conversely, near the top wall, the inward flow about the CAT post (see Fig. 5a) pushes the fluid away from CAT. Analogously, at the top wall, the outward flow around the UR pump pulls the fluid toward the UR coated post. In the region between CAT and UR, the combined flows form one coherent vortex, which directs the flow toward the UR post in the top fluid layer and toward the CAT post in the bottom fluid layer. In this sense, it is useful to view the pusher (UR pump) and puller (CAT pump) as forming a fluidic “dipole”, which controls the overall flow pattern2. The patterned flow spans the entire chamber as demonstrated by the streamlines in Fig. 5b, which are plotted along the diagonal plane of the chamber at a specific point in time, and fluid velocities at the bottom wall plotted in Fig. 5d.
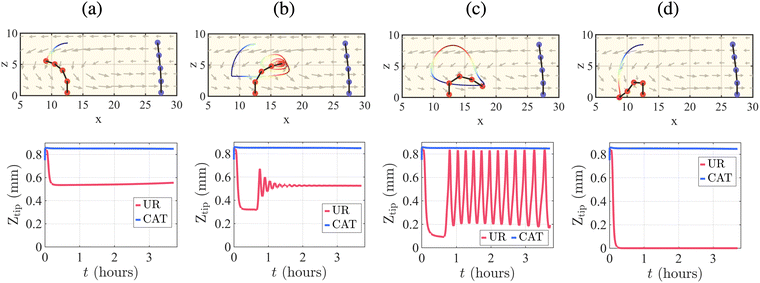
While the bending stiffness for the UR and CAT post are both set equal to κb = 0.17 pN mm2, the shapes and deformation of the posts are quite different. Notably, the extensive flow in the upper fluid layer (Fig. 5a) is directed toward the tip of the UR pump. The tip of the post is more flexible than its anchored base, and thus can be readily dragged by the fluid. Conversely, the flow in the bottom layer is directed toward the base of the CAT post (Fig. 5d), where it has less influence on the post's shape, causing the CAT post to remain relatively upright. Fig. 5d shows the trajectory of the tip of UR-coated post within one period, as well as the flow field at the bottom wall.
The hydrodynamic forces imposed by the flow on the UR-coated post causes the post to display different modes of motion, depending on the bending stiffness of the post (Fig. 6). For higher stiffness (κb = 0.5 pN mm2), the UR-coated post displays a stable mode. For this relatively high value of κb, the tip extends into the flow near the top surface, where fluid moves away from the CAT-coated post and toward the UR-coated post. Consequently, the UR-coated post bends away from the CAT post (Fig. 6a). A decrease in the bending stiffness makes the UR-coated post sufficiently flexible that the tip lies close to the bottom surface and experiences the flow near that wall (Fig. 6b and c). The latter flow moves toward the CAT-coated post, opposite the flow at the top. Hence, the post bends in the direction opposite to that shown in Fig. 6a. In the case where κb = 0.28 pN mm2, the UR-coated post undergoes damped oscillatory motion while a less stiff post (κb = 0.17 pN mm2) at the same position shows full oscillatory behavior (Fig. 6c). The frequency of oscillation for the case in Fig. 6c (having the same bending stiffness as in Fig. 5d, with κb = 0.17 pN mm2) is f = 1.125 mHz, which corresponds to period of T = 14.8 min.
If, however, the bending stiffness is decreased to κb = 0.057 pN mm2, the tip of the post touches the bottom of the chamber and remains there (see Fig. 6d and Movie S4 in ESI,† Appendix). Notably, for the system with two active posts, we observe oscillatory dynamics at a higher bending stiffness (approximately, three times in the Young's modulus) than for one active post. The behavior is a result of the stronger average flow induced in the domain with two active posts.
F. Fluidic “dipole” is effective at prompting oscillations in the array
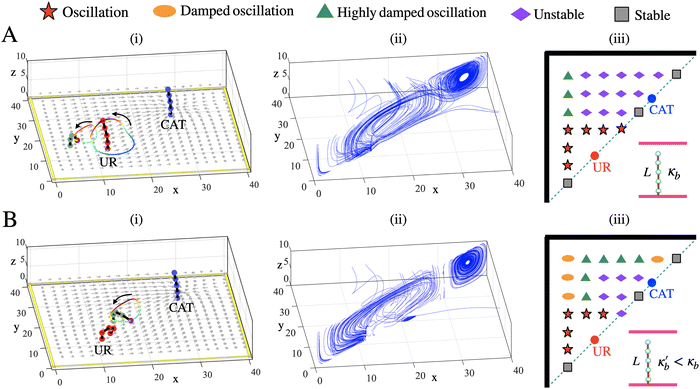
To demonstrate the influence of the “dipolar” flow discussed above, a passive post is placed near the two active ones. The passive posts shown in green in Fig. 7A(i) and B(i) lie at different locations, which were chosen to test the ability of a single passive post to sense and respond to the oscillatory behavior arising from the “dipole” generated flow. As in the cases above, the passive post is sequentially placed at 24 different locations to generate a phase map.To examine the effect of bending stiffness, we focused on two representative values of κb, with Fig. 7A portraying results for the stiffer post and Fig. 7B showing the results for the more flexible ones. (Note that at a chosen value of κb, all three posts have the same bending stiffness.) As discussed below, a comparison of the results shown in Fig. 7A and B reveals how the combination of the dipolar motif with the posts’ flexibility affects the oscillatory behavior in the array.
The panels in Fig. 7 show: (i) the position of a passive post with the corresponding trajectories of the post tips, (ii) the streamlines in the diagonal plane and (iii) the state diagram that summarizes different modes of motion of the passive post in the presence of the active CAT-UR pair. We consider only half of the domain due to the symmetry of the system.
For the cases presented in Fig. 7A, the bending stiffness for all the posts was set to κb = 0.17 pN mm2. Of the two active posts, only the UR-coated post exhibits oscillatory behavior at the specific separation distances depicted in Fig. 7A(i). The phase map (Fig. 7A(iii)) reveals that the dipolar flow pattern generated by the two active posts enables passive posts closest to the UR-coated one (shown by stars) to sense and respond to the oscillatory behavior enforced by this active post. An oscillating active post can propagate oscillations to a nearby passive one. This oscillatory signal has a limited range; it is not propagated to posts that lie farther away in the chamber. In the latter regions, a passive post only exhibits highly damped behavior, stable and unstable modes.
Fig. 7B shows the behavior for the more flexible posts, which have κb = 0.057 pN mm2. A particular example with the passive post located to the left of the line that connects the active posts is shown in Fig. 7B(i). At the smaller value of κb, the UR-coated post does not oscillate since its tip remains near the bottom wall (Fig. 6d). The phase diagram shown in Fig. 7B(iii), however, indicates that the generated “dipolar” flow profile still enables even the non-oscillatory UR-coated post to prompt the oscillations of the nearby passive posts. Here, the flow around the UR-coated post causes the passive posts’ free-ends to bend toward the UR-coated post, whereupon these ends dip into the fluid layer in the bottom half plane, which flows in a direction opposite to the flow in the upper half of the box (see streamlines in Fig. 7B(ii)). This flow pattern enabled by the dipole arrangement of the active posts (coupled to fluid motion reflected from the wall), ultimately produces oscillatory motion of the passive posts in the same region of the phase map as in the case above, where the UR-coated post did oscillate.
Relative to Fig. 7A, the decrease in the bending stiffness for Fig. 7B affects the behavior of posts near the walls in the upper half plane. The posts at the unstable points in Fig. 7A show highly damped behavior in the corresponding locations in Fig. 7B. Similarly, posts with the highly damped behavior in Fig. 7A show damped dynamics in Fig. 7B for the same locations.
G. Collective behavior in arrays containing multiple passive posts
We consider an array that encompasses additional posts, which alter the hydrodynamic interactions in the entire array. As shown below, the altered hydrodynamic interactions can, for example, cause non-oscillatory points in the sparse domain to now exhibit oscillatory behavior in the crowded environment.We focus on the two different scenarios presented in Fig. 8A and B, respectively. In Fig. 8A(i), the array of 5 × 5 posts encompass 24 passive posts arranged around one central CAT-coated post (shown in blue). In Fig. 8B(i), the array of 5 × 5 posts include 23 passive posts and two active ones arranged along the diagonal line of the domain: the UR-coated post (shown in red) and CAT-coated post (shown in blue). The passive posts are colored green, with tips shown in magenta.
To analyze the dynamics, we monitor oscillations performed by a representative passive post, P2, and compare its oscillation frequencies for the cases when all other passive posts are present in the array, or they are absent. We plot: (ii) the evolution of the tip height and (iii) corresponding frequency of oscillations for these two cases.
When the dynamics of the array are driven by a single central active post (as shown in Fig. 8A) different passive posts display distinct modes of motion. Besides the post P2, there are another 16 passive posts that oscillate with different amplitudes and frequencies. These moving posts actively perturb the fluid flow around the representative post P2, (see Movie S5 in ESI,† Appendix). (Note, that the central CAT-coated post always remains straight and eight passive posts located near the walls contact the walls.) We observe that all the posts located in the vicinity of the CAT-coated post display oscillatory behavior in contrast to the phase diagram in Fig. 2 (for a single passive post driven by a central active post), where passive posts at the corresponding positions show stable or unstable modes of behavior. The results in Fig. 8 indicate that the collective action of multiple passive posts contribute to the observed oscillatory behavior. Moreover, the presence of other passive posts in the array decreases the velocities of the circular fluid flow and, therefore, reduces the oscillation frequency of post P2. (Fig. S5 in the ESI,† Appendix reveals how the extensive flow streamlines in chamber are perturbed by the local motion of the individual posts.)
In the case shown in Fig. 8B(i), where the dipolar flow is produced by the UR-coated and CAT-coated posts, the representative passive post P2 displays almost the same oscillation frequencies in the absence and presence of other passive posts in the array (see Fig. 8B(ii) and (iii)). Here, the collective and extensive dipolar flow pattern can regulate the overall behavior of the system. For this case, we chose the same bending stiffness (κb = 0.17 pN mm2) as that for the post shown in (Fig. 6(c)), where the UR-coated post oscillates. In the presence of other passive posts, the collective hydrodynamic interactions between the posts now enable the UR-coated post to change orientation, bend toward the CAT-coated post, and remain there. Note that only two passive posts (post P2 and its counterpart at the opposite corner) exhibit the oscillatory mode of motion, while remaining passive posts follow the dipolar flow pattern. The former posts lie near corners, where the reflected fluid flow can promote oscillations.
IV. Conclusion
In summary, we used theory and simulation to design a system of flexible microposts in solution that convert non-oscillatory chemical input into self-organized oscillatory output, which enabled the posts to spontaneously propagate a chemical signal over long distances (i.e., comparable to the characteristic length in the system). Here, the oscillations arise due to activated chemo-mechanical processes and the resultant fluid–structure interactions. The fluid provides the medium by which these interactions and “messages” can be transmitted over significant distances.In the simplest system considered here, we focused on one passive post placed near a side wall and one centrally located active post that converts reactants in the solution into less dense products. In this fluidic system, the reaction at the active post generates radially symmetric flow that kept the central post up-right. The fluid–structure interaction with the surrounding walls and the passive post broke this local symmetry and lead to the nontrivial behavior of the passive structure. The flow moved toward this passive post along the top wall and away from this structure near the bottom wall, thereby forming circular streamlines. This circular flow pattern enabled a non-oscillatory chemical input to produce oscillatory chemo-mechanical output.
For the observed non-reciprocal behavior, the fluid–structure interactions bent the tip of the passive post in the closed chamber. Due to the latter interactions, the bent post serves as the fundamental dynamic unit. The specific conformation of this fundamental unit depends on its position in the array and bending stiffness. Hence, the posts can exhibit the range of dynamic motion seen here.
We also observe that the oscillation frequencies in the system are sensitive to the post's position inside the chamber, the magnitude of the buoyancy-driven force, the bending stiffness of the post and the presence of enclosing walls. Notably, the oscillation frequency exhibited by the passive posts can be modified, for example, by introducing additional passive posts into the array (see Fig. 4 and 8). The latter finding demonstrates the presence of cooperative activity between the posts in the array.
We also examined systems that involved two active posts, which were coated with distinct catalysts, UR and CAT. Here, the combination of the local inward and outward flows (promoted by the CAT-coated and UR-coated posts, respectively) led to a specifically oriented fluidic motion, which flowed toward UR-coated post at the top and away from UR at the bottom, forming an oriented vortex about the UR-coated post. In this flow pattern, the fluid in the central region organized into a “dipolar” flow pattern with the CAT-coated pole being the “pusher” and the UR-coated post serving as the “puller”. The combined effects of the pusher and puller led to the flow pattern shown in Fig. 5d. By taking into account the flow patterns for the two individual pumps, and the relative placement of the pumps, flow profiles can be combined to enhance, suppress or reverse the fluid motion in the chamber. The coupling of the different flows generated at the pump (outward and inward) provides a distinct means of controlling the global circulation of the fluid, transporting a chemical message along a particular path and producing the desired mechanical response of the tethered posts.
For the dipolar flow created by the UR-CAT coated pumps, the flow deforms the pusher post and enables it to undergo different modes of motions. The imposed dipolar flow profile enabled the oscillatory behavior on just the UR-coated post even though the two posts were placed at symmetric positions along the diagonal line that cuts through the box and they both exhibited the same bending stiffness. This example elucidates principles for the rational design of the flow profile in the immersed array.
The calculated phase maps allow the designer to select the appropriate parameters (placement in the array, bending stiffness) and thereby access a particular dynamic state and desired functionality. For a given array containing a specified number, location and type of active and passive posts, the system can still be reconfigured by specifying which of the appropriate reactants are to be added and the sequence in which they are added. Additional dynamic motions of passive elastic posts could be induced by cascade reactions, where the product of one reaction is the reactant for the next. Once all the reagents have been consumed, the chamber can be reinvigorated by adding new reactants, and thus, the system can be used multiple times. With this wealth of dynamic behavior, each mode of motion can serve different purposes and offer a range of utility. Ultimately, these self-oscillating systems can facilitate the development of autonomously moving robots in solution and the directed transport of specific chemicals in the chamber.
V. Methods
A. Numerical simulation
The continuity and Navier–Stokes equations are solved using the lattice Boltzmann method44 (LBM) with a single relaxation time D3Q19 scheme.45 A finite difference approach with a forward-time central-space (FTCS) scheme is used to solve the advection–reaction–diffusion of chemicals. The immersed boundary (IB) approach is used to capture the fluid–structure interactions between the elastic posts and fluid. In the IB model, each node of elastic post is modeled by a sphere with effective hydrodynamics radius a that experiences fluid drag, characterized by the mobility M = (6πηa)−1. The forces Fel exerted by the nodes of the elastic post on the fluid, which are calculated using the IB method, provide zero fluid velocities at the discretization nodes of the elastic post. Therefore, the IB approach approximates no-slip conditions for the fluid velocities at the boundary nodes, as well as no fluid permeation through the nodes of the posts. Moreover, all these nodes are assumed to have the same reaction rate, which is given by SKd, where S is the surface area per each node (see eqn (5)).The size of computational domain is 40Δx × 40Δx × 10Δx where the lattice Boltzmann unit Δx is 100 μm. The time step of the simulation is Δt = 1.67 × 10−3 s. In the IB approach, each of the discretized nodes of the post is treated as a sphere with radius a ≈ 1.3Δx. Each post is discretized into N = 5 beads with the equilibrium distance between the beads as 1.75Δx. Moreover, we place the first bead at distance Δx from the wall, so that the total length of the post is L = 8Δx.
B. Dimensionless Grashof number
The behavior of the system is characterized by the ratio of buoyancy to viscous forces, expressed by the dimensionless Grashof number, Gr = gβΔCH3/ν2, where β is the solutal expansion coefficient, ΔC is the chemical variations in the domain, ν is the kinematic viscosity of the fluid and H is the height of the chamber. For a chosen set of parameters, the relationship indicates how to adjust the other parameters to ensure that the system will yield a similar class of behavior. This relationship allows us to generalize our findings to a range of conditions and chemistries. The typical Grashof number in our system is about 102.C. Elasto-hydrodynamic theory
For the semi-analytical calculation, we couple elasticity theory and overdamped viscous hydrodynamics46–52 to obtain the time-dependent motion of the posts, where the external background flow is taken from the flow induced by one CAT-coated post at the center of the domain. We consider a slender inextensible elastic post of length L, with circular cross section of radius a at its midpoint, where the centerline is identified by X(s,t) which is a function of both time, t and arc length 0 ≤ s ≤ L. The end s = 0 is clamped against a no-slip wall, and s = L is free. The surrounding fluid has a viscosity η, and the flow is assumed to be sufficiently slow that the Reynolds number is small. At any local point along the post, the instantaneous force balance satisfies| fe + fh = 0, | (9) |
| fe = −BXssss + (TXs)s, | (10) |
| Xt − U∞ = −M0[I + (ξ − 1)XsXs]·fh, | (11) |
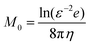 is the perpendicular mobility of the post, ξ is the ratio between parallel to perpendicular mobility54 (ξ = 2 for ε → 0), I is the identity tensor, and U∞ is the background flow. If we rescale the length by L, time with inverse of shear rate,
is the perpendicular mobility of the post, ξ is the ratio between parallel to perpendicular mobility54 (ξ = 2 for ε → 0), I is the identity tensor, and U∞ is the background flow. If we rescale the length by L, time with inverse of shear rate, ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) −1, and tension with
−1, and tension with 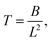 we get:55
we get:55![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) (Xt − U∞) = −Xssss − (Xssss·Xs)Xs + 2TsXs + TXss, (Xt − U∞) = −Xssss − (Xssss·Xs)Xs + 2TsXs + TXss, | (12) |
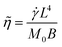 is the ratio between viscous to elastic force. The limit
is the ratio between viscous to elastic force. The limit ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) → 0 and ∞ corresponds to a rigid rod and a flexible thread,56 respectively. Taking the derivative of both side of the equation with respect to s and then taking dot product of both sides by Xs gives us the other scalar equation:
→ 0 and ∞ corresponds to a rigid rod and a flexible thread,56 respectively. Taking the derivative of both side of the equation with respect to s and then taking dot product of both sides by Xs gives us the other scalar equation:7Xssss·Xss + 6Xsss·Xsss + 2Tss − TXss·Xss + ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) U∞s·Xs − α(JN,1 − Xs·Xs) = 0, U∞s·Xs − α(JN,1 − Xs·Xs) = 0, | (13) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) ∼ 10−3 s−1, aspect ratio of ε ∼ 0.1, L = 0.8 mm, and flexural rigidity B ∼ 0.01 pN mm2, we obtain
∼ 10−3 s−1, aspect ratio of ε ∼ 0.1, L = 0.8 mm, and flexural rigidity B ∼ 0.01 pN mm2, we obtain ![[small eta, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e110.gif) ∼ 140 for our system.
∼ 140 for our system.
To obtain the motion of the post, we assume that a single passive post is placed in the flow generated by the CAT-coated post. This flow in general is time dependent, due to advection and diffusion of the chemicals, but in the limit of small Reynolds number (Re = ρLU/η ∼ 10−3), we can approximate the background flow as a steady flow. We insert the background velocity field, U∞, in eqn (12) and (13) from the simulation at some specified time to obtain solutions for the time-dependent motion of passive elastic posts placed at a specified distance from the active post.
Data availability
All study data are included in the article and/or ESI.†Conflicts of interest
There are no conflicts to declare.Acknowledgements
ACB gratefully acknowledges funding from NSF grant number 2234135 to support the development of the analytical models and the DOE under grant DE-FG02-90ER45438 for support to develop the computational models. This research was supported in part by the University of Pittsburgh Center for Research Computing, RRID:SCR_022735, through the resources provided. Specifically, this work used the H2P cluster, which is supported by NSF award number OAC-2117681.References
- P. J. de Jong, F. Trigka and M. M. Lerch, Towards Autonomous Materials–Challenges in Chemical Communication, ChemSystemsChem, 2024, 6(3), e202400005 CrossRef CAS.
- M. Moradi, O. E. Shklyaev and A. C. Balazs, Integrating chemistry, fluid flow, and mechanics to drive spontaneous formation of three-dimensional (3D) patterns in anchored microstructures, Proc. Natl. Acad. Sci. U. S. A., 2024, 121(11), e2319777121 CrossRef CAS.
- R. K. Manna, A. Laskar, O. E. Shklyaev and A. C. Balazs, Harnessing the power of chemically active sheets in solution, Nat. Rev. Phys., 2022, 4(2), 125–137 CrossRef.
- J. Song, O. E. Shklyaev, A. Sapre, A. C. Balazs and A. Sen, Self-propelling macroscale sheets powered by enzyme pumps, Angew. Chem., 2024, 136(6), e202311556 CrossRef.
- A. Laskar, R. K. Manna, O. E. Shklyaev and A. C. Balazs, Computer modeling reveals modalities to actuate mutable, active matter, Nat. Commun., 2022, 13(1), 2689 CrossRef CAS.
- R. K. Manna, O. E. Shklyaev and A. C. Balazs, Chemically Driven Multimodal Locomotion of Active, Flexible Sheets, Langmuir, 2023, 39(2), 780–789, DOI:10.1021/acs.langmuir.2c02666 From NLM Medline.
- J. Song, J. Zhang, J. Lin, O. E. Shklyaev, S. Shrestha, A. Sapre and A. C. Balazs, Programming Fluid Motion Using Multi-Enzyme Micropump Systems, ACS Appl. Mater. Interfaces, 2024, 16(34), 45660–45670 CrossRef CAS.
- J. Zhang, A. Laskar, J. Song, O. E. Shklyaev, F. Mou, J. Guan, A. C. Balazs and A. Sen, Light-powered, fuel-free oscillation, migration, and reversible manipulation of multiple cargo types by micromotor swarms, ACS Nano, 2022, 17(1), 251–262 CrossRef.
- J. E. Kauffman, A. Laskar, O. E. Shklyaev, A. C. Balazs and A. Sen, Light-induced dynamic control of particle motion in fluid-filled microchannels, Langmuir, 2020, 36(34), 10022–10032 CrossRef CAS.
- B. M. Tansi, M. L. Peris, O. E. Shklyaev, A. C. Balazs and A. Sen, Organization of Particle Islands through Light-Powered Fluid Pumping, Angew. Chem., 2019, 131(8), 2317–2321 CrossRef.
- R. K. Manna, O. E. Shklyaev, J. Kauffman, B. Tansi, A. Sen and A. C. Balazs, Light-Induced Convective Segregation of Different Sized Microparticles, ACS Appl. Mater. Interfaces, 2019, 11(19), 18004–18012 CrossRef CAS.
- S. Maiti, O. E. Shklyaev, A. C. Balazs and A. Sen, Self-Organization of Fluids in a Multienzymatic Pump System, Langmuir, 2019, 35(10), 3724–3732, DOI:10.1021/acs.langmuir.8b03607.
- I. Ortiz-Rivera, H. Shum, A. Agrawal, A. Sen and A. C. Balazs, Convective flow reversal in self-powered enzyme micropumps, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(10), 2585–2590 CrossRef CAS.
- R. K. Manna, K. Gentile, O. E. Shklyaev, A. Sen and A. C. Balazs, Self-Generated Convective Flows Enhance the Rates of Chemical Reactions, Langmuir, 2022, 38(4), 1432–1439, DOI:10.1021/acs.langmuir.1c02593.
- S. Arnaboldi, G. Salinas, S. Bichon, S. Gounel, N. Mano and A. Kuhn, Bi-enzymatic chemo-mechanical feedback loop for continuous self-sustained actuation of conducting polymers, Nat. Commun., 2023, 14(1), 6390 CrossRef CAS.
- X. He, M. Aizenberg, O. Kuksenok, L. D. Zarzar, A. Shastri, A. C. Balazs and J. Aizenberg, Synthetic homeostatic materials with chemo-mechano-chemical self-regulation, Nature, 2012, 487(7406), 214–218 CrossRef CAS.
- S. Li, M. M. Lerch, J. T. Waters, B. Deng, R. S. Martens, Y. Yao, D. Y. Kim, K. Bertoldi, A. Grinthal and A. C. Balazs, et al., Self-regulated non-reciprocal motions in single-material microstructures, Nature, 2022, 605(7908), 76–83, DOI:10.1038/s41586-022-04561-z.
- J. T. Waters, S. Li, Y. Yao, M. M. Lerch, M. Aizenberg, J. Aizenberg and A. C. Balazs, Twist again: dynamically and reversibly controllable chirality in liquid crystalline elastomer microposts, Sci. Adv., 2020, 6(13), eaay5349 CrossRef CAS.
- V. V. Yashin, S. Suzuki, R. Yoshida and A. C. Balazs, Controlling the dynamic behavior of heterogeneous self-oscillating gels, J. Mater. Chem., 2012, 22(27), 13625–13636 RSC.
- I. C. Chen, O. Kuksenok, V. V. Yashin, R. M. Moslin, A. C. Balazs and K. J. Van Vliet, Shape-and size-dependent patterns in self-oscillating polymer gels, Soft Matter, 2011, 7(7), 3141–3146 RSC.
- O. Kuksenok, V. V. Yashin, M. Kinoshita, T. Sakai, R. Yoshida and A. C. Balazs, Exploiting gradients in cross-link density to control the bending and self-propelled motion of active gels, J. Mater. Chem., 2011, 21(23), 8360–8371 RSC.
- I. C. Chen, O. Kuksenok, V. V. Yashin, A. C. Balazs and K. J. Van Vliet, Mechanical resuscitation of chemical oscillations in Belousov–Zhabotinsky gels, Adv. Funct. Mater., 2012, 22(12), 2535–2541 CrossRef CAS.
- P. Yuan, O. Kuksenok, D. E. Gross, A. C. Balazs, J. S. Moore and R. G. Nuzzo, UV patternable thin film chemistry for shape and functionally versatile self-oscillating gels, Soft Matter, 2013, 9(4), 1231–1243 RSC.
- S. Atis, B. T. Weinstein, A. W. Murray and D. R. Nelson, Microbial range expansions on liquid substrates, Phys. Rev. X, 2019, 9(2), 021058 CAS.
- C. Wang, H. Tang and X. Zhang, Fluid–structure interaction of bio-inspired flexible slender structures: a review of selected topics, Bioinspiration Biomimetics, 2022, 17(4), 041002 CrossRef.
- W.-X. Huang and S. Alben, Fluid–structure interactions with applications to biology, Acta Mech. Sin., 2016, 32, 977–979 CrossRef CAS.
- X. Dong, G. Z. Lum, W. Hu, R. Zhang, Z. Ren, P. R. Onck and M. Sitti, Bioinspired cilia arrays with programmable nonreciprocal motion and metachronal coordination, Sci. Adv., 2020, 6(45), eabc9323 CrossRef CAS.
- K. Ni and Z. Wang, Recent Progress on the Development of Magnetically-Responsive Micropillars: Actuation, Fabrication, and Applications, Adv. Funct. Mater., 2023, 33(14), 2213350 CrossRef CAS.
- S. Zhang, X. Hu, M. Li, U. Bozuyuk, R. Zhang, E. Suadiye, J. Han, F. Wang, P. Onck and M. Sitti, 3D-printed micrometer-scale wireless magnetic cilia with metachronal programmability, Sci. Adv., 2023, 9(12), eadf9462 CrossRef CAS.
- Z. Ren, M. Zhang, S. Song, Z. Liu, C. Hong, T. Wang, X. Dong, W. Hu and M. Sitti, Soft-robotic ciliated epidermis for reconfigurable coordinated fluid manipulation, Sci. Adv., 2022, 8(34), eabq2345 CrossRef CAS.
- S. Sharma, L. C. Jung, N. Lee, Y. Wang, A. Kirk-Jadric, R. Naik and X. Dong, Wireless Peristaltic Pump for Transporting Viscous Fluids and Solid Cargos in Confined Spaces, Adv. Funct. Mater., 2024, 2405865 CrossRef.
- B. Zuo, M. Wang, B.-P. Lin and H. Yang, Visible and infrared three-wavelength modulated multi-directional actuators, Nat. Commun., 2019, 10(1), 4539 CrossRef.
- M. Lahikainen, H. Zeng and A. Priimagi, Design principles for non-reciprocal photomechanical actuation, Soft Matter, 2020, 16(25), 5951–5958 RSC.
- M. Wang, Y. Han, L.-X. Guo, B.-P. Lin and H. Yang, Photocontrol of helix handedness in curled liquid crystal elastomers, Liq. Cryst., 2019, 46(8), 1231–1240 CrossRef CAS.
- Z. Deng, H. Zhang, A. Priimagi and H. Zeng, Light-Fueled Nonreciprocal Self-Oscillators for Fluidic Transportation and Coupling, Adv. Mater., 2024, 36(12), 2209683 CrossRef CAS.
- H. Zeng, M. Lahikainen, L. Liu, Z. Ahmed, O. M. Wani, M. Wang, H. Yang and A. Priimagi, Light-fuelled freestyle self-oscillators, Nat. Commun., 2019, 10(1), 5057 CrossRef.
- G. Cicconofri, V. Damioli and G. Noselli, Nonreciprocal oscillations of polyelectrolyte gel filaments subject to a steady and uniform electric field, J. Mech. Phys. Solids, 2023, 173, 105225 CrossRef CAS.
- S. Sengupta, D. Patra, I. Ortiz-Rivera, A. Agrawal, S. Shklyaev, K. K. Dey, U. Cordova-Figueroa, T. E. Mallouk and A. Sen, Self-powered enzyme micropumps, Nat. Chem., 2014, 6(5), 415–422, DOI:10.1038/nchem.1895 From NLM Medline.
- O. E. Shklyaev, H. Shum, A. Sen and A. C. Balazs, Harnessing surface-bound enzymatic reactions to organize microcapsules in solution, Sci. Adv., 2016, 2(3), e1501835 CrossRef.
- S. Lim, A. Ferent, X. S. Wang and C. S. Peskin, Dynamics of a closed rod with twist and bend in fluid, SIAM J. Sci. Comput., 2008, 31(1), 273–302 CrossRef.
- C. Chandrasekhar, Hydrodynamic and hydromagnetic stability, Clarendon Press, Oxford, 1961 Search PubMed.
- K. A. Johnson and R. S. Goody, The original Michaelis constant: translation of the 1913 Michaelis–Menten paper, Biochemistry, 2011, 50(39), 8264–8269 CrossRef CAS.
- O. Kuksenok, V. V. Yashin and A. C. Balazs, Mechanically induced chemical oscillations and motion in responsive gels, Soft Matter, 2007, 3(9), 1138–1144 RSC.
- S. Succi, The lattice Boltzmann equation: for fluid dynamics and beyond, Oxford University Press, 2001 Search PubMed.
- A. J. Ladd and R. Verberg, Lattice–Boltzmann simulations of particle-fluid suspensions, J. Stat. Phys., 2001, 104, 1191–1251 CrossRef CAS.
- C. H. Wiggins, D. Riveline, A. Ott and R. E. Goldstein, Trapping and wiggling: elastohydrodynamics of driven microfilaments, Biophys. J., 1998, 74(2), 1043–1060 CrossRef CAS.
- G. De Canio, E. Lauga and R. E. Goldstein, Spontaneous oscillations of elastic filaments induced by molecular motors, J. R. Soc., Interface, 2017, 14(136), 20170491 CrossRef.
- A.-K. Tornberg and M. J. Shelley, Simulating the dynamics and interactions of flexible fibers in Stokes flows, J. Comput. Phys., 2004, 196(1), 8–40 CrossRef.
- T. R. Powers, Dynamics of filaments and membranes in a viscous fluid, Rev. Mod. Phys., 2010, 82(2), 1607 CrossRef.
- C. Pozrikidis, Shear flow past slender elastic rods attached to a plane, Int. J. Solids Struct., 2011, 48(1), 137–143 CrossRef.
- Y.-N. Young, M. Downs and C. R. Jacobs, Dynamics of the primary cilium in shear flow, Biophys. J., 2012, 103(4), 629–639 CrossRef CAS.
- S. Gueron and N. Liron, Ciliary motion modeling, and dynamic multicilia interactions, Biophys. J., 1992, 63(4), 1045–1058 CrossRef CAS.
- R. Cox, The motion of long slender bodies in a viscous fluid Part 1. General theory, J. Fluid Mech., 1970, 44(4), 791–810 CrossRef.
- E. Lauga and T. R. Powers, The hydrodynamics of swimming microorganisms, Rep. Prog. Phys., 2009, 72(9), 096601 CrossRef.
- O. Du Roure, A. Lindner, E. N. Nazockdast and M. J. Shelley, Dynamics of flexible fibers in viscous flows and fluids, Annu. Rev. Fluid Mech., 2019, 51, 539–572 CrossRef.
- L. E. Becker and M. J. Shelley, Instability of elastic filaments in shear flow yields first-normal-stress differences, Phys. Rev. Lett., 2001, 87(19), 198301 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4mh01111b |
| This journal is © The Royal Society of Chemistry 2024 |