Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Theory of flow-induced covalent polymer mechanochemistry in dilute solutions†
Etienne
Rognin
 ,
Niamh
Willis-Fox
,
Niamh
Willis-Fox
 and
Ronan
Daly
and
Ronan
Daly
 *
*
Department of Engineering, University of Cambridge, Cambridge, UK. E-mail: rd439@cam.ac.uk
First published on 6th February 2024
Abstract
Predicting polymer mechanochemistry in arbitrary flows is challenging due to the diversity of chain conformations, competition among stretched bonds, and flow heterogeneity. Here, we demonstrate that the vast diversity of polymer unravelling pathways must be accounted for, rather than considering an averaged chain conformation. We propose a model that describes both mechanophore activation and non-specific backbone scission, where the reaction rates depend solely on fluid kinematics. Validated with coarse-grained molecular dynamics simulations in complex flows, the model captures mechanochemistry onset, intact chain half-life, and non-specific scission.
1 Introduction
Covalent bonds of polymers in solution can break under mechanical tension imparted by large velocity gradients. While this phenomenon is of practical importance when macromolecules need to be preserved from flow-induced degradation,1–3 it has also inspired scientists to develop an abundance of macromolecular compounds known as mechanophores, which can exhibit a change in a physico-chemical property such as color or conductivity under large tensile stress.4–6 Although mechanophores have been extensively studied at the molecular level, how they react to macroscopic stress is still poorly understood. In liquid solutions in particular, the state-of-the-art activation method is sonication, but the chaotic nature of this flow prevents any detailed understanding of the link between fluid mechanics and reaction kinetics, impeding generalization to arbitrary flows and translation to industrial applications.7–9While flow-induced polymer degradation has been studied for decades, existing models are still restricted to specific types of flow such as developed turbulence,10–12 porous media,13 and microfluidic constrictions,14,15 or they focus on the onset of scission rather than its actual rate.16 These models cannot be generalized to arbitrary flows nor be extended to predict mechanophore activation without substantial reformulation.
In fact, the final outcome of mechanochemistry in an arbitrary transient flow is the intricate convolution of at least three factors: first, the heterogeneity of the flow producing different forcing sequences for polymers flowing along different Lagrangian trajectories; second, the wide variety of polymer conformations responding differently to a given flow (this variation being amplified by molecular weight dispersity); and third, for a given polymer conformation, the vast number of bonds being stretched simultaneously inducing a competition between mechanophore activation and non-specific chain scission. The aim of this paper is to show that this complexity can be factorized to a large extent, so that reaction rates can be derived directly from the solvent velocity field.
2 Model
2.1 The critical force hypothesis in flows
Covalent mechanochemistry is usually interpreted within the framework of thermally activated reaction rates.17,18 Furthermore, assuming Bell's model for the force-induced decrease of the free-energy barrier, then at bond scale the activation rate, k, is given by:19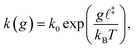 | (1) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ‡ is the reaction coordinate of the transition state, and kBT is the thermal energy. Bell's model assumes that the distortion of the energy landscape is small and the reaction coordinate is aligned with the force. Non-conventional mechanophores may exhibit non-monotonic or even strain-hardening changes in activation energy,20 in which case a more elaborate theory than the one developed here may be necessary. Nevertheless, for common backbone bonds and a vast class of mechanophores, we expect the decrease in energy barrier to be roughly proportional to the tensile force, at least in the range of relevant forces. The theory presented in this paper is based on a separation of time scales for which an accurate description of reaction rates is not necessary.
‡ is the reaction coordinate of the transition state, and kBT is the thermal energy. Bell's model assumes that the distortion of the energy landscape is small and the reaction coordinate is aligned with the force. Non-conventional mechanophores may exhibit non-monotonic or even strain-hardening changes in activation energy,20 in which case a more elaborate theory than the one developed here may be necessary. Nevertheless, for common backbone bonds and a vast class of mechanophores, we expect the decrease in energy barrier to be roughly proportional to the tensile force, at least in the range of relevant forces. The theory presented in this paper is based on a separation of time scales for which an accurate description of reaction rates is not necessary.
For single-molecule pulling experiments, the tensile force is uniform between the two anchor points, and the loading rate is controlled. By contrast, in flow-induced mechanochemistry non-uniform and transient force distributions occur. Once a molecule is fully unravelled, the tension along the backbone has a quasi-parabolic profile with a maximum value at the center of the chain given by:21
gmax = ζ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) L2, L2, | (2) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is the strain rate of the solvent, and L is the chain length. Typically, ζ depends on monomer type and is proportional to solvent viscosity. According to slender-body hydrodynamics,22ζ also has a slow variation in (ln
is the strain rate of the solvent, and L is the chain length. Typically, ζ depends on monomer type and is proportional to solvent viscosity. According to slender-body hydrodynamics,22ζ also has a slow variation in (ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) L)−1 which is neglected for now. The overall scission rate of an unravelled chain made of n independent links which react according to Bell's model is given by the Thermally Activated Bond Scission (TABS) model:23
L)−1 which is neglected for now. The overall scission rate of an unravelled chain made of n independent links which react according to Bell's model is given by the Thermally Activated Bond Scission (TABS) model:23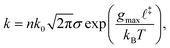 | (3) |
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ‡), and where we have assumed gmax
‡), and where we have assumed gmax![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ‡ ≫ kBT. Indeed, typical covalent mechanochemical systems are observed when the reaction is accelerated by many orders of magnitude (for example reducing the half-life from months to microseconds), suggesting that g
‡ ≫ kBT. Indeed, typical covalent mechanochemical systems are observed when the reaction is accelerated by many orders of magnitude (for example reducing the half-life from months to microseconds), suggesting that g![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ‡/kBT is at least of the order of 20. A critical strain rate
‡/kBT is at least of the order of 20. A critical strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c can be defined by combining eqn (2) and (3), which, because of the exponential scaling, amounts to defining a bond-scale critical force gc = ζ
c can be defined by combining eqn (2) and (3), which, because of the exponential scaling, amounts to defining a bond-scale critical force gc = ζ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) cL2. Odell et al.23 and others used this model to rationalize the experimental scaling law that
cL2. Odell et al.23 and others used this model to rationalize the experimental scaling law that ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c ∼ L−2 in flows with stagnation points like cross slots. Nevertheless, this paradigm fails to explain the
c ∼ L−2 in flows with stagnation points like cross slots. Nevertheless, this paradigm fails to explain the ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c ∼ L−1 scaling observed in constriction flows24,25 and therefore cannot be generalized to arbitrary scenarios. In a transient flow, the variation of both solvent strain rate and polymer conformation have to be properly accounted for.
c ∼ L−1 scaling observed in constriction flows24,25 and therefore cannot be generalized to arbitrary scenarios. In a transient flow, the variation of both solvent strain rate and polymer conformation have to be properly accounted for.
For this purpose, we first consider a fully unravelled chain subject to an increasing strain rate in the vicinity of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c. If the strain rate is doubled then tension is doubled, so that the scission rate is roughly multiplied by a factor exp(gc
c. If the strain rate is doubled then tension is doubled, so that the scission rate is roughly multiplied by a factor exp(gc![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) ‡/kBT) ≳ 108; likewise halving the force would roughly divide the rate by 104. Consequently, scission is clearly a threshold phenomenon with respect to the time scale of the flow. Let us now consider unravelling polymer chains at constant solvent strain rate. We define the Weissenberg number as Wi = τ
‡/kBT) ≳ 108; likewise halving the force would roughly divide the rate by 104. Consequently, scission is clearly a threshold phenomenon with respect to the time scale of the flow. Let us now consider unravelling polymer chains at constant solvent strain rate. We define the Weissenberg number as Wi = τ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , with τ the polymer longest relaxation time. For
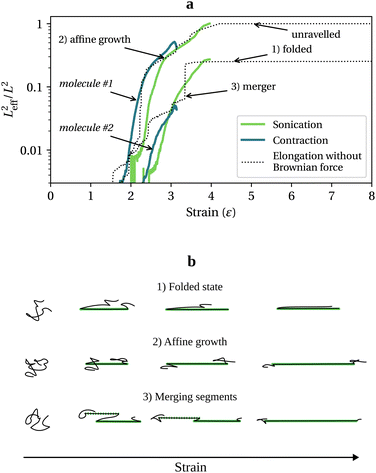
, with τ the polymer longest relaxation time. For 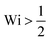 , molecules unravel, but the time it takes to reach the final elongated state differs vastly from one molecule to another, depending on their initial random conformation.26,27 To illustrate the implication for chain scission, we have simulated an ensemble of 103 free-draining bead-rod chains,14,21 each made of N = 1000 links, under three scenarios: (1) a steady uniaxial extensional flow without Brownian forces (neglecting Brownian forces is equivalent to assuming the chain or any of its part does not have time to relaxation during the deformation, in other words it is equivalent to considering the limit Wi = +∞); (2) the collapse of a sonication bubble (Rayleigh–Plesset equation with parameters taken from Turetta and Lattuada28); and (3) the center line of a steady laminar 4
, molecules unravel, but the time it takes to reach the final elongated state differs vastly from one molecule to another, depending on their initial random conformation.26,27 To illustrate the implication for chain scission, we have simulated an ensemble of 103 free-draining bead-rod chains,14,21 each made of N = 1000 links, under three scenarios: (1) a steady uniaxial extensional flow without Brownian forces (neglecting Brownian forces is equivalent to assuming the chain or any of its part does not have time to relaxation during the deformation, in other words it is equivalent to considering the limit Wi = +∞); (2) the collapse of a sonication bubble (Rayleigh–Plesset equation with parameters taken from Turetta and Lattuada28); and (3) the center line of a steady laminar 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 contraction flow. The sonication and contraction flows are normalised so that Wimax ∼ 103. Bead-rod polymer modelling and simulation settings are described in more detail in sections 2 and 3 of the ESI.† For each molecule, we capture the effective length, Leff, at time t as:
1 contraction flow. The sonication and contraction flows are normalised so that Wimax ∼ 103. Bead-rod polymer modelling and simulation settings are described in more detail in sections 2 and 3 of the ESI.† For each molecule, we capture the effective length, Leff, at time t as:
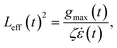 | (4) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . Tension grows in proportion to Leff2, and there are three ways straight segments grow at Wi = +∞: (1) a quasi-frozen folded state, (2) an affine growth (deforming with the solvent), and (3) a sudden growth resulting from merging two unravelled segments. These chain unravelling pathways due to solvent strain, which have been extensively studied both theoretically (reported as kinks dynamics)26,27 and experimentally,29,30 are sketched in Fig. 1b. In the folded state, the chain loses internal mobility and the segment growth is almost stopped. The affine growth represents the regular uncoiling from one or two ends of a straight segment and scales as exp(2
. Tension grows in proportion to Leff2, and there are three ways straight segments grow at Wi = +∞: (1) a quasi-frozen folded state, (2) an affine growth (deforming with the solvent), and (3) a sudden growth resulting from merging two unravelled segments. These chain unravelling pathways due to solvent strain, which have been extensively studied both theoretically (reported as kinks dynamics)26,27 and experimentally,29,30 are sketched in Fig. 1b. In the folded state, the chain loses internal mobility and the segment growth is almost stopped. The affine growth represents the regular uncoiling from one or two ends of a straight segment and scales as exp(2![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) t), while the growth by merging happens when two significantly stretched segments are eventually joined.
t), while the growth by merging happens when two significantly stretched segments are eventually joined.
At finite Wi, small coiled parts of the chains can relax. As a result, in the contraction and sonication flows (Fig. 1a), the growth of Leff2 follows the infinite Wi uniaxial extension behaviour to a large extent albeit being smoother.
2.2 Ensemble of polymer chains
For a given molecule, considering the rapid growth of Leff, scission should occur as soon as Leff2 ≥ gc/(ζ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ), except in the unlikely circumstance where the chain is stuck in the folded conformation at exactly Leff2 = gc/(ζ
), except in the unlikely circumstance where the chain is stuck in the folded conformation at exactly Leff2 = gc/(ζ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ). Remarkably, because of the variety of unravelling pathways, the thresholding hypothesis applied to an ensemble of random coils subject to a constant solvent strain rate
). Remarkably, because of the variety of unravelling pathways, the thresholding hypothesis applied to an ensemble of random coils subject to a constant solvent strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c still results in a pseudo first-order reaction with rate k ∼
c still results in a pseudo first-order reaction with rate k ∼ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c.31,32 This is because chains which develop elongated segments sooner due to their initial random conformation break first while it requires more time (or strain in the general case) for more tangled coils. But importantly, there is an initial idle time, or equivalently a critical solvent strain εc before which no reaction occurs. A detailed analysis of the whole simulated ensemble shows that
c.31,32 This is because chains which develop elongated segments sooner due to their initial random conformation break first while it requires more time (or strain in the general case) for more tangled coils. But importantly, there is an initial idle time, or equivalently a critical solvent strain εc before which no reaction occurs. A detailed analysis of the whole simulated ensemble shows that 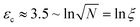 , where ξ is the polymer extensibility (for a chain in a theta-solvent,
, where ξ is the polymer extensibility (for a chain in a theta-solvent, 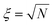 ). In other words, the critical strain scales with the unravelling of a typical coil.
). In other words, the critical strain scales with the unravelling of a typical coil.
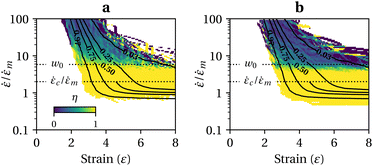
In addition, we can see from Fig. 1a that Leff2 is a function of ε and in good approximation independent of the type of flow. Indeed, if we assume that covalent mechanochemistry occurs at Wi ≫ 1, the unravelling pathways of the largest structures depend only on the accumulated strain. Consequently, the resulting proportion of intact chains, c, is also a function of ε and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) only, and can be learnt from only one flow, for example a steady elongation at Wi = +∞. The result is reported in Fig. 2a for a mono-dispersed ensemble of 103 chains of N = 1000 identical links (no mechanophore moiety), and Fig. 2b for a dispersed ensemble of the same size, the number of links being sampled from a log-normal distribution of average 〈N〉 = 1000, with a polydispersity index (PDI) of 1.01 (or equivalently a standard deviation of about 10% of the average length). The contour at 0.97 represents the arbitrary limit for the onset of scission: at large strain, the limit is given by
only, and can be learnt from only one flow, for example a steady elongation at Wi = +∞. The result is reported in Fig. 2a for a mono-dispersed ensemble of 103 chains of N = 1000 identical links (no mechanophore moiety), and Fig. 2b for a dispersed ensemble of the same size, the number of links being sampled from a log-normal distribution of average 〈N〉 = 1000, with a polydispersity index (PDI) of 1.01 (or equivalently a standard deviation of about 10% of the average length). The contour at 0.97 represents the arbitrary limit for the onset of scission: at large strain, the limit is given by ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) =
= ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c. At strain below ln
c. At strain below ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ, the limit is given by a function of both
ξ, the limit is given by a function of both ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) and ε, accounting for scission occurring in a partially unravelled coils. In addition, the main effect of length dispersity is to smooth the transition around
and ε, accounting for scission occurring in a partially unravelled coils. In addition, the main effect of length dispersity is to smooth the transition around ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c, as we can see by comparing Fig. 2a and b. We can understand this feature by imagining an ensemble of chains pre-stretched below
c, as we can see by comparing Fig. 2a and b. We can understand this feature by imagining an ensemble of chains pre-stretched below ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c (up to a solvent strain of 6 for example), then suddenly subject to
c (up to a solvent strain of 6 for example), then suddenly subject to ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c: if the ensemble is monodisperse, all chains would break at the same time, while with dispersity the longer chains would break first.
c: if the ensemble is monodisperse, all chains would break at the same time, while with dispersity the longer chains would break first.
 | ||
| Fig. 2 (a) Contours of the proportion of intact chains in the limit of high Wi for a monodispersed ensemble of 103 free-draining chains, ξ2 = 1000, identical links; (b) same as (a) but with chain length dispersity, PDI = 1.01; (c) effect of HI on the unravelling of the same initial random coil; (d) same as (b) but including HI and for a subset of 100 chains. In (a), (b) & (d) solid lines show simulation results, dashed lines show fit to eqn (5). | ||
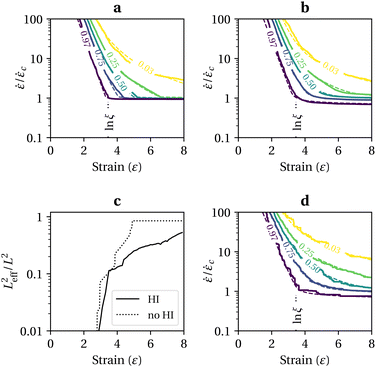
For further analysis, we propose the following functional approximation of c(ε,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ):
):
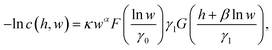 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ and w =
ξ and w = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c, and smooth onset of scission given by F(x) = (1 + exp(−x))−1, and G(x) = ln(1 + exp(x)). Values of the fitted parameters κ, α, β, γ0, and γ1 are reported in Table 1 for various molecular models and ensemble properties. Fitted eqn (5) is represented as dashed lines in Fig. 2. The onset of scission with respect to w is of course w > 1 by definition of
c, and smooth onset of scission given by F(x) = (1 + exp(−x))−1, and G(x) = ln(1 + exp(x)). Values of the fitted parameters κ, α, β, γ0, and γ1 are reported in Table 1 for various molecular models and ensemble properties. Fitted eqn (5) is represented as dashed lines in Fig. 2. The onset of scission with respect to w is of course w > 1 by definition of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c. On the other hand, the onset with respect to strain is h > −β0
c. On the other hand, the onset with respect to strain is h > −β0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ln
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) w, which means that activation is reached at lower strain for larger strain rates, as quantified by β0.
w, which means that activation is reached at lower strain for larger strain rates, as quantified by β0.
We recover the first order reaction kinetics at constant strain rate:31,32 for w = 1 and large h, −ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c ∼ κh which implies d(−ln
c ∼ κh which implies d(−ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c)/dt ∼ κ
c)/dt ∼ κ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) . Also, for a constant w > 1, k ∼
. Also, for a constant w > 1, k ∼ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 1.9, which is consistent with our previous simplified modelling (k ∼
1.9, which is consistent with our previous simplified modelling (k ∼ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) 2).33 The value of α depends on whether mechanophore activation is due to a much weaker bond compared to backbone bond strength, and will be discussed below. Parameters γ0 and γ1 control the smoothness of the onset. γ0 in particular increases with chain length dispersity.
2).33 The value of α depends on whether mechanophore activation is due to a much weaker bond compared to backbone bond strength, and will be discussed below. Parameters γ0 and γ1 control the smoothness of the onset. γ0 in particular increases with chain length dispersity.
To assess the influence of Hydrodynamic Interactions (HI) within polymer chains, a small ensemble of 100 chains has been simulated using the standard Rotne–Prager–Yamakawa hydrodynamic coupling tensor with an HI parameter h* = 0.25 and without Brownian forces (see ESI, section 2†). The results are shown in Fig. 2c and d.34 HI have a negligible impact on the tension in fully stretched chains or long unravelled segments (so long as the friction coefficient is re-scaled). However, because polymer segments of the outer part of the coil shield the inner part from the stretching effect of the flow, they can considerably slow down the unravelling process.34,35 To illustrate this effect, the normalised effective square length is plotted in Fig. 2c for the same initial random coil subject to stretching with or without HI. In the absence of HI, the coil is fully elongated at a solvent strain of 5, while with HI it is still partially coiled at a strain of 8. Fitted coefficients from Fig. 2d are reported in Table 1, line 3. They are similar to the free-draining model, except for κ which is about half of the free-draining value, confirming the slowing-down effect of HI. Remarkably, the critical strain still scales with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ξ, which supports previous studies reporting no significant influence of HI on the onset of scission.21,28
ξ, which supports previous studies reporting no significant influence of HI on the onset of scission.21,28
2.3 Polymer degradation through constrictions
Before moving on to more complex mechanochemistry, it is worth discussing the implications of this theory on non-specific chain scission in flows through constrictions. As mentioned above, a scaling of the critical strain rate as![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c ∼ L−1 is typically reported for transient flows through an orifice, in apparent contradiction with the TABS model (
c ∼ L−1 is typically reported for transient flows through an orifice, in apparent contradiction with the TABS model (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c ∼ L−2). The scaling for transient flows has been explained by assuming chains break while still mainly in a coiled conformation, in contradiction with mid-chain scission observations.24,25 This paradox is solved instead by recognising the rich diversity of unravelling pathways in an ensemble of chains. To this aim, we consider a polymer molecule of relaxation time τ flowing through an abrupt contraction of radius R and volumetric flow rate Q. Ignoring the effects of boundary layers, we have, along a Lagrangian path until the orifice:
c ∼ L−2). The scaling for transient flows has been explained by assuming chains break while still mainly in a coiled conformation, in contradiction with mid-chain scission observations.24,25 This paradox is solved instead by recognising the rich diversity of unravelling pathways in an ensemble of chains. To this aim, we consider a polymer molecule of relaxation time τ flowing through an abrupt contraction of radius R and volumetric flow rate Q. Ignoring the effects of boundary layers, we have, along a Lagrangian path until the orifice: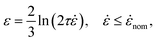 | (6) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) nom = Q/(πR3) is the nominal strain rate in the constriction. Experiments would consist of reporting
nom = Q/(πR3) is the nominal strain rate in the constriction. Experiments would consist of reporting ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) nom at the onset of degradation for a range of molecular weights. We now assume that the onset is in fact governed by the critical strain. Then, combining eqn (6) with the scaling of G(x) in eqn (5) yields:
nom at the onset of degradation for a range of molecular weights. We now assume that the onset is in fact governed by the critical strain. Then, combining eqn (6) with the scaling of G(x) in eqn (5) yields: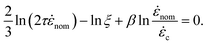 | (7) |
Polymer relaxation scales as τ ∼ Lδ with δ = 2 for free-draining chains or 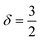 for Zimm chains in a theta-solvent;
for Zimm chains in a theta-solvent; 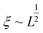 (theta-solvent), and
(theta-solvent), and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c ∼ L−2 (eqn (2)). β is given in Table 1, line 2 or 3 for the free-draining or Zimm chain respectively. The overall scaling is therefore
c ∼ L−2 (eqn (2)). β is given in Table 1, line 2 or 3 for the free-draining or Zimm chain respectively. The overall scaling is therefore ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) nom ∼ L−1.4 (free-draining) or
nom ∼ L−1.4 (free-draining) or ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) nom ∼ L−1.1 (Zimm chain), in agreement with simulations and experiments. Chains breaking at the onset of degradation are the ones which are significantly stretched, albeit not fully unravelled: this is why mid-chain scission is observed even if the vast majority of chains are still coiled as they pass the orifice.
nom ∼ L−1.1 (Zimm chain), in agreement with simulations and experiments. Chains breaking at the onset of degradation are the ones which are significantly stretched, albeit not fully unravelled: this is why mid-chain scission is observed even if the vast majority of chains are still coiled as they pass the orifice.
2.4 Mechanophore activation versus non-specific scission
We now discuss the additional complexity of considering two competing reactions: activation of a mechanophore moiety versus non-specific backbone scission. In the following, we assume there is only one mechanophore site located at the center of the chain. Our bead-rod mechanophore model is therefore a chain of identical links as above, except that we also monitor tension at the central link.The direct competition between moiety activation and scission of the closest neighbour bonds, which can be assessed by quantum chemistry computations, is beyond the scope of this work.36 Here, we study chain scission far from the mechanophore active site as it can occur in a non-fully unravelled chain. We note ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m the strain rate at which mechanophores activate in a fully stretched chain, and
m the strain rate at which mechanophores activate in a fully stretched chain, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c the strain rate for non-specific scission as above. In this illustration we set
c the strain rate for non-specific scission as above. In this illustration we set ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c = 2
c = 2![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m (activation would occur at 2 nN at the central link, for example, while scission would require 4 nN anywhere else). As above, these critical strain rates are defined with respect to the average chain length in the case of a polydisperse distribution. To obtain the activation yield, η, we consider the poly-dispersed bead-rod molecules ensemble of Fig. 2b and compare both the tension at the center of the chain and the maximum tension elsewhere to their respective thresholds. We count at every point (ε,
m (activation would occur at 2 nN at the central link, for example, while scission would require 4 nN anywhere else). As above, these critical strain rates are defined with respect to the average chain length in the case of a polydisperse distribution. To obtain the activation yield, η, we consider the poly-dispersed bead-rod molecules ensemble of Fig. 2b and compare both the tension at the center of the chain and the maximum tension elsewhere to their respective thresholds. We count at every point (ε,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ) and in the two directions δε and δ
) and in the two directions δε and δ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , the proportion of mechanophore activation. Results are reported in Fig. 3. Naturally, in the vicinity
, the proportion of mechanophore activation. Results are reported in Fig. 3. Naturally, in the vicinity ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ∼
∼ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m we obtain maximum yield, and for
m we obtain maximum yield, and for ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) ≫
≫ ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c significant non-specific scission occurs. Yet, a transition for non-exclusive mechanophore activation is found far beyond
c significant non-specific scission occurs. Yet, a transition for non-exclusive mechanophore activation is found far beyond ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c. A chain would need to unravel from one end first to break before mechanophore activation. Using the fact that tension is parabolic along the straight segment, one can show that a chain would break if at least
c. A chain would need to unravel from one end first to break before mechanophore activation. Using the fact that tension is parabolic along the straight segment, one can show that a chain would break if at least ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m ≥ w0, with:
m ≥ w0, with:
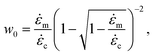 | (8) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , and is a function of
, and is a function of ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) only. The efficiency can be approximated by:
only. The efficiency can be approximated by: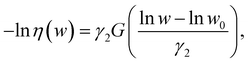 | (9) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) /
/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m, w0 given by eqn (8), and γ2 ≈ 0.2. This expression is justified when the mechanophore is located at the center of the chain, but could vary significantly with embedding position.
m, w0 given by eqn (8), and γ2 ≈ 0.2. This expression is justified when the mechanophore is located at the center of the chain, but could vary significantly with embedding position.
2.5 General implementation
Finally, we would like to discuss general implementation aspects. First, the solvent strain rate is well defined for uniaxial elongation. To capture more complex flows, we can use an effective strain rate,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff, defined by:
eff, defined by: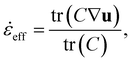 | (10) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff. The additional cost is low as simulating C is a standard procedure in viscoelastic flow simulations. For example, the Finite-Extensible Non-linear Elastic Peterlin (FENE-P) closure can be used.37
eff. The additional cost is low as simulating C is a standard procedure in viscoelastic flow simulations. For example, the Finite-Extensible Non-linear Elastic Peterlin (FENE-P) closure can be used.37
Let us now consider a flow with multiple stretching events. If the time between two events is longer than the relaxation time of the molecules, then conformations are reshuffled in the population of intact chains and the second stretching should be characterised by the same probability of activation. Therefore it is natural to model the mechanochemistry by a first order reaction. On the other hand, if the pause is much shorter than the relaxation time, no mechanochemistry should occur until the exact same segments are fully stretched again. To capture this behaviour, we can split the overall solvent strain into a positive strain, ε, which can only vanish by relaxation, and a negative buckling strain, φ, evolving as:
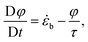 | (11) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) b =
b = ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff if
eff if ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff < 0 or φ < 0, and
eff < 0 or φ < 0, and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) b = 0 otherwise. Then the positive strain is found by integrating:
b = 0 otherwise. Then the positive strain is found by integrating: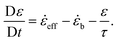 | (12) |
This means that for fast strain rates, ε will not grow unless ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff is large, positive and φ = 0 (no previous buckling to compensate for). The last subtlety is to take into account the fact that in uniaxial elongation
eff is large, positive and φ = 0 (no previous buckling to compensate for). The last subtlety is to take into account the fact that in uniaxial elongation ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff is equal to
eff is equal to ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) only when C becomes significantly anisotropic. Meanwhile, the Lagrangian strain unaccounted for is
only when C becomes significantly anisotropic. Meanwhile, the Lagrangian strain unaccounted for is 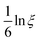 , leading to a different normalised strain in eqn (5):
, leading to a different normalised strain in eqn (5): 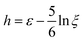 .
.
We can now summarize the flow-induced mechanochemistry model as follows:
1. The conformation tensor is modelled by a standard closure equation;
2. The effective strain rate is derived from eqn (10);
3. The strain is computed by combining eqn (11) and (12);
4. The concentration of intact chains, ci, is modelled by a first order reaction where the reaction rate, k, is computed from the total variation of eqn (5):
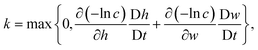 | (13) |
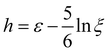 and w = max{0,
and w = max{0,![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) eff/
eff/![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m}. The rate is cropped at zero since reactions are assumed irreversible.
m}. The rate is cropped at zero since reactions are assumed irreversible.
5. The creation of activated mechanophores per unit time is ηkci where η is the chain efficiency defined by eqn (9).
3 Results
To validate the model, we consider the sonication and 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 contraction scenarios used above, plus an inkjet flow (transient nozzle flow and filament breakup) and a turbulent channel flow (Johns Hopkins Turbulence Database38). For each scenario, 5 Lagrangian trajectories are extracted, normalised so that Wimax ∼ 103, then used as forcing sequences for the bead-rod model simulations (100 free-draining chains, PDI = 1.01, 〈ξ2〉 = 1000). See ESI, section 3,† for a detailed description of how the Lagrangian trajectories are obtained in each scenario. We set Wim = τ
1 contraction scenarios used above, plus an inkjet flow (transient nozzle flow and filament breakup) and a turbulent channel flow (Johns Hopkins Turbulence Database38). For each scenario, 5 Lagrangian trajectories are extracted, normalised so that Wimax ∼ 103, then used as forcing sequences for the bead-rod model simulations (100 free-draining chains, PDI = 1.01, 〈ξ2〉 = 1000). See ESI, section 3,† for a detailed description of how the Lagrangian trajectories are obtained in each scenario. We set Wim = τ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m = 50 and
m = 50 and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) c = 2
c = 2![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m (situation depicted in Fig. 3). We then compare the concentrations of intact chains, ci and activated mechanophores, cm, obtained from the molecular simulations to those predicted by our model (with parameters from line 4 in Table 1). For each trajectory, mean and maximum errors are reported in Fig. 4. The maximum error is typically of the order of 0.1 while the average over an entire trajectory is tenfold smaller. Mechanochemistry is not occurring in the 5th sonication trajectory and the 2nd to the 4th inkjet trajectories, for both the bead-rod simulations and the model. The data supports that the model is able to capture the onset of mechanochemical activation, the half-life of initial chains, and the proportion of non-specific backbone scission.
m (situation depicted in Fig. 3). We then compare the concentrations of intact chains, ci and activated mechanophores, cm, obtained from the molecular simulations to those predicted by our model (with parameters from line 4 in Table 1). For each trajectory, mean and maximum errors are reported in Fig. 4. The maximum error is typically of the order of 0.1 while the average over an entire trajectory is tenfold smaller. Mechanochemistry is not occurring in the 5th sonication trajectory and the 2nd to the 4th inkjet trajectories, for both the bead-rod simulations and the model. The data supports that the model is able to capture the onset of mechanochemical activation, the half-life of initial chains, and the proportion of non-specific backbone scission.
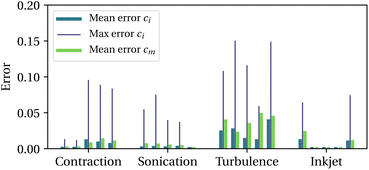 | ||
| Fig. 4 Model errors normalised by the initial concentration of chains, with 5 trajectories per scenario. | ||
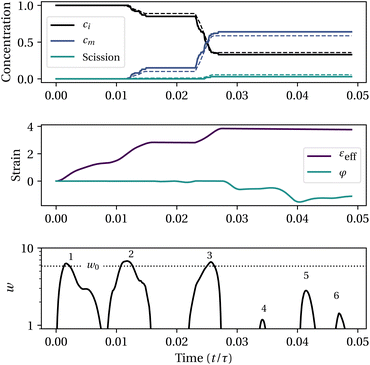
Finally, to get more insight on the model, Fig. 5 shows an example of mechanochemistry simulated along a turbulent Lagrangian trajectory. This trajectory features multiple straining events above the critical strain rate, numbered from 1 to 6 in the bottom plot. The first event does not lead to activation because the strain is still modest. The second and third events are responsible for mechanophore activation and moderate non-specific scission. After the third event, the buckling strain becomes non-zero, which explains why events 4 to 6 do not result in activation even though ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) >
> ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) m. This illustrates the importance of accounting for buckling deformation in arbitrary flows. Other trajectories can be inspected in the ESI, section 3.3.†
m. This illustrates the importance of accounting for buckling deformation in arbitrary flows. Other trajectories can be inspected in the ESI, section 3.3.†
4 Conclusion
In conclusion, we have shown that polymer mechanochemistry in transient flows should be in large part governed by the unravelling dynamics of chains. For a particular initial conformation, mechanochemistry is described as a thresholding phenomenon due to the rapid growth of straight segments and the large change in activation energy. In addition, the unravelling state is only a function of the Lagrangian strain at large Weissenberg numbers, and therefore the survival indicator for this initial conformation is only a function of strain and strain rate. This enables performance of an ensemble average over many different initial conformations and dispersed molecular lengths, and model the proportion of intact chains as a function of strain and strain rate. To take into account the competition between mechanophore activation and non-specific scission, the model is formulated as a pseudo first order reaction with a strain rate dependent yield. The model shows good performance on realistic flow scenarios and is able to capture the onset of mechanochemistry, the half-life of intact chains and the proportion of non-specific scission.Throughout this study we have assumed a relatively small polymer length dispersity. The theory should hold as long as the characteristics of the vast majority of the chains in an ensemble are within the same order of magnitude. For highly polydisperse or multimodal distributions, we might encounter situations where short mechanophores start activating while the longer ones have already undergone multiple scissions, or the coil-stretch transition of the shorter polymer may not occur at all.39 This complexity goes beyond the scope of this paper. Future work should also focus on the effect of finite polymer concentration. Furthermore, the approach can be extended to model chains with different number and location of active mechanophore moieties. Finally, this model requires the flow to be fully resolved, which might be difficult in some cases like full-beaker sonication, porous media, or turbulence. However it should help develop closure models where Lagrangian statistics are known, and significantly improve the understanding and interpretation of mechanochemistry in simple and controlled flows.
Data availability
The simulation dataset and post-processing code used for this study are available at https://doi.org/10.17863/CAM.101595 under open access license CC BY 4.0.Author contributions
E. R.: conceptualization, software, formal analysis, writing – original draft; N. W.-F.: conceptualization, writing – review & editing; R. D.: conceptualization, supervision, writing – review & editing.Conflicts of interest
The authors declare no competing interests.Acknowledgements
This work was supported by the Engineering and Physical Sciences Research Council (EPSRC), grant no. EP/S009000/1.Notes and references
- E. J. Soares, J. Non-Newtonian Fluid Mech., 2020, 276, 104225 CrossRef CAS.
- S. E. Evans, T. S. Harrington, M. C. R. Rivero, E. Rognin, T. R. Tuladhar and R. Daly, Int. J. Pharm., 2021, 599, 120443 CrossRef CAS PubMed.
- S. Wu, T. Fu, R. Qiu and L. Xu, Soft Matter, 2021, 17, 9047–9056 RSC.
- N. Willis-Fox, E. Rognin, T. A. Aljohani and R. Daly, Chem, 2018, 4, 2499–2537 CAS.
- H.-A. Klok, A. Herrmann and R. Göstl, ACS Polym. Au, 2022, 2, 208–212 CrossRef CAS PubMed.
- R. T. O'Neill and R. Boulatov, Nat. Rev. Chem, 2021, 5, 148–167 CrossRef PubMed.
- N. Willis-Fox, E. Rognin, C. Baumann, T. A. Aljohani, R. Göstl and R. Daly, Adv. Funct. Mater., 2020, 30, 2002372 CrossRef CAS.
- N. Willis-Fox, E. Watchorn-Rokutan, E. Rognin and R. Daly, Trends Chem., 2023, 5, 415–431 CrossRef CAS.
- R. T. O'Neill and R. Boulatov, Nat. Chem., 2023, 15, 1214–1223 CrossRef PubMed.
- D. Vincenzi, T. Watanabe, S. S. Ray and J. R. Picardo, J. Fluid Mech., 2020, 912, A18 CrossRef.
- I. Martins, E. J. Soares and R. do Nascimento Siqueira, J. Non-Newtonian Fluid Mech., 2022, 301, 104740 CrossRef CAS.
- A. S. Pereira, G. Mompean and E. J. Soares, J. Non-Newtonian Fluid Mech., 2018, 256, 1–7 CrossRef CAS.
- A. Lohne, O. M. Nødland, A. Stavland and A. Hiorth, Comput. Geosci., 2016, 21, 1289–1312 CrossRef.
- E. Rognin, N. Willis-Fox, T. A. Aljohani and R. Daly, J. Fluid Mech., 2018, 848, 722–742 CrossRef CAS.
- S. Garrepally, S. Jouenne, P. D. Olmsted and F. Lequeux, J. Rheol., 2019, 64, 601–614 CrossRef.
- S. A. Vanapalli, S. L. Ceccio and M. J. Solomon, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 16660–16665 CrossRef CAS PubMed.
- O. K. Dudko, G. Hummer and A. Szabó, Phys. Rev. Lett., 2006, 96, 108101 CrossRef PubMed.
- J. Ribas-Ariño and D. Marx, Chem. Rev., 2012, 112, 5412–5487 CrossRef PubMed.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- S. Akbulatov, Y. Tian, Z. Huang, T. J. Kucharski, Q.-Z. Yang and R. Boulatov, Science, 2017, 357, 299–303 CrossRef CAS PubMed.
- H. G. Sim, B. Khomami and R. Sureshkumar, J. Rheol., 2007, 51, 1223–1251 CrossRef CAS.
- G. K. Batchelor, J. Fluid Mech., 1970, 44, 419–440 CrossRef.
- J. A. Odell, A. Keller and Y. Rabin, J. Chem. Phys., 1988, 88, 4022–4028 CrossRef CAS.
- Y. Rabin, J. Chem. Phys., 1987, 86, 5215–5216 CrossRef CAS.
- T. Q. Nguyen and H.-H. Kausch, J. Non-Newtonian Fluid Mech., 1988, 30, 125–140 CrossRef CAS.
- R. G. Larson, Rheol. Acta, 1990, 29, 371–384 CrossRef CAS.
- E. J. Hinch, J. Non-Newtonian Fluid Mech., 1994, 54, 209–230 CrossRef CAS.
- L. Turetta and M. Lattuada, Ind. Eng. Chem. Res., 2021, 60, 10539–10550 CrossRef.
- T. T. Perkins, D. E. Smith and S. Chu, Science, 1997, 276, 2016–2021 CrossRef CAS.
- S. Sachdev, A. Muralidharan and P. E. Boukany, Macromolecules, 2016, 49, 9578–9585 CrossRef CAS PubMed.
- J. J. López Cascales and J. García de la Torre, J. Chem. Phys., 1992, 97, 4549–4554 CrossRef.
- J. G. Hernández Cifre and J. García de la Torre, J. Chem. Phys., 2001, 115, 9578–9584 CrossRef.
- E. Rognin, N. Willis-Fox, T. Z. Zhao, T. A. Aljohani and R. Daly, J. Fluid Mech., 2021, 924, A24 CrossRef CAS.
- C.-C. Hsieh and R. G. Larson, J. Rheol., 2004, 48, 995–1021 CrossRef CAS.
- V. S. Krishna, P. Kumar, B. Sharma and I. S. Dalal, arXiv, 2022, preprint, arXiv:2208.06559, DOI:10.48550/arXiv.2208.06559.
- S. Kumar and T. Stauch, RSC Adv., 2020, 11, 7391–7396 RSC.
- M. A. Alves, P. J. Oliveira and F. T. Pinho, Annu. Rev. Fluid Mech., 2021, 53, 509–541 CrossRef.
- Y. Li, E. Perlman, M. Wan, Y. Yang, C. Meneveau, R. C. Burns, S. Chen, A. S. Szalay and G. L. Eyink, J. Turbul., 2008, 9, N31 CrossRef.
- K. S. Sorbie and L. J. Roberts, SPE Enhanced Oil Recovery Symposium, 1984, pp. SPE-12654-MS Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mr00009e |
| This journal is © The Royal Society of Chemistry 2024 |