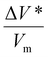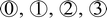Open Access Article
Open Access ArticleElucidating tribochemical reaction mechanisms: insights into tribofilm formation from hydrocarbon adsorbates coupled with tribochemical substrate wear†
Yu-Sheng
Li
 a,
Fakhrul H.
Bhuiyan
a,
Fakhrul H.
Bhuiyan
 b,
Jongcheol
Lee
b,
Jongcheol
Lee
 a,
Ashlie
Martini
a,
Ashlie
Martini
 b and
Seong H.
Kim
b and
Seong H.
Kim
 *a
*a
aDepartment of Chemical Engineering and Materials Research Institute, Pennsylvania State University, University Park, PA 16802, USA. E-mail: shk10@psu.edu
bDepartment of Mechanical Engineering, University of California, Merced, CA 95343, USA
First published on 19th June 2024
Abstract
Tribochemical reactions, chemical processes that occur by frictional shear at sliding interfaces, lead to tribofilm formation or substrate wear that directly affect the efficiency of machinery. Here, we report tribofilm growth through tribopolymerization and tribochemical wear of a silica surface due to reactions with organic precursors methylcyclopentane, cyclohexane, cyclohexene, and α-pinene. The activation volume determined from the stress dependence of reaction yield is correlated to the chemical reactivity of the precursor molecules. The molecules with higher tribochemical reactivity exhibited smaller activation volume, implying that less mechanical energy was required to initiate tribochemical reactions. Nudged elastic band calculations for the hypothetical pathways for the observed tribochemical reactions suggested that the smaller activation volume could be related to smaller thermal activation energy at the rate-limiting step. The tribofilm formation yield was found to increase with load whereas the load dependence of tribochemical wear was negligible. The environment dependence of the sliding processes was also analyzed. Results showed that, compared to a dry N2 environment, the tribopolymerization reaction yield increased in dry air but decreased in N2 with 40% relative humidity, while the wear rate remained unchanged. This finding suggested that during sliding, the reactive sites exposed at the worn surface could be re-oxidized by even trace amounts of oxygen or water vapor in the environment. This analysis of tribofilm yield and substrate wear in various environments showed that ambient gas can change the tribochemical reactivities of the reactant, which leads to different load dependencies of tribopolymerization and tribochemical wear.
1. Introduction
Mechanochemistry is the subfield of chemistry investigating or utilizing chemical reactions that are facilitated by mechanical stress in milling, grinding, stretching, compressing, and shearing processes. Unlike conventional chemical reactions that rely on thermal activation or catalysis, mechanochemistry involves mechanical energy as the primary driving force to initiate or facilitate chemical reactions. Mechanochemistry can offer several advantages over solution-based chemistry.1,2 For example, ball-milling process can be an efficient and solvent-free synthetic route at room temperature, while the same reaction in solution in a conventional reactor may require high temperatures.3 Twin screw extrusion has been demonstrated to be an efficient process for large-scale organic synthesis by enabling continuous reactions without solvent, providing products with high conversion yields and minimal post-synthesis purification.4 Tribofilms containing polymeric species can be formed from adsorbate molecules or additives under frictional shear conditions, which can provide lubrication effect and reduce wear of the substrate.5–8 Chemical reactions that are driven by interfacial friction are specifically called tribochemical reactions. Such reactions are ubiquitous in lubrication systems in industrial machineries and polishing processes.9Tribochemical reactions have been investigated using various experimental and computation methods which include macroscale tribometers, atomic force microscopy (AFM), and molecular dynamics simulations. Studies using tribometers have shown that tribochemical polymerization, i.e., formation of tribopolymers, is sensitive to the applied frictional force,10,11 surface chemistry,12,13 environmental gas,14,15 and the presence of various additives in base oil.16,17 Using AFM, the growth of tribofilms from lubricant additives in single-asperity sliding nanocontacts followed an exponential dependence on the applied compressive stress or temperature.18 Molecular dynamics simulations have been widely employed to gain atomic insights into underlying reaction pathways.19–22
From those studies, it is now clear that shear stress of friction plays a key role in driving tribochemical reaction,11,23–26 but it is still unclear how the mechanical energy of interfacial shear is transferred or channeled into the reaction coordinate. The most extensively used model to describe the energetics of triobochemical reactions is the Bell model (also called the stress-assisted thermal activation model).27,28 In this model, reaction kinetics is expressed as:
 | (1) |
| Em = FΔx* = τΔV* | (2) |
 | (3) |
Activation volume can be readily calculated from the slope of the semi-log plot of reaction rate constant (k) versus shear stress (τ) assuming that the temperature change during friction is negligible:15
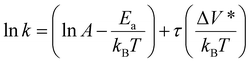 | (4) |
However, despite the ease of estimation, interpreting the physical meaning of the activation volume is not straightforward. It has been proposed to be the change in molecular volume between the reactant state and transition state during tribochemical reactions,22,31–33 the physical volume of the reactant,24,34,35 or a hypothetical parameter that quantifies the sensitivity of a tribological system to mechanical forces.11,32 Understanding the physical meaning of the activation volume is crucial for gaining insight into the mechanisms underlying tribochemical reactions and for facilitating the development of a new tribological system.36
One approach to study the underlying reaction mechanisms of tribochemistry is to investigate the yield of tribofilms remaining on the substrate under varying shear stress conditions. In the chemical process of tribofilm formation, the tribochemical wear of substrate could occur simultaneously.15,25,26,37,38 This type of surface wear is different from abrasive or adhesive wear. The involvement of surface atoms from the substrate as a key reaction step in the formation of tribofilms through tribochemical reactions of organic precursors has been shown in several studies.25,26,37 This process can lead to changes in chemical states of surface atoms or even surface wear within the sliding interface. Wear of metal surfaces was reported to occur concurrently with the formation of tribofilms in several lubricant additive studies using a macroscale tribometer.15,37–39 However, the correlation between yield of tribofilms and wear volume of the substrate appeared to be quite complicated. The tribochemical reactivity of organic reactants was found to vary depending on the substrate being rubbed and the ambient gas environments, while the wear rate of the substrate remained relatively constant.15,39 In some studies, less wear of a steel substrates was observed when more carbon-containing oligomeric films were formed from liquid lubricants in the boundary lubrication regime using a macroscale tribometer at substrate.12,40,41 It was suggested that the formation of tribofilms at the sliding interfaces can prevent direct contact between the two surfaces, thereby reducing wear. In contrast, other studies reported a larger wear volume of a metal substrate when more tribofilms were present in a macroscale tribotest due to higher tribochemical wear.13,42,43 In vapor phase lubrication (VPL) with n-pentanol where the tribofilm formation was not observed at all, frictional wear was almost completely suppressed.44,45 Analyzing the correlation between surface wear volume and tribofilm reaction yield as a function of shear stress is therefore important not only for better comprehending the role of surface atoms in tribochemistry but also for gaining deeper insight into the fundamental processes of tribochemistry.
In this study, we aimed to elucidate two aspects of tribochemistry: (i) the correlation between ΔV* and the molecular structures of organic model compounds in tribopolymerization reactions on a model surface (silica) and (ii) the interplay between the tribopolymerization and tribochemical wear. The model compounds chosen for the study were methylcyclopentane, cyclohexane, cyclohexene, and α-pinene, which were supplied to the sliding interface through adsorption from the gas phase. These were chosen to evaluate the relative importance of three factors: (i) internal molecular strain, (ii) presence of unsaturated bonds, (iii) equilibrium dimensions (size). To confirm the role of internal ring strain energy, methylcyclopentane and cyclohexane were selected in this study. The estimated strain energies of cyclohexane, cyclohexene, and cyclopentane are 0.8 kcal mol−1, 1.3 kcal mol−1, and 7.4 kcal mol−1, respectively.46 The methyl group on cyclopentane would not change the strain energy by much.47 Cyclohexane and cyclohexene were chosen to not only study the effect of internal ring strain energy but also the presence of unsaturated bonds on tribochemical reactivity. α-Pinene has a four-membered ring and a six-membered ring with unsaturated bond. The four-member ring of cyclobutane has a strain energy of about 25 kcal mol−1.48 The comparison of α-pinene with cyclic hydrocarbons reveals that molecular size can affect tribochemical reactivity as well.
The activation volume was deduced from the slope of the semi-log plot of reaction yield versus shear stress using the Bell model, and the tribochemical reactivity was inferred from the intercept (eqn (4)). These analyses were complemented by nudged elastic band (NEB) calculations within the framework of a reactive empirical potential to calculate the activation energy barrier for selected reaction pathways. To study the role of the substrate wear in tribopolymerization of adsorbates, the wear rate of the silica surface was measured over varying shear stress conditions and in three different environmental conditions (dry N2, dry air, and humid N2). Putting all these results together, we found the interplay among various parameters such as ΔV*, environmental gas, molecular structure, and surface chemistry. This suggested that a full mechanistic understanding may not be obtained by studying the effect of a single parameter.
2. Methods
2.1 Experimental
All tribotests were carried out using a custom-built ball-on-flat tribometer with the capability to control the vapor environment. In this study, a silicon wafer with thermally grown oxide layers was used as the substrate, and the counter surface was a sodium borosilicate sphere (Thermo Fisher Scientific) with a diameter of 3 mm. The root-mean-square surface roughness of the ball was estimated to be ∼4 nm after removal of the ball curvature.49 A new ball surface was used in each experiment. A silicon (100) wafer (Wafer World, Inc. (West Palm Beach, FL, USA)) was cleaned with RCA-1 solution (water![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) H2O2
H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) NH4OH = 5
NH4OH = 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) at 75–80 °C for 20 minutes to remove organic and inorganic contaminants followed by rinsing with deionized water. After cleaning, the silicon wafer was heated in a tube furnace at 450 °C for 15 hours in dry N2 and then cooled to room temperate at 1 °C/min. The thickness of the resulting oxide layer was determined to be 5–7 nm from ellipsometry analysis.49,50 The water contact angle of the thermally-treated silica was 42 ± 1°, while the RCA-1 cleaned surface had a contact angle of less than 5° (Fig. S1 in the ESI†). Hereafter, the silicon wafer prepared in this way is called dehydroxylated silica.
1) at 75–80 °C for 20 minutes to remove organic and inorganic contaminants followed by rinsing with deionized water. After cleaning, the silicon wafer was heated in a tube furnace at 450 °C for 15 hours in dry N2 and then cooled to room temperate at 1 °C/min. The thickness of the resulting oxide layer was determined to be 5–7 nm from ellipsometry analysis.49,50 The water contact angle of the thermally-treated silica was 42 ± 1°, while the RCA-1 cleaned surface had a contact angle of less than 5° (Fig. S1 in the ESI†). Hereafter, the silicon wafer prepared in this way is called dehydroxylated silica.
Before the tribotest, the dehydroxylated silica substrate and the counter surface were rinsed with acetone and ethanol, followed by deionized water, and subjected to UV/O3 treatment for 20 minutes.51 The gas flow with the saturation vapor pressure (Psat) of α-pinene (98%; Sigma-Aldrich), methylcyclopentane (97%; Sigma-Aldrich), cyclohexane (≥99%; Sigma-Aldrich), cyclohexene (99%; Thermo Fisher Scientific), and n-pentanol (99%; fisher scientific) were generated by flowing dry N2 into a flask filled with those chemicals at room temperature. Note that the dry N2 gas used in this study contained ∼500 ppm of oxygen and![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∼10 ppm of water (based on the purity and dew point provided by vendor). Partial pressures of the organic vapors relative to its saturated vapor pressure (P/Psat) were controlled at 30% by mixing the N2 stream saturated with organic vapor with the dry N2 stream at a specific ratio calculated for each precursor to be tested. Details of the tribotest set-up were discussed previously.15 A constant load was applied to the counter surface and the substrate was reciprocated at a speed of 3.2 mm s−1. The applied load ranged from 50 g to 300 g, which corresponded to an average Hertzian contact pressure varying from 0.23 to 0.42 GPa. The substrate was reciprocated at a stroke length of 2.3 mm. In this condition, the maximum flash temperature rise was calculated to be less than 5 °C.52 The shear stress was calculated as the average contact pressure multiplied by the measured friction coefficient.53 The friction coefficient data and friction loops are provided in the ESI (Fig. S2 and S3).†
∼10 ppm of water (based on the purity and dew point provided by vendor). Partial pressures of the organic vapors relative to its saturated vapor pressure (P/Psat) were controlled at 30% by mixing the N2 stream saturated with organic vapor with the dry N2 stream at a specific ratio calculated for each precursor to be tested. Details of the tribotest set-up were discussed previously.15 A constant load was applied to the counter surface and the substrate was reciprocated at a speed of 3.2 mm s−1. The applied load ranged from 50 g to 300 g, which corresponded to an average Hertzian contact pressure varying from 0.23 to 0.42 GPa. The substrate was reciprocated at a stroke length of 2.3 mm. In this condition, the maximum flash temperature rise was calculated to be less than 5 °C.52 The shear stress was calculated as the average contact pressure multiplied by the measured friction coefficient.53 The friction coefficient data and friction loops are provided in the ESI (Fig. S2 and S3).†
Tribo-products formed and remained inside and around the sliding tracks were analyzed with atomic force microscopy (AFM; Digital Instruments MultiMode scanning probe microscope). The tapping mode imaging method was used to collect the 3D topographic images of tribopolymers at various segments of sliding tracks (covering both ends of the sliding track and one place in the middle of the track). Tapping mode AFM tips were purchased from Bruker (TESPA-V2), and the spring constant of cantilever was calibrated to be 50 ± 2 N m−1 using the Sader method.54 The reaction yield was calculated by adding up the volumes above reference plane from multiple AFM images. It was assumed that the unimaged area of the track has the same amount of tribofilm calculated from the image in the middle. The total volume calculated along the entire sliding tract was then divided by the sliding area and time to get the normalized yield. The wear volume of the substrate was estimated from the images taken by optical profilometry (Zygo NewView 7300) after rinsing off the tribopolymers with acetone, ethanol, and deionized water. Detailed information regarding the calculation of reaction yield and wear volume can be found in a previous study.15
The photothermal AFM-IR analysis was conducted in the spectral range of 800–1800 cm−1 using a Bruker IconIR system in contact mode. In this mode, a gold-coated AFM probe (PR-U-CnIR; k = 0.2 N m−1; resonant frequency = 13 kHz) maintained contact with the surface across the sample scan while it was illuminated by IR pulses (MIRcatTM). The IR pulse frequency was modulated at a contact resonance frequency which was determined for each sample (for example, ∼696 kHz for cyclohexene and ∼732 kHz for cyclohexane), and the signal was detected at the same frequency. Areas of 15 μm × 10 μm were scanned with 64 pixels per line at a scan rate of 0.4 Hz at two locations of each sliding track – the pile-up region at the end and the side region in the middle with small islands. The AFM-IR imaging was done for the tribopolymers formed from cyclohexene and cyclohexane.
2.2 Computational
The nudged elastic band (NEB) method in LAMMPS55 was used to calculate the energy barriers for the key steps associated with cyclohexane and cyclohexene oligomerization reactions.56–58 The oligomerization reactions were observed in reactive molecular dynamics (MD) simulations in a previous study, where the simulation system consisted of 50 precursor molecules (cyclohexane or cyclohexene) between two silica slabs.59 The precursor molecules in the reactive MD simulations were compressed at 2 GPa normal stress and then sheared between the two silica slabs at 300 K to induce oligomerization reactions, mimicking the ball-on-flat tribometer experiments and described in detail in previous papers.25,59,60 The normal stresses used in the simulations are standard in the literature and such normal stress values are routinely used in reactive MD simulations to accelerate reaction kinetics.19,22,60–63 However, the magnitude of the stress in the dynamic simulations did not affect the NEB calculations directly since the initial (reactant state) and the final (product state) replicas were energy minimized and structurally optimized via LAMMPS before performing the NEB calculations.The initial and final images for the NEB calculations were taken from the dynamic simulations by deleting all non-relevant atoms that did not participate directly in the reactions. The initial configurations of the intermediate replicas were automatically generated by the NEB method through a linear interpolation of the atomic coordinates based on the initial and the final replicas. The minimum energy path for the reaction was then calculated by the NEB method by optimizing the replicas along the reaction path.
The replicas were connected by virtual springs parallel to the transition path to ensure equal spacing between the replicas. Another virtual spring perpendicular to the transition path was applied to maintain a straight path for transition. The total force acting on each replica was then calculated by combining all the force components acting parallel and perpendicular to the tangent to a replica on the reaction path. The force components included the gradient of the atomic interaction perpendicular to the tangent, the spring force along the tangent, and the perpendicular component of the spring force regulated by a switching function.57,64 The total force acting on the replicas was minimized through damped dynamics until a force criterion of 0.1 eV Å−1 was met for the saddle point to calculate the minimum energy path.56,64,65 These calculations used the climbing image method to prevent the replica with the highest energy from slipping down along the reaction path and to force the replica to climb upwards to maximize its energy.66 All NEB calculations were performed using a ReaxFF forcefield previously developed to model the interactions among H, C, O, and Si atoms to study the mechanical properties of a two-phase solid–liquid polymer system in water.67,68
3. Results and discussion
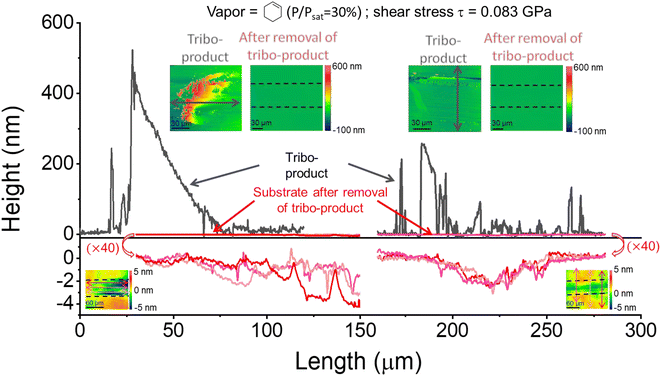
Fig. 1 displays the height profiles taken at the left end and in the middle of the sliding track, before and after rinsing off the tribo-products. The tribo-products were mostly accumulated at the end or periphery of the sliding track. There were relatively few tribo-products remaining inside the sliding track, which means that they were pushed to both ends of the reciprocating motion by the counter-surface during the tribotesting. After the removal of the tribo-products, the height profile along the same sliding track shows that the wear of the substrate occurred during the tribofilm formation. The substrate wear amount is considerably smaller than the volume of tribo-products. Note that the wear of the ball and the volume of tribofilm adhered to the ball were negligible compared to the wear of the substrate and the yield on the substrate.15 In the previous tribotesting of silica in a vapor phase lubrication condition with chemically inert precursor molecules (such as pentanol vapor), neither abrasive nor adhesive wear was observed in a mechanical load condition similar to the one used in this study.45 Thus, the observed wear in this system must originate from tribochemical reactions involving the surface atoms of the substrate in the process of producing tribofilms from the adsorbed molecules. In the following, the shear stress dependence of the normalized tribofilm yield and the tribochemical wear volume will be discussed separately.3.1 Activation volume associated with tribofilm formation from adsorbed organic precursors
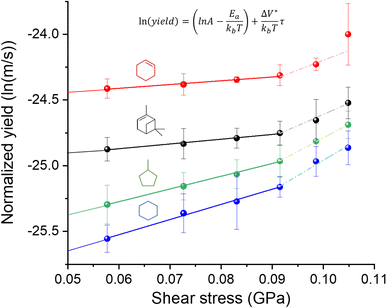
In Fig. 2, the normalized tribofilm yields measured in four precursor vapor environments are plotted on a log scale against the shear stress which was calculated by multiplying the contract stress with the friction coefficient.53 From the change in slope of the data on the semi-log plot, two different stress dependence regimes can be identified – linear dependence on shear stress at ≤0.091 GPa and deviation from this linearity with different slopes at τ ≥ 0.091 GPa. The difference in the slope might indicate a non-linear distortion of the potential energy profile along the reaction coordinate,69,70 or an onset of competition with a new reaction pathway at high shear stress conditions.70 Exploring the exact mechanism of the difference between low and high-stress regimes is beyond the scope of this study. The reason we only use the first four shear stress data points in the fitted model is to leave room for the possibility that the nonlinear effect of force on PES may become significant at the high stress condition. In fact, including all the data points in the linear fitting does not change the conclusions or trends found in the results (Fig. S4 in the ESI†). Additionally, the highest load applied in this study reached the capacity limit of our load cell, preventing us from increasing the load further to evaluate possible nonlinear behavior at high stress. In the reactive MD simulations, a linear trend was still observed up to the contact pressure of 4 GPa.60 For the linear regime at τ ≤ 0.091 GPa, the activation volume and intercept for each precursor were obtained for each precursor, which are summarized in Table 1, along with the volume per molecule (Vm) of four precursors. Interestingly, cyclohexene and α-pinene exhibited significantly smaller ΔV* than cyclohexane and methylcyclopentane. Since the reaction condition was identical for all four cases, the higher yield can be interpreted as a higher tribochemical reactivity. Here, the tribochemical reactivity refers to the combination of the pre-exponential factor A and the energy barrier Ea, solely Ea, or corresponding to the reaction yield at the same shear stress. This correlation suggested that the reactants with higher tribochemical reactivity tend to have smaller ΔV*.Between the two precursors with high reactivities, cyclohexene had ΔV* about ∼15% smaller than α-pinene, while the molecular volume (Vm) calculated from the molar volume in the liquid state is ∼36% smaller for cyclohexene than α-pinene. Between the two precursors with low activities, ΔV* of methylcyclopentane was ∼16% smaller than that of cyclohexane, although Vm of methylcyclopentane is ∼3% larger than that of cyclohexane. These comparisons indicate that ΔV* is not a function of the size of molecule in the equilibrium state. If the ΔV* is assumed to represent the molecular deformation from its equilibrium structure, then the ΔV*/Vm ratio could be viewed as a measure of deformation needed to lower the effective activation barrier of the rate-determining step along the tribochemical reaction pathway. The two highly reactive precursors had a ΔV*/Vm ratio equal to or less than 0.07, while those with lower reactivities exhibited a ratio larger than 0.20.
From the semi-log plot in Fig. 2, it is also noted that the molecules with higher tribochemical reactivities (cyclohexene and α-pinene) have smaller negative intercepts at zero shear stress than those with lower reactivities (methylcyclopentane and cyclohexane). In the Bell model (eqn (4)), the intercept of the semi-log plot contains the thermal activation energy (−Ea) term for the reaction observed in the tribological experiment. Note that, since the log of normalized reaction yield was used in the analysis of the experimental data with the Bell model, instead of the reaction rate constant, the intercept value cannot be converted to the activation energy in the unit of cal mol−1. Calculating the reaction rate constant is not straightforward. This difficulty arises from the fact that the contact diameter (∼100 μm) is much smaller than the length of the sliding track (∼2300 μm); thus, the reaction at a given location of the track occurs intermittently. During the period when the counter-surface is not in contact at a given location of the sliding track between two reciprocating slides, intermediate species at that location may desorb into the gas phase or further reactions may occur with molecules impinging from the gas phase. In some studies, the pre-exponential factor was assumed to be 1013 or 1014 s−1,8,10,69,71,72 which is a reasonable approximation only for the first-order unimolecular reactions.10,73 Although the reaction order of tribopolymerization reactions is not known or could not be determined, it is not expected to be first order.13,74,75 All these details make it difficult (if not impossible) to accurately determine the reaction rate constant and reliably convert the experimentally-determined intercept value to the effective energy barrier.36 Even if such a conversion was possible, reactions that occur in tribochemical conditions are not readily observable under thermal reaction conditions. Thus, it is difficult to compare mechanochemical reaction parameters with those of the same reaction occurring in the absence of mechanical activation.
Nonetheless, if the pre-exponential factor term (A) is assumed to be similar or comparable for the four molecules studied here,32,69 the smaller magnitude of the negative intercept in the semi-log plot could be interpreted as a smaller thermal activation energy (Ea). Then, it is noted that the decreasing order of Ea is the same as the decreasing order of ΔV*. Similar trends have been observed when comparing the tribopolymerization of α-pinene on different substrates, tribopolymerization of α-pinene, pinane, and n-decane on stainless steel and the Diels–Alder cycloaddition reaction with different dienophiles.13,32,74 The activation volume calculated from the slope of semi-log plot of normalized yield against contact pressure on highly reactive surfaces (CuO, NiO and Cr2O3) was smaller than that on low reactive surface (SiO2). Additionally, the absolute value of intercept of the high-yield substrate was smaller than the low-yield substrate, indicating that Ea of the tribopolymerization of α-pinene was smaller on CuO, NiO and Cr2O3 than on SiO2.13 When comparing the tribopolymerization of α-pinene, pinane, and n-decane on stainless steel, α-pinene exhibited the highest tribopolymerization yield (smallest Ea) and the smallest activation volume.74 Though a similar trend was shown in this previous study, they did not discuss this trend at all (only the effect of ring strain energy on ΔV* was discussed).74 In the study on the force-activated Diels–Alder cycloaddition reaction with different dienophiles, it was found that the reactions with larger activation energy (Ea) were more sensitive to mechanochemical activation as indicated by larger activation volume ΔV*.32 This correlation could mean that less assistance from mechanical energy is needed to initiate tribochemical reactions for molecules that have a smaller activation barrier. If ΔV* is associated with the molecular deformation,22,31–33 this trend means that the molecule with a smaller activation barrier can undergo tribochemical reactions even at small deformation from the equilibrium geometry or structure, as observed in our previous work.74
In the homologous series of cyclic saturated hydrocarbons, the five-membered ring compound has a slightly higher ring strain than the six-membered ring.46,76 Maybe, the slightly smaller ΔV* and negative intercept values for methylcyclopentane than cyclohexane could be attributed to the difference in ring strain energies (0.8 kcal mol−1 for cyclohexane; 7.4 kcal mol−1 for cyclopentane.)46,47 Despite a slightly larger ring strain energy in methylcyclopentane compared to cyclohexene (1.4 kcal mol−1), the tribochemical reactivity of methylcyclopentane was found to be lower than that of cyclohexene. This finding suggests that ring strain energy is not the only parameter governing the tribochemical reactivity of a reactant, especially when comparing a cycloalkene to a cycloalkane. The higher reactivity of cyclohexene (indicated by smaller Ea) and lower sensitivity to stress (indicated by smaller ΔV*) than cycloalkane can be attributed to the fact that they follow different reaction pathways and thus their activation energy barriers are different.25,59 α-Pinene has both the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond in the six-membered ring and the four-membered ring with even larger ring strain, but its tribochemical reactivity was found to be slightly smaller than that of cyclohexene. Currently, we do not have any definitive explanation. A speculative hypothesis is the role of entropy in the activation process. α-Pinene consists of 10 carbon molecules, while cyclohexene has only 6 carbon atoms. Thus, α-pinene would have more degrees of freedom in stress-induced deformation than cyclohexene. If so, the assumption of “similar” pre-exponential factor used to interpret the magnitude of the negative intercept may need to be modified as least for the α-pinene case.32,77,78 Another possible reason is that the methyl group near the unsaturated bond (or the two methyl groups near the four-membered ring) hindered the access of double bond to react with the surface.25 The comparison of α-pinene with cyclohexene provides a new insight that was not obvious in the previous studies comparing homologous series with the same number of carbon atoms74 – not only the ring structure and unsaturated bond could alter reactivities, but also molecular size and the accessibility of reactive sites to the surface could have an impact.25,32 This suggests that the accessibility to reactive site or physical hindrance also affects ΔV* and Ea.
C double bond in the six-membered ring and the four-membered ring with even larger ring strain, but its tribochemical reactivity was found to be slightly smaller than that of cyclohexene. Currently, we do not have any definitive explanation. A speculative hypothesis is the role of entropy in the activation process. α-Pinene consists of 10 carbon molecules, while cyclohexene has only 6 carbon atoms. Thus, α-pinene would have more degrees of freedom in stress-induced deformation than cyclohexene. If so, the assumption of “similar” pre-exponential factor used to interpret the magnitude of the negative intercept may need to be modified as least for the α-pinene case.32,77,78 Another possible reason is that the methyl group near the unsaturated bond (or the two methyl groups near the four-membered ring) hindered the access of double bond to react with the surface.25 The comparison of α-pinene with cyclohexene provides a new insight that was not obvious in the previous studies comparing homologous series with the same number of carbon atoms74 – not only the ring structure and unsaturated bond could alter reactivities, but also molecular size and the accessibility of reactive sites to the surface could have an impact.25,32 This suggests that the accessibility to reactive site or physical hindrance also affects ΔV* and Ea.
3.2 NEB calculation of activation energy involved in tribofilm formation
To gain molecular-level insight into the trends observed in the experiments, we have carried out NEB calculations to quantify the activation energy barrier of the rate-determining step involved in the tribochemical reactions. In our previous studies, we used reactive MD simulations to capture the shear-activated oligomerization reaction pathways for all four molecules.25,59 Cyclohexane and methylcyclopentane followed a similar pathway, which began with the hydrogen elimination of an intact precursor molecule, while cyclohexene and α-pinene followed another similar pathway, which started with oxidative chemisorption of an intact molecule at the double bond. Hence, it is reasonable to assume that the rate-limiting steps for methylcyclopentane and cyclohexane tribopolymerization are similar. The same assumption can be applied to α-pinene and cyclohexene. Here, NEB calculations were performed for cyclohexane and cyclohexene only. This choice was based on the categorization of the four molecules into two groups in Table 1: one group with high yield and low ΔV* (α-pinene and cyclohexene), and the other with low yield and high ΔV* (methylcyclopentane and cyclohexane). Since cyclohexene and cyclohexane have similar chemical structures in terms of atom number and ring structure, they were chosen for comparative study of these two groups.Previously, reactive MD simulations of cyclohexane and cyclohexene captured the reaction pathways for oligomerization.59 Although only oligomers were observed in MD simulations, MD can still provide the potential energies of various reaction steps involved in tribopolymerization because polymers are produced by repeating the same steps involved in the oligomerization reaction. Simulations showed that tribo-oligomerization of cyclohexane starts with hydrogen elimination from the precursor molecule by the surface oxygen in the chemisorption step followed by association reaction of this chemisorbed species with another incoming molecule.43 In contrast, cyclohexene undergoes oxidative chemisorption at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bond first and then the addition of another molecule to the surface oxygen that is already covalently bonded to the previous cyclohexene molecule.25,59 Following the identification of these reaction steps, NEB calculations were performed to quantify the thermal activation energy in the hydrogen elimination (for cyclohexane) and oxidative chemisorption (for cyclohexene) followed by the association reaction step to (1) determine the rate-limiting step, and (2) compare the activation energy barriers of the rate-limiting steps in tribochemical reactions of the representative molecules of the high-yield and low-yield groups.
C double bond first and then the addition of another molecule to the surface oxygen that is already covalently bonded to the previous cyclohexene molecule.25,59 Following the identification of these reaction steps, NEB calculations were performed to quantify the thermal activation energy in the hydrogen elimination (for cyclohexane) and oxidative chemisorption (for cyclohexene) followed by the association reaction step to (1) determine the rate-limiting step, and (2) compare the activation energy barriers of the rate-limiting steps in tribochemical reactions of the representative molecules of the high-yield and low-yield groups.
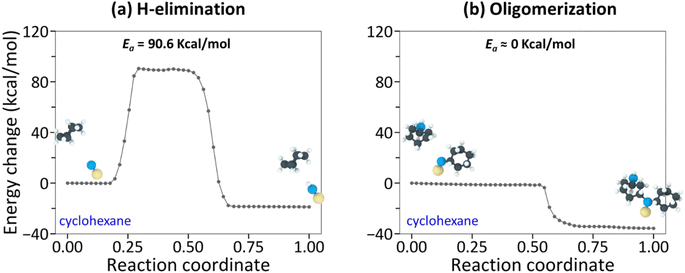
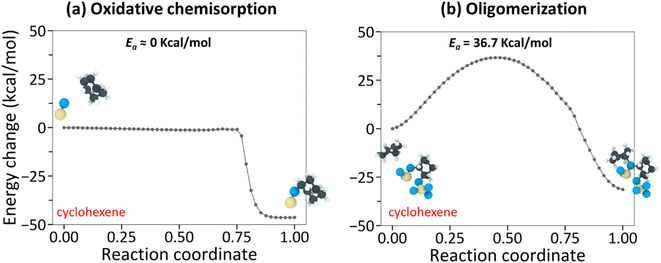
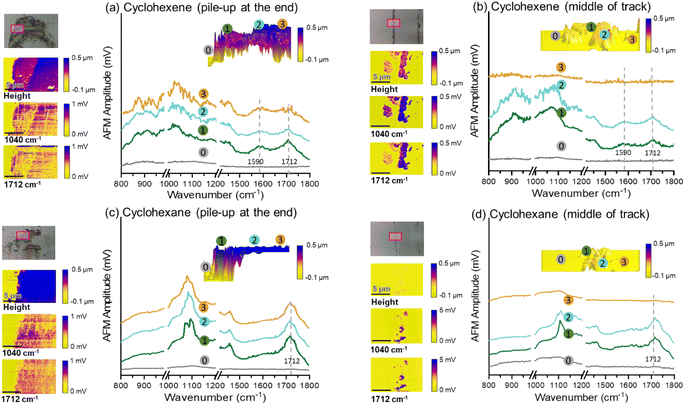
The NEB-calculated minimum-energy paths and associated energy barriers involved in the tribochemical processes of cyclohexane and cyclohexene are shown in Fig. 3 and 4. Fig. 3a and (b) correspond to (i) hydrogen elimination needed prior to initial chemisorption and (ii) association reaction of the chemisorbed species, respectively.43 The NEB calculations showed that the rate-limiting step is the hydrogen-elimination with an activation energy of 90.6 kcal mol−1. The second step involving the association of the chemisorbed species with another molecule appears to be an energetically downhill process without a significant barrier. The oxidative chemisorption of the cyclohexane molecule (Fig. 3b insets) with an undercoordinated carbon molecule after H-elimination had a low energy barrier like the oligomerization step and thus is not shown here as a key step.
In the case of cyclohexene, the oxidative chemisorption (Fig. 4a) appeared to occur without any significant energy barrier (less than 1 kcal mol−1), and the association reaction of the chemisorbed species with incoming molecule (Fig. 4a) was found to be an activated process with a barrier of 36.7 kcal mol−1. Therefore, the rate-limiting step in the cyclohexene tribopolymerization must be the association reaction. The NEB-calculated energy barrier for oxidative chemisorption of cyclohexene was less than 1 kcal mol−1, which is lower than the previous DFT calculation results (1.6 kcal mol−1 to 13.2 kcal mol−1) for similar reaction steps in epoxidation or hydroxylation of cyclohexene.79–81 This could be due to the differences in the reactants and the reaction mechanisms involved in this study compared to the previous DFT calculations, and the approximations involved in parameterizing reactive force fields. Nevertheless, the NEB calculations revealed a stark difference between the reactivity of the two precursor molecules and showed that the rate-limiting step of cyclohexene oligomerization has a thermal activation energy that is ∼2.5 times lower than the rate-limiting step of cyclohexane oligomerization.
Although quantitative comparison of the NEB calculation results with the experimentally determined ΔV* and the negative intercept is not possible, a qualitative comparison could still provide valuable insight. First, the large difference in the negative intercept magnitude could be explained by the finding that different reactions are involved in the rate-limiting step. Second, the large difference in activation barriers (Ea) of these rate-limiting steps may explain the large difference in ΔV*. The hydrogen elimination step of cyclohexane by the surface oxygen has much higher Ea (H-elimination; Fig. 3a) than the association step of cyclohexene to the chemisorbed species (oligomerization; Fig. 4b) and thus more assistance from Em (=τΔV*) is required for the cyclohexane tribopolymerization to occur under the same shear stress, which supports the larger ΔV* found for cyclohexane than for cyclohexene. In other words, cyclohexane has higher sensitivity to stress. Although the NEB calculations were done for the dimerization only, we think the subsequent reactions forming polymers will exhibit similar trends. The reaction pathways for cyclohexene and cyclohexane oligomerization mentioned earlier remained consistent up to hexamers, as observed in the reactive MD simulations. Since no other energy or heat source is available in the experiments, the reaction mechanisms identified from the simulations should be relevant to longer polymer chains.
3.3 Chemical and mechanical properties of tribofilm
The exact chemical composition or molecular weight distribution of the tribopolymers produced could not be determined because the amount of tribofilm inside and around the sliding track was too small for chemical analysis. Nonetheless, the chemical differences between the tribopolymer formed from cyclohexene and cyclohexane could be assessed using AFM-based analyses. Fig. 5 compares the photothermal AFM-IR analysis results of the tribofilms formed from cyclohexene and cyclohexane, representative ones from the high-yield and low-yield groups. The tribopolymers in the pile-up region at the end of the sliding track exhibited an absorption peak at 1712 cm−1, characteristic of the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O group, and a broad bands with peaks in the 1000–1100 cm−1 region, which could be attributed to the C–O stretching modes.82–84 The Si–O stretch of the silica layer can also give a broad absorption band in the 1000–1100 cm−1 region in AFM-IR;85 but the contribution from the substrate was found to be negligible. The 1040 cm−1 signal in the bare substrate region (regions marked with
O group, and a broad bands with peaks in the 1000–1100 cm−1 region, which could be attributed to the C–O stretching modes.82–84 The Si–O stretch of the silica layer can also give a broad absorption band in the 1000–1100 cm−1 region in AFM-IR;85 but the contribution from the substrate was found to be negligible. The 1040 cm−1 signal in the bare substrate region (regions marked with  in Fig. 5) was much smaller than the intensity in the tribofilm region. The presence of these oxygenated species is consistent with previous elemental analysis results.15,33 Since the precursor molecules did not contain oxygen, these oxygen species in the tribofilm must originate from the surface oxygen. In fact, our previous MD simulations showed the involvement of surface oxygen species in the oxidative chemisorption and/or subsequent association reactions.25,59 This aspect will be elaborated further in the next section where the tribochemical wear of the substrate is discussed.
in Fig. 5) was much smaller than the intensity in the tribofilm region. The presence of these oxygenated species is consistent with previous elemental analysis results.15,33 Since the precursor molecules did not contain oxygen, these oxygen species in the tribofilm must originate from the surface oxygen. In fact, our previous MD simulations showed the involvement of surface oxygen species in the oxidative chemisorption and/or subsequent association reactions.25,59 This aspect will be elaborated further in the next section where the tribochemical wear of the substrate is discussed.
The difference in the band shape of the 800–1200 cm−1 region could be due to the difference in the tribochemical reaction mechanisms of cyclohexene and cyclohexane. However, the spectral resolution was not good enough to resolve the heterogeneous polymeric species in the triobofilm, making further interpretation not possible. Nonetheless, it is noted that, in Fig. 5, the peak at 1590 cm−1 is clearly discernible in the AFM-IR spectrum of the tribofilm from cyclohexene, while it is absent in the cyclohexane tribofilm spectrum. This peak can be attributed to the stretch mode of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bonds.83,84 This may imply that not all cyclohexene molecules are activated through the oxidative chemisorption or association reaction at the C
C bonds.83,84 This may imply that not all cyclohexene molecules are activated through the oxidative chemisorption or association reaction at the C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C bond sites. In fact, our previous MD simulation study found that not all C
C bond sites. In fact, our previous MD simulation study found that not all C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C participate in the initial oxidative chemisorption.25,59 Therefore, it is likely that some fraction of C
C participate in the initial oxidative chemisorption.25,59 Therefore, it is likely that some fraction of C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C double bonds remain unreacted (or re-formed) and is detected in the AFM-IR spectra of the final product.
C double bonds remain unreacted (or re-formed) and is detected in the AFM-IR spectra of the final product.
Inside the sliding tracks (regions marked with ③ in Fig. 5b and d), the tribopolymer signal was found to be very weak or not larger than the detection limit of the contact-mode AFM-IR analysis. The contact mode of AFM-IR does not have sufficient surface sensitivity to detect ultra-thin layer of tribopolymer. As an alternative means to check if some tribofilm remained in the middle of the sliding track, we compared the adhesion behavior by collecting the amplitude-distance curve in the tapping-mode AFM analysis. The cantilever oscillation amplitude was measured as the tip approached and retracted from the surface. When the adhesion force between the tip and the sample becomes larger than the oscillating force of the cantilever, then the oscillation amplitude drops to zero. During the tip retraction, the cantilever oscillation recovers from zero to the free-standing value when the cantilever pull-off force becomes larger than the tip-sample adhesion force.86,87
Fig. 6 displays the amplitude-distance curves measured on the bare surface, the pile-up region of the tribofilm, and the region inside the sliding track without tribopolymer. At the end of the sliding track, the hysteresis between snap-in and pull-out of the AFM tip is much larger at the location with a thick layer of tribopolymers compared to the silica substrate region. This large hysteresis indicates that the tribopolymers exhibit more viscoelastic behavior compared to silica, requiring a longer pull-off distance to separate the tip from the surface during the retraction.82,88 Thus, the tribofilm appears quite compliant.
To get more quantitative comparison, the experiments with the contact-mode force–distance curve were conducted at two locations marked as ② at the pile-up at the track end and at the track side. The results of these experiments are presented in Fig. S6 in the ESI.† The elastic modulus of tribopolymers was estimated by analyzing the compression curve using a JKR model;29 the triboproducts piled up at the end of the track showed an elastic modulus of about 105–130 MPa, the ones pushed to the side of the track exhibited about 283–305 MPa. The products at the end of the track showed more hysteresis between loading and unloading cycles than the ones at the side of the track; but we could not tell if this is due to the difference in the amount or the genuine property. In any case, both exhibited viscoelastic behavior.
For the side region of the sliding track, three locations were analyzed: silica substrate, thick islands with tribopolymers, and the inside region of the track. The hysteresis in the amplitude-distance curve inside the track (locations ③ in the right panels of Fig. 6a and b) is observed to be significantly smaller than the thick pile-up regions at the end of the sliding track but slightly larger than on the silica substrate. This suggested that a small amount of tribopolymer remained inside the sliding track. For the region inside the sliding track, there was too little tribopolymer present to confidently perform force-separation measurements.
3.4 Tribochemical wear of substrate during tribofilm formation
The previous elemental analysis of tribopolymers14,26,89,90 and the AFM-IR analysis of this study (Fig. 5) indicated that tribo-products produced from oxygen-free hydrocarbon precursors contain oxygenated functional groups. One possible mechanism suggested by reactive MD simulations is the transfer of surface oxygen species to the reaction product.25,59 If the oxygen atoms from the substrate were the only source of oxygen species in the tribopolymers, an increase in the tribopolymerization yield would result in an increase in the wear volume of the surface as well. However, the load dependence of the wear rate did not follow this expectation.Fig. 7a shows the line profiles of the wear track in the substrate surface after 600 reciprocating cycles in different organic vapor conditions. The 3D profilometry images of each wear track and the locations where height profiles were taken are provided in the ESI.†Fig. 7b compares the wear rate of the dehydroxylated silica surface at various shear stresses in five vapor environments. Here, the n-pentanol data are included to show that there is no wear of the substrate in the absence of tribofilm formation under the same mechanical load condition used in this study.44,45 Thus, the wear of substrate found after removal of the tribofilm must be due to tribochemical processes associated with the formation of tribofilms, not due to mechanical wear. In the absence of vapor phase lubrication or tribopolymerization, there was substantial wear of the substrate in the same mechanical condition (as shown in Fig. 7b).
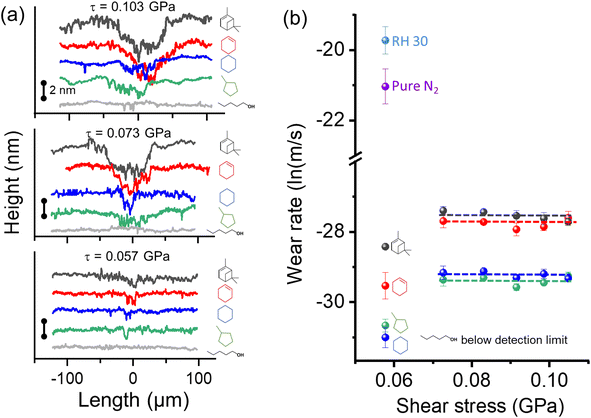 | ||
| Fig. 7 (a) Wear profiles taken on the surface after tribotests in different organic precursors at shear stresses ranging from 0.057–0.103 GPa. Results for three shear stresses are shown here and the others are in ESI as Fig. S5.† (b) Wear rate as a function of shear stress calculated after tribotests in different vapor environments. Tribotests without organic precursors conducted in relative humidity of 30% in N2 and pure N2 environments were added to compare wear volume with and without boundary lubrication. Error bars are from three multiple measurements. | ||
Comparing the different organic precursors, the wear tracks found after removal of tribopolymers formed from cyclohexene and α-pinene were deeper and wider compared to those formed in cyclohexane and methylcyclopentane conditions. This could be attributed to the different reaction pathways associated with the highly reactive group (cyclohexene and α-pinene undergoing oxidative chemisorption first) and the less reactive group (cyclohexane and methylcyclopentane undergoing hydrogen elimination first), as discussed in Fig. 3 and 4.59
For all precursors, the load dependence of the wear rate was negligible, except for the lowest shear stress case (τ = 0.057 GPa). In the lowest shear stress condition tested here, the efficacy of spreading or pushing tribopolymer products from the sliding region might have been lower than other cases. Setting aside this outlier case, it was quite surprising to see no stress dependence of wear, while the tribopolymerization yield increased exponentially with the applied shear stress (Fig. 2).
To understand these trends, we conducted a mass balance analysis for oxygen. The amount of oxygen consumed from the surface over 600 reciprocating cycles could be estimated from the wear volume (Fig. 7b) and the stoichiometry and density of silicon dioxide.91 The amount of oxygen incorporated into the tribopolymer could be estimated from the total volume of the tribofilm (Fig. 2) and the atomic percentage of oxygen determined from elemental analysis (∼6%) from the previous study.15,92 Then, it can be seen that, at τ = 0.073 GPa, only 60% of the oxygen incorporated into the cyclohexene tribopolymer comes from the surface wear, and at τ = 0.103 GPa, this fraction decreases to 40%.
This analysis suggested that there should be another source of oxygen involved in the tribological experiment in dry N2. One possible source could be a trace amount of impurity in the dry N2 gas.93 Based on the purity of the dry N2 gas used in this study, the partial pressure of O2 and H2O were estimated to be ∼40 mTorr and ∼8 mTorr, respectively, in the gas stream continuously flowing at ambient pressure (760 torr). A simple kinetics theory predicts that the bombardment rate of these O2 and H2O molecules onto the surface is 1018–1019 collisions per cm2. If the atomic density of the silica surface is ∼1014 per cm2, then we can see that the single atomic site is being bombarded by O2 and H2O molecules 104–105 times per second. If the reaction probability of O2 or the sticking probability of H2O is 10−3–10−2,94,95 it would take a fraction of second to form a full monolayer on the substrate surface; this time is shorter than the exposure time of the surface to the environment between consecutive sliding cycles. If so, the reactive oxygen sites at the sliding interface may get replenished by the O2 and H2O molecules impinging from the gas phase.
To test this hypothesis, we conducted tribopolymerization tests of cyclohexene in dry air (152 torr of O2) and measured the product yield and the wear volume. Comparing the yield of tribopolymers produced in dry N2 with 40 mTorr of O2, the tribopolymer yield was increased while the wear volume was relatively unchanged (Fig. 8). This supports the hypothesis that ambient O2 participates in tribochemical reactions through re-population of the oxygen vacancy site produced by the transfer of surface oxygen to the tribopolymer. Another possible control experiment that could be done would be the tribotest at a lower partial pressure of O2. But it was practically difficult to do due to the limitation in the purity of the carrier gas or precursor liquid that can be obtained.
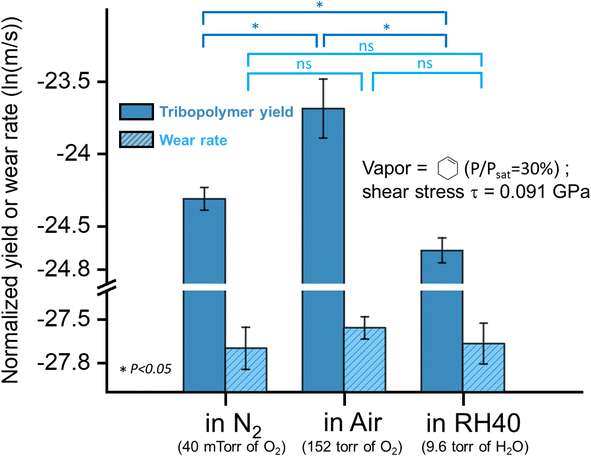 | ||
| Fig. 8 The normalized tribopolymerization yield produced in cyclohexene vapor in N2, air, and RH40 at shear stress τ = 0.091 GPa, along with the wear rate of the substrate after sliding in different environments. Optical images and AFM images of the sliding tracks after tribotest in cyclohexene in dry N2, dry air, and N2 with relative humidity of 40% were in the ESI as Fig. S7.† Error bars represent the standard deviations from three multiple measurements, and the p-value from the Student's t-test between each group is shown. | ||
In the control experiment conducted in N2 with 40% RH (9.6 torr of H2O), the tribopolymerization yield of cyclohexene was decreased as compared to the dry N2 condition, while the wear volume was about the same. In our previous study, we have shown that the tribopolymerization yield on the fully-hydroxylated silica surface was lower than that on the dehydroxylated surface.15,49,96 So, seeing the reduced tribopolymerization yield at higher H2O partial pressure further corroborates the hypothesis that the surface sites exposed by friction react with not only the precursor molecules, but also other oxidative reactants co-present in the carrier gas. In the case of humid environments, H2O molecules impinging from the gas phase can hydroxylate the oxygen vacancy site produced by the transfer of surface oxygen to the tribopolymer, which leads to a lower tribopolymerization activity in the subsequent sliding cycle.
These findings indicate that tribochemical reactivities are affected by not only the chemical structure of the reactant, but also the chemical composition of the ambient (carrier) gas. The latter affects the reactivity of the surface exposed by friction or sweeping off the product by the counter-surface. This explains why the chemical compositions and elastic modulus of the tribopolymers produced from the same precursor can vary depending on the composition of the carrier gas.96 That is because the chemistry of the reactive surface site can vary depending on the environmental condition. In the literature, some studies reported that oxygen or water in air suppressed the formation of tribofilm from organic precursors leading to increased surface wear,14,15,97–100 while other papers reported the presence of oxygen or water in environment could increase the reaction yield of vapor reactants with negligible impacts on wear.15,96,101 These studies reporting contrary effects must mean that the role of oxygen and water in the surrounding environment vary depending on the type of tribofilm formation reactions.
Conclusions
In this study, the correlation between activation volume (ΔV*), thermal activation energy (Ea), and molecular structures of organic precursors in tribopolymerization, as well as the role of oxygen and water in the surrounding environment are elucidated. The key findings are summarized as follows:(1) The activation volume ΔV* determined from the load dependence of tribofilm formation does not correlate with the volume of reactant molecule in its thermodynamic equilibrium state.
(2) Saturated species (cyclohexane and methylcyclopentane) have lower tribochemical reactivity but higher sensitivity to stress and larger ΔV* than unsaturated species (cyclohexene and α-pinene) as observed in macroscale tribological experiments.
(3) The magnitude of ΔV* observed in experiments for cyclohexane and cyclohexene appears to negatively correlate with the magnitude of the thermal activation energy (Ea) calculated from ReaxFF-based NEB calculations of the reaction pathway that would occur in the absence of mechanical stress. Similar trends were observed on force-activated Diels–Alder reactions on anthracene monolayers32 and the tribopolymerization of α-pinene, pinane, and n-decane on 440C stainless steel substrate.33
(4) In the tribopolymerization of cyclohexane, the rate-limiting step was the hydrogen elimination of an intact precursor activated by a surface siloxane. For cyclohexene tribopolymerization, the rate-limiting step was the association reaction of the chemisorbed species with incoming molecules.
(5) The tribochemical wear of substrate can occur concurrently with the tribofilm formation if the surface atoms of the substrate are involved in the reaction mechanism and consumed in the formation of the final product. Nonetheless, the tribochemical wear yield may not correlate with the tribofilm yield if reactive surface sites are reproduced and replenished via reactions with ambient gases.
Conflicts of interest
The authors declare no competing financial interest.Acknowledgements
This work was supported by the National Science Foundation (Grant No. CMMI-2038494 and 2038499).References
- X. Liu, Y. Li, L. Zeng, X. Li, N. Chen, S. Bai, H. He, Q. Wang and C. Zhang, Adv. Mater., 2022, 34, 2108327 CrossRef CAS PubMed.
- J.-L. Do and T. Friščić, ACS Cent. Sci., 2017, 3, 13–19 CrossRef CAS PubMed.
- G. Dayaker, D. Tan, N. Biggins, A. Shelam, J. L. Do, A. D. Katsenis and T. Friščić, ChemSusChem, 2020, 13, 2966–2972 CrossRef CAS PubMed.
- D. E. Crawford, C. K. Miskimmin, A. B. Albadarin, G. Walker and S. L. James, Green Chem., 2017, 19, 1507–1518 RSC.
- Y. Shimizu and H. A. Spikes, Tribol. Lett., 2016, 64, 1–11 CrossRef.
- J. M. Martin, Tribol. Lett., 1999, 6, 1–8 CrossRef CAS.
- M. Kasrai, J. Cutler, K. Gore, G. Canning, G. Bancroft and K. Tan, Tribol. Trans., 1998, 41, 69–77 CrossRef CAS.
- O. Furlong, B. Miller and W. T. Tysoe, Wear, 2012, 274, 183–187 CrossRef.
- H. Carlton, D. Huitink and H. Liang, Lubricants, 2020, 8, 87 CrossRef.
- W. Tysoe, Tribol. Lett., 2017, 65, 1–16 CrossRef CAS.
- L. Fang, S. Korres, W. A. Lamberti, M. N. Webster and R. W. Carpick, Faraday Discuss., 2023, 241, 394–412 RSC.
- A. M. Khan, J. Ahmed, S. Liu, T. Martin, S. Berkebile, Y.-W. Chung and Q. J. Wang, Tribol. Lett., 2023, 71, 63 CrossRef CAS.
- X. He and S. H. Kim, Langmuir, 2018, 34, 2432–2440 CrossRef CAS PubMed.
- J. Zhang, S. Campen, J. Wong and H. Spikes, Tribol. Int., 2022, 165, 107287 CrossRef CAS.
- Y.-S. Li, S. Jang, F. H. Bhuiyan, A. Martini and S. H. Kim, Tribol. Lett., 2023, 71, 49 CrossRef CAS.
- V. Brizmer, H. Pasaribu and G. E. Morales-Espejel, Tribol. Trans., 2013, 56, 739–748 CrossRef CAS.
- S. A. Bhat and M. Charoo, Mater. Today: Proc., 2019, 18, 4416–4420 Search PubMed.
- N. Gosvami, J. Bares, F. Mangolini, A. Konicek, D. Yablon and R. Carpick, Science, 2015, 348, 102–106 CrossRef CAS PubMed.
- A. Martini, S. J. Eder and N. Dörr, Lubricants, 2020, 8, 44 CrossRef.
- P. A. Romero, L. Mayrhofer, P. Stoyanov, R. Merz, M. Kopnarski, M. Dienwiebel and M. Moseler, Front. Mech. Eng., 2019, 5, 6 CrossRef.
- D.-C. Yue, T.-B. Ma, Y.-Z. Hu, J. Yeon, A. C. van Duin, H. Wang and J. Luo, Langmuir, 2015, 31, 1429–1436 CrossRef CAS PubMed.
- J. Yeon, X. He, A. Martini and S. H. Kim, ACS Appl. Mater. Interfaces, 2017, 9, 3142–3148 CrossRef CAS PubMed.
- R. Rana, N. Hopper, F. Sidoroff and W. T. Tysoe, Chem. Sci., 2022, 13, 12651–12658 RSC.
- J. Zhang and H. Spikes, Tribol. Lett., 2016, 63, 1–15 CrossRef CAS.
- F. H. Bhuiyan, S. H. Kim and A. Martini, Appl. Surf. Sci., 2022, 591, 153209 CrossRef CAS.
- R. Rana, R. Bavisotto, N. Hopper and W. T. Tysoe, Tribol. Lett., 2021, 69, 1–8 CrossRef.
- H. Spikes and W. Tysoe, Tribol. Lett., 2015, 59, 1–14 CrossRef CAS.
- G. I. Bell, Science, 1978, 200, 618–627 CrossRef CAS PubMed.
- F. H. Bhuiyan, Y.-S. Li, S. H. Kim and A. Martini, Sci. Rep., 2024, 14, 2992 CrossRef CAS PubMed.
- H. Spikes, Friction, 2018, 6, 1–31 CrossRef.
- B. Johnson, H. Wu, M. Desanker, D. Pickens, Y.-W. Chung and Q. Jane Wang, Tribol. Lett., 2017, 66, 1–13 Search PubMed.
- Y. S. Zholdassov, L. Yuan, S. R. Garcia, R. W. Kwok, A. Boscoboinik, D. J. Valles, M. Marianski, A. Martini, R. W. Carpick and A. B. Braunschweig, Science, 2023, 380, 1053–1058 CrossRef CAS PubMed.
- X. He, A. J. Barthel and S. H. Kim, Surf. Sci., 2016, 648, 352–359 CrossRef CAS.
- B. Gotsmann and M. A. Lantz, Phys. Rev. Lett., 2008, 101, 125501 CrossRef PubMed.
- Z. Cao, W. Zhao, A. Liang and J. Zhang, Adv. Mater. Interfaces, 2017, 4, 1601224 CrossRef.
- A. Martini and S. H. Kim, Tribol. Lett., 2021, 69, 1–14 CrossRef.
- B. Tripathy, M. Furey and C. Kajdas, Wear, 1995, 181, 138–147 CrossRef.
- L. Hu, J. Chen, W. Liu, Q. Xue and C. Kajdas, Wear, 2000, 243, 60–67 CrossRef CAS.
- G. De-Li, Z. Bing, X. Qun-Ji and W. Hong-Li, Wear, 1990, 137, 267–273 CrossRef.
- Q. Ma, A. M. Khan and Q. J. Wang, Tribol. Lett., 2020, 68, 1–10 CrossRef.
- Y. Gong, A. Morina, C. Wang, Y. Wang, Y. Tamura, A. Ishihara, A. Ghanbarzadeh and A. Neville, Tribol. Int., 2022, 176, 107888 CrossRef CAS.
- A. Akchurin and R. Bosman, Tribol. Lett., 2017, 65, 1–9 CrossRef CAS.
- R. Heuberger, A. Rossi and N. D. Spencer, Lubr. Sci., 2008, 20, 79–102 CrossRef CAS.
- A. L. Barnette, D. B. Asay, D. Kim, B. D. Guyer, H. Lim, M. J. Janik and S. H. Kim, Langmuir, 2009, 25, 13052–13061 CrossRef CAS PubMed.
- A. J. Barthel and S. H. Kim, Langmuir, 2014, 30, 6469–6478 CrossRef CAS PubMed.
- F. Agapito, P. M. Nunes, B. J. Costa Cabral, R. M. Borges dos Santos and J. A. Martinho Simoes, J. Org. Chem., 2008, 73, 6213–6223 CrossRef CAS PubMed.
- R. D. Bach and O. Dmitrenko, J. Am. Chem. Soc., 2004, 126, 4444–4452 CrossRef CAS PubMed.
- A. L. Ringer and D. H. Magers, J. Org. Chem., 2007, 72, 2533–2537 CrossRef CAS PubMed.
- A. Khajeh, X. He, J. Yeon, S. H. Kim and A. Martini, Langmuir, 2018, 34, 5971–5977 CrossRef CAS PubMed.
- C.-H. Lin, in Encyclopedia of Microfluidics and Nanofluidics, ed. D. Li, Springer US, Boston, MA, 2008, pp. 1584, DOI:10.1007/978-0-387-48998-8_1173.
- A. J. Barthel, J. Luo, K. S. Hwang, J.-Y. Lee and S. H. Kim, Wear, 2016, 350–351, 21–26 CrossRef CAS.
- Y.-S. Li, S. Jang, A. M. Khan, T. V. Martin, A. L. Ogrinc, Q. J. Wang, A. Martini, Y.-W. Chung and S. H. Kim, Tribol. Lett., 2023, 71, 57 CrossRef CAS.
- X. He, Z. Liu, L. B. Ripley, V. L. Swensen, I. J. Griffin-Wiesner, B. R. Gulner, G. R. McAndrews, R. J. Wieser, B. P. Borovsky and Q. J. Wang, Tribol. Int., 2021, 155, 106780 CrossRef CAS.
- J. E. Sader, J. W. Chon and P. Mulvaney, Rev. Sci. Instrum., 1999, 70, 3967–3969 CrossRef CAS.
- S. Plimpton, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS.
- A. Nakano, Comput. Phys. Commun., 2008, 178, 280–289 CrossRef CAS.
- G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985 CrossRef CAS.
- B. J. Berne, G. Ciccotti and D. F. Coker, Classical and Quantum Dynamics in Condensed Phase Simulations: Proceedings of the International School of Physics, World Scientific, 1998 Search PubMed.
- F. H. Bhuiyan, Y.-S. Li and S. Kim, Faraday Discuss., 2022, 241, 194–205 RSC.
- F. H. Bhuiyan, Y.-S. Li, S. H. Kim and A. Martini, Sci. Rep., 2024, 14, 2992 CrossRef CAS PubMed.
- E. Ogbomo, F. H. Bhuiyan, C. A. Latorre, A. Martini and J. P. Ewen, Phys. Chem. Chem. Phys., 2024, 26, 278–292 RSC.
- C. Ayestarán Latorre, J. E. Remias, J. D. Moore, H. A. Spikes, D. Dini and J. P. Ewen, Commun. Chem., 2021, 4, 178 CrossRef PubMed.
- X. Chen, K. Kawai, H. Zhang, K. Fukuzawa, N. Koga, S. Itoh and N. Azuma, J. Phys. Chem. C, 2020, 124, 22496–22505 CrossRef CAS.
- E. Maras, O. Trushin, A. Stukowski, T. Ala-Nissila and H. Jonsson, Comput. Phys. Commun., 2016, 205, 13–21 CrossRef CAS.
- O.-P. Koistinen, V. Ásgeirsson, A. Vehtari and H. Jónsson, J. Chem. Theory Comput., 2019, 15, 6738–6751 CrossRef CAS PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- A. Chipara, T. Tsafack, P. Owuor, J. Yeon, C. Junkermeier, A. van Duin, S. Bhowmick, S. Asif, S. Radhakrishnan and J. Park, Mater. Today Chem., 2018, 9, 149–157 CrossRef CAS.
- T. P. Senftle, S. Hong, M. M. Islam, S. B. Kylasa, Y. Zheng, Y. K. Shin, C. Junkermeier, R. Engel-Herbert, M. J. Janik and H. M. Aktulga, npj Comput. Mater., 2016, 2, 1–14 CrossRef.
- H. L. Adams, M. T. Garvey, U. S. Ramasamy, Z. Ye, A. Martini and W. T. Tysoe, J. Phys. Chem. C, 2015, 119, 7115–7123 CrossRef CAS.
- J. Ribas-Arino, M. Shiga and D. Marx, Angew. Chem., Int. Ed., 2009, 48, 4190–4193 CrossRef CAS PubMed.
- P. A. Redhead, Vacuum, 1962, 12, 203–211 CrossRef CAS.
- H. Adams, B. P. Miller, P. V. Kotvis, O. J. Furlong, A. Martini and W. T. Tysoe, Tribol. Lett., 2016, 62, 1–9 CrossRef CAS.
- K. L. Johnson, Contact Mechanics, Cambridge University Press, Cambridge, UK, 1985 Search PubMed.
- X. He and S. H. Kim, Langmuir, 2017, 33, 2717–2724 CrossRef CAS PubMed.
- J. Zhang, J. P. Ewen, M. Ueda, J. S. Wong and H. A. Spikes, ACS Appl. Mater. Interfaces, 2020, 12, 6662–6676 CrossRef CAS PubMed.
- E. V. Anslyn and D. A. Dougherty, Modern Physical Organic Chemistry, University science books, 2006 Search PubMed.
- A. Bhan, R. Gounder, J. Macht and E. Iglesia, J. Catal., 2008, 253, 221–224 CrossRef CAS.
- W. C. Conner Jr, J. Catal., 1982, 78, 238–246 CrossRef.
- R. Gupta, X.-X. Li, K.-B. Cho, M. Guo, Y.-M. Lee, Y. Wang, S. Fukuzumi and W. Nam, J. Phys. Chem. Lett., 2017, 8, 1557–1561 CrossRef CAS PubMed.
- P. Rydberg, R. Lonsdale, J. N. Harvey, A. J. Mulholland and L. Olsen, J. Mol. Graphics Modell., 2014, 52, 30–35 CrossRef CAS PubMed.
- R. Lonsdale, J. N. Harvey and A. J. Mulholland, J. Phys. Chem. Lett., 2010, 1, 3232–3237 CrossRef CAS.
- J.-W. Wu, M.-Y. Chen, S.-K. Hung and L.-C. Fu, in 2011 8th Asian Control Conference (ASCC), IEEE, 2011, pp. 1030–1035 Search PubMed.
- A. O. Balogun, O. A. Lasode, H. Li and A. G. McDonald, Waste Biomass Valorization, 2015, 6, 109–116 CrossRef.
- M. Mecozzi, M. Pietroletti, M. Scarpiniti, R. Acquistucci and M. E. Conti, Environ. Monit. Assess., 2012, 184, 6025–6036 CrossRef PubMed.
- Y.-T. Lin, H. He, H. Kaya, H. Liu, D. Ngo, N. J. Smith, J. Banerjee, A. Borhan and S. H. Kim, Anal. Chem., 2022, 94, 5231–5239 CrossRef CAS PubMed.
- M. C. Strus, A. Raman, C.-S. Han and C. Nguyen, Nanotechnology, 2005, 16, 2482 CrossRef CAS.
- A. San Paulo and R. García, Biophys. J., 2000, 78, 1599–1605 CrossRef CAS PubMed.
- D. P. Allison, N. P. Mortensen, C. J. Sullivan and M. J. Doktycz, Wiley Interdiscip. Rev.: Nanomed. Nanobiotechnol., 2010, 2, 618–634 Search PubMed.
- H. Wu, A. M. Khan, B. Johnson, K. Sasikumar, Y. W. Chung and Q. J. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 16139–16146 CrossRef CAS PubMed.
- P. Herrera-Fierro, B. A. Shogrin and W. R. Jones Jr, in Tribology Conference (No. NAS 1.15:107299), 1996 Search PubMed.
- C. R. Helms and E. H. Poindexter, Rep. Prog. Phys., 1994, 57, 791 CrossRef CAS.
- C. Campanale, I. Savino, I. Pojar, C. Massarelli and V. F. Uricchio, Sustainability, 2020, 12, 6755 CrossRef CAS.
- M. J. Marino, E. Hsiao, Y. Chen, O. L. Eryilmaz, A. Erdemir and S. H. Kim, Langmuir, 2011, 27, 12702–12708 CrossRef CAS PubMed.
- J. Eisinger and J. Law, J. Chem. Phys., 1959, 30, 410–412 CrossRef CAS.
- J. Law, J. Phys. Chem. Solids, 1958, 4, 91–100 CrossRef CAS.
- X. He, A. Pollock and S. H. Kim, Tribol. Lett., 2019, 67, 1–9 CrossRef CAS.
- J. Appeldoorn, I. Goldman and F. Tao, ASLE Trans., 1969, 12, 140–150 CrossRef CAS.
- P. Parsaeian, M. C. Van Eijk, I. Nedelcu, A. Neville and A. Morina, Tribol. Int., 2017, 107, 135–143 CrossRef CAS.
- P. Parsaeian, A. Ghanbarzadeh, M. Wilson, M. C. Van Eijk, I. Nedelcu, D. Dowson, A. Neville and A. Morina, Wear, 2016, 358, 23–31 CrossRef.
- H. Cen, A. Morina, A. Neville, R. Pasaribu and I. Nedelcu, Tribol. Int., 2012, 56, 47–57 CrossRef CAS.
- X. He, D. Ngo and S. H. Kim, Langmuir, 2019, 35, 15451–15458 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3mr00036b |
| This journal is © The Royal Society of Chemistry 2024 |