Tetrahedron clusters serving as a platform for foam-like structure design

Abstract

There are a number of exceptional examples indicating the unique position of tetrahedral symmetry in the vast landscape of different spatial organization pathways which can be sampled by matter. This work shows that the design and analysis of relatively simple tetrahedron clusters can lead to the formulation of a new type of dendritic structure together with unique periodic frameworks resembling clathrates and foams. A simple sequential protocol leading from regular tetrahedron clusters to more complex structural motifs can be employed to determine interesting repetitive building units. Accordingly, four different hierarchical superstructures are introduced, in which the dominant population of nodes is based on tetrahedral symmetry. The introduced architectures could be of particular interest for the field of regenerative medicine and metamaterial engineering.

---

Introduction

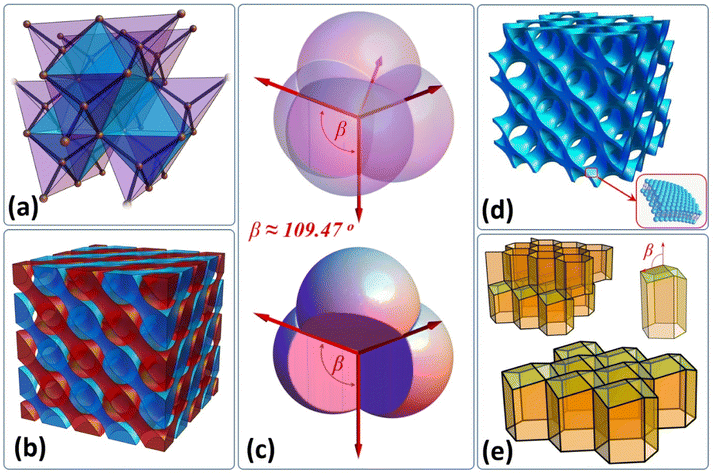
The regular tetrahedron is the simplest Platonic solid. By connecting the central point of this polyhedron with its four vertices a basic mesh element can be obtained, which is one of the most frequently observed and inherent structural motifs present in molecular and crystalline architectures. The beauty of equivalently positioned hydrogens around the central carbon within the methane molecule manifests the local space isotropy and directly displays the symmetry of sp³ orbitals. All inter-bond angles of this simple, organic molecule are the same and are known as tetrahedral angles. There are a number of fascinating examples where the tetrahedral angle remains an intrinsic feature of the system or emerges spontaneously due to interactions. Quite remarkably, the angle reappears in fundamental spin interactions i.e. the dipolar coupling between a pair of polarized spins (magnetic moments) vanishes when the inter-spin vector is tilted one half of the tetrahedral angle with respect to the polarization field direction. This specific condition is known as the magic angle¹ in the NMR field and the effect is directly related to the inherent symmetry of a magnetic field generated by an isolated magnetic moment.² An example from the atomic theory is also worth mentioning, where the electron density distribution in the case of the 3dz² orbital is described by second order spherical harmonics Y₂⁰(θ,φ), and hence the electron density disappears onto the conical surfaces with a solid tetrahedral angle. In crystallography, both commonly used materials i.e. crystalline silicone and the hardest allotrope of carbon display a diamond cubic structure (see Fig. 1(a)). Moreover, there is also a large family of zinc blende structures which adopt the same crystallographic order. Frozen water (for instance ice I_h and I_c) can also be tetrahedrally coordinated.³

Fig. 1 Several examples of tetrahedral symmetry naturally present on nanoscopic, mesoscopic and macroscopic scales: (a) crystal structure of diamond, (b) Double Diamond (DD) order of self-assembled copolymer domains, (c) cluster of four, equal sized soap bubbles, (d) DD ordered lipid structure discovered in cubosomes, (e) honeycomb structure.

However, the most intriguing are examples of tetrahedral symmetry spontaneously emerging in mesoscopic and macroscopic scales. One of them is the bicontinuous, double diamond (DD) phase (see Fig. 1(b)) which forms via thermodynamically driven microphase separation taking place in block copolymer systems.^4,5 Recently, Chang et al.⁶ reported that controlled annealing protocols enable sampling of metastable phases and observation of order–order transitions from double primitive to double diamond and then to double gyroid (DG) for simple diblock copolymers. Interestingly, both diamond and gyroid structures (see animation 1 and 2 in the ESI†) were also discovered in naturally developed scaffolds, first in the case of the exoskeleton of the Lamprocyphus augustus beetle⁷ and the second in the case of the Lycaenid butterfly's wing structure.⁸ The authors emphasize that besides their unique mechanical properties, they exhibit features typical of photonic crystals, which are responsible for the brilliant iridescence observed in these particular species. Following the idea of this natural assembly, Li et al.⁹ have demonstrated a method to fabricate a DD photonic crystal scaffold using a reverse core–shell microphase templating system, employing amphiphilic copolymers. Another example in which the tetrahedral symmetry emerges spontaneously concerns congruent spherical particles which self-assemble into colloidal nanocrystals¹⁰ accordingly gathering into either hexagonal close packing or face centered cubic phases. Wang et al.¹¹ demonstrated a method for growing DD colloidal photonic crystals from 400 nm diameter, DNA-grafted microspheres, reaching a lattice spacing comparable to that of visible light wavelengths. Moreover, Damasceno et al.¹² predicted that besides spheres there is a relatively large family of polyhedra which can also self-assemble into FCC (HCP) lattices and some of their results were already confirmed experimentally.^13,14 Interestingly, the DD structure was also discovered in lipid or polymer based bicontinuous networks (see. Fig. 1(d)) called cubosomes,^15,16 which provide two non-intersecting water-channels and which have been extensively investigated due to their potential medical applications. On macroscopic scales the tetrahedral angle naturally reappears in foam architecture,¹⁷ which satisfies Plateau's laws. Soap bubbles meet in fours at a vertex and the angle between interbubble boundaries equals ∼109.47°. Fig. 1(c) illustrates four equal sized bubbles joined into a cluster. A foam structure inspired Lord Kelvin to pose the following partition problem: how can space be divided into cells of equal volume with the least surface area between them. The structure was theoretically calculated by Denis Weaire and Robert Phelan¹⁸ and experimentally confirmed by Gabbrielli et al.¹⁹ The Weaire–Phelan structure consists of two kinds of cells, a pyritohedron (possessing tetrahedral symmetry) and truncated hexagonal trapezohedron. Finally, the most remarkable example of tetrahedral angle in nature is directly related to Apis honey bees and their natural ability to construct honeycomb cells satisfying minimalization of cell surface conditions (accordingly they minimize the amount of building material).²⁰ Each cell is closed at the bottom with three congruent rhombuses with tetrahedral acute angles (see Fig. 1(e)). All the abovementioned examples signify the unique position of tetrahedral symmetry in the vast landscape of different spatial organization pathways which can be sampled by matter. Therefore, it is not surprising that tetrahedron packing remains an actively studied problem among mathematicians, chemists and physicists alike.^21–23 The mystery of tetrahedron packing persists because the ultimate and the most efficient packing strategy of these solids remains unknown. The best packing fraction Φ ≈ 0.856 to date was reported by Chen et al.,²⁴ relying on Kallus–Elser–Gravel's²⁵ packing strategy. Haji-Akbari et al.,²⁶ employing thermodynamic computer simulations, have shown that regular tetrahedra can also pack in an unexpected way and form a dodecagonal quasicrystalline phase revealing very high Φ ≈ 0.8324. This result was the first example of a quasicrystal formed from non-spherical particles. There are also a number of computational^27–29 and experimental^30,31 works concerning random tetrahedron packing. Jin et al.³² examined disordered packings of tetrahedra and performed cluster analysis. They found out that two special types of clusters are dominant, i.e. dimer and 5-unit wagon wheels. Wang et al.³³ presented experimentally the remarkable structural diversity of gold nanotetrahedron assemblies by tailoring nanocrystal interactions. It is, however, difficult to find any reports concerning larger tetrahedron cluster designs and their analysis, except the work of Nagaoka et al.,³⁴ who reported on superstructures generated experimentally from tetrahedral quantum dots. Below, we show that relatively simple tetrahedron clusters have the potential to become an interesting platform to formulate a new class of dendritic structures together with interesting scaffolds (frameworks), which could be implemented in both metamaterial design and construction engineering.

Results and discussion

Construction of clusters

The tetrahedron clusters are designed using a relatively simple strategy, which has been introduced earlier.³⁵ The method relies on sequential decoration of a central tetrahedron with additional layers, which produce subsequent G_i generations, where i can grow from 1 to an arbitrarily specified N. There are only two conditions which have to be satisfied when constructing the cluster: (a) cluster G_i is decorated via a face–face joint step (i.e. two adjacent tetrahedra always share one common face), (b) the cluster must retain tetrahedral symmetry. A detailed description of the protocol can be found in the ESI (Fig. S1 to S7†). As shown in Fig. 2(a) this simple algorithm can produce very interesting objects: green represents G₄ and blue G₅ generation respectively (see animation 3 in the ESI†). The first consists of 77 tetrahedra, while the second consists of 125 tetrahedra. It has been shown³⁵ that some of these clusters can be used to design more complex superstructures.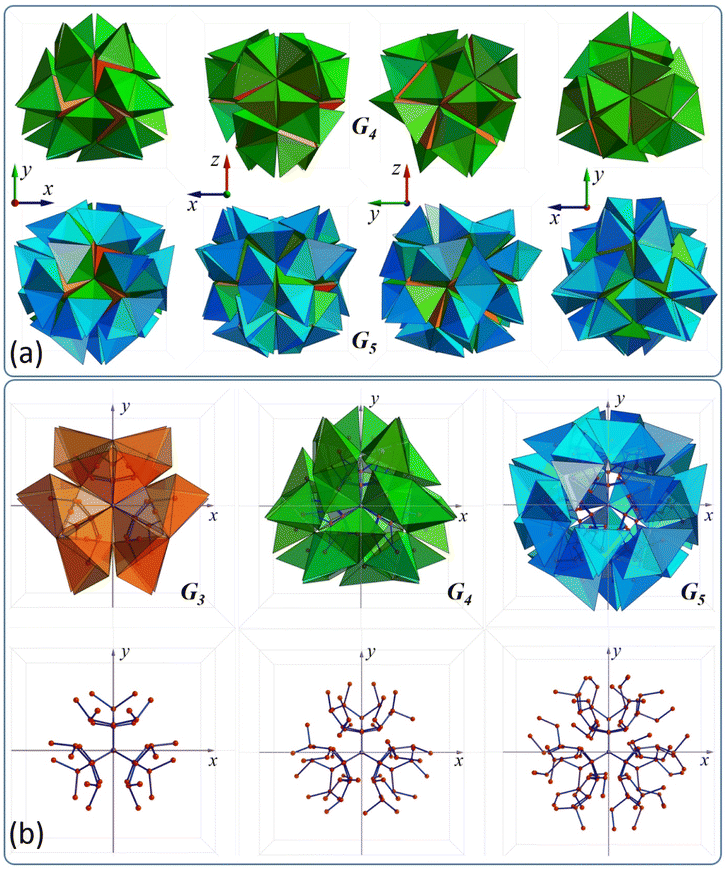

Fig. 2 (a) Two different tetrahedron clusters G₄ and G₅ viewed from four different angles, (b) G₃, G₄, and G₅ clusters and their corresponding dendrimers.

Construction of dendrimers

The obtained clusters can be employed as platforms to formulate perfectly tetrahedral dendrimers, which are illustrated in Fig. 2(b) for three different generations (see also animation 4a in the ESI†). The produced dendrimers reveal tetrahedral symmetry and, more importantly, every single inter-bond angle within the structure is also a tetrahedral angle. In general, one can construct an infinitely large dendritic network of this kind (with N → ∞) having only one unique central point. It is also worth adding that all bonds (internode distances) of these structures have the same length. In order to construct these objects, a very straightforward protocol has to be implemented (see Fig. S8 to S11 in the ESI†). Initially, all central points (centres of gravity) of individual tetrahedra have to be specified and, subsequently, the connections are constituted only between those tetrahedra which share one common face. The obtained network to some extent resembles the spatial distribution of Voronoi seeds determined for a specific cluster. In other words, all faces which are shared by two adjacent tetrahedra would be a part of the Voronoi diagram³⁶ determined for this particular network of seeds (generators). Interestingly, the formulated dendritic structures can become a structural platform to design foam-like architectures. This idea is illustrated in Fig. 3(a)–(c). First, we stretch membranes onto a dendritic scaffold, obtaining a lattice of interconnected pentagonal polygons (see Fig. 3(d)). At this stage, the structure provides several open, foam-like pockets (see animation 4b in the ESI†). Subsequently, we artificially close these pockets with additional pentagonal membranes, thus forming closed cells (see Fig. 3(e) and S13 in the ESI†), which resemble pentagonal dodecahedra. Accordingly, we can specify three types of clusters α, β, and γ. Since all the inter-membrane angles within the structure are either exactly equal or close to 120°, the presented clusters of cells satisfy Plateau's law and hence it is expected that very similar formations can locally develop in actual foams.^17,37 It is worth emphasizing that this work limits the analysis only to relatively primitive networks based on G₅ clusters and we are aware that further studies are required to discover and examine more interesting and complex foam-like structures determined for larger N.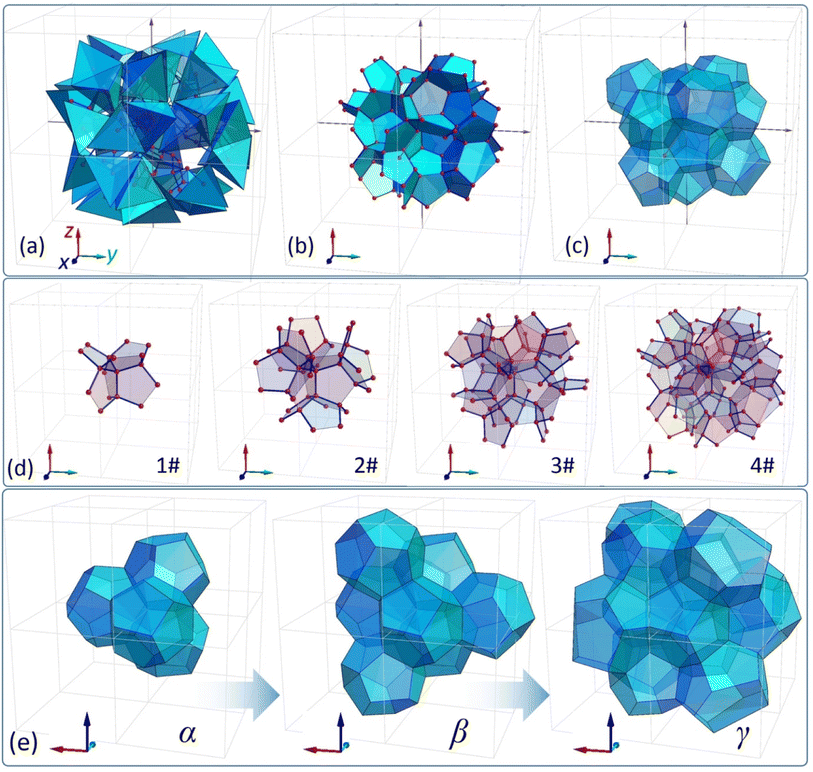

Fig. 3 (a)–(c) illustrate the sequence of foam-like unit formation, (d) shows membranes stretched onto a dendritic scaffold, and (e) illustrates foam-like unit cells.

Construction of new frameworks

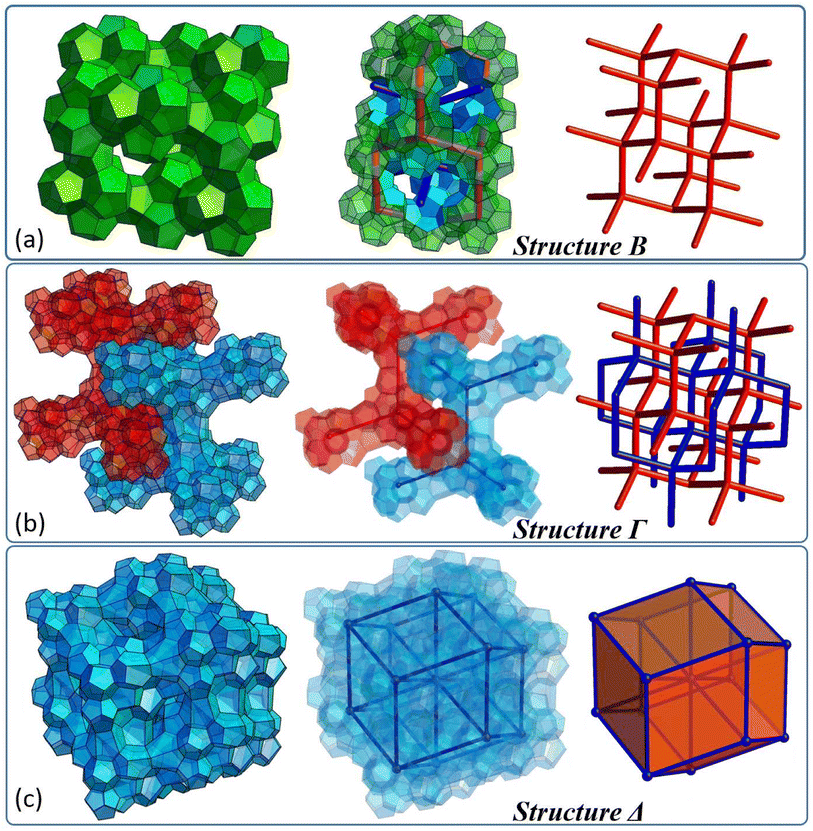
Below, we would like to introduce and discuss four different types of structures, which are originally based on specific tetrahedron clusters and their complementary dendritic networks. The first structure (called here structure A) is illustrated in Fig. 4(d) and one can design it relying on G₂ clusters assembled into a diamond like superstructure (Fig. 4(b)), which has already been introduced elsewhere.³⁵Fig. 4 sequentially depicts how the corresponding dendritic scaffold becomes a platform to formulate more complex, foam-like architecture consisting of two types of solids, one resembling a pentagonal dodecahedron with 12 pentagonal faces (small cage 5¹²-purple) and the second resembling a hexakaidecahedron with 12 pentagonal and four hexagonal faces (large cage 5¹²6⁴-blue).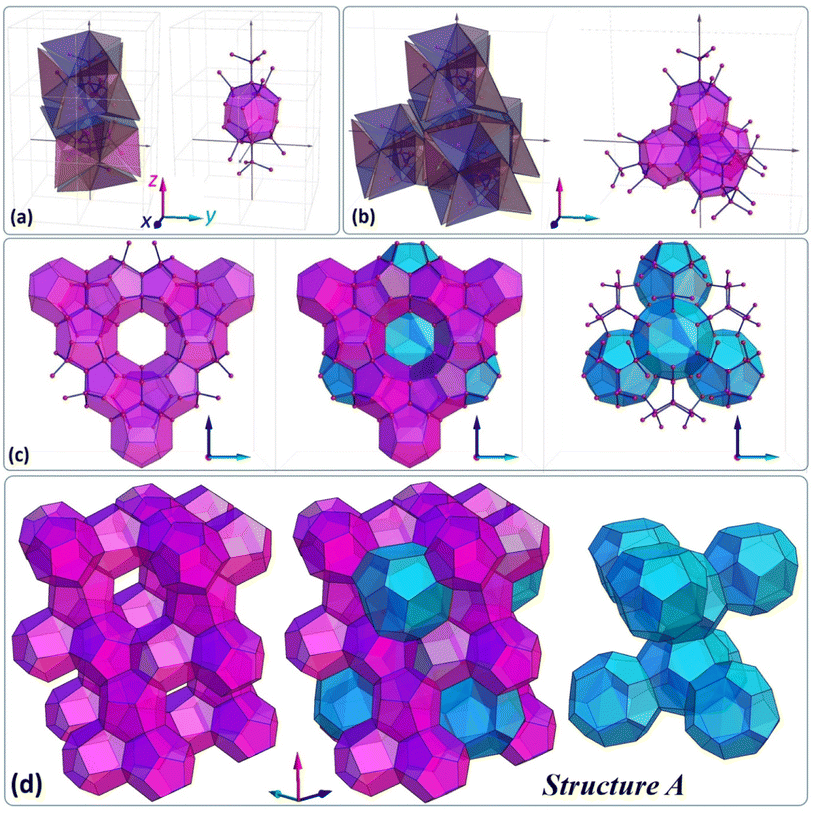

Fig. 4 (a) Pair of G₂ clusters and corresponding dendrimers, which define the 5¹² cage, (b) five G₂ clusters forming a larger superstructure and corresponding dendritic network, (c) and (d) the foam-like structure A based on a dendritic network, which resembles the sII structure typical of hydrates (see also Fig. S14 in the ESI†).

Fig. 5 illustrates three additional structures, which can be originally designed relying on tetrahedron clusters. Their unique architecture, which locally resembles the structure of foam, can be particularly interesting in the field of regenerative medicine and metamaterials design. Structure B displays chains of 5¹²-like solids which are specifically assembled onto a diamond lattice (see also animations 5a/5b and Fig. S15–17 in the ESI†). Accordingly, a continuous void is left around it, which also exhibits diamond symmetry. The architecture is based on clusters α, shown in Fig. 3(e), which sit in each node of the diamond lattice and which are interconnected via an additional pentagonal polyhedron. Structure Γ displays the same superstructure geometry and may be designed as a single diamond or double diamond. Fig. 5(b) depicts a DD form (see also animation 6 and Fig. S18–23 in the ESI†), which does not tile the space and leaves voids between two diamond superstructures (red and blue). Both forms are designed relying on γ clusters introduced in Fig. 3(e). There is a special connection (linker) introduced between each pair of γ clusters consisting of three solids resembling an irregular dodecahedron (Fig. S18†). Structure Δ in fact represents the third variant of Γ, and differs solely in terms of the coordination number characteristic of each nodal point. In the case of Δ, each γ cluster is directly connected with its 8 closest neighbours. Linker geometry remains the same as in Γ. Accordingly, the superstructure of Δ resembles a rhombic dodecahedron, which is a tessellating space convex polyhedron. As shown in Fig. 5(c), the structure does not tile the space and there is, interestingly, a continuous void network present in this framework (see Fig. S24 and 25 in the ESI†). The presented superstructure has 12 interconnected chambers which are visualised in animation 7 available in the ESI.†

Fig. 5 Three different, periodic superstructures based on tetrahedron clusters. (a) Structure B following a diamond lattice, (b) structure Γ following a DD lattice, (c) structure Δ following the lattice based on a space-filling rhombic dodecahedron.

Confrontation with structures reported by other authors

Interestingly, very similar structures to the ones introduced above have been reported for gas hydrates,^38,39 silica clathrates^39–41 and carbon clathrates.⁴² Gas hydrates are solid compounds naturally present on Earth and other celestial bodies (planets, moons and comets), which can be formed under specific conditions within gas/water mixtures. They consist of a hydrogen-bonded water framework (host molecules) providing cavities for guest molecules which also stabilize the framework. Importantly, various types of guest molecules can be accommodated and stored in the structure, for instance hydrogen, nitrogen, CO₂ or methane. Therefore, gas-hydrate-based-technologies are attracting ongoing attention due to their potential application in CO₂ capture, gas separation, water desalination and energy storage. Moreover, the enormous mass of gases naturally stored in hydrates (vast reserves of methane hydrates mostly accumulated in submarine continental margins) on our planet constitutes a large portion of energy resources and hence methods for safe extraction are going to be identified and implemented. Natural hydrates are classified into three structural types: (a) structure sI including two types of cage units i.e. (5¹²) and (5¹²6²), (b) structure sII including two types of cage units i.e. (5¹²) and (5¹²6⁴), and structure (c) including three types of cage units i.e. (5¹²), (5¹²6⁸) and (4³5⁶6³).³⁸ Interestingly, clathrate hydrates form nonstoichiometric compounds and there is large population of empty cages present in the system. Falenty et al.⁴³ confirmed experimentally that the sII structure can stand as an empty hydrate lattice even without the presence of stabilizing guest molecules and thus they formally established the seventeenth crystalline ice phase, which corresponds directly to structure A presented here. It appears to be the least dense of all known crystalline water phases. The authors showed that the initially present neon guest molecules can be pumped out from the framework cages (they can migrate through six-membered rings of water) leaving behind a metastable water network. In terms of architecture, one analogue to clathrate hydrates is silica clathrates, which possess a pure silica framework. Among these zeolite-like materials three specific topologies can be found, which directly correspond to the frameworks found in hydrates i.e. (a) MEP, which is isotypic with the cubic sI, (b) DOH, which is identical to sH topology and (c) MTN, which coincides with sII hydrate topology.⁴⁰ Momma et al.⁴⁴ reported the discovery of two new silica clathrate minerals that are isostructural with sII and sH. They were formed in marine sediments at temperatures above the stability fields of gas hydrates and they store hydrocarbons. One of them is chibaite,⁴⁵ a mineral analogous to the synthetic MTN silica,⁴⁶ which corresponds directly to structure A (Fig. 4). Inspired by clathrate hydrates, Zhu et al.⁴² postulated new carbon allotropes based on sI, sII and sH structures and performed ab initio calculations in order to examine their potential mechanical and electronic properties. The authors found that all of these allotropes would be thermodynamically stable and exhibit remarkable mechanical characteristics, indicating that they could potentially become lightweight 3D structures for important engineering applications. Carbon framework sII, which corresponds directly to structure A, exhibits higher ideal tensile strength (defined by the upper limit of material tensile strength) in the <111> loading direction than diamond, despite its lower mass density.

Although the hydrate structures are well defined, an accurate description of nucleation and growth mechanisms leading to the formation of these unique arrangements remains unclear. The major difficulty in achieving a complete description of the molecular events leading to the crystallization of a hydrate structure from a disordered state has been that of overcoming the metastability occurring during molecular simulations.⁴⁷ Among several nucleation and growth mechanisms proposed,³⁸ the labile-cluster hypothesis (LCH)⁴⁸ is particularly interesting with regard to the design protocol employed here. According to the LCH, hydrate nucleation is initiated by an agglomeration of unstable entities featuring a guest molecule surrounded by water molecules. These entities diffuse and form larger, more stable clusters, which may become a platform to initiate further growth of the crystal. Intriguingly, the sequential pattern illustrated in Fig. 4 corresponds to some extent to the LCH mechanism. The 5¹² cage illustrated in Fig. 4(a) can be treated as an unstable cluster of water molecules coordinated around a guest molecule, whereas the structure shown in Fig. 4(b) represents a more stable cluster, which could possibly initiate further growth. It is worth emphasizing that structure A was designed solely relying on specific tetrahedron cluster assembly (thus representing a colloidal crystal growth approach), and this approach independently led to the structure resembling sII (MTN) architecture. It is also worth mentioning that structure B, illustrated in Fig. 5(a), to some extent resembles clathrate-IX,^41,49 which consists solely of 5¹²-like solids. The latter consists of pentagonal polyhedra gathered into helical chains, which do not tile the space, and leave large void channels in between.

The frameworks introduced here could be treated as an extracellular matrix for three dimensional cellular colony growth or as a scaffold for ultralight and mechanically robust materials. It has been shown that cellular packing organization regulates communication and growth, and determines the mechanical properties of the tissue.⁵⁰ Hayashi et al.⁵¹ reported that the assembly pattern observed in the spatial arrangement of cells during the development of the retina can be driven by surface tension minimization. In other words, the tissue architecture can partially follow the packing strategy, which is characteristic of foams. On the other hand, Alsous et al.⁵² analysed geometrically frustrated cell assemblies (egg chamber) and suggested that topological constraints can control cell positioning during early oogenesis and embryogenesis. Therefore, the geometry of an extracellular matrix can have a significant impact on cells' spatial packing and their eventual properties and functions. It is important to emphasize that all of the architectures presented in Fig. 5 are fully periodic and the repetitive structural motifs can be arbitrarily scaled and thus it is possible to manufacture arbitrarily shaped objects displaying a precisely defined microstructure. This feature makes them particularly interesting in the field of high-performance ultra-lightweight materials based on well-defined scaffold or cellular architectures, which are referred to as metamaterials.^53–55 It has been shown that properly designed truss architecture can reveal remarkably high mechanical strength despite the low density of the overall material, which can be treated as a porous substance. In other words, it is the microstructural geometry, rather than the material composition, which determines the unusual properties of metamaterials. A number of different geometries have been examined, including stochastic and periodic structures both closed and open cellular,^56–58 some of them inspired by architectures developed by living organisms, for instance triply periodic minimal surfaces such as gyroids.^59,60 Metamaterials are continuously treated as an emerging technology which is strongly coupled to rapid developments observed in 3D printing. Therefore, there is an ongoing effort to design and examine novel truss topologies displaying desired properties. It is worth mentioning that the frameworks introduced here belong to hierarchical metamaterials⁶¹ in which the dominant population of nodes is based on tetrahedral symmetry. Importantly, the exact same symmetry refers to the superstructure, too. This structural feature guarantees uniform stress distribution on both levels i.e. microstructural and superstructural.

Conclusions

It has been shown that tetrahedron clusters are interesting and intriguing objects which can be treated as an initial platform for identification of more complex architectures. Among these architectures are (a) a new class of dendritic structures and (b) periodic foam-like frameworks. The simple algorithm employed here leads to remarkable dendritic objects, which alone would require separate and thorough studies. This work limits its analysis solely to the trivial G₅ generation and hence there are a number of additional questions to address, for instance (i) what is the structural evolution of these dendritic objects for larger N? and (ii) is there any repetitive structural motive observed for larger N? Finally, the work reveals that the mentioned dendrites can be treated as scaffolds to design unique frameworks consisting solely of pentagonal membranes. These structures could become particularly useful in metamaterial engineering or regenerative medicine. Again, a question remains concerning frameworks determined for larger N. In general, the protocol introduced here allows construction of open cell frameworks for arbitrarily large N, the most intriguing of which would be the one in which N goes to infinity, thus forming a continuous foam-like framework.

Data availability

The datasets generated and/or analysed during the current study are available from the corresponding author on reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This work was supported by the National Centre for Research and Development under grant NanoHEART DWM/WPC2/285/2020.

References

1. E. R. Andrew, A. Bradbury and R. G. Eades, Nuclear Magnetic Resonance Spectra from a Crystal rotated at High Speed, Nature, 1958, 182, 1659.
2. J. Jenczyk, Effective nuclear magnetic field under Zeeman splitting conditions, J. Magn. Magn. Mater., 2020, 505, 166735.
3. C. G. Salzmann and B. J. Murray, Ice goes fully cubic, Nat. Mater., 2020, 19, 586–587.
4. A. Reddy, X. Feng, E. L. Thomas and G. M. Grason, Block Copolymers beneath the Surface: Measuring and Modeling Complex Morphology at the Subdomain Scale, Macromolecules, 2021, 54, 9223–9257.
5. Q. Sheng, H. Chen, W. Mao, C. Cui, S. Che and L. Han, Self-Assembly of Single-Diamond-Surface Networks, Angew. Chem., Int. Ed., 2021, 60, 15236–15242.
6. C.-Y. Chang, G.-M. Manesi, C.-Y. Yang, Y.-C. Hung, K.-C. Yang, P.-T. Chiu, A. Avgeropoulos and R.-M. Ho, Mesoscale networks and corresponding transitions from self-assembly of block copolymers, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2022275118.
7. J. W. Galusha, L. R. Richey, J. S. Gardner, J. N. Cha and M. H. Bartl, Discovery of a diamond-based photonic crystal structure in beetle scales, Phys. Rev. E, 2008, 77, 050904.
8. R. W. Corkery and E. C. Tyrode, On the colour of wing scales in butterflies: iridescence and preferred orientation of single gyroid photonic crystals, Interface focus, 2017, 7, 20160154.
9. H. Li, Y. Liu, X. Cao, L. Han, C. Jiang and S. Che, A Shifted Double-Diamond Titania Scaffold, Angew. Chem., 2017, 56 3, 806–811.
10. M. A. Boles, M. Engel and D. V. Talapin, Self-Assembly of Colloidal Nanocrystals: From Intricate Structures to Functional Materials, Chem. Rev., 2016, 116, 11220–11289.
11. Y. Wang, I. C. Jenkins, J. T. McGinley, T. Sinno and J. C. Crocker, Colloidal crystals with diamond symmetry at optical lengthscales, Nat. Commun., 2017, 8, 14173.
12. P. F. Damasceno, M. Engel and S. C. Glotzer, Predictive Self-Assembly of Polyhedra into Complex Structures, Science, 2012, 337, 453–457.
13. J. Gong, R. S. Newman, M. Engel, M. Zhao, F. Bian, S. C. Glotzer and Z. Tang, Shape-dependent ordering of gold nanocrystals into large-scale superlattices, Nat. Commun., 2017, 8, 14038.
14. C. Avci, I. Imaz, A. Carné-Sánchez, J. A. Pariente, N. Tasios, J. Pérez-Carvajal, M. I. Alonso, A. Blanco, M. Dijkstra, C. López and D. Maspoch, Self-assembly of polyhedral metal–organic framework particles into three-dimensional ordered superstructures, Nat. Chem., 2018, 10, 78–84.
15. Y. La, J. Song, M. G. Jeong, A. Cho, S.-M. Jin, E. Lee and K. T. Kim, Templated synthesis of cubic crystalline single networks having large open-space lattices by polymer cubosomes, Nat. Commun., 2018, 9, 5327.
16. J. Jagielski, Ł. Przysiecka, D. Flak, M. Diak, Z. Pietralik-Molińska, M. Kozak, S. Jurga and G. Nowaczyk, Comprehensive and comparative studies on nanocytotoxicity of glyceryl monooleate- and phytantriol-based lipid liquid crystalline nanoparticles, J. Nanobiotechnol., 2021, 19, 168.
17. W. Drenckhan and S. Hutzler, Structure and energy of liquid foams, Adv. Colloid Interface Sci., 2015, 224, 1–16.
18. D. Weaire and R. Phelan, A counter-example to Kelvin's conjecture on minimal surfaces, Philos. Mag. Lett., 1994, 69, 107–110.
19. R. Gabbrielli, A. J. Meagher, D. Weaire, K. A. Brakke and S. Hutzler, An experimental realization of the Weaire–Phelan structure in monodisperse liquid foam, Philos. Mag. Lett., 2012, 92, 1–6.
20. S. Yang, X. Gong, D. Zhou, X. Zhang, H. Kuang and K. Dong, Structure of Fejes Tóth cells in natural honey bee combs, Apidologie, 2022, 53, 6.
21. J. Lagarias and C. Zong, Mysteries in packing regular tetrahedra, Not. Am. Math. Soc., 2012, 59, 1540–1549.
22. J. H. Conway and S. Torquato, Packing, tiling, and covering with tetrahedra, Proc. Natl. Acad. Sci. U. S. A., 2006, 103, 10612–10617.
23. S. Torquato and Y. Jiao, Dense packings of the Platonic and Archimedean solids, Nature, 2009, 460, 876–879.
24. E. R. Chen, M. Engel and S. C. Glotzer, Dense Crystalline Dimer Packings of Regular Tetrahedra, Discrete Comput. Geom., 2010, 44, 253–280.
25. Y. Kallus, V. Elser and S. Gravel, Dense Periodic Packings of Tetrahedra with Small Repeating Units, Discrete Comput. Geom., 2010, 44, 245–252.
26. A. Haji-Akbari, M. Engel, A. S. Keys, X. Zheng, R. G. Petschek, P. Palffy-Muhoray and S. C. Glotzer, Disordered, quasicrystalline and crystalline phases of densely packed tetrahedra, Nature, 2009, 462, 773–777.
27. S. Zhao, X. Zhou, W. Liu and C. Lai, Random packing of tetrahedral particles using the polyhedral discrete element method, Particuology, 2015, 23, 109–117.
28. S. Li, P. Lu, W. Jin and L. Meng, Quasi-random packing of tetrahedra, Soft Matter, 2013, 9, 9298–9302.
29. B. Zhao, X. An, Y. Wang, Q. Qian, X. Yang and X. Sun, DEM dynamic simulation of tetrahedral particle packing under 3D mechanical vibration, Powder Technol., 2017, 317, 171–180.
30. A. Jaoshvili, A. Esakia, M. Porrati and P. M. Chaikin, Experiments on the Random Packing of Tetrahedral Dice, Phys. Rev. Lett., 2010, 104, 185501.
31. J. Baker and A. Kudrolli, Maximum and minimum stable random packings of Platonic solids, Phys. Rev. E, 2010, 82, 061304.
32. W. Jin, P. Lu, L. Liu and S. Li, Cluster and constraint analysis in tetrahedron packings, Phys. Rev. E, 2015, 91, 042203.
33. Y. Wang, J. Chen, Y. Zhong, S. Jeong, R. Li and X. Ye, Structural Diversity in Dimension-Controlled Assemblies of Tetrahedral Gold Nanocrystals, J. Am. Chem. Soc., 2022, 144, 13538–13546.
34. Y. Nagaoka, R. Tan, R. Li, H. Zhu, D. Eggert, Y. A. Wu, Y. Liu, Z. Wang and O. Chen, Superstructures generated from truncated tetrahedral quantum dots, Nature, 2018, 561, 378–382.
35. J. Jenczyk, Densely packed tetrahedra clusters displaying diamond-like superstructures, Particuology, 2021, 58, 147–152.
36. G. Angelucci and F. Mollaioli, Voronoi-Like Grid Systems for Tall Buildings, Front. Built Environ., 2018, 4, 78.
37. S. Andrieux, A. Quell, C. Stubenrauch and W. Drenckhan, Liquid foam templating – A route to tailor-made polymer foams, Adv. Colloid Interface Sci., 2018, 256, 276–290.
38. A. Hassanpouryouzband, E. Joonaki, M. Vasheghani Farahani, S. Takeya, C. Ruppel, J. Yang, N. J. English, J. M. Schicks, K. Edlmann, H. Mehrabian, Z. M. Aman and B. Tohidi, Gas hydrates in sustainable chemistry, Chem. Soc. Rev., 2020, 49, 5225–5309.
39. G. Tabacchi, Supramolecular Organization in Confined Nanospaces, ChemPhysChem, 2018, 19, 1249–1297.
40. K. Momma, Clathrate compounds of silica, J. Phys.: Condens. Matter, 2014, 26, 103203.
41. J.-A. Dolyniuk, B. Owens-Baird, J. Wang, J. V. Zaikina and K. Kovnir, Clathrate thermoelectrics, Mater. Sci. Eng. R Rep., 2016, 108, 1–46.
42. J. Zhu, K. Xu, Z. Zhang, X. Cao, S. Huang and J. Wu, Carbon clathrates as strong lightweight structures, Int. J. Mech. Sci., 2021, 202–203, 106509.
43. A. Falenty, T. C. Hansen and W. F. Kuhs, Formation and properties of ice XVI obtained by emptying a type sII clathrate hydrate, Nature, 2014, 516, 231–233.
44. K. Momma, T. Ikeda, K. Nishikubo, N. Takahashi, C. Honma, M. Takada, Y. Furukawa, T. Nagase and Y. Kudoh, New silica clathrate minerals that are isostructural with natural gas hydrates, Nat. Commun., 2011, 2, 196.
45. A. Y. Likhacheva, S. V. Goryainov, Y. V. Seryotkin, K. D. Litasov and K. Momma, Raman spectroscopy of chibaite, natural MTN silica clathrate, at high pressure up to 8 GPa, Microporous Mesoporous Mater., 2016, 224, 100–106.
46. J. Dong, X. Tong, J. Yu, H. Xu, L. Liu and J. Li, Synthesis of large single crystals of a clathrate compound MTN (a zeolite-like material) by the vapor-phase method, Mater. Lett., 2008, 62, 4–6.
47. A. K. Sum, D. T. Wu and K. Yasuoka, Energy science of clathrate hydrates: Simulation-based advances, MRS Bull., 2011, 36, 205–210.
48. E. D. Sloan Jr and F. Fleyfel, A molecular mechanism for gas hydrate nucleation from ice, AIChE J., 1991, 37, 1281–1292.
49. A. V. Shevelkov and K. Kovnir, Zintl Clathrates, in Zintl Phases: Principles and Recent Developments, ed. T. F. Fässler, Springer Berlin Heidelberg, Berlin, Heidelberg, 2011, pp. 97–142.
50. P. Gómez-Gálvez, S. Anbari, L. M. Escudero and J. Buceta, Mechanics and self-organization in tissue development, Semin. Cell Dev. Biol., 2021, 120, 147–159.
51. T. Hayashi and R. W. Carthew, Surface mechanics mediate pattern formation in the developing retina, Nature, 2004, 431, 647–652.
52. J. Imran Alsous, P. Villoutreix, N. Stoop, S. Y. Shvartsman and J. Dunkel, Entropic effects in cell lineage tree packings, Nat. Phys., 2018, 14, 1016–1021.
53. X. Yu, J. Zhou, H. Liang, Z. Jiang and L. Wu, Mechanical metamaterials associated with stiffness, rigidity and compressibility: A brief review, Prog. Mater. Sci., 2018, 94, 114–173.
54. A. J. D. Shaikeea, H. Cui, M. O'Masta, X. R. Zheng and V. S. Deshpande, The toughness of mechanical metamaterials, Nat. Mater., 2022, 21, 297–304.
55. S. J. Yeo, M. J. Oh and P. J. Yoo, Structurally Controlled Cellular Architectures for High-Performance Ultra-Lightweight Materials, Adv. Mater., 2019, 31, 1803670.
56. J. B. Berger, H. N. G. Wadley and R. M. McMeeking, Mechanical metamaterials at the theoretical limit of isotropic elastic stiffness, Nature, 2017, 543, 533–537.
57. J. Bauer, J. A. Kraus, C. Crook, J. J. Rimoli and L. Valdevit, Tensegrity Metamaterials: Toward Failure-Resistant Engineering Systems through Delocalized Deformation, Adv. Mater., 2021, 33, 2005647.
58. J. J. Andrew, P. Verma and S. Kumar, Impact behavior of nanoengineered, 3D printed plate-lattices, Mater. Des., 2021, 202, 109516.
59. Z. Gan, D. Turner Mark and M. Gu, Biomimetic gyroid nanostructures exceeding their natural origins, Sci. Adv., 2016, 2, e1600084.
60. E. Yang, M. Leary, B. Lozanovski, D. Downing, M. Mazur, A. Sarker, A. Khorasani, A. Jones, T. Maconachie, S. Bateman, M. Easton, M. Qian, P. Choong and M. Brandt, Effect of geometry on the mechanical properties of Ti-6Al-4V Gyroid structures fabricated via SLM: A numerical study, Mater. Des., 2019, 184, 108165.
61. X. Zheng, W. Smith, J. Jackson, B. Moran, H. Cui, D. Chen, J. Ye, N. Fang, N. Rodriguez, T. Weisgraber and C. M. Spadaccini, Multiscale metallic metamaterials, Nat. Mater., 2016, 15, 1100–1106.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00470h

---