 Open Access Article
Open Access ArticleOverview of solar thermal applications of heat exchangers with thermophysical features of hybrid nanomaterials
Muhammad Naveed
Khan
a,
F. M.
Aldosari
b,
Zhentao
Wang
*a,
Muhammad
Yasir
 c,
Mohammad
Afikuzzaman
d and
Ibrahim E.
Elseesy
e
c,
Mohammad
Afikuzzaman
d and
Ibrahim E.
Elseesy
e
aSchool of Energy and Power Engineering, Jiangsu University, PO Box 28, Zhenjiang, Jiangsu 212013, China. E-mail: zhentao.wang@ujs.edu.cn
bDepartment of Physics, College of Science and Humanities, Prince Sattam bin Abdulaziz University, Al-Kharj, Saudi Arabia
cDepartment of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
dUniSA STEM, University of South Australia, Adelaide, SA 5000, Australia
eMechanical Engineering Department, College of Engineering, King Khalid University, Abha, 61421, Saudi Arabia
First published on 29th November 2023
Abstract
With their notable thermal characteristics, fluids incorporating nanoparticles have significant importance in industrial processes. Due to the higher proficiency of hybrid nanofluid, this study is organized to observe the flow phenomenon and thermal characteristics of kerosene-oil-based hybrid ferrofluid in relation to the modified versions of two imperative Yamada–Ota and Xue models. A performance-based comparison is conducted for an incompressible hybrid ferrofluid in relation to the upgraded Yamada–Ota and Xue models. The magnetized flow mechanism in two dimensions is explored over a stretchable, curved sheet. With the ordinary kerosene oil liquid, the ferroparticles, namely cobalt ferrite and magnetite, are merged to form (CoFe2O4–Fe3O4/kerosene oil) hybrid ferrofluid. Mass and heat transport mechanisms are scrutinized with the execution of activation energy, convective constraints, Joule heating, exponential heat sources, and thermal radiation. Suitable ansatzes are utilized to achieve the dimensionless pattern of the equations that regulate the problem. To numerically explore the dimensionless equations, a powerful bvp4c strategy is implemented. On behalf of both considered models, the characteristics of hybrid ferrofluid relative to pertinent parameters are graphically investigated and comparatively analyzed. This study ensures that the improved Yamada–Ota model yields more proficient outcomes in comparison to the Xue model. Moreover, the concentration field demonstrates an escalating trend with the enhanced activation energy parameter.
1. Introduction
With the greatest accomplishment of nanofluids in multifarious disciplines, the focus on the study of nanofluids has been enhanced. Nanofluid originated by introducing a nanoparticle of nanometer size into a regular fluid. As an ordinary fluid has a low capability to conduct heat, the addition of nanoparticles uplifts the thermal features of classical fluids. Initially, nanofluid was developed through the concept of Choi.1 To excessively elevate the base fluid's thermal attributes, two nanoparticles are included in a carrier fluid, termed a hybrid nanofluid. As compared to nanofluids, the category of hybrid nanofluids is more effective with their excessive abilities to improve the rate of heat transport in classical fluids. Illustrations of such fluids include nanotechnology, heat exchangers, nuclear systems, solar energy, manufacturing processes, and biomedical engineering.2 Numerous researchers investigate the thermal features of classical fluids corresponding to the inclusion of nanoparticles. Sreedevi et al.3 carried out an unsteady investigation of a magnetized hybrid nanofluid corresponding to physical constraints. The immersion of distinct nanoparticles into the two-dimensional flow phenomenon of a regular liquid through a stretchable curved medium was deliberated by Madhukesh et al.4 The radiative magnetized flow mechanism affected by slip conditions in a non-Newtonian fluid with the participation of a hybrid nanofluid was inspected by Qureshi.5 An exploration of the physical impacts on the thermal analysis of liquid-carrying nanoparticles was carried out by Santhi et al.6 The consequences of various physical characteristics on the steady flow phenomenon generated by a porous exponential medium in a hybrid nanofluid were investigated by Neethu et al.7 The thermal characteristics of a magnetized hybrid nanofluid flow phenomenon based on Yamada–Ota and Xue models were explored by Ishtiaq et al.8 They compared the various properties of the considered fluid corresponding to the two distinct models. The study of a hybrid nanofluid subjected to a time-dependent three-dimensional flow mechanism produced by a stretched medium was deliberated by Mohana and Kumar.9 Nadeem et al.10 discussed the thermal features of a non-Newtonian fluid with the contribution of nanoparticles in a steady flow mechanism.The movement of electrically conducting fluids with the significance of the magnetic field has been widely studied by numerous researchers. The field of magnetohydrodynamics (MHD) has a diverse range of applications, including Teltron tubes, transformers, metal working procedures, Helmholtz coils, electric motors, and magnetic levitation. Khader and Babatin11 conducted an examination of the mechanism of heat transport and steady flow characteristics in an Eyring–Powell fluid under the influence of a magnetic field. A scrutinization of the magnetized flow properties dependent on a two-phase model in a Casson nanofluid was revealed by Ishtiaq and Nadeem.12 Seid et al.13 assumed a stretchable medium to examine the flow phenomenon influenced by magnetic and various physical properties in an electrically conductive fluid. With the significance of the variable magnetic field, the properties of the micropolar fluid on distinct mediums were explored by Nadeem et al.14 Through a stretched, slender medium, the thermal analysis and flow mechanism based on magnetic properties in a fluid containing distinct nanoparticles were addressed by Elsebaee et al.15 Recent studies on the magnetized flow of hybrid nanofluids can be found in ref. 16–24.
In industrial procedures, the purpose of chemical reactions is to obtain material of good quality from low-quality material. The minimum requirement of energy to start the reactions is characterized by activation energy, first addressed by researcher S. Arrhenius. The study of activation energy has grabbed the attention of researchers with its effective utilization in engineering and industrial fields. The significance of the activation energy in the time-independent flow properties of Casson fluid subject to physical constraints was shown by Salahuddin et al.25 The thermal mechanism with the contribution of activation energy in a non-Newtonian fluid and a two-dimensional flow process was demonstrated by Bilal and Urva.26 The flow aspects with the consequence of activation energy and physical thermal conditions in a Williamson fluid were exhibited by Asjad et al.27 Jayaprakash et al.28 performed a numerical evaluation to analyze the diverse flow features of a hybrid nanofluid in relation to activation energy. The consequence of the activation energy on the flow phenomenon of a hybrid nanofluid with the application of partial slips was deliberated by Algehyne et al.29 Further, the related studies are in ref. 30–36.
After analyzing the aforementioned investigations, it is noticed that hybrid nanofluids flow with different physical properties subject to stretched surfaces have been explored, but the magnetized flow phenomenon of kerosene oil-based hybrid nanofluids with the extended version of Yamada–Ota and Xue models over a curved stretching sheet has not been observed until now. The novelty of the current study comprises the execution of updated Yamada–Ota and Xue models on the two-dimensional magnetized flow of a hybrid nanofluid relative to a stretchable curved surface. The mechanisms of mass and heat transport are addressed through the utilization of exponential heat sources, activation energy, Joule heating, and thermal radiation effects. The dimensionless equations in relation to the Xue model and Yamada–Ota model are numerically handled through the bvp4c methodology. For both models under consideration, a graphical comparison of the flow characteristics relative to numerous parameters is elucidated. Moreover, a numerical scrutinization of the heat and mass transport rates along with the surface drag force in relation to relevant parameters is demonstrated.
2. Problem's mathematical description
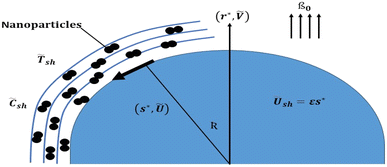
Let us take a stretchable sheet of curved shape to analyze the movement of an incompressible hybrid ferrofluid in two dimensions. The considered sheet is assumed to form a circular shape with radius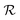 . For the preparation of the desirable hybrid ferrofluid, two different nanoparticles, namely magnetite Fe3O4 and cobalt ferrite CoFe2O4, merge with regular kerosene oil liquid. With the velocity Ũsh = εs*, the considered curved surface is extended towards the s*-direction. In the framework of a magnetized flow mechanism, in the r*-direction, a magnetic field of β0 strength is deployed. Moreover, the thermal analysis experiences the impacts of an exponential heat source, convective constraint, Joule heating, and radiation, while the consequences of activation energy are incorporated into mass transfer. The physical visualization of the ongoing problem is portrayed in Fig. 1.
. For the preparation of the desirable hybrid ferrofluid, two different nanoparticles, namely magnetite Fe3O4 and cobalt ferrite CoFe2O4, merge with regular kerosene oil liquid. With the velocity Ũsh = εs*, the considered curved surface is extended towards the s*-direction. In the framework of a magnetized flow mechanism, in the r*-direction, a magnetic field of β0 strength is deployed. Moreover, the thermal analysis experiences the impacts of an exponential heat source, convective constraint, Joule heating, and radiation, while the consequences of activation energy are incorporated into mass transfer. The physical visualization of the ongoing problem is portrayed in Fig. 1.
By taking the above suppositions, the appropriate equations are defined in the curvilinear coordinates (r*, s*) as follows:37,38
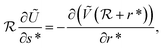 | (1) |
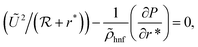 | (2) |
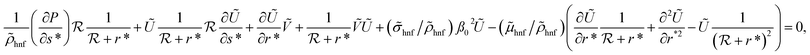 | (3) |
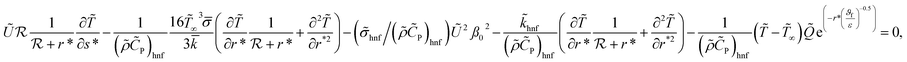 | (4) |
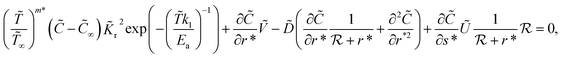 | (5) |
The relevant set of conditions at the boundary is illustrated in the following way:37
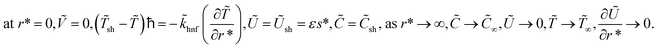 | (6) |
Now, let us familiarize ourselves with the following similar ansatz:36,37
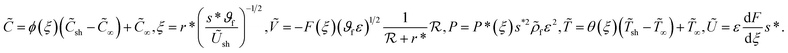 | (7) |
The above eqn (7) satisfy eqn (1) and transform eqn (2)–(5) into the following form:
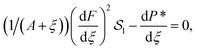 | (8) |
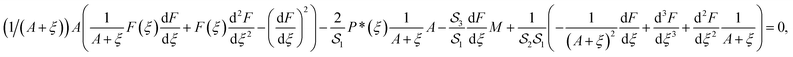 | (9) |
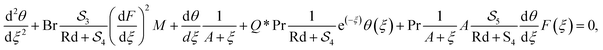 | (10) |
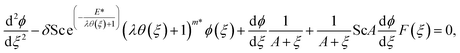 | (11) |
The elimination of the pressure term from eqn. (8) and (9) yields the following equation:
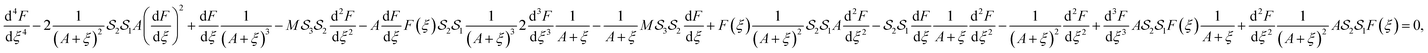 | (12) |
In view of eqn (6) and (7) has the following expressions:
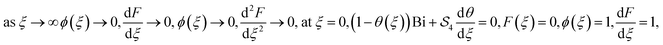 | (13) |
The parameters involved in the above equations are expressed as follows:
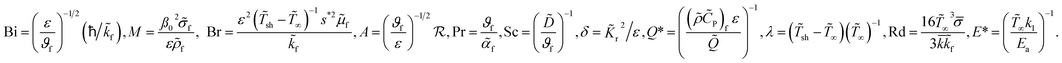 | (14) |
The thermophysical characteristics involved in the dimensionless equations are36
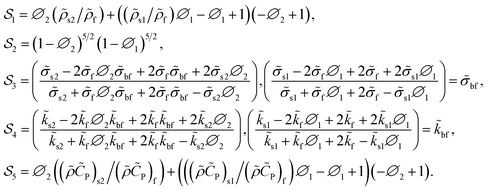 | (15) |
The two nanoparticles considered in this problem have numerical thermophysical characteristics, which are disclosed in the following Table 1.
| Thermophysical features | Cobalt ferrite (CoFe2O4) | Kerosene oil | Magnetite Fe3O4 |
|---|---|---|---|
(m S−1)−1![[small sigma, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e10d.gif) |
1.1 × 107 | 21 × 10−6 | 0.74 × 106 |
(K−1 J kg−1)![[C with combining tilde]](https://www.rsc.org/images/entities/i_char_0043_0303.gif) P P |
700 | 2090 | 670 |
(K−1 W m−1)![[k with combining tilde]](https://www.rsc.org/images/entities/i_char_006b_0303.gif) |
3.7 | 0.145 | 9.7 |
(1/kg m−3)−1![[small rho, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e4.gif) |
4907 | 783 | 5180 |
3. Model-dependent approach to hybrid ferrofluid
The two familiar models, namely Yamada–Ota40 and Xue,41 for the flow mechanism of nanofluid have been studied. However, these two substantial models are now upgraded for hybrid nanofluid with their vigorous expressions. In the ongoing study, we observe these modified models on the flow and thermal characteristics of a kerosene oil-based hybrid nanofluid with cobalt ferrite and magnetite nanoparticles. The Xue model, with its modified version of hybrid nanofluid, has the following pattern:8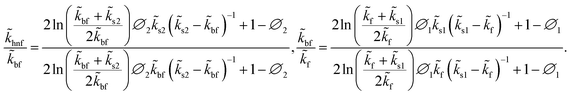 | (16) |
The following expressions are from the Yamada–Ota model with its upgraded form:8
 | (17) |
4. Physical quantities
The interesting quantities of the Sherwood number, coefficient of skin friction, and Nusselt number are incorporated in the current analysis. Mathematically, these quantities are illustrated in the following way:37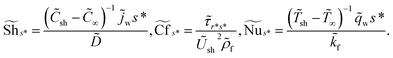 | (18) |
Here,
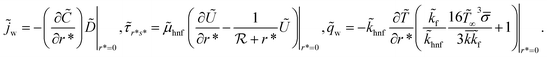 | (19) |
With the assistance of eqn (7), (18) and (19) has the following expressions:
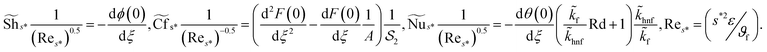 | (20) |
5. Outcomes and discussion
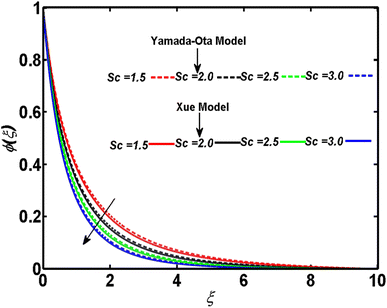
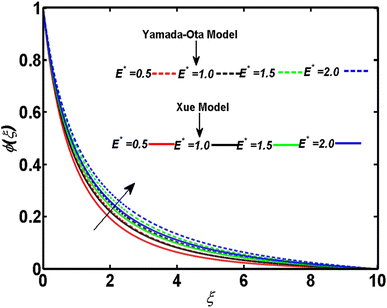
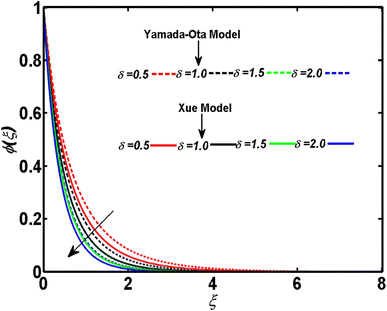
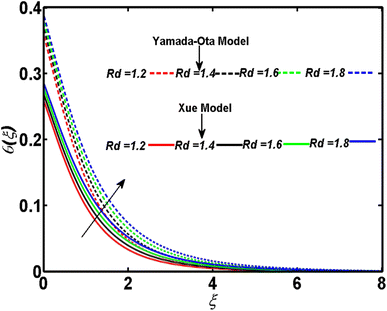
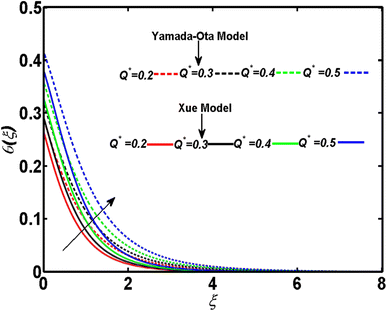
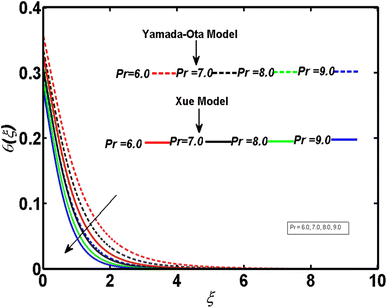
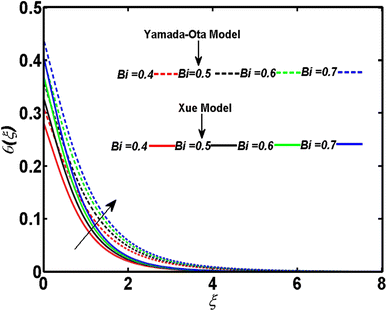
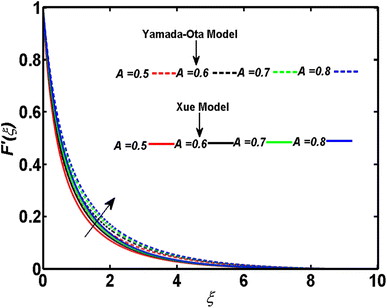
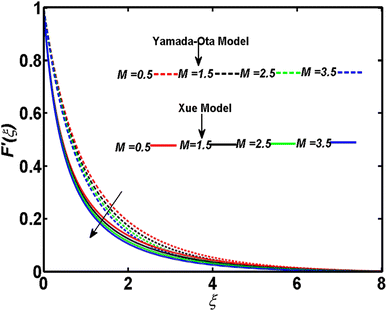
In relation to the improved version of the Xue and Yamada–Ota models, an incompressible two-dimensional flow of Al2O3–Cu/kerosene oil hybrid nanofluid with various physical effects is explored. An efficient technique called bvp4c is employed to numerically tackle the setup of dimensionless equations. A comparison between the current outcomes and the previously reported study is given in Table 2. Table 2 demonstrates that a strong bonding of numerical values is found between previous and current results. This ensures the affirmation and validity of the ongoing analysis. This section is arranged to analyze the significance of the relevant parameters corresponding to both models of Xue and Yamada–Ota on the concentration, velocity, and temperature distributions through graphics. A reduction is observed in the concentration distribution corresponding to both considered models and the higher magnitude of the Schmidt number, as depicted in Fig. 2. Physically, the mass diffusivity deteriorates with the acceleration of the Schmidt number. Consequently, there is a decrement in the concentration boundary layer thickness, and the concentration field yields the declining behavior. This diminishing phenomenon is more noticeable in the Yamada–Ota model. Fig. 3 is sketched to examine the field of concentration in relation to both considered models and the higher parameter of activation energy. The greater activation energy parameter yields an augmentation in the concentration distribution, particularly in correspondence to the Yamada–Ota model. This phenomenon occurs because the energy is excessively enhanced in the system due to the improved parameter of activation energy. Further, the rate of the chemical reaction increases, which consequently heightens the concentration. The declining nature of the concentration curve with consideration of both models and the higher rate of the chemical reaction are demonstrated in Fig. 4. An enhancement in the considered parameter upgrades the chemical reaction's destructive rate. Accordingly, the fluid particles are discarded, and their concentration reveals deteriorating behavior. This visual phenomenon holds greater significance when considering the Yamada–Ota model. In relation to both models under consideration, Fig. 5 is organized to explore the significance of the radiation parameter on the curve of the temperature. There is a rise in the temperature profile with the escalation of the radiation parameter. The fluid particle's kinetic energy amplifies with the accelerating radiation parameter. Thus, an augmentation in the temperature distribution is detected. An escalation of the temperature profile subject to the improved heat generation parameter and considered models is portrayed in Fig. 6. The fluid particles gain more heat with the augmentation of heat generation, and consequently, the rate of heat transfer increases. The model of Yamada–Ota provides more notable results for temperature distribution. Fig. 7 exhibits the nature of the temperature curve affected by the intensifying Prandtl number. The improved Prandtl number leads to a reduction in the temperature field. Physically, an inverse connection is found between thermal diffusivity and the Prandtl number. The increment of the Prandtl number minimizes the heat diffusivity within the system. As a result, the rate of heat transfer becomes lower. Variation of the Biot number develops an intensification in the curve of the temperature corresponding to both models, as elucidated in Fig. 8. The rate of thermal transport through a convection process is incredibly upgraded with the improved Biot number. Accordingly, the temperature profile yields an augmented behavior in relation to both models under consideration. However, this graphical phenomenon in the case of the Yamada–Ota model yields a vital effect. Fig. 9 has the objective of presenting the optimized velocity behavior related to the considered models and improved curvature parameters. Physically, the radius of the surface becomes elongated due to the amplification of the curvature parameter. As a result, the velocity field yields an upgraded result. The purpose of the improved magnetic field is to decrease the velocity field, as disclosed in Fig. 10. In the movement of fluid, an oppositional Lorentz force is generated with the escalation of the magnetic field. The fluid motion diminishes as it encounters resistance from this force. As a result, the velocity distribution experiences a decrease. A comparative analysis of physical parameters corresponding to both considered models is given in Table 3. The physical quantities and their numerical values relative to the specific pertinent parameters are exhibited. It is noticed that the curvature parameter yields an enhancement in the surface drag force but lowers the transport rates of heat and mass. These effects are more noticeable in the context of the Yamada–Ota model. Both the heat and mass transport rates are progressively influenced by the rising magnetic field values. There is an escalation in the surface drag force with the higher volume fraction of magnetite nanoparticles. On the other hand, the rate of mass transport and the rate of heat transport yield results opposite to the surface drag force.| M | ||
|---|---|---|
| Present values | Mabood and Das42 | |
| 1 | 1.4080 | 1.4142 |
| 5 | 2.4306 | 2.4495 |
| 10 | 3.2982 | 3.3166 |
| A | M | ∅ 2 | Yamada–Ota Model | Xue Model | ||||
|---|---|---|---|---|---|---|---|---|
| Sherwood | Skin | Nusselt | Sherwood | Skin | Nusselt | |||
| 0.3 | 0.5 | 0.02 | 1.3532 | −6.7464 | 0.7178 | 1.2706 | −6.7408 | 0.7020 |
| 0.5 | 1.1385 | −4.1421 | 0.1222 | 1.1213 | −4.1341 | 0.1019 | ||
| 0.7 | 1.0067 | −3.0692 | 0.1028 | 1.0057 | −3.0599 | 0.0054 | ||
| 0.6 | 1.3554 | −6.7492 | 0.7151 | 1.3528 | −6.7436 | 0.7013 | ||
| 0.7 | 1.3556 | −6.7464 | 0.7159 | 1.3529 | −6.7408 | 0.7020 | ||
| 0.8 | 1.3557 | −6.7391 | 0.7298 | 1.3541 | −6.7380 | 0.7028 | ||
| 0.02 | 1.3532 | −6.7464 | 0.7178 | 1.2706 | −6.7408 | 0.7020 | ||
| 0.04 | 1.2314 | −6.4047 | 0.5359 | 1.2107 | −6.3964 | 0.5274 | ||
| 0.06 | 1.2200 | −6.0785 | 0.1633 | 1.1518 | −6.0705 | 0.1531 | ||
6. Concluding remarks
The application of the improved Xue model and Yamada–Ota model to the magnetized 2D flow mechanism developed by a stretched curved sheet in a hybrid ferrofluid is discussed in the article. Various physical impacts are incorporated into the mechanisms of mass and heat transport. A numerical scrutinization of the flow problem is conducted through the execution of the bpv4c approach. The current study yields the following crucial outcomes:• The improved Prandtl number in the context of both considered models develops a deterioration in the thermal field.
• A growing trend in the temperature curve is identified, corresponding to a greater magnitude of the Biot number, radiation, and heat source parameters.
• With the execution of both models and the augmentation of the curvature parameter, the velocity profile exhibits an accelerating mechanism.
• Both the fields of concentration and velocity yield reducing behavior in the context of the amplification of the Schmidt number and magnetic field, respectively.
• The purpose of the improved activation energy corresponding to both models is to upgrade the concentration distribution.
• A stronger rate of chemical reaction produces an opposition in the field of concentration.
• In comparison to the Xue model, the graphical outcomes are more favorable with respect to the Yamada–Ota model.
Nomenclature
Subscripts
| s1 | Cobalt ferrite nanoparticle |
| bf | Base fluid |
| f | Fluid |
| s2 | Magnetite nanoparticle |
| ∞ | Free stream condition |
| hnf | Hybrid nanofluid |
Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through a large group Research Project under grant number RGP2/153/44.References
- S. U. Choi, and J. A. Eastman, Enhancing Thermal Conductivity of Fluids with Nanoparticles (No. ANL/MSD/CP-84938; CONF-951135-29), Argonne National Lab.(ANL), Argonne, IL (United States), 1995 Search PubMed.
- S. M. Hussain and W. Jamshed, A comparative entropy based analysis of tangent hyperbolic hybrid nanofluid flow: Implementing finite difference method, Int. Commun. Heat Mass Transfer, 2021, 129, 105671 CrossRef CAS.
- P. Sreedevi, P. S. Reddy and A. Chamkha, Heat and mass transfer analysis of unsteady hybrid nanofluid flow over a stretching sheet with thermal radiation, SN Appl. Sci., 2020, 2, 1222 CrossRef CAS.
- J. K. Madhukesh, R. N. Kumar, R. P. Gowda, B. C. Prasannakumara, G. K. Ramesh, M. I. Khan and Y. M. Chu, Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-Fourier heat flux model approach, J. Mol. Liq., 2021, 335, 116103 CrossRef CAS.
- M. A. Qureshi, A case study of MHD driven Prandtl–Eyring hybrid nanofluid flow over a stretching sheet with thermal jump conditions, Case Stud. Therm. Eng., 2021, 28, 101581 CrossRef.
- M. Santhi, K. V. S. Rao, P. S. Reddy and P. Sreedevi, Heat and mass transfer characteristics of radiative hybrid nanofluid flow over a stretching sheet with chemical reaction, Heat Transfer, 2021, 5, 2929–2949 CrossRef.
- T. S. Neethu, A. S. Sabu, A. Mathew, A. Wakif and S. Areekara, Multiple linear regression on bioconvective MHD hybrid nanofluid flow past an exponential stretching sheet with radiation and dissipation effects, Int. Commun. Heat Mass Transfer, 2022, 135, 106115 CrossRef CAS.
- B. Ishtiaq, A. M. Zidan, S. Nadeem and M. K. Alaoui, Scrutinization of MHD stagnation point flow in hybrid nanofluid based on the extended version of Yamada-Ota and Xue models, Ain Shams Eng. J., 2023, 14, 101905 CrossRef.
- C. M. Mohana and B. R. Kumar, Shape effects of Darcy–Forchheimer unsteady three-dimensional CdTe-C/H2O hybrid nanofluid flow over a stretching sheet with convective heat transfer, Phys. Fluids, 2023, 35, 092002 CrossRef CAS.
- S. Nadeem, B. Ishtiaq, M. B. B. Hamida, S. Almutairi, H. A. Ghazwani, S. M. Eldin and A. S. Al-Shafay, Reynolds nano fluid model for Casson fluid flow conveying exponential nanoparticles through a slandering sheet, Sci. Rep., 2023, 13, 1953 CrossRef CAS PubMed.
- M. M. Khader and M. M. Babatin, Numerical study for improvement the cooling process through a model of Powell–Eyring fluid flow over a stratified stretching sheet with magnetic field, Case Stud. Therm. Eng., 2022, 31, 101786 CrossRef.
- B. Ishtiaq and S. Nadeem, Theoretical Analysis of Casson Nanofluid over a Vertical Exponentially Shrinking Sheet with Inclined Magnetic Field, Waves Random Complex Media, 2022, pp. 1–17 Search PubMed.
- E. Seid, E. Haile and T. Walelign, Multiple slip, Soret and Dufour effects in fluid flow near a vertical stretching sheet in the presence of magnetic nanoparticles, Int. J. Thermofluids, 2022, 13, 100136 CrossRef CAS.
- S. Nadeem, B. Ishtiaq, J. Alzabut, H. A. Ghazwani and A. M. Hassan, Unsteady magnetized flow of micropolar fluid with prescribed thermal conditions subject to different geometries, Results Phys., 2023, 53, 106946 CrossRef.
- F. A. A. Elsebaee, M. Bilal, S. R. Mahmoud, M. Balubaid, M. Shuaib, J. K. Asamoah and A. Ali, Motile micro-organism based trihybrid nanofluid flow with an application of magnetic effect across a slender stretching sheet: Numerical approach, AIP Adv., 2023, 13, 035237 CrossRef CAS.
- S. Sarkar, R. N. Jana and S. Das, Activation energy impact on radiated magneto-Sisko nanofluid flow over a stretching and slipping cylinder: entropy analysis, Multidiscip. Model. Mater. Struct., 2020, 16, 1085–1115 CrossRef CAS.
- A. Ali, R. N. Jana and S. Das, Radiative CNT-based hybrid magneto-nanoliquid flow over an extending curved surface with slippage and convective heating, Heat Transfer, 2021, 50, 2997–3020 CrossRef.
- S. Nadeem, B. Ishtiaq, N. Akkurt and H. A. Ghazwani, Entropy optimized flow of hybrid nanofluid with partial slip boundary effects and induced magnetic field, Int. J. Mod. Phys. B, 2023, 37, 2350252 CrossRef CAS.
- M. G. Murtaza, T. Akter, E. E. Tzirtzilakis and M. Ferdows, Numerical study of biomagnetic fluid flow over an unsteady curved stretching sheet in the presence of magnetic field, Adv. Appl. Fluid Mech., 2023, 30, 35–62 Search PubMed.
- B. Ishtiaq, S. Nadeem and J. Alzabut, Effects of variable magnetic field and partial slips on the dynamics of Sutterby nanofluid due to biaxially exponential and nonlinear stretchable sheets, Heliyon, 2023, 9, e17921 CrossRef PubMed.
- K. Rafique, Z. Mahmood and U. Khan, Mathematical analysis of MHD hybrid nanofluid flow with variable viscosity and slip conditions over a stretching surface, Mater. Today Commun., 2023, 36, 106692 CrossRef CAS.
- T. A. Assiri, F. A. A. Elsebaee, A. M. Alqahtani, M. Bilal, A. Ali and S. M. Eldin, Numerical simulation of energy transfer in radiative hybrid nanofluids flow influenced by second-order chemical reaction and magnetic field, AIP Adv., 2023, 13, 035020 CrossRef CAS.
- R. Akhter, M. M. Ali and M. A. Alim, Magnetic field impact on double diffusive mixed convective hybrid-nanofluid flow and irreversibility in porous cavity with vertical wavy walls and rotating solid cylinder, Results Eng., 2023, 19, 101292 CrossRef CAS.
- S. U. Jan, U. Khan, S. Islam and M. Ayaz, Impact of variable thermal conductivity on flow of trihybrid nanofluid over a stretching surface, Nanotechnol, 2023, 34, 465301 CrossRef.
- T. Salahuddin, M. Arshad, N. Siddique, A. S. Alqahtani and M. Y. Malik, Thermophyical properties and internal energy change in Casson fluid flow along with activation energy, Ain Shams Eng. J., 2020, 11, 1355–1365 CrossRef.
- M. Bilal and Y. Urva, Analysis of non-Newtonian fluid flow over fine rotating thin needle for variable viscosity and activation energy, Arch. Appl. Mech., 2021, 91, 1079–1095 CrossRef.
- M. I. Asjad, M. Zahid, M. Inc, D. Baleanu and B. Almohsen, Impact of activation energy and MHD on Williamson fluid flow in the presence of bioconvection, Alex. Eng. J., 2022, 61, 8715–8727 CrossRef.
- M. C. Jayaprakash, M. D. Alsulami, B. Shanker and R. S. V. Kumar, Investigation of Arrhenius Activation Energy and Convective Heat Transfer Efficiency in Radiative Hybrid Nanofluid Flow, Waves Random Complex Media, 2022, pp. 1–13 Search PubMed.
- E. A. Algehyne, A. Saeed, M. Arif, M. Bilal, P. Kumam and A. M. Galal, Gyrotactic microorganism hybrid nanofluid over a Riga plate subject to activation energy and heat source: numerical approach, Sci. Rep., 2023, 13, 13675 CrossRef CAS.
- J. K. Madhukesh, R. N. Kumar, R. P. Gowda, B. C. Prasannakumara, G. K. Ramesh, M. I. Khan and Y. M. Chu, Numerical simulation of AA7072-AA7075/water-based hybrid nanofluid flow over a curved stretching sheet with Newtonian heating: A non-Fourier heat flux model approach, J. Mol. Liq., 2021, 335, 116103 CrossRef CAS.
- S. Das, R. R. Patra and R. N. Jana, The layout of Boussinesq couple-stress fluid flow over an exponentially stretching sheet with slip in porous space subject to a variable magnetic field, Multidiscip. Model. Mater. Struct., 2020, 16, 1131–1154 CrossRef CAS.
- A. Ali, R. N. Jana and S. Das, Hall effects on radiated magneto-power-law fluid flow over a stretching surface with power-law velocity slip effect, Multidiscip. Model. Mater. Struct., 2020, 17, 103–125 CrossRef.
- S. Das, A. Ali and R. N. Jana, Darcy–Forchheimer flow of a magneto-radiated couple stress fluid over an inclined exponentially stretching surface with Ohmic dissipation, World J. Eng., 2021, 18, 345–360 CrossRef CAS.
- Z. Mahmood, S. M. Eldin, K. Rafique and U. Khan, Numerical analysis of MHD tri-hybrid nanofluid over a nonlinear stretching/shrinking sheet with heat generation/absorption and slip conditions, Alex. Eng. J., 2023, 76, 799–819 CrossRef.
- Z. Mahmood, U. Khan, S. Saleem, K. Rafique and S. M. Eldin, Numerical analysis of ternary hybrid nanofluid flow over a stagnation region of stretching/shrinking curved surface with suction and lorentz force, J. Magn. Magn. Mater., 2023, 573, 170654 CrossRef CAS.
- U. Khan, H. A. Wahab, H. Syed, B. Ullah and Adnan, Numerical study of heat transport mechanism in hybrid nanofluid [Cu-(Al2O3)/water] over a stretching/shrinking porous wedge, Proc. Inst. Mech. Eng., Part C, 2023, 237, 635–644 CAS.
- K. Sarada, F. Gamaoun, A. Abdulrahman, S. O. Paramesh, R. Kumar, G. D. Prasanna and R. P. Gowda, Impact of exponential form of internal heat generation on water-based ternary hybrid nanofluid flow by capitalizing non-Fourier heat flux model, Case Stud. Therm. Eng., 2022, 38, 102332 CrossRef.
- F. Ahmad, S. Abdal, H. Ayed, S. Hussain, S. Salim and A. O. Almatroud, The improved thermal efficiency of Maxwell hybrid nanofluid comprising of graphene oxide plus silver/kerosene oil over stretching sheet, Case Stud. Therm. Eng., 2021, 27, 101257 CrossRef.
- S. Zainodin, A. Jamaludin, R. Nazar and I. Pop, Effects of higher order chemical reaction and slip conditions on mixed convection hybrid ferrofluid flow in a Darcy porous medium, Alex. Eng. J., 2023, 68, 111–126 CrossRef.
- E. Yamada and T. Ota, Effective thermal conductivity of dispersed materials, Heat Mass Transfer, 1980, 13, 27–37 CAS.
- Q. Z. Xue, Model for thermal conductivity of carbon nanotube-based composites, Phys. B, 2005, 368, 302–307 CrossRef CAS.
- F. Mabood and K. Das, Melting heat transfer on hydromagnetic flow of a nanofluid over a stretching sheet with radiation and second-order slip, Eur. Phys. J. Plus, 2016, 131, 1–12 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |

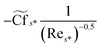
![[Q with combining tilde]](https://www.rsc.org/images/entities/i_char_0051_0303.gif)
![[j with combining tilde]](https://www.rsc.org/images/entities/i_char_006a_0303.gif)
![[T with combining tilde]](https://www.rsc.org/images/entities/i_char_0054_0303.gif)
![[q with combining tilde]](https://www.rsc.org/images/entities/i_char_0071_0303.gif)
![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif)
![[k with combining macron]](https://www.rsc.org/images/entities/i_char_006b_0304.gif)
![[small sigma, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d2.gif)
![[small tau, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e5.gif)
![[K with combining tilde]](https://www.rsc.org/images/entities/i_char_004b_0303.gif)
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)