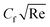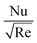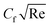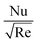Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Multiscale tribology analysis of MHD hybrid nanofluid flow over a curved stretching surface
Khursheed
Muhammad
 *a,
Bilal
Ahmed
b,
Mohamed
Sharaf
*a,
Bilal
Ahmed
b,
Mohamed
Sharaf
 c,
Mohammad
Afikuzzaman
d and
Emad A.
Az-Zo'bi
e
c,
Mohammad
Afikuzzaman
d and
Emad A.
Az-Zo'bi
e
aDepartment of Humanities and Sciences, School of Electrical Engineering and Computer Science (SEECS), National University of Sciences and Technology (NUST), Islamabad, Pakistan. E-mail: khursheed.muhammad@seecs.edu.pk
bSchool of Energy and Power Engineering, Jiangsu University, Zhenjiang, China
cIndustrial Engineering Department, College of Engineering, King Saud University, P. O. Box 800, Riyadh 11421, Saudi Arabia
dUniSA STEM, University of South Australia, Adelaide, SA 5000, Australia
eDepartment of Mathematics, Mutah University, Al Karak, Jordan
First published on 1st December 2023
Abstract
In this study, we investigate the interactions of a hybrid nanofluid on a curved surface that is being stretched. The magnetic field is perpendicular to the flow and interacts with a mixture of molybdenum disulfide and argentum nanoparticles suspended in pure water, forming a hybrid nanomaterial. Our investigation considers heat transport analysis under different conditions, such as magnetohydrodynamic, Darcy–Forchheimer porous medium flow, Joule heating, and a convective boundary condition. We employ numerical and statistical methods to study the problem's intricacies comprehensively. Our findings indicate that Darcy–Forchheimer flow includes viscous and inertial forces, which results in higher flow rates and reduced skin friction. Additionally, the convective boundary condition leads to uniform temperature distribution within the hybrid material due to rapid internal heat transfer relative to surface resistance, significantly increasing the heat transfer rate.
1. Introduction
Hybrid nanofluids are advanced colloidal suspensions that combine nanoparticles from different materials to create unique and synergistic properties. Incorporating different nanoparticles involves blending these nanoparticles to create a specialized nanofluid with enhanced thermal, electrical, and other functional characteristics. Lee et al.1 reviewed conflicting findings on the thermal conductivity of nanofluids. The study highlighted experimental milestones, proposed mechanisms and models, addressed data inconsistencies, and suggested directions for future research. The aim was to optimize nanofluids for enhanced thermal properties in various applications. Lee et al.2 developed surfactant-free zinc oxide nanofluids using a pulsed wire evaporation method in ethylene glycol. Five labs conducted round-robin tests to measure the thermal conductivity of three samples using in-house setups and a commercial device. Choi et al.3 discussed nanofluids' internal forced convective heat transfer attributes with experimental features. Nadeem et al.4 inspected hybrid nanomaterial distribution by considering two distinct nanoparticles in pure water over a curved surface. Waqas et al.5 numerically computed melting heat transfer in the nonlinear radiative flow of hybrid nanofluids due to permeable stretching curved surface. Wahid et al.6 explored the flow and heat transfer of a hybrid nanofluid induced by an exponentially stretching/shrinking curved surface. More interesting studies regarding nanofluids are addressed in ref. 7–22.Regression analysis is a statistical technique used to establish empirical correlations between parameters. It has practical applications in fluid mechanics, allowing researchers to understand, predict, and optimize various fluid behaviors. These correlations are crucial for characterizing flow patterns, predicting pressure drops, and modeling turbulence in complex fluid systems. It also supports the analysis of experimental data and validation of numerical simulations and helps to design efficient systems while making informed decisions in fluid mechanics. Moreover, quadratic and multiple quadratic regression analyses are specialized approaches that can accommodate linear and non-linear relationships between variables and establish predictive models that enhance the understanding and manipulation of fluid behavior. Najm23 examined polynomial chaos methods for probabilistic uncertainty quantification in computational fluid dynamics (CFD) predictions. The study reviewed various CFD applications and challenges, such as flow in porous media, incompressible and compressible flows, thermofluid and reacting flows, and cross-cutting challenges related to time unsteadiness and longtime horizons. Zhang et al.24 presented an improved airfoil design using a modified shape function transformation. The design was validated through computational fluid dynamics and experimental testing. Optimization was performed using a modified multi-island genetic algorithm combined with non-linear programming. The resulting optimized airfoil demonstrated enhanced performance and lift-to-drag ratio, providing insights for future airfoil design. Kumar et al.25 employed spectral relaxation to investigate nanofluid flow over a porous stretching sheet, considering slip, mixed convection, dissipations, and nanoparticle control. The study discussed velocity, temperature, and concentration graphs; verified prior findings; conducted regression analysis for local Nusselt numbers; and highlighted the impact of thermophoretic and Eckert number factors on diffusion. Liu et al.26 used quadratic regression orthogonal combination (QROC) and a genetic algorithm (GA) to optimize the coal pyrolysis filtration system's performance and extend the filter tube lifespan with compelling predictions and low mean square error. References are provided for studies discussing issues associated with regression analysis (ref. 27–33).
The significance of this study lies in examining the combined effects of molybdenum disulfide and argentum nanoparticles suspended in a water solution over a curved surface, influenced by an inward magnetic field, magnetohydrodynamics, Darcy–Forchheimer porous medium flow, Joule heating, and a convective boundary condition. This yields insights into intricate heat transport interactions through a hybrid nanomaterial and porous medium. The reason we have combined molybdenum disulfide (MoS2) and silver (Ag) nanoparticles is their versatility and compatibility with different nanomaterials (their mixture can be customized to achieve specific results). The investigation employs numerical and statistical methodologies for a comprehensive study of the intricacies of the problem. The findings of this study hold relevance in various applications such as advanced thermal management systems, nanoparticle-enhanced heat exchangers, and innovative cooling technologies where the combined effects of molybdenum disulfide and argentum nanoparticles suspended in a water solution can be harnessed to optimize heat transfer efficiency and system performance.
The article was structured as follows: Section 2 encompassed mathematical modeling, Section 3 presented regression analysis, Section 3 contained a discussion of results, and Section 4 offered a summary of the findings.
2. Modeling of the problem
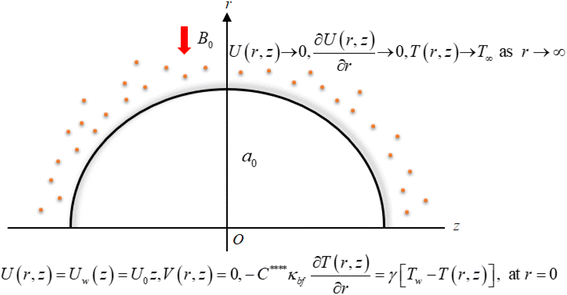
A two-dimensional flow of a hybrid nanofluid is considered over a curved surface with a radius “a0,” which is undergoing stretching. The problem is formulated in curved coordinates (r,z), and an applied magnetic field of intensity “B0” with an inward perpendicular direction to the flow is present. This field interacts with a mixture of molybdenum disulfide (MoS2) and argentum (Ag) nanoparticles suspended in a pure water (H2O) solution, creating the hybrid nanomaterial. The velocity field is V = [U(r,z), V(r,z), 0]. The analysis encompasses heat transfer effects while accounting for magnetohydrodynamics, Darcy–Forchheimer porous medium flow, Joule heating, and a convective boundary condition. The investigation involves both numerical and statistical approaches to study the problem comprehensively. Fig. 1 provides a visual representation of the problem's geometry, while Table 1 offers essential thermophysical values for both the nanoparticles and the base fluid.| Materials/characteristics | ρ (kg m−3) | κ (W m−1 K−1) | σ (S m−1) | c p (J kg−1 K−1) | Pr |
|---|---|---|---|---|---|
| H2O | 997 | 0.613 | 5.5 × 10−6 | 4179 | 6.2 |
| Ag | 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 490 490 |
429 | 6.3 × 107 | 235 | — |
| MoS2 | 5060 | 34.5 | 2.09 × 104 | 397.746 | — |
By incorporating the assumptions mentioned above and considering conditions such as negligible viscous dissipation and the application of boundary layer approximations (O(U) = O(z) = O(ρbf) = O(ρhnf) = O(1), O(V) = O(r) = O(δ), and O(μhnf) = O(μf) = O(δ2)), the following set of PDEs can be derived (following ref. 7):
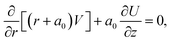 | (1) |
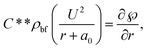 | (2) |
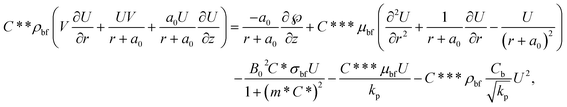 | (3) |
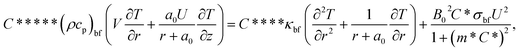 | (4) |
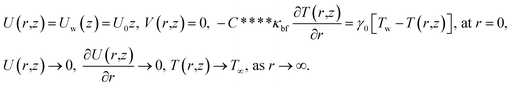 | (5) |
For hybrid nanofluid the electrical conductivity is defined by
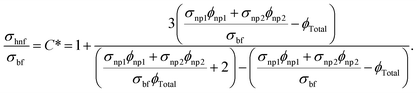 | (6) |
Hybrid nanomaterial density by the Xuan and Li model is
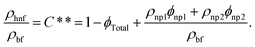 | (7) |
Dynamic viscosity via the Brinkman model for the hybrid nanomaterial is
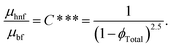 | (8) |
The Maxwell model defined thermal conductivity of the hybrid nanomaterial using
 | (9) |
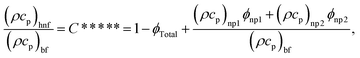 | (10) |
| ϕTotal = ϕnp1 + ϕnp2. | (11) |
For the conversion of flow as mentioned above and heat transfer related PDEs and associated BCs into non-dimensional form, we introduce the following dimensionless non-similar variables (following ref. 7).
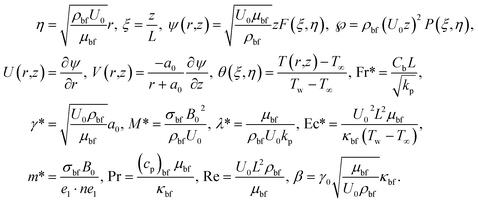 | (12) |
After making use of the associated velocity component in terms of stream function, we get eqn (1) identically satisfied, and the rest of the equations (eqn (2)–(5)) take the following form after using first-order truncation 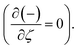 :
:
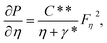 | (13) |
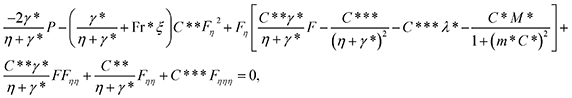 | (14) |
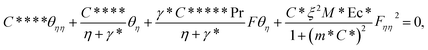 | (15) |
Eliminating P from eqn (13) and (14), we get
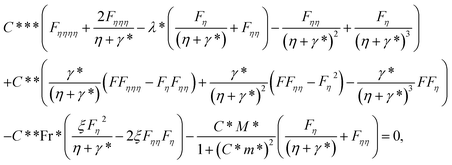 | (16) |
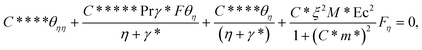 | (17) |
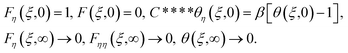 | (18) |
Dimensional skin friction 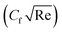 and Nusselt number
and Nusselt number 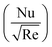 are (following ref. 7)
are (following ref. 7)
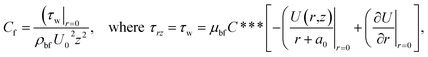 | (19) |
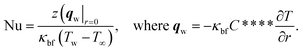 | (20) |
After using appropriate substitutions in eqn (19) and (20), we get non-dimensional 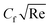 and
and 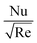 as
as
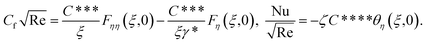 | (21) |
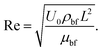
3. Regression analysis
To study the comparative effectiveness of two physical parameters on the skin friction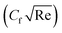 and Nusselt number
and Nusselt number 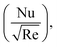 we have used the multiple quadratic regression model. A multiple quadratic regression model is a statistical technique for modeling the relationship between a dependent variable and one or more independent variables. For this purpose we have taken 51 values of λ* and Fr*, such that λ* ∈ [0.1,0.5] and Fr* ∈ [0.1,0.7]. In the case of regression analysis of
we have used the multiple quadratic regression model. A multiple quadratic regression model is a statistical technique for modeling the relationship between a dependent variable and one or more independent variables. For this purpose we have taken 51 values of λ* and Fr*, such that λ* ∈ [0.1,0.5] and Fr* ∈ [0.1,0.7]. In the case of regression analysis of 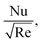 we have chosen 51 values of Ec* and β such that β ∈ [0.1,0.5] and Ec* ∈ [0.1,0.3]. During these analyses all other physical parameters are kept fixed. The multiple quadratic regression model for skin friction
we have chosen 51 values of Ec* and β such that β ∈ [0.1,0.5] and Ec* ∈ [0.1,0.3]. During these analyses all other physical parameters are kept fixed. The multiple quadratic regression model for skin friction 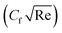 and Nusselt number
and Nusselt number 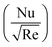 is defined according to Kumbhakar et al.33
is defined according to Kumbhakar et al.33| (Cf)Predicted = C + c1Fr* + c2λ* + c3(Fr*)2 + c4(λ*)2 + c5Fr*λ*, | (22) |
| (Nu)Predicted = N + d1β + d2Ec* + d3(β)2 + d4(Ec*)2 + d5Ec*β. | (23) |
4. Discussion
The primary objective of this section is to analyze the responses of flow (Fη(ξ,η)), temperature (θ(ξ,η)), skin friction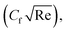 and Nusselt number
and Nusselt number 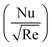 with the variation of different physical parameters.
with the variation of different physical parameters.
4.1 Discussion of methodology
The governing non-dimensional PDEs and their BCs are solved using the NDSolve numerical tool in Mathematica. It simplifies the solving process by automatically selecting the most appropriate method and controlling the adaptive step size, making it easier for users to solve complex differential equations with high accuracy. Similarity transformations are applied to simplify the PDEs, treating them as ODEs. NDSolve automatically selects a numerical method suitable for the equations and desired precision. The size of time or space steps is adjusted using NDSolve as the solution progresses, focusing computational effort where it is needed. Starting from the initial conditions and progressing to the desired final time or spatial domain, NDSolve integrates the equations over the specified range. It returns the numerical solution, often as interpolating function objects, which can be used for analysis and visualization. Mathematica's built-in functions can create plots and visual representations of the solution. The technique also provides information about the accuracy of the solution, including error estimates.Each graph presented in this section offers a comparative analysis of the behavior of hybrid (MoS2 + Ag + water) and nanofluid (MoS2 + water) solutions. The nanofluid consists of MoS2 nanoparticles suspended in a water base fluid, while the hybrid nanofluid incorporates two types of nanoparticles: MoS2 and Ag, both dispersed in a water base fluid. Throughout the comparative study, ϕnp1 = 0.05 = ϕnp2 is kept constant for the MoS2 + Ag + water case, whereas ϕnp1 = 0.1 and ϕnp2 = 0 are fixed for MoS2 + water. The results are visually depicted using solid lines for hybrid nanofluid (MoS2 + Ag + water) and dashed lines for nanofluid (MoS2 + water) solutions. Moreover, Table 1 is constructed for thermophysical properties of nanoparticles and base fluid while Tables 2 and 3 are for regression coefficients of skin friction and Nusselt number respectively.
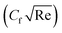 during multiple quadratic regression analysis for higher estimations of γ*
during multiple quadratic regression analysis for higher estimations of γ*
| γ* | C f | c 1 | c 2 | c 3 | c 4 | c 5 |
|---|---|---|---|---|---|---|
| Hybrid nanofluids (MoS 2 + Ag + water) | ||||||
| 0.1 | −17.575 | −3.22112 | 1.97122 | −0.294866 | −0.075453 | 0.320673 |
| 0.2 | −9.51135 | −1.72027 | 1.08551 | −0.157455 | −0.0457487 | 0.171275 |
| 0.3 | −6.76872 | −1.20441 | 0.788643 | −0.108862 | −0.0359474 | 0.121005 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Nanofluids (MoS 2 + water) | ||||||
| 0.1 | −17.5709 | −3.299 | 1.9067 | −0.304304 | −0.0600063 | 0.326598 |
| 0.2 | −9.50444 | −1.79253 | 1.02482 | −0.169154 | −0.0331203 | 0.174443 |
| 0.3 | −6.7593 | −1.27487 | 0.728769 | −0.12193 | −0.0245564 | 0.122779 |
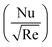 during multiple quadratic regression analysis for higher estimations of M*
during multiple quadratic regression analysis for higher estimations of M*
| M* | Nu | d 1 | d 2 | d 3 | d 4 | d 5 |
|---|---|---|---|---|---|---|
| Hybrid nanofluids (MoS 2 + Ag + water) | ||||||
| 0.1 | −0.0333674 | 0.603027 | 0.682105 | −0.415122 | 0.568414 | −0.028235 |
| 0.2 | −0.0332625 | 0.602356 | 0.681424 | −0.417831 | 0.562702 | −0.0322668 |
| 0.3 | −0.0331631 | 0.60172 | 0.680778 | −0.420374 | 0.557327 | −0.036058 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
||||||
| Nanofluids (MoS 2 + water) | ||||||
| 0.1 | −0.0333137 | 0.602791 | 0.681885 | −0.416022 | 0.566507 | −0.0295857 |
| 0.2 | −0.0332078 | 0.602112 | 0.681195 | −0.418731 | 0.56078 | −0.0336241 |
| 0.3 | −0.0331074 | 0.601468 | 0.680541 | −0.421278 | 0.555383 | −0.0374266 |
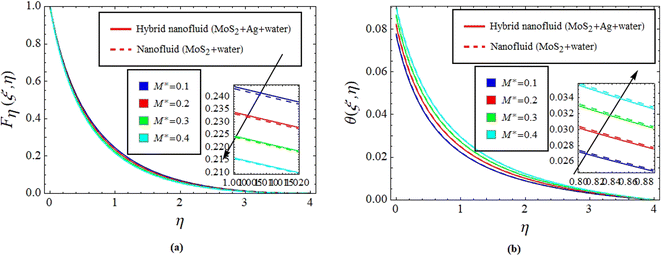
Fig. 2(a) and (b) illustrate the response of M* on Fη(ξ,η) and θ(ξ,η). It is seen that with the variation of M* from 0.1 to 0.4, the opposition force created by B0 causes the flow field to decline. Physically, this is because particles experience resistance which slows their motion and consequently, lowers Fη(ξ,η), see Fig. 2(a). However, due to B0, Joule heating promotes the energy transport among the particles. Physically, the system's kinetic energy boosts, which eventually enhances θ(ξ,η), see Fig. 2(b). The behavior is the same for hybrid nanofluid (MoS2 + Ag + water) and nanofluid (MoS2 + water) solutions. However, the MoS2 + Ag + water solution causes a more prominent effect. Fig. 3(a) and (b) depict the outcome of m* on Fη(ξ,η) and θ(ξ,η). The variation is recorded from 0.1 to 0.4. This parameter is generated due to the Hall effect. Physically, it causes charged particles in the fluid to experience a Lorentz force as the particles move through a magnetic field. The fluid's dynamics is affected by this interaction, which leads to an increase in Fη(ξ,η), see Fig. 3(a). Specifically, it amplifies existing driving forces for fluid motion, resulting in accelerated flow in certain regions. On the other hand, the Hall effect's Lorentz force does not only impact Fη(ξ,η) but can also affect θ(ξ,η). When charged particles move through the magnetic field, their trajectories can be altered by the force, leading to changes in θ(ξ,η). This effect can even cause a decrease in θ(ξ,η) in some regions of the fluid due to the redistribution of thermal energy resulting from the interaction between the Lorentz force and the fluid flow, see Fig. 3(b). Fig. 4(a) and (b) depict the impact of M* against m* on 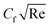 and
and 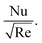 . The variation of M* is from 0.1 to 0.4. The opposing force causes the particles to experience resistance, which is skin drag. Thus, due to variation of M*,
. The variation of M* is from 0.1 to 0.4. The opposing force causes the particles to experience resistance, which is skin drag. Thus, due to variation of M*, 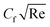 enhances, but m* causes
enhances, but m* causes 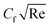 to lessen, see Fig. 4(a). However, the opposite trend is visible for
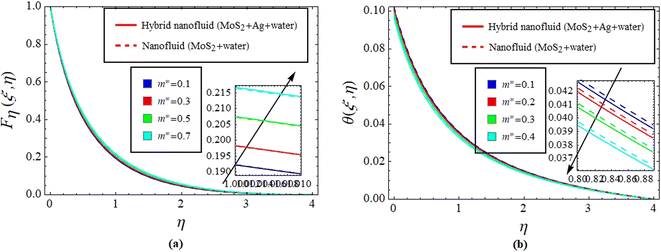
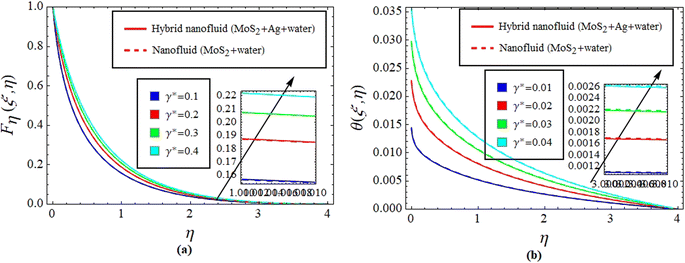
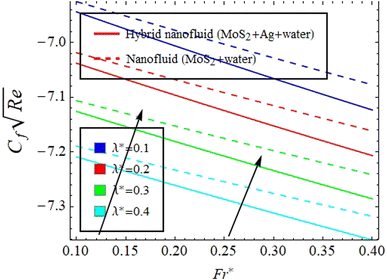
to lessen, see Fig. 4(a). However, the opposite trend is visible for 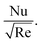 Physically, due to the complex interplay between the Hall effect and magnetic field the energy transport rate is declined, see Fig. 4(b). Fig. 5(a) and (b) describe the effect of γ* on Fη(ξ,η) and θ(ξ,η). The impression noted suggests that when fluid flows through a curved path, its inertia causes curvature to generate centrifugal forces. These forces are directed away from the center of curvature and can lead to an increase in Fη(ξ,η) on the outer side of the curve, see Fig. 5(a). This increase in velocity often results in higher kinetic energy, which can elevate θ(ξ,η) due to the conversion of kinetic energy into thermal energy through dissipation, see Fig. 5(b). Fig. 6(a) and (b) explain the impact of Fr* and λ* on Fη(ξ,η). Fig. 7 identifies the influence of Fr* against λ* on
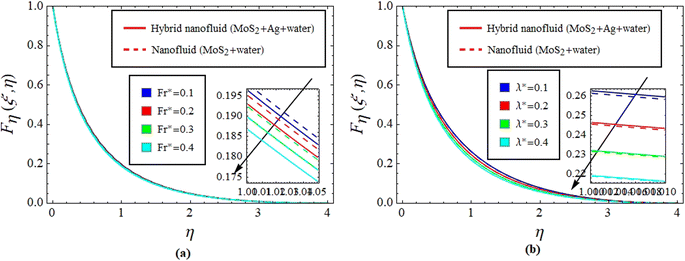
Physically, due to the complex interplay between the Hall effect and magnetic field the energy transport rate is declined, see Fig. 4(b). Fig. 5(a) and (b) describe the effect of γ* on Fη(ξ,η) and θ(ξ,η). The impression noted suggests that when fluid flows through a curved path, its inertia causes curvature to generate centrifugal forces. These forces are directed away from the center of curvature and can lead to an increase in Fη(ξ,η) on the outer side of the curve, see Fig. 5(a). This increase in velocity often results in higher kinetic energy, which can elevate θ(ξ,η) due to the conversion of kinetic energy into thermal energy through dissipation, see Fig. 5(b). Fig. 6(a) and (b) explain the impact of Fr* and λ* on Fη(ξ,η). Fig. 7 identifies the influence of Fr* against λ* on 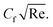 . The Darcy–Forchheimer law expands upon Darcy's law to account for inertial effects in porous media. It highlights that as Fη(ξ,η) decreases, see Fig. 6(a), inertial forces accounted for result in lower flow rates compared to predictions made using Darcy's law (which only considers viscous forces). However, the effect of Fr* on
. The Darcy–Forchheimer law expands upon Darcy's law to account for inertial effects in porous media. It highlights that as Fη(ξ,η) decreases, see Fig. 6(a), inertial forces accounted for result in lower flow rates compared to predictions made using Darcy's law (which only considers viscous forces). However, the effect of Fr* on 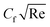 is more complex.
is more complex. 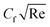 is determined using the τw at the solid–fluid interface, and both viscous and inertial affect it. Physically, an increase in inertial forces counteract the increase in
is determined using the τw at the solid–fluid interface, and both viscous and inertial affect it. Physically, an increase in inertial forces counteract the increase in 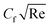 caused by lower velocity, resulting in a net inclination of
caused by lower velocity, resulting in a net inclination of 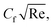 and see Fig. 7 for the behavior of hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. However, λ* suggests that due to porosity, there are more spaces available for fluid to flow through. This increased porosity creates additional pathways for fluid movement, resulting in higher Fη(ξ,η). The availability of open spaces allows fluid to move more freely through the medium, leading to greater Fη(ξ,η), whereas λ* results in a lower volume of the solid material within the medium, which reduces the resistance against fluid flow. Therefore, there is less interaction between the fluid and solid surfaces, resulting in
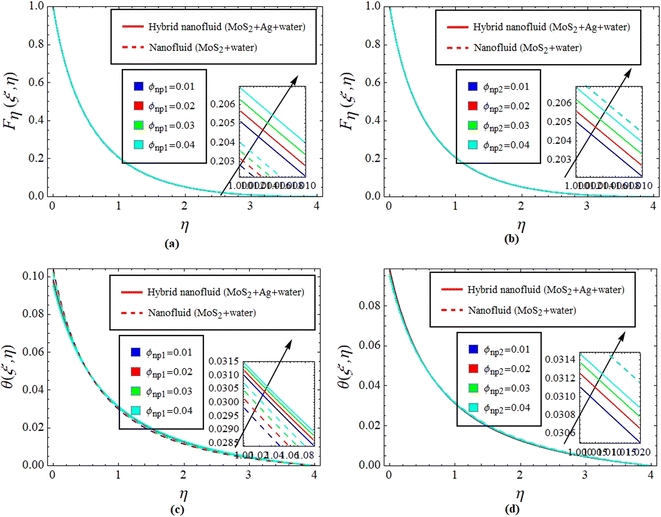
and see Fig. 7 for the behavior of hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. However, λ* suggests that due to porosity, there are more spaces available for fluid to flow through. This increased porosity creates additional pathways for fluid movement, resulting in higher Fη(ξ,η). The availability of open spaces allows fluid to move more freely through the medium, leading to greater Fη(ξ,η), whereas λ* results in a lower volume of the solid material within the medium, which reduces the resistance against fluid flow. Therefore, there is less interaction between the fluid and solid surfaces, resulting in 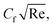 , see Fig. 7. Fig. 8(a)–(d) define the reaction of ϕnp1 and ϕnp2 on Fη(ξ,η) and θ(ξ,η) for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. The ϕnp1 notation is for MoS2 and ϕnp2 is for Ag. Due to the increment in ϕnp1 and ϕnp2, Fη(ξ,η) is augmented. Physically, by increasing ϕnp1 and ϕnp2, Fη(ξ,η) and θ(ξ,η) are heightened due to the enhanced thermal conductivity of the nanoparticles. This increases heat transfer rates within the fluid, creating a temperature gradient that drives fluid motion through thermally induced convection. The energy absorption by the nanoparticles and their transfer to the fluid contribute to increasing θ(ξ,η). Note that the MoS2 + Ag + water solution causes a more prominent effect. Thus, an increment in ϕnp1 and ϕnp2 improves heat transfer properties and thermally driven fluid motion, leading to enhanced Fη(ξ,η) and θ(ξ,η), see Fig. 8(a)–(d). Fig. 9(a)–(d) provide physical significance of γ* and ϕnp2 against ϕnp1 on
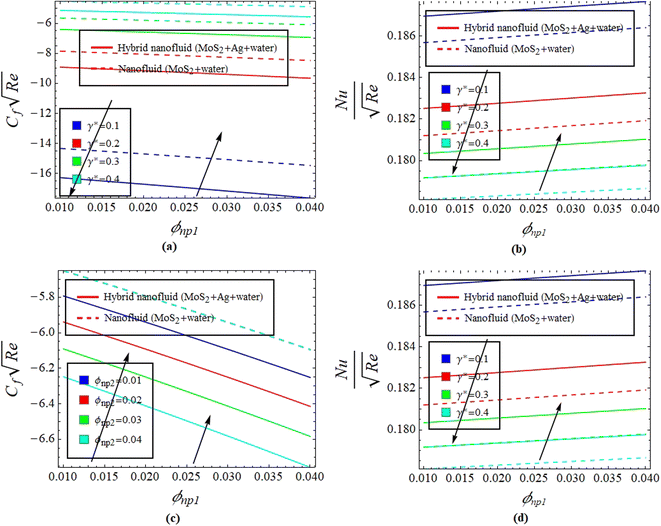
, see Fig. 7. Fig. 8(a)–(d) define the reaction of ϕnp1 and ϕnp2 on Fη(ξ,η) and θ(ξ,η) for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. The ϕnp1 notation is for MoS2 and ϕnp2 is for Ag. Due to the increment in ϕnp1 and ϕnp2, Fη(ξ,η) is augmented. Physically, by increasing ϕnp1 and ϕnp2, Fη(ξ,η) and θ(ξ,η) are heightened due to the enhanced thermal conductivity of the nanoparticles. This increases heat transfer rates within the fluid, creating a temperature gradient that drives fluid motion through thermally induced convection. The energy absorption by the nanoparticles and their transfer to the fluid contribute to increasing θ(ξ,η). Note that the MoS2 + Ag + water solution causes a more prominent effect. Thus, an increment in ϕnp1 and ϕnp2 improves heat transfer properties and thermally driven fluid motion, leading to enhanced Fη(ξ,η) and θ(ξ,η), see Fig. 8(a)–(d). Fig. 9(a)–(d) provide physical significance of γ* and ϕnp2 against ϕnp1 on 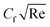 and
and 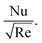 The graphs are designed for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. As γ* enhanced Fη(ξ,η), see Fig. 5(a), it causes a reduction in opposition forces, see Fig. 9(a). Therefore,
The graphs are designed for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. As γ* enhanced Fη(ξ,η), see Fig. 5(a), it causes a reduction in opposition forces, see Fig. 9(a). Therefore, 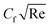 declines but due to ϕnp1,
declines but due to ϕnp1, 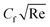 is boosted up. Similarly, the heat transfer rate is reduced due to an augmentation in γ*, see Fig. 9(b). The effect of ϕnp1 causes
is boosted up. Similarly, the heat transfer rate is reduced due to an augmentation in γ*, see Fig. 9(b). The effect of ϕnp1 causes 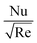 as well. The physics behind this is that the better thermal conductive properties of MoS2 augment
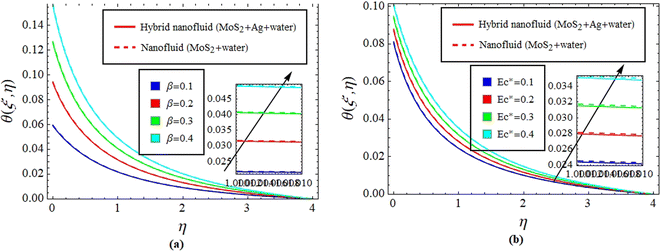
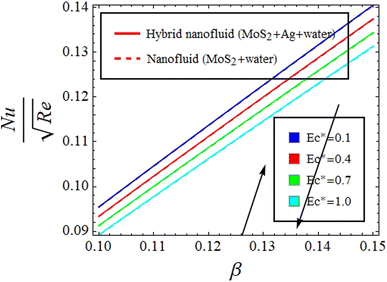
as well. The physics behind this is that the better thermal conductive properties of MoS2 augment 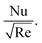 Fig. 10(a) and (b) give explanation of the impact of β and Ec* on θ(ξ,η). Fig. 11 identifies the influence of Ec* against β on
Fig. 10(a) and (b) give explanation of the impact of β and Ec* on θ(ξ,η). Fig. 11 identifies the influence of Ec* against β on 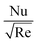 for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. An increment in β represents a shift from efficient internal heat transfer to surface resistance as the dominant factor in heat transfer processes
for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions. An increment in β represents a shift from efficient internal heat transfer to surface resistance as the dominant factor in heat transfer processes 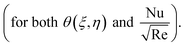 . For β ≪ 1, a uniform temperature distribution increment is seen within the material due to rapid internal heat transfer relative to surface resistance. In contrast, β ≫ 1 indicates slower internal heat transfer than surface heat transfer, which can result in temperature gradients within the material and notable differences between surface and bulk temperatures, see Fig. 10(a) and 11. Meanwhile, increasing Ec* signifies a greater significance of kinetic energy changes in a fluid than heat transfer rates. This can increase θ(ξ,η), while decreasing
. For β ≪ 1, a uniform temperature distribution increment is seen within the material due to rapid internal heat transfer relative to surface resistance. In contrast, β ≫ 1 indicates slower internal heat transfer than surface heat transfer, which can result in temperature gradients within the material and notable differences between surface and bulk temperatures, see Fig. 10(a) and 11. Meanwhile, increasing Ec* signifies a greater significance of kinetic energy changes in a fluid than heat transfer rates. This can increase θ(ξ,η), while decreasing 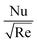 for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions, see Fig. 10(b) and 11.
for hybrid nanofluid (MoS2 + Ag + water) and for nanofluid (MoS2 + water) solutions, see Fig. 10(b) and 11.
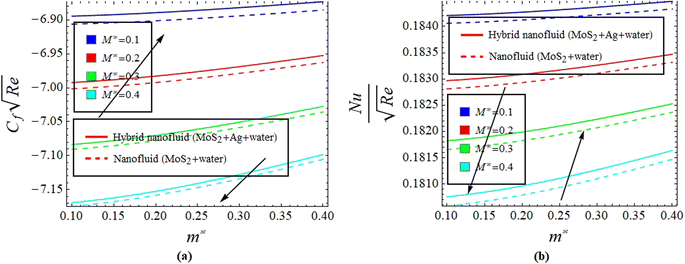
From Table 2, it is seen that the absolute value of the regression coefficient of M* is greater than the regression coefficient of m*. Hence, the effect of M* is prominent over m* on skin friction 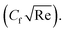 Similarly, from Table 3, it is observed that the absolute regression coefficient of Ec* is more than that of γ*. Therefore, it is concluded that Ec* is more effective for Nusselt number
Similarly, from Table 3, it is observed that the absolute regression coefficient of Ec* is more than that of γ*. Therefore, it is concluded that Ec* is more effective for Nusselt number 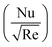 in comparison with γ*.
in comparison with γ*.
5. Final remarks
This study investigated the complex interactions of a hybrid nanofluid flowing over a curved surface subjected to stretching. A magnetic field perpendicular to the flow and directed inward engaged with a composite of molybdenum disulfide and argentum nanoparticles suspended in a pure water solution, forming a hybrid nanomaterial. The study analyzed heat transport through magnetohydrodynamics, Darcy–Forchheimer porous medium flow, Joule heating, and a convective boundary condition. Using numerical and statistical methods, the study gained valuable insights into the behavior of the hybrid nanofluid system under specified conditions. The main key points are:❖ The MoS2 + Ag + water solution caused a more prominent effect than MoS2 + water.
❖ Joule heating promoted the energy transport among the particles, while Lorentz force caused the flow field to lessen, resulting in an increment in skin friction.
❖ The Hall effect affected fluid's dynamics by increasing velocity, while decreasing skin friction. However, thermal transport declined but the Nusselt number boosted up.
❖ Curvature augmented velocity and causes conversion of kinetic energy into thermal energy, which inclined thermal transport.
❖ The volume fraction improved heat transfer properties and thermally driven fluid motion.
❖ Darcy–Forchheimer flow included viscous and inertial forces which resulted in higher flow rates and diminished skin friction.
❖ Porosity declined flow and enhanced skin friction.
❖ The Biot number caused uniform temperature distribution within the material due to rapid internal heat transfer relative to surface resistance.
❖ The biot number augmented the heat transfer rate significantly.
❖ The Eckert number caused heat capacity to enhance and elevated thermal transport; however, it lessened the Nusselt number.
❖ Regression analysis suggested that the effect of the Eckert number on the Nusselt number was more than that of the Biot number.
❖ The impact of Darcy–Forchheimer flow through regression analysis was prominent over the porosity parameter on skin friction.
5.1 Limitations and scope of future work
The study's use of numerical and statistical methods demonstrates its potential for insightful analysis. However, experimental validation is necessary to enhance the model's credibility further and ensure its practical application accuracy. Although the findings are specific to the investigated parameters, they provide a valuable basis for comprehending the behavior of hybrid nanofluids and allow for customized applications in a broad range of scenarios. Real-world complexity, including factors such as turbulence and impurities, emphasizes the importance of future research to expand on this foundation, considering the intricate nature of dynamics of fluid in various environments.Conflicts of interest
The authors declare that there is no conflict of interest amongst them.Abbreviations
Nomenclature for the involved expressions
| U(r,z) and W(r,z) | Velocity components |
| F η (ξ,η) | Non-dimensional velocity |
| U 0 | Reference stretching velocity |
| θ(ξ,η) | Non-dimensional temperature |
| T w | Surface/wall temperature |
| e 1 | Electron charge |
| L | Characteristic length |
| Fr* | Forchheimer parameter |
| B 0 | Magnetic field strength |
| γ* | Curvature parameter |
| m* | Hall parameter |
| Re | Reynolds number |
| τ w = τrz | Wall shear stress |
| λ* | Porosity parameter |
| r,z | Coordinates |
| ψ(r,z) | Stream function |
| U w(x) | Stretching velocity |
| T(r,z) | Temperature |
| T ∞ | Ambient temperature |
| ne 1 | Free electron density |
| a 0 | Radius of a curved surface |
| C b | Drag coefficient |
| M* | Dimensionless magnetic parameter |
| Pr | Prandtl number |
| Ec* | Eckert number |
| Nu | Nusselt number |
| C f | Skin friction |
| k p | Porous medium permeability |
Thermophysical features (MoS2, Ag, and water)
| Ag | Argentum |
| μ hnf | Dynamic viscosity |
| ρ hnf | Density |
| κ hnf | Thermal conductivity |
| κ np1 | MoS2 thermal conductivity |
| ϕ np1 | MoS2 volume fraction |
| (cp)hnf | Specific heat |
| σ hnf | Electrical conductance |
| ν hnf | Kinematic viscosity |
| α hnf | Thermal diffusivity |
| MoS2 | Molybdenum dioxide |
| μ bf | Base fluid dynamic viscosity |
| ρ bf | Base fluid density |
| κ bf | Base fluid thermal conductivity |
| κ np2 | Ag thermal conductivity |
| ϕ np2 | Agvolume fraction |
| (cp)bf | Base fluid specific heat |
| σ bf | Base fluid electrical conductivity |
| ν bf | Base fluid kinematic viscosity |
| α bf | Base fluid thermal diffusivity |
Note added after first publication
This article replaces the version published on 1st December 2023, which contained errors in equation 14.Acknowledgements
The authors present their appreciation to King Saud University for funding this research through Researchers Supporting Program number (RSPD2023R704), King Saud University, Riyadh, Saudi Arabia.References
- J. H. Lee, S. H. Lee, C. Choi, S. Jang and S. Choi, A review of thermal conductivity data, mechanisms and models for nanofluids, Int. J. Micro-Nano Scale Transp., 2011, 1085–1110 CAS.
- W. H. Lee, C. K. Rhee, J. Koo, J. Lee, S. P. Jang, S. U. Choi, K. W. Lee, H. Y. Bae, G. J. Lee, C. K. Kim and S. W. Hong, Round-robin test on thermal conductivity measurement of ZnO nanofluids and comparison of experimental results with theoretical bounds, Nanoscale Res. Lett., 2011, 6, 1–11 Search PubMed.
- T. J. Choi, B. Subedi, H. J. Ham, M. S. Park and S. P. Jang, A review of the internal forced convective heat transfer characteristics of nanofluids: experimental features, mechanisms and thermal performance criteria, J. Mech. Sci. Technol., 2018, 32, 3491–3505 CrossRef.
- S. Nadeem, N. Abbas and M. Y. Malik, Inspection of hybrid based nanofluid flow over a curved surface, Comput. Methods Progr. Biomed., 2020, 189, 105193 CrossRef CAS PubMed.
- H. Waqas, F. F. Bukhari, U. Farooq, M. S. Alqarni and T. Muhammad, Numerical computation of melting heat transfer in nonlinear radiative flow of hybrid nanofluids due to permeable stretching curved surface, Case Stud. Therm. Eng., 2021, 27, 101348 CrossRef.
- N. S. Wahid, N. M. Arifin, N. S. Khashi'ie, I. Pop, N. Bachok and M. E. H. Hafidzuddin, Flow and heat transfer of hybrid nanofluid induced by an exponentially stretching/shrinking curved surface, Case Stud. Therm. Eng., 2021, 25, 100982 CrossRef.
- K. Muhammad, T. Hayat and A. Alsaedi, Numerical study of Newtonian heating in flow of hybrid nanofluid (SWCNTs+ CuO+ ethylene glycol) past a curved surface with viscous dissipation, J. Therm. Anal. Calorim., 2021, 143, 1291–1302 CrossRef CAS.
- M. Hassan, M. Marin, R. Ellahi and S. Z. Alamri, Exploration of convective heat transfer and flow characteristics synthesis by Cu–Ag/water hybrid-nanofluids, Heat Tran. Res., 2018, 49(18), 1837–1848 CrossRef.
- M. I. Khan, K. Muhammad, T. Hayat, S. Farooq and A. Alsaedi, Numerical simulation for Darcy-Forchheimer flow of carbon nanotubes due to convectively heated nonlinear curved stretching surface, Int. J. Numer. Methods Heat Fluid Flow, 2019, 29(9), 3290–3304 CrossRef.
- T. Hayat, K. Muhammad, A. Alsaedi and B. Ahmed, Melting effect in squeezing flow of third-garde fluid with non-Fourier heat flux model, Phys. Scr., 2019, 94(10), 105705 CrossRef CAS.
- M. I. Khan, K. Muhammad, T. Hayat, S. Farooq and A. Alsaedi, Numerical simulation for Darcy-Forchheimer flow of carbon nanotubes due to convectively heated nonlinear curved stretching surface, Int. J. Numer. Methods Heat Fluid Flow, 2019, 29(9), 3290–3304 CrossRef.
- R. Ellahi, S. M. Sait, N. Shehzad and Z. Ayaz, A hybrid investigation on numerical and analytical solutions of electro-magnetohydrodynamics flow of nanofluid through porous media with entropy generation, Int. J. Numer. Methods Heat Fluid Flow, 2020, 30(2), 834–854 CrossRef.
- R. Ellahi, F. Hussain, S. Asad Abbas, M. M. Sarafraz, M. Goodarzi and M. S. Shadloo, Study of two-phase Newtonian nanofluid flow hybrid with Hafnium particles under the effects of slip, Inventions, 2020, 5(1), 6 CrossRef.
- A. Ali, R. N. Jana and S. Das, Radiative CNT-based hybrid magneto-nanoliquid flow over an extending curved surface with slippage and convective heating, Heat Transfer, 2021, 50(3), 2997–3020 CrossRef.
- A. Riaz, R. Ellahi and S. M. Sait, Role of hybrid nanoparticles in thermal performance of peristaltic flow of Eyring–Powell fluid model, J. Therm. Anal. Calorim., 2021, 143, 1021–1035 CrossRef CAS.
- T. Hayat, K. Muhammad and A. Alsaedi, Numerical study of melting heat transfer in stagnation-point flow of hybrid nanomaterial (MWCNTs+ Ag+ kerosene oil), Int. J. Numer. Methods Heat Fluid Flow, 2021, 31(8), 2580–2598 CrossRef.
- K. Muhammad, T. Hayat and A. Alsaedi, Heat transfer analysis in slip flow of hybrid nanomaterial (ethylene glycol+ Ag+ CuO) via thermal radiation and Newtonian heating, Waves Random Complex Media, 2021, 1–21 CAS.
- M. Sarfraz and M. Khan, Magnetized homann flow comprising GO and Co3O4 nanoparticles past a biaxially stretching surface, Phys. Scr., 2023, 98(3), 035218 CrossRef.
- M. Sarfraz and M. Khan, Thermodynamic irreversibility analysis of water conveying argentum and titania nanoparticles subject to inclined stretching surface, Phys. Scr., 2023, 98(2), 025205 CrossRef.
- T. Hayat, A. Fatima, K. Muhammad and A. Alsaedi, Heat transfer and entropy analysis in squeezing flow of hybrid nanofluid (Au-CuO/NaAlg) with DF (Darcy-Forchheimer) and CC (Cattaneo-Christov) heat flux, Mater. Sci. Eng. B, 2023, 288, 116150 CrossRef CAS.
- M. Sarfraz and M. Khan, Heat transfer efficiency in planar and axisymmetric ternary hybrid nanofluid flows, Case Stud. Therm. Eng., 2023, 44, 102857 CrossRef.
- M. Sarfraz, M. Khan, A. Al-Zubaidi and S. Saleem, Tribology-informed analysis of convective energy transfer in ternary hybrid nanofluids on inclined porous surfaces, Tribol. Int., 2023, 188, 108860 CrossRef CAS.
- H. N. Najm, Uncertainty quantification and polynomial chaos techniques in computational fluid dynamics, Annu. Rev. Fluid. Mech., 2009, 41, 35–52 CrossRef.
- T. T. Zhang, W. Huang, Z. G. Wang and L. Yan, A study of airfoil parameterization, modeling, and optimization based on the computational fluid dynamics method, J. Zhejiang Univ., Sci., A, 2016, 17(8), 632–645 CrossRef CAS.
- B. Kumar, G. S. Seth and R. Nandkeolyar, Quadratic multiple regression model and spectral relaxation approach to analyse stagnation point nanofluid flow with second-order slip, Proc. Inst. Mech. Eng., Part E, 2020, 234(1), 3–14 CrossRef.
- J. Liu, T. Zhao, K. Liu, B. Sun and C. Bai, Optimization of structure parameters in a coal pyrolysis filtration system based on CFD and quadratic regression orthogonal combination and a genetic algorithm, Eng. Appl. Comput. Fluid Mech., 2021, 15(1), 815–829 Search PubMed.
- N. Islam, A. A. Pasha, W. Jamshed, R. W. Ibrahim and R. Alsulami, On Powell-Eyring hybridity nanofluidic flow based Carboxy-Methyl-Cellulose (CMC) with solar thermal radiation: a quadratic regression estimation, Chaos, Solitons Fractals, 2022, 138, 106413 CAS.
- B. Ali, N. A. Ahammad, A. U. Awan, K. Guedri, E. M. Tag-ElDin and S. Majeed, Dynamics of Rotating Micropolar Fluid over a Stretch Surface: The Case of Linear and Quadratic Convection Significance in Thermal Management, Nanomaterials, 2022, 12(18), 3100 CrossRef CAS PubMed.
- M. Turkyilmazoglu and M. Altanji, Fractional models of falling object with linear and quadratic frictional forces considering Caputo derivative, Chaos, Solitons Fractals, 2023, 166, 112980 CrossRef.
- T. Sajid, W. Jamshed, R. W. Ibrahim, M. R. Eid, A. Abd-Elmonem and M. Arshad, Quadratic regression analysis for nonlinear heat source/sink and mathematical Fourier heat law influences on Reiner-Philippoff hybrid nanofluid flow applying Galerkin finite element method, J. Magn. Magn. Mater., 2023, 568, 170383 CrossRef CAS.
- F. Wang, M. Sohail, U. Nazir, E. R. El-Zahar, M. Singh, A. Singh, C. R. Mohan and S. M. Eldin, Applications of triadic hybridized-cross nanomaterials suspended in engine oil using quadratic and linear convection with magnetic dipole, Case Stud. Therm. Eng., 2023, 44, 102873 CrossRef.
- K. Sarkodie, A. Fergusson-Rees, M. Abdulkadir and N. Y. Asiedu, Gas-liquid flow regime identification via a non-intrusive optical sensor combined with polynomial regression and linear discriminant analysis, Ann. Nucl. Energy, 2023, 180, 109424 CrossRef CAS.
- B. Kumbhakar, S. Nandi and A. J. Chamkha, Unsteady hybrid nanofluid flow over a convectively heated cylinder with inclined magnetic field and viscous dissipation: a multiple regression analysis, Chin. J. Phys., 2022, 79, 38–56 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |