Open Access Article
Open Access ArticleStrength, number, and kinetics of hydrogen bonds for water confined inside boron nitride nanotubes†
Bhargav Sai
Chava
and
Siddhartha
Das
 *
*
Department of Mechanical Engineering, University of Maryland, College Park, MD 20742, USA. E-mail: sidd@umd.edu
First published on 29th April 2024
Abstract
Water has shown a myriad of highly interesting properties and behaviors, such as very low friction, phase transition under unexpected conditions, massive property alterations, etc. inside strong nanoconfinements of few-nanometer to sub-nanometer diameters. Water–water hydrogen bonding is one of the most important factors dictating such water behavior and properties inside such strong nanoconfinements. In this paper, we employ Reactive Force Field (ReaxFF) molecular dynamics (MD) simulations for studying multiple facets of such water–water hydrogen bonds (HBs) inside boron-nitride nanotubes (BNNTs) having diameters ranging from a few nanometers to sub-nanometers. First, the strength of the water–water HB interactions, as a function of the HB configuration, is quantified by studying the corresponding PMF (potential of mean force). For water present in extreme confinements (BNNTs with sub-nanometric diameters), we see completely isolated HB basins. On the other hand, for bulk water the HB basin is connected (via a saddle point) to a nearby second PMF well. Therefore, our analysis successfully distinguishes the HB characteristics between the cases of water in extreme confinement and bulk water. Second, we study the kinetics of such water–water HBs: HBs formed by a given pair of water molecules in extreme confinements show a much larger probability of remaining intact once formed or re-forming after they have been broken. Both these results, which shed new light on water–water hydrogen bonding inside strong nanoconfinements, can be explained by the single-file structure formed by the water molecules in extreme BNNT confinements.
Introduction
Water structure in the presence of strong (few nanometers or sub-nanometers) confinements has been extensively studied,1–11 owing to some of the most fascinating effects demonstrated by water in such confinements, including ultra-fast transport,12–14 spontaneous filling of hydrophobic nanotubes,15 phase transition under the most unexpected conditions,16 use in the fabrication of hybrid materials,17 significant changes in properties such as melting point, boiling point, density, and surface tension,18etc. Non-bonded water–water interactions, such as water–water hydrogen bonding, are an important factor governing water behavior in such extreme confinements.19–21 For example, hydrogen bonding has been known to dictate the nature of water diffusion inside CNTs of varying diameters,22–24 graphene nanochannels of different heights,25,26 and self-assembled ionic liquid crystals,27 unidirectional proton transport in fluorinated CNTs,28etc. Water–water hydrogen bonds (HBs) trigger water clusters inside a confinement: such clusters are broken when in contact with certain types of nanoconfinement material (e.g., nanomaterials composed of fluorous compounds) resulting in very fast water transport in such nanoconfinements.29 In our recent study, we established that such disruption of hydrogen bond (HB) formation, associated with the presence of dangling –OH bonds, leads to the spontaneous filling of boron nitride nanotubes (BNNTs) of sub-nanometric diameters.30While the importance of water–water hydrogen bonding inside strong confinements has been thoroughly established, there remain several gaps in understanding the very nature of such HBs inside confinements. For example, the manner in which the progressive increase in the extent of confinement leads to the alterations of the conditions that define the formation of water–water HBs and the corresponding energetics of such hydrogen bonding, the confinement-driven changes in the kinetics of hydrogen bonding (e.g., how stable a hydrogen bond is, or once an HB is broken, how quickly it re-forms), etc. have not been extensively explored. For example, in a very recent study the water behavior inside nanometric to sub-nanometric diameter CNTs was probed using MD simulations; however, such confinement-driven changes in the conditions associated with the HB formation and the corresponding HB energetics and kinetics were not probed.31 In this paper, we address these issues considering water confined inside BNNTs of varying diameters of nanometer to sub-nanometer ranges. In our previous study, we have delineated in great detail the manner in which BNNTs of different diameters lead to entropy-driven water filling of BNNTs, with the factors dictating the favorable entropy changes and the corresponding water structure being strongly dictated by the BNNT diameters.30 In this paper, through all-atom molecular dynamics (MD) simulations, we study two critical issues: (1) the effect of confinement on the water–water interactions that govern the hydrogen bonding and (2) the effect of confinement on the kinetics of the water–water HBs. In order to understand the effect of confinement on the interactions governing the water–water hydrogen bonding, we probe the PMFs (potential of mean forces) dictating the water–water HBs. Our results demonstrate that these PMFs, which are expressed as functions of r and θ (r denotes the inter-oxygen distance or the distance between the oxygen atoms of the two water molecules participating in the hydrogen bonding and θ denotes the angle between the OH bond and the line joining the oxygen atoms), are significantly affected by the extent of the BNNT confinement. For example, we observe completely isolated HB basins in BNNTs with strong confinement, which is in stark contrast to the HBs in bulk water or in larger diameter BNNTs where there is a second nearby PMF well to which the primary HB basin is connected via a saddle point. The second major contribution of this paper is to unveil the most remarkable BNNT-diameter-dependent kinetics of the water–water HBs. The specific single-file water structure inside sub-nanometer-diameter BNNTs ensures that the water–water HBs formed inside such BNNTs are stable over a much longer time period. This is confirmed by the corresponding auto-correlation function (dictating the lifetime of the HBs) that decays to a large non-zero constant value at long times. Similarly, the same water structure ensures that such HBs, once broken, show a strong tendency to re-form. Overall, the findings of this paper create new knowledge of the specific water–water hydrogen bonding behavior inside extreme nano- and sub-nano-confinements.
Results and discussion
Water–water interactions dictating the hydrogen bonding inside BNNTs
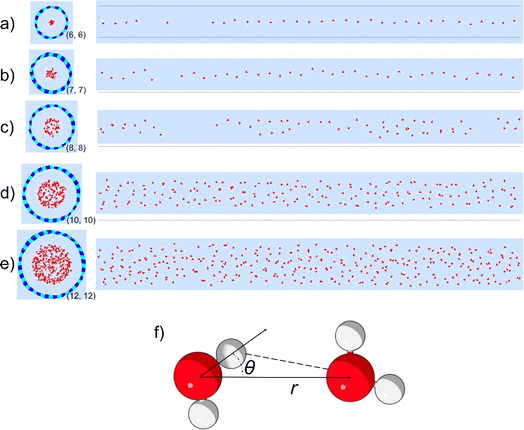
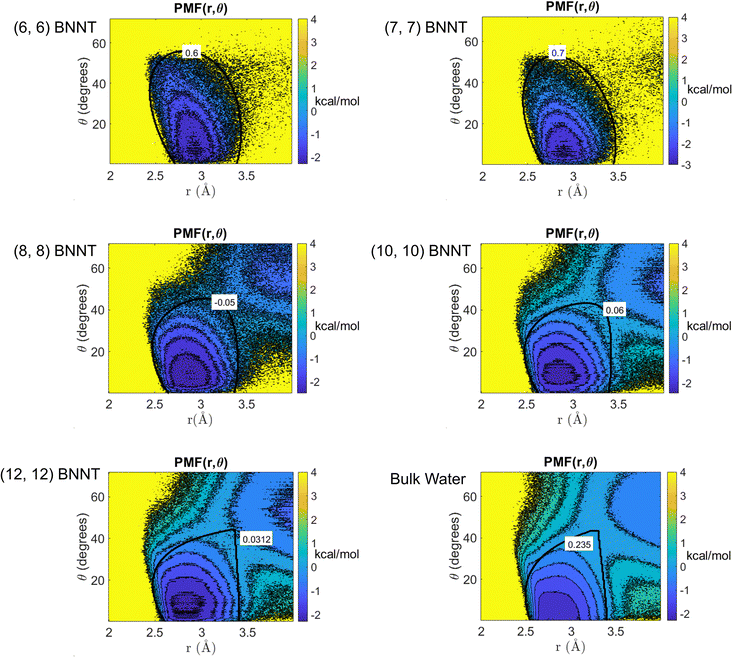
To study the hydrogen bonding thermodynamics for water confined in BNNTs, we performed the ReaxFF MD simulations of water confined in five different BNNTs with chiral indices (6, 6), (7, 7), (8, 8), (10, 10), and (12, 12) respectively [see Fig. 1(a)–(e) and the Methods section for more details]. The diameters of these BNNTs range from 0.85 nm to 1.69 nm with the (6, 6) BNNTs having the smallest diameter and the (12, 12) BNNTs having the largest diameter. In addition, we also carried out bulk water simulations to highlight the effect of the BNNT-based confinement on water–water hydrogen bonding relative to water in the absence of any confinement. The detailed water structure and the energetics dictating these structures have been discussed in our previous paper;30 we avoid repeating such discussions here for the sake of brevity.In order to identify hydrogen bonding configurations between pairs of water molecules, we need to devise appropriate HB definitions for the various systems considered in this study. The generic geometry-based HB definition for water involves cutoff values for the inter-oxygen distance (r) and the angle (θ) between the OH bond and the line joining the oxygen atoms [see Fig. 1(f)].32–34 The most widely used criteria (for the formation of water–water HBs) for bulk water are r < 3.5 Å and θ < 30°.33–35 However, these specific cutoff values and the resulting rectangular boundary, located on the 2D PMF [W(r,θ)] mapped using (r, θ) coordinates, may not be appropriate for identifying HB configurations among water molecules present inside nanoconfinements (i.e., in non-bulk-like environments). In particular, for water inside the sub-nanometer and nanometer wide nanotubes, the shape and size of the PMF basin corresponding to the HB configurations can differ significantly from that of the bulk water.
Fig. 2 shows the 2D PMFs [W(r,θ)] corresponding to water–water interactions for all the systems considered in this study. In these PMF plots, we identify the HB basin (i.e., identify the r and θ values that correspond to water–water hydrogen bonding) and the boundary distinguishing between the water–water hydrogen bonding interactions (characterized by large negative PMF values) and other types of water–water interactions (characterized by weaker negative PMF values). From these results, we can easily confirm that the ensemble of configurations (r, θ) associated with the formation of the water–water HBs are different for water confined in BNNTs (of various diameters) as compared to water in the bulk. To be specific, we see a striking contrast between the PMFs of bulk water and water confined in (6, 6) and (7, 7) BNNTs (with diameters of 0.85 nm and 1 nm, respectively). For water present in these extreme confinements, we see completely isolated HB basins. On the other hand, for bulk water the HB basin is connected (via a saddle point) to a nearby second PMF well, which is centered around larger r and θ values and corresponds to the second hydration shell. In our previous study,30 we identified that water forms an axially ordered single-file structure in (6, 6) and (7, 7) BNNTs. As a result, in these extreme confinements, a given water molecule is well separated from other water molecules that are not its nearest neighbors (i.e., not a part of its first solvation shell). For water in (6,6) and (7,7) BNNTs, as shown in Fig. 3, the r value of the second peak of the corresponding water O–O RDF – this second peak denotes the water molecules in the second solvation shell of a given water molecule – is significantly large compared to the other systems considered in this study. Also, the minimum between the first and second O–O RDF peaks in these systems [water inside (6, 6) and (7, 7) BNNTs] reaches a near zero value indicating that no pathways exist for water molecules to travel between the first and second solvation shells. This justifies such a completely isolated HB basin for water molecules in (6, 6) and (7, 7) BNNTs.
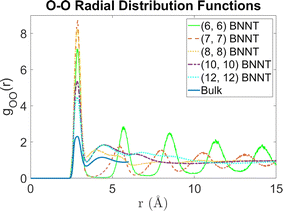 | ||
| Fig. 3 Radial distribution functions between oxygen atoms for water molecules in the bulk and in BNNTs with chiral indices (6, 6), (7, 7), (8, 8), (10, 10) and (12, 12). | ||
In the (8, 8) BNNTs, as the nanotube diameter increases, the ordered single-file structure disappears, and we start to see high-density clusters of water molecules joined by low-density chain-like regions.30 This water structure results in the appearance of the second hydration PMF well situated close to the HB basin (see Fig. 2). Similarly, with further weakening of confinement in (10, 10) and (12, 12) BNNTs, the PMF maps approach a behavior similar to the water molecules in the bulk and accordingly, the HB basin becomes separated from the nearby well by a saddle region (see Fig. 2). The possibility of such a saddle region connecting the HB basin and the nearby second hydration basin (for bulk water and water inside larger diameter BNNTs) creates pathways for water molecules to travel between these basins.
Additionally, we performed a ReaxFF MD simulation of a water slab on a hexagonal Boron Nitride (h-BN) sheet and obtained the water HB PMF for the h-BN-sheet-supported interfacial water molecules. Results (see Fig. S1 in the ESI†) confirm that the HB PMF of h-BN-sheet-supported interfacial water shows a near identical behavior to that of bulk water.
Number of hydrogen bonds inside BNNTs
From the 2D PMF results provided in Fig. 2, we determine the appropriate water HB definitions for all the systems considered in this study by choosing a continuous iso-surface with a PMF value beyond which the volume enclosed by the iso-surface increases discontinuously (please refer to the Methods section for details). The iso-surface corresponding to the HB definition for each system can be found in Fig. 2. Using these definitions, we compute the average number of HBs formed by a water molecule (NHB) in each system (see Table 1). For bulk water, our findings show the NHB to be 3.62, which is close to the values reported in previous studies35 (ref. 35 reported 3.6 hydrogen bonds per molecule in bulk water) following similar approaches to develop HB definitions. Inside the BNNTs, NHB decreases significantly: the smaller the BNNT diameter (or more pronounced the degree of nanoconfinement), the more prominent is this decrease. For single-file water [in (6, 6) and (7, 7) BNNTs],30 we obtain NHB values less than 2 indicating that each water molecule is connected to less than or equal to two adjacent water molecules in the single file structure. Such a behavior stems from the water molecules taking an axially ordered single-file structure in (6, 6) and (7, 7) BNNTs (see ref. 30) causing the water molecules to be well separated from other water molecules that are not their nearest neighbors. On the other hand, for water confined in wider BNNTs [i.e., in (10, 10) and (12, 12) BNNTs], we see NHB values greater than 3 with a significant fraction of water molecules forming three or more HBs with surrounding water molecules in these systems.| System | N HB |
|---|---|
| Bulk water | 3.62 |
| (6, 6) | 1.74 |
| (7, 7) | 1.88 |
| (8, 8) | 2.35 |
| (10, 10) | 3.04 |
| (12, 12) | 3.29 |
Kinetics of water–water hydrogen bonds inside BNNTs
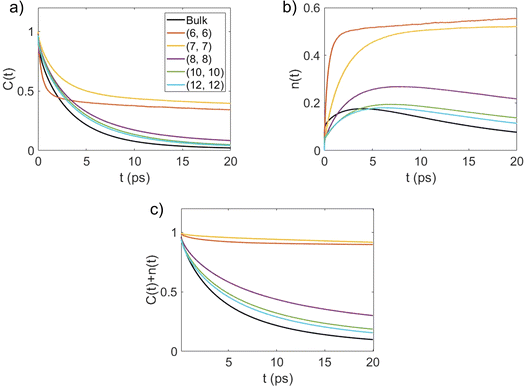
The second important contribution of this study is investigating the effect of nanoconfinement on the kinetics of the water–water HBs. We have explored the HB kinetics for nanoconfined and bulk water using a chemical-dynamics-based analysis.33 In this process, we first compute the HB autocorrelation function, C(t), using an HB population operator, h(t), which equals 1 if an HB is present between a given pair of water molecules and 0 otherwise. As such, the HB autocorrelation function is given by: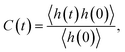 | (1) |
This function gives the conditional probability that a pair of water molecules are hydrogen bonded at time t, given that there exists an HB between this pair at time zero.33 As shown in Fig. 4(a), C(t) decays the fastest to zero for bulk water and the rate of decay generally decreases with an increase in the degree of confinement (i.e., as the BNNT diameter decreases) except for (6, 6) BNNTs. However, unlike other systems, C(t) for the water molecules confined in (6, 6) and (7, 7) BNNTs tends to decay to a finite value below 0.5. In these extreme confinements, i.e., in (6, 6) and (7, 7) BNNTs, where water takes a single-file structure30 with NHB close to 2 (see Table 1), a given water molecule is forced to form HBs with the same two neighboring water molecules for the entire duration of the simulations. As a result, if a pair of water molecules is found to form an HB through one of the four hydrogen atoms at t = 0, the probability of finding the same HB at t = ∞ would be approximately 0.25 (one of four possible HBs). In Fig. 4(a), we report our calculations for a finite time of 20 ps and we can see that C(t) converges to 0.25. For bulk water as well as water in larger diameter BNNTs, a given water molecule has close interactions with its second solvation shell and water molecules can travel between the first solvation shell (HB basin) and the second solvation shell through the saddle region (see Fig. 2); accordingly, in bulk water and water in large diameter BNNTs water molecules diffuse away from each other at larger times, and therefore, the chances that a given water molecule will form the HB (at time t) with the same molecule with which it formed the HB at time t = 0 becomes progressively small (and approaches zero) with time. This justifies the decay of C(t) to zero at larger times for bulk water as well as water in larger diameter BNNTs.
Fig. 4(b) shows the time dependent conditional probability [n(t)] that an initially hydrogen bonded pair of water molecules stay within the HB vicinity with the initial bond broken. In a given system, a pair of water molecules is considered to be in the HB vicinity if their inter-oxygen distance is less than the maximum value of r that lies on the HB boundary (as indicated in Fig. 2).
This conditional probability, n(t), can be expressed as:
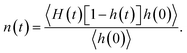 | (2) |
For single-file water in (6, 6) and (7, 7) BNNTs, n(t) relaxes to a value larger than 0.5 for the same reason that the corresponding C(t) approaches a finite value below 0.5 at large t. In the single file structure, almost all the pairs of adjacent water molecules stay hydrogen bonded, via one of four possible hydrogens, for the entire simulation period. Accordingly, for any given pair of water molecules that always stay connected via an HB, there is a three-in-four probability that an initial HB between these molecules is broken at large t. In other systems, namely bulk water and water in BNNTs with larger diameters, n(t) increases at shorter times and then relaxes to zero at longer times. This behavior indicates that, in these systems, once an HB breaks between a pair of water molecules, these water molecules either relax back to form the same HB or diffuse away from each other at large t.33 Here, the latter seems to be the case (for bulk water and water in larger diameter BNNTs) as evident from Fig. 4(c), which shows the time dependence of C(t) + n(t). Here, C(t) + n(t) gives the time dependent conditional probability that a pair of initially hydrogen bonded water molecules stay within the HB vicinity. For systems where water molecules do not form a single-file structure [i.e., in bulk and in (8, 8), (10, 10) and (12, 12) BNNTs], C(t) + n(t) rapidly decays to zero indicating that as time progresses, pairs of water molecules diffuse away from each other after an HB is broken. In contrast, for single file water, i.e., for water confined in (6, 6) and (7, 7) BNNTs, C(t) + n(t) decays to values near 0.9 since nearly every pair of adjacent water molecules stays within the HB vicinity forming one of four possible HBs.
The description of the kinetics of the water–water hydrogen bonding inside nanoconfinements will be further harnessed if one can determine the effect of confinement on the forward rate constant (k) of HB breaking and the backward rate constant (k′) of HB formation. To obtain these rate constants, we computed the reactive flux HB correlation function K(t), as a function of the autocorrelation C(t), as:33,36
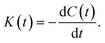 | (3) |
K(t) can be further related to C(t) and n(t) via the following relation:33,36
| K(t) = kC(t) − k′n(t). | (4) |
From the above relations, the HB lifetime can be obtained using33,36
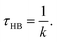 | (5) |
Assuming that hydrogen bond breakage can be described as an Eyring process,36 we can relate ΔGHB (the Gibbs free energy of HB breaking) to τHB using the following equation:
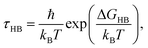 | (6) |
Table 2 shows the HB lifetimes (τHB) and ΔGHB for water in all the systems studied in this work. We see that bulk water has the smallest ΔGHB, followed by water confined in the (6, 6) BNNTs. For other confined systems, ΔGHB is inversely proportional to the nanotube diameter with water in the (7, 7) BNNTs exhibiting the largest ΔGHB. For bulk water, there is an entropic gain associated with HB breaking due to water exchange between the first and second hydration shells of a given water molecule. In the (7, 7) BNNTs, as a given water molecule only has access to the same two water molecules to form an HB with, such exchange entropic gain associated with HB breaking is absent. Thus, HBs are less prone to breaking and are stronger in the (7, 7) BNNTs compared to the bulk water. As the BNNT diameter increases and the single file nature of water disappears, the water exchange entropic gain resulting from HB breaking increases resulting in progressively weaker HBs.
| System | ΔGHB (kcal mol−1) | τ HB (ps) | k (ps−1) | k' (ps−1) |
|---|---|---|---|---|
| Bulk water | 1.8142 | 3.3550 | 0.29806 | 0.0719 |
| (6, 6) | 1.8999 | 3.8735 | 0.25816 | 0.1698 |
| (7, 7) | 2.0129 | 4.6815 | 0.21360 | 0.1686 |
| (8, 8) | 1.9629 | 4.3051 | 0.23228 | 0.0831 |
| (10, 10) | 1.9483 | 4.2011 | 0.23803 | 0.0746 |
| (12, 12) | 1.9277 | 4.0587 | 0.24638 | 0.0752 |
Our previous study30 has shown that in the (6, 6) BNNTs, water molecules have low translational entropy due to extreme radial confinement restricting the in-plane translational motions of the water molecules. However, in the (6, 6) BNNTs, water molecules possess high rotational entropy, on account of the flipping rotations of water molecules in this system and such water flipping involves regular HB breakage. Thus, the small ΔGHB for water in the (6, 6) BNNTs can be associated with the corresponding significant rotational entropic gain associated with the HB breakage.
Conclusions
In summary, we use ReaxFF MD simulations to study the effect of BNNT induced nanoconfinement on (1) water–water interactions, the resulting conditions associated with the corresponding water–water hydrogen bonding, and the total number of HBs and (2) the kinetics of such hydrogen bonding. First the 2D PMF maps dictating the water–water interactions in BNNTs of different diameters and bulk water are obtained. This data is subsequently used to identify the conditions dictating the water–water hydrogen bonding in boron nitride nanoconfinements. In very narrow BNNTs (with sub-nanometric diameters), we observe completely isolated HB basins; in contrast, in bulk water, the HB basin is connected to a nearby PMF well via a saddle point. Such a behavior is entirely attributed to the unique single-file structure of water in such BNNTs with sub-nanometric diameters. This same single-file water structure dictates the kinetics of water–water HBs in such strong sub-nanometric confinements. The single-file structure ensures that a given water molecule always remains in close proximity to two or less other water molecules: hence the probability that the HB between the same pair of water molecules survives or re-forms after being broken is significantly high for water molecules in such strong confinements. Overall, our study sheds light on some of the most pressing fundamental issues of water properties inside very strong confinements, and we anticipate that such new information will be potentially useful in explaining the vast number of highly non-intuitive events associated with water entrapped in strong confinements.Methods
All the simulations were performed using the ReaxFF37 package implemented in the LAMMPS MD engine.38,39 The ReaxFF force field parameters were obtained from Verma et al.40 The Qeq41 charge equilibration scheme was used for all the simulations. BNNTs with chiral indices (6, 6), (7, 7), (8, 8), (9, 9), (10,10), (11,11) and (12,12) were considered in this study. In all the simulations involving BNNTs, the nanotubes were modeled to be flexible using the ReaxFF force field parameters. The production data was obtained by simulating bulk water and confined water (in approximately 10 nm long BNNTs) in the canonical ensemble (NVT). During the production runs, the 10 nm long BNNTs were modeled to be periodic in the axial direction to simulate infinitely long water-filled nanotubes. These production trajectories were 5 ns long for BNNT systems, and 1.5 ns long for bulk water. The temperature was maintained at 300 K using the Nosé–Hoover thermostat42,43 with a damping constant of 100 time-steps and a time step of 0.25 fs was used for all the simulations. More details regarding the simulation procedure such as the equilibration process, bulk water simulations, and obtaining appropriate confined water densities can be found in our previous study.30We obtained the hydrogen bonding definitions based on the distance–angle (r,θ) coordinates using the corresponding two-dimensional potentials of mean force W(r,θ). Here, r and θ represent the inter-oxygen distance and the angle between the OH bond and the vector joining the oxygen atoms ∠HOdOa (Fig. 1). Only the smallest θ among the four possible values, for a given pair of water molecules, was considered for sampling. W(r,θ) is given by the following equation:
| W(r,θ) = −kBTg(r,θ). | (7) |
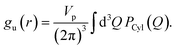 | (8) |
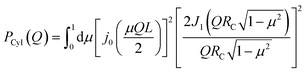 | (9) |
In Fig. 2, we show the 2D PMF for water in all the systems considered in this study. The boundary demarcating the HB boundary was obtained by considering the iso-surface with a PMF value beyond which the volume enclosed by such a surface increased discontinuously. The HB boundary for each system is shown using a continuous black contour line in Fig. 2.
Conflicts of interest
There are no conflicts to declare.References
- J. C. Rasaiah, S. Garde and G. Hummer, Water in nonpolar confinement: From nanotubes to proteins and beyond, Annu. Rev. Phys. Chem., 2008, 59, 713–740 CrossRef CAS PubMed
.
- S. Chakraborty, H. Kumar, C. Dasgupta and P. K. Maiti, Confined water: structure, dynamics, and thermodynamics, Acc. Chem. Res., 2017, 50, 2139–2146 CrossRef CAS PubMed
.
- S. Cerveny, F. Mallamace, J. Swenson, M. Vogel and L. Xu, Confined water as model of supercooled water, Chem. Rev., 2016, 116, 7608–7625 CrossRef CAS PubMed
.
- C. I. Lynch, S. Rao and M. S. Sansom, Water in nanopores and biological channels: A molecular simulation perspective, Chem. Rev., 2020, 120, 10298–10335 CrossRef CAS PubMed
.
- Y. P. Sirkin, M. Tagliazucchi and I. Szleifer, Transport in nanopores and nanochannels: some fundamental challenges and nature-inspired solutions, Mater. Today Adv., 2020, 5, 100047 CrossRef
.
- Z. Zhu, D. Wang, Y. Tian and L. Jiang, Ion/molecule transportation in nanopores and nanochannels: From critical principles to diverse functions, J. Am. Chem. Soc., 2019, 141, 8658–8669 CrossRef CAS PubMed
.
- N. Kavokine, R. R. Netz and L. Bocquet, Fluids at the nanoscale: from continuum to subcontinuum transport, Annu. Rev. Fluid. Mech., 2021, 53, 377–410 CrossRef
.
- B. S. Chava, Y. Wang, V. S. Sivasankar and S. Das, Water-free localization of anion at anode for small-concentration water-in-salt electrolytes confined in Boron-Nitride nanotube, Cell Rep. Phys. Sci., 2020, 1, 100246 CrossRef
.
- H. S. Sachar, B. S. Chava, T. H. Pial and S. Das, All-atom molecular dynamics simulations of the temperature response of densely grafted polyelectrolyte brushes, Macromolecules, 2021, 54, 6342–6354 CrossRef CAS
.
- Q. Dong, X. Zhang, J. Qian, S. He, Y. Mao, A. H. Brozena, Y. Zhang, T. P. Pollard, O. A. Borodin, Y. Wang, B. S. Chava, S. Das, P. Zavalij, C. U. Segre, D. Zhu, L. Xu, Y. Liang, Y. Yao, R. M. Briber, T. Li and L. Hu, A cellulose-derived supramolecule for fast ion transport, Sci. Adv., 2022, 8, eadd2031 CrossRef CAS PubMed
.
- H. S. Sachar, T. H. Pial, B. S. Chava and S. Das, All-atom molecular dynamics simulations of weak polyionic brushes: influence of charge density on the properties of polyelectrolyte chains, brush-supported counterions, and water molecules, Soft Matter, 2020, 16, 7808–7822 RSC
.
- M. Whitby and N. Quirke, Fluid flow in carbon nanotubes and nanopipes, Nat. Nanotechnol., 2007, 2, 87–94 CrossRef CAS PubMed
.
- M. Majumder, N. Chopra, R. Andrews and B. J. Hinds, Enhanced flow in carbon nanotubes, Nature, 2005, 438, 44 CrossRef CAS PubMed
.
- E. Secchi, S. Marbach, A. Niguès, D. Stein, A. Siria and L. Bocquet, Massive radius-dependent flow slippage in carbon nanotubes, Nature, 2016, 537, 210–213 CrossRef CAS PubMed
.
- T. A. Pascal, W. A. Goddard and Y. Jung, Entropy and the driving force for the filling of carbon nanotubes with water, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 11794–11798 CrossRef CAS PubMed
.
- K. V. Agrawal, S. Shimizu, L. W. Drahushuk, D. Kilcoyne and M. S. Strano, Observation of extreme phase transition temperatures of water confined inside isolated carbon nanotubes, Nat. Nanotechnol., 2017, 12, 267–273 CrossRef CAS PubMed
.
- B. S. Chava, Y. Wang and S. Das, Boron nitride nanotube–salt–water hybrid: Toward zero-dimensional liquid water and highly trapped immobile single anions inside one-dimensional nanostructures, J. Phys. Chem. C, 2021, 125, 14006–14013 CrossRef CAS
.
- A. W. Knight, N. G. Kalugin, E. Coker and A. G. Ilgen, Water properties under nano-scale confinement, Sci. Rep., 2019, 9, 8246 CrossRef PubMed
.
- O. Byl, J. C. Liu, Y. Wang, W. L. Yim, J. K. Johnson and J. T. Yates, Unusual hydrogen bonding in water-filled carbon nanotubes, J. Am. Chem. Soc., 2006, 128, 12090–12097 CrossRef CAS PubMed
.
- S. Dalla Bernardina, E. Paineau, J. B. Brubach, P. Judeinstein, S. Rouzière, P. Launois and P. Roy, Water in carbon nanotubes: the peculiar hydrogen bond network revealed by infrared spectroscopy, J. Am. Chem. Soc., 2016, 138, 10437–10443 CrossRef CAS PubMed
.
- H. S. Sachar, B. S. Chava, T. H. Pial and S. Das, Hydrogen bonding and its effect on the orientational dynamics of water molecules inside polyelectrolyte brush-induced soft and active nanoconfinement, Macromolecules, 2021, 54, 2011–2021 CrossRef CAS
.
- D. N. de Freitas, B. H. Mendonça, M. H. Köhler, M. C. Barbosa, M. J. Matos, R. J. Batista and A. B. de Oliveira, Water diffusion in carbon nanotubes under directional electric fields: Coupling between mobility and hydrogen bonding, Chem. Phys., 2020, 537, 110849 CrossRef CAS
.
- Q. Chen, Q. Wang, Y. C. Liu and T. Wu, The effect of hydrogen bonds on diffusion mechanism of water inside single-walled carbon nanotubes, J. Chem. Phys., 2014, 140, 214507 CrossRef PubMed
.
- A. Barati Farimani and N. R. Aluru, Spatial diffusion of water in carbon nanotubes: from Fickian to ballistic motion, J. Phys. Chem. B, 2011, 115, 12145–12149 CrossRef CAS PubMed
.
- M. Wu, M. Wei, X. Liu, K. Liu and S. Li, Structure and dynamic properties of stretched water in graphene nanochannels by molecular dynamics simulation: effects of stretching extent, Phys. Chem. Chem. Phys., 2019, 21, 19163–19171 RSC
.
- H. Duan, Z. Ying, L. Tian, Y. Cheng and L. Shi, Aqueous proton transportation in graphene-based nanochannels, Langmuir, 2022, 38, 15413–15421 CrossRef CAS PubMed
.
- Y. Ishii, N. Matubayasi, G. Watanabe, T. Kato and H. Washizu, Molecular insights on confined water in the nanochannels of self-assembled ionic liquid crystal, Sci. Adv., 2021, 7, eabf0669 CrossRef CAS PubMed
.
- J. K. Clark II and S. J. Paddison, Ab initio molecular dynamics simulations of water and an excess proton in water confined in carbon nanotubes, Phys. Chem. Chem. Phys., 2014, 16, 17756–17769 RSC
.
- Y. Itoh, S. Chen, R. Hirahara, T. Konda, T. Aoki, T. Ueda, I. Shimada, J. J. Cannon, C. Shao, J. Shiomi, K. V. Tabata, H. Noji, K. Sato and T. Aida, Ultrafast water permeation through nanochannels with a densely fluorous interior surface, Science, 2022, 376, 738–743 CrossRef CAS PubMed
.
- B. S. Chava, G. R. Chandel and S. Das, Water-structure-specific entropic dominance in the filling of boron nitride nanotubes, J. Phys. Chem. C, 2023, 127, 7009–7018 CrossRef CAS
.
- Z. Wan, Y. Gao, X. Chen, X. C. Zeng, J. S. Francisco and C. Zhu, Anomalous water transport in narrow-diameter carbon nanotubes, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2211348119 CrossRef CAS PubMed
.
- P. Wernet, D. Nordlund, U. Bergmann, M. Cavalleri, M. Odelius, H. Ogasawara, L. Å. Naslund, T. K. Hirsch, L. Ojamae, P. Glatzel, L. G. M. Pettersson and A. Nilsson, The structure of the first coordination shell in liquid water, Science, 2004, 304, 995–999 CrossRef CAS PubMed
.
- A. Luzar and D. Chandler, Hydrogen-bond kinetics in liquid water, Nature, 1996, 379, 55–57 CrossRef CAS
.
- A. Luzar and D. Chandler, Effect of environment
on hydrogen bond dynamics in liquid water, Phys. Rev. Lett., 1996, 76, 928 CrossRef CAS PubMed
.
- R. Kumar, J. R. Schmidt and J. L. Skinner, Hydrogen bonding definitions and dynamics in liquid water, J. Chem. Phys., 2007, 126, 204107 CrossRef CAS PubMed
.
- D. van der Spoel, P. J. van Maaren, P. Larsson and N. Tîmneanu, Thermodynamics of hydrogen bonding in hydrophilic and hydrophobic media, J. Phys. Chem. B, 2006, 110, 4393–4398 CrossRef CAS PubMed
.
- A. C. van Duin, S. Dasgupta, F. Lorant and W. A. Goddard, ReaxFF: a reactive force field for hydrocarbons, J. Phys. Chem. A, 2001, 105, 9396–9409 CrossRef CAS
.
- S. Plimpton, Fast parallel algorithms for short-range molecular dynamics, J. Comput. Phys., 1995, 117, 1–19 CrossRef CAS
.
- H. M. Aktulga, J. C. Fogarty, S. A. Pandit and A. Y. Grama, Parallel reactive molecular dynamics: Numerical methods and algorithmic techniques, Parallel Comput., 2012, 38, 245–259 CrossRef
.
- A. Verma, W. Zhang and A. C. van Duin, ReaxFF reactive molecular dynamics simulations to study the interfacial dynamics between defective h-BN nanosheets and water nanodroplets, Phys. Chem. Chem. Phys., 2021, 23, 10822–10834 RSC
.
- A. K. Rappe and W. A. Goddard III, Charge equilibration for molecular dynamics simulations, J. Phys. Chem., 1991, 95, 3358–3363 CrossRef CAS
.
- W. G. Hoover, Canonical dynamics: equilibrium phase-space distributions, Phys. Rev. A, 1985, 31, 1695–1697 CrossRef PubMed
.
- S. Nosé, A unified formulation of the constant temperature molecular dynamics methods, J. Chem. Phys., 1984, 81, 511–519 CrossRef
.
- A. K. Soper, The excluded volume effect in confined fluids and liquid mixtures, J. Phys.: Condens. Matter, 1997, 9, 2399 CrossRef CAS
.
- C. Hartnig, W. Witschel, E. Spohr, P. Gallo, M. A. Ricci and M. Rovere, Modifications of the hydrogen bond network of liquid water in a cylindrical SiO2 pore, J. Mol. Liq., 2000, 85, 127–137 CrossRef CAS
.
-
Small Angle X-Ray Scattering, ed. O. Glatter, O. Kratky and H. C. Kratky, Academic Press, 1982 Search PubMed
.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3na00948c |
| This journal is © The Royal Society of Chemistry 2024 |