Open Access Article
Open Access ArticleAgglomeration compaction promotes corrosion of gold nanoparticles†
Borys A.
Snopok
 *a,
Shavkat N.
Nizamov
*a,
Shavkat N.
Nizamov
 b,
Tetiana V.
Snopok
b,
Tetiana V.
Snopok
 a and
Vladimir M.
Mirsky
a and
Vladimir M.
Mirsky
 b
b
aVE Lashkaryov Institute of Semiconductor Physics, NAS of Ukraine, 41 pr. Nauki, Kyiv, 03028, Ukraine. E-mail: snopok@isp.kiev.ua
bNanobiotechnology – Institute of Biotechnology, Brandenburg Technical University, Cottbus-Senftenberg, Universitätsplatz 1, Senftenberg, 01968, Germany
First published on 10th June 2024
Abstract
Engineered nanoparticles are increasingly being used in various areas of human activity. However, the degradation mechanism of nanobodies in harsh environments is still a puzzle for theory and experiment. We report here the results of optical spectroscopy and nanoparticle tracking analysis, quantifying agglomeration and sizing of 50 nm citrate stabilized gold nanoparticles (GNPs) in HCl solutions containing H2O2. The mechanism of a consecutive corrosion reaction of GNPs is discussed within the framework of the near-field approach. We found that the disappearance of single nanoparticles from a suspension does not occur due to their dissolution per se, but is a consequence of the formation of aggregates. The neutralization of electrostatic shielding at high ionic strength allows gold nanoparticles to approach the subnanometer distance within the region of capping defects, at which the Casimir and van der Waals attractive forces dominate. It is suggested that electric field fluctuations in the confined space between highly conductive gold nanoparticles cause complexant-stimulated loss of metal from the core in the contact area. Going beyond the charge screening limitations by constraining the reaction space and reducing the double electrical layer thickness allows for chemical processes flow along otherwise not accessible reaction pathways.
1. Introduction
The nanoscale manipulation of matter is expanding the variety of natural chemical compositions with characteristics not always easily predicted from current knowledge. Moreover, quite often nanomaterials are involved in reactions which are not typical for bulk materials.1–5 Nevertheless, engineered metal nanoparticles (EMP) are being developed and incorporated in a number of commercial products, raising the potential of human exposure during manufacture, use, and disposal. Within the nearly limitless diversity of these materials, some happen to be toxic to biological systems (e.g. antimicrobial properties) and environment (i.e. toxic pollution); others are relatively benign, while others confer health benefits (drug carriers etc.). A deep understanding of the nanoscale specific properties of such structures is needed to minimize possible harm caused by these materials, while supporting continued study and appropriate industrial development. The widespread and well-characterized citrate stabilized gold nanoparticles (GNP) with potent health and environmental risks are one of the best models for studying the behaviour of classical EMP in a reactive environment.6–9Transformation of GNPs is a universal stage of EMP's life and important property that influences their mode of action. An EMP integration with a formation of “weakly” (association) or more “strongly” (soft agglomeration or aggregation) – bound irregular clusters as well as a release of ionic species (“leaching” of metal due to oxidative dissolution) are considered as two independent fates of metallic nanoparticles during their life cycle.10,11 However, an elucidation of the EMP degradation mechanism in liquids is often hampered by the ambiguity in separating the contributions of complex and poorly controllable processes. Thermodynamic and kinetic stability of GNP ensembles in acidic media is as well a hot topic, since in most practical applications GNPs are often surrounded by chloride containing environment. Indeed, HCl is one of the most abundant environmental pollutants.12,13 Chloride ion is an indispensable component of biological fluids, while hydrochloric acid in the stomach of mammals can decrease pH below 2.14 Hydrochloric acid is widely used in industry, for example, in chemical technologies, pharmaceutical industry, food production, microelectronics, etc., often in the presence of nanostructured components.15 In some technological approaches HCl is applied in combination with hydrogen peroxide, this leads to more reactive environment owing to oxidation–chlorination process.16 That is why in this work we study the behaviour of GNPs in aqueous solutions containing HCl also in the presence of hydrogen peroxide as an oxidizing booster.
The evolution of gold nanoparticles in chloride-containing media is not well covered in the literature, probably due to the mutually conflicting daily practice. An opinion on high chemical inertness of macroscopic gold samples is widespread.17 At the same time, everyday practice indicates a high efficiency of dissolving gold nanostructures (island films, nanoparticles, etc.) in aqueous solutions of HCl or HCl–H2O2 with a formation of Au3+.18,19 Despite the degradation of gold nanoparticles in acidic chloride-containing media was repeatedly confirmed experimentally in ref. 20–26, a relationship between various stages and general mechanism of the process remains unclear. In, particular the relationship between the agglomeration (collecting in a mass of nanoparticles which does not change the phase composition of the system, i.e. soft agglomerates) and release of material from the metal core to the aqueous phase in the form of ions is still a puzzle for theory and experiment. To identify this relationship and establish the main route of disappearance of single nanoparticles freely moving in highly dilute suspension, we used in this work a combination of in situ optical spectroscopy (UV-VIS) with Nanoparticle Tracking Analysis (NTA).
The hyphenation of size-dependent NTA and nanoscale specific local plasmon resonance spectroscopy (LSPR) opens the way to direct sizing of nanobodies in liquids; this allows the characterization of both individual nanoparticles and their aggregates in undistorted form, typical for isotropic solutions. For the optimal NTA imaging of freely diffusing nanobodies, GNPs with a diameter of 50 nm were selected.27,28 For GNPs of a given size, there is the best agreement between the equivalent spherical hydrodynamic diameter Dh of nanoparticles determined by the NTA method and the size of the metal core according to TEM data (see ESI, Fig. S1†). The choice of the concentration of hydrochloric acid and hydrogen peroxide was based on our previously obtained results.29 Under such conditions and at a low concentration of metal nanoparticles, the reaction medium can be considered isotropic and homogeneous for optical measurements, since fluctuations in the solution density caused by gaseous reaction products can be neglected.
2. Results
2.1. Single gold nanoparticles in solution
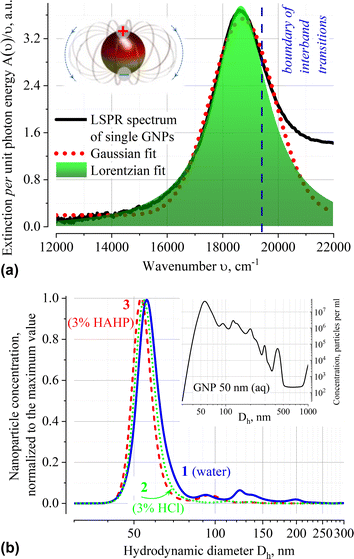
The extinction spectrum A(ν) normalized to the quantum of light ν of very diluted (ca. 3 × 108 single particles of dominated size per ml according to the NTA data) GNP suspension in water is shown in Fig. 1a. Approximation of A(ν)/ν using various profiles shows that the localized surface plasmon resonance (LSPR) band at 536 nm (18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 cm−1) is well fitted by the Lorentzian function. It differs from solutions of organic compounds, for which the Gaussian shape of the absorption band is typical. The Gaussian profile indicates that the external environment directly influences the electron transition in chromophore; in this case, averaging performs over an ensemble of chromophores that have slightly different transition energy owing to variation in their immediate environment.30,31
657 cm−1) is well fitted by the Lorentzian function. It differs from solutions of organic compounds, for which the Gaussian shape of the absorption band is typical. The Gaussian profile indicates that the external environment directly influences the electron transition in chromophore; in this case, averaging performs over an ensemble of chromophores that have slightly different transition energy owing to variation in their immediate environment.30,31
The Lorentzian profile of the extinction band means that the broadening is due to fluctuations in the characteristics of the transition itself (i.e., dispersion of the dimensions of the metal core, presence of structural defects on the metal surface or inside the organic stabilizer layer, etc.), and not due to local variations in density, composition or environment temperature. The reasons for neglecting the influence of local variations of the medium on the conditions of LSPR excitation are related to the collective oscillations of electron density in plasmons and presence of an organic stabilizer that forms a uniform dielectric layer on the surface. The citrate capping is capable of damping local fluctuations in the dynamics of the solvent molecules and contributes to the constancy of the composition of the electrostatic double layer in the immediate vicinity of the nanoparticle. The integrity of the surface layer is maintained by the process of dynamic “healing” of the arising defects by the citrate molecules present in the solution (nanoparticles are supplied as a stabilized suspension in a citrate buffer).
The position of the dominant peak in the NTA size distribution confirms that particles with a core size of ∼50 nm predominate in aqueous suspension of GNP. According to the product specification, this suspension has mean hydrodynamic diameter Dh of nanoparticles in the range of 58–65 nm (Fig. 1b). No substantial shift in the position of the NTA peak of freshly prepared suspensions in different solvents (Dh = 56.0; 54.5 and 53.0 nm for distilled water, 3% HCl (aq, v/v) and 3% HAHP ((3)HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (3)H2O2
(3)H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (94)H2O (v/v/v)) correspondingly) is observed.
(94)H2O (v/v/v)) correspondingly) is observed.
2.2. GNP agglomerates in acidic suspensions
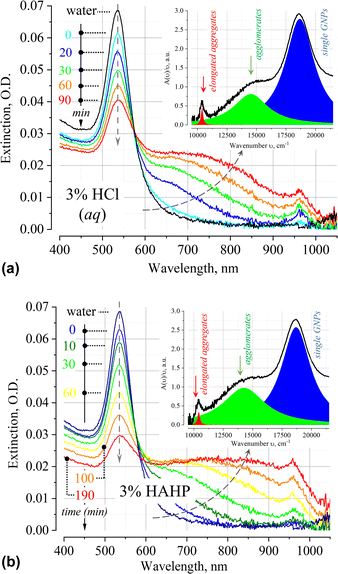
The time dependence of the extinction spectrum A(ν) of nanoparticles in 3% HCl is shown in Fig. 2a. A qualitative analysis of the spectrum shows that a decrease in the intensity of the LSPR band is accompanied by an increase in the extinction in the longer wavelength region of the spectrum. Typical deconvolution of the extinction spectra into elementary bands of the Lorentzian profile are shown in the insets of Fig. 2 (see Fig. S2, ESI† for more results). In addition to the LSPR band of single particles at 18![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 657 cm−1 (536 nm), a broad band is observed in the region of 11
657 cm−1 (536 nm), a broad band is observed in the region of 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–17
000–17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 (900–600 nm). The position of the band is in good agreement with the results of other authors, who also attribute this band to irregular agglomerates/clusters/“oligomers” of gold nanoparticles.32–40 Most likely, soft clusters consist of a few particles, since their mean hydrodynamic diameter will typically not exceed 200 nm. At t > 20 min also an absorption band at 10
000 cm−1 (900–600 nm). The position of the band is in good agreement with the results of other authors, who also attribute this band to irregular agglomerates/clusters/“oligomers” of gold nanoparticles.32–40 Most likely, soft clusters consist of a few particles, since their mean hydrodynamic diameter will typically not exceed 200 nm. At t > 20 min also an absorption band at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 cm−1 (ca. 950 nm) appears, which, by analogy with other researchers, can be attributed to the impact of nanoparticle aggregation in elongated geometry.41–43
500 cm−1 (ca. 950 nm) appears, which, by analogy with other researchers, can be attributed to the impact of nanoparticle aggregation in elongated geometry.41–43
At times above ∼80 min, absorption bands in UV-VIS spectrum essentially overlap. The uncertainty of the process of deconvolution of the A(ν)/ν spectra into elementary bands and the large residuals of the approximating functional do not allow to apply this procedure in such case. This is evidenced by the broadening of the highly constructed (complex) long-wavelength band in the region of 13![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000–15
000–15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cm−1 over time (see Fig. S2, ESI†).
000 cm−1 over time (see Fig. S2, ESI†).
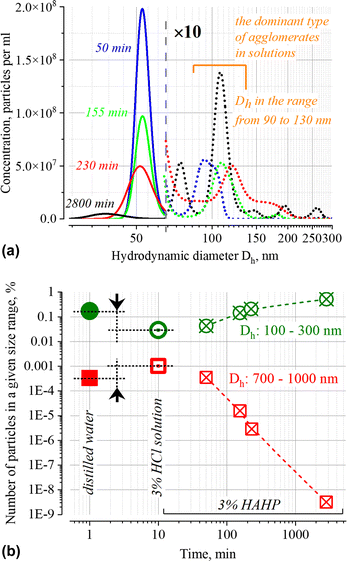
The NTA results (Fig. 4 and inset in Fig. 1b) confirm the presence of particles with Dh > 50 nm both in the initial suspension and over time; the presence of these particles can be associated both with soft agglomerates (100 ≤ Dh ≤ 300 nm) and very loosely connected associates (700 ≤ Dh ≤ 1000 nm) of GNPs, as well as with some foreign particles which may be present in the stock suspension of nanoparticles and in purified distilled water used to prepare the working solutions. Since the method does not allow one to establish the nature of these particles and unambiguously interpret individual peaks, below we will use only the total number of particles in the size ranges of interest which characterize the relative changes in the number of submicron particles within the indicated boundaries Dh.
2.3. Nanoparticle dissolution kinetics in HCl and HAHP
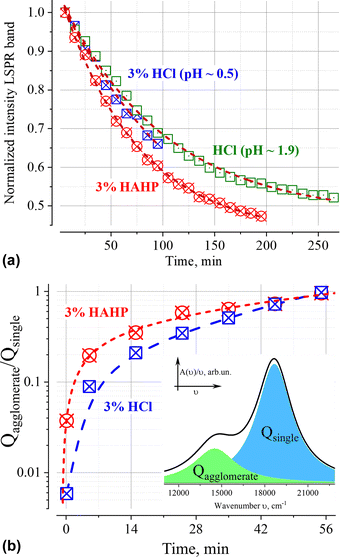
Similar phenomena of the appearance of long-wavelength bands are observed in the time dependence of the extinction spectrum A(ν) of nanoparticles in both a 3% HAHP (Fig. 2b) and a 3% HCl solutions (Fig. 2a). The kinetics of spectral changes, however, are different. The dependences of the extinction value at the maximum of the single particle's LSPR band (536 nm) on time in HCl (at pH ∼0.5 (3% HCl) and ∼1.9) and 3% HAHP are shown in Fig. 3a. These dependences are well approximated by an exponential decay function, which describes the irreversible reduction in the number of suspended single nanoparticles in a one-step process with unique outcome (a first-order reaction whose product is clusters of nanoparticles). Within this model, the addition of hydrogen peroxide to the reaction volume (HAHP) increases the rate of this process as compared to a 3% HCl (Fig. 3a).The NTA results confirm an increase in the number of objects in the range 100 ≤ Dh ≤ 300 nm, especially for the clusters with Dh from 90 to 130 nm, typical for soft agglomerates of two or three particles are held together by weak physical forces. However, the particles with Dh < 50 nm are not detected for several hours while the peak corresponding to single particles of the initial size decreases monotonically over time (Fig. 4a). Note, that for suspensions of gold nanoparticles, NTA size detection limit is ca. 20 nm. So, NPs with 30–40 nm in diameter would be detected by NTA.
This observation is fundamentally important for the current work since it allows us to conclude that the agglomeration of single particles is the dominant process of reducing the number of single nanoparticles in the suspension. At the same time, no decrease in the single particle size is observed in this time interval. Similar results for silver nanoparticles were obtained in ref. 44. Broadening of the NTA peak into a region of smaller sizes than that of single particles is observed only after few hours; it is likely that these are the original dimers or trimers of particles that have already undergone significant corrosion during this time.
Also noteworthy is the growth of the submicron-sized structures (700 ≤ Dh ≤ 1000 nm, see Fig. 4b) immediately after injection of GNP into aqueous solution with pH < 2. It is not accompanied by significant changes in the UV-VIS extinction. Formation of large associates can be caused by suppression of electrostatic repulsion at low pH. Indeed, the pK values of carboxy group of citric acid are 3.13, 4.76 and 6.39; therefore, less than 0.3% of the total amount of these groups exposed into aqueous phase will be deprotonated at pH ∼1. Notably, the number of such associates at t > 100 minutes decreases (Fig. 4b) while the structures with Dh ∼70 and 110 nm (with concentration ca. (4–8) × 106 particles per ml, approximately 100 times less than the initial one) remain until the final stage (ca. 48 h) of the degradation process. Probably, in addition to single nanoparticles coated with an intact layer of organic stabilizer, some elongated aggregates are also retained. Similar architectures were observed at the final stage of degradation of gold43 and silver nanoparticles.45 A wide peak on the NTA distribution for a sample with an exposure time of ca. 2800 min (Fig. 4) indicates that only at this time the “small” objects with Dh ∼30 nm (this is close to the size detection limit of the NTA) dominate in the suspension.
2.4. Changes in populations of single particles and their aggregates over time
Deconvolution of the A(ν)/ν spectra makes it possible to eliminate the overlap of extinction bands and directly identify changes in populations of single particles and their aggregates. The ratio of the areas of correspondent elementary bands over time is shown on Fig. 3b. It is necessary to highlight, that the addition of hydrogen peroxide leads to a faster increase in the number of aggregates. This fact indicates that some chemical transformations on the surface of nanoparticles reinforced by hydrogen peroxide booster can contribute to the process of their aggregation.The agglomeration process is characterized by the presence of an isosbestic point, which provides evidence in favour of our assumption about a single dominate channel for the “disappearance” of GNPs (Fig. 2).46 Indeed, the observation of isosbestic point indicates that the stoichiometry of the reaction remains unchanged over time and there is no competition between parallel reactions (such as, the dissolution of nanoparticles etc.) occur within the considered time range (for more details see ESI†).47,48 Moreover, this indicates that the agglomeration products are clusters of similar composition.
Analysis of the dependence between the intensity of the LSPR band of single particles (Fig. 3a) and the ratio of agglomerates/single particles (Fig. 3b) indicates a linear correlation (Pearson coefficients > 0.98) of these values for t ≤ 60 min (Fig. S3, ESI†). In this time interval, the intensity of the LSPR band makes it possible to quantitatively characterize the aggregation process, since its value is directly proportional to the ratio of the number of aggregated and single gold nanoparticles.
Deconvolution of the A(ν)/ν spectra into elementary bands confirms the broadening of the extinction bands over time (Fig. 5a and b, see Fig. S2 for more details, ESI†). The strong broadening of the long-wavelength band of aggregates (Fig. 5b) is due to the growth of their configuration/composition diversity over time leads, in particular, to the formation of increasingly dense clusters.49 Indeed, a “plasmon ruler” allows us to estimate changes in the average distance, s (Fig. 5c), between constituent nanoparticles in gold agglomerates using the shift of their resonance wavelength λ (for sub – 10 nm interparticle distances,50–52). Using the results of the spectra's deconvolution (Fig. S2, ESI†), the estimated average distance s monotonically decreases over time from an initial value of about 1.2 nm (5 min) to ca. 0.8 nm (>60 min) at a rate of about 5 pm per min for 3% HCl and ca. 10 pm per min for 3% HAHP at the beginning (Fig. 5c).
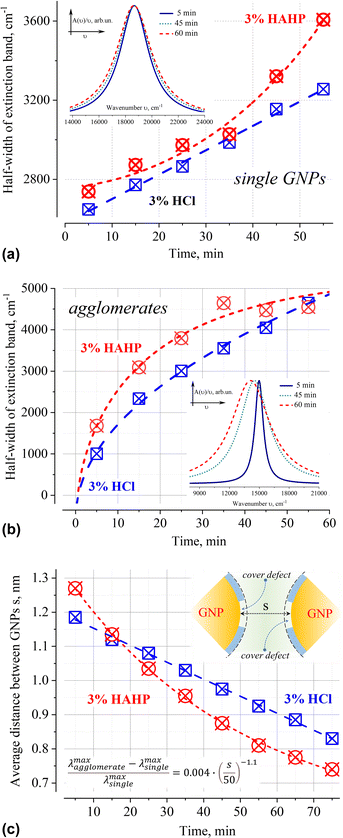 | ||
| Fig. 5 Time dependence of the half-width of extinction bands of 50 nm GNPs as single particles (a) and their agglomerates (b) in 3% HCl (aq) and 3% HAHP. The average distance between nanoparticles within gold agglomerates, s, over time (c). The formula for calculation of distance between nanoparticles according to “plasmonic rulers”50 shown in the inset (all values in nm). The presented results used the decomposition of extinction spectrum normalized to the unit photon energy A(ν)/ν into elementary Lorentzian bands. The insets in (a) and (b) show the corresponding extinction bands in 3% HCl normalized to the maximum value to demonstrate the broadening effect. | ||
In the case of single particles, the weak broadening of the LSPR band (Fig. 5a) is not accompanied by a change in its position (535 ± 2 in HCl and 536 ± 2 nm in HAHP). This broadening can be caused by inevitable background level in the extinction spectra and the decomposition fitting. An overlap with another broad band or unpredictable scattering can, of course, as well change a background level. In these cases, such broadening can be neglected as a specular. However, given the low concentration of gold nanoparticles (and, accordingly, corrosion products), and the fact that these products do not absorb/scatter in the energy range characteristic of LSPR, deconvolution was carried out for a fixed (zero optical density) baseline value.
Broadening can as well hint on some physical–chemical processes. Indeed, a slight broadening of the LSPR band is observed immediately after sample preparation: 2554, 2648 (+94) or 2738 (+184) cm−1 for water, HCl or HAHP respectively. The half-width of the LSPR band continued to increase further, again stronger for a more aggressive medium containing hydrogen peroxide (Fig. 5a).
In general, the LSPR resonant conditions depend on (1) the size of metal core, (2) the optical constants of the environment (Lorenz profile allow us to neglect fluctuations of this factor) and (3) the capping layer.32,53–55 If we assume that the broadening is associated with a “symmetrical” change in the size of the metal core, then this means that the processes of gold oxidation and reduction have close efficiency under strongly acidic conditions. This seems to be an unlikely scenario owing to the high concentrations of chloride ions prevent the spontaneous formation of a metal phase, since the AuCl4− anion is a stable gold compound at [H+] and [Cl−] values of more than 10−2 M.56
Variations in the density/integrity of the surface coating due to its partial removal, local stacking faults, or as the result of chemical transformation as well affect the conditions of resonant excitation under near-field coupling of light. Indeed, all these defects cause local changes in the refractive index in the immediate vicinity of the surface where the electron density flows beyond the geometric boundaries of the metal nanoparticle (“spill-out effect”).57–60 The occurrence of such defects in a chlorine-containing medium is due to the adsorption of chlorine on the gold surface, which leads to a change in coordination from mono- to bidentate conformation of citric acid on the gold surface,61 the unique capabilities of the H2O2–HCl (aq) system for the one-pot oxidation–chlorination of various organics16,62 or is a consequence of the presence of steps at the intersections of the crystal lattice faces on the surface. This allows us to suggest that the broadening of the LSPR band of single nanoparticles is caused by an increase in the inhomogeneity of the organic capping layer, which causes an increase in the dispersion of the LSPR excitation conditions over time. The results in more aggressive solutions containing hydrogen peroxide confirm this suggestion – broadening is more intensively under exposure in HAHP (Fig. 5).
3. Discussion
It is generally accepted that the fate of metal nanoparticles of very different nature in reactive environment are subjected to a variety of processes: (i) redistribution of material between the cores of nanoparticles (e.g. Ostwald ripening in which the average particle size increases); (ii) oxidation of the metal and subsequent dissolution of the cores, while the average particle size monotonically decreases; (iii) aggregation of nanoparticles with follow-up (iv) precipitation/sedimentation. Both redistribution of the material (from smaller to larger nanoparticles) and association/aggregation are thermodynamically-controlled enthalpy-driven process tending to reduce the surface energy.63,64 Charge and integrity of organic shell also influence on the surface energy (solvation etc.) as well as on the kinetics of the system evolution towards the state with a lower energy (e.g., by electrostatic repulsion or Coulomb blockade of core oxidation etc.).65 Therefore, the dominance of one or another process depends on the environment, pH value (i.e. surface potential of GNPs, etc.), presence of active chemical compounds (complexing or/and oxidizing agents etc.) capable of reacting either with stabilizer molecules or with the metal core.3.1. A critical analysis of processes in colloidal suspensions of gold nanoparticles containing hydrochloric acid
According to the NTA and UV-VIS results, the efficiency of spontaneous dissolution of single 50 nm citrate stabilized gold nanoparticles, even in the presence of chloride ions at low pH values, is rather low: particles/corroded units whose size is smaller than the initial ones of single nanoparticles are observed only at the final stage of degradation of all nano-objects in suspension. This is not surprising, given the very high value of the redox potential of gold and the obstacles to the formation of oxidized gold on the surface of a citrate-stabilized nanoparticle. Indeed, even for fast electrochemically driven dissolution of much easily oxidizable silver nanoparticles, a complexation of the formed ions is required to shift reaction balance towards dissolution.66Although the Ostwald's ripening is energetically favourable, we also consider it to be unlikely for gold nanoparticles. The reason is that it requires a consequence of few processes, at least, an oxidation of gold with a formation of soluble products diffusing in the solution up to final reduction on the larger particles. From electrochemical point of view, this process is driven by the difference in the redox potentials of small and large particles. However, the value of this potential difference between the particles of 50 nm and of infinity curvature (flat) is rather low. Moreover, a final product under similar conditions is oxidized Au3+ compound;18–26,67–70 therefore, the conditions for the final reduction of the formed metallic ions into the larger NPs can hardly be achieved.
Another typical pathway of nanoparticle fate involves aggregation to form larger bodies, which often cause nanoparticle precipitation/sedimentation.71 However, in the case under consideration, single particles disappear within several hours. This happens much faster than gravitational sedimentation which occurs for similar suspensions in the time scale of hundreds of hours.72,73 Intensive mixing of the suspension confirms this conclusion – no changes in the spectral characteristics of suspensions were observed after mixing.
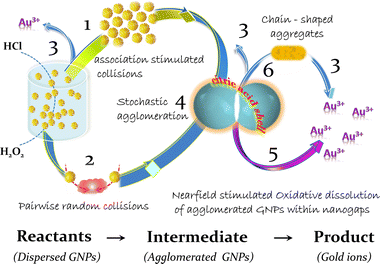
The inability to interpret experimental results within the framework of typical degradation models necessitates a more thorough analysis of the agglomeration process. Taking into account all available experimental results, it is reasonable to assume that the process of GNP dissolution goes over aggregation stage. Thus, (i) approaching of nanoparticles in aggregates follows by (ii) formation of a unique reaction space within nanoparticle clusters and, finally, (iii) activation of nanoscale specific chemical processes of gold dissolution.
3.2. Forces driving an aggregation of citrate stabilized gold nanoparticles in acidic chloride-containing media
Interaction between large dry elastic particles can be described by the repulsive Hertz-Mindlin stress model with negligible attractive forces. For capped metallic nanoparticles with a large surface area to volume ratio in suspension, a number of additional enforcements is needed. This includes (i) hydrodynamic/cohesive forces arise from particle velocity/acceleration or liquid shape; (ii) solvation/hydration/structuring forces driving interface pack around a constraining boundary; (iii) double layer forces occurring across liquids as osmotic pressure and generated by the differences in the ionic concentrations within the gap between charged objects with respect to the bulk solution;74 (iv) short-range Casimir and van der Waals forces as well as (v) contact force, which is only present when the particle is sintered to another one.75 The question is which of the known interactions between colloidal particles in solution can initiate the process of their corrosion.A classic tool for solving issues related to the aggregation and kinetic stability of aqueous dispersions is the DLVO theory.76,77 It takes into account the combined effect of van der Waals (at very close distances) and double layer force (at larger distances). Thus, it allows one to describe the force between charged surfaces interacting through a liquid medium. In kinetically stable suspensions, it is the diffuse part of electric double layer that separates particles and actually does not allow them to get close enough to engage in chemical reactions. The double layer force decays exponentially as a function of distance and is mainly dependent on the surface charge of the particles and ionic strength of the solution. The effective interaction distance is controlled by the Debye screening length which is in sub-nanometre range (ca. 0.5 nm, see for details in ESI†) for the solutions under consideration (ca. 0.36 M HCl); thus, diffusive part of double layer force in this particular case can be neglected. This allows us to conclude that the aggregation is a kinetically controlled process and the formation/growth of clusters is only due to the stochastic collisions of particles in solution; high ionic strength of the solution eliminates any long-range electrostatic interactions between nanoparticles occurring across liquid.
Within the concept of double layer, the first layer corresponds to the charged surface. As for most organic covered metallic nanoparticles, these charges originate from dissociated surface groups. At pH > 4, citric acid possessing first pKa 3.13 is deprotonated. Thus, the citrate capping gives the gold nanoparticles a negative surface charge and GNP suspension is kinetically stable. Deprotonated citric acid has an excellent binding to the gold surface and forms strongly charged layer on the metal surface. However, when pH approached 2, almost all ionic groups are protonated and the citrate molecules are uncharged; their adsorption to the gold layer is expected to be much lower because of disappearance of mirror forces.
If electrostatic repulsion does not prevent approaching of particles and the citrate capping does not have structural defects (i.e., it completely covers the surface of the metal core), a formation of low-density particle's associates possible. Weakly bound associates up to submicron size are stabilized by reducing the total surface tension and expelling excess water molecules (i.e., solvation) (Fig. 4b).
If the contact of the nanoparticles is in the area of the exposed metal surface (organic coating defect), Brownian motion will push the particles closer together, allowing the short-range attractive Casimir and then van der Waals forces to become dominant; nanoparticles approach so close to each other that the distance between them becomes in the (sub)nanometer range (Fig. 5c).
3.3. Near-field effects in the nanogaps of metallic nanoparticles
Despite the fact that the overwhelming majority of publications are devoted to light induced interactions between plasmonic nanoparticles, an association and agglomeration of nanoparticles proceed also in the dark. Therefore, the discussed here interactions do not imply external stimulation, in particular, by light.When metal particles approach to a distance of tens of nanometers, a Casimir (at larger nanoscale distances) and then van der Waals forces (at very close distances) arises between them. The Casimir force is the strongest force acting on two uncharged conducting objects separated by confined space gaps in nanometer range due to the restructuring of the quantum vacuum fluctuations of a field.78–80 Moreover, it was shown that the Casimir interaction between two objects of the same material results in passive Casimir trapping so that two objects can remain without contact at a specific distance (Casimir equilibrium).81 With further approach of uncharged metal particles without own dipole moments, dispersion interactions caused by van der Waals forces begin to dominate at subnanometer distances.82,83
It was found that for the system of two spherical shelled nanoparticles interaction potential is similar to the well-known Lennard-Jones potential where the overall two-body contribution yields an attractive interaction.84,85 These forces are caused by fluctuations of electrons and quantum fluctuations whose spectrum is altered by the presence of boundaries.86–88 It is reasonable to stress that according to theoretical calculations, the light-induced interaction for strongly focused laser beams becomes comparable in strength to the action of Casimir force.89 When the nonlinear polarizability of nanoparticles is also taken into account, an additional interaction appears, leading to the attractive ponderomotive forces in the system of two nanoparticles.90Thereby, an interaction of metal nanoparticles does not require a presence of light for sure, but is limited by the possibility to approach to the distance at which near-field effects can manifest. In our case due to the small Debye length and defects in the organic coating layer, nanoparticles can approach each other to the sub-nanometer distance (Fig. 5).
Since the stochastically oscillated local fields play an important role in the near-field, their spatial distribution leads to the formation of local electrostatic gradients. In the nanogaps the electric field distribution depends on the number, size and mutual arrangement of constituent nanoparticle aggregate; configurations can arise in which nanoparticles can both compensate or even suppress each other's action, and, conversely, significantly enhance the local fields in the nanogaps.32,40,78,89,91–93
To summarize, we can conclude that the aggregation of nanoparticles in solutions with sub-nanometer Debye length is caused by fluctuations-based near-field electrostatic interactions. In this case the “unusual” chemical reactions can occur within the confined space between closely approached nanoparticles. This conclusion is in good agreement with the results of other authors, who showed that the gold nanoparticles exhibited different dissolution behaviors as ensembles compared to the single particles.94 Similar results were obtained for polycrystalline films, which showed that surface corrugations induce fluctuating near-field variation and modulate corrosion reaction.29,92
The corrosion resistance of gold under normal conditions is caused by the high standard potential of this material.17,95 However, the high energy required for the oxidation can be lowered by decreasing of the energy of gold ions in the aqueous phase. This can be achieved by complexation (decrease of the chemical component of electrochemical potential), addition of oxidizers such as hydrogen peroxide (to reduce the electrode potential of gold) and by application of electric field (decrease of the electrical component of electrochemical potential). The second well known effect of the electric field is the influence on the activation energy of this process. The formation of a complex also reduces the energy consumption for detachment of surface gold atoms due to the redistribution of the electron density of the complexing agent, which weakens the bonds that fix the atom in the crystal lattice. Therefore, we can suggest that the high concentration of chloride ions and the presence of high electric field within the nanogap can promote local corrosion of metal in nanoparticles in the area of their contacts. The anticipated corrosion mechanism is similar to oxidative intergranular or crevice dissolution of metals in polar solutions of halogens occurring at high fluctuations of local electric field in confined space.96
3.4. The irreversible consecutive mechanism for the degradation of gold nanoparticles in acidic aqueous suspensions
The analysis of obtained experimental results and their interpretation within the framework of the near-field approach indicates that the corrosion of gold nanoparticles in chlorine-containing medium is a multistage process. It includes the partial destruction of the stabilizer layer in acidic conditions, which in turn leads to the closest agglomeration of GNPs, which are consecutively dissolved in the area of interparticle contacts (Fig. 6). This process is more intensive in the presence of hydrogen peroxide, which provides strong oxidation conditions for capping agents and reduce electrode potential of gold at acidic pH. As the metal phase dissolves within the strongly confined space of the nanogaps, a part of the agglomerates can transform into stable capped “clusters” through oriented attachment in a common crystallographic alignment. Similar elongated structures are observed at the initial stages of synthesis of nanostructures (nuclei line up in chains due to the features of the crystal structure of gold97 or silver45); potentially the same architectures are ones of the most “long-lived” in the process of GNP degradation (Fig. 4).4. Experimental
4.1. Chemicals and reagents
Chemicals (hydrochloric acid) (HCl, 37%, Roth 9277-1, 1.19 g ml−1), hydrogen peroxide (H2O2, 30%, Roth) and gold nanoparticles (the stock solution Aldrich 741![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 957 (10 nm); Aldrich 741
957 (10 nm); Aldrich 741![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 965 (20 nm); Aldrich 741
965 (20 nm); Aldrich 741![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 973 (30 nm); Aldrich 741
973 (30 nm); Aldrich 741![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 981 (40 nm); Aldrich 742
981 (40 nm); Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007 (50 nm); Aldrich 742
007 (50 nm); Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 015 (60 nm); Aldrich 742
015 (60 nm); Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 023 (80 nm); Aldrich 742
023 (80 nm); Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 031 (100 nm); Aldrich 742
031 (100 nm); Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 866 (200 nm)) were purchased from the above commercial suppliers and were used without further purification. All solutions were prepared according to the standard procedures using Milli-Q-purified water.
866 (200 nm)) were purchased from the above commercial suppliers and were used without further purification. All solutions were prepared according to the standard procedures using Milli-Q-purified water.
HCl working solution, was prepared by dissolving of 3 ml of hydrochloric acid (HCl, 37%) in 97 ml of distilled water leading to referred to below as “3% HCl” solution with pH ∼ 0.5 (0.36 M). Water solutions of hydrochloric acid and hydrogen peroxide (HAHP) were prepared by mixing of 3 ml of hydrochloric acid (HCl, 37%), 3 ml aliquots of hydrogen peroxide (H2O2, 30%) and 94 ml of distilled water; in this case the volumetric ratio was (x)HCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (x)H2O2
(x)H2O2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) (100 − 2x)H2O (v/v/v) for x = 3 (referred to below as “3% HAHP” solution). Notable, if x > 3, the bubbles of gaseous reaction products were generated both in the bulk of the solution and on the glass surface of the cuvette during the dissolution of gold; the bubbles can create local variations in the concentration of active components and may lead to a non-uniform condition for chemical conversions as well disturb measurement owing to additional light scattering at the solution/bubble/glass interfaces.
(100 − 2x)H2O (v/v/v) for x = 3 (referred to below as “3% HAHP” solution). Notable, if x > 3, the bubbles of gaseous reaction products were generated both in the bulk of the solution and on the glass surface of the cuvette during the dissolution of gold; the bubbles can create local variations in the concentration of active components and may lead to a non-uniform condition for chemical conversions as well disturb measurement owing to additional light scattering at the solution/bubble/glass interfaces.
Working samples of GNPs were prepared from the stock suspension (Aldrich 742![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 007) immediately before measurements by 1
007) immediately before measurements by 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 15 dilution by water or above-described aqueous solutions of HCl or HAHP in glass vials. The concentrations of the single GNP of dominant size (maximum of NTA distributions at Dh = 56 nm) after preparation were ∼3 × 108 particles per ml, the mean hydrodynamic diameter of nanoparticle Dh according to NTA measurements was 56 nm. The samples in glass vials were stored in the dark using aluminium foil to prevent a possible light exposure. Thus, irradiation (low intensity, capturing about 2% of the suspension volume) occurred only during spectrum measurement (scanning range 200–1100 nm, scanning time 5 min). The experiments were performed at 21 ± 1 °C.
15 dilution by water or above-described aqueous solutions of HCl or HAHP in glass vials. The concentrations of the single GNP of dominant size (maximum of NTA distributions at Dh = 56 nm) after preparation were ∼3 × 108 particles per ml, the mean hydrodynamic diameter of nanoparticle Dh according to NTA measurements was 56 nm. The samples in glass vials were stored in the dark using aluminium foil to prevent a possible light exposure. Thus, irradiation (low intensity, capturing about 2% of the suspension volume) occurred only during spectrum measurement (scanning range 200–1100 nm, scanning time 5 min). The experiments were performed at 21 ± 1 °C.
4.2. Characterization methods: optical measurements
The UV-VIS spectra of samples were recorded using Evolution 220 spectrometer (Thermo Scientific, Germany). The spectra were recorded using a glass cuvette (10 mm, QG Precision Cells, 6030-10-10, Hellma Analytics) with the same solvent as a reference; an interval of 10 minutes was used for kinetic analysis. Totally up to 20 scans were collected for each measurement with a resolution of 2 cm−1.4.3. Characterization methods: nanoparticle tracking analysis (NTA)
Direct visualization, sizing and counting of suspended GNPs was performed using a NanoSight™ NS300 Nanoparticle Analysis System (Malvern Panalytical Ltd, Malvern, Worcs, UK https://www.malvernpanalytical.com) equipped with a homemade injection system based on automatic autosampler (for details see Fig. S3, ESI†).Before measurements the water carrier for suspensions of GNP were filtered through 0.2 μm filter (Millipore). Between experiments, the system was flushed with a large volume of filtered water at a high flow rate (up to 2 ml min−1). Scattered light from the suspended nanoparticles interrupting the green (532 nm) laser beam passing through the sample chamber was recorded as a video file of the particles undergoing Brownian motion. Camera focus, gain and shutter settings were adjusted in unison to generate optimally exposed blur-free images of particles and a capture duration of 60 s was employed. Image processing was done in standard mode for 5 repetitions with all other analysis parameters set to recommended default values.
Data analysis was performed using the software provided by the manufacturer (NanoSight NTA software version 3.4, Build 3.4.4), no additional initial data conversions or calculations were performed. The results of the analysis are presented as a histogram of the number of particles of a given size against the equivalent spherical hydrodynamic diameter of the particles Dh, calculated on the basis of the measured change in the position of the particle using the Stokes–Einstein equation. Estimations of viscosity of HCl and H2O2 solutions based on linear approximation of data98,99 indicate that the difference of used solutions of HCl and HAHP from pure water is ∼2%; therefore, viscosity of pure water was used in the calculation of Dh.
In order to minimize the systematic errors caused by the peculiarities of the implementation of the NTA method,28 the Dh value of commercially available gold nanoparticles was measured in the range of 20–200 nm. The results are presented in Fig. S1, ESI†. Considering that in this work we are interested in changes in the initial size of GNPs, particles with a diameter of ∼50 nm were selected. According to the results of interlaboratory testing presented in ref. 28, the hydrodynamic diameter Dh of these nanoparticles best corresponds to the size of nanoparticles obtained using transmission electron spectroscopy (determining the size of the metal core d), taking into account the thickness of the organic stabilizer layer (less than 1 nm).61,100 Notably, nanoparticles with a diameter of 50 nm are located in the center of the linear part of the dependence of Dhversus d (Fig. S2, ESI†), ensuring the correct registration of changes in the size of individual nanoparticles. For a qualitative assessment of the number of submicron particles in a certain range of Dh, integral values were calculated, i.e. the total number of particles whose hydrodynamic diameter was in the ranges 100 ≤ Dh ≤ 300 and 700 ≤ Dh ≤ 1000 nm.
4.4. Data processing of GNP extinction spectra
The extinction of individual spherical gold particles is caused by the processes of absorption and coherent scattering (changing the angular distribution) of light. In the basic Mie theory, the expected contour of the extinction band under the local surface plasmon resonance conditions is described by Lorentzian function including both equilibrium (plasma oscillations) and nonequilibrium (inter-band transitions) free charge carriers.32,33The shape of a suspension extinction spectrum is the result of the summation of a large number of spectra of individual nanoparticles. In order to match the statistical theoretical models (formulated in terms of the number of particles of a given property) and the measured spectra, it is necessary to represent the extinction band as a result of cumulative behaviour of nanoparticles sets with a given energy. In order to move into a probabilistic representation of optical spectra, the concept of Einstein coefficients is usually used: the Einstein coefficients are quantities describing the probability of electron transition per unit frequency (light quantum).30,31,101–103 To obtain a value directly proportional to the corresponding Einstein coefficient, it is necessary to divide the extinction spectrum A(ν) to the value of the quantum energy ν (e.g. wavenumber); in this case, the random variable A(ν)/ν does not more depend on the transition energy and its quantity is proportional to the number of particles having electron transition with a given quantum energy ν. This procedure is widely used in molecular spectroscopy and photovoltaics.101–103
Deconvolution of the A(ν)/ν spectrum by individual symmetrical components makes it possible to improve resolution and identify a particular band shape specific for the corresponding electronic processes.30,31,104,105 The shape of the band indicates the dominant broadening mechanism.106–108 If the broadening is due to fluctuations of the transition moment itself (intrinsic properties), the band profile is described by the Lorentzian curve. If the influence of the external environment dominates, i.e. due to a presence of other objects close to the absorber, an inhomogeneous thermal (or proximity) broadening is observed which results in a Gaussian absorption band profile.
The procedures of Origin (OriginLab Corporation) were used for spectra deconvolution and analysis.
5. Conclusion
Near-field engineering utilizing local fields can drive chemical reactions along otherwise not accessible reaction pathways. Many approaches based on manipulation of photon energy flow in plasmonic chemistry have been proposed and practically implemented, including near-field etching,109 photooxidative dissolution of gold,110 near-field assisted chemical reactions,90,111,112 and the generation of localized magnetic field.113 Here we would like to draw attention to the fact that atypical reaction pathways can be activated also without optical excitation. We demonstrate that near-field assisted chemical transformation proceeds as well in darkness, given that GNPs able to come very close to each other.In the search for nanoscale specific effects of transformation of metallic nanoparticles it usually assumed that particle agglomeration can result in reduced near-field effects.114 This is explained by a decrease of the free surface/volume ratio. In this study, we argue that closest agglomeration paves also the way for unique nanogap-based reactors with otherwise hidden near-field effects. In such strongly confined space between conducting boundaries chemical processes are activated and enhanced by fluctuating local electrostatic field in Casimir or van der Waals bound nanostructures.
One of the most important practical takeaways of this report is that the integrity of the capping coating of gold nanoparticles is the key factor determining their behaviour in chloride-containing media. Despite the fact that a number of authors emphasize the problem,115–117 the implications of coating breakdown are often vainly overlooked. It can be of a great importance, for instance, when examining GNP applicability in biological liquids where the thickness of the diffuse part of double layer is often less than 1 nm under physiological conditions.118 As shown in this work, chemically induced defects in the coating of nanoparticles can promote the dissolution of the metal in nanogaps and ultimately lead to the disappearance of the nanocarrier. Having ways to maintain the kinetic stability of gold nanoparticle suspensions in different environments is a prerequisite, for example, for the development of pharmaceuticals using GNP based formulations intended for oral administration, or the successful application of a new type of plasmonic nanoparticle etching-based optical sensors.119
It is also important to emphasize that the degradation of nanostructured metals is a multiscale consecutive reaction in which structural transformations and chemical reactions are mutually coordinated through stochastic processes of transport of objects whose mass differs by 7–8 orders of magnitude (aggregates, particles and ions). In this case, some new functional architectures built from the initially inert elements acts as a nanoreactors (temporal intermediate), those newly acquired properties open the way for the implementation of the “unusual” chemical transformations. Thus, in contrast to homogeneous processes in isotropic solutions an evolution of colloidal nanosystems is influenced by their spatial (self)organization and exhibit typical features of complex systems.120–122
The results obtained in this work focus the reader's attention on near-field processes specific for Casimir or van der Waals bound nanostructures,123–128 in particular, transformation in agglomerates of metal nanoparticles in chloride-containing media. This knowledge is important for risk assessment and product development in industry and pharmacology assuming their potential threats to environmental health and safety risks. Clearly understood mechanisms, integrity limits and conditions under which a GNP's protective capping fails, opens the ways for conscious and purposeful development of task-oriented stable nanomaterials to derive the benefits of nanoscale-based technologies while limiting adverse health impacts or industrial mismatch.
Author contributions
Conceptualization, B. S. and V. M.; methodology, B. S. and S. N.; software, S. N.; formal analysis, B. S. and T. S.; investigation, B. S.; resources, S. N. and T. S.; data curation, B. S. and T. S.; writing—original draft preparation, B. S.; writing—review and editing, V. M. and S. N.; visualization, B. S. and T. S.; project administration, V. M.; funding acquisition, V. M. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
There are no conflicts of interests to declare.Acknowledgements
Authors thanks DFG-Projekt – GZ: MI 599/12-1 and DAAD (B. S., Grant 57507440) for support this work. This work has received as well funding through the MSCA4Ukraine project (Grant ID 1119494), which is funded by the European Union.Notes and references
- R. Abbasi, G. Shineh, M. Mobaraki, S. Doughty and L. Tayebi, J. Nanopart. Res., 2023, 25, 43 CrossRef CAS PubMed.
- L. Li and Y. J. Zhu, J. Colloid Interface Sci., 2006, 303(2), 415–418 CrossRef CAS PubMed.
- A. L. Suherman, G. Zampardi, S. Kuss, E. E. L. Tanner, H. M. A. Amin, N. P. Young and G. Richard, Phys. Chem. Chem. Phys., 2018, 20, 28300 RSC.
- B. Snopok and O. Snopok, in NATO Science for Peace and Security Series A: Chemistry and Biology, Advanced Nanomaterials for Detection of CBRN, ed. J. Bonca and S. Kruchinin, Springer, Nature, B.V, 2020 Search PubMed.
- C. Girard, C. Joachim and S. Gauthier, Rep. Prog. Phys., 2000, 63, 893 CrossRef CAS.
- S. J. Amina and B. Guo, Int. J. Nanomed., 2020, 15, 9823 CrossRef CAS PubMed.
- A. Sani, C. Cao and D. Cui, Biochem. Biophys. Rep., 2021, 26, 100991 CAS.
- R. Stein, B. Friedrich, M. Mühlberger, N. Cebulla, E. Schreiber, R. Tietze, I. Cicha, C. Alexiou, S. Dutz, A. R. Boccaccini and H. Unterweger, Molecules, 2020, 25, 4425 CrossRef CAS PubMed.
- X. Hu, Y. Zhang, T. Ding, J. Liu and H. Zhao, Front. Bioeng. Biotechnol., 2020, 8, 990 CrossRef PubMed.
- S. McCarrick, K. Midander, M. Krausová, U. Carlander and H. L. Karlsson, in the Presence of Human Macrophages, Int. J. Nanomed., 2021, 16, 5895 CrossRef PubMed.
- M. Z. Iqbal, I. Ali, W. S. Khan, X. Kong and E. Dempsey, Mater. Des., 2021, 205, 109694 CrossRef.
- C. D. Evans, D. T. Monteith, D. Fowler, J. N. Cape and S. Brayshaw, Environ. Sci. Technol., 2011, 45(5), 1887 CrossRef CAS PubMed.
- I. V. Kruglenko and B. A. Snopok, Theor. Exp. Chem., 2018, 54, 53 CrossRef CAS.
- O. Mbanga, E. Cukrowska and M. Gulumian, J. Nanopart. Res., 2021, 23, 29 CrossRef CAS.
- V.-P. Thai, H. D. Nguyen, N. Saito, K. Takahashi, T. Sasaki and T. Kikuchi, Nanoscale Adv., 2022, 4, 4490–4501 RSC.
- G. I. Nikishin, N. I. Kapustina, L. L. Sokova, O. V. Bityukov and A. O. Terent'ev, Tetrahedron Lett., 2020, 61, 152154 CrossRef CAS.
- S. Cherevko, A. A. Topalov, A. R. Zeradjanin, I. Katsounarosa and K. J. J. Mayrhofer, RSC Adv., 2013, 3, 16516 RSC.
- H. Shi, H. Bi, B. Yao and L. Zhang, Appl. Surf. Sci., 2000, 161, 276 CrossRef CAS.
- S. R. King, J. Massicot and A. M. McDonagh, Metals, 2015, 5, 1454 CrossRef.
- S. K. Misra, A. Dybowska, D. Berhanu, S. N. Luoma and E. Valsami-Jones, Sci. Total Environ., 2012, 438, 225 CrossRef CAS PubMed.
- J. Hedberg, E. Blomberg and I. O. Wallinder, Environ. Sci. Technol., 2019, 53(8), 4030 CrossRef CAS PubMed.
- H. Shi, H. Bi, B. Yao and L. Zhang, Appl. Surf. Sci., 2000, 161(1–2), 276 CrossRef CAS.
- M. N. Martin, A. J. Allen, R. I. MacCuspie and V. A. Hackley, Langmuir, 2014, 30(38), 11442 CrossRef CAS PubMed.
- S. Riaz, L. Qu, E. K. Fodjo, W. Ma and Y.-T. Long, RSC Adv., 2014, 4, 14031 RSC.
- J. R. Reimers, M. J. Ford, A. Halder, J. Ulstrup and N. S. Hush, Proc. Natl. Acad. Sci. U. S. A., 2016, 113(11), E1424 CrossRef CAS PubMed.
- S. K. Tripathy, J. Y. Woo and C.-S. Han, Anal. Chem., 2011, 83(24), 9206 CrossRef CAS PubMed.
- Product Specification Product Number: 742007 “50 Nm Diameter, OD 1, Stabilized Suspension in Citrate Buffer”, https://www.sigmaaldrich.com/UA/en/product/aldrich/742007 Search PubMed.
- S. M. Briffa, J. Sullivan, A. Siupa, P. Carnell-Morris, M. Carboni, K. Jurkschat, R. J. B. Peters, C. Schultz, K. H. Seol, S. J. Kwon, S. Park, T. H. Yoon, C. Johnston, S. Lofts and E. Valsami-Jones, J. Visualized Exp., 2020, 164, e61741 Search PubMed.
- B. Snopok, A. Laroussi, C. Cafolla, K. Voïtchovsky, T. Snopok and V. M. Mirsky, Surf. Interfaces, 2021, 22, 100818 CrossRef CAS.
- B. A. Snopok and Ya. D. Lampeka, Opt. Spectrosc., 1992, 73(4), 400 Search PubMed.
- B. A. Snopok and Y. D. Lampeka, Opt. Spectrosc., 1993, 75(2), 189 Search PubMed.
- V. Klimov, Nanoplasmonics, Jenny Stanford Publishing, 2014 Search PubMed.
- I. M. Krishchenko, É. G. Manoilov, S. A. Kravchenko and B. A. Snopok, Theor. Exp. Chem., 2020, 56, 67 CrossRef CAS.
- Y. Liu, W. Fu, Z. Xu, L. Zhang, T. Sun, M. Du, X. Kang, S. Xiao, C. Zhou, M. Gong and D. Zhang, Front. Chem., 2021, 9, 675491 CrossRef CAS PubMed.
- V. A. Dhumale, R. K. Gangwar, S. S. Datar and R. B. Sharma, Mater. Express, 2012, 2(4), 311 CrossRef CAS.
- E. Moaseri, J. A. Bollinger, B. Changalvaie, L. Johnson, J. Schroer, K. P. J. Orcid and T. M. Truskett, Langmuir, 2017, 33(43), 12244 CrossRef CAS PubMed.
- S. Shrestha, B. Wang and P. Dutta, Adv. Colloid Interface Sci., 2020, 279, 102162 CrossRef CAS PubMed.
- B. D. Dana, A. N. Koya, X. Song and J. Lin, Phys. B, 2022, 631, 413706 CrossRef CAS.
- M. Loumaigne, C. Midelet, T. Doussineau, P. Dugourd, R. Antoine, M. Stamboul, A. Débarrecd and M. H. V. Werts, Nanoscale, 2016, 8(12), 6555 RSC.
- Y. Zhou, J. Zhu, J. Xi, K. Li and W. Huang, J. Phys. Chem. A, 2023, 127(1), 390 CrossRef CAS PubMed.
- X. Gu, V. Timchenko, Y. G. Heng, L. Dombrovsky and R. Taylor, Appl. Sci., 2018, 8(7), 1132 CrossRef.
- L. V. Melendez, S. J. Barrow, A. Liu, T. U. Connell and D. E. Gómez, Optica, 2020, 7, 1666 CrossRef.
- W. Wei, R. Gou, C. Shu and Z. Guo, J. Phys. Chem. C, 2023, 127(16), 7808–7815 CrossRef CAS.
- J. L. Axson, D. I. Stark, A. L. Bondy, S. S. Capracotta, A. D. Maynard, M. A. Philbert, I. L. Bergin and A. P. Ault, J. Phys. Chem. C, 2015, 119(35), 20632 CrossRef CAS PubMed.
- I. Fernando and Y. Zhou, Chemosphere, 2019, 216, 297 CrossRef CAS PubMed.
- F. Kaspar, ChemBioChem, 2023, 24, e202200744 CrossRef CAS PubMed.
- Compendium of Chemical Terminology, ed. A. D. McNaught and A. Wilkinson, IUPAC the “Gold Book”, Blackwell Scientific Publications, Oxford, 2nd edn, 1997 Search PubMed.
- E. H. Mohamed, H. M. Lotfy, M. A. Hegazy and S. Mowaka, Chem. Cent. J., 2017, 11, 43 CrossRef CAS PubMed.
- J. H. Yoon, F. Selbach, L. Schumacher, J. Jose and S. Schlücker, ACS Photonics, 2019, 6(3), 642 CrossRef CAS.
- G. A. Kelesidis, D. Gao, F. H. L. Starsich and S. E. Pratsinis, Anal. Chem., 2022, 94(13), 5310 CrossRef CAS PubMed.
- R. T. Hill, J. J. Mock, A. Hucknall, S. D. Wolter, N. M. Jokerst, D. R. Smith and A. Chilkoti, ACS Nano, 2012, 6(10), 9237 CrossRef CAS PubMed.
- X. Ma, Y. Guo, M. Pu, X. Li and X. Luo, Plasmonics, 2019, 14, 845 CrossRef.
- S. Manzhosa, G. Giorgib, J. Lüderd and M. Ihara, Adv. Phys.: X, 2021, 6(1), 1908848 Search PubMed.
- L. Cheng, G. Zhu, G. Liu and L. Zhu, Mater. Res. Express, 2020, 7(12), 125009 CrossRef CAS.
- J. Shin, M. Song, H. Hafeez, P. J. Jeusraj, D. H. Kim, J. C. Lee, W. H. Lee, D. K. Choi, C. H. Kim, T. S. Bae, S. M. Yu, K. Kim, H. G. Park, K. B. Chung, A. Song, Y. C. Kang, J. Park, C. Kim and S. Ryu, Org. Electron., 2019, 66, 94 CrossRef CAS.
- I. V. Mironov, Medium Effects and Complexation in the Electrolyte Solutions, Novosibirsk, SB RAS, Institute of Inorganic Chemistry, 2003 Search PubMed.
- R. Javed, A. Sajjad, S. Naz, H. Sajjad and Q. Ao, J. Mol. Sci., 2022, 23, 10521 CrossRef CAS PubMed.
- S. J. Zalyubovskiy, M. Bogdanova, A. Deinega, Y. Lozovik, A. D. Pris, K. H. An, W. P. Hall and R. A. Potyrailo, J. Opt. Soc. Am. A, 2012, 29, 994 CrossRef CAS PubMed.
- A. Bonyár, Biosensors, 2021, 11(12), 527 CrossRef PubMed.
- L. Guo, J. A. Jackman, H.-H. Yang, P. Chen, N.-J. Cho and D.-H. Kim, Nano Today, 2015, 10(2), 213 CrossRef CAS.
- D.-B. Grys, B. de Nijs, A. R. Salmon, J. Huang, W. Wang, W.-H. Chen, O. A. Scherman and J. J. Baumberg, ACS Nano, 2020, 14(7), 8689 CrossRef CAS PubMed.
- G. I. Nikishin, N. I. Kapustina, L. L. Sokova, O. V. Bityukov and A. O. Terent'ev, Tetrahedron Lett., 2020, 61(31), 152154 CrossRef CAS.
- N. T. K. Thanh, N. Maclean and S. Mahiddine, Chem. Rev., 2014, 114, 7610 CrossRef CAS PubMed.
- A. A. Eliseev and A. V. Lukashyn, in Functional Nanomaterials, ed. Y. D. Tretyakov, Fizmatlyt, Moscow, 2010 Search PubMed.
- M. Z. Iqbal, I. Ali, W. S. Khan, X. Kong and E. Dempsey, Mater. Des., 2021, 205, 109694 CrossRef.
- S. Nizamov, O. Kasian and V. M. Mirsky, Angew. Chem., Int. Ed., 2016, 55(25), 7247 CrossRef CAS PubMed.
- H. Shi, H. Bi, B. Yao and L. Zhang, Appl. Surf. Sci., 2000, 161(1–2), 276 CrossRef CAS.
- S. McCarrick, K. Midander, M. Krausová, U. Carlander and H. L. Karlsson, Int. J. Nanomed., 2021, 16, 5895 CrossRef PubMed.
- U. Carlander, K. Midander, Y. S. Hedberg, G. Johanson, M. Bottai and H. L. Karlsson, ACS Appl. Bio Mater., 2019, 2(3), 1006 CrossRef CAS PubMed.
- K. Oya, K. Aoshika, M. Ageishi, H. Magara, S. Ogawa, Y. Takakuwa and T. Takami, Chem. Lett., 2021, 50, 191 CrossRef CAS.
- C. M. Alexander, J. C. Dabrowiak and J. Goodisman, J. Colloid Interface Sci., 2013, 396, 53 CrossRef CAS PubMed.
- J. Midelet, A. El-Sagheer, T. Brown, A. G. Kanaras and M. H. V. Werts, Part. Part. Syst. Charact., 2017, 34(10), 1700095 CrossRef.
- C. M. Alexander, J. C. Dabrowiak and J. Goodisman, J. Colloid Interface Sci., 2013, 396, 53 CrossRef CAS PubMed.
- J. N. Israelachvili, in Intermolecular and Surface Forces, Elsevier eBooks, 2011 Search PubMed.
- S. C. Endres, L. C. Ciacchi and L. Mädler, J. Aerosol Sci., 2021, 153, 105719 CrossRef CAS.
- V. A. Hernández, ChemTexts, 2023, 9, 10 CrossRef.
- B. Derjaguin and L. Landau, Acta Phys.-Chim., 1941, 14, 633 Search PubMed.
- T. Gong, M. R. Corrado, A. R. Mahbub, C. Shelden and J. N. Munday, Nanophotonics, 2021, 10(1), 523 CrossRef CAS.
- E. Marino, O. A. Vasilyev, B. B. Kluft, M. J. B. Stroink, S. Kondrat and P. Schall, Nanoscale Horiz., 2021, 6, 751 RSC.
- J. R. Villanueva-Valencia, H. Guo, R. Castañeda-Priego and Y. Liu, Phys. Chem. Chem. Phys., 2021, 23, 4404 RSC.
- R. Zhao, L. Li, S. Yang, W. Bao, X. Yang, P. Ashby, Y. Wang and X. Zhang, Science, 2019, 364, 984 CrossRef CAS PubMed.
- S. Y. Buhmann, Dispersion Forces I, Macroscopic Quantum Electrodynamics and Ground-State Casimir, Casimir-Polder and van der Waals Forces, Springer-Verlag, Berlin, Heidelberg, 2012 Search PubMed.
- C. Girard, C. Joachim and S. Gauthier, Rep. Prog. Phys., 2000, 63(6), 893 CrossRef CAS.
- H. Demchenko and N. Rusinchuk, J. Nanotechnol., 2019, 4270454 CAS.
- V. Lozovski and V. Piatnytsia, J. Comput. Theor. Nanosci., 2013, 10, 2288 CrossRef CAS.
- H. B. G. Casimir and D. Polder, Phys. Rev., 1948, 73, 360 CrossRef CAS.
- P. Barcellona and R. Passante, Ann. Phys., 2015, 355, 282 CAS.
- G. L. Klimchitskaya and V. M. Mostepanenko, Mod. Phys. Lett. A, 2020, 35(03), 2040007 CrossRef.
- L. Novotny and C. Henkel, Opt. Lett., 2008, 33, 1029 CrossRef CAS PubMed.
- I. Yavuz, J. Schötz, M. F. Ciappina, P. Rosenberger, Z. Altun, M. Lewenstein and M. F. Kling, Phys. Rev. A, 2018, 98, 043413 CrossRef CAS.
- V. Lozovski, V. Lysenko and N. Rusinchuk, Sci. Rep., 2022, 12, 17768 CrossRef CAS PubMed.
- J. H. K. Pfisterer, M. Baghernejad, G. Giuzio and K. F. Domke, Nat. Commun., 2019, 10(1), 5702 CrossRef CAS PubMed.
- V. Z. Lozovski, V. S. Lysenko and N. M. Rusinchuk, Adv. Nat. Sci: Nanosci. Nanotechnol., 2020, 11, 015014 CAS.
- A. L. Suherman, G. Zampardi, S. Kuss, E. E. L. Tanner, H. M. A. Amin, N. P. Young and R. G. Compton, Phys. Chem. Chem. Phys., 2018, 20(14), 28300 RSC.
- L. D. Burke and P. F. Nugent, Gold Bull., 1997, 30, 43 CrossRef CAS.
- C. Cardell and I. Guerra, Sci. Adv., 2022, 9(36), 8 Search PubMed.
- X. Ji, X. Song, J. Li, Y. Bai, W. Yang and X. Peng, J. Am. Chem. Soc., 2007, 129, 13939 CrossRef CAS PubMed.
- E. Nishikata, T. Ishii and T. Ohta, J. Chem. Eng. Data, 1981, 26(3), 254 CrossRef CAS.
- X. Huang, L. Sheng, Y. Lu and S. Li, Micromachines, 2022, 13(5), 771 CrossRef PubMed.
- P. M. Boltovets, S. A. Kravchenko and B. A. Snopok, Plasmonics, 2010, 5(4), 395 CrossRef CAS.
- C. N. Banwell and E. M. McCash, Fundamentals of Molecular Spectroscopy, McGraw-Hill, 1994 Search PubMed.
- R. C. Hilborn, Am. J. Phys., 1982, 50, 982 CrossRef CAS.
- O. Axner, J. Gustafsson, N. Omenetto and J. D. Winefordner, Spectrochim. Acta, Part B, 2004, 59(1), 1 CrossRef.
- W. E. Blass and G. W. Halsey, Deconvolution of Absorption Spectra, Academic Press, 1981 Search PubMed.
- W. F. Maddams, Appl. Spectrosc., 1980, 34(3), 245 CrossRef CAS.
- D. Applebaum, Lévy Processes and Stochastic Calculus, Cambridge University Press, 2009 Search PubMed.
- S. L. Li and D. G. Truhlar, J. Chem. Theory Comput., 2017, 13(6), 2823 CrossRef CAS PubMed.
- J. H. R. Clarke, in Advances in Infrared and Raman Spectroscopy, ed. R. J. H. Clark and R. E. Hester, 1978, vol. 4, p. 109 Search PubMed.
- T. Yatsui, M. Yamaguchi and K. Nobusada, Prog. Quantum Electron., 2017, 55, 166 CrossRef.
- A. Al-Zubeidi, B. S. Hoener, S. S. E. Collins, W. Wang, S. R. Kirchner, S. a. H. Jebeli, A. Joplin, W. Chang, S. Link and C. F. Landes, Nano Lett., 2019, 19(2), 1301 CrossRef CAS PubMed.
- H. Bockmann, “Far- and Near-Field Photochemistry of Single Molecules on a Metal Surface” PhDT, 2019 Search PubMed.
- Y. Ohmi, S. Nishimura and K. Ebitani, ChemSusChem, 2013, 6(12), 2259 CrossRef CAS PubMed.
- T. Yatsui, in 2017 OPJ-OSA Joint Symposia on Nanophotonics and Digital Photonics, ed. T. Omatsu, OSA Technical Digest (online) Optica Publishing Group, 2017 Search PubMed.
- J. Hedberg, E. Blomberg and I. O. Wallinder, Environ. Sci. Technol., 2019, 53, 4030 CrossRef CAS PubMed.
- M. N. Martin, A. J. Allen, R. I. MacCuspie and V. A. Hackley, Langmuir, 2014, 30(38), 11442 CrossRef CAS PubMed.
- D. E. Kim, J. Y. Kim, I. C. Sun, D. Schellingerhout, S. K. Lee, C. H. Ahn, I. C. Kwon and K. Kim, Ann. Neurol., 2013, 73(5), 617 CrossRef CAS PubMed.
- Y. Wang, J. E. Q. Quinsaat and T. Ono, et al. , Nat. Commun., 2020, 11, 6089 CrossRef CAS PubMed.
- V. Kesler, B. Murmann and H. T. Soh, ACS Nano, 2020, 14(12), 16194 CrossRef CAS PubMed.
- E. T. Athira and J. Satija, Analyst, 2023, 148, 6188 RSC.
- B. A. Snopok and O. B. Snopok, in Nanostructured Materials for the Detection of CBRN, Springer, 2018 Search PubMed.
- S. İlday, G. Makey, G. B. Akgüç, Ö. Yavuz, O. Tokel, I. Pavlov, O. Gülseren and F. Ö. İlday, Nat. Commun., 2017, 8, 14942 CrossRef PubMed.
- N. A. Kotov, ACS Nano, 2009, 3(6), 1307 CrossRef CAS PubMed.
- M. Stöhr, M. Sadhukhan, Y. S. Al-Hamdani, J. Hermann and A. Tkatchenko, Nat. Commun., 2021, 12, 137 CrossRef PubMed.
- T. Ocampo-Delgado and B. Ivlev, J. Exp. Theor. Phys., 2010, 110, 367 CrossRef CAS.
- A. Rao, S. Roy and P. P. Pillai, Langmuir, 2021, 37(5), 1843 CrossRef CAS PubMed.
- H. M. Lee, Y. K. Kim, E. M. Go, C. Revadekar, K. H. Choi, Y. Cho, S. K. Kwak and B. J. Park, Nat. Commun., 2023, 14, 3838 CrossRef CAS PubMed.
- L. M. Woods, D. A. R. Dalvit, A. Tkatchenko, P. Rodriguez-Lopez, A. W. Rodriguez and R. Podgornik, Rev. Mod. Phys., 2016, 88, 045003 CrossRef.
- R. Esquivel-Sirvent, Physics, 2023, 5(1), 322 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00109e |
| This journal is © The Royal Society of Chemistry 2024 |