DOI:
10.1039/D4NA00153B
(Paper)
Nanoscale Adv., 2024,
6, 3306-3319
Side-view optical microscopy-assisted atomic force microscopy for thickness-dependent nanobiomechanics†
Received
22nd February 2024
, Accepted 6th April 2024
First published on 8th April 2024
Abstract
The mechanical properties of biomaterials play an important role in regulating life processes, and thus accurately delineating the mechanical properties of biomaterials is critical to understand their functionality. Particularly, atomic force microscopy (AFM) has become a powerful and standard tool for characterizing and analyzing the nanomechanical properties of biomaterials, and providing a capability to visualize the thickness of the specimen during AFM-based force spectroscopy experiments benefits the biomedical applications of AFM. Here, we present a study of side-view optical microscopy-assisted AFM based on the integration of AFM and a detachable side-view optical microscopy module, which is able to image in real time the AFM indentation process from the side-view perspective and consequently facilitates the utilization of AFM-based indentation assay to precisely detect the mechanical properties of a specimen by taking its thickness into account. The effectiveness of side-view optical microscopy-assisted AFM was confirmed on four different types of biomaterial systems, including microfabricated structures, hydrogels, living cells, and cell spheroids, and the experimental results significantly show that the mechanical properties of samples at the micro/nanoscale are closely related to their thickness, vividly illustrating side-view optical microscopy-assisted AFM as a promising approach for accurate nanomechanics of biomaterial systems. The study provides additional possibilities for measuring the thickness-dependent nanomechanical properties of biomaterials by AFM, which will enable AFM-based force spectroscopy technology to address more biological issues with enhanced precision and will benefit the field of mechanobiology.
1. Introduction
Mechanical cues are crucial for life activities. Normal tissue cells are generally not viable when suspended in a fluid and they must adhere to a solid to perform cellular physiological activities, which is called anchorage dependence.1 The solid supporting cellular attachment is called the extracellular matrix (ECM), which is a three-dimensional, non-cellular structure that is present in all tissues and is essential for life.2 The ECM is composed of two main classes of macromolecules, including proteoglycans and fibrous proteins.3 Cells adhere to the ECM via cell surface receptors to sense mechanical cues from the ECM and respond in an appropriate manner (for example, changes in cell shape and size and responses), which is known as mechanotransduction.4 The stiffness of ECMs has been shown to significantly affect a variety of cellular processes, including cell spreading, cell migration, stem cell differentiation, cell division, cell apoptosis, and cancer progression.5 Particularly, ECMs are not only linearly elastic materials, but also exhibit other complex mechanical behaviors (such as viscoelasticity, plasticity, and nonlinear elasticity),6 which all affect cellular behaviors. It is increasingly apparent that any modern tissue engineering strategy has to consider the stiffness of the native biological tissue, as well as the implications of this stiffness for the behaviors of resident cells.7 The role of the physical microenvironment in tumor development, progression, metastasis, and treatment is considerably gaining appreciation.8 In addition to the mechanical properties of ECMs, the mechanical properties of cells themselves influence cellular and subcellular functions, including adhesion, migration, polarization, and differentiation, as well as organelle organization and trafficking inside the cytoplasm.9 For example, invasive and metastatic cancer cells have often been reported to be softer than normal cells, which facilitates the migration of cancer cells through the narrow tissue spaces for dissemination.10,11 Therefore, developing methods to accurately characterize the mechanical properties of biomaterials is of fundamental significance for exploring the regulatory roles of mechanical cues in physiological and pathological processes to advance life sciences and healthcare.
The atomic force microscopy (AFM)-based force spectroscopy technique12,13 has been an important and standard method for measuring the nanomechanical properties of soft materials (e.g., hydrogels,14 biological membrane proteins,15 viruses,16 extracellular vesicles,17 cells,18 and tissues19) by controlling the AFM probe to perform indentation assay in the vertical direction on the specimens, contributing much to the field of mechanobiology.20,21 In AFM-based indentation assay, the Hertz–Sneddon model is the most commonly used theoretical model to extract the Young's modulus of the specimen from the force curves,22–24 which assumes that the specimen being indented is infinitely thick and thus neglects the effect of specimen thickness on the measured mechanics. Researchers have improved the Hertz–Sneddon model to make it suitable for measuring the mechanical properties of samples with finite thickness,25–27 which rely on utilizing AFM to perform line/topographic scans on the specimen previously to obtain the thickness of each measurement point and thus providing a capability to expediently measure the thickness of the specimen benefits the applications of the AFM-based force spectroscopy technique. Combining AFM with confocal microscopy allows the rendering of a side-view optical image of the cell being detected by AFM,28 but it is not real-time. Researchers have also explored attaching side-view optical microscopy systems to AFM to visualize in real time the AFM indentation process from the side-view perspective for the mechanical studies of cells.29–32 Nevertheless, combining side-view optical microscopy with AFM to examine the effect of specimen thickness on specimen mechanics at the micro/nanoscale is still rarely reported. Here, we developed a detachable side-view optical microscopy module for a commercial AFM without any modifications to the AFM itself, and the constructed side-view optical microscopy-assisted AFM was then utilized to perform force measurements on diverse biomaterial systems (microfabricated structures, hydrogels, living cells, and cell spheroids) to comprehensively analyze the effect of specimen thickness on specimen mechanics. The experimental results reveal the remarkable effects of specimen thickness on specimen mechanics measured by AFM, providing novel possibilities for utilizing AFM to accurately characterize the thickness-dependent nanomechanics of biomaterials for better biomedical applications.
2. Materials and methods
2.1 Cell culture and cell sample preparation
HEK-293 cells (a human embryonic kidney cell line), MGC-803 cells (a human gastric cancer cell line), HGC-27 cells (a human undifferentiated gastric cancer cell line), and Raji cells (a human B lymphoblastoid cell line) were purchased from the Cell Bank of Chinese Academy of Sciences (Shanghai, China). The RPMI-1640 medium, Dulbecco's Modified Eagle Medium (DMEM) with high glucose, and phosphate-buffered saline (PBS) were purchased from the DearyTech Company (Shanghai, China). The penicillin-streptomycin solution was purchased from the Solarbio Company (Beijing, China). The Leibovitz's L-15 medium, trypsin solution, and fetal bovine serum (FBS) were purchased from Thermo Fisher Scientific (Waltham, Massachusetts, USA). HEK-293 cells were cultured in DMEM medium containing 10% FBS and 1% penicillin-streptomycin at 37 °C (5% CO2 and 95% air). MGC-803 cells, HGC-27 cells, and Raji cells were cultured in RPMI-1640 medium containing 10% FBS and 1% penicillin-streptomycin at 37 °C (5% CO2 and 95% air). HEK-293 cells, MGC-803 cells, and HGC-27 cells were cultured in dishes. Raji cells were cultured in flasks.
For utilizing the established side-view optical microscopy-assisted AFM to detect adherent cells (HEK-293 cells, MGC-803 cells, HGC-27 cells), cells were seeded on coverslips (10 mm × 10 mm) and incubated at 37 °C (5% CO2 and 95% air) for 18 h. After adding 20 mL of L-15 medium into the square dish of the side-view optical microscopy-assisted AFM system, the coverslip was placed in the square dish, and the heating plate under the square dish was turned on for subsequent AFM experiments of adherent cells at 37 °C. For detecting Raji cells, the micropillar substrate used for cell trapping was placed in the square dish of the side-view optical microscopy-assisted AFM system in L-15 medium (the heating plate was turned on), and then the Raji suspension solution was directly dropped onto the micropillar substrate and allowed to sit for 2 min. After that, AFM experiments of Raji cells were performed at 37 °C.
2.2 Micropillar structure fabrication
The polydimethylsiloxane (PDMS) micropillar substrates were prepared according to a previous protocol based on maskless photolithography and PDMS molding.33 Briefly, the AZ P4620 photoresist (Merck KGaA Company, Darmstadt, Germany) was first coated on a glass slide by using a spin coater. The glass slide was then heated at 90 °C for 180 s. Next, a maskless lithography system (miDALIX Company, Slovenia) was used to generate the patterns with desired geometries on the photoresist on the glass slide by laser direct imaging. Subsequently, a developer (Changchun Tok Company, Changshu, China) was used to treat the glass slide to form the mold. After that, the PDMS monomer and cross-linker (Dow Corning Corporation, Midland, Michigan, USA) were mixed in a specified ratio (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 5
1 or 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and the mixture was poured onto the mold. The mold was then degassed for 1 h, after which the mold was heated at 80 °C for 2 h. The micropillar substrates were then obtained by directly peeling the hardened PDMS from the mold. For the fabrication of cuboid micropillars, the designed geometries of cuboid micropillars are the following: the side length is 50 μm, the height is 15 μm, and the distance between two adjacent micropillars is 50 μm. The designed geometries of cylindrical micropillars (used for cell trapping) are the following: the diameter is 10 μm, the height is 10 μm, and the axial distance between two adjacent cylindrical micropillars is 20 μm.
1) and the mixture was poured onto the mold. The mold was then degassed for 1 h, after which the mold was heated at 80 °C for 2 h. The micropillar substrates were then obtained by directly peeling the hardened PDMS from the mold. For the fabrication of cuboid micropillars, the designed geometries of cuboid micropillars are the following: the side length is 50 μm, the height is 15 μm, and the distance between two adjacent micropillars is 50 μm. The designed geometries of cylindrical micropillars (used for cell trapping) are the following: the diameter is 10 μm, the height is 10 μm, and the axial distance between two adjacent cylindrical micropillars is 20 μm.
2.3 Hemisphere structure fabrication
The hemisphere structures were fabricated by using two-photon lithography (Photonic Professional GT2, Nanoscribe GmbH & Co. KG, Germany). With the use of the SolidWorks software (Dassault Systemes, Velizy-Villacoublay, France), two types of hemisphere structures (the radii are 5 μm and 10 μm respectively) were designed and the STL file was generated. The STL file was imported into the print job development software (DeScribe) of the two-photon lithography system to set the 3D print parameters. The print material is resin (IP-DIP). The hemisphere structures were formed on the fused silica substrate with the use of a 63× objective lens. The laser source is a 780 nm femtosecond laser, and the laser intensity is 20 MW. Different laser scanning speeds were used, including 1000 μm s−1, 3000 μm s−1, 5000 μm s−1, 7000 μm s−1, and 9000 μm s−1. After fabrication, the substrate was treated with propylene glycol methyl ether acetate (PGMEA) for 20 min, and then the substrate was treated with isopropyl alcohol (IPA) for 30 s to remove the residual resin and to form the hemisphere structures.
2.4 Hydrogel preparation
The gelatin methacryloyl (GelMA) hydrogels were prepared according to previous protocols.34 Briefly, the purchased GelMA material (Engineering For Life Company, Suzhou, China) with an amino substitution degree of 30 was used to prepare hydrogels. First, 0.05 g of photoinitiator was dissolved in 20 mL of PBS to prepare the photoinitiator solution. Next, a specified amount of GelMA was added into a centrifuge tube containing 5 mL of photoinitiator solution, for example, 0.5 g GelMA was added to prepare the GelMA hydrogel with a concentration of 10% (w/v). The centrifuge tube was then heated at 50 °C in the dark for 30 min (the tube was shaken several times). Subsequently, the GelMA solution was dropped onto a fresh coverslip, and then a digital mirror device (DMD)-based optical projection lithography system35 was used to irradiate the hydrogel solution with UV light for polymerization, after which hydrogel patches of different heights were obtained.
2.5 Preparation of cell spheroids
Raji cells can naturally form cell spheroids, and Raji cell spheroids could be observed after culturing Raji cells for 1 day at 37 °C (5% CO2 and 95% air). For preparing spheroids of adherent cells (HEK-293 cells), the digested HEK-293 cells were added into the wells of the ultra-low attachment cell culture plate (LABSELECT Company, Hefei, China) and cultured at 37 °C (5% CO2 and 95% air) for 24 h, during which cell spheroids were formed. A micropillar substrate was placed in the square dish containing L-15 medium, and then the cell spheroid solution was dropped onto the micropillar substrate and allowed to sit for 2 min. Subsequently, force measurement experiments by the side-view optical microscopy-assisted AFM were performed on the cell spheroids at 37 °C.
2.6 Side-view optical microscopy module
The side-view optical microscopy module mainly consists of a 10× objective lens (Zhaoyi Opto-electronics Technology Company, Shanghai, China), a CCD camera (Oplenic Company, Hangzhou, China), a 3D mobile platform (Hengyang Electronic Technology Company, Guangzhou, China), a coaxial light source (Topray Technology Company, Shenzhen, China), a breadboard (Thorlabs, Newton, New Jersey, USA), and the supporting frame. By manually controlling the 3D mobile platform, the focus plane of the side-view optical microscopy system was positioned on the AFM probe to allow observing the thickness of the sample being indented as well as the contact process between the AFM probe and the sample during AFM-based force spectroscopy experiments. Particularly, the square Petri dish (the length, width and height are 10 cm, 10 cm, and 1.7 cm respectively) was used instead of the regular round Petri dish for better obtaining the side-view optical microscopy images of the specimen (a round dish filled with liquid can be approximated as a convex lens, which can blur the imaging of objects in the dish by the side-view optical microscopy). Besides, an aluminum alloy supporting block (the reason for using aluminum alloy is its good thermal conductivity) was fabricated and placed in the dish for the integration of the AFM and the side-view optical microscopy module. In addition, in order to improve the imaging result of the transmitted light path, a mirror was added to the side of the supporting block and a silicon chip was placed on the supporting block. In order to maintain the growth environment of living cells during AFM experiments, the square dish was placed on a heating plate.
2.7 Preparation of microsphere-modified AFM probes for indentation assay
The microsphere-modified AFM probes were prepared by gluing a microsphere to an AFM probe based on the micromanipulations using a commercial AFM (Dimension Icon, Bruker, Santa Barbara, CA, USA).34 Briefly, the two parts of the epoxy adhesive (3M, Maplewood, Minnesota, USA) were mixed on one end of a fresh glass slide, and the polystyrene microsphere solution was dropped on the other end of the glass slide. Next, under the guidance of AFM's optical microscopy, the AFM probe (the spring constant of the cantilever is 0.12 N m−1) (DNP-10-B, Bruker, Santa Barbara, CA, USA) was controlled to contact with the epoxy adhesive, after which the glue-modified AFM probe was controlled to touch a microsphere for 3 min. Subsequently, the AFM probe was controlled to retract, and then the prepared spherical probe was placed in an AFM probe box and left at room temperature for 12 h before being used for AFM experiments.
2.8 Preparation of the AFM single-cell probe for SCFS assay
The single-cell AFM probe used for SCFS assay was prepared according to a previous protocol.36 The reagents for single-cell probe functionalization, including biotin-conjugated bovine serum albumin (BSA), streptavidin, and biotin-conjugated concanavalin A (ConA), were purchased from the Solarbio Company (Beijing, China). Briefly, the tipless AFM cantilever (the spring constant of the cantilever is 0.12 N m−1) (NP-O10-B, Bruker, Santa Barbara, CA, USA) was irradiated with UV light for 45 min, after which the cantilever was placed in 50 μL of biotin-BSA solution at 37 °C overnight. The cantilever was then washed with PBS three times, after which the cantilever was placed in 50 μL of streptavidin solution at room temperature for 30 min. After washing the cantilever three times with PBS, the cantilever was placed in 50 μL of biotin-ConA solution at room temperature for 30 min. After washing the cantilever three times with PBS, the functionalized cantilever was used to adsorb single living MGC-803 cell. For doing so, the ConA-functionalized tipless cantilever was controlled to gently touch a living digested MGC-803 cell with a contact force of 5 nN for 15 s, and then the AFM cantilever was controlled to retract and was kept in the medium for 20 min (ref. 37) to allow the formation of firm binding between the cell and the cantilever before being used in SCFS experiments.
2.9 AFM experiments
For each situation, the force curves were obtained with identical experimental parameters to make the results comparable with each other. For obtaining force curves on cuboid micropillars in air, the ramp size was 8 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 16 μm s−1. For obtaining force curves on cuboid micropillars in pure water, the ramp size was 2 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 4 μm s−1. For obtaining force curves on hemispheres in air, the ramp size was 2 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 4 μm s−1. For obtaining force curves on hydrogels in the PBS, the ramp size was 7 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 14 μm s−1. For obtaining force curves on living HEK-293 cells and Raji cells, the ramp size was 3 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 6 μm s−1. For obtaining force curves on living MGC-803 cells, the ramp size was 2 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 4 μm s−1. For performing approach-dwell-retract cycles on living cells, the dwell time of the AFM probe on the cell after the approach was 1 s. For SCFS assay, the ramp size was 12 μm, the ramp rate was 1 Hz, the approaching velocity of the AFM probe was 24 μm s−1, and the dwell time was 1 s. For obtaining force curves on cell spheroids, the ramp size was 5 μm, the ramp rate was 1 Hz, and the approaching velocity of the AFM probe was 10 μm s−1.
2.10 Scanning electron microscopy
Scanning electron microscopy (SEM) images were obtained using a commercial SEM called Quattro SEM (Thermo Fisher, Waltham, Massachusetts, USA). For imaging hydrogels by SEM, the prepared GelMA hydrogels were added into a centrifuge tube which was then placed in liquid nitrogen for 20 min. Next, the centrifuge tube was placed in a lyophilizer at −80 °C under 0.85 Pa for 24 h. The freeze-dried hydrogels were then cut into small pieces and gilded for SEM imaging. For imaging spherical AFM probes, microfabricated micropillar substrates and hemisphere structures, they were directly gilded and imaged by SEM.
2.11 Image dehazing
In experiments, the different refractive indices of air and water as well as the influence of the AFM's own light path can commonly degrade the side-view optical microscopy images obtained by the established side-view optical microscopy system. In order to improve the image quality, an image dehazing method based on the use of dark channel prior38 was utilized to treat the obtained side-view optical microscopy images. This method has been widely applied in the task of removing fog effects in the field of image processing, and its simplicity and efficiency allow it to quickly treat blurred images in practice. The image dehazing algorithm was written in C++ language and codes of the image dehazing algorithm were downloaded from the GitHub website (https://github.com/).
2.12 Data analysis
The Young's modulus of the specimen was calculated from the force curve by applying the original Hertz model and the thickness-corrected Hertz model25–27 respectively:| | 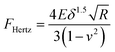 | (1) |
| | 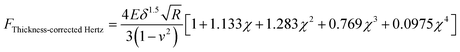 | (2) |
| | 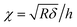 | (3) |
where F is the loading force exerted by the AFM probe, E is the Young's modulus of the specimen, R is the radius of the microsphere of the AFM spherical probe, δ is the indentation depth, υ is the Poisson ratio of the sample (here υ = 0.5), and h is the thickness of the specimen (obtained by the side-view optical microscopy module). The loading force was obtained from Hooke's law:where k is the spring constant of the AFM cantilever and x is the deflection of the AFM cantilever. According to the contact point in the approach curve, the approach curve was converted into the indentation curve by subtracting the cantilever deflection from the vertical displacement of the piezoelectric tube. The contact point was determined by analyzing the slope changes of the approach curve.39 Briefly, for each point in the approach curve, the ratio of the variance over the small interval N (here N = 10) to the right of this point to the variance over the small interval N to the left of the point, which is called ratio of variances (ROV), is calculated by using the program written by Matlab (MathWorks, Natick, Massachusetts, USA)34 and thus the point of the maximum ROV corresponds to the contact point. The indentation curve was then fitted by the Hertz model or the thickness-corrected Hertz model to obtain the Young's modulus of the specimen, which was performed using the program written by Matlab. Notably, for calculating the Young's modulus of Raji cells, since Raji cells are round, the effective radius40 was used:| | 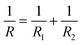 | (5) |
where R is the effective radius, R1 is the radius of the microsphere on the AFM cantilever, and R2 is the radius of the Raji cell.
The relaxation time of the cell was obtained by fitting the obtained relaxation curve with the Maxwell spring-dashpot model:34
where
A0 is the instantaneous response,
A1 is the force amplitude, and
τ is the cellular relaxation time. Notably, the relaxation curve was obtained by an external oscilloscope here, and the signals of the cantilever deflections during the relaxation process were voltages. The voltages were converted into forces:
where
F is the force of the AFM cantilever,
V is the voltage,
S is the deflection sensitivity of the AFM cantilever, and
k is the spring constant of the AFM cantilever. Fitting the relaxation curve with the Maxwell model was performed with the program written by Matlab. After obtaining the Young's modulus and relaxation time of the cell, the viscosity of the cell is then obtained:
where
η is the viscosity,
E is the Young's modulus, and
τ is the relaxation time. The significant differences were analyzed by two-tailed Student's
t-test using GraphPad Prism (San Diego, CA, USA).
3. Results and discussion
3.1 Construction of the side-view optical microscopy-assisted AFM
The side-view optical microscopy-assisted AFM system was first constructed. We designed a detachable side-view optical microscopy module (denoted by the dashed blue box in Fig. 1A) to observe in real time the indentation process of AFM-based force spectroscopy experiments from the side-view viewpoint. The side-view optical microscopy module (Fig. 1B and S1†) is positioned close to one side of the square Petri dish (II in Fig. 1B) which is placed on the AFM's sample stage. For better biomedical applications, a heating plate (Fig. S1†) is placed under the square dish to provide a temperature-controlled environment (for example, 37 °C is required for the activities of living cells). A supporting block (III in Fig. 1B) is placed in the dish to lift the sample so that the sample can be viewed using the side-view optical microscopy system. A mirror is placed sideways on the supporting block and a silicon chip is placed flat on the supporting block, which are used to enhance side-view optical imaging. A merit of the presented side-view optical microscopy module is that it does not require any changes/modifications to the AFM itself. Therefore, in addition to the AFM's own optical image (IV in Fig. 1B), the side-view optical microscopy-assisted AFM provides extra side-view optical images of the specimen being probed by AFM (V in Fig. 1B), which significantly facilitates better understanding of AFM-based force measurements. An image dehazing algorithm38 was exploited to improve the quality of side-view optical images obtained in solution. For better characterizing the mechanical properties of biomaterials, AFM spherical probes (a microsphere is glued to the AFM probe cantilever) were used here (the inset surrounded by the dashed grey box in Fig. 1A).
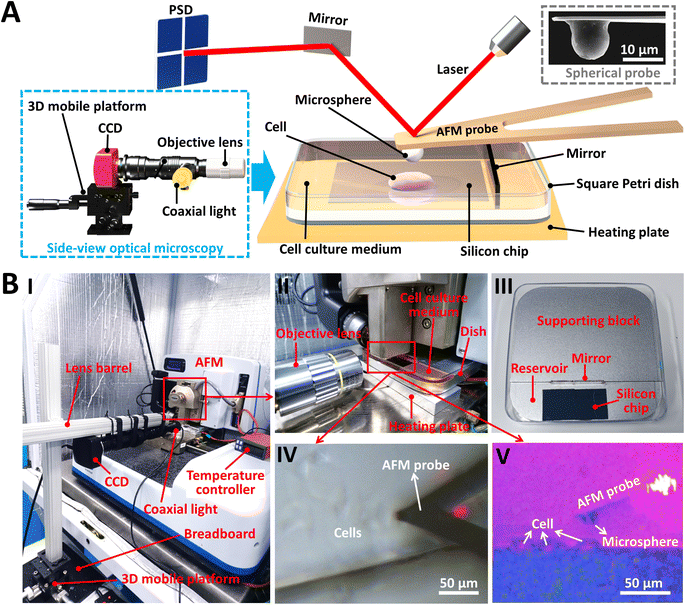 |
| | Fig. 1 Side-view optical microscopy-assisted AFM. (A) Schematic illustration of a side-view optical microscopy system for AFM force measurements. With the use of the side-view optical microscopy (denoted by the dashed blue box), the vertical contact process between the AFM probe and the specimen during AFM-based force spectroscopy experiments can be observed in real time, which can be exploited to analyze the effects of specimen thickness on the nanomechanical properties of the specimen measured by AFM. An example of a living cell being measured using the AFM spherical probe under aqueous conditions is shown. The inset denoted by the dashed grey box is a scanning electron microscopy (SEM) image of a prepared AFM spherical probe. (B) The actual photograph of the established side-view optical microscopy-assisted AFM system. (I) The whole system. (II) Magnified image showing the integration of AFM and the side-view optical microscopy. (III) The square Petri dish with a supporting block inside. (IV) Optical microscopy image of the AFM probe at work (an example of detecting living cells is shown) obtained by AFM's own optical microscopy system. (V) The simultaneously obtained optical image using the side-view optical microscopy module. | |
3.2 Indentation assay of microstructures by side-view optical microscopy-assisted AFM
The established side-view optical microscopy-assisted AFM was then utilized to measure the mechanical properties of individual microfabricated structures. Fig. 2 shows the results obtained on polydimethylsiloxane (PDMS) cuboid micropillars. Vertically aligned micropillars have been important biomaterials and have been widely used to sense and regulate cellular behaviors,41,42 and thus we fabricated micropillars (Fig. 2A) to test the performance of side-view optical microscopy-assisted AFM. The side-view optical images obtained during AFM indentation assay clearly show the AFM tip (microsphere) and the micropillar as well as their geometries (Fig. 2B). With the use of the micropillar thickness determined by the side-view optical image, the mechanical properties of the micropillars were conveniently measured by applying the thickness-corrected Hertz model.25–27 The mechanical properties of micropillars were measured in air (Fig. 2C) and in solution (Fig. 2D) respectively to examine the environmental effect on measurements. The real-time AFM indentation process on a single micropillar recorded by the side-view optical microscopy is shown in ESI Movie 1.† The results of fitting indentation curves obtained in both air (II and III in Fig. 2C) and solution (II and III in Fig. 2D) as well as the statistical results (Fig. 2E) show that the Young's modulus obtained by the thickness-corrected Hertz model was significantly smaller than that obtained by the Hertz model, indicating the influence of micropillar height on micropillar mechanics. An interesting point is that the Young's modulus of PDMS micropillars measured in water is much smaller than that measured in air, showing the impact of the environment on the mechanical properties of PDMS materials. We performed experiments on two types of PDMS micropillars with different ratios of monomers and cross-linkers (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to examine the effect of micropillar thickness on micropillar mechanics, and experimental results on both the two types of PDMS micropillars show a significant decrease in Young's modulus when the micropillar thickness is taken into account (Fig. 2E). However, we can also see that there is no significant difference in the Young's modulus of the prepared two types of PDMS micropillars (10
1) to examine the effect of micropillar thickness on micropillar mechanics, and experimental results on both the two types of PDMS micropillars show a significant decrease in Young's modulus when the micropillar thickness is taken into account (Fig. 2E). However, we can also see that there is no significant difference in the Young's modulus of the prepared two types of PDMS micropillars (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), which may be due to the fabrication of PDMS micropillars here. A previous study has shown that the Young's modulus of PDMS films was in the range of 0.1–1.6 MPa depending on the weight ratio (the ratio of monomers to cross-linkers) and curing time, and particularly there is no significant difference in the mechanical properties between the two PDMS films (10
1), which may be due to the fabrication of PDMS micropillars here. A previous study has shown that the Young's modulus of PDMS films was in the range of 0.1–1.6 MPa depending on the weight ratio (the ratio of monomers to cross-linkers) and curing time, and particularly there is no significant difference in the mechanical properties between the two PDMS films (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respectively) when the curing time is 16 h.43 Another study has shown that the Young's modulus (1.36 MPa) of PDMS films prepared with a weight ratio of 10
1 respectively) when the curing time is 16 h.43 Another study has shown that the Young's modulus (1.36 MPa) of PDMS films prepared with a weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is slightly smaller than the Young's modulus (1.5 MPa) of PDMS films prepared with a weight ratio of 5
1 is slightly smaller than the Young's modulus (1.5 MPa) of PDMS films prepared with a weight ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,44 in which the curing time was 20 min. Hence, we can optimize the weight ratio and curing time to prepare the PDMS micropillars with different mechanical properties in future studies. We also applied side-view optical microscopy-assisted AFM to measure the mechanics of single resin hemisphere structures fabricated by two-photon lithography, and the results show that the Young's modulus obtained by thickness-corrected Hertz model was smaller than that obtained by the Hertz model (Fig. S2†). Engineering biomaterials with microscale topographies and exploiting them to tune the behaviors of cells (such as from proliferation to differentiation and migration) at the cell–substrate interface has been a promising way for regenerative medicine and oncology.45–47 The established side-view optical microscopy-assisted AFM allows easily obtaining the geometric sizes of microstructures during AFM indentation assay and the consequent precise analysis of their mechanical properties by applying the thickness-corrected Hertz model, which therefore benefits comprehensive understanding of the structures and properties of engineered microtopographies and their roles in tuning the behaviors of cells.
1,44 in which the curing time was 20 min. Hence, we can optimize the weight ratio and curing time to prepare the PDMS micropillars with different mechanical properties in future studies. We also applied side-view optical microscopy-assisted AFM to measure the mechanics of single resin hemisphere structures fabricated by two-photon lithography, and the results show that the Young's modulus obtained by thickness-corrected Hertz model was smaller than that obtained by the Hertz model (Fig. S2†). Engineering biomaterials with microscale topographies and exploiting them to tune the behaviors of cells (such as from proliferation to differentiation and migration) at the cell–substrate interface has been a promising way for regenerative medicine and oncology.45–47 The established side-view optical microscopy-assisted AFM allows easily obtaining the geometric sizes of microstructures during AFM indentation assay and the consequent precise analysis of their mechanical properties by applying the thickness-corrected Hertz model, which therefore benefits comprehensive understanding of the structures and properties of engineered microtopographies and their roles in tuning the behaviors of cells.
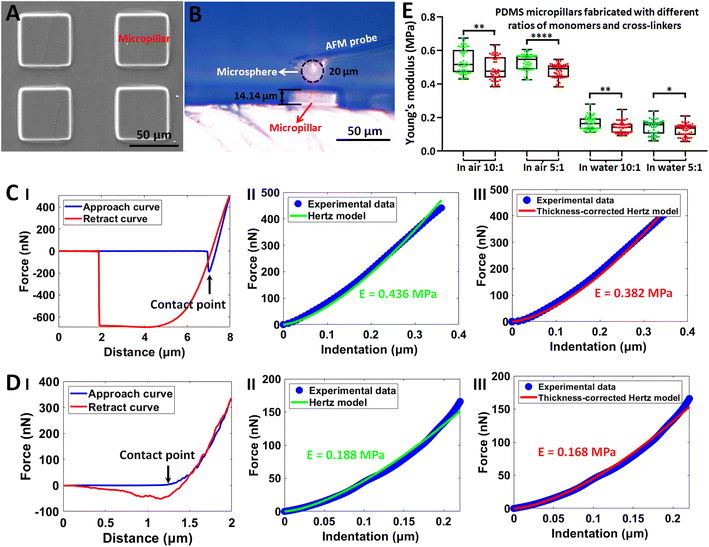 |
| | Fig. 2 Measuring the Young's modulus of single PDMS cuboid micropillars by side-view optical microscopy-assisted AFM to analyze the effects of specimen thickness on specimen mechanics. (A) SEM image of the fabricated PDMS cuboid micropillars. (B) The optical image recorded by the integrated side-view optical microscopy system showing the indentation process between the AFM spherical probe and a PDMS cuboid micropillar. (C and D) Measurements of the Young's modulus of micropillars performed in air (C) and in pure water (D) respectively. (I) Typical force curves. (II and III) The corresponding fitting results of the indentation curve converted from (I) by Hertz model (II) and thickness-corrected Hertz model (III) respectively. Contact points in the approach curves are indicated by black arrows. (E) Statistical results (box plots) of measuring the Young's modulus of two types of PDMS micropillars (the ratio between monomers and cross-linkers was 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5 1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respectively) under different conditions (in air and in pure water). Each dot represents a Young's modulus value. The green dots are the Young's modulus values calculated from the Hertz model, and the red dots are the Young's modulus values calculated from the thickness-corrected Hertz model. Statistical significance was set at the following levels: *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns not significant. 1 respectively) under different conditions (in air and in pure water). Each dot represents a Young's modulus value. The green dots are the Young's modulus values calculated from the Hertz model, and the red dots are the Young's modulus values calculated from the thickness-corrected Hertz model. Statistical significance was set at the following levels: *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns not significant. | |
3.3 Indentation assay of hydrogels by side-view optical microscopy-assisted AFM
The side-view optical microscopy-assisted AFM was next utilized to measure the mechanical properties of hydrogels in their native states (under aqueous conditions). Hydrogels are biomaterials that are widely used in cell culture systems to imitate critical features of the natural extracellular matrix,48 and particularly AFM has been a standard tool to assess the mechanics of hydrogel films.49 However, current studies utilizing AFM to characterize the mechanics of hydrogels commonly ignore the influence of hydrogel film thickness on hydrogel mechanics.50–52 Here, the effect of hydrogel film thickness on hydrogel mechanics was revealed by side-view optical microscopy-assisted AFM, as shown in Fig. 3. GelMA53 is an engineered gelatin-based hydrogel and has been widely used in the field of biomedicine, and thus we used GelMA as an example of hydrogel to test the side-view optical microscopy-assisted AFM. Three types of GelMA hydrogels with different concentrations (5%, 7.5%, and 10%) were prepared. Three-dimensional porous structures are significantly observed from the SEM images of hydrogels, and hydrogel with a higher concentration has a smaller pore size and a denser network than hydrogel with a smaller concentration (Fig. 3A and S3†). The side-view optical images clearly show the AFM indentation process on hydrogels (real-time side-view optical microscopy images of AFM indentation processes on hydrogels are shown in ESI Movie 2–4† respectively), from which the thickness of the hydrogel being indented by the AFM spherical probe can be directly obtained (Fig. 3B). One can see that the thickness-corrected Hertz model (III in Fig. 3C) fits the indentation curve better than the regular Hertz model (II in Fig. 3C). Statistical results (Fig. 3D) show that the Young’s modulus obtained by the thickness-corrected Hertz model is smaller than that obtained by the Hertz model, and the difference between the thickness-corrected Hertz model-derived Young's modulus and Hertz model-derived Young's modulus becomes larger with the decrease of hydrogel thickness, indicating that the effects of hydrogel thickness on hydrogel mechanics become more obvious with the decrease of the hydrogel thickness. Besides, regardless of the Hertz model or thickness-corrected Hertz model, the Young's modulus of the hydrogel decreases exponentially or linearly with increasing thickness (Fig. 3D and S4†). Notably, there is no significant difference in the Young's modulus of the three types of hydrogels prepared here (Fig. 3D), which is due to the raw material of the hydrogel used here. Here, the three types of hydrogels were prepared by using the same GelMA material with a low amino substitution degree (30), and the mechanical properties of the prepared three types of hydrogels with different concentrations (5%, 7.5%, and 10%) were similar. Previously, we have successfully fabricated hydrogels with different mechanical properties by using GelMA materials with different amino substitution degrees (30, 60 or 90).34 Hence, we can use the GelMA materials with different amino substitution degrees and also increase the concentration of the prepared hydrogels to fabricate hydrogels with different mechanical properties.
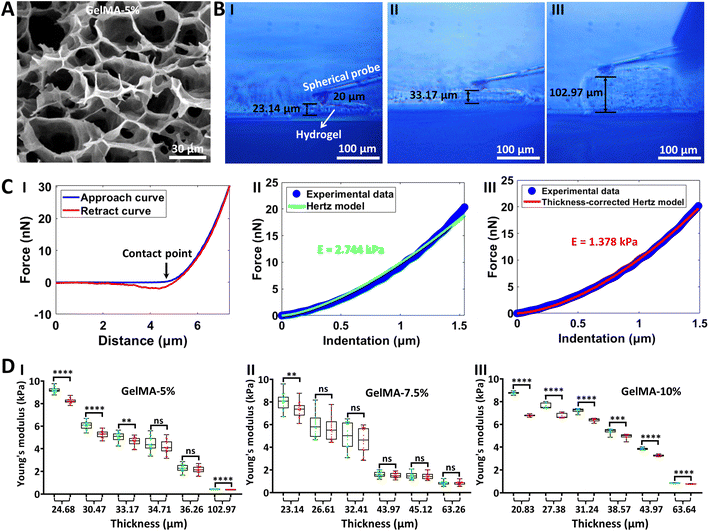 |
| | Fig. 3 Measuring the Young's modulus of hydrogels in aqueous conditions by side-view optical microscopy-assisted AFM. Experiments were performed in PBS in the native (hydrated) states of hydrogels. (A) SEM image of the prepared GelMA hydrogel with a concentration of 5%. (B) Optical images recorded by the side-view optical microscopy system showing the measurement process of hydrogels with different thicknesses. (I) Hydrogel with a thickness of 23.14 μm. (II) Hydrogel with a thickness of 33.17 μm. (III) Hydrogel with a thickness of 102.97 μm. (C) A typical force curve (I) obtained on the hydrogel and the corresponding fitting results of the indentation curve with the use of the Hertz model (II) and thickness-corrected Hertz model (III) respectively. The black arrow denotes the contact point. (D) Statistical results (box plots) revealing the thickness-dependent Young's modulus of hydrogels measured by AFM. Three different concentrations of GelMA hydrogels were measured (5%, 7.5%, and 10%). Each dot represents a Young's modulus value. The green dots are the results obtained from the Hertz model, and the red dots are the results obtained from the thickness-corrected Hertz model. Statistical significance was set at the following levels: *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns not significant. | |
3.4 Indentation assay of living cells by side-view optical microscopy-assisted AFM
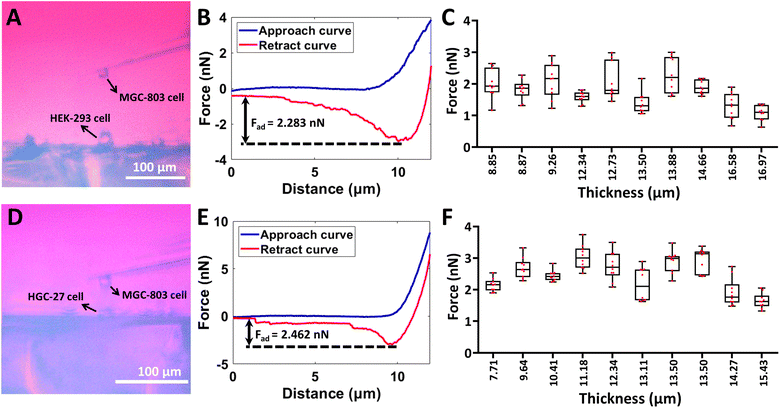
The side-view optical microscopy-assisted AFM was also used to analyze the effect of cell thickness on the multiple mechanical properties (Young's modulus, relaxation time, and viscosity) of single living cells by controlling the AFM spherical probe to perform approach-dwell-retract cycles54 on cells, as shown in Fig. 4. Two types of adherent cells (HEK-293 cells and MGC-803 cells) and one type of mammalian suspended cells (Raji cells) were used to examine the generalization of measurements. Fig. 4(A–D) show the process of measuring the viscoelasticity of single HEK-293 cells by side-view optical microscopy-assisted AFM. The side-view optical image clearly shows the HEK-293 cell being indented by an AFM spherical probe (Fig. 4A). Notably, since the AFM probe was controlled to dwell on the cell for 1 s after the approach step to measure the viscous properties of the cell, there is a large gap between the approach curve and the retract curve (Fig. 4B). One can see that the thickness-corrected Hertz model (II in Fig. 4C) can better match the indentation curve than the Hertz model (I in Fig. 4C), which is consistent with the results obtained on hydrogels (Fig. 3C). Fitting the relaxation curve with the Maxwell model gives the relaxation time of the cell (II in Fig. 4D). The cell viscosity is then obtained by multiplying Young's modulus and relaxation time.34 The measurement process of MGC-803 cells is the same as that for HEK-293 cells, which is shown in Fig. S5.† Since Raji cells are suspended cells and they cannot naturally attach to the substrate, micropillar substrates were used to physically trap single living Raji cells (Fig. S6†) for side-view optical microscopy-assisted AFM (Fig. S7†). Real-time side-view optical microscopy images of indentation processes of these three types of cells are shown in ESI Movie 5–7† respectively. Statistical results (I in Fig. 4(E–G)) show that, as the cell thickness decreased, the cell Young's modulus increased exponentially or linearly (Fig. S8 and S9†), and the difference between cell Young's modulus obtained by the thickness-corrected Hertz model and cell Young's modulus obtained by the Hertz model became larger, which are consistent with the results of hydrogels (Fig. 3D). However, cell thickness has little effect on the measured cell relaxation time (II in Fig. 4(E–G)). The cell viscosity also increased with decreasing cell thickness on the whole (III in Fig. 4(E–G)). The experimental results (Fig. 4) show the diversity of the effects of cell thickness on cell mechanics, which are associated with the mechanical property parameter (Young's modulus, relaxation time, or viscosity). Further studies, such as observing cytoskeletons55 during AFM indentation assay, will be beneficial for revealing the biological mechanisms of these effects. In addition to the AFM spherical probe, side-view optical microscopy-assisted AFM could also clearly visualize the single-cell probe (Fig. S10†) used in single-cell force spectroscopy (SCFS) assay to quantify cell adhesion force. We used side-view optical microscopy-assisted AFM to perform SCFS assay on HEK-293 cells (ESI Movie 8†) and HGC-27 cells respectively, and the results (Fig. 5) show that changes in cell thickness had no significant effect on intercellular adhesion force, which may be reasonably due to the fact that cell adhesion force measured by SCFS is mainly determined by the cell surface adhesion receptors.56
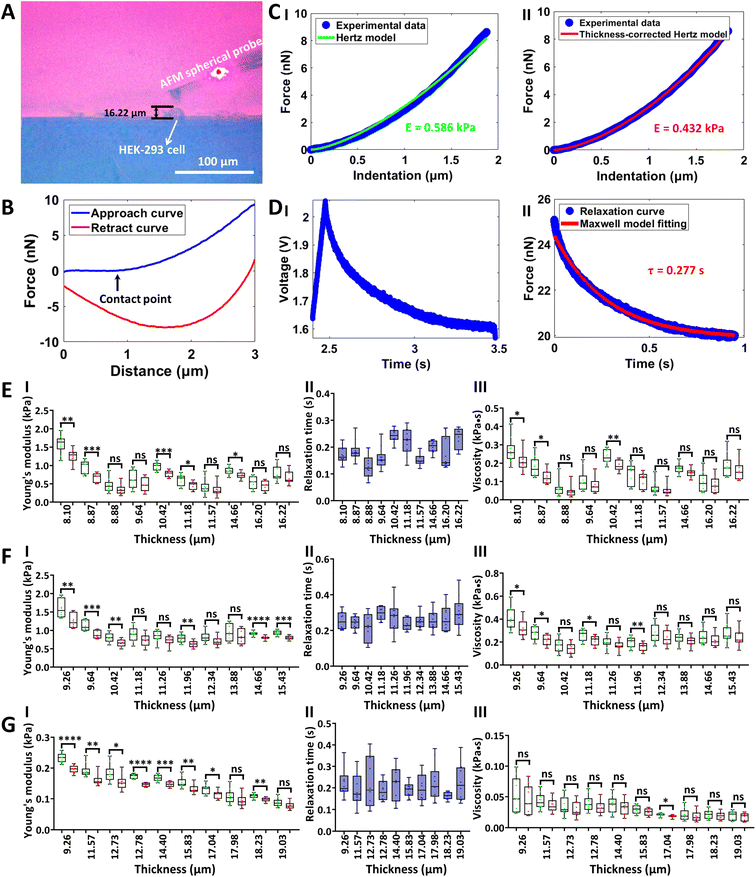 |
| | Fig. 4 Measuring the viscoelastic properties of single living cells by side-view optical microscopy-assisted AFM. Experiments were performed at 37 °C with the use of CO2-independent cell culture medium. (A) Side-view optical image showing that the microsphere-modified AFM probe was controlled to indent a target HEK-293 cell. (B) A typical force curve (the contact point is denoted by the black arrow) recorded during the approach-dwell-retract cycle of the AFM spherical probe on the cell. (C) Fitting results of the indentation curve using the Hertz model (I) and thickness-corrected Hertz model (II) respectively to calculate cell Young's modulus. (D) A typical relaxation curve recorded during the approach-dwell-retract cycle of the AFM spherical probe on the cell (I) and the fitting result of the relaxation curve with the Maxwell model (II) to extract the relaxation time of the cell. (E–G) Statistical results (box plots) of the effect of cell thickness on cell Young's modulus (I), cell relaxation time (II), and cell viscosity (III). Three types of living cells were measured, including HEK-293 cells (E), MGC-803 cells (F), and Raji cells (G). Each dot represents a Young's modulus (I)/relaxation time (II)/viscosity (III) value. (I) The green dots are the results obtained from the Hertz model, and the red dots are the results obtained from the thickness-corrected Hertz model. (III) The green dots are the viscosity calculated from the Young's modulus values obtained by the Hertz model, and the red dots are the viscosity calculated from the Young's modulus values obtained by the thickness-corrected Hertz model. Statistical significance was set at the following levels: *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns not significant. | |
 |
| | Fig. 5 Side-view optical microscopy-assisted AFM for the SCFS assay to measure the cellular adhesion force. Experiments were performed at 37 °C with the use of CO2-independent cell culture medium. Adhesion forces were measured on two types of cells, including HEK-293 cells (A–C) and HGC-27 cells (D–F). The MGC-803 cell was attached to the AFM tipless cantilever to prepare the single-cell probe. (A and C) Side-view optical images of AFM-based SCFS assay. (B and E) Typical force curves obtained during SCFS experiments. The cellular adhesion forces (Fad) calculated from the retract curves were denoted by the black double arrow lines. (C and F) Statistical results (box plots) of the adhesion forces measured on cells with different thicknesses. Each dot represents a cellular adhesion force value. | |
3.5 Indentation assay of cell spheroids by side-view optical microscopy-assisted AFM
The side-view optical microscopy-assisted AFM was also used to measure the mechanical properties of single living cell spheroids, and the results are shown in Fig. 6. Two types of cell spheroids, including Raji cell spheroids (I in Fig. 6A) and HEK-293 cell spheroids (II in Fig. 6A), were used. Raji cell spheroids could be naturally formed by culturing Raji cells, and HEK-293 cell spheroids were formed by culturing HEK-293 cells with the ultra-low attachment cell culture plate (more images of the formed cell spheroids are shown in Fig. S11†). One can see that the side-view optical microscopy module could clearly visualize the AFM-based indentation process on single cell spheroids from the side-view perspective (III and IV in Fig. 6A). For Raji cell spheroids, the fitting results of the thickness-corrected Hertz model were slightly better than that of the Hertz model (II and III in Fig. 6B). For HEK-293 cell spheroids, there were no significant differences between the fitting results of the Hertz model and thickness-corrected Hertz model (II and III in Fig. 6C). This is because that HEK-293 cell spheroids were much larger than Raji cell spheroids and the advantages of the thickness-corrected Hertz model weaken for thick specimens, which is confirmed by the statistical results (Fig. 6D and E). From the statistical results, we can also see that the Young's modulus of Raji cell spheroids decreased with the increase of the thickness of the Raji cell spheroids (I in Fig. 6D). For HEK-293 cell spheroids, the thickness effect disappeared when the thickness of the spheroid was larger than 80 μm (I in Fig. 6E). For AFM-based mechanical assays, it is well known that the depth of indentation should be no more than 10% of the sample thickness to avoid the bottom effect.57 We then obtained the statistical results of the changes in Young's modulus values versus the ratio of indentation depth to spheroid thickness (II in Fig. 6D and E). For Raji cell spheroids, we can observe the remarkable thickness effect when the ratio of indentation depth to spheroid thickness was larger than 12.5% (II in Fig. 6D). For HEK-293 cell spheroids, the results were all obtained when the indentation depth was less than 10% of the spheroid thickness, but we can still observe the gradual appearance of the thickness effect when the ratio of indentation depth to spheroid thickness approached 5% (II in Fig. 6E), providing novel insights into our understanding of the influence of specimen thickness on specimen mechanics as well as the underlying bottom effect in AFM-based mechanical assays. Cell spheroids are gaining enormous interest for modeling tissue development and disease to advance personalized medicine, drug screening and cell therapy.58 The results (Fig. 6) show that side-view optical microscopy-assisted AFM is able to quantify the effect of spheroid thickness on spheroid mechanics for accurately characterizing the mechanical properties of single cell spheroids, which will facilitate revealing the mechanical cues involved in cell spheroid-related processes.
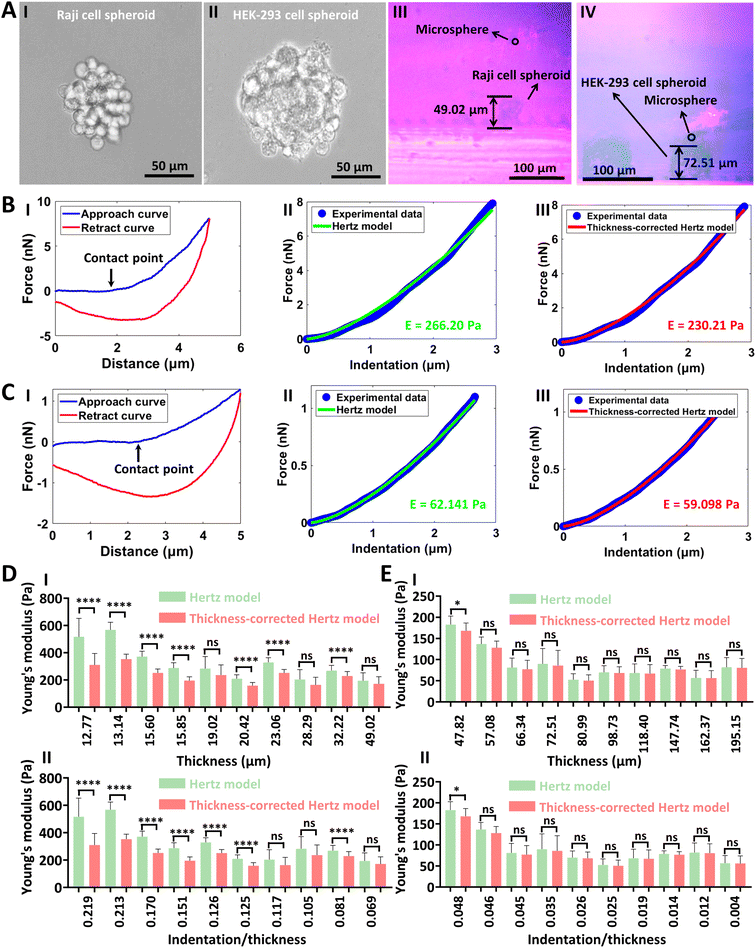 |
| | Fig. 6 Measuring the mechanical properties of single living cell spheroids by side-view optical microscopy-assisted AFM. Experiments were performed at 37 °C with the use of a CO2-independent cell culture medium. (A) Inverted optical microscopy images (I and II) and side-view optical microscopy images (III and IV) of cell spheroids. (I and III) Raji cell spheroids. (II and IV) HEK-293 cell spheroids. (B and C) Typical force curves obtained on Raji cell spheroids (B) and HEK-293 cell spheroids (C) as well as theoretical fitting results. (I) Force curves. (II) Fitting results of the indentation curves with the Hertz model. (III) Fitting results of the indentation curves with the thickness-corrected Hertz model. The black arrow denotes the contact point. (D and E) Statistical results (mean ± SD) of the effect of spheroid thickness on spheroid Young's modulus. (D) Raji cell spheroids. (E) HEK-293 cell spheroids. (I) Plots of Young's modulus values versus thickness. (II) Plots of Young's modulus values versus the ratio of indentation depth to spheroid thickness (indentation/thickness). Statistical significance was set at the following levels: *p < 0.05, **p < 0.01, ***p < 0.001, ****p < 0.0001, ns not significant. | |
The experimental results illustrate that side-view optical microscopy-assisted AFM offers new possibilities for thickness-dependent nanobiomechanics. It is now well recognized that the mechanical properties of biological tissues, from nanoscale to macroscale dimensions, are fundamental for cellular behavior and consequent tissue functionality, but standardization of characterizing the mechanical properties of living tissues at the micro/nanoscale is still largely blank.7 In this work, a side-view optical microscopy module was developed and integrated with a commercial AFM, allowing real-time visualization of the contact process between the AFM probe and the specimen from the side-view perspective during AFM-based force spectroscopy assay. Side-view optical microscopy-assisted AFM is able to conveniently obtain the thickness of the specimen during AFM indentation assay which is subsequently used as a factor to determine the exact mechanical properties of the specimen, allowing accurate measurements of the mechanical properties of biomaterials. Therefore, side-view optical microscopy-assisted AFM benefits the standardization of AFM-based mechanical assay at the micro/nanoscale for biomedical applications. Notably, researchers previously have already explored realizing side-view optical microscopy imaging for AFM-based single-cell mechanical assay,30,31 but these studies require the fabrication of specific AFM probe holders (such as permanently attaching a mirror to the probe holder). Here, the presented side-view optical microscopy-assisted AFM maintain the full capabilities of AFM and does not require any changes/modifications to AFM (or AFM accessories) itself, which therefore facilitates the biomedical applications of the presented methodology of side-view optical microscopy-assisted AFM. The experimental results on diverse biomaterial systems (microstructures, hydrogels, living cells, and cell spheroids) reveal the significant impact of specimen thickness on specimen mechanics, providing experimental access to thickness-dependent nanomechanics and demonstrating the broad application prospects of side-view optical microscopy-assisted AFM. However, it should be noted that the spatial resolution of the side-view optical microscopy module presented here is still limited, and integrating fluorescence microscopy with the side-view optical microscopy module will increase the spatial resolution to visualize the subcellular structures for better applications.31 Further applications of side-view optical microscopy-assisted AFM, such as accurately measuring the mechanical properties of cells/spheroids and their physical microenvironments as well as monitoring mechanical dynamics,59 exploring interplay between mechanics and signaling in regulating cell fate,60 will benefit better unveiling the important role of mechanical cues in life activities and diseases.
4. Conclusions
This work has demonstrated that side-view optical microscopy-assisted AFM offers a convenient solution for the precise measurements of the thickness-dependent nanomechanical properties of biomaterials. The side-view optical microscopy-assisted AFM can capture in real time the vertical profile dynamics of AFM-based indentation assay to detail the contact process between the AFM probe and the specimen, helping to better understand the AFM force spectroscopy experiments and allowing accurate measurement of the mechanical properties of the specimen. Applications of side-view optical microscopy-assisted AFM on various biomaterial systems (microstructures, hydrogels, living cells, and cell spheroids) significantly reveal the diversity of the effect of specimen thickness on the mechanical properties of the specimen, which are associated with the thickness and indentation depth as well as the type of the mechanics being measured. The study provides more possibilities for the standardization of AFM-based nanobiomechanics, which will facilitate utilizing AFM to address biological issues and will benefit the field of mechanobiology.
Author contributions
Conceptualization (M. L.); funding acquisition (M. L.); investigation (Y. Y.); formal analysis (Y. Y.); methodology (Y. Y. and M. L.); resources (M. L.); project administration (M. L.); supervision (M. L.); writing – original draft (M. L. and Y. Y.); writing – review & editing (M. L. and Y. Y.).
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (62273330), the Key Research Program of Frontier Sciences CAS (ZDBS-LY-JSC043), and the CAS Project for Young Scientists in Basic Research (YSBR-041).
References
- D. E. Discher, P. Janmey and Y. L. Wang, Tissue cells feel and respond to the stiffness of their substrate, Science, 2005, 310, 1139–1143 CrossRef CAS PubMed
 .
.
- C. Bonnans, J. Chou and Z. Werb, Remodelling the extracellular matrix in development and disease, Nat. Rev. Mol. Cell Biol., 2014, 15, 786–801 CrossRef CAS PubMed
 .
.
- C. Frantz, K. M. Stewart and V. M. Weaver, The extracellular matrix at a glance, J. Cell Sci., 2010, 123, 4195–4200 CrossRef CAS PubMed
 .
.
- F. M. Watt and W. T. S. Huck, Role of the extracellular matrix in regulating stem cell fate, Nat. Rev. Mol. Cell Biol., 2013, 14, 467–473 CrossRef CAS PubMed
 .
.
- A. Saraswathibhatla, D. Indana and O. Chaudhuri, Cell-extracellular matrix mechanotransduction in 3D, Nat. Rev. Mol. Cell Biol., 2023, 24, 495–516 CrossRef CAS PubMed
 .
.
- O. Chaudhuri, J. Cooper-White, P. A. Janmey, D. J. Mooney and V. B. Shenoy, Effects of extracellular matrix viscoelasticity on cellular behaviour, Nature, 2020, 584, 535–546 CrossRef CAS PubMed
 .
.
- C. F. Guimaraes, L. Gasperini, A. P. Marques and R. L. Reis, The stiffness of living tissues and its implications for tissue engineering, Nat. Rev. Mater., 2020, 5, 351–370 CrossRef
 .
.
- H. T. Nia, L. L. Munn and R. K. Jain, Physical traits of cancer, Science, 2020, 370, eaaz0868 CrossRef CAS PubMed
 .
.
- P. H. Wu, D. R. B. Aroush, A. Asnacios, W. C. Chen, M. E. Dokukin, B. L. Doss, P. Durand-Smet, A. Ekpenyong, J. Guck, N. V. Guz, P. A. Janmey, J. S. H. Lee, N. M. Moore, A. Ott, Y. C. Poh, R. Ros, M. Sander, I. Sokolov, J. R. Staunton, N. Wang, G. Whyte and D. Wirtz, A comparison of methods to assess cell mechanical properties, Nat. Methods, 2018, 15, 491–498 CrossRef CAS PubMed
 .
.
- C. Alibert, B. Goud and J. B. Manneville, Are cancer cells really softer than normal cells?, Biol. Cell, 2017, 109, 167–189 CrossRef PubMed
 .
.
- C. Rianna, M. Radmacher and S. Kumar, Direct evidence that tumor cells soften when navigating confined spaces, Mol. Biol. Cell, 2020, 31, 1726–1734 CrossRef CAS PubMed
 .
.
- R. Garcia, Nanomechanical mapping of soft materials with the atomic force microscope: methods, theory and applications, Chem. Soc. Rev., 2020, 49, 5850–5884 RSC
 .
.
- A. Viljoen, M. Mathelie-Guinlet, A. Ray, N. Strohmeyer, Y. J. Oh, P. Hinterdorfer, D. J. Muller, D. Alsteens and Y. F. Dufrene, Force spectroscopy of single cells using atomic force microscopy, Nat. Rev. Methods Primers, 2021, 1, 63 CrossRef CAS
 .
.
- M. D. A. Norman, S. A. Ferreira, G. M. Jowett, L. Bozec and E. Gentleman, Measuring the elastic modulus of soft culture surfaces and three-dimensional hydrogels using atomic force microscopy, Nat. Protoc., 2021, 16, 2418–2449 CrossRef CAS PubMed
 .
.
- F. Rico, C. Su and S. Scheuring, Mechanical mapping of single membrane proteins at submolecular resolution, Nano Lett., 2011, 11, 3983–3986 CrossRef CAS PubMed
 .
.
- W. H. Roos, R. Bruinsma and G. J. L. Wuite, Physical virology, Nat. Phys., 2010, 6, 733–743 Search PubMed
 .
.
- Y. Feng, M. Liu, X. Li, M. Li, X. Xing and L. Liu, Nanomechanical signatures of extracellular vesicles from hematologic cancer patients unraveled by atomic force microscopy for liquid biopsy, Nano Lett., 2023, 23, 1591–1599 CrossRef CAS PubMed
 .
.
- S. E. Cross, Y. S. Jin, J. Rao and J. K. Gimzewski, Nanomechanical analysis of cells from cancer patients, Nat. Nanotechnol., 2007, 2, 780–783 CrossRef CAS PubMed
 .
.
- M. Plodinec, M. Loparic, C. A. Monnier, E. C. Obermann, R. Zanetti-Dallenbach, P. Oertle, J. T. Hyotyla, U. Aebi, M. Bentires-Alj, R. Y. H. Lim and C. A. Schoenenberger, The nanomechanical signature of breast cancer, Nat. Nanotechnol., 2012, 7, 757–765 CrossRef CAS
 .
.
- M. Krieg, G. Flaschner, D. Alsteens, B. M. Gaub, W. H. Roos, G. J. L. Wuite, H. E. Gaub, C. Gerber, Y. F. Dufrene and D. J. Muller, Atomic force microscopy-based mechanobiology, Int. Rev. Phys., 2019, 1, 41–57 Search PubMed
 .
.
- Y. F. Dufrene and A. Persat, Mechanomicrobiology: how bacteria sense and respond to forces, Nat. Rev. Microbiol., 2020, 18, 227–240 CrossRef CAS PubMed
 .
.
- M. Radmacher, Measuring the elastic properties of living cells by the atomic force microscope, Methods Cell Biol., 2002, 68, 67–90 CrossRef PubMed
 .
.
- M. Lekka, K. Pogoda, J. Gostek, O. Klymenko, S. Prauzner-Bechcicki, J. Wiltowska-Zuber, J. Jaczewska, J. Lekki and Z. Stachura, Cancer cell recognition-mechanical phenotype, Micron, 2012, 43, 1259–1266 CrossRef PubMed
 .
.
- S. Kasas, G. Longo and G. Dietler, Mechanical properties of biological specimens explored by atomic force microscopy, J. Phys. D Appl. Phys., 2013, 46, 133001 CrossRef
 .
.
- E. K. Dimitriadis, F. Horkay, J. Maresca, B. Kachar and R. S. Chadwick, Determination of elastic moduli of thin layers of soft material using the atomic force microscope, Biophys. J., 2002, 82, 2798–2810 CrossRef CAS PubMed
 .
.
- N. Gavara and R. S. Chadwick, Determination of the elastic moduli of thin samples and adherent cells using conical atomic force microscope tips, Nat. Nanotechnol., 2012, 7, 733–736 CrossRef CAS PubMed
 .
.
- P. D. Garcia and R. Garcia, Determination of the elastic moduli of a single cell cultured on a rigid support by force microscopy, Biophys. J., 2018, 114, 2923–2932 CrossRef CAS PubMed
 .
.
- M. P. Stewart, A. W. Hodel, A. Spielhofer, C. J. Cattin, D. J. Muller and J. Helenius, Wedged AFM-cantilevers for parallel plate cell mechanics, Methods, 2013, 60, 186–194 CrossRef CAS PubMed
 .
.
- O. Chaudhuri, S. H. Parekh, W. A. Lam and D. A. Fletcher, Combined atomic force microscopy and side-view optical imaging for mechanical studies of cells, Nat. Methods, 2009, 6, 383–387 CrossRef CAS PubMed
 .
.
- C. Gonnermann, C. Huang, S. F. Becker, D. R. Stamov, D. Wedlich, J. Kashef and C. M. Franz, Quantitating membrane bleb stiffness using AFM force spectroscopy and an optical sideview setup, Integr. Biol., 2015, 7, 356–363 CrossRef CAS PubMed
 .
.
- K. Beicker, E. O'Brien, M. R. Falvo and R. Superfine, Vertical light sheet enhanced side-view imaging for AFM cell mechanics studies, Sci. Rep., 2018, 8, 1504 CrossRef PubMed
 .
.
- X. Meng, X. Wu, J. Song, H. Zhang, M. Chen and H. Xie, Quantification of the microrheology of living cells using multi-frequency magnetic force modulation atomic force microscopy, IEEE Trans. Instrum. Meas., 2022, 71, 7501609 Search PubMed
 .
.
- Y. Feng and M. Li, Micropipette-assisted atomic force microscopy for single-cell 3D manipulations and nanomechanical measurements, Nanoscale, 2023, 15, 13346–13358 RSC
 .
.
- J. Wei and M. Li, Interplay of fluid mechanics and matrix stiffness in tuning the mechanical behaviors of single cells probed by atomic force microscopy, Langmuir, 2023, 39, 1309–1319 CrossRef CAS PubMed
 .
.
- Z. Ge, H. Yu, W. Yang, J. Yang, B. Liu, X. Wang, Z. Liu and L. Liu, Development of multi-dimensional cell co-culture via a novel microfluidic chip fabricated by DMD-based optical projection lithography, IEEE Trans. NanoBiosci., 2019, 18, 679–686 Search PubMed
 .
.
- J. Friedrichs, J. Helenius and D. J. Muller, Quantifying cellular adhesion to extracellular matrix components by single-cell force spectroscopy, Nat. Protoc., 2010, 5, 1353–1361 CrossRef CAS PubMed
 .
.
- J. Wei, Y. Yang and M. Li, Single-cell force spectroscopy of fluid flow-tuned cell adhesion for dissecting hemodynamics in tumor metastasis, Nanoscale, 2024, 16, 360–372 RSC
 .
.
- K. He, J. Sun and X. Tang, Single image haze removal using dark channel prior, IEEE Trans. Pattern Anal. Mach. Intell., 2011, 33, 2341–2353 Search PubMed
 .
.
- N. Gavara, Combined strategies for optimal detection of the contact point in AFM force-indentation curves obtained on thin samples and adherent cells, Sci. Rep., 2016, 6, 21267 CrossRef CAS PubMed
 .
.
- M. Li, L. Liu, N. Xi, Y. Wang, Z. Dong, X. Xiao and W. Zhang, Atomic force microscopy imaging and mechanical properties measurement of red blood cells and aggressive cancer cells, Sci. China: Life Sci., 2012, 55, 968–973 CrossRef PubMed
 .
.
- L. Trichet, J. L. Digabel, R. J. Hawkins, S. R. K. Vedula, M. Gupta, C. Ribrault, P. Hersen, R. Voituriez and B. Ladoux, Evidence of a large-scale mechanosensing mechanism for cellular adaptation to substrate stiffness, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 6933–6938 CrossRef CAS PubMed
 .
.
- Z. Jahed, R. Zareian, Y. Y. Chau, B. B. Seo, M. West, T. Y. Tsui, W. Wen and M. R. K. Mofrad, Differential collective- and single-cell behaviors on silicon micropillar arrays, ACS Appl. Mater. Interfaces, 2016, 8, 23604–23613 CrossRef CAS PubMed
 .
.
- M. L. Fitzgerald, S. Tsai, L. M. Bellan, R. Sappington, Y. Xu and D. Li, The relationship between the Young's modulus and dry etching rate of polydimethylsiloxane (PDMS), Biomed. Microdevices, 2019, 21, 26 CrossRef PubMed
 .
.
- Y. S. Yu, Z. Q. Wang and Y. P. Zhao, Experimental study of evaporation of sessile water droplet on PDMS surfaces, Acta Mech. Sin., 2013, 29, 799–805 CrossRef
 .
.
- K. Kulangara and K. W. Leong, Substrate topography shapes cell function, Soft Matter, 2009, 5, 4072–4076 RSC
 .
.
- M. Nikkhah, F. Edalat, S. Manoucheri and A. Khademhosseini, Engineering microscale topographies to control the cell-substrate interface, Biomaterials, 2012, 33, 5230–5246 CrossRef CAS PubMed
 .
.
- M. J. Mitchell, R. K. Jain and R. Langer, Engineering and physical sciences in oncology: challenges and opportunities, Nat. Rev. Cancer, 2017, 17, 659–675 CrossRef CAS PubMed
 .
.
- J. Lou and D. J. Mooney, Chemical strategies to engineer hydrogels for cell culture, Nat. Rev. Chem, 2022, 6, 726–744 CrossRef CAS PubMed
 .
.
- S. R. Caliari and J. A. Burdick, A practical guide to hydrogels for cell culture, Nat. Methods, 2016, 13, 405–414 CrossRef CAS PubMed
 .
.
- T. R. Matzelle, G. Geuskens and N. Kruse, Elastic properties of poly(N-isopropylacrylamide) and poly(acrylamide) hydrogels studies by scanning force microscopy, Macromolecules, 2003, 36, 2926–2931 CrossRef CAS
 .
.
- A. J. Engler, S. Sen, H. L. Sweeney and D. E. Discher, Matrix elasticity directs stem cell lineage specification, Cell, 2006, 126, 677–689 CrossRef CAS PubMed
 .
.
- A. Gimenez, J. J. Uriarte, J. Vieyra, D. Navajas and J. Alcaraz, Elastic properties of hydrogels and decellularized tissue sections used in mechanobiology studies probed by atomic force microscopy, Microsc. Res. Tech., 2017, 80, 85–96 CrossRef CAS PubMed
 .
.
- M. Zhu, Y. Wang, G. Ferracci, J. Zheng, N. J. Cho and B. H. Lee, Gelatin methacryloyl and its hydrogels with an exceptional degree of controllability and batch-to-batch consistency, Sci. Rep., 2019, 9, 6863 CrossRef PubMed
 .
.
- M. Li, N. Xi, Y. Wang and L. Liu, Atomic force microscopy in probing tumor physics for nanomedicine, IEEE Trans. Nanotechnol., 2019, 18, 83–113 CAS
 .
.
- D. A. Fletcher and R. D. Mullins, Cell mechanics and the cytoskeleton, Nature, 2010, 463, 485–492 CrossRef CAS PubMed
 .
.
- J. T. Parsons, A. R. Horwitz and M. A. Schwartz, Cell adhesion: integrating cytoskeletal dynamics and cellular tension, Nat. Rev. Mol. Cell Biol., 2010, 11, 633–643 CrossRef CAS PubMed
 .
.
- M. Stolz, R. Raiteri, A. U. Daniels, M. R. VanLandingham, W. Baschong and U. Aebi, Dynamic elastic modulus of porcine articular cartilage determined at two different levels of tissue organization by indentation-type atomic force microscopy, Biophys. J., 2004, 86, 3269–3283 CrossRef CAS PubMed
 .
.
- M. Hofer and M. P. Lutolf, Engineering organoids, Nat. Rev. Mater., 2021, 6, 402–420 CrossRef CAS PubMed
 .
.
- J. D. Humphrey, E. R. Dufresne and M. A. Schwartz, Mechanotransduction and extracellular matrix homeostasis, Nat. Rev. Mol. Cell Biol., 2014, 15, 802–812 CrossRef CAS PubMed
 .
.
- H. De Belly, E. K. Paluch and K. J. Chalut, Interplay between mechanics and signalling in regulating cell fate, Nat. Rev. Mol. Cell Biol., 2022, 23, 465–480 CrossRef CAS PubMed
 .
.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *abc
*abc
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 or 5
1 or 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) and the mixture was poured onto the mold. The mold was then degassed for 1 h, after which the mold was heated at 80 °C for 2 h. The micropillar substrates were then obtained by directly peeling the hardened PDMS from the mold. For the fabrication of cuboid micropillars, the designed geometries of cuboid micropillars are the following: the side length is 50 μm, the height is 15 μm, and the distance between two adjacent micropillars is 50 μm. The designed geometries of cylindrical micropillars (used for cell trapping) are the following: the diameter is 10 μm, the height is 10 μm, and the axial distance between two adjacent cylindrical micropillars is 20 μm.
1) and the mixture was poured onto the mold. The mold was then degassed for 1 h, after which the mold was heated at 80 °C for 2 h. The micropillar substrates were then obtained by directly peeling the hardened PDMS from the mold. For the fabrication of cuboid micropillars, the designed geometries of cuboid micropillars are the following: the side length is 50 μm, the height is 15 μm, and the distance between two adjacent micropillars is 50 μm. The designed geometries of cylindrical micropillars (used for cell trapping) are the following: the diameter is 10 μm, the height is 10 μm, and the axial distance between two adjacent cylindrical micropillars is 20 μm.
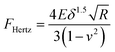
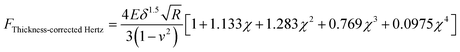
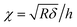
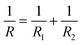
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) to examine the effect of micropillar thickness on micropillar mechanics, and experimental results on both the two types of PDMS micropillars show a significant decrease in Young's modulus when the micropillar thickness is taken into account (Fig. 2E). However, we can also see that there is no significant difference in the Young's modulus of the prepared two types of PDMS micropillars (10
1) to examine the effect of micropillar thickness on micropillar mechanics, and experimental results on both the two types of PDMS micropillars show a significant decrease in Young's modulus when the micropillar thickness is taken into account (Fig. 2E). However, we can also see that there is no significant difference in the Young's modulus of the prepared two types of PDMS micropillars (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), which may be due to the fabrication of PDMS micropillars here. A previous study has shown that the Young's modulus of PDMS films was in the range of 0.1–1.6 MPa depending on the weight ratio (the ratio of monomers to cross-linkers) and curing time, and particularly there is no significant difference in the mechanical properties between the two PDMS films (10
1), which may be due to the fabrication of PDMS micropillars here. A previous study has shown that the Young's modulus of PDMS films was in the range of 0.1–1.6 MPa depending on the weight ratio (the ratio of monomers to cross-linkers) and curing time, and particularly there is no significant difference in the mechanical properties between the two PDMS films (10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 5
1 and 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 respectively) when the curing time is 16 h.43 Another study has shown that the Young's modulus (1.36 MPa) of PDMS films prepared with a weight ratio of 10
1 respectively) when the curing time is 16 h.43 Another study has shown that the Young's modulus (1.36 MPa) of PDMS films prepared with a weight ratio of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 is slightly smaller than the Young's modulus (1.5 MPa) of PDMS films prepared with a weight ratio of 5
1 is slightly smaller than the Young's modulus (1.5 MPa) of PDMS films prepared with a weight ratio of 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1,44 in which the curing time was 20 min. Hence, we can optimize the weight ratio and curing time to prepare the PDMS micropillars with different mechanical properties in future studies. We also applied side-view optical microscopy-assisted AFM to measure the mechanics of single resin hemisphere structures fabricated by two-photon lithography, and the results show that the Young's modulus obtained by thickness-corrected Hertz model was smaller than that obtained by the Hertz model (Fig. S2†). Engineering biomaterials with microscale topographies and exploiting them to tune the behaviors of cells (such as from proliferation to differentiation and migration) at the cell–substrate interface has been a promising way for regenerative medicine and oncology.45–47 The established side-view optical microscopy-assisted AFM allows easily obtaining the geometric sizes of microstructures during AFM indentation assay and the consequent precise analysis of their mechanical properties by applying the thickness-corrected Hertz model, which therefore benefits comprehensive understanding of the structures and properties of engineered microtopographies and their roles in tuning the behaviors of cells.
1,44 in which the curing time was 20 min. Hence, we can optimize the weight ratio and curing time to prepare the PDMS micropillars with different mechanical properties in future studies. We also applied side-view optical microscopy-assisted AFM to measure the mechanics of single resin hemisphere structures fabricated by two-photon lithography, and the results show that the Young's modulus obtained by thickness-corrected Hertz model was smaller than that obtained by the Hertz model (Fig. S2†). Engineering biomaterials with microscale topographies and exploiting them to tune the behaviors of cells (such as from proliferation to differentiation and migration) at the cell–substrate interface has been a promising way for regenerative medicine and oncology.45–47 The established side-view optical microscopy-assisted AFM allows easily obtaining the geometric sizes of microstructures during AFM indentation assay and the consequent precise analysis of their mechanical properties by applying the thickness-corrected Hertz model, which therefore benefits comprehensive understanding of the structures and properties of engineered microtopographies and their roles in tuning the behaviors of cells.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.






