Open Access Article
Open Access ArticleUnveiling the mechanism of tuning elemental distribution in high entropy alloys and its effect on thermal stability†
Panhua
Shi
a,
Yiying
Yang
a,
Baodian
Yao
b,
Jiaxuan
Si
ac and
Yuexia
Wang
 *a
*a
aKey Laboratory of Nuclear Physics and Ion-beam Application (MOE), Institute of Modern Physics, Fudan University, Shanghai, 200433, China. E-mail: yxwang@fudan.edu.cn
bShandong Peninsula Engineering Research Center of Comprehensive Brine Utilization, Weifang University of Science and Technology, Shouguang, Shandong 262700, China
cThe Fourth Sub-Institute, Nuclear Power Institute of China, Chengdu, 610005, China
First published on 11th June 2024
Abstract
The issue of elemental distribution such as chemical short range order (SRO) in high entropy alloys (HEAs) has garnered increased attention in both experimental and theoretical realms. A comprehensive and urgently required elucidation of this atomic-level phenomenon is the focus of this study. In this work, we systematically analyzed atomic-level information, involving atomic volume, charge transfer, local chemical ordering and atomic stress in 3d HEAs. We assess the hotly debated issue by attributing it to Cr atoms with negative atomic stress in the sublattice site, whereas other atoms with positive atomic stress have larger electronegativity and greater atomic volume, through which the interplay of positive and negative atomic stresses balances the local atomic environment. Additionally, we assume that Mn promotes the homogeneity of the HEA and the temperature-dependent chemical SRO enhances the thermal stability of HEAs. Our work contributes to advancing our understanding of the mechanistic aspects of elemental distribution in HEAs and their thermodynamic implications.
1. Introduction
High entropy alloys (HEAs),1,2 characterized by the inclusion of four or more principal elements at approximately equal atomic percentages, exhibit a substantial chemical complexity marked by a vast array of distinct local atomic environment, which serves as the basis for a diverse range of macroscopic properties.3–6 The alloying strategy addresses the specific concern of grain instability7,8 observed in nanocrystalline (NC) materials when subjected to elevated temperatures, accomplished by incorporating high mixing entropy and sluggish diffusion, which are two of the core effects of HEAs,9 making them more stable than intermetallic compounds.The impact of a complex local atomic environment on the stability of HEAs has been confirmed through both experimental and theoretical research. As the initial presumption of random solid solution states in HEAs, X-ray diffraction results from a bulk PtPdFeCoNi HEA nanoparticle film validated the stabilization of these five elements in a unified face-centered cubic (FCC) structure.10 However, these multi-principal element alloys involved chemical ordering at the atomic scale, namely short range order (SRO). It was observed that phase decomposition was initiated by Ni and Mn co-segregation at GBs in a NC-CrMnFeCoNi Cantor alloy using atom probe tomography.11 In contrast, energy dispersive X-ray mapping in transmission electron microscopy of CrMnFeCoNi samples deposited through high-temperature magnetron sputtering demonstrated that phase separation occured without the necessity of elemental segregation.12 To understand the elemental behavior in the thermal stability, Ghosh et al.13 discovered a first-order order–disorder transition from a high-temperature random structure to an ordered one occurring at approximately 975 K in the CrCoNi HEA utilizing on-lattice machine learning interatomic potentials and canonical Monte Carlo (MC) simulations. Moreover, different degrees of chemical SRO in the nanoscratching process have been examined by hybrid MC/molecular dynamics (MD) simulations, revealing that the SRO-600K sample displayed enhanced resistance to plastic deformation and increased structural stability.14 As a result, the issue of the chemical SRO effect has attracted growing interest in the past 20 years within the community,15e.g., studies on the thermal stability of local chemical ordering and its impact on the mechanical properties of HEAs.16–18
Some efforts have been made to provide explanations for the phenomenon of the chemical SRO effect in these complex multi-principal element alloys. The grain and phase stabilities were attributed to the so-called self-stabilization effect of Cr and Fe in NC-(AlCoCrFe)1−xZrx and NC-AlCoCrFe HEAs by Adaan-Nyiak et al.19,20 They posited that the large negative enthalpies of segregation for Cr and Fe promoted GB segregation and contributed to nanograin stabilization, aligning with the conceptual framework that the segregation enthalpy concept has historically guided extensive research on binary and ternary nanoscale alloys.21 However, this framework is not applicable to multi-principal element alloys, as the contradictory nature arises from the negative mixing enthalpy between Ni and 3d transition elements, despite both experimental and theoretical observations consistently indicating Ni segregation.22–24 Furthermore, the self-stabilization effect may be a phenomenon instead of a proper explanation for the atomic-level SRO effect. Besides, Chen et al.25 proposed that differences in atomic size and electronegativity, viewed from an elemental perspective, were insufficient to elucidate the variations in atomic segregation and the SRO effect within these HEAs; nevertheless, the correlation between these two parameters remains unclear.
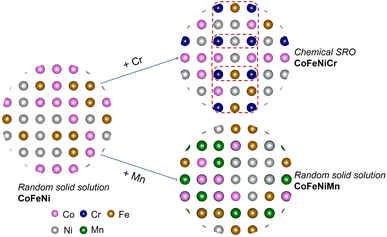
Herein, we systematically assess atomic-level information, involving atomic volume, atomic charge, local chemical ordering and atomic stress in 3d HEAs, with the objective of identifying suitable descriptors for the local atomic environment that can facilitate a more explicit elucidation of elemental precipitation. The atomic stress serves as a cohesive link between elemental information and the local atomic structure, contributing to diverse macroscopic properties such as glass transition and mechanical failure.26 Initially, we explored the chemical ordering in equiatomic CoFeNiM (M = Cr, Mn) alloys by employing a combination of the Metropolis Monte Carlo (MMC) method and density functional theory (DFT). CoFeNi, CoFeNiCr and CoFeNiMn are commonly studied nanocrystalline FCC derivative alloys of the Cantor alloy.27–30 Subsequently, we unveiled the intrinsic correlations among atomic volume, atomic stress and charge transfer, contributing to a better comprehension of the distinctly different SRO effects observed in CoFeNiCr and CoFeNiMn, where CoFeNiCr exhibited Cr chemical ordering and CoFeNiMn was in a random solid solution matrix, as is shown in Fig. 1. Following this, we systematically explored the influence of Cr chemical ordering on structural stability by modulating the composition of Cr within the alloy. Given the experimental observations indicating the emergence of secondary phases in HEAs during heat treatment, our final investigation focused on examining the impact of the chemical SRO effect at different temperatures on the thermal stability of the system. This study aims to provide an atomic perspective on the mechanism of elemental distribution and its impact on structural stability.
2. Methods
2.1 First principles calculations
Firstly, the SQS algorithm31 was utilized in the initial supercell towards an ideal random state. Subsequently, we performed calculations for 5000 samples in each studied high entropy alloy system using our in-house MMC-DFT algorithm.32 Then we optimized the lattice structures and obtained system energy using the VASP package.33 The interaction between ions and electrons adopted the projector augmented wave (PAW) method.34 The exchange–correlation potential employed the Perdew–Burke–Ernzerhof (PBE) method under the generalized gradient approximation.35 The plane wave cut-off energy was set at 350 eV, with a total energy convergence criterion of 1 × 10−5 eV per atom. The conjugate gradient method was employed for structure relaxation, relaxing force components to below 0.02 eV Å−1. The k-point grids were set as 4 × 4 × 4.To capture the electronic interactions of atoms, we employed an atomic stress approximation method based on quantum mechanics derivation. Key points in defining atomic stress include: (i) decomposing the system energy into contributions from individual atoms; (ii) observing the response change in atomic energy to cell deformations. Here, we utilized the Voronoi volume division method embedded in the locally self-consistent multiple scattering (LSMS) approach36 to calculate atomic energies within each polyhedron. The LSMS method initially computed the electronic density at each atomic position, and then solved the Poisson equation with periodic boundary conditions to obtain the Hartree potential. Subsequently, the exchange–correlation potential was added to obtain the effective Kohn–Sham potential and iterative cycles were performed until self-consistency was achieved. The exchange–correlation energy was treated using Von Barth and Hedin's local approximation function.37 Calculating atomic energies within Voronoi polyhedra, the LSMS method considered multiple scattering contributions only within the local interaction zone of each atom, capturing electron density at that position. This ordered process ensured accurate modelling of the system's electronic structure.
The first principles calculations of atomic stress involve two steps: (i) geometry optimization of the supercell using the VASP package; (ii) calculation of atomic stress using the LSMS method. The atomic stress tensor is defined as38
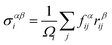 | (1) |
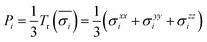 | (2) |
For applied volume strain on the supercell, the atomic stress for each atom can be calculated as the negative derivative of energy with respect to atomic volume. Therefore, energy calculation for each atom was performed at two different volumes, and the derivative was obtained by dividing the energy difference between the two volume strains by the volume strain, with each volume subjected to a minor perturbation of 1.5%. Positive values of the computed stress indicate compressive (repulsive) atomic stress, while negative values indicate tensile (attractive) atomic stress.
2.2 MC-DFT calculations
The Monte Carlo (MC) method, predicated upon the Metropolis algorithm,39 serves as a computational tool for addressing equilibrium phenomena within alloy structures. It efficaciously circumvents the protracted temporal scales inherent in physical dynamics process, notably diffusion, whilst concurrently furnishing insight into average compositional distributions within thermodynamically equilibrated systems. The method presupposes that, prior to the exchange of atomic positions within the crystalline lattice, the total energy of crystal A, designated as E1, delineates the incumbent structural state, colloquially referred to as the “old structure”. Subsequent to the positional exchange, the total energy of crystal B, denoted as E2, delineates the resultant structural state, herein dubbed the “new structure”. In instances where E1 surpasses E2, indicating a lower energy configuration and thus enhancing structural stability, the optimised structure is retained with a probability denoted by PAB in eqn (3), which assumes a value of 1. This iterative process persists, with the “new structure” supplanting the incumbent “old structure” as dictated by the probabilistic criterion. If E1 < E2, then the new optimised structure is retained with a probability denoted by PAB,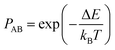 | (3) |
2.3 Warren-Cowley short range order
The Warren-Cowley order parameter40 is used to characterize the degree of chemical short range order at various annealing temperatures. This parameter can be defined by considering the deviation of the two-point correlation function at lattice positions (i, j, k) and (p, q, r)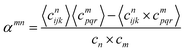 | (4) |
In the formula, cijkn represents the local occupancy of species n at the lattice position (i, j, k), and the angle brackets denote averaging over all lattice sites. cn is the concentration of the entire system.
The two-point correlation function is expected to be symmetric with respect to element types, i.e. 〈cijkn〉〈cpqrm〉 = cnPnm = cmPmn, where Pnm describes the conditional probability of an atom of element type m having an atom of element type n as a nearest neighbour. Additionally, considering that the local concentration is equal to the global concentration on average, we can derive the expression for the Warren-Cowley parameter:
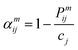 | (5) |
In the formula, Pijm represents the probability of finding an atom of type j in the mth nearest coordination shell of an atom of type i, and cj is the atomic concentration of element j. A parameter value of 0 indicates an ideal random solid solution, positive values represent ordered structures and negative values indicate a tendency towards segregation.
3. Results and discussion
3.1 Element dependence of chemical SRO
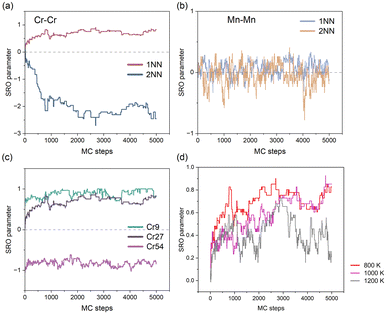
We initially investigated the chemical ordering in the CoFeNiCr HEA matrix. In Fig. 2(a), the convergence of the first-nearest neighbour (1NN) SRO parameter for Cr–Cr atomic pairs during MC iterations indicates a chemical ordering characteristic of Cr in the CoFeNiCr HEA. To delve deeper into this spatial distribution feature, we computed the SRO parameter for Cr–Cr atomic pairs in the second-nearest neighbour (2NN), revealing a converging trend with MC iterations. In contrast to the positive order parameter values of +0.75 observed at the 1NN distance, the 2NN SRO parameter is approximately −2.5. This signifies a typical arrangement where Cr atoms occupy the 2NN sites, i.e., sub-lattice points, forming an L12 structure, as reported in similar literature.5,41,42 In contrast, the Mn–Mn pair in the CoFeNiMn HEA exhibits no distinguished trend but rather a random distribution, in both the 1NN and 2NN SRO analyses (see Fig. 2(b)). This suggests that the role of Mn in the CoFeNiMn HEA is to promote the homogeneity of the structure. Gutierrez et al.43 believed that the addition of Mn to the CoCrFeNi matrix contributed favourably to the mixing configurational entropy that promoted a homogeneous solid solution using the Bozzolo–Ferrante–Smith (BFS) method. However, the appearance of Mn seems to be detrimental to the corrosion resistance. Torbati-Sarraf et al.44 examined the pitting corrosion of equiatomic CrMnFeCoNi and CrFeCoNi alloys to clarify the effect of Mn addition on pitting, revealing that the inclusion of Mn resulted in a reduction of the protective ability of the passive film against chloride ions. Besides, Fig. S1† illustrates all the atomic pairs in the first-nearest neighbours for both CoFeNiCr and CoFeNiMn HEAs to provide a more comprehensive comparison.We proceeded to investigate the variation in SRO parameters for Cr–Cr pairs across different concentrations of Cr element. As is depicted in Fig. 2(c), different concentrations of Cr element in the CoFeNiCr HEA represent the chemical ordering/cluster phenomenon. Here, it is elucidated that while maintaining a constant total number of atoms in the system, we varied the number of Cr atoms to investigate Cr's compositional impact. For ease of description, we assigned distinct names to different HEAs based on the number of Cr atoms in the system, such as denoting (CoFeNi)33Cr9 as Cr9. From Fig. 2(c), a similar trend in chemical ordering for the Cr9 and equiatomic Cr27 alloys can be observed, indicating that Cr would occupy the 2NN sites of other Cr atoms in both types of HEAs. For Cr54, where Cr constitutes half of the composition, the chemical SRO parameter converges around −1 and no random behaviour similar to Mn–Mn atomic pairs is observed. This is attributed to the abundant Cr atoms, which, in addition to occupying the sublattice at the 2NN lattice site of other Cr atoms, also extend to the 1NN lattice site, resulting in a clustering phenomenon. That's to say, it is the inherent character of Cr that leads to the sublattice occupation behaviour. Experimental observations also indicate that changes in Cr concentration have an impact on the ordering of Cr in the system. Combining in situ synchrotron XRD with containerless levitation techniques, Jeon et al.45 discovered that short range order in the Fe–Cr–Ni melt became more pronounced as the Cr concentration decreased.
Next, we identified the impact of temperature on chemical SRO. As is shown in Fig. 2(d), the chemical SRO parameter of Cr–Cr atomic pairs in the CoFeNiCr HEA gradually fluctuates with increasing temperature, implying that elevated temperatures lead to the tendency of Cr atoms in the HEA to be more disordered. It is noteworthy that the chemical SRO parameter for Cr–Cr in CoFeNiCr at 800 K stabilizes around 0.7. For the case of 1200 K, the solid solution in the HEA is typically considered to be in an ideally random state, a reasonable approximation particularly at elevated temperatures where configurational entropy dominates the free energy, stabilizing the random alloy. Our work is consistent with the SRO research on the Co30Fe16.67Ni36.67Ti16.67 alloy via hybrid MD/MC simulations, yielding notable chemical SRO that intensified with decreasing annealing temperature.46
3.2 Mechanism of the SRO effect
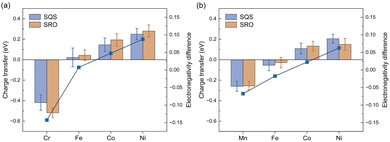
To thoroughly investigate the chemical SRO effect in the multi-component system of HEAs, we initially examined the impact of the electronic effects of individual elements on the SRO effect. As depicted in Fig. 3(a), there exists a progressive shift in the extent of charge transfer for Cr, Fe, Co and Ni from the loss of charge to gaining more charge via Bader charge analysis.47 A similar trend is observed for the CoFeNiMn HEA, as illustrated in Fig. 3(b). For example in the CoFeNiCr HEA (Fig. 3(a)), Cr, Fe, Co and Ni are in the sequential order of 3d transition metals in the periodic table, each possessing distinct electronegativity that increases with the atomic number. Subsequently, we explored the electronegativity difference among different elements in HEAs, as shown in the line graph in Fig. 3. The electronegativity differences are computed as the disparity between the Allen electronegativity48 of each constituent element in HEAs and the average electronegativity. It is evident that there is a strong positive correlation between the charge transfer and electronegativity difference. In other words, as the electronegativity increases with the rising atomic number, the charge transfer in the alloy transitions from electron loss to electron gain. In the CoFeNiCr HEA, Cr atoms with the lowest electronegativity in the alloy system experience the highest degree of electron loss. Conversely, the atoms of the other three elements exist in an electron-gaining state, where Ni atoms with the highest electronegativity acquire the largest number of electrons. Moreover, the phenomenon of charge transfer is dependent on the specific composition. In the CoFeNiMn HEA, where the electronegativities of constituent elements are relatively close, Mn and Fe atoms undergo electron loss, while Co and Ni atoms undergo electron gain. Due to the higher electronegativity of Mn compared to Cr, it is less prone to electron loss. Consequently, atoms more inclined to gain electrons will compete for electrons from elements excluding Mn in the CoFeNiMn HEA. This competition results in the phenomenon of charge loss observed in Fe.The relationship between elemental charge transfer and the SRO effect is dependent on the alloy composition. As depicted in Fig. 3(a), the CoFeNiCr HEA exhibits a more pronounced charge transfer due to the SRO effect. However, in Fig. 3(b), the charge transfer in the CoFeNiMn HEA is unrelated to SRO, indicating the presence of an element averaging effect in the CoFeNiMn HEA. Besides, a notable correlation is observed between charge transfer and Bader volume in Fig. S2,† a relationship influenced by the method of Bader volume determination. This implies that atoms undergoing loss of electrons will result in the reduction of atomic volume. For instance, in the CoFeNiCr HEA, Cr atoms lose electrons due to their lowest electronegativity, leading to the smallest atomic volume as depicted in Fig. S2(b).† Ni atoms with the largest electronegativity in both CoFeNiMn and CoFeNiCr HEAs exhibit the largest atomic volume, acquiring the maximum number of electrons.
Based on the analysis of variations in atomic volumes within these alloy systems, we proceeded to investigate the atomic stress of each atom in the HEAs. Fig. 4 illustrates the correlation between atomic stress and Voronoi volume in the CoFeNiMn and CoFeNiCr HEAs. On one hand, the atomic stress of each element exhibits positive compressive stress and negative tensile stress in the CoFeNiMn HEA, roughly distributed around the equilibrium line in the middle of Fig. 4(a). This balanced distribution of atomic stress for different alloys contributes to the stability of the structure. From the perspective of Voronoi volume, despite Co, Fe and Mn atoms in the CoFeNiMn HEA occupying comparable Voronoi volumes, it is evident that the Ni atoms, with the increased atomic volume due to electron gain, occupy the largest Voronoi volume. The relationship between atomic volume and Voronoi volume is illustrated in Fig. S4,† where the region above the red asymptotic line indicates Bader volume exceeding Voronoi volume. By comparing Mn and Cr, it is evident that the atomic volume of Cr atoms, which lose a larger number of electrons, is significantly smaller than its Voronoi volume at the respective sites. On the other hand, in the CoFeNiCr HEA, characterized by distinct chemical ordering, the atomic stress of Cr atoms is consistently negative, and this phenomenon becomes more pronounced with an increasing degree of chemical SRO. To further elucidate the distribution characteristics of atomic stress and volume in the alloy system, we plotted the average charge transfer and average Bader Volume, as shown in Fig. S3.† It is apparent that the average atomic stress of Cr atoms in the SRO structure of CoFeNiCr is much smaller than that in the SQS structure, and the reduced error bars reflect a more consistent distribution of Cr's atomic stress. The majority of atomic stress for the other three atoms (Co, Fe, and Ni) in the SRO structure is predominantly positive. Combining this analysis with the examination of Cr occupying sublattices in Fig. 2, we posit that Cr atoms with negative atomic stress occupy sublattice sites at the second-nearest neighbour, which promotes the formation of an L12 structure, while other atoms with positive atomic stress are randomly distributed throughout the system. Through this alternating interaction of positive and negative atomic stress, the local atomic environment is balanced, leading to a stable structure. Prior studies have reported the selection of atomic occupancy in L12 sites to achieve phase stability. The DFT calculations of Kulo et al. indicated that the most stable structure for Ni3X-type intermetallic compounds was the L12 structure, wherein Cr and Mo occupied the Ni-sublattice.49 Similarly, experimental findings by Gwalani et al.50 revealed the precipitation of highly refined ordered L12 precipitated in Al0.3CoFeCrNi, demonstrating stability at 550 °C, using scanning electron microscopy, transmission electron microscopy and 3D atom probe tomography. To date, recognizing the SRO structure of HEAs in experiments has been fairly challenging. Mössbauer spectroscopy is a good tool to exactly probe SRO, but it is usually limited in binary alloys containing Fe. It is because the neighbouring atom (the species different from Fe) around the 57Fe nuclei probe is assumed to be measurable by analysing the variation of spectral hyperfine parameters. However, with increasing constituent elements, the spectral hyperfine parameters become much more sophisticated so that it hardly distinguishes the individual element effect around the 57Fe nuclei probe. Another experimental method, transmission electron microscopy, observed the SRO in VCoNi.51 Unfortunately, the evidence of SRO from experiments is missing for HEAs composed of more constituent elements. Nevertheless, the study on Fe–Cr binary alloys52 revealed the SRO phenomenon in the Fe–Cr samples. This may also be related to the low electronegativity and the resulting negative stress of Cr, similar to our study. We expect more novel experimental methods to unleash feasible and explicit evidence of the SRO phenomenon in multi-principal element alloys.
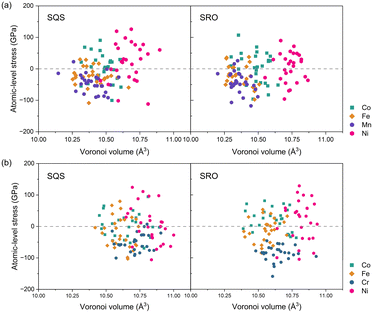 | ||
| Fig. 4 Correlation between atomic stress and Voronoi volume: (a) CoFeNiMn and (b) CoFeNiCr. Left corresponds to SQS structures, and right corresponds to equilibrium structures. | ||
3.3 SRO effect on thermal stability
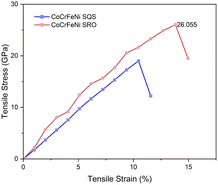
The ongoing debate on whether controlling the occurrence of chemical SRO enables tailoring of the mechanical properties of HEAs is at the forefront of discussion. We conducted static stress–strain calculations (see the method in the ES I†) for SQS and SRO structures, as illustrated in Fig. 5. The stress–strain curve is pretty linear in the SQS structure more than in the SRO model. The possible reason is that valence electronic concentration (VEC) is distributed homogeneously over the whole SQS matrix. Fig. 5 indicates that structures with chemical ordering exhibit greater tensile stress and strain compared to random structures, thus overcoming the strength-ductility trade-off. Experimental evidence indicated that the macroscopic yield strength of the single-phase equiatomic CrMnFeCoNi HEA was not impacted by heat treatment, where the development of short range order was expected.53 However, theoretical calculations conducted by Ji et al.54 showed that the presence of SRO in NbMoTaW refractory HEAs could concurrently bolster both strength and toughness, with a more pronounced enhancement observed at lower temperatures attributed to a higher degree of SRO. The observed disparities may stem from variations in experimental heat treatment process and sample preparation methods.Experimental observations have indicated the occurrence of secondary phases in HEAs during heat treatment.55–57 Consequently, we investigated the influence of the SRO effect at different temperatures on the thermal stability of the system. Based on the schematic of the addition of Cr/Mn into the CoFeNi alloy in Fig. 1, we calculated the change of Gibbs free energy for the synthesis process. For the alloys with order/disorder states,
| x·CoFeNi + (1 − x)·M → CoFeNixM1−x | (6) |
| S = −kB∑xm × lnxm | (7) |
As a result, we established linear correlations between the change of Gibbs free energy and temperature within the multicomponent systems utilizing the following equation:
| ΔG = ΔH − TΔS | (8) |
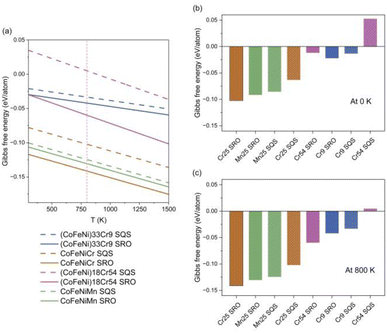
Fig. 6 illustrates the impact of chemical SRO on the thermal stability of HEAs. In Fig. 6(a) depicting linear correlations between the change in Gibbs free energy and temperature, the dashed lines represent SQS structures, while the solid lines represent SRO structures. This approximation indicates that HEAs become more stable with increasing temperature, highlighting their potential applications at elevated temperatures.
From Fig. 6(a), it is evident that equiatomic CoFeNiCr and CoFeNiMn HEAs exhibit correlations positioned at the lower end, implying that this equiatomic elemental composition promotes the thermal stability of the alloy system, thus validating the requirement of equiatomic or nearly equiatomic composition in the definition of HEAs. The thermal stability of the Cr-rich Cr54 HEA is comparatively worse, and according to the correlations between the change in Gibbs free energy and temperature, a phase transition in this alloy system occurs at T = 883 K. Comparing the SQS and SRO structures of the CoFeNiCr HEA, it is observed that the thermal stability of the structure after MC iterations is better than that of the initial random structure. This suggests that chemical ordering contributes to the enhancement of the thermal stability of HEAs. In the case of the CoFeNiMn HEA, lacking chemical ordering, the correlations between the change in Gibbs free energy and temperature in the structures before and after MC iterations are relatively close. In particular, we investigated the thermal stability of different HEAs at 0 K and 800 K, through Gibbs free energy, primarily from the contribution of entropy. The temperature 800 K considered here is due to factors such as the practical application temperature range,58 and variations in material properties observed at elevated temperatures.59 As is depicted in Fig. 6(b) and (c), it is evident that the equiatomic CoFeNiCr HEA is the most stable sample at both 0 K and 800 K, with the initial structure of the Cr54 HEA being the least stable, indicating a phase separation.
4. Conclusions
By introducing Cr and Mn into CoFeNi HEAs, we identified distinct elemental distributions within the matrix. Through analyses of the electronegativity difference, charge transfer, atomic volume and atomic stress of HEA constituent elements, we elucidated the origin of chemical short range order. Building upon this foundation, we investigated the impact of the SRO effect on the thermal stability of HEAs. The specific findings are summarized as follows:(1) Cr consistently occupied sublattice sites in HEAs, regardless of Cr concentration, while Mn promoted the homogeneity of composition in HEAs.
(2) Chemical SRO was temperature-dependent, becoming more pronounced at lower temperatures.
(3) Cr atoms, possessing the lowest electronegativity in the alloy system, underwent the highest degree of electron loss, resulting in the smallest atomic volume.
(4) Cr atoms with negative atomic stress occupied sublattice sites at the second-nearest neighbour position, while other atoms with positive atomic stress were randomly distributed. This interplay of positive and negative atomic stress balanced the local atomic environment, contributing to structural stability.
(5) Chemical ordering enhanced the thermal stability of HEAs, with equiatomic HEAs suggested as the most thermally stable.
Author contributions
Panhua Shi: conceptualization, methodology, validation, writing – original draft, data curation, investigation, and writing – review & editing. Yiying Yang: validation and investigation. Baodian Yao: data curation and investigation. Jiaxuan Si: validation. Y. X. Wang: conceptualization, writing – review & editing, and supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the National Natural Science Foundation of China under Grant No. 12275055 and U2067218.References
- J. W. Yeh, S. K. Chen, S. J. Lin, J. Y. Gan, T. S. Chin, T. T. Shun, C. H. Tsau and S. Y. Chang, Adv. Eng. Mater., 2004, 6, 299–303 CrossRef CAS.
- B. Cantor, I. T. H. Chang, P. Knight and A. J. B. Vincent, Mater. Sci. Eng., A, 2004, 375–377, 213–218 CrossRef.
- K. M. B. Urs, N. K. Katiyar, R. Kumar, K. Biswas, A. K. Singh, C. S. Tiwary and V. Kamble, Nanoscale, 2020, 12, 11830–11841 RSC.
- S. Tsianikas, Y. Chen, J. Jeong, S. Zhang and Z. Xie, Nanoscale, 2021, 13, 3602–3612 RSC.
- A. Smekhova, A. Kuzmin, K. Siemensmeyer, C. Luo, J. Taylor, S. Thakur, F. Radu, E. Weschke, A. G. Buzanich, B. Xiao, A. Savan, K. V. Yusenko and A. Ludwig, Nano Res., 2023, 16, 5626–5639 CrossRef CAS.
- B. Song, Y. Yang, M. Rabbani, T. T. Yang, K. He, X. Hu, Y. Yuan, P. Ghildiyal, V. P. Dravid, M. R. Zachariah, W. A. Saidi, Y. Liu and R. Shahbazian-Yassar, ACS Nano, 2020, 14, 15131–15143 CrossRef CAS PubMed.
- Y. Huang, S. Sabbaghianrad, A. I. Almazrouee, K. J. Al-Fadhalah, S. N. Alhajeri and T. G. Langdon, Mater. Sci. Eng., A, 2016, 656, 55–66 CrossRef CAS.
- K. S. Kumar, H. Van Swygenhoven and S. Suresh, Acta Mater., 2003, 51, 5743–5774 CrossRef CAS.
- B. Gludovatz, E. P. George and R. O. Ritchie, JOM, 2015, 67, 2262–2270 CrossRef CAS.
- H. Qiao, M. T. Saray, X. Wang, S. Xu, G. Chen, Z. Huang, C. Chen, G. Zhong, Q. Dong, M. Hong, H. Xie, R. Shahbazian-Yassar and L. Hu, ACS Nano, 2021, 15, 14928–14937 CrossRef CAS PubMed.
- Y. J. Li, A. Savan and A. Ludwig, Appl. Phys. Lett., 2021, 119, 201910 CrossRef CAS.
- L. Zendejas Medina, L. Riekehr and U. Jansson, Surf. Coat. Technol., 2020, 403, 126323 CrossRef CAS.
- S. Ghosh, V. Sotskov, A. V. Shapeev, J. Neugebauer and F. Körmann, Phys. Rev. Mater., 2022, 6, 113804 CrossRef CAS.
- J. Zhang, G. Deng, W. Li, L. Su, X. Liu, T. Ma and L. Gao, Tribol. Int., 2024, 191, 109191 CrossRef CAS.
- N. Rasooli, W. Chen and M. Daly, Nanoscale, 2024, 16, 1650–1663 RSC.
- S. Chen, T. Wang, X. Li, Y. Cheng, G. Zhang and H. Gao, Acta Mater., 2022, 238, 118201 CrossRef CAS.
- S. Yin, Y. Zuo, A. Abu-Odeh, H. Zheng, X.-G. Li, J. Ding, S. P. Ong, M. Asta and R. O. Ritchie, Nat. Commun., 2021, 12, 4873 CrossRef CAS PubMed.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, D. J. Srolovitz, P. K. Liaw and Y.-W. Zhang, Mater. Today, 2023, 65, 14–25 CrossRef CAS.
- M. A. Adaan-Nyiak, I. Alam, E. Jossou, S. Hwang, K. Kisslinger, S. K. Gill and A. A. Tiamiyu, Small, 2024, e2309631, DOI:10.1002/smll.202309631.
- M. A. Adaan-Nyiak, I. Alam, G. A. Arcuri and A. A. Tiamiyu, Mater. Des., 2023, 236, 112482 CrossRef CAS.
- T. Chookajorn, H. A. Murdoch and C. A. Schuh, Science, 2012, 337, 951–954 CrossRef CAS PubMed.
- Y. Wang, J. Yin, H. Hou, S. Hu, X. Liu, F. Xue, C. H. Henager and J. Wang, Nucl. Instrum. Methods Phys. Res., Sect. B, 2019, 456, 32–36 CrossRef CAS.
- M. N. Hasan, J. Gu, S. Jiang, H. J. Wang, M. Cabral, S. Ni, X. H. An, M. Song, L. M. Shen and X. Z. Liao, Scr. Mater., 2021, 190, 80–85 CrossRef CAS.
- D. Litvinov, K. Lu, M. Walter and J. Aktaa, Mater. Today Commun., 2023, 35, 106030 CrossRef CAS.
- S. Chen, Z. H. Aitken, S. Pattamatta, Z. Wu, Z. G. Yu, R. Banerjee, D. J. Srolovitz, P. K. Liaw and Y.-W. Zhang, Acta Mater., 2021, 206, 116638 CrossRef CAS.
- T. Egami, Prog. Mater. Sci., 2011, 56, 637–653 CrossRef CAS.
- S. Praveen, B. S. Murty and R. S. Kottada, JOM, 2013, 65, 1797–1804 CrossRef CAS.
- P. T. Hung, M. Kawasaki, J.-K. Han, J. L. Lábár and J. Gubicza, Mater. Charact., 2021, 171, 110807 CrossRef CAS.
- M. K. Kini, S. Lee, A. Savan, B. Breitbach, Y. Addab, W. Lu, M. Ghidelli, A. Ludwig, N. Bozzolo, C. Scheu, D. Chatain and G. Dehm, Surf. Coat. Technol., 2021, 410, 126945 CrossRef CAS.
- S. Mehrizi, M. J. Molaei and M. H. Sohi, J. Mater. Res. Technol., 2022, 21, 2547–2554 CrossRef CAS.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- X. L. Ren, P. H. Shi, W. W. Zhang, X. Y. Wu, Q. Xu and Y. X. Wang, Acta Mater., 2019, 180, 189–198 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- Y. Wang, G. M. Stocks, W. A. Shelton, D. M. C. Nicholson, Z. Szotek and W. M. Temmerman, Phys. Rev. Lett., 1995, 75, 2867–2870 CrossRef CAS PubMed.
- U. Von Barth and L. Hedin, J. Phys. C: Solid State Phys., 1972, 5, 1629–1642 CrossRef CAS.
- T. Egami and Y. Waseda, J. Non-Cryst. Solids, 1984, 64, 113–134 CrossRef CAS.
- N. Metropolis, A. W. Rosenbluth, M. N. Rosenbluth, A. H. Teller and E. Teller, J. Chem. Phys., 1953, 21, 1087–1092 CrossRef CAS.
- D. De Fontaine, J. Appl. Crystallogr., 1971, 4, 15–19 CrossRef CAS.
- C. Niu, A. J. Zaddach, A. A. Oni, X. Sang, J. W. Hurt, J. M. LeBeau, C. C. Koch and D. L. Irving, Appl. Phys. Lett., 2015, 106, 161906 CrossRef.
- H.-W. Hsiao, R. Feng, H. Ni, K. An, J. D. Poplawsky, P. K. Liaw and J.-M. Zuo, Nat. Commun., 2022, 13, 6651 CrossRef CAS PubMed.
- M. A. Gutierrez, G. D. Rodriguez, G. Bozzolo and H. O. Mosca, Comput. Mater. Sci., 2018, 148, 69–75 CrossRef CAS.
- H. Torbati-Sarraf, M. Shabani, P. D. Jablonski, G. J. Pataky and A. Poursaee, Mater. Des., 2019, 184, 108170 CrossRef CAS.
- S. Jeon, M. P. Sansoucie, O. Shuleshova, I. Kaban and D. M. Matson, J. Chem. Phys., 2020, 152, 094501 CrossRef CAS PubMed.
- E. Antillon, C. Woodward, S. I. Rao, B. Akdim and T. A. Parthasarathy, Acta Mater., 2020, 190, 29–42 CrossRef CAS.
- R. F. W. Bader and R. F. Bader, Atoms in Molecules: A Quantum Theory, Clarendon Press, 1990 Search PubMed.
- J. B. Mann, T. L. Meek, E. T. Knight, J. F. Capitani and L. C. Allen, J. Am. Chem. Soc., 2000, 122, 5132–5137 CrossRef CAS.
- N. Kulo, S. He, W. Ecker, R. Pippan, T. Antretter and V. I. Razumovskiy, Intermetallics, 2019, 114, 106604 CrossRef CAS.
- B. Gwalani, V. Soni, D. Choudhuri, M. Lee, J. Y. Hwang, S. J. Nam, H. Ryu, S. H. Hong and R. Banerjee, Scr. Mater., 2016, 123, 130–134 CrossRef CAS.
- X. Chen, Q. Wang, Z. Cheng, M. Zhu, H. Zhou, P. Jiang, L. Zhou, Q. Xue, F. Yuan, J. Zhu, X. Wu and E. Ma, Nature, 2021, 592, 712–716 CrossRef CAS PubMed.
- S. M. Dubiel and J. Żukrowski, J. Alloys Compd., 2015, 624, 165–169 CrossRef CAS.
- D. Zhou, Z. Chen, K. Ehara, K. Nitsu, K. Tanaka and H. Inui, Scr. Mater., 2021, 191, 173–178 CrossRef CAS.
- W. Ji and M. S. Wu, Intermetallics, 2022, 150, 107707 CrossRef CAS.
- E. A. Anber, N. C. Smith, P. K. Liaw, C. M. Wolverton and M. L. Taheri, APL Mater., 2022, 10, 101108 CrossRef CAS.
- A. E. Mann and J. W. Newkirk, Adv. Eng. Mater., 2023, 25, 2201614 CrossRef CAS.
- P. Sliwa, K. Berent, J. Przewoznik and J. Cieslak, J. Alloys Compd., 2020, 814, 151757 CrossRef CAS.
- M. Rieth, S. L. Dudarev, S. M. Gonzalez De Vicente, J. Aktaa, T. Ahlgren, S. Antusch, D. E. J. Armstrong, M. Balden, N. Baluc, M. F. Barthe, W. W. Basuki, M. Battabyal, C. S. Becquart, D. Blagoeva, H. Boldyryeva, J. Brinkmann, M. Celino, L. Ciupinski, J. B. Correia, A. De Backer, C. Domain, E. Gaganidze, C. García-Rosales, J. Gibson, M. R. Gilbert, S. Giusepponi, B. Gludovatz, H. Greuner, K. Heinola, T. Höschen, A. Hoffmann, N. Holstein, F. Koch, W. Krauss, H. Li, S. Lindig, J. Linke, C. Linsmeier, P. López-Ruiz, H. Maier, J. Matejicek, T. P. Mishra, M. Muhammed, A. Muñoz, M. Muzyk, K. Nordlund, D. Nguyen-Manh, J. Opschoor, N. Ordás, T. Palacios, G. Pintsuk, R. Pippan, J. Reiser, J. Riesch, S. G. Roberts, L. Romaner, M. Rosiński, M. Sanchez, W. Schulmeyer, H. Traxler, A. Ureña, J. G. Van Der Laan, L. Veleva, S. Wahlberg, M. Walter, T. Weber, T. Weitkamp, S. Wurster, M. A. Yar, J. H. You and A. Zivelonghi, J. Nucl. Mater., 2013, 432, 482–500 CrossRef CAS.
- G. Bonny, A. Bakaev, P. Olsson, C. Domain, E. E. Zhurkin and M. Posselt, J. Nucl. Mater., 2017, 484, 42–50 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00202d |
| This journal is © The Royal Society of Chemistry 2024 |