Open Access Article
Open Access ArticleUnderstanding mono- and bi-metallic Au and Ni nanoparticle responses to fast heating†
Tatiana E.
Itina
 *
*
Université Jean Monnet Saint-Etienne, CNRS, Institut d Optique Graduate School, Laboratoire Hubert Curien UMR 5516, F-42023, Saint-Etienne, France. E-mail: tatiana.itina@univ-st-etienne.fr
First published on 9th September 2024
Abstract
Nanoparticle assembly, alloying and fragmentation are fundamental processes with significant implications in various fields such as catalysis, materials science, and nanotechnology. Understanding these processes under fast heating conditions is crucial for tailoring nanoparticle properties and optimizing their applications. For this, we employ molecular dynamics simulations to obtain atomic-level insights into nanoparticle behavior. The performed simulations reveal intricate details of sintering, alloying and fragmentation mechanisms shedding light on the underlying physical phenomena governing these processes. The calculation results help to visualize nanoparticle evolution upon undercritical and supercritical heating elucidating not only the role of temperature, but also of nanoparticle sizes and composition. In particular, it is shown that surface tension and surface energy play important roles not only in nanoparticle melting but also in its fragmentation. When the added energy exceeds a critical threshold, the nanoparticle begins to experience alternating compression and expansion. If the tensile stress surpasses the material's strength limit, fragmentation becomes prominent. For very small particles (with radius smaller than ∼10 nm), this occurs more rapidly, whereas sub-nano-cavitation precedes the final fragmentation in larger particles, which behave more like droplets. Interestingly, this effect depends on composition in the case of AuNi alloy nanoparticles, as expected from the phase diagrams and excess energy. The heating level required to overcome the mixing barrier is also determined and is shown to play an important role in the evolution of AuNi nanoparticles, in addition to their size. Furthermore, our findings provide insights into controlling nanoparticle synthesis for various applications in numerous nanotechnological domains, such as catalysis, sensors, material analysis, as well as deseas diagnostics and treatment. This study bridges the gap between experimental observations and theoretical predictions paving the way for designing advanced nanomaterials with enhanced functionalities.
1. Introduction
Nanoparticle (NP) assembly, mixing and fragmentation represent fundamental phenomena with profound implications across diverse scientific and technological domains.1–3 The ability to understand, to alter and to control the behavior of nanoparticles under varying thermal conditions is paramount for advancing numerous fields of modern nanotechnology in various domains such as chemistry, optics and photonics, energy storage, catalysis and medicine.4–12 Nanoparticles are also promising candidates for environmental remediation applications, such as pollutant removal and wastewater treatment. In fact, high surface area-to-volume ratio13 and unique chemical, optical, magnetic and/or electronic properties make nanomaterials particularly attractive.1–3 Additionally, nano-objects are known to be efficient photo-thermal converters14 and color modifiers.15 Particularly, the extraordinary capacities of plasmonic nanomaterials to locally enhance electromagnetic field16 were extensively studied during last decades.In modern nanotechnology, nanoparticles often serve as building blocks for synthesizing advanced materials with tailored properties. In fact, sintering and controllable assembly of nanoparticles17 enable not only the three-dimensional (3D) fabrication of nanostructured materials with enhanced properties, but also provide possibilities of numerous combinations, or so-called “smart” materials.18 Particularly, two or multi-material complexes can create, such as Janus nanoparticles,19 core-satellites structures,20 alloys,21 nanoparticle chains, lattices, etc. By changing the fabrication conditions, such as temperature, pressure and ambient medium, the properties of the fabricated nanomaterials can be adjusted, but it is still difficult to efficiently control over engineering new functional materials. Sintering and fragmentation processes are strongly material-dependent.22,23 These processes not only affect properties of nanoparticles, but can constantly and profoundly impact the fabrication process. In addition to traditional chemical fabrication methods, efforts were focused on the development of physical or even biological synthesis of nanomaterials.24 Many of the recent achievements in the experimental research have showcased the potential of pulsed heating techniques to engineer nanoparticle morphology and structure with unprecedented precision, demonstrating their utility across various applications. Thus, many investigations revealed the capacities and versatilities of laser systems ranging from continuous wave (CW) to nanosecond, picosecond and even femtosecond pulsed lasers.25–27 Additionally, plasma discharges, such as corona, spark, RF, magnetron, as well as plasma jets and sprays also lead to nanoparticle formation and growth.28–30 These studies elucidated the effects of rapid heating on various materials and offered valuable insights into the mechanisms governing particle melting, evaporation, sintering, etc.
In recent years, molecular dynamics (MD) simulations have emerged as a powerful numerical approach for unraveling the intrinsic atomic-scale processes underlying nanoparticle behavior.31–33 Namely, MD simulations have significantly contributed to our understanding of nanoparticle behavior under rapidly changing thermal conditions. By faithfully replicating atomic interactions, MD simulations have already provided numerous insights into the mechanisms driving nanoparticle melting, aggregation and fragmentation.23,34–41 These simulations not only helped to better understand experimental results, but also uncovered intricate details of nanoparticle dynamics, shedding light on phenomena that are challenging to observe experimentally. Notably, recent MD studies have elucidated the role of nanoparticle properties, environment, heating rate, surface interactions, and diffusion kinetics in governing nanoparticle evolution under pulsed heating, paving the way for predictive modeling and design of nanomaterials with tailored properties.35–41 On one hand, the phenomenon of nanoparticle sintering, wherein adjacent nanoparticles merge due to diffusion and surface energy minimization, plays a key role in determining material properties and functionality. On the other hand, nanoparticle fragmentation, characterized by the breaking apart of nanoparticles into smaller entities, influences nanoparticle stability, reactivity, and assembly.
Experimentally, effects, such as spectral changes or bleaching in optical measurements, as well as changes in X-ray scattering indicated that either reversible or irreversible changes could be induced by laser heating of nanoparticles at different fluences.37,42–45 In experiments, such as laser ablation for instance, commonly two distinguished nanoparticle populations are observed with diameters smaller than ∼10 nm and around 20–50 nm requiring additional targeted fragmentation to remove to larger population. For this, nanoparticles are often rapidly heated and exploded by an additional laser irradiation.46 Thus, instead of slow evaporation, they may experience rapid and non-equilibrium phase transformations and breakage. Similar effects are known to occur in wire explosion and in fast and ultra-fast laser ablation when super-critical heating of materials is achieved followed by the formation of a metastable super-heated liquid phases, phase explosion and spinodal decomposition.47–49 These effects remain not enough understood, particularly in the case of such small objects as nanoparticles. Fast and strong heating, furthermore, leads to new structures and phase formation enhancing atomic diffusion and mixing of even immiscible elements, creating irreversible sintering, dislocations or amorphous phases, complete or partial alloying, or leading to Janus nanocomposite formation. Contrary to the long and slow annealing, fast cooling helps freezing such structures.
Despite tremendous interest, most of the above-mentioned non-equilibrium phenomena are still far from being understood. This knowledge is, however, essential for both theoretical and applicative developments. That is why, herein we present the results of several MD simulations that are focused on the nuanced dynamics of nanoparticle fragmentation and assembly upon fast and rather strong heating during only 20 ps followed by a rather fast cooling. We consider monoatomic Au and bi-atomic Au–Ni nanoparticles. The choice of the material is based on the important catalytic applications. Thus, Au–Ni nanoparticles can serve as catalysts in hydrogenation reactions, where they help in the selective addition of hydrogen to various substrates. These nanoparticles are used in fuel cells and electrochemical sensors, enhancing the efficiency and performance of reactions like the oxygen reduction reaction (ORR) and hydrogen evolution reaction (HER). Catalysis impacts numerous industries, including energy, pharmaceuticals, and environmental technology, making it a critical area of research and application for Au–Ni nanoparticles. Not only alloy, but also Janus nanoparticles offer unique advantages for catalytic applications due to their dual functionality, enhanced catalytic activity, improved stability, and versatility. For Au–Ni nanoparticles, the Janus structure can be particularly advantageous in multiphase reactions and in applications where different catalytic processes need to be optimized simultaneously. This makes Janus Au–Ni nanoparticles a promising candidate for advanced catalytic systems, potentially outperforming traditional alloy or core–shell configurations in specific scenarios. The fabrication procedures of such structures, however, remain challenging. To better understand the effect of picosecond heating, both near-critical and supercritical conditions are considered. By probing these processes at the atomic level, we aim to elucidate the underlying mechanisms governing nanoparticle evolution and morphology in response to intense thermal stimuli.
2. Methodology and simulation details
The study is based on classical molecular dynamics simulations to investigate nanoparticle dynamics under pulsed heating conditions. In these simulations, the behaviour of atoms within the nanoparticle system is simulated over time based on Newton's equations of motion. Interatomic interactions are described using a suitable force field, allowing for the calculation of forces between atoms and the determination of particle trajectories.50In the present model, the initial nanoparticles may consist either of one type of atoms (Au, Ni) or a mixture of these metallic atoms with various atomic fractions. They are modelled as spherical entities with the corresponding lattice structure. The interatomic interactions between metal atoms are modelled by using the Embedded Atom (EAM) potential:51
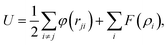 | (1) |
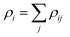 is the electron density of the atom i, ρij is the electron density function. For the interaction of different metallic atoms, we use specifically built EAM potentials that were previously verified to give reasonable values of material elastic constant, equilibrium lattice constant, bulk modulus, and vacancy formation energy.52–54 The equations of motion are integrated using the velocity Verlet algorithm55 available in LAMMPS,56 which is known for its numerical stability and conservation of energy. This algorithm allows for the efficient propagation of the system dynamics over time. In the third simulation model, two or several different metallic particles are placed in a close vicinity. They are allowed to stick together during heating and then cooled down to room temperature. Then, the sample is heated and cooled again following the same procedure as for a single nanoparticle. We start each simulation by a sample preparation procedure. Initially, atoms are placed in the positions according to the structure of the corresponding components forming one or several spherical particles with centers at the pre-defined positions. The initial center to mass velocity is zero in the presented simulations. Before each simulation, the initially built samples are firstly pre-heated above the corresponding melting point, then quenched to 0.1 K, heated to room temperature and equilibrated. This procedure allows us to be sure that particles have a correct atomic structure and surface energy (surface tension). The typical time step is as short as 1 fs to insure the correct energy of the system which is systematically monitored. Commonly, open boundary conditions are used. Simulations are then performed by increasing system temperature during a short time of several picoseconds (20 ps here) simulating the temperature rise from 300 K to Tmax that can be higher that the thermodynamic critical temperature through the canonical Nosé–Hoover NVT procedure.57 After the heating, the system is slowly cooled back to room temperature during a much longer time (200 ps here). For the cooling stage, the NVT procedure is also used. The simulation parameters and techniques are tailored to accurately represent the system of interest while minimizing computational overhead. High performance computing using MPI (The Message Passing Interface) was used.
is the electron density of the atom i, ρij is the electron density function. For the interaction of different metallic atoms, we use specifically built EAM potentials that were previously verified to give reasonable values of material elastic constant, equilibrium lattice constant, bulk modulus, and vacancy formation energy.52–54 The equations of motion are integrated using the velocity Verlet algorithm55 available in LAMMPS,56 which is known for its numerical stability and conservation of energy. This algorithm allows for the efficient propagation of the system dynamics over time. In the third simulation model, two or several different metallic particles are placed in a close vicinity. They are allowed to stick together during heating and then cooled down to room temperature. Then, the sample is heated and cooled again following the same procedure as for a single nanoparticle. We start each simulation by a sample preparation procedure. Initially, atoms are placed in the positions according to the structure of the corresponding components forming one or several spherical particles with centers at the pre-defined positions. The initial center to mass velocity is zero in the presented simulations. Before each simulation, the initially built samples are firstly pre-heated above the corresponding melting point, then quenched to 0.1 K, heated to room temperature and equilibrated. This procedure allows us to be sure that particles have a correct atomic structure and surface energy (surface tension). The typical time step is as short as 1 fs to insure the correct energy of the system which is systematically monitored. Commonly, open boundary conditions are used. Simulations are then performed by increasing system temperature during a short time of several picoseconds (20 ps here) simulating the temperature rise from 300 K to Tmax that can be higher that the thermodynamic critical temperature through the canonical Nosé–Hoover NVT procedure.57 After the heating, the system is slowly cooled back to room temperature during a much longer time (200 ps here). For the cooling stage, the NVT procedure is also used. The simulation parameters and techniques are tailored to accurately represent the system of interest while minimizing computational overhead. High performance computing using MPI (The Message Passing Interface) was used.
3. Modeling results and discussion
Nanoparticle behaviour is known to depend on their sizes. Thus, their melting temperature is often described by the Gibbs–Thomson equation: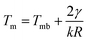 , where γ is the surface energy of the nanoparticle material, k is Boltzmann constant; and Tmb is bulk melting temperature.58–60
, where γ is the surface energy of the nanoparticle material, k is Boltzmann constant; and Tmb is bulk melting temperature.58–60
Nanoparticles possess high surface energy due to the large fraction of atoms residing at the surface, this effect being more pronounced for particles with diameter smaller than D* ∼ 20 nm (radius R ∼ 10 nm). Size-dependent melting temperatures of single mono-metallic nanoparticles composed of Au or Ni are shown in Fig. 1. The theoretical predictions were compared with the results of the MD simulations and a good agreement was obtained in the range of D between 5 and 100 nm.59,60
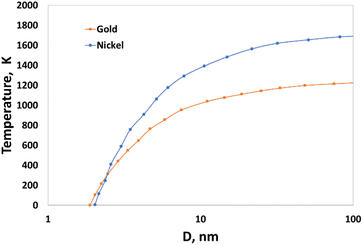 | ||
| Fig. 1 Size-dependent melting temperature of gold and nickel nanoparticles.59,60 | ||
The high surface-to-volume ratio means that surface atoms, which are less tightly bound than those in the interior, play a crucial role in determining the nanoparticle's mechanical properties. Commonly, the relationship between melting point and pressure is described by the Clapeyron equation. The melting point of a metal generally increases under high compression. This is because increased pressure reduces the volume, making it harder for the atoms to move into a liquid state. Under tensile stress or high extension, the melting point of a metal typically decreases. This effect is attributed to the reduced cohesive forces between atoms when the material is under tension, making it easier for the atoms to break free from the solid structure. The melting point of nanoparticles also depends on pressure, but the effect is more complex. For nanoparticles, the surface energy plays a significant role, and under compression, the melting point may increase, but not as significantly as in bulk materials.
To get more information about material properties, thermodynamic phase diagrams are commonly used.49,61,62 An example of previously calculated phase diagram of gold in temperature–density coordinates is presented in Fig. 2a. The presence of metastable states, such as superheated liquid region and saturated gas is particularly important for fast and strong heating. The life time of the of metastable liquid state [region (l) in Fig. 1a] drops to zero when approaching the spinodal, whereas it tends to infinity in the vicinity of the binodal line. In the case of small nanoparticles, this diagram should be corrected. The primary change for nanoparticles smaller than 10–20 nm is observed in the melting curve (as in Fig. 1), where the melting temperature decreases with smaller nanoparticle sizes (as indicated by the dash-dotted black line in Fig. 2a). The behavior of other curves remains an open question. However, because surface tension decreases with rising temperature, the surface effects on the main lines defining the metastable and unstable regions (binodal and spinodal lines) are significantly less pronounced at higher temperatures. Noticeable differences can be, nevertheless, observed in nanoparticle behavior due to their small size. To clarify, Fig. 2a presents a sketch of two typical temperature–density trajectories: one for a slice of a bulk target heated by an ultra-short laser pulse (blue line) and another for a nanoparticle with a radius of 20 nm (yellow line). While a slice of a bulk target can be heated almost at constant density in a vacuum, its trajectory enters the metastable superheated liquid region with negative pressure only once, during cooling. In contrast, for nanoparticles, the pressure and radius oscillate during heating, causing the corresponding curve to repeatedly enter and exit the metastable superheated liquid zone with negative pressure, then return to positive pressure during the heating process. To characterize binary systems, Au–Ni phase diagrams the corrections corresponding to the changes in properties for nanoparticles (Fig. 2b) were also calculated.63–65
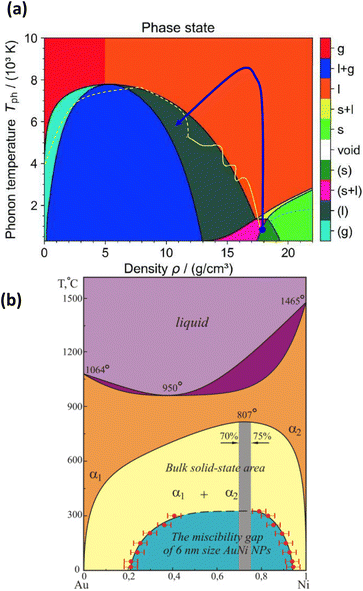 | ||
| Fig. 2 (a) – Temperature–density phase diagram of gold with phase states:61 s—solid; l—liquid; g—gas; l + g—liquid–gas mixture; s + l—melting; (s)—metastable solid; (s + l)—metastable melting; (l)—metastable liquid; (g)—metastable gas. bn and sp are binodal and spinodal curves, respectively. (b) – Binary Au–Ni phase diagram.63–65 | ||
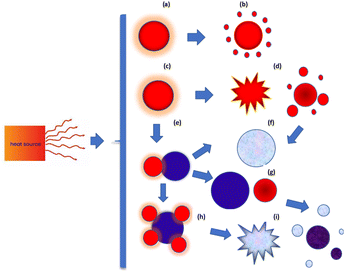
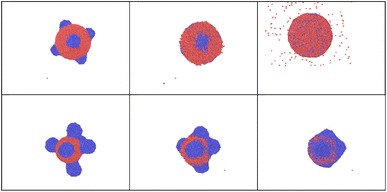
Under rapid heating, the system reaches strongly non-equilibrium conditions, and many mechanisms governing nanoparticle responses under such conditions remain insufficiently studied. Depending on the energy input, as well as the rates of heating and cooling, nanoparticles may undergo a range of transformations (Fig. 3) such as partial or complete melting, evaporation, fragmentation, aggregation, coalescence, and mixing.
A series of molecular dynamic simulations are performed to investigate the behavior of nanoparticles under rapid heating, with particular emphasis on mono- and bi-atomic metallic systems. As we will demonstrate, rapid heating can induce not only nanoparticle melting and evaporation but also fragmentation into smaller pieces. Additionally, sintering and mixing processes can be significantly enhanced.
3.1 Fast heating and decay of a single mono-metallic nanoparticle
Firstly, we consider the rapid heating of single metallic nanoparticles (Au) of varying sizes. A series of all-atom three-dimensional simulations were conducted with a heating rate as high as 3.85 × 1014 K s−1 during 20 ps. The considered heating rate and temperature ranges well above material boiling point can be easily obtained in experiments with ultra-short (femtosecond) laser pulses, as can be understood based on a well-known two-temperature model for metals. In this model, two coupled heat equations are commonly written for small nanoparticles as follows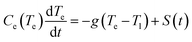 | (2) |
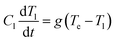 | (3) |
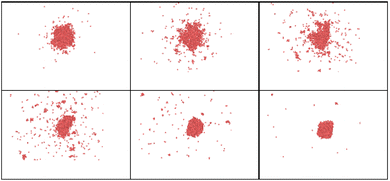
It is interesting to examine the role of nanoparticle size under heating well above melting point. Upon such rapid and intense heating, surface pre-melting occurs within the first few picoseconds for the smaller particle (R = 20 uc). This causes significant surface instability, leading to rapid disintegration and irreversible nanoparticle fragmentation (Fig. 4 and 5).
An important observation is that to achieve even partial nanoparticle decay, the temperatures must exceed the thermodynamic critical temperature of bulk material. One can see in Fig. 4 and 5 that while the smaller cluster is evaporated, the bigger cluster starts experiencing expansion, followed by multiple nanocavitation that finally leads to the particle decomposition into a number of smaller clusters. In addition, a large number of atoms and very small clusters are ejected in the form of monomers. Both the atoms and the daughter clusters expand rapidly outward from the cluster center. This result with the fact that nanoparticle formation and fragmentation by short heat sources often results in a bimodal fragment size distribution, producing bigger particles along with many smaller clusters and monomers.66,67
Complete nanoparticle melting is achieved within ∼2–10 ps depending on nanoparticle size. The difference between uncompleted and compete melting is evident in the radial distribution function (Fig. 6 for R = 20 au, and Fig. 1S in ESI† for R = 50 au), where Fig. 6a reveals a mixture of liquid and solid phases at 0.1 ps, while Fig. 6b corresponds to a complete melting of the same nanoparticles at t = 10 ps. The subsequent dynamics are characterized by intensive bond breaking and atomic expansion, occurring not only at the surface but also deeper within the nanoparticle.
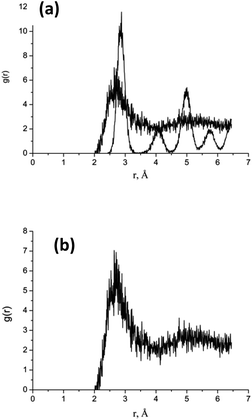 | ||
| Fig. 6 Calculated radial distribution function (RDF) for Au cluster with R = 20 uc, (a) at t = 0.1 ps and (b) – the same at t = 10 ps. | ||
Because particle melting take place, surface instabilities can be observed like in liquid droplets, where a competition exists between forces driving expansion and those attempting to retain the droplet's shape. As for particle decay, which generally occurs due to a combination of both thermal and mechanical effects, several criteria were proposed mostly for bulk material. It is clear that particle fragmentation leads to the formation of new surfaces, so that the system energy should be high enough for this. Again, it is important to note that the fraction of surface energy in the energy balance is larger for smaller nanoparticles (smaller than 10 nm). Upon heating, the absolute value of the potential energy decreases, while the part of kinetic energy in total energy rises. During cooling, the inverse process is observed (Fig. 7). From thermodynamic point of view fragmentation can enter into play if the formation of new surfaces is energetically profitable, so that the corresponding potential energy 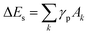 is smaller than the one the system would have without fragmentation, where γp is the interfacial energy per unit area of the particle p; Ak is the area of the new surface k formed.68,69
is smaller than the one the system would have without fragmentation, where γp is the interfacial energy per unit area of the particle p; Ak is the area of the new surface k formed.68,69
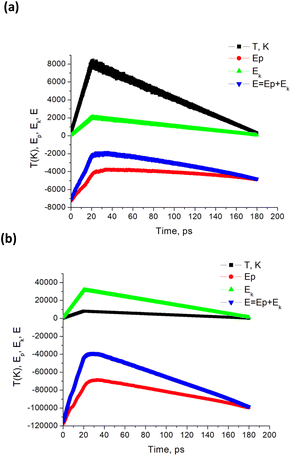 | ||
| Fig. 7 Calculated temperature and NP energies vs. time for Tmax = 8000 K. Here, simulations are performed for a single Au NP with radius (a) R = 20 uc, and (b) R = 50 uc. Energy units are cal mol−1. | ||
Therefore, depending on particle size and material, rapid heating can lead to not only fast melting, surface instabilities, dynamic fragmentation, but also the formation of growing nanopores inside the heated material. This phenomenon is similar to the well-known sub-surface boiling and cavitation observed in ultra-fast ablation or explosive boiling, arising from tensile stresses, thermal nucleation, and defect diffusion and aggregation.
When a gold nanoparticle is subjected to thermal stress, the stress is concentrated intensely due to its limited volume, leading to a regime of stress confinement. As the tensile stress increases, it can overcome the cohesive forces that hold the surface atoms together, resulting in the initiation of cracks or voids. For a gold nanoparticle, the radius can be expressed in terms of the number of unit cells. The lattice constant of gold, a, is approximately 0.407 nm. If the radius of the nanoparticle is 50 uc, the actual radius R = 20.4 nm. The volume of a spherical nanoparticle can be calculated as 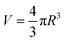 . The onset of fracture can be estimated by comparing the tensile stress σ (or, a negative pressure, P) with the material's cohesive strength σc. For a gold nanoparticle under tensile stress:
. The onset of fracture can be estimated by comparing the tensile stress σ (or, a negative pressure, P) with the material's cohesive strength σc. For a gold nanoparticle under tensile stress: 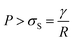 , where γ is the surface energy (approximately 1.5 J m−2 for gold), and r is the radius of the nanoparticle. Substituting the values, we obtain σs = 73.5 MPa. Thus, when the applied tensile stress exceeds approximately 73.5 MPa, it can overcome the cohesive forces in a gold nanoparticle with a radius of 50 uc, leading to fracture or the formation of cracks and voids.
, where γ is the surface energy (approximately 1.5 J m−2 for gold), and r is the radius of the nanoparticle. Substituting the values, we obtain σs = 73.5 MPa. Thus, when the applied tensile stress exceeds approximately 73.5 MPa, it can overcome the cohesive forces in a gold nanoparticle with a radius of 50 uc, leading to fracture or the formation of cracks and voids.
The calculated pressure–temperature dependencies are shown in Fig. 8. The calculated pressure oscillates, as shown in Fig. 8, due to the fact that rapid heating induces pressure waves or even shock waves, which are known to form under such conditions. In the case of a nanoparticle, these waves propagate toward the center and then return to the surface, with energy being dissipated in the processes of particle deformation and bond breaking. The period of such dumped oscillations can be estimated as 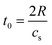 , where R is particle radius and cs is sound velocity. An estimation of a gold nanoparticle with of 20 nm gives a value of ∼16 ps at cs = 2.4 × 103 m s−1. This period decreases with size. More precisely, it is also possible to describe such oscillations by using Lamb Rayleigh theory, where different modes can be considered. Considering breathing mode, again oscillations frequencies close to the one obtained in MD calculations are obtains. For particles with radius smaller than 10 nm, the frequency stays constant since such objects do not obey to classical mechanical description anymore. In a simplified approach, one can consider the balance between internal pressure and surface pressure, which is especially significant for small nanoparticles. The internal pressure Pint due to thermal expansion can be expressed as
, where R is particle radius and cs is sound velocity. An estimation of a gold nanoparticle with of 20 nm gives a value of ∼16 ps at cs = 2.4 × 103 m s−1. This period decreases with size. More precisely, it is also possible to describe such oscillations by using Lamb Rayleigh theory, where different modes can be considered. Considering breathing mode, again oscillations frequencies close to the one obtained in MD calculations are obtains. For particles with radius smaller than 10 nm, the frequency stays constant since such objects do not obey to classical mechanical description anymore. In a simplified approach, one can consider the balance between internal pressure and surface pressure, which is especially significant for small nanoparticles. The internal pressure Pint due to thermal expansion can be expressed as 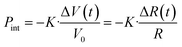 , and the surface pressure
, and the surface pressure 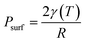 , where r is nanoparticle radius, and K is the bulk modulus of gold. The total pressure P(t) is:
, where r is nanoparticle radius, and K is the bulk modulus of gold. The total pressure P(t) is:
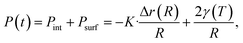 | (4) |
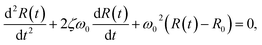 | (5) |
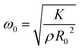 is the natural angular frequency of oscillation, with K being the bulk modulus and ρ the density of the nanoparticle material. ζ is the damping coefficient, which accounts for energy loss due to internal friction and other dissipative processes; R0 is the equilibrium radius of the nanoparticle. The solution to this equation depends on the damping coefficient ζ. If the damping is small (ζ < 1), the solution represents underdamped oscillations:
is the natural angular frequency of oscillation, with K being the bulk modulus and ρ the density of the nanoparticle material. ζ is the damping coefficient, which accounts for energy loss due to internal friction and other dissipative processes; R0 is the equilibrium radius of the nanoparticle. The solution to this equation depends on the damping coefficient ζ. If the damping is small (ζ < 1), the solution represents underdamped oscillations:R(t) = R0 + Ae−ζω0t![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos(ω1t + ϕ), cos(ω1t + ϕ), | (6) |
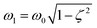 is the damped angular frequency, ϕ is the phase angle.
is the damped angular frequency, ϕ is the phase angle.
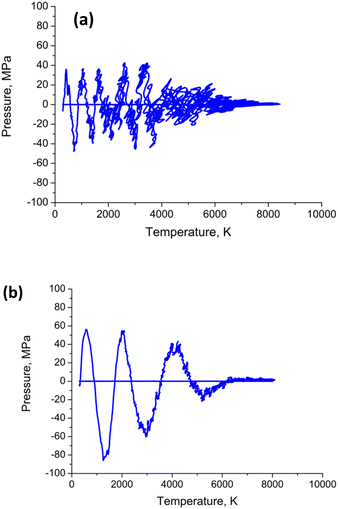 | ||
| Fig. 8 Calculated pressure–temperature dependencies (a) for Au nanoparticle with radius R = 20 uc; (b) – the same for radius R = 50 uc. The heating–cooling conditions are the same as in Fig. 4–7. | ||
Both the frequency and the damping coefficient are influenced by the size of the nanoparticle, as evidenced by the calculation results. The frequency typically increases as nanoparticle size decreases until ∼10 nm, and then remains constant. On the contrary, for smaller nanoparticles, the damping effect often increases due to enhanced surface. The surface tension 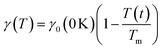 and the temperature-dependent strength limit σs(T) decrease with temperature
and the temperature-dependent strength limit σs(T) decrease with temperature 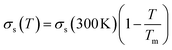 , at T < Tm. If P(t) = σs(T), stress exceeds strength limit and voids and crack may appear. The maximum strength strongly depends on the heating rate. Given that the temperature increases linearly with time at a rate
, at T < Tm. If P(t) = σs(T), stress exceeds strength limit and voids and crack may appear. The maximum strength strongly depends on the heating rate. Given that the temperature increases linearly with time at a rate 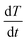 , the temperature change is
, the temperature change is 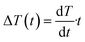 .
.
The time tm at which the temperature reaches the melting point, given the maximum temperature is 8000 K and the heating rate 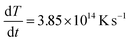 depends on nanoparticle size, and is between ∼1.3 and ∼2.6 ps for gold nanoparticles. Then additional time is required for a complete melting is required when size-dependent additional heat is required for bond breaking corresponding to the particle melting enthalpy Hm. So, the complete melting time rises with size from ∼2 to ∼8 ps. Beyond these time delays, the models of liquid nanodroplet oscillations become justified. In particular, several instabilities may occur. For instance, Rayleigh instability may take place when a liquid droplet (or a larger molten nanoparticle) becomes unstable due to the minimization of surface energy. This instability may cause the particle to break into smaller droplets. Given that the most unstable mode corresponds to a wavelength of approximately the circumference of the original droplet, the droplet typically breaks into two fragments (for n ≈ 2). Thus, the expected radius of fragments
depends on nanoparticle size, and is between ∼1.3 and ∼2.6 ps for gold nanoparticles. Then additional time is required for a complete melting is required when size-dependent additional heat is required for bond breaking corresponding to the particle melting enthalpy Hm. So, the complete melting time rises with size from ∼2 to ∼8 ps. Beyond these time delays, the models of liquid nanodroplet oscillations become justified. In particular, several instabilities may occur. For instance, Rayleigh instability may take place when a liquid droplet (or a larger molten nanoparticle) becomes unstable due to the minimization of surface energy. This instability may cause the particle to break into smaller droplets. Given that the most unstable mode corresponds to a wavelength of approximately the circumference of the original droplet, the droplet typically breaks into two fragments (for n ≈ 2). Thus, the expected radius of fragments 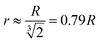 . For a gold nanoparticle with a radius R = 20 nm, the resulting fragments would each have a radius of approximately 16.1 nm, which basically agrees with the MD simulation results. This is a simplified estimation that assumes equal-sized fragments. Note that a distribution of bigger fragments and smaller clusters is obtained in both MD simulations and in common experiments.
. For a gold nanoparticle with a radius R = 20 nm, the resulting fragments would each have a radius of approximately 16.1 nm, which basically agrees with the MD simulation results. This is a simplified estimation that assumes equal-sized fragments. Note that a distribution of bigger fragments and smaller clusters is obtained in both MD simulations and in common experiments.
Furthermore, at very high energy levels and ultra-fast heating, phase explosion is known to take place. For bulk material, this limit was defined as T ∼ 0.9 Tc, where Tc is thermodynamic critical temperature of the material.70 For a nanoparticle, this would give E* ∼ 0.9 (3kTcNPN), where TcNP is thermodynamic critical temperature of nanoparticles N = (4/3) πR3ρ/M and S = 2πR2; R is the nanoparticle radius; and M is the atomic weight. The present simulation shows that super-critical energy per atom is commonly required for phase explosion of a nanoparticle. This result can be attributed to the facts that nanoparticle expand, vibrate, move, their structure and shape change. All these processes consume energy. When nanoparticle material becomes sufficiently overheated, bonds get broken, strong tensile stress leads to the expansion and nanopores nucleation due to explosive boiling and dynamic fragmentation.
3.2 Fast heating of bimetallic alloy nanoparticles
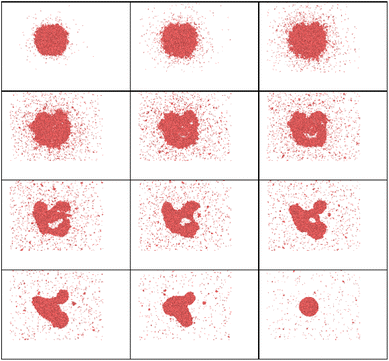
In the case of a bi-metallic particle, the above-derived criterion depends not only on the nanoparticle size, but also on its composition, as we show in the next section. In general, it should also depend on nanoparticle shape, but this is beyond the scope of this paper. In addition to monometallic nanoparticles, it is also interesting to examine the effect of atomic fractions in bimetallic alloys on the nanoparticle decay process. In this study, nanoparticles were heated to temperatures just above the fragmentation threshold. For this, we consider an intense and fast heating of AuNi nanoparticles with different initial compositions (Fig. 9). The obtained calculation results show that, at the considered border-line heating level, in some cases (small or high Ni atomic fraction) mostly surface evaporation can be observed, whereas partial particle fragmentation takes place in other cases (near equal Ni and Au atomic fractions). Therefore, the calculation results indicate that the nanoparticle is particularly stable when the Ni fraction is either small or large. However, it is easier to fragment the nanoparticle when it contains approximately 50–60% of Ni element. We note, however, that if heating level is increased, it is also possible to fragment all the particles.To understand such effects, thermodynamic phase diagrams are often employed. Detailed mono- and bi-metallic phase diagrams for nanoparticles were measured and calculated in several studies, either taking into account metastable phases, or neglecting them.63–65 We note, however, these diagrams are only suitable for equilibrium conditions71–73 and are hardly applicable for fast and strong heatings. Even though fragmentation is a strongly out-of-equilibrium process, mixing or so-called “excess” energy can still provide valuable insights, particularly regarding the composition dependency for the bi-metallic systems. For Au Ni nanoparticles, the “excess energy” was calculated (Fig. 10) based on the model presented in (ref. 63–65).
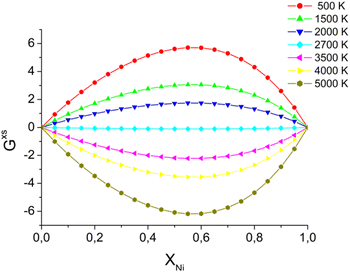 | ||
| Fig. 10 Excess energy, calculated for AuNi alloy,63–65 by using eqn (S1).† Energy units are J K−1 mol−1. | ||
3.3 Rapid heating of AuNi Janus nanoparticles and nanosatellites
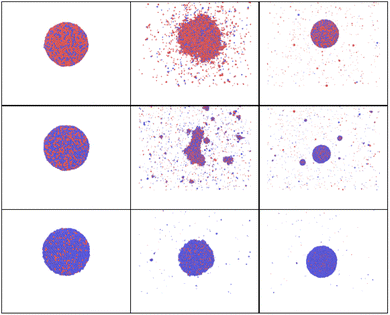
In this section, attention is focused on sintered or Janus nanoparticles. They are firstly obtained in a preliminary simulation and then heated back to room temperature before the second fast and strong heating. Such nanoparticle sintering is known to be driven by minimization of the total Gibbs free energy of the system, G. However, it is still unclear how the sintered bi-metallic nanoparticles would response to an additional fast heating: Will they be separated, destroyed or mix together? To bring more light on such processes, a series of calculations are carried out for Ni–Au Janus nanoparticles74,75 with the same sizes and rapidly heated to the same temperature following the same heating algorithm as in previous sections.The snapshots obtained in MD calculations at this maximum temperature calculation are shown in Fig. 11. The corresponding temperature evolution, potential, kinetic and total energy curves are shown in ESI, see Fig. 3S(a)† for Tmax = 2700K. The corresponding radial correlation functions are demonstrated in Fig. 12. One can see that during the heating Au and Ni nanoparticle parts start approaching, while particles start to melt. Then, surface diffusion enters into play, so that Ni atoms start covering Au core forming one larger particle at the end of the heating stage (at 20 ps).
 | ||
| Fig. 11 Snapshots obtained in the heating of Janus AuNi nanoparticles (6125 atoms, where 3061 atom of Au and 3064 of Ni) with heating shown in Fig. 3S.†Tmax = 2700 K, time delays are 0, 10, 20 ps (upper row), 50, 70, and 90 ps (bottom row), from left to right. | ||
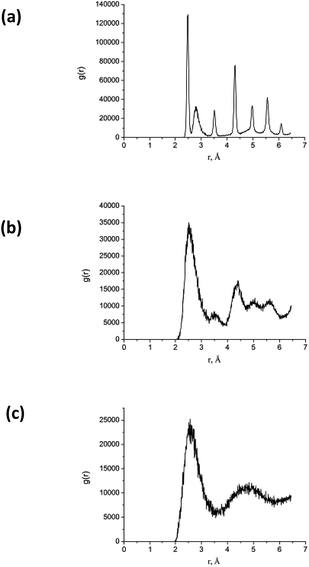 | ||
| Fig. 12 RDF calculated for the AuNi Janus nanoparticle shown in Fig. 11 at time delays (a) 0 ps, (b) – 10 ps, and (b) – 20 ps. Here, the maximum temperature Tmax = 2700 K. | ||
We note that when nanoparticles stay solid inside, the inner interatomic diffusion remains low. The final effect depends on the maximum temperature, as we will show in what follows. Furthermore, with the increase in T, kinetic energy rises here again while the value of potential energy decreases (and inversely during the cooling stage). The particle is molten at the end of the heating stage, but it remains Janus so that only partial mixing is observed (Fig. 2S ESI Mat.†).
Fast heating at sufficient energy level helps to efficiently mix Au and Ni compounds. For this, diffusion should be promoted, so that temperature should reach or overcome a certain value ∼2700 K, based on the calculated excess energy (Fig. 10). By reaching or surpassing this temperature, the increased atomic mobility allows Au and Ni atoms to interdiffuse more rapidly, leading to a more uniform alloy.
The calculated energy difference can be also used to characterize atomic mixing that can be reached (Fig. 3S in ESI Mat.†) and to indicate when the mixing barrier can be overcome.
A series of calculations are then performed for higher maximum temperatures (4000 K and 8000 K). As shown in Fig. 13 and 14, these elevated temperatures significantly enhance the mixing process. However, the mixing remains incomplete. In fact, rapid heating and the following cooling may freeze the system before complete mixing occurs, trapping the elements in a partially mixed state. Finally, the formation of stable phases or intermetallic compounds during heating could also inhibit full mixing by creating regions where further diffusion is energetically unfavorable. To balance effective alloying with structural integrity, it is crucial to identify an optimal temperature range where diffusion and mixing are maximized without causing significant particle degradation.
 | ||
| Fig. 13 Simulation snapshots for AuNi obtained at time delays t = 0, 10, 20, 50, 70 and 90 ps for Tmax = 4000 K. | ||
 | ||
| Fig. 14 Simulation snapshots for AuNi Janus NP and Tmax = 8000 K, at time t = 10, 20, 30, 50, 70, 90 ps. | ||
Fig. 14 clearly demonstrates that at high temperatures, the particle starts experiencing strong deformation. Additionally, it is partially evaporated and partly destroyed. Such high heating should be, therefore, avoided if alloying is the main objective. Thus, to enhance the nanoparticle mixing, there is a temperature window that can be chosen. In fact, temperature should be high enough to overcome diffusion and mixing barriers, but lower than the one at with nanoparticle starts to decay.
The most favorable conditions are to be determined based on the excess energy calculations and on the potential energy curves. When Tmax is larger than 2700 K as expected from the diagram shown in Fig. 8, mixing barrier vanishes. Additionally, jumps that are observed in potential energy indicate phase transitions and sintering, while energy difference is also influenced by the excess energy that is either released or consumed. Furthermore, the importance of particle sizes, and in particular, of their ratio, was previously emphasized. However, it was generally noticed that comparable sizes are more favorable for alloying. Here we have chosen such configurations because we are more interested by mixing and alloying. The other sizes and atomic fractions can be more favorable for core–shell formation and will be considered elsewhere.
In addition to Janus structures, nanoparticles often form more complex aggregates or core-satellite structures76,77 (Fig. 15) if their sizes are different. Addition fast heating of such complexes can modify them considerably promoting either alloying or core–shell formation at different energy levels, as show our MD results. If, however, only one kind of particles is heated (as in some well-targeted laser interactions), on the contrary satellite removal becomes possible. Thus, the presented results clearly demonstrate exciting possibilities that fast heating of nanoparticles provides. In this paper we did not consider surface chemistry, solvent effects, and/or molecular attachments. These processes are to be considered in separate studies.
We note, finally, that catalytic properties of small Au–Ni nanoparticles were extensively studied.78–84 Recently, in catalytic characterization by the probe reaction of semi-hydrogenation of butadiene showed that the nickel-based nanocatalysts containing a small amount of gold exhibited higher selectivity to butenes than pure nickel catalysts and a high level of activity, closer to that of pure nickel catalysts than to that of pure gold catalysts.78 It was particularly emphasized that these improved catalytic performances could come from the incorporation of Ni within the gold surface and/or from surface lattice relaxation and subsurface misfit defects. Therefore, the results of our study open particularly interesting routes for such catalytic applications. Au and Ni nanoparticles can also form core–shell bimetallic Au–Ni particles,85,86 that could be reshaped by heating, which is also promising for such applications.
4. Summary and conclusions
In conclusion, this study provides atomistic insights into the non-equilibrium dynamics of nanoparticle sintering and fragmentation under rapid and intense heating conditions through molecular dynamics (MD) simulations. The methodologies and simulation setups used offer a framework for investigating the dynamic behavior of single nanoparticles or multiple nanoparticles under fast heating conditions, enabling exploration of sintering and fragmentation processes at a detailed atomic scale.The main findings reveal distinct morphological transformations in metallic nanoparticles. Particularly, it is confirmed that partial melting of nanoparticles starts from the surface. When the added energy exceeds a critical threshold, nanoparticle fragmentation becomes prominent. The energy per atom required for this process corresponds to the superheating and the required heating rate is such that the maximum temperature is supercritical. In addition, our simulations revealed that the fragmentation threshold is highly sensitive to nanoparticle size, with smaller nanoparticles exhibiting faster fragmentation rates and more pronounced morphological changes. The study also explained the critical heating rates required to initiate these processes. Furthermore, our results demonstrated that bimetallic nanoparticles exhibit unique fragmentation behaviors compared to monometallic ones, due to the interplay between their distinct melting points and surface energies. Specifically, Au–Ni nanoparticles showed enhanced mixing and alloying under rapid heating, leading to the formation of complex, metastable structures prior to fragmentation.
We have furthermore numerically examined and analyzed the effects of fast heating on nanoparticle mixing. Specifically, diffusion, mixing and alloying are significantly enhanced in the considered regimes due to the required changes in the excess energy. Unlike the subtle morphological changes observed at slow and weak heating, the results presented here illustrate extremely pronounced non-equilibrium transformations. These findings demonstrate the capacities of molecular dynamics (MD) simulations as a powerful tool for exploring nanoscale phenomena with atomic-level detail. By accurately capturing the dynamics of nanoparticle systems under various heating conditions, MD simulations offer critical insights into the mechanisms driving sintering and fragmentation processes. This study also provides valuable information for the design and optimization of nanoparticle-based materials and devices. Understanding the dynamics of nanoparticle sintering and fragmentation is essential for controlling material properties, optimizing fabrication processes, and developing novel nanomaterials with tailored characteristics for diverse applications. The insights gained from MD simulations can also aid in analyzing experimental studies, optimizing synthesis protocols, and designing nanomaterials with enhanced performance and functionality.
Commonly, in addition to thermodynamic factors, the behavior of bimetallic materials is affected by their composition, temperature dependence of key mechanical properties, such as elastic–plastic and brittle-ductile characteristics. Chemical activities, including segregation, evaporation of the more volatile component, and the formation of chemical barriers, also play a significant role. We emphasize, finally, that in the presence of an ambient medium, such as a liquid solvent or a solid matrix, significant cooling, substantial drag force, ambient pressure, damage, bubble formation, and chemical reactions may influence the energy transfer from the particle to the medium, as well as subsequent dissipation and dynamics. During multi-pulse heating, both growth and fragmentation may occur cyclically, with fragmentation prevailing at very high supercritical fast heating. Multi-pulsed heating is also commonly used in experiments, when created atoms can nucleate into clusters again, fragments or daughter nanoparticles may coalesce or aggregate, and the process can become cyclic. These effects become significant if nanoparticle concentration is sufficiently high. All these phenomena are beyond the scope of the present study and will be addressed elsewhere.
Data availability
The data that support the findings of this study, “Understanding mono- and bi-metallic Au–Ni nanoparticle responses to fast heating” by Tatiana E. Itina, are available from the corresponding author upon reasonable request. The datasets generated and analyzed during the current study are not publicly available due to privacy but are available from the corresponding author on reasonable request.Author contributions
TEI has conceived the ideas, performed the simulations, written and edited the manuscript, and obtained funds for the project.Conflicts of interest
The author declares no conflicts of interests.Acknowledgements
The author gratefully acknowledges Dr S. Selezneva for critical reading of the manuscript. Computer support was provided by CINES of France under the project AD010814604R1.Notes and references
- Synthesis and Applications of Nanoparticles, ed. A. Thakur, P. Thakur and S. M. P. Khurana, Spinger, 2022 Search PubMed.
- I. Linkov, Nanomaterials, Springer, New York, 2008 Search PubMed.
- D. Vollath, Nanomaterials: an Introduction to Synthesis, Properties and Application, Wiley-VCH, Weinheim, 2008 Search PubMed.
- G. A. Somorjai and Y. Li, Introduction to Surface Chemistry and Catalysis, John Wiley & Sons, Inc., Hoboken, NJ, 2010 Search PubMed.
- Y. Li and G. A. Somorjai, Nanoscale advances in catalysis and energy applications, Nano Lett., 2010, 10(7), 2289–2295 CrossRef CAS.
- C. Vito, D. Forrer and V. Amendola, Recent developments in plasmonic alloy nanoparticles: synthesis, modelling, properties and applications, ChemPhysChem, 2022, 23(21), e202200136 CrossRef.
- Z. Swiatkowska-Warkocka, A. Pyatenko, F. Krok, B. R. Jany and M. Marszalek, Synthesis of new metastable nanoalloys of immiscible metals with a pulse laser technique, Sci. Rep., 2015, 5(1), 9849 CrossRef CAS.
- V. Amendola and M. Meneghetti, Laser ablation synthesis in solution and size manipulation of noble metal nanoparticles, Phys. Chem. Chem. Phys., 2009, 11(20), 3805–3821 RSC.
- G. Zhan, Y. Hong, V. T. Mbah, J. Huang, A. R. Ibrahim, M. Du and Q. Li, Bimetallic Au–Pd/MgO as efficient catalysts for aerobic oxidation of benzyl alcohol: a green bio-reducing preparation method, Appl. Catal., A, 2012, 439, 179–186 CrossRef.
- D. Zhang, B. Gokce and S. Barcikowski, Laser synthesis and processing of colloids: fundamentals and applications, Chem. Rev., 2017, 117(5), 3990–4103 CrossRef CAS PubMed.
- T. P. Otanicar, D. DeJarnette, Y. Hewakuruppu and R. A. Taylor, Filtering light with nanoparticles: a review of optically selective particles and applications, Adv. Opt. Photonics, 2016, 8(3), 541–585 CrossRef.
- A. Rudenko, K. Ladutenko, S. Makarov and T. E. Itina, Photogenerated Free Carrier-Induced Symmetry Breaking in Spherical Silicon Nanoparticle, Adv. Opt. Mater., 2018, 6(7), 1701153 CrossRef.
- J. N. Sharma, D. K. Pattadar, B. P. Mainali and F. P. Zamborini, Size determination of metal nanoparticles based on electrochemically measured surface-area-to-volume ratios, Anal. Chem., 2018, 90(15), 9308–9314 CrossRef CAS.
- X. Cui, Q. Ruan, X. Zhuo, X. Xia, J. Hu, R. Fu, Y. Li, J. Wang and H. Xu, Photothermal nanomaterials: a powerful light-to-heat converter, Chem. Rev., 2023, 123(11), 6891–6952 CrossRef CAS.
- M. Quinten, The color of finely dispersed nanoparticles, Appl. Phys. B, 2001, 73, 317–326 CrossRef CAS.
- K. Tanabe, Field enhancement around metal nanoparticles and nanoshells: a systematic investigation, J. Phys. Chem. C, 2008, 112(40), 15721–15728 CrossRef CAS.
- L. Wang, L. Xu, H. Kuang, C. Xu and N. A. Kotov, Dynamic nanoparticle assemblies, Acc. Chem. Res., 2012, 45(11), 1916–1926 CrossRef CAS PubMed.
- H. Zhou, F. Zou, K. Koh and J. Lee, Multifunctional magnetoplasmonic nanomaterials and their biomedical applications, J. Biomed. Nanotechnol., 2014, 10(10), 2921–2949 CrossRef CAS.
- M. Lattuada and T. A. Hatton, Synthesis, properties and applications of Janus nanoparticles, Nano Today, 2011, 6(3), 286–308 CrossRef CAS.
- J. H. Yoon, J. Lim and S. Yoon, Controlled assembly and plasmonic properties of asymmetric core–satellite nanoassemblies, ACS Nano, 2012, 6(8), 7199–7208 CrossRef CAS.
- H. You, S. Yang, B. Ding and H. Yang, Synthesis of colloidal metal and metal alloy nanoparticles for electrochemical energy applications, Chem. Soc. Rev., 2013, 42(7), 2880–2904 RSC.
- M. L. Eggersdorfer and S. E. Pratsinis, Agglomerates and aggregates of nanoparticles made in the gas phase, Adv. Powder Technol., 2014, 25(1), 71–90 CrossRef CAS.
- E. Goudeli, Nanoparticle growth, coalescence, and phase change in the gas-phase by molecular dynamics, Curr. Opin. Chem. Eng., 2019, 23, 155–163 CrossRef.
- S. Iravani, H. Korbekandi, S. V. Mirmohammadi and B. Zolfaghari, Synthesis of silver nanoparticles: chemical, physical and biological methods, Res. Pharm. Sci., 2014, 9(6), 385–406 CAS.
- A. H. Hamad, Effects of Different Laser Pulse Regimes (Nanosecond, Picosecond and Femtosecond) on the Ablation of Materials for Production of Nanoparticles in Liquid Solution, IntechOpen, London, UK, 2016, p. 21 Search PubMed.
- D. B. Geohegan, A. A. Puretzky, G. Duscher and S. J. Pennycook, Time-resolved imaging of gas phase nanoparticle synthesis by laser ablation, Appl. Phys. Lett., 1998, 72(23), 2987–2989 CrossRef CAS.
- S. Barcikowski and G. Compagnini, Advanced nanoparticle generation and excitation by lasers in liquids, Phys. Chem. Chem. Phys., 2013, 15(9), 3022–3026 RSC.
- P. Pohl, Plasma-Based Synthesis and Modification of Nanomaterials, Nanomaterials, 2019, 9(2), 278 CrossRef CAS.
- I. Adamovich, S. D. Baalrud, A. Bogaerts, P. J. Bruggeman, M. Cappelli, V. Colombo, U. Czarnetzki, U. Ebert, J. G. Eden, P. Favia and A. Vardelle, The 2017 Plasma Roadmap: Low temperature plasma science and technology, J. Phys. D: Appl. Phys., 2017, 50(32), 323001 CrossRef.
- T. Belmonte, A. V. Nominé, C. Noël, T. Gries, A. Nominé, V. Milichko, M. Belmahi and M. Y. Awaji, Submerged discharges in liquids for nanoobject synthesis: expectations and capabilities, Plasma Chem. Plasma Process., 2023, 1–56 Search PubMed.
- P. Tian, Molecular dynamics simulations of nanoparticles, Annu. Rep. Prog. Chem. Sect. C Phys. Chem., 2008, 104, 142–164 RSC.
- M. R. Zachariah and M. J. Carrier, Molecular dynamics computation of gas-phase nanoparticle sintering: a comparison with phenomenological models, J. Aerosol Sci., 1999, 30(9), 1139–1151 CrossRef CAS.
- D. Bhandary, V. Valechi, M. N. D. Cordeiro and J. K. Singh, Janus gold nanoparticles from nanodroplets of alkyl thiols: a molecular dynamics study, Langmuir, 2017, 33(12), 3056–3067 CrossRef CAS PubMed.
- V. M. Samsonov, I. V. Talyzin, V. V. Puytov, S. A. Vasilyev, A. A. Romanov and M. I. Alymov, When mechanisms of coalescence and sintering at the nanoscale fundamentally differ: Molecular dynamics study, J. Chem. Phys., 2022, 156(21), 214302 CrossRef CAS PubMed.
- M. D. Manning, A. L. Kwansa, T. Oweida, J. S. Peerless, A. Singh and Y. G. Yingling, Progress in ligand design for monolayer-protected nanoparticles for nanobio interfaces, Biointerphases, 2018, 13(6), 06D502 CrossRef CAS PubMed.
- M. S. Shakeri, Z. Swiatkowska-Warkocka, O. Polit, T. Itina, A. Maximenko, J. Depciuch, J. Gurgul, M. Mitura-Nowak, M. Perzanowski, A. Dziedzic and J. Nęcki, Alternative Local Melting-Solidification of Suspended Nanoparticles for Heterostructure Formation Enabled by Pulsed Laser Irradiation, Adv. Funct. Mater., 2023, 33(43), 2304359 CrossRef CAS.
- A. Plech, M. Tack, H. Huang, M. Arefev, A. R. Ziefuss, M. Levantino, H. Karadas, C. Chen, L. V. Zhigilei and S. Reichenberger, Physical Regimes and Mechanisms of Picosecond Laser Fragmentation of Gold Nanoparticles in Water from X-ray Probing and Atomistic Simulations, ACS Nano, 2024, 18(15), 10527–10541 CrossRef CAS PubMed.
- R. Fahdiran and H. M. Urbassek, Ultrafast laser irradiation of spherical nanoparticles: Molecular-dynamics results on fragmentation and small-angle scattering, Eur. Phys. J. D, 2015, 69, 1–7 CrossRef CAS.
- T. E. Itina, L. V. Zhigilei and B. J. Garrison, Matrix-assisted pulsed laser evaporation of polymeric materials: a molecular dynamics study, Nucl. Instrum. Methods Phys. Res., Sect. B, 2001, 180(1–4), 238–244 CrossRef CAS.
- K. Gouriet, M. Sentis and T. E. Itina, Molecular dynamics study of nanoparticle evaporation and condensation in a gas, J. Phys. Chem. C, 2009, 113(43), 18462–18467 CrossRef CAS.
- L. Delfour and T. E. Itina, Mechanisms of ultrashort laser-induced fragmentation of metal nanoparticles in liquids: numerical insights, J. Phys. Chem. C, 2015, 119(24), 13893–13900 CrossRef CAS.
- S. Noël, J. Hermann and T. Itina, Investigation of nanoparticle generation during femtosecond laser ablation of metals, Appl. Surf. Sci., 2007, 253(15), 6310–6315 CrossRef.
- J. Hermann, S. Noël, T. E. Itina, E. Axente and M. E. Povarnitsyn, Correlation between ablation efficiency and nanoparticle generation during the short-pulse laser ablation of metals, Laser Phys., 2008, 18, 374–379 CrossRef CAS.
- D. Werner, S. Hashimoto, T. Tomita, S. Matsuo and Y. Makita, In-situ spectroscopic measurements of laser ablation-induced splitting and agglomeration of metal nanoparticles in solution, J. Phys. Chem. C, 2008, 112(43), 16801–16808 CrossRef CAS.
- D. Werner, A. Furube, T. Okamoto and S. Hashimoto, Femtosecond laser-induced size reduction of aqueous gold nanoparticles: In situ and pump− probe spectroscopy investigations revealing Coulomb explosion, J. Phys. Chem. C, 2011, 115(17), 8503–8512 CrossRef CAS.
- K. Maximova, A. Aristov, M. Sentis and A. V. Kabashin, Size-controllable synthesis of bare gold nanoparticles by femtosecond laser fragmentation in water, Nanotechnology, 2015, 26(6), 065601 CrossRef CAS.
- M. M. Martynyuk, Phase explosion of a metastable fluid, Combust., Explos. Shock Waves, 1977, 13(2), 178–191 CrossRef.
- M. V. Shugaev, M. He, Y. Levy, A. Mazzi, A. Miotello, N. M. Bulgakova and L. V. Zhigilei, Laser-induced thermal processes: heat transfer, generation of stresses, melting and solidification, vaporization, and phase explosion, Handbook of Laser Micro-and Nano-Engineering, Springer International Publishing, Cham, 2021, pp. 83–163 Search PubMed.
- M. E. Povarnitsyn, T. E. Itina, M. Sentis, K. V. Khishchenko and P. R. Levashov, Material decomposition mechanisms in femtosecond laser interactions with metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75(23), 235414 CrossRef.
- D. Frenkel and B. Smit, Understanding Molecular Simulation: from Algorithms to Applications, Elsevier, 2023 Search PubMed.
- R. A. Johnson, Alloy models with the embedded-atom method, Phys. Rev. B: Condens. Matter Mater. Phys., 1989, 39(17), 12554 CrossRef PubMed.
- R. Freitas, M. Asta and M. De Koning, Nonequilibrium free-energy calculation of solids using LAMMPS, Comput. Mater. Sci., 2016, 112, 333–341 CrossRef CAS.
- A. Maulana, A. Arkundato, S. Sutisna and H. Trilaksana, Mechanical properties of Fe, Ni and Fe-Ni alloy: Strength and stiffness of materials using lammps molecular dynamics simulation, AIP Conf. Proc., 2020, 2314(1), 020008 CrossRef CAS.
- D. S. Ivanov and L. V. Zhigilei, Combined atomistic-continuum modeling of short-pulse laser melting and disintegration of metal films, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 68(6), 064114 CrossRef.
- H. Grubmüller, H. Heller, A. Windemuth and K. Schulten, Generalized Verlet algorithm for efficient molecular dynamics simulations with long-range interactions, Mol. Simul., 1991, 6(1–3), 121–142 CrossRef.
- LAMMPS Stands for Large-Scale Atomic/Molecular Massively Parallel Simulator. Copyright, Sandia Corporation, 2003 Search PubMed.
- M. Krief and Y. Ashkenazy, Calculation of elastic constants of embedded-atom-model potentials in the NVT ensemble, Phys. Rev. E, 2021, 103(6), 063307 CrossRef CAS.
- J. Sun and S. L. Simon, The melting behavior of aluminum nanoparticles, Thermochim. Acta, 2007, 463(1–2), 32–40 CrossRef CAS.
- M. V. Kharlamova, Investigation of growth dynamics of carbon nanotubes, Beilstein J. Nanotechnol., 2017, 8(1), 826–856 CrossRef CAS.
- A. van Teijlingen, S. A. Davis and S. R. Hall, Size-dependent melting point depression of nickel nanoparticles, Nanoscale Adv., 2020, 2(6), 2347–2351 RSC.
- M. E. Povarnitsyn, T. E. Itina, R. P. Levashov and K. V. Khishchenko, Mechanisms of nanoparticle formation by ultra-short laser ablation of metals in liquid environment, Phys. Chem. Chem. Phys., 2013, 15(9), 3108–3114 RSC.
- M. E. Povarnitsyn, V. B. Fokin, P. R. Levashov and T. E. Itina, Molecular dynamics simulation of subpicosecond double-pulse laser ablation of metals, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92(17), 174104 CrossRef.
- S. Bogatyrenko, A. Kryshtal, A. Minenkov and A. Kruk, Miscibility gap narrowing on the phase diagram of AuNi nanoparticles, Scr. Mater., 2019, 170, 57–61 CrossRef CAS.
- H. Okamoto, Phase Diagrams for Binary Alloys, ASM International, 2000, p. 828 Search PubMed.
- J. Sopoušek, A. Kryštofová, M. Premović, O. Zobač, S. Polsterová, P. Brož and J. Buršík, Au-Ni nanoparticles: Phase diagram prediction, synthesis, characterization, and thermal stability, Calphad, 2017, 58, 25–33 CrossRef.
- A. F. Thunemann, S. Rolf, P. Knappe and S. Weidner, In situ analysis of a bimodal size distribution of superparamagnetic nanoparticles, Anal. Chem., 2009, 81(1), 296–301 CrossRef CAS.
- C. Y. Shih, R. Streubel, J. Heberle, A. Letzel, M. V. Shugaev, C. Wu and L. V. Zhigilei, Two mechanisms of nanoparticle generation in picosecond laser ablation in liquids: the origin of the bimodal size distribution, Nanoscale, 2018, 10(15), 6900–6910 RSC.
- T. E. Glover, Hydrodynamics of particle formation following femtosecond laser ablation, J. Opt. Soc. Am. B, 2003, 20(1), 125–131 CrossRef CAS.
- D. E. Grady and M. E. Kipp, Mechanisms of dynamic fragmentation: factors governing fragment size, Mech. Mater., 1985, 4(3–4), 311–320 CrossRef.
- B. J. Garrison, T. E. Itina and L. V. Zhigilei, Limit of overheating and the threshold behavior in laser ablation, Phys. Rev. E, 2003, 68(4), 041501 CrossRef.
- F. Pittaway, L. O. Paz-Borbón, R. L. Johnston, H. Arslan, R. Ferrando, C. Mottet, G. Barcaro and A. Fortunelli, Theoretical studies of palladium− gold nanoclusters: Pd− Au clusters with up to 50 atoms, J. Phys. Chem. C, 2009, 113(21), 9141–9152 CrossRef CAS.
- R. Ferrando, Determining the equilibrium structures of nanoalloys by computational methods, J. Nanopart. Res., 2018, 20(7), 179 CrossRef.
- H. Peng, W. Qi, S. Li and W. Ji, Modeling the phase stability of Janus, core–shell, and alloyed Ag–Cu and Ag–Au nanoparticles, J. Phys. Chem. C, 2015, 119(4), 2186–2195 CrossRef CAS.
- H. Wang, D. Liu and C. Xu, Directed synthesis of well dispersed and highly active AuCu and AuNi nanoparticle catalysts, Catal. Sci. Technol., 2016, 6(19), 7137–7150 RSC.
- R. Brayner, T. Coradin, M. J. Vaulay, C. Mangeney, J. Livage and F. Fiévet, Preparation and characterization of metal (Au)–and bimetallic alloys (AuNi)–gelatin nanocomposites, Colloids Surf., A, 2005, 256(2–3), 191–197 CrossRef CAS.
- J. Li, Q. L. Zhu and Q. Xu, Non-noble bimetallic CuCo nanoparticles encapsulated in the pores of metal–organic frameworks: synergetic catalysis in the hydrolysis of ammonia borane for hydrogen generation, Catal. Sci. Technol., 2015, 5(1), 525–530 RSC.
- A. A. Popov, Z. Swiatkowska-Warkocka, M. Marszalek, G. Tselikov, I. V. Zelepukin, A. Al-Kattan, S. M. Deyev, S. M. Klimentov, T. E. Itina and A. V. Kabashin, Laser-ablative synthesis of ultrapure magneto-plasmonic core-satellite nanocomposites for biomedical applications, Nanomaterials, 2022, 12(4), 649 CrossRef CAS.
- J. Reboul, Z. Y. Li, J. Yuan, K. Nakatsuka, M. Saito, K. Mori, H. Yanashita, Y. Xia and C. Louis, Synthesis of small Ni-core–Au-shell catalytic nanoparticles on TiO 2 by galvanic replacement reaction, Nanoscale Adv., 2021, 3(3), 823–835 RSC.
- M. A. Keane, S. Gomez-Quero, F. Cardenas-Lizana and W. Shen, Alumina-Supported Ni-Au: Surface Synergistic Effects in Catalytic Hydrodechlorination, ChemCatChem, 2009, 1(2), 270–278 CrossRef CAS.
- G. Yuan, C. Louis, L. Delannoy and M. A. Keane, Silica- and titania-supported Ni-Au: Application in catalytic hydrodechlorination, J. Catal., 2007, 247(2), 256–268 CrossRef CAS.
- Z. Wu, Z. Zhao and M. Zhang, Synthesis by Replacement Reaction and Application of TiO2-Supported Au-Ni Bimetallic Catalyst, ChemCatChem, 2010, 2(12), 1606–1614 CrossRef CAS.
- F. Cardenas-Lizana, S. Gomez-Quero, G. Jacobs, Y. Ji, B. H. Davis, L. Kiwi-Minsker and M. A. Keane, Alumina Supported Au-Ni: Surface Synergism in the Gas Phase Hydrogenation of Nitro-Compounds, J. Phys. Chem. C, 2012, 116(20), 11166–11180 CrossRef CAS.
- F. Cardenas-Lizana and M. A. Keane, Gas phase selective hydrogenation over oxide supported Ni-Au, Phys. Chem. Chem. Phys., 2015, 17(42), 28088–28095 RSC.
- H. Wei, X. Wei, X. Yang, G. Yin, A. Wang, X. Liu, Y. Huang and T. Zhang, Supported Au-Ni nano-alloy catalysts for the chemoselective hydrogenation of nitroarenes, Cuihua Xuebao, 2015, 36(2), 160–167 CAS.
- X. Zhang, S. Han and B. Zhu, et al., Reversible loss of core–shell structure for Ni–Au bimetallic nanoparticles during CO2 hydrogenation, Nat. Catal., 2020, 3, 411–417 CrossRef CAS.
- Z. Zhao, H. Xu, Y. Gao and D. Cheng, Universal description of heating-induced reshaping preference of core–shell bimetallic nanoparticles, Nanoscale, 2019, 11(3), 1386–1395 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00634h |
| This journal is © The Royal Society of Chemistry 2024 |