Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Efficient spin filtering through Fe4GeTe2-based van der Waals heterostructures†
Masoumeh
Davoudiniya
and
Biplab
Sanyal
 *
*
Department of Physics and Astronomy, Uppsala University, Sweden. E-mail: Biplab.Sanyal@physics.uu.se
First published on 9th October 2024
Abstract
Utilizing ab initio simulations, we study the spin-dependent electronic transport characteristics within Fe4GeTe2-based van der Waals heterostructures. The electronic density of states for both free-standing and device-configured Fe4GeTe2 (F4GT) confirms its ferromagnetic metallic nature and reveals a weak interface interaction between F4GT and PtTe2 electrodes, enabling efficient spin filtering. The ballistic transport through a double-layer F4GT with a ferromagnetic configuration sandwiched between two PtTe2 electrodes is predicted to exhibit an impressive spin polarization of 97% with spin-up electrons exhibiting higher transmission probability than spin-down electrons. Moreover, we investigate the spin transport properties of Fe4GeTe2/GaTe/Fe4GeTe2 van der Waals heterostructures sandwiched between PtTe2 electrodes to explore their potential as magnetic tunnel junctions in spintronic devices. The inclusion of monolayer GaTe as a 2D semiconducting spacer between F4GT layers results in a tunnel magnetoresistance of 487% at a low bias and decreases with increasing bias voltage. Overall, our findings underscore the potential of F4GT/GaTe/F4GT heterostructures in advancing spintronic devices based on van der Waals materials.
1 Introduction
Quantum transport through two-dimensional (2D) magnetic structures has emerged as a fascinating field of research with promising implications for spintronics.1–7 Spintronic aims to harness both the charge and spin degrees of freedom to enable the development of novel electronic devices with enhanced functionalities. Moreover, 2D magnetic structures, such as atomically thin ferromagnetic films and magnetic heterostructures, possess distinct spin-dependent properties that enable efficient control and manipulation of electron spins. Understanding spin transport in these systems is crucial for the development of spin-based electronic devices and spintronic circuits. Historically, most magnetic tunnel junctions (MTJs) were constructed using perovskite-oxide materials. However, these conventional MTJs have limitations, notably a large resistance-area product, which restricts their practicality in device applications.8 In contrast, van der Waals (vdW) materials have shown promise in overcoming the challenges associated with traditional magnetic thin films. They lead to significantly high tunnel magnetoresistance (TMR) values, as evidenced by numerous experimental studies.9–14 The vdW heterostructures, composed of atomically thin layers stacked on top of each other, have emerged as promising platforms to explore and exploit such quantum transport phenomena.2,15–23 The weak vdW forces facilitate the formation of a clean and atomically sharp interface between layers, enabling efficient transfer of spin-polarized electrons between the magnetic materials.Recent discoveries of FenGeTe2 (n = 3, 4, 5) (FGT), a class of 2D itinerant ferromagnets with a Curie temperature approaching room temperature, provide exciting prospects for 2D spintronic advancements.24–27 A comparative study of FGT family has been done in ref. 28 with the aid of ab initio calculations. FGT exhibits a notable advantage stemming from its metallic nature, which facilitates the manipulation of both electronic spin and charge. Furthermore, FGT has been suggested as a rare-earth-free material with strong magnetism and electronic correlation.29 Recent experimental reports have confirmed that the tunneling resistance behavior in hBN sandwiched between two Fe3GeTe2(F3GT) layers follows established patterns, exhibiting minimum (maximum) resistance when the magnetizations of the electrodes are parallel (antiparallel). Remarkably, a significant magnetoresistance of 160% is observed at low temperatures, indicating a spin polarization of 0.66 in F3GT.18 Moreover, the formation of ohmic contacts in F3GT/MoS2 interfaces is confirmed by linear current–voltage curves, indicating a conducting layer rather than a tunneling one. This is a positive result as ohmic contacts enable efficient charge transport with minimal resistance, whereas tunneling contacts can obstruct current flow and reduce device performance. It has been also observed that magnetoresistance of F3GT/MoS2/F3GT heterostructures reaches 3.1% at 10 K, which is approximately 8 times larger than conventional spin valves with MoS2 and conventional ferromagnetic electrodes.30 While F3GT has been extensively explored, the focus on Fe4GeTe2 (F4GT) has been relatively limited, despite its higher Curie temperature, making it a promising avenue for further research.31 Investigating F4GT can provide valuable insights into its exceptional electronic, magnetic, and structural properties. By understanding the distinctive characteristics of F4GT, one can unlock its potential for technological applications such as spintronics, magnetic storage, and other advanced electronic devices. FGT-based heterostructures are highly promising for spintronic devices due to their strong spin-filtering and spin polarization, making them ideal for MTJs and spin valves, which are critical components in advanced non-volatile memory technologies like magnetoresistive random access memory (MRAM).5,11,32,33 The tunable magnetic properties and spin–orbit coupling in the FGT family also enhance their use in spin–orbit torque devices, enabling efficient, high-speed magnetic switching for logic and memory applications.34 These materials are valuable in quantum computing as spin filters, facilitating selective spin transmission essential for spin-based quantum gates and complex computing systems. Moreover, FGT's high sensitivity to magnetic fields makes it useful for magnetic sensors and detectors, boosting performance in automotive, aerospace, and other industrial technologies.35
Here, the nonequilibrium Green's function (NEGF) formalism and ab initio simulations were utilized to analyze the transport characteristics of vdW heterostructures consisting of F4GT. This approach is a robust method for studying ballistic transmission across ultrathin magnetic films.2,36–46 The focus of this study is also on investigating the electronic and magnetic properties of these heterostructures. Specifically, we investigated spin-dependent ballistic transport in both mono- and bi-layer F4GT structures that were sandwiched between PtTe2 electrodes. To assess the tunneling magnetoresistance behavior, we analyzed the spin-dependent electronic transport across F4GT/GaTe/F4GT junctions, connected to PtTe2 electrodes, serving as vdW MTJs.
2 Methodology
We employed the QuantumATK software package47 to investigate quantum transport properties. The calculations involved the combination of density functional theory (DFT) and the NEGF formalism. The DFT calculations were carried out using the generalized gradient approximation (GGA) to describe the exchange–correlation functional. We obtained the electronic band structure and density of states (DOS) of F4GT to gain insights into its electronic properties. Realistic device structures, including the scattering region and leads, were constructed to simulate the transport properties. The NEGF formalism was employed to calculate the transmission spectra and current–voltage characteristics of the F4GT-based devices under external biases. To accurately account for vdW interactions, we applied the DFT-D3 method with Becke–Jonson damping.48,49 Structural relaxations were performed using the linear combination of atomic orbitals (LCAO) basis set with PseudoDojo for pseudopotentials. A Monkhorst–Pack grid of 14 × 14 × 1 has been used and a cutoff density of 140 hartree was chosen to ensure convergence. Moreover, a force tolerance of 10−3 eV Å−1 was used for relaxations. Convergence was achieved when the total energy difference between consecutive steps was below 10−4 eV. The source and drain electrodes were set to a length of 10.402 Å, and the same LCAO settings were applied for the quantum transport simulations. For the gate-all-around (GAA) structure, the Poisson solver utilized the Dirichlet boundary condition in all directions. We utilized a Monkhorst–Pack grid with dimensions of 16 × 16 × 1 to assess the transmission and current. To maintain reasonable simulation times, the parallel conjugate gradient method was employed. To calculate the magnetocrystalline anisotropy energy (MAE), we included spin–orbit coupling (SOC) using a full k-point grid, and the Brillouin zone integration was performed using a 55× 55 × 1 Γ-centered Monkhorst–Pack grid. Moreover, previous studies28 have demonstrated that GGA + U calculations are incompatible with experimental results for FGT materials. This incompatibility extends to parameters such as unit cell dimensions, magnetic moments, magnetic anisotropy energy, and transition temperature. Consequently, utilizing static electron correlation is not suitable for accurately characterizing a metallic magnet like FGT. Therefore, we have neglected the Hubbard U correction in our calculations.The spin-dependent transmission coefficient was determined using Green's functions, as expressed by the following equation50
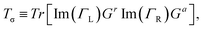 | (1) |
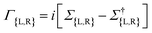 is the line width function and ΣL(R) in the equation corresponds to the retarded self-energy of the left (right) electrode, representing the coupling between the central region and the semi-infinite leads. This term accounts for the interaction and exchange of electrons between the central region and the electrodes. The Gr(a) term refers to the retarded (advanced) Green's function matrices, which describe the propagation of electrons through the system in the spin and orbital spaces.
is the line width function and ΣL(R) in the equation corresponds to the retarded self-energy of the left (right) electrode, representing the coupling between the central region and the semi-infinite leads. This term accounts for the interaction and exchange of electrons between the central region and the electrodes. The Gr(a) term refers to the retarded (advanced) Green's function matrices, which describe the propagation of electrons through the system in the spin and orbital spaces.
To find the transmission eigenstates, we utilize a linear combination of Bloch states, ∑neαnψn, with coefficients eαn that diagonalize the transmission matrix. This transmission matrix is mathematically defined as
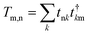 | (2) |
To calculate the spin-dependent tunneling current, the Landauer–Büttiker formula was employed,51
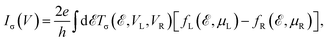 | (3) |
The tunneling current is determined by the electrochemical potentials μL(μR), Fermi distribution functions fL(fR), and bias voltages VL(VR) applied to the left (right) lead at room temperature. The transmission coefficient 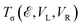 is energy-dependent and varies with the bias voltages and energy of the system. In the calculations of current for the device mentioned in this paper, we used a voltage-dependent transmission function. This means the transmission function is evaluated at each bias voltage, taking into account the changes in electronic structure and transmission properties under finite bias. This approach ensures that the calculated current accurately reflects the influence of the applied voltage, rather than relying on the zero-bias transmission function. We performed the current calculations at room temperature (300 K). For the transmission and electric current calculations, the cross-sectional area of the device is defined as the transverse unit cell area, which is perpendicular to the direction of electron transport. We report the total transmission and electric current for each spin channel, indicating that the current density is multiplied by this cross-sectional area.
is energy-dependent and varies with the bias voltages and energy of the system. In the calculations of current for the device mentioned in this paper, we used a voltage-dependent transmission function. This means the transmission function is evaluated at each bias voltage, taking into account the changes in electronic structure and transmission properties under finite bias. This approach ensures that the calculated current accurately reflects the influence of the applied voltage, rather than relying on the zero-bias transmission function. We performed the current calculations at room temperature (300 K). For the transmission and electric current calculations, the cross-sectional area of the device is defined as the transverse unit cell area, which is perpendicular to the direction of electron transport. We report the total transmission and electric current for each spin channel, indicating that the current density is multiplied by this cross-sectional area.
3 Results and discussion
3.1 Characterization of PtTe2/F4GT/PtTe2 heterostructure
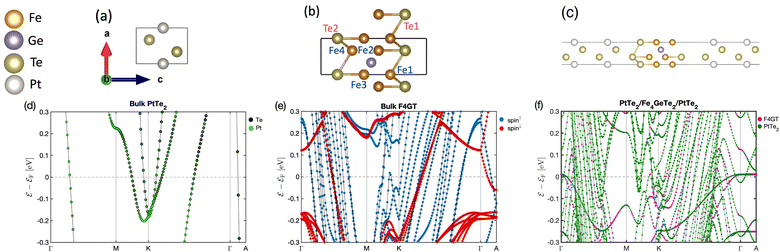
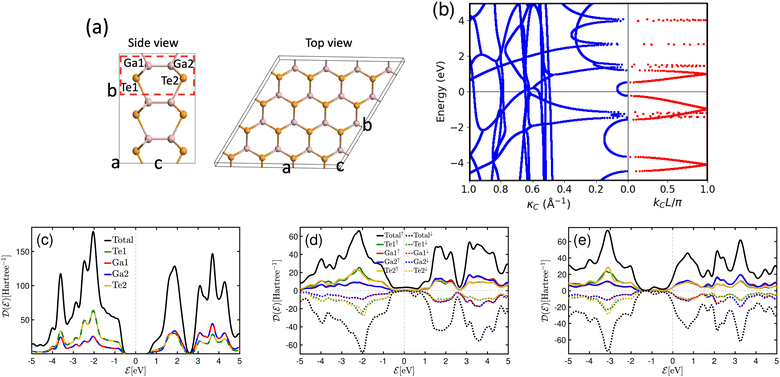
The unit cell of PtTe2 is depicted in Fig. 1a. It possesses a layered crystal structure within the trigonal space group P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1.52 The structure comprises Pt atoms situated between two layers of Te atoms. The stacking of these layers repeats in a hexagonal pattern along the c-axis, generating a three-dimensional structure. The interlayer interactions are governed by weak vdW forces. The lattice constants obtained using the GGA functional are a = b = 4.01 Å and c = 5.201 Å. Fig. 1b indicates the layered crystal structure of F4GT, which shares the same space group (P
m1.52 The structure comprises Pt atoms situated between two layers of Te atoms. The stacking of these layers repeats in a hexagonal pattern along the c-axis, generating a three-dimensional structure. The interlayer interactions are governed by weak vdW forces. The lattice constants obtained using the GGA functional are a = b = 4.01 Å and c = 5.201 Å. Fig. 1b indicates the layered crystal structure of F4GT, which shares the same space group (P![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m1) as PtTe2.53 Each layer consists of four Fe atoms surrounded by Ge and Te atoms. The Ge and Te atoms form a distorted hexagonal lattice, with the Fe atoms occupying the centers of distorted octahedra formed by the coordination with Ge and Te. Magnetic moment of Fe1 (Fe4) and Fe2 (Fe3) have been calculated to be 2.72 μB and 1.71 μB, respectively, which is in good agreement with ref. 54. The calculated lattice constant of F4GT is found to be a = b = 3.968 Å, which is remarkably close to the lattice constant of PtTe2. This similarity in lattice constants suggests a strong structural resemblance between F4GT and PtTe2, indicating potential similarities in their crystal structures and bonding arrangements. We initiate our investigation by examining a two-probe system consisting of a single-layer F4GT situated between two PtTe2 electrodes (Fig. 1c). In this setup, the F4GT layer is subjected to a tensile strain of 0.7%. The distance between the Te atoms on the surface of F4GT and the surface layer of PtTe2 is approximately 2.88 Å. This distance is larger than the interlayer distances in bulk PtTe2, which is around 2.33 Å, and smaller than the interlayer distances in bulk F4GT, which is approximately 3.28 Å. Moreover, in the device configuration, the magnetic moment of Fe1 and Fe4 remains unchanged at 2.72 μB. However, the magnetic moment of Fe2 and Fe3 slightly increases to 1.81 μB.
m1) as PtTe2.53 Each layer consists of four Fe atoms surrounded by Ge and Te atoms. The Ge and Te atoms form a distorted hexagonal lattice, with the Fe atoms occupying the centers of distorted octahedra formed by the coordination with Ge and Te. Magnetic moment of Fe1 (Fe4) and Fe2 (Fe3) have been calculated to be 2.72 μB and 1.71 μB, respectively, which is in good agreement with ref. 54. The calculated lattice constant of F4GT is found to be a = b = 3.968 Å, which is remarkably close to the lattice constant of PtTe2. This similarity in lattice constants suggests a strong structural resemblance between F4GT and PtTe2, indicating potential similarities in their crystal structures and bonding arrangements. We initiate our investigation by examining a two-probe system consisting of a single-layer F4GT situated between two PtTe2 electrodes (Fig. 1c). In this setup, the F4GT layer is subjected to a tensile strain of 0.7%. The distance between the Te atoms on the surface of F4GT and the surface layer of PtTe2 is approximately 2.88 Å. This distance is larger than the interlayer distances in bulk PtTe2, which is around 2.33 Å, and smaller than the interlayer distances in bulk F4GT, which is approximately 3.28 Å. Moreover, in the device configuration, the magnetic moment of Fe1 and Fe4 remains unchanged at 2.72 μB. However, the magnetic moment of Fe2 and Fe3 slightly increases to 1.81 μB.
Fig. 1d displays the atom-projected band structure plots of the monolayer PtTe2. Additionally, Fig. 1e presents the spin-polarized bands of F4GT, while Fig. 1f shows bands projected onto both the total F4GT layer and the PtTe2 layer of the PtTe2/F4GT/PtTe2 system. The band structure analysis reveals that both monolayer PtTe2 and F4GT exhibit metallic behavior. In the case of F4GT, the states around the Fermi level are primarily dominated by the spin-up channel, accompanied by a smaller contribution from the spin-down channel. As observed in Fig. 1f of the weight-projected band structure plot, numerous bands intersect and cross the Fermi level. These crossing points indicate the presence of potential conductance channels within the device configuration. The majority of states near the Fermi level originate from Te and Pt atoms from PtTe2 layers. This difference can be attributed to the larger number of Te and Pt atoms present in the electrodes of the device, leading to a higher contribution from these elements to the electronic states near the Fermi level. Furthermore, upon closer examination near the Fermi level at the M and K points (see Fig. 1f), it is evident that the F4GT bands in the device configuration exhibit minimal changes compared to the isolated F4GT (see Fig. 1e). This observation suggests a weak vdW interaction at the interface between F4GT and the electrodes. The relatively unchanged Fe bands indicate that the electronic structure of F4GT is preserved within the device, implying that the interface interaction does not significantly affect the Fe electronic states.
The spin-polarized DOS calculations were performed to investigate the spin-dependent electronic properties of the monolayer F4GT (a) and the F4GT sandwiched between two PtTe2 electrodes (b), as shown in Fig. 2. Panel (a) reveals a significant electron density at the Fermi level 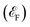 with an exchange splitting, indicating the ferromagnetic nature of F4GT. This finding is consistent with previous ab initio calculations.55 The states near the Fermi level are primarily dominated by the Fe atoms in F4GT, contributing to the majority spin channel. The orbital-decomposed d-band DOS for the 3d orbitals of Fe atoms in a freestanding monolayer of F4GT, shown in Fig. S1,† reveals significant contributions at the Fermi level. The dxz and dz2 orbitals exhibit pronounced spin-split peaks near the Fermi level, with the spin-up states being more prominent than the spin-down states. The dxy orbitals also contribute, though less significantly. In panel (b), the DOS plot showcases the impact of the PtTe2 layers on the electronic states of the F4GT sandwiched structure. It is observed that the redistribution and shifting of the electronic states in the Fe atoms are relatively unchanged, indicating a weak interaction between the F4GT and PtTe2 layers. This suggests that the electronic properties of F4GT remain largely preserved within the device configuration. Furthermore, the DOS values from panel (b) highlight the spin filtering mechanism of the device configuration. The electronic states at
with an exchange splitting, indicating the ferromagnetic nature of F4GT. This finding is consistent with previous ab initio calculations.55 The states near the Fermi level are primarily dominated by the Fe atoms in F4GT, contributing to the majority spin channel. The orbital-decomposed d-band DOS for the 3d orbitals of Fe atoms in a freestanding monolayer of F4GT, shown in Fig. S1,† reveals significant contributions at the Fermi level. The dxz and dz2 orbitals exhibit pronounced spin-split peaks near the Fermi level, with the spin-up states being more prominent than the spin-down states. The dxy orbitals also contribute, though less significantly. In panel (b), the DOS plot showcases the impact of the PtTe2 layers on the electronic states of the F4GT sandwiched structure. It is observed that the redistribution and shifting of the electronic states in the Fe atoms are relatively unchanged, indicating a weak interaction between the F4GT and PtTe2 layers. This suggests that the electronic properties of F4GT remain largely preserved within the device configuration. Furthermore, the DOS values from panel (b) highlight the spin filtering mechanism of the device configuration. The electronic states at 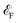 in the majority spin channel are more abundant compared to the minority spin channel. This indicates the potential for spin-polarized currents when a bias voltage is applied to the device.
in the majority spin channel are more abundant compared to the minority spin channel. This indicates the potential for spin-polarized currents when a bias voltage is applied to the device.
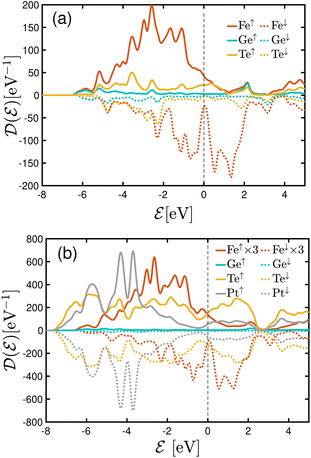 | ||
| Fig. 2 DOS plots for (a) the freestanding monolayer F4GT and (b) the F4GT sandwiched between two layers of PtTe2. | ||
To assess the impact of SOC on the transport properties of the device, we have calculated the noncollinear transmission coefficient for the device composed of F4GT sandwiched between two PtTe2 electrodes, as demonstrated in Fig. S3.† Our findings indicate that SOC has a negligible effect on the transmission coefficient of the device. This can be primarily attributed to the use of non-magnetic electrodes in our calculations. The magnetic properties influencing transport are derived from the Fe atoms in the F4GT layer. For the purpose of focusing on transport phenomena, we intentionally excluded SOC from our consideration in the model.
3.2 Spin filtering
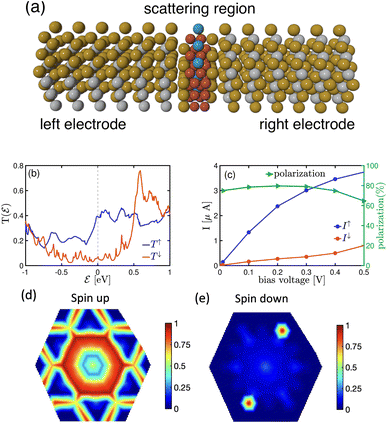
Fig. 3 presents the transmission spectrum of a monolayer F4GT sandwiched between two PtTe2 electrodes (panel a) under zero bias voltage. The results show ballistic transport near the Fermi level with distinct spin polarization (Fig. 3b). In the vicinity of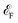 , the transmission coefficient for the spin-up channel is higher, while the spin-down channel exhibits a broad transmission peak reaching its maximum value of 0.75 at
, the transmission coefficient for the spin-up channel is higher, while the spin-down channel exhibits a broad transmission peak reaching its maximum value of 0.75 at 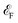 +0.6 eV. In contrast, the transmission coefficient for the spin-up channel remains comparatively lower at this energy level. This behavior is also supported by the DOS plot in Fig. 2, where a peak for the spin-down channel is observed at the same energy level (
+0.6 eV. In contrast, the transmission coefficient for the spin-up channel remains comparatively lower at this energy level. This behavior is also supported by the DOS plot in Fig. 2, where a peak for the spin-down channel is observed at the same energy level (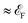 +0.6 eV). This peak results in a higher contribution of the spin-down channel to the transport properties of the system. The difference in the transmission behavior between the two spin channels strongly indicates the presence of spin-polarized transport properties in the F4GT-based device configuration. This can be seen in Fig. 3c, which exhibits a non-zero spin-polarized current for both spin channels. The I–V curve shows that the spin-up channel has a higher value of current, indicating a preferential flow of electrons with specific spin orientations. Similar spin filtering behavior in F3GT has been reported in conjunction with Cu electrodes.4
+0.6 eV). This peak results in a higher contribution of the spin-down channel to the transport properties of the system. The difference in the transmission behavior between the two spin channels strongly indicates the presence of spin-polarized transport properties in the F4GT-based device configuration. This can be seen in Fig. 3c, which exhibits a non-zero spin-polarized current for both spin channels. The I–V curve shows that the spin-up channel has a higher value of current, indicating a preferential flow of electrons with specific spin orientations. Similar spin filtering behavior in F3GT has been reported in conjunction with Cu electrodes.4
Additionally, we have conducted calculations to determine the spin polarization of the current, which is defined as P = |I↑ − I↓|/(I↑ + I↓). Since we require a finite bias voltage for polarization calculations, we have included polarization plots for all cases starting from 0.01 V throughout the paper. In Fig. 3c, the current spin polarization exhibits an impressive value of 80%, which remains consistently high in the voltage range of 0.1–0.4 V, comparable to the polarization observed at very low bias voltages. However, as the bias voltage is further increased to 0.5 V, the polarization gradually decreases and reaches 64%. This indicates that single-layer F4GT serves as an effective material for achieving substantial spin polarization, particularly at lower bias voltages. The significant transport polarization observed in F4GT agrees well with experimental results. A very recent study employing spin-resolved Andreev reflection spectroscopy on F4GT revealed an exceptionally high transport spin polarization, surpassing 50%.56
The k‖-resolved transmission probability offers a comprehensive understanding of how electrons with different spin orientations propagate through the material at the Fermi level. Thus, we performed calculations to determine the momentum-dependent transmission for Fig. 3d spin-up and Fig. 3e spin-down electrons at the Fermi energy under zero bias voltage. As expected, the transmission probability for spin-up electrons surpasses that of spin-down electrons, indicating a significant degree of spin polarization in the material. Furthermore, we found that the transmission in both the spin-up and spin-down channels does not change with the reversal of k‖ due to the two-fold rotational symmetry of the system. This is consistent with the structural symmetry of the system.
Quantum transmission eigenstates, which characterize electron propagation within a device, are depicted via isosurface plots in Fig. 4. The figure shows a monolayer F4GT placed between two PtTe2 electrodes for both (a) spin-up and (b) spin-down channels at the Fermi energy level under zero bias. A quantum transmission eigenstate can be thought of as a combination of two distinct electron states. One of these states represents electrons moving from the left electrode to the right electrode, while the other describes electrons going from the right electrode to the left electrode. Their relative phase depends on their proximity to the respective electrodes. This phase difference results in an interference-like pattern in the isosurface plot, particularly in the PtTe2 layers on the left and right sides of F4GT, far from the scattering region. A π phase shift is observed for the transmission eigenstates localized on the left electrode in the spin-down channel (panel b) compared to the spin-up channel (panel a). Nevertheless, for the PtTe2 layers on the right side of F4GT, the phase of eigenstates is the same for both channels. In Fig. 4a, the transmission eigenstate in the scattering region exhibits a pattern characterized by dz2 orbitals on Fe atoms for the spin-up channel. Interestingly, we observe that in the right electrode region, the transmission eigenstates pertaining to the spin-up channel (panel a) exhibit greater dominance when compared to those of the spin-down channel (panel b).
A comprehensive examination of the fundamental mechanisms contributing to this spin-filtering phenomenon reveals that the dominant transmission eigenstates in the spin-up channel establish a robust transmission channel in the heterojunction. This enables the efficient movement of electrons from the left electrode to the right electrode. Conversely, the spin-down channel experiences a relative scarcity of transmission eigenstates (Fig. 4b), resulting in a restricted transmission of electrons to the right side. The observed spin-filtering effect originates from the channel-selective transmission behavior, where the spin-up channel displays a more pronounced transmission, allowing a larger number of electrons to traverse from the left to the right side. The orbital-projected local density of states is presented in Fig. 5 for distinct orbitals, focusing on (a) the left electrode's PtTe2 layer interfacing with F4GT, (b) F4GT itself, and (c) the right electrode's PtTe2 layer interfacing with F4GT. The figure highlights a substantial contribution from both p and d orbitals, resulting in discernible d–p hybridization states near the Fermi level.
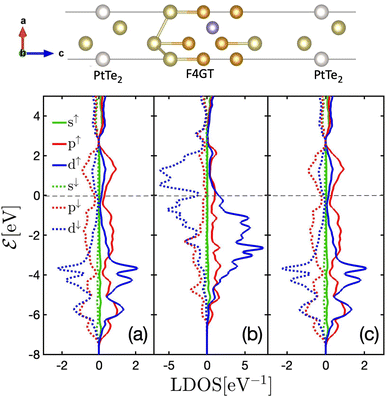 | ||
| Fig. 5 Orbital-projected local density of states for (a) the left electrode's PtTe2 layer interfacing with F4GT, (b) F4GT itself, and (c) the right electrode's PtTe2 layer interfacing with F4GT. | ||
Furthermore, we have calculated the spin-polarized electronic structure and transport properties for the bilayer F4GT placed between two PtTe2 electrodes. The AB-stacking for two F4GT layers is selected due to its higher stability in terms of energy compared to the AA-stacking configuration. The ground state energy for AA-stacked bilayer F4GT is found to be −92.21 eV, whereas the ground state energy for AB-stacked bilayer F4GT is −92.26 eV. The two-probe model for the NEGF calculations of this bilayer system is illustrated in Fig. 6a. Fig. 6b displays the spin-resolved energy-dependent transmission function of the system at zero voltage, with the energy measured relative to the Fermi level and the bilayer F4GT in a ferromagnetic (FM) configuration. Similar to the monolayer system, the zero-bias ballistic transport near the Fermi level exhibits spin polarization. However, in the bilayer system, there is a broad transmission peak between approximately 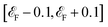 eV, with its maximum at
eV, with its maximum at 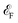 for the spin-up channel. In contrast, the transmission coefficient in the spin-down channel is suppressed. This behavior results in a spin filtering effect, allowing only one spin type to flow through the constriction at this particular energy range. The I–V calculation (Fig. 6c) reveals that the difference in spin-up and spin-down currents is more pronounced in the bilayer system compared to the single-layer F4GT, leading to higher polarization of the current. This value of spin polarization surpasses the reported spin polarization values for a device comprising a bilayer of F3GT placed between Cu electrodes. The highest spin polarization value for the Cu/F3GT/Cu heterostructure with a ferromagnetic configuration is documented as 85% at a very low bias voltage.4 The significantly enhanced spin polarization in our FM system indicates its potential for efficient spin transport in spintronic devices.
for the spin-up channel. In contrast, the transmission coefficient in the spin-down channel is suppressed. This behavior results in a spin filtering effect, allowing only one spin type to flow through the constriction at this particular energy range. The I–V calculation (Fig. 6c) reveals that the difference in spin-up and spin-down currents is more pronounced in the bilayer system compared to the single-layer F4GT, leading to higher polarization of the current. This value of spin polarization surpasses the reported spin polarization values for a device comprising a bilayer of F3GT placed between Cu electrodes. The highest spin polarization value for the Cu/F3GT/Cu heterostructure with a ferromagnetic configuration is documented as 85% at a very low bias voltage.4 The significantly enhanced spin polarization in our FM system indicates its potential for efficient spin transport in spintronic devices.
To gain further insight into the transport properties of the systems, we analyzed the distribution of transmission coefficients at the Fermi level under zero bias voltage, as depicted in Fig. 6d and e. In comparison to the spin-down channel shown in panel (e), the 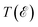 for the spin-up channel in panel (d) exhibits higher values and is distributed across most of the first Brillouin zone region. However, for the spin-down channel, the transmission contours are primarily concentrated around the Γ point. This indicates that the spin-up electrons have a significantly higher probability of transmission, while the transmission of the spin-down electrons is largely suppressed.
for the spin-up channel in panel (d) exhibits higher values and is distributed across most of the first Brillouin zone region. However, for the spin-down channel, the transmission contours are primarily concentrated around the Γ point. This indicates that the spin-up electrons have a significantly higher probability of transmission, while the transmission of the spin-down electrons is largely suppressed.
3.3 Magnetic tunnel junction
The study of MTJs is important in spintronics, as they are key components in spin-based devices.57 The structure of an MTJ consists of ferromagnetic layers separated by a tunneling barrier between them. The MTJs can come in different sizes, use low energy, and could potentially last without wearing out. These properties make the MTJ highly valuable for various applications like MRAM,58 magnetic sensors,59 hard disk drive etc60.In our investigation, we have introduced GaTe as a barrier between the ferromagnetic electrodes. GaTe is a member of the group-VIII metal chalcogenide family and is a semiconductor with an indirect bandgap. It crystallizes in the P![[6 with combining macron]](https://www.rsc.org/images/entities/char_0036_0304.gif) m2 space group,61,62 and its lattice parameter for a single layer is approximately 4.09 Å, closely matching that of F4GT and PtTe2. This close lattice match minimizes material mismatches in the heterostructure, promoting better interface quality. Fig. 7a presents side and top views of monolayer GaTe's atomic structure, consisting of four atoms in its unit cell: two Ga and two Te atoms.
m2 space group,61,62 and its lattice parameter for a single layer is approximately 4.09 Å, closely matching that of F4GT and PtTe2. This close lattice match minimizes material mismatches in the heterostructure, promoting better interface quality. Fig. 7a presents side and top views of monolayer GaTe's atomic structure, consisting of four atoms in its unit cell: two Ga and two Te atoms.
Accurately evaluating the exponential decay of wave transmission necessitates a comprehensive analysis of the dispersion spectrum, considering both propagating and evanescent wave modes. In Fig. 7b, we present the computed complex band structures of bulk GaTe, showcasing the real bands on the right panel and the imaginary bands on the left. Here, L in the imaginary bands represents the set at 17.52 Å for semiconducting GaTe with AB stacking. The right panel of the plot illustrates the real bands, while the left part exhibits the complex bands plotted against the imaginary part, κC. The calculated band gap of 0.78 eV for bulk GaTe aligns with findings from ref. 63. Evanescent states exhibit a characteristic decay length inversely proportional to the imaginary wave vector κC. Thus, our primary focus is on states where κC remains small within the gap. Notably, the presence of states with increasing κC indicates a progressive enhancement of the damping or broadening parameter in the complex band structure, signifying the temporal decay of electronic states.
The total and atomic projected density of states for freestanding monolayer GaTe is displayed in Fig. 7c, revealing a semiconductor phase with a band gap of approximately 1.05 eV. Notably, the projected density of states for atoms of the same type within the unit cell exhibits similar behavior. To investigate changes in the electronic structure of monolayer GaTe when integrated into the PtTe2/F4GT/GaTe/F4GT/PtTe2 heterostructure, we computed the spin-polarized projected density of states for both parallel and antiparallel configurations. These results are presented in panels (d) and (e) of Fig. 7, respectively. Our findings indicate that the incorporation of a GaTe monolayer in the device heterostructure leads to the observation of non-zero states in the DOS of GaTe at the Fermi level in both configurations. These states are known as metal-induced gap states (MIGS) and are responsible for the tunneling process. Moreover, the behavior of the density of states for atoms of the same type within the unit cell is altered due to the influence of the electrodes. MIGS arise from the interaction between the GaTe monolayer and the adjacent metallic electrodes. Their formation can be described by two primary mechanisms. The first mechanism involves charge transfer at the interface, where the wave functions of the metal penetrate into the semiconductor's band gap in the energy range where the metal's conduction band overlaps with the semiconductor gap. This interaction generates a continuum of metal-induced gap states derived from the virtual gap states of the semiconductor's complex band structure. Additionally, MIGS can be associated with intrinsic interface states on the semiconductor side, which may pin the Fermi level. These intrinsic states create localized energy levels within the band gap, further enhancing the presence of MIGS at the interface.64 Furthermore, in panel d, it is observed that in the parallel configuration, the monolayer GaTe becomes polarized as a result of its interaction with the ferromagnetic electrodes. In contrast, no such polarization is observed in the antiparallel configuration, as depicted in panel e. This lack of polarization in the antiparallel configuration arises from the opposing spin orientations in the left and right electrodes, which effectively cancel out their individual polarization effects on the barrier. Moreover, the magnetic moment calculations for the device with parallel configuration confirm a slight polarization of GaTe when it is positioned between two F4GT layers. The magnetic moments of Te and Ga are found to be 0.002 μB and 0.004 μB, respectively. These results suggest that GaTe experiences a subtle magnetic influence in the heterostructure, due to its interaction with the adjacent F4GT layers.
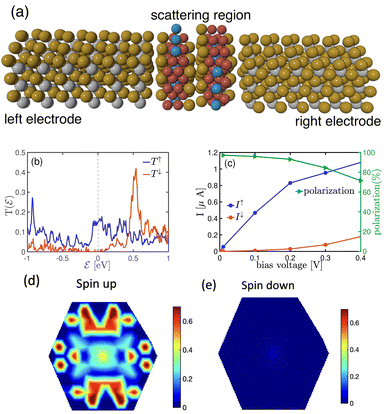
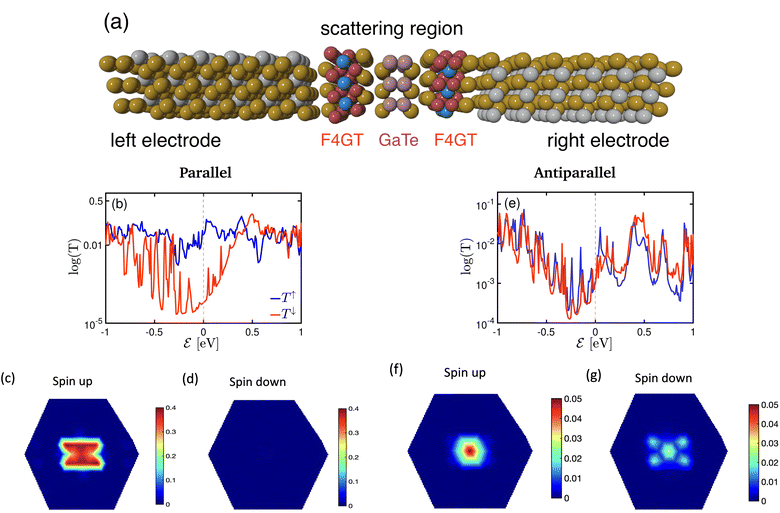
A schematic view of a single layer of GaTe as a spacer between two layers of F4GT, creating a heterostructure of PtTe2/F4GT/monolayer GaTe/F4GT/PtTe2 is shown in Fig. 8a. The distance between the GaTe layer and left (right) F4GT electrodes was obtained as 3.2 (3.08) Å which is less than the distance between GaTe layers in AB stacking form (3.81 Å). Fig. 8 indicates the transmission probability for the parallel (P) and antiparallel (AP) spin states in panels (b–d) and (e–g), respectively. Upon introducing GaTe as a spacer between F4GT layers, a decrease in the transmission probability is observed, as shown in panel 8b in comparison to Fig. 6b. In Fig. 8b, a very high spin polarization is observed in the transmission spectrum for the P state at the Fermi level, indicating a preference for one spin orientation over the other. Notably, near the Fermi level, perfect spin filtering occurs, where the transmission is non-zero only for the spin-up channel. This demonstrates that the system acts as an efficient spin filter, allowing only spin-up electrons to pass through the constriction. This nearly perfect spin polarization of transmission can be attributed to the specific electronic and magnetic properties of the F4GT layers in MTJ. In the parallel configuration, the aligned magnetic moments of the F4GT layers create a coherent magnetic environment that favors the transmission of spin-up electrons, minimizing scattering and enhancing spin-dependent transport. The interface between F4GT and PtTe2 acts as an efficient spin filter, where spin-up electrons experience less resistance, contributing more to the transmission while spin-down electrons are suppressed. High-quality interfaces between the layers ensure minimal scattering and defects, which is critical for maintaining high spin polarization. Additionally, the alignment of specific orbitals, such as the d-orbitals of Fe and the p-orbitals of Te, supports efficient spin-up electron transport in the parallel configuration.
The k‖-resolved transmission probability at the Fermi energy for the spin-up and spin-down channels, presented in panels (c) and (d) of Fig. 8, shows that the transmission channels for spin-up electrons are significantly higher than those for spin-down electrons. There is a relatively large transmission probability only around the Γ point (k‖ = 0) in the 2D Brillouin zone for the spin-up channel (Fig. 8c), indicating efficient spin-filtering due to aligned magnetic moments. Electron tunneling is highly sensitive to momentum conservation laws. The Γ point, being a high-symmetry point in the Brillouin zone, has lower in-plane momentum (k‖), which makes it easier for these electrons to tunnel through the barrier with minimal scattering, resulting in higher transmission probabilities near this point. This high transmission probability is consistent with typical behavior in ferromagnetic MTJs, where majority spins encounter less resistance. For spin-down electrons (Fig. 8d), the transmission probability is significantly lower, demonstrating the spin-filtering effect.
In the AP configuration (Fig. 8e), the system exhibits reduced spin polarization and less efficient spin filtering behavior near the Fermi level. However, the transmission for up and down-spin electrons is not the same in the AP configuration. This discrepancy is due to slight asymmetries in the atomic structure at the interfaces of F4GT and GaTe after relaxation, as shown in Fig. S4.† These asymmetries can lead to differences in the magnetic moments of Fe atoms in the F4GT layers and the spin-dependent transmission for an antiparallel configuration of the MTJ. These structural asymmetries, along with differences in the magnetic moments of Fe atoms, contribute to the observed variations in spin-dependent transport properties. The transmission probability through the device is less sensitive to the electron spin orientation, resulting in a more balanced transmission for both spin-up and spin-down electrons. As can be seen in Fig. 8f and g, in the antiparallel configuration, the k‖-resolved transmission probabilities for both spin-up and spin-down electrons are notably reduced compared to the parallel configuration. The reduced transmission in k‖ space and the absence of transmission channels in regions away from the Γ point indicate that the transmission is confined to a specific momentum range for both spin orientations. This confinement and reduced transmission efficiency are due to the anti-aligned magnetic moments at the interfaces, leading to increased scattering and less efficient electron transport. Consequently, the transport properties of the system in the AP configuration suggest a less pronounced spin-dependent behavior compared to the P configuration. This observation is consistent with the reported values for P and AP transmission of F3GT/h-BN/F3GT and F3GT/graphene/F3GT heterostructures.45 Furthermore, we calculated the resistance–area (RA) product from the transmission using the formula 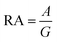 , where
, where 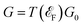 and
and 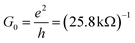 is the spin-conductance quantum. Here, A is the unit cell area of our setup, calculated as
is the spin-conductance quantum. Here, A is the unit cell area of our setup, calculated as 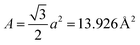 , with a = 4.01 Å being the in-plane lattice constant of the device. Then, the resistance-area product is:
, with a = 4.01 Å being the in-plane lattice constant of the device. Then, the resistance-area product is:
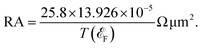 | (4) |
For the PtTe2/F4GT/GaTe/F4GT/PtTe2 MTJ, the resistance–area values obtained are 0.137 Ω μm2 and 1.618 Ω μm2 for parallel and antiparallel configurations, respectively. It is evident that when the MTJ is in the parallel state, it exhibits lower resistance, resulting in higher transmission values than in the antiparallel state.
Moreover, we focused on the implementation of a bilayer of GaTe as the barrier layer. Transmission coefficient of the Fe4GeTe2/bilayer GaTe/Fe4GeTe2 in the (b) parallel and (b) antiparallel state under zero bias voltage is shown in Fig. 9. The total transmission coefficients at the Fermi level for the Fe4GeTe2/bilayer GaTe/Fe4GeTe2 system were determined to be 0.002 and 1.4316 × 10−4 in the parallel and antiparallel magnetic states under zero bias voltage, respectively. Notably, these values are lower than the total transmission coefficients observed when utilizing a monolayer of GaTe as the barrier layer, where they were found to be 0.0250 and 0.0021 for the parallel and antiparallel magnetic states under zero bias voltage, respectively. This outcome highlights the introduction of a bilayer of GaTe as a more effective hindrance to electron transport in the MTJ. Specifically, the bilayer GaTe barrier demonstrates significantly reduced transmittance in both parallel and antiparallel magnetic configurations compared to its monolayer counterpart.
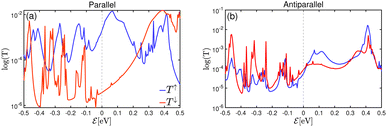 | ||
| Fig. 9 Transmission characteristics of the Fe4GeTe2/bilayer GaTe/Fe4GeTe2 in the (b) parallel and (b) antiparallel state under zero bias voltage on a logarithmic scale. | ||
The total charge current of the device is calculated as the sum of two components: I = I↑ + I↓ (eqn (3)). By measuring the currents at different voltages, the TMR ratio can be determined using the formula:65
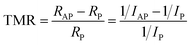 | (5) |
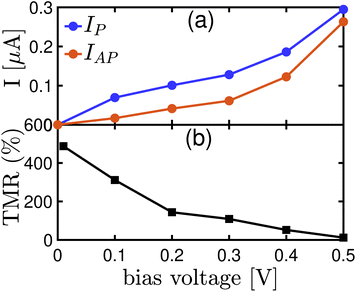
Fig. 10a illustrates the I–V curve for the Fe4GeTe2/monolayer GaTe/Fe4GeTe2 magnetic tunnel junction sandwiched between two PtTe2 electrodes in both parallel and antiparallel configurations. The current in the P state is higher than the current in the AP state under the given bias voltage, indicating more efficient electron transport when the magnetic moments of the Fe4GeTe2 layers are aligned parallel. This suggests that electrons with parallel spins have a higher probability of transmitting through the device, leading to more efficient transport of charge carriers. This behavior is consistent with the spin-filtering effect observed in the P state (Fig. 8b), where the majority spins experience less resistance and are favored in the transport process. On the other hand, in the AP state, the transmission of both spin-up and spin-down (Fig. 8e–g) electrons is more restricted due to the anti-alignment of the magnetic moments. As a result, the total current in the AP configuration is reduced compared to the P configuration.
Tunnel magnetoresistance is a key parameter used to quantify the difference in resistance between the P and AP configurations of an MTJ. A higher TMR indicates a more efficient spin-filtering effect and a larger difference in current between the two spin states, while a lower TMR suggests a reduced difference in current. In Fig. 10b, TMR is plotted for PtTe2/Fe4GeTe2/monolayer GaTe/Fe4GeTe2/PtTe2 MTJ within a bias range starting from 0.01 V, as it requires a finite bias voltage for accurate representation. The system exhibits a high TMR of 487% at low bias, surpassing the reported TMR value of 89% for PtTe2/F4GT/α-In2Se3/F3GT/PtTe2 heterostructures.2 However, as the bias voltage increases, the TMR gradually decreases, reaching 12% at 0.5 V. This decline suggests that the efficiency of the spin-filtering effect diminishes under higher voltage conditions. The higher voltage leads to stronger carrier injection in the device, which can modify the spin-dependent transport properties and result in the observed reduction in TMR. Additionally, the investigation into spin filtering and the potential utilization of other members within the FGT family has produced notable findings. For example, an experiment involving a spin valve device integrated a vertical F3GT/h-BN/F3GT magnetic MTJ with an electrolyte gate, resulting in a MR ratio of 36% for the intrinsic MTJ. Electrolyte gating further enhanced the TMR ratio of the F3GT/h-BN/F3GT heterostructure from 26% to 65%33 which is less than the observed value of TMR for F4Gt-based MTJ, especially in low bias voltages. Also, a TMR value of 141% has been documented in van der Waals magnetic heterostructures comprising F3GT and FePSe3 at 5 K.12 The ability to modulate magnetic fields and magnetoresistance switches presents a promising avenue for controlling the magnetization configuration of the MTJ. In the context of F3GT/Cr2Ge2Te6/F3GT van der Waals junctions, a transition from negative-to-positive magnetoresistance was observed with an increasing bias voltage.32 This transition, attributed to the changing spin polarizations, was supported by calculated spin-dependent density of states under bias conditions.
4 Conclusion
In conclusion, we have investigated the spin-dependent transport properties of Fe4GeTe2/GaTe/Fe4GeTe2 vdW heterostructures sandwiched between PtTe2 electrodes using first-principles calculations and non-equilibrium Green's function method. We analyzed the electronic DOS of F4GT in both freestanding and device configurations, revealing its ferromagnetic metallic nature and sensitivity to local environments. Through our study, we have demonstrated the formation of spin valves with well-defined spin filtering behavior. Transmission eigenstates of a monolayer F4GT sandwiched between PtTe2 reveal interference patterns influenced by relative phases and localization differing in spin-up and spin-down channels. The transport characteristics of a double-layer F4GT with a ferromagnetic configuration, placed between two PtTe2 electrodes, are found to display remarkable spin polarization of 97%. This indicates a strong tendency for one spin orientation to dominate the transport process. The transport properties of F4GT-based MTJs by introducing monolayer GaTe as a spacer between F4GT layers show a remarkable value of 487% of TMR at low bias surpassing the existing values reported for similar systems in literature. TMR decreases with increasing bias voltage, indicating the modification of spin-dependent transport properties under carrier injection. These findings open up new opportunities for the design and optimization of spintronic devices based on FGT and related heterostructures, advancing the field of spintronics and offering the potential for future technological advancements.Data availability
All the data presented in this paper are available from the authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We gratefully acknowledge Prof. Mads Brandbyge of DTU, Denmark for useful discussions. B.S. acknowledges financial support from Swedish Research Council (grant no. 2022-04309), STINT Mobility Grant for Internationalization (grant no. MG2022-9386), Energymyndigheten (Diary no. 2018-004434 & Project number 46621-1) and DST-SPARC, India (Ref. No. SPARC/2019-2020/P1879/SL). The computations were enabled by resources provided by the National Academic Infrastructure for Supercomputing in Sweden (NAISS) at UPPMAX (NAISS 2024/5-258) and at NSC and PDC (NAISS 2023/3-42) partially funded by the Swedish Research Council through grant agreement no. 2022-06725. B. S. also acknowledges the allocation of supercomputing hours within EuroHPC JU Development Access call in LUMI-C supercomputer (grant no. EHPC-DEV-2024D04-071) in Finland.Notes and references
- D. Awschalom and N. Samarth, J. Magn. Magn. Mater., 1999, 200, 130–147 CrossRef CAS.
- Y. Su, X. Li, M. Zhu, J. Zhang, L. You and E. Y. Tsymbal, Nano Lett., 2021, 21, 175–181 CrossRef CAS.
- D. Li, J. Phys. Chem. C, 2021, 125, 16228–16234 CrossRef CAS.
- Z.-Z. Lin and X. Chen, Adv. Electron. Mater., 2020, 6, 1900968 CrossRef CAS.
- D. Li, T. Frauenheim and J. He, ACS Appl. Mater. Interfaces, 2021, 13, 36098–36105 CrossRef CAS.
- S. Xiong, X. Dong, L. Xie, Z. Guan, M. Long and T. Chen, J. Phys.: Condens. Matter, 2023, 35, 395302 CrossRef CAS.
- T. Chen, W. Ding, H. Li and G. Zhou, J. Mater. Chem. C, 2021, 9, 3652–3660 RSC.
- J. P. Velev, C.-G. Duan, J. D. Burton, A. Smogunov, M. K. Niranjan, E. Tosatti, S. S. Jaswal and E. Y. Tsymbal, Nano Lett., 2009, 9, 427–432 CrossRef CAS.
- M. Arai, R. Moriya, N. Yabuki, S. Masubuchi, K. Ueno and T. Machida, Appl. Phys. Lett., 2015, 107, 103107 CrossRef.
- B. Karpiak, A. W. Cummings, K. Zollner, M. Vila, D. Khokhriakov, A. M. Hoque, A. Dankert, P. Svedlindh, J. Fabian, S. Roche and S. P. Dash, 2D Materials, 2019, 7, 015026 CrossRef.
- W. Zhu, Y. Zhu, T. Zhou, X. Zhang, H. Lin, Q. Cui, F. Yan, Z. Wang, Y. Deng, H. Yang, L. Zhao, I. Žutić, K. D. Belashchenko and K. Wang, Nat. Commun., 2023, 14, 5371 CrossRef CAS.
- X. Huang, L. Zhang, L. Tong, Z. Li, Z. Peng, R. Lin, W. Shi, K.-H. Xue, H. Dai, H. Cheng, D. de Camargo Branco, J. Xu, J. Han, G. J. Cheng, X. Miao and L. Ye, Nat. Commun., 2023, 14, 2190 CrossRef CAS.
- T. Song, X. Cai, M. W.-Y. Tu, X. Zhang, B. Huang, N. P. Wilson, K. L. Seyler, L. Zhu, T. Taniguchi, K. Watanabe, M. A. McGuire, D. H. Cobden, D. Xiao, W. Yao and X. Xu, Science, 2018, 360, 1214–1218 CrossRef CAS.
- D. R. Klein, D. MacNeill, J. L. Lado, D. Soriano, E. Navarro-Moratalla, K. Watanabe, T. Taniguchi, S. Manni, P. Canfield, J. Fernández-Rossier and P. Jarillo-Herrero, Science, 2018, 360, 1218–1222 CrossRef CAS.
- N. Devaraj and K. Tarafder, Advanced Theory and Simulations, 2022, 5, 2200178 CrossRef CAS.
- H. Kurebayashi, J. H. Garcia, S. Khan, J. Sinova and S. Roche, Nat. Rev. Phys., 2022, 4, 150–166 CrossRef CAS.
- J. F. Sierra, J. Fabian, R. K. Kawakami, S. Roche and S. O. Valenzuela, Nat. Nanotechnol., 2021, 16, 856–868 CrossRef CAS.
- Z. Wang, D. Sapkota, T. Taniguchi, K. Watanabe, D. Mandrus and A. F. Morpurgo, Nano Lett., 2018, 18, 4303–4308 CrossRef CAS.
- A. F. May, S. Calder, C. Cantoni, H. Cao and M. A. McGuire, Phys. Rev. B, 2016, 93, 014411 CrossRef.
- X. Li, Y. Su, M. Zhu, F. Zheng, P. Zhang, J. Zhang and J.-T. Lü, Phys. Rev. Appl., 2021, 16, 034052 CrossRef CAS.
- Y. Yu, G. Liu, C. Luo, W. Yang, X. Xiao and T. Chen, ACS Appl. Nano Mater., 2024, 7, 18299–18308 CrossRef CAS.
- X. Dong, T. Chen and G. Zhou, J. Alloys Compd., 2024, 977, 173417 CrossRef CAS.
- L. Xie, T. Chen, X. Dong, G. Liu, H. Wang and X. Xiao, J. Phys.: Condens. Matter, 2022, 34, 465302 CrossRef CAS.
- H.-J. Deiseroth, K. Aleksandrov, C. Reiner, L. Kienle and R. K. Kremer, Eur. J. Inorg. Chem., 2006, 2006, 1561–1567 CrossRef.
- B. Zhao, R. Ngaloy, S. Ghosh, S. Ershadrad, R. Gupta, K. Ali, A. M. Hoque, B. Karpiak, D. Khokhriakov, C. Polley, B. Thiagarajan, A. Kalaboukhov, P. Svedlindh, B. Sanyal and S. P. Dash, Adv. Mater., 2023, 35, 2209113 CrossRef CAS.
- H. Wang, H. Lu, Z. Guo, A. Li, P. Wu, J. Li, W. Xie, Z. Sun, P. Li, H. Damas, A. M. Friedel, S. Migot, J. Ghanbaja, L. Moreau, Y. Fagot-Revurat, S. Petit-Watelot, T. Hauet, J. Robertson, S. Mangin, W. Zhao and T. Nie, Nat. Commun., 2023, 14, 2483 CrossRef CAS.
- S. Ershadrad, S. Ghosh, D. Wang, Y. Kvashnin and B. Sanyal, J. Phys. Chem. Lett., 2022, 13, 4877–4883 CrossRef CAS.
- S. Ghosh, S. Ershadrad, V. Borisov and B. Sanyal, npj Comput. Mater., 2023, 9, 86 CrossRef CAS.
- J.-X. Zhu, M. Janoschek, D. S. Chaves, J. C. Cezar, T. Durakiewicz, F. Ronning, Y. Sassa, M. Mansson, B. L. Scott, N. Wakeham, E. D. Bauer and J. D. Thompson, Phys. Rev. B, 2016, 93, 144404 CrossRef.
- H. Lin, F. Yan, C. Hu, Q. Lv, W. Zhu, Z. Wang, Z. Wei, K. Chang and K. Wang, ACS Appl. Mater. Interfaces, 2020, 12, 43921–43926 CrossRef CAS.
- J. Seo, D. Y. Kim, E. S. An, K. Kim, G.-Y. Kim, S.-Y. Hwang, D. W. Kim, B. G. Jang, H. Kim, G. Eom, S. Y. Seo, R. Stania, M. Muntwiler, J. Lee, K. Watanabe, T. Taniguchi, Y. J. Jo, J. Lee, B. I. Min, M. H. Jo, H. W. Yeom, S.-Y. Choi, J. H. Shim and J. S. Kim, Sci. Adv., 2020, 6, eaay8912 CrossRef.
- Z.-A. Wang, X. Zhang, W. Zhu, F. Yan, P. Liu, Z. Yuan and K. Wang, Chin. Phys. Lett., 2023, 40, 077201 CrossRef CAS.
- L. Zhou, J. Huang, M. Tang, C. Qiu, F. Qin, C. Zhang, Z. Li, D. Wu and H. Yuan, InfoMat, 2023, 5, e12371 CrossRef CAS.
- H. Wang, H. Wu, J. Zhang, Y. Liu, D. Chen, C. Pandey, J. Yin, D. Wei, N. Lei, S. Shi, H. Lu, P. Li, A. Fert, K. L. Wang, T. Nie and W. Zhao, Nat. Commun., 2023, 14, 5173 CrossRef CAS.
- Y. Wang, C. Wang, S.-J. Liang, Z. Ma, K. Xu, X. Liu, L. Zhang, A. S. Admasu, S.-W. Cheong, L. Wang, M. Chen, Z. Liu, B. Cheng, W. Ji and F. Miao, Adv. Mater., 2020, 32, e2004533 CrossRef.
- D. Li, S. Haldar and S. Heinze, Nano Lett., 2024, 24, 2496–2502 CrossRef CAS.
- B. Wu, J. Yang, S. Liu, S. Fang, Z. Liu, Z. Lin, J. Shi, W. Yang, Z. Luo, C. Wang, H. Du, J. Yang and J. Lu, Phys. Rev. Appl., 2023, 19, 064008 CrossRef CAS.
- A. Melnikov, L. Brandt, N. Liebing, M. Ribow, I. Mertig and G. Woltersdorf, Phys. Rev. B, 2022, 106, 104417 CrossRef CAS.
- A. Khater, L. Saim, R. Tigrine and D. Ghader, Surf. Sci., 2018, 672–673, 47–55 CrossRef CAS.
- E. A. Moujaes, A. Khater, M. Abou Ghantous and V. Ashokan, Materialia, 2018, 4, 373–387 CrossRef CAS.
- F. Mireles and G. Kirczenow, Phys. Rev. B, 2001, 64, 024426 CrossRef.
- J. Yang, B. Wu, J. Zhou, J. Lu, J. Yang and L. Shen, Nanoscale, 2023, 15, 16103–16111 RSC.
- J. Zhou, J. Qiao, C.-G. Duan, A. Bournel, K. L. Wang and W. Zhao, ACS Appl. Mater. Interfaces, 2019, 11, 17647–17653 CrossRef CAS.
- W. Yang, Y. Cao, J. Han, X. Lin, X. Wang, G. Wei, C. Lv, A. Bournel and W. Zhao, Nanoscale, 2021, 13, 862–868 RSC.
- X. Li, J.-T. Lü, J. Zhang, L. You, Y. Su and E. Y. Tsymbal, Nano Lett., 2019, 19, 5133–5139 CrossRef CAS.
- D. Marian, D. Soriano, E. Cannavó, E. G. Marin and G. Fiori, npj 2D Mater. Appl., 2023, 7, 42 CrossRef CAS.
- S. Smidstrup, T. Markussen, P. Vancraeyveld, J. Wellendorff, J. Schneider, T. Gunst, B. Verstichel, D. Stradi, P. A. Khomyakov, U. G. Vej-Hansen, M.-E. Lee, S. T. Chill, F. Rasmussen, G. Penazzi, F. Corsetti, A. Ojanperä, K. Jensen, M. L. N. Palsgaard, U. Martinez, A. Blom, M. Brandbyge and K. Stokbro, J. Phys.: Condens. Matter, 2019, 32, 015901 CrossRef.
- S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104 CrossRef.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456–1465 CrossRef CAS.
- H. Wang, J. Zhou, X. Liu, C. Yao, H. Li, L. Niu, Y. Wang and H. Yin, Appl. Phys. Lett., 2017, 111, 172408 CrossRef.
- S. Datta, Quantum Transport: Atom to Transistor, Cambridge University Press, 2005 Search PubMed.
- P. C. Aguilar, F. Calleja, C.-N. Kuo, C. S. Lue, B. Ghosh, A. Agarwal, A. Politano, A. L. V. de Parga, R. Miranda, J. A. Silva-Guillén and M. Garnica, J. Phys.: Mater., 2022, 5, 044003 Search PubMed.
- Q. Liu, J. Xing, Z. Jiang, Y. Guo, X. Jiang, Y. Qi and J. Zhao, Commun. Phys., 2022, 5, 140 CrossRef CAS.
- D. Kim, C. Lee, B. G. Jang, K. Kim and J. H. Shim, Sci. Rep., 2021, 11, 17567 CrossRef CAS.
- K. Kim, J. Seo, E. Lee, K.-T. Ko, B. S. Kim, B. G. Jang, J. M. Ok, J. Lee, Y. J. Jo, W. Kang, J. H. Shim, C. Kim, H. W. Yeom, B. Il Min, B.-J. Yang and J. S. Kim, Nat. Mater., 2018, 17, 794–799 CrossRef CAS.
- D. Rana, M. Bhakar, B. G., S. Bera, N. Saini, S. K. Pradhan, M. Mondal, M. Kabir and G. Sheet, Phys. Rev. B, 2023, 107, 224422 CrossRef CAS.
- S. Peng, Y. Zhang, M. Wang, Y. Zhang and W. Zhao, in Magnetic Tunnel Junctions for Spintronics: Principles and Applications, John Wiley & Sons, Ltd, 2014, pp. 1–16 Search PubMed.
- W. J. Gallagher and S. S. P. Parkin, IBM J. Res. Dev., 2006, 50, 5–23 CAS.
- J. Y. Chen, J. F. Feng and J. M. D. Coey, Appl. Phys. Lett., 2012, 100, 142407 CrossRef.
- B.-Y. Jiang, K. Zhang, T. Machita, W. Chen and M. Dovek, J. Magn. Magn. Mater., 2023, 571, 170546 CrossRef CAS.
- S. Demirci, N. Avazl ı, E. Durgun and S. Cahangirov, Phys. Rev. B, 2017, 95, 115409 CrossRef.
- M. N. Çınar, G. O. Sargı n, K. Sevim, B. Özdamar, G. Kurt and H. Sevinçli, Phys. Rev. B, 2021, 103, 165422 CrossRef.
- K. Lai, S. Ju, H. Zhu, H. Wang, H. Wu, B. Yang, E. Zhang, M. Yang, F. Li, S. Cui, X. Deng, Z. Han, M. Zhu and J. Dai, Commun. Phys., 2022, 5, 143 CrossRef CAS.
- W. Mönch, Appl. Surf. Sci., 1990, 41–42, 128–138 CrossRef.
- S. S. P. Parkin, C. Kaiser, A. Panchula, P. M. Rice, B. Hughes, M. Samant and S.-H. Yang, Nat. Mater., 2004, 3, 862–867 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00639a |
| This journal is © The Royal Society of Chemistry 2024 |