Tunable insulator–metal transition in epitaxial VO₂ thin films via strain and defect engineering

Abstract

The Metal to Insulator Transition (MIT) in materials, particularly vanadium dioxide (VO₂), has garnered significant research interest due to its potential applications in smart windows, memristors, transistors, sensors, and optical switches. The transition from an insulating, monoclinic phase to a conducting, tetragonal phase involves changes in optical and electrical properties, opening avenues in adaptive radiative coolers, optical memories, photodetectors, and optical switches. VO₂ exhibits MIT close to 68 °C, thereby requiring tuneable transition temperatures (T_c) in VO₂ thin films for practical device applications. In this work, we explore the role of strain and defect engineering in tuning the MIT temperature in epitaxial VO₂ thin films deposited on c-cut sapphire using Pulsed Laser Deposition (PLD). The study involves tuning the metal-to-insulator transition (MIT) by varying growth parameters, mainly temperature and oxygen partial pressure. Strain engineering along the b-axis helped tune the transition temperature from 65 °C to 82 °C with the out-of-plane b-strain varying from −0.71% to −0.44%. Comprehensive structural and property analyses, including X-ray diffraction (XRD), Reciprocal Space Mapping (RSM), X-ray Photoelectron Spectroscopy (XPS), Raman spectroscopy, and resistivity–temperature (R–T) measurements, were performed to correlate structural properties with T_c. Additionally, density functional theory (DFT) calculations were performed using Quantum Espresso within the generalized gradient approximation of the revised Perdew–Burke–Ernzerhof (PBEsol) functional to provide theoretical validity to the experimentally obtained results. Our study provides critical insights into the interplay between strain and oxygen vacancies and their effect on the physical properties of VO₂ thin films with DFT calculations supporting the experimental findings.

---

Introduction

Metal to Insulator Transition (MIT) has been a hot topic amongst researchers in the recent past owing to its potential in applications such as smart windows, memristors, transistors, sensors and optical switches.^1–4 A material which exhibits MIT can transform from an insulating, transparent low temperature phase to a conducting, opaque high temperature phase with application of sufficient energy to trigger the transition. Vanadium dioxide (VO₂) in particular has been a subject of interest due to its metal-to-insulator transition temperature (T_c) at approximately 68 °C, a value very close to room temperature compared with the other alternatives.^5,6 With increasing temperature, VO₂ transitions from high resistance, transparent, monoclinic P2₁/c to low resistance, opaque, tetragonal P4₂/mnm.^7–9 This is accompanied by a change in optical and electrical properties (optical changes being visible in the IR region), thereby leading to exciting applications in optical devices including adaptive radiative coolers, optical memories, photodetectors, and optical switches.^5,10,11

However, for application in practical devices, tuneable T_c in VO₂ thin films is required for different operating conditions. This has been mainly achieved through strain engineering and elemental doping in the past.¹² Recent studies have demonstrated the tuneable T_c in VO₂ by using different substrates.¹³ For example, T_c of 340 K and 292 K has been obtained, when epitaxial VO₂ films were deposited on (0006) Al₂O₃ and (001) TiO₂ substrates, respectively.^14,15 VO₂-based nanocomposites deposited on c-cut sapphire have also shown a bidirectional T_c tuning from 323.5 K (Au–VO₂ nanocomposite) and 366.7 K (Pt–VO₂ nanocomposite), compared to a T_c of 344 K, which was obtained for pure VO₂ on c-cut sapphire.^16,17 Studies have also reported an increase in T_c for higher substrate deposition temperatures, consequently as a way of changing the size of gold nanoparticles embedded within the VO₂ matrix.¹⁷ Similar reports have been published on nanocomposites of VO₂ embedded with platinum, nickel and tungsten.^18–20 Yang et al. fabricated a VO₂–Nb:TiO₂ heterojunction whose optical properties were studied with respect to thermally actuated MIT.²¹ Moatti et al. studied the effect of oxygen vacancies introduced via vacuum annealing on VO₂/NiO/c-Al₂O₃ heterostructures.²² However, limited research has been done on the role of oxygen vacancies introduced directly by changing the partial pressure of oxygen inside the deposition chamber. Since oxygen vacancies are positively charged in nature, they act as conducting channels which stabilize the conducting, high temperature phase and therefore bring T_c closer to room temperature. Studies have shown that increasing the oxygen partial pressure during growth reduces the b-axis spacing up to a certain limit.^23,24 A further increase in oxygen flow rate results in an increase in the b-axis lattice parameter of the (020) VO₂ on (0006) sapphire which might be due to the lack of opportunities for the oxygen ions to diffuse into the VO₂ surface.²⁴ Some review reports have discussed how the oxygen vacancies influence the transition temperature.^5,10 Fan et al. studied the role of vacancies in the growth of VO₂ films on MgF₂ substrates by rf-plasma assisted MBE.²⁵ Koussi et al. studied the effect of oxygen vacancies introduced by post-deposition rapid thermal annealing (RTA).²⁶ Lu et al. studied the role of vacancies formed at the grain boundaries in VO₂ growth on Pt-coated silicon substrates.²⁷ However, study of the correlation between the role of oxygen vacancies and change in lattice strain using structural and electrical characterization, especially for epitaxial VO₂ films grown on c-sapphire has been very limited. In addition, limited computational studies have been performed on the phase stability of strained epitaxial VO₂ thin films, which can provide critical insights into strain engineering for obtaining tuneable MIT.

In this work, we have explored the effect of oxygen vacancies and strain in epitaxial VO₂ thin films deposited on c-cut sapphire using Pulsed Laser Deposition (PLD) as shown schematically in Fig. 1(d). This was enabled by varying the deposition parameters, including the deposition temperature and oxygen partial pressure, giving rise to tuneable T_c. Detailed structural and property analyses including X-ray diffraction (XRD), Reciprocal Space Mapping (RSM), X-ray Photoelectron Spectroscopy (XPS), Raman spectroscopy, and resistivity–temperature (R–T) measurements were conducted to correlate the structural properties with the tuneable T_c. In addition, DFT calculations were also performed to study the effect of strain on the phase stability and the transition temperature.

Fig. 1 Schematics of the VO₂ thin film stack on (0001) Al₂O₃ showing an epitaxial relationship. (a) Cross sectional view of the stack; (b) 3 : 2 domain matching epitaxy of (020) VO₂ along [001] deposited on (0001) Al₂O₃ along [11̄00]; (c) 10 : 7 domain matching epitaxy of (020) VO₂ along [100] deposited on (0001) Al₂O₃ along [011̄0]; (d) a 3D schematic of the VO₂ thin film deposited on c-Al₂O₃.

Methodology

Thin film growth

VO₂ thin films were deposited on a c-cut sapphire substrate using a Coherent COMPex Pro laser system (248 nm KrF excimer laser). Prior to the deposition, the substrates were cleaned using an ultra-sonicator for 20 minutes each in acetone, ethyl alcohol and deionized water respectively, in that sequence, followed by dry blowing in N₂. The base pressure of the chamber was 3.5 × 10⁻⁶ mbar (2.625 × 10⁻⁶ Torr) or lower before deposition. A frequency of 5 Hz and laser fluence of 2.5 J cm⁻² were used for all the depositions. The depositions were carried out at three different substrate temperatures (550 °C, 600 °C and 650 °C), and three different oxygen pressures (2.5 mTorr, 5 mTorr, and 7.5 mTorr). After depositions were completed, the films were annealed for 30 minutes, followed by cooling to 25 °C in 30 minutes.

Structural and property characterization

A Malvern Panalytical Empyrean was used for X-Ray Diffraction (XRD), in which high resolution XRD scans were performed in thin film mode for step size of 0.004° and scan rate of 0.6 s per degree. Confocal Raman spectroscopy was performed using an Acton Spectrapro 2500i spectrometer from Princeton Instruments to further characterize the samples. All the samples were excited with a laser wavelength of 532 nm with 40 mW power. The data was accumulated twenty times, with exposure time of 2 s. UV-vis-NIR spectroscopy was used to measure the film reflectance in a 250–1500 nm wavelength range using a Jasco V-770 spectrophotometer in reflectance mode. XPS scans were performed using a PHI 5000 Versa Probe II from FEI Inc., utilizing an X-ray of diameter 100 μm from a 100 W power source. The scans were performed from 0 to 1200 eV for all the samples, with a resolution of 0.8 eV at a vacuum of 10⁻⁷ mbar to confirm the quantity of each element (C, V and O) present in the film. For R–T analysis, a custom four-point probe station was used to measure the resistivity as a function of temperature. The distance between consecutive probes was approximately 2 mm, and depending on the resistance offered by the film, input current ranging from 5 mA to 100 mA was used for a temperature range of 25 °C to 100 °C. The thickness of the films was measured using a Bruker DektakXT stylus profilometer.

Computational study

Quantum Espresso was used to perform DFT calculations within the generalized gradient approximation of the revised Perdew–Burke–Ernzerhof (PBEsol).^28–31 Projector augmented wave (PAW) pseudopotentials parameterized for PBEsol with 13 valence electrons for V and 6 valence electrons for O were used.^32,33 Because of the strong Coulomb repulsion among the V 3d electrons, the PBE+U method was used for the calculations.³⁴ Setting the effective parameters, i.e., U_eff = U − J, where U is the Hubbard parameter and J is the screened exchange parameter, accurately describes the electronic structure and strong correlation of VO₂.^35–37 Values of U and J were chosen to be 4.2 eV and 0.8 eV, respectively, resulting in a U_eff of 3.4 eV, identical to those used by Yao et al.³⁵ The electron density and wavefunctions were expanded in plane waves with energy cutoffs of 560 and 70 Ry, respectively. Fermi–Dirac smearing with a Gaussian spreading of 0.001 Ry was used. Gamma-centered 5 × 6 × 5 and 6 × 6 × 5 k-meshes for sampling the reciprocal space were used for monoclinic and rutile phases, respectively. We used a 10⁻⁶ Ry energy difference as a convergence criterion for electronic relaxation. Atomic positions were relaxed until the force on every atom was less than 10⁻⁵ Ry bohr⁻¹. All calculations were spin-polarized to accurately describe the magnetic properties of VO₂.

We studied 12 atom supercells (4 V and 8 O) of monoclinic (M₁) (1 × 1 × 1) and rutile (R) (1 × 1 × 2) phases. The initial cell parameters of M₁ and R were used as: M₁ → a = 5.75 Å, b = 4.53 nm, c = 5.38 nm, α = γ = 90°, β = 122.6° and R → a = b = 4.55 nm, c = 5.90 nm, α = β = γ = 90°. These cell parameters are consistent with the experimental study by Moatti et al.³⁸ Starting from these structures, we performed a full relaxation via energy minimization with respect to atomic positions, cell shape, and cell volume. To mimic the effect of the sapphire substrate, we applied the in-plane strain on the x–z plane of both monoclinic and rutile phases. We used the value of misfit strains measured by Moatti et al. experimentally, i.e., −4.42% and +2.27% along (100) and (001), respectively, and β = 120° for the M₁ phase; +3.36% and −3.37% along (100) and (001), respectively, keeping all the angles at 90° for the R phase.³⁸ The out-of-plane cell parameter along (010) and atomic positions were relaxed to minimize energy.

Results and discussion

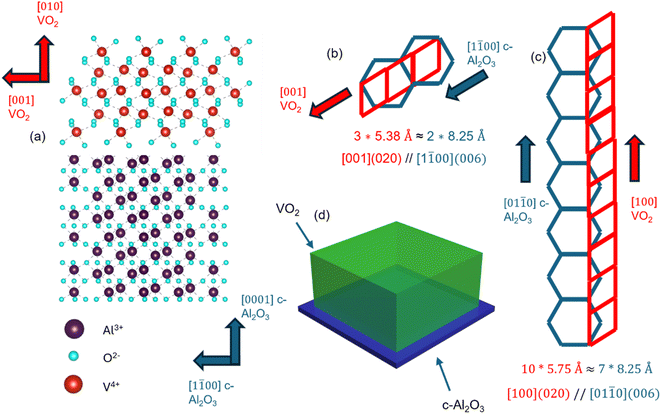
All the VO₂ thin film samples were deposited using PLD (see the Methodology). Fig. 1(a) shows the schematic of the lattice plane matching of VO₂ and c-Al₂O₃ involved in the film. The epitaxy relation was confirmed using XRD (discussed later). The [001] direction of VO₂ on the (020) interface has a domain-matching relationship with the (0006) face of c-cut sapphire, along the [11̄00] direction. The lattice parameter of VO₂ in the (020) plane along its c-plane i.e. [001] direction is 5.38 Å, while that for (0006) c-Al₂O₃ in the [11̄00] direction is 8.25 Å, hence forming an approximately 3 : 2 relationship, as shown in Fig. 1(b).^39,40 VO₂ also achieves domain matching with (0001) Al₂O₃ along the a-axis i.e. [100] direction, as it is in an approximately 10 : 7 ratio, along the [011̄0] direction of the (0001) sapphire face, as shown in Fig. 1(c).^39,40 A schematic of the VO₂ thin film stack is shown in Fig. 1(d).

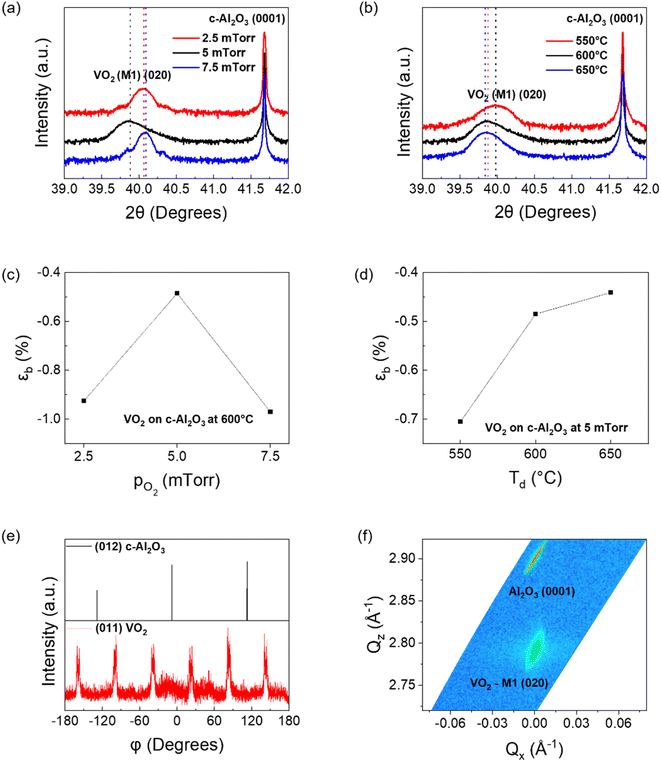
To confirm the above epitaxy relationship, XRD was performed. Fig. 2(a) and (b) show the XRD plots of the VO₂ films deposited on (0001) Al₂O₃. While Fig. 2(a) is a comparison of films deposited at 5 mTorr oxygen chamber pressure at 550 °C, 600 °C, and 650 °C substrate temperatures, Fig. 2(b) is a comparison of VO₂ deposited at three different oxygen pressures of 2.5 mTorr, 5 mTorr and 7.5 mTorr, with the substrate temperature during deposition for all three films being 600 °C. The XRD θ–2θ scans of the VO₂ thin films confirm the highly textured growth of VO₂ along the (020) out-of-plane for all cases with compressive strain present along the out-of-plane direction, indicative of the in-plane tensile strain (2θ value for bulk M₁-VO₂ (020) = 39.68°). The data shows that with increasing deposition temperatures, the FWHM of the VO₂ samples decreases, while the d-spacing increases, leading to a decrease in the compressive strain from −0.71% to −0.44% as shown in Fig. 2(d). This is due to the increase in the film crystallinity as the deposition temperature increases, along with a continuous reduction in compressive strain along the b-axis.⁴¹ With respect to oxygen partial pressure during deposition, the compressive strain along the b-axis is minimum at −0.48% for the sample deposited at 5 mTorr, while it increases to −0.93% and −0.97% for samples deposited at 2.5 mTorr and 7.5 mTorr oxygen pressure as shown in Fig. 2(c). This may be due to the three-dimensional nature of the V–O bond, as extension of the lattice parameter along the out-of-plane b-axis usually leads to compression along the other two axes, and vice versa, owing to the lattice distortion by oxygen vacancies (discussed later).⁴² The non-linear effects of increasing oxygen content in the chamber have been reported earlier.²⁴ In summary, due to the three-dimensional nature of V–O bonds, since compression in one direction leads to stretching along the other two, there is a possibility that the VO₂ film has an optimal zone of minimum compressive strain along the b-axis with respect to the in situ oxygen partial pressure. Any change in oxygen pressure from 5 mTorr will increase the out-of-plane compressive strain in the film.

Fig. 2 XRD analysis of the VO₂ samples – the temperature-wise comparisons for VO₂ films deposited at 5 mTorr oxygen pressure (a), the changes in the XRD scans with respect to oxygen pressure keeping the deposition substrate temperature constant at 600 °C (b), and the respective strains calculated (c and d). φ scan results confirming the epitaxial nature of the VO₂ film (e), and the RSM plot of the VO₂ film deposited at 5 mTorr oxygen pressure and 600 °C substrate temperature (f).

Phi (φ) scans of the 5 mTorr sample, deposited at 600 °C, are shown in Fig. 2(e). Here, the φ scan of the (012) plane (also called r-plane) of sapphire (2θ = 25.56°; ψ = 57.7°) showed three-fold symmetry, each peak spaced 120° apart, confirming the three-fold symmetry of the trigonal substrate. φ scans of VO₂ for the (011) plane (2θ = 27.87°; ψ = 44.9°) confirmed the two-fold symmetry of monoclinic VO₂ on each of the three r-planes, thus giving six peaks in φ scan.^38,43 The (011) VO₂ scans demonstrated 30° rotation with respect to the [11̄02] sapphire axis, which matches well with earlier reports.³⁸ The (020) as well as (002) peaks of VO₂ have approximately the same d-spacing (2.27 Å), as well as similar tilts with respect to the (011) plane (45° and 44.9°). Hence, the out-of-plane XRD results cannot confirm on their own if the VO₂ peaks obtained in this setup are from (020) or (002) orientation. To clarify further on this issue, the φ scans for the (110) peak with respect to (020) and (002) out of plane VO₂ orientations are shown in ESI Fig. S1.† The (110) orientation for VO₂ has Bragg angle 2θ = 26.92°, with its tilt with respect to the (020) and (002) planes being ψ₍₀₂₀₎ = 43.1° and ψ₍₀₀₂₎ = 68.4° respectively. Fig. S1(a)† confirms the (020) out-of-plane orientation for the VO₂ film grown on (0001) sapphire, as the other configuration yields a much poorer XRD plot, as shown in Fig. S1(b).† Moatti et al. have shown the critical thickness for VO₂ grown on c-sapphire with an NiO buffer layer to be approximately 15 nm, while all of the films grown in this study were determined by the profilometer to be approximately 50 nm.⁴⁴ This is also confirmed by the study of Moatti et al., in which they showed that VO₂ films grown epitaxially on c-Al₂O₃ substrates grow with (200) and (020) out of plane grown for thickness below and above the critical limit respectively.⁴⁵ Han et al. have reported the critical thickness of an epitaxial VO₂ thin film on c-sapphire to be approximately 4 nm.⁴⁶ The (020) orientation growth observed in the VO₂ films grown thus confirms that films have thickness above the critical limit. Reciprocal Space Mapping (RSM) of the VO₂ film deposited at 5 mTorr oxygen pressure and 600 °C is shown in Fig. 2(f), which confirms the epitaxial nature of the film. The film shows a very small spread in the reciprocal axis (ΔQ_x = 0.02 Å⁻¹ along Q_x and ΔQ_z = 0.5 Å⁻¹ along Q_z) confirming the high quality of the film. A larger spread is associated with more defects, such as edge dislocations and grain boundaries, and therefore likely to be nucleation sites for other phases, such as M₂.⁴⁷ From these ΔQ_x and ΔQ_z values, the in-plane and out-of-plane correlation length can be calculated as d_ip = 2π/ΔQ_x and d_op = 2π/ΔQ_z respectively. The d_ip and d_op have been calculated to be 31.4 nm and 1.26 nm respectively. d_ip being much larger than d_op is indicative of in-plane nucleation of VO₂ being the dominant factor, rather than layer-by-layer growth.^48,49

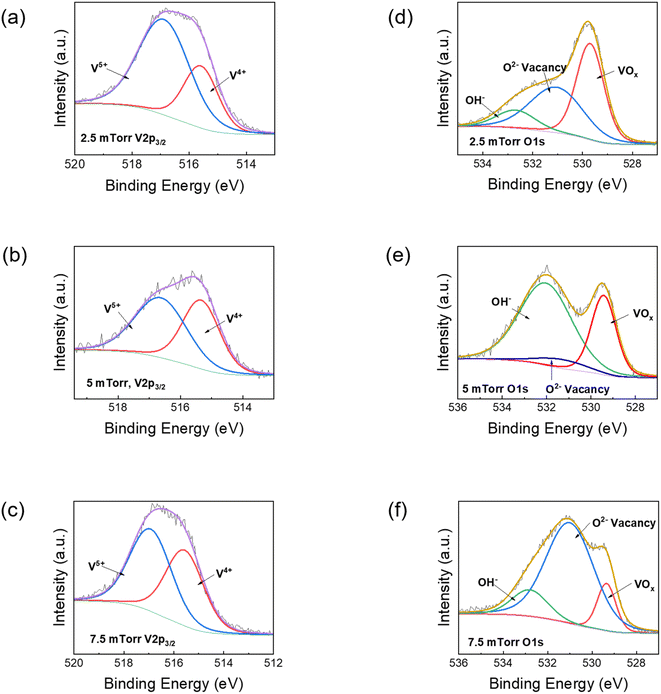
Further, the effect of oxygen partial pressure on the oxygen vacancies was studied using XPS. Fig. 3 shows the XPS data, in which the de-convoluted peaks of the V 2p_1/2, V 2p_3/2 and O 1s_1/2 for films deposited at 2.5 mTorr, 5 mTorr and 7.5 mTorr are presented. The de-convolution of V 2p peaks is explained in Fig. 3(a), (c) and (e), while the analysis of O 1s spectra is shown in Fig. 3(b), (d) and (f) for VO₂ films deposited at 2.5 mTorr, 5 mTorr and 7.5 mTorr respectively. The substrate temperature for all the films was 600 °C. The V 2p_3/2 peaks are used for comparison. The V 2p_3/2 peak is de-convoluted into two peaks for every sample, centred at 515.6 eV (corresponding to V⁴⁺) and 516.8 eV (corresponding to V⁵⁺), with the values matching with the literature.^24,50,51 The XPS results did not validate the presence of any V³⁺ ions. The lack of any V₂O₃ peaks in XRD results can be used in conjunction as evidence that V₂O₃ did not play any role in the SMT analysis of the VO₂ films. The results in Fig. 3(a), (c) and (e) show the lowest V⁴⁺ content for the VO₂ film formed at 2.5 mTorr partial oxygen pressure (30.54%), while higher values of V⁴⁺ at 45.28% and 45.83% are observed at oxygen pressures of 5 mTorr and 7.5 mTorr respectively. This might be due to overaccumulation of O²⁻ ions on the substrate surface, which results in a smaller number of oxygen ions being able to diffuse into the film and both with vanadium ions, a phenomenon observed in previous reports.^23,24 It also explains why the VO₂ samples deposited at 5 mTorr and 7.5 mTorr oxygen pressure have higher switching ratios in the resistivity vs. temperature plots, as it is VO₂ that is primarily responsible for the metal-to-insulator transition (discussed later). The binding energy of V⁴⁺ for the VO₂ fabricated at 5 mTorr is also the lowest among the three (515.33 eV), which suggests increased electronegativity compared to the other films (515.59 eV for 2.5 mTorr and 515.56 eV for 7.5 mTorr respectively). In the case of the O 1s peak, the one attributed to VO_x bonding at 529.42 ± 0.2 eV has the highest percentage for the film fabricated at 2.5 mTorr, shown in Fig. 3(b), while it decreases with increases in oxygen pressure. However, in the case of a film fabricated at 2.5 mTorr, fewer V⁴⁺ ions are available compared to V⁵⁺ for bonding with O²⁻, while in the case of 7.5 mTorr oxygen pressure, the VO_x content within the sample is the lowest, both in terms of intensity as well as percentage. Hence, it is plausible that the VO₂ content is best formed in the film fabricated at 5 mTorr oxygen pressure.

Fig. 3 XPS plots of the VO₂ samples deposited on (0001) Al₂O₃ – (a, b and c) the de-convolution of V 2p peaks for VO₂ films formed at varying oxygen pressure levels (substrate temperature being 600 °C), and (d, e and f) the de-convoluted XPS data points of the O 1s level corresponding to the V 2p peaks in (a), (b) and (c) respectively.

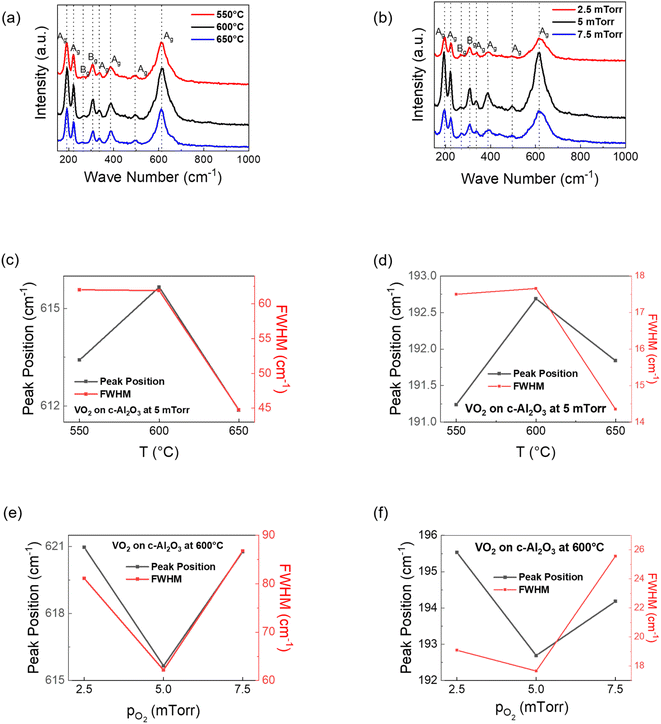
To further understand the effect of temperature and oxygen partial pressure on the VO₂ film quality, Raman spectroscopy was performed. The peaks in Raman spectroscopy plots are categorized as per the wave number at which they're located (<400 cm⁻¹ for V–O–V bending spectra, 400 to 800 cm⁻¹ for V–O–V stretching mode and >800 cm⁻¹ for V=O stretching mode),⁵² with the Raman peak at 192 cm⁻¹ being also attributed to V–V twisting vibrations.^53,54 For both V–O and V–V peaks, it is seen that the shift to higher frequencies is highest for the VO₂ film deposited at 600 °C as shown in Fig. 4(a). This indicates that the lattice parameter stretching for the sample deposited at 600 °C is the lowest. A smaller V–O bond length should drive up the transition temperature, since it makes it difficult for free electrons to be available for conduction. This correlates with the R–T results (discussed later), in which the transition temperature for the 600 °C VO₂ sample is the highest. However, a shorter V–V bond should reduce the transition temperature. Since for the film deposited at 600 °C, both the V–V as well as V–O bonds are the smallest, it suggests that the entire cell shrinks at certain deposition parameters, with the competition between V–O and V–V bonds determining whether the MIT increases or decreases. XRD plots indicate increasing relaxation along the b-axis with increasing deposition temperatures. From these three results, it can be understood that for lower deposition temperatures (550 °C and 600 °C), increasing deposition temperatures initiates b-axis relaxation as well as contraction along the in-plane axes. But for deposition at 650 °C, the VO₆ cell expands in all directions. Comparing between VO₂ films deposited at different oxygen pressures (substrate temperature for all of them being 600 °C), the trend in Fig. 4(b) is the opposite. The stretching frequency for the 5 mTorr VO₂ film is the lowest in both V–O and V–V bonds, indicating larger bond length for VO₂ deposited at 5 mTorr.⁵³ This is probably due to the lowest out-of-plane compressive strain for the 5 mTorr film, compared to the other films. Here, the peak corresponding to the V–O as well as V–V stretching shifts to higher frequency (i.e. lower bond length) for 2.5 mTorr as well 7.5 mTorr VO₂ samples as shown in Fig. 4(d). This means that the entire cell shrinks for films deposited at 2.5 mTorr as well as 7.5 mTorr oxygen pressure, with maximum cell volume for VO₂ films deposited at 5 mTorr in oxygen pressure-wise comparison. Moatti et al. have suggested that increasing vacancy leads to densification of the VO₂ lattice.⁵⁵ But the sudden shrinking of the lattice parameters at higher oxygen pressure (7.5 mTorr) suggests the relationship is not linear, since the trend of increasing MIT with increasing oxygen pressure continues to hold (discussed later) despite non-linear XRD and Raman trends. The FWHM comparison from Fig. 4(c)–(f) shows a minimum value for the VO₂ film deposited at 5 mTorr and 600 °C in oxygen pressure-wise comparison (for both V–V and V–O bonds), indicating that VO₂ films formed at this pressure are of better quality. However, the substrate temperature-wise comparison shows a further drop in FWHM at 650 °C, since higher deposition temperature leads to a more refined crystallinity. The signal-to-noise ratio for all the VO₂ attributed peaks was also the highest for the film deposited at 5 mTorr, further validating the observation that optimal VO₂ films on (0001) Al₂O₃ are formed at 5 mTorr oxygen pressure and 600 °C substrate temperature. The reflectivity analysis performed for the VO₂ films grown at 5 mTorr oxygen pressure, with varying substrate temperature is shown in ESI Fig. S2.† From the plots, we obtained the direct band gap values for the films grown at 550 °C, 600 °C and 650 °C substrate temperatures to be respectively 0.64 eV, 0.82 eV and 0.78 eV respectively. These are all close to the direct band gap for bulk VO₂ as reported in the literature.^5,10 These values also match with the T_c values obtained, which have been discussed later. Larger T_c implies an unstable metallic rutile phase, which should correspond to a larger band gap value, and vice versa. The Kubelka–Munk model was used for this analysis, as reported in the literature.⁵⁶

Fig. 4 Raman analysis of the VO₂ samples – (a) the Raman analysis of the substrate temperature-wise, and (b) the variation in Raman plot with change in oxygen pressure during deposition; (c and d) the respective FWHM and position of the main V–O and V–V stretching peaks with respect to deposition temperature respectively, and (e and f) oxygen pressure-wise comparison for the V–O and V–V peaks respectively.

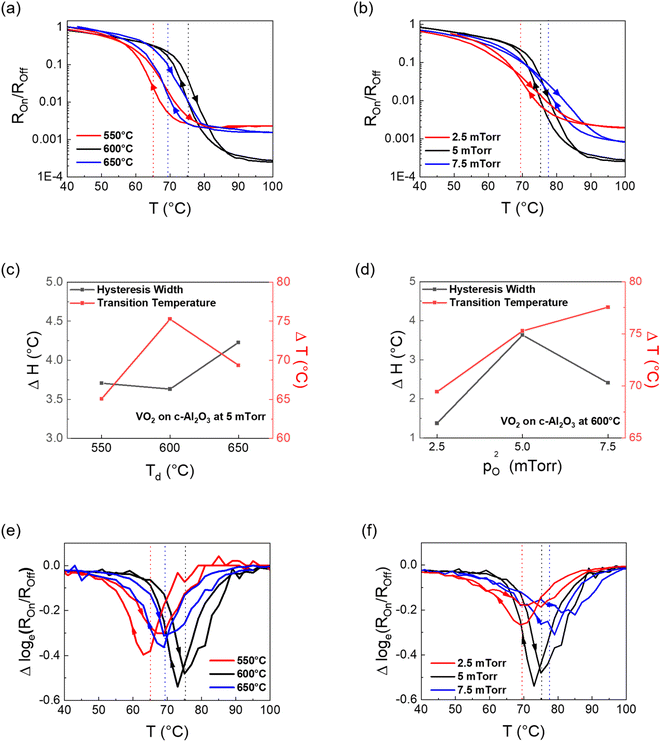
Finally, the phase transition in VO₂ thin films was studied by measuring the resistivity of the film as a function of temperature using a custom four-point-probe setup. The resistivity vs. temperature (R–T) plots of the VO₂ samples are shown in Fig. 5. The heating and cooling curves for each sample have been indicated by arrows. The T_c for each sample was calculated by Gaussian fitting (not shown here) of both the logarithmic differential curves (heating and cooling) in Fig. 5(e) and (f), followed by averaging the value of both the troughs. All the plots show good switching (3 orders or more) with transition temperature greater than the 68 °C value of bulk VO₂. From Fig. 5(a), it is seen that the switching ratio reaches a maximum of 2 × 10⁻⁴ for the VO₂ film deposited at 600 °C substrate temperature, while it reduces to 1.9 × 10⁻³ and 1.2 × 10⁻³ for VO₂ films deposited at 550 °C and 650 °C respectively. Overall, the results match well with the inferences derived from XRD, XPS and Raman spectroscopy discussions in previous sections. This can possibly indicate a reduction in quality of the VO₂ formed for substrate temperatures other than 600 °C. From the XRD plots, it should be presumed that the transition temperature should be highest for the VO₂ film deposited at 550 °C, since it has the highest out-of-plane compressive strain. However, that is not the case. In fact, the 550 °C sample has lower transition temperature (65.06 °C) compared to the VO₂ film deposited at 600 °C (75.26 °C), as shown in Fig. 5(e). This could be explained by competition between different axial strains as well as the changes in V–O bond length alongside V–V bond length, as explained in the previous section. While the interplanar spacing along the b-axis increases with increasing substrate deposition temperature, as shown by the XRD plots in Fig. 2(a), it also means that the lattice parameter along the other two axes should reduce. Hence, for VO₂ films formed at 650 °C, it is possible that the V–O bond length expansion overcompensates for the V–V bond length expansion, thus causing the T_c to reduce again. The hysteresis width comparison for the three samples is given in Fig. 5(c). The difference between the heating and cooling curves is the smallest for the VO₂ film deposited at 600 °C. Compared with higher switching amplitude, it indicates higher film quality and lower grain boundary density translating to lower interfacial energy.¹⁹Fig. 5(b) and (d) compare the R–T results with a change in oxygen partial pressure during deposition, where all the VO₂ films were deposited at 600 °C. Clearly, the T_c reduces with the reduction in oxygen partial pressure during deposition (69.4 °C for 2.5 mTorr, 75.3 °C for 5 mTorr and 77.6 °C for 7.5 mTorr), as shown by the differential plots in Fig. 5(f). The increasing T_c with a corresponding increase in oxygen pressure can be attributed to oxygen vacancies, since oxygen vacancies act as conducting channels and help to stabilize the metallic tetragonal phase of VO₂.²³ The hysteresis width for the film deposited at 600 °C, however, is the highest when compared across oxygen partial pressures. Compressive strain along the c-axis is associated with a reduction in MIT owing to the stabilization of the denser, high-temperature metallic phase.⁴¹ Since the XRD results in this case show compressive strain along the b-axis, DFT calculations were done to understand the strain effect on the phase stability.

Fig. 5 Resistivity analysis of the VO₂ on c-cut sapphire as a function of temperature – (a) the comparison between three VO₂ films deposited at 550 °C, 600 °C and 650 °C substrate temperatures, with the oxygen pressure constant at 5 mTorr, (b) the R–T comparisons for the three films with varying oxygen pressures of 2.5 mTorr, 5 mTorr and 7.5 mTorr, with the substrate temperature being kept constant at 600 °C in all of them, (c and d) their corresponding ΔH and T_c analysis; (e and f) the differential plots of the results in (a) and (b), from which T_c is calculated (heating and cooling curves in all the plots are indicated by arrows and the T_c for each sample is shown by a vertical dashed line).

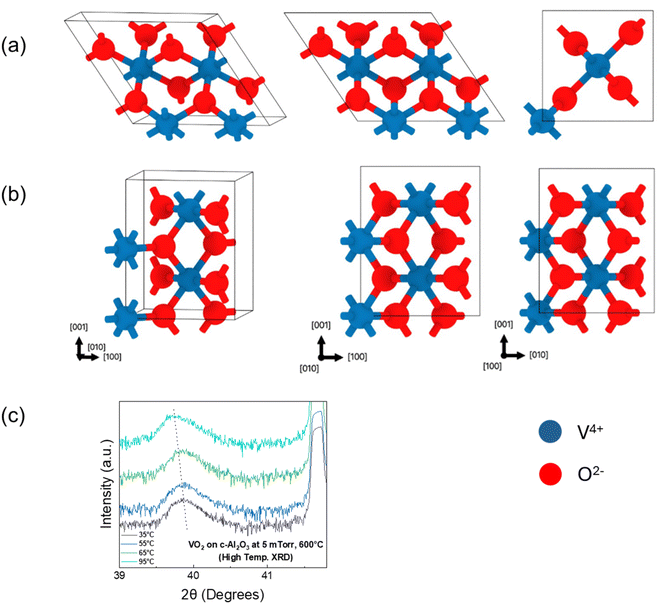
Table 1 summarizes the lattice parameters and the energetics of the bulk and strained M₁ & R phases. Our relaxed parameters for bulk VO₂ are within 4% of experimental lattice parameters which is typical in DFT calculations. Our calculations reveal the energy difference between the high temperature R and low temperature M₁ phases to be 82.1 meV per VO₂ at 0 K. We find that the in-plane strains on M₁ mimic the sapphire substrate, resulting in −1.98% strain along the out-of-plane direction (010) as compared to the bulk M₁ phase.³⁸ The value for this out-of-plane strain on the R phase is found to be −1.03%, which is lower and consistent with the experimental results in this study. Moreover, the in-plane strains associated with the sapphire substrate increase the 0 K energy difference between R and M₁ phases to 118.8 meV per VO₂, which corresponds to higher stability of the M₁ phase at 0 K and higher M₁ → R transformation temperatures.³⁸ We find similar behaviour experimentally where the deposition of the VO₂ thin film on the sapphire substrate increases the transformation temperature as compared to the bulk VO₂. In experiments, n unit cells of the substrate can match with m unit cells of the film to minimize the epitaxial strain. We note that we are using an upper limit where n = m, which provides the upper bound. The experimental strain will be some fraction n/m, impacting the quantitative predictions (which will lie in between our bulk and strained calculation). However, the qualitative picture and two main conclusions will remain the same: (i) the presence of substrate results in lower out-of-plane strain in the R phase compared to M₁ and (ii) the c-Al₂O₃ substrate stabilizes the M₁ phase and will lead to higher transformation temperature. Fig. 6(a) and (b) show the relaxed structures of the bulk VO₂ for monoclinic and tetragonal phases. At higher temperatures, VO₂ retains its (020) out-of-plane orientation, but it is characterized by a reduction in d-spacing. High-temperature XRD was performed for the VO₂ film deposited at 5 mTorr oxygen pressure and 600 °C substrate temperature, the results of which are plotted in Fig. 6(c). At 35 °C, the film has a d-spacing of 2.258 Å (2θ = 39.87°), which shifts to a d-spacing of 2.264 Å (2θ = 39.76°), when heated up to temperatures at which complete transition from the monoclinic M₁ (020) to tetragonal T (020) phase has occurred, which is consistent with the DFT calculations.

Table 1 Lattice parameters and the energetics of the bulk and strained monoclinic (M₁) and rutile (R) phases. The energy of the M₁ phase is used as a reference for both bulk and strained cases. The in-plane lattice parameters (a, c, and β) for the strained case correspond to the experimental values for the sapphire substrate. The out-of-plane lattice parameters (b) are fully relaxed

	Phase	a (Å)	b (Å)	c (Å)	α (°)	β (°)	γ (°)	E − EM1 (meV per VO2)
Bulk	M1	6.01	4.43	5.36	90	124.12	90	0
	R	4.54	4.54	5.71	90	90	90	82.1
Strained	M1	5.74	4.35	5.48	90	120	90	0
	R	4.69	4.49	5.51	90	90	90	118.8

---

Fig. 6 Schematic of the VO₂ in bulk mode for (a) monoclinic and (b) tetragonal phases, and (c) the corresponding experimental results of high temperature X-ray diffraction, with the shift in the 2θ value confirming the transition at high temperatures.

Conclusion

In this work, we successfully fabricated epitaxial VO₂ thin films on c-Al₂O₃ substrates by the pulsed laser deposition technique. T_c tuning was achieved by varying the two main parameters of deposition – substrate temperature and partial pressure of oxygen during deposition. The epitaxial nature of VO₂ films was confirmed by XRD scans, while Raman spectroscopy identified the various phonon modes associated with VO₂. The XPS scans confirmed the C, V and O contents in the sample, and described the changing of quantity of each element due to varying the deposition parameters. The R–T results showed maximum switching for the VO₂ film deposited at 600 °C substrate temperature and 5 mTorr oxygen pressure, with high switching unlocking potential for its use in memristive devices. DFT calculations supported the experimental findings. Our study provides a better understanding of the interplay between strain and oxygen vacancies and their effect on the physical properties of VO₂ thin films.

Data availability

The data supporting the findings presented in this study are not publicly available at this time, but may be obtained from the corresponding author upon reasonable request.

Conflicts of interest

There are no conflicts to declare.

References

1. R. Xie, C. T. Bui, B. Varghese, Q. Zhang, C. H. Sow, B. Li and J. T. L. Thong, Adv. Funct. Mater., 2011, 21, 1602–1607.
2. S. Lee, C. Cheng, H. Guo, K. Hippalgaonkar, K. Wang, J. Suh, K. Liu and J. Wu, J. Am. Chem. Soc., 2013, 135, 4850–4855.
3. B. Hu, Y. Ding, W. Chen, D. Kulkarni, Y. Shen, V. V. Tsukruk and Z. L. Wang, Adv. Mater., 2010, 22, 5134–5139.
4. E. Strelcov, A. Tselev, I. Ivanov, J. D. Budai, J. Zhang, J. Z. Tischler, I. Kravchenko, S. V. Kalinin and A. Kolmakov, Nano Lett., 2012, 12, 6198–6205.
5. Z. Shao, X. Cao, H. Luo and P. Jin, NPG Asia Mater., 2018, 10, 581–605.
6. S. H. Bae, S. Lee, H. Koo, L. Lin, B. H. Jo, C. Park and Z. L. Wang, Adv. Mater., 2013, 25, 5098–5103.
7. Z. Khan, P. Singh, S. A. Ansari, S. R. Manippady, A. Jaiswal and M. Saxena, Small, 2021, 17(4), e2006651.
8. P. Schofield, A. Bradicich, R. M. Gurrola, Y. Zhang, T. D. Brown, M. Pharr, P. J. Shamberger and S. Banerjee, Adv. Mater., 2023, 35, 2205294.
9. Y. Yang, X. Mao, Y. Yao, H. Huang, Y. Lu, L. Luo, X. Zhang, G. Yin, T. Yang and X. Gao, J. Appl. Phys., 2019, 125, 082508.
10. W. K. Hong, S. Cha, J. I. Sohn and J. M. Kim, J. Nanomater., 2015, 538954.
11. J. D. Budai, A. Tselev, J. Z. Tischler, E. Strelcov, A. Kolmakov, W. J. Liu, A. Gupta and J. Narayan, Acta Mater., 2013, 61, 2751–2762.
12. K. Liu, S. Lee, S. Yang, O. Delaire and J. Wu, Mater. Today, 2018, 21, 875–896.
13. X. Gao, C. M. M. Rosário and H. Hilgenkamp, AIP Adv., 2022, 12, 015218.
14. M. Samizadeh Nikoo, R. Soleimanzadeh, A. Krammer, G. Migliato Marega, Y. Park, J. Son, A. Schueler, A. Kis, P. J. W. Moll and E. Matioli, Nature Electronics, 2022, 5, 596–603.
15. Y. Yang, L. Wang, H. Huang, C. Kang, H. Zong, C. Zou, Y. Lu, X. Li, B. Hong and C. Gao, Ceram. Int., 2018, 44, 3348–3355.
16. T. H. Yang, R. Aggarwal, A. Gupta, H. Zhou, R. J. Narayan and J. Narayan, J. Appl. Phys., 2010, 107, 053514.
17. J. Jian, X. Wang, S. Misra, X. Sun, Z. Qi, X. Gao, J. Sun, A. Donohue, D. G. Lin, V. Pol, J. Youngblood, H. Wang, L. Li, J. Huang and H. Wang, Adv. Funct. Mater., 2019, 29, 1903690.
18. Z. He, J. Jian, S. Misra, X. Gao, X. Wang, Z. Qi, B. Yang, D. Zhang, X. Zhang and H. Wang, Nanoscale, 2020, 12, 17886–17894.
19. Z. He, J. Jian, L. Quigley, N. A. Bhatt, J. P. Barnard, C. A. Mihalko, H. Wang, X. L. Phuah, J. Lu, X. Xu and H. Wang, Adv. Phys. Res., 2023, 2, 2300031.
20. K. Mulchandani, A. Soni, K. Pathy and K. R. Mavani, Superlattices Microstruct., 2021, 154, 106883.
21. Y. Yang, G. Wang, W. Huang, C. Wang, Y. Yao, X. Mao, H. Lin, T. Zhang, H. Qiu, Z. Li, H. Zhang, Y. Yin, J. Guo, Y. Guan, W. Yan, Z. Luo, C. Zou, Y. Tian, G. Xiao, X. Li and C. Gao, Sci. China Mater., 2021, 64, 1687–1702.
22. A. Moatti, R. Sachan and J. Narayan, J. Appl. Phys., 2020, 128, 045302.
23. S. Kittiwatanakul, J. Laverock, D. Newby, K. E. Smith, S. A. Wolf and J. Lu, J. Appl. Phys., 2013, 114, 053703.
24. S. A. Bukhari, S. Kumar, P. Kumar, S. P. Gumfekar, H. J. Chung, T. Thundat and A. Goswami, Appl. Surf. Sci., 2020, 529, 146995.
25. L. Fan, X. Wang, F. Wang, Q. Zhang, L. Zhu, Q. Meng, B. Wang, Z. Zhang and C. Zou, RSC Adv., 2018, 8, 19151–19156.
26. E. K. Koussi, F. Bourquard, T. Tite, D. Jamon, F. Garrelie and Y. Jourlin, Appl. Surf. Sci., 2020, 521, 146267.
27. W. Lu, L. M. Wong, S. Wang and K. Zeng, Journal of Materiomics, 2018, 4, 360–367.
28. P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. De Gironcoli, P. Delugas, R. A. Distasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kücükbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Otero-De-La-Roza, L. Paulatto, S. Poncé, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys.: Condens. Matter, 2017, 29, 465901.
29. P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. De Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502.
30. P. Giannozzi, O. Baseggio, P. Bonfà, D. Brunato, R. Car, I. Carnimeo, C. Cavazzoni, S. De Gironcoli, P. Delugas, F. Ferrari Ruffino, A. Ferretti, N. Marzari, I. Timrov, A. Urru and S. Baroni, J. Chem. Phys., 2020, 152(15), 154105.
31. J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406.
32. P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953.
33. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758.
34. S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505.
35. T. Yao, X. Zhang, Z. Sun, S. Liu, Y. Huang, Y. Xie, C. Wu, X. Yuan, W. Zhang, Z. Wu, G. Pan, F. Hu, L. Wu, Q. Liu and S. Wei, Phys. Rev. Lett., 2010, 105, 226405.
36. J. Wei, H. Ji, W. Guo, A. H. Nevidomskyy and D. Natelson, Nat. Nanotechnol., 2012, 7, 357–362.
37. Y. Cui, S. Shi, L. Chen, H. Luo and Y. Gao, Phys. Chem. Chem. Phys., 2015, 17, 20998–21004.
38. A. Moatti, R. Sachan, J. Prater and J. Narayan, ACS Appl. Mater. Interfaces, 2017, 9, 24298–24307.
39. A. Ainabayev, D. Mullarkey, B. Walls, D. Caffrey, K. Zhussupbekov, A. Zhussupbekova, C. Ilhan, A. Kaisha, P. Biswas, A. Tikhonov, O. Murtagh and I. Shvets, ACS Appl. Nano Mater., 2023, 6, 2917–2927.
40. J. Jian, A. Chen, Y. Chen, X. Zhang and H. Wang, Appl. Phys. Lett., 2017, 111, 153102.
41. S. A. Howard, E. Evlyukhin, G. Páez Fajardo, H. Paik, D. G. Schlom and L. F. J. Piper, Adv. Mater. Interfaces, 2021, 8, 2001790.
42. C. Zhang, G. Liu, X. Geng, K. Wu and M. Debliquy, Sens. Actuators, A, 2020, 309, 112026.
43. L. Diebold, T. Maroutian, L. Largeau, N. Guiblin, R. Bude, G. Garry, O. M. Ishchenko and P. Aubert, Appl. Phys. Lett., 2023, 123, 131601.
44. A. Moatti, R. Sachan and J. Narayan, Mater. Res. Lett., 2020, 8, 16–22.
45. A. Moatti, R. Sachan, V. R. Cooper and J. Narayan, Sci. Rep., 2019, 9, 3009.
46. K. Han, L. Wu, Y. Cao, H. Wang, C. Ye, K. Huang, M. Motapothula, H. Xing, X. Li, D.-C. Qi, X. Li and X. R. Wang, ACS Appl. Mater. Interfaces, 2021, 13, 16688–16693.
47. Y. Ji, Y. Zhang, M. Gao, Z. Yuan, Y. Xia, C. Jin, B. Tao, C. Chen, Q. Jia and Y. Lin, Sci. Rep., 2014, 4, 4854.
48. E. Ekström, S. Hurand, A. le Febvrier, A. Elsukova, P. O. Å. Persson, B. Paul, F. Eriksson, G. Sharma, O. Voznyy, D. G. Sangiovanni, G. Ramanath and P. Eklund, Mater. Des., 2023, 229, 111864.
49. R. Yue, Y. Nie, L. A. Walsh, R. Addou, C. Liang, N. Lu, A. T. Barton, H. Zhu, Z. Che, D. Barrera, L. Cheng, P. R. Cha, Y. J. Chabal, J. W. P. Hsu, J. Kim, M. J. Kim, L. Colombo, R. M. Wallace, K. Cho and C. L. Hinkle, 2D Mater., 2017, 4, 045019.
50. G. Silversmit, D. Depla, H. Poelman, G. B. Marin and R. De Gryse, J. Electron Spectrosc. Relat. Phenom., 2004, 135, 167–175.
51. M. J. Powell, I. J. Godfrey, R. Quesada-Cabrera, D. Malarde, D. Teixeira, H. Emerich, R. G. Palgrave, C. J. Carmalt, I. P. Parkin and G. Sankar, J. Phys. Chem. C, 2017, 121, 20345–20352.
52. M. Taha, S. Walia, T. Ahmed, D. Headland, W. Withayachumnankul, S. Sriram and M. Bhaskaran, Sci. Rep., 2017, 7, 17899.
53. E. Evlyukhin, S. A. Howard, H. Paik, G. J. Paez, D. J. Gosztola, C. N. Singh, D. G. Schlom, W. C. Lee and L. F. J. Piper, Nanoscale, 2020, 12, 18857–18863.
54. K. Okimura, N. Hanis Azhan, T. Hajiri, S. I. Kimura, M. Zaghrioui and J. Sakai, J. Appl. Phys., 2014, 115, 153501.
55. A. Moatti, R. Sachan, S. Gupta and J. Narayan, ACS Appl. Mater. Interfaces, 2019, 11, 3547–3554.
56. K. Brajesh, S. Ranjan, R. Kumar, R. Gupta, A. Dixit and A. Garg, J. Am. Ceram. Soc., 2023, 106, 6769–6777.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4na00682h

---