Designing 2D stripe winding network through crown-ether intermediate Ullmann coupling on Cu(111) surface

Abstract

Chemical synthesis typically yields the most thermodynamically stable ordered arrangement, a principle also governing surface synthesis on an atomically level two-dimensional (2D) surface, fostering the creation of structured 2D formations. The linear connection arising from energetically stable chemical bonding precludes the generation of a 2D random network comprised of one-dimensional (1D) convoluted stripes through on-surface synthesis. Nonetheless, we underscored that on-surface synthesis possesses the capability not solely to fashion a 2D ordered linear network but also to fabricate a winding 2D network employing a precursor with a soft ring and intermediate state bonding within the Ullmann reaction. Here, on-surface synthesis was exhibited on Cu(111) employing a 2D self-assembled monolayer array of 4,4′,5,5′-tetrabromodibenzo[18]crown-6 ether (BrCR) precursors. These precursors were purposefully structured, with a crown ether ring at the core and Br atoms positioned at the head and tail ends, facilitating preferential connections along the elongated axis to foster a 1D stripe configuration. We illustrate how adjustments in the quantities of the intermediate state, serving as a primary linkage, can yield a labyrinthine, convoluted winding 2D network of stripes. The progression of growth, underlying mechanisms, and electronic structures were scrutinized using an ultrahigh vacuum low-temperature scanning tunneling microscopy and spectroscopy (STM/STS) setup combined with density functional theory (DFT) calculations. This experimental evidence opens a novel functionality in leveraging on-surface synthesis for the formation of a 2D random network. This discovery holds promise as a pioneering constituent in the construction of a ring host supramolecule, augmenting its capability to ensnare guest atoms, molecules, or ions.

---

New concepts

The STM experimental investigation illustrated the creation of a 2D monolayer film comprising randomly connected stripe networks formed by linking individual tetrabrominated crown ether molecules through three distinct connections. While intermediate states have conventionally been deemed energetically unstable, our experiments substantiated the stability of the resultant 2D network at room temperature (300 K) and its formation feasibility at a relatively lower temperature of 453 K. This sheds new light on a novel approach for 2D network synthesis. Leveraging the flexibility and resilience of these stripes, a densely packed 2D network film was achieved on a flat Cu(111) surface. Given the inherent flexibility of the crown ether molecule's core ring, this breakthrough holds significant promise as a foundational building block in fabricating ring host supramolecules, thereby enhancing its capacity to encapsulate guest atoms, molecules, or ions.

1. Introduction

Exploration of on-surface synthesis stands as an advanced bottom-up approach for fabricating expansive two-dimensional (2D) molecular assemblies,^1–12 notably graphene (Gr) or graphene nanoribbons (GNR)^13–22 and porous organic frameworks (POFs)^23,24 encompassing covalent organic molecular frameworks (COFs).^25,26

This method harnesses highly functional, adaptable monolayer organic films, significantly broadening their potential applications across diverse fields, including gas storage and separation, catalysis, optoelectronics, sensing, and adsorption of small molecules.^27–39

The Ullmann reaction^40–42 conducted on noble metal surfaces extensively employs inflexible and planar benzene ring compounds as precursors for COFs creation. Principally, the reaction mechanism on Cu surfaces has undergone rigorous investigation, leading to the elucidation of its procedural intricacies.^43–45 For example, in the case of the Ullmann reaction from bromotriphenylene to bistriphenylene on a Cu(111) surface, it was found that halogen, first, dissociates and adsorbs on Cu and leaves a phenyl radical. Second, a phenyl–Cu–phenyl intermediate state is formed from a Cu adatom.^43,46 Third, when heating above 660 K, the C–C (phenyl–phenyl) bonding is made, and the Cu atom disappears. However, organic molecules can be easily damaged or sublimated at such a high temperature. Therefore, understanding and controlling the on-surface synthesis process at appropriate temperatures in the range of 300–500 K could be crucial.

In this study, we demonstrate the generation of a non-superimposing 2D stripe random network via on-surface synthesis employing pliable precursors and their intermediate-state bonding. Such random networks elude formation through the use of rigid, durable, and flat precursors like phthalocyanines or porphyrins, which, however, yield ordered networks.⁴⁷

Furthermore, this growth process prohibits the emergence of a second-layer stripe formation, thereby precluding three-dimensional (3D) phase formation. This stands in contrast to the construction of 3D overlapping stripes achieved through the conventional drop-casting of graphene nanoribbons or carbon nanotube solutions.^48–50

The internal ring within the crown ether molecule stands as a potential candidate among flexible precursors for the generation of a random network. A 4,4′,5,5′-tetrabromodibenzo[18]crown-6 ether (BrCR) molecule, consisting of a center crown ether ring with two phenyl rings at both sides, was used.⁵¹ Owing to the pliability in the crown-ether ring, both bulk crystal and gas phase configurations exhibit bent ring structures.⁵²

Moreover, the design of 2D stripes utilizing BrCR precursors poses a challenge due to conventional bulk methods that yield aggregation when employing BrCR and Cu powder synthesis in bulk, rendering the synthesis of the stripe unattainable.

The precise alignment control of BrCR precursors on Cu(111) assumes a pivotal role, as it is imperative for stripe formation that the Ullmann reaction selectively occurs between two BrCR molecules orientated in the same direction. This orientation ensures that the ‘head’ and ‘tail’ ends of the molecules, housing the Br atoms, face each other—a condition satisfied by the BrCR monolayer on Cu(111).^52–55 Repetition of such a linear connection in a consistent direction yields stripes. By selecting the annealing temperature conducive to intermediate state connections, successful growth of a 2D random stripe network becomes feasible, thereby exploring the potential of on-surface synthesis in generating amorphous-like, asymmetrical nanopatterns.

This CR ring polymer exhibits significantly greater durability compared to individual molecules, demonstrating stability even at 300 K. Moreover, the crown ring component within the CR polymer possesses the capacity to encapsulate guest atoms, molecules, and ions, presenting vast potential for a diverse array of applications. For instance, incorporating a guest transition-metal atom could yield polymers with enhanced functionality,⁵⁶ spanning quantum dot networks,^57–60 spintronics,^61,62 biomedicine,^63,64 drug delivery,^65,66 catalysts,^67–69 and water purification.⁷⁰ Furthermore, integrating the host “wheel” BrCR ring molecule with the guest “axel” molecule could result in the formation of nanomolecular machine polymers.^71–73

2. Experimental section

2.1 Characterization of synthesized BrCR precursors

First, BrCR was synthesized and characterized based on the method described in the literature.²⁹ Field-desorption mass spectra (FDMS) of Ullmann coupling products were observed by JEOL JMS-T200GC AccuTOF GCx. CCDC 1901496 contains the supplementary crystallographic data (see Fig. S4–S6, ESI†).

2.2 Sample preparations

A Cu(111) single crystal (diameter 6 mm, MatecK, purity 99.999%) was carefully sputtered and annealed to obtain clean and atomically flat surfaces in the preparation chambers (<5.0 × 10⁻⁸ Pa). Cleaning parameters were Ar⁺ sputtering (+1.0 keV, 0.4 μA) with subsequent annealing (∼820 K). Then, BrCR molecules were deposited on the Cu(111) substrate at 300 K in the deposition chamber (<3.0 × 10⁻⁷ Pa). We used a quartz SiO₂ crucible and a homebuilt molecular evaporator. The quartz crystal microbalance (QCM) parameters (z-ratio = 1, density = 1) were taken to operate QCM.⁷⁴ The quarts crucible was radiatively heated by flowing current through a tungsten wire filament (diameter 0.3 mm). The crucible temperature was monitored by using the alumel–chromel thermocouple contacting the bottom of the crucible. The Cu(111) substrate was put ∼110 mm above the crucible. Before the deposition, we always checked the BrCR evaporation rate by setting a QCM at the same distance position. We used the evaporation speed of 0.03 nm min⁻¹ at ∼361 K. Since the QCM parameters of z-ratio and molecule density, the estimated deposition amounts, as well as the adsorption probability on the substrate, were unknown, the molecule thickness estimated by QCM was only used as an index. STM checked the precise deposited molecular monolayer (ML).

2.3 STM/STS measurements

STM measurements combined with the Nanonis SPM controller BP4 were used to obtain topographic images of sample surfaces in a constant current mode. The STM data were analyzed using WSxM 5.0 Develop 10.2 software and Gwyddion 2.56.⁷⁵ The home-built UHV-STM equipment consisted of STM, preparation, and deposition chambers. The base pressures of each chamber were below 5.0 × 10⁻⁸ Pa, 2.0 × 10⁻⁸ Pa, and 1.0 × 10⁻⁷ Pa, respectively.⁷⁶ Samples and STM tips were transferred between chambers using transfer rods without breaking the UHV. Gate valves separated each chamber. A UHV cryostat (CryoVAC) in the STM chamber was used to cool down the STM setup. All STM results were obtained at 78 K in UHV. We used sharp tungsten tips as STM probe tips.^77–80

2.4 DFT calculation

DFT calculations of possible intermediate and final conformations of the BrCR Ullmann coupling have been performed using the projector-augmented wave method as implemented in the VASP package.^81,82 The PBE exchange–correlation function was employed with a plane wave cut-off energy of 400 eV. Sufficiently large supercells were used such that the distance between periodic images was at least 1 nm. All structures were fully optimized until the forces on all atoms were less than 0.1 eV Å⁻¹. The energies of all these systems were computed using the same method (VASP, PBE-functional, same plane-wave energy cut-off). The adsorption energy of Br/Cu(111) was computed using a five monolayer Cu(111) slab with one Br atom in a 4 × 4 surface supercell and a 6 × 6 × 1 Gamma-centered k-point mesh. Similar computational settings were recently used for F adsorption on Cu(001).⁸³ When adsorbed at the stable hollow fcc site, the adsorption energy per Br atom is −1.70 eV for the Br₂ molecule in the gas phase or −2.96 eV for Br single atoms. This agrees well with the value of −3.05 eV reported by Migani and Illas.⁸⁴

3. Results and discussion

3.1 On-surface design of 2D stripe random network

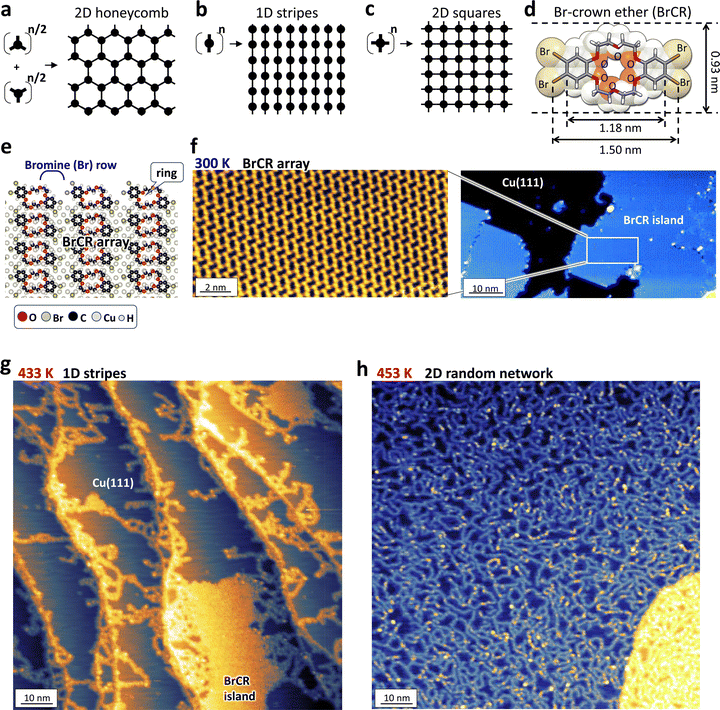
Fig. 1(a)–(c) shows how the precursor symmetry determines the on-surface synthesized 2D network coordination. Here, C₃, C₂, and C₄ symmetry precursors could ideally produce honeycomb, straight stripes, and squared lattice structures on a 2D surface. During the on-surface synthesis, the connection reaction between precursors was governed by the Arrhenius equation. This means the reaction process is strongly dependent on the temperature.

Fig. 1 (a)–(c) Bonding models of precursors. (a) Honeycomb network with C₃, 1D stripes with C₂, and 2D squares with C₄ precursors. (d) Single-crystal X-ray crystallographic structure of BrCR. Stick and space-fill models are overlaid. (e) Sphere models of 2D BrCR self-assembled monolayer array on Cu(111). (f)–(h) STM topographic images obtained at 77.8 K on BrCR grown on Cu(111) (f) before and after the thermal annealing of (g) 433 K and (h) 453 K: (f) left panel: 20 × 10 nm², −0.8 V, 10 pA, right panel: 100 × 50 nm², −2.5 V, 10 pA. (g) 100 × 100 nm², −2.5 V, 10 pA, (h) 100 × 100 nm², −1.6 V, 100 pA.

For example, 1,3,5-tris(4-bromophenyl)benzene (TBB) precursors,^12,85,86 known as a precursor to creating the honeycomb porous lattice (Fig. 1(a)), generate not only hexagons but also pentagons and heptagons, producing an incomplete 2D honeycomb network because bromine (Br) desorption,^12,85 thermal diffusion, and covalent bonding formation simultaneously occur.

Still, rigid and flat benzene ring compounds produced a flat 2D linear structure because of the strong covalent bonding between benzene rings. The π-orbital from the benzene ring is preferentially coupled with s-orbitals of the noble metal substrate, leading to a flat surface, i.e., the benzene ring parallel to the substrate surface. This means the 2D random network of tortuous stripes cannot be produced using the normal rigid π-conjugated precursors.

To design the 2D stripe random network, (1) the precursor requires a flexible structure with the functionality of bending or twisting, and (2) the formation of a one-dimensional (1D) stripe requires that the Ullman reaction happens only at the head and tail position of the precursor. Thus, we designed the precursor with a crown ether at the center, Br atoms were set at head and tail positions, and two benzene rings were used to bond with the substrate, keeping the flatness. The BrCR molecule (see Fig. 1(d)) consists of a center crown ether ring with two phenyl rings on both sides.⁵¹

In a bulk state, Ullmann coupling of BrCR in the presence of Cu powder produced 3D aggregations, including various compounds of mono-coupling, biphenylene, and triphenylene products observed by field desorption mass spectra (FDMS, Fig. S4–S6, ESI†), suggesting uncontrollability of the chemical reactions (Fig. S7, ESI†).

In this study, we used the ordered self-assembled BrCR monolayer film formed on Cu(111).^52–55Fig. 1(e) shows a spherical model of an ordered (7 × 4) 2D BrCR array. Although the BrCR in the gas phase has a C₂ symmetry, the BrCR single molecules are slightly distorted, losing the symmetry.

Notably, the long axis of the BrCR molecule on the Cu(111) surface aligns parallel to each other, producing Br atom rows. Namely, when the thermal annealing could preferentially occur the Ullmann reaction at these rows, the BrCR precursors could connect along the long axis since one single BrCR has two Br atoms on each side. Therefore, the free-bonding hands could have a higher chance of bonding with neighbors after the Ullmann reaction.

Fig. 1(f) presents the STM topographic depiction acquired on the BrCR array structure prepared on Cu(111) at 300 K under UHV conditions, distinctly demonstrating the absence of on-surface synthesis at this temperature. This stands in stark contrast to observations with 4,4′′-dibromo-p-terphenyl⁸⁷ or TBB,^12,85,86 wherein Br deposition at 300 K on Cu(111) initiated on-surface synthesis, yielding a planar polymer chain. However, the BrCR arrangement on Cu(111) at 300 K did not manifest such synthesis, as evidenced in Fig. 1(f), implying that the crown ether ring attenuates the interaction with the Cu substrate, thus inhibiting Br desorption. Nonetheless, the BrCR array on Cu(111) does exhibit on-surface synthesis commencing at an annealing temperature of 433 K, as depicted in Fig. 1(g) and (h).

Before our annealing experiments, the following results were reported: (1) ortho-dibromobenzene molecules conducted on-surface Ullmann coupling produce biphenylene and triphenylene groups.⁸⁸ (2) TBB precursors generate intermediate bonds on Cu(111) at the annealing temperature of 370 K, and this intermediate state transforms to the final C–C bonding states above 410 K.⁸⁹ Therefore, we expected a 2D network consisting of the biphenylene and triphenylene groups, suggesting major straight and trident connections. Then, we set the annealing temperature at 433–453 K.

After the thermal annealing treatment at 433 K in UHV for the BrCR array on Cu(111) provided the 1D stripe formation, as depicted in Fig. 1(g). Markedly, we observed a drastic change on the surface after the further thermal annealing at 453 K in UHV. In Fig. 1(h), the ordered array disappeared, but a 2D stripe random network was produced.

3.2 Theoretically predicted stable connections

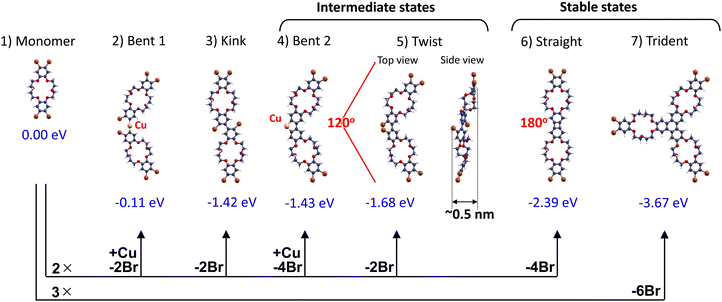
To better understand the chemical reactions of BrCR precursors on Cu(111), DFT calculations were performed to investigate the energetically stable connections (Fig. 2). Except for the adsorption of Br on Cu(111), all calculations were done in the gas phase.

Fig. 2 DFT calculation results of possible optimized bonding configurations of two BrCR monomers via Ullmann reaction. From left to right, (1) monomer, (2) 120° bent structure no. 1 with a Cu atom, (3) kink structure, (4) 120° bent structure no. 2 with a Cu atom, (5) twist structure, (6) 180° straight structure, and (7) trident structure. Although energetically stable configurations are (6) and (7), intermediate states of (4) and (5) introduce the 120° bent structure. Especially, the intermediate “twist” configuration provides corrugation of approximately 0.5 nm. Blue energy values denote reaction energies ΔE, given per reactant BrCR molecule concerning the reference states Br/Cu(111) and bulk Cu for structures (2) and (4). ΔE < 0 means an exothermic reaction.

We consider a product molecule X, formed by the Ullmann coupling reaction between n BrCR precursor molecules (n = 2 or 3). In the process, m Br atoms are dissociated, which we assume will adsorb on the Cu surface. Thus, the reaction can be written as: nBrCR + Cu(111) → X + (mBr)/Cu(111) or, when X is a Cu-containing intermediate: nBrCR + Cu (S) + Cu(111) → X + (m Br)/Cu(111).

In Fig. 2, the DFT optimized structures are shown together with their reaction energies ΔE, which are given per one BrCR reactant molecule and with respect to the following reference states: BrCR: free molecule, Br: adsorbed on Cu(111), Cu: bulk. All energies are negative, which means exothermic reactions. The reaction energy of the Cu-containing intermediate state (no. 2) is minimal, making this configuration rather unlikely or short-lived.

It should be noted that the Cu-containing intermediates (no. 2 and no. 4) are gas phase models. In reality, the Cu atoms in the intermediate states of the Ullmann coupling are likely to be attached to the Cu surface, either as a Cu adatom or a partially lifted surface Cu atom.⁴³ Such adsorbed structures should be more stable than the gas phase models considered here. All reactions in Fig. 2 (except for no. 2) are exothermic and thus thermodynamically possible. Note that the Br adsorption on Cu (calculated adsorption energy −1.70 eV per half Br₂ molecule) contributes a large part to the reaction energy. If the reaction product is Br₂ gas instead of adsorbed Br, all reaction energies will increase by m/n × 1.70 eV. The corresponding reaction energies become: (2) bent 1: 1.97 eV, (3) kink: 0.28 eV, (4) bent 2: 1.59 eV, (5) twist: 0.02 eV, (6) straight: 1.01 eV, and (7) trident: −0.27 eV. Then, all reactions except trident formation would become endothermic, and no linear connections could be formed. This implies that apart from the ordered arrangement of the BrCR monolayer on Cu, a second important factor for the formation of a 2D stripe network is that for a monolayer of BrCR molecules, the dissociated Br atoms can efficiently adsorb on the Cu surface, which makes the straight connection energetically stable. Indeed, the present calculations suggest that when Br adsorption on Cu is impossible (or saturated), a straight connection cannot be formed.

Thus, the DFT results in Fig. 2 suggested that the most energetically stable formation using Ullmann coupling could be (6) straight and (7) trident in agreement with the previously reported results of ortho-dibromobenzene molecules conducted on-surface Ullmann coupling producing biphenylene and triphenylene groups.⁸⁸ However, 2D tortuous stripe networks presented in Fig. 1(h) cannot be made using only straight and trident connections. This leads to a requirement of intermediate 120° bent connections suggested by the DFT results in Fig. 2.

Another crucial aspect highlighted by the theoretical projections in Fig. 2 is that solely the intermediate states of the (4) bent 2 and (5) twisted configurations exhibit corrugation, while alternative configurations such as the (2) bent 1, (3) kink, (6) straight, and (7) trident maintain flatness subsequent to bonding. The (5) twisted arrangement demonstrates a maximum width of approximately 0.5 nm between H–H atoms. Subsequently, this corrugation will be discernible in the STM images.

3.3 Necessity of intermediate states for 2D stripe random network formation

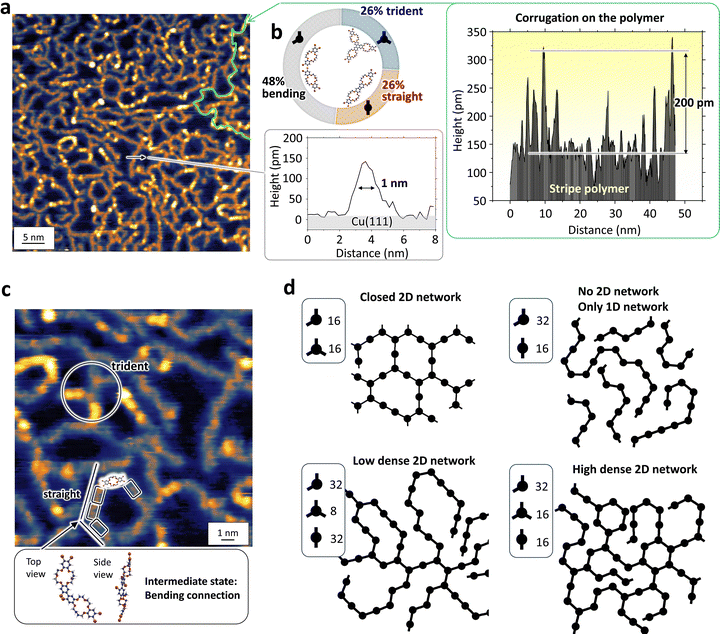
Fig. 3 shows STM experimental results obtained on the 2D stripe network grown on Cu(111). Fig. 3(a) shows a magnified STM topographic image. Single chains have an identical width of approximately 1 nm, as shown by the height profile along the arrow in smaller-right panel, which is comparable to the BrCR width estimated from a single-crystal X-ray crystallographic spacefill model and the BrCR unit cell vector of a = 0.93 nm as depicted in Fig. 1(d).

Fig. 3 (a) STM topographic image obtained at 77.8 K on the BrCR/Cu(111) surface after the thermal annealing at 453 K for 10 min in UHV (50 × 50 nm², −1.6 V, 100 pA). The right panels denote the height profiles along the arrow and the green line. (b) Histogram of the connections: stable straight (26%) and trident (26%) connections, but the intermediate state of the 120° bent structures are found to be majority (48%). (c) Magnified STM topographic image: 18 × 18 nm². The chain polymers consist of three connections: straight, bent, and trident connections. A box denotes the single BrCR precursor size. (d) 2D network models formed with different precursors. From left to right, the network consisting of 16 bent and 16 trident precursors, the network composed of 32 bent and 16 straight precursors, the network consisting of 32 bent, eight trident, and 32 straight precursors, and the network consisting of 32 bent, 16 trident, and 16 straight precursors. The last one corresponds to the experimentally obtained ratio in (b).

We additionally assessed the height profile along a single long chain, marked by the green line in Fig. 3(a). This height profile, presented in the right panel, conspicuously reveals a surface that is not atomically flat on the polymer chain. This stands in stark contrast to polymer chains synthesized using precursors composed solely of benzene rings.^12,85–87 Such corrugations, reaching a maximum height of approximately 200 pm, may signify the existence of the intermediate state as anticipated in Fig. 2 (twist structure).

We measured the angle between the connections and summarized in the histogram (ESI,† Fig. S8). It is clear that the connection angle is widely distributed between 60–180 degrees and therefore this could a proof of the randomness of the network. Such a random network cannot be produced by using the rigid precursors, such as phthalocyanines or porphyrins.⁴⁷ The Fourier transformed (FT) image displayed no apparent symmetry (no spots). (Other images are also shown in ESI,† Fig. S1–S3.)

From the image in Fig. 3(a), we found the following facts. (1) One stripe structure continuously connects and grows with a length longer than 50 nm. (2) All stripes are separated and do not bind together, indicating a repulsive interaction. (3) Interestingly, the stripes seem connected randomly, as depicted by the magnified image in Fig. 3(c) (12 × 12 nm²); however, this indicates that the local chains consist of mainly three connections. Namely, 120° bent, 180° straight, and trident connections. One BrCR precursor size (∼1.5 nm) is marked as a box in Fig. 3(c). We classified 746 connections in the STM topographic images, and Fig. 3(b) shows the results. Surprisingly, the theoretically predicted energetically stable straight and trident connections were limited to 26%. On the contrary, the intermediate 120° bent connection was found to be the major connection, 48%.

Fig. 3(d) shows network models using 120° bent, 180° straight, and trident connections. These simple models help us understand the network formation process. The two networks on the upper side consist of only two connections. These networks do not fit the experimental observation; the first has closed stripe loops, and the second has only 1D stripes. Thus, these two models exclude the possibility of creating a 2D network using only two connections. The third and fourth models used three connections, but the ratio was modified: bent : trident : straight = 32 : 8 : 32 and 32 : 16 : 16; the former led to a more considerable distance between stripes, but the latter produced a dense stripe network, in agreement with the experimental results, and this ratio (2 : 1 : 1) corresponds to the experimentally obtained ratio of 48% : 26% : 26%. Therefore, the network models in Fig. 3(d) strongly indicate that the formation of the 2D stripe random network is governed by the presence of the intermediate 120° bent connection.

Moreover, the ratio of 48% : 26% : 26% following the 453 K annealing closely mirrors that of 54% : 20% : 26% following the 433 K annealing. No substantial alteration was discerned, suggesting the stability of intermediate states within this temperature range.

3.4 Electronic structures in 2D random network

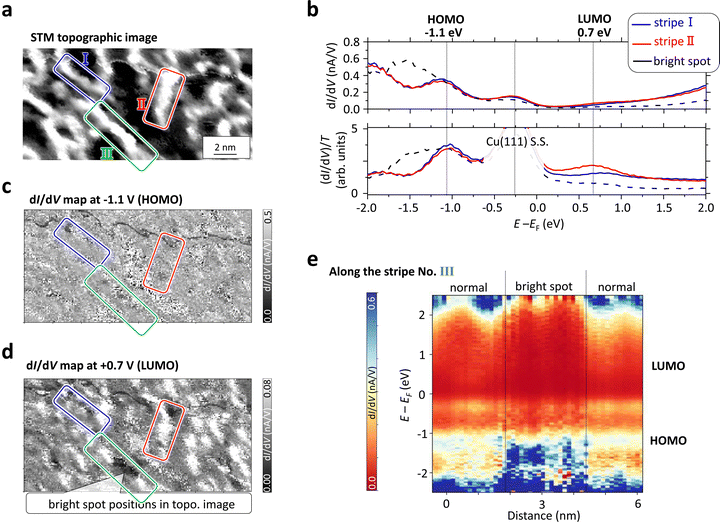
Another aspect of the stripes lies in the corrugation observed on the polymer surface, as depicted in Fig. 3(a), stemming from the formation of intermediate states, which could potentially alter the molecular orbitals. To investigate this phenomenon, scanning tunneling spectroscopy (STS) measurements were conducted on the polymer surface depicted in Fig. 4.

Fig. 4 STS results obtained on the 2D stripe network. (a) Topographic image (20 × 10 nm²). (b) dI/dV spectra, corresponding to the surface LDOS, obtained on the regular stripe (blue and red lines) and the bright spot position in the stripe (black dotted line). (c) and (d) dI/dV maps obtained on the same area as (a) at (c) −1.1 V and (d) +0.7 V. (e) dI/dV 3D plot along the stripe no. III in (a) as a function of the energy: x-axis: distance (nm), y-axis: E − E_F (eV), and z-axis: dI/dV value.

Fig. 4(a) shows an STM topographic image showing 2D stripes on Cu(111). At each pixel position in this area, we measured dI/dV curves, proportional to the sample LDOS, as a function of the bias voltage. Fig. 4(b) shows dI/dV curves, in which E_F denotes the Fermi energy and positive and negative bias sides represent unoccupied and occupied LDOS, respectively. We observed a peak around −0.3 eV just below the Fermi energy, which might be an in-gap state inside the molecular gap or the Cu(111) surface state (S.S.) located at −0.35 eV below the Fermi energy,⁹⁰ through the molecular gap.

The dI/dV curves delineated in Fig. 4(b), extracted from two polymers demarcated by blue (I) and red (II) boxes in Fig. 4(a), exhibit identical dI/dV variation with respect to the energy. This indicates that the on-surface synthesized 1D stripe polymers using the BrCR could possess a uniform electronic structure despite the corrugated surface topology. Since the HOMO and LUMO peaks are often obscured by the exponential background in the dI/dV curve, namely, the tunneling probability function (T), a well-established normalization method is employed to recover the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) peaks.^91–94

The normalized (dI/dV)/T curves depicted in the lower panel of Fig. 4(b) elucidates the recovered HOMO and LUMO peaks positioned at approximately −1.1 eV and +0.7 eV, respectively. These energy levels are slightly shifted from the HOMO/LUMO positions of the original 2D BrCR array: −1.5 eV and +1.4 eV.^52,54 This implies that the original HOMO–LUMO gap of approximately 2.9 eV has been narrowed to approximately 1.8 eV, in agreement with theoretical predictions. Density of states (DOS) plots of the BrCR monomer and dimers in Fig. 2 (gas phase) shown in ESI,† Fig. S9 suggest that all dimer connections exhibit a narrower band gap compared to the monomer.

Fig. 4(c) and (d) depict dI/dV maps acquired at −1.1 V and +0.7 eV, corresponding to the energy positions of the HOMO and LUMO peaks, respectively. Three strips are delineated by I, II, and III, wherein the majority of regions exhibit uniform HOMO levels, while local disparities are discernible in the LUMO energy map, suggesting the presence of at least two types of chemical bonding within the stripe.

The black dashed line in Fig. 4(b) represents the dI/dV curve derived from the region marked by the arrow in the stripe III, aligning with the location of heightened corrugation (bright spot), which manifests an additional peak around −1.5 eV and the suppression of the LUMO peak. As the DFT calculated DOS in ESI,† Fig. S9, shows, the straight and the bent 2 connections have slightly different HOMO and LUMO peak positions. If the bright spot with a high corrugation (∼200 pm) in the strips every ∼5 nm, corresponding to the length of about three precursors, it suggests that about 30% of the connections (ESI,† Fig. S3) could be originated by the intermediate bent configuration, thus aligning with both DFT and experimentally obtained results. A similar heightened appearance due to the intermediate state was observed for other on-surface syntheses,⁸⁹ which could also suggests a metal atom from the substrate in the covalent bonding, possibly CuBr₂ (bent structures in Fig. 2).

We further investigate the variation of LDOS concerning the position within the stripe. Fig. 4(e) illustrates a 3D plot of dI/dV acquired along the stripe III the x-axis represents distance, the y-axis denotes energy relative to the Fermi energy, and the z-axis illustrates dI/dV values (with higher and lower values depicted in blue and red, respectively). This 3D plot suggests that the bright spot within the stripe may exhibit a locally distinct LDOS.

3.5 Initial growth of stripe formation

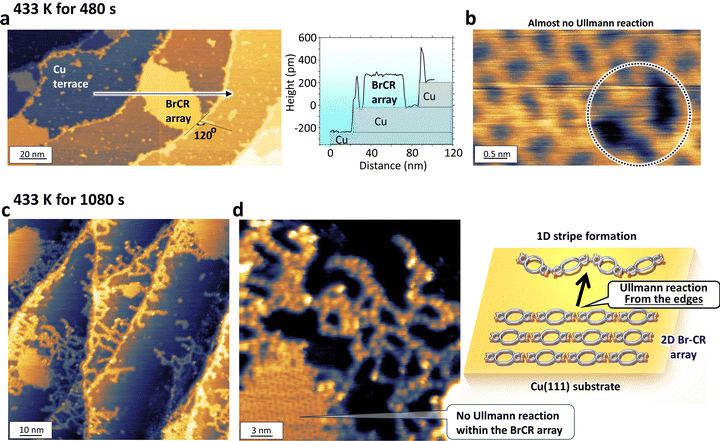
Although the complete 2D stripe random network was accomplished using the thermal annealing temperature of 453 K for 10 min (Fig. 1(h)), tuning the temperature by thermal heating could control the intermediate states since the chemical reaction follows the Arrhenius equation. To investigate the initial growth of the stripes, we reduced the heating temperature from 453 K to 433 K.

Fig. 5(a) and (b) show the STM results after heating at 433 K for 480 s. In contrast to Fig. 1(h), Cu terraces in Fig. 5(a) are not coated by stripes, and we could observe the original BrCR monolayer array. Interestingly, the STM image magnified inside the array showed an identical orderliness with the original BrCR array, the same as Fig. 1(f). It is entirely unexpected that the stripe formation did not start from the array. Still, the stripe began to grow from Cu atomic steps, only at descending steps (no ascending steps). This indicates that the onset of the stripe formation requires a Cu atom since the Cu atom at the steps has a higher chance of contact with the diffusing BrCR molecules, leading to the intermediate state connection. These stripes along the steps observed in Fig. 5(a) consist of only straight and 120° bent connections (no trident). A height profile along the arrow in the upper image, as depicted in the lower panel of Fig. 5(a), represents the stripe formation that occurred only at the descending steps.

Fig. 5 (a) STM topographic images obtained at 77.8 K on BrCR/Cu(111) after the thermal annealing at 433 K for 480 s (200 × 100 nm², −2.5 V, 10 pA). The right panel denotes the height profile along the arrow. (b) Magnified STM image inside the CR array (5 × 3 nm², −1.5 V, 11 pA). (c) and (d) STM topographic images obtained on the same sample surface after the thermal annealing at 433 K for 1080 s; (c) 100 × 100 nm² and (d) 30 × 30 nm², 2.5 V, 10 pA. The model shows the stripe formation started from the BrCR island edge.

We found a tiny change inside the array in one out of 62 BrCR molecules in Fig. 5(b) (marked by a dotted circle). Here, the difference includes 30 pm higher spots with 20 pm deeper holes, indicating one Ullmann reaction occurred between two BrCR molecules. Interestingly, the dimer formation already produced a buckled structure instead of maintaining a flat surface. Such a buckling should not happen by the stable straight or trident structures suggested by DFT in Fig. 2. Namely, the intermediate state generated a non-flat molecular surface and dominated the connection from the beginning.

Next, we maintained the sample temperature at 433 K but kept it longer. Fig. 5(c) and (d) show STM topographic images obtained after 1080 s annealing time. Here, many stripes started to grow and covered the terraces while the BrCR array remained, and the orderliness was also maintained. So how were the BrCR precursors supplied to grow the stripes? The hint was shown in Fig. 5(c) where stripes grew not equivalently but densely at local areas between the BrCR array and Cu steps. Also, many stripes were produced from the Cu steps, and their length became longer. Then, one could imagine that the growing stripes contact with the BrCR array, more and more BrCR connected to the stripe, making the stripe longer and scraped off the BrCR array one by one, as shown in the model in Fig. 5(d). These results could indicate that the stripe formation requires step defects on the substrate, which becomes a trigger to form the stripe. Also, no Ullmann reaction occurred at this temperature for the BrCR array; the step defects could have an essential role in lowering the activation energy of the Ullmann reaction. When a growing stripe touches the BrCR array, the stripe absorbs the BrCR precursors to change the stripe, producing dense stripes on the surface. This could repeat until all the BrCRs were completely switched to CR stripe polymers. It should be noted that there are no second monolayers of the stripe; this stripe formation is only limited to one monolayer film. Thus, this on-surface synthesis occurred only on the Cu surface, leading to an ultrathin one-monolayer-thickness 2D stripe random network.

4. Conclusions

The growth of the 2D stripe random network using BrCR precursors was effectively showcased on the atomically flat and pristine Cu(111) surface. This process underwent scrutiny employing experimental STM/STS configurations and DFT calculations. Success ensued by employing a precursor embedding a pliable crown ether ring and adjusting the thermal annealing temperature to enhance the prevalence of the intermediate 120-degree bent structure as a primary connection.

The initiation of stripe formation was ascertained to be prompted by Cu step defects, with the intermediate state assuming dominance from the inception of dimer formation. As the stripe extends, it assimilates the BrCR array, elongating itself and engendering densely patterned stripes on the surface. This process can iterate until all BrCRs are entirely transformed into CR stripe polymers. The pliability of the crown ether ring allows for facile bending of the stripe, contributing to the randomness of the pattern. Notably, this stripe formation is confined to a sole monolayer film; there are no second monolayer of the stripe observed. Our empirical evidence substantiates that on-surface synthesis is not confined solely to the creation of linearly ordered systems via rigid and planar precursors like phthalocyanines or porphyrins, but also extends to the production of a 2D winding network using precursors featuring a soft ring and intermediate state connections in the Ullmann reaction.

The creation of a 1D polymer composed of crown ether hoops formed on the 2D surface offers promising prospects as foundational units for molecular complexes. Moreover, it facilitates the modulation of surface-based electric and morphological properties. Given the chain's incorporation of numerous rings, these structures possess the capacity to encapsulate supplementary guest materials within, engendering diverse functionalities, such as the formation of single-atom catalysts through the introduction of metal atoms.

Author contributions

T. K. Y. conceived and designed the project. T. K. Y., R. N., and F. N. performed all STM/STS experiments. C. H. W., Y. H. C., and M. H. synthesized and evaluated the BrCR molecules. P. K. performed DFT calculations. T. K. Y, H. I., and M. H. analyzed the data. T. K. Y. wrote the first draft, and M. H. and P. K. corrected and added synthesis and theoretical discussion in the manuscript. All authors discussed the results and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by JSPS KAKENHI Grant Numbers 17K19023 and 23H02033, the Murata Science Foundation, the Shorai Foundation for Science and Technology, TEPCO Memorial Foundation, Casio Science Promotion Foundation, and Toshiaki Ogasawara Memorial Foundation. We thank Dr Eiichi Inami for carefully reading our manuscript and fruitful discussion. We thank Ms Ayano Yoshida for STM experimental support.

References

1. K. Wedeking, Z. Mu, G. Kehr, J. Cano Sierra, C. Mück Lichtenfeld, S. Grimme, G. Erker, R. Fröhlich, L. Chi, W. Wang, D. Zhong and H. Fuchs, Oligoethylene Chains Terminated by Ferrocenyl End Groups: Synthesis, Structural Properties, and Two-Dimensional Self-Assembly on Surfaces, Chem. – Eur. J., 2006, 12(6), 1618–1628,  DOI:10.1002/chem.200500552.
2. Y. Zhang, J. Lu, B. Li, W. Chen, W. Xiong, Z. Ruan, H. Zhang, S. Sun, L. Chen, L. Gao and J. Cai, On-Surface Synthesis and Characterization of Nitrogen-Doped Covalent-Organic Frameworks on Ag(111) Substrate, J. Chem. Phys., 2022, 157(3), 031103,  DOI:10.1063/5.0099995.
3. E. Virmani, J. M. Rotter, A. Mähringer, T. Von Zons, A. Godt, T. Bein, S. Wuttke and D. D. Medina, On-Surface Synthesis of Highly Oriented Thin Metal–Organic Framework Films through Vapor-Assisted Conversion, J. Am. Chem. Soc., 2018, 140(14), 4812–4819,  DOI:10.1021/jacs.7b08174.
4. J. I. Urgel, J. Bock, M. Di Giovannantonio, P. Ruffieux, C. A. Pignedoli, M. Kivala and R. Fasel, On-Surface Synthesis of π-Conjugated Ladder-Type Polymers Comprising Nonbenzenoid Moieties, RSC Adv., 2021, 11(38), 23437–23441,  10.1039/D1RA03253D.
5. K. Sun, O. J. Silveira, Y. Ma, Y. Hasegawa, M. Matsumoto, S. Kera, O. Krejčí, A. S. Foster and S. Kawai, On-Surface Synthesis of Disilabenzene-Bridged Covalent Organic Frameworks, Nat. Chem., 2023, 15(1), 136–142,  DOI:10.1038/s41557-022-01071-3.
6. J. Su, W. Fan, P. Mutombo, X. Peng, S. Song, M. Ondráček, P. Golub, J. Brabec, L. Veis, M. Telychko, P. Jelínek, J. Wu and J. Lu, On-Surface Synthesis and Characterization of [7]Triangulene Quantum Ring, Nano Lett., 2021, 21(1), 861–867,  DOI:10.1021/acs.nanolett.0c04627.
7. V. M. Santhini, O. Stetsovych, M. Ondráček, J. I. Mendieta Moreno, P. Mutombo, B. Torre, M. Švec, J. Klívar, I. G. Stará, H. Vázquez, I. Starý and P. Jelínek, On-Surface Synthesis of Polyferrocenylene and Its Single-Chain Conformational and Electrical Transport Properties, Adv. Funct. Mater., 2021, 31(5), 2006391,  DOI:10.1002/adfm.202006391.
8. Z. Chen, R. Berger, K. Müllen and A. Narita, On-Surface Synthesis of Graphene Nanoribbons through Solution-Processing of Monomers, Chem. Lett., 2017, 46(10), 1476–1478,  DOI:10.1246/cl.170606.
9. H. Denawi, M. Koudia, R. Hayn, O. Siri and M. Abel, On-Surface Synthesis of Spin Crossover Polymeric Chains, J. Phys. Chem. C, 2018, 122(26), 15033–15040,  DOI:10.1021/acs.jpcc.8b04171.
10. M. Di Giovannantonio, K. Eimre, A. V. Yakutovich, Q. Chen, S. Mishra, J. I. Urgel, C. A. Pignedoli, P. Ruffieux, K. Müllen, A. Narita and R. Fasel, On-Surface Synthesis of Antiaromatic and Open-Shell Indeno[2,1-b]Fluorene Polymers and Their Lateral Fusion into Porous Ribbons, J. Am. Chem. Soc., 2019, 141(31), 12346–12354,  DOI:10.1021/jacs.9b05335.
11. C. Dobner, G. Li, M. Sarker, A. Sinitskii and A. Enders, Diffusion-Controlled on-Surface Synthesis of Graphene Nanoribbon Heterojunctions, RSC Adv., 2022, 12(11), 6615–6618,  10.1039/D2RA01008A.
12. C. M. Doyle, C. McGuinness, A. P. Lawless, A. B. Preobrajenski, N. A. Vinogradov and A. A. Cafolla, Surface Mediated Synthesis of 2D Covalent Organic Networks: 1,3,5-Tris(4-bromophenyl)Benzene on Au(111), Phys. Status Solidi B, 2019, 256(2), 1800349,  DOI:10.1002/pssb.201800349.
13. Z. Chen, A. Narita and K. Müllen, Graphene Nanoribbons: On-Surface Synthesis and Integration into Electronic Devices, Adv. Mater., 2020, 32(45), 2001893,  DOI:10.1002/adma.202001893.
14. Q. Fan, D. Martin-Jimenez, S. Werner, D. Ebeling, T. Koehler, T. Vollgraff, J. Sundermeyer, W. Hieringer, A. Schirmeisen and J. M. Gottfried, On-Surface Synthesis and Characterization of a Cycloarene: C108 Graphene Ring, J. Am. Chem. Soc., 2020, 142(2), 894–899,  DOI:10.1021/jacs.9b10151.
15. L. Gao, J. R. Guest and N. P. Guisinger, Epitaxial Graphene on Cu(111), Nano Lett., 2010, 10(9), 3512–3516,  DOI:10.1021/nl1016706.
16. J. Cai, P. Ruffieux, R. Jaafar, M. Bieri, T. Braun, S. Blankenburg, M. Muoth, A. P. Seitsonen, M. Saleh, X. Feng, K. Müllen and R. Fasel, Atomically Precise Bottom-up Fabrication of Graphene Nanoribbons, Nature, 2010, 466(7305), 470–473,  DOI:10.1038/nature09211.
17. Ç. Ö. Girit, J. C. Meyer, R. Erni, M. D. Rossell, C. Kisielowski, L. Yang, C.-H. Park, M. F. Crommie, M. L. Cohen, S. G. Louie and A. Zettl, Graphene at the Edge: Stability and Dynamics, Science, 2009, 323(5922), 1705–1708,  DOI:10.1126/science.1166999.
18. T. Ahmed, S. Kilina, T. Das, J. T. Haraldsen, J. J. Rehr and A. V. Balatsky, Electronic Fingerprints of DNA Bases on Graphene, Nano Lett., 2012, 12(2), 927–931,  DOI:10.1021/nl2039315.
19. K. S. Novoselov, A. K. Geim, S. V. Morozov, D. Jiang, Y. Zhang, S. V. Dubonos, I. V. Grigorieva and A. A. Firsov, Electric Field Effect in Atomically Thin Carbon Films, Science, 2004, 306(5696), 666–669,  DOI:10.1126/science.1102896.
20. P. Ruffieux, S. Wang, B. Yang, C. Sánchez-Sánchez, J. Liu, T. Dienel, L. Talirz, P. Shinde, C. A. Pignedoli, D. Passerone, T. Dumslaff, X. Feng, K. Müllen and R. Fasel, On-Surface Synthesis of Graphene Nanoribbons with Zigzag Edge Topology, Nature, 2016, 531(7595), 489–492,  DOI:10.1038/nature17151.
21. S. Song, J. Su, M. Telychko, J. Li, G. Li, Y. Li, C. Su, J. Wu and J. Lu, On-Surface Synthesis of Graphene Nanostructures with π-Magnetism, Chem. Soc. Rev., 2021, 50(5), 3238–3262,  10.1039/D0CS01060J.
22. L. M. Mateo, Q. Sun, K. Eimre, C. A. Pignedoli, T. Torres, R. Fasel and G. Bottari, On-Surface Synthesis of Singly and Doubly Porphyrin-Capped Graphene Nanoribbon Segments, Chem. Sci., 2021, 12(1), 247–252,  10.1039/D0SC04316H.
23. A. P. Cote, A. I. Benin, N. W. Ockwig, M. O’Keeffe, A. J. Matzger and O. M. Yaghi, Porous, Crystalline, Covalent Organic Frameworks, Science, 2005, 310.
24. H. Xu, J. Gao and D. Jiang, Stable, Crystalline, Porous, Covalent Organic Frameworks as a Platform for Chiral Organocatalysts, Nat. Chem., 2015, 7(11), 905–912,  DOI:10.1038/nchem.2352.
25. M.-X. Wu and Y.-W. Yang, Applications of Covalent Organic Frameworks (COFs): From Gas Storage and Separation to Drug Delivery, Chin. Chem. Lett., 2017, 28(6), 1135–1143,  DOI:10.1016/j.cclet.2017.03.026.
26. X. Feng, X. Ding and D. Jiang, Covalent Organic Frameworks, Chem. Soc. Rev., 2012, 41(18), 6010,  10.1039/c2cs35157a.
27. G. Das, B. P. Biswal, S. Kandambeth, V. Venkatesh, G. Kaur, M. Addicoat, T. Heine, S. Verma and R. Banerjee, Chemical Sensing in Two Dimensional Porous Covalent Organic Nanosheets, Chem. Sci., 2015, 6(7), 3931–3939,  10.1039/C5SC00512D.
28. H. V. Babu, M. G. M. Bai and M. Rajeswara Rao, Functional π-Conjugated Two-Dimensional Covalent Organic Frameworks, ACS Appl. Mater. Interfaces, 2019, 11(12), 11029–11060,  DOI:10.1021/acsami.8b19087.
29. Q. Gao, X. Li, G.-H. Ning, K. Leng, B. Tian, C. Liu, W. Tang, H.-S. Xu and K. P. Loh, Highly Photoluminescent Two-Dimensional Imine-Based Covalent Organic Frameworks for Chemical Sensing, Chem. Commun., 2018, 54(19), 2349–2352,  10.1039/C7CC09866A.
30. Y. Peng, Z. Hu, Y. Gao, D. Yuan, Z. Kang, Y. Qian, N. Yan and D. Zhao, Synthesis of a Sulfonated Two-Dimensional Covalent Organic Framework as an Efficient Solid Acid Catalyst for Biobased Chemical Conversion, ChemSusChem, 2015, 8(19), 3208–3212,  DOI:10.1002/cssc.201500755.
31. Y. Jin, Y. Hu and W. Zhang, Tessellated Multiporous Two-Dimensional Covalent Organic Frameworks, Nat. Rev. Chem., 2017, 1(7), 0056,  DOI:10.1038/s41570-017-0056.
32. J. Li, X. Zhou, J. Wang and X. Li, Two-Dimensional Covalent Organic Frameworks (COFs) for Membrane Separation: A Mini Review, Ind. Eng. Chem. Res., 2019, 58(34), 15394–15406,  DOI:10.1021/acs.iecr.9b02708.
33. N. Huang, X. Chen, R. Krishna and D. Jiang, Two-Dimensional Covalent Organic Frameworks for Carbon Dioxide Capture through Channel-Wall Functionalization, Angew. Chem., Int. Ed., 2015, 54(10), 2986–2990,  DOI:10.1002/anie.201411262.
34. A. K. Mandal, J. Mahmood and J.-B. Baek, Two-Dimensional Covalent Organic Frameworks for Optoelectronics and Energy Storage, ChemNanoMat, 2017, 3(6), 373–391,  DOI:10.1002/cnma.201700048.
35. M. Mu, Y. Wang, Y. Qin, X. Yan, Y. Li and L. Chen, Two-Dimensional Imine-Linked Covalent Organic Frameworks as a Platform for Selective Oxidation of Olefins, ACS Appl. Mater. Interfaces, 2017, 9(27), 22856–22863,  DOI:10.1021/acsami.7b05870.
36. M. Zhang, G. Feng, Z. Song, Y.-P. Zhou, H.-Y. Chao, D. Yuan, T. T. Y. Tan, Z. Guo, Z. Hu, B. Z. Tang, B. Liu and D. Zhao, Two-Dimensional Metal–Organic Framework with Wide Channels and Responsive Turn-On Fluorescence for the Chemical Sensing of Volatile Organic Compounds, J. Am. Chem. Soc., 2014, 136(20), 7241–7244,  DOI:10.1021/ja502643p.
37. Y. Peng, Y. Li, Y. Ban and W. Yang, Two-Dimensional Metal–Organic Framework Nanosheets for Membrane-Based Gas Separation, Angew. Chem., Int. Ed., 2017, 129(33), 9889–9893,  DOI:10.1002/ange.201703959.
38. M. Wang, M. Ballabio, M. Wang, H.-H. Lin, B. P. Biswal, X. Han, S. Paasch, E. Brunner, P. Liu, M. Chen, M. Bonn, T. Heine, S. Zhou, E. Cánovas, R. Dong and X. Feng, Unveiling Electronic Properties in Metal–Phthalocyanine-Based Pyrazine-Linked Conjugated Two-Dimensional Covalent Organic Frameworks, J. Am. Chem. Soc., 2019, 141(42), 16810–16816,  DOI:10.1021/jacs.9b07644.
39. S. Xu, M. Richter and X. Feng, Vinylene-Linked Two-Dimensional Covalent Organic Frameworks: Synthesis and Functions, Acc. Mater. Res., 2021, 2(4), 252–265,  DOI:10.1021/accountsmr.1c00017.
40. J. Eichhorn, D. Nieckarz, O. Ochs, D. Samanta, M. Schmittel, P. J. Szabelski and M. Lackinger, On-Surface Ullmann Coupling: The Influence of Kinetic Reaction Parameters on the Morphology and Quality of Covalent Networks, ACS Nano, 2014, 8(8), 7880–7889,  DOI:10.1021/nn501567p.
41. H. Lin and D. Sun, Recent Synthetic Developments and Applications of the Ullmann Reaction. A Review, Org. Prep. Proced. Int., 2013, 45(5), 341–394,  DOI:10.1080/00304948.2013.816208.
42. E. Sperotto, G. P. M. Van Klink, G. Van Koten and J. G. De Vries, The Mechanism of the Modified Ullmann Reaction, Dalton Trans., 2010, 39(43), 10338,  10.1039/c0dt00674b.
43. S. Zint, D. Ebeling, T. Schlöder, S. Ahles, D. Mollenhauer, H. A. Wegner and A. Schirmeisen, Imaging Successive Intermediate States of the On-Surface Ullmann Reaction on Cu(111): Role of the Metal Coordination, ACS Nano, 2017, 11(4), 4183–4190,  DOI:10.1021/acsnano.7b01109.
44. T. A. Pham, F. Song, M.-T. Nguyen, Z. Li, F. Studener and M. Stöhr, Comparing Ullmann Coupling on Noble Metal Surfaces: On-Surface Polymerization of 1,3,6,8-Tetrabromopyrene on Cu(111) and Au(111), Chem. – Eur. J., 2016, 22(17), 5937–5944,  DOI:10.1002/chem.201504946.
45. A. Rastgoo Lahrood, J. Björk, W. M. Heckl and M. Lackinger, 1,3-Diiodobenzene on Cu(111) – an Exceptional Case of on-Surface Ullmann Coupling, Chem. Commun., 2015, 51(68), 13301–13304,  10.1039/C5CC04453G.
46. Y. Kim, S. Park, S.-J. Shin, W. Choi, B. K. Min, H. Kim, W. Kim and Y. J. Hwang, Time-Resolved Observation of C–C Coupling Intermediates on Cu Electrodes for Selective Electrochemical CO₂ Reduction, Energy Environ. Sci., 2020, 13(11), 4301–4311,  10.1039/D0EE01690J.
47. L. Lafferentz, V. Eberhardt, C. Dri, C. Africh, G. Comelli, F. Esch, S. Hecht and L. Grill, Controlling On-Surface Polymerization by Hierarchical and Substrate-Directed Growth, Nat. Chem., 2012, 4(3), 215–220,  DOI:10.1038/nchem.1242.
48. T. K. Yamada, H. Fukuda, T. Fujiwara, P. Liu, K. Nakamura, S. Kasai, A. L. Vazquez de Parga and H. Tanaka, Energy Gap Opening by Crossing Drop Cast Single-Layer Graphene Nanoribbons, Nanotechnology, 2018, 29(31), 315705,  DOI:10.1088/1361-6528/aac36b.
49. H. Tanaka, R. Arima, M. Fukumori, D. Tanaka, R. Negishi, Y. Kobayashi, S. Kasai, T. K. Yamada and T. Ogawa, Method for Controlling Electrical Properties of Single-Layer Graphene Nanoribbons via Adsorbed Planar Molecular Nanoparticles, Sci. Rep., 2015, 5(1), 12341,  DOI:10.1038/srep12341.
50. Y. Goto, S. Ando, K. Kakugawa, S. Takahara and T. K. Yamada, Unzipping Process of Wet Carbon Nanotubes Adsorbed on Cu(111) in Ultra-High Vacuum: an STM/STS study, Vac. Surf. Sci., 2021, 64(1), 40–46,  DOI:10.1380/vss.64.40.
51. C. J. Pedersen, The Discovery of Crown Ethers, Science, 1988, 241(4865), 536–540,  DOI:10.1126/science.241.4865.536.
52. R. Nemoto, P. Krüger, T. Hosokai, M. Horie, S. Kera and T. K. Yamada, Room-Temperature Deposition of Cobalt Monolayer on (7 × 4) Crown-Ether Ring Molecular Array: Ultra-High Vacuum STM and UPS Study, Vac. Surf. Sci., 2020, 63(9), 465–469,  DOI:10.1380/vss.63.465.
53. A. Ohira, M. Sakata, C. Hirayama and M. Kunitake, 2D-Supramolecular Arrangements of Dibenzo-18-Crown-6-Ether and Its Inclusion Complex with Potassium Ion by Potential Controlled Adsorption, Org. Biomol. Chem., 2003, 1(2), 251–253,  10.1039/b208717k.
54. R. Nemoto, P. Krüger, A. N. Putri Hartini, T. Hosokai, M. Horie, S. Kera and T. K. Yamada, Well-Ordered Monolayer Growth of Crown-Ether Ring Molecules on Cu(111) in Ultra-High Vacuum: An STM, UPS, and DFT Study, J. Phys. Chem. C, 2019, 123(31), 18939–18950,  DOI:10.1021/acs.jpcc.9b03335.
55. T. Hosokai, M. Horie, T. Aoki, S. Nagamatsu, S. Kera, K. K. Okudaira and N. Ueno, Change in Molecular Conformation of Dibenzo-Crown Ether Induced by Weak Molecule−Substrate Interaction, J. Phys. Chem. C, 2008, 112(12), 4643–4648,  DOI:10.1021/jp710835b.
56. T. K. Yamada, R. Nemoto, F. Nishino, T. Hosokai, C.-H. Wang, M. Horie, Y. Hasegawa, S. Kera and P. Krüger, On-Surface Growth of Transition-Metal Cobalt Nanoclusters Using a 2D Crown-Ether Array, J. Mater. Chem. C, 2024, 12, 874–883,  10.1039/D3TC03339B.
57. J. Tejada, E. M. Chudnovsky, E. D. Barco, J. M. Hernandez and T. P. Spiller, Magnetic Qubits as Hardware for Quantum Computers, Nanotechnology, 2001, 12(2), 181–186,  DOI:10.1088/0957-4484/12/2/323.
58. S. Bertaina, S. Gambarelli, T. Mitra, B. Tsukerblat, A. Müller and B. Barbara, Quantum Oscillations in a Molecular Magnet, Nature, 2008, 453(7192), 203–206,  DOI:10.1038/nature06962.
59. D. K. Yi, S. T. Selvan, S. S. Lee, G. C. Papaefthymiou, D. Kundaliya and J. Y. Ying, Silica-Coated Nanocomposites of Magnetic Nanoparticles and Quantum Dots, J. Am. Chem. Soc., 2005, 127(14), 4990–4991,  DOI:10.1021/ja0428863.
60. R. Di Corato, N. C. Bigall, A. Ragusa, D. Dorfs, A. Genovese, R. Marotta, L. Manna and T. Pellegrino, Multifunctional Nanobeads Based on Quantum Dots and Magnetic Nanoparticles: Synthesis and Cancer Cell Targeting and Sorting, ACS Nano, 2011, 5(2), 1109–1121,  DOI:10.1021/nn102761t.
61. S. Singamaneni, V. N. Bliznyuk, C. Binek and E. Y. Tsymbal, Magnetic Nanoparticles: Recent Advances in Synthesis, Self-Assembly and Applications, J. Mater. Chem., 2011, 21(42), 16819,  10.1039/c1jm11845e.
62. C. Wang, J. Meyer, N. Teichert, A. Auge, E. Rausch, B. Balke, A. Hütten, G. H. Fecher and C. Felser, Heusler Nanoparticles for Spintronics and Ferromagnetic Shape Memory Alloys, J. Vac. Sci. Technol., B: Nanotechnol. Microelectron.: Mater., Process., Meas., Phenom., 2014, 32(2), 020802,  DOI:10.1116/1.4866418.
63. C. C. Berry and A. S. G. Curtis, Functionalisation of Magnetic Nanoparticles for Applications in Biomedicine, J. Phys. Appl. Phys., 2003, 36(13), R198–R206,  DOI:10.1088/0022-3727/36/13/203.
64. Q. A. Pankhurst, J. Connolly, S. K. Jones and J. Dobson, Applications of Magnetic Nanoparticles in Biomedicine, J. Phys. Appl. Phys., 2003, 36(13), R167–R181,  DOI:10.1088/0022-3727/36/13/201.
65. V. I. Shubayev, T. R. Pisanic and S. Jin, Magnetic Nanoparticles for Theragnostics, Adv. Drug Delivery Rev., 2009, 61(6), 467–477,  DOI:10.1016/j.addr.2009.03.007.
66. J. Dobson, Magnetic Nanoparticles for Drug Delivery, Drug Dev. Res., 2006, 67(1), 55–60,  DOI:10.1002/ddr.20067.
67. J. Govan and Y. Gun’ko, Recent Advances in the Application of Magnetic Nanoparticles as a Support for Homogeneous Catalysts, Nanomaterials, 2014, 4(2), 222–241,  DOI:10.3390/nano4020222.
68. Q. M. Kainz and O. Reiser, Polymer- and Dendrimer-Coated Magnetic Nanoparticles as Versatile Supports for Catalysts, Scavengers, and Reagents, Acc. Chem. Res., 2014, 47(2), 667–677,  DOI:10.1021/ar400236y.
69. R. Abu-Reziq, H. Alper, D. Wang and M. L. Post, Metal Supported on Dendronized Magnetic Nanoparticles: Highly Selective Hydroformylation Catalysts, J. Am. Chem. Soc., 2006, 128(15), 5279–5282,  DOI:10.1021/ja060140u.
70. R. D. Ambashta and M. Sillanpää, Water Purification Using Magnetic Assistance: A Review, J. Hazard. Mater., 2010, 180(1–3), 38–49,  DOI:10.1016/j.jhazmat.2010.04.105.
71. M. Horie and C.-H. Wang, Stimuli-Responsive Dynamic Pseudorotaxane Crystals, Mater. Chem. Front., 2019, 3(11), 2258–2269,  10.1039/C9QM00483A.
72. C.-H. Wang, K.-J. Chen, T.-H. Wu, H.-K. Chang, Y. Tsuchido, Y. Sei, P.-L. Chen and M. Horie, Ring Rotation of Ferrocene in Interlocked Molecules in Single Crystals, Chem. Sci., 2021, 12(11), 3871–3875,  10.1039/D0SC06876D.
73. C.-H. Wang and M. Horie, Photo and Thermal Responsive Pseudorotaxane Crystals Comprising Ferrocene-Containing Ammonium Salts and Crown Ethers, Mater. Today Chem., 2022, 24, 100852,  DOI:10.1016/j.mtchem.2022.100852.
74. E. Inami, M. Yamaguchi, T. Yamaguchi, M. Shimasaki and T. K. Yamada, Controlled Deposition Number of Organic Molecules Using Quartz Crystal Microbalance Evaluated by Scanning Tunneling Microscopy Single-Molecule-Counting, Anal. Chem., 2018, 90(15), 8954–8959,  DOI:10.1021/acs.analchem.8b01118.
75. I. Horcas, R. Fernández, J. M. Gómez-Rodríguez, J. Colchero, J. Gómez-Herrero and A. M. Baro, WSXM: A Software for Scanning Probe Microscopy and a Tool for Nanotechnology, Rev. Sci. Instrum., 2007, 78(1), 013705,  DOI:10.1063/1.2432410.
76. N. K. M. Nazriq, P. Krüger and T. K. Yamada, Carbon Monoxide Stripe Motion Driven by Correlated Lateral Hopping in a 1.4 × 1.4 Monolayer Phase on Cu(111), J. Phys. Chem. Lett., 2020, 11(5), 1753–1761,  DOI:10.1021/acs.jpclett.9b03645.
77. T. K. Yamada, T. Abe, N. M. K. Nazriq and T. Irisawa, Electron-Bombarded 〈110〉-Oriented Tungsten Tips for Stable Tunneling Electron Emission, Rev. Sci. Instrum., 2016, 87(3), 033703,  DOI:10.1063/1.4943074.
78. T. Yamaguchi, E. Inami, Y. Goto, Y. Sakai, S. Sasaki, T. Ohno and T. K. Yamada, Fabrication of Tungsten Tip Probes within 3 s by Using Flame Etching, Rev. Sci. Instrum., 2019, 90(6), 063701,  DOI:10.1063/1.5085251.
79. Y. Goto, R. Suizu, Y. Noguchi and T. K. Yamada, Oxidative Vaporization Etching for Molybdenum Tip Formation in Air, Appl. Surf. Sci., 2021, 542, 148642,  DOI:10.1016/j.apsusc.2020.148642.
80. N. K. M. Nazriq, E. Minamitani and T. K. Yamada, CO-Tip Manipulation Using Repulsive Interactions, Nanotechnology, 2018, 29(49), 495701,  DOI:10.1088/1361-6528/aae0df.
81. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54(16), 11169–11186,  DOI:10.1103/PhysRevB.54.11169.
82. G. Kresse and D. Joubert, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59(3), 1758–1775,  DOI:10.1103/PhysRevB.59.1758.
83. M. N. Petukhov, P. Krüger, A. I. Oreshkin, D. A. Muzychenko and S. I. Oreshkin, 2D Missing Row Structure of Cuprous Fluoride on Cu(001), J. Phys. Chem. C, 2022, 126(50), 21390–21395,  DOI:10.1021/acs.jpcc.2c06295.
84. A. Migani and F. Illas, A Systematic Study of the Structure and Bonding of Halogens on Low-Index Transition Metal Surfaces, J. Phys. Chem. B, 2006, 110(24), 11894–11906,  DOI:10.1021/jp060400u.
85. R. Gutzler, H. Walch, G. Eder, S. Kloft, W. M. Heckl and M. Lackinger, Surface Mediated Synthesis of 2D Covalent Organic Frameworks: 1,3,5-Tris(4-Bromophenyl)Benzene on Graphite(001), Cu(111), and Ag(110), Chem. Commun., 2009, 4456,  10.1039/b906836h.
86. T. K. Yamada, S. Kanazawa, K. Fukutani and S. Kera, Growth of Transition-Metal Cobalt Nanoclusters on 2D Covalent Organic Frameworks, J. Phys. Chem. C, 2024, 128(3), 1477–1486,  DOI:10.1021/acs.jpcc.3c07435.
87. W. Wang, X. Shi, S. Wang, M. A. Van Hove and N. Lin, Single-Molecule Resolution of an Organometallic Intermediate in a Surface-Supported Ullmann Coupling Reaction, J. Am. Chem. Soc., 2011, 133(34), 13264–13267,  DOI:10.1021/ja204956b.
88. C. Sánchez-Sánchez, A. Nicolaï, F. Rossel, J. Cai, J. Liu, X. Feng, K. Müllen, P. Ruffieux, R. Fasel and V. Meunier, On-Surface Cyclization of Ortho -Dihalotetracenes to Four- and Six-Membered Rings, J. Am. Chem. Soc., 2017, 139(48), 17617–17623,  DOI:10.1021/jacs.7b10026.
89. L. Dong, P. N. Liu and N. Lin, Surface-Activated Coupling Reactions Confined on a Surface, Acc. Chem. Res., 2015, 48(10), 2765–2774,  DOI:10.1021/acs.accounts.5b00160.
90. G. Hörmandinger, Imaging of the Cu(111) Surface State in Scanning Tunneling Microscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49(19), 13897–13905,  DOI:10.1103/PhysRevB.49.13897.
91. Y. Yamagishi, S. Nakashima, K. Oiso and T. K. Yamada, Recovery of Nanomolecular Electronic States from Tunneling Spectroscopy: LDOS of Low-Dimensional Phthalocyanine Molecular Structures on Cu(111), Nanotechnology, 2013, 24(39), 395704,  DOI:10.1088/0957-4484/24/39/395704.
92. L. Gerhard, T. K. Yamada, T. Balashov, A. F. Takács, R. J. H. Wesselink, M. Däne, M. Fechner, S. Ostanin, A. Ernst, I. Mertig and W. Wulfhekel, Magnetoelectric Coupling at Metal Surfaces, Nat. Nanotechnol., 2010, 5(11), 792–797,  DOI:10.1038/nnano.2010.214.
93. T. K. Yamada, M. M. J. Bischoff, G. M. M. Heijnen, T. Mizoguchi and H. van Kempen, Observation of Spin-Polarized Surface States on Ultrathin Bct Mn(001) Films by Spin-Polarized Scanning Tunneling Spectroscopy, Phys. Rev. Lett., 2003, 90(5), 056803,  DOI:10.1103/PhysRevLett.90.056803.
94. V. A. Ukraintsev, Data Evaluation Technique for Electron-Tunneling Spectroscopy, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 53(16), 11176–11185,  DOI:10.1103/PhysRevB.53.11176.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nh00586k

---