Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Synthesis, structure, and magnetic properties of diamagnetic Co(III) ion-based heterometallic CoIII–LnIII (Ln = Dy, Tb, Ho, Er) complexes†
Nandini
Barman
a,
Purbashree
Halder
a,
Subrata
Mukhopadhyay
a,
Björn
Schwarz
 *b,
Enrique
Colacio
*b,
Enrique
Colacio
 *c,
Rajanikanta
Rana
d,
Gopalan
Rajaraman
*d and
Joydeb
Goura
*c,
Rajanikanta
Rana
d,
Gopalan
Rajaraman
*d and
Joydeb
Goura
 *aef
*aef
aDepartment of Chemistry, Jadavpur University, Kolkata 700032, India. E-mail: jgoura@chemistry.du.ac.in; joydebgoura@gmail.com
bKarlsruhe Institute of Technology (KIT) – Institute for Applied Materials (IAM), Hermann-von-Helmholtz-Platz 1, 76344 Eggenstein-Leopoldshafen, Germany. E-mail: bjoern.schwarz@kit.edu
cDepartamento de Química Inorgánica, Facultad de Ciencias, Universidad de Granada, Av. Fuentenueva S/N, 18071 Granada, Spain. E-mail: ecolacio@ugr.es
dDepartment of Chemistry, Indian Institute of Technology, Bombay, Powai, Mumbai, Maharashtra 400076, India. E-mail: rajaraman@chem.iitb.ac.in
eDepartment of Chemistry, University of Delhi, Delhi 110007, India
fDepartment of Chemistry, Bangabasi College, Kolkata 700009, India
First published on 3rd July 2024
Abstract
The reaction of Schiff base ligand N,N′-bis(salicylidene)ethylenediamine (H2L) with [CoII2(μ-OH2)(O2CCMe3)4(HO2CCMe3)4] (CoII2-Piv) (Piv = pivalate) and Ln(NO3)3·xH2O (for 1, 3, 4x = 5; for 2, x = 6) salts in the presence of triethylamine afforded [CoIIILnIII(L)(μ-Piv)2(η1-Piv)2(η1-OHMe)2] [where Ln = Dy, for 1; Tb, for 2; Ho, for 3; and Er, for 4] complexes. The heterometallic dinuclear ensemble is built via the bridging coordination action of [L]2− and four [Piv]− ligands. Further, the Ln(III) center is coordinated by two η1-OHMe ligands. Shape analysis of all the Ln(III) centers in 1–4 reveals the existence of a distorted triangular dodecahedron geometry. Magnetic studies revealed that compound 1 shows slow magnetic relaxation under zero-field at low temperatures whereas compound 4 displays field-induced slow magnetic relaxation. This phenomenon is in agreement with the results of theoretical studies.
Introduction
In recent years, 3d/4f containing heterometallic polynuclear complexes have obtained increasing attention due to their potential applications in a variety of fields such as magnetism,1 magnetic refrigeration,2 quantum computation,3 spintronics,4 and luminescence.5 Interesting magnetic properties arise for such systems, due to the strong interaction between paramagnetic 3d and 4f electrons of the metal ions. In addition, the presence of spin–orbit coupling in many lanthanide metal ions leads to a large total angular momentum (J) and many lanthanide ions possess significant single-ion magnetic anisotropy due to the splitting of the J levels by the ligand crystal field.6 As a result, they exhibit single-molecule magnet (SMM) behavior with high energy barriers for reversal of magnetization (Ueff) and blocking temperatures (TB).7From recent developments, it is realized that replacing paramagnetic 3d metal ions with diamagnetic metal ions (e.g. Zn(II), Mg(II), Co(III) in specific co-ordinations environments etc.) can lead to more desired magnetic properties. It is observed that the presence of diamagnetic metal ions increases the negative charge density on the bridging oxide ligands to make it more rigid, and allows tighter binding with the lanthanide metal ions, which stabilizes the ground state of lanthanide metal ions, hence increasing the energy gap between the ground and the excited state.8 There are various types of organic ligands utilized for the preparation of 3d/4f ensembles. Among them, salen Schiff base type ligands are appropriate for the construction of 3d–4f metal complexes as they possess two types of coordination pockets, (i) the (N, O) sites are suitable for transition metal ions, and (ii) the (O, O) sites are suitable for lanthanoid ions. As a result, they can act as multi-site coordination ligands leading to 3d/4f heterometallic ensembles of diverse topology.
Chandrasekhar and coworkers have reported Ln–M complexes with diamagnetic Mn+ ions {Mn+ = Co(III) and Zn(II)} behaving as SMM complexes.9 In 2015, they reported heterometallic trinuclear CoIII2Ln complexes and in these instances, CoIII2Dy shows zero field SMM behavior and the highest energy barrier of 88 K for reversal of magnetization,9a while Tb and Er analogs show field-induced slow relaxation of magnetization. In 2017, they prepared diamagnetic Zn(II) metal ion containing double triangular topology-based heterometallic hexanuclear Zn3IIILn3 complexes. Here, Zn3IIIDy3 displayed SMM behavior with an energy barrier of 48 K.5b Mohanta et al. prepared a CoIII–Dy heterometallic system based on an o-vanillin and ethylene diamine ligand. AC susceptibility measurements pointed out that this complex exhibited a field-induced slow magnetic relaxation with two relaxation processes.10 Sun and co-workers reported a series of Zn(II) or Co(III) ions-based heterometallic 3d/4f ensembles that were assembled via an o-vanillin based compartmental ligand and a beta-diketonate as auxiliary ligand. They have shown that replacing the square pyramidal Zn(II) ion by a Co(III) ion for Co(III)–Dy systems leads to better SMM behavior.11
Therefore, N,N′-bis(salicylidene)ethylenediamine (H2L) represents a very interesting ligand as it can be synthesized by commercial reagents and it has two different coordination pockets. Moreover, it may possibly to form a Ln(III) center with a reduced coordination number due to the lack of an extra OMe group in salicylaldehyde. It is well documented that the low coordinated lanthanide(III) complexes exhibit better SMM performance than any other system.12
Herein, we report the synthesis and the structural/magnetic characterization of [CoIIILnIII(L)(μ-Piv)2(η1-Piv)2(η1-OHMe)2] [where Ln = Dy, for 1; Tb, for 2; Ho, for 3; and Er, for 4] complexes that are discussed with respect to results from theoretical studies.
Experimental
Reagents and general procedures
Solvents and other general reagents used in this work were purified according to standard procedures.13 2-Hydroxy benzaldehyde, ethylenediamine (S. D. Fine Chemicals, Mumbai, India), Dy(NO3)3·5H2O, Tb(NO3)3·6H2O, Ho(NO3)3·5H2O and Er(NO3)3·5H2O were obtained from Alfa Aesar and were used as received. The Schiff base ligand, N,N′-bis(salicylidene)ethylenediamine (H2L) and [CoII2(μ-OH2)(O2CCMe3)4(HO2CCMe3)4] (CoII2-Piv) were prepared using a reported procedure.14,15Instrumentation
Melting points were measured using a JSGW melting point apparatus and are uncorrected. 1H NMR spectra were recorded in DMSO-d6 solutions on a JEOL JNM LAMBDA 400 model spectrometer operating at 400 MHz. Chemical shifts are reported in parts per million (ppm) and are referenced with respect to internal tetramethylsilane (1H). FT-IR spectra were recorded using a PerkinElmer LX-1 FTIR spectrophotometer operating at 400–4000 cm−1 by using a modern diamond attenuated total reflectance (ATR) accessory method. Elemental analyses of the compounds were performed using a PerkinElmer 2400 Series-II CHN analyzer. Powder X-ray diffraction (PXRD) patterns were measure using a Bruker D8 Advanced powder diffractometer with CuKα radiation.X-Ray crystallography
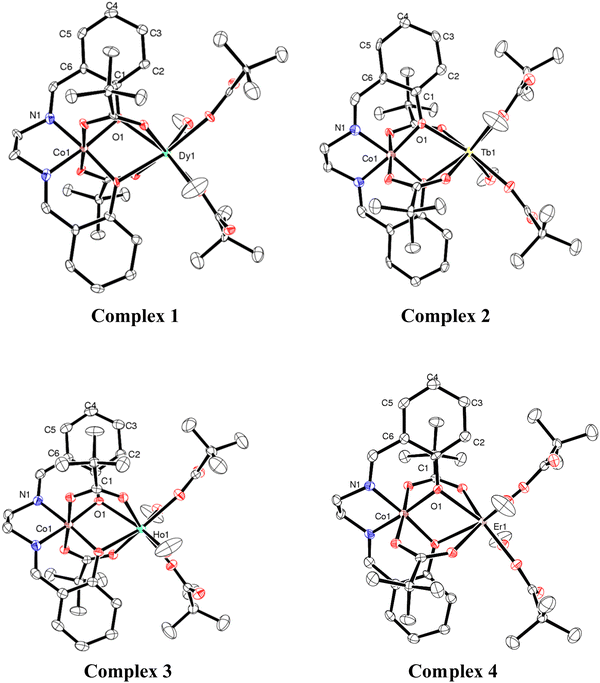
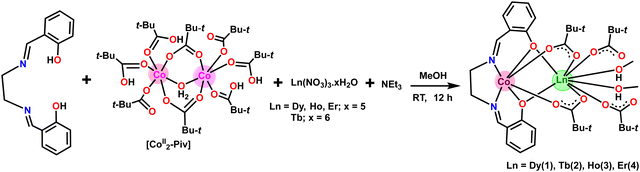
Single-crystal X-ray structural studies of 1–4 were performed on a Bruker SMART APEX II CCD diffractometer. Data were collected using a graphite-monochromated MoKα radiation (λα = 0.71073 Å). The crystals did not degrade/decompose during the data collection. Data collection, structure solution, and refinement were performed using the SMART, SAINT, and SHELXTL programs respectively.16a–f All of the non-hydrogen atoms were refined anisotropically using full-matrix least-square procedures. All of the hydrogen atoms were fixed at idealized positions and a riding model was used. All of the mean plane analyses and molecular drawings were obtained using Diamond (version 3.1). The ORTEP diagrams of all the complexes are represent in Fig. 1.Synthesis
AC susceptibility was measured with a ACMS-II option from 10 Hz to 10 kHz at 35 frequencies (for 4, from 100 Hz to 10 kHz at 40 frequencies) with log-distribution at 1.8 K (for 1 also at 2.0, 2.35 and 2.56 K and for 4 also at 2.0 K) at various magnetic DC fields up to 1 T for 1 and 4, up to 2000 Oe for 3, and up to 500 Oe for 2, respectively. For the AC measurements, the polypropylene sample capsule was attached to the polymer straw sample holder (AGC2 from Quantum Design) with the help of some polyimid tape. The AC excitation field was 5 Oe with an averaging time per measuring point of 10 seconds. The AC raw data sets have not been corrected for diamagnetic contributions.
Results and discussion
Synthesis
Chandrasekhar and coworkers reported heterometallic trinuclear bent-shaped CoIII2Ln complexes by utilized o-vanillin Schiff base.9 This is the first example of this series that shows zero-field SMM behavior.9 In the current instance replacement of o-vanillin by salicylaldehyde generates a simple Schiff base ligand, N,N′-bis(salicylidene)ethylenediamine (H2L) (Scheme 1). H2L possesses N and O donor sites and helps to bind the selectively Co(III) and Ln(III) ions due to hard–hard combinations of the O and Ln sites. Therefore, the reaction of H2L ligand with CoII2-Piv and Ln(NO3)3·xH2O (for 1, 3, 4x = 5; for 2, x = 6) salts in the presence of triethylamine as a base afforded heterometallic dinuclear CoIII–LnIII family. Here the conversion of Co(II) to Co(III) is due to the aerial oxidation, and has been confirmed by bond valence sum (BVS) calculations (Table S2, ESI†).18 The molecular geometries of these complexes have been ascertained by single-crystal X-ray diffraction and are discussed below.Molecular structures of 1–4
The crystallographic parameters of 1–4 are given in Table 1. Compounds 1–4 are isostructural and crystallize in the monoclinic C2/c (Z = 4) space group. In view of the structural similarity of all the compounds, only the representative structure of 1 will be described here. The detailed structural parameters of all four compounds are given in the ESI† (Fig. S1–S3 and Tables S3–S8).| Compound | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| Formula | C38H58CoDyN2O12 | C38H58CoTbN2O12 | C38H58CoHoN2O12 | C38H58CoErN2O12 | |
| Formula weight (g mol−1) | 956.29 | 952.27 | 958.72 | 961.05 | |
| Temp. (K) | 100(2) | 100(2) | 100(2) | 100(2) | |
| Crystal system | Monoclinic | Monoclinic | Monoclinic | Monoclinic | |
| Space group | C2/c | C2/c | C2/c | C2/c | |
| Unit cell dimensions | a (Å) | 16.1016(11) | 16.1293(10) | 16.1250(10) | 16.1225(11) |
| b (Å) | 10.6366(8) | 10.6538(10) | 10.6664(10) | 10.6783(11) | |
| c (Å) | 25.107(2) | 25.171(2) | 25.1229(2) | 25.104(2) | |
| α (°) | 90 | 90 | 90 | 90 | |
| β (°) | 107.172(5) | 107.014(3) | 107.197(3) | 107.219(3) | |
| γ (°) | 90 | 90 | 90 | 90 | |
| Volume (Å3); Z | 4108 (5); 4 | 4136 (6); 4 | 4127(6); 4 | 4128(6); 4 | |
| Density (Mg m−3) | 1.546 | 1.530 | 1.543 | 1.546 | |
| Abs. coef. (mm−1) | 2.270 | 2.158 | 2.366 | 2.482 | |
| F (000) | 1956 | 1952 | 1960 | 1964 | |
| Crystal size (mm) | 0.12 × 0.09 × 0.08 | 0.12 × 0.11 × 0.09 | 0.12 × 0.11 × 0.09 | 0.16 × 0.12 × 0.08 | |
| θ range (°) | 2.609 to 25 | 2.602 to 24.994 | 2.604 to 25 | 2.603 to 25 | |
| Limiting indices | −19 ≤ h ≤ 18 | −19 ≤ h ≤ 19 | −19 ≤ h ≤ 19 | −19 ≤ h ≤ 19 | |
| −12 ≤ k ≤ 12 | −12 ≤ k ≤ 12 | −12 ≤ k ≤ 12 | −12 ≤ k ≤ 12 | ||
| −29 ≤ l ≤ 29 | −29 ≤ l ≤ 29 | −29 ≤ l ≤ 29 | −29 ≤ l ≤ 29 | ||
| Reflections collected | 24![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 951 951 |
30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 810 810 |
32![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 055 055 |
31![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 599 599 |
|
| Unique reflections [Rint] | 3620 [0.0890] | 3647 [0.0493] | 3638 [0.0394] | 3640 [0.0656] | |
| Completeness to θ | 99.8% (25.00°) | 99.9% (24.994°) | 99.9% (25.00°) | 99.9% (25.00°) | |
| Data/restraints/parameters | 3620/0/253 | 3647/0/253 | 3638/0/253 | 3640/0/253 | |
| GOOF on F2 | 1.173 | 1.454 | 1.226 | 1.266 | |
| Final R indices [I > 2σ(I)] | R 1 = 0.0420, wR2 = 0.0874 | R 1 = 0.0505, wR2 = 0.1249 | R 1 = 0.0235, wR2 = 0.0544 | R 1 = 0.0343, wR2 = 0.0709 | |
| R indices (all data) | R 1 = 0.0528, wR2 = 0.0915 | R 1 = 0.0520, wR2 = 0.1254 | R 1 = 0.0250, wR2 = 0.0549 | R 1 = 0.0381, wR2 = 0.0719 | |
| Largest residual peaks (e Å−3) | 2.18 and −1.19 | 1.63 and −3.32 | 1.44 and −0.70 | 0.70 and −1.81 | |
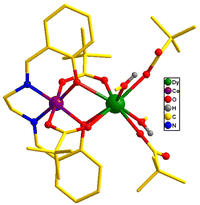
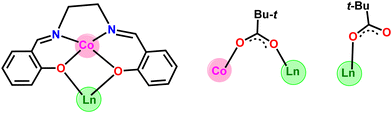
The heterometallic dinuclear CoIII–DyIII compound is formed by the combination of a Co(III) and a Dy(III) ion which are held together by [L]2−, and four [Piv]− ligands. There are two types of binding coordination modes of the pivalate ligand. Out of four pivalate ligands two of them are bridges between Co(III) and Dy(III) center and the remaining two are η1-coordinated to the Dy(III) center. In addition, two η1-OHMe ligands are coordinated to the Dy(III) (Fig. 2 and Scheme 1). The coordination modes of the ligands are summarized in Chart 1.
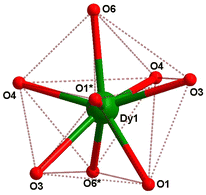
In compound 1, the Dy(III) center is eight-fold coordinated with a coordination sphere DyO8. Systematic Shape analysis of compounds 1–4, using SHAPE 2.1,19 reveals that the individual Ln(III) coordination sphere is best described as a distorted triangular dodecahedron geometry (Fig. 3). Full results of the geometric analyses can be found in the ESI† (Table S8). The isomorphism and phase purity of these complexes was further check using powder X-ray diffraction analysis (Fig. S4–S7, ESI†).
The core structure and magnetic properties of the reported CoIII–LnIII complexes have been compared with the current instances to their formula and the magnetic properties (Table S9, ESI†).10,11,20 All the CoIII–LnIII complexes possess linear core structure with different coordination geometry around the lanthanide ions. Interestingly, compound [L1Co(III)Br2Dy(III)(acac)2]·CH2Cl2 show the largest energy barrier Ueff = 167 K, among the reported systems (Table S9, ESI†)11 while [CoIIIDyIII(HL)(AcO)3(H2O)3]·(AcO)(H2O) possesses Ueff = 113 K.20c The different energy barrier explained due to the change in the coordination number and geometry around the Dy(III) center. In the former case it is eight-coordinated with biaugmented trigonal prismatic geometry while the later one possesses nine coordinated with distorted monocapped square antiprism geometry. Another derivatives of [Co(H0.5L)Dy(DBM)2H2O](ClO4)0.5(H2O)3 show Ueff = 88.9 K20b and it is similar effective energy barrier reported the trinuclear bent-geometry of [CoIII2Ln(L)2(μ-O2CCH3)2(H2O)3]·NO3·MeOH·4H2O (LH3 = 2-methoxy-6-[{2-(2-hydroxyethylamino)ethylimino}methyl]phenol), in a zero applied field.9a Overall, the different magnetic properties of the diamagnetic metal ion containing CoIII–LnIII complexes are mostly attributed by the lanthanide coordination number and geometry, as well magnetic anisotropy 4f-metal ions.9–11,20
Magnetic properties
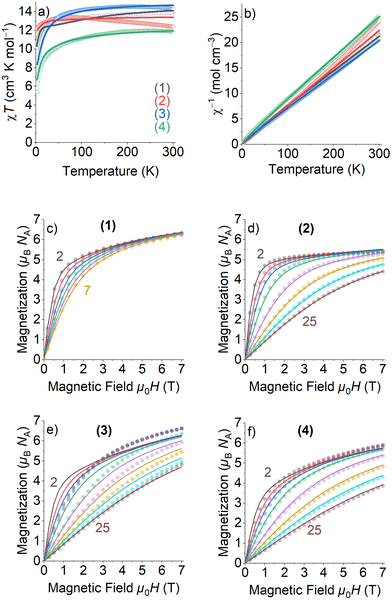
The electronic configurations, total spin quantum numbers S, total orbital angular momentum quantum number L and total angular momentum quantum number J of Dy3+ (1), Tb3+ (2), Ho3+(3), and Er3+ (4), as well as the refined magnetic parameters as obtained by fits to the experimental data sets for these complexes are listed in Table 2. The magnetic properties of 1–4 in the form of the temperature dependence of the χMT (where χM is the molar susceptibility), in the temperature range 300–2 K and under an applied magnetic field of 1000 Oe, are given in Fig. 4(a).| Lanthanoide Ln | (1) | (2) | (3) | (4) |
|---|---|---|---|---|
| Dysprosium (Dy) | Terbium (Tb) | Holmium (Ho) | Erbium (Er) | |
| a Calculated from the total angular momentum quantum number J and the refined effective giso value. | ||||
| Electr. Conf. | [Xe] 4f106s2 | [Xe] 4f96s2 | [Xe] 4f116s2 | [Xe] 4f126s2 |
| Ln3+ | 4f9 | 4f8 | 4f10 | 4f11 |
| Spin quantum nr. S | 5/2 | 3 | 2 | 3/2 |
| Orbital quantum nr. L | 5 | 3 | 6 | 6 |
| Total quantum nr. J | 15/2 | 6 | 8 | 15/2 |
| Ground term | 6H15/2 | 7F6 | 5I8 | 4I15/2 |
| Theoretical magnetic parameters | ||||
| Landé g factor | 1.33 | 1.5 | 1.25 | 1.2 |
| Paramagnetic moment μtheo (μB) | 10.646 | 9.721 | 10.6066 | 9.5812 |
| Curie constant Ctheo (cm3 K mol−1) | 14.17 | 11.82 | 14.07 | 11.48 |
| Saturation moment Mtheo (μB) | 10 | 9 | 10 | 9 |
| Experimentally observed magnetic parameters | ||||
| χ M T at room temperature (cm3 K mol−1) | 13.90 | 12.39 | 14.30 | 11.88 |
| χ M T at 2 K (cm3 K mol−1) | 10.16 | 12.00 | 5.42 | 5.82 |
| Measured moment at 2 K and 7 T Mmax (μB) | 6.33(1) | 5.41(1) | 6.62(1) | 5.90(1) |
| Refined magnetic parameters from experimental DC magnetometry | ||||
| Effective giso | 1.3372(5) | 1.594(2) | 1.280(1) | 1.234(1) |
| Effective paramagnetic moment μeffa (μB) | 10.677(1) | 10.330(1) | 10.861(1) | 9.953(1) |
| Curie constant Ca (cm3 K mol−1) | 14.25(1) | 13.34(1) | 14.75(1) | 12.14(1) |
| Saturation moment Ma (μB) | 10.03(1) | 9.56(1) | 10.24(1) | 9.26(1) |
| CFP B02 (cm−1) | −5.55(5) | −7.9(4) | −3.3(2) | −4.9(1) |
| CFP B04 (cm−1) | 0.0232(2) | 0.021(1) | 0.014(1) | 0.025(1) |
| Fit residual | 0.45 | 49 | 709 | 19 |
The room temperature χMT values of complexes 1–4 are in rather good agreement with the expected theoretical values using the free ion approximation (see Table 2). The χMT product decreases with decreasing temperature, first slowly down to 75–100 K for 1, 2 and 4 and then rapidly down to 2.0 K to reach the values indicated in Table 2. In the case of 3, the χMT very slightly increases to reach a maximum at approximately 100 K and then decreases down to 2 K. The decreases in χMT for 1–4 are mainly due to the effects of the thermal depopulation of the mJ sublevels of the 2S+1ΓJ ground state of the Ln3+ ion, which are originated by the crystal field, together with possible very weak Ln3+⋯Ln3+ antiferromagnetic interactions.
The experimental curves were fitted by means of a phenomenological Hamiltonian approach with an angular momentum basis set that represents the magnetic lanthanoid ion using the program PHI.21 In this magnetic model, the lanthanoid ion was defined by its corresponding total angular momentum quantum number J. A refinable effective isotropic g-factor giso was introduced with the theoretical g-factors as listed in Table 2 as starting values for the refinements. Besides this, two crystal field parameters (CFP) B02 and B04 were introduced to account for uniaxial local site anisotropy (see eqn (S1), ESI† for description and definition of applied Hamiltonian). The fits of the magnetic model simulations to the experimentally measured data are quite satisfying, except the low temperature and high field part of the field scans of 3 which could not be modelled adequately. Most importantly, the refined isotropic giso factors for 1–4 (Table 2) are all quite close to the theoretical values, verifying thereby that the magnetic properties can exclusively be ascribed to the Ln3+ ion and that Co(III) is diamagnetic. For all compounds 1–4, negative values for B02 and positive values for B04 have been refined, with the absolute values of B04 being much smaller than those of B02. Because of the crude model used to simulate the magnetic data, the refinement of the CFPs should still rather be considered as a parameter fit, and the application of more sophisticated spectroscopic methods would be needed to extract more reasonable parameters to characterize the crystal field. The magnetization values at the highest applied DC magnetic field of 7 T are almost half of those calculated for the theoretical saturation moments Mtheo of hypothetical free ions (see Table 2), which can be mainly attributed to crystal-field effects giving rise to significant magnetic anisotropy.
The AC susceptibility measurements were firstly performed at the lowest available temperature of 1.8 K and up to the highest experimentally available excitation frequency of 10 kHz to investigate whether slow magnetic relaxation is present in these compounds. Furthermore, the AC susceptibility was not only measured at zero DC magnetic field, but at various external DC fields as outlined in the Experimental section. 1 and 4 are the only compounds of the series that exhibit slow magnetic relaxation within the available parameter space of the experiment. In the case of 1, the frequency dependence of the 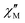 at 1.8 K and applied magnetic fields in the 0–10
at 1.8 K and applied magnetic fields in the 0–10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 Oe (= 1 T) range (see Fig. S8, ESI†) shows weak slow relaxation from zero Oe (with a maximum at a frequency of about 10 kHz), until approximately 3500 Oe (with maximum at a frequency about 3 kHz). The intensity of the maxima increases until 588 Oe (at about 8 kHz) and decreases and shifts to lower frequencies when the DC field increases from this value, so that at about 5000 Oe no cusp can be observed any more. Maxima are observed until 2.35 K (Fig. S8–S10, ESI†), but at 2.56 K (Fig. S11, ESI†) the broad maxima peaks have shifted to frequencies that are higher than those available in our equipment. Concerning 4, as shown in Fig. S12 (ESI†), there are no indications for slow magnetic relaxation neither at zero nor at fields up to 175 Oe at 1.8 K. But from 231 Oe on, there is a cusp in the imaginary χ′′ part around 8 kHz that is slightly shifting to lower frequencies when the DC field is increased to 1236 Oe. For even higher fields up to 1 T, the overall signal reduces again and a cusp in χ′′ is only visible up to 2162 Oe (see Fig. S12, ESI†). The cusp in the imaginary χ′′ part, together with a simultaneously present steep decreasing real
000 Oe (= 1 T) range (see Fig. S8, ESI†) shows weak slow relaxation from zero Oe (with a maximum at a frequency of about 10 kHz), until approximately 3500 Oe (with maximum at a frequency about 3 kHz). The intensity of the maxima increases until 588 Oe (at about 8 kHz) and decreases and shifts to lower frequencies when the DC field increases from this value, so that at about 5000 Oe no cusp can be observed any more. Maxima are observed until 2.35 K (Fig. S8–S10, ESI†), but at 2.56 K (Fig. S11, ESI†) the broad maxima peaks have shifted to frequencies that are higher than those available in our equipment. Concerning 4, as shown in Fig. S12 (ESI†), there are no indications for slow magnetic relaxation neither at zero nor at fields up to 175 Oe at 1.8 K. But from 231 Oe on, there is a cusp in the imaginary χ′′ part around 8 kHz that is slightly shifting to lower frequencies when the DC field is increased to 1236 Oe. For even higher fields up to 1 T, the overall signal reduces again and a cusp in χ′′ is only visible up to 2162 Oe (see Fig. S12, ESI†). The cusp in the imaginary χ′′ part, together with a simultaneously present steep decreasing real 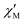 part points to the realization of a field-induced slow magnetic relaxation in 4. However, already at 2 K the slow relaxation has already shifted to higher frequencies, so that it is no longer observable within the available frequency range of this experiment (see Fig. S13, ESI†). The behavior observed for 1 and 4 could be due to either a very low energy barrier for the flipping of the magnetization, which is not high enough to trap the magnetization above 2 K, or the existence of a very fast resonant zero-field quantum tunneling of the magnetization (QTM), which leads to a flipping rate that is too fast to observe the maximum in the
part points to the realization of a field-induced slow magnetic relaxation in 4. However, already at 2 K the slow relaxation has already shifted to higher frequencies, so that it is no longer observable within the available frequency range of this experiment (see Fig. S13, ESI†). The behavior observed for 1 and 4 could be due to either a very low energy barrier for the flipping of the magnetization, which is not high enough to trap the magnetization above 2 K, or the existence of a very fast resonant zero-field quantum tunneling of the magnetization (QTM), which leads to a flipping rate that is too fast to observe the maximum in the 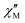 above 2 K (Fig. S13, ESI†). In contrast for 2 and 3 (see Fig. S14 and S15, ESI† respectively) no maxima in the imaginary
above 2 K (Fig. S13, ESI†). In contrast for 2 and 3 (see Fig. S14 and S15, ESI† respectively) no maxima in the imaginary 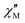 signals could be observed at 1.8 K, neither in zero field nor in a present DC external field with the available experimental parameter space.
signals could be observed at 1.8 K, neither in zero field nor in a present DC external field with the available experimental parameter space.
The AC data for 1 could not be fitted adequately, neither by a Debye model nor by a generalized Debye model including a distribution of relaxation times, because the relaxation rates are too close to the experimental limit of the experiment of 10 kHz. To overcome this problem, an alternative approach has been applied to obtain the relaxation parameters from the AC data, which is based on the fact that the ratio between the out-of-phase 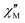 and in-phase
and in-phase 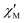 AC susceptibility can be expressed in an approximate manner as22
AC susceptibility can be expressed in an approximate manner as22
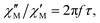 | (1) |
The substitution in this equation of the relaxation time (τ) by its expression for each relaxation mechanism (Orbach or Raman) allows for determining the respective relaxation parameters. If, hypothetically, the relaxation would occur entirely through an Orbach relaxation mechanism, for which τ = τ0·exp(Ueff/kBT), the equation becomes as follows after applying natural logarithms:
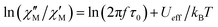 | (2) |
The effective energy barrier Ueff could be approximately assessed by fitting the experimental 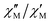 data in the high-frequency region to this equation, which allows roughly evaluating Ueff and τ0 (Fig. 5).
data in the high-frequency region to this equation, which allows roughly evaluating Ueff and τ0 (Fig. 5).
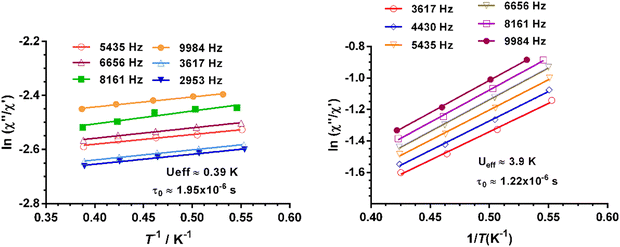 | ||
Fig. 5 Temperature dependence of the 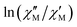 at different frequencies under a magnetic field of zero (left) and 588 Oe for 1. Solid lines correspond to the fit of the experimental data to eqn (2). at different frequencies under a magnetic field of zero (left) and 588 Oe for 1. Solid lines correspond to the fit of the experimental data to eqn (2). | ||
The extracted parameters Ueff and τ0 were ≈0.3 K and ≈1.9 × 10−6 s, respectively, at zero field and ≈3.9 K and ≈1.2 × 10−6 s at 588 Oe. The small value of the energy barrier agrees well with the fact that no maxima could be observed for 1 above 2.5 K. The increase of Ueff in the presence of a small field could be related to the quenching of the QTM. Nevertheless, the Ueff values should be taken as phenomenological ones and may not represent the actual relaxation processes. In the presence of a magnetic field, direct/Raman processes should dominate in the studied low-temperature range. Bearing this in mind, the 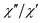 data have also been fitted by the following equation:
data have also been fitted by the following equation:
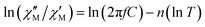 | (3) |
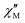 is larger) were fitted to the equation using frequencies between 3617 and 9984 Hz, leading to the parameters C ≈ 2.8 × 10−5 s and n ≈ 2 (Fig. 6).
is larger) were fitted to the equation using frequencies between 3617 and 9984 Hz, leading to the parameters C ≈ 2.8 × 10−5 s and n ≈ 2 (Fig. 6).
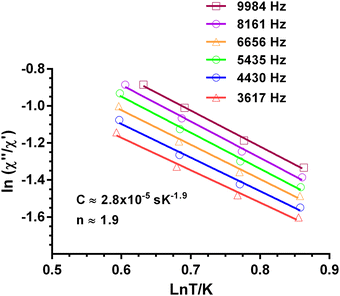 | ||
Fig. 6 Dependence of the ratio of the ln(χ′′M/χ′M) with ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) T at different frequencies under a magnetic field of 588 Oe for 1. Solid lines correspond to the fit of the experimental data to eqn (3). T at different frequencies under a magnetic field of 588 Oe for 1. Solid lines correspond to the fit of the experimental data to eqn (3). | ||
The inverse of the relaxation times follows a τ ∝ T2 dependence, which could be ascribed to a resonance phonon trapping (RPT) mechanism. This process occurs when there are phonon-bottleneck effects, so that the energy of the lattice modes generated by the relaxing spins cannot be liberate appropriately fast into a thermal reservoir. These phonons can be reabsorbed by other spins, and the effective relaxation time becomes longer. It is worth mentioning that this alternative approach of fitting could not be applied to 4.
To explain the dynamic behaviour of these compounds we have to inspect the distribution of oxygen donor atoms and Ln–O distances in the Ln3+ ion coordination sphere. The shortest Ln–O distances in all these complexes involve oxygen donor atoms of the phenoxido bridges (Ln–O ∼2.3 Å). Moreover, all other distances are larger by up to approximately 0.12 Å. The relatively large Dy–O distances and the rather spherical distribution of the donor oxygen atoms around the Ln3+ are not appropriate to create neither strong axial nor equatorial crystal fields and therefore small axial anisotropy are expected in all cases. In agreement, uniaxial anisotropies were implemented in the magnetic models by introducing the crystal field parameters B02 and B04. As a result, the energy gap between the ground and first excited Kramers doublets (KD) states, which determine the thermal energy barrier, is expected to be very small. This prediction is in good accord with the experimental results, which as indicated above, show no maxima in the χMvs. T plot below 2 K.
The fact that complexes 2 and 3 do not show slow relaxation even in the presence of an applied magnetic field is not unexpected taking into consideration that non-Kramers ions, such as Tb3+ and Ho3+, present an intrinsic tunnelling gap in the ground state favouring QTM. Moreover, to exhibit an axial bistable ground state and slow relaxation of the magnetization, these ions require a strict axial symmetry and this is not the case of compounds 2 and 3. Besides, in the case of the Ho3+ ion, the intrinsic low anisotropy of the 4f shell makes more difficult the adoption of an axial bistable ground state.
Theoretical calculation
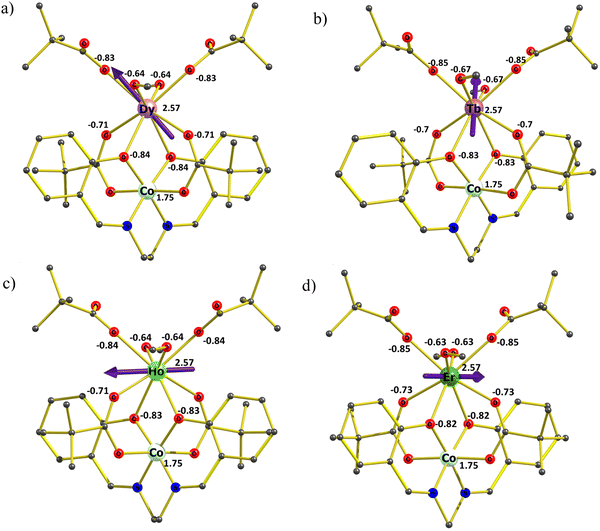
Ab initio calculations on complexes 1–4 were performed with the MOLCAS 8.223 program of the CASSCF/RASSI-SO/SINGLE_ANISO type (see computational details in ESI†). Experimental findings indicate that complexes 2, 3, and 4 lack zero-field single-molecule magnet (SMM) behavior and are not field-induced SMMs either. Meanwhile, 1 exhibits non-SMM behavior but demonstrates minimal field-induced SMM characteristics. Ab initio calculations reflect these experimental results accurately. The g tensors of complexes 1 and 4 exhibit non-axial behavior, with a notable contribution from transverse anisotropy. Ground state analysis further reveals substantial quantum tunneling of magnetization (QTM) and minimal involvement of mJ = 15/2, alongside a mixture of other mJ levels shown in Table 3. In the case of complexes 2 and 3, our calculations reveal a significant tunneling gap between the ground-state single-ion TbIII and HoIII sites: approximately 8.93 cm−1 (for 2) and 1.87 cm−1 (for 3), as detailed in Table 3. This aligns with the experimental findings of the absence of single-molecule magnet (SMM) behavior in AC measurements without a DC field for complexes 2 and 3. Examining the anisotropy axes of 1–4 depicted in Fig. 7(a)–(d), it is evident that there is an absence of a strong-field ligand along the anisotropy axis, contributing to a reduction in the molecule's overall anisotropy.| Energy (cm−1) | |||
|---|---|---|---|
| 1 (Dy) | 2 (Tb) | 3 (Ho) | 4 (Er) |
| 0 | 0 | 0 | 0 |
| 12.2 | 1.87 | 8.9 | 15.3 |
| 97.5 | 132.4 | 10.3 | 55.1 |
| 127.8 | 163.4 | 25.6 | 83.8 |
| 157.3 | 169.8 | 50.8 | 150.6 |
| 170.9 | 244.4 | 101.9 | 165.7 |
| 210.2 | 254.5 | 110.4 | 245.0 |
| 461.8 | 305.2 | 121.7 | 271.0 |
| 307.4 | 131.1 | ||
| 368.5 | 161.9 | ||
| 371.7 | 181.3 | ||
| g x | g y | g z | Wavefunction | |
|---|---|---|---|---|
| Ground Kramers doublet (1) | 11.62 | 7.31 | 0.12 | 5|±15/2〉 + 22|±13/2〉 + 19|±11/2〉 + 78|±1/2〉 |
| Ground Ising doublet (2) | 0.00 | 0.00 | 17.61 | 97|±6〉 + 19|±4〉 |
| Ground Ising doublet (3) | 0.00 | 0.00 | 11.83 | 9|±8〉 + 50|±7〉 + 19|±6〉 + 40|±5〉 + 19|±4〉 + 43|±0〉 |
| Ground Kramers doublet (4) | 0.76 | 2.92 | 14.80 | 89|±15/2〉 + 21|±13/2〉 + 11|±11/2〉 + 20|±5/2〉 |
To gain further insight into the anisotropy axis and its alignment, we have calculated LoProp charges for complexes 1–4, as depicted in Fig. 7(a)–(d). Notably, high charges are observed among all the coordinated atoms on the μ2- and μ3-oxygen atoms linked to the CoIII ion. Given that the electron density of DyIII, TbIII, and HoIII ions exhibits an oblate shape, the β-electron density is expected to align perpendicular to the direction of maximum electrostatic repulsion. Meanwhile, the gzz axis aligns with the atoms possessing the “largest” charges, elucidating the parallel gzz orientation observed in complexes 1 to 3. Considering the electrostatic interactions remain consistent for the TbIII and HoIII complexes compared to DyIII, a similar trend is anticipated. However, TbIII exhibits a relatively more oblate shape than DyIII, whereas HoIII is less oblate. Consequently, the electrostatic repulsion from the strongly negative oxygen atoms linked to the CoIII ion exerts the most significant influence on the electronic structure of TbIII ions, followed by DyIII, with the weakest impact on HoIII ions. For complex 4, where ErIII exhibits prolate electron density, the anisotropy will align in the direction of the lowest charge.
To investigate the impact of the charge of the diamagnetic ion on the anisotropy barrier and the resulting single-molecule magnet (SMM) properties, we conducted a study by substituting the tricationic diamagnetic ion in complex 1 with monocationic, dicationic, and tetracationic diamagnetic ions. Specifically, potassium (KI), zinc (ZnII), and titanium (TiIV) ions were chosen for this purpose, and the CoIII ions in complex 1 were modeled as K+ (model 1a), ZnII (model 1b), and TiIV (model 1c), respectively. Ab initio calculations were performed for models 1a, 1b, and 1c, revealing that in the cases of 1a and 1b, there was an observed increase in the anisotropy, leading to a partial suppression of quantum tunneling of magnetization (QTM) in the ground state, as detailed in Table 4. Conversely, in the case of model 1c, the transverse anisotropy was notably higher, accompanied by increased QTM in the ground state. This trend strongly indicates that a decrease in the oxidation state of the diamagnetic ion results in enhanced electronic repulsion with the bridging atoms, consequently increasing the anisotropy barrier and partially quenching QTM.
| Model | g x | g y | g z | QTM |
|---|---|---|---|---|
| 1a (KIDyIII) | 1.15 | 2.21 | 16.16 | 0.94 |
| 1b (ZnIIDyIII) | 1.53 | 3.21 | 12.16 | 1.02 |
| 1 (CoIIIDyIII) | 11.62 | 7.31 | 0.12 | 2.67 |
| 1c (TiIVDyIII) | 10.6 | 6.31 | 0.18 | 2.68 |
In examining complexes 1–4, both experimental and computational results indicate the absence of zero-field single-molecule magnet (SMM) behavior. This could be attributed to the anisotropy of the molecules, influenced by the electron density of the metal. Complexes 1–3 exhibit an oblate electron density, necessitating strong axial and weak equatorial ligands, whereas complex 4 has a prolate shape, requiring weak axial and strong equatorial ligands. However, none of the ligands in 1–4 fit these criteria. Complex 4 shows slow magnetic relaxation under a small magnetic field but lacks field-induced SMM behavior in theoretical investigations. Theoretical calculations were conducted without considering the impact of the magnetic field on the compound's electronic structure, as is customary. These calculations reveal a high ground state quantum tunneling of magnetization (QTM), indicating that relaxation occurs within the ground state itself, as shown in Fig. S16–S18 (ESI†), resulting in a theoretical barrier height of zero. However, when a small magnetic field is applied, compound 4 exhibits slow magnetic relaxation, demonstrating its behavior under experimental conditions. Additionally, it is observed that the CASSCF-calculated CFPs closely align with the experimentally fitted CFPs. While they are not an exact match, the trends are consistent as shown in Table 5.
| Compound | B 02 (cm−1) | B 04 (cm−1) | ||
|---|---|---|---|---|
| Experimental | CASSCF | Experimental | CASSCF | |
| 1 | −5.5 | −2.7 | 0.023 | 0.008 |
| 2 | −7.9 | −6.0 | 0.021 | 0.007 |
| 3 | −3.3 | −1.8 | 0.014 | 0.006 |
| 4 | −4.9 | −2.9 | 0.025 | 0.008 |
Conclusion
In summary, we used a multi-site coordination Schiff base ligand to prepare heterometallic dinuclear CoIII–LnIII assembly. The magnetic properties of the Ln(III) center are influenced by the diamagnetic Co(III) ion. The magnetic study revealed that compound 1 shows slow magnetic relaxation at low temperatures under zero-field, whereas compound 4 needs the application of a small magnetic field to exhibit such a behavior. Ab initio calculations and experimental investigations on complexes 1–4 reveal their magnetic behavior, with complex 1 showing minimal single-molecule magnet (SMM) characteristics, while complexes 2, 3, and 4 lack both zero-field and field-induced SMM properties. Anisotropy analysis, supported by charge distribution and electron density considerations, highlights the role of ligand geometry in modulating magnetic behavior. Substituting diamagnetic ions in complex 1 with different oxidation states impacts anisotropy and quantum tunneling of magnetization (QTM), suggesting a correlation between ion charge and SMM properties. Experimental and computational data underscore the influence of metal electron density on the absence of SMM behavior and the importance of ligand geometry in optimizing magnetic performance.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank the Department of Science Engineering Research Board (SERB), India, for Ramanujan fellowship (SERB/F/10742/202-2022) for financial support. JG is thankful to the Department of Chemistry, Jadavpur University, University of Delhi, and Institution of Eminence (IoE) for FRP research grant (ref. no. IoE/2023-24/12/FRP). E. C. would like to acknowledge financial support from the Ministerio de Ciencia e Innovación (Project PID2022-138090NB-C21), Junta de Andalucía (FQM-195 and project I + D + i P20_00692), and the University of Granada.References
- (a) A. Zabala-Lekuona, J. Manuel Seco and E. Colacio, Single-Molecule Magnets: From Mn12-ac to dysprosium metallocenes, a travel in time, Coord. Chem. Rev., 2021, 441, 213984, DOI:10.1016/j.ccr.2021.213984; (b) J. Wang, M. Feng, M. Nadeem Akhtar and M.-L. Tong, Recent advance in heterometallic nanomagnets based on TMxLn4−x cubane subunits, Coord. Chem. Rev., 2019, 387, 129–153, DOI:10.1016/j.ccr.2019.02.008; (c) J. Goura, R. Guillaume, E. Rivière and V. Chandrasekhar, Hexanuclear, Heterometallic, Ni3Ln3 Complexes Possessing O-Capped Homo- and Heterometallic Structural Subunits: SMM Behavior of the Dysprosium Analogue, Inorg. Chem., 2014, 53, 7815–7823, DOI:10.1021/ic403090z; (d) J. Goura and V. Chandrasekhar, Molecular Metal Phosphonates, Chem. Rev., 2015, 115, 6854–6965, DOI:10.1021/acs.chemrev.5b00107; (e) E. Moreno Pineda, F. Tuna, R. G. Pritchard, A. C. Regan, R. E. P. Winpenny and E. J. L. McInnes, Molecular amino-phosphonate cobalt–lanthanide clusters, Chem. Commun., 2013, 49, 3522–3524, 10.1039/C3CC40907D.
- Y.-Z. Zheng, G.-J. Zhou, Z. Zheng and R. E. P. Winpenny, Molecule-based magnetic coolers, Chem. Soc. Rev., 2014, 43, 1462–1475, 10.1039/C3CS60337G.
- C. H. Bennett and D. P. DiVincenzo, Quantum information and computation, Nature, 2000, 404, 247–255, DOI:10.1038/35005001.
- L. Bogani and W. Wernsdorfer, Molecular spintronics using single-molecule magnets, Nat. Mater., 2008, 7, 179, DOI:10.1038/nmat2133.
- (a) J. Long, Y. Guari, R. A. S. Ferreira, L. D. Carlos and J. Larionova, Recent advances in luminescent lanthanide based Single-Molecule Magnets, Coord. Chem. Rev., 2018, 363, 57–70, DOI:10.1016/j.ccr.2018.02.019; (b) J. Goura, E. Colacio, J. M. Herrera, E. A. Suturina, I. Kuprov, Y. Lan, W. Wernsdorfer and V. Chandrasekhar, Heterometallic Zn3Ln3 Ensembles Containing (μ6-CO3) Ligand and Triangular Disposition of Ln3+ ions: Analysis of Single-Molecule Toroic (SMT) and Single-Molecule Magnet (SMM) Behavior, Chem. – Eur. J., 2017, 23, 16621–16636, DOI:10.1002/chem.201703842; (c) D. A. Gálico and M. Murugesu, Controlling the Energy-Transfer Processes in a Nanosized Molecular Upconverter to Tap into Luminescence Thermometry Application, Angew. Chem., Int. Ed., 2022, 61, e202204839, DOI:10.1002/anie.202204839; (d) S. Titos-Padilla, J. Ruiz, J. M. Herrera, E. K. Brechin, W. Wersndorfer, F. Lloret and E. Colacio, Dilution-Triggered SMM Behavior under Zero Field in a Luminescent Zn2Dy2 Tetranuclear Complex Incorporating Carbonato-Bridging Ligands Derived from Atmospheric CO2 Fixation, Inorg. Chem., 2013, 52, 9620–9626, DOI:10.1021/ic401378k; (e) L.-X. Chang, G. Xiong, L. Wang, P. Cheng and B. Zhao, A 24-Gd nanocapsule with a large magnetocaloric effect, Chem. Commun., 2013, 49, 1055–1057, 10.1039/C2CC35800J.
- D. N. Woodruff, R. E. P. Winpenny and R. A. Layfield, Lanthanide Single-Molecule Magnets, Chem. Rev., 2013, 113, 5110–5148, DOI:10.1021/cr400018q.
- F.-S. Guo, B. M. Day, Y.-C. Chen, M.-L. Tong, A. Mansikkamäki and R. A. Layfield, Magnetic hysteresis up to 80 kelvin in a dysprosium metallocene single-molecule magnet, Science, 2018, 362, 1400–1403, DOI:10.1126/science.aav065.
- (a) A. Upadhyay, S. K. Singh, C. Das, R. Mondol, S. K. Langley, K. S. Murray, G. Rajaraman and M. Shanmugam, Enhancing the effective energy barrier of a Dy(III) SMM using a bridged diamagnetic Zn(II) ion, Chem. Commun., 2014, 50, 8838, 10.1039/C4CC02094D; (b) A. Chakraborty, J. Goura, P. Kalita, A. Swain, G. Rajaraman and V. Chandrasekhar, Heterometallic 3d–4f single molecule magnets containing diamagnetic metal ions, Dalton Trans., 2018, 47, 8841–8864, 10.1039/C8DT01883A; (c) L. Zhao, J. Wu, S. Xue and J. Tang, A Linear 3d–4f Tetranuclear CoIII2DyIII2 Single-Molecule Magnet: Synthesis, Structure, and Magnetic Properties, Chem. – Asian J., 2012, 7, 2419–2423, DOI:10.1002/asia.201200548; (d) G.-F. Xu, P. Gamez, J. Tang, R. Clérac, Y.-N. Guo and Y. Guo, MIIIDy3III (M = FeIII, CoIII) Complexes: Three-Blade Propellers Exhibiting Slow Relaxation of Magnetization, Inorg. Chem., 2012, 51, 5693–5698, DOI:10.1021/ic300126q; (e) J. Wu, L. Zhao, P. Zhang, L. Zhang, M. Guo and J. Tang, Linear 3d–4f compounds: synthesis, structure, and determination of the d–f magnetic interaction, Dalton Trans., 2015, 44, 11935–11942, 10.1039/C5DT01382H; (f) P. Zhang, L. Zhang, S.-Y. Lin and J. Tang, Tetranuclear [MDy]2 Compounds and Their Dinuclear [MDy] (M = Zn/Cu) Building Units: Their Assembly, Structures, and Magnetic Properties, Inorg. Chem., 2013, 52, 6595–6602, DOI:10.1021/ic400620j.
- (a) J. Goura, J. Brambleby, P. Goddard and V. Chandrasekhar, A Single-Ion Magnet Based on a Heterometallic CoIII2DyIII Complex, Chem. – Eur. J., 2015, 21, 4926–4930, DOI:10.1002/chem.201406021; (b) J. Goura, J. Brambleby, C. V. Topping, P. A. Goddard, R. Suriya Narayanan, A. K. Bar and V. Chandrasekhar, Heterometallic trinuclear {CoIII2LnIII} (Ln = Gd, Tb, Ho and Er) complexes in a bent geometry. Field-induced single-ion magnetic behavior of the ErIII and TbIII analogues, Dalton Trans., 2016, 45, 9235–9249, 10.1039/C5DT03871E.
- S. Hazra, J. Titiš, D. Valigura, R. Boča and S. Mohanta, Bis-phenoxido and bis-acetato bridged heteronuclear {CoIIIDyIII} single molecule magnets with two slow relaxation branches, Dalton Trans., 2016, 45, 7510–7520, 10.1039/C6DT00848H.
- J.-W. Yang, Y.-M. Tian, J. Tao, P. Chen, H.-F. Li, Y.-Q. Zhang, P.-F. Yan and W.-B. Sun, Modulation of the Coordination Environment around the Magnetic Easy Axis Leads to Significant Magnetic Relaxations in a Series of 3d-4f Schiff Complexes, Inorg. Chem., 2018, 57, 8065–8077, DOI:10.1021/acs.inorgchem.8b00056.
- (a) D. Errulat1, K. L. M. Harriman, D. A. Gálico, A. A. Kitos, A. Mansikkamäki and M. Murugesu, A trivalent 4f complex with two bis-silylamide ligands displaying slow magnetic relaxation, Nat. Chem., 2023, 15, 1100–1107, DOI:10.1038/s41557-023-01208-y; (b) N. F. Chilton, C. A. P. Goodwin, D. P. Mills and R. E. P. Winpenny, The first near-linear bis(amide) f-block complex: a blueprint for a high temperature single molecule magnet, Chem. Commun., 2015, 51, 101–103, 10.1039/C4CC08312A; (c) Z. Zhu, X. Ying, C. Zhao, Y.-Q. Zhang and J. Tang, A new breakthrough in low-coordinate Dy(III) single-molecule magnets, Inorg. Chem. Front., 2022, 9, 6061–6066, 10.1039/D2QI01940J; (d) C. A. P. Goodwin, F. Ortu, D. Reta, N. F. Chilton and D. P. Mills, Molecular magnetic hysteresis at 60 kelvin in dysprosocenium, Nature, 2017, 548, 439–442, DOI:10.1038/nature23447; (e) P. Zhang, L. Zhang, C. Wang, S. Xue, S.-Y. Lin and J. Tang, Equatorially Coordinated Lanthanide Single Ion Magnets, J. Am. Chem. Soc., 2014, 136, 4484–4487, DOI:10.1021/ja500793x; (f) Y.-S. Ding, N. F. Chilton, R. E. P. Winpenny and Y.-Z. Zheng, On Approaching the Limit of Molecular Magnetic Anisotropy: A Near-Perfect Pentagonal Bipyramidal Dysprosium(III) Single-Molecule Magnet, Angew. Chem., Int. Ed., 2016, 55, 16071–16074, DOI:10.1002/anie.201609685; (g) S. Xue, L. Ungur, Y.-N. Guo, J. Tang and L. F. Chibotaru, Field-Induced Multiple Relaxation Mechanism of CoIII2DyIII Compound with the Dysprosium Ion in a Low-Symmetrical Environment, Inorg. Chem., 2014, 53, 12658–12663, DOI:10.1021/ic502443g.
- B. S. Furniss, A. J. Hannaford, P. W. G. Smith and A. R. Tatchell, Vogel's Textbook of Practical Organic Chemistry, Longman, London, 5th edn, 1989 Search PubMed.
- W. Ghann, H. Sobhi, H. Kang, T. Chavez-Gil, F. Nesbitt and J. Uddin, Synthesis and Characterization of Free and Copper(II) Complex of N,N′-Bis(Salicylidene)Ethylenediamine for Application in Dye Sensitized Solar Cells, J. Mater. Sci. Chem. Eng., 2017, 5, 46–66, DOI:10.4236/msce.2017.56005.
- G. AromÌ, A. S. Batsanov, P. Christian, M. Helliwell, A. Parkin, S. Parsons, A. A. Smith, G. A. Timco and R. E. P. Winpenny, Synthetic and Structural Studies of Cobalt–Pivalate Complexes, Chem. – Eur. J., 2003, 9, 5142–5161, DOI:10.1002/chem.200304993.
- (a) SMART & SAINT Software Reference manuals, Version 6.45, Bruker Analytical X-ray Systems, Inc., Madison, WI, 2003 Search PubMed; (b) G. M. Sheldrick, SADABS, a software for empirical absorption correction, Ver. 2.05, University of Göttingen, Göttingen, Germany, 2002 Search PubMed; (c) SHELXTL Reference Manual, Ver. 6.c1, Bruker Analytical X-ray Systems, Inc., Madison, WI, 2000 Search PubMed; (d) G. M. Sheldrick, SHELXTL, Ver. 6.12, Bruker AXS Inc., Madison, WI, 2001 Search PubMed; (e) G. M. Sheldrick, SHELXL97, Program for Crystal Structure Refinement, University of Göttingen, Göttingen, Germany, 1997 Search PubMed; (f) K. Bradenburg, Diamond, Ver. 3.1eM, Crystal Impact GbR, Bonn, Germany, 2005 Search PubMed.
- H. Lueken, Magnetochemie, Eine Einführung in Theorie und Anwendung, Teubner Studienbücher (TSBC), 1999 Search PubMed.
- (a) I. D. Brown and K. K. Wu, Empirical Parameters for Calculating Cation-Oxygen Bond Valences, Acta Crystallogr., 1976, B32, 1957, DOI:10.1107/S0567740876006869; (b) W. Liu and H. H. Thorp, Bond valence sum analysis of metal-ligand bond lengths in metalloenzymes and model complexes. 2. Refined distances and other enzymes, Inorg. Chem., 1993, 32, 4102–4105, DOI:10.1021/ic00071a023; (c) R. M. Wood and G. J. Palenik, Bond Valence Sums in Coordination Chemistry. A Simple Method for Calculating the Oxidation State of Cobalt in Complexes Containing Only Co-O Bonds, Inorg. Chem., 1998, 37, 4149–4151, DOI:10.1021/ic980176q; (d) I. D. Brown and D. Altermatt, Bond-Valence Parameters Obtained from a Systematic Analysis of the Inorganic Crystal Structure Database, Acta Crystallogr., 1985, B41, 244, DOI:10.1107/S0108768185002063.
- S. Alvarez, P. Alemany, D. Casanova, J. Cirera, M. Llunell and D. Avnir, Shape maps and polyhedral interconversion paths in transition metal chemistry, Coord. Chem. Rev., 2005, 249, 1693–1708, DOI:10.1016/j.ccr.2005.03.031.
- (a) Y. Yamada, M. Tanabe, Y. Miyashita and K.-I. Okamoto, Oxalato-bridged di- and trinuclear Co(III)/Dy(III) complexes derived from mononuclear Co(III) complex with nitrilotriacetate, Polyhedron, 2003, 22, 1455–1459, DOI:10.1016/S0277-5387(03)00122-0; (b) M.-J. Liu, J. Yuan, B.-L. Wang, S.-T. Wu, Y.-Q. Zhang, C.-M. Liu and H.-Z. Kou, Spontaneous Resolution of Chiral Co(III)-Dy(III) Single-Molecule Magnet Based on an Achiral Flexible Ligand, Cryst. Growth Des., 2018, 18, 7611–7617, DOI:10.1021/acs.cgd.8b01410; (c) M. Dolai, M. Ali, J. Titiš and R. Boča, Cu(II)–Dy(III) and Co(III)–Dy(III) based single molecule magnets with multiple slow magnetic relaxation processes in the Cu(II)–Dy(III) complex, Dalton Trans., 2015, 44, 13242–13249, 10.1039/c5dt00960j.
- N. F. Chilton, R. P. Anderson, L. D. Turner, A. Soncini and K. S. Murray, PHI: A powerful new program for the analysis of anisotropic monomeric and exchange-coupled polynuclear d- and f-block complexes, J. Comput. Chem., 2013, 34, 1164–1175, DOI:10.1002/jcc.23234.
- J. Bartolomé, G. Filoti, V. Kuncser, G. Schinteie, V. Mereacre, C. E. Anson, A. K. Powell, D. Prodius and C. Turta, Magnetostructural correlations in the tetranuclear series of {Fe3LnO2} butterfly core clusters: Magnetic and Mössbauer spectroscopic study, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 014430, DOI:10.1103/PhysRevB.80.014430.
- F. Aquilante, T. B. Pedersen, V. Veryazov and R. Lindh, MOLCAS a software for multiconfigurational quantum chemistry calculations, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2013, 3, 143–149, DOI:10.1002/wcms.1117.
Footnote |
| † Electronic supplementary information (ESI) available: Figures and tabulated bond angles/lengths for the crystal structures of compounds 1–4. Bond valence sum calculations for the Co(III) atoms of compound 1–4. Full results of the SHAPE analysis for the Ln(III) centers in 1–4. Fig. S8–S15 are AC susceptibility measurements for compounds 1–4. Fig. S19 is the IR spectrum of complexes 1–4. CCDC 2332342 (1), 2332343 (3), 2332344 (2) and 2332345 (4). For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4nj02058h |
| This journal is © The Royal Society of Chemistry and the Centre National de la Recherche Scientifique 2024 |