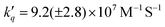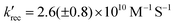Tracking photoinduced charge separation in a perfluorinated Zn-tetraphenylporphyrin sensitizer

Abstract

The development of artificial biomimetic systems with real-world applications relies on a profound understanding of all photophysical and photochemical processes taking place upon light absorption by a chromophoric unit. Efficient photoinduced charge separation in photosensitizers or specialized photocatalysts is the process triggering most of the chemical reactions in the production of solar fuels, and hence, its proper characterization is of utmost importance. In this work, we investigated photoinduced charge separation processes in a perfluorinated Zn-tetraphenylporphyrin photosensitizer (ZnF₂₀). Ascorbate and 1,4-diazabicyclo[2.2.2]octane (DABCO) were used as reversible electron donors for nanosecond-resolved pump–probe experiments using both optical absorption and resonance Raman scattering as probes. Our results indicate that in spite of similar charge separation efficiencies, the DABCO-containing system exhibits a much faster kinetics of charge-separated state formation and decay. This is attributed to its inherent ability to coordinate to the metal center. Time-resolved resonance Raman measurements allow for the detection of vibrational modes specific to both the triplet excited state of ZnF₂₀ and its reduced state, complementing transient absorption data to fully characterize the charge separation process.

---

Introduction

The daring promise of artificial photosynthesis to mitigate carbon dioxide (CO₂) emissions heavily relies on the fundamental comprehension of photoinduced charge transfer processes in carefully engineered biomimetic systems capable of both charge separation and accumulation of redox equivalents.^1–5 The very development of the next generation of dedicated materials can only be accomplished by fine-tuning their behaviors once exposed to photonic excitations as a way to induce chemical transformations. Achieving this requires a great deal of burdensome spectroscopy-based mechanistic investigations, supported by their theoretical counterparts, to shed some light on the principles that must guide molecular design towards long-lived charge-separated states.⁶

Be as troubling as it may, we now have access to proper experimental tools to investigate such fundamental processes in a myriad of biomimetic systems that can be engineered with different strategies. Some of the most well-known approaches employ basic donor-photosensitizer-acceptor (D-PS-A) units, either covalently constructed^7–9 or in a multicomponent configuration,^10,11 to mimic photoinduced processes (multiple electron transfers and accumulation) taking place in natural systems. Built on the blueprints of the natural photosynthetic apparatus, such systems take us ever closer to realizing an actual functional biomimetic system that could potentially fulfill the promise of solar fuel production.

As far as light-absorbing units, photosensitizers, are concerned, prototypical Ru(II) polypyridyl complexes remain unchallenged in terms of photochemical and photophysical properties,^12–16 but porphyrin-based compounds have been attracting attention as reasonable alternatives. Among them, zinc tetraphenylporphyrin (ZnTPP) derivatives not only have been widely used as photosensitizers for different applications^17–22 and in supramolecular self-assemblies,^23–25 but have even shown photocatalytic²⁶ proton reduction activities, which make them an even more valuable class of compounds. Because of these capabilities, they can also be used as photocatalysts for light-induced reduction reactions in artificial photosystems.

Bimolecular electron transfer processes of both singlet and triplet excited states of zinc porphyrins in the presence of donors/acceptors, along with subsequent charge recombination, have already been extensively studied. Ultrafast charge transfer from the S₂ excited state followed by rapid charge recombination of the photogenerated ion pair to populate the S₁ excited state has been demonstrated by fluorescence upconversion experiments.^27,28 Other studies revealed electron transfer from the S₁ and S₂ states, followed by picosecond charge recombination to form ground-state reactants when the energy of the ion pair is located below that of the S₁ excited state.^20,29,30 Bimolecular charge transfer from the triplet state of these compounds has also been previously reported.³¹ Importantly, geminate ion pairs formed by electron transfer quenching of an excited singlet state remain in a state with a singlet multiplicity and, therefore, charge recombination to the ground state is spin-allowed and rapid. Conversely, if the triplet excited state is quenched, the resulting geminate ion pair is also in the triplet state and charge recombination is spin-forbidden, resulting in a longer-lived geminate ion pair that may break through the solvent cage during its lifetime.^31–33

On the donor/acceptor side, not only their thermodynamic compatibility with the photosensitizer's excited state has to be taken into account, but the implications in the charge separation kinetics are also relevant depending on whether these species are covalently bound or not. Consequently, the complete reversible cycle of reductive/oxidative quenching of the photosensitizer has to be investigated in detail prior to any systematic attempt at using the charge-separated species to trigger chemical transformations of any kind.

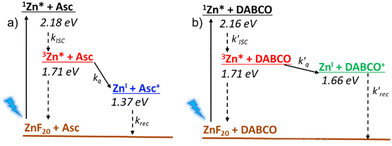
It is in this context that we now report the complete characterization of the photoinduced and reversible electron transfer processes taking place in a perfluorinated Zn-tetraphenylporphyrin photosensitizer (referred to as ZnF₂₀, Fig. 1). For this, we use complementary time-resolved probes of optical light absorption and resonance Raman scattering in the standard pump–probe approach. This molecule shows two reversible reductions (Fig. S1, ESI†) in acetonitrile (CH₃CN), both centered on the tetraphenylporphyrin ligand,³⁴ with E_red (ZnF₂₀/ZnF₂₀˙⁻) = −0.68 V vs. the normal hydrogen electrode (NHE) and E_red (ZnF₂₀˙⁻/ZnF₂₀˙˙²⁻) = −1.07 V vs. NHE. Hereafter, for simplicity, [ZnF₂₀˙⁻] and [ZnF₂₀˙˙²⁻] will be referred to as Zn^I and Zn⁰, respectively.

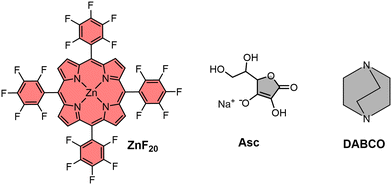Fig. 1 Molecular structures of the Zn porphyrin photosensitizer (ZnF₂₀) and electron donors (DABCO and Asc).

To investigate the reductive quenching mechanism, 1,4-diazabicyclo[2.2.2]octane (DABCO, E_ox = 0.98 V vs. NHE)³⁵ and sodium ascorbate (Asc, E_ox = 0.70 V vs. NHE)³⁶ were used as reversible electron donors (Fig. 1) in CH₃CN and acetonitrile/water (CH₃CN/H₂O = 6/4) solutions, respectively. The choice of these electron donors responds to their intrinsically different properties – DABCO, soluble in organic solvents, is known to coordinate to the metal center of the porphyrin,³⁷ whereas ascorbate can be used in water-containing mixtures,³⁶ which is desirable for artificial photosystems envisaging future practical applications.³⁸

Experimental

Materials

DABCO, sodium ascorbate and acetonitrile are commercially available and were purchased from Sigma Aldrich. 1,3-Dimethyl-2-phenyl-2,3-dihydro-1Hbenzo[d]imidazole (BIH) was prepared according to the literature.³⁹

For the synthesis of ZnF₂₀, porphyrin-F₂₀ (C₄₄H₁₀F₂₀N₄, 110 mg, 123 μmol) was dissolved in a 100 mL chloroform/methanol (CHCl₃/MeOH = 5/1) mixture. Then, zinc acetate (Zn(OAc)₂, 207 mg, 1.23 mmol) and sodium acetate (NaOAc, 93 mg, 1.23 mmol) were added, and the reaction mixture was refluxed overnight. The reaction mixture was then filtered to remove the excess of salt and the solvent was evaporated under vacuum. The reaction crude product was dissolved in 50 mL of CHCl₃, and 50 mL aqueous solution of 1 M sodium bicarbonate (NaHCO₃) was then added to separate the two phases. The organic phase containing the final ZnF₂₀ complex was filtered through a silica plug and evaporated under vacuum to obtain a purple powder in 90% yield (105 mg).

Photoaccumulation and spectroelectrochemistry

Photoaccumulation experiments were performed in a 1 cm quartz cuvette purged with Ar. A single-beam SPECORD s600 spectrophotometer (Analytik Jena) was used to probe the UV-vis absorption of the samples. Vigorous stirring conditions were maintained during 405 nm (∼58 mW) continuous laser excitation. Spectroelectrochemistry (SEC) experiments were performed in a quartz cuvette with a 1 mm optical path, with a Pt-mesh used as the working electrode, a Pt wire as the counter electrode and Ag/Ag⁺ as the pseudo-reference. The chronoamperometry method was used to induce reduction.

Nanosecond optical transient absorption spectroscopy

The experimental setup used for optical transient absorption (OTA) measurements has been described in detail in previous reports.^10,11 Briefly, a tunable OPO laser set to 10 Hz was used as a pump and a supercontinuum white light laser operating at 20 Hz was used as an absorption probe. The pump–probe delays are electronically controlled as the differential spectra are obtained by subtracting the signals before and after the pump excitation.

Time-resolved resonance Raman spectroscopy

Similarly, the time-resolved resonance Raman (TR3) experimental setup has been described elsewhere.⁴⁰ Two tunable OPO lasers were used as the pump and probe, both operating at 20 Hz. The wavelength of the probe laser was adjusted to match the electronic transitions of the photogenerated products, thus ensuring the resonance conditions and the concomitant signal enhancement. UV-vis absorption spectra of the sample were recorded before and after laser excitation experiments to ensure stability under the operational experimental conditions.

Fluorescence lifetime measurements

Time-resolved fluorescence measurements were carried out using a Leica TCS SP5 confocal microscope (Leica Microsystems, Germany; implemented at the Centre de Photonique pour la biologie et les matériaux (CPBM) in Orsay) coupled with a femtosecond Ti:sapphire laser (Chameleon-XR, Coherent, USA) running at a 80 MHz repetition rate and delivering 150-fs pulses. ZnF₂₀ was biphotonically excited at 800 nm. The laser beam was focused on the sample using a high–numerical aperture (1.4) 63× oil-immersion objective. The fluorescence signal was collected by the same objective and directed on an avalanche photodiode coupled with a PicoHarp 300 device based on the time-correlated single-photon counting method. An 800 nm short-pass emission filter was used to remove any residual laser light, and the emitted fluorescence was recorded within the range of 400 to 800 nm. The observed time-resolved decays were deconvoluted with a simulated instrumental response function. It was possible here to fit all the fluorescence decays, with a single exponential function giving the fluorescence lifetime of the sample with a 100 ps time resolution.

Computational calculations

Fully unconstrained geometry optimizations were carried out using the CAM-B3LYP functional as implemented in the Gaussian 16 package.⁴¹ The Def2-TZVP basis set was applied to C, H, N, and F atoms. The inner electrons of Zn were treated with the effective core potential LANL2DZ⁴² and the valence electrons with the associated double-ς basis set. The nature of all the optimized geometries was confirmed through the analysis of the harmonic vibrational frequencies at the same level of theory. Resonance Raman spectra were computed at the TD-DFT level of theory (CAM-B3LYP) using the aforementioned basis sets. The modified vibronic theory of Albrecht with the independent mode displaced harmonic oscillator (IMDHO) model was employed.^43–45 The resulting theoretical resonance stick spectra were convoluted with Voigt functions (1 : 1, half-width 5 cm⁻¹) and normalized at the most intense mode. No scaling was applied to the resulting spectra.

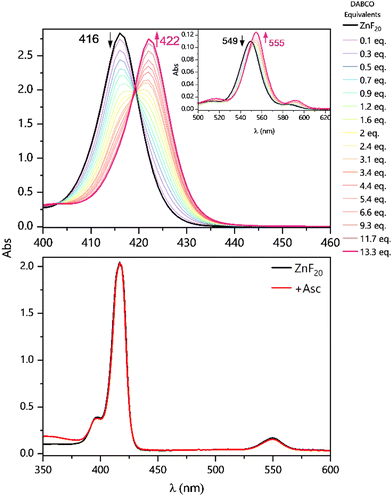
Results and discussion

The ability of DABCO to coordinate the porphyrin's metal center in CH₃CN is the very first aspect to be considered in this system. With a binding constant in the order of 10⁵–10⁸ M⁻¹,⁴⁶ this coordination has previously been described and built upon in the context of supramolecular self-assemblies.^37,47–54 Since the effect of DABCO's ligation can easily be observed in steady-state UV-vis absorption spectra, we performed a titration of ZnF₂₀ in the presence of the binding donor (Fig. 2, top panel). ZnF₂₀ exhibits two absorption bands at 416 and 549 nm corresponding, respectively, to the Soret and Q bands. The band positions are similar to those observed for the parent ZnTPP.⁵⁵ Upon coordination, both the Soret and the Q-bands of ZnF₂₀ are subject to a red shift of approximately 6 nm.

Fig. 2 Absorption changes in the Soret band region and in the Q-bands (inset) upon titration of 4.9 μM ZnF₂₀ with DABCO (top panel) in CH₃CN. Absorption spectrum of 4.9 μM ZnF₂₀ in the absence and presence of 100 mM Asc (bottom panel) in CH₃CN/H₂O (6 : 4).

It is well known that, for micromolar-ranged concentrations of the porphyrin, a 1 : 1 complex with DABCO is formed, with further 2 : 1 aggregation being possible at millimolar concentrations.⁴⁸ However, our titration dataset at a micromolar concentration of ZnF₂₀ revealed that 1 : 1 [ZnF₂₀–DABCO] and 1 : 2 [ZnF₂₀–(DABCO)₂] complexes were successively formed with equilibrium constants of β₁₁ = 4.5 (±1.3) × 10⁵ M⁻¹ and β₁₂ = 1.7 (±0.5) × 10¹⁰ M⁻¹, respectively (Fig. S2 and S3, ESI†). Equilibrium constants were determined using the KEV software.⁵⁶ When Asc was used as an electron donor, no changes were observed in the absorption spectrum of ZnF₂₀ (Fig. 2, bottom panel) and so no relevant ground-state interaction was expected to take place. Similarly, no significant changes were detected in the emission spectra of ZnF₂₀ in the presence of Asc (Fig. S4, ESI†).

However, the same DABCO coordination effects can be observed in the red shift of the emission spectra of ZnF₂₀ in its initial Zn^II oxidation state (Fig. S5, ESI†) and in its chemically prepared reduced form, Zn^I (Fig. S6, ESI†). For the chemical preparation of Zn^I, cobaltocene (CoCp₂) was used as a reducing agent (E_red = −0.96 V vs. NHE).⁵⁷ We also measured the time-resolved fluorescence of ZnF₂₀, whose decay was fitted with a single exponential and showed a lifetime of 3.2 ns (Fig. S7, ESI†).⁵⁵ In the presence of 100 mM DABCO, the lifetime decreased to 1.1 ns. The fluorescence quenching and the decrease in the lifetime can be attributed to either: (i) the axial ligation of DABCO to the Zn center, resulting in a red shift and a quenching of the fluorescence (Fig. S5, ESI†), previously attributed to the acceleration of non-radiative relaxation pathways, such as internal conversion, in the DABCO-coordinated complex;⁵⁸ or (ii) an electron transfer from DABCO to the singlet excited state of ZnF₂₀, followed by a rapid charge recombination of the geminate ion pair to the ground state, which is a spin-allowed process. The upper limit of this electron transfer rate was estimated to be k_ET = 1/τ − 1/τ₀ = 6 × 10⁸ s⁻¹, where τ and τ₀ correspond to the fluorescence lifetimes of ZnF₂₀ with and without DABCO, respectively. Since these particular behaviors of ZnF₂₀ with different electron donors are likely to have implications on the photoinduced charge separation dynamics, we set to look deeper into this process by means of time-resolved spectroscopic approaches.

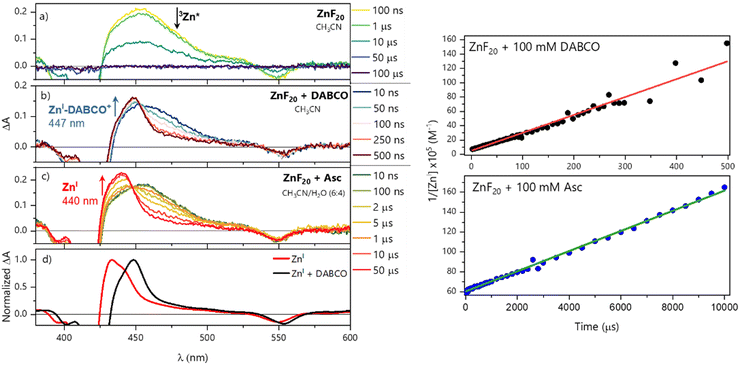
For OTA experiments, solutions of 5.8 μM of ZnF₂₀ were consistently used and porphyrin was excited at its Soret band (423 nm, 1 mJ per pulse). Excitation of ZnF₂₀ alone in CH₃CN shows the formation of its triplet state (denoted ³Zn*) with a broad excited-state absorption (ESA) band centered at 453 nm (Fig. 3a) and a monoexponential decay fitted with a time constant of 11.6 ± 0.2 μs (Fig. S8, ESI†). The same absorption signature was obtained in CH₃CN/H₂O (6 : 4) with a similar time constant of 26.0 ± 0.5 μs (Fig. S9, ESI†). In both cases, ∼38 ± 5% of the ground-state population was converted into ³Zn*. This estimation is based on the analysis of the bleaching Q-band with ε(553 nm) = ∼20 500 M⁻¹ cm⁻¹ in CH₃CN.

Fig. 3 Transient absorption spectra (left panel) of a solution containing (a) 5.8 μM ZnF₂₀ and upon addition of (b) 100 mM DABCO in CH₃CN or (c) ascorbate in CH₃CN/H₂O 6 : 4; (d) spectral references for Zn^I obtained via photoaccumulation experiments with BIH in the presence and absence of DABCO. Time profiles of the inverse values of the concentrations (1/C) of reduced ZnF₂₀, indicating the second-order charge recombination kinetics, are shown in the right panel for DABCO (top) and ascorbate (bottom). λ_exc = 423 nm, 1 mJ per pulse.

To investigate the reductive quenching mechanism, both DABCO and Asc were added in excess (100 mM) to samples containing 5.8 μM ZnF₂₀. The resulting absorption spectra are shown in Fig. 2 (bottom) for the ZnF₂₀ solution with ascorbate and in Fig. S10 (ESI†) for the DABCO-containing sample. In the presence of DABCO, upon excitation, ∼1.4 ± 0.3 μM of ³Zn* was formed, corresponding to an efficiency of ∼24 ± 3%, which is lower than what has been observed for ZnF₂₀ alone. The aforementioned fluorescence quenching of ZnF₂₀ due to the axial coordination of DABCO, naturally, affects the yield of the triplet state by favoring other non-radiative deactivation pathways that compete with intersystem crossing. Reductive quenching of the excited state is observed with the decay of ³Zn* at 453 nm as a new transient band rises at 447 nm (Fig. 3b). The charge separation efficiency was estimated to be 24 ± 3% for a maximal transient concentration of Zn^I-DABCO⁺ of 1.4 (±0.4) μM. Since the electron transfer in the Zn-DABCO complex is thought to be intramolecular, we estimated the quenching rate constant from global analysis of the transient dataset (Fig. S11, ESI†). The fits generated a triplet-state quenching constant k_q = 1.3 (±0.1) × 10⁷ s⁻¹ from a lifetime of 75 (±7) ns. Furthermore, the charge recombination reaction is shown to follow a second-order kinetics (Fig. 3, top right), fitted with a bimolecular rate k_rec = 2.6 (±0.8) × 10¹⁰ M⁻¹ s⁻¹. The fact that the charge recombination follows a bimolecular kinetics suggests that the ions in the geminate ion pair break through the solvent cage and diffuse away from each other, which is possible considering the triplet state nature of the geminate ion pair when the triplet excited state is reductively quenched.

In the case of ascorbate, the absorption band due to the formation of Zn^I appears blue-shifted (λ_max = 440 nm) with respect to DABCO (Fig. 3c and d). Bimolecular kinetic simulations carried out using the SK-Ana software⁵⁹ yielded quenching and recombination rate constants of k_q = 1.5 (±0.5) × 10⁶ M⁻¹ s⁻¹ and k_rec = 1.3 (±0.4) × 10⁸ M⁻¹ s⁻¹, respectively (Table S1, ESI†). As expected, the charge recombination in the ascorbate-containing system follows a second-order kinetics (Fig. 3, bottom right). This time, a similar yield of ³Zn* with and without Asc was obtained, and a slightly higher charge separation efficiency of ∼31 ± 3% was observed. The details on the spectro-kinetic simulations are available in the ESI† (Table S1 and Fig. S11, S12). The formation of Zn^I-DABCO⁺ and Zn^I in solutions containing DABCO and ascorbate, respectively, was confirmed by photoaccumulation (PA) experiments performed with 1,3-dimethyl-2-phenyl-2,3-dihydro-1Hbenzo[d]imidazole (BIH) as a nonbinding sacrificial electron donor (Fig. 3d and Fig. S13, S14, ESI†) and by spectroelectrochemistry (SEC, Fig. S15 and S16, ESI†).

Although these systems have similar charge separation efficiencies, their kinetics are intrinsically different. This is mainly manifested in the values of k_rec – the recombination takes place with a hundredfold increase in the order of magnitude for DABCO as compared to the ascorbate-containing system (Table S1, ESI†). Since both processes are diffusion-driven, this difference in kinetics can be tentatively explained by the coulombic attraction between the negatively charged ZnF₂₀˙⁻ and the positively charged DABCO˙⁺ species. Consequently, the reduced porphyrin generated when Asc is used has a much longer lifetime.

We then tried to look deeper into the reductive quenching mechanism by probing vibrational changes in the Zn porphyrin. In order to perform time-resolved resonant Raman experiments, we set the laser pump to 554 nm (2.2 mJ per pulse) to excite ZnF₂₀ at its Q-band and the laser probe was set to 447 nm (2.2 mJ per pulse), in resonance with the T₁ excited state ³Zn* and the reduced state Zn^I of the porphyrin. For TR3, we increased the concentration to 12.6 μM ZnF₂₀ due to the lower extinction coefficient of the Q-band.

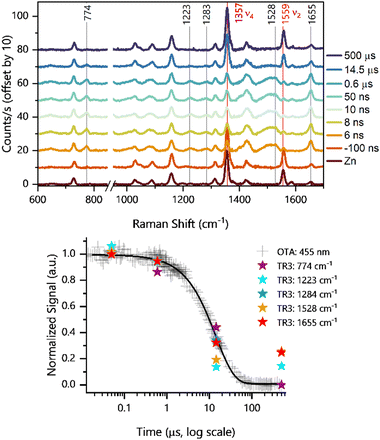
We first investigated the formation of the triplet state by exciting the porphyrin alone. Pump excitation led to the formation and decay of new bands at 1655, 1528, 1283, 1223, and 774 cm⁻¹ (Fig. 4). Similar bands of the triplet excited state have been previously identified for ZnTPP⁶⁰ under similar Soret resonance conditions. The assignments of these bands have been discussed in the literature,^60,61 and they are available in Table 1 together with the corresponding calculated DFT frequencies. It is noteworthy that, with respect to ZnTPP, the presence of perfluorinated phenyl rings in ZnF₂₀ causes frequency shifts due to increased force constants, particularly on the modes with a strong phenyl character, such as the one observed at 1655 cm⁻¹ (Fig. S17, ESI†). Other modes are also strongly affected by fluorination. The corresponding theoretical spectra for the ground and excited states under resonance conditions are available in Fig. S18 (ESI†).

Fig. 4 TR3 spectra (top panel) obtained upon exciting 12.6 μM ZnF₂₀ in CH₃CN. Solid vertical lines represent time-evolving bands due to the formation of ³Zn*. Overlapped kinetic decays (bottom panel) obtained by OTA and TR3 under the same experimental conditions. λ_pump = 554 nm, 2.2 mJ per pulse; λ_probe = 447 nm, 2.2 mJ per pulse.

Table 1 Vibrational frequencies (in cm⁻¹) of the main peaks observed in TR3 experiments attributed to ZnF₂₀, ³Zn* and Zn^I. Mode notations are taken from ref. 62

ZnF20			^3Zn*			Zn^I			Assignment^c
Exp.	DFT^a	Lit.^b	Exp.	DFT^a	Lit.^b	Exp.	DFT^a	Lit.^b
a Unscaled vibrational frequencies obtained from our CAM-B3LYP/Def2-TZVP/LANL2DZ calculations. b Literature values observed either for ZnTPP^60 or NiTPP.^62 c Tentative assignments of relevant vibrational modes according to the metalloporphyrin core classification and the numbering scheme commonly used in the literature.^62
1656	1714	1598^60	1655	1714	1596^60				Φ 4 (phenyl)
1559	1632	1548^60	1528	1618	1508^60	1540	1554	1532^60	ν 2, ν(Cα–Cm)
1357	1412	1352^60							ν 4, ν(Cα–N)
1313	1353	1302^62							ν 12, ν(Cα–N)
			1283	1302	1287^60	1277	1282	1257^60	ν 27, ν(Cm–Cph)
			1223	1285	1233^60				ν 1, ν(Cm–Cph)
1158	1188	1179^60							Φ 6 (phenyl)
730	755	639^62							Φ 9 (phenyl)
			774	801	846^62				ν 16, δ(pyr def)sym
		684^62				636	672		π3′, γ(CF)

---

Interestingly, the ν₂ mode observed at 1559 cm⁻¹ for ZnF₂₀ in its ground state (solid red line in Fig. 4) exhibits a strong time-dependent decrease in intensity upon formation of the triplet state (−100 ns to 0.6 μs) concomitant with the rise of a new band at 1528 cm⁻¹. This indicates that this mode is strongly spin-state-sensitive as in the case for iron-based porphyrins.³⁴ In fact, a similar downshift of 40 cm⁻¹ has been previously demonstrated upon populating the triplet state of ZnTPP.⁶⁰ Although a weaker intensity loss was observed in the ν₄ mode at 1357 cm⁻¹, it did not exhibit any shift in frequency.

In addition, we observed a new band of ³Zn* at 774 cm⁻¹ that can be assigned to ν₁₆ according to our DFT calculations. This feature presents a strong component of the δ(CαNCα) mode and a strong phenyl contribution, having previously been described as symmetric pyrrole deformation in the metalloporphyrin D_4h-core.⁶² Finally, we show (Fig. 4, bottom panel) that all detected TR3 vibrations follow the same kinetics as the ESA band of ³Zn*, further corroborating their nature.

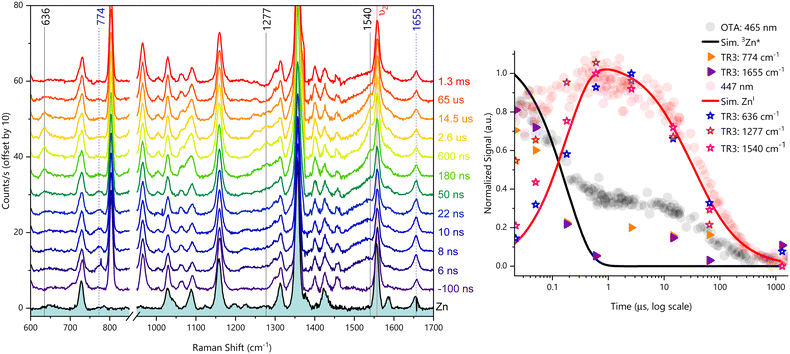
We then investigated the reductive quenching mechanism in the presence of both electron donors. Since no differences were observed in the resonant Raman spectra in the presence of either DABCO or ascorbate (Fig. S19, ESI†), as additionally shown by our DFT calculations (Fig. S20, ESI†), only the results related to the DABCO-containing system will be discussed. The excitation of 12.6 μM ZnF₂₀ in the presence of 100 mM DABCO in CH₃CN led to the time-resolved evolution of new bands detected at 636, 1277, and 1540 cm⁻¹ (Fig. 5, left panel). The reference spectrum of the chemically prepared Zn^I species in the presence of 100 mM DABCO is displayed in Fig. S21 (ESI†), together with the corresponding theoretical resonance Raman spectrum of Zn^I shown in Fig. S22 (ESI†).

Fig. 5 TR3 spectra (left panel) obtained upon exciting 12.6 μM ZnF₂₀ in the presence of 100 mM DABCO in CH₃CN. Black solid lines represent time-evolving bands due to the formation of Zn^I and dashed blue lines indicated the bands of ³Zn*. Overlapped kinetic decays (right panel) obtained by OTA and TR3 under the same experimental conditions, with solid lines showing the simulated evolution of relevant photogenerated species. λ_pump = 554 nm, 2.2 mJ per pulse; λ_probe = 447 nm, 2.2 mJ per pulse.

Once again, we observed a downshift of 19 cm⁻¹ in the ν₂ mode detected, this time, at 1540 cm⁻¹. This indicates that, in addition to being spin-state-sensitive, this mode is sensitive to the oxidation state of the Zn–porphyrin. Due to these two features, this mode constitutes an excellent probe for photochemical processes involving ZnF₂₀ as a photosensitizer. The downshift of this band, due to the formation of both the triplet and reduced states, can be explained by the population of the LUMO orbital of the porphyrin macrocycle, weakening the π bonds of the conjugated rings.⁶⁰

The mode at 1277 cm⁻¹ has also been previously observed and assigned to the reduced state of ZnTPP in previous studies,^63,64 and it has been identified as ν(C_m–C_ph). Our calculations are in agreement with this assignment for ZnF₂₀ and, because this mode is of totally symmetric nature,⁶³ it can be attributed to ν₂₇.⁶² Finally, we have detected a new band at 636 cm⁻¹, also predicted by our DFT calculations, assigned to an out-of-plane phenyl vibration involving the fluorine atoms. A similar phenyl mode has been observed for NiTPP and it can be tentatively assigned to π₃′, a mode described by a γ(CH) component in the hydrogenated phenyl ring that, naturally, becomes γ(CF) for ZnF₂₀ (Fig. S23, ESI†).

Remarkably, the time evolutions of the three reduced-state bands of ZnF₂₀ follow the same kinetics observed for the 447 nm band in OTA experiments (Fig. 5, right panel). Not only the reduced-state bands are visible in the presence of DABCO, but the excited state bands at 774 cm⁻¹ and 1655 cm⁻¹ are also present and are likewise shown to evolve with the same kinetics observed under the same conditions in OTA. Indeed, these results illustrate the complementarity of these two experimental approaches to track the fate of transient species through the lenses of different probing strategies, thus providing valuable information on the nature and dynamics of molecular photosystems.

Finally, we investigated the charge separation thermodynamics in both DABCO and ascorbate-containing systems. The energy level diagrams with the reaction pathways of all relevant photoinduced processes are presented in Fig. 6. It should be noted that the energy of ³Zn* (∼1.71 eV) was estimated from the phosphorescence spectrum recorded in an ethanol/methanol solvent mixture at 77 K (Fig. S24, ESI†). Because the energy of the first excited singlet state (¹Zn* + DABCO) is virtually unaffected by the presence of DABCO, we assume that its effect is also negligible for the lowest lying triplet state (³Zn* + DABCO). The energy level diagram of Fig. 6 makes it evident that DABCO provides an electron transfer driving force that is 290 mV lower than that of ascorbate. Despite this, reductive quenching of the excited state is observed with DABCO, with faster reaction rates of electron transfer and recombination that are probably associated with its coordination to the metal center.

Fig. 6 Jablonski energy level diagram and reaction pathways for ZnF₂₀ in the presence of (a) ascorbate and (b) DABCO as reversible electron donors. k_q = 1.5 (±0.5) × 10⁶ M⁻¹ s⁻¹, k_rec = 1.3 (±0.5) × 10⁸ M⁻¹ s⁻¹, , .

Conclusions

Although the systems containing ZnF₂₀ and DABCO/ascorbate have similar charge separation efficiencies, they display intrinsically different kinetic properties, exhibiting much faster quenching and charge recombination reaction rates with DABCO. Indeed, the estimated rate constants with DABCO are more compatible with intramolecular electron transfer processes than ascorbate-containing samples. In the latter, the same processes are clearly governed by diffusion and so the charge-separated state has a much longer lifetime. This prolonged lifetime increases its probability of engaging in bimolecular electron transfer reactions with other molecular species such as specialized catalysts. Overall, we provide a complete photophysical characterization of ZnF₂₀ in reductive quenching reaction mechanisms using complementary time-resolved techniques to generate and probe transient charge-separated states. Such studies contribute to the very fundamental understanding of primordial light-induced processes operating in artificial photosynthetic systems.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work has been supported by the French National Research Agency (LOCO, grant No. ANR-19-CE05-0020-01). DFT calculations performed using computational resources from the Moulon Mésocentre – Ruche. DHCN is grateful for the MESRI grant (2021-2024). We thank Paris-Saclay University and CNRS for additional financial support. We acknowledge CPBM/ISMO-UMR8214 for providing access to the fluorescence confocal microscope.

References

1. V. Balzani, A. Credi and M. Venturi, ChemSusChem, 2008, 1, 26–58.
2. D. Gust, T. A. Moore and A. L. Moore, Acc. Chem. Res., 2009, 42, 1890–1898.
3. J. W. Wang, D. C. Zhong and T. B. Lu, Coord. Chem. Rev., 2018, 377, 225–236.
4. B. Zhang and L. Sun, Chem. Soc. Rev., 2019, 48, 2216–2264.
5. C. Herrero, A. Quaranta, W. Leibl, A. W. Rutherford and A. Aukauloo, Energy Environ. Sci., 2011, 4, 2353–2365.
6. E. Romero, V. I. Novoderezhkin and R. Van Grondelle, Nature, 2017, 543, 355–365.
7. M. H. Ha-Thi, V. T. Pham, T. Pino, V. Maslova, A. Quaranta, C. Lefumeux, W. Leibl and A. Aukauloo, Photochem. Photobiol. Sci., 2018, 17, 903–909.
8. M. Kuss-Petermann and O. S. Wenger, Helv. Chim. Acta, 2017, 100, 1–7.
9. M. Kuss-Petermann, M. Orazietti, M. Neuburger, P. Hamm and O. S. Wenger, J. Am. Chem. Soc., 2017, 139, 5225–5232.
10. T. T. Tran, T. Pino and M. H. Ha-Thi, J. Phys. Chem. C, 2019, 123, 28651–28658.
11. T. T. Tran, M. H. Ha-Thi, T. Pino, A. Quaranta, C. Lefumeux, W. Leibl and A. Aukauloo, J. Phys. Chem. Lett., 2018, 9, 1086–1091.
12. J. G. Vos and J. M. Kelly, Dalton Trans., 2006, 4869–4883.
13. F. E. Poynton, S. A. Bright, S. Blasco, D. C. Williams, J. M. Kelly and T. Gunnlaugsson, Chem. Soc. Rev., 2017, 46, 7706–7756.
14. F. Heinemann, J. Karges and G. Gasser, Acc. Chem. Res., 2017, 50, 2727–2736.
15. D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820.
16. P. Herr, C. Kerzig, C. B. Larsen, D. Häussinger and O. S. Wenger, Nat. Chem., 2021, 13, 956–962.
17. C. D. Windle, M. W. George, R. N. Perutz, P. A. Summers, X. Z. Sun and A. C. Whitwood, Chem. Sci., 2015, 6, 6847–6864.
18. T. Gatti, P. Cavigli, E. Zangrando, E. Iengo, C. Chiorboli and M. T. Indelli, Inorg. Chem., 2013, 52, 3190–3197.
19. D. Il Won, J. S. Lee, Q. Ba, Y. J. Cho, H. Y. Cheong, S. Choi, C. H. Kim, H. J. Son, C. Pac and S. O. Kang, ACS Catal., 2018, 8, 1018–1030.
20. M. Andersson, J. Davidsson, L. Hammarström, J. Korppi-Tommola and T. Peltola, J. Phys. Chem. B, 1999, 103, 3258–3262.
21. J. Petersson, M. Eklund, J. Davidsson and L. Hammarström, J. Phys. Chem. B, 2010, 114, 14329–14338.
22. K. Kiyosawa, N. Shiraishi, T. Shimada, D. Masui, H. Tachibana, S. Takagi, O. Ishitani, D. A. Tryk and H. Inoue, J. Phys. Chem. C, 2009, 113, 11667–11673.
23. Y. Hee Kim, D. Hong Jeong, D. Kim, S. Chae Jeoung, H. Sun Cho, S. Keun Kim, N. Aratani and A. Osuka, J. Am. Chem. Soc., 2001, 123, 76–86.
24. I. W. Hwang, H. S. Cho, D. H. Jeong, D. Kim, A. Tsuda, T. Nakamura and A. Osuka, J. Phys. Chem. B, 2003, 107, 9977–9988.
25. P. Osswald, C. C. You, V. Stepanenko and F. Würthner, Chem. – Eur. J., 2010, 16, 2386–2390.
26. S. S. Nurttila, R. Becker, J. Hessels, S. Woutersen and J. N. H. Reek, Chem. – Eur. J., 2018, 24, 16395–16406.
27. A. Morandeira, L. Engeli and E. Vauthey, J. Phys. Chem. A, 2002, 106, 4833–4837.
28. B. R. Danger, K. Bedient, M. Maiti, I. J. Burgess and R. P. Steer, J. Phys. Chem. A, 2010, 114, 10960–10968.
29. A. M. Brun, A. Harriman and S. M. Hubig, J. Phys. Chem., 1992, 96, 254–257.
30. S. L. Logunov and M. A. J. Rodgers, J. Phys. Chem., 1992, 96, 8697–8700.
31. A. Harriman, G. Porter and A. Wilowska, J. Chem. Soc., Faraday Trans. 2, 1983, 79, 807–816.
32. S. M. Hubig, T. M. Bockman and J. K. Kochi, J. Am. Chem. Soc., 1997, 119, 2926–2935.
33. M. Gouterman and D. Holten, Photochem. Photobiol., 1977, 25, 85–92.
34. C. Römelt, S. Ye, E. Bill, T. Weyhermüller, M. Van Gastel and F. Neese, Inorg. Chem., 2018, 57, 2141–2148.
35. M. Jonsson, A. Houmam, G. Jocys and D. D. M. Wayner, J. Chem. Soc., Perkin Trans. 2, 1999, 425–429.
36. Y. Pellegrin and F. Odobel, C. R. Chim., 2017, 20, 283–295.
37. C. C. Mak, N. Bampos and J. K. M. Sanders, Angew. Chem., Int. Ed., 1998, 37, 3020–3023.
38. Y. Yamazaki, H. Takeda and O. Ishitani, J. Photochem. Photobiol., C, 2015, 25, 106–137.
39. E. Hasegawa, T. Seida, N. Chiba and C. Hart, J. Org. Chem., 2005, 70, 9632–9635.
40. D. H. Cruz Neto, J. Soto, N. Maity, C. Lefumeux, T. Nguyen, P. Pernot, K. Steenkeste, D. Peláez, M. H. Ha-Thi and T. Pino, J. Phys. Chem. Lett., 2023, 14, 4789–4795.
41. M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision C.01, Gaussian, Inc., Wallingford CT, 2016.
42. P. J. Hay and W. R. Wadt, J. Chem. Phys., 1985, 82, 299–310.
43. D. Aranda, F. J. Avila, I. López-Tocón, J. F. Arenas, J. C. Otero and J. Soto, Phys. Chem. Chem. Phys., 2018, 20, 7764–7771.
44. M. R. Lopez-Ramirez, D. Aranda Ruiz, F. J. Avila Ferrer, S. P. Centeno, J. F. Arenas, J. C. Otero and J. Soto, J. Phys. Chem. C, 2016, 120, 19322–19328.
45. J. Soto, E. Imbarack, I. López-Tocón, S. Sánchez-Cortés, J. C. Otero and P. Leyton, RSC Adv., 2019, 9, 14511–14519.
46. H. W. Wang, C. H. Chen, T. S. Lim, S. L. Huang and T. Y. Luh, Chem. - Asian J., 2011, 6, 524–533.
47. H. L. Anderson, C. A. Hunter, M. Nafees Meah and J. K. M. Sanders, J. Am. Chem. Soc., 1990, 112, 5780–5789.
48. L. Baldini, P. Ballester, A. Casnati, R. M. Gomila, C. A. Hunter, F. Sansone and R. Ungaro, J. Am. Chem. Soc., 2003, 125, 14181–14189.
49. M. C. Lensen, S. J. T. Van Dingenen, J. A. A. W. Elemans, H. P. Dijkstra, G. P. M. Van Klink, G. Van Koten, J. W. Gerritsen, S. Speller, R. J. M. Nolte and A. E. Rowan, Chem. Commun., 2004, 762–763.
50. D. I. Schuster, K. Li, D. M. Guldi and J. Ramey, Org. Lett., 2004, 6, 1919–1922.
51. P. Ballester, A. I. Oliva, A. Costa, P. M. Deyà, A. Frontera, R. M. Gomila and C. A. Hunter, J. Am. Chem. Soc., 2006, 128, 5560–5569.
52. S. Hecht and J. M. J. Fréchet, Angew. Chem., Int. Ed., 2001, 40, 74–91.
53. T. Ishida, Y. Morisaki and Y. Chujo, Tetrahedron Lett., 2006, 47, 5265–5268.
54. T. Kishida, N. Fujita, O. Hirata and S. Shinkai, Org. Biomol. Chem., 2006, 4, 1902–1909.
55. F. D’Souza and V. Krishnan, J. Chem. Soc., Dalton Trans., 1992, 2873–2876.
56. A. N. Meshkov and G. A. Gamov, Talanta, 2019, 198, 200–205.
57. A. Badalyan, Z. Y. Yang and L. C. Seefeldt, ACS Catal., 2019, 9, 1366–1372.
58. T. Sakuma, H. Sakai and Y. Araki, Phys. Chem. Chem. Phys., 2016, 18, 5453–5463.
59. P. Pernot, SK-Ana: Analysis of Spectro-Kinetic Data (Version 3.4), 2018.
60. R. A. Reed, R. Purrello, K. Prendergast and T. G. Spiro, J. Phys. Chem., 1991, 95, 9720–9727.
61. V. A. Walters, J. C. De Paula, G. T. Babcock and G. E. Leroi, J. Am. Chem. Soc., 1989, 111, 8300–8302.
62. X. Y. Li, R. S. Czernuszewicz, J. R. Kincaid, Y. O. Su and T. G. Spiro, J. Phys. Chem., 1990, 94, 31–47.
63. M. Atamiaiv, R. J. Donohoe, J. S. Lidnsay and D. F. Bocian, J. Phys. Chem., 1989, 93, 2236–2243.
64. H. Yamaguchi, A. Soeta, H. Toeda and K. Itoh, J. Electroanal. Chem., 1983, 159, 347–359.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nj02484b

---