Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Probing spin waves in Co3O4 nanoparticles for magnonics applications†
Mikhail
Feygenson
 *abc,
Zhongyuan
Huang‡
d,
Yinguo
Xiao
*abc,
Zhongyuan
Huang‡
d,
Yinguo
Xiao
 d,
Xiaowei
Teng
d,
Xiaowei
Teng
 e,
Wiebke
Lohstroh
f,
Nileena
Nandakumaran
g,
Jörg C.
Neuefeind
h,
Michelle
Everett
h,
Andrey A.
Podlesnyak
e,
Wiebke
Lohstroh
f,
Nileena
Nandakumaran
g,
Jörg C.
Neuefeind
h,
Michelle
Everett
h,
Andrey A.
Podlesnyak
 h,
Germán
Salazar-Alvarez
h,
Germán
Salazar-Alvarez
 c,
Seda
Ulusoy
c,
Mario
Valvo
c,
Seda
Ulusoy
c,
Mario
Valvo
 i,
Yixi
Su
j,
Sascha
Ehlert
b,
Asma
Qdemat
g,
Marina
Ganeva
i,
Yixi
Su
j,
Sascha
Ehlert
b,
Asma
Qdemat
g,
Marina
Ganeva
 j,
Lihua
Zhang
k and
Meigan C.
Aronson
l
j,
Lihua
Zhang
k and
Meigan C.
Aronson
l
aEuropean Spallation Source ERIC, SE-221 00 Lund, Sweden. E-mail: mikhail.feygenson@ess.eu
bJülich Centre for Neutron Science (JCNS-1) at Forschungszentrum Jülich, D-52425 Jülich, Germany
cDepartment of Materials Science and Engineering, Uppsala University, Box 35, 751 03, Uppsala, Sweden
dSchool of Advanced Materials, Peking University, Shenzhen Graduate School, Shenzhen 518055, China
eWorcester Polytechnic Institute, Department of Chemical Engineering, Worcester 01609, USA
fHeinz Maier-Leibnitz Zentrum (MLZ), Technische Universität München, Lichtenbergstr. 1, 8574 Garching, Germany
gJülich Centre for Neutron Science (JCNS-2) and Peter Grünberg Institute (PGI-4), Jülich GmbH, 52425, Jülich, Germany
hNeutron Scattering Division, Oak Ridge National Laboratory, Oak Ridge, Tennessee 37831, USA
iDepartment of Chemistry, Uppsala University, 75121 Uppsala, Sweden
jJülich Centre for Neutron Science (JCNS-4) at Heinz Maier-Leibnitz-Zentrum (MLZ), Forschungszentrum Jülich GmbH, Lichtenbergstr. 1, 85747 Garching, Germany
kCenter for Functional Nanomaterials, Brookhaven National Laboratory, Upton, New York 11973-5000, USA
lStewart Blusson Quantum Matter Institute, University of British Columbia, Vancouver, BC V6T 1Z4, Canada
First published on 22nd December 2023
Abstract
The magnetic properties of spinel nanoparticles can be controlled by synthesizing particles of a specific shape and size. The synthesized nanorods, nanodots and cubic nanoparticles have different crystal planes selectively exposed on the surface. The surface effects on the static magnetic properties are well documented, while their influence on spin waves dispersion is still being debated. Our ability to manipulate spin waves using surface and defect engineering in magnetic nanoparticles is the key to designing magnonic devices. We synthesized cubic and spherical nanoparticles of a classical antiferromagnetic material Co3O4 to study the shape and size effects on their static and dynamic magnetic proprieties. Using a combination of experimental methods, we probed the magnetic and crystal structures of our samples and directly measured spin wave dispersions using inelastic neutron scattering. We found a weak, but unquestionable, increase in exchange interactions for the cubic nanoparticles as compared to spherical nanoparticle and bulk powder reference samples. Interestingly, the exchange interactions in spherical nanoparticles have bulk-like properties, despite a ferromagnetic contribution from canted surface spins.
1 Introduction
The magnetic nanomaterials offer a unique opportunity to broaden our understanding of fundamental exchange interactions inside a solid-state matter on an atomic scale that underlines its macroscopic properties. The interactions are tailored by virtue of the finite-size effects resulting from a large fraction of the surface atoms. It is possible to further affect exchange interactions in nanoparticles by deliberately changing their shape to expose selected crystal planes. The nanoparticles of different shapes retain their chemical composition, in contrast to the bulk materials, in which the exchange interactions can only be altered by an isotope substitution, application of high pressure and extreme magnetic fields.Here, we present a comprehensive study of the dynamic magnetic properties of the spherical and cubic Co3O4 nanoparticles using a combination of advanced neutron scattering methods. The bulk Co3O4 crystallizes in a normal spinel structure and it becomes antiferromagnetic below the Néel temperature (TN) of about 40 K.1 The origin of the antiferromagnetic (AFM) ordering in Co3O4 is ascribed to the exchange interactions between magnetic Co2+ ions via non-magnetic intervening O2− ion.1–3 The strength of the interactions is defined by the exchange constants J1 and J2, corresponding to the AFM interactions between the nearest Co2+ ions and weak ferromagnetic (FM) interactions between the next-nearest Co2+ ions. The strength of AFM interactions depends on Co–O bond lengths, the titling angle between them, and occupancies of the atoms within the exchange path.4 Although the earliest study of the origin of the antiferromagnetic order in the bulk powder of Co3O4 dates back to 1964,1 the interest in the Co3O4 nanoparticles was recently revived by advances in shape and surface engineering that resulted in the synthesis of nanocubes, nanorods, nanoplates, nanotubes and 3D-nanonet hollow structures of Co3O4.5–16 These nanostructured Co3O4 materials have shown particular characteristics and superior performance in a variety of applications, including thermoelectric power generation, advanced supercapacitors, quantum tunneling, phonon transmission and lithium storage capacity.15,17–19
The AFM ordering of the Co3O4 makes it also possible to use the Co3O4 nanoparticles in magnonics applications. In this revolutionary concept, spin waves or magnons are used to carry information.20–23 The manipulation of the spin waves is a cornerstone of magnonics applications, that was successfully achieved in thin films and millimeter-sized ferrimagnetic crystal.24–26 The spin wave detection in magnetic nanoparticles is the next step in the same direction, aiming to miniaturize magnonic devices by bringing them to the nanoscale. The AFM nanoparticles are particularly attractive for applications due to the higher energy required for switching between different magnetic states and hence operating into the THz range.27–29 However, the finite-size and shape effects on the spin wave properties are needed to be understood first. In the particular case of the Co3O4 nanoparticles, a direct impact of surface engineering on exchange interactions has been demonstrated.30,31 The Co3O4 nanoparticles with exposed (100) and (111) crystal planes showed an induced magnetic moment on nominally non-magnetic Co3+ ions, while for (110) planes, Co3+ ions remain non-magnetic.
We used inelastic neutron scattering to experimentally study spin waves dispersions and to directly measure J1 and J2 exchange constants in spherical and cubic Co3O4 nanoparticles, as well as in their bulk powder counterpart. The inelastic neutron scattering measurements were successfully used in the past to detect the spin waves in a variety of magnetic nanoparticles.32–34 We also revised the experimental J1 value for the bulk Co3O4 powder, in order to provide an additional input for density functional theory calculations, that currently estimate values of J1 varied by an order of magnitude.35,36
2 Experimental
We synthesized cubic Co3O4 nanoparticles using Co nanoparticles prepared by the thermal decomposition of Co2(CO)8 in hot oleic acid as described in.37,38 Once the particles have fully formed, we annealed them at 400 °C for 4 hours inside a vacuum furnace. The use of the annealing temperature above the boiling point of the oleic acid (360 °C) ensured the absence of the surfactant coating of the cubic nanoparticles. The spherical Co3O4 nanoparticles and reference bulk powder of Co3O4 were purchased from Sigma-Aldrich.TEM measurements were carried out in the Ernst Ruska-Centre at Forschungszentrum Jülich with a Philips CM20 TEM and FEITecnai G2 F20 using an accelerating voltage of 200 kV. The SEM studies were performed using a Hitachi SU8000 instrument at an electron acceleration voltage of 20 kV. Additional HRTEM measurements were performed at Uppsala University. The samples were dispersed in toluene and drop-casted on 400 mesh carbon-coated copper grids. The particles were investigated using a FEI Titan Themis microscope with a Schottky field-emission gun operating at an accelerating voltage of 200 kV. The images were acquired using a BM-Ceta Camera.
The DC magnetization measurements were carried out using a Quantum Design Magnetic Property Measurement System (MPMS). For the measurements, 10 μL of the original aliquots were dispersed in 50 μL of liquid paraffin and then injected into a standard gelatin capsule to reduce inter-particle interactions. The gelatin capsules were fastened in plastic straws for immersion into the magnetometer. In order to measure the exchange bias field, a sample is cooled from 300 K to 5 K in an applied magnetic field of 70 kOe. The magnetization is then measured as a function of an applied magnetic field. The exchange bias field is calculated as HEB = |Hc1 + Hc2|/2, where Hc1 and Hc2 are the negative and positive coercive fields, respectively. The standard field-cooled (FC) and zero-field-cooled (ZFC) measurements of temperature-dependent magnetization were used to determine TN. FC and ZFC measurements were carried out in the field of 500 Oe.
The time-of-flight (TOF) neutron diffraction experiments were performed on the Nanoscale-Ordered Materials Diffractometer (NOMAD) at Spallation Neutron Source (SNS) at Oak Ridge National Laboratory.39 The low-temperature measurements were done using an Orange-type cryostat. NOMAD detectors were calibrated using scattering from diamond powder. The magnetic structure refinements of the data were done using Jana2006 software,40 which was adopted for handling neutron TOF diffraction data from six detector banks. In order to obtain the structural factor S(Q) the scattering intensity was normalized to the scattering from a solid vanadium rod and the background was subtracted. The pair-distribution function (PDF) was obtained by the Fourier transform of S(Q) at Qmin = 0.08 Å−1 and Qmax = 31.5 Å−1:
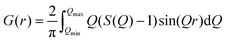 | (1) |
We used the Cold Neutron Chopper Spectrometer (CNCS) at the SNS at Oak Ridge National Laboratory41 to perform zero field TOF inelastic neutron scattering experiments on nanoparticle powders with the incident wavelength of λi = 2.34 Å (Ei = 15 meV). Additional temperature-dependent inelastic neutron scattering measurements were carried out at TOFTOF instrument at Heinz Maier-Leibnitz Zentrum. Two incident wavelengths λi,1 = 2 Å (Ei,1 = 9 meV) and λi,2 = 5 Å (Ei,2 = 3.3 meV) were used for accessing the medium and high energy resolutions, respectively. The empty sample container and vanadium solid rod were measured with both instruments. The vanadium measurements were used to define the resolution function of each instrument. The CNCS data have provided access to the energy gain and the energy loss parts of excitations (Fig. S5†), while only the energy gain part of the TOFTOF data was analyzed. The TOFTOF data were reduced using Mantid software.42
Room temperature Raman measurements were conducted at Uppsala University using a Renishaw (inVia) spectrometer with a built-in optical microscope (Leica) and by employing two different excitation wavelengths of 532 and 785 nm, respectively. The latter were provided by different solid-state laser diodes. Prior to the analyses, the spectrometer was calibrated using a Si wafer to obtain a characteristic reference peak at ∼520 cm−1. A low laser power was utilized for the respective measurements and the laser beam was focused onto the surface of the various samples via a 50× lens.
3 Results and discussion
Three samples were investigated in our work: spherical Co3O4 nanoparticles, cubic Co3O4 nanoparticles and reference bulk powder. The properties of all samples are summarized in Table 1.| Sample | d (nm) | T N (K) | a (Å) | m (μB) | J 1 (meV) | J 2 (meV) | D S (meV) |
|---|---|---|---|---|---|---|---|
| Sphere | 33(3) | 30.1(2) | 8.075(2) | 2.76(2) | −7.60 | 1.10 | 0.0154 |
| Cubic | 61(2) | 32.2(1) | 8.086(3) | 2.88(2) | −7.72 | 1.10 | 0.0154 |
| Bulk | 2500(1) | 42.4(8) | 8.086(3) | 3.01(2) | −7.60 | 1.10 | 0.0154 |
3.1 Structural characterization
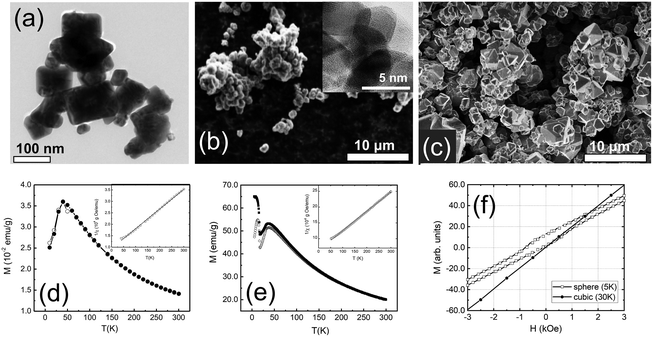
A combination of transmission electron microscopy (TEM) and scanning electron microscopy (SEM) measurements was used to characterize the overall size, shape, and crystallinity of our samples. Representative TEM and SEM images are shown in Fig. 1. The cubic sample shows polydisperse nanoparticles. The majority of the nanoparticles are best described by a rectangular shape with clear-cut edges (Fig. 1a). The spherical nanoparticles appear to be globular with a high degree of agglomeration (Fig. 1b). The spherical nanoparticles appeared to be amorphous, but high-resolution TEM (Fig. 1b, inset) and X-ray powder diffraction studies (Fig. S1†) confirmed their crystallinity. The bulk sample shows polyhedron crystallites as large as several micrometers in size (Fig. 1c).3.2 Magnetization measurements
The ZFC and FC magnetizations of the cubic and spherical nanoparticles peak at TN ∼45 K (Fig. 1d and e). At temperatures above TN, the long-range AFM order is lost and nanoparticles are transitioned into the paramagnetic phase. In this phase, the temperature dependence of the ZFC and FC magnetizations is well described by the Curie–Weiss law. The strength of AFM interactions can be estimated by fitting magnetic susceptibility χ to the modified Curie–Weiss equation (χ = χ0 + [C/(T + θ)]) well above TN. The fits are shown in the insets of Fig. 1d and e for cubic and spherical nanoparticles. In the case of cubic nanoparticles, we derived C = 1.16 × 10−2 emu K g−1 Oe, θ = 109 K and χ0 = 1.06 × 10−4 emu g−1 Oe, in good agreement with the previous reports for the bulk Co3O4.43,44 For spherical nanoparticles we obtained C = 1.63 × 10−2 emu K g−1 Oe, θ = 103 K and χ0 = 1.57 × 10−5 emu g−1 Oe. The negative sign of θ suggests dominating AFM interactions for all samples. The strength of the interactions is rather similar because values of θ for nanoparticles are close 110 K, previously reported for the bulk Co3O4.16,45The magnetic properties of cubic and spherical nanoparticles are distinctively different at low temperatures. ZFC magnetization of the spherical nanoparticles peaks at ∼25 K, while FC magnetization gradually increases and saturates below 25 K. Other researchers have observed similar DC magnetization dependence in Co3O4 nanoparticles, attributed to the coexistence of AFM-ordered core and FM-like surface shell of uncompensated spins with a freezing temperature of 25 K.46–48 The alternative explanation of this transition is a spin glass-like phase of the surface magnetic moments.49,50 However, we found no signatures of the spin-glass phase below 25 K in our neutron diffraction and inelastic neutron scattering data,51 at least within the experimental uncertainty. The existence of an FM-like surface shell is further confirmed by the observation of an exchange bias field (HEB) below 25 K. The maximum field HEB = 357(8) Oe was obtained at 5 K after cooling in 70 kOe field from the room temperature (Fig. 1f). The presence of the exchange bias effect is a clear indication of the coupling between the AFM core and the FM-like surface shell, previously documented in the literature for Co3O4 nanoparticles.52–57 In the case of cubic nanoparticles, no exchange bias was observed under similar experimental conditions.
3.3 Raman scattering
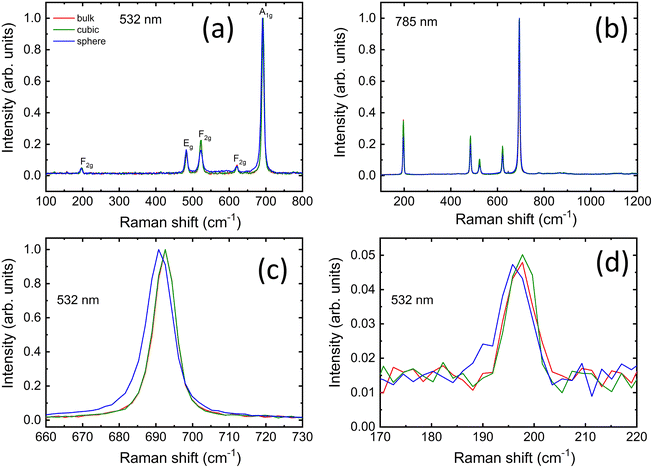
We examine the structural properties of our samples with Raman scattering measurements at two wavelengths of 532 and 785 nm. A comparison of the normalized spectra for both nanoparticles and the bulk reference powder is presented in Fig. 2a and b, while their respective as-recorded spectral signals are shown in Fig. S2.† All the samples exhibit five Raman-active modes confirming the formation of the pure cubic phase of Co3O4 with a normal spinel structure.58–60 The peaks for all samples are centered at around similar positions: 197 cm−1 (F2g), 483 cm−1 (Eg), 523 cm−1 (F2g), 621 cm−1 (F2g), and 692 cm−1 (A1g) as shown in Fig. 2a and b. The position of each peak is ascribed to a characteristic vibration mode (see ESI†).All normalized Raman spectra look very similar and spherical nanoparticles are the only sample that displays a slight red-shift of ∼2 cm−1 for the A1g mode when measured with a 532 nm wavelength (Fig. 2c). Moreover, the spherical nanoparticles show a moderate broadening of all the peaks compared to those displayed by the other two samples (Table S1†). The peak broadening is less visible in the spectra recorded with 785 nm excitation wavelength (Table S2†) and no shift is detected for any peak position in this case, while the intensities of the remaining modes appear more pronounced. The most likely explanation for both phenomena is a higher degree of a structural disorder in spherical nanoparticles, previously suggested for the similar Co3O4 nanostructures.59,61,62
Interestingly, the slight red shift in Fig. 2c, d and Fig. S2a† affects only the A1g mode at ∼690 cm−1 and the F2g vibration at ∼196 cm−1, whereas the positions of the other peaks are not influenced. If it were an optical phonon confinement effect,63,64 the peak positions of the five active modes would sensibly be shifted toward lower wavenumbers, while this is not the case. Pronounced agglomeration for the spherical nanoparticles (see also Fig. 1b), due to their larger surface-to-volume ratio compared to the other samples, could influence their thermal response,18 especially under conditions of elevated light absorption, e.g. during resonant Raman scattering (RRS). RRS causes excitation of electronic levels and substantial enhancement of some vibrational modes. Under such conditions and high absorption, the light penetration is typically limited to a few tens of nanometers,64 thereby making this analysis more surface sensitive. Using 532 nm instead of 785 nm should in principle allow a shallower penetration depth (δp = λexc/4πnk) and thus probe more effectively the particle surface via RRS.64 Considering the reduced number of counts compared to the as-recorded spectra obtained with the 785 nm laser (see Fig. S2a and b†) and the negligible influence of thermal effects due to the purposeful use of low laser power, the results in Fig. 2a and Fig. S2a† suggest that surface defects, local lattice distortions and disorder represent the main cause for the slight changes in the spectral features of the spherical nanoparticles under RRS at 532 nm. In fact, the peaks remained sharp and hardly shifted to lower wavenumbers, while the peak broadening for the spherical nanoparticles appeared moderate, especially when compared to those reported for agglomerated Co3O4 nanoparticles measured with similar laser power, whose spectral features sensibly red-shifted and exhibited much broader lines.18,65 Therefore, this confirms that the surface properties of the spherical nanoparticles differ from those of the cubic nanoparticles and bulk powder.
3.4 Neutron diffraction studies
We combined neutron powder diffraction and pair-distribution function (PDF) measurements, to unambiguously determine our samples’ crystal and magnetic structures. The quality of Rietveld refinements of the neutron diffraction data is demonstrated in Fig. 3a and b. The refined average crystal structure is cubic for all samples with the space group Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m.66 It is a normal spinel with the Co2+ and Co3+ ions occupying tetrahedral and octahedral sites, respectively. While positions of structural peaks are the same for all samples, the peak width of nanoscaled samples is broader as compared to the bulk counterpart due to the finite particle size. The crystalline sizes equal to 33(3) and 61(2) nm for spherical and cubic nanoparticles, respectively were derived from the Rietveld refinements (Tables S3 and S4†). The most intriguing conclusion of the average crystal structure study is a difference in lattice constant values between the three samples shown in Fig. 3c. The lattice constant of cubic nanoparticles is higher than the bulk sample, while the lattice constant of spherical nanoparticles is smaller.
m.66 It is a normal spinel with the Co2+ and Co3+ ions occupying tetrahedral and octahedral sites, respectively. While positions of structural peaks are the same for all samples, the peak width of nanoscaled samples is broader as compared to the bulk counterpart due to the finite particle size. The crystalline sizes equal to 33(3) and 61(2) nm for spherical and cubic nanoparticles, respectively were derived from the Rietveld refinements (Tables S3 and S4†). The most intriguing conclusion of the average crystal structure study is a difference in lattice constant values between the three samples shown in Fig. 3c. The lattice constant of cubic nanoparticles is higher than the bulk sample, while the lattice constant of spherical nanoparticles is smaller.
 | ||
| Fig. 3 NOMAD TOF diffraction data for cubic Co3O4 nanoparticles from the forward scattering bank at 10 K (a) and the backscattering bank at 100 K (b), with experimental data as blue open circles, the calculated pattern in red, and the difference curve in green. Inset shows an expanded view of the same data, with no indications of magnetic Bragg peaks. Temperature dependencies of the lattice constant (c) and the magnetic moment per Co2+ (d) for the spherical, cubic and bulk samples. Solid lines are mean-field fits with TN listed in Table 1. | ||
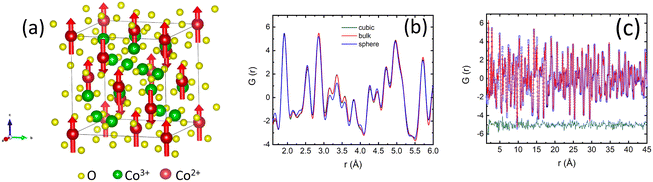
The magnetic structure of our samples was refined from neutron diffraction data collected below TN. In agreement with previous neutron diffraction studies of Co3O4 powders,1,46,67 we found that the magnetic structure is best described by a propagation vector k = (0, 0, 0), i.e. the magnetic unit cell is identical to the nuclear one. The two primary peaks below TN can be indexed to the (111) and (200) peaks of the bulk Co3O4 structure. The first peak at Q111 = 1.33 Å−1 constitutes structural and magnetic contributions, while the second peak Q200 = 1.56 Å−1 is purely magnetic. Additional diffuse scattering had to be added in the modeling of the intensity of Q111 peak for all three samples (see Fig. S3†). This magnetic diffuse scattering was previously observed with neutron diffraction studies of the bulk Co3O4. It corresponds to the disordered short-range magnetic state resembling spiral spin liquid. The correlation length of the disordered state was estimated using the Scherrer formula68ζ = d2111/Δd111, where d111 is the position and Δd111 is the full width at half-maximum of the Q111 peak. We found ζ equal to 9.8(2) nm, 6.7(3) nm and 12.4(1) nm, for the spherical, cubic and bulk samples. The correlation length in spherical nanoparticles is about 30% of their crystalline size, implying a non-negligible role of this magnetically disordered phase in their magnetic properties.
In our model, only Co2+ ions bear magnetic moments. The magnetic moment of spherical nanoparticles is reduced down to 2.76(2)μB from the value of 3.01(2)μB observed for the bulk and cubic nanoparticles at 10 K. We found no deviation from a cubic symmetry in the crystal structural or additional magnetic phase transitions below TN in both of our nanoparticle samples. We obtained TN for each sample from mean-field fits of the magnetic moment temperature dependence (Fig. 3d). TN is decreasing from its bulk value of 42.4(8) K with the particle size down to 32.2(1) K and 30.1(2) K, for cubic and spherical particles, respectively. The result agrees well with the finite-size effects reduction of TN previously reported for Co3O4 nanoparticles.45,47,69,70
We further investigate the local crystal structure of our samples using neutron PDF measurements. The purpose of PDF studies was to verify any deviations from the average crystal structure derived from Rietveld refinements. Nanoparticles are prone to dislocations, stress, vacancies and anti-phase boundaries, which all can influence local crystal structure and consequently, the strength of the AFM interactions.71,72 Most recent examples include modification of the local structure of iron oxide nanoparticles due to vacancies and non-stoichiometry.73,74 Specifically for Co3O4 samples, we used PDF measurements to investigate local structural transitions, which were suggested as one of the reasons for the incommensurate AFM order observed with muon spin rotation and relaxation method in bulk Co3O4.43
Neutron PDF data for all three samples are qualitatively similar. We fitted neutron PDF data using the average crystal structure obtained with the Rietveld refinements as a starting model (Fig. 4a). The PDF analysis indicated no deviations of the local structure from the cubic symmetry or any signs of inverse spinel structure for both nanoparticle samples. The lattice constants obtained from the refinement of the PDF data are consistent with Rietveld refinement results (Fig. S4a†). The spherical nanoparticles have the smallest lattice constant. The most significant difference between the samples is observed for the spherical nanoparticles between 3.0 and 3.7 Å at 10 K. The intensities of the three peaks at 3.15, 3.35 and 3.57 AA are reduced (Fig. 4b). The position of the first peak at 3.15 Å corresponds to an O–O atomic pair. The second peak is a superposition of Co–Co and Co–O atomic pairs, while the last peak corresponds to Co–O pair (Fig. S4b†). The reduction of intensity in PDF peaks compared to the bulk indicates that the atoms in corresponding pairs have a lower coordination number. We refined the occupancies of O and Co atoms while modeling the neutron PDF data (Table S4†). The results of the PDF data refinements for cubic nanoparticles are shown in Fig. 4c and for the bulk in Fig. S4c.† We found that occupancies of O and Co atoms are reduced for the spherical nanoparticles, as compared to the bulk and cubic nanoparticles (Table S3†). Neutron diffraction is not sensitive to the valence state of Co atoms, however previous density function theory (DFT) calculations confirmed that the formation of the Co2+ defects is more likely than the formation of Co3+ defects, because of the lower formation energy of Co2+ vacancies.59
3.5 Inelastic neutron scattering measurements
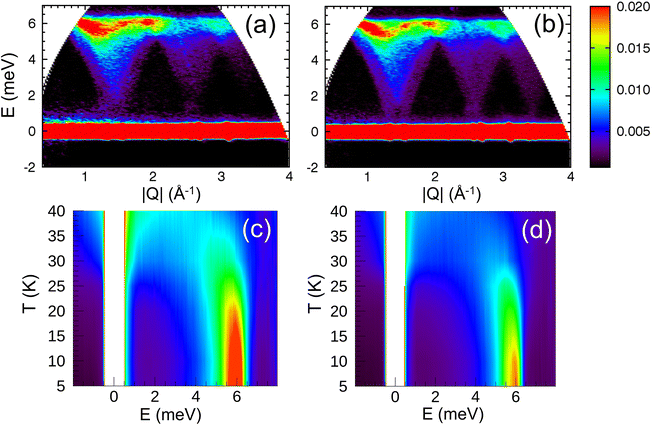
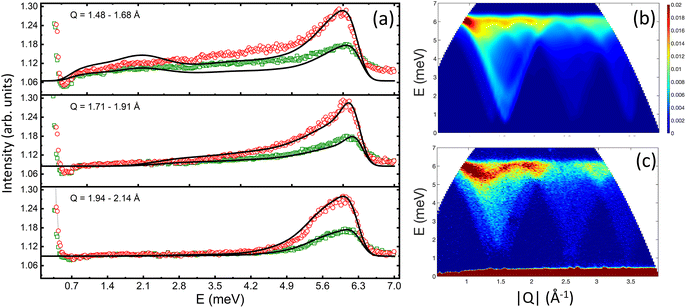
The spin wave properties of our samples were studied with TOF inelastic neutron scattering measurements (INS). We found no previous reports on TOF INS of polycrystalline a powder or single crystal of Co3O4. Growing a single crystal of Co3O4 is extremely challenging. The main issue is the decomposition of Co3O4 at 900 °C which limits applications of conventional crystal growth methods. The Co3O4 is carcinogenic and extraordinary safety measures have to be taken in order to handle it at elevated temperatures.75The overview of INS data is shown in Fig. 5. The energy and wave-vector dependence of the scattered intensity I(Q,E) is plotted for T = 5 K for the cubic nanoparticles and bulk powder (Fig. 5a and b). Similar for all three samples, the inelastic excitation peaked near 6 meV, and shows dispersion over the entire Q-range with its intensity decreasing strongly with increased wave vector Q. The dispersion is periodic and matches perfectly the periodicity of the Bravais magnetic lattice derived from the magnetic structure (Fig. S6 and S7†). The excitations are only observed below TN for each individual sample. Since the excitation signals in the spectrum possess a characteristic dispersion in the low-energy regions and the scattering intensity decreases with increasing Q following the magnetic form factor, it is fair to conclude that the signals are contributions from magnetic spin waves. Similar spin wave dispersions for the nanoparticle and bulk samples confirm that they are inherently specific to the magnetic properties of Co3O4. We found no evidence of finite-size induced phonon dispersions nor excitations associated with the collective nanoparticle modes, at least within our experimental energy window of 15 meV. Fig. 5c and d show the energy E dependence of the scattered intensity I(E) for the cubic nanoparticles and bulk powder, integrated over wave vectors Q, for temperatures above and below TN. Above TN, the scattering is quasielastic (QE) for both samples. As the temperature is reduced, the QE linewidth is reduced and the overall scattering intensity decreases. QE scattering collapses below TN, for both samples and the inelastic peak begins to emerge. It changes its position and becomes more intense as the temperature further decreases. At the lowest temperature of 5 K, the peak position for the cubic nanoparticles is slightly but visibly increased to E = 6.2 meV, compared to the value of 6.0 meV for both bulk powder and spherical nanoparticles.
The neutron diffraction studies of our samples showed a relatively large magnetic moment of Co2+ ions, therefore the spin wave dispersion can be analyzed by the Heisenberg model with a spin Hamiltonian:
 | (2) |
 | (3) |
In order to directly compare the calculations with the experimental INS data on the powder samples, the calculated INS cross-section (eqn (3)) was averaged over different Q vectors lying on a constant-Q sphere. The exchange constants for all samples were obtained by fitting the energy spectra at different momentum transfers (Fig. 6a). We found that for the bulk and spherical nanoparticle samples, J1 = −7.60 meV, J2 = 1.10 meV, and DS = 0.015 meV. Using these values we were able to calculate neutron scattering spectra that compare well and reproduce all the features of the experimental data (Fig. 6b and c). However, the best fit of the energy spectra for the cubic nanoparticles was obtained with a slightly increased J1 = −7.72 meV. The calculated neutron scattering spectra with these exchange parameters can reproduce the experimental data quite well (Fig. S8†). Increased value of J1 can also explain the shift of the inelastic peak position in I(E) data, experimentally observed for the cubic nanoparticles (Fig. 5c). The increase of J1 value in the cubic nanoparticles is rather weak compared to the bulk value, presumably due to a large polydispersity of the cubic nanoparticles and their shape irregularities observed in TEM studies. Additional neutron scattering experiments on monodisperse cubic nanoparticles of various sizes might show an even larger increase of J1 value.
The values obtained in this experiment are considerably higher than previously reported in the literature. DFT calculations with Dudraev correction for on-site Coulomb interactions (DFT+U) found the value of J1 ranging from −0.2 to 4.8 meV for the bulk Co3O4, depending on the functional.77–80 The only reported experimental value of J1 obtained by INS measurements with a monochromatic beam on the polycrystalline Co3O4 powder is equal to 0.63 meV.81
The most likely explanation for the FM-shell in spherical nanoparticles is the reduced coordination number of the surface atoms56 or the surface spins pinning by the ligand atoms.82–85 Both effects can induce a net magnetic moment at the surface due to incomplete AFM alignment of the magnetic moments of the surface atoms. The exchange interactions between this FM-like magnetic moment and AFM inner core lead to non-zero HEB, only observed in the spherical nanoparticles. The lower coordination number of the surface atoms might lead to a defective crystal structure at the surface. Indeed, according to our neutron diffraction studies O and Co atoms deficiencies are the most prominent in the spherical nanoparticles. According to first-principle studies, oxygen vacancies lead to FM-like behavior in Co3O4 thin films because they affect exchange interactions between metallic ions.86 The detailed model of the vacancies distribution in our samples is missing, but independent magnetization and Raman scattering measurements, both suggest that the vacancies are distributed at the surface of the spherical nanoparticles. Another consequence of the surface disorder in the spherical nanoparticles is the reduction of their lattice constant. The defective surface structure induces a tensile surface stress that in turn compresses the lattice constant to minimize the surface energy.16,87,88 Our explanation is supported by the previous X-ray absorption fine structure measurements and DFT calculations on similarly sized Co3O4 nanostructures.59 The cubic nanoparticles appear to be more ordered than the spherical ones, showing only small deviations in the crystal and magnetic structures from their bulk counterpart. The most prominent structural feature of the cubic nanoparticles is their surface. They are exposing well-defined crystal planes formed by high-temperature annealing in a vacuum. Previous studies have concluded that for the cubic Co3O4 nanoparticles, the most likely exposed planes at their surface are (111) and (100).16 These two planes have a larger fraction of Co2+ ions, compared to a number of non-magnetic Co3+ ions. The size of Co2+ ions (0.745 Å) is larger than the size of Co3+ ions (0.545 Å), hence negative stress is induced on the surface of those planes.66,87 That results in an increase of the lattice constant observed in our cubic sample and in previous studies of cubic Co3O4 nanoparticles prepared by a similar high-temperature annealing method.61,89
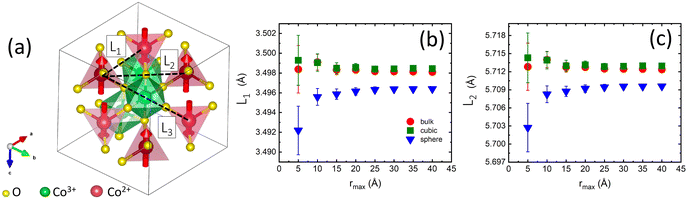
One would expect increased values of J1 in nanoparticles with the smallest lattice constants due to a higher degree of 3d electron cloud overlap.90Fig. 7a shows the nearest (L1) and the next-nearest (L2) neighbor distances between Co2+ ions for all three samples obtained from neutron data refinements. The best Rietveld refinements were obtained with the position of all atoms fixed. Thus both distances follow the same dependencies as the lattice constants, i.e. the shortest bond lengths were found for the spherical nanoparticles. We further examine any possible local distortions of L1 and L2 by relaxing the positions of Co atoms in tetrahedral and octahedral sites during neutron PDF data boxcar refinements in the range r = 1.5–40 Å, with a step of rmax = 5 Å (Fig. 7b and c). The obtained values of L1 and L2 show no rmax-dependence and remain constants within experimental error, as well as Co–O and O–O bond lengths (Fig. S9†). We tried to relax and fit the positions of all atoms simultaneously, but it led to the over-parametrization of the model and the fits were unstable. In conclusion, we found no local distortions of the bond lengths in the superexchange path in our samples that could have explained the increased values of J1 in the cubic nanoparticles.
Another parameter to consider when explaining the exchange interactions in a normal spinel is inversion.86,91 Our cubic nanoparticles might be susceptible to inversion because they were exposed to high temperatures of 400 °C. We accurately calculated the inversibility parameter using the spinel anion parameter u, according to92 for all our samples, using lattice constants and bond lengths at 10 K derived from neutron diffraction studies. The value of 0.26(1) for all three samples is consistent with the bulk values of 0.26–0.27 previously reported for a normal spinel structure.92,93
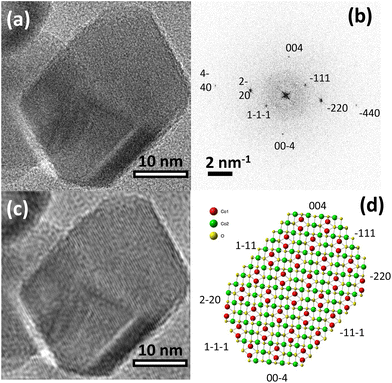
As we discussed in the preceding sections, the enhancement of J1 observed in cubic nanoparticles cannot be explained by either decreased lattice constants, ligand interactions, or inversion. Thus, the shape effects must be considered. The previous reports have already indicated that the shape effects modify the magnetic structure of Co3O4 nanoparticles in a significant way. For example, 7 nm Co3O4 single-crystal nanowires showed an induced FM-moment due to the symmetry breaking of Co3+ ions on (111) surfaces.52 Similarly, cubic and platelet-like Co3O4 nanoparticles displayed a variation in the net magnetic moment depending on the coordination number of Co ions at a dominant crystal plane.16 In the case of our cubic nanoparticles, the high-resolution TEM study verified that the dominant (100) and (111) planes are exposed on the surface (Fig. 8). Presumably, exposure of these planes seen only in cubic nanoparticles is responsible for enhancing J1. Previous studies of larger Co3O4 particles in the shape of cubes with the (001) plane, truncated octahedrons with (001) and (111) planes and an octahedron with the (111) show remarkably different physicochemical behaviors, as for example indicated by their respective electrochemical performances.8 Accordingly, the key role of specifically exposed surface planes in Co3O4 nanoparticles with well-defined shapes must be considered. In the same vein, DFT calculations of the magnetic interactions on (100) and (111) surfaces of our cubic nanoparticles, including an experimental crystal structure can help to elucidate the origin of J1 increase. However, given the relatively large size of the cubic nanoparticles (61 nm), those calculations are extremely time-consuming and difficult to handle. The large polydispersity of our cubic nanoparticles will further complicate the understanding of the DFT calculation results.
Finally, we considered an alternative explanation of AFM-order in our samples and a possible reason for the FM-like phase observed in the spherical Co3O4 nanoparticles. The idea was first put forward by W. Roth in his original work in 1964.1 He suggested another exchange parameter J3 between the next-next nearest neighbor of Co2+ ions separated by 6.68 Å and including 180° bond angle between O–Co3+–O (see Fig. 7a). This is a weak interaction, but it becomes dominant if the multiplicity of exchange paths is taken into account. Each of the FM and AFM exchange paths via 90° O–Co3+–O bonds have the same multiplicity of 24 and cancel each other out. Only the AFM exchange path via 180° O–Co3+–O bond with a multiplicity of 12 remains responsible for AFM order in Co3O4. However, in Co3O4 nanoparticles with well-defined shapes, the multiplicity on the surface is broken and additional FM or AFM interactions are emerging.16 We found no experimental evidence of this scenario in our samples. Using additional exchange parameter J3 in the spin Hamiltonian had no effect on the calculated spin wave spectrum for all three samples, however, the determination of J3 might be hindered by the powder averaged data. Additional INS measurements of a single crystal are needed for a proper assessment of the J3 contribution to the spin wave spectrum of Co3O4.
4 Conclusions
We carried out extensive experimental studies of the structural and magnetic properties of spherical and cubic Co3O4 nanoparticles and compared them with the bulk powder. The spherical nanoparticles showed a pronounced effect of the canted surface spins, resulting in the appearance of an FM-like phase below 25 K. Despite, this surface disorder the exchange constants J1 and J2 of the spherical nanoparticles remained the same as in bulk, within the experimental error of our experiment. For the cubic nanoparticles, the lattice constant is increased as compared to the lattice constant of their bulk counterpart. It is a direct consequence of the negative surface stress caused by the high-temperature annealing. The importance of the particle's shape was further reinforced by the inelastic neutron scattering experiments, which showed increased exchange constant J1 only for the cubic nanoparticles. Our results imply that magnetic nanoparticles with selectively exposed surface planes can strengthen the exchange interactions and hence be more attractive for magnonics applications. Those applications can also benefit from the use of the spherical Co3O4 nanoparticles with magnetically disordered surfaces because they still retain their bulk-like spin waves dispersion.Author contributions
MF corresponding author, concept, measurements, data analysis, writing and editing; ZH, YX INS data analysis, writing; XT sample preparation; WL, NN, AP, MG, YS INS measurements, data reduction, editing; JCN, ME neutron PDF measurements, data reduction, editing; GSA, SU, LZ, SE HRTEM measurements, editing, data analysis, writing; MV Raman measurements, data analysis, writing; AQ SEM measurements, editing, data analysis, MCA concept, INS measurements.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank Paul Hering and Dr Moo-Sung Kim for their help with laboratory X-ray diffraction measurements. We gratefully acknowledge fruitful discussions with Dr Jörg Perβon, Dr Nicolo Violini and Dr Jörg Voigt. We also thank Dr Mark Hagen for his help with CNCS measurements. We thank Dr Vaclav Petříček for modifying Jana2006 program to adopt TOF neutron diffraction data. This work is based upon experiments performed at the TOFTOF instrument operated by Technische Universität München at the Heinz Maier-Leibnitz Zentrum (MLZ), Garching, Germany. A portion of this research at Oak Ridge National Laboratory's Spallation Neutron Source was sponsored by the Scientific User Facilities Division, Office of Basic Energy Sciences, U.S. Department of Energy. This research used JEOL2100F of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. G. S. A. and S. U. thank the financial support of the Swedish Research Agency, VR (Grant No. 2016-06959) and also acknowledge Myfab Uppsala for providing facilities and experimental support. Myfab is funded by the Swedish Research Council (Grant No. 2019-00207) as a national research infrastructure.References
- W. Roth, J. Phys. Chem. Solids, 1964, 25, 1–10 CrossRef CAS.
- D. Scheerlinck, S. Hautecler and W. Wegener, Phys. Status Solidi B, 1975, 68, 535–541 CrossRef CAS.
- Y. Ichiyanagi and S. Yamada, Polyhedron, 2005, 24, 2813–2816 CrossRef CAS.
- W. Söllinger, W. Heiss, R. T. Lechner, K. Rumpf, P. Granitzer, H. Krenn and G. Springholz, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 155213 CrossRef.
- R. Zhang, L. Pan, B. Guo, Z.-F. Huang, Z. Chen, L. Wang, X. Zhang, Z. Guo, W. Xu, K. P. Loh and J.-J. Zou, J. Am. Chem. Soc., 2023, 145, 2271–2281 CrossRef CAS PubMed.
- M. A. Boles, D. Ling, T. Hyeon and D. V. Talapin, Nat. Mater., 2016, 15, 141–153 CrossRef CAS PubMed.
- X. Xie, Y. Li, Z.-Q. Liu, M. Haruta and W. Shen, Nature, 2009, 458, 746–749 CrossRef CAS PubMed.
- X. Xiao, X. Liu, H. Zhao, D. Chen, F. Liu, J. Xiang, Z. Hu and Y. Li, Adv. Mater., 2012, 24, 5762–5766 CrossRef CAS PubMed.
- C. Gao, Q. Meng, K. Zhao, H. Yin, D. Wang, J. Guo, S. Zhao, L. Chang, M. He, Q. Li, H. Zhao, X. Huang, Y. Gao and Z. Tang, Adv. Mater., 2016, 28, 6485–6490 CrossRef CAS PubMed.
- J. Mu, L. Zhang, G. Zhao and Y. Wang, Phys. Chem. Chem. Phys., 2014, 16, 15709–15716 RSC.
- T. He, D. Chen, X. Jiao and Y. Wang, Adv. Mater., 2006, 18, 1078–1082 CrossRef CAS.
- D. Su, X. Xie, P. Munroe, S. Dou and G. Wang, Sci. Rep., 2014, 4, 6519 CrossRef CAS PubMed.
- R. Jing, A. Shan, R. Wang and C. Chen, CrystEngComm, 2013, 15, 3587–3592 RSC.
- Y. Hou, H. Kondoh, M. Shimojo, T. Kogure and T. Ohta, J. Phys. Chem. B, 2005, 109, 19094–19098 CrossRef CAS PubMed.
- Y. Wang, Y. Lei, J. Li, L. Gu, H. Yuan and D. Xiao, ACS Appl. Mater. Interfaces, 2014, 6, 6739–6747 CrossRef CAS PubMed.
- M. Shepit, V. K. Paidi, C. A. Roberts and J. van Lierop, Sci. Rep., 2020, 10, 20990 CrossRef CAS PubMed.
- S. Takada, M. Fujii, S. Kohiki, T. Babasaki, H. Deguchi, M. Mitome and M. Oku, Nano Lett., 2001, 1, 379–382 CrossRef CAS.
- I. Lorite, J. J. Romero and J. F. Fernández, J. Raman Spectrosc., 2012, 43, 1443–1448 CrossRef CAS.
- Y. Liu, H. Wan, H. Zhang, J. Chen, F. Fang, N. Jiang, W. Zhang, F. Zhou, H. Arandiyan, Y. Wang, G. Liu, Z. Wang, S. Luo, X. Chen and H. Sun, ACS Appl. Nano Mater., 2020, 3, 3892–3903 CrossRef CAS.
- H. Qin, R. B. Holländer, L. Flajšman, F. Hermann, R. Dreyer, G. Woltersdorf and S. van Dijken, Nat. Commun., 2021, 12, 2293 CrossRef CAS PubMed.
- S. Neusser and D. Grundler, Adv. Mater., 2009, 21, 2927–2932 CrossRef CAS.
- A. Kamra and L. G. Johnsen, Nat. Phys., 2023, 19, 469–470 Search PubMed.
- V. Sluka, T. Schneider, R. A. Gallardo, A. Kákay, M. Weigand, T. Warnatz, R. Mattheis, A. Roldán-Molina, P. Landeros, V. Tiberkevich, A. Slavin, G. Schütz, A. Erbe, A. Deac, J. Lindner, J. Raabe, J. Fassbender and S. Wintz, Nat. Nanotechnol., 2019, 14, 328–333 CrossRef CAS PubMed.
- R. Salikhov, I. Ilyakov, L. Körber, A. Kákay, R. A. Gallardo, A. Ponomaryov, J.-C. Deinert, T. V. A. G. de Oliveira, K. Lenz, J. Fassbender, S. Bonetti, O. Hellwig, J. Lindner and S. Kovalev, Nat. Phys., 2023, 19, 529–535 Search PubMed.
- J. Pelliciari, S. Lee, K. Gilmore, J. Li, Y. Gu, A. Barbour, I. Jarrige, C. H. Ahn, F. J. Walker and V. Bisogni, Nat. Mater., 2021, 20, 188–193 CrossRef CAS PubMed.
- D. Lachance-Quirion, S. P. Wolski, Y. Tabuchi, S. Kono, K. Usami and Y. Nakamura, Science, 2020, 367, 425–428 CrossRef CAS PubMed.
- O. Gomonay, T. Jungwirth and J. Sinova, Phys. Status Solidi RRL, 2017, 11, 1700022 CrossRef.
- E. Albisetti, S. Tacchi, R. Silvani, G. Scaramuzzi, S. Finizio, S. Wintz, C. Rinaldi, M. Cantoni, J. Raabe, G. Carlotti, R. Bertacco, E. Riedo and D. Petti, Adv. Mater., 2020, 32, 1906439 CrossRef CAS PubMed.
- M. Ishibashi, Y. Shiota, T. Li, S. Funada, T. Moriyama and T. Ono, Sci. Adv., 2020, 6, eaaz6931 CrossRef CAS PubMed.
- Z. Cai, Y. Bi, E. Hu, W. Liu, N. Dwarica, Y. Tian, X. Li, Y. Kuang, Y. Li, X.-Q. Yang, H. Wang and X. Sun, Adv. Energy Mater., 2018, 8, 1701694 CrossRef.
- W. Li, Y. Wang, X. Y. Cui, S. Yu, Y. Li, Y. Hu, M. Zhu, R. Zheng and S. P. Ringer, ACS Appl. Mater. Interfaces, 2018, 10, 19235–19247 CrossRef CAS PubMed.
- E. M. Jefremovas, M. de la Fuente Rodríguez, F. Damay, B. Fåk, A. Michels, J. A. Blanco and L. F. Barquín, Phys. Rev. B, 2021, 104, 134404 CrossRef CAS.
- E. M. Jefremovas, M. de la Fuente Rodríguez, D. Alba Venero, C. Echevarría-Bonet, P. Bender, B. Fåk, J. A. Blanco and L. Fernández Barquín, Commun. Mater., 2023, 4, 56 CrossRef CAS.
- M. Feygenson, X. Teng, S. E. Inderhees, Y. Yiu, W. Du, W. Han, J. Wen, Z. Xu, A. A. Podlesnyak, J. L. Niedziela, M. Hagen, Y. Qiu, C. M. Brown, L. Zhang and M. C. Aronson, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 174414 CrossRef.
- O. M. Sousa, J. S. Lima, A. F. Lima and M. V. Lalic, J. Magn. Magn. Mater., 2019, 484, 21–30 CrossRef CAS.
- A. Lima, J. Phys. Chem. Solids, 2016, 91, 86–89 CrossRef CAS.
- V. P. Puntes, K. M. Krishnan and P. A. Alivisatos, Science, 2001, 291, 2115–2117 CrossRef CAS PubMed.
- M. Feygenson, Y. Yiu, A. Kou, K.-S. Kim and M. C. Aronson, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 195445 CrossRef.
- J. Neuefeind, M. Feygenson, J. Carruth, R. Hoffmann and K. K. Chipley, Nucl. Instrum. Methods Phys. Res., Sect. B, 2012, 287, 68–75 CrossRef CAS.
- V. Petříček, M. Dušek and L. Palatinus, Z. Kristallogr. – Cryst. Mater., 2014, 229, 345–352 CrossRef.
- G. Ehlers, A. A. Podlesnyak, J. L. Niedziela, E. B. Iverson and P. E. Sokol, Rev. Sci. Instrum., 2011, 82, 085108 CrossRef CAS PubMed.
- O. Arnold, J. Bilheux, J. Borreguero, A. Buts, S. Campbell, L. Chapon, M. Doucet, N. Draper, R. F. Leal, M. Gigg, V. Lynch, A. Markvardsen, D. Mikkelson, R. Mikkelson, R. Miller, K. Palmen, P. Parker, G. Passos, T. Perring, P. Peterson, S. Ren, M. Reuter, A. Savici, J. Taylor, R. Taylor, R. Tolchenov, W. Zhou and J. Zikovsky, Nucl. Instrum. Methods Phys. Res., Sect. A, 2014, 764, 156–166 CrossRef CAS.
- Y. Ikedo, J. Sugiyama, H. Nozaki, H. Itahara, J. Brewer, E. Ansaldo, G. Morris, D. Andreica and A. Amato, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 054424 CrossRef.
- T. Fukai, Y. Furukawa, S. Wada and K. Miyatani, J. Phys. Soc. Jpn., 1996, 65, 4067–4071 CrossRef CAS.
- P. Sahoo, H. Djieutedjeu and P. F. P. Poudeu, J. Mater. Chem. A, 2013, 1, 15022–15030 RSC.
- A. H. Hill, A. Harrison, C. Ritter, W. Yue and W. Zhou, J. Magn. Magn. Mater., 2011, 323, 226–231 CrossRef CAS.
- L. He, C. Chen, N. Wang, W. Zhou and L. Guo, J. Appl. Phys., 2007, 102, 103911 CrossRef.
- D. von Dreifus, E. C. Pereira and A. J. A. de Oliveira, Mater. Res. Express, 2015, 2, 116102 CrossRef.
- D. Branković, V. Jokanović, B. Babić-Stojić, Z. Jagličić, D. Lisjak and D. Kojić, J. Phys.: Condens. Matter, 2009, 21, 095303 CrossRef PubMed.
- S. Sarkar, A. Mondal, N. Giri and R. Ray, Phys. Chem. Chem. Phys., 2019, 21, 260–267 RSC.
- M. Kofu, R. Watanuki, T. Sakakibara, S. Ohira-Kawamura, K. Nakajima, M. Matsuura, T. Ueki, K. Akutsu and O. Yamamuro, Sci. Rep., 2021, 11, 12098 CrossRef CAS PubMed.
- P. Lv, Y. Zhang, R. Xu, J. C. Nie and L. He, J. Appl. Phys., 2012, 111, 013910 CrossRef.
- E. L. Salabaş, A. Rumplecker, F. Kleitz, F. Radu and F. Schuth, Nano Lett., 2006, 6, 2977–2981 CrossRef PubMed.
- Z. Dong, Y. Fu, Q. Han, Y. Xu and H. Zhang, J. Phys. Chem. C, 2007, 111, 18475–18478 CrossRef CAS.
- S. D. Li, H. Bi, J. L. Fang, W. Zhong and Y. W. Du, Chin. Phys. Lett., 2004, 21, 737–740 CrossRef CAS.
- P. Dutta, M. S. Seehra, S. Thota and J. Kumar, J. Phys.: Condens.Matter, 2008, 20, 015218 CrossRef.
- M. J. Benitez, O. Petracic, H. Tüysüz, F. Schüth and H. Zabel, Europhys. Lett., 2009, 88, 1–6 CrossRef.
- V. G. Hadjiev, M. N. Iliev and I. V. Vergilov, J. Phys. C: Solid State Phys., 1988, 21, L199 CrossRef.
- R. Zhang, Y.-C. Zhang, L. Pan, G.-Q. Shen, N. Mahmood, Y.-H. Ma, Y. Shi, W. Jia, L. Wang, X. Zhang, W. Xu and J.-J. Zou, ACS Catal., 2018, 8, 3803–3811 CrossRef CAS.
- H. Shirai, Y. Morioka and I. Nakagawa, J. Phys. Soc. Jpn., 1982, 51, 592–597 CrossRef CAS.
- S. R. Gawali, A. C. Gandhi, S. S. Gaikwad, J. Pant, T.-S. Chan, C.-L. Cheng, Y.-R. Ma and S. Y. Wu, Sci. Rep., 2018, 8, 249 CrossRef PubMed.
- L. C. Schumacher, I. B. Holzhueter, I. R. Hill and M. J. Dignam, Electrochim. Acta, 1990, 35, 975–984 CrossRef CAS.
- C. Stella, N. Soundararajan and K. Ramachandran, AIP Adv., 2015, 5, 087104 CrossRef.
- G. Gouadec and P. Colomban, Prog. Cryst. Growth Charact. Mater., 2007, 53, 1–56 CrossRef CAS.
- D. Gallant, M. Pézolet and S. Simard, J. Phys. Chem. B, 2006, 110, 6871–6880 CrossRef CAS PubMed.
- P. Meena, R. Kumar and K. Sreenivas, AIP Conf. Proc., 2013, 1204–1205 CrossRef CAS.
- T. D. Sparks, A. Gurlo, M. F. Bekheet, M. W. Gaultois, G. Cherkashinin, L. Laversenne and D. R. Clarke, Phys. Rev. B, 2019, 99, 1–10 CrossRef.
- N. Golosova, D. Kozlenko, D. Nicheva, T. Petkova, S. Kichanov, E. Lukin, G. Avdeev, P. Petkov and B. Savenko, J. Magn. Magn. Mater., 2020, 508, 166874 CrossRef CAS.
- S. Thota, A. Kumar and J. Kumar, J. Mater. Sci. Eng. B, 2009, 164, 30–37 CrossRef CAS.
- D. A. Resnick, K. Gilmore, Y. U. Idzerda, M. T. Klem, M. Allen, T. Douglas, E. Arenholz and M. Young, J. Appl. Phys., 2006, 99, 08Q501 CrossRef.
- K. M. Jensen and S. R. Cooper, Reference Module in Chemistry, Molecular Sciences and Chemical Engineering, Elsevier, 2021 Search PubMed.
- T. Köhler, A. Feoktystov, O. Petracic, N. Nandakumaran, A. Cervellino and T. Brückel, J. Appl. Crystallogr., 2021, 54, 1719–1729 CrossRef PubMed.
- A. Lappas, G. Antonaropoulos, K. Brintakis, M. Vasilakaki, K. N. Trohidou, V. Iannotti, G. Ausanio, A. Kostopoulou, M. Abeykoon, I. K. Robinson and E. S. Bozin, Phys. Rev. X, 2019, 9, 041044 CAS.
- H. L. Andersen, B. A. Frandsen, H. P. Gunnlaugsson, M. R. V. Jørgensen, S. J. L. Billinge, K. M. Ø. Jensen and M. Christensen, IUCrJ, 2021, 8, 33–45 CrossRef CAS PubMed.
- Private communications with Dr. Jörg Perβon, 2020.
- Theory of neutron scattering from condensed matter. Vol. 1. Nuclear scattering .
- A. Cadi-Essadek, A. Roldan, D. Santos-Carballal, P. E. Ngoepe, M. Claeys and N. H. de Leeuw, S. Afr. J. Chem., 2021, 74, 8–16 CrossRef CAS.
- J. Chen, X. Wu and A. Selloni, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–7 Search PubMed.
- V. Singh, M. Kosa, K. Majhi and D. T. Major, J. Chem. Theory Comput., 2015, 11, 64–72 CrossRef CAS PubMed.
- P. Gopal, R. D. Gennaro, M. S. dos Santos Gusmao, R. A. R. A. Orabi, H. Wang, S. Curtarolo, M. Fornari and M. B. Nardelli, J. Phys.: Condens. Matter, 2017, 29, 444003 CrossRef PubMed.
- D. Scheerlinck and S. Hautecler, Phys. Status Solidi B, 1976, 73, 223–228 CrossRef CAS.
- R. H. Kodama, A. E. Berkowitz, E. McNiff Jr. and S. Foner, Phys. Rev. Lett., 1996, 77, 394 CrossRef CAS PubMed.
- A. Berkowitz, J. Lahut, I. Jacobs, L. M. Levinson and D. Forester, Phys. Rev. Lett., 1975, 34, 594 CrossRef CAS.
- D. Lin, A. Nunes, C. Majkrzak and A. Berkowitz, J. Magn. Magn. Mater., 1995, 145, 343–348 CrossRef CAS.
- L. Shan-Dong, B. Hong, F. Jiang-Lin, Z. Wei and D. You-Wei, Chin. Phys. Lett., 2004, 21, 737 CrossRef.
- P. Wang, C. Jin, P. Li, D. X. Zheng, J. L. Gong and H. L. Bai, Thin Solid Films, 2018, 660, 287–293 CrossRef CAS.
- P. M. Diehm, P. Ágoston and K. Albe, ChemPhysChem, 2012, 13, 2443–2454 CrossRef CAS PubMed.
- M. Casas-Cabanas, G. Binotto, D. Larcher, A. Lecup, V. Giordani and J. M. Tarascon, Chem. Mater., 2009, 21, 1939–1947 CrossRef CAS.
- P. P. Rodenbough, C. Zheng, Y. Liu, C. Hui, Y. Xia, Z. Ran, Y. Hu, S. W. Chan and W. Wong-Ng, J. Am. Ceram. Soc., 2017, 100, 384–392 CrossRef CAS.
- H. Ueda and Y. Ueda, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 224411 CrossRef.
- W. Chen, C. Chen and L. Guo, J. Appl. Phys., 2010, 108, 073907 CrossRef.
- R. J. Hill, J. R. Craig and G. V. Gibbs, Phys. Chem. Miner., 1979, 4, 317–339 CrossRef CAS.
- K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82, 3279–3292 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr04424f |
| ‡ This author contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |