Open Access Article
Open Access ArticleGiant supermagnonic Bloch point velocities in cylindrical ferromagnetic nanowires†
Felipe
Tejo
 a,
Jose Angel
Fernandez-Roldan
a,
Jose Angel
Fernandez-Roldan
 b,
Konstantin Y.
Guslienko
cd,
Rubén M.
Otxoa
b,
Konstantin Y.
Guslienko
cd,
Rubén M.
Otxoa
 ef and
Oksana
Chubykalo-Fesenko
ef and
Oksana
Chubykalo-Fesenko
 *g
*g
aUniversidad Central de Chile, Escuela de Ingeniería, Santiago de Chile, 8330601, Chile
bInstitute of Ion Beam Physics and Materials Research, Helmholtz-Zentrum Dresden-Rossendorf e.V., Bautzner Landstrasse 400, Dresden, 01328, Germany
cDepto. Polímeros y Materiales Avanzados: Física, Química y Tecnología, Universidad del País Vasco, UPV/EHU, San Sebastian, 20018, Spain
dIKERBASQUE, the Basque Foundation for Science, Bilbao, 48009, Spain
eHitachi Cambridge Laboratory, J. J. Thomson Avenue, Cambridge, CB3 0HE, UK
fDonostia International Physics Center, San Sebastian, 20018, Spain
gInstituto de Ciencias de Materiales de Madrid, CSIC, Sor Juana Ines de la Cruz, 3, Madrid, 28049, Spain. E-mail: oksana@icmm.csic.es
First published on 30th April 2024
Abstract
Achieving high velocities of magnetic domain walls is a crucial factor for their use as information carriers in modern nanoelectronic applications. In nanomagnetism and spintronics, these velocities are often limited either by internal domain wall instabilities, known as the Walker breakdown phenomenon, or by spin wave emission, known as the magnonic regime. In the rigid domain wall model, the maximum magnon velocity acts as an effective “speed of light”, providing a relativistic analogy for the domain wall speed limitation. Cylindrical magnetic nanowires are an example of systems without the Walker breakdown phenomenon. Here we demonstrate that the magnonic limit could be outstandingly surpassed in cylindrical nanowires with high magnetization, such as iron. Our numerical modeling shows the Bloch point domain wall velocities as high as 14 km s−1, well above the magnonic limit estimated in the interval 1.7–2.0 km s−1. The key ingredient is the three-dimensional conical shape of the domain wall, which elongates and breaks during the dynamics, expelling backwards pairs of Bloch points. This leads to domain wall acceleration, the effect, which resembles the “jet propulsion”. This effect will be very important for three-dimensional networks based on cylindrical magnetic nanowires.
Introduction
Domain walls (DWs) are topological magnetic solitons with a huge area of potential applications in modern nanoelectronics and spintronics. Magnetic domain walls (DWs) are currently used for many applications such as the race-track memory in information technologies,1,2 logical circuits,3 neuromorphic computing,4etc. Apart from technological perspectives, there is a fundamental question of the key mechanism limiting the propagation of any traveling wave in a given media. Generally, the maximum speed of information transmission cannot surpass the maximum group velocity of elementary excitations. Thus, this maximum velocity, defined as an effective “speed of light”, can be viewed as analogous to limiting velocity in the special theory of relativity.5 Additionally, topological solitons propagation is limited by wave emission (e.g., acoustic or electromagnetic), similar to the Cherenkov effect6,7 (“speed of sound”). The question arises of how solid are the above restrictions and if even higher velocities can be achieved.Achieving high domain wall velocities in magnetic media is a key ingredient for many applications because they determine the device operation time. Unfortunately, in ferromagnetic materials, the domain wall velocity also suffers from the so-called Walker breakdown phenomenon.8 In permalloy (FeNi alloy) stripes (widely used for spintronic and magnonic studies), DW velocity cannot exceed few hundreds of m s−1.9 Consequently, extensive research has been performed to find solutions to this problem. The manipulation of ferromagnetic DWs with spin–orbit torques in insulator/metal heterostructures with the Dzyaloshinskii–Moriya exchange interactions and out-of-plane magnetization resulted in DW velocities up to 400 m s−1.10 In low dissipative insulating garnets, DW velocities up to 4.3 km s−1 have been recently reported.5 Unlike the above materials, antiferromagnets and ferrimagnets close to the angular momentum compensation point, do not have the Walker breakdown phenomena. In ferrimagnetic materials for temperatures around a net angular momentum compensation point high velocities up to 2 km s−1 have been measured.11 In pure antiferromagnets with special crystal lattice symmetries such as Mn2Au even higher velocities up to 40 km s−1 were theoretically predicted.12–15 Within the 1D model the DW speed in these materials is limited by the magnon group velocity,14,16 used as an analog to the “speed of light” for their dynamics which obey equations similar to ones in the special theory of relativity. However, numerical modelling shows that antiferromagnetic DWs can propagate with velocities above the magnonic limit.16 Also, after reaching the corresponding velocity, the DW is slowed down, and a proliferation of multiple domain walls arising from the initial wall has been observed in numerical modeling.14
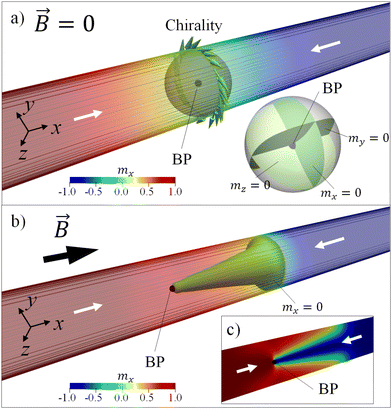
Cylindrical magnetic nanowires are viewed as building blocks for three-dimensional applications such as the Internet of nano things.17 They constitute another example of systems where the absence of the Walker breakdown phenomenon has been predicted.18 Starting with some diameters, cylindrical magnetic nanowires possess a very special DW of the Bloch point (BP) type (BP-DW),18–20 in which head-to-head or tail-to-tail magnetic domains are separated by a vortex domain wall containing a Bloch point (see Fig. 1). The BP-DW is a 3D magnetic topological soliton, whose configuration has a singularity of the magnetization field with an excess of the exchange energy. It is stabilized by the minimization of the magnetostatic energy and at rest it has a cylindrically symmetric structure. In finite nanostructures such as magnetic spheres, it is characterized by the non-zero and not integer 3D topological charge due to a variable helicity arising from magnetostatic energy minimization,21 configuring magnetic fields with a quadrupolar nature,22 which could be used in technological applications.23 It was predicted that BP has a large mobility in response to external driving magnetic field.24 Recent numerical simulations reported the BP-DW velocity in permalloy cylindrical nanowire circa 1 km s−1, slightly higher than the magnon group velocity.25 After that, the DW dynamics enter a so-called turbulent regime characterized by the proliferation of magnetic “drops”.26 Unfortunately, the dynamics of BP-DWs have another problem since it has been shown that they undergo dynamical transformation to the vortex–antivortex domain wall.27,28 This phenomenon would significantly impact and may limit possible applications of cylindrical magnetic nanowires.27
In this article, we show that the BP-DW velocity in ferromagnetic cylindrical nanowires of high magnetization (such as iron) can reach very high values after overcoming the turbulent magnonic regime, i.e., in the “super-sonic” regime. Fig. 1 illustrates the internal magnetization texture of the BP-DW. Being initially of a symmetrical shape at rest (Fig. 1a), as it moves along the nanowire under an applied field, the BP-DW develops a conical shape in which the BP is positioned at the vertex of the cone (Fig. 1b). The length of the cone increases as time progresses. As we show later, some internal instabilities break the cone-shaped DW, creating a pair of new BPs which are emitted backwards. This produces a “jet propulsion” effect, accelerating the DW. Our numerical modeling shows the BP DW velocity values up to 14 km s−1, much higher than any value reported previously in numerical modeling of ferromagnetic nanowires.
Results
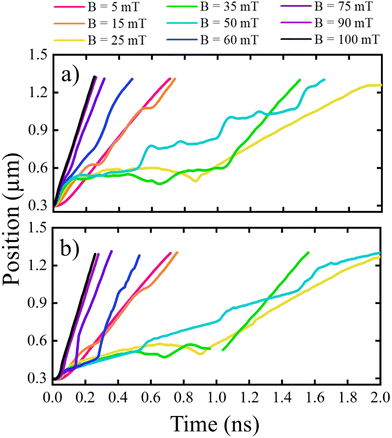
As an illustrative example, we first discuss the dynamics of a BP-DW in a nanowire with the radius R = 30 nm, length L = 1.5 μm (see ESI† for nanowires with different diameters). The details of the model can be found in the Methods section.An important parameter to describe BP-DW is its chirality, i.e., the direction of the magnetization circulation in the yz plane perpendicular to the nanowire x-axis. We start our simulations with DW of “good” chirality, as defined by ref. 18, i.e., the one with a circular polarisation direction favored by the torque induced by internal field (depicted in Fig. 1). Then, an external magnetic field B is applied parallel to the nanowire axis. Fig. 2a shows an “effective” DW position as a function of time, evaluated from the zero value of the average magnetization along the nanowire axis, i.e., 〈mx(t)〉 = 0 (an experimentally measured quantity) for different driving magnetic field magnitudes. Fig. 2b shows the BP position along the nanowire axis for the same driving fields. The BP position has been calculated by intersecting three iso-surfaces corresponding to zero values of the magnetization components mx = 0, my = 0, mz = 0. We stress that although the value 〈mx(t)〉 could be close to what is measured experimentally by imaging techniques, it is not a good characterization of the non-rigid domain wall dynamics. Nevertheless, both figures show similar tendencies except for the void region in Fig. 2b, which corresponds to the absence of the BP in simulations.
Fig. 2 presents three regimes for the BP-DW motion. In the regime I, for applied fields B < 15 mT, the DW propagation is approximately linear in time, and DW velocity increases as the magnitude of the external field increases. In the regime II, the DW mobility is significantly decreased for applied fields 15 mT < B < 60 mT. This regime is characterized by a large emission of small-amplitude spin waves from the BP-DW towards the nanowire edges, which was associated previously with the spin-Cherenkov effect.7,18,25 Note that the Cherenkov radiation starts when the moving DW reaches the minimal phase velocity of the linear spin waves and exceeds it.7 Also, in this regime the DW texture may undergo a series of complex transformations. Indeed, for B = 35 mT, during some time interval, the BP does not exist. These effects are similar to previous works on transforming BP-DW into vortex–antivortex DW.27 This regime has been reported previously as the one limiting BP-DW propagation.27 Additional illustrations can be found in the ESI.† The novelty comes in the regime III for B > 60 mT, where surprisingly, we again discover a quasi-linear DW motion with time with a very high velocity. This is a regime in which we will mostly pay our attention.
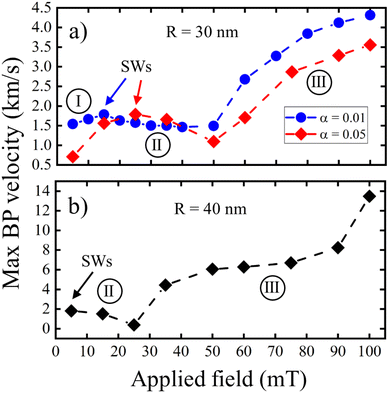
Fig. 3 summarizes the maximum BP velocity as a function of the applied magnetic field for two different nanowire radii and two damping parameter values (note that in the initial interval of time for B = 60 mT and B = 75 mT in Fig. 3b, the BP mobility is low and we extract the velocity from the high mobility region). We observe that the critical magnetic fields limiting the transition between different regimes displace to higher values as the nanowire radius decreases. For R = 20 nm (see ESI†), we observed only the first and the second DW motion regimes within the same field interval as considered in Fig. 3. In contrast, for R = 40 nm, the first regime is displaced to small fields. This transition between the first and the second regime occurs in all cases for velocities of approximately 1.7–2.0 km s−1, which we associate with the spin Cherenkov effect, reported previously in ref. 7, 25 and 26. Theoretical estimation of the minimum phase magnon velocity, determining the start of the magnon emission can be found in our ESI.† Its value is in the interval of 1.5–1.8 km s−1; it decreases as a function of nanowire radius and slightly increases as a function of the applied field. In simulations, approaching this velocity produces a significant spin wave emission and either a stagnation or a decrease of the DW velocity. Note that as it can be seen in Fig. 5 of the ESI,† spinwaves in this regime are mainly emitted backwards and are small-amplitude. However, in the third regime, the velocity is significantly increased up to circa 4 km s−1 for nanowires with 30 nm radius and 14 km s−1 for 40 nm radius. We also notice that the velocities increase as the nanowire radius increases or the damping value decreases. The latter is in clear contradiction with the standard Walker 1D model,8 which predicts that above the Walker breakdown field, the Zeeman energy input is compensated by magnetic relaxation and thus the DW velocity is proportional to the damping value.29 We highlight that this model is not applicable for our 3D DW which dynamically changes its shape.
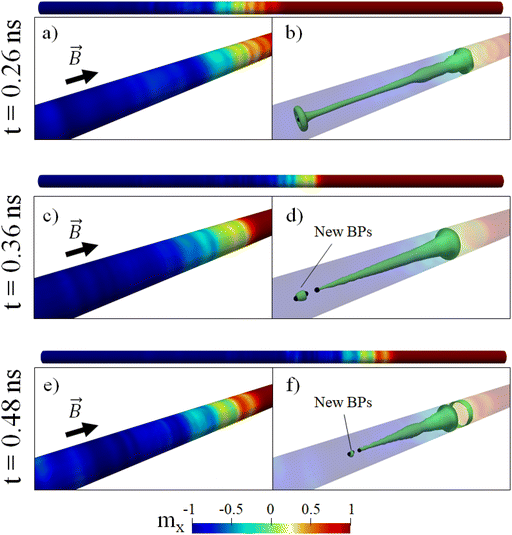
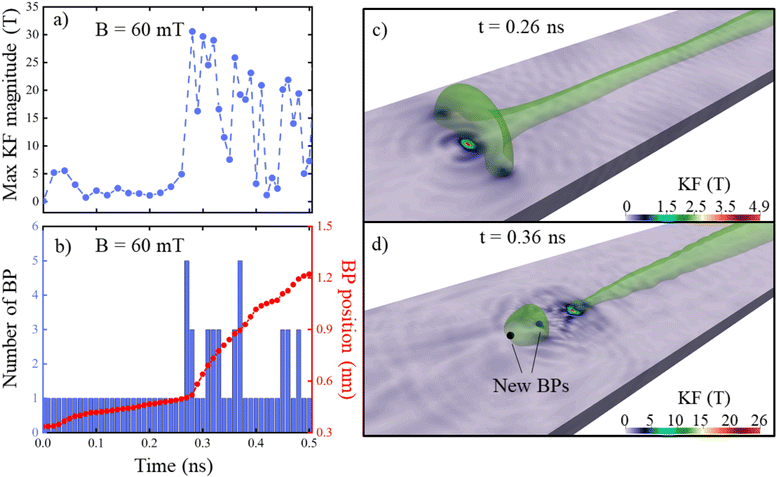
To clarify the origin of these behaviors, we show in Fig. 4 snapshots of the magnetization dynamics for B = 60 mT. Since the Bloch point moves faster than the effective “speed of sound”, the emission of spin waves is very relevant, especially visible on the nanowire surface magnetization. Similar to regime II, small-amplitude spinwaves propagating backward are present. However, unlike the regime II, the Bloch point is also surrounded by large-amplitude spinwaves forming a cloud around it (see available ESI Video†). Most importantly, during the dynamics, in this regime the length of the cone substantially increases with time, and the cone breaks at some instant, giving rise to the spontaneous creation of pairs of BPs near the cone end. This pair forms head-to-head and tail-to-tail BP-DWs containing BPs surrounded by magnetisation configurations with opposite chiralities. The original BP (part of the head-to-head BP-DW) detaches from the cone together with one of the newborn BPs (part of the tail-to-tail BP-DW), and the other new BP (identical to the original one) is now located at the DW cone end. Additional illustrations can be found in the ESI Video.† After some time, the detached part of the cone annihilates, leading to further spin wave emission. In our simulations, we always follow the dynamics of the BP, which is attached to the main cone, i.e., forms part of the main DW. This mechanism of expelling backwards additional BPs provides a propulsion-like effect on the main DW cone, leading to a change in the slope for the DW (i.e. 〈mx〉(t)) or BP positions in Fig. 2 and allowing the BP-DW to reach high velocities.
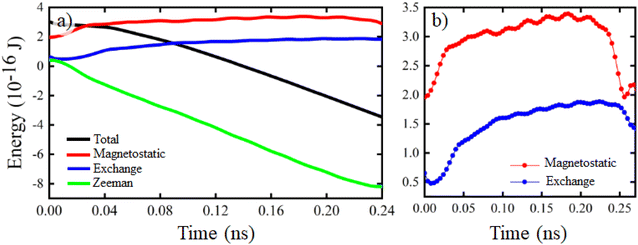
Several effects are important here. First, the main contribution to increasing the cone length comes from the magnetostatic interactions. Indeed, due to the difference of magnetostatic fields at the nanowire's surface and center, surface magnetization propagates faster, and the one in the center lags behind, producing an elongation of the DW cone. This effect is more significant in nanowires with high saturation magnetization, such as Fe, as well as it is larger in nanowires with larger diameters. Fig. 5 shows time evolution of magnetic energies during the domain wall propagation. Note the dominant role of the magnetostatic energy. The elongation of the domain wall cone leads to an increase of interaction energies, both magnetostatic and exchange.
The next essential ingredient of the process is the fact that the cone breaks due to dynamical instabilities. This effect was noticed previously in ref. 26 as a drop generation behind DW; however, its significance for the DW velocity was not discussed, and the large velocity increase was not reported. For better understanding, we systematically study the dynamics of the so-called kinetic field, used in the studies of dynamical instabilities of magnetic solitons such as reversal of the core polarity in magnetic vortices by vortex–antivortex pair nucleation30 or DW-pairs proliferation in layered antiferromagnets such Mn2Au.14 The kinetic field is defined via the gauge vector potential introduced to keep the Lagrangian invariant31 and is written as 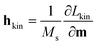 , where
, where 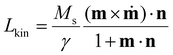 corresponds to the kinetic part of the Lagrangian density of our system, where m is a unit vector in the direction of magnetization and n is a unit vector of Cartesian coordinates. Note that the kinetic field is not a real magnetic field. It is a heuristic concept introduced for visualization of the points in configurational space with large dynamical instabilities where the fracture of the continuous magnetisation can be expected.
corresponds to the kinetic part of the Lagrangian density of our system, where m is a unit vector in the direction of magnetization and n is a unit vector of Cartesian coordinates. Note that the kinetic field is not a real magnetic field. It is a heuristic concept introduced for visualization of the points in configurational space with large dynamical instabilities where the fracture of the continuous magnetisation can be expected.
Fig. 6a and b compare the maximum kinetic field magnitude and the number of existing BPs along the BP DW dynamical trajectory. Importantly, new BPs are constantly generated and annihilated (in pairs and with opposite chiralities of BP-DWs); in this case, up to five BPs can exist simultaneously in the system. One can relate the appearance of additional BPs with a burst in the kinetic field. The increase of the DW velocity is associated with the appearance of new Bloch points, i.e., the DW velocity was low when only one BP was present in the system, and the DW accelerates due to the appearance of the newborn BP pair. The rate of additional BP production increases with the driving field increasing. For higher fields (see ESI† for B = 100 mT), the process of creation/annihilation of the BP pairs occurs continuously during the propagation of the BP-DW, and it takes place very close to the BP that is part of the DW, allowing the BP-DW to achieve a continuous displacement at high velocity and additional acceleration, comparatively to the B = 60 mT case, where the velocities boost are visible in the DW trajectory.
Finally, the acceleration of the BP, attached to the DW main cone, is due to the effect, similar to “jet propulsion”. Indeed, by breaking the cone, the cone size substantially decreases and the detached part, expelled in the opposite direction, accelerates the dynamics of the main cone. The energy dissipation due to the annihilation of detached Bloch points is visible as oscillations in Fig. 5, both in magnetostatic and in exchange energies. We have also analysed large-amplitude spinwaves on the nanowire surface in this regime (see ESI†). Their maximum amplitude occurs at the moment when the new-born Bloch points are annihilated. Their group velocity coincides with that of the Bloch point which is positioned slightly in front of the point of their maximum amplitude. Thus, in this regime the massive spinwave emission forms part of the same process of the energy release from the conical domain wall: first the cone breaks and creates two Bloch points, in the subsequent time moments they annihilate and create large-amplitude spinwaves.
We note here that the rigorous definition of the jet propulsion effect would require the proof of the linear momentum conservation. Unfortunately, the peculiarity of magnetic dynamics, the complexity of the 3D non-rigid domain wall and the presence of damping does not allow us to introduce this conservation law rigorously. However, as it is clearly seen in Fig. 6(a and b), the DW accelerates forward in the moment when it ejects backward new BPs, in a qualitative agreement with the “jet propulsion” effect. The underlying mechanism, in this case, is related more to the exchange interactions than the magnetostatic ones. Indeed, the magnetisation configuration around BP in the cone has an opposite chirality to the one around the newborns closest to it (see additional illustration in ESI†), and the exchange interaction produces a repulsion effect between the main DW and the new BP.
Discussion
Cylindrical geometry offers possibilities to achieve very high velocities of magnetic domain walls due to the absence of the Walker breakdown phenomenon. However, because of the possible dynamical instabilities of the BP-DWs and their transformation to other magnetization configurations, this possibility has been questioned.27 In our numerical modeling, we report very high velocity (up to 14 km s−1) of the BP-DW in cylindrical magnetic nanowires of high magnetization value, such as Fe. These velocities are much higher than the “magnonic limit”, estimated here as being close to 2 km s−1. We associate the velocity increase with the “jet propulsion” effect by a constant ejection of new BPs from the domain wall. The key to this effect is the cone shape of the DW due to different magnetization propagation speeds on the nanowire surface and in its center. Due to its magnetostatic origin, the effect is more significant in nanowires with high saturation magnetization. The internal instabilities break the cone and give birth to a pair of DWs that are ejected by the main DW. This creates a jet propulsion effect, accelerating the DW propagation along the nanowire axis. The emission of BPs from the main domain wall provides an efficient dissipation mechanism.Our findings raise again the question about the limits for the domain wall velocities in ferromagnets. In our view, the “relativistic limit” of the domain wall velocity related to the magnon extreme velocities is valid only for the case of (almost) rigid domain wall dynamics in the 1D case, while our case is very far from this. We demonstrated that the magnonic limit does not restrict the velocity for Bloch point domain wall in the ferromagnetic nanowires with essentially 3D magnetization configurations and that the energy dissipation in the form of Bloch points and repulsive interactions between them helps to overcome it to a very large extent. We stress again that the concepts of the Walker breakdown phenomenon and the “relativistic” magnonic limit are the results of the rigid 1D domain wall model. In this model, the energetic balance requires the input energy to be compensated by the dissipation and thus large DW velocity would require high dissipation rate. The situation changes when the DW constantly alters its shape and is moving in a turbulent regime emitting highly energetic objects since the complete energy balance would include now more complex interactions. Thus, real limitations of DW propagation speed are not known, especially when complex DW transformations and consequent energy transfer are expected.
Our results will be very important for developing devices based on three-dimensional magnetization textures since the magnetic nanowires will most probably be their parts. It is important that, in this case, there are only little limitations in terms of magnetic materials. For example, there is no need for materials having special crystallographic symmetry, antiferromagnetic coupling, Dzyaloshinskii–Moriya interaction, or large spin–orbit torque effects. It should be also highlighted that the propagation dynamics of a BP-DW driven by magnetic fields differ significantly from those driven by spin-polarized currents.28,32 In the latter case, the combined action of the spin-transfer torque and the Oersted field leads to a very different butterfly-like dynamical domain wall shape and the velocities are significantly lower. Additionally, the increment of the velocity is constrained by the domain wall widening at high current densities.
Our results can also find analogies in other area of research related to propagation of nonlinear waves. A relevant example beyond the field of nano-magnetism can be found in the plastic deformation of a crystalline structure where under low applied stress the mobility of the dislocation can be successfully explained by the linear elastic theory. However, under large excitation, the dislocation dynamics is able to enter into a super-sonic regime surpassing the sonic barrier. Several studies have demonstrated this effect in iron and bcc Tungsten screw dislocations.33,34 Interestingly, the underlying reason for this supersonic behavior lies in the generation of secondary kinks (topological defects) via the so-called mother–daughter nucleation with opposite Burgers vectors. We found this effect similar to what we report here for a BP-DW dynamics in a cylindrical ferromagnetic nanowire.
Methods
Simulations were performed using the GPU-accelerated micromagnetic solver MuMax3, which numerically integrates the Landau–Lifshitz–Gilbert equation of magnetization motion.35 We considered a single nanowire with three different radii Ri, each associated with different lengths Li, conserving approximately the wire aspect ratio L/R, that is: R1 = 20 nm, L1 = 1200 nm; R2 = 30 nm, L2 = 1500 nm and R3 = 40 nm, L3 = 2500 nm. These parameters were chosen to ensure the existence of BP-DW.20 We used the magnetic parameters of Fe, where the saturation magnetization is Ms = 1700 kA m−1, and the exchange stiffness is Aex = 21 pJ m−1. We also considered a polycrystalline system, so we disregarded the magnetocrystalline anisotropy. Discretization size was chosen at 1 × 1 × 1 nm3, which produces very little effect on DW dynamics (see ESI†). Unless specified, we used the damping parameter value α = 0.01. The system's initial state is a BP-DW positioned at one of the free ends of the nanowire (see Fig. 1a). This configuration is obtained by relaxing a forced head-to-head configuration. We have ensured that the chirality of the BP-DW is appropriate to favor its movement due to the direction of the applied magnetic field.18 To avoid the nucleation of other domain walls at the ends of the nanowire, we eliminated the surface magnetic charges at its ends. In this way, we imitated an infinitely long wire, which allows the BP-DW to move longitudinally along the nanowire axis.Author contributions
F. T., J. A. F.-R. and O. C.-F. conceived the project, F. T. performed micromagnetic modelling, K. G. performed spinwave calculations. All authors analysed the results and were involved in discussions and critical assessment. O. C.-F. coordinated the project. F. T. and O. C.-F. wrote the paper. All authors reviewed and contributed to the paper.Conflicts of interest
There are no conflicts to declare. The authors declare no competing financial interest.Acknowledgements
The authors acknowledge financial support by the grants PID2019-108075RB-C31 and PID2019-108075RB-C33 funded by Ministry of Science and Innovation of Spain MCIN/AEI/10.13039/501100011033. The work of F. T. was supported by ANID + Fondecyt de Postdoctorado, convocatoria 2022 + Folio 3220527. K. G. acknowledges support by IKERBASQUE (the Basque Foundation for Science). The work of K. G. was partially supported by the Norwegian Financial Mechanism 2014–2021 through the project UMO-2020/37/K/ST3/02450. J. A. Acknowledges the support of the Alexander von Humboldt Foundation. This research was partially supported by the supercomputing infrastructure of the NLHPC (ECM-02). Finally, the research was partially funded by project CIP2022035 of the Universidad Central de Chile.References
- S. Parkin, M. Hayashi and L. Thomas, Science, 2008, 320, 190 CrossRef CAS PubMed.
- O. Boulle, G. Malinowski and M. Klaui, Mater. Sci. Eng., R, 2011, 72, 159 CrossRef.
- Z. Luo, A. Hrabec, T. Dao, G. Sala, S. Finizio, J. Feng, S. Mayr, J. Raabe, P. Gambardella and L. Heyderman, Nature, 2020, 579, 214 CrossRef CAS PubMed.
- R. Ababei, M. Ellis, I. Vidamour, D. Devadasan, D.-A. Allwood, E. Vasilaki and T. Hayward, Sci. Rep., 2021, 11, 15587 CrossRef CAS PubMed.
- L. Caretta, S. Oh, T. Fakhrul, D.-K. Lee, B. Lee, C. Kim, S. K. Ross, K.-J. Lee and G. Beach, Science, 2020, 370, 1438 CrossRef CAS PubMed.
- N. Akhmediev and M. Karlsson, Phys. Rev. A, 1995, 51, 2602 CrossRef CAS PubMed.
- M. Yan, A. Kakay, C. Andreas and R. Hertel, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 88, 220412 CrossRef.
- N. L. Schryer and L. R. Walker, J. Appl. Phys., 1974, 45, 5406 CrossRef CAS.
- M. Hayashi, L. Thomas, C. Rettner, R. Moriya, Y. Bazaliy and S. Parkin, Phys. Rev. Lett., 2007, 98, 037204 CrossRef PubMed.
- S. Velez, J. Schaab, M. Wornle, M. Muller, E. Gradauskaite, P. Welter, C. Gutgsell, C. Nistor, C. Degen, M. Trassin, M. Fiebig and P. Gambardella, Nat. Commun., 2019, 10, 4750 CrossRef PubMed.
- K.-J. Kim, S. K. Kim, Y. Hirata, S.-H. Oh, T. Tono, D.-H. Kim, T. Okuno, S. Ham, S. Kim, G. Go, Y. Tserkovnyak, A. Tsukamoto, T. Moriyama, K.-J. Lee and T. Ono, Nat. Mater., 2017, 16, 1187 CrossRef CAS PubMed.
- T. Shiino, S.-H. Oh, P. M. Haney, S.-W. Lee, G. Go, B.-G. Park and K.-J. Lee, Phys. Rev. Lett., 2016, 117, 087203 CrossRef PubMed.
- R. M. Otxoa, U. Atxitia, P. E. Roy and O. Chubykalo-Fesenko, Commun. Phys., 2020, 3, 1–7 CrossRef.
- R. Otxoa, P. Roy, R. Rama-Eiroa, J. Godinho, K. Guslienko and J. Wunderlich, Commun. Phys., 2020, 3, 190 CrossRef CAS.
- O. Gomonay, T. Jungwirth and J. Sinova, Phys. Rev. Lett., 2016, 117, 017202 CrossRef CAS PubMed.
- H. Yang, H. Yuan, M. Yan, H. Zhang and P. Yan, Phys. Rev. B, 2019, 100, 024407 CrossRef CAS.
- A. Fernandez-Pacheco, R. Streubel, O. Fruchart, R. Hertel, P. Fischer and R. Cowburn, Nat. Commun., 2017, 8, 15756 CrossRef PubMed.
- R. Hertel, J. Phys.: Condens. Matter, 2016, 28, 483002 CrossRef CAS PubMed.
- S. Da Col, S. Jamet, N. Rougemaille, A. Locatelli, T. T. O. Mentes, B. Santos Burgos, R. Afid, M. Darques, L. Cagnon, J. Toussaint and O. Fruchart, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 180405(R) CrossRef.
- R. Moreno, V. Carvalho-Santos, D. Altbir and O. Chubykalo-Fesenko, J. Magn. Magn. Mater., 2022, 542, 168495 CrossRef CAS.
- F. Tejo, R. Hernandez Heredero, O. Chubykalo-Fesenko and K. Guslienko, Sci. Rep., 2021, 11, 21714 CrossRef CAS PubMed.
- C. Zambrano-Rabanal, B. Valderrama, F. Tejo, R. G. Elías, A. S. Nunez, V. L. Carvalho-Santos and N. Vidal-Silva, Sci. Rep., 2023, 13, 7171 CrossRef CAS PubMed.
- F. Tejo, C. Zambrano-Rabanal, V. Carvalho-Santos and N. Vidal-Silva, Appl. Phys. Lett., 2023, 123, 102405 CrossRef CAS.
- R. Wieser, U. Nowak and K. Usadel, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 69, 064401 CrossRef.
- X.-P. Ma, J. Zheng, H.-G. Piao, D.-H. Kim and P. Fischer, Appl. Phys. Lett., 2020, 117, 062402 CrossRef.
- R. Hertel and J. Kirschner, J. Magn. Magn. Mater., 2004, 278, L291 CrossRef CAS.
- A. Wartelle, B. Trapp, M. Stano, C. Thirion, S. Bochmann, J. Bachmann, M. Foerster, L. Aballe, T. Mentes, A. Locatelli, A. Sala, L. Cagnon, J.-C. Toussaint and O. Fruchart, Phys. Rev. B, 2019, 99, 024433 CrossRef CAS.
- J. Fernandez-Roldan and O. Chubykalo-Fesenko, APL Mater., 2022, 10, 111101 CrossRef CAS.
- A. Thiaville and Y. Nakatani, Domain-Wall Dynamics in Nanowires and Nanostrips, in Spin Dynamics in Confined Magnetic Structures III, 2006, vol. 101, p. 261 Search PubMed.
- K. Y. Guslienko, K.-S. Lee and S.-K. Kim, Phys. Rev. Lett., 2008, 100, 027203 CrossRef PubMed.
- K. Guslienko, Europhys. Lett., 2016, 113, 67002 CrossRef.
- M. M. Schobitz, A. De Riz, S. Martin, S. Bochmann, C. Thirion, J. Vogel, M. Foerster, L. Aballe, T. Menteş, A. Locatelli, F. Genuzio, S. Le-Denmat, L. Cagnon, J. Toussaint, D. Gusakova, J. Bachmann and O. Fruchart, Phys. Rev. Lett., 2019, 123, 217201 CrossRef CAS PubMed.
- A. N. Stroh, Stud. Appl. Math., 1962, 41, 77 Search PubMed.
- F. C. Frank and J. H. van der Merwe, Proc. R. Soc. London, Ser. A, 1949, 198, 205 CAS.
- A. Vansteenkiste, J. Leliaert, M. Dvornik, M. Helsen, F. Garcia-Sanchez and B. Van Waeyenberge, AIP Adv., 2014, 4, 107133 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05013k |
| This journal is © The Royal Society of Chemistry 2024 |