Coulomb interactions for mediator-enhanced sensitized triplet–triplet annihilation upconversion in solution

Abstract

Sensitized triplet–triplet annihilation upconversion offers an attractive possibility to replace a high-energy photon by two photons with lower energy through the combination of a light-harvesting triplet sensitizer and an annihilator for the formation of a fluorescent singlet state. Typically, high annihilator concentrations are required to achieve an efficient initial energy transfer and as a direct consequence the most highly energetic emission is often not detectable due to intrinsic reabsorption by the annihilator itself. Herein, we demonstrate that the addition of a charge-adapted mediator drastically improves the energy transfer efficiency at low annihilator concentrations via an energy transfer cascade. Inspired by molecular dyads and recent developments in nanocrystal-sensitized upconversion, our system exploits a concept to minimize intrinsic filter effects, while boosting the upconversion quantum yield in solution. A sensitizer-annihilator combination consisting of a ruthenium-based complex and 9,10-diphenylanthracene (DPA) is explored as model system and a sulfonated pyrene serves as mediator. The impact of opposite charges between sensitizer and mediator – to induce coulombic attraction and subsequently result in accelerated energy transfer rate constants – is analyzed in detail by different spectroscopic methods. Ion pairing and the resulting static energy transfer in both directions is a minor process, resulting in an improved overall performance. Finally, the more intense upconverted emission in the presence of the mediator is used to drive two catalytic photoreactions in a two-chamber setup, illustrating the advantages of our approach, in particular for photoreactions requiring oxygen that would interfere with the upconversion system.

---

Christoph Kerzig (photographer: Stefan F. Sämmer)

Christoph Kerzig studied chemistry at MLU Halle (Germany), where he obtained his PhD under the supervision of Martin Goez in 2017. He then joined the group of Oliver Wenger at the University of Basel with a Leopoldina postdoc fellowship. During his research stay in Basel, he was also a visiting scientist in Gothenburg, working on upconversion with Karl Börjesson. In 2020, Christoph joined JGU Mainz as a tenure-track Professor. His research focuses on mechanistic photochemistry, spectroscopy and photocatalysis. When not at work, he enjoys cycling (to get new scientific ideas, of course) and spending time with his family.

---

1. Introduction

Triplet–triplet annihilation upconversion is an interesting photophysical phenomenon capable of converting two low-energy photons into one high-energy photon, and this process has been explored towards applications in various fields.^1–10 For sensitized triplet–triplet annihilation upconversion (sTTA-UC) typically a light-harvesting unit (sensitizer) that introduces the possibility to populate a triplet state is combined with an annihilator, that is after energy transfer able to convert these two excited triplet states by triplet–triplet annihilation to one singlet state with higher energy.^11–14 In recent years, different systems were successfully designed to enhance the sTTA-UC efficiency by using a mediated energy transfer approach (Fig. 1a). The introduction of a preorganized organic chromophore as an energy transfer mediator can be regarded as key concept in these systems. This new component in the sTTA-UC system leads to a fast initial energy transfer step (TTET₁ in Fig. 1a), populating a long-lived triplet state of the mediator. As a consequence, decreased annihilator concentrations are usable and/or lower energy transfer rate constants are sufficient for obtaining similar or even enhanced upconversion quantum yields. This general concept was realized with nanocrystals,^15–20 quantum dots,^21–24 and molecular dyads^25–31 in solution. Additionally, similar sensitizer-mediator-annihilator combinations were explored in solid state perovskite solar cells.³² Focusing on the systems in solution, the main trick for the efficient population of the triplet-excited mediator seemingly relies on a permanent attachment of the mediator through a covalent bond or non-covalent interactions resulting in high binding constants. For metal complexes the guidelines to tune the excited states towards the desired properties are in principle known, however, especially the introduction of an additional chromophore typically requires a tailored ligand design and multi-step synthesis. A modular approach with commercially available components is therefore highly desirable. Very recently a three component upconversion system using singlet oxygen as mediator has been reported, but the design intrinsically limits its applicability to annihilators with very low triplet energies.³³ We were aiming to develop a mediator-supported concept in solution without the time-consuming synthesis of a permanently linked mediator (Fig. 1b). As a model system, a ruthenium-based sensitizer in combination with the popular annihilator 9,10-diphenylanthracene (DPA) was chosen.^34–37 The triplet energy of a suitable mediator has to be between those of the sensitizer and the annihilator. Inspired by the triplet reservoir effect with covalently attached pyrenes^{28,30,38–40} as well as studies on diffusion-controlled triplet energy transfer to pyrene derivatives in solution,^41–43 together with a ∼0.3 eV driving force for a triplet energy transfer from the pyrene to the anthracene triplet,⁴⁴ qualifies this basic structure as a potentially useful mediator (Fig. 1b). Kinetically, more efficient quenching can be achieved by (i) longer excited-state lifetimes of the sensitizers, (ii) higher concentrations of the quenchers and/or (iii) increased bimolecular quenching rate constants. In general, these parameters essentially depend on the local concentration of the annihilator in close proximity of the sensitizer. With a positively charged sensitizer and a negatively charged mediator, we anticipated a locally increased concentration of the mediator by coulombic interactions and consequently a more efficient energy transfer. Furthermore, we believe that this Coulomb approach has a less pronounced effect on the individual energy levels of the sensitizer and the mediator compared to the spacer-dependent effects observed with covalently linked bichromophores.^45–47 While ionic interactions were considered in (photo)catalysis^48–53 and self-assembled upconversion systems^54–56 previously, these interactions have not been exploited for mediated sTTA-UC systems in homogeneous solution.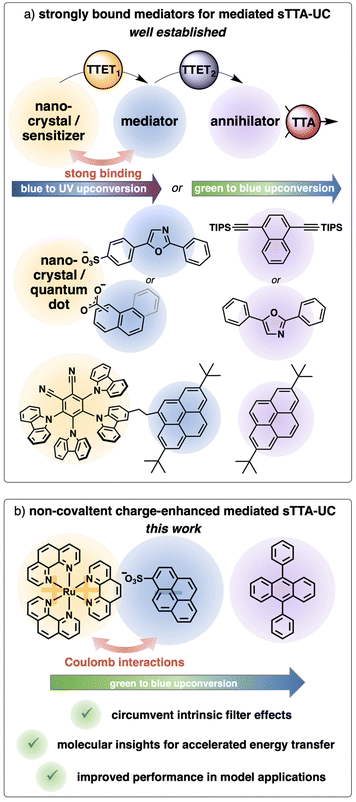

Fig. 1 (a) Different systems for sensitized triplet–triplet annihilation upconversion (sTTA-UC) with mediators that are strongly bound to the sensitizers.^15,17,18,25 (b) Our new system with Coulomb-enhanced mediated sTTA-UC.

Herein, we report the successful use of a sensitizer-mediator-annihilator combination exploiting coulombic interactions for an enhanced initial energy transfer to the mediator, resulting in a six-fold increase of the sTTA-UC quantum yield in a green-to-blue upconversion model system. The system allows minimizing intrinsic filter effects of the most highly energetic upconverted emission caused by the ground state absorption of the annihilator. This is particularly relevant for annihilators with very small Stokes shifts and high extinction coefficients,^34,57–60 which holds true for many annihilators especially in blue-to-UV upconversion systems, a field that has recently received increased attention.^5,26,61–64 Also in systems where the comparably short lifetimes of the sensitizers call for high concentrations of the annihilators, filter effects can significantly limit the output of high-energy photons.^21,65–70 These performance improvements are important for applications in which the upconversion system is used as light source to drive secondary reactions.^1,71–76 With our new approach using a commercially available charge-adapted mediator in solution, a modular exchange of the annihilator to other anthracene-based structures is possible with similar enhancements of the upconversion quantum yields induced by the mediator. Our new upconversion strategy is furthermore employed for proof-of-principle applications for the endoperoxide formation of anthracene and the oxidation of triphenylphosphine, highlighting the use of a two-chamber approach for the combination of an oxygen-sensitive sTTA-UC system and a photocatalytic system relying on dissolved oxygen.

2. Results and discussion

2.1. Concept and key ideas

Inspired by the textbook-like system consisting of a dicationic ruthenium-based sensitizer and an anthracene-based annihilator,³⁴ we started our investigations with DPA as annihilator and selected sodium pyrene-1-sulfonate (PMS) as mediator. Initial solubility tests indicated that N,N-dimethylformamide (DMF) is a suitable solvent to dissolve all components at reasonable concentrations. A general mechanistic scheme is presented in Fig. 2a. Excitation of the sensitizer and relaxation to the triplet state after intersystem crossing (³*[Ru^II] in Fig. 2a) is followed by a first energy transfer (TTET) to PMS (step 1) to populate the triplet state of PMS (³*PMS). In a second TTET, the annihilator quenches ³*PMS to generate ³*DPA (step 2) and by the encounter of two excited triplet DPA molecules, triplet–triplet annihilation (step 3) can result in the generation of ¹*DPA producing upconverted blue emission. Initial screening experiments indicated that [Ru(phen)₃]²⁺ is better suited than the widely used [Ru(bpy)₃]²⁺ as sensitizer for the sTTA-UC system under study (data not shown). This is most likely due to the slightly higher triplet energy of the former metal complex (by ∼0.1 eV).⁷⁷ Hence, the detailed study was performed with [Ru(phen)₃]²⁺.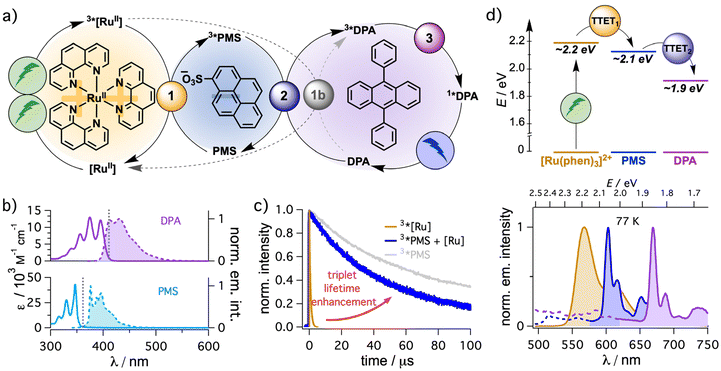

Fig. 2 (a) Concept for sensitized triplet–triplet annihilation upconversion using an energy mediator with [Ru(phen)₃]²⁺ as sensitizer, pyrene-1-sulfonate (PMS) as energy mediator and 9,10-diphenylanthracene (DPA) as annihilator. The key elementary reaction steps including (1) triplet–triplet energy transfer (TTET) from the sensitizer to the mediator, (2) TTET from the mediator to the annihilator and (3) triplet–triplet annihilation (TTA) are distinguished with differently colored cycles. The alternative direct triplet–triplet energy transfer from [Ru(phen)₃]²⁺ to DPA is included in gray as step 1b. (b) UV-vis and emission spectra of DPA and PMS. Vertical dotted lines indicate the maximum wavelengths at which filter effects are less pronounced because the extinction coefficients for re-absorption are below 1000 M⁻¹ cm⁻¹. (c) Lifetime of ³*[Ru(phen)₃]²⁺ (50 μM) in the absence (orange trace) of PMS and of ³*PMS after TTET from ³*[Ru(phen)₃]²⁺ (2.5 mM PMS, kinetic transient absorption detection at 525 nm, blue trace) upon excitation at 532 nm. The triplet decay of PMS (50 μM) in the absence of the sensitizer is provided in pale gray (excitation at 355 nm, kinetic transient absorption detection at 425 nm, a similar initial ³*PMS concentration to that after sensitization was obtained). (d) Energy transfer cascade (top) and corresponding triplet emission spectra at 77 K in 4 : 1 ethanol-methanol solvent mixtures (bottom). Further details are provided in section 4.1.1 of the ESI.†

In general, there are several prerequisites for the mediator to be useful for the performance enhancement of sTTA-UC systems. First, both energy transfer steps need a slightly exergonic driving force enabling fast bimolecular energy transfer quenching constants (∼10⁸–10¹⁰ M⁻¹ s⁻¹) and consequently high TTET efficiencies at millimolar or even micromolar concentrations of energy acceptors, while ensuring minimal energy loss. Hence, the mediator ideally has a triplet energy in-between the triplet energy of the sensitizer and the annihilator for an energy transfer cascade. Indeed, triplet energy estimations from 77 K emission measurements in frozen ethanol-methanol (4 : 1) matrix clearly show an energetically downhill process from [Ru(phen)₃]²⁺ (∼2.2 eV) to PMS (∼2.1 eV) and finally the anthracene-based annihilator. Due to the absence of any phosphorescence of DPA under these conditions, its triplet energy was estimated from the phosphorescence of unsubstituted anthracene in frozen matrix (∼1.9 eV). The estimated triplet energy is reasonably close to the literature value for DPA (∼1.8 eV)⁴⁴ and it is clearly suitable for the intended energy transfer cascade (Fig. 2d). Second, the excited state lifetime of the mediator should be significantly longer compared to that of the sensitizer, ensuring high TTET efficiencies at lower annihilator concentrations. Organic chromophores lacking heavy atoms are typically explored as mediators (see Fig. 1) due to their triplet state lifetimes in the microsecond or even millisecond time range.⁴⁴ In our case, the unquenched triplet lifetime of the organic mediator (∼476 μs, ESI section 4.41†) is almost three orders of magnitude longer than that of [Ru(phen)₃]²⁺ (728 ns, Fig. 2, ocher trace). At higher triplet concentrations the observed ³*PMS lifetime upon direct excitation is on the order of ∼90 μs (gray trace in Fig. 2c) and also a sensitized population of ³*PMS results in a significantly prolonged lifetime (∼55 μs, blue trace in Fig. 2c). Analyzing the quenching efficiencies (η = 1 − (1 + τ₀·k_Q·[Q])⁻¹), the second TTET step from the mediator to the annihilator (step 2 in Fig. 2a) is expected to require significantly reduced concentrations of DPA to reach the same quenching efficiency η compared to a direct quenching of the sensitizer (step 1b) assuming the same rate constant k_Q.⁷⁸ As discussed in the next section in more detail, the thoughtful choice of the mediator even allows an enhanced energy transfer quenching rate constant k_TTET from ³*[Ru(phen)₃]²⁺ to the anionic mediator PMS compared to the neutral annihilator DPA. Overall, this offers the possibility to use very small concentrations of the annihilator (∼100 μM, see below). In fact, the small Stokes shift of DPA makes the annihilator concentration crucial to prevent the reabsorption of the high-energy photons in the emission spectrum (section 4.4.5 in the ESI†). With lowered concentrations the intrinsic inner filter effect of the annihilator is prevented or significantly minimized (Fig. 2b), which is highly beneficial when the UC emission is used as light source for the excitation of a secondary absorber such as a photocatalyst. Third and related to that point, the mediator should not absorb the upconverted light. Indeed, the combination of pyrene derivatives as mediators with anthracene-based annihilators is extremely promising in this regard as even at high mediator concentrations the filter effects caused by the mediator for the upconverted emission are negligibly small (Fig. 2b). PMS is therefore well suited for a closer analysis as mediator to enhance sTTA-UC with [Ru(phen)₃]²⁺ as sensitizer and DPA as annihilator.

2.2. Mediated triplet–triplet energy transfer

As explained in the preceding section, the usage of the mediator should enhance the overall energy transfer efficiency from ³*[Ru(phen)₃]²⁺ to ³*DPA. This approach holds great promise for DPA as it is clearly among the most efficient annihilators regarding achievable efficiencies,^57,79–82 but its poor solubility in most solvents does not allow quantitative energy transfer in several conventional (i.e. non-mediated) UC systems.^{34,65,69,75,83} To demonstrate the feasibility of our key idea, we investigated our system by transient absorption spectroscopy to gain insights into the formation of the annihilator triplet state (Fig. 3). [Ru(phen)₃]²⁺ (50 μM) in the presence of 100 μM DPA was excited with a 532 nm laser pulse. Right after the laser pulse the characteristic ground-state bleach corresponding to [Ru(phen)₃]²⁺ is visible (negative signals around 450 nm in gray spectra in Fig. 3a).³⁸ Over time a weak positive transient absorption band with an absorption maximum at 445 nm is observable (e.g. red spectrum in Fig. 3a), and this species can be assigned to ³*DPA based on several studies in the literature.^44,82,84 In line with a long-lived triplet excited state, this absorption feature decays over several hundreds of microseconds (Fig. 3a/c). Performing the same measurements with additionally added PMS (500 μM), the initial ground state bleach of [Ru(phen)₃]²⁺ is still present (Fig. 3b), but shortly after the laser pulse new transient absorption signals with maxima at 425 nm and around 525 nm are formed. This clearly provides evidence for the formation of ³*PMS as transient intermediate after (predominantly dynamic) triplet energy transfer from the sensitizer (TTET₁).⁸⁵ On a timescale of a few microseconds the signals from ³*PMS disappear again while the characteristic absorption band from ³*DPA starts to increase. After a post-pulse delay of about 10 μs the ³*DPA signals are essentially the only remaining characteristics in the TA spectrum (purple spectrum in Fig. 3b). These observations are in perfect agreement with the expectation for a stepwise energy transfer from the ruthenium-based sensitizer to DPA via the formation of ³*PMS as intermediate. Importantly, the ³*DPA signal intensity is higher by almost one order of magnitude in the presence of PMS as mediator in comparison to the measurement without mediator under otherwise identical conditions. This is also confirmed by kinetic measurements at the TA maximum of ³*DPA (445 nm), where the trace in the presence of PMS shows a much higher intensity (compare purple and red trace in Fig. 3c). In fact, due to the spectral overlap between ³*PMS and ³*DPA around 445 nm the kinetic trace with mediator present has a more rapid initial change followed by a slower growing of the signal intensity and therefore this dataset also points towards a stepwise energy transfer cascade (further information in section 4.2.6 of the ESI†). Hence, the results of this section clearly demonstrate that the additional mediator can strongly enhance the population of the desired annihilator triplet state in solution, eventually leading to a superincrease of the UC performance at low annihilator concentrations and negligible filter effects accordingly.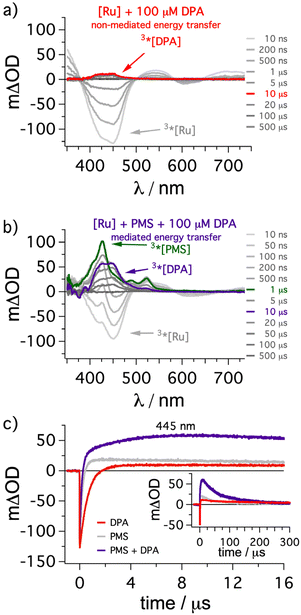

Fig. 3 Transient absorption measurements of the conventional or mediated formation of ³*DPA via sensitization. (a) [Ru(phen)₃](PF₆)₂ (50 μM) in de-aerated dimethylformamide was excited with a constant laser pulse energy (∼30 mJ) at 532 nm in the presence of DPA (100 μM) and transient absorption (TA) spectra were measured with different time delays after the laser pulse. (b) TA measurements with additionally added PMS (500 μM) as energy transfer mediator under otherwise identical conditions. All spectra were time-integrated for 50 ns and the specific delay times are indicated in the figure. The traces detected 10 μs after the laser pulse are highlighted in red (non-mediated energy transfer) and purple (mediated energy transfer). The TA spectrum with the highest ³*PMS concentration is highlighted in green. (c) Kinetic traces at 445 nm on short (main plot) and long (inset) timescales for the abovementioned solutions together with a reference containing [Ru(phen)₃](PF₆)₂ (50 μM) and PMS (500 μM) in the absence of DPA (shown in gray). Further details are discussed in the ESI in section 4.2.6.†

The determined bimolecular rate constants for the main steps in the mechanism under investigation (Fig. 2a) are summarized in Table 1 and the corresponding measurements are discussed in the following section.

Table 1 Rate constants (k) for different sensitizers and quenchers as well as reference measurements for the individual elementary processes illustrated in Fig. 2. All values for de-aerated DMF at 20 °C

Step no.	Description of step	k /M^−1 s^−1
a Time-resolved measurements. Steady state data (Table S3†) and further details are given in section 4.2 of the ESI.† b Pyrene serves as uncharged reference compound of the mediator.
1	TTET from ^3*[Ru(phen)3]^2+ to PMS	9.1 × 10^9
1 with Py^b	TTET from ^3* [Ru(phen)3]^2+ to Py	1.4 × 10^9
2	TTET from ^3*PMS to DPA	2.4 × 10^9
1b	TTET from ^3*[Ru(phen)3]^2+ to DPA	2.0 × 10^9
3	TTA-UC of DPA	2.4 × 10^9

---

2.3. Coulomb interactions for accelerated triplet–triplet energy transfer

After providing spectroscopic evidence that the mediator can increase the concentration of ³*DPA in solution, we investigated the different elementary steps in more detail. A Stern–Volmer study analyzing the energy transfer step from [Ru(phen)₃]²⁺ to PMS (step 1 in Fig. 2a) and DPA (step 1b in Fig. 2a) by time-resolved emission quenching gave bimolecular energy transfer rate constants of 9.1 × 10⁹ M⁻¹ s⁻¹ and 2.0 × 10⁹ M⁻¹ s⁻¹, respectively (Table 1). The quenching rate constant with the mediator is even slightly higher than the tabulated diffusion limit in DMF (7.6 × 10⁹ M⁻¹ s⁻¹),⁴⁴ which is calculated for uncharged reaction partners with identical molecular radii.⁸⁶ Interestingly, the apparent rate constant with PMS measured by steady-state emission spectroscopy was significantly smaller (6.1 × 10⁹ M⁻¹ s⁻¹, ESI section 4.2.3†) than the value determined by time-resolved spectroscopy, while there is essentially no difference for DPA when comparing Stern–Volmer data sets based on steady-state and time-resolved measurements. The triplet energy difference between the sensitizer [Ru(phen)₃]²⁺ (∼2.2 eV, Fig. 2) and PMS (∼2.1 eV) is sufficiently small for a thermal repopulation of ³*[Ru(phen)₃]²⁺via back energy transfer and consequently there is an excited-state equilibrium between the sensitizer and the mediator. As additional support for this interpretation, the sensitized triplet state lifetime of PMS is slightly diminished compared to the value determined by direct excitation and intersystem crossing (Fig. 2c). Delayed emission of ³*[Ru(phen)₃]²⁺ is detectable by time-resolved spectroscopy at longer delay times, which is in line with this observation (ESI, section 4.2.5†). Interestingly, this closely resembles the properties of molecular dyads with (covalently) permanently linked chromophores, but without the need to synthesize the tailor-made bichromophores (Fig. 1).^25–28 The rate constant for back energy transfer is estimated to amount to ∼4 × 10⁸ M⁻¹ s⁻¹ (section 4.2.5 in the ESI†), which is slower than the forward energy transfer by more than one order of magnitude. The lifetime of ³*PMS obtained via TTET is on the order of 50 μs under our typical conditions. This is longer than what is typically observed for most ruthenium complex–pyrene dyads.^{29,38,39,87–90} We regard the absence of efficient ion-pairing (see below) and the possibility to use PMS in large excess over [Ru(phen)₃]²⁺ as the main reasons for these favorable properties of our mediator system. In the presence of the annihilator, the equilibrium in our dyad-like combination is disturbed. Hence, even with similar concentrations of sensitizer and mediator, the energy transfer to the annihilator is highly favored. This is also confirmed by a Stern–Volmer analysis for the triplet–triplet energy transfer step from ³*[Ru(phen)₃]²⁺ to PMS in the presence of DPA, where the rate constants from steady-state measurements and time-resolved measurements are more similar than in the absence of DPA (ESI section 4.2.7†).

As indicated above, we expected that the negatively charged PMS as mediator might permit beneficial coulombic effects on the energy transfer step from the dicationic sensitizer. Hence, unsubstituted pyrene (Py) was chosen as uncharged reference energy acceptor to gain further insights into the role of ionic interactions. The rate constant determined with Py amounts to 1.4 × 10⁹ M⁻¹ s⁻¹ (section 4.2.8 in the ESI†) and therefore this TTET is almost one order of magnitude slower than observed for the sulfonated pyrene analogue PMS. The triplet energy difference between [Ru(phen)₃]²⁺ and PMS is relatively small and in principle the observed effect on the TTET kinetics might also be caused small changes in the energy transfer driving force. However, the triplet energy of pyrene (2.1 eV)⁴⁴ is expected to be very similar to PMS. Hence, it seems natural to assume that the TTET rate constant enhancement is mainly caused by the introduction of the charged sulfonate group, resulting in coulombic attraction and faster diffusion.⁹¹ To obtain a better understanding of the interplay between sensitizer and mediator, different spectroscopic techniques were used. In principle, an association through ion pairing between the charged compounds eventually leading to static quenching contributions could be present in solution.^92,93 An NMR titration of PMS to [Ru(phen)₃]²⁺ in DMF-d₇ was performed, the data were analyzed by the Benesi–Hildebrand method^94–96 and an association constant K_A of 30 (±2) M⁻¹ was estimated for the aggregation between [Ru(phen)₃]²⁺ and PMS (Fig. 4a) with a 1 : 1 stoichiometry (ESI, section 4.5.1†). Similar experiments in DMSO-d₆ gave an almost identical association constant (∼35 (± 4) M⁻¹, see ESI section 4.5.1†). Re-evaluating the time-resolved Stern–Volmer data (blue traces in Fig. 4b) revealed that also small contributions from static quenching are determined (details in section 4.5.2 of the ESI†) and a slightly higher (but still low) association constant is estimated. Evidently, TTET through static quenching is in all investigated cases a minor contribution; with 2.5 mM PMS as used in the upconversion experiments, the static contribution can be calculated as follows, using the association constant obtained from NMR measurements: η = 1 − (1 + K_A·[Q])⁻¹ = 1 − (1 + 30 M⁻¹ × 2.5 mM)⁻¹ ≈ 7%.⁸⁶ To obtain further evidence for Coulomb-enhanced energy transfer rates, the influence of ammonium hexafluorophosphate as additional salt to increase the ionic strength in solution was investigated. The bimolecular rate constant for the excited state quenching of ³*[Ru(phen)₃]²⁺ with PMS was determined with an excess of external salt (20 mM) in solution (Fig. 4b). The energy transfer rate constant is significantly smaller with a higher ionic strength. In fact, the value of 2.6 × 10⁹ M⁻¹ s⁻¹ is much closer to the rate constant for unsubstituted pyrene (1.4 × 10⁹ M⁻¹ s⁻¹) than to the value determined for PMS in neat DMF (9.1 × 10⁹ M⁻¹ s⁻¹). This pronounced kinetic salt effect decelerating the diffusion between the oppositely charged reaction partners is in perfect agreement with our hypothesis of coulombic interactions between sensitizer and mediator. Control experiments with pyrene and DPA acting as quenchers in the presence of the salt indicated only minor effects caused by changing the ionic strength (Table 2). The absorption band shape in UV-vis and transient absorption spectra of PMS and [Ru(phen)₃]²⁺ are completely unaffected by salt addition, pointing towards an influence of the charge and not a change of the energy levels. Additional quenching experiments with PMS using mono-cationic and neutral iridium complexes as sensitizers result in quenching constants of 5.7 × 10⁹ M⁻¹ s⁻¹ and 2.5 × 10⁹ M⁻¹ s⁻¹ respectively (Table 2). Taking into account the increased driving force for energy transfer to PMS with these two complexes, an effect caused by TTET driving force changes is unlikely, while a pronounced effect of the overall charge of the complex for coulombic interactions with the anionic mediator is in line with this observation. All these experiments strongly support our hypothesis that coulombic interactions enhance the first energy transfer step from the ruthenium-based sensitizer to the charged mediator.

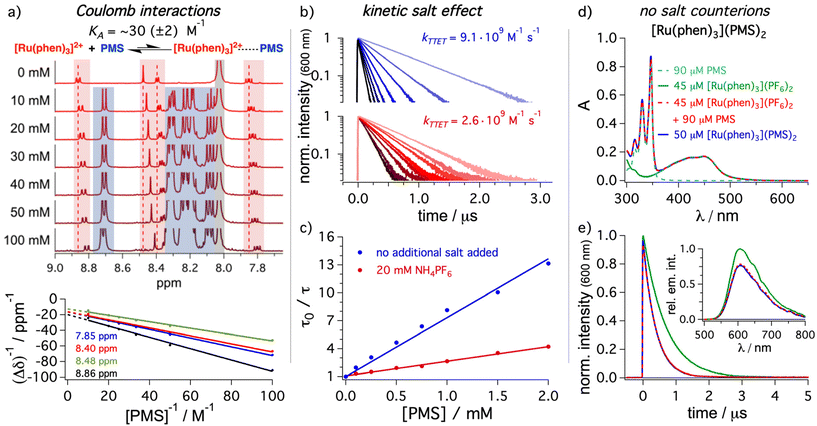Fig. 4 Investigations of the molecular interactions between [Ru(phen)₃]²⁺ and PMS by different spectroscopic techniques. (a) ¹H NMR titration of different concentrations of PMS to a solution of [Ru(phen)₃](PF₆)₂ (500 μM) in DMF-d₇ and the corresponding Benesi–Hildebrand plot (bottom) following the signals of [Ru(phen)₃]²⁺ at different chemical shifts δ. A singlet corresponding to non-deuterated solvent traces at 8.03 ppm is marked in gray. Kinetic emission traces (b) and Stern–Volmer analysis (c) of [Ru(phen)₃]²⁺ (50 μM) were analyzed with PMS as quencher at different concentrations. Measurements were performed in the absence (blue traces) and presence of 20 mM ammonium hexafluorophosphate (NH₄PF₆). Comparison of the UV-vis absorption (d) as well as time-resolved (e) and steady-state emission spectra (inset) of the synthesized salt dyad [Ru(phen)₃](PMS)₂ with the results obtained for the mixture of commercially available salts with photochemically inactive counterions and [Ru(phen)₃](PF₆)₂ alone in de-aerated DMF. Color code and concentrations are given in the figure and the overlapping traces are presented as dotted lines. Further details are provided in the ESI in section 4.2.14 and 4.5.1.†

Table 2 Rate constants (k) with different sensitizers or salt additives. All values for de-aerated DMF at 20 °C

Sensitizer^a	E T/eV	k TTET/M^−1 s^−1 PMS	k TTET/M^−1 s^−1 pyrene	k TTET/M^−1 s^−1 DPA
a Hexafluorophosphate counter anions are present for cationic complexes. b The concentration of ammonium hexafluorophosphate (NH4PF6) is 20 mM. Further details are given in section 4.2.9 and 4.2.14 of the ESI.†
[Ru(phen)3]^2+	2.2	9.1 × 10^9	1.4 × 10^9	2.0 × 10^9
[Ru(phen)3]^2+ + NH4PF6 ^b	2.2	2.6 × 10^9	1.6 × 10^9	1.4 × 10^9
[Ir(dFppyCF3)2(bpy)]^+	2.7^97	5.7 × 10^9	3.4 × 10^9	—
fac-[Ir(ppy)3]	2.5^78,98	2.5 × 10^9	3.5 × 10^9	—

---

Looking on the nanoscale and taking the abovementioned results into account, the combination of cationic sensitizer and anionic mediator in principle allows the direct synthesis of a salt with 1 : 2 stoichiometry, [Ru(phen)₃](PMS)₂. This strategy avoids the presence of additional non-chromophoric counterions that could potentially influence the coulombic interactions and change the bimolecular quenching rate constant. Hence, the direct sensitizer-mediator salt was synthesized and spectroscopically characterized (section 3.1.1 in ESI†). The expected ratio between sensitizer and mediator was confirmed by ¹H NMR. Furthermore, the UV-vis absorption is essentially a superposition of one [Ru(phen)₃]²⁺ and two PMS units (Fig. 4d), although the extinction coefficient is slightly below that of the expected value. We attribute this to remaining crystal water in the new sensitizer–mediator salt. Recording the steady-state emission spectra and the time-resolved emission lifetimes for both the synthesized [Ru(phen)₃](PMS)₂ and a freshly prepared solution with the commercial salts possessing identical ground-state absorption properties (as the [Ru(phen)₃](PMS)₂ solution) results in essentially two identical datasets (Fig. 4d and e). The low concentrations of the non-chromophoric counterions obviously do not cause detrimental kinetic salt effects. Hence, it is not necessary to synthesize sensitizer–mediator salts and a direct combination of the commercially available compounds is similarly well suited for exploiting our new approach.

Next, the energy transfer from of the dark triplet state ³*PMS to DPA was analyzed by transient absorption spectroscopy. In a Stern–Vomer-type analysis, a bimolecular rate constant of 2.4 × 10⁹ M⁻¹ s⁻¹ was found and, together with the long excited-state lifetime of the mediator under the conditions suitable for upconversion (≥50 μs), quenching efficiencies above 90% are achievable with DPA concentrations as low as 100 μM. Also, the rate constant for triplet–triplet annihilation for DPA was determined by a power-dependent triplet state decay analysis under our conditions (section 4.4.1 in ESI† for details), resulting in a value of 2.4 × 10⁹ M⁻¹ s⁻¹ (Table 2). This is reasonably close to the k_TTA values obtained for DPA in other solvents.^79,99,100 The detailed kinetic insights from this section will allow us to select meaningful conditions for photon upconversion experiments.

2.4. Triplet–triplet annihilation upconversion

As our study is especially focused on minimizing filter effects (ESI, section 4.4.5†), especially the concentration of DPA is important to prevent intrinsic reabsorption. Initial screening experiments for the mediated UC system revealed a reasonably good correlation between the predicted energy transfer efficiencies based on the rate constants determined above and the measured upconverted emission intensity upon variation of the mediator or annihilator concentration (details in ESI section 4.4.2†). To study the influence of the mediator in detail a PMS concentration of 2.5 mM and a DPA concentration of 100 μM was chosen. This PMS concentration permits not only highly efficient (94%) initial quenching but it also shifts the excited-state equilibrium between ³*[Ru(phen)₃]²⁺ and ³*PMS towards the latter. UC experiments without DPA revealed that ³*PMS undergoes annihilation with mixed monomer and excimer emission, which is why PMS itself can be regarded as poor annihilator while being an excellent mediator in our system. Interestingly, PMS excimer emission does not occur in the prompt emission spectrum upon direct excitation ruling out (i) pre-aggregation effects of ground-state PMS molecules and (ii) a diffusion-mediated mechanisms between singlet-excited PMS and PMS in its ground state at our selected concentration (see section 4.2.5 of the ESI† and corresponding text for details). However, the PMS excimer can also be observed in the delayed emission spectrum even in the absence of [Ru(phen)₃]²⁺, indicating that the special geometry of the triplet pair is (partially) responsible for the observed excimer formation.¹⁰¹ In any case, excimer formation is rather inefficient and it is regarded to be unimportant in the presence of DPA under our conditions used for upconversion (the triplet population is almost completely DPA-localized).

Under the standardized conditions mentioned above, the threshold intensity and upconversion quantum yields as two main figures of merit for upconversion systems were investigated (Fig. 5). The threshold intensity I_th for a DMF solution containing 50 μM [Ru(phen)₃]²⁺ was measured with a 514 nm continuous-wave (cw) laser by a variation of the laser power and a value of ∼60 mW cm⁻² resulted after converting the total laser output to power densities (see Fig. 5 and ESI† for details). This value compares favorably with many other upconversion systems,⁵ and is quite close to current state-of-the art reports.^82,102–106 Especially the long-lived triplet state introduced by the mediator plays a crucial role here.^13,14,26,82 The relative emission quantum yield Φ_em of ∼6.8(±0.1)% for ³*[Ru(phen)₃]²⁺ in de-aerated DMF determined with our steady-state setup is very close to the literature value of 6.3% in the same solvent.⁴⁴ Therefore, all upconversion quantum yields were measured against the unquenched [Ru(phen)₃]²⁺ phosphorescence in de-aerated DMF with the same absorbance at the excitation wavelength of the cw laser as used for the upconversion sample. A standardized laser intensity (30 mW, 1 W cm⁻²) in the linear region of the upconversion system was selected. The upconversion quantum yield of a solution with sensitizer, mediator and annihilator under these conditions is 3.2(±0.15)% based on a theoretical maximum of 50% (Fig. 5c) and this value is more than six times higher than obtained in the absence of the mediator (0.5(±0.03)%, Fig. 5d). In fact, the increase in the upconversion quantum yield by a factor of ∼6.4 strongly resembles the expected value based on the relative quenching efficiencies in the presence and absence of mediator (∼6.9, details in the ESI section 4.4.3†). Taking the laser wavelength and the global maximum of the UC emission, a moderate anti-Stokes shift of ∼0.6 eV with mediator in solution can be calculated, but with more sophisticated systems using a mediator concept we expect that this could also help to improve this property due to the detection of the most highly energetic emission. A reference system with 5 mM of DPA in the absence of PMS – where according to the different quenching constants a similar ³*DPA concentration is reached – clearly demonstrates the filter effects caused by the intense ground state absorption of DPA. Consequently, the detected emission quantum yield is with ∼2.4(±0.1)% about one third smaller than the value for the mediated upconversion system (Fig. 5d). Notably, the high-energy vibrational emission band is not even resolved anymore and overall, the emission maximum is red-shifted by 19 nm, which corresponds to ∼0.14 eV in that spectral region. These results clearly demonstrate that the introduction of a mediator can almost completely prevent filter effects caused by the annihilator and drastically increase the number of emitted photons. While the usefulness of the mediator approach has been demonstrated clearly, all upconversion quantum yields for the [Ru(phen)₃]²⁺—DPA pair presented in our paper are significantly lower than what can be achieved with highly optimized sensitizer—DPA couples. This is a result of efficient optical losses in our system, because the sensitizer absorption maximum is very close to the emission maximum of the annihilator.¹¹

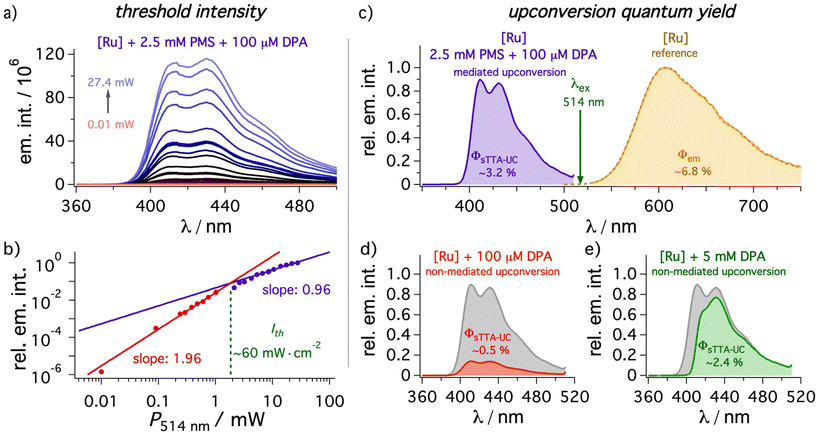Fig. 5 Upconverted emission with different conditions sensitized by [Ru(phen)₃]²⁺ ([Ru], 50 μM) in de-aerated DMF at 20 °C. Excitation occurred with a 514 nm cw laser in all cases. (a and b) The power dependence at various excitation conditions in the presence of PMS (2.5 mM) and DPA (100 μM). With a beam size of 3 mm² a threshold intensity of ∼60 mW cm⁻² is calculated. (c–e) Upconversion quantum yields Φ_sTTA-UC with DPA (100 μM) in the (c) presence and (d) absence of PMS (2.5 mM) determined relative to the unquenched [Ru(phen)₃]²⁺ emission (ocher spectrum, Φ_em = ∼6.8(±0.1)%). (e) Additional measurement with high concentrations of DPA (5 mM) in the absence of mediator. The gray spectra in (d) and (e) are reference spectra for the mediated system taken from (c). All quantum yields were measured in triplicate with a constant laser intensity in the linear regime (30 mW, corresponding to 1 W cm⁻²). Further details are given in section 4.4 of the ESI.†

As expected from the reasonably low threshold intensity, also LEDs as light sources instead of cw laser setups are in principle usable to achieve upconverted emission from DPA. Indeed, the measured threshold intensity (∼40 mW cm⁻²) and upconversion quantum yield of ∼1.6(±0.05)% is in line with the expectation based on the maximum output of the LED light source and the modified measurement setup (details in section 2 of the ESI†). Interestingly, the inner filter effects are more pronounced with an LED as light source. We observed an emission intensity increase by more than one order of magnitude caused by the mediator, and also for the reference system with 5 mM DPA, an upconversion quantum yield as low as ∼0.5(±0.03)% was detected. The significant differences between laser and LED measurements are attributed to the illumination of the full cuvette with the LED: the average reabsorption path length is longer compared to the laser experiments, in which the irradiation volume close to the detector is illuminated. Taking into consideration the strongly distance-dependent power density of the used LED, a small distance between the light source and the cuvette would be required, but this is challenging for our experimental setup used for UC-driven photoreactions (see below). Hence, we decided to employ the green cw laser as light source for investigating different applications in an overall standardized fashion.

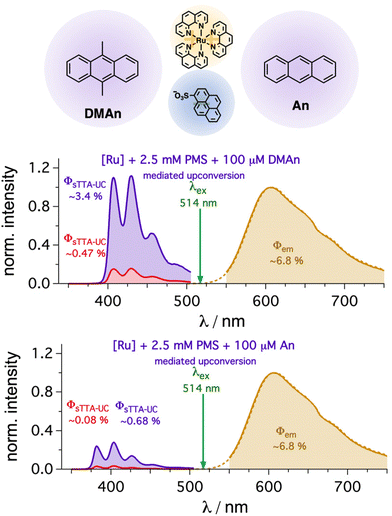
Owing to the introduction of a mediator with a long-lived triplet state, the influence of the second energy transfer rate constant is expected to be smaller for the overall efficiency compared to the direct quenching of sensitizers with sub-microsecond excited state lifetimes. Hence, this concept offers the opportunity exchange the annihilator in a straightforward manner with other annihilators having similar or lower triplet energies. Indeed, anthracene-based annihilators such as 9,10-dimethylanthracene (DMAn) or unsubstituted anthracene (An) instead of DPA were successfully investigated for mediated sTTA-UC. While the upconversion quantum yield with 100 μM of DMAn (∼3.4(±0.003)%, Fig. 6) is very similar to the value with DPA (∼3.2(±0.15)%), the detected emission with An is significantly smaller (∼0.68(±0.02)%, Fig. 6). This can be clearly attributed to the lower fluorescence quantum yield of anthracene (0.27 in ethanol)⁴⁴ compared to the values near unity for the other anthracene-based annihilator structures (section 4.1.1 in the ESI†). Correcting this emission quantum yield difference and assuming an identical spin-statistical factor for simplicity,^79,107,108 we estimated very similar quantum yields (∼2.9%) for the generated singlet states. Furthermore, the roughly six-fold emission enhancement in the presence compared to the absence of the PMS mediator is very similar with all three annihilator structures (Fig. 6). These measurements clearly show how versatile our system is and that this mediator-enhanced upconversion might help to use different annihilator structures in a more straightforward design, e.g., to pave the wave for using hardly soluble annihilator structures or for expensive annihilators with tailored redox properties.⁶⁵

Fig. 6 Sensitized upconversion with different anthracene-based annihilator structures. [Ru(phen)₃]²⁺ (50 μM) in DMF was excited at 514 nm with a cw laser (30 mW, 1 W cm⁻²) in the presence of PMS (2.5 mM) and different annihilators (100 μM). Upconversion quantum yields Φ_sTTA-UC in the absence (red) and the presence (purple) of the mediator were measured using the unquenched emission of [Ru(phen)₃]²⁺ as reference (ocher spectrum, Φ_em = ∼6.8(±0.1)%). All quantum yields were measured in triplicate.

2.5. Application of mediated sTTA-UC system for photo(redox) catalysis

In recent years, triplet–triplet annihilation has received some attention in light-driven photoredox catalysis.^{1,61,65,71,72,109–113,114,115} To demonstrate the practical usability of our upconversion system and to compare the performance with and without mediator, a setup consisting of two chambers was chosen.^75,116,117 A schematic presentation of the irradiation setup is provided in Fig. 7b. The spatial separation with two chambers allows the use of different solvents or the addition of reagents that would interfere with the upconversion system. We selected two photoreactions from the literature that are known to be fast. This ensures that our UC systems are sufficiently stable during photoirradiation (stability measurements can be found in section 4.4.4 of the ESI†), allowing us to exclude pronounced contributions of decomposition effects in the analysis. Both investigated reactions rely on molecular oxygen as reagent for a substrate activation by energy or electron transfer in the reaction mixture. Molecular oxygen strongly interferes with sTTA-UC systems and special reaction conditions and sophisticated concepts are needed to allow the coexistence of both in the same reaction flask.^{33,61,114,118–122} The physical separation introduces an additional approach that permits the possibility of an individual optimization of the upconversion system and the photocatalytic mixture. The first investigated reaction is the light-driven oxygenation of triphenylphosphine with 9,10-dicyanoanthracene as photocatalyst and naphthalene as redox mediator (Fig. 7a).^123–125 Our UC system serves as light source for photocatalyst excitation. The irradiation of a stirred upconversion solution with [Ru(phen)₃]²⁺ (50 μM), PMS (2.5 mM) and DPA (100 μM) in de-aerated DMF for 20 minutes under green cw laser irradiation (800 mW) generated enough light for a triphenylphosphine conversion of 90% in the second aerated reaction chamber. Without PMS as energy transfer mediator the yield is reduced to 26% and also with a high DPA concentration (5 mM) lower yields of 76% were found based on ¹H NMR analysis. These results are in line with the observed UC quantum yield increase caused by the mediator and they underline the importance of the most highly energetic emission for the spectral overlap between UC emission and photocatalyst absorption (see ESI section 4.6.2† for details). The proposed reaction sequence for the mechanism is provided in the ESI† (section 4.6.2). Briefly, after excitation of the sensitizer and the energy transfer sequence and subsequent TTA-UC with DPA as annihilator, the emitted light is absorbed by DCA and with the help from a naphthalene redox mediator, the triphenylphosphine substrate is oxidized. Triphenylphosphine (1.9 × 10¹⁰ M⁻¹ s⁻¹ in 2 : 98 water/acetonitrile,¹²³ 2.7 × 10¹⁰ M⁻¹ s⁻¹ in acetonitrile)¹²⁶ and naphthalene (1.5 × 10¹⁰ M⁻¹ s⁻¹ in acetonitrile)^65,127 quench excited DCA with almost diffusion-limited rate constants, and it has been shown previously for light-driven catalysis with DCA that a higher cage escape with the mediator enables a faster overall product formation.^65,128–130 Electron transfer from the radical anion of DCA (DCA˙⁻) to molecular oxygen closes the catalytic cycle and overall, the phosphine is oxidized to its phosphine oxide. With the different reaction chambers, it is possible to scale the reaction volume without diluting the upconversion solution. Turnover numbers exceeding 1500 with respect to the ruthenium sensitizer and over 750 for the annihilator can be calculated with the actual amounts employed in this initial test reaction (see ESI sections 3.1.2 and 4.6.2 for details†).

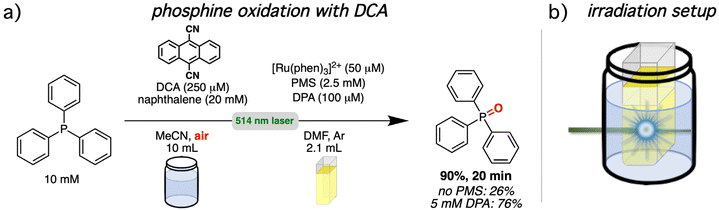Fig. 7 Phosphine oxidation via green-to-blue sTTA-UC (in argon-saturated solution) and subsequent excitation of 9,10-dicyanoanthracene (DCA) by upconverted light (under aerobic conditions). (a) Reaction conditions under cw laser excitation. Further details and a mechanistic scheme are provided in sections 3.1.2 and 4.6.2 of the ESI.† (b) Schematic representation of the irradiation setup exploiting a two-chamber approach.

Finally, we investigated a model reaction that enables a straightforward comparison of the different upconversion conditions. In this case, the generation of singlet oxygen by a thioxanthone derivative (MeOTX)^131,132 with a long-lived triplet state was selected as model reaction for energy transfer (Fig. 8) in combination with DMAn as well-established actinometer substrate for singlet oxygen to form the corresponding endoperoxide.¹³³ While DMAn has distinct absorption bands with a fine structure characteristic for anthracenes, the resulting endoperoxide does not absorb above 300 nm.¹³⁴ Hence, a rapid quantification through the decreasing absorption intensity in the UVA range is possible. The use of 2 mm cuvettes allowed the direct analysis of an aerated DMAn solution with an initial concentration of 1 mM by UV-vis absorption spectroscopy without further dilution. Taking into consideration the shape and the position of the long-wavelength absorption band of MeOTX, significant photocatalytic performance differences for the upconversion systems are expected (Fig. 8b). Irradiation with the mediated upconversion system for 150 minutes led to 71% conversion of the DMAn starting material (Fig. 8a). In striking contrast, the yields in the absence of the mediator (21%) or with high concentrations of DPA (28%) were significantly lower. Analyzing the spectral changes over time clearly highlights the differences between the upconversion systems (Fig. 8b). Surprisingly, even in the absence of the upconversion system a slow degradation of DMAn is detectable (details in section 4.6.3 of the ESI†). However, this background reaction amounts to about 10% conversion after 120 minutes of irradiation (gray line in right panel of Fig. 8b). It is thus significantly slower than the conversion with any upconversion system investigated herein. As a 495 nm longpass filter did not prevent the background reaction, we speculate that a weak direct singlet–triplet absorption band of MeOTX or DMAn or a green-light absorbing impurities (with essentially undetectable concentrations) might cause the observed background reactivity.¹³⁵ Gratifyingly, after correcting the time-resolved conversion for the upconversion-independent background reaction, the ratios of the initial reaction rates are in good agreement with the estimated (relative) overlap integral between MeOTX absorption and upconverted emission. Specifically, the reaction rate for the mediated UC system so obtained is about ∼6.4 times faster than for the non-mediated system, and almost the same factor was obtained for the overlap integral. Using high DPA concentrations without mediator results in reaction rates as well as overlap integrals in-between these two scenarios with a much more pronounced performance decrease (factor of ∼3.6) than what would be expected from the slight absolute quantum yield differences shown in Fig. 5. Hence, this model reaction clearly highlights the advantages that can be achieved by minimizing inner filter effects when upconversion systems are exploited as light source for photocatalytic reactions. Furthermore, it is worth mentioning, that for both investigated reactions either the substrate (DMAn) or the organic photocatalyst (DCA) would interfere with the upconversion system due to their accessible triplet energies on the order of (∼1.8 eV)⁴⁴ and significantly higher concentrations compared to that of the annihilator. Notably, while using a metal-containing sensitizer for light-harvesting, the photocatalytic systems spatially separated from the upconversion system are purely organic in our case, avoiding heavy metal contaminations in the product.

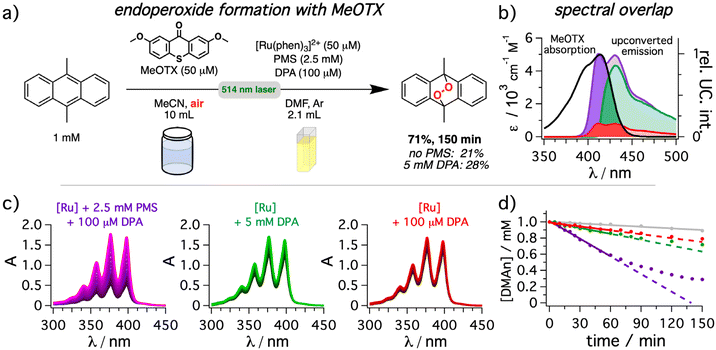Fig. 8 9,10-Dimethylanthracene (DMAn) endoperoxide formation via singlet oxygen generation (¹O₂) by 2,7-dimethoxy-9H-thioxanthen-9-one (MeOTX) under aerobic conditions in a two-chamber system using green-to-blue sTTA-UC. (a) General reaction scheme and concentrations in both chambers for the endoperoxide formation from 9,10-dimethylanthracene (DMAn). A 514 nm cw laser (800 mW) was used as light source. (b) Spectral overlap between the photosensitizer (MeOTX, black) absorption and the normalized upconverted emission resulting from solutions of [Ru(phen)₃](PF₆)₂ in de-aerated DMF as sensitizer in the absence (red) or presence of 2.5 mM PMS (purple) or with 5 mM of DPA (green) corrected for illumination in the middle of the cuvette. (c) UV-vis absorption spectra of the 9,10-dimethylanthracene solution measured in 2 mm cuvettes after different times of exposure to upconversion solutions with the same conditions as described in (b). The different components in the upconversion cuvette are indicated as insets. (d) The change of DMAn concentration was monitored following the absorption at 358 nm over time together with a reference measurement without any upconversion system present (gray trace). The same color code as in panel (c) was used. Details are provided in section 4.6.3 of the ESI.†

3. Conclusions

In summary, we report here a three-component upconversion system that exploits a triplet energy transfer cascade to enhance the population of the triplet state of the annihilator and the upconversion quantum yield accordingly. In addition to the general photophysical properties, the important role of the ionic charges of the sensitizer and the mediator are thoroughly investigated. Different spectroscopic measurements indicate that accelerated diffusion resulting from coulombic attraction rather than static quenching plays a crucial role in our system to enhance the bimolecular rate constant for the initial energy transfer step, while avoiding fast deactivation through static back energy transfer. Starting from a short-lived ruthenium sensitizer triplet, the organic mediator introduces a long-lived triplet state and offers the possibility to lower the annihilator concentrations to the micromolar range. Hence, our study demonstrates that intrinsic filter effects caused by the ground state absorption of the annihilator, reabsorbing the most highly energetic upconverted photons, can be minimized by the introduction of a long-lived mediator triplet in solution. We have demonstrated the modularity of our approach that permits the opportunity to exchange annihilators with similar triplet energies easily.^72,136–138 As a further scientific question related to this study, the mediator approach can potentially be developed into (underexplored) hetero TTA systems^139,140 when a charge-adapted annihilator is used as well, i.e. a cationic DPA derivative in our case.

Furthermore, the improved emission output of our mediated sTTA-UC system (regarding both its intensity and photon energy) is capable of activating a secondary photosensitizer/photocatalyst in physically separated reaction containers. Two proof-of-principle reactions highlight the combination of sTTA-UC with photocatalysis under aerobic conditions using a secondary absorber for energy or electron transfer. From a conceptual viewpoint, this facilitates the individual tuning of UC system and photocatalytic reaction mixture, and prevents optimization side effects that are typically observed when UC system and photocatalyst are in the same phase, such as divergent solvent effects on key reaction steps or solubility issues.^{65,71,110,115,141} Our work complements recently reported concepts to exploit sensitized triplet–triplet annihilation upconversion in solution under air (ESI, section 4.6.1†)^{61,118–121,142–146} that have also in some cases received attention for applications in photo(redox) catalysis.^61,113,114 While our work demonstrates a straightforward way to improve an upconversion system that is in a non-mediated version suitable to learn sTTA-UC in undergraduate courses,³⁴ the general concept is potentially important for developing more efficient upconversion systems and new applications thereof in the future.^4,5,110,111

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge generous financial support from the JGU Mainz and the German Research Foundation (DFG, grant number KE 2313/7-1). We thank Till Zähringer for insightful discussions.

References

1. S. Y. Hwang, D. Song, E. J. Seo, F. Hollmann, Y. You and J. B. Park, Sci. Rep., 2022, 12, 6–12.
2. Q. Liu, M. Xu, T. Yang, B. Tian, X. Zhang and F. Li, ACS Appl. Mater. Interfaces, 2018, 10, 9883–9888.
3. V. Gray, D. Dzebo, M. Abrahamsson, B. Albinsson and K. Moth-Poulsen, Phys. Chem. Chem. Phys., 2014, 16, 10345–10352.
4. T. Schloemer, P. Narayanan, Q. Zhou, E. Belliveau, M. Seitz and D. N. Congreve, ACS Nano, 2023, 17, 3259–3288.
5. M. Uji, T. J. B. Zähringer, C. Kerzig and N. Yanai, Angew. Chem., Int. Ed., 2023, 62, e202301506.
6. D. Beery, T. W. Schmidt and K. Hanson, ACS Appl. Mater. Interfaces, 2021, 13, 32601–32605.
7. S. H. C. Askes and S. Bonnet, Nat. Rev. Chem., 2018, 2, 437–452.
8. N. Yanai and N. Kimizuka, Angew. Chem., Int. Ed., 2020, 59, 10252–10264.
9. Z. A. Vanorman and L. Nienhaus, ACS Energy Lett., 2021, 6, 3686–3694.
10. S. N. Sanders, T. H. Schloemer, M. K. Gangishetty, D. Anderson, M. Seitz, A. O. Gallegos, R. C. Stokes and D. N. Congreve, Nature, 2022, 604, 474–478.
11. Y. Zhou, F. N. Castellano, T. W. Schmidt and K. Hanson, ACS Energy Lett., 2020, 5, 2322–2326.
12. L. Naimovičius, P. Bharmoria and K. Moth-Poulsen, Mater. Chem. Front., 2023, 7, 2297–2315.
13. N. A. Durandin, J. Isokuortti, A. Efimov, E. Vuorimaa-Laukkanen, N. V. Tkachenko and T. Laaksonen, J. Phys. Chem. C, 2019, 123, 22865–22872.
14. P. Bharmoria, H. Bildirir and K. Moth-Poulsen, Chem. Soc. Rev., 2020, 49, 6529–6554.
15. L. Hou, A. Olesund, S. Thurakkal, X. Zhang and B. Albinsson, Adv. Funct. Mater., 2021, 31, 1–12.
16. Z. Huang, Z. Xu, M. Mahboub, Z. Liang, P. Jaimes, P. Xia, K. R. Graham, M. L. Tang and T. Lian, J. Am. Chem. Soc., 2019, 141, 9769–9772.
17. M. Koharagi, N. Harada, K. Okumura, J. Miyano, S. Hisamitsu, N. Kimizuka and N. Yanai, Nanoscale, 2021, 13, 19890–19893.
18. S. He, X. Luo, X. Liu, Y. Li and K. Wu, J. Phys. Chem. Lett., 2019, 10, 5036–5040.
19. C. J. Imperiale, P. B. Green, M. Hasham and M. W. B. Wilson, Chem. Sci., 2021, 12, 14111–14120.
20. Z. A. Vanorman, C. R. Conti, G. F. Strouse and L. Nienhaus, Chem. Mater., 2021, 33, 452–458.
21. K. Wang, R. P. Cline, J. Schwan, J. M. Strain, S. T. Roberts, L. Mangolini, J. D. Eaves and M. L. Tang, Nat. Chem., 2023, 15, 1172–1178.
22. Z. Xu, Z. Huang, T. Jin, T. Lian and M. L. Tang, Acc. Chem. Res., 2021, 54, 70–80.
23. X. Lin, Z. Chen, Y. Han, C. Nie, P. Xia, S. He, J. Li and K. Wu, ACS Energy Lett., 2022, 7, 914–919.
24. J. De Roo, Z. Huang, N. J. Schuster, L. S. Hamachi, D. N. Congreve, Z. Xu, P. Xia, D. A. Fishman, T. Lian, J. S. Owen and M. L. Tang, Chem. Mater., 2020, 32, 1461–1466.
25. Q. Chen, Y. Liu, X. Guo, J. Peng, S. Garakyaraghi, C. M. Papa, F. N. Castellano, D. Zhao and Y. Ma, J. Phys. Chem. A, 2018, 122, 6673–6682.
26. H. Li, C. Wang, F. Glaser, N. Sinha and O. S. Wenger, J. Am. Chem. Soc., 2023, 145, 11402–11414.
27. S. Liu, X. Wang, H. Liu, L. Shen, D. Zhao and X. Li, J. Mater. Chem. C, 2020, 8, 3536–3544.
28. M.-S. Bertrams, K. Hermainski, J.-M. Mörsdorf, J. Ballmann and C. Kerzig, Chem. Sci., 2023, 14, 8583–8591.
29. C. Kerzig and O. S. Wenger, Chem. Sci., 2018, 9, 6670–6678.
30. F. Deng, M. S. Lazorski and F. N. Castellano, Philos. Trans. R. Soc., A, 2015, 373, 20140322.
31. Y. Lu, J. Wang, N. McGoldrick, X. Cui, J. Zhao, C. Caverly, B. Twamley, G. M. Ó. Máille, B. Irwin, R. Conway-Kenny and S. M. Draper, Angew. Chem., Int. Ed., 2016, 55, 14688–14692.
32. W. Sheng, J. Yang, X. Li, J. Zhang, Y. Su, Y. Zhong, Y. Zhang, L. Gong, L. Tan and Y. Chen, CCS Chem., 2023, 5, 729–740.
33. R. Forecast, F. Campaioli, T. W. Schmidt and J. H. Cole, J. Phys. Chem. A, 2023, 127, 1794–1800.
34. B. M. Wilke and F. N. Castellano, J. Chem. Educ., 2013, 90, 786–789.
35. A. J. Tilley, B. E. Robotham, R. P. Steer and K. P. Ghiggino, Chem. Phys. Lett., 2015, 618, 198–202.
36. T. N. Singh-Rachford and F. N. Castellano, J. Phys. Chem. A, 2009, 113, 9266–9269.
37. K. Fujimoto, K. Kawai, S. Masuda, T. Mori, T. Aizawa, T. Inuzuka, T. Karatsu, M. Sakamoto, S. Yagai, T. Sengoku, M. Takahashi and H. Yoda, Langmuir, 2019, 35, 9740–9746.
38. A. C. Sell, J. C. Wetzel, M. Schmitz, A. W. Maijenburg, G. Woltersdorf, R. Naumann and C. Kerzig, Dalton Trans., 2022, 51, 10799–10808.
39. D. S. Tyson, J. Bialecki and F. N. Castellano, Chem. Commun., 2000, 2355–2356.
40. D. S. Tyson, K. B. Henbest, J. Bialecki and F. N. Castellano, J. Phys. Chem. A, 2001, 105, 8154–8161.
41. M. S. Coles, G. Quach, J. E. Beves and E. G. Moore, Angew. Chem., Int. Ed., 2020, 59, 9522–9526.
42. I. Ghosh, R. S. Shaikh and B. König, Angew. Chem., Int. Ed., 2017, 56, 8544–8549.
43. C. Kerzig and M. Goez, Chem. Sci., 2016, 7, 3862–3868.
44. M. Montalti, A. Credi, L. Prodi and M. T. Gandolfi, Handbook of Photochemistry, CRC Press: Taylor & Francis Group, Boca Raton, FL, USA, 3rd edn, 2006.
45. Y. Sasaki, N. Yanai and N. Kimizuka, Inorg. Chem., 2022, 61, 5982–5990.
46. K. Choroba, M. Penkala, J. Palion-Gazda, E. Malicka and B. Machura, Inorg. Chem., 2023, 62, 19256–19269.
47. C. Reichardt, T. Sainuddin, M. Wächtler, S. Monro, S. Kupfer, J. Guthmuller, S. Gräfe, S. McFarland and B. Dietzek, J. Phys. Chem. A, 2016, 120, 6379–6388.
48. R. Brimioulle, D. Lenhart, M. M. Maturi and T. Bach, Angew. Chem., Int. Ed., 2015, 54, 3872–3890.
49. J. D. Earley, A. Zieleniewska, H. H. Ripberger, N. Y. Shin, M. S. Lazorski, Z. J. Mast, H. J. Sayre, J. K. McCusker, G. D. Scholes, R. R. Knowles, O. G. Reid and G. Rumbles, Nat. Chem., 2022, 14, 746–753.
50. T. E. Schirmer and B. König, J. Am. Chem. Soc., 2022, 144, 19207–19218.
51. H. J. Davis, M. T. Mihai and R. J. Phipps, J. Am. Chem. Soc., 2016, 138, 12759–12762.
52. C. C. Clark, A. Marton and G. J. Meyer, Inorg. Chem., 2005, 44, 3383–3385.
53. E. P. Farney, S. J. Chapman, W. B. Swords, M. D. Torelli, R. J. Hamers and T. P. Yoon, J. Am. Chem. Soc., 2019, 141, 6385–6391.
54. V. Gray, K. Moth-Poulsen, B. Albinsson and M. Abrahamsson, Coord. Chem. Rev., 2018, 362, 54–71.
55. Y. Kawashima, H. Kouno, K. Orihashi, K. Nishimura, N. Yanai and N. Kimizuka, Mol. Syst. Des. Eng., 2020, 5, 792–796.
56. R. Fayad, A. T. Bui, S. G. Shepard and F. N. Castellano, ACS Appl. Energy Mater., 2020, 3, 12557–12564.
57. C. Wang, F. Reichenauer, W. R. Kitzmann, C. Kerzig, K. Heinze and U. Resch-Genger, Angew. Chem., Int. Ed., 2022, 61, e202202238.
58. C. Ye, V. Gray, K. Kushwaha, S. Kumar Singh, P. Erhart and K. Börjesson, Phys. Chem. Chem. Phys., 2020, 22, 1715–1720.
59. R. Haruki, Y. Sasaki, K. Masutani, N. Yanai and N. Kimizuka, Chem. Commun., 2020, 56, 7017–7020.
60. W. Sun, A. Ronchi, T. Zhao, J. Han, A. Monguzzi and P. Duan, J. Mater. Chem. C, 2021, 9, 14201–14208.
61. R. Jeyaseelan, M. Utikal, C. G. Daniliuc and L. Næsborg, Chem. Sci., 2023, 14, 11040–11044.
62. A. Olesund, J. Johnsson, F. Edhborg, S. Ghasemi, K. Moth-Poulsen and B. Albinsson, J. Am. Chem. Soc., 2022, 144, 3706–3716.
63. T. J. B. Zähringer, M.-S. Bertrams and C. Kerzig, J. Mater. Chem. C, 2022, 10, 4568–4573.
64. A. Olesund, S. Ghasemi, K. Moth-Poulsen and B. Albinsson, J. Am. Chem. Soc., 2023, 145, 22168–22175.
65. F. Glaser and O. S. Wenger, Chem. Sci., 2023, 14, 149–161.
66. Z. Yuan, J. He, Z. Mahmood, L. Xing, S. Ji, Y. Huo and H. L. Zhang, Dyes Pigm., 2022, 199, 110049.
67. W. R. Kitzmann, M. S. Bertrams, P. Boden, A. C. Fischer, R. Klauer, J. Sutter, R. Naumann, C. Förster, G. Niedner-Schatteburg, N. H. Bings, J. Hunger, C. Kerzig and K. Heinze, J. Am. Chem. Soc., 2023, 145, 16597–16609.
68. C. E. McCusker and F. N. Castellano, Chem. Commun., 2013, 49, 3537–3539.
69. Y. Wei, M. Zheng, L. Chen, X. Zhou and S. Liu, Dalton Trans., 2019, 48, 11763–11771.
70. C. Wang, C. Wegeberg and O. S. Wenger, Angew. Chem., Int. Ed., 2023, 62, e202311470.
71. B. D. Ravetz, A. B. Pun, E. M. Churchill, D. N. Congreve, T. Rovis and L. M. Campos, Nature, 2019, 565, 343–346.
72. L. Huang, W. Wu, Y. Li, K. Huang, L. Zeng, W. Lin and G. Han, J. Am. Chem. Soc., 2020, 142, 18460–18470.
73. M. Wu, B. A. Moser, T. M. Steeves, A. Figueroa, B. M. Wallace, S. T. Kim, A. P. Esser-Kahn and R. C. Steinhardt, RSC Adv., 2019, 9, 26172–26175.
74. R. S. Khnayzer, J. Blumhoff, J. A. Harrington, A. Haefele, F. Deng and F. N. Castellano, Chem. Commun., 2012, 48, 209–211.
75. J. B. Bilger, C. Kerzig, C. B. Larsen and O. S. Wenger, J. Am. Chem. Soc., 2021, 143, 1651–1663.
76. M. Barawi, F. Fresno, R. Pérez-Ruiz and V. A. De La Peña O'Shea, ACS Appl. Energy Mater., 2019, 2, 207–211.
77. A. A. Vlcek, E. S. Dodsworth, W. J. Pietro and A. B. P. Lever, Inorg. Chem., 1995, 34, 1906–1913.
78. D. M. Arias-Rotondo and J. K. McCusker, Chem. Soc. Rev., 2016, 45, 5803–5820.
79. V. Gray, A. Dreos, P. Erhart, B. Albinsson, K. Moth-Poulsen and M. Abrahamsson, Phys. Chem. Chem. Phys., 2017, 19, 10931–10939.
80. A. Monguzzi, R. Tubino, S. Hoseinkhani, M. Campione and F. Meinardi, Phys. Chem. Chem. Phys., 2012, 14, 4322–4332.
81. C. Fan, L. Wei, T. Niu, M. Rao, G. Cheng, J. J. Chruma, W. Wu and C. Yang, J. Am. Chem. Soc., 2019, 141, 15070–15077.
82. M. Yang, S. Sheykhi, Y. Zhang, C. Milsmann and F. N. Castellano, Chem. Sci., 2021, 12, 9069–9077.
83. L. A. Büldt, X. Guo, R. Vogel, A. Prescimone and O. S. Wenger, J. Am. Chem. Soc., 2017, 139, 985–992.
84. S. K. Chattopadhyay, C. V. Kumar and P. K. Das, Chem. Phys. Lett., 1983, 98, 250–254.
85. C. Bohne, E. B. Abuin and J. C. Scaiano, J. Am. Chem. Soc., 1990, 112, 4226–4231.
86. J. R. Lakowicz, Principles of Fluorescence Spectroscopy, Springer US, Boston, MA, 2006.
87. Y. Leydet, F. J. Romero-Salguero, C. Jiménez-Sanchidrián, D. M. Bassani and N. D. McClenaghan, Inorg. Chim. Acta, 2007, 360, 987–994.
88. S. Ji, W. Wu, W. Wu, P. Song, K. Han, Z. Wang, S. Liu, H. Guo and J. Zhao, J. Mater. Chem., 2010, 20, 1953–1963.
89. D. S. Tyson, J. Phys. Chem. A, 1999, 103, 10921–10934.
90. G. J. Wilson, W. H. F. Sasse and A. W. H. Mau, Chem. Phys. Lett., 1996, 250, 583–588.
91. P. Debye, Trans. Electrochem. Soc., 1942, 82, 265.
92. D. Genovese, M. Cingolani, E. Rampazzo, L. Prodi and N. Zaccheroni, Chem. Soc. Rev., 2021, 50, 8414–8427.
93. L. Troian-Gautier, W. B. Swords and G. J. Meyer, Acc. Chem. Res., 2019, 52, 170–179.
94. L. Fielding, Tetrahedron, 2000, 56, 6151–6170.
95. P. Thordarson, Chem. Soc. Rev., 2011, 40, 1305–1323.
96. H. A. Benesi and J. H. Hildebrand, J. Am. Chem. Soc., 1949, 71, 2703–2707.
97. D. Hanss, J. C. Freys, G. Bernardinelli and O. S. Wenger, Eur. J. Inorg. Chem., 2009, 2009, 4850–4859.
98. K. A. King, P. J. Spellane and R. J. Watts, J. Am. Chem. Soc., 1985, 107, 1431–1432.
99. F. Edhborg, A. Olesund and B. Albinsson, Photochem. Photobiol. Sci., 2022, 21, 1143–1158.
100. A. Olesund, V. Gray, J. Mårtensson and B. Albinsson, J. Am. Chem. Soc., 2021, 143, 5745–5754.
101. C. Ye, V. Gray, J. Mårtensson and K. Börjesson, J. Am. Chem. Soc., 2019, 141, 9578–9584.
102. P. Duan, N. Yanai and N. Kimizuka, Chem. Commun., 2014, 50, 13111–13113.
103. N. Harada, Y. Sasaki, M. Hosoyamada, N. Kimizuka and N. Yanai, Angew. Chem., 2021, 133, 144–149.
104. Y. Wei, Y. Li, M. Zheng, X. Zhou, Y. Zou and C. Yang, Adv. Opt. Mater., 2020, 8, 1902157.
105. M. Uji, N. Harada, N. Kimizuka, M. Saigo, K. Miyata, K. Onda and N. Yanai, J. Mater. Chem. C, 2022, 10, 4558–4562.
106. A. Ronchi and A. Monguzzi, Chem. Phys. Rev., 2022, 3, 041301.
107. F. Deng, J. Blumhoff and F. N. Castellano, J. Phys. Chem. A, 2013, 117, 4412–4419.
108. Y. Y. Cheng, B. Fückel, T. Khoury, R. G. C. R. Clady, M. J. Y. Tayebjee, N. J. Ekins-Daukes, M. J. Crossley and T. W. Schmidt, J. Phys. Chem. Lett., 2010, 1, 1795–1799.
109. M. Majek, U. Faltermeier, B. Dick, R. Pérez-Ruiz and A. Jacobi von Wangelin, Chem. – Eur. J., 2015, 21, 15496–15501.
110. R. Pérez-Ruiz, Top. Curr. Chem., 2022, 380, 23.
111. F. Glaser, C. Kerzig and O. S. Wenger, Angew. Chem., Int. Ed., 2020, 59, 10266–10284.
112. L. Huang, L. Zeng, Y. Chen, N. Yu, L. Wang, K. Huang, Y. Zhao and G. Han, Nat. Commun., 2021, 12, 122.
113. O. S. Kwon, J. H. Kim, J. K. Cho and J. H. Kim, ACS Appl. Mater. Interfaces, 2015, 7, 318–325.
114. M. Häring, R. Pérez-Ruiz, A. Jacobi von Wangelin and D. D. Díaz, Chem. Commun., 2015, 51, 16848–16851.
115. B. Pfund, D. M. Steffen, M. R. Schreier, M.-S. Bertrams, C. Ye, K. Börjesson, O. S. Wenger and C. Kerzig, J. Am. Chem. Soc., 2020, 142, 10468–10476.
116. W. Larsson, M. Morimoto, M. Irie, J. Andréasson and B. Albinsson, Chem. – Eur. J., 2023, 29, e202203651.
117. Y. Wei, H. Xian, X. Lv, F. Ni, X. Cao and C. Yang, Mater. Horiz., 2021, 8, 606–611.
118. L. Huang, T. Le, K. Huang and G. Han, Nat. Commun., 2021, 12, 1898.
119. D. Dzebo, K. Moth-Poulsen and B. Albinsson, Photochem. Photobiol. Sci., 2017, 16, 1327–1334.
120. H. Kouno, Y. Sasaki, N. Yanai and N. Kimizuka, Chem. – Eur. J., 2019, 25, 6124–6130.
121. S. Baluschev, K. Katta, Y. Avlasevich and K. Landfester, Mater. Horiz., 2016, 3, 478–486.
122. L. Ding, J. Zhou, Q. Fu, G. Bao, Y. Liu and D. Jin, Anal. Chem., 2021, 93, 4641–4646.
123. M. Nakamura, M. Miki and T. Majima, J. Chem. Soc., Perkin Trans. 2, 2000, 1447–1452.
124. S. Yasui, S. Tojo and T. Majima, J. Org. Chem., 2005, 70, 1276–1280.
125. E. Vauthey, P. Suppan and E. Haselbach, Helv. Chim. Acta, 1988, 71, 93–99.
126. M. E. R. Marcondes, V. G. Toscano and R. G. Weiss, J. Am. Chem. Soc., 1975, 97, 4485–4490.
127. T. Tamai, N. Ichinose, T. Tanaka, T. Sasuga, I. Hashida and K. Mizuno, J. Org. Chem., 1998, 63, 3204–3212.
128. E. Vauthey, D. Pilloud, E. Haselbach, P. Suppan and P. Jacques, Chem. Phys. Lett., 1993, 215, 264–268.
129. F. D. Lewis and M. Kojima, J. Am. Chem. Soc., 1988, 110, 8664–8670.
130. L. M. Kammer, B. Lipp and T. Opatz, J. Org. Chem., 2019, 84, 2379–2392.
131. L. D. Elliott, S. Kayal, M. W. George and K. Booker-Milburn, J. Am. Chem. Soc., 2020, 142, 14947–14956.
132. T. J. B. Zähringer, M. Wienhold, R. Gilmour and C. Kerzig, J. Am. Chem. Soc., 2023, 145, 21576–21586.
133. A. Gomes, E. Fernandes and J. L. F. C. Lima, J. Biochem. Biophys. Methods, 2005, 65, 45–80.
134. A. Klein, M. Kalb and M. S. Gudipati, J. Phys. Chem. A, 1999, 103, 3843–3853.
135. M. Nakajima, S. Nagasawa, K. Matsumoto, T. Kuribara, A. Muranaka, M. Uchiyama and T. Nemoto, Angew. Chem., 2020, 132, 6914–6919.
136. K. J. Fallon, E. M. Churchill, S. N. Sanders, J. Shee, J. L. Weber, R. Meir, S. Jockusch, D. R. Reichman, M. Y. Sfeir, D. N. Congreve and L. M. Campos, J. Am. Chem. Soc., 2020, 142, 19917–19925.
137. A. B. Pun, L. M. Campos and D. N. Congreve, J. Am. Chem. Soc., 2019, 141, 3777–3781.
138. Y. Wei, K. An, X. Xu, Z. Ye, X. Yin, X. Cao and C. Yang, Adv. Opt. Mater., 2023, 2301134.
139. X. Cao, B. Hu and P. Zhang, J. Phys. Chem. Lett., 2013, 4, 2334–2338.
140. B. Nickel and G. Roden, Chem. Phys., 1982, 66, 365–376.
141. F. Glaser, C. Kerzig and O. S. Wenger, Chem. Sci., 2021, 12, 9922–9933.
142. F. Marsico, A. Turshatov, R. Peköz, Y. Avlasevich, M. Wagner, K. Weber, D. Donadio, K. Landfester, S. Baluschev and F. R. Wurm, J. Am. Chem. Soc., 2014, 136, 11057–11064.
143. P. Bharmoria, S. Hisamitsu, H. Nagatomi, T. Ogawa, M. A. Morikawa, N. Yanai and N. Kimizuka, J. Am. Chem. Soc., 2018, 140, 10848–10855.
144. H. Lee, M. S. Lee, M. Uji, N. Harada, J. M. Park, J. Lee, S. E. Seo, C. S. Park, J. Kim, S. J. Park, S. H. Bhang, N. Yanai, N. Kimizuka, O. S. Kwon and J. H. Kim, ACS Appl. Mater. Interfaces, 2022, 14, 4132–4143.
145. J. Ma, S. Chen, C. Ye, M. Li, T. Liu, X. Wang and Y. Song, Phys. Chem. Chem. Phys., 2019, 21, 14516–14520.
146. H. Zhou, J. Lin, S. Wan and W. Lu, Phys. Chem. Chem. Phys., 2022, 24, 29151–29158.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr05265f

---