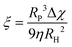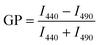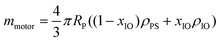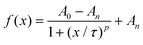Magnetic micromotors crossing lipid membranes†
Miguel A.
Ramos Docampo
 a,
Ondrej
Hovorka
b and
Brigitte
Städler
a,
Ondrej
Hovorka
b and
Brigitte
Städler
 *a
*a
aInterdisciplinary Nanoscience Center (iNANO), Aarhus University, Gustav Wieds Vej 14, 8000 Aarhus, Denmark. E-mail: bstadler@inano.au.dk
bFaculty of Engineering and Physical Sciences, University of Southampton, SO16 7QF, Southampton, UK
First published on 16th January 2024
Abstract
Nano/micromotors are self-propelled particles that show enhanced motion upon being triggered by a stimulus. Their use in nanomedicine has been widely explored, with special focus on imaging or drug delivery. However, a thorough understanding of the requirements for more efficient locomotion is still lacking. In this paper, we assembled magnetically propelled motors of different sizes (i.e., 0.5, 1 and 4 μm) and surface chemistries (positive charge or PEGylated) and assessed their motion in the presence of giant unilamellar lipid vesicles (GUVs) of varying compositions (zwitterionic, negatively charged and saturated lipids). Unexpectedly, the size does not seem to be the dominating characteristics that governs the ability of the motors to cross lipid membranes. Specifically, the 0.5 μm PEGylated motors have very limited ability to cross the lipid membrane of GUVs due to their non-interacting nature compared to their equally sized positively charged counterparts. Furthermore, membranes made of saturated lipids and, in particular, in combination with a weak magnetic field facilitate motors’ crossing, regardless of their size. The results were validated by in-house data-driven statistical analysis that employs experimental data to allow for the identification of individual motor motion in the ensemble when meeting the lipid membranes. Altogether, we provide insight into motor locomotion when they interact with a biological barrier considering both the entire ensemble and the individual motors, which has the potential to support considerations of future motor designs.
Introduction
Nano- and micromotors are active particles that can self-propel outperforming Brownian motion by converting input energy into kinetic energy. Great advances have been witnessed in this field, especially towards their potential in nanomedicine.1–5 From the first examples in simple, aqueous environments, efforts have evolved towards more complex media (i.e., gels, cellulose, cell media) and eventual in vitro and in vivo experimentations, as reviewed in detail.6–11 In contrast, the motion of motors in patterned or confined environments12 and controlling motor swarming13–15 are still ongoing endeavors.When it comes to the interaction of motors with mammalian cells, endocytosis is still predominant. There exist some examples where magnetic coatings were used to facilitate the incorporation of nanoparticles inside cells.16 In addition, the active motion of motors was employed to increase the chances of uptake by cells compared to passive particles17 or to increase the mobility when performing a task (e.g., drug delivery).18 Nonetheless, the use of motors’ power to cross or penetrate membranes with the aim to either enter the cell's cytosol or to escape from the endo/lysosomes remains to be thoroughly explored. Although atomic force microscopy experiments have determined that the minimum force to break a bacterial cell membrane was ∼20 nN,19 the corresponding force for mammalian cells remains debated, as well as it is the impulse (thrust) that a motor needs to achieve during locomotion to cross such membranes. Simulations have been performed with the aim to estimate the dynamics of motors approaching or crossing lipid membranes.20–22 These models assumed that the motor size was comparable to the thickness of the membrane (few nanometers) and that the viscosity was constant. Furthermore, most of the model-based studies considered magnetic particles, meaning that an active field pulled the particles, due to which they obtained ballistic motion. Complementarily, the interaction between motors and lipid vesicles has been experimentally addressed before.23,24 Interestingly, these efforts demonstrated that the motors did not cross the membrane to enter the void of the vesicles, but instead, they orbited around the vesicles, which was also supported by theoretical evaluations.25–28 A recent approach considered encapsulated coacervate-based motors inside lipid vesicles.29 These motors were equipped with catalase for propulsion by the conversion of hydrogen peroxide (H2O2) into water and oxygen molecules with diffusion coefficients of up to ∼0.24 μm2 s−1 when 3.4 vol% H2O2 was used. However, the motors never escaped the lipid vesicles.
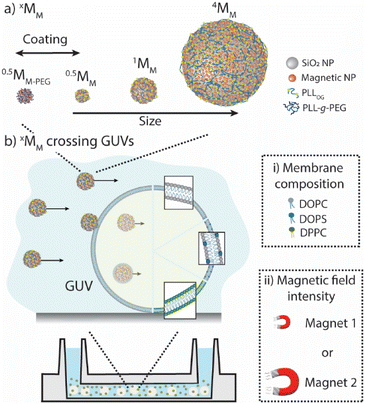
Herein, we experimentally explored how magnetic motors cross the lipid membranes of giant unilamellar vesicles (GUVs). Specifically, we (i) designed magnetic motors with different core sizes and ζ-potentials to determine their maximum speed in an isotonic solution when different magnetic forces were applied; (ii) assembled GUVs with varying membrane compositions to identify the role of membrane fluidity and charge affecting the motors’ crossing; and (iii) evaluated the locomotion of the motors in the presence of GUVs to identify the proportion of the motors in an ensemble that were able to cross the lipid membranes (Scheme 1).
Results and discussion
Fundamental characterization of the magnetic motors and giant unilamellar vesicles
We chose the simplest magnetic motor that could be reliably driven and stopped depending on an external magnetic field, as the goal was to identify how they interacted with lipid membranes and not to establish a new type of motor. The magnetic motors were prepared by depositing magnetic, iron oxide nanoparticles onto polystyrene cores of different sizes (i.e., 0.5, 1 and 4 microns), yielding in xMM where x identifies the core size. Note that smaller cores could not be visualized with a regular bright-field microscope, and larger cores sedimented too fast and were too heavy to be pulled by the magnets. Non-interacting motors were prepared by coating xMM with an outer layer of poly(L-lysine)-graft-poly(ethylene glycol) and were referred to as xMM-PEG. (For details about fabrication and characterization, please refer to ESI Fig. S1 and related text and Table S1.†) The mobility of xMM and xMM-PEG was assessed in an isotonic solution (i.e., a solution containing 5 wt% glucose and 0.9 wt% NaCl) and a sucrose solution when exposed to a magnetic field in a microfluidic channel (ESI Fig. S2–S4 and related text and Movie panels S1–S4†). The magnetic field was created using a magnet with a pulling force of either 0.3 N or 2 N, which produced a magnetic flux gradient the motors would be pulled towards. (Note: the magnetic force refers to the force the magnet has to hold a magnetic object, given the provider specifications. The specific magnetic force of the 2 N magnet is ∼8× higher than that of the 0.3 N magnet. For simplicity, the notations magnet 1 and magnet 2 referring to the 0.3 N magnet and the 2 N magnet, respectively, will be used in this article). The maximum velocities were ∼3 μm s−1 for 0.5MM and 1MM and ∼7 μm s−1 for 4MM in isotonic solution and ∼2× lower in sucrose solution when magnet 2 was used. 0.5MM-PEG had a maximum velocity of ∼22 μm s−1 in isotonic solution using magnet 2.Giant unilamellar vesicles (GUVs) were employed as a simplified model of the cell membrane. GUVs with different membrane properties were assembled, i.e., flexible and zwitterionic (GUVZ), flexible and negatively charged (GUV−), and rigid and zwitterionic (GUVS), using different lipids (for details about fabrication and characterization, please refer to ESI Fig. S5 and related text and Table S2†). With the aim to assess the motors’ motion behavior when encountering the GUV membranes, xMM were encapsulated in the GUVs’ void by an emulsion transfer method. These samples were employed in all the subsequent experiments, unless specified otherwise.
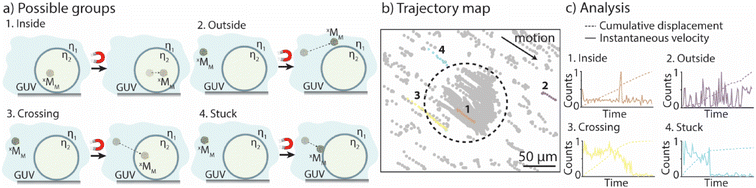
Data-driven statistical analysis of xMM locomotion
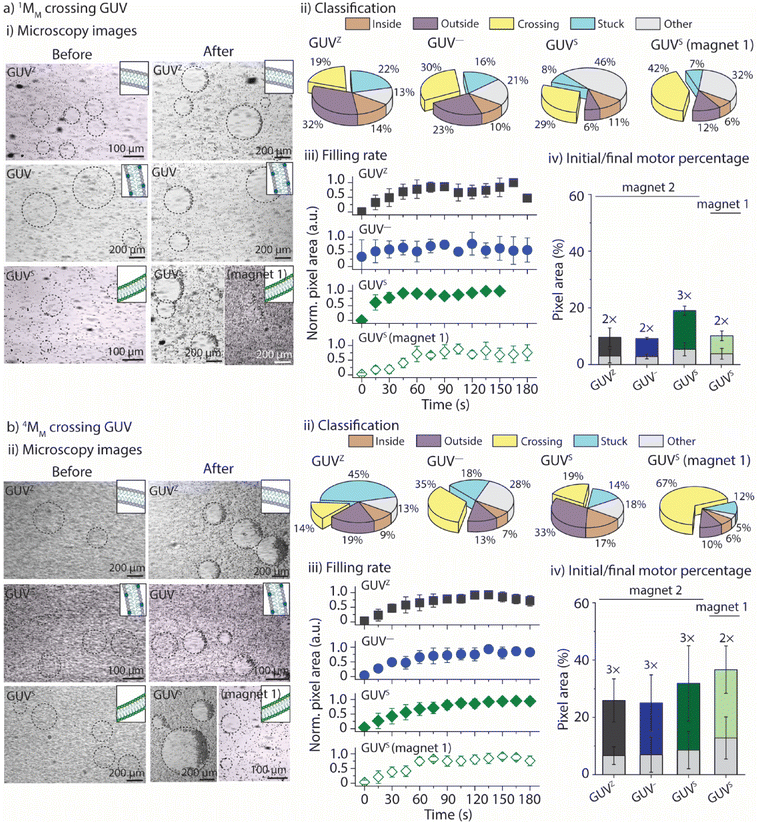
The goal was to evaluate if and when xMM were able to cross the GUV membranes. The solutions with the GUVs and motors were suspended in a non-coated ibidi microfluidic channel, bright-field images were taken before a magnetic field was applied and movies of the moving motors when exposed to the magnets were recorded for up to 3 min. The motor's motion was tracked as previously described30 (for details, please refer to the Experimental section). In addition, an in-house Python code was developed, which allowed to separate the motors into five groups depending on their motion properties (see the Experimental section for more details). Group 1 and group 2 contained motors that moved only in the void of the GUVs and in the surrounding solution, respectively. Motors that crossed the membranes of the GUVs were part of group 3, while group 4 contained the motors that got stuck either in the membrane of the GUVs or on the surface of the microfluidic channels (Fig. 1a). The trajectory maps of a sample were extracted and analyzed using the Python code (Fig. 1b). The code uses the cumulative displacement and the instantaneous velocity of each individual motor in an ensemble of ∼300 motors for their classification (Fig. 1c). Motors that exhibited linear fits to their cumulative displacement and had velocities below the average velocity of the ensemble were assigned to group 1, representing motors confined within the GUVs. Motors that displayed linear fits but had velocities surpassing the average velocity of the ensemble were designated as group 2, signifying motors remaining outside the GUVs. A piecewise linear (wedge) function was applied to their cumulative displacement curves for motors exhibiting variable velocities. If the slope following the wedge was found to be non-zero, the motors were categorized as group 3, indicating their ability to cross the GUV membrane. If the slope following the wedge was close to zero, the motors were assigned to group 4, representing motors that were immobilized or trapped within the GUV membrane or on the surface of the channel. (We would like to note that we cannot distinguish between these two phenomena thus far.) Motors that did not meet any of the aforementioned criteria were classified in an additional group referred to as “other”. Note that this group also contained motors with a velocity profile where the slope before the wedge was lower than that after the wedge, pointing towards motors that might be able to escape the GUVs. However, it was challenging to observe these motors in the movies due to their very low number and the low resolution of the microscope.Effect of surface chemistry and medium viscosity
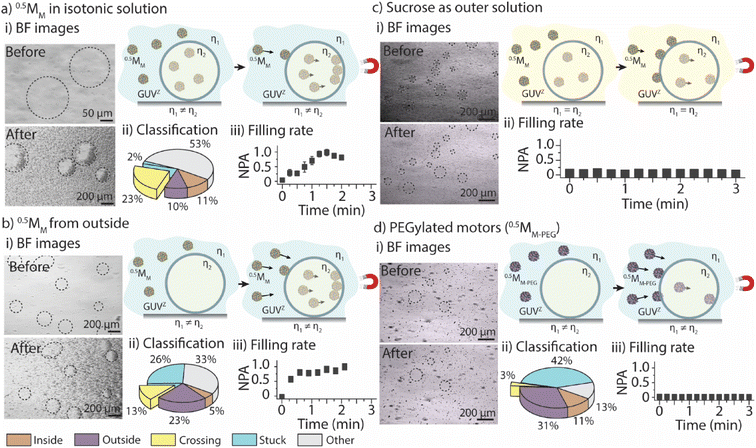
The first goal was to determine the parameters that govern the motors’ ability to cross the GUVZ membranes depending on the viscosity of the medium by comparing the positively charged 0.5MM with the inert 0.5MM-PEG. The inside of the GUVs (i.e., the sucrose solution) had a ∼2× higher viscosity than the isotonic solution in the surrounding. Magnet 2 was employed for the experiments. (For details about the setup, please refer to ESI Fig. S6.†)Initially, GUVZs containing 0.5MM were evenly distributed in the microfluidic channel. Following the application of a magnetic field, the GUVZs partially filled with 0.5MM were able to cross the membranes, showing an accumulation of 0.5MM in one hemisphere of the GUVZs (Fig. 2ai and ESI Movie panel S5†). This accumulation indicated that 0.5MM decelerated after having crossed the membranes, which resulted in the inability of 0.5MM to leave the void of the GUVZ. This observation was ascribed to the reduced magnetophoretic mobility of 0.5MM in the viscous environment inside the GUVZs. It is noteworthy to emphasize that the GUVZs were not disrupted upon 0.5MM crossing and accumulation. We speculated that the pressure exerted in the GUVZs’ membrane was rather low, and the flexibility of the membrane allowed for rapid self-healing after the crossing of 0.5MM.31,32
Following the determination of the cumulative displacement and the instantaneous velocity, 0.5MM were classified into the above defined five groups (Fig. 2aii). A similar amount of ∼10% of 0.5MM was part of group 1 and group 2 (moving only inside or outside of the GUVZ, respectively), while close to zero 0.5MM remained stuck (group 4) and ∼23% of 0.5MM were able to cross the lipid membranes (group 3) and accumulated inside the GUVZ. We also noticed that a fraction of 0.5MM in the “other” group represented ∼53% of the total number of motors. However, we cannot explain this observation.
The accumulation of 0.5MM inside the GUVZ was semi-quantitatively analyzed by extracting the movie frames, followed by their conversion into binary images (where the white pixels correspond to the motors and the black pixels correspond to the background). The white pixel area inside the regions of interest (i.e., the GUVZ) was obtained as a function of time (Fig. 2aiii) and normalized to the highest value (white pixel area at t = 3 min). 0.5MM showed an accumulation inside the GUVZ that reached a plateau after ∼60 s.
In the next step, we aimed to verify that the increase in the number of 0.5MM in the void of the GUVZs upon exposure to the magnetic field was due to the penetration of 0.5MM from outside and not only due to the accumulation of the encapsulated 0.5MM in the GUVZ. To this end, empty GUVZs were mixed with 0.5MM, added to the microfluidic channels and movies were recorded when the magnetic field was applied, followed by the classification of the individual 0.5MM in the 4 groups (Fig. 2bi and ESI Movie panel S5†). Only ∼5% of 0.5MM were moving inside of the GUVZ, but importantly ∼13% of 0.5MM crossed the membrane (Fig. 2bii). The majority of 0.5MM either remained in the surrounding solution or were trapped in the membrane of GUVZ. It should be noted that a rather large portion of 0.5MM was stuck compared to the first outlined situation. We attributed this observation to the fact that the organization of the GUVZ membrane was affected by the presence of 0.5MM during assembly. Nonetheless, the increment of the pixel area corresponding to 0.5MM inside of the GUVZ was calculated and found to be similar as above, confirming that 0.5MM were indeed able to cross the lipid membranes and accumulate in the GUVZ's void (Fig. 2biii).
Next, we aimed to understand if 0.5MM with lower velocity could also cross the membrane of the GUVZ. To this end, GUVZs containing 0.5MM were added in the microfluidic channel filled with sucrose before recording movies with the applied magnetic field (Fig. 2di and ESI Movie panel S5†). In this context, it was not possible to analyze the differences in motion with the current model, due to the similar velocities 0.5MM displayed inside and outside the GUVZs. However, the filling rate analysis showed only a little penetration of 0.5MM to the inside of the GUVZs (Fig. 2dii), which was explained by the fact that the magnetophoretic mobility of the motors was inversely proportional to the viscosity of the medium.
Finally, 0.5MM-PEG were considered as an inert alternative to the positively charged 0.5MM to determine the impact of the surface chemistry of the motors on their ability to cross the membrane of the GUVZ. Empty GUVZs were mixed with 0.5MM-PEG, added to the microfluidic channels, and the movies were recorded when the magnetic field was applied. Representative bright-field microscopy images suggested that very limited penetration of 0.5MM-PEG across the membrane occurred (Fig. 2ci and ESI Movie panel S5†). The classification revealed that most 0.5MM-PEG in the ensemble belonged either to group 2 or 4, i.e., they either moved outside of the GUVZs or were trapped in the membrane or on the surface of the microfluidic channel, respectively. Only a very low fraction of 0.5MM-PEG was able to cross the membrane (Fig. 2cii), which was also confirmed by analyzing the filling rate (Fig. 2ciii). We would like to note that 0.5MM-PEG had higher velocities than 0.5MM, which means that not only the velocities, but also the interaction of the lipid membrane with the surface of the motors was an important aspect to consider. In the current case, the inert nature of 0.5MM-PEG was the dominating factor over the motor size.
Effect of the GUV membrane fluidity and composition
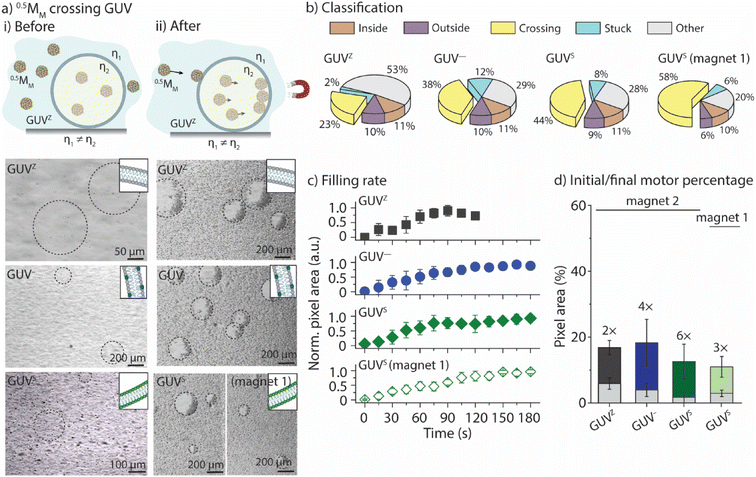
We aimed to correlate the lipid composition of the GUV membrane with the ability of 0.5MM to cross the membranes. To this end, 0.5MM were employed together with the GUVZ, GUV−, and GUVS. Bright-field microscopy images were taken before and after 0.5MM were exposed to the magnetic field for 3 min (Fig. 3a and ESI Movie panel S6†). In general, 0.5MM were able to cross the membranes of all four types of GUVs. Next, the locomotion of the individual 0.5MM was classified into the five groups (Fig. 3b). The percentage of 0.5MM crossing the membranes increased from ∼23% to ∼38% for the GUVZ and GUV−, respectively, when magnet 2 was used. We hypothesized that negatively charged membranes of GUV− had a beneficial interaction with the positively charged 0.5MM when they approached, which increased the chances of penetration. The percentage of 0.5MM that were able to cross was also higher when GUVSs were considered (∼44%). We attributed this observation to the fact that the less fluid membranes in the GUVS![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 19 compared to the GUVZ and GUV− might have absorbed a smaller part of the energy transferred during the impact and therefore increased the crossing probability. Additionally, ∼58% 0.5MM were able to cross the membrane of the GUVS when magnet 1 was used. The reason behind this might be ascribed to the slow velocities 0.5MM reached in this case, which increased the retention time in the membrane and favored the crossing since the magnetic field was still pulling.
19 compared to the GUVZ and GUV− might have absorbed a smaller part of the energy transferred during the impact and therefore increased the crossing probability. Additionally, ∼58% 0.5MM were able to cross the membrane of the GUVS when magnet 1 was used. The reason behind this might be ascribed to the slow velocities 0.5MM reached in this case, which increased the retention time in the membrane and favored the crossing since the magnetic field was still pulling.
The movies were analyzed as outlined before to obtain the time-dependent normalized white pixel area inside of the GUVs (Fig. 3c). Furthermore, a logistic function was fitted to these data in order to obtain a more quantitative analysis (ESI Fig. S7†). A logistic function is an S-shaped curve that allows for sequential analysis to a distribution-free accumulation of data within a boundary. The function has two main parameters, named here τ and p. τ relates to the half-time the motors needed to fill the GUVs that is associated with the permeation time, i.e., τ depends on the motor velocity, membrane fluidity and medium viscosity. p is the rate by which 0.5MM filled up the GUVs, and is related to the permeability of the membrane towards the motors.17τ obtained from the fitting was below 70 s in all cases when magnet 2 was used (ESI Table S3†), meaning that the GUVs were filled to half of their final capacity within the same time, independent of the membrane composition. As expected, τ became longer when magnet 1 was used, indicating that the motors needed more time to cross the membrane as they moved slower. The fitted value for p ranged from 1.6 s−1 to 1.9 s−1, independent of the membrane composition or the magnetic field strength.
Furthermore, the difference between the initial amount of 0.5MM encapsulated inside the GUV and the final amount present after the application of the magnetic field was calculated (Fig. 3d). To do so, the images were converted into binary and the number of white pixels related to the motors was determined and expressed as a percentage related to the total number of pixels in the image. The initial area occupied by the motors in all cases was smaller than the end-point value, indicating an increase in the number of motors inside the GUV, i.e., 0.5MM crossed the membranes upon applying the magnetic field. However, 0.5MM showed differences in the crossing efficiency as indicated by varied final areas depending on the membrane composition (Fig. 6d). Specifically, the final number of 0.5MM increased 2-fold when GUVZs were used. In contrast, a 4× increase was found for the GUV−. This observation suggested that the interaction of the negatively charged GUV− with the positively charged 0.5MM had a positive effect on the crossing ability of 0.5MM. The concentration of the negatively charged DOPS lipids was increased from 10 vol% to 50 vol% (resulting in GUV50−) in an attempt to support this explanation. The results showed that 0.5MM were able to cross with values of τ and p of 8 s and 2.3 s−1, respectively, suggesting that the GUV50− membranes were much more permeable toward 0.5MM than the GUV− (ESI Fig. S8 and Movie panel S7†). This analysis also confirmed that 0.5MM could more easily cross the membrane of the GUVS than the GUVZ already observed when classifying the individual 0.5MM in the ensemble. It should be noted that when magnet 1 was employed, 0.5MM were half as efficient in entering the GUVS void compared to when magnet 2 was used. This observation was ascribed to the constant time frame that 0.5MM had to cross the GUVs, as they moved slower compared to when magnet 2 was employed.
Effect of the motor size
In the next step, we aimed to identify how the motors’ size affected their ability to cross the GUV membranes. To do so, 1MM and 4MM were used, and their interaction with the four different GUVs was assessed. Samples were prepared as outlined before, and the movies were recorded up to 3 min during exposure to either magnet 1 or magnet 2 (Fig. 4ai, bi and ESI Movie panel S8 and S9†). Even these larger motors were able to cross the membrane without disrupting the GUVs, independent of the lipid composition. Their locomotion was classified into the five groups as outlined above (Fig. 4aii and bii). Both 1MM and 4MM displayed a similar behavior to 0.5MM with the percentages of crossing motors varying from ∼19% to ∼30% and ∼29% for 1MM crossing GUVZ, GUV− and GUVS, respectively, and from ∼14% to ∼35% and ∼19% for 4MM crossing the GUVZ, GUV− and GUVS, respectively, in the presence of magnet 2. While the percentages of 1MM and 4MM crossing the membranes of GUVZ and GUV− were similar, higher numbers of 1MM seemed to have crossed the membrane of GUVS compared to 4MM, but with the available data it was difficult to speculate about the origin of this observation. Furthermore, the percentage of 1MM and 4MM crossing the GUVS when magnet 1 was used increased up to ∼42% and ∼67%, respectively, as they moved slower and had more time to interact with the GUV membrane to eventually cross.The quantification of pixels corresponding to the presence of 1MM and 4MM trapped inside the GUVs indicated a lower count compared to GUVs where 0.5MM used. The normalized white pixel area inside the GUVs was determined as a function of time and fitted to a logistic function to calculate the parameters τ and p (Fig. 4aiii and biii). First, τ became generally shorter with increasing motor size from ∼44 s to ∼35 s and ∼24 s for 0.5MM, 1MM and 4MM, respectively, independent of the GUV lipid composition. This observation agreed with the fact that larger motors had faster velocities, and thus they needed less time to fill the same area inside the GUV's cavity. It should also be noted that the motor size for 1MM and 4MM dominated over the lipid composition of the GUVs. As expected, τ became longer when magnet 1 was used, indicating that the motors needed more time to cross the membrane since they moved slower. In addition, there was a general trend to smaller p with increasing motor size from 1.9 s−1 to 1.2 s−1 and 0.8 s−1 for 0.5MM, 1MM and 4MM, respectively, suggesting that the GUVs showed lower permeability towards larger motors, independent of their lipid composition. This observation can be rationalized by considering that the motors and membranes of GUVs approximate the Hertzian model,33 which involves a hard sphere and a soft plane. According to this model, the contact area between the two materials increases as the spherical particle size decreases. Finally, both 1MM and 4MM showed that a similar number of motors was able to cross into the GUVs’ voids (within the experimental error), independent of the membrane composition (Fig. 4aiv and biv). It is noteworthy to mention that 4MM displayed the largest total number of motors entrapped inside the GUVs due to the inherent larger area these motors occupied and that was not considered (i.e., normalized) when analyzing the pixel count.
Taking these observations together, we aimed to estimate the thrust (impulse) that the 0.5MM, 1MM and 4MM needed to cross the membranes of the GUVZ, GUV− and GUVS, calculated as the linear momentum (Fig. 5). To this end, we considered the mass of the motors and the difference in velocity before and after crossing the membranes. These findings suggested that first 4MM had more potential to cross the GUV membranes compared to 1MM or 0.5MM, as expected since they had the highest mass. Second, 1MM and 4MM had a higher momentum when crossing the GUVZ and GUV− membranes, which might indicate that these more fluid membranes required a lower energy penalty to be penetrated compared to the more rigid GUVS membranes. This observation might seem counterintuitive when considered the results discussed above, where more rigid membranes increased the chances of crossing. However, we hypothesized that the energy cost (i.e., transfer of momentum) when the motors crossed the GUVS was higher, as they had to overcome a stiffer membrane compared to the GUVZ and GUV−. Third, there was a trend observable that all motors crossing the GUV− had the highest momentum, which might be explained by the electrostatic attraction between the motors and the GUV−. Finally, there were barley any differences in momentum for 0.5MM, and we assumed that the smallest motors required less energy to deform the membrane and cross, reducing the transfer of momentum.
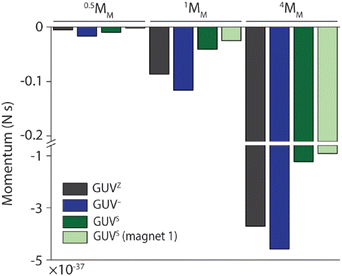 | ||
| Fig. 5 Thrust (impulse) calculated as the linear momentum of 0.5MM, 1MM and 4MM crossing GUV membranes. | ||
GUV membrane integrity upon xMM crossing
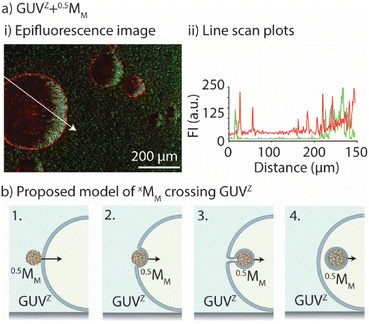
In common phago/endocytosis, the mammalian cell engulfs molecules, fluids, or nanomaterials for transport inside of the cell via invagination of the membrane, without any negative effect on the membrane integrity.34,35 In this context, artificial endocytosis/recruitment of nanoparticles using either GUVs36,37 or coacervates38,39 has been experimentally illustrated. Consequently, we aimed to get a better understanding of how xMM crossed the GUVs’ membrane by determining if xMM had lipids deposited on their surface following the crossing and how the membrane permeability was affected by the crossing of xMM.First, we evaluated whether the motors had a lipid coating after crossing the GUV's membrane. To do so, epifluorescence microscopy images were taken after GUVZ containing 0.5MM were exposed to magnet 2 (Fig. 6a). Regardless of whether 0.5MM or 4MM were considered, the outcome was similar because the presence of lipids adhering to the surface of motors after crossing the membrane was anticipated to be unrelated to their size (ESI Fig. S9a and b†). Overlapping of the fluorescence signals originating from the fluorescent-labelled lipid Rho-PE and the motors coated with PLLOG (resulting in yellow color in the images) was observed independent of the type of used GUV, confirming that the mechanism of crossing was very likely the same for all types of motors and GUVs (ESI Fig. S8a and b†). (Please note that motors that did not cross the membranes had only a fluorescence signal originating from PLLOG, shown in green.) Furthermore, line scan plots were extracted from the epifluorescence microscopy images (path indicated as a white arrow). The intensity maxima for the signal originating from Rho-PE were found in the positions that match with the GUV membrane (indicated by dotted white lines) as well as in the positions where the motors accumulated inside of the GUVs. In contrast, the signal originating from PLLOG had the maxima corresponding to the area where 4MM accumulated due to the magnetic field. In an attempt to more quantitatively assess the images, the Manders’ correlation coefficient40 was calculated to determine the level of colocalization between the fluorescence signal from Rho-PE (red) and PLLOG (green) (ESI Table S4†). There was a strong correlation in the green-to-red signal, indicating that many 0.5MM and 4MM overlapped with the lipids, suggesting that the motors had parts of the GUV lipid membrane on their surface. It should be noted that not all motors that crossed the membrane showed a fluorescence signal originating from the lipids. We hypothesized that the visible inhomogeneous distribution of Rho-PE in the GUV membrane and/or that the amount of Rho-PE was too small, and thus not all the motors that crossed the GUV membrane picked up a detectable amount of Rho-PE.
Following on, the recovery of the GUV membrane upon motor crossing was assessed by employing 5(6)-carboxy-X-rhodamine (RhoX), a molecule that could only trespass to the inside of the GUV through defects in the membrane. In other words, RhoX was used as a tracer to determine if there were changes in the membrane integrity due to the crossing motors. 0.5MM, 1MM and 4MM were added to RhoX solution and mixed with the empty GUVZ, followed by recording epifluorescence microscopy images before and after exposure to magnet 2 (ESI Fig. S9c†). Initially, a homogeneous fluorescence signal originating from RhoX in the environment of the GUVZ was observed. After exposure to the magnet, red fluorescent aggregates were observed in the void of the GUVZ, suggesting that RhoX crossed the membranes by sticking to the motor's surfaces and not as free molecules. The surrounding showed similar fluorescent aggregates, supporting this explanation together with the fact that RhoX has carboxylic groups that likely interacted with the positive surface charge of the motors. The line scan plots supported these findings. The minima of the plots before applying the magnetic field matched the voids of the empty GUVs. The same minima displayed spikes after exposure to the magnet due to the accumulation of RhoX associated with the motors inside the GUVs.
Taking these observations together, we proposed a mechanism to explain the process of crossing (Fig. 6b). First, the motors met the GUV membrane and associated with it (1). Due to the pulling force of the magnet field, the motors were pushed inside of the GUVs (2). This process occurred through membrane engulfment (similar to cell phagocytosis). The motors crossed the GUV membrane grasping part of the membrane (3). The GUV self-healed rapidly due to the fast lateral mobility of the lipids, avoiding the disruption of the vesicle. Finally, the motors ended up inside of the GUV (partly) coated with the lipid membrane (4). This mechanism is in agreement with our findings including, e.g., the efficient crossing of the GUV− membranes due to electrostatic interactions or the limited crossing of 0.5MM-PEG due to the hindered interaction with the GUV membranes.
Conclusion
We assessed the ability of magnetic motors to cross lipid vesicles of diverse compositions and developed an analysis approach that allowed for the classification of individual motors in an ensemble according to their interaction with the membranes. The main findings illustrated that the motors’ size did not play a key role in crossing the membranes, but more importantly stiffer membranes (made of saturated lipids) and weaker magnetic fields enabled the crossing, owing to the increased retention time of the motors on the membranes and the better interaction. Non-interacting (PEGylated) motors showed limited crossing, which was dominant over the motors’ size or speed. Furthermore, due to the interaction of the motors’ surface with the membranes, the crossing motors got (partly) coated with lipids, pointing towards artificial endocytosis. This kind of analysis is envisioned to contribute to the design of motors with sufficient thrust (impulse) to overcome hurdles.In the case of biomedical applications, the next step would involve calculating/estimating the energy barrier that biological membranes pose and identifying the minimum energy required for the motors to cross them. This might improve the design of motors able to propel through cell membranes, escape lysosomal entrapment or penetrate tissues. From our data, we can conclude that this energy barrier is not only related to the speed of the motors and the membrane composition, but other factors such as interaction energies between the motors and the membranes and the viscosity of the medium are important parameters to consider.
In a broader sense, the mathematical model used in this paper allows for the estimation of individual velocities even when the medium is not homogeneous and could be generalized in other fields where motors navigate complex, viscosity-changing media (e.g., water–oil mixtures).
Experimental
Materials
Sodium chloride (NaCl, 99%), poly(allylamine hydrochloride) (PAH, MW 17.5 kDa), poly(sodium 4-styrenesulfonate) (PSS, MW 70 kDa), poly(L-lysine) hydrobromide (PLL, MW 30–70 kDa), 5(6)-carboxy-X-rhodamine (RhoX), 4-(2-hydroxyethyl)piperazine-1-ethane-sulfonic acid (HEPES), Laurdan probe (6-dodecanoyl-N,N-dimethyl-2-naphthylamine), sucrose, glucose, mineral oil, and polystyrene particles (PS, 0.5 μm, 1 μm, and 4 μm, 5 wt%) were purchased from Sigma-Aldrich. Methoxypolyethylene glycol carboxylic acid (mPEG-COOH, MW 2 kDa) was purchased from Abbexa Ltd. 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (Rho-PE) were purchased from Avanti Polar Lipids, Inc. Ltd. μ-Slides VI0.4 uncoated were purchased from ibidi GmbH. Different NdFeB magnets (2 N and 0.3 N pulling force) were purchased from Supermagnete. Ultrapure water (18.2 MΩ cm resistivity) was obtained using an ELGA Purelab Ultra system (ELGA LabWater, Lane End).Oregon Green 488-labeled poly(L-lysine) (PLLOG) and poly(L-lysine)-grafted-poly(ethylene glycol) (PLL-g-PEG, grafting ratio ∼17%, i.e., 1 out of 6 PEG chains contained 1 PLL chain) were synthesized following a previous method.41
Micromotor (MM) assembly
The magnetic motors consisted of a carboxylate-modified polystyrene (PS) core (i.e., 0.5, 1 or 4 μm in diameter) decorated with iron oxide nanoparticles. The iron oxide nanoparticles were synthesized employing the Massart's method. This resulted in magnetite/hematite (Fe3O4/α-Fe2O3) nanoparticles of an average diameter of 10.5 */1.5 nm (95.5% population, log–normal fit) and a positive surface charge (ζ-potential ∼ +30 mV).41,42The assembly was achieved using the layer-by-layer technique. First, 200 μL of commercial PS solution (5 wt%) were dispersed in PAH solution (2 mg mL−1 in 0.5 M NaCl) and stirred for 15 min at room temperature. Then, the excess of PAH was removed by centrifugation and the particles were washed with ultrapure water (4500–6500 rpm, 5 min, 3×). Second, the PAH-coated particles were dispersed in PSS solution (2 mg mL−1 in 0.5 M NaCl), incubated for 15 min and washed as above. Then, 500 μL of iron oxide nanoparticles (40 mg mL−1 in ultrapure water) were added to the previously coated particles, incubated for 30 min, and washed as above, resulting in magnetic motors xMM (x represents the PS core size in microns). For visualization purposes, the motors were fluorescence labelled by adding a layer of Oregon Green™-labelled poly(L-lysine) (PLLOG) instead of PLL. For non-interacting motors, PLL-g-PEG was added as the terminating layer instead of PLL, resulting in xMM-PEG.
The ζ-potentials of the particles after each deposition step were measured in ultrapure water using a Malvern Zetasizer 4. Scanning electron microscopy (SEM) images of the assemblies were recorded using a Nova NanoSEM 600 operating at an acceleration voltage of 5 kV with a working distance of 5 mm and using an ETD detector. The samples were coated with a thin layer of Pt (6 nm). Magnetic measurements were performed using the VSM option in a physical property measurement system from Quantum Design. Virgin curves were recorded at 300 K up to an external field of 1 T. M–T curves were measured in the range of 290–310 K by applying a magnetic field of 10 mT. The magnetophoretic mobility coefficient (ξ) was calculated according to the following expression:
Giant unilamellar vesicle (GUV) assembly
Giant unilamellar vesicles (GUVs) with different lipid compositions were assembled by an emulsion transfer method. For example, 0.5 μL of biotinyl-PE (10 mg mL−1 in chloroform), 0.5 μL of lissamine rhodamine PE (for visualization, 1 mg mL−1 in chloroform) and 9.5 μL of DOPC (10 mg mL−1 in chloroform) were mixed in 50 μL of chloroform before 500 μL of mineral oil were added. The mixture was vortexed and heated at 80 °C for 40 min to remove the remaining chloroform. Next, to a 1.5 mL Eppendorf tube containing 200 μL of an isotonic solution, 300 μL of the mixture were added carefully and allowed to stand for at least 10 min. (Note: isotonic solution contains 0.9% NaCl and 5% glucose dissolved in ultrapure water.) To prepare empty GUVs, 20 μL of sucrose solution (300 mM) were added to the previous mixture and vortexed at high speed for 30 s. The emulsion was centrifuged at 3000 rpm for 30 min at RT and the GUVs were collected from the bottom of the Eppendorf tube, termed GUVZ. GUVs were always stored at 4 °C and used within 24 h. To encapsulate xMM inside the GUV, 20 μL of the xMM stock solution were added instead of the sucrose solution. The GUVs were visualized on a bright-field microscope (Olympus IX81) equipped with a fluorescence lamp. The images were pseudo-colored for visualization purposes using Fiji.Other lipid-based GUVs were prepared by changing the lipid composition in the initial step. Specifically, to prepare GUV−, 1 μL of DOPS (10 mg mL−1 in chloroform) and 8.5 μL of DOPC (10 mg mL−1 in chloroform) were used instead of only 9.5 μL of DOPC. GUVs containing saturated lipids were prepared by replacing DOPC with DPPC (10 mg mL−1 in chloroform), resulting in the GUVS. For experiments made in sucrose, a sucrose solution (300 mM) was used instead of the isotonic solution. A summary of all compositions can be found in ESI Table S2.†
The general polarization (GP) values were determined as an indication of membrane packing (fluidity) of the GUVs using the Laurdan probe.43,44 For this, 100 μL of GUVs including 2.5 μL of Laurdan (100 μM stock solution in DMSO, final concentration of 2.5 μM) were added to a black 96-well plate, followed by shaking the plate (300 rpm) for 45 min and recording the emission spectra from λem = 390–590 nm using an excitation wavelength of λex = 340 nm in a multi-well plate reader (PerkinElmer Ensight). The Laurdan spectra were normalized to the intensity peak at λem = 490 nm. The GP was calculated according to the following equation:
Locomotion
| ΔL2 = 2DeffΔt + v2Δt2, |
(1) If |R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) linear − R2
linear − R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wedge| < 0.1, then consider the fit as linear. R2
wedge| < 0.1, then consider the fit as linear. R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) linear and R2
linear and R2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) wedge are the coefficinets of multiple correlation resulting from the linear and wedge funtion fits, as described in the main text.
wedge are the coefficinets of multiple correlation resulting from the linear and wedge funtion fits, as described in the main text.
(2) If linear, then decide if slow (inside the GUVs) or fast (outside the GUVs) swimming as:
Slow (inside): if νmean < νensemble (group 1)
Fast (outside): if νmean > νensemble (group 2)
Here, νmean represents the mean velocity calculated over the trajectory of a motor, and νensemble is the mean velocity of the entire batch (ensemble) of motors.
(3) If not linear (then wedge), then analyze only those motors whose maximum velocities are above the standard deviation of the noise in the velocity data across the trajectory. Next, decide if motion is:
Slow–fast: if νinside < νoutside (group 5)
Fast–slow: if νinside > νoutside (group 3)
Move–stop: if νinside > 0.2 × νensemble (i.e., increase the scale from 5% to 20% of the ensemble mean velocity) (group 4).
(4) Otherwise not classified (group 5).
| Momentum = mmotor(νinside − νoutside), |
where RP is the particle (motor) radius, xIO is the fraction of the magnetic material calculated from the VSM data and ρPS = 1050 kg m−3 and ρIO = 5240 kg m−3 are the densities of polystyrene and iron oxide, respectively.
GUV membrane crossing
where A0 and An are the initial and final values of the curve, and τ and p are parameters that describe the half-time when the motors filled the GUV and the rate which with they do so, respectively.
Author contributions
MARD: conceptualization, investigation, methodology, validation, visualization, writing – original draft, and writing – review and editing. OH: software, data curation, and writing – review and editing. BS: conceptualization, funding acquisition, project administration, resources, writing – original draft, and writing – review and editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by a Carlsberg Foundation Distinguished Associate Professor Fellowship (B.S. CF16-0233) and the Lundbeck Foundation. The authors thank Prof. Mogens Christensen (Department of Chemistry, Aarhus University) and Dr Kasper Borup (Department of Chemistry, Aarhus University) for performing the magnetic measurements of the samples.References
- A. Ghosh, W. Xu, N. Gupta and D. H. Gracias, Nano Today, 2020, 31, 100836 CrossRef CAS PubMed.
- G. T. van Moolenbroek, T. Patiño, J. Llop and S. Sánchez, Adv. Intell. Syst., 2020, 2, 2000087 CrossRef.
- A. Rastmanesh, M. Tavakkoli Yaraki, J. Wu, Z. Wang, P. Ghoderao, Y. Gao and Y. N. Tan, Mol. Syst. Des. Eng., 2021, 6, 566–593 RSC.
- J. Lv, Y. Xing, T. Xu, X. Zhang and X. Du, Appl. Mater. Today, 2021, 23, 101034 CrossRef.
- L. Wang, X. Hao, Z. Gao, Z. Yang, Y. Long, M. Luo and J. Guan, Interdiscip. Mater., 2022, 1, 256–280 CrossRef.
- P. L. Venugopalan, B. Esteban-Fernández De Ávila, M. Pal, A. Ghosh and J. Wang, ACS Nano, 2020, 14, 9423–9439 CrossRef CAS PubMed.
- H. Yuan, X. Liu, L. Wang and X. Ma, Bioact. Mater., 2021, 6, 1727–1749 CrossRef CAS PubMed.
- X. Arqué, T. Patiño and S. Sánchez, Chem. Sci., 2022, 13, 9128–9146 RSC.
- C. Lv, Y. Yang and B. Li, Micromachines, 2022, 13, 307 CrossRef PubMed.
- M. Fernández-Medina, M. A. Ramos-Docampo, O. Hovorka, V. Salgueiriño and B. Städler, Adv. Funct. Mater., 2020, 30, 1–17 CrossRef.
- M. A. Ramos Docampo, Adv. Biol., 2023, 7, 2200308 CrossRef PubMed.
- Z. Xiao, M. Wei and W. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 6667–6684 CrossRef CAS PubMed.
- F. Mou, J. Zhang, Z. Wu, S. Du, Z. Zhang, L. Xu and J. Guan, iScience, 2019, 19, 415–424 CrossRef PubMed.
- K. Yuan, M. Pacheco, B. Jurado-Sánchez and A. Escarpa, Adv. Intell. Syst., 2021, 3, 2100002 CrossRef.
- M. Yang, Y. Zhang, F. Mou, C. Cao, L. Yu, Z. Li and J. Guan, Sci. Adv., 2023, 9, eadk7251 CrossRef CAS PubMed.
- M. A. Ramos-Docampo, P. Hurtado, A. B. Dávila-Ibáñez, R. Piñeiro, M. L. Fanarraga and V. Salgueiriño, J. Colloid Interface Sci., 2022, 629, 287–296 CrossRef PubMed.
- M. A. R. Docampo, X. Qian, C. Ade, T. F. Marcelino, M. Ceccato, M. Foss, O. Hovorka and B. Städler, Adv. Mater. Interfaces, 2022, 2201509 Search PubMed.
- G. Tezel, S. S. Timur, F. Kuralay, R. N. Gürsoy, K. Ulubayram, L. Öner and H. Eroğlu, J. Drug Targeting, 2020, 29, 29–45 CrossRef PubMed.
- A. Del Valle, J. Torra, P. Bondia, C. M. Tone, P. Pedraz, V. Vadillo-Rodriguez and C. Flors, ACS Appl. Mater. Interfaces, 2020, 12, 31235–31241 CrossRef CAS PubMed.
- C. Liu, P. Elvati, S. Majumder, Y. Wang, A. P. Liu and A. Violi, ACS Nano, 2019, 13, 10221–10232 CrossRef CAS PubMed.
- A. Singhal and G. J. Agur Sevink, Nanoscale Adv., 2021, 3, 6635–6648 RSC.
- X. Zhang, G. Ma and W. Wei, NPG Asia Mater., 2021, 13, 52 CrossRef CAS.
- V. Sharma, E. Azar, A. P. Schroder, C. M. Marques and A. Stocco, Soft Matter, 2021, 17, 4275–4281 RSC.
- M. Winkens, A. Vilcan, P. J. De Visser, F. V. De Graaf and P. A. Korevaar, Small, 2023, 2206800 CrossRef CAS PubMed.
- D. Takagi, J. Palacci, A. B. Braunschweig, M. J. Shelley and J. Zhang, Soft Matter, 2014, 10, 1784–1789 RSC.
- S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411 RSC.
- S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147 CrossRef.
- N. Desai, V. A. Shaik and A. M. Ardekani, Soft Matter, 2018, 14, 264–278 RSC.
- S. Song, A. Llopis-Lorente, A. F. Mason, L. K. E. A. Abdelmohsen and J. C. M. Van Hest, J. Am. Chem. Soc., 2022, 144, 13831–13838 CrossRef CAS PubMed.
- J. Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90 CrossRef CAS PubMed.
- W. Rawicz, K. C. Olbrich, T. Mcintosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339 CrossRef CAS PubMed.
- K. Olbrich, W. Rawicz, D. Needham and E. Evans, Biophys. J., 2000, 79, 321–327 CrossRef CAS PubMed.
- A. C. Fischer-Cripps, J. Mater. Sci., 1999, 34, 129–137 CrossRef CAS.
- M. Sousa De Almeida, E. Susnik, B. Drasler, P. Taladriz-Blanco, A. Petri-Fink and B. Rothen-Rutishauser, Chem. Soc. Rev., 2021, 50, 5397–5434 RSC.
- J. J. Rennick, A. P. R. Johnston and R. G. Parton, Nat. Nanotechnol., 2021, 16, 266–276 CrossRef CAS PubMed.
- F. G. Strobl, D. M. Czubak, A. Wixforth and C. Westerhausen, J. Phys. D: Appl. Phys., 2019, 52, 294001 CrossRef CAS.
- C. Contini, J. W. Hindley, T. J. Macdonald, J. D. Barritt, O. Ces and N. Quirke, Commun. Chem., 2020, 3, 1–12 CrossRef PubMed.
- Y. Qiao, M. Li, R. Booth and S. Mann, Nat. Chem., 2017, 9, 110–119 CrossRef CAS PubMed.
- N. Gao, C. Xu, Z. Yin, M. Li and S. Mann, J. Am. Chem. Soc., 2022, 144, 3855–3862 CrossRef CAS PubMed.
- K. W. Dunn, M. M. Kamocka and J. H. McDonald, Am. J. Physiol.: Cell Physiol., 2011, 300, 723–742 CrossRef PubMed.
- P. De Dios Andres, M. A. Ramos-Docampo, X. Qian, M. Stingaciu and B. Städler, Nanoscale, 2021, 13, 17900–17911 RSC.
- P. de Dios Andres and B. Städler, Small, 2022, 19, 2201251 CrossRef PubMed.
- T. Parasassi, G. De Stasio, G. Ravagnan, R. M. Rusch and E. Gratton, Biophys. J., 1991, 60, 179–189 CrossRef CAS PubMed.
- A. G. Jay and J. A. Hamilton, J. Fluoresc., 2017, 27, 243–249 CrossRef PubMed.
- N. Tarantino, J.-Y. Tinevez, E. F. Crowell, B. Boisson, R. Henriques, M. Mhlanga, F. Agou, A. Israel and E. Laplantine, J. Cell Biol., 2014, 204, 231–245 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Magnetic motor assembly and locomotion analyses, locomotion of PEGylated motors, GUV assembly and details, experimental setup and specific cases of motors crossing GUVs. See DOI: https://doi.org/10.1039/d3nr05462d |
| This journal is © The Royal Society of Chemistry 2024 |