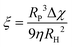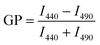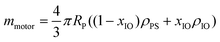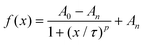Magnetic micromotors crossing lipid membranes

Abstract

Nano/micromotors are self-propelled particles that show enhanced motion upon being triggered by a stimulus. Their use in nanomedicine has been widely explored, with special focus on imaging or drug delivery. However, a thorough understanding of the requirements for more efficient locomotion is still lacking. In this paper, we assembled magnetically propelled motors of different sizes (i.e., 0.5, 1 and 4 μm) and surface chemistries (positive charge or PEGylated) and assessed their motion in the presence of giant unilamellar lipid vesicles (GUVs) of varying compositions (zwitterionic, negatively charged and saturated lipids). Unexpectedly, the size does not seem to be the dominating characteristics that governs the ability of the motors to cross lipid membranes. Specifically, the 0.5 μm PEGylated motors have very limited ability to cross the lipid membrane of GUVs due to their non-interacting nature compared to their equally sized positively charged counterparts. Furthermore, membranes made of saturated lipids and, in particular, in combination with a weak magnetic field facilitate motors’ crossing, regardless of their size. The results were validated by in-house data-driven statistical analysis that employs experimental data to allow for the identification of individual motor motion in the ensemble when meeting the lipid membranes. Altogether, we provide insight into motor locomotion when they interact with a biological barrier considering both the entire ensemble and the individual motors, which has the potential to support considerations of future motor designs.

---

Introduction

Nano- and micromotors are active particles that can self-propel outperforming Brownian motion by converting input energy into kinetic energy. Great advances have been witnessed in this field, especially towards their potential in nanomedicine.^1–5 From the first examples in simple, aqueous environments, efforts have evolved towards more complex media (i.e., gels, cellulose, cell media) and eventual in vitro and in vivo experimentations, as reviewed in detail.^6–11 In contrast, the motion of motors in patterned or confined environments¹² and controlling motor swarming^13–15 are still ongoing endeavors.

When it comes to the interaction of motors with mammalian cells, endocytosis is still predominant. There exist some examples where magnetic coatings were used to facilitate the incorporation of nanoparticles inside cells.¹⁶ In addition, the active motion of motors was employed to increase the chances of uptake by cells compared to passive particles¹⁷ or to increase the mobility when performing a task (e.g., drug delivery).¹⁸ Nonetheless, the use of motors’ power to cross or penetrate membranes with the aim to either enter the cell's cytosol or to escape from the endo/lysosomes remains to be thoroughly explored. Although atomic force microscopy experiments have determined that the minimum force to break a bacterial cell membrane was ∼20 nN,¹⁹ the corresponding force for mammalian cells remains debated, as well as it is the impulse (thrust) that a motor needs to achieve during locomotion to cross such membranes. Simulations have been performed with the aim to estimate the dynamics of motors approaching or crossing lipid membranes.^20–22 These models assumed that the motor size was comparable to the thickness of the membrane (few nanometers) and that the viscosity was constant. Furthermore, most of the model-based studies considered magnetic particles, meaning that an active field pulled the particles, due to which they obtained ballistic motion. Complementarily, the interaction between motors and lipid vesicles has been experimentally addressed before.^23,24 Interestingly, these efforts demonstrated that the motors did not cross the membrane to enter the void of the vesicles, but instead, they orbited around the vesicles, which was also supported by theoretical evaluations.^25–28 A recent approach considered encapsulated coacervate-based motors inside lipid vesicles.²⁹ These motors were equipped with catalase for propulsion by the conversion of hydrogen peroxide (H₂O₂) into water and oxygen molecules with diffusion coefficients of up to ∼0.24 μm² s⁻¹ when 3.4 vol% H₂O₂ was used. However, the motors never escaped the lipid vesicles.

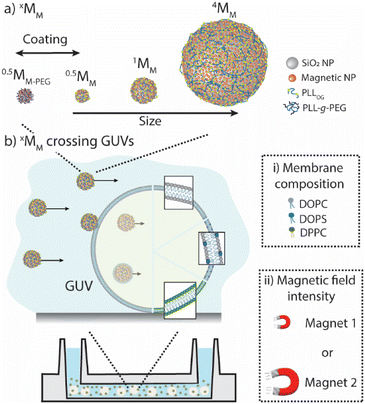
Herein, we experimentally explored how magnetic motors cross the lipid membranes of giant unilamellar vesicles (GUVs). Specifically, we (i) designed magnetic motors with different core sizes and ζ-potentials to determine their maximum speed in an isotonic solution when different magnetic forces were applied; (ii) assembled GUVs with varying membrane compositions to identify the role of membrane fluidity and charge affecting the motors’ crossing; and (iii) evaluated the locomotion of the motors in the presence of GUVs to identify the proportion of the motors in an ensemble that were able to cross the lipid membranes (Scheme 1).

Scheme 1 Magnetic motors that cross lipid membranes. (a) Magnetic motors of different sizes (^xM_M) and terminating coatings assembled using the layer-by-layer technique. (b) Giant unilamellar vesicles (GUVs) prepared by varying the membrane composition (i), which affects their fluidity and ζ-potential. The ability of ^xM_M to cross the lipid membranes of GUVs was evaluated in the presence of different magnetic fields (ii).

Results and discussion

Fundamental characterization of the magnetic motors and giant unilamellar vesicles

We chose the simplest magnetic motor that could be reliably driven and stopped depending on an external magnetic field, as the goal was to identify how they interacted with lipid membranes and not to establish a new type of motor. The magnetic motors were prepared by depositing magnetic, iron oxide nanoparticles onto polystyrene cores of different sizes (i.e., 0.5, 1 and 4 microns), yielding in ^xM_M where x identifies the core size. Note that smaller cores could not be visualized with a regular bright-field microscope, and larger cores sedimented too fast and were too heavy to be pulled by the magnets. Non-interacting motors were prepared by coating ^xM_M with an outer layer of poly(L-lysine)-graft-poly(ethylene glycol) and were referred to as ^xM_M-PEG. (For details about fabrication and characterization, please refer to ESI Fig. S1 and related text and Table S1.†) The mobility of ^xM_M and ^xM_M-PEG was assessed in an isotonic solution (i.e., a solution containing 5 wt% glucose and 0.9 wt% NaCl) and a sucrose solution when exposed to a magnetic field in a microfluidic channel (ESI Fig. S2–S4 and related text and Movie panels S1–S4†). The magnetic field was created using a magnet with a pulling force of either 0.3 N or 2 N, which produced a magnetic flux gradient the motors would be pulled towards. (Note: the magnetic force refers to the force the magnet has to hold a magnetic object, given the provider specifications. The specific magnetic force of the 2 N magnet is ∼8× higher than that of the 0.3 N magnet. For simplicity, the notations magnet 1 and magnet 2 referring to the 0.3 N magnet and the 2 N magnet, respectively, will be used in this article). The maximum velocities were ∼3 μm s⁻¹ for ^0.5M_M and ¹M_M and ∼7 μm s⁻¹ for ⁴M_M in isotonic solution and ∼2× lower in sucrose solution when magnet 2 was used. ^0.5M_M-PEG had a maximum velocity of ∼22 μm s⁻¹ in isotonic solution using magnet 2.

Giant unilamellar vesicles (GUVs) were employed as a simplified model of the cell membrane. GUVs with different membrane properties were assembled, i.e., flexible and zwitterionic (GUV^Z), flexible and negatively charged (GUV⁻), and rigid and zwitterionic (GUV^S), using different lipids (for details about fabrication and characterization, please refer to ESI Fig. S5 and related text and Table S2†). With the aim to assess the motors’ motion behavior when encountering the GUV membranes, ^xM_M were encapsulated in the GUVs’ void by an emulsion transfer method. These samples were employed in all the subsequent experiments, unless specified otherwise.

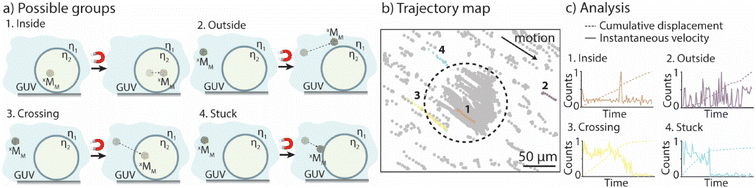
Data-driven statistical analysis of ^xM_M locomotion

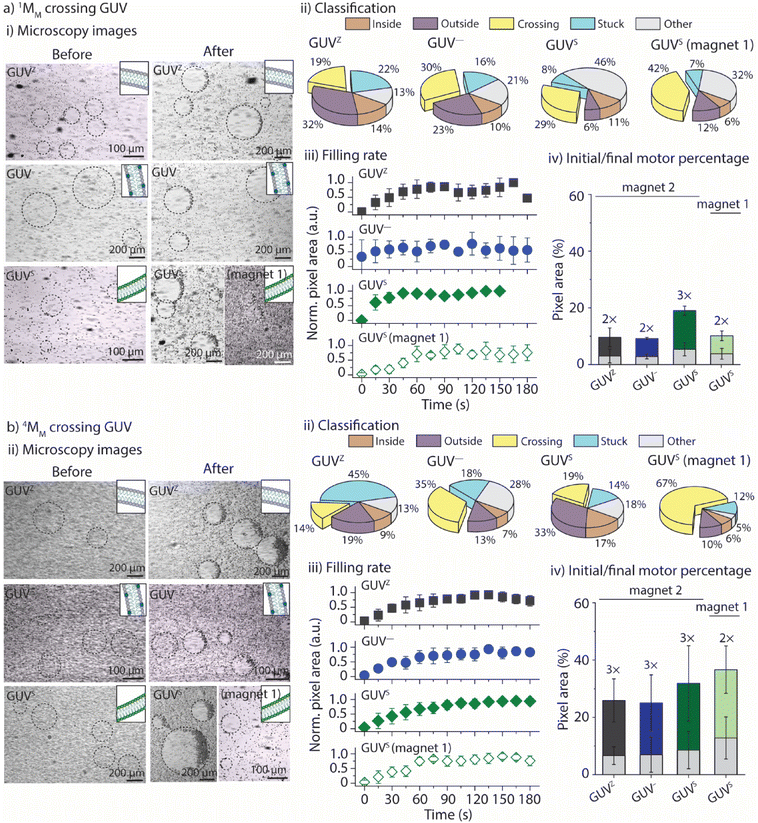
The goal was to evaluate if and when ^xM_M were able to cross the GUV membranes. The solutions with the GUVs and motors were suspended in a non-coated ibidi microfluidic channel, bright-field images were taken before a magnetic field was applied and movies of the moving motors when exposed to the magnets were recorded for up to 3 min. The motor's motion was tracked as previously described³⁰ (for details, please refer to the Experimental section). In addition, an in-house Python code was developed, which allowed to separate the motors into five groups depending on their motion properties (see the Experimental section for more details). Group 1 and group 2 contained motors that moved only in the void of the GUVs and in the surrounding solution, respectively. Motors that crossed the membranes of the GUVs were part of group 3, while group 4 contained the motors that got stuck either in the membrane of the GUVs or on the surface of the microfluidic channels (Fig. 1a). The trajectory maps of a sample were extracted and analyzed using the Python code (Fig. 1b). The code uses the cumulative displacement and the instantaneous velocity of each individual motor in an ensemble of ∼300 motors for their classification (Fig. 1c). Motors that exhibited linear fits to their cumulative displacement and had velocities below the average velocity of the ensemble were assigned to group 1, representing motors confined within the GUVs. Motors that displayed linear fits but had velocities surpassing the average velocity of the ensemble were designated as group 2, signifying motors remaining outside the GUVs. A piecewise linear (wedge) function was applied to their cumulative displacement curves for motors exhibiting variable velocities. If the slope following the wedge was found to be non-zero, the motors were categorized as group 3, indicating their ability to cross the GUV membrane. If the slope following the wedge was close to zero, the motors were assigned to group 4, representing motors that were immobilized or trapped within the GUV membrane or on the surface of the channel. (We would like to note that we cannot distinguish between these two phenomena thus far.) Motors that did not meet any of the aforementioned criteria were classified in an additional group referred to as “other”. Note that this group also contained motors with a velocity profile where the slope before the wedge was lower than that after the wedge, pointing towards motors that might be able to escape the GUVs. However, it was challenging to observe these motors in the movies due to their very low number and the low resolution of the microscope.

Fig. 1 Classification of the motors according to their motion behavior. (a) Schematic showing the different groups in a population of motors. Group 1: motors in the void of the GUVs; group 2: motors in the surrounding solution; group 3: motors crossing the GUV membrane; group 4: motors getting trapped in the membrane. (b) Simplified trajectory map of ^0.5M_M (light grey) in the presence of GUV^Z (dotted black line). Representative trajectories for the four groups are indicated as colored trajectories. Group 1 (orange), group 2 (purple), group 3 (yellow) and group 4 (light blue). (c) Examples of the cumulative displacement (solid lines) and the instantaneous velocity (dotted lines) of a representative motor in each of the four groups.

Effect of surface chemistry and medium viscosity

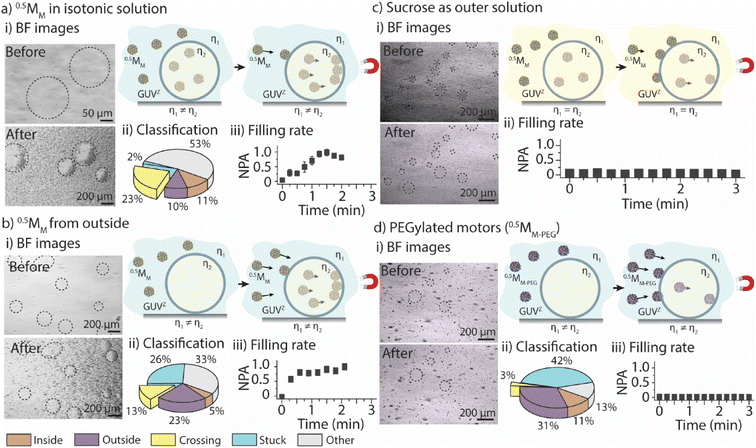
The first goal was to determine the parameters that govern the motors’ ability to cross the GUV^Z membranes depending on the viscosity of the medium by comparing the positively charged ^0.5M_M with the inert ^0.5M_M-PEG. The inside of the GUVs (i.e., the sucrose solution) had a ∼2× higher viscosity than the isotonic solution in the surrounding. Magnet 2 was employed for the experiments. (For details about the setup, please refer to ESI Fig. S6.†)

Initially, GUV^Zs containing ^0.5M_M were evenly distributed in the microfluidic channel. Following the application of a magnetic field, the GUV^Zs partially filled with ^0.5M_M were able to cross the membranes, showing an accumulation of ^0.5M_M in one hemisphere of the GUV^Zs (Fig. 2ai and ESI Movie panel S5†). This accumulation indicated that ^0.5M_M decelerated after having crossed the membranes, which resulted in the inability of ^0.5M_M to leave the void of the GUV^Z. This observation was ascribed to the reduced magnetophoretic mobility of ^0.5M_M in the viscous environment inside the GUV^Zs. It is noteworthy to emphasize that the GUV^Zs were not disrupted upon ^0.5M_M crossing and accumulation. We speculated that the pressure exerted in the GUV^Zs’ membrane was rather low, and the flexibility of the membrane allowed for rapid self-healing after the crossing of ^0.5M_M.^31,32

Fig. 2 ^0.5M_M interacting with the GUV^Z. Comparative analysis of ^0.5M_M in isotonic solution when motors are (a) encapsulated, (b) added from outside, and using (c) sucrose as the outer solution and (d) PEGylated motors. Representative bright-field (BF) microscopy images of the interaction with the GUV^Z before and after pulling the motors with the magnetic field (i), classification of the motors represented as pie charts (aii, bii, and dii), and filling rate curves (aiii, biii, cii, and diii; NPA: normalized pixel area). Data are shown as the mean ± standard deviation (n = 3–5). Cartoons illustrate the different scenarios before and after applying the magnetic field.

Following the determination of the cumulative displacement and the instantaneous velocity, ^0.5M_M were classified into the above defined five groups (Fig. 2aii). A similar amount of ∼10% of ^0.5M_M was part of group 1 and group 2 (moving only inside or outside of the GUV^Z, respectively), while close to zero ^0.5M_M remained stuck (group 4) and ∼23% of ^0.5M_M were able to cross the lipid membranes (group 3) and accumulated inside the GUV^Z. We also noticed that a fraction of ^0.5M_M in the “other” group represented ∼53% of the total number of motors. However, we cannot explain this observation.

The accumulation of ^0.5M_M inside the GUV^Z was semi-quantitatively analyzed by extracting the movie frames, followed by their conversion into binary images (where the white pixels correspond to the motors and the black pixels correspond to the background). The white pixel area inside the regions of interest (i.e., the GUV^Z) was obtained as a function of time (Fig. 2aiii) and normalized to the highest value (white pixel area at t = 3 min). ^0.5M_M showed an accumulation inside the GUV^Z that reached a plateau after ∼60 s.

In the next step, we aimed to verify that the increase in the number of ^0.5M_M in the void of the GUV^Zs upon exposure to the magnetic field was due to the penetration of ^0.5M_M from outside and not only due to the accumulation of the encapsulated ^0.5M_M in the GUV^Z. To this end, empty GUV^Zs were mixed with ^0.5M_M, added to the microfluidic channels and movies were recorded when the magnetic field was applied, followed by the classification of the individual ^0.5M_M in the 4 groups (Fig. 2bi and ESI Movie panel S5†). Only ∼5% of ^0.5M_M were moving inside of the GUV^Z, but importantly ∼13% of ^0.5M_M crossed the membrane (Fig. 2bii). The majority of ^0.5M_M either remained in the surrounding solution or were trapped in the membrane of GUV^Z. It should be noted that a rather large portion of ^0.5M_M was stuck compared to the first outlined situation. We attributed this observation to the fact that the organization of the GUV^Z membrane was affected by the presence of ^0.5M_M during assembly. Nonetheless, the increment of the pixel area corresponding to ^0.5M_M inside of the GUV^Z was calculated and found to be similar as above, confirming that ^0.5M_M were indeed able to cross the lipid membranes and accumulate in the GUV^Z's void (Fig. 2biii).

Next, we aimed to understand if ^0.5M_M with lower velocity could also cross the membrane of the GUV^Z. To this end, GUV^Zs containing ^0.5M_M were added in the microfluidic channel filled with sucrose before recording movies with the applied magnetic field (Fig. 2di and ESI Movie panel S5†). In this context, it was not possible to analyze the differences in motion with the current model, due to the similar velocities ^0.5M_M displayed inside and outside the GUV^Zs. However, the filling rate analysis showed only a little penetration of ^0.5M_M to the inside of the GUV^Zs (Fig. 2dii), which was explained by the fact that the magnetophoretic mobility of the motors was inversely proportional to the viscosity of the medium.

Finally, ^0.5M_M-PEG were considered as an inert alternative to the positively charged ^0.5M_M to determine the impact of the surface chemistry of the motors on their ability to cross the membrane of the GUV^Z. Empty GUV^Zs were mixed with ^0.5M_M-PEG, added to the microfluidic channels, and the movies were recorded when the magnetic field was applied. Representative bright-field microscopy images suggested that very limited penetration of ^0.5M_M-PEG across the membrane occurred (Fig. 2ci and ESI Movie panel S5†). The classification revealed that most ^0.5M_M-PEG in the ensemble belonged either to group 2 or 4, i.e., they either moved outside of the GUV^Zs or were trapped in the membrane or on the surface of the microfluidic channel, respectively. Only a very low fraction of ^0.5M_M-PEG was able to cross the membrane (Fig. 2cii), which was also confirmed by analyzing the filling rate (Fig. 2ciii). We would like to note that ^0.5M_M-PEG had higher velocities than ^0.5M_M, which means that not only the velocities, but also the interaction of the lipid membrane with the surface of the motors was an important aspect to consider. In the current case, the inert nature of ^0.5M_M-PEG was the dominating factor over the motor size.

Effect of the GUV membrane fluidity and composition

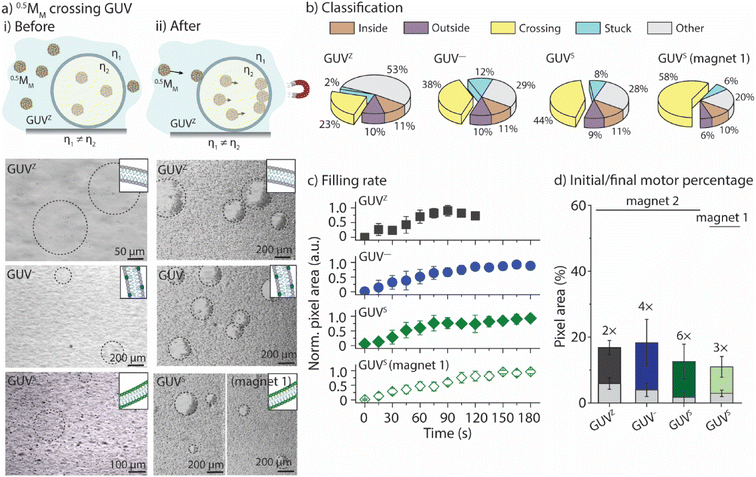
We aimed to correlate the lipid composition of the GUV membrane with the ability of ^0.5M_M to cross the membranes. To this end, ^0.5M_M were employed together with the GUV^Z, GUV⁻, and GUV^S. Bright-field microscopy images were taken before and after ^0.5M_M were exposed to the magnetic field for 3 min (Fig. 3a and ESI Movie panel S6†). In general, ^0.5M_M were able to cross the membranes of all four types of GUVs. Next, the locomotion of the individual ^0.5M_M was classified into the five groups (Fig. 3b). The percentage of ^0.5M_M crossing the membranes increased from ∼23% to ∼38% for the GUV^Z and GUV⁻, respectively, when magnet 2 was used. We hypothesized that negatively charged membranes of GUV⁻ had a beneficial interaction with the positively charged ^0.5M_M when they approached, which increased the chances of penetration. The percentage of ^0.5M_M that were able to cross was also higher when GUV^Ss were considered (∼44%). We attributed this observation to the fact that the less fluid membranes in the GUV^S 19 compared to the GUV^Z and GUV⁻ might have absorbed a smaller part of the energy transferred during the impact and therefore increased the crossing probability. Additionally, ∼58% ^0.5M_M were able to cross the membrane of the GUV^S when magnet 1 was used. The reason behind this might be ascribed to the slow velocities ^0.5M_M reached in this case, which increased the retention time in the membrane and favored the crossing since the magnetic field was still pulling.

Fig. 3 ^0.5M_M crossing GUV membranes. (a) Representative bright-field microscopy images of the interaction with the GUV^Z, GUV^–, and GUV^S before (i) and after (ii) exposure to magnet 2 or magnet 1. (b) Classification of ^0.5M_M and (c) their filling rate curves into the GUVs. (d) Percentage of ^0.5M_M trapped inside the GUVs after exposure to the magnetic field, represented as the pixel area. Light grey and colored bars refer to the pixel counting of the number of ^0.5M_M before and after exposure to the magnets, respectively. Data are shown as the mean ± standard deviation (n = 3–5).

The movies were analyzed as outlined before to obtain the time-dependent normalized white pixel area inside of the GUVs (Fig. 3c). Furthermore, a logistic function was fitted to these data in order to obtain a more quantitative analysis (ESI Fig. S7†). A logistic function is an S-shaped curve that allows for sequential analysis to a distribution-free accumulation of data within a boundary. The function has two main parameters, named here τ and p. τ relates to the half-time the motors needed to fill the GUVs that is associated with the permeation time, i.e., τ depends on the motor velocity, membrane fluidity and medium viscosity. p is the rate by which ^0.5M_M filled up the GUVs, and is related to the permeability of the membrane towards the motors.¹⁷τ obtained from the fitting was below 70 s in all cases when magnet 2 was used (ESI Table S3†), meaning that the GUVs were filled to half of their final capacity within the same time, independent of the membrane composition. As expected, τ became longer when magnet 1 was used, indicating that the motors needed more time to cross the membrane as they moved slower. The fitted value for p ranged from 1.6 s⁻¹ to 1.9 s⁻¹, independent of the membrane composition or the magnetic field strength.

Furthermore, the difference between the initial amount of ^0.5M_M encapsulated inside the GUV and the final amount present after the application of the magnetic field was calculated (Fig. 3d). To do so, the images were converted into binary and the number of white pixels related to the motors was determined and expressed as a percentage related to the total number of pixels in the image. The initial area occupied by the motors in all cases was smaller than the end-point value, indicating an increase in the number of motors inside the GUV, i.e., ^0.5M_M crossed the membranes upon applying the magnetic field. However, ^0.5M_M showed differences in the crossing efficiency as indicated by varied final areas depending on the membrane composition (Fig. 6d). Specifically, the final number of ^0.5M_M increased 2-fold when GUV^Zs were used. In contrast, a 4× increase was found for the GUV⁻. This observation suggested that the interaction of the negatively charged GUV⁻ with the positively charged ^0.5M_M had a positive effect on the crossing ability of ^0.5M_M. The concentration of the negatively charged DOPS lipids was increased from 10 vol% to 50 vol% (resulting in GUV⁵⁰⁻) in an attempt to support this explanation. The results showed that ^0.5M_M were able to cross with values of τ and p of 8 s and 2.3 s⁻¹, respectively, suggesting that the GUV⁵⁰⁻ membranes were much more permeable toward ^0.5M_M than the GUV⁻ (ESI Fig. S8 and Movie panel S7†). This analysis also confirmed that ^0.5M_M could more easily cross the membrane of the GUV^S than the GUV^Z already observed when classifying the individual ^0.5M_M in the ensemble. It should be noted that when magnet 1 was employed, ^0.5M_M were half as efficient in entering the GUV^S void compared to when magnet 2 was used. This observation was ascribed to the constant time frame that ^0.5M_M had to cross the GUVs, as they moved slower compared to when magnet 2 was employed.

Effect of the motor size

In the next step, we aimed to identify how the motors’ size affected their ability to cross the GUV membranes. To do so, ¹M_M and ⁴M_M were used, and their interaction with the four different GUVs was assessed. Samples were prepared as outlined before, and the movies were recorded up to 3 min during exposure to either magnet 1 or magnet 2 (Fig. 4ai, bi and ESI Movie panel S8 and S9†). Even these larger motors were able to cross the membrane without disrupting the GUVs, independent of the lipid composition. Their locomotion was classified into the five groups as outlined above (Fig. 4aii and bii). Both ¹M_M and ⁴M_M displayed a similar behavior to ^0.5M_M with the percentages of crossing motors varying from ∼19% to ∼30% and ∼29% for ¹M_M crossing GUV^Z, GUV⁻ and GUV^S, respectively, and from ∼14% to ∼35% and ∼19% for ⁴M_M crossing the GUV^Z, GUV⁻ and GUV^S, respectively, in the presence of magnet 2. While the percentages of ¹M_M and ⁴M_M crossing the membranes of GUV^Z and GUV⁻ were similar, higher numbers of ¹M_M seemed to have crossed the membrane of GUV^S compared to ⁴M_M, but with the available data it was difficult to speculate about the origin of this observation. Furthermore, the percentage of ¹M_M and ⁴M_M crossing the GUV^S when magnet 1 was used increased up to ∼42% and ∼67%, respectively, as they moved slower and had more time to interact with the GUV membrane to eventually cross.

Fig. 4 ¹M_M (a) and ⁴M_M (b) crossing GUV membranes. Representative bright-field microscopy images of the interaction with the GUV^Z before and after pulling the motors with the magnets (i), classification of the motors (ii), filling rate curves (iii) and percentage of motors trapped inside the GUVs after exposure to the magnetic field, represented as the pixel area (iv). Light grey and colored bars refer to the number of motors before and after exposure to the magnetic field, respectively. Data are shown as the mean ± standard deviation (n = 3).

The quantification of pixels corresponding to the presence of ¹M_M and ⁴M_M trapped inside the GUVs indicated a lower count compared to GUVs where ^0.5M_M used. The normalized white pixel area inside the GUVs was determined as a function of time and fitted to a logistic function to calculate the parameters τ and p (Fig. 4aiii and biii). First, τ became generally shorter with increasing motor size from ∼44 s to ∼35 s and ∼24 s for ^0.5M_M, ¹M_M and ⁴M_M, respectively, independent of the GUV lipid composition. This observation agreed with the fact that larger motors had faster velocities, and thus they needed less time to fill the same area inside the GUV's cavity. It should also be noted that the motor size for ¹M_M and ⁴M_M dominated over the lipid composition of the GUVs. As expected, τ became longer when magnet 1 was used, indicating that the motors needed more time to cross the membrane since they moved slower. In addition, there was a general trend to smaller p with increasing motor size from 1.9 s⁻¹ to 1.2 s⁻¹ and 0.8 s⁻¹ for ^0.5M_M, ¹M_M and ⁴M_M, respectively, suggesting that the GUVs showed lower permeability towards larger motors, independent of their lipid composition. This observation can be rationalized by considering that the motors and membranes of GUVs approximate the Hertzian model,³³ which involves a hard sphere and a soft plane. According to this model, the contact area between the two materials increases as the spherical particle size decreases. Finally, both ¹M_M and ⁴M_M showed that a similar number of motors was able to cross into the GUVs’ voids (within the experimental error), independent of the membrane composition (Fig. 4aiv and biv). It is noteworthy to mention that ⁴M_M displayed the largest total number of motors entrapped inside the GUVs due to the inherent larger area these motors occupied and that was not considered (i.e., normalized) when analyzing the pixel count.

Taking these observations together, we aimed to estimate the thrust (impulse) that the ^0.5M_M, ¹M_M and ⁴M_M needed to cross the membranes of the GUV^Z, GUV⁻ and GUV^S, calculated as the linear momentum (Fig. 5). To this end, we considered the mass of the motors and the difference in velocity before and after crossing the membranes. These findings suggested that first ⁴M_M had more potential to cross the GUV membranes compared to ¹M_M or ^0.5M_M, as expected since they had the highest mass. Second, ¹M_M and ⁴M_M had a higher momentum when crossing the GUV^Z and GUV⁻ membranes, which might indicate that these more fluid membranes required a lower energy penalty to be penetrated compared to the more rigid GUV^S membranes. This observation might seem counterintuitive when considered the results discussed above, where more rigid membranes increased the chances of crossing. However, we hypothesized that the energy cost (i.e., transfer of momentum) when the motors crossed the GUV^S was higher, as they had to overcome a stiffer membrane compared to the GUV^Z and GUV⁻. Third, there was a trend observable that all motors crossing the GUV⁻ had the highest momentum, which might be explained by the electrostatic attraction between the motors and the GUV⁻. Finally, there were barley any differences in momentum for ^0.5M_M, and we assumed that the smallest motors required less energy to deform the membrane and cross, reducing the transfer of momentum.

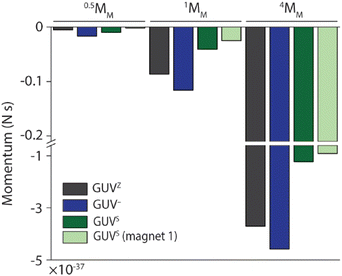Fig. 5 Thrust (impulse) calculated as the linear momentum of ^0.5M_M, ¹M_M and ⁴M_M crossing GUV membranes.

GUV membrane integrity upon ^xM_M crossing

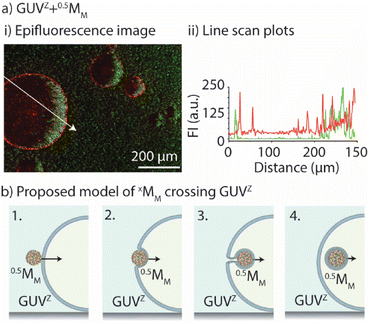
In common phago/endocytosis, the mammalian cell engulfs molecules, fluids, or nanomaterials for transport inside of the cell via invagination of the membrane, without any negative effect on the membrane integrity.^34,35 In this context, artificial endocytosis/recruitment of nanoparticles using either GUVs^36,37 or coacervates^38,39 has been experimentally illustrated. Consequently, we aimed to get a better understanding of how ^xM_M crossed the GUVs’ membrane by determining if ^xM_M had lipids deposited on their surface following the crossing and how the membrane permeability was affected by the crossing of ^xM_M.

First, we evaluated whether the motors had a lipid coating after crossing the GUV's membrane. To do so, epifluorescence microscopy images were taken after GUV^Z containing ^0.5M_M were exposed to magnet 2 (Fig. 6a). Regardless of whether ^0.5M_M or ⁴M_M were considered, the outcome was similar because the presence of lipids adhering to the surface of motors after crossing the membrane was anticipated to be unrelated to their size (ESI Fig. S9a and b†). Overlapping of the fluorescence signals originating from the fluorescent-labelled lipid Rho-PE and the motors coated with PLL_OG (resulting in yellow color in the images) was observed independent of the type of used GUV, confirming that the mechanism of crossing was very likely the same for all types of motors and GUVs (ESI Fig. S8a and b†). (Please note that motors that did not cross the membranes had only a fluorescence signal originating from PLL_OG, shown in green.) Furthermore, line scan plots were extracted from the epifluorescence microscopy images (path indicated as a white arrow). The intensity maxima for the signal originating from Rho-PE were found in the positions that match with the GUV membrane (indicated by dotted white lines) as well as in the positions where the motors accumulated inside of the GUVs. In contrast, the signal originating from PLL_OG had the maxima corresponding to the area where ⁴M_M accumulated due to the magnetic field. In an attempt to more quantitatively assess the images, the Manders’ correlation coefficient⁴⁰ was calculated to determine the level of colocalization between the fluorescence signal from Rho-PE (red) and PLL_OG (green) (ESI Table S4†). There was a strong correlation in the green-to-red signal, indicating that many ^0.5M_M and ⁴M_M overlapped with the lipids, suggesting that the motors had parts of the GUV lipid membrane on their surface. It should be noted that not all motors that crossed the membrane showed a fluorescence signal originating from the lipids. We hypothesized that the visible inhomogeneous distribution of Rho-PE in the GUV membrane and/or that the amount of Rho-PE was too small, and thus not all the motors that crossed the GUV membrane picked up a detectable amount of Rho-PE.

Fig. 6 Membrane integrity and permeability upon motor crossing. (a) Representative epifluorescence microscopy images of ^0.5M_M (i) crossing the GUV^Z upon applying the magnetic field and line scan plots of the epifluorescence image (ii). (Green: PLL_OG, red: Rho-PE.) The white arrow indicates the profile path (n = 2). (b) Schematics 1–4 illustrate the proposed process of crossing and membrane engulfment. The decreasing size of the black arrows indicates the deceleration of the motor after crossing.

Following on, the recovery of the GUV membrane upon motor crossing was assessed by employing 5(6)-carboxy-X-rhodamine (RhoX), a molecule that could only trespass to the inside of the GUV through defects in the membrane. In other words, RhoX was used as a tracer to determine if there were changes in the membrane integrity due to the crossing motors. ^0.5M_M, ¹M_M and ⁴M_M were added to RhoX solution and mixed with the empty GUV^Z, followed by recording epifluorescence microscopy images before and after exposure to magnet 2 (ESI Fig. S9c†). Initially, a homogeneous fluorescence signal originating from RhoX in the environment of the GUV^Z was observed. After exposure to the magnet, red fluorescent aggregates were observed in the void of the GUV^Z, suggesting that RhoX crossed the membranes by sticking to the motor's surfaces and not as free molecules. The surrounding showed similar fluorescent aggregates, supporting this explanation together with the fact that RhoX has carboxylic groups that likely interacted with the positive surface charge of the motors. The line scan plots supported these findings. The minima of the plots before applying the magnetic field matched the voids of the empty GUVs. The same minima displayed spikes after exposure to the magnet due to the accumulation of RhoX associated with the motors inside the GUVs.

Taking these observations together, we proposed a mechanism to explain the process of crossing (Fig. 6b). First, the motors met the GUV membrane and associated with it (1). Due to the pulling force of the magnet field, the motors were pushed inside of the GUVs (2). This process occurred through membrane engulfment (similar to cell phagocytosis). The motors crossed the GUV membrane grasping part of the membrane (3). The GUV self-healed rapidly due to the fast lateral mobility of the lipids, avoiding the disruption of the vesicle. Finally, the motors ended up inside of the GUV (partly) coated with the lipid membrane (4). This mechanism is in agreement with our findings including, e.g., the efficient crossing of the GUV⁻ membranes due to electrostatic interactions or the limited crossing of ^0.5M_M-PEG due to the hindered interaction with the GUV membranes.

Conclusion

We assessed the ability of magnetic motors to cross lipid vesicles of diverse compositions and developed an analysis approach that allowed for the classification of individual motors in an ensemble according to their interaction with the membranes. The main findings illustrated that the motors’ size did not play a key role in crossing the membranes, but more importantly stiffer membranes (made of saturated lipids) and weaker magnetic fields enabled the crossing, owing to the increased retention time of the motors on the membranes and the better interaction. Non-interacting (PEGylated) motors showed limited crossing, which was dominant over the motors’ size or speed. Furthermore, due to the interaction of the motors’ surface with the membranes, the crossing motors got (partly) coated with lipids, pointing towards artificial endocytosis. This kind of analysis is envisioned to contribute to the design of motors with sufficient thrust (impulse) to overcome hurdles.

In the case of biomedical applications, the next step would involve calculating/estimating the energy barrier that biological membranes pose and identifying the minimum energy required for the motors to cross them. This might improve the design of motors able to propel through cell membranes, escape lysosomal entrapment or penetrate tissues. From our data, we can conclude that this energy barrier is not only related to the speed of the motors and the membrane composition, but other factors such as interaction energies between the motors and the membranes and the viscosity of the medium are important parameters to consider.

In a broader sense, the mathematical model used in this paper allows for the estimation of individual velocities even when the medium is not homogeneous and could be generalized in other fields where motors navigate complex, viscosity-changing media (e.g., water–oil mixtures).

Experimental

Materials

Sodium chloride (NaCl, 99%), poly(allylamine hydrochloride) (PAH, MW 17.5 kDa), poly(sodium 4-styrenesulfonate) (PSS, MW 70 kDa), poly(L-lysine) hydrobromide (PLL, MW 30–70 kDa), 5(6)-carboxy-X-rhodamine (RhoX), 4-(2-hydroxyethyl)piperazine-1-ethane-sulfonic acid (HEPES), Laurdan probe (6-dodecanoyl-N,N-dimethyl-2-naphthylamine), sucrose, glucose, mineral oil, and polystyrene particles (PS, 0.5 μm, 1 μm, and 4 μm, 5 wt%) were purchased from Sigma-Aldrich. Methoxypolyethylene glycol carboxylic acid (mPEG-COOH, MW 2 kDa) was purchased from Abbexa Ltd. 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phospho-L-serine (DOPS), 1,2-dipalmitoyl-sn-glycero-3-phosphocholine (DPPC) and 1,2-dipalmitoyl-sn-glycero-3-phosphoethanolamine-N-(lissamine rhodamine B sulfonyl) (ammonium salt) (Rho-PE) were purchased from Avanti Polar Lipids, Inc. Ltd. μ-Slides VI^0.4 uncoated were purchased from ibidi GmbH. Different NdFeB magnets (2 N and 0.3 N pulling force) were purchased from Supermagnete. Ultrapure water (18.2 MΩ cm resistivity) was obtained using an ELGA Purelab Ultra system (ELGA LabWater, Lane End).

Oregon Green 488-labeled poly(L-lysine) (PLL_OG) and poly(L-lysine)-grafted-poly(ethylene glycol) (PLL-g-PEG, grafting ratio ∼17%, i.e., 1 out of 6 PEG chains contained 1 PLL chain) were synthesized following a previous method.⁴¹

Micromotor (M_M) assembly

The magnetic motors consisted of a carboxylate-modified polystyrene (PS) core (i.e., 0.5, 1 or 4 μm in diameter) decorated with iron oxide nanoparticles. The iron oxide nanoparticles were synthesized employing the Massart's method. This resulted in magnetite/hematite (Fe₃O₄/α-Fe₂O₃) nanoparticles of an average diameter of 10.5 */1.5 nm (95.5% population, log–normal fit) and a positive surface charge (ζ-potential ∼ +30 mV).^41,42

The assembly was achieved using the layer-by-layer technique. First, 200 μL of commercial PS solution (5 wt%) were dispersed in PAH solution (2 mg mL⁻¹ in 0.5 M NaCl) and stirred for 15 min at room temperature. Then, the excess of PAH was removed by centrifugation and the particles were washed with ultrapure water (4500–6500 rpm, 5 min, 3×). Second, the PAH-coated particles were dispersed in PSS solution (2 mg mL⁻¹ in 0.5 M NaCl), incubated for 15 min and washed as above. Then, 500 μL of iron oxide nanoparticles (40 mg mL⁻¹ in ultrapure water) were added to the previously coated particles, incubated for 30 min, and washed as above, resulting in magnetic motors ^xM_M (x represents the PS core size in microns). For visualization purposes, the motors were fluorescence labelled by adding a layer of Oregon Green™-labelled poly(L-lysine) (PLL_OG) instead of PLL. For non-interacting motors, PLL-g-PEG was added as the terminating layer instead of PLL, resulting in ^xM_M-PEG.

The ζ-potentials of the particles after each deposition step were measured in ultrapure water using a Malvern Zetasizer 4. Scanning electron microscopy (SEM) images of the assemblies were recorded using a Nova NanoSEM 600 operating at an acceleration voltage of 5 kV with a working distance of 5 mm and using an ETD detector. The samples were coated with a thin layer of Pt (6 nm). Magnetic measurements were performed using the VSM option in a physical property measurement system from Quantum Design. Virgin curves were recorded at 300 K up to an external field of 1 T. M–T curves were measured in the range of 290–310 K by applying a magnetic field of 10 mT. The magnetophoretic mobility coefficient (ξ) was calculated according to the following expression:

where R_P and R_H stand for the solid and hydrodynamic radii of the particle, Δχ is the magnetic susceptibility of the particle relative to the fluid, and η is the viscosity of the fluid (in this case, an isotonic solution and a sucrose solution). The hydrodynamic radii (R_H) were determined by dynamic light scattering (DLS, (Malvern Zeta sizer Nano-590 at λ = 632 nm at 25 °C)).

Giant unilamellar vesicle (GUV) assembly

Giant unilamellar vesicles (GUVs) with different lipid compositions were assembled by an emulsion transfer method. For example, 0.5 μL of biotinyl-PE (10 mg mL⁻¹ in chloroform), 0.5 μL of lissamine rhodamine PE (for visualization, 1 mg mL⁻¹ in chloroform) and 9.5 μL of DOPC (10 mg mL⁻¹ in chloroform) were mixed in 50 μL of chloroform before 500 μL of mineral oil were added. The mixture was vortexed and heated at 80 °C for 40 min to remove the remaining chloroform. Next, to a 1.5 mL Eppendorf tube containing 200 μL of an isotonic solution, 300 μL of the mixture were added carefully and allowed to stand for at least 10 min. (Note: isotonic solution contains 0.9% NaCl and 5% glucose dissolved in ultrapure water.) To prepare empty GUVs, 20 μL of sucrose solution (300 mM) were added to the previous mixture and vortexed at high speed for 30 s. The emulsion was centrifuged at 3000 rpm for 30 min at RT and the GUVs were collected from the bottom of the Eppendorf tube, termed GUV^Z. GUVs were always stored at 4 °C and used within 24 h. To encapsulate ^xM_M inside the GUV, 20 μL of the ^xM_M stock solution were added instead of the sucrose solution. The GUVs were visualized on a bright-field microscope (Olympus IX81) equipped with a fluorescence lamp. The images were pseudo-colored for visualization purposes using Fiji.

Other lipid-based GUVs were prepared by changing the lipid composition in the initial step. Specifically, to prepare GUV⁻, 1 μL of DOPS (10 mg mL⁻¹ in chloroform) and 8.5 μL of DOPC (10 mg mL⁻¹ in chloroform) were used instead of only 9.5 μL of DOPC. GUVs containing saturated lipids were prepared by replacing DOPC with DPPC (10 mg mL⁻¹ in chloroform), resulting in the GUV^S. For experiments made in sucrose, a sucrose solution (300 mM) was used instead of the isotonic solution. A summary of all compositions can be found in ESI Table S2.†

The general polarization (GP) values were determined as an indication of membrane packing (fluidity) of the GUVs using the Laurdan probe.^43,44 For this, 100 μL of GUVs including 2.5 μL of Laurdan (100 μM stock solution in DMSO, final concentration of 2.5 μM) were added to a black 96-well plate, followed by shaking the plate (300 rpm) for 45 min and recording the emission spectra from λ_em = 390–590 nm using an excitation wavelength of λ_ex = 340 nm in a multi-well plate reader (PerkinElmer Ensight). The Laurdan spectra were normalized to the intensity peak at λ_em = 490 nm. The GP was calculated according to the following equation:

GP values range between −1 (disordered membrane) and 1 (ordered membrane).

Locomotion

Locomotion in isotonic solution. The locomotion of the micromotors was assessed in isotonic solution (0.9% NaCl and 5% glucose in ultrapure water). To do so, 2 μL of GUV stock solutions containing ^xM_M were dispersed in 98 μL of isotonic solution and added to uncoated ibidi microfluidic channels. ^xM_M were allowed to equilibrate for 2 min before taking the movies using an inverted bright-field microscope (Olympus IX81) equipped with a 40× or 60× oil objective. Next, magnet 1 or 2 was placed next to the channel, and the movies were recorded for 300 frames at a speed of 16.67 fps. (Note: the magnetic force refers to the force of the magnet to hold a magnetic material. In terms of our experiments, magnet 2 exerts a force ∼8× higher than magnet 1.) For control experiments, no magnets were used. The locomotion in sucrose solution was assessed employing a 300 mM sucrose solution instead of the isotonic solution. The trajectories were extracted every frame and analyzed using the plugin TrackMate of Fiji.³⁰ The mean-squared displacement (MSD) was calculated in Matlab employing a protocol published elsewhere,⁴⁵ and plotted for every analysis. The following equation for two-dimensional motion:

ΔL² = 2D_effΔt + v²Δt^2,

where ΔL² is the averaged MSD over an interval of time Δt, D_eff stands for the effective diffusion coefficient and v is the average velocity of the ensemble of particles, was fitted to the MSD plots. Accordingly, the MSD plots show a linear trend for particles displaying only Brownian (random) motion. The MSD fits to a parabola for particles displaying ballistic (directed) motion. (It should be noted that the error bars of the MSD plots became larger at longer times because of the error cumulated for every time shift.) The velocities were calculated and plotted as whisker plots. The whisker plots (or box plots) represent the median (line crossing each box) and average (triangle) velocity. The lower and upper edges of the box represent the 1^st (25% of the data) and 3^rd (75% of the data) quartiles. Outliers are represented as crosses. Two independent repeats were exercised per experiment and the analyses show the averaged values, unless indicated otherwise. All movies were accelerated 2× for visualization purposes.

Locomotion in the presence of GUVs. The locomotion of ^xM_M was assessed in the presence of GUVs. For that, GUVs containing motors were added to uncoated ibidi microfluidic channels, and the movies were recorded as aforementioned using a 10× or 40× objective. Magnet 1 or 2 was placed next to the channel, and the movies were recorded for up to 3000 frames at a speed of 16.67 fps. Controls consisted of GUVs suspended in sucrose solution (300 mM). The trajectories were extracted every 10^th frame and analyzed using the plugin TrackMate of Fiji. At least two independent repeats were exercised per experiment and the analyses show the averaged values, unless indicated otherwise. All movies were accelerated 10× for visualization purposes.

Mathematical analysis. ^x M_M were classified into five groups according to their behavior in the presence of GUVs. An in-house Python code was developed to separate the motors into groups depending on their motion properties. For that, the following criteria was applied:

(1) If |R² linear − R² wedge| < 0.1, then consider the fit as linear. R² linear and R² wedge are the coefficinets of multiple correlation resulting from the linear and wedge funtion fits, as described in the main text.

(2) If linear, then decide if slow (inside the GUVs) or fast (outside the GUVs) swimming as:

Slow (inside): if ν_mean < ν_ensemble (group 1)

Fast (outside): if ν_mean > ν_ensemble (group 2)

Here, ν_mean represents the mean velocity calculated over the trajectory of a motor, and ν_ensemble is the mean velocity of the entire batch (ensemble) of motors.

(3) If not linear (then wedge), then analyze only those motors whose maximum velocities are above the standard deviation of the noise in the velocity data across the trajectory. Next, decide if motion is:

Slow–fast: if ν_inside < ν_outside (group 5)

Fast–slow: if ν_inside > ν_outside (group 3)

Move–stop: if ν_inside > 0.2 × ν_ensemble (i.e., increase the scale from 5% to 20% of the ensemble mean velocity) (group 4).

(4) Otherwise not classified (group 5).

^x M_M thrust (impulse). ^x M_M thrust was calculated as the linear momentum, according to the following expression:

Momentum = m_motor(ν_inside − ν_outside),

where m_motor is the motor mass and can be estimated as:
where R_P is the particle (motor) radius, x_IO is the fraction of the magnetic material calculated from the VSM data and ρ_PS = 1050 kg m⁻³ and ρ_IO = 5240 kg m⁻³ are the densities of polystyrene and iron oxide, respectively.

GUV membrane crossing

Penetration ability of ^xM_M. The number of ^xM_M crossing the GUVs was determined. To do so, GUVs containing motors were added to uncoated ibidi microfluidic channels, and the movies were recorded as aforementioned using a 10× or 40× objective. Magnet 1 or 2 was placed next to the channel, and the movies were recorded for up to 3000 frames at a speed of 16.67 fps. Controls consisted of GUVs suspended in sucrose solution (300 mM). The trajectories were extracted every 150^th frame and analyzed using Fiji. The images were converted into black and white only (where black represented the background and white represented the motors) and the white pixel areas were determined over time. Logistic curves were fitted to the data to determine the increase in pixel number (motors) over time according to the following function:
where A₀ and A_n are the initial and final values of the curve, and τ and p are parameters that describe the half-time when the motors filled the GUV and the rate which with they do so, respectively.

Membrane integrity. The capacity of ^xM_M disrupting the GUV membranes was evaluated. Epifluorescence images of the ^xM_M and GUVs were collected using a bright-field microscope (Olympus IX81) equipped with a fluorescence lamp using filters at λ_ex/em values of 467–498/513–556 nm and 513–556/570–613 nm for PLL_OG (terminating layer of ^xM_M) and Rho-PE (fluorescent lipid in the GUV membrane), respectively.

Rhodamine X (RhoX) permeability. 10 μL of RhoX solution (5 μM) were mixed with 95 μL of unlabeled GUV solution and added into an uncoated ibidi microfluidic channel. Next, 5 μL of ^xM_M stock solution were added and allowed to equilibrate for 10 min. Then, magnet 2 was placed next to the channel, and the pictures were taken right after using a bright-field microscope (Olympus IX81, 10× objective) at λ_ex/em = 513–556/570–613 nm and 200 ms exposure.

Author contributions

MARD: conceptualization, investigation, methodology, validation, visualization, writing – original draft, and writing – review and editing. OH: software, data curation, and writing – review and editing. BS: conceptualization, funding acquisition, project administration, resources, writing – original draft, and writing – review and editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This project was supported by a Carlsberg Foundation Distinguished Associate Professor Fellowship (B.S. CF16-0233) and the Lundbeck Foundation. The authors thank Prof. Mogens Christensen (Department of Chemistry, Aarhus University) and Dr Kasper Borup (Department of Chemistry, Aarhus University) for performing the magnetic measurements of the samples.

References

1. A. Ghosh, W. Xu, N. Gupta and D. H. Gracias, Nano Today, 2020, 31, 100836.
2. G. T. van Moolenbroek, T. Patiño, J. Llop and S. Sánchez, Adv. Intell. Syst., 2020, 2, 2000087.
3. A. Rastmanesh, M. Tavakkoli Yaraki, J. Wu, Z. Wang, P. Ghoderao, Y. Gao and Y. N. Tan, Mol. Syst. Des. Eng., 2021, 6, 566–593.
4. J. Lv, Y. Xing, T. Xu, X. Zhang and X. Du, Appl. Mater. Today, 2021, 23, 101034.
5. L. Wang, X. Hao, Z. Gao, Z. Yang, Y. Long, M. Luo and J. Guan, Interdiscip. Mater., 2022, 1, 256–280.
6. P. L. Venugopalan, B. Esteban-Fernández De Ávila, M. Pal, A. Ghosh and J. Wang, ACS Nano, 2020, 14, 9423–9439.
7. H. Yuan, X. Liu, L. Wang and X. Ma, Bioact. Mater., 2021, 6, 1727–1749.
8. X. Arqué, T. Patiño and S. Sánchez, Chem. Sci., 2022, 13, 9128–9146.
9. C. Lv, Y. Yang and B. Li, Micromachines, 2022, 13, 307.
10. M. Fernández-Medina, M. A. Ramos-Docampo, O. Hovorka, V. Salgueiriño and B. Städler, Adv. Funct. Mater., 2020, 30, 1–17.
11. M. A. Ramos Docampo, Adv. Biol., 2023, 7, 2200308.
12. Z. Xiao, M. Wei and W. Wang, ACS Appl. Mater. Interfaces, 2019, 11, 6667–6684.
13. F. Mou, J. Zhang, Z. Wu, S. Du, Z. Zhang, L. Xu and J. Guan, iScience, 2019, 19, 415–424.
14. K. Yuan, M. Pacheco, B. Jurado-Sánchez and A. Escarpa, Adv. Intell. Syst., 2021, 3, 2100002.
15. M. Yang, Y. Zhang, F. Mou, C. Cao, L. Yu, Z. Li and J. Guan, Sci. Adv., 2023, 9, eadk7251.
16. M. A. Ramos-Docampo, P. Hurtado, A. B. Dávila-Ibáñez, R. Piñeiro, M. L. Fanarraga and V. Salgueiriño, J. Colloid Interface Sci., 2022, 629, 287–296.
17. M. A. R. Docampo, X. Qian, C. Ade, T. F. Marcelino, M. Ceccato, M. Foss, O. Hovorka and B. Städler, Adv. Mater. Interfaces, 2022, 2201509.
18. G. Tezel, S. S. Timur, F. Kuralay, R. N. Gürsoy, K. Ulubayram, L. Öner and H. Eroğlu, J. Drug Targeting, 2020, 29, 29–45.
19. A. Del Valle, J. Torra, P. Bondia, C. M. Tone, P. Pedraz, V. Vadillo-Rodriguez and C. Flors, ACS Appl. Mater. Interfaces, 2020, 12, 31235–31241.
20. C. Liu, P. Elvati, S. Majumder, Y. Wang, A. P. Liu and A. Violi, ACS Nano, 2019, 13, 10221–10232.
21. A. Singhal and G. J. Agur Sevink, Nanoscale Adv., 2021, 3, 6635–6648.
22. X. Zhang, G. Ma and W. Wei, NPG Asia Mater., 2021, 13, 52.
23. V. Sharma, E. Azar, A. P. Schroder, C. M. Marques and A. Stocco, Soft Matter, 2021, 17, 4275–4281.
24. M. Winkens, A. Vilcan, P. J. De Visser, F. V. De Graaf and P. A. Korevaar, Small, 2023, 2206800.
25. D. Takagi, J. Palacci, A. B. Braunschweig, M. J. Shelley and J. Zhang, Soft Matter, 2014, 10, 1784–1789.
26. S. E. Spagnolie, G. R. Moreno-Flores, D. Bartolo and E. Lauga, Soft Matter, 2015, 11, 3396–3411.
27. S. E. Spagnolie and E. Lauga, J. Fluid Mech., 2012, 700, 105–147.
28. N. Desai, V. A. Shaik and A. M. Ardekani, Soft Matter, 2018, 14, 264–278.
29. S. Song, A. Llopis-Lorente, A. F. Mason, L. K. E. A. Abdelmohsen and J. C. M. Van Hest, J. Am. Chem. Soc., 2022, 144, 13831–13838.
30. J. Y. Tinevez, N. Perry, J. Schindelin, G. M. Hoopes, G. D. Reynolds, E. Laplantine, S. Y. Bednarek, S. L. Shorte and K. W. Eliceiri, Methods, 2017, 115, 80–90.
31. W. Rawicz, K. C. Olbrich, T. Mcintosh, D. Needham and E. Evans, Biophys. J., 2000, 79, 328–339.
32. K. Olbrich, W. Rawicz, D. Needham and E. Evans, Biophys. J., 2000, 79, 321–327.
33. A. C. Fischer-Cripps, J. Mater. Sci., 1999, 34, 129–137.
34. M. Sousa De Almeida, E. Susnik, B. Drasler, P. Taladriz-Blanco, A. Petri-Fink and B. Rothen-Rutishauser, Chem. Soc. Rev., 2021, 50, 5397–5434.
35. J. J. Rennick, A. P. R. Johnston and R. G. Parton, Nat. Nanotechnol., 2021, 16, 266–276.
36. F. G. Strobl, D. M. Czubak, A. Wixforth and C. Westerhausen, J. Phys. D: Appl. Phys., 2019, 52, 294001.
37. C. Contini, J. W. Hindley, T. J. Macdonald, J. D. Barritt, O. Ces and N. Quirke, Commun. Chem., 2020, 3, 1–12.
38. Y. Qiao, M. Li, R. Booth and S. Mann, Nat. Chem., 2017, 9, 110–119.
39. N. Gao, C. Xu, Z. Yin, M. Li and S. Mann, J. Am. Chem. Soc., 2022, 144, 3855–3862.
40. K. W. Dunn, M. M. Kamocka and J. H. McDonald, Am. J. Physiol.: Cell Physiol., 2011, 300, 723–742.
41. P. De Dios Andres, M. A. Ramos-Docampo, X. Qian, M. Stingaciu and B. Städler, Nanoscale, 2021, 13, 17900–17911.
42. P. de Dios Andres and B. Städler, Small, 2022, 19, 2201251.
43. T. Parasassi, G. De Stasio, G. Ravagnan, R. M. Rusch and E. Gratton, Biophys. J., 1991, 60, 179–189.
44. A. G. Jay and J. A. Hamilton, J. Fluoresc., 2017, 27, 243–249.
45. N. Tarantino, J.-Y. Tinevez, E. F. Crowell, B. Boisson, R. Henriques, M. Mhlanga, F. Agou, A. Israel and E. Laplantine, J. Cell Biol., 2014, 204, 231–245.

---

Footnote

† Electronic supplementary information (ESI) available: Magnetic motor assembly and locomotion analyses, locomotion of PEGylated motors, GUV assembly and details, experimental setup and specific cases of motors crossing GUVs. See DOI: https://doi.org/10.1039/d3nr05462d

---