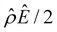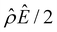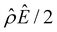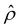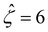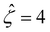Diffusioosmotic flow reversals due to ion–ion electrostatic correlations
Shengji
Zhang
 a and
Henry C. W.
Chu
a and
Henry C. W.
Chu
 *b
*b
aDepartment of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
bDepartment of Chemical Engineering and Department of Mechanical and Aerospace Engineering, University of Florida, Gainesville, FL 32611, USA. E-mail: h.chu@ufl.edu
First published on 23rd April 2024
Abstract
Existing theories of diffusioosmosis have neglected ion–ion electrostatic correlations, which are important in concentrated electrolytes. Here, we develop a mathematical model to numerically compute the diffusioosmotic mobilities of binary symmetric electrolytes across low to high concentrations in a charged parallel-plate channel. We use the modified Poisson equation to model the ion–ion electrostatic correlations and the Bikerman model to account for the finite size of ions. We report two key findings. First, ion–ion electrostatic correlations can cause a unique reversal in the direction of diffusioosmosis. Such a reversal is not captured by existing theories, occurs at ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 M for a monovalent electrolyte, and at a much lower concentration of ≈
0.4 M for a monovalent electrolyte, and at a much lower concentration of ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 M for a divalent electrolyte in a channel with the same surface charge. This highlights that diffusioosmosis of a concentrated electrolyte can be qualitatively different from that of a dilute electrolyte, not just in its magnitude but also its direction. Second, we predict a separate diffusioosmotic flow reversal, which is not due to electrostatic correlations but the competition between the underlying chemiosmosis and electroosmosis. This reversal can be achieved by varying the magnitude of the channel surface charge without changing its sign. However, electrostatic correlations can radically change how this flow reversal depends on the channel surface charge and ion diffusivity between a concentrated and a dilute electrolyte. The mathematical model developed here can be used to design diffusioosmosis of dilute and concentrated electrolytes, which is central to applications such as species mixing and separation, enhanced oil recovery, and reverse electrodialysis.
0.003 M for a divalent electrolyte in a channel with the same surface charge. This highlights that diffusioosmosis of a concentrated electrolyte can be qualitatively different from that of a dilute electrolyte, not just in its magnitude but also its direction. Second, we predict a separate diffusioosmotic flow reversal, which is not due to electrostatic correlations but the competition between the underlying chemiosmosis and electroosmosis. This reversal can be achieved by varying the magnitude of the channel surface charge without changing its sign. However, electrostatic correlations can radically change how this flow reversal depends on the channel surface charge and ion diffusivity between a concentrated and a dilute electrolyte. The mathematical model developed here can be used to design diffusioosmosis of dilute and concentrated electrolytes, which is central to applications such as species mixing and separation, enhanced oil recovery, and reverse electrodialysis.
1. Introduction
Diffusioosmosis refers to the deterministic fluid motion over a surface induced by a solute concentration gradient.1–7 Diffusioosmosis comprises a chemiosmotic and an electroosmotic component. The chemiosmotic flow is generated by the osmotic pressure gradient induced by the solute gradient, which acts to drive fluid from a region of high to low solute concentration. The electroosmotic flow is generated by an electric field, which is induced by the ionic solute gradient to ensure no net ionic current in the bulk. The electroosmotic flow may drive fluid up or down the ionic solute gradient, depending on the diffusivities of ions and the charge of the surface. The diffusioosmotic flow velocity follows the ‘log-sensing’ relation, u = M∇![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n,8 where n is the ion concentration and a positive (negative) diffusioosmotic mobility M corresponds to fluid driven up (down) the solute gradient. Diffusioosmosis has received much attention in recent years due to its impact on a wide range of applications, such as mixing and separation,9–36 reverse electrodialysis,37–42 and enhanced oil recovery.43–47
n,8 where n is the ion concentration and a positive (negative) diffusioosmotic mobility M corresponds to fluid driven up (down) the solute gradient. Diffusioosmosis has received much attention in recent years due to its impact on a wide range of applications, such as mixing and separation,9–36 reverse electrodialysis,37–42 and enhanced oil recovery.43–47
The main objective of this article is to demonstrate that ion–ion electrostatic correlations can lead to a unique reversal in the direction of diffusioosmosis of a binary, symmetric, concentrated electrolyte solution, relative to diffusioosmosis of the same but dilute electrolyte solution. Existing theories of diffusioosmosis have focused on dilute electrolyte solutions4,8,11,12,48–54 and cannot capture this reversal. In a dilute electrolyte solution, the electric potential is typically modeled by the Poisson equation, where ions respond to the average potential in the electric double layer and the space charge density decays monotonically from the charged surface. The Poisson equation neglects electrostatic correlations between ions. Ion–ion electrostatic correlations are prominent in concentrated electrolytes and cause overscreening of charges on a surface, where the space charge density oscillates in sign near the charged surface.55–57 By using molecular dynamics simulations and other non-local approaches,58–67 it has been demonstrated that the causes of overscreening are ion–ion electrostatic correlations. Although these approaches can capture overscreening accurately, the high computational cost largely restricts their use to model equilibrium systems. Building on the work of Santangelo68 and Hatlo and Lue,66 Bazant et al.69,70 derived a continuum-level, modified Poisson equation to robustly model overscreening. The equation is applicable to dilute and concentrated electrolyte solutions, room-temperature ionic liquids, and molten salts. For a binary electrolyte, the modified Poisson equation reads69–71
| ε(l2c∇4ϕ − ∇4ϕ) = ρ = en+z+ + en−z−, | (1) |
In this article, we develop a mathematical model that predicts the diffusioosmotic mobilities of binary symmetric electrolytes across low to high concentrations in a channel comprising two charged parallel plates. We use the modified Poisson equation69 to model the electric potential and electrostatic correlations. We incorporate the Bikerman model75 to account for the finite size of ions. We report two key findings. First, we compute the diffusioosmotic mobilities of common electrolytes and demonstrate that the direction of diffusioosmosis of a monovalent electrolyte reverses as the electrolyte concentration increases beyond ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 M. This unique diffusioosmotic flow reversal is not captured by existing theories and we identify its origin to be overscreening of channel surface charges by ion–ion electrostatic correlations. In a channel with the same surface charge, we show that the diffusioosmotic flow reversal occurs at a much lower concentration of ≈
0.4 M. This unique diffusioosmotic flow reversal is not captured by existing theories and we identify its origin to be overscreening of channel surface charges by ion–ion electrostatic correlations. In a channel with the same surface charge, we show that the diffusioosmotic flow reversal occurs at a much lower concentration of ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 M for a divalent electrolyte. Second, we present flow direction diagrams of diffusioosmosis as a function of the electrolyte concentration, valence, diffusivity, and channel surface charge. The diagrams predict a separate diffusioosmotic flow reversal to that shown in prior work.4,8,50,52 This reversal is not due to electrostatic correlations but the competition between the chemiosmosis and electroosmosis that constitute diffusioosmosis. The reversal can be realized by varying the magnitude of the channel surface charge without changing its sign. However, due to electrostatic correlations, this reversal has a distinct dependence on the product of the channel surface charge and ion diffusivity between a concentrated and a dilute electrolyte.
0.003 M for a divalent electrolyte. Second, we present flow direction diagrams of diffusioosmosis as a function of the electrolyte concentration, valence, diffusivity, and channel surface charge. The diagrams predict a separate diffusioosmotic flow reversal to that shown in prior work.4,8,50,52 This reversal is not due to electrostatic correlations but the competition between the chemiosmosis and electroosmosis that constitute diffusioosmosis. The reversal can be realized by varying the magnitude of the channel surface charge without changing its sign. However, due to electrostatic correlations, this reversal has a distinct dependence on the product of the channel surface charge and ion diffusivity between a concentrated and a dilute electrolyte.
The rest of this article is outlined as follows. In section 2, we formulate the problem by presenting the governing equations and boundary conditions for the electric potential, induced electric field, and diffusioosmotic flow field and mobility. In section 3, we present our results and elaborate on the two above-mentioned key findings. In section 4, we summarize this study and offer ideas for future work.
2. Problem formulation
Consider a channel that comprises two parallel plates of constant surface charge density q (or constant surface potential ζ) and a length L separated by a distance of 2H (Fig. 1). A constant concentration gradient of a binary, symmetric electrolyte ∇ni∞ is applied across the channel, where i = (+) and i = (−) are the cationic and anionic species, respectively, and n+∞(x) = n−∞(x) = n∞(x). Following prior work,4,8,12,48–54 we focus on typical regimes of diffusioosmosis, where the electrolyte concentration gradient across the channel length is much smaller than the background concentration, L|∇n∞|/n∞ ≪ 1 with n∞ = n∞(0). A diffusioosmotic flow with a constant velocity u is induced parallel to ∇ni∞ along the x-direction. The velocity u is an unknown. In the following, we will determine the electric potential inside the channel in section 2.1 and the electric field induced by the electrolyte gradient in section 2.2. We will use this information to determine u in section 2.3.2.1. Electric potential
The Bikerman model75 describes the electrochemical potential of each ionic species as μ± = kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log
log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n± + z±eϕ − kT
n± + z±eϕ − kT![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log[1 − a3(n+ + n−)], where the first two terms represent an ideal solution and the last term accounts for the steric effect of the finite size of ions. The steric effect is controlled by the bulk volume fraction of ions, ν = 2a3n∞. At equilibrium, ∇μ± = 0, the ion concentration follows the Fermi-like, modified Boltzmann distribution as14,52,76
log[1 − a3(n+ + n−)], where the first two terms represent an ideal solution and the last term accounts for the steric effect of the finite size of ions. The steric effect is controlled by the bulk volume fraction of ions, ν = 2a3n∞. At equilibrium, ∇μ± = 0, the ion concentration follows the Fermi-like, modified Boltzmann distribution as14,52,76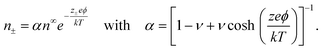 | (2) |
Substituting eqn (2) into (1) yields a Poisson–Fermi equation that governs the electric potential accounting for both the finite size of ions and ion–ion electrostatic correlations69,70
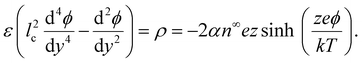 | (3) |
We non-dimensionalize eqn (3) using the following schemes: ŷ = y/H,  ,
, 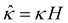 , and
, and 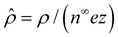 , where quantities with carets are non-dimensional and the Debye length
, where quantities with carets are non-dimensional and the Debye length 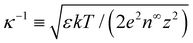 is the length scale over which the space charge density varies. The non-dimensionalized eqn (3) reads,
is the length scale over which the space charge density varies. The non-dimensionalized eqn (3) reads,
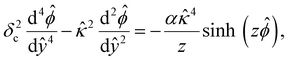 | (4) |
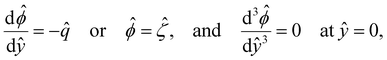 | (5) |
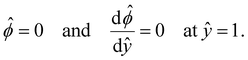 | (6) |
In eqn (5), the first two conditions indicate that the channel surface charge density ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = qeH/(εkT) or the channel surface potential
= qeH/(εkT) or the channel surface potential 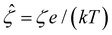 is specified. The third condition is demanded by the Poisson–Fermi equation. In eqn (6), the conditions indicate that the electrostatic potential and its derivative approach zero smoothly away from the channel surface. The first condition is guaranteed, where our analyses focus on electrolyte solutions with n∞ ≥ 10–3 M (κ−1 ≲ 10–8 m) in typical microscale channels with H ≳ 10–7 m so that
is specified. The third condition is demanded by the Poisson–Fermi equation. In eqn (6), the conditions indicate that the electrostatic potential and its derivative approach zero smoothly away from the channel surface. The first condition is guaranteed, where our analyses focus on electrolyte solutions with n∞ ≥ 10–3 M (κ−1 ≲ 10–8 m) in typical microscale channels with H ≳ 10–7 m so that 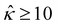 and
and 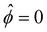 at ŷ = 1. When δc = 0 (lc = 0) and α = 1 (ν = 0), eqn (4) reduces to the classical Poisson–Boltzmann equation for a dilute electrolyte solution, where the last condition in eqn (5) and (6) is not required.
at ŷ = 1. When δc = 0 (lc = 0) and α = 1 (ν = 0), eqn (4) reduces to the classical Poisson–Boltzmann equation for a dilute electrolyte solution, where the last condition in eqn (5) and (6) is not required.
2.2. Induced electric field
In diffusioosmosis, the electric field E is generated by the imposed electrolyte concentration gradient to ensure no net ionic current in the bulk:8| J = z+ej+ + z−ej− = 0, | (7) |
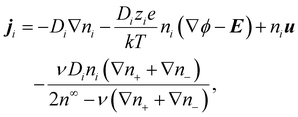 | (8) |
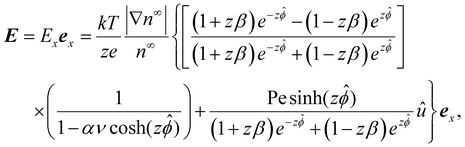 | (9) |
2.3. Diffusioosmotic flow field and mobility
Inertial forces are negligible in microscale transport. The fluid dynamics is described by the continuity equation, ∇·u = 0, in addition to the Stokes equation with an electric body force, 0 = η∇2u − ∇p + ρ(E − ∇ϕ). For a fully developed flow, ux = ux(y) and the continuity equation suggest that the y-component of u is zero. Thus, the y- and x-components of the Stokes equation are written as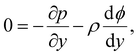 | (10) |
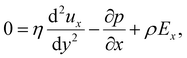 | (11) |
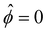 at ŷ = 1,
at ŷ = 1,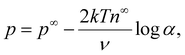 | (12) |
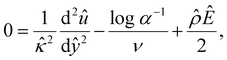 | (13) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α−1)/ν and
α−1)/ν and 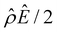 are the chemiosmotic and electroosmotic driving forces to the diffusioosmotic flow, respectively, and Ê = Ex/(kT|∇n∞|/zen∞). Eqn (13) is subject to the no-slip condition at the channel walls and the symmetry condition about the channel centerline
are the chemiosmotic and electroosmotic driving forces to the diffusioosmotic flow, respectively, and Ê = Ex/(kT|∇n∞|/zen∞). Eqn (13) is subject to the no-slip condition at the channel walls and the symmetry condition about the channel centerline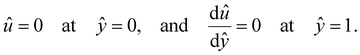 | (14) |
We further define the mean diffusioosmotic velocity as
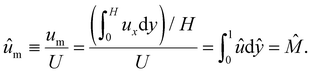 | (15) |
Note that ûm is equivalent to the non-dimensionalized diffusioosmotic mobility ![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) = Mηe2z2/(εk2T2), which together recover the dimensional log-sensing relation um = M
= Mηe2z2/(εk2T2), which together recover the dimensional log-sensing relation um = M![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∇log
∇log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) n∞. In sum, we solved eqn (4)–(6) for
n∞. In sum, we solved eqn (4)–(6) for 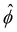 . The potential
. The potential 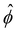 is then used to compute
is then used to compute 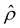 viaeqn (3) and is substituted into eqn (13) and (15) to solve for û and ûm. We use a combination of the finite difference method and Newton's method in Wolfram Mathematica to solve these equations and converged solutions are obtained with mesh size Δŷ = 10–5. Details of the numerical scheme are given in Appendix A. We validated our model by recovering the results of prior work50,52 in Appendix B.
viaeqn (3) and is substituted into eqn (13) and (15) to solve for û and ûm. We use a combination of the finite difference method and Newton's method in Wolfram Mathematica to solve these equations and converged solutions are obtained with mesh size Δŷ = 10–5. Details of the numerical scheme are given in Appendix A. We validated our model by recovering the results of prior work50,52 in Appendix B.
3. Results and discussion
In this section, we compute the non-dimensionalized diffusioosmotic mobilities![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) of common binary, symmetric electrolytes. Their cation diffusivity, anion diffusivity, diffusivity ratio, and saturation concentration are listed in Table 1. In section 3.1, we present the mobilities as a function of the bulk molar concentration of the electrolyte C, which relates to the bulk number density of ions via n∞ = 103AC, where A is the Avogadro constant. In section 3.2, we present flow direction diagrams that show the direction of the diffusioosmotic flow as a function of the electrolyte concentration, valence, diffusivity, and channel surface charge. In section 3.1 and 3.2, we account for the fact that varying C varies ν,
of common binary, symmetric electrolytes. Their cation diffusivity, anion diffusivity, diffusivity ratio, and saturation concentration are listed in Table 1. In section 3.1, we present the mobilities as a function of the bulk molar concentration of the electrolyte C, which relates to the bulk number density of ions via n∞ = 103AC, where A is the Avogadro constant. In section 3.2, we present flow direction diagrams that show the direction of the diffusioosmotic flow as a function of the electrolyte concentration, valence, diffusivity, and channel surface charge. In section 3.1 and 3.2, we account for the fact that varying C varies ν, 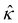 , and δc; see section 2.1 for parameter definitions. We set T = 298 K, a = 0.3 nm,70,76lc = z2lB,77 and Pe = 4n∞U/[(D+ + D−)|∇n∞|] = 1, which is justified by typical diffusioosmosis with U ∼ 10–6 ms−1, n∞/|∇n∞| ∼ 10–3 m, and D± ∼ 10–9 m2 s−1.10,50
, and δc; see section 2.1 for parameter definitions. We set T = 298 K, a = 0.3 nm,70,76lc = z2lB,77 and Pe = 4n∞U/[(D+ + D−)|∇n∞|] = 1, which is justified by typical diffusioosmosis with U ∼ 10–6 ms−1, n∞/|∇n∞| ∼ 10–3 m, and D± ∼ 10–9 m2 s−1.10,50
| Electrolyte | D + [×10–9 m2 s−1] | D − [×10–9 m2 s−1] | β | Saturation concentration [M] |
|---|---|---|---|---|
| Hydrogen chloride (HCl) | 9.31 | 2.03 | 0.64 | 19.7 |
| Potassium acetate (CH3COOK) | 1.96 | 1.09 | 0.29 | 27.4 |
| Potassium chloride (KCl) | 1.96 | 2.03 | −0.02 | 4.61 |
| Sodium chloride (NaCl) | 1.33 | 2.03 | −0.21 | 6.16 |
| Sodium hydroxide (NaOH) | 1.33 | 5.27 | −0.60 | 25 |
| Zinc sulphate (ZnSO4) | 0.72 | 1.07 | −0.10 | 3.57 |
| Magnesium chromate (MgCrO4) | 0.71 | 1.13 | −0.12 | 5.15 |
| Beryllium sulphate (BeSO4) | 0.60 | 1.07 | −0.14 | 3.81 |
3.1. Variation of diffusioosmotic mobilities with bulk electrolyte concentrations
![[M with combining circumflex]](https://www.rsc.org/images/entities/i_char_004d_0302.gif) of five monovalent electrolytes: HCl (β = 0.64), CH3COOK (β = 0.29), KCl (β = −0.02), NaCl (β = −0.21), and NaOH (β = −0.60). The channel height H = 100 nm. Thus,
of five monovalent electrolytes: HCl (β = 0.64), CH3COOK (β = 0.29), KCl (β = −0.02), NaCl (β = −0.21), and NaOH (β = −0.60). The channel height H = 100 nm. Thus, 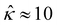 at C = 10–3 M and
at C = 10–3 M and 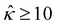 as C increases. The channel surface charge density q = 0.014 C m−2 (
as C increases. The channel surface charge density q = 0.014 C m−2 (![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 78.4) corresponds to a channel surface potential ζ = 100 mV
= 78.4) corresponds to a channel surface potential ζ = 100 mV 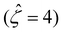 at C = 10–3 M. We use the same
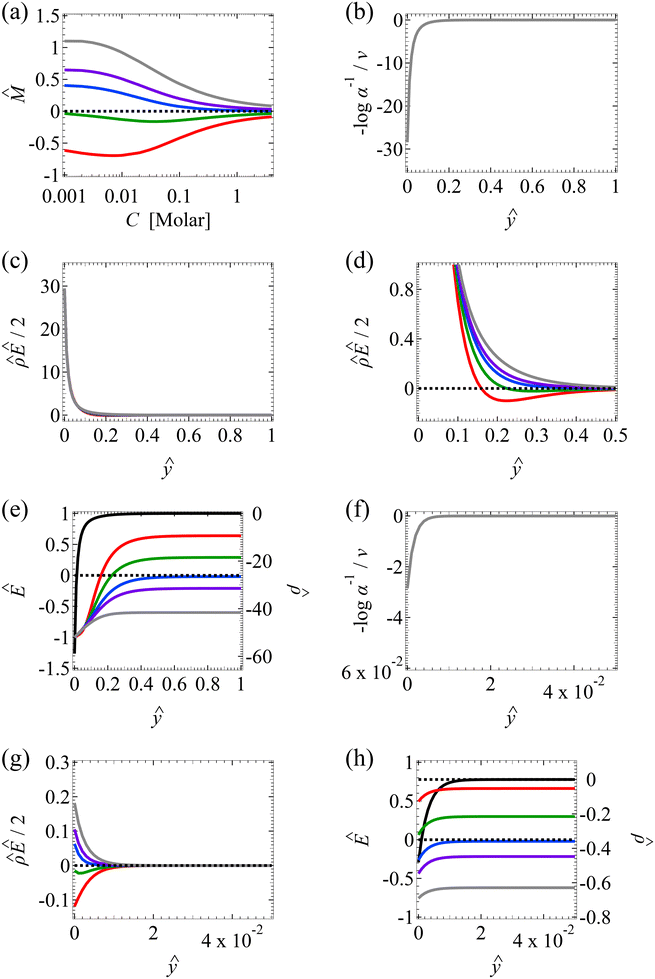
at C = 10–3 M. We use the same ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) to compute the mobilities at other electrolyte concentrations. Fig. 2 includes the effect of finite-ion-size, i.e., ν is non-zero, but ignores electrostatic correlations by setting δc = 0. By definition (Fig. 1), a positive (negative) mobility corresponds to a diffusioosmotic flow from a region of low (high) to high (low) electrolyte concentration.
to compute the mobilities at other electrolyte concentrations. Fig. 2 includes the effect of finite-ion-size, i.e., ν is non-zero, but ignores electrostatic correlations by setting δc = 0. By definition (Fig. 1), a positive (negative) mobility corresponds to a diffusioosmotic flow from a region of low (high) to high (low) electrolyte concentration.
The first observation from Fig. 2(a) is that, at a low electrolyte concentration C = 10–3 M for a strongly negative β = −0.60 (grey line), the diffusioosmotic mobility is positive. That is, the diffusioosmotic flow is from a region of low to high electrolyte concentration. To understand this observation, we show the chemiosmotic driving force –(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α−1)/ν in Fig. 2(b) and the electroosmotic driving force
α−1)/ν in Fig. 2(b) and the electroosmotic driving force  in Fig. 2(c) and (d) [see eqn (13)]; panel (d) is a zoom-in of panel (c). Fig. 2(b) shows that the chemiosmotic driving force is negative, meaning that a chemiosmotic flow is generated from a region of high to low electrolyte concentration, consistent with prior work.8 The chemiosmotic driving force is independent of β, which explains the overlap of data for five different β values. Fig. 2(c) and (d) show that, for β = −0.60, the electroosmotic driving force is always positive away from the channel surface (ŷ = 0), meaning that an electroosmotic flow is generated from a region of low to high electrolyte concentration. The positive electroosmotic driving force
in Fig. 2(c) and (d) [see eqn (13)]; panel (d) is a zoom-in of panel (c). Fig. 2(b) shows that the chemiosmotic driving force is negative, meaning that a chemiosmotic flow is generated from a region of high to low electrolyte concentration, consistent with prior work.8 The chemiosmotic driving force is independent of β, which explains the overlap of data for five different β values. Fig. 2(c) and (d) show that, for β = −0.60, the electroosmotic driving force is always positive away from the channel surface (ŷ = 0), meaning that an electroosmotic flow is generated from a region of low to high electrolyte concentration. The positive electroosmotic driving force 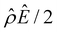 for β = −0.60 is confirmed by its negative components
for β = −0.60 is confirmed by its negative components 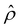 and Ê as shown in Fig. 2(e). To sum, since the magnitude of the electroosmotic driving force [Fig. 2(c)] is larger than the chemiosmotic driving force [Fig. 2(b)], the direction of the resulting diffusioosmotic flow is governed by the former, which goes from a region of low to high electrolyte concentration, i.e., a positive mobility.
and Ê as shown in Fig. 2(e). To sum, since the magnitude of the electroosmotic driving force [Fig. 2(c)] is larger than the chemiosmotic driving force [Fig. 2(b)], the direction of the resulting diffusioosmotic flow is governed by the former, which goes from a region of low to high electrolyte concentration, i.e., a positive mobility.
The second observation from Fig. 2(a) is that, at a low electrolyte concentration C = 10−3 M for a strongly positive β = 0.64 (red line), the diffusioosmotic mobility is negative. That is, the diffusioosmotic flow is from a region of high to low electrolyte concentration. This can be understood by the same reasoning as in the above paragraph. Specifically, Fig. 2(b) shows that the chemiosmotic driving force –(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α−1)/ν is negative, meaning that a chemiosmotic flow is generated from a region of high to low electrolyte concentration. Fig. 2(c) and (d) show that, for β = 0.64, the electroosmotic driving force
α−1)/ν is negative, meaning that a chemiosmotic flow is generated from a region of high to low electrolyte concentration. Fig. 2(c) and (d) show that, for β = 0.64, the electroosmotic driving force 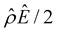 is positive near the channel wall (ŷ ≲ 0.16) and becomes negative away from the channel wall (ŷ ≳ 0.16). Such a change in the direction of the electroosmotic driving force is caused by a sign change in the induced electric field Ê but not in the space charge density
is positive near the channel wall (ŷ ≲ 0.16) and becomes negative away from the channel wall (ŷ ≳ 0.16). Such a change in the direction of the electroosmotic driving force is caused by a sign change in the induced electric field Ê but not in the space charge density 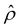 [Fig. 2(e)]. Thus, the net electroosmotic flow for β = 0.64 is weaker than that for β = −0.60. Consequently, when the electroosmotic flow couples with the chemiosmotic flow for β = 0.64, the resulting diffusioosmotic flow is governed by the latter, which goes from a region of high to low electrolyte concentration, i.e., a negative mobility.
[Fig. 2(e)]. Thus, the net electroosmotic flow for β = 0.64 is weaker than that for β = −0.60. Consequently, when the electroosmotic flow couples with the chemiosmotic flow for β = 0.64, the resulting diffusioosmotic flow is governed by the latter, which goes from a region of high to low electrolyte concentration, i.e., a negative mobility.
Combining the first and second observations, at a low electrolyte concentration, the mobility transitions from positive to increasingly negative as β becomes more positive.
The third observation from Fig. 2(a) is that the magnitude of the mobility decreases and approaches zero with an increasing electrolyte concentration C. This can be understood by recalling that we consider a constant channel surface charge density ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 78.4. This corresponds to a channel surface potential
= 78.4. This corresponds to a channel surface potential 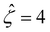 at a low electrolyte concentration C = 10–3 M. On increasing the electrolyte concentration, the channel surface potential decreases and approaches zero, e.g.,
at a low electrolyte concentration C = 10–3 M. On increasing the electrolyte concentration, the channel surface potential decreases and approaches zero, e.g., 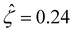 at C = 1 M which can be obtained by solving eqn (4)–(6), and so does the mobility.
at C = 1 M which can be obtained by solving eqn (4)–(6), and so does the mobility.
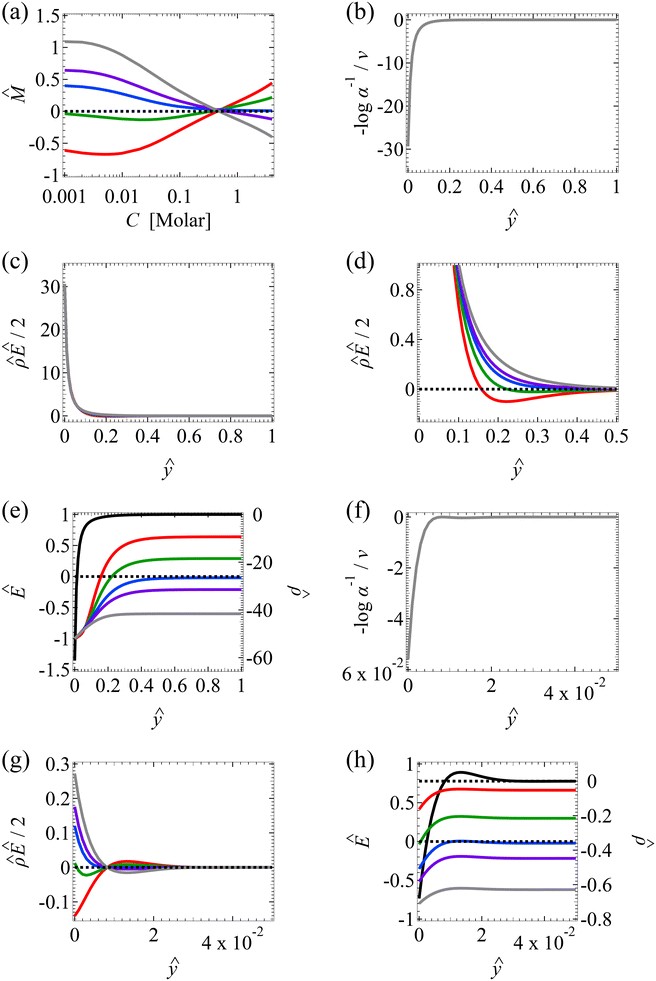 | ||
| Fig. 3 Diffusioosmosis of monovalent electrolytes accounting for electrostatic correlations (δc = κlc). Figure captions are the same as those in Fig. 2, except that electrostatic correlations are accounted for. | ||
We start by stating the similarities between Fig. 3(a) and 2(a). These similarities occur when C < 0.1 M, where the effect of electrostatic correlations is weak. First, Fig. 3(a) shows that, at a low electrolyte concentration C = 10–3 M, the mobility is negative for a strongly positive β (grey line) and transitions to be negative for a strongly positive β (red line). This trend and the physical explanations are identical to those presented in Fig. 2(a) at a low electrolyte concentration (the first and the second observation in section 3.1.1). In fact, the mobilities at C = 10–3 M in Fig. 3(a) and their constitutive driving forces in Fig. 3(b)–(e) are almost identical to those in Fig. 2(a)–(e). This is because, at C = 10–3 M, δc = 0.074 ≪ 1 in Fig. 3(a)–(e) indicates that electrostatic correlations are negligible and can be approximated accurately by neglecting electrostatic correlations (δc = 0) as presented in Fig. 2(a)–(e). Second, the same as in Fig. 2(a), Fig. 3(a) shows that the magnitude of the mobility decreases with an increasing electrolyte concentration. This echoes the third observation in section 3.1.1.
Next, let us state and discuss the new phenomena caused by electrostatic correlations, as shown by the dissimilarities between Fig. 3(a) and 2(a). These dissimilarities occur when C ≳ 0.1 M, where the effect of electrostatic correlations is prominent. The first new phenomenon caused by electrostatic correlations is that, for a fixed β value, there is a substantial deviation of the mobility as shown in Fig. 3(a) relative to Fig. 2(a) at C ≥ 0.2 M where δc ≥ 1. This is consistent with the Poisson–Fermi eqn (4) in that the effect of electrostatic correlations is important when δc ≳ O(1).77
The second new phenomenon caused by electrostatic correlations is that the aforementioned deviation of the mobility in Fig. 3(a) subsequently evolves into a unique sign reversal in the mobility at C ≳ 0.4 M, which is absent in Fig. 2(a). For instance, in Fig. 3(a) for β = −0.60 (grey line) the mobility is positive at C = 10–3 M and becomes negative at C ≳ 0.4 M, whereas in Fig. 2(a) for β = −0.60 the mobility is positive at all concentrations C. A comparison between Fig. 3(f)–(h) (which accounts for electrostatic correlations) and Fig. 2(f)–(h) (which ignores electrostatic correlations) shows that electrostatic correlations are at the origin of such a sign reversal in the mobility at a high electrolyte concentration. First, by comparing Fig. 3(f) and 2(f), the chemiosmotic driving force –(log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) α−1)/ν in the two panels are found to be qualitatively the same, indicating that the chemiosmotic flow is not a cause of the diffusioosmotic mobility reversal at a high electrolyte concentration. Second, by comparing Fig. 3(g) and 2(g), the electroosmotic driving force
α−1)/ν in the two panels are found to be qualitatively the same, indicating that the chemiosmotic flow is not a cause of the diffusioosmotic mobility reversal at a high electrolyte concentration. Second, by comparing Fig. 3(g) and 2(g), the electroosmotic driving force ![[small rho, Greek, circumflex]](https://www.rsc.org/images/entities/i_char_e0b7.gif) Ê/2 presented in Fig. 3(g) shows a sign reversal near ŷ = 0.01, which is absent in Fig. 2(g). This indicates that the electroosmotic flow reversal away from the channel surface is the cause of the diffusioosmotic mobility reversal at a high electrolyte concentration. We remark that such a sign reversal in
Ê/2 presented in Fig. 3(g) shows a sign reversal near ŷ = 0.01, which is absent in Fig. 2(g). This indicates that the electroosmotic flow reversal away from the channel surface is the cause of the diffusioosmotic mobility reversal at a high electrolyte concentration. We remark that such a sign reversal in 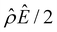 is due to the electrostatic correlation-induced overscreening of the channel surface charge, which is manifested in a sign change in the space charge density
is due to the electrostatic correlation-induced overscreening of the channel surface charge, which is manifested in a sign change in the space charge density 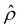 near the channel surface as shown in Fig. 3(h). This sign change in
near the channel surface as shown in Fig. 3(h). This sign change in 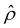 is absent when electrostatic correlations are ignored in Fig. 2(h). This sign change in
is absent when electrostatic correlations are ignored in Fig. 2(h). This sign change in 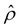 has been reported in prior work and causes various anomalous electrokinetic phenomena, including electroosmotic flow reversal,70 electrophoretic mobility reversal,72 dielectrophoretic polarization reversal,73 and ionic current rectification reversal.74 In sum, electrostatic correlations cause overscreening of the channel surface charge that leads to a sign change in the space charge density near the channel surface. Such a sign change in the space charge density in turn causes a reversal in the electroosmotic driving force
has been reported in prior work and causes various anomalous electrokinetic phenomena, including electroosmotic flow reversal,70 electrophoretic mobility reversal,72 dielectrophoretic polarization reversal,73 and ionic current rectification reversal.74 In sum, electrostatic correlations cause overscreening of the channel surface charge that leads to a sign change in the space charge density near the channel surface. Such a sign change in the space charge density in turn causes a reversal in the electroosmotic driving force 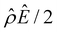 that generates the electroosmotic flow, leading to a sign reversal in the diffusioosmotic mobility.
that generates the electroosmotic flow, leading to a sign reversal in the diffusioosmotic mobility.
A further note to the above-mentioned second new phenomenon is that the unique sign reversal in the mobility is absent for β = −0.02 (blue line) in Fig. 3(a), despite accounting for electrostatic correlations. This is because for β = −0.02 a sign change in Ê and in 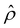 [Fig. 3(h)] cancel each other, leading to no sign change in
[Fig. 3(h)] cancel each other, leading to no sign change in 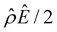 [Fig. 3(g)] and the electroosmotic flow. Thus, without a sign change in the electroosmotic flow, there is no sign change in the diffusioosmotic mobility.
[Fig. 3(g)] and the electroosmotic flow. Thus, without a sign change in the electroosmotic flow, there is no sign change in the diffusioosmotic mobility.
The third new phenomenon caused by electrostatic correlations is that, after the unique sign reversal in the mobility at C ≳ 0.4 M, the mobility continues to increase in magnitude as shown in Fig. 3(a). The two physical underpinnings of this new phenomenon are as follows. First, in the presence of electrostatic correlations, the magnitude of the electroosmotic driving force 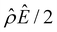 [Fig. 3(g)] is larger than that when electrostatic correlations are neglected [Fig. 2(g)]. Second, overscreening as described by the Poisson–Fermi equation causes a non-vanishing and increasing channel surface potential at an electrolyte concentration of C ≳ 0.4 M. Physically, the charge on the channel surface is overcompensated by a layer of counterions,69,72 resulting in an increasing surface potential as the electrolyte concentration increases and electrostatic correlations become increasingly important. This is in contrast to the classical Poisson equation, which overlooks overscreening and predicts a vanishing channel surface potential at a high electrolyte concentration. For instance, at C = 1 M, in Fig. 3(a) the channel surface potential
[Fig. 3(g)] is larger than that when electrostatic correlations are neglected [Fig. 2(g)]. Second, overscreening as described by the Poisson–Fermi equation causes a non-vanishing and increasing channel surface potential at an electrolyte concentration of C ≳ 0.4 M. Physically, the charge on the channel surface is overcompensated by a layer of counterions,69,72 resulting in an increasing surface potential as the electrolyte concentration increases and electrostatic correlations become increasingly important. This is in contrast to the classical Poisson equation, which overlooks overscreening and predicts a vanishing channel surface potential at a high electrolyte concentration. For instance, at C = 1 M, in Fig. 3(a) the channel surface potential 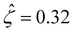 whereas in Fig. 2(a) the channel surface potential
whereas in Fig. 2(a) the channel surface potential 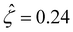 . In sum, under electrostatic correlations, with a larger
. In sum, under electrostatic correlations, with a larger 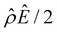 value and an increasing
value and an increasing 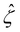 value at a high electrolyte concentration, the diffusioosmotic mobility continues to increase in magnitude after the unique sign reversal.
value at a high electrolyte concentration, the diffusioosmotic mobility continues to increase in magnitude after the unique sign reversal.
 at C = 10–3 M and
at C = 10–3 M and  as C increases. The channel surface charge density q = 0.014 C m−2 (
as C increases. The channel surface charge density q = 0.014 C m−2 (![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) = 78.4) corresponds to a channel surface potential ζ = 50 mV
= 78.4) corresponds to a channel surface potential ζ = 50 mV 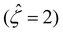 at C = 10–3 M. We use the same
at C = 10–3 M. We use the same ![[q with combining circumflex]](https://www.rsc.org/images/entities/i_char_0071_0302.gif) to compute the mobility at other electrolyte concentrations. Fig. 4 includes the effect of finite-ion-size, i.e., ν is non-zero, but ignores electrostatic correlations by setting δc = 0. A positive (negative) mobility corresponds to a diffusioosmotic flow from a region of low (high) to high (low) electrolyte concentration. The observations from Fig. 4 and explanations largely follow those from Fig. 2 for monovalent electrolytes. We have summarized them below.
to compute the mobility at other electrolyte concentrations. Fig. 4 includes the effect of finite-ion-size, i.e., ν is non-zero, but ignores electrostatic correlations by setting δc = 0. A positive (negative) mobility corresponds to a diffusioosmotic flow from a region of low (high) to high (low) electrolyte concentration. The observations from Fig. 4 and explanations largely follow those from Fig. 2 for monovalent electrolytes. We have summarized them below.
First, Fig. 4(a) shows that, at a low electrolyte concentration C = 10–3 M, the mobility transitions from a large positive number to a small positive number as β is increasingly positive. This trend and the physical explanations are identical to that in Fig. 2(a) at a low electrolyte concentration (the first and the second observation in section 3.1.1). Specifically, in Fig. 4(a) at C = 10–3 M, the positive mobility for β = −0.14 (grey line) arises from the electroosmotic flow [Fig. 4(c)–(e)] dominating the chemiosmotic flow [Fig. 4(b)], where the former flows from a region of low to high electrolyte concentration, i.e., a positive mobility. The smaller positive mobility for β = −0.10 (red line) is due to the fact that the electroosmotic flow is weaker than that for β = −0.14 [Fig. 4(c)–(e)], despite that it still dominates the chemiosmotic flow [Fig. 4(b)].
Second, Fig. 4(a) shows that the mobility decreases in magnitude with an increasing electrolyte concentration. This trend is identical to the third observation in section 3.1.1. The physical explanations are the same and not repeated here for brevity.
 | ||
| Fig. 5 Diffusioosmosis of divalent electrolytes accounting for electrostatic correlations (δc = κlc). Figure captions are the same as those in Fig. 4, except that electrostatic correlations are accounted for. | ||
The first new phenomenon caused by electrostatic correlations is that, for a fixed β, there is a substantial deviation of the mobility in Fig. 5(a) compared to that in Fig. 4(a). This observation is similar to the first new phenomenon in section 3.1.2 for monovalent electrolytes. Specifically, this deviation is observed in monovalent electrolytes at C ≥ 0.2 M by comparing Fig. 3(a) and 2(a). However, this deviation occurs at a lower electrolyte concentration C ≥ 10–3 M for divalent electrolytes as observed by comparing Fig. 5(a) and 4(a). This can be understood as follows. First, the inverse Debye length of a divalent electrolyte is twice that of a monovalent electrolyte, κdi = 2κmono. Second, the electrostatic correlation length of a divalent electrolyte is four times that of a monovalent electrolyte, lc,di = 4lc,mono. Combining these two statements, it is computed that, at C = 10–3 M, δc(= κlc) = 0.59 for a divalent electrolyte whereas δc = 0.074 for a monovalent electrolyte. That is, at C = 10–3 M, the effect of electrostatic correlations is prominent in divalent electrolytes but not in monovalent electrolytes. Hence, consistent with the Poisson–Fermi equation that the impact of electrostatic correlations increases with δc, at the same concentration the deviation of the mobility in divalent electrolytes [comparing Fig. 5(a) and 4(a)] is more prominent than that in monovalent electrolytes [comparing Fig. 3(a) and 2(a)].
The second new phenomenon caused by electrostatic correlations is that there is a unique sign reversal in the mobility at C ≈ 0.003 M in Fig. 5(a), which is absent in Fig. 4(a). A comparison between Fig. 5(f)–(h) (which accounts for electrostatic correlations) and Fig. 4(f)–(h) (which ignores electrostatic correlations) shows that electrostatic correlations are at the origin of such a sign reversal. The phenomenon and physical explanations here are identical to those in the discussion of the second new phenomenon in section 3.1.2 and are reiterated briefly as follows. Electrostatic correlations result in overscreening of the channel surface charge and a sign change in the space charge density near the channel surface [Fig. 5(h)]. Such a sign change in the space charge density in turn induces a reversal in the electroosmotic driving force 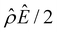 and electroosmotic flow [Fig. 5(g)], leading to a sign reversal in the diffusioosmotic mobility [Fig. 5(a)]. We note that such a mobility reversal due to electrostatic correlations occurs at a lower concentration of a divalent electrolyte [C ≈ 0.003 M in Fig. 5(a)] relative to that of a monovalent electrolyte [C ≈ 0.4 M in Fig. 3(a)].
and electroosmotic flow [Fig. 5(g)], leading to a sign reversal in the diffusioosmotic mobility [Fig. 5(a)]. We note that such a mobility reversal due to electrostatic correlations occurs at a lower concentration of a divalent electrolyte [C ≈ 0.003 M in Fig. 5(a)] relative to that of a monovalent electrolyte [C ≈ 0.4 M in Fig. 3(a)].
The third new phenomenon caused by electrostatic correlations is that, at C ≳ 0.003 M, the mobility continues to increase in magnitude as shown in Fig. 5(a). The physical underpinnings of this phenomenon are the same as the third new phenomenon in section 3.1.2 and are not repeated for brevity.
3.2. Diffusioosmotic flow direction diagrams
So far, we have presented results of how the sign and magnitude of the diffusioosmotic mobility (flow) vary with the electrolyte concentration, ion diffusivity difference, and ion valence, at a fixed channel surface charge. In this section, we plot diffusioosmotic flow direction diagrams that show how the sign of the mobility changes with these parameters at varying channel surface charges. The channel height H = 100 nm. Electrostatic correlations are accounted for by incorporating a non-zero δc = κlc. These diagrams are efficient to identify the range of parameters that generates diffusioosmosis of the desired direction.We present the diffusioosmotic flow direction diagrams for monovalent electrolytes at C = 10–3 M in Fig. 6(a) and at C = 1 M in Fig. 6(b). The blue lines are obtained by determining the values of β that generate a zero diffusioosmotic mobility (mean diffusioosmotic velocity) at each q by setting a tolerance of M ≤ 10–4. Thus, the blue lines separate each figure into four domains, each of them corresponding to diffusioosmosis flowing from a region of high to low electrolyte concentration or vice versa. We state three key observations associated with electrostatic correlations from these figures as follows.
First, at C = 10–3 M, when q is positive and as β changes from negative to positive [going from left to right in the top half of Fig. 6(a)], the direction of diffusioosmosis changes from “flowing from a region of low to high electrolyte concentration” (positive mobility) to “flowing from a region of high to low electrolyte concentration” (negative mobility). This observation corresponds to the first and the second observation in section 3.1.1. In contrast, at C = 1 M, when q is positive and as β changes from negative to positive [going from left to right in the top half of Fig. 6(b)], the direction of diffusioosmosis changes from “flowing from a region of high to low electrolyte concentration” (negative mobility) to “flowing from a region of low to high electrolyte concentration” (positive mobility). This observation corresponds to the second new phenomenon in section 3.1.2. A diffusioosmotic flow reversal due to electrostatic correlations is demonstrated by comparing the same domain across Fig. 6(a) and (b).
Second, when the magnitude of q is large (e.g., |q| = 0.014 C m−2) and β is small (e.g., |β| = 0.02), the direction of diffusioosmosis remains the same across a low [Fig. 6(a)] and a high electrolyte concentration [Fig. 6(b)]. One example of this observation is KCl (β = −0.02) shown in Fig. 3(a), where the mobility remains positive from low to high electrolyte concentrations.
Third, at a low electrolyte concentration, when βq > 0 a diffusioosmotic flow reversal can occur by varying the magnitude of the channel surface charge without changing its sign [e.g., the two arrows in Fig. 6(a)], whereas at a high electrolyte concentration this can only be achieved when βq < 0 [e.g., the two arrows in Fig. 6(b)]. This diffusioosmotic flow reversal has been observed in prior work that did not consider electrostatic correlations.4,8,50,52 That is, this reversal is not due to electrostatic correlations but is a consequence of the competition between the chemiosmotic and electroosmotic components of diffusioosmosis, since it occurs even at a low electrolyte concentration. However, here we remark that electrostatic correlations can radically change the dependence of this reversal on βq between a dilute and a concentrated electrolyte. Before ending, we show the diffusioosmotic flow direction diagrams for divalent electrolytes at C = 10–3 M in Fig. 6(c) and at C = 1 M in Fig. 6(d). These figures are qualitatively similar to Fig. 6(a) and (b).
4. Conclusions
In this work, we have developed a mathematical model for quantifying the diffusioosmotic flow driven by a binary symmetric electrolyte concentration gradient in a charged parallel-plate channel. The key distinction between this and prior work is the incorporation of ion–ion electrostatic correlations in modeling diffusioosmosis, which is important in concentrated electrolytes but has been ignored in prior theories. The present model also incorporates the steric effect of finite-ion-size, which has been shown to be important in diffusioosmosis of concentrated electrolytes.14,52 To demonstrate our model, we have computed and analyzed the diffusioosmotic flow mobilities of a list of common monovalent and divalent electrolytes.In the first part of this article, we have analyzed the variation of the mobilities with respect to the electrolyte concentration. For both monovalent and divalent electrolytes, we have shown that ion–ion electrostatic correlations can lead to a unique reversal of the diffusioosmotic flow. Specifically, electrostatic correlations overscreen the channel surface charge and cause a sign change in the space charge density near the channel surface. This in turn causes a reversal in the electroosmotic driving force of diffusioosmosis, leading to a sign reversal in the diffusioosmotic mobility. Existing theories that ignore electrostatic correlations cannot capture this unique diffusioosmotic flow reversal. Accounting only for the steric effect of the finite size of ions is not sufficient to capture this flow reversal. This reversal occurs at ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.4 M for a monovalent electrolyte and at a much lower concentration of ≈
0.4 M for a monovalent electrolyte and at a much lower concentration of ≈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0.003 M for a divalent electrolyte in a channel with the same surface charge. These results demonstrate the significant impact of electrostatic correlations on diffusioosmosis, where not just its magnitude but its direction can be altered.
0.003 M for a divalent electrolyte in a channel with the same surface charge. These results demonstrate the significant impact of electrostatic correlations on diffusioosmosis, where not just its magnitude but its direction can be altered.
In the second part of this article, we have constructed flow direction diagrams that enable efficient identification of the diffusioosmotic flow direction for a given set of electrolyte concentration, ion diffusivity, ion valence, and channel surface charge. These diagrams predict a separate diffusioosmotic flow reversal that has been identified in prior work.4,8,50,52 This reversal can occur even at a low electrolyte concentration where electrostatic correlations are negligible. Thus, this reversal is not due to electrostatic correlations but the competition between the chemiosmosis and electroosmosis that constitute diffusioosmosis. This reversal can be achieved by varying the magnitude of the channel surface charge without varying its sign. We show that electrostatic correlations can alter qualitatively how this reversal depends on the product of the channel surface charge and the ion diffusivity difference βq across low to high electrolyte concentrations. Namely, this reversal occurs at a low electrolyte concentration only when βq > 0 and at a high electrolyte concentration only when βq < 0.
The present analysis can be extended in several directions. First, a natural extension is to relax the assumption that the equilibrium electric double layer is not perturbed by the diffusioosmotic flow. This can be done by numerically solving the coupled nonlinear systems of the Poisson–Fermi equation, conservation of individual ionic species, and the Stokes equation with an electric body force. However, we note that this extension will likely give quantitative modifications to our present results only and will not alter our conclusions, since the Peclet number is weak [Pe ≤ O(1)] in diffusioosmosis.10,50 Second, other effects can be incorporated into the present model, e.g., a concentration-dependent viscosity, diffusivity, and permittivity.77,79 These effects are, however, prominent only in a solution whose concentration is higher than a few molars. Thus, they will not qualitatively alter the flow reversal predicted from this work, which occurs much below one molar concentration. Third, diffusioosmosis experiments have matured in recent years9,21 and can measure the diffusioosmotic flow reversal predicted in this work.
Appendix A: Numerical schemes for solving the electric potential and diffusioosmotic mobility
We describe the numerical schemes for solving the electric potential and diffusioosmotic velocity. Let us start with the governing equation and boundary conditions eqn (4)–(6) for the electric potential. We first discretize the domain ŷ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ∈
∈![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) [0, 1] into m + 1 grid points ŷ0, ŷ1,…ŷm, where ŷi = ŷ0 + iΔŷ with Δŷ the grid size and i = 0, 1,…m. The electric potential at the grid point ŷi is
[0, 1] into m + 1 grid points ŷ0, ŷ1,…ŷm, where ŷi = ŷ0 + iΔŷ with Δŷ the grid size and i = 0, 1,…m. The electric potential at the grid point ŷi is 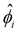 . We approximate the first- and third-order derivatives using a forward finite-difference scheme with a first-order accuracy, and the second- and fourth-order derivatives using a central finite-difference scheme with a second-order accuracy as follows,80
. We approximate the first- and third-order derivatives using a forward finite-difference scheme with a first-order accuracy, and the second- and fourth-order derivatives using a central finite-difference scheme with a second-order accuracy as follows,80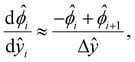 | (16) |
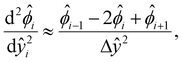 | (17) |
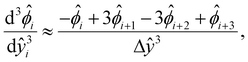 | (18) |
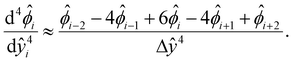 | (19) |
Upon finite-differencing, eqn (4)–(6) form a system of m + 1 nonlinear equations with m + 1 unknown 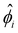 , which are solved by the Newton's method via the built-in solver FindRoot in Wolfram Mathematica. The diffusioosmotic velocity is solved by the same finite-difference method, except that the highest-order derivative in its governing equation and boundary conditions eqn (13) and (14) is second order. A converged solution of the mean diffusioosmotic velocity, equivalently the diffusioosmotic mobility, is obtained with Δŷ = 10–5. For instance, as shown in Fig. 7, the mobilities at C = 10–3 M obtained with Δŷ = 10–5 (solid lines) differ by less than 0.2% from those obtained with Δŷ = 5 × 10–6 (circles).
, which are solved by the Newton's method via the built-in solver FindRoot in Wolfram Mathematica. The diffusioosmotic velocity is solved by the same finite-difference method, except that the highest-order derivative in its governing equation and boundary conditions eqn (13) and (14) is second order. A converged solution of the mean diffusioosmotic velocity, equivalently the diffusioosmotic mobility, is obtained with Δŷ = 10–5. For instance, as shown in Fig. 7, the mobilities at C = 10–3 M obtained with Δŷ = 10–5 (solid lines) differ by less than 0.2% from those obtained with Δŷ = 5 × 10–6 (circles).
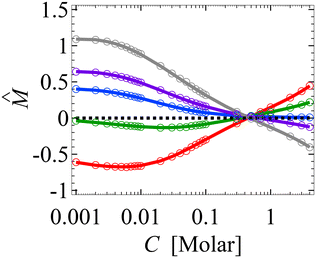 | ||
| Fig. 7 Figure captions are the same as those in Fig. 3(a). Solid lines denote results obtained with the grid size Δŷ = 10–5 and circles denote results obtained with Δŷ = 5 × 10–6. | ||
Appendix B: Model validation by recovering prior work
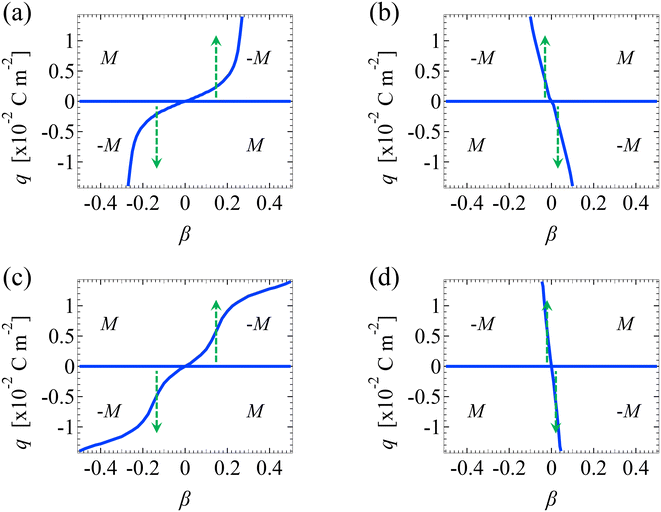
We validate our model by recovering the results of prior work, which computed the diffusioosmotic mobilities that account for the finite size of ions but ignore electrostatic correlations52 and those that ignore the finite size of ions and electrostatic correlations.50 Specifically, as shown by the solid lines in Fig. 8(a), our model recovers the mobilities computed by Hoshyargar et al.52 with ν = 0.05,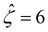 and Pe = 1, in the limit of δc = 0. As shown by the squares in Fig. 8(a), our model recovers the mobilities computed by Ma and Keh50 with
and Pe = 1, in the limit of δc = 0. As shown by the squares in Fig. 8(a), our model recovers the mobilities computed by Ma and Keh50 with 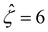 and Pe = 1, in the limit of ν = 0 and δc = 0. In short, Fig. 8(a) in this work shows the recovery of Fig. 2(b) in ref. 52, which compares model predictions with and without the finite size of ions in the absence of electrostatic correlations. For an additional reference, we generate a similar set of mobilities with
and Pe = 1, in the limit of ν = 0 and δc = 0. In short, Fig. 8(a) in this work shows the recovery of Fig. 2(b) in ref. 52, which compares model predictions with and without the finite size of ions in the absence of electrostatic correlations. For an additional reference, we generate a similar set of mobilities with 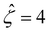 as shown in Fig. 8(b).
as shown in Fig. 8(b).
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors acknowledge the funding support from the Division of Sponsored Programs, Department of Chemical Engineering, and Herbert Wertheim College of Engineering at University of Florida. This material is based upon work supported by the U.S. Department of Energy, Office of Science, Office of Basic Energy Sciences, Geosciences program under Award Number DE-SC0018676.References
- B. V. Derjaguin, G. P. Sidorenkov, E. A. Zubashchenkov and E. V. Kiseleva, Kolloidyni Zh., 1947, 9, 335–348 Search PubMed.
- J. L. Anderson, Annu. Rev. Fluid Mech., 1989, 21, 61–99 CrossRef.
- D. Velegol, A. Garg, R. Guha, A. Kar and M. Kumar, Soft Matter, 2016, 12, 4686–4703 RSC.
- H. J. Keh, Curr. Opin. Colloid Interface Sci., 2016, 24, 13–22 CrossRef CAS.
- S. Marbach and L. Bocquet, Chem. Soc. Rev., 2019, 48, 3102–3144 RSC.
- S. Shin, Phys. Fluids, 2020, 32, 101302 CrossRef CAS.
- S. Shim, Chem. Rev., 2022, 122, 6986–7009 CrossRef CAS PubMed.
- D. C. Prieve, J. L. Anderson, J. P. Ebel and M. E. Lowell, J. Fluid Mech., 1984, 148, 247–269 CrossRef CAS.
- C. Lee, C. Cottin-Bizonne, A. L. Biance, P. Joseph, L. Bocquet and C. Ybert, Phys. Rev. Lett., 2014, 112, 244501 CrossRef CAS PubMed.
- S. Shin, E. Um, B. Sabass, J. T. Ault, M. Rahimi, P. B. Warren and H. A. Stone, Proc. Natl. Acad. Sci. U. S. A., 2016, 113, 257–261 CrossRef CAS PubMed.
- N. Shi, R. Nery-Azevedo, A. I. Abdel-Fattah and T. M. Squires, Phys. Rev. Lett., 2016, 117, 258001 CrossRef PubMed.
- V. Hoshyargar, S. N. Ashrafizadeh and A. Sadeghi, Phys. Fluids, 2017, 29, 012001 CrossRef.
- S. Marbach, H. Yoshida and L. Bocquet, J. Chem. Phys., 2017, 146, 194701 CrossRef PubMed.
- R. F. Stout and A. S. Khair, Phys. Rev. Fluids, 2017, 2, 014201 CrossRef.
- J. T. Ault, S. Shin and H. A. Stone, J. Fluid Mech., 2018, 854, 420–448 CrossRef CAS.
- F. Raynal, M. Bourgoin, C. Cottin-Bizonne, C. Ybert and R. Volk, J. Fluid Mech., 2018, 847, 228–243 CrossRef CAS.
- J. T. Ault, S. Shin and H. A. Stone, Soft Matter, 2019, 15, 1582–1596 RSC.
- F. Raynal and R. Volk, J. Fluid Mech., 2019, 876, 818–829 CrossRef CAS.
- D. Ha, S. Seo, K. Lee and T. Kim, ACS Nano, 2019, 13, 12939–12948 CrossRef CAS PubMed.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2020, 16, 238–246 RSC.
- M. K. Rasmussen, J. N. Pedersen and R. Marie, Nat. Commun., 2020, 11, 2337 CrossRef CAS PubMed.
- V. S. Doan, S. Chun, J. Feng and S. Shin, Nano Lett., 2021, 21, 7625–7630 CrossRef CAS PubMed.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2021, 917, A52 CrossRef CAS.
- B. M. Alessio, S. Shim, E. Mintah, A. Gupta and H. A. Stone, Phys. Rev. Fluids, 2021, 6, 054201 CrossRef.
- S. Chanda and P. A. Tsai, Phys. Fluids, 2021, 33, 032008 CrossRef CAS.
- H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, Soft Matter, 2022, 18, 1896–1910 RSC.
- B. E. McKenzie, H. C. W. Chu, S. Garoff, R. D. Tilton and A. S. Khair, J. Fluid Mech., 2022, 949, A17 CrossRef CAS.
- R. E. Migacz and J. T. Ault, Phys. Rev. Fluids, 2022, 7, 034202 CrossRef.
- R. Volk, M. Bourgoin, C. Brehier and F. Raynal, J. Fluid Mech., 2022, 948, A42 CrossRef CAS.
- S. Lee, J. Lee and J. T. Ault, Colloids Surf., A, 2023, 659, 130775 CrossRef CAS.
- S. Sambamoorthy and H. C. W. Chu, Soft Matter, 2023, 19, 1131–1143 RSC.
- J. Xu, Z. Wang and H. C. W. Chu, RSC Adv., 2023, 13, 9247–9259 RSC.
- I. Ertugrul and O. Ulkir, RSC Adv., 2020, 10, 33731–33738 RSC.
- A. Sharma, M. Bekir, N. Lomadze, S. Jung, A. Pich and S. Santer, Langmuir, 2022, 38, 6343–6351 CrossRef CAS PubMed.
- X. Wang and D. Jing, J. Phys. D: Appl. Phys., 2022, 55, 145401 CrossRef CAS.
- S. K. Mehta and P. K. Mondal, Electrophoresis, 2023, 44, 44–52 CrossRef CAS PubMed.
- B. E. Logan and M. Elimelch, Nature, 2012, 488, 313–319 CrossRef CAS PubMed.
- A. Siria, P. Poncharal, A. Biance, R. Fulcrand, X. Blase, S. T. Purcell and L. Bocquet, Nature, 2013, 494, 455–458 CrossRef CAS PubMed.
- B. D. Kang, H. J. Kim, M. G. Lee and D. Kim, Energy, 2015, 86, 525–538 CrossRef CAS.
- S. Chanda and P. A. Tsai, Energy, 2019, 176, 531–543 CrossRef CAS.
- M. Karimzadeh, M. Khatibi, S. N. Ashrafizadeh and P. K. Mondal, Phys. Chem. Chem. Phys., 2022, 24, 20303–20317 RSC.
- D. Pandey, P. K. Mondal and S. Wongwises, Soft Matter, 2023, 19, 1152–1163 RSC.
- A. Kar, T. Chiang, I. O. Rivera, A. Sen and D. Velegol, ACS Nano, 2015, 9, 746–753 CrossRef CAS PubMed.
- S. W. Park, J. Lee, H. Yoon and S. Shin, Energy Fuels, 2021, 35, 4885–4892 CrossRef CAS.
- N. Shi and A. Abdel-Fattah, Phys. Rev. Fluids, 2021, 6, 053103 CrossRef.
- H. Tan, A. Banejee, N. Shi, X. Tang, A. Abdel-Fattah and T. M. Squires, Sci. Adv., 2021, 7, eabh0638 CrossRef CAS PubMed.
- H. Zhang, D. Y. Moh, S. Wang and R. Qiao, Phys. Fluids, 2022, 34, 092017 CrossRef CAS.
- H. J. Keh and J. H. Wu, Langmuir, 2001, 17, 4216–4222 CrossRef CAS.
- H. J. Keh and H. C. Ma, Colloids Surf., A, 2004, 233, 87–95 CrossRef CAS.
- H. C. Ma and H. J. Keh, J. Colloid Interface Sci., 2006, 298, 476–486 CrossRef CAS PubMed.
- T. Chiang and D. Velegol, J. Colloid Interface Sci., 2014, 424, 120–123 CrossRef CAS PubMed.
- V. Hoshyargar, S. N. Ashrafizadeh and A. Sadeghi, Phys. Chem. Chem. Phys., 2015, 17, 29193–29200 RSC.
- H. Jing and S. Das, Phys. Chem. Chem. Phys., 2018, 20, 10204–10212 RSC.
- A. Gupta, B. Rallabandi and H. A. Stone, Phys. Rev. Fluids, 2019, 4, 043702 CrossRef.
- A. Y. Grosberg, T. T. Nguyen and B. I. Shklovskii, Rev. Mod. Phys., 2002, 74, 329–345 CrossRef CAS.
- Y. Levin, Rep. Prog. Phys., 2002, 65, 1577–1632 CrossRef CAS.
- M. Mezger, H. Schroder, H. Reichert, S. Schramm, J. S. Okasinski, S. Schoder, V. Honkimake, M. Deutsch, B. M. Ocko, J. Ralston, M. Rohwerder, M. Stratmann and H. Dosch, Science, 2008, 322, 424–428 CrossRef CAS PubMed.
- G. M. Torrie and J. P. Valleau, J. Chem. Phys., 1980, 73, 5807–5816 CrossRef CAS.
- E. Gonzales-Tovar, M. Lozada-Cassou and D. Henderson, J. Chem. Phys., 1985, 83, 361–372 CrossRef CAS.
- R. Kjellander and S. Marcelja, J. Phys. Chem. A, 1986, 90, 1230–1232 CrossRef CAS.
- P. Attard, D. J. Mitchell and B. W. Ninham, J. Chem. Phys., 1988, 89, 4358–4367 CrossRef CAS.
- J. Ennis, S. Marcelja and R. Kjellander, Electrochim. Acta, 1996, 41, 2115–2124 CrossRef CAS.
- R. R. Netz and H. Orland, Eur. Phys. J. E: Soft Matter Biol. Phys., 2000, 1, 203–214 CrossRef CAS.
- A. Martin-Molina, M. Quesada-Perez, F. Galisteo-Gonzalez and R. Hidalgo-Alvarez, J. Chem. Phys., 2003, 118, 4183–4189 CrossRef CAS.
- M. V. Fedorov and A. A. Kornyshev, J. Phys. Chem. B, 2008, 112, 11868–11872 CrossRef CAS PubMed.
- M. M. Hatlo and L. Lue, Europhys. Lett., 2010, 89, 25002 CrossRef.
- D. Gillespie, A. S. Khair, J. P. Bardhan and S. Pennathur, J. Colloid Interface Sci., 2011, 359, 520–529 CrossRef CAS PubMed.
- C. D. Santangelo, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 73, 041512 CrossRef PubMed.
- M. Bazant, B. D. Storey and A. A. Kornyshev, Phys. Rev. Lett., 2011, 106, 046102 CrossRef PubMed.
- B. D. Storey and M. Z. Bazant, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 056303 CrossRef PubMed.
- M. He, P. Sun and H. Zhao, Comput. Math. Appl., 2022, 117, 229–244 CrossRef.
- R. F. Stout and A. S. Khair, J. Fluid Mech., 2014, 752, R1 CrossRef CAS.
- E. Alidoosti and H. Zhao, Langmuir, 2018, 34, 5592–5599 CrossRef CAS PubMed.
- E. Alidoosti and H. Zhao, Electrophoresis, 2019, 40, 2655–2661 CrossRef CAS PubMed.
- J. J. Bikerman, Philos. Mag., 1942, 33, 384–397 CAS.
- M. S. Kilic, M. Z. Bazant and A. Ajdari, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2007, 75, 021502 CrossRef PubMed.
- M. Bazant, M. S. Kilic, B. D. Storey and A. Ajdari, Adv. Colloid Interface Sci., 2009, 152, 48–88 CrossRef CAS PubMed.
- P. Vanysek, CRC Handbook of Chemistry and Physics, CRC Press, Boca Raton, 1992 Search PubMed.
- Y. Nakayama and D. Andelman, J. Chem. Phys., 2015, 142, 044706 CrossRef PubMed.
- R. J. LeVeque, Finite difference methods for ordinary and partial differential equations, Society for Industrial and Applied Mathematics, Philadelphia, 2007 Search PubMed.
| This journal is © The Royal Society of Chemistry 2024 |