Nanometrology based control: taming radical grafting reactions with attoliter precision

Abstract

Precisely controlled micropatterning with organic moieties is a promising route for designing smart surfaces, enabling the development of microsensors and actuators with optimal usage of reactants. Such applications require fine control over the surface modification process, which in turn demands detailed knowledge about the surface modification process. As complex surface kinetics often emerge as a result of even slight modifications of the grafting entity, non-invasive, sensitive and precise closed loop control strategies are highly desirable. In this paper we demonstrate that a nanometrology approach based on quantitative phase imaging (QPI) fulfill all these requirements. We first use the technique to monitor surface photografting kinetics of aryl radicals, comprehensively analyzing the effect of substituents on surface addition reactions. We demonstrate that several aspects of the grafting process are affected in complex ways, rendering open-loop strategies impossible to implement precisely. Then, we show that the operando optical phase signal can be used as a direct feedback, guiding the grafting reaction process. Using relatively simple instrumentation, we demonstrate that general and precise control strategies can be designed and used to control the volume of the grafting material with attoliter precision, in spite of radically different surface modification kinetics spanning several orders of magnitude.

---

Introduction

Microstructured functional surfaces are highly desirable targets for the development of chemically complex tasks (sensors,¹ actuators,^2,3 anchoring,^4–6etc.) with minimal usage of reactants. Their implementation requires the development of precise surface modification methodologies, able to locally control the addition of chemical functions onto surfaces, preferably with large scope both in terms of chemical groups and surfaces. Photoactivated radical based strategies are particularly appealing in this regard, as photoactivation enables high spatial and temporal resolutions, while radical methodologies offer highly reactive intermediates bearing a variety of substituents,^7–9 which can be added to several different surfaces.^10–15 Such reactivity, however, often compromises the controllability of surface modification processes. Therefore, when quantitative grafting methodologies are sought (i.e. locally controlling the number of added molecules), it is essential to carefully consider the surface reaction kinetics.

Surface reactions intermediated by aryl radicals constitute a particularly pathological example of uncontrolled radical reactivity. Indeed, these intermediates react at different rates towards different surfaces (e.g. pristine glass, metal surfaces or previously grafted layers), leading to non-linear addition rates which often develop into inhomogeneities.^16–20 Moreover, aryl-radicals are relatively stable and thus able to diffuse for at least a few tens of nanometers before reacting,^21,22 often leading to resolution loss and decreasing the fabrication precision. The benefits of developing controlled aryl-radical addition is however high, motivating considerable efforts towards methodologies for their generation^23,24 and surface addition control.^22,25–29 Indeed, several precursors have emerged for triggering aryl radicals formation, such as aryl halides, aryltriflates,⁸ aryl iodonium salts,³⁰ arylazosulfonates,²⁴etc.

Within the context of surface modification, diazonium salts arguably remain the most popular and interesting platform for generating aryl-radicals,^8,31 being easily prepared from abundant aniline precursors,^11,31–33 compatible with aqueous media, and directly activatable through a variety of pathways, including electro-,^{12,15,34–37} thermo-²⁶ and photochemical methods.^{14,20,28,38–40} In particular, the attractiveness of photochemical routes has recently considerably increased, as our group has demonstrated that the reaction can be conducted in mild conditions (light in the visible range, low power sources) in very simple aqueous media, containing only the diazonium salt.^20,40 Therefore, in spite of the generality of the methods presented here, we chose to focus on this class of radical precursors.

Methodologies for controlling the extent of surface modification through diazonium salts activation are scarce, and almost exclusively focused in electrochemical activation. For instance, dynamic control over electrografting of diazonium salts has been attempted using charge, applied potential¹⁰ and time^25,41 as control parameters, with limited degree of success. Self-limiting and chemical strategies, such as radical scavengers,^35,42 monomer engineering,^{13,27,29,43,44} or grafting from viscous solvents,²⁶ have yielded better results, but such reactions only enable preparation of very thin layers (often monolayers), require considerable complexification of the reaction medium, and/or limit the precursor substituents. They therefore do not explore the chemical flexibility and practicity of diazonium salts to their full extent. Ideally, one would like to develop a strategy to stop the reaction on demand at a fixed volume or thickness.

For that, in situ monitoring and control seem required, and a few strategies have been proposed, such as capacitive,⁴⁵ optical⁴⁶ or quartz microbalances based.^34,47 No general control strategy has however emerged, as global surface indicators cannot easily be adapted to local modification, while reported high resolution methods provide little quantitative information about the distribution of the surface modification reaction. Control efforts are further complicated by lack of data on substituent effects in aryl-reactivity surface addition reactions. Existing literature data mostly deals with electrografted layers,^{34,36,47,51–53} reflecting the conductivity of the layer, rather than the intrinsic aryl-radical surface reactivity.

In this paper, we approach the problem from a nanometrology perspective, based on quantitative optical monitoring of surface modification kinetics. As we have previously shown,^20,40 quantitative phase imaging (QPI) enables monitoring the appearance of grafted layers in real-time with nanometric precision, and can be used to extract local surface modification kinetics. We now put these techniques in the service of reactivity control. First, we perform an extensive analysis of the influence of substituents on aryl-radicals surface reactivity, showing how the arylradical structure can impact several reactivity-determining parameters. Then, we attempt to use the resulting information to design strategies to quantitatively control the reaction extent (the amount of grafted material). We show that, in spite of grafting kinetics differences spanning several orders of magnitude, it is possible to design a control strategy to obtain local layers of precisely controlled volume.

Results and discussion

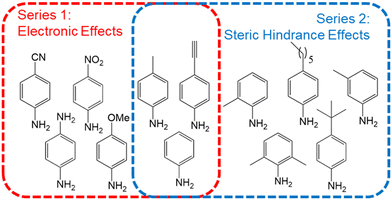
Within the context of surface modification, one of the most attractive features of using diazonium salts as aryl radical sources is that they can be formed in situ, avoiding isolation or purification steps, which are time consuming and potentially hazardous.^48,49 We thus start our substituent effect analysis from aniline precursors instead of directly the diazonium salts. We analyze the formation and surface modification dynamics of diazonium salts bearing a variety of substituents, as indicated in Fig. 1. A qualitative understanding of how substituents affect the stability and photografting efficiency of arylradical species is a necessary step to design control algorithms. Therefore, before explicitly attempting to design a general control strategy, we analyze how they affect several parameters which determine the grafting efficiency. The substituent scope is classified in two groups, indicated by different colors. The first series, indicated in red, is based on the electronic structure of the resulting diazonium salts and spans from strongly electron withdrawing (e.g. –NO₂) to electron donating moieties (e.g. –OMe). The second chemical series, composed of alkyl substituents of different structures and geometries, highlights the influence of steric hindrance effects on the grafting kinetics.

Fig. 1 Chemical structure of the diazonium precursors used in this study. The substituents are organized in two series, highlighting the substituents electronic properties (red) and steric hindrance ability (blue).

Diazotization kinetics and photophysical properties

As direct photografting of diazonium salts has been shown to proceed through direct photoabsorption,⁴⁰ it depends on the absorption coefficient at the excitation wavelength and on the concentration of the diazonium salts. Incomplete diazotization, presence of degradation kinetics and differential light absorbing properties are therefore some of the potential factors that could arise and directly impact the observed grafting rate. We therefore first analyze how substituents can impact these features during the diazonium salt formation, and consequently the diazonium salts concentration during photografting reactions. Diazotization reactions are monitored in situ by adding 1 eq. of diazotization agent (NaNO₂) to solutions of the aniline precursors (200 μM) inside a UV Vis cuvette. Fig. 2A shows typical spectral evolution associated with the diazotization reaction, along with the kinetic traces obtained by integration of the main emerging peak, indicated in gray (other substituents are shown in ESI section S2†). One can readily see how different the diazotization kinetics can be. For instance, diazonium formation takes place monotonically for 4-tertbutyl-aniline, leading to the appearance of a clear characteristic band (λ_max = 280 nm, ε_max = 5.5 × 10³ M⁻¹cm⁻¹) which remains stable at the timescale of the experiment, while other substituents, such as 2,6-dimethyl and 2-methyl, lead to an observable decrease in the formed bands after a few minutes. These observations show that (at least some of) the formed diazonium species are not completely stable in aqueous medium, and eventually degrade into other products. Conversely, species for which complex kinetics were expected, such as 4-phenylene-diamine (ESI section S2†), which could in principle lead to a proportion of bis-diazonium salts, in fact lead to simple diazotization reactions, as evidenced by the presence of a single peak in the resulting absorption spectrum, in agreement with literature data.⁵³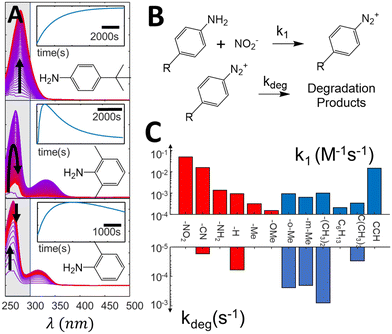

Fig. 2 (A) Evolution of difference absorption spectra of selected aniline precursors during the diazotization, showing the spectral evolution associated with the formation of diazonium salts. The spectra are normalized (see ESI section S2† for the original data). The highlighted zone is integrated to form the kinetic traces indicated in the insets. (B) simplified reaction mechanism used to fit the spectra evolution, (C) kinetic constants extracted from the kinetic fit, showcasing variation of almost three orders of magnitude in the formation constants and up to two orders for the degradation ones.

Diazotization kinetic traces are further analyzed by fitting the reaction kinetics to a simple model, indicated in Fig. 2B (see ESI section S3† for a detailed description of the fitting procedure). In our model, the formation of diazonium salts takes place through a second order reaction, while the degradation reaction is assumed to present first order kinetics. The rate constants extracted from the fits are summarized in Fig. 2C, and demonstrate how different the diazotization kinetics can be. While formation kinetics span three orders of magnitude, degradation constants can be quite substantial for some substituents, achieving rate constants as high as 10⁻³ s⁻¹. Although in most cases the salt formation takes place at a much higher rate than degradation, enabling reasonable control over the solution concentration, some of the formed salts degrade in a few minutes, posing a challenge for quantitative control strategies. Clearly, the diazotization kinetics and degradation behavior show sufficient variability to raise questions about the feasibility of open loop dosing strategies for control.

Influence of substituents on grafting kinetics

The identified difficulties in predicting the diazonium concentration could in principle be circumvented, at the expense of the convenience of one-pot in situ synthesis methods. Indeed, one could optimize the diazotization time and reactants concentration, isolate and purify the salts and pragmatically measure the absorbance of samples to enable a functional methodology to control the diazonium concentration in the grafting solution. Indeed, by increasing the aniline and diazotization agent concentrations, diazonium salts form much faster, enabling the reaction to reach completion before any measurable degradation can occur.

Therefore, we proceed our analysis by measuring the grafting kinetics for diazonium salts formed at high (5 mM) aniline and diazotization agent concentrations, and using only fresh (<2 h) solutions.

As detailed in the Methods section, the grafting reaction is excited locally with a laser beam (λ_exc = 474 nm) focused onto a glass surface (coverslip, ∼1μm² zone) immersed in the diazonium solution. Upon illumination, the diazonium moieties generate reactive species which graft onto the inert surface and onto previously grafted molecules, leading to formation of a organic layer which grows as more radicals are continuously photogenerated in the surface vicinity. The layer thickness is monitored with the QPI setup, which measures optical path differences between the surface initial state (before excitation), and operando during the grafting reaction. Representative data is shown in ESI section S1,† along with the experimental setup. Integration of the optical path difference in vicinity of the focused laser beam yields the optical volume difference (OVD) and allows a global and quantitative evaluation of the advancement of the surface modification process.

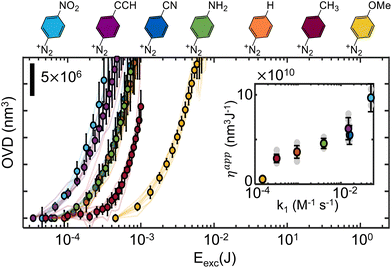
Since the measured molar absorption coefficients in the visible range are roughly similar (section S3, ESI†), it is expected that any observed grafting rate change stem from variation of the addition efficiencies. Such variability is indeed observed, as the apparent grafting efficiencies, defined here as the ratio between the grafted volume and the total excitation energy, are observed to span almost three orders of magnitude. While such result was expected on the grounds of radical stability, mobility, and steric hindrance, it signals the need to more finely understand the effect of substituents on the grafting efficiency, which is carried out next. In order to simplify the analysis, we separate the substrates in two series – aiming at extracting the influence of the aryl radicals’ electronic structure and steric properties.

Electronic structure. This series of substituents is selected to limit the effects of steric hindrance, and is therefore restricted to p-substituted diazonium salts bearing small groups. The grafting rates (or equivalently the apparent efficiencies) are expected to correlate with the lifetime of the radical species, as more stable radicals would be able to diffuse longer, increasing the reaction efficiency and grafting rate.

Fig. 3 shows the observed evolution of the grafted volume as a function of the total excitation energy for several p-substituted diazonium salts, monitored with QPI. As previously observed for Dz-NO₂,²⁰ the grafting dynamics can be divided in two characteristic regions: an induction period for low exposure dose, on which an apparently exponential relationship is observed (only visible for slow kinetics), and a linear regime. This behavior is assigned to a nucleation and growth mechanism, consistent with the fact that the underlying surface state only affects the inductive period, and has no significant influence on the linear regime, as shown in ESI section S8.† Both regimes are influenced by the substituents in non-monotonic ways, sometimes leading to curves which cross each other. Interestingly, the grafting rate in the linear regime (and consequently the apparent grafting efficiency) shows good correlation with the kinetic constant for diazonium formation, enabling Hammett-like analysis, as shown in the inset of Fig. 3. These trends are consistent with previous studies on radical reactivity triggered electrochemically, which also observed a correlation between the reduction potential and the electronic nature of substituents.^36,51 The existence of such linear relationships supports the hypothesis that, within this series, radical stability and addition rate are governed by electronic structure features. It enables some degree of predictive power over the grafting kinetics to be obtained in cases where the nucleation can be neglected in comparison to the linear growth regime (OVD ≫ 10⁷ nm³). Indeed, a open-loop strategy could be designed by extrapolating the observed η(k₁) relationship to determine the appropriate dosage required to graft a desired volume, as it will be shown later.

Fig. 3 Comparison of the grafting curves for p-substituted diazonium salts with small substituents (electronic series). Actual grafting curves are represented by continuous lines, while the averages between several (at least 3) experiments are indicated by the round markers. The inset compares the apparent efficiency, obtained by taking the slope of the OVD = f(E_exc) curves in the linear regime, compared to the diazotization formation rate constant on a semi-log scale. In both plots, the corresponding diazonium chemical structure is indicated by color.

Steric effects. If some degree of rationalization still seemed possible within the electronic series, such perspective gets considerably more complex when more general chemical structures are considered. This is exemplified by the data shown in Fig. 4. Grafting of three –CH₃ substituted diazonium salts isomers is shown for instance in Fig. 4A and perfectly illustrates the difficulty: although their structures only vary through the position of the methyl group, the grafting rate and efficiency are sharply modified, by more than an order of magnitude. Moreover, one can also observe differences in the induction regime, which appears to get longer for substituents located close to the radical position. While rough qualitative rationalization is possible on the basis of steric hindrance with respect to radical stability, layer organization, and/or radical addition hindrance, no clear quantitative trend can in fact be extracted.

Fig. 4 Comparison of several grafting curves within the steric series. (A) The grafting kinetics of three isomers is investigated, leading to different grafting kinetics. (B) grafting kinetics of different p-substituted diazonium salts, with varying hindrance potentials. (C) Comparison of the apparent grafting efficiencies, showcasing almost two orders of magnitude differences in grafting efficiency.

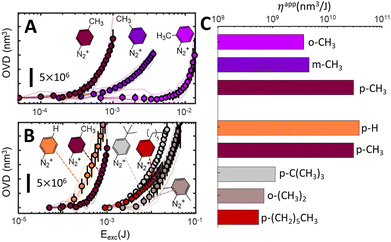
The situation is similar when more hindering structures are considered, as shown in Fig. 4B. It portraits a series of grafting experiments performed on diazonium salts bearing progressively larger substituents in the para position and a doubly hindered o-(CH₃)₂ substituent. Generally, one can clearly observe that crowded aryl radicals (p-C₆H₁₃, p-C(CH₃)₃, o-(CH₃)₂) graft considerably slower than less crowded ones (–H, –CH₃). Any comparison among the “sterically hindered” radicals is however purely qualitative, and all our attempts to quantitively describe the observed tendencies have remained inconclusive. Moreover, as the substituents get larger, more complex effects start to set in, such as the apparent saturation of p-C₆H₁₃ (ESI S3†), indicating that radical addition reactions are less likely to occur on grafted polymer than on pristine glass for some substituents. Hindering the positions next to the radical also progressively impairs the grafting rate (ESI section S6†). Indeed these substituents severely limit the number of suitable configurations for a radical attack onto the surface, prolonging the induction regime, and making the radical more prone to other deactivation mechanisms (such as radical–radical deactivation). As a consequence, low grafting efficiencies are observed. The linear growth regime is also impacted, but to a lesser extent, as the irregular distribution of the first grafted film increases the number of orientations leading to successful additions (i.e. with the attacking aryl radical perpendicularly oriented with respect to grafted species). As similarly observed in electrografting literature, where bulky radicals limit growth to thin layers, monolayers, or avoid grafting altogether,^13,51,52 only qualitative trends can be extracted, and a quantitative description of the influence of steric effects on grafting rates remains elusive.

Taken together, these results show that the grafting kinetics results from a complex mix between the substituted aryl ability to stabilize the radical, to enable surface attack, and to form easily (releasing N₂). Interplay between all these factors makes any predictive model difficult to implement, again raising serious questions about the feasibility of open loop control strategies.

Optical based control

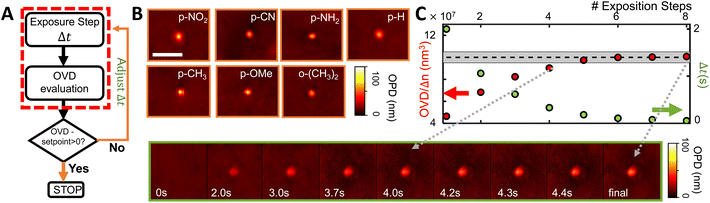
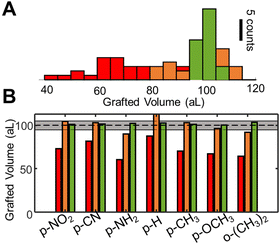
As shown by many aspects of the collected results, several properties which determine the grafting rate are strongly influenced by the presence of substituents, often in unpredictable ways. Consequently, the perspective of generally controlling diazonium photografting solely based on predictive strategies seems very grim. If nevertheless attempted, our results signal the need for extensive calibration of the chemical and optical systems before any quantitative predictions can be made, which is at best unpractical and usually unfeasible. Instead, we explore a different strategy to control the grafting reaction, using the operando QPI measurements as a feedback for the grafting process. Two simply implemented control algorithms are tested, incorporating a stop condition and using adaptative illumination steps, indicated in Fig. 5A in orange and green comparatively with open loop control in red.

Fig. 5 Implemented Control strategies. (A) Progressively more complex algorithms used for controlling the amount of grafted material. Each strategy is indicated by a different color. (B) Examples of grafted spots obtained with a fixed Setpoint Stop Condition, showcasing a fixed optical volume 1 ± 0.1 × 10⁸ nm³ (=100 ± 10 aL) for several substituted diazonium salts presenting very different grafting kinetics. The scale bar represents 5 μm. (C) Evolution of a grafting spot controlled by the Adaptative Exposure Time method, in which each exposure time (in green) is reduced proportionally to the distance between the measured grafted object (red) and the setpoint (indicated by the gray rectangle). The scale is the same as in B.

Setpoint stop condition. The most straightforward way of using the operando information is by integrating a stop condition into the illumination loop. In this case, the illumination shutter only opens if the measured optical volume (OVD) is below a predefined threshold value (orange in Fig. 5). Application of the methodology for deposition of grafted layers bearing different substituents but fixed optical volume (OVD = 10⁸ nm³ or 100 attoliters) shows that the methodology sensibly improves the surface modification precision. The resulting QPI images of seven different diazonium salts is shown in Fig. 5B, and demonstrates success of the strategy. With respect to model-based grafting (open loop control), the procedure significantly improves the grafting precision, leading to objects within 20% of the targeted optical volume. The process can be readily adapted for equal physical volumes by integrating knowledge about the refractive index of each resulting polymer.

As indicated in the Methods section (ESI S7†), this parameter can be readily obtained by taking the ratio between the optical volume of grafted layers and their actual volume, evaluated with atomic force microscopy (AFM). Using the measured refractive indices, we redefine the stop condition as OVD/Δn = 10⁸ nm³ (=100 aL). The efficiency of the method and reliability of refractive index estimations are confirmed, leading to physical grafted volumes within 20% of the target volume, as confirmed by AFM measurements, and shown in orange in Fig. 6.

Fig. 6 Comparison between the different control strategies. (A) histogram gathering grafted volumes over a large number of grafting operations, spanning different substituents. The volumes are determined from AFM height images by numerical integration. In (B) the same data is represented separated by the substituents, showcasing a superior performance of the adaptative method in all diazonium classes.

Adaptive exposure time. The process can be further improved by adapting the illumination dose to the grafting evolution. Indeed, during the previous experiment series, a systematic deviation with respect to the setpoint was observed, indicating that the grafting imprecisions are dominated by discretization error (the amount of material grafted at each step). In such case, reducing the duration of the illumination steps should improve the control precision. We design an improved version of the grafting experiment on which the duration of each grafting step (Δt_i) is automatically adapted after each OVD measurement. 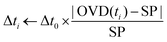The updated Δt is evaluated as the initial Δt₀ multiplied by the distance between the evaluated OVD and the setpoint (SP), accordingly to eqn (1).

As the grafted volume approaches the target setpoint, the added volume becomes proportionally smaller, asymptotically tending to SP. This configuration corresponds to a conservative proportional control strategy which takes into account the irreversibility of the grafting operation (one cannot “ungraft” material), and therefore that the amount of grafted material should never surpass the target value. A typical controlled grafting curve obtained using this strategy is shown in Fig. 5C (p-NO₂ substituent). Initial expositions quickly lead the grafted volume to within 10% of the grafted volume, while subsequent expositions of proportionally smaller doses refine the operation, asymptotically arriving at the target. Once the grafting procedure is within 5% of the target, the operation is stopped.

The performances of the three proposed strategies are compared in Fig. 6. Fig. 6A shows the AFM measured final grafted volume of several grafting operations, using the open loop control (red), setpoint stop condition (orange), and the adaptative method (green). The performance is homogeneous throughout all diazonium derivatives tested, as indicated in Fig. 6B. The dashed line indicates the target value (10⁸ nm³ ± 5%, 100 ± 5 aL). One can clearly see that, in spite of almost 4 orders of magnitude differences in the surface grafting kinetics, we were able to obtain grafted regions within 5% of the target volume, demonstrating attoliter level control over the volume of modified material.

Experimental

Diazotization of aniline precursors

The substituted diazonium salts are freshly prepared from their parent aniline precursors using one pot diazotization protocol before each experiment. The chosen precursors are indicated in Fig. 1 and were selected on the basis of the substituents chemical properties in order to constitute a representative electronic and steric hindrance series, as indicated in the main text. Unless noted otherwise, the reactions are carried out by mixing aqueous (pH 2, adjusted with HCl) 5 mM solutions of anilines with one equivalent NaNO₂ as diazotization agent. 5% DMSO are systematically added as a cosolvent to avoid solubility issues along all the chemical series.

Grafting setup

Grafting experiments were carried out as described previously.^20,40 In short, the grafting reactions are excited by a 474 nm pulsed laser (LDH-P-C-470, Picoquant, 40 MHz) focused on the surface of the substrate with the help of a ×100 oil immersion objective (Nikon, NA = 1.49), leading to a focused laser spot waist in the micrometer range (typ. FWHM = 800 nm). A thin (10 μm) grafting cell is put together by associating a glass coverslip (VWR international) and a quartz spacer (106-QS, Suprasil, Hellma), except for the data shown in section S5 of the ESI,† where Au and ITO surfaces were used to analyze the influence of the underlying surface in the grafting kinetics. The microscope native ×1.5 tube lens was used in combination with a ×2.5 relay lens to further magnify the image, reaching a total magnification of ×375. The grafting extent is monitored with a diffuser-based phase sensing and imaging (DIPSi) module implemented in the detection path of the microscope, consisting in the addition of a thin diffuser located at a distance d (3 mm) from the focal plane of the CCD camera, generating a speckle pattern. A Demon Image registration algorithm, implemented in Matlab (imregdemons), was used to track deformations of the speckle pattern, which can be directly related to the optical path difference, as described in detail elsewhere.^20,50 The experimental setup is shown in ESI section S1,† along with representative data. In all experiments, the irradiation power is kept in the 20–200 μW range, adjusted to enable a reasonable sampling rate for the grafting curves. The incident power is systematically measured in the sample focal plane with a hand held powermeter (Ophir NOVA II), and the total irradiation energy is reported. A precision shutter (Edmund Optics) was used to block the excitation beam during the image acquisition and control the excitation time. The shutter was controlled with the help of an Arduino Mega board, interfaced with the help of Matlab, enabling the control routines to be implemented.

Apparent grafting efficiency evaluation (η^app)

Apparent grafting efficiencies are calculated by taking the ratio between the layer volume increase (nm³ s⁻¹), and the incident laser power (J s⁻¹, measured in the sample focal place). It can be directly extracted from the reported grafting curves by taking the slope of the OVD as a function of the total incident energy. It estimates how much energy is required, on average, to graft a certain volume of grafted species (or equivalently, how many photons are required per molecule). Noteworthy, η^app is dependent on the laser fluency and experimental setup, and therefore should only be used to compare relative efficiencies obtained in the same grafting conditions, as done throughout the paper.

Data treatment

All grafting experiments were repeated at least 3 times, and both the raw data and the averaged values are reported in the figures (respectively by the transparent traces and dots). Error bars indicate 3 standard deviation for the mean values. The standard deviation of mean values are estimated from a population consisting of N standard measurements as σ/√N, where σ is the unweighted standard deviation of the measurements. All grafting curves are displayed in a semi log scale in the main paper in order to facilitate visualization, while the same data are shown in linear scales in section S6 of the ESI.†

Atomic force microscopy (AFM) measurements

All atomic force microscopy measurements were carried out with a Dimension Icon (Bruker) equipped with PointProbePlus tips (PPP-NCHR, NanoSensors) on tapping mode. All AFM measurements were carried out after carefully rinsing the grafted samples with milliQ water and drying the samples under N₂ flow. The volume of the deposited material was evaluated from AFM height images by numerically integrating the zone around the grafted spot, using the trapezoid rule.

Refractive index evaluation procedure

The refractive index of grafted layer (n_layer) allows transforming the optical path difference (OPD) into the actual thickness of the grafted layer (L), according to eqn (2), in which n_m is the refractive index of the grafting medium:

OPD = (n_layer−n_m) × L (2)

n_m is evaluated at the observation wavelength (λ_obs = 633 nm) using an Abbe refractometer (Bausch & Lomb), leading to the value of 1.335 ± 0.001 for all grafting solutions. For each aniline precursor, we conduct a large number (∼10) of grafting experiments, leading to a series of grafted spots which are later evaluated with the help of an AFM. section S7 of the ESI† section recapitulates these measurements.

Conclusions

In this paper, we employ a nanometrology approach to quantitatively analyze and control surface modification reactions. The role of substituents on the photografting kinetics of diazonium salts was first analyzed, leading to the first large scale analysis of the photografting efficiency of such salts. We have shown that substituents of the aryl ring globally affect the surface modification kinetics in several ways: (i) by modifying the diazonium salts formation rate and stability, leading to unprecise concentrations when one pot methodologies are used. (ii) By altering the photophysical properties of the resulting diazonium salts, and (iii) by modifying the efficiency of the radical addition onto the surface. In particular cases it was possible to rationalize the observed trends, notably when electronic effects dominate the radical stability, on which case a predictive model could be developed for estimating the grafting rate from the kinetics of diazonium formation from aniline precursors. In the general case, however, no global trend was observed, precluding efficient implementation of open loop strategies.

We solved the problem by designing a closed loop strategy based on the real time monitoring methodology. We demonstrate the surface grafting and polymerization of reactive aryl radicals can be physically controlled with great precision using the optical phase information as feedback for modulating the photografting process. Using an adaptative strategy to tune the exposition rate, we show that, regardless of the surface modification kinetics, surface layers of controlled volume can be obtained with attoliter precision.

Considering the generality and noninvasive nature of the optical nanometrology technique, we foresee that this methodology can find broad applicability in surface modification reactions. Indeed, any photochemically induced additive manufacturing process could in principle be finely controlled using the developed techniques, as long as the surface modification reaction induces a detectable refractive index change.

Author contributions

BM performed the experiments, BM and VB analysed the data, JFA, and VB designed the methodology and implemented the experimental setup, VB and FM were responsible for funding acquisition. VB designed the research, wrote the original draft and supervised the experiments. This manuscript was prepared through contribution of all authors. All authors have revised and approved the final version of this manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

BM acknowledges funding from ENS Paris Saclay. We gracefully acknowledge funding from Agence Nationale de la Recherche (ANR-19-CE09-0013 APMJ). This project has received financial support from the CNRS through the MITI interdisciplinary programs through its exploratory research program (MITI “Instrumentation, données et analyse in situ ou operando”).

References

1. L. P. C. Gomez, A. Spangenberg, X. A. Ton, Y. Fuchs, F. Bokeloh, J. P. Malval, B. Tse Sum Bui, D. Thuau, C. Ayela, K. Haupt and O. Soppera, Adv. Mater., 2016, 28, 5931–5937.
2. L. Y. Hsu, P. Mainik, A. Münchinger, S. Lindenthal, T. Spratte, A. Welle, J. Zaumseil, C. Selhuber-Unkel, M. Wegener and E. Blasco, Adv. Mater. Technol., 2023, 8, 2200801.
3. X. Lu, C. P. Ambulo, S. Wang, L. K. Rivera-Tarazona, H. Kim, K. Searles and T. H. Ware, Angew. Chem., Int. Ed., 2021, 60, 5536–5543.
4. L. Wang, U. S. Schubert and S. Hoeppener, Chem. Soc. Rev., 2021, 50, 6507–6540.
5. X. T. Le, P. Viel, P. Jégou, A. Garcia, T. Berthelot, T. H. Bui and S. Palacin, J. Mater. Chem., 2010, 20, 3750–3757.
6. G. S. Kumar and Q. Lin, Chem. Rev., 2021, 121, 6991–7031.
7. Z. X. Chen, Y. Li and F. Huang, Chem, 2021, 7, 288–332.
8. N. Kvasovs and V. Gevorgyan, Chem. Soc. Rev., 2021, 50, 2244–2259.
9. S. Usgaonkar, S. Deshmukh, B. Biswas, N. Karjule, P. Yadav, J. Nithyanandhan and G. Kumaraswamy, Angew. Chem., Int. Ed., 2019, 58, 2715–2719.
10. P. Allongue, C. Henry de Villeneuve, G. Cherouvrier, R. Cortès and M. C. Bernard, J. Electroanal. Chem., 2003, 550–551, 161–174.
11. D. Bélanger and J. Pinson, Chem. Soc. Rev., 2011, 40, 3995–4048.
12. J. Pinson and F. I. Podvorica, Curr. Opin. Electrochem., 2020, 24, 44–48.
13. C. Combellas, F. Kanoufi, J. Pinson and F. I. Podvorica, J. Am. Chem. Soc., 2008, 130, 8576–8577.
14. M. Busson, A. Berisha, C. Combellas, F. Kanoufi and J. Pinson, Chem. Commun., 2011, 47, 12631–]12633.
15. G. Ambrosio, A. Brown, L. Daukiya, G. Drera, G. Di Santo, L. Petaccia, S. De Feyter, L. Sangaletti and S. Pagliara, Nanoscale, 2020, 12, 9032–9037.
16. A. Adenier, C. Combellas, F. Kanoufi, J. Pinson and F. I. Podvorica, Chem. Mater., 2006, 18, 2021–2029.
17. A. Adenier, E. Cabet-Deliry, A. Chaussé, S. Griveau, F. Mercier, J. Pinson and C. Vautrin-Ul, Chem. Mater., 2005, 17, 491–501.
18. M. C. Bernard, A. Chaussé, E. Cabet-Deliry, M. M. Chehimi, J. Pinson, F. Podvorica and C. Vautrin-Ul, Chem. Mater., 2003, 15, 3450–3462.
19. J. K. Kariuki and M. T. McDermott, Langmuir, 1999, 15, 6534–6540.
20. V. Brasiliense, J.-F. Audibert, T. Wu, G. Tessier, P. Berto and F. Miomandre, Small Methods, 2022, 6, 2100737.
21. L. Pichereau, L. Fillaud, N. Kostopoulos, E. Maisonhaute, T. Cauchy, M. Allain, J. M. Noël, C. Gautier and T. Breton, J. Phys. Chem. Lett., 2022, 13, 11866–11871.
22. K. Torbensen, K. Malmos, F. Kanoufi, C. Combellas, S. U. Pedersen and K. Daasbjerg, ChemPhysChem, 2012, 13, 3303–3307.
23. K. F. Clark, S. Tyerman, L. Evans, C. M. Robertson, D. J. Nelson, A. R. Kennedy and J. A. Murphy, J. Am. Chem. Soc., 2023, 145(38), 20849–20858.
24. L. Nicchio, J. Médard, P. Decorse, S. Gam-Derouich, A. Chevillot-Biraud, Y. Luo, C. Mangeney, A. Berisha, F. Averseng, M. Fagnoni, S. Protti and J. Pinson, Chem. – Eur. J., 2023, 29, e202301006.
25. F. Lebon, R. Cornut, V. Derycke and B. Jousselme, Electrochim. Acta, 2019, 318, 754–761.
26. M. Barrejón, Z. Syrgiannis and M. Prato, Nanoscale, 2018, 10, 15782–15787.
27. L. T. Nielsen, K. H. Vase, M. Dong, F. Besenbacher, S. U. Pedersen and K. Daasbjerg, J. Am. Chem. Soc., 2007, 129, 1888–1889.
28. P. Schroll, C. Fehl, S. Dankesreiter and B. König, Org. Biomol. Chem., 2013, 11, 6510–6514.
29. J. Billon, V. Shkirskiy, S. Dabos-Seignon, T. Breton and C. Gautier, Phys. Chem. Chem. Phys., 2022, 24, 14294–14298.
30. J. Médard, C. Combellas, F. Kanoufi, J. Pinson, J. Chauvin and A. Deronzier, J. Phys. Chem. C, 2018, 122, 19722–19730.
31. S. Baranton and D. Bélanger, J. Phys. Chem. B, 2005, 109, 24401–24410.
32. C. Cougnon, F. Gohier, D. Belanger and J. Mauzeroll, Angew. Chem., Int. Ed., 2009, 48, 4006–4008.
33. J. Lyskawa and D. Bélanger, Chem. Mater., 2006, 18, 4755–4763.
34. S. Bouden, J. Pinson and C. Vautrin-Ul, Electrochem. Commun., 2017, 81, 120–123.
35. T. Menanteau, E. Levillain and T. Breton, Chem. Mater., 2013, 25, 2905–2909.
36. T. Menanteau, M. Dias, E. Levillain, A. J. Downard and T. Breton, J. Phys. Chem. C, 2016, 120, 4423–4429.
37. O. Fernandez-Delgado, A. R. P. Santiago, J. G. Betancourth, M. F. Sanad, S. T. Sreenivasan and L. Echegoyen, Nanoscale, 2021, 14, 3858–3864.
38. M. Bouriga, M. M. Chehimi, C. Combellas, P. Decorse, F. Kanoufi, A. Deronzier and J. Pinson, Chem. Mater., 2013, 25, 90–97.
39. P. Bléteau, M. Bastide, S. Gam-Derouich, P. Martin, R. Bonnet and J.-C. Lacroix, ACS Appl. Nano Mater., 2020, 3, 7789–7794.
40. B. Maillot, M. Johnson, J. F. Audibert, F. Miomandre and V. Brasiliense, Nanoscale, 2023, 15, 8754–8761.
41. B. M. Simons, J. Lehr, D. J. Garrett and A. J. Downard, Langmuir, 2014, 30, 4989–4996.
42. T. Menanteau, E. Levillain, A. J. Downard and T. Breton, Phys. Chem. Chem. Phys., 2015, 17, 13137–13142.
43. J. Seibel, D. B. Amabilino and S. De Feyter, Angew. Chem., Int. Ed., 2019, 58, 12964–12968.
44. A. Mattiuzzi, I. Jabin, C. Mangeney, C. Roux, O. Reinaud, L. Santos, J. F. Bergamini, P. Hapiot and C. Lagrost, Nat. Commun., 2012, 3, 1130.
45. V. Shkirskiy, E. Levillain and C. Gautier, ChemPhysChem, 2021, 22, 1074–1078.
46. S. Munteanu, N. Garraud, J. P. Roger, F. Amiot, J. Shi, Y. Chen, C. Combellas and F. Kanoufi, Anal. Chem., 2013, 85, 1965–1971.
47. X. Zhang, F. Rösicke, V. Syritski, G. Sun, J. Reut, K. Hinrichs, S. Janietz and J. Rappich, Z. Phys. Chem., 2014, 228, 557–573.
48. J. D. Firth and I. J. S. Fairlamb, Org. Lett., 2020, 22, 7057–7059.
49. M. Sheng, D. Frurip and D. Gorman, J. Loss Prev. Process Ind., 2015, 38, 114–118.
50. P. Berto, H. Rigneault and M. Guillon, Opt. Lett., 2017, 42, 5117–5120.
51. K. Tahara, Y. Kubo, B. Lindner, S. Hashimoto, S. Hirose, A. Brown, B. Hirsch, L. Daukiya, S. De Feyter and Y. Tobe, Langmuir, 2019, 35(6), 2089–2098.
52. C. Combellas, D. Jiang, F. Kanoufi, J. Pinson and F. Podvorica, Langmuir, 2009, 25(1), 286–293.
53. J. Lyskawa and D. Bélanger, Chem. Mater., 2006, 18, 4755–4763.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3nr06324k

---