Open Access Article
Open Access ArticleLight-driven dynamical tuning of the thermal conductivity in ferroelectrics†
Claudio
Cazorla
 a,
Sebastian
Bichelmaier
a,
Sebastian
Bichelmaier
 b,
Carlos
Escorihuela-Sayalero
a,
Jorge
Íñiguez
b,
Carlos
Escorihuela-Sayalero
a,
Jorge
Íñiguez
 cd,
Jesús
Carrete
cd,
Jesús
Carrete
 b and
Riccardo
Rurali
b and
Riccardo
Rurali
 *e
*e
aDepartament de Física, Universitat Politècnica de Catalunya, Campus Nord B4-B5, Barcelona 08034, Spain
bInstitute of Materials Chemistry, TU Wien, A-1060 Vienna, Austria
cMaterials Research and Technology Department, Luxembourg Institute of Science and Technology (LIST), Avenue des Hauts-Fourneaux 5, L-4362 Esch/Alzette, Luxembourg
dDepartment of Physics and Materials Science, University of Luxembourg, 41 Rue du Brill, L-4422 Belvaux, Luxembourg
eInstitut de Ciència de Materials de Barcelona, ICMAB-CSIC, Campus UAB, 08193 Bellaterra, Spain. E-mail: rrurali@icmab.es
First published on 2nd April 2024
Abstract
Dynamical tuning of the thermal conductivity in crystals, κ, is critical for thermal management applications, as well as for energy harvesting and the development of novel phononic devices able to perform logic operations with phonons. Such a desired κ control can be achieved in functional materials that experience large structural and phonon variations as a result of field-induced phase transformations. However, this approach is only practical within reduced temperature intervals containing zero-bias phase transition points, since otherwise the necessary driving fields become excessively large and the materials’ performances are detrimentally affected. Here, based on first-principles calculations, we propose an alternative strategy for dynamically tuning κ that is operative over broad temperature conditions and realizable in a wide class of materials. By shining light on the archetypal perovskite oxide KNbO3, we predict that ultrafast and reversible ferroelectric-to-paraelectric phase transitions are induced, yielding large and anisotropic κ variations (up to ≈30% at T = 300 K). These light-induced thermal transport shifts can take place at temperatures spanning several hundreds of kelvin and are essentially the result of anharmonic effects affecting the phonon lifetimes.
1 Introduction
Current strategies to design materials with tailored thermal properties typically rely on the creation of structural inhomogeneities that scatter phonons and reduce the thermal conductivity (e.g., lattice defects,1 grain boundaries2 and nanostructure surfaces3) and the engineering of periodic heterostructures (superlattices), in which wave interference induces the appearance of phonon frequency gaps.4 These approaches, however, yield changes in the thermal properties of materials that are static and irreversible. Applications in the context of thermal management and energy harvesting, however, would benefit from the possibility of dynamically tuning the thermal conductivity of materials, κ.5–7 Likewise, the design of phononic devices capable of performing logic operations with phonons, analogous to what their electronic counterparts do with charge carriers, may also be envisaged on the basis of the concept of active κ control.8,9 Such a technological goal can be achieved, for instance, via strain10 and chemical intercalation11 in layered materials. However, these approaches appear to be rather impractical due to their long response times and complex setups.A promising approach for dynamical κ tuning involves the exploitation of the effects of field-induced phase transitions on the thermal properties of functional materials like ferroelectric and magnetic crystals.12–19 The ensuing electrophononic and magnetophononic effects are expected to lead to fast and dynamical manipulation of the heat carriers, thus yielding à la carte thermal properties for on-demand applications. Nevertheless, for these phononic phenomena to be practical, the operating conditions need to be close to the phase-transition points at zero bias since otherwise the required driving fields may grow unfeasibly large and the materials’ performances may be seriously compromised owing to the presence of leakage/eddy currents and dielectric/magnetic losses.
On the other hand, the possibility of manipulating κ with light has received very little attention thus far, although some promising results in azobenzene-doped liquid crystals have been recently reported.20 Light-driven control of the thermal conductivity could bypass some of the issues posed by the schemes described above (e.g., application of large driving fields) and simplify the design of logic devices (i.e., no need for electrical contacts). Macroscopic light-driven phase transitions21,22 involving collective phenomena such as electronic correlation, spin–lattice and charge–lattice couplings are especially appealing in this regard. Photoinduced phase transitions of these types have been reported for π-conjugated polymers,23 transition metal oxides24 and molecular crystals,25 to cite a few examples. Remarkably, the dynamics of this class of light-driven phase transformation is ultrafast, in the scale of subpicoseconds for VO2,24 ≈1 ps for LaTe3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 26 and 100–500 ps for inorganic perovskite nanocrystals.27 More recently, ultrafast photo-driven control of the incipient ferroelectric KTaO3
26 and 100–500 ps for inorganic perovskite nanocrystals.27 More recently, ultrafast photo-driven control of the incipient ferroelectric KTaO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 28 and hydrogen-bonded ferroelectric crystals29 has also been experimentally demonstrated, while it has been theoretically proposed that light-excited carriers can thermodynamically stabilize three-dimensional nanoscale polar structures in ferroelectric superlattices.30
28 and hydrogen-bonded ferroelectric crystals29 has also been experimentally demonstrated, while it has been theoretically proposed that light-excited carriers can thermodynamically stabilize three-dimensional nanoscale polar structures in ferroelectric superlattices.30
In this Communication, we use predictive first-principles calculations to demonstrate dynamical tuning of the thermal conductivity in a ferroelectric perovskite oxide resulting from a reversible light-induced phase transition. These photophononic effects rely on large changes in phonon dispersion and phonon lifetimes caused by the suppression of ferroelectricity upon irradiation.31 We explore this effect in the prototypical ferroelectric perovskite KNbO3 (KNO), finding large and highly anisotropic κ variations (up to ≈30%) within a wide temperature interval spanning over several hundreds of kelvin. Our results can be qualitatively generalized to other ferroelectrics displaying displacive-like phase transitions such as BaTiO3.31
2 Results and discussion
2.1 Light-induced phase transitions
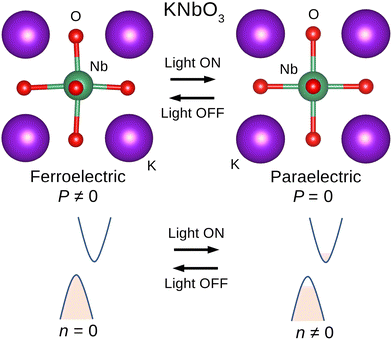
At temperatures lower than 225 K, KNO exhibits a non-centrosymmetric rhombohedral R3m phase with electric polarization oriented along the pseudocubic direction [111]. According to our first-principles calculations based on density functional theory (for DFT calculations, see Methods), this structure is characterized by a lattice parameter of 4.034 Å, a rhombohedral angle of 89.89° and a ferroelectric polarization of P = 35.05 μC cm−2. These results compare notably well with the corresponding experimental values of 4.016 Å, 89.83° and 30–40 μC cm−2, respectively.32–34 Upon (above-bandgap) light irradiation, some electrons are photoexcited and promoted from the valence to the conduction band, where they can move more freely and become delocalized throughout the crystal. These carriers turn out to screen the long-range dipole–dipole interactions that sustain polar order in the rhombohedral phase.31,35 As a consequence, the nonpolar cubic phase Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, which under dark conditions is only stable at temperatures T ≥ 703 K,32 can potentially become the new ground state (Fig. 1).
m, which under dark conditions is only stable at temperatures T ≥ 703 K,32 can potentially become the new ground state (Fig. 1).
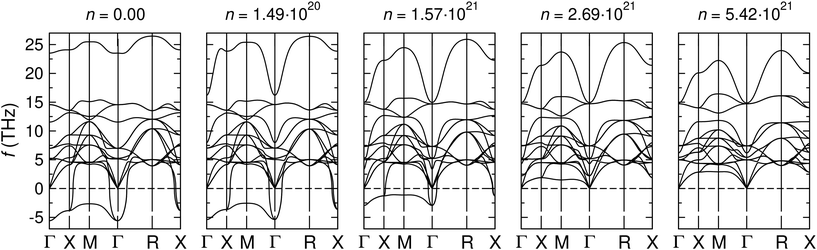
In particular, our zero-temperature DFT calculations show that the nonpolar Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase becomes stable at photoexcited electron densities of n >
m phase becomes stable at photoexcited electron densities of n > ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) = 2.69 × 1021 cm−3. This effect is illustrated in Fig. 2 where we plot the phonon dispersion of paraelectric KNO estimated at five different conduction electron densities. Let us also note that the cell volume of the paraelectric phase slightly expands under photoexcitation (e.g., the lattice parameter increases from 4.019 Å at n = 0 to 4.028 Å at
= 2.69 × 1021 cm−3. This effect is illustrated in Fig. 2 where we plot the phonon dispersion of paraelectric KNO estimated at five different conduction electron densities. Let us also note that the cell volume of the paraelectric phase slightly expands under photoexcitation (e.g., the lattice parameter increases from 4.019 Å at n = 0 to 4.028 Å at ![[n with combining macron]](https://www.rsc.org/images/entities/i_char_006e_0304.gif) ). This is the likely reason for the generalized softening of the phonon spectrum observed with increasing n that particularly affects the high frequency region.
). This is the likely reason for the generalized softening of the phonon spectrum observed with increasing n that particularly affects the high frequency region.
At a temperature of ≈225 K, KNO transforms into a polar orthorhombic phase (space group Amm2) that is stable up to T ≈ 493 K.32 For this phase, we estimated at zero temperature a 5-atom cell defined by a = 3.996 Å, b = c = 4.053 Å, α = 90.182°, and β = γ = 90°, and a ferroelectric polarization of P = 38.53 μC cm−2 along the pseudocubic direction [011], which are again in very good agreement with the corresponding experimental values 3.973 Å, 4.098 Å and ≈40 μC cm−2.32,33 At zero temperature, the phonon spectrum of this phase exhibits several imaginary frequencies, indicating dynamical instability against a distortion taking the system to the rhombohedral ground state. Nevertheless, by performing phonon calculations that take the effect of temperature into account, it is possible to obtain well-behaved dispersion curves that are consistent with the experimentally observed stability of the Amm2 phase (see Methods, ESI Fig. 3, and Table 1:† our T-renormalized phonon calculations were performed with two different approaches, namely, normal-mode-decomposition methods36 and QSCAILD,37,38 that provided identical results). Interestingly, in this polar orthorhombic phase, it is also possible to stabilize the paraelectric cubic phase by means of photoexcitation; hence, we also considered it in our subsequent thermal conductivity study. The underlying mechanism is analogous to the case discussed above (i.e., screening of dipole–dipole interactions by photoexcited carriers). It is worth stressing that both the polar rhombohedral and orthorhombic phases spontaneously relax into the paraelectric cubic phase under sufficiently high light irradiation (or, equivalently, density of photoexcited electron–hole pairs), so they are unstable, rather than metastable, under such conditions. All phonon dispersion relations are shown in ESI Fig. 1–3.†
Let us note that photoinduced ferroelectric-to-paraelectric phase transitions analogous to those reported here for KNO have been recently predicted for BaTiO3.31 Remarkably, in the same material, the ferroelectric instability can also be suppressed by means of impurity doping, as has been theoretically and experimentally demonstrated.39–41 In this case, electrons are injected into the conduction band from impurity states rather than promoted from the valence band via photoexcitation. Our DFT calculations explicitly reproduce this behavior in KNO as well.
2.2 Thermal conductivity and photophononic coupling
In what follows, we analyze the thermal conductivity changes that accompany the two photoinduced phase transitions: R3m → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (at temperatures below 225 K, when the rhombohedral phase is observed to be stable) and Amm2 → Pm
m (at temperatures below 225 K, when the rhombohedral phase is observed to be stable) and Amm2 → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (at and near room temperature, when the orthorhombic phase is observed to be stable). We compute the thermal conductivity of the different phases as specified in ESI Table 1.† Our results, expressed as a function of temperature, are shown in Fig. 3, where we plot the diagonal elements of the heat conductivity tensor along the two independent pseudocubic directions separately. A very rich scenario emerges from these plots, in which both the size and sign of κ change depend on the direction and phase transition involved. Of special interest is the κxx reduction of ≈30% that can be achieved at room temperature upon the light-induced Amm2 → Pm
m (at and near room temperature, when the orthorhombic phase is observed to be stable). We compute the thermal conductivity of the different phases as specified in ESI Table 1.† Our results, expressed as a function of temperature, are shown in Fig. 3, where we plot the diagonal elements of the heat conductivity tensor along the two independent pseudocubic directions separately. A very rich scenario emerges from these plots, in which both the size and sign of κ change depend on the direction and phase transition involved. Of special interest is the κxx reduction of ≈30% that can be achieved at room temperature upon the light-induced Amm2 → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase transition. This large heat conductivity change could be exploited in various applications, such as thermal logic,8,42 solid-state refrigeration5,6 and waste heat scavenging.7 We also tested the effect of considering room-temperature renormalized phonons (see the ESI†) in the calculation of the thermal conductivity of the light-stabilized cubic phase. We obtained a slightly larger value of κ and thus the photoswitching ratio of the Amm2 → Pm
m phase transition. This large heat conductivity change could be exploited in various applications, such as thermal logic,8,42 solid-state refrigeration5,6 and waste heat scavenging.7 We also tested the effect of considering room-temperature renormalized phonons (see the ESI†) in the calculation of the thermal conductivity of the light-stabilized cubic phase. We obtained a slightly larger value of κ and thus the photoswitching ratio of the Amm2 → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m transition decreases to 20%. However, this effect is most likely overestimated since we are not taking into account the thermal expansion of the material, which certainly would compensate for the aforementioned thermal conductivity increase. On the other hand, the κ changes accompanying the photoinduced R3m → Pm
m transition decreases to 20%. However, this effect is most likely overestimated since we are not taking into account the thermal expansion of the material, which certainly would compensate for the aforementioned thermal conductivity increase. On the other hand, the κ changes accompanying the photoinduced R3m → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase transition at low temperatures are modest (≈5%). It should be noted that the cubic phase is thermodynamically unstable under dark conditions, thus – disregarding possible hysteresis effects – the low conductivity state can only be accessed when light is shone on the material. Therefore, our prediction is that, when light is turned off, reverse paraelectric-to-ferroelectric transitions occur spontaneously. Note also that a critical parameter is the light penetration depth, Δz, which in the case of being too small could result in a limiting factor for practical applications. Fortunately, from the optical absorption data reported by Kaifu and coworkers43 we could estimate Δz ≈ 30 μm, which safely exceeds the typical thickness of thin films (∼10–100 nm).
m phase transition at low temperatures are modest (≈5%). It should be noted that the cubic phase is thermodynamically unstable under dark conditions, thus – disregarding possible hysteresis effects – the low conductivity state can only be accessed when light is shone on the material. Therefore, our prediction is that, when light is turned off, reverse paraelectric-to-ferroelectric transitions occur spontaneously. Note also that a critical parameter is the light penetration depth, Δz, which in the case of being too small could result in a limiting factor for practical applications. Fortunately, from the optical absorption data reported by Kaifu and coworkers43 we could estimate Δz ≈ 30 μm, which safely exceeds the typical thickness of thin films (∼10–100 nm).
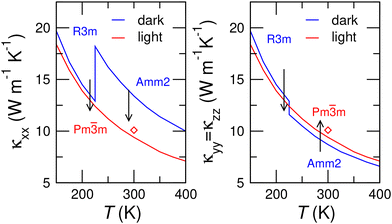 | ||
Fig. 3 Thermal conductivity of KNO along the three Cartesian axes expressed as a function of temperature. Results are shown for the ferroelectric ground state (R3m at T ≤ 225 K and Amm2 at T ≥ 225 K) and the light-stabilized cubic nonpolar phase (Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m). Arrows indicate the sign of the photoinduced κ shifts: up is positive and down is negative. The diamonds in the figure represent the room-temperature κ estimated for the cubic nonpolar phase when that is stabilized by increasing temperature under dark conditions (see the main text). See ESI Table 1† for a summary of the details of the calculation of κ in the different phases. m). Arrows indicate the sign of the photoinduced κ shifts: up is positive and down is negative. The diamonds in the figure represent the room-temperature κ estimated for the cubic nonpolar phase when that is stabilized by increasing temperature under dark conditions (see the main text). See ESI Table 1† for a summary of the details of the calculation of κ in the different phases. | ||
It is worth noting that the anisotropy of the thermal conductivity tensor in each phase can be understood in terms of symmetry and electric polarization arguments. In the R3m and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases, the three diagonal κ components are equal along the three pseudocubic directions, just like their electric polarization components (null in the case of the cubic phase). On the other hand, in the Amm2 phase, it is found that κxx > κyy = κzz. In this latter case, the equivalence between the yy and zz components also follows from the orientation of the corresponding electric polarization, [011], while the difference in the xx component value can be explained by the fact that there is a mirror plane along the corresponding direction13,15,44 (and thus the projection of the electric polarization along the x direction is null).
m phases, the three diagonal κ components are equal along the three pseudocubic directions, just like their electric polarization components (null in the case of the cubic phase). On the other hand, in the Amm2 phase, it is found that κxx > κyy = κzz. In this latter case, the equivalence between the yy and zz components also follows from the orientation of the corresponding electric polarization, [011], while the difference in the xx component value can be explained by the fact that there is a mirror plane along the corresponding direction13,15,44 (and thus the projection of the electric polarization along the x direction is null).
The two photoinduced phase transitions analyzed here involve a volume reduction of ∼1%, which taken alone has a non-negligible effect on the phonon frequencies and velocities. Nevertheless, it is not always possible to rationalize the changes in the thermal conductivity based exclusively on volume changes.45 A volume reduction, for instance, can lead to an overall hardening of the phonon frequencies, through shortening of the interatomic bonds, and thus to an increase in phonon velocities: both these factors should result in an increase of κ. Conversely, the phonon population decreases as a consequence of the increase of phonon frequencies, which should lead to lower values of κ.
A simple and effective way to ascertain the role of harmonic effects on the thermal conductivity, and thus their effect on its relative change upon the photoinduced phase transitions analyzed here, is based on the estimation of the thermal conductivity in the small-grain limit.46 In this type of calculation, the thermal conductivity is factorized into a product of two terms. One of them is an effective global mean free path for phonons, λ, which captures the anharmonic effects. The other, κSG, is a proportionality coefficient depending only on the phonon frequencies and group velocities, both harmonic properties. λ can only be interpreted as a true uniform mean free path in a highly idealized model of a nanograined crystal in which phonon transport is limited by the grain size. In a more general setting, it is a global proxy for the intensity of phonon scattering per unit length, which in a single crystal is dominated by anharmonicity. Fig. 4 compares the κ shifts obtained in the full calculation and under the small-grain approximation for the two photoinduced polar → nonpolar phase transitions analyzed in this work. As can be appreciated therein, there is a clear contrast between both sets of data. Even at the qualitative level, the overall Δκxx trend is not correctly reproduced by ΔκSGxx, while in the case of Δκyy and Δκzz, the small-grain limit considerably overestimates the variations. These results indicate that the changes in the thermal conductivity across the phase transitions are mostly driven by anharmonic effects (particularly for Δκxx since a prediction based on κSG alone would be qualitatively incorrect). We can quantify that influence by plotting λ = κ/κSG (Fig. 4). These results account for the phase and temperature trends obtained for Δκxx – the largest variation of the κ tensor –, which was not even qualitatively captured by the small-grain model (i.e., solely based on harmonic effects).
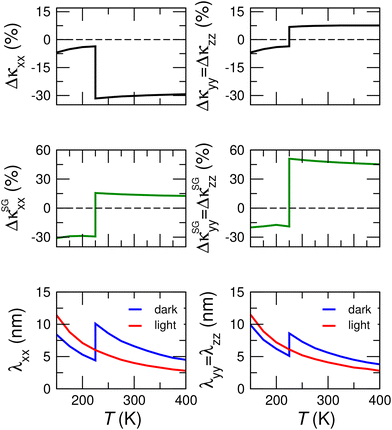 | ||
| Fig. 4 Thermal conductivity variations in KNO upon the light-induced polar → nonpolar phase transformation. (Top) Directly deduced from Fig. 3. (Middle) Considering a uniform phonon mean free path of 1 nm (small-grain approximation). (Bottom) Effective global phonon mean free path, λ, computed as κ/κSG. | ||
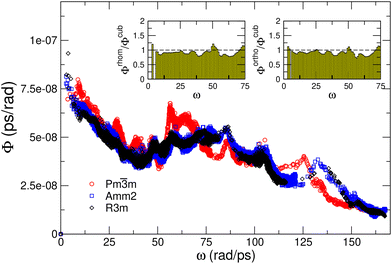
To gain closer insight into the phonon–phonon anharmonic scattering, we first analyze the phonon phase space, Φ, which measures the number of three-phonon processes allowed by the conservation of energy and momentum. With all other factors being equal, the larger Φ is, the more likely the resistive collision processes are to occur; hence, this quantity is normally negatively correlated with the lattice thermal conductivity.47 The Φ(ω) results shown in Fig. 5 reveal very similar phonon phase space features for the three analyzed crystalline phases, with that corresponding to the cubic phase slightly exceeding the others. This finding is quantitatively confirmed by the insets in the same figure: the Φrhom/Φcub and Φortho/Φcub ratios are close to unity, but smaller at all frequencies. These results can be understood by noting that the phonon phase space is essentially reflecting the unit cell complexity; the three phases involved, despite presenting different symmetries, are all described by 5-atom primitive cells; hence, their respective three-phonon collision spaces turn out to be very similar. It is worth noting that in principle one could expect the Φ of the more symmetric cubic phase to be smaller. However, a larger number of nondegenerate phonon bands in the less symmetric phase does not necessarily imply a larger number of allowed phonon collision processes and thus larger Φ. Consequently, we may conclude that the thermal conductivity shifts shown in Fig. 3 are in part caused by differences in the phase space of three-phonon processes.
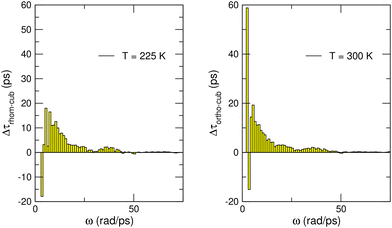
Next, we analyze the degree of anharmonicity of the different phases in terms of another relevant aspect, namely, the phonon scattering matrix elements. Fig. 6 shows the differences in the phonon lifetime, τ, of the polar and nonpolar phases averaged over frequency intervals of 1 rad ps−1. In the two cases considered here, that is, R3m → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 225 K and Amm2 → Pm
m at 225 K and Amm2 → Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m at 300 K, the phonon lifetimes of the polar phases are noticeably longer than those of the light-stabilized nonpolar phase at most frequencies. Remarkably, there is a low-frequency range in which the phonon lifetimes of the room-temperature Amm2 phase are about 60 ps higher than those of the photostabilized Pm
m at 300 K, the phonon lifetimes of the polar phases are noticeably longer than those of the light-stabilized nonpolar phase at most frequencies. Remarkably, there is a low-frequency range in which the phonon lifetimes of the room-temperature Amm2 phase are about 60 ps higher than those of the photostabilized Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. These giant τ differences are the main cause of the largest thermal conductivity variations reported in Fig. 3 (i.e., Δκxx ≈ −30% at room temperature). At temperatures below 225 K, the estimated Δτ's are not as large but still substantial (e.g., ∼15 ps at low frequencies), which accounts for the estimated Δκxx ≈ −5% (Fig. 3). The phonon lifetimes depend on the number of anharmonic scattering processes, which we quantified by the phase space, Φ, and the magnitude of the phonon–phonon anharmonic couplings. The slightly larger Φ of the cubic phase appears to be an important driving factor. It is more difficult to ascertain the role of the anharmonic couplings because of the rather similar force constants. Yet, the computed Grüneisen parameter, usually considered as a good proxy of a system's anharmonicity, suggests a certain level of synergy with the phase space (see ESI Fig. 4†), i.e., the cubic phase has a larger Φ and larger anharmonic couplings.
m phase. These giant τ differences are the main cause of the largest thermal conductivity variations reported in Fig. 3 (i.e., Δκxx ≈ −30% at room temperature). At temperatures below 225 K, the estimated Δτ's are not as large but still substantial (e.g., ∼15 ps at low frequencies), which accounts for the estimated Δκxx ≈ −5% (Fig. 3). The phonon lifetimes depend on the number of anharmonic scattering processes, which we quantified by the phase space, Φ, and the magnitude of the phonon–phonon anharmonic couplings. The slightly larger Φ of the cubic phase appears to be an important driving factor. It is more difficult to ascertain the role of the anharmonic couplings because of the rather similar force constants. Yet, the computed Grüneisen parameter, usually considered as a good proxy of a system's anharmonicity, suggests a certain level of synergy with the phase space (see ESI Fig. 4†), i.e., the cubic phase has a larger Φ and larger anharmonic couplings.
Electron–phonon scattering is not included in our lattice thermal conductivity calculations. It should however be noted that this additional source of scattering could only play a relevant role in the light-stabilized cubic phase, where mobile charges are present in the conduction band, further decreasing its thermal conductivity and enhancing the effect of illumination. This means that the κ change that we estimate is a lower bound of the actual value.
2.3 Cubic phase stabilized by temperature
A valid question at this stage is whether the light-stabilized cubic phase is qualitatively different from the usual cubic phase stabilized by temperature. To answer this point, we carried out T-renormalized phonon and κ calculations for the centrosymmetric phase at 300 and 800 K. In these calculations, we constrained the volume of the system to that of the light-stabilized cubic phase, allowing for direct comparisons. The results obtained are very interesting for several reasons. Firstly, at 300 K, we get rid of the dynamical instability of the cubic phase under dark conditions, namely, all its phonon branches are well-behaved (Fig. 7). In principle, this phase is experimentally not accessible since the orthorhombic Amm2 phase is the most stable at that temperature. However, according to our simulations the centrosymmetric phase is metastable, rather than being unstable, at T = 300 K; consequently, it is physically meaningful to compare the κ of the different cubic phases stabilized by either light or temperature. Secondly, the results obtained at T = 800 K are of practical relevance since at that temperature KNO is stable in the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase.
m phase.
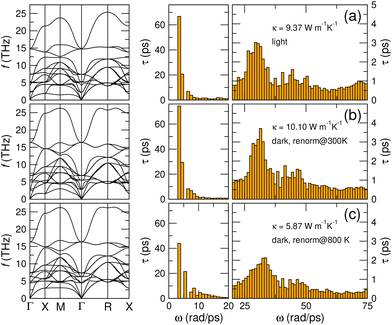 | ||
Fig. 7 Phonon dispersions and lifetimes of the cubic phase. Phonon dispersions and lifetimes averaged over frequency intervals of 1 rad ps−1 for the cubic Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase stabilized by (a) photoexcitation, (b) temperature at T = 300 K, and (c) temperature at T = 800 K (the calculation conditions for each case are detailed in ESI Table 1†). In (a), phonons are computed at zero temperature, while phonon lifetimes and the thermal conductivity are calculated at 300 K by considering the corresponding phonon population at that temperature. In (b and c), phonons are explicitly computed at the target temperature by means of phonon renormalization calculations (see Methods). Low- and mid-frequency lifetimes are displayed in separate panels to improve their visualization. m phase stabilized by (a) photoexcitation, (b) temperature at T = 300 K, and (c) temperature at T = 800 K (the calculation conditions for each case are detailed in ESI Table 1†). In (a), phonons are computed at zero temperature, while phonon lifetimes and the thermal conductivity are calculated at 300 K by considering the corresponding phonon population at that temperature. In (b and c), phonons are explicitly computed at the target temperature by means of phonon renormalization calculations (see Methods). Low- and mid-frequency lifetimes are displayed in separate panels to improve their visualization. | ||
Fig. 7 shows the phonon dispersions and phonon lifetimes of centrosymmetric KNO stabilized by either light or temperature. As can be appreciated therein, the two systems at room temperature are remarkably similar: not only the phonon dispersions, but also the frequency resolved lifetimes and thermal conductivities, 9.37 vs. 10.10 W m−1 K−1, are nearly identical. These results suggest that, for all practical effects of interest here, the ferroelectric-to-paraelectric phase transition remains essentially the same regardless of its driving force – either light or temperature – and underlying mechanisms. Regarding the experimentally accessible high temperature cubic phase, we estimated a relatively small thermal conductivity of 5.87 W m−1 K−1 at a temperature of 800 K, which mainly results from shorter phonon lifetimes caused by stronger phonon–phonon couplings. Nevertheless, at the qualitative level, the three computed τ distributions do not feature any major difference, with the mid-frequency region being dominated by vibrations of around 30 rad ps−1 and the rest of the optical phonons displaying similar relative weights.
2.4 Electronic contribution to the thermal conductivity
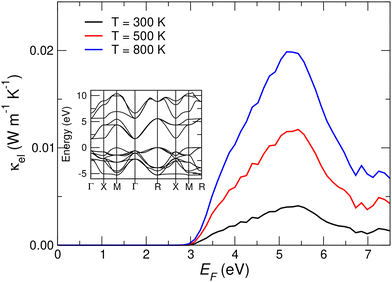
Up to this point, we have assumed that heat was entirely transported by phonons, that is, our κ analysis has been restricted to its lattice component. This is a standard and very reasonable assumption when dealing with non-magnetic insulators and semiconductors, since the electronic contribution to the thermal conductivity, κel, is usually negligible due to the ultralow density of free charge carriers. KNO falls into this category because its electronic band gap for the different phases ranges from 3.1 to 3.8 eV.32 The light-stabilized nonpolar phase, however, is different in this respect since photoexcitation partially metallizes the crystal. A non-negligible κel in the cubic phase, therefore, could diminish the large κxx reduction found at room temperature upon the light-induced orthorhombic → cubic phase transition.To assess this possibility in KNO, we explicitly computed κel for the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase by considering electronic relaxation times obtained from ab initio electron–phonon coupling calculations (see Methods). Our κel results are shown in Fig. 8. It can be appreciated that, regardless of the value of the electronic chemical potential, electronic contributions to the heat conductivity are always at least two orders of magnitude smaller than those stemming from the lattice vibrations. This conclusion holds true even when considering temperatures much higher than those relevant to the present work (i.e., 500 and 800 K) and is attributed to the presence of very low electronic group velocities (note the abundant flat bands in the electronic structure shown in the inset of Fig. 8). Besides the fact that κel depends quadratically on the velocities, their low values result in a high density of states near the band edges, which in turn leads to a considerable scattering of electrons.
m phase by considering electronic relaxation times obtained from ab initio electron–phonon coupling calculations (see Methods). Our κel results are shown in Fig. 8. It can be appreciated that, regardless of the value of the electronic chemical potential, electronic contributions to the heat conductivity are always at least two orders of magnitude smaller than those stemming from the lattice vibrations. This conclusion holds true even when considering temperatures much higher than those relevant to the present work (i.e., 500 and 800 K) and is attributed to the presence of very low electronic group velocities (note the abundant flat bands in the electronic structure shown in the inset of Fig. 8). Besides the fact that κel depends quadratically on the velocities, their low values result in a high density of states near the band edges, which in turn leads to a considerable scattering of electrons.
Based on these results, we can safely neglect electronic contributions to κ for the three crystalline KNO phases considered in this study, including the light-stabilized cubic phase, since phononic heat transport is unquestionably dominant. In other materials, however, κel could be more significant in relative terms and therefore it might be necessary to take it into consideration when estimating overall thermal conductivity changes.
3 Conclusions
In conclusion, we have theoretically demonstrated light-driven dynamical tuning of the heat conductivity in KNbO3, a prototypical perovskite oxide exhibiting soft-mode-driven ferroelectric phase transitions. We predicted that it is possible to induce polar to non-polar phase transitions in this material upon photoexcitation and that such transformations may entail a large decrease in κ, e.g. about 30% at room temperature. Interestingly, the originating phase transition mechanisms, namely, photoinduced screening of the dipole–dipole interactions in the ferroelectric phases and consequent stabilization of a paraelectric phase, are operative within ample temperature intervals extending over several hundreds of kelvin. The superior heat conductivity estimated for the polar phases can be traced back to a lower level of phonon–phonon scattering resulting from weaker phonon–phonon anharmonic couplings and smaller phase space.Analogous photophononic effects are expected to occur in other akin ferroelectric materials as well (e.g., BaTiO3), thus opening new avenues for the realization of innovative thermal logic, solid-state refrigeration and waste heat scavenging applications.
4 Methods
4.1 Density functional calculations
We performed density functional theory (DFT) calculations with the VASP code48 and projector augmented waves49,50 with an energy cutoff of 520 eV and the generalized-gradient approximation PBEsol.51 The following electrons were explicitly treated as valence electrons: K 4s13p63s2, Nb 4d45s14p6, and O 2s22p4. The Brillouin zone was sampled with a 12 × 12 × 12 k-point grid and the atomic positions were optimized until all the atomic forces were smaller than 0.005 eV Å−1. All the phases were described by 5-atom unit cells. Electric polarizations were calculated with the Born effective charge method.52The second-order interatomic force constants were computed by finite differences with Phonopy53 in 5 × 5 × 5 supercells for the R3m and Amm2 phases, while we used 4 × 4 × 4 supercells for the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phase. Non-analytical corrections proved to induce contamination of the acoustic branches that led to spurious instability in the Amm2 phase, and thus were only included in the R3m and Pm
m phase. Non-analytical corrections proved to induce contamination of the acoustic branches that led to spurious instability in the Amm2 phase, and thus were only included in the R3m and Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m phases. For the third-order interatomic force constants we used thirdorder.py54 and 3 × 3 × 3 supercells with a cutoff of 4.4 Å in the three-phonon scattering processes, which spans up to the 8th nearest neighbors in the R3m phase. We then solved the phonon Boltzmann transport equation (BTE) beyond the relaxation time approximation (RTA) on a 18 × 18 × 18 grid of q-points with the almaBTE code.55 Scattering from isotopic disorder was accounted for through the model of Tamura.56 The lattice thermal conductivity was estimated as:
m phases. For the third-order interatomic force constants we used thirdorder.py54 and 3 × 3 × 3 supercells with a cutoff of 4.4 Å in the three-phonon scattering processes, which spans up to the 8th nearest neighbors in the R3m phase. We then solved the phonon Boltzmann transport equation (BTE) beyond the relaxation time approximation (RTA) on a 18 × 18 × 18 grid of q-points with the almaBTE code.55 Scattering from isotopic disorder was accounted for through the model of Tamura.56 The lattice thermal conductivity was estimated as:
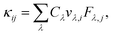 | (1) |
Although phonon–phonon scattering processes beyond third-order have not been considered in this study, further works should address their influence on the photophononic effects reported here. While in general fourth-order phonon–phonon processes are relevant for situations in which three-phonon scattering is weak57 or at high temperatures, none of which apply to the present study, those may be non-negligible in other cases as well (see e.g., ref. 58 and 59).
Photoexcitation of the cubic phase was achieved by constraining the partial occupancies of each electronic orbital through adjustment of the Fermi distribution smearing, σ. For sufficiently large values of σ, the valence (conduction) band is partially emptied (filled). We estimated the density of photoexcited carriers by integrating the number of electrons in the conduction band over all k-points (see Table 1). This effective DFT approach is equivalent to those previously employed in other works.31,60 In particular, Paillard et al.31 demonstrated that, with regard to light-driven transitions and the suppression of ferroelectricity in perovskite oxides, electronic smearing correctly reproduces the results obtained with more sophisticated approaches to treat the photoexcited state. They compared the results obtained by imposing a Fermi–Dirac smearing, similarly to the present work, with those obtained by running a constrained DFT calculation with a fixed concentration of electron–hole pairs via the introduction of two adjustable quasi-Fermi levels. They found that the results were qualitatively the same, which justifies the use of this effective method for a proof-of-concept study as the present one.
![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m KNO for different values of smearing applied on the Fermi–Dirac occupation distribution
m KNO for different values of smearing applied on the Fermi–Dirac occupation distribution
| σ | n [cm−3] |
|---|---|
| 0.10 | 2.02 × 1018 |
| 0.20 | 1.49 × 1020 |
| 0.30 | 6.91 × 1020 |
| 0.40 | 1.57 × 1021 |
| 0.50 | 2.69 × 1021 |
| 0.60 | 3.99 × 1021 |
| 0.70 | 5.42 × 1021 |
| 0.80 | 6.96 × 1021 |
| 0.90 | 8.57 × 1021 |
| 1.00 | 1.02 × 1022 |
In this scheme, charge neutrality is always preserved, as in the case of photodoping. Therefore, no compensating background must be added, thus avoiding potential artifacts that, as previously reported, can lead to spurious pressure effects.61
4.2 Anharmonic lattice dynamics from ab initio molecular dynamics simulations
The DynaPhoPy code36 was used to calculate the anharmonic lattice dynamics of KNbO3 (e.g., T-renormalized phonons) from ab initio molecular dynamics (AIMD) simulations. To this end, a normal-mode-decomposition technique was employed in which the atomic velocities vjl(t) (j and l represent particle and Cartesian direction indexes) generated during fixed-temperature AIMD simulation runs were expressed as: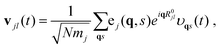 | (2) |
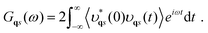 | (3) |
Finally, this power spectrum was approximated by a Lorentzian function of the form:
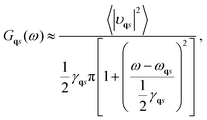 | (4) |
AIMD simulations based on DFT (performed with the VASP code) were carried out in the (N, V, T) ensemble for bulk KNbO3 in the orthorhombic phase at a temperature of 300 K. The selected volume was that of equilibrium determined at zero temperature; hence, thermal expansion effects were neglected. The temperature in the AIMD simulations was kept fluctuating around a set-point value by using Nosé–Hoover thermostats. A large simulation cell containing N = 625 atoms was employed with periodic boundary conditions applied along the three Cartesian directions. Newton's equations of motion were integrated by using the customary Verlet's algorithm and a time-step length of 15−3 ps. Γ-point sampling for integration within the first Brillouin zone was employed and the total duration of the AIMD simulations was 40 ps.
4.3 Self-consistent finite-temperature phonon calculations
An adapted version of the QSCAILD method,37 as introduced in ref. 38, is used to calculate finite-temperature phonon spectra through effective harmonic potentials. Using the eigenvectors, ej(q,s), and -values, ωqs, of the finite-displacement force constants corresponding to the first trial potential,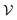 , a trial density matrix, ρ, is constructed as a function of mass-weighted displacements ujl = m−1/2j(Rjl − R0jl):
, a trial density matrix, ρ, is constructed as a function of mass-weighted displacements ujl = m−1/2j(Rjl − R0jl):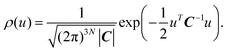 | (5) |
The blocks of the covariance matrix, C, are obtained as
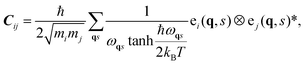 | (6) |
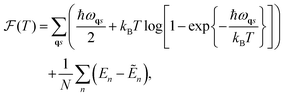 | (7) |
 , for each of the N structures.
, for each of the N structures.
4.4 Electron–phonon scattering calculations
We use the electron–phonon averaged approximation (EPA)64 to treat electron scattering by phonons, the main mechanism determining the electronic lifetime. Under that approximation, electron–phonon matrix elements are averaged over wave vectors, resulting in an energy-dependent contribution to the electronic scattering rates.We use the reference software implementation of the EPA in combination with BoltzTraP2.65 We run the required DFT calculations with Quantum ESPRESSO66 employing ultrasoft pseudopotentials, charge-density and wave-function plane-wave cutoffs of 600 and 75 Ry, respectively, a Fermi–Dirac smearing parameter matching the VASP calculations and an 11 × 11 × 11 k-point grid that is later non-self-consistently refined to 32 × 32 × 32.
Conflicts of interest
There are no conflicts to declare.Acknowledgements
We acknowledge financial support by MCIN/AEI/10.13039/501100011033 under grant PID2020-119777GB-I00, TED2021-130265B-C22, the “Ramón y Cajal” fellowship RYC2018-024947-I and the Severo Ochoa Centres of Excellence Program (CEX2019-000917-S), and by the Generalitat de Catalunya under grant no. 2021 SGR 01519. J. Í. acknowledges the financial support from the Luxembourg National Research Fund through grant C21/MS/15799044/FERRODYNAMICS. Calculations were performed at the Centro de Supercomputación de Galicia (CESGA) within action FI-2022-1-0012 of the Red Española de Supercomputación (RES).References
- R. Gurunathan, R. Hanus and G. J. Snyder, Mater. Horiz., 2020, 7, 1452–1456 RSC.
- M. Sledzinska, R. Quey, B. Mortazavi, B. Graczykowski, M. Placidi, D. Saleta Reig, D. Navarro-Urrios, F. Alzina, L. Colombo, S. Roche and C. M. Sotomayor Torres, ACS Appl. Mater. Interfaces, 2017, 9, 37905–37911 CrossRef CAS PubMed.
- N. Mingo, L. Yang, D. Li and A. Majumdar, Nano Lett., 2003, 3, 1713–1716 CrossRef CAS.
- M. Maldovan, Nat. Mater., 2015, 14, 667–674 CrossRef CAS PubMed.
- R. I. Epstein and K. J. Malloy, J. Appl. Phys., 2009, 106, 064509 CrossRef.
- Y. Jia and Y. Sungtaek Ju, Appl. Phys. Lett., 2012, 100, 242901 CrossRef.
- G. Wehmeyer, T. Yabuki, C. Monachon, J. Wu and C. Dames, Appl. Phys. Rev., 2017, 4, 041304 Search PubMed.
- N. Li, J. Ren, L. Wang, G. Zhang, P. Hänggi and B. Li, Rev. Mod. Phys., 2012, 84, 1045–1066 CrossRef.
- M. Maldovan, Nature, 2015, 14, 209–217 Search PubMed.
- K. Nakagawa, K. Satoh, S. Murakami, K. Takei, S. Akita and T. Arie, Sci. Rep., 2021, 11, 19533 CrossRef CAS PubMed.
- A. Sood, F. Xiong, S. Chen, H. Wang, D. Selli, J. Zhang, C. J. McClellan, J. Sun, D. Donadio, Y. Cui, E. Pop and K. E. Goodson, Nat. Commun., 2018, 9, 4510 CrossRef PubMed.
- G. Qin, Z. Qin, S.-Y. Yue, Q.-B. Yan and M. Hu, Nanoscale, 2017, 9, 7227–7234 RSC.
- J. A. Seijas-Bellido, H. Aramberri, J. Íñiguez and R. Rurali, Phys. Rev. B, 2018, 97, 184306 CrossRef CAS.
- P. Torres, J. A. Seijas-Bellido, C. Escorihuela-Sayalero, J. Íñiguez and R. Rurali, Phys. Rev. Mater., 2019, 3, 044404 CrossRef CAS.
- P. Torres, J. Íñiguez and R. Rurali, Phys. Rev. Lett., 2019, 123, 185901 CrossRef CAS PubMed.
- C. Liu, Y. Chen and C. Dames, Phys. Rev. Appl., 2019, 11, 044002 CrossRef CAS.
- Z. Yang, K. Yuan, J. Meng and M. Hu, Nanoscale, 2020, 12, 19178–19190 RSC.
- C. Cazorla and R. Rurali, Phys. Rev. B, 2022, 105, 104401 CrossRef CAS.
- C. Cazorla, M. Stengel, J. Íñiguez and R. Rurali, npj Comput. Mater., 2023, 9, 97 CrossRef CAS.
- N. Varela-Domínguez, C. López-Bueno, A. López-Moreno, M. S. Claro, G. Rama, V. Leborán, M. d. C. Giménez-López and F. Rivadulla, J. Mater. Chem. C, 2023, 11, 4588–4594 RSC.
- K. Nasu, H. Ping and H. Mizouchi, J. Phys.: Condens. Matter, 2001, 13, R693 CrossRef CAS.
- S. Koshihara, J. Phys.: Conf. Ser., 2005, 21, 7 CrossRef CAS.
- S. Koshihara, Y. Tokura, K. Takeda and T. Koda, Phys. Rev. Lett., 1992, 68, 1148–1151 CrossRef CAS PubMed.
- A. Cavalleri, C. Tóth, C. W. Siders, J. A. Squier, F. Ráksi, P. Forget and J. C. Kieffer, Phys. Rev. Lett., 2001, 87, 237401 CrossRef CAS PubMed.
- F. O. Karutz, J. U. von Schütz, H. Wachtel and H. C. Wolf, Phys. Rev. Lett., 1998, 81, 140–143 CrossRef CAS.
- A. Zong, A. Kogar, Y.-Q. Bie, T. Rohwer, C. Lee, E. Baldini, E. Ergeçen, M. B. Yilmaz, B. Freelon, E. J. Sie, H. Zhou, J. Straquadine, P. Walmsley, P. E. Dolgirev, A. V. Rozhkov, I. R. Fisher, P. Jarillo-Herrero, B. V. Fine and N. Gedik, Nat. Phys., 2019, 15, 27–31 Search PubMed.
- M. S. Kirschner, B. T. Diroll, P. Guo, S. M. Harvey, W. Helweh, N. C. Flanders, A. Brumberg, N. E. Watkins, A. A. Leonard, A. M. Evans, M. R. Wasielewski, W. R. Dichtel, X. Zhang, L. X. Chen and R. D. Schaller, Nat. Commun., 2019, 10, 504 Search PubMed.
- V. Krapivin, M. Gu, D. Hickox-Young, S. W. Teitelbaum, Y. Huang, G. de la Peña, D. Zhu, N. Sirica, M.-C. Lee, R. P. Prasankumar, A. A. Maznev, K. A. Nelson, M. Chollet, J. M. Rondinelli, D. A. Reis and M. Trigo, Phys. Rev. Lett., 2022, 129, 127601 CrossRef CAS PubMed.
- K. Iwano, Y. Shimoi, T. Miyamoto, D. Hata, M. Sotome, N. Kida, S. Horiuchi and H. Okamoto, Phys. Rev. Lett., 2017, 118, 107404 CrossRef CAS PubMed.
- T. Yang, C. Dai and L.-Q. Chen, Nano Lett., 2023, 23, 2551–2556 CrossRef CAS PubMed.
- C. Paillard, E. Torun, L. Wirtz, J. Íñiguez and L. Bellaiche, Phys. Rev. Lett., 2019, 123, 087601 CrossRef CAS PubMed.
- D. Wang, G. Wang, Z. Lu, Z. Al-Jlaihawi and A. Feteira, Front. Mater., 2020, 7, 91 CrossRef.
- A. I. Frenkel, F. M. Wang, S. Kelly, R. Ingalls, D. Haskel, E. A. Stern and Y. Yacoby, Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 56, 10869–10877 CrossRef CAS.
- M. D. Fontana, G. Metrat, J. L. Servoin and F. Gervais, J. Phys. C: Solid State Phys., 1984, 17, 483 CrossRef CAS.
- R. E. Cohen, Nature, 1992, 358, 136–138 CrossRef CAS.
- A. Carreras, A. Togo and I. Tanaka, Comput. Phys. Commun., 2017, 221, 221–234 CrossRef CAS.
- A. van Roekeghem, J. Carrete and N. Mingo, Comput. Phys. Commun., 2021, 263, 107945 CrossRef CAS.
- S. Bichelmaier, J. Carrete, M. Nelhiebel and G. K. H. Madsen, Phys. Status Solidi RRL, 2022, 16, 2100642 CrossRef CAS.
- Y. Wang, X. Liu, J. D. Burton, S. S. Jaswal and E. Y. Tsymbal, Phys. Rev. Lett., 2012, 109, 247601 CrossRef PubMed.
- H. J. Zhao, A. Filippetti, C. Escorihuela-Sayalero, P. Delugas, E. Canadell, L. Bellaiche, V. Fiorentini and J. Íñiguez, Phys. Rev. B, 2018, 97, 054107 CrossRef.
- J. Fujioka, A. Doi, D. Okuyama, D. Morikawa, T. Arima, K. N. Okada, Y. Kaneko, T. Fukuda, H. Uchiyama, D. Ishikawa, A. Q. R. Baron, K. Kato, M. Takata and Y. Tokura, Sci. Rep., 2015, 5, 13207 CrossRef CAS PubMed.
- L. Wang and B. Li, Phys. Rev. Lett., 2007, 99, 177208 CrossRef PubMed.
- Y. Kaifu, T. Komatsu, T. Hirano and T. Inoguchi, J. Phys. Soc. Jpn., 1967, 23, 903–903 CrossRef CAS.
- J. A. Seijas-Bellido, I. J. Íñiguez and R. Rurali, Appl. Phys. Lett., 2019, 115, 192903 CrossRef.
- L. Lindsay, D. A. Broido, J. Carrete, N. Mingo and T. L. Reinecke, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 121202(R) CrossRef.
- J. Carrete, W. Li, N. Mingo, S. Wang and S. Curtarolo, Phys. Rev. X, 2014, 4, 011019 CAS.
- L. Lindsay and D. A. Broido, J. Phys.: Condens. Matter, 2008, 20, 165209 CrossRef.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169 CrossRef CAS PubMed.
- P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953 CrossRef PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- C. Menéndez and C. Cazorla, Phys. Rev. Lett., 2020, 125, 117601 CrossRef PubMed.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- J. Carrete, B. Vermeersch, A. Katre, A. van Roekeghem, T. Wang, G. K. Madsen and N. Mingo, Comput. Phys. Commun., 2017, 220, 351–362 CrossRef CAS.
- S. Tamura, Phys. Rev. B: Condens. Matter Mater. Phys., 1983, 27, 858–866 CrossRef CAS.
- A. Kundu, X. Yang, J. Ma, T. Feng, J. Carrete, X. Ruan, G. K. H. Madsen and W. Li, Phys. Rev. Lett., 2021, 126, 115901 CrossRef CAS PubMed.
- Y. Zhao, S. Zeng, G. Li, C. Lian, Z. Dai, S. Meng and J. Ni, Phys. Rev. B, 2021, 104, 224304 CrossRef CAS.
- J. Zheng, D. Shi, Y. Yang, C. Lin, H. Huang, R. Guo and B. Huang, Phys. Rev. B, 2022, 105, 224303 CrossRef CAS.
- B. Peng, Y. Hu, S. Murakami, T. Zhang and B. Monserrat, Sci. Adv., 2020, 6, eabd1618 CrossRef CAS PubMed.
- D. Hickox-Young, D. Puggioni and J. M. Rondinelli, Phys. Rev. Mater., 2023, 7, 010301 CrossRef CAS.
- F. Eriksson, E. Fransson and P. Erhart, Adv. Theory Simul., 2019, 2, 1800184 CrossRef.
- P. Pulay, J. Comput. Chem., 1982, 3, 556–560 CrossRef CAS.
- G. Samsonidze and B. Kozinsky, Adv. Energy Mater., 2018, 8, 1800246 CrossRef.
- G. K. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin-Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr00100a |
| This journal is © The Royal Society of Chemistry 2024 |