Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Mechanistic insights into on-surface reactions from isothermal temperature-programmed X-ray photoelectron spectroscopy†
Lukas
Grossmann
 ab,
Manuela
Hocke
a,
Gianluca
Galeotti
b,
Giorgio
Contini
ab,
Manuela
Hocke
a,
Gianluca
Galeotti
b,
Giorgio
Contini
 cd,
Luca
Floreano
cd,
Luca
Floreano
 e,
Albano
Cossaro
e,
Albano
Cossaro
 eh,
Amit
Ghosh
eh,
Amit
Ghosh
 f,
Michael
Schmittel
f,
Michael
Schmittel
 f,
Johanna
Rosen
g,
Wolfgang M.
Heckl
ab,
Jonas
Björk
f,
Johanna
Rosen
g,
Wolfgang M.
Heckl
ab,
Jonas
Björk
 *g and
Markus
Lackinger
*g and
Markus
Lackinger
 *ab
*ab
aPhysics Department, Technical University of Munich, James-Franck-Str. 1, 85748 Garching, Germany. E-mail: markus@lackinger.org
bDeutsches Museum, Museumsinsel 1, 80538 Munich, Germany
cIstituto di Struttura della Materia-CNR (ISM-CNR), Via Fosso del Cavaliere 100, Roma, Italy
dDepartment of Physics, University of Rome Tor Vergata, Via della Ricerca Scientifica 1, 00133, Roma, Italy
eIstituto Officina dei Materiali Consiglio Nazionale delle Ricerche, S.S. 14, km 163.5, Trieste, 34149, Italy
fCenter of Micro and Nanochemistry and (Bio)Technology, Organische Chemie I, Universität Siegen, Adolf-Reichwein-Str. 2, 57068 Siegen, Germany
gLinköping University, Department of Physics, Chemistry and Biology, IFM, 581 83 Linköping, Sweden. E-mail: jonas.bjork@liu.se
hDepartment of Chemical and Pharmaceutical Sciences, Università degli Studi di Trieste, via L. Giorgieri 1, 34100, Trieste, Italy
First published on 15th March 2024
Abstract
On-surface synthesis often proceeds under kinetic control due to the irreversibility of key reaction steps, rendering kinetic studies pivotal. The accurate quantification of reaction rates also bears potential for unveiling reaction mechanisms. Temperature-Programmed X-ray Photoelectron Spectroscopy (TP-XPS) has emerged as an analytical tool for kinetic studies with splendid chemical and sufficient temporal resolution. Here, we demonstrate that the common linear temperature ramps lead to fitting ambiguities. Moreover, pinpointing the reaction order remains intricate, although this key parameter entails information on atomistic mechanisms. Yet, TP-XPS experiments with a stepped temperature profile comprised of isothermal segments facilitate the direct quantification of rate constants from fitting time courses. Thereby, rate constants are obtained for a series of temperatures, which allows independent extraction of both activation energies and pre-exponentials from Arrhenius plots. By using two analogous doubly versus triply brominated aromatic model compounds, we found that their debromination on Ag(111) is best modeled by second-order kinetics and thus proceeds via the involvement of a second, non-obvious reactant. Accordingly, we propose that debromination is activated by surface supplied Ag adatoms. This hypothesis is supported by Density Functional Theory (DFT) calculations. We foresee auspicious prospects for this TP-XPS variant for further exploring the kinetics and mechanisms of on-surface reactions.
Introduction
Reaction pathways in on-surface synthesis, and ultimately also the products, are frequently governed by kinetics rather than thermodynamics. The reason is that key reaction steps are irreversible either due to the large associated exothermic reaction enthalpies or the concomitant irretrievable loss of reaction byproducts by desorption.1–3 Accordingly, advancement in the understanding and control of on-surface reaction products can be expected from detailed kinetic studies. Thereby, the temperature dependence of the rate constants provides access to key parameters as pre-exponentials and activation energies. In addition, determination of the reaction order, that is the power law which describes how the reaction rate depends on reactant concentrations, allows the derivation of the overall chemical equation. This may reveal decisive but non-obvious reactants, thereby opening a window for atomistic insights into reaction mechanisms.Various analytical tools are feasible for kinetic studies of chemical reactions on solid surfaces. For instance, Scanning-Probe-Microscopy (SPM) facilitates real space studies at the atomic level with unique possibilities to identify reaction sites.4 In favorable cases, video-rate image acquisition can even provide a glimpse on reaction mechanisms provided that the reaction site is immobile.5 Nevertheless, it remains challenging to obtain a time-resolved integral picture from SPM. Alternatively, X-ray Photoelectron Spectroscopy (XPS) offers enhanced chemical and sufficient temporal resolution. Advantageously, XPS readily provides a statistically significant ensemble average, because photoelectrons are excited and collected from macroscopic surface areas. Unfortunately, this global picture can obscure the role of active sites, where reaction rates are greatly enhanced. But compared to heterogeneous catalysis with gaseous reactants and products that are only transiently adsorbed, active sites play a minor role in on-surface synthesis: the reactants are comparatively large molecules that remain adsorbed during and after the reaction, and surface coverages in the monolayer regime are used. Accordingly, the reaction is necessarily distributed over larger portions of the surface and is therefore less driven by active sites. For thermally activated reactions, studies are established where XP spectra are acquired while the temperature is increased to enhance reaction rates until the turnover becomes detectable. In its conventional implementation as Temperature-Programmed XPS (TP-XPS), the temperature is linearly ramped and spectra are swiftly acquired in the binding energy range of the studied element. Many of the prevalent studies tackle surface-assisted Ullmann type couplings.6–14 Its two elementary reaction steps, that is initial dehalogenation and subsequent conversion of organometallic intermediates commonly observed on copper and silver surfaces into covalent products,15–18 can be monitored in the halogen (e.g. Br 3d) and carbon C 1s core levels, respectively. For instance, based on TP-XPS experiments a two-staged nucleation and growth mechanism was inferred for the on-surface synthesis of poly-para-phenylene from dihalobenzene precursors.6
Here, we explore the initial debromination of 2,4,6-tris(4-bromophenyl)-1,3,5-triazine (3BPT) and 2,4-bis(4-bromophenyl)-6-phenyl-1,3,5-triazine (2BPT) precursor molecules on Ag(111) (see Fig. 1 for chemical structures and ESI, Section 7† for synthesis and characterization). Their different bromine substitution has profound consequences for structure formation. Three-fold brominated 3BPT results in two-dimensional reticulated networks,19 whereas two-fold brominated 2BPT affords a non-uniform mixture of one-dimensional topologies, i.e. closed rings as well as straight and curved chains. This not only applies to the final covalent structures, but already to the organometallic intermediates (ESI, Fig. S1† and ref. 19). The conceptual idea of this study is to explore possible influences of bromine substitution pattern and dimensionality effects already in the initial debromination.
Results
Linear temperature ramps
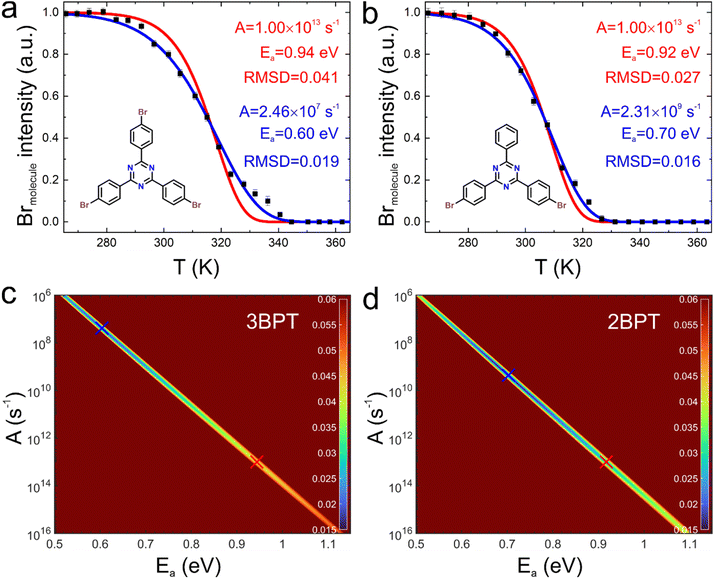
Initially, traces of debromination versus temperature were acquired with linear temperature ramps at the ALOISA beamline20 of Elettra Synchrotron (Trieste, Italy) for 3BPT and 2BPT on Ag(111) (Methods and ESI, Fig. S2†). Low molecular coverages in the submonolayer regime were deliberately used to avoid additional influences from molecular crowding at the surface, although this is associated with lower signal-to-noise ratios (see Methods section). In principal, kinetic reaction parameters can be extracted from fitting. In our previous study of the closely related compound 1,3,5-tris(4-bromophenyl)benzene (TBB, similar to 3BPT, but with a central phenyl instead of a triazine ring) on Ag(111), we fitted analogous traces by underlying first-order reaction kinetics.10 A coarse fit was obtained for TBB on Ag(111) using the Density Functional Theory (DFT) calculated activation energy of Ea = 0.98 eV, resulting in a pre-exponential of A = 3.25 × 1016 s−1. Here, for 3BPT and 2BPT on Ag(111), to elucidate finer details and to also judge the appropriateness of the employed model, a higher density of data points has been obtained by a slower heating rate and enhanced acquisition speed for individual spectra (Fig. 1(a) and (b)). Instead of resorting to calculated activation energies, we aimed to derive both Ea and A from fitting. Yet, even linear temperature ramps do not allow for an analytical solution of the temperature traces, but their numerical simulation is straightforward and computationally inexpensive. To systematize the fitting procedure and to make it more efficient, we now applied a grid search algorithm: the fitting parameters Ea and A were both independently varied in a sensible range on a fine grid. For each grid point in this two-dimensional parameter space a debromination versus temperature trace was numerically computed according to the respective model (ESI, Section 3†). Then the root mean square deviation (RMSD) between simulated and measured curve was calculated and plotted as figure of merit of the fit, that is the closer the RMSD is to zero the better the fit. For both molecules the respective fitting maps for first-order kinetics in an extened range of A and Ea are shown in Fig. 1(c) and (d). Interestingly, the best fit values display a linear correlation between Ea and ln(A) in the fitting map over many orders of magnitude in the pre-exponential, implying that the two parameters cannot be independently quantified within this approach. Assuming A = 1 × 1013 s−1 for the pre-exponential as a standard value derived from transition state theory for unimolecular reactions in the gas phase, the corresponding optimized activation energies are Ea = 0.94 eV and Ea = 0.92 eV for 3BPT and 2BPT, respectively (red crosses in Fig. 1(c) and (d)). These figures compare favorably with DFT-calculated activation energies of debromination on Ag(111) terraces (vide infra), but the corresponding simulated temperature traces (red lines in Fig. 1(a) and (b)) result in unsatisfactory fit quality with comparatively high RMSD values. However, the extended parameter spaces of the grid searches, also reveal weakly pronounced global minima for unexpectedly low values of Ea and A as indicated in Fig. 1(a) and (b). The activation energies of 0.60 eV (3BPT) and 0.70 eV (2BPT) are 0.2–0.3 eV lower than reported values from DFT calculations,2,21–23 and the pre-exponentials in the order of 107–109 s−1 also appear to be small. Yet, the corresponding simulated temperature traces (blue lines in Fig. 1(a) and (b)) provide visibly improved fit quality with significantly lower RMSD. On the other hand, comparatively small pre-exponentials are not uncommon for surface reactions and are often associated with diffusion control.24 In conclusion, the situation of the global minima in the grid searches (blue crosses in Fig. 1(c) and (d)) challenges the simple view of debromination on Ag(111) as a unimolecular reaction proceeding with first-order kinetics on atomically flat terraces without the need for mass transport.Stepped temperature profiles
To resolve the fitting ambiguity experienced for the linear temperature ramps, we devised an experimental approach with the aim to independently determine Ea and A. For that purpose, we propose an alternative temperature profile for TP-XPS comprised of isothermal segments and stepwise temperature changes instead of the commonly applied linear ramps. Thereby, the time dependence of the reaction turnover is disentangled from the dominating exponential temperature influence. Consequently, rate constants can be directly inferred at the respective temperatures from fitting the time traces with analytical functions. Depending on the reaction order, different time courses are expected: first-order results in an exponential decay of reactant concentration in time, whereas second-order yields a reciprocal relation between reactant concentration and time (ESI, Section 5†). Acquisition of debromination versus time traces for a series of temperatures grants access to the temperature dependence of the rate constant, from which Ea and A can be independently extracted. The applied temperature profiles and the measured photoelectron yield of molecule-bound bromine are depicted in Fig. 2(a) and (b) for 3BPT and 2BPT, respectively. For each of the isothermal segments we have extracted the time course of the debromination. However, contrary to our expectations, these kinetic traces did not allow a clear distinction between first- and second-order rate laws (ESI, Fig. S7†).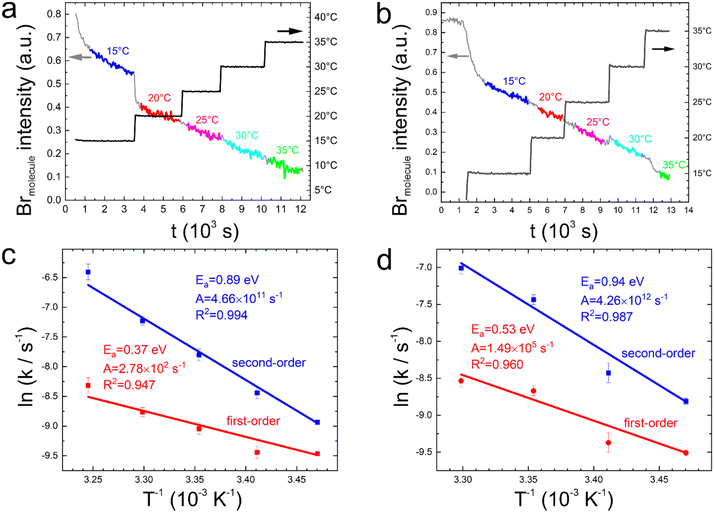 | ||
| Fig. 2 Debromination versus time traces for (a) 3BPT and (b) 2BPT acquired with a stepped temperature profile comprised of isothermal segments. The respective temperature profiles are depicted as black lines. The grey lines represent the continuously measured integrated photoelectron yield from the Br 3d5/2 peak of bromine covalently bound to the molecule (Brmolecule). Segments of the time traces that were used for deriving rate constants are colored and the associated temperatures are indicated. For 3BPT in (a), a beam dump occurred at the end of the 15 °C segment, where the sample was preserved by cooling to a lower temperature and resuming the measurement at 20 °C when the beam was stable again. Corresponding Arrhenius plots of the rate constants k for (c) 3BPT and (d) 2BPT obtained for assuming either first-order (red) or second-order (blue) reaction kinetics (for 2BPT the last data point at 35 °C was discarded, because this short trace yielded an unacceptably large fitting error). The activation energies and pre-exponentials extracted from the respective slopes are indicated. For both compounds the first-order Ea appear unreasonably low, while the second-order Ea are largely consistent with DFT calculations. Moreover, a second-order kinetics results in improved R2 values in the Arrhenius plots. The error bars represent only fitting errors of the time traces (ESI, Table S1†). The actual error bars are expected to be larger because they include additional contributions from temperature measurement uncertainties, X-ray intensity variations, and detector noise. | ||
Accordingly, we fitted the debromination traces acquired at constant temperatures with the analytical functions for both first- and second-order kinetics as the most plausible reaction orders, noting here that the reaction order does not necessarily have to be an integer for more complex reaction scenarios. Note that the lowest target temperature of 15 °C was approached with a fairly high temperature rate, accordingly, a long enough equilibration time ensured thermal equilibration across the samples. From fitting, we obtained two data sets of temperature dependent rate constants k for both first- and second-order (ESI, Table S1†). Fig. 2(c) and (d) show the corresponding Arrhenius plots for 3BPT and 2BPT, respectively. In both cases, underlying a first-order rate law yields unexpectedly low activation energies of Ea = 0.37 eV (3BPT) and Ea = 0.55 eV (2BPT), especially compared to the 0.80–1.0 eV obtained from DFT calculations.2,21–23 In addition, to match the experimentally measured reaction rates, the low activation energies are accompanied by small pre-exponentials of A = 2.73 × 102 s−1 (3BPT) and A = 1.49 × 105 s−1 (2BPT). Although the values of these kinetic parameters derived under the assumption of a first-order kinetics are much smaller than expected, they qualitatively reflect the global minima obtained by fitting the temperature-dependent conversion with first-order reaction kinetics (Fig. 1). In summary, the assumption of first-order kinetics consistently results in low pre-exponentials for both linear and stepped temperature profiles. One possible interpretation is to attribute this to surface diffusion as a rate limiting step.24 On the contrary, presuming second-order reaction kinetics yields activation energies of Ea = 0.89 eV (3BPT) and Ea = 0.94 eV (2BPT) in the Arrhenius plots (Fig. 2), which are more consistent with DFT calculations, indicating the involvement of a second reaction partner (vide infra). The description of debromination as a second-order process can be viewed as an alternative approach to account for the diffusion control indicated by the low pre-exponentials of the first-order description. Similarly, optimization of the fit parameters of the temperature traces shown in Fig. 1(a) and (b) for second-order kinetics by means of a grid search leads to global minima with enhanced activation energies (ESI, Fig. S9†). Moreover, the kinetic reaction parameters obtained by either fitting the temperature traces or from the Arrhenius plots exhibit a reasonable level of consistency (ESI, Fig. S10†). Finally, we also performed grid searches with the reaction order and the pre-exponential as the free parameters (ESI, Fig. S3 and S4†). In each individual grid search, the activation energy was kept fixed and multiple grid searches were performed over an activation energy range of 0.70 eV to 1.10 eV. Both 2BPT and 3BPT showed the same trend: the optimal reaction order shifts monotonically from lower values around one to values of two and above as Ea is increased. Interestingly, for a given activation energy the optimal reaction order was always larger for 3BPT. This ambiguity in the optimal reaction order may indicate more complex processes.
Second-order reaction kinetics
Second-order reaction kinetics indicates two reactants either of the same or a different kind, thereby challenging the view of debromination on metal surfaces being a unimolecular reaction, a scenario often used as a premise for calculations.23,25–27 Surface-supplied metal adatoms appear to be the most plausible second reactant, in part because debromination on silver and copper surfaces results in metastable organometallic intermediates with molecules linked by carbon–metal–carbon bonds15,28 as similarly observed for both 2BPT (ESI, Fig. S1†) and 3BPT,19 with only a few reported exceptions.29 Although it is difficult to elucidate a decisive contribution of the adatoms, they are conjectured as being important for a variety of chemical reactions on metals,5,30–34 and in particular for formation of metal-coordinated and organometallic structures.35–41 For surface-assisted Ullmann coupling, the role of metal adatoms has mostly been studied for the organometallic intermediates,42–44 but less so for the initial dehalogenation.21,45In order to evaluate a possible kinetic advantage of the Ag adatom-activated debromination on Ag(111), we calculated energy profiles by DFT for the comparison of activation energies (see Methods for details). It should be noted that this type of calculation does not take entropy into account. In this context, halobenzenes have previously been introduced as model system.2,21,22,44 Yet, their strongly tilted adsorption geometry contradicts the flat adsorption of commonly employed larger aromatic precursors, with a potential impact on calculated activation and reaction energies.10 To arrive at a more realistic picture, we calculated the debromination of 3BPT and 2BPT on Ag(111) with and without the assistance of Ag adatoms. Energy profiles of triple and double debromination of 3BPT and 2BPT alongside structures of the corresponding transition and final states are depicted in Fig. 3 (cf. ESI, Fig. S11† for a more detailed depiction). Importantly, we did not include an additional energy contribution for providing the Ag adatom, because they are supplied from a 2D gas that originates in a dynamic equilibrium of evaporation and condensation from substrate step-edges.46 Consequently, Ag adatoms are readily available for surface chemistry, although their potential participation will depend on if and by how much they lower the activation energy. Further, their local concentration will matter, which is projected to be in the order of 10−9 with respect to surface atoms at room temperature.46 In fact, measuring the concentration of intrinsic adatoms is challenging, and the extremely low value in the order of parts per billion is, to the best of our knowledge, the only quantitative statement of adatom concentration in the literature. On the other hand, self-assembly of molecular structures with interspersed Ag adatoms has been observed at about 100 K on Ag(111), indicating their sufficient availability even at lower temperatures.40 Our DFT calculations indicate appreciable differences for debromination of 3BPT with and without Ag adatoms (Fig. 3(a)): (1) activation energies become markedly reduced with Ag adatoms, that is 0.80 eV versus 1.02 eV for the first debromination; (2) without Ag adatoms the activation energies for all subsequent debromination reactions are virtually constant, whereas they become significantly lower for the second (0.66 eV) and third (0.70 eV) debromination of 3BPT with Ag adatoms. Differences in debromination temperatures have previously been observed not only for inequivalent bromine substituents,47 but also for nominally equivalent sites,23,48 suggesting a more general phenomenon. By contrast, for 2BPT (Fig. 3(b)) we find nearly similar activation energies for its first (0.71 eV) and second (0.69 eV) debromination that correspond to the second and third debromination of 3BPT. (3) Debromination reactions without Ag adatoms are energetically neutral. Hence, the entropy gained from releasing bromine atoms would decisively contribute to the thermodynamic driving force. By contrast, the Ag adatom-activated debromination results in a nearly equal energy gain of approximately −0.50 eV for each successive debromination for both 3BPT and 2BPT. The reason for the lower final state energy is presumably two-fold. Firstly, an organometallic bond between the debrominated carbon atom and an Ag adatom is less strained, hence energetically more favorable than forming bonds with Ag surface atoms, even though the phenyl group still bends down to the lower lying Ag adatom.19 Secondly, adatoms are less coordinated than surface atoms, rendering them more reactive. On the other hand, adatom-activated debromination comes with an entropic cost for immobilizing the Ag adatom.
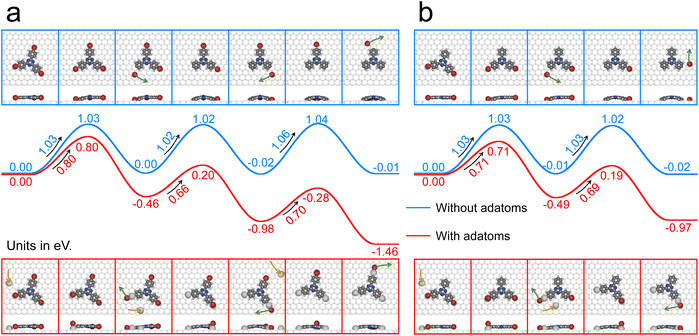 | ||
| Fig. 3 DFT calculated energy profiles for the debromination of (a) 3BPT and (b) 2BPT on Ag(111) terraces without (upper part, blue curve) and with (lower part, red curve) Ag adatoms. Full debromination of the entire 3BPT (2BPT) molecule by three (two) successive debromination reactions was calculated. The relative energy with respect to the intact initial state was calculated with eqn (1) (Methods). Essentially, the final state energy of each debromination was evaluated with the bromine atom adsorbed on Ag(111), but isolated from the molecule as indicated by the green arrows. No additional energy contribution was considered for providing the Ag adatom (yellow arrow). | ||
Since our DFT calculations indicate the possibility of different activation energies for the debromination of 3BPT, as also suggested by other studies,23,48 we have refined our model (ESI, Section 3 and Fig. S5†). In the corresponding grid search, we again use a second-order rate law in a two-dimensional parameter space, now consisting of two different activation energies, while using fixed values for the pre-exponential in each grid search over a representative range. However, in all optimizations we obtain fairly similar activation energies with differences of less than 50 meV. In fact, larger differences in the two activation energies result in discernible steps in the temperature versus debromination curves, calling for a re-examination of the reported studies by TP-XPS.23,48
Alternative reaction pathways
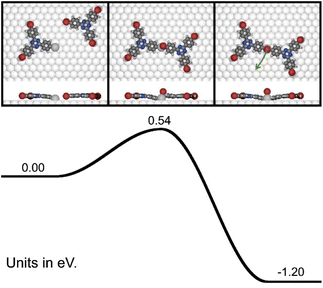
In the final state of the adatom-activated debromination, the Ag atom remains bonded to the molecule. Hence, it is conceivable that this immobilized organometallic Ag atom could become an active site for ongoing debromination reactions. Consequently, we also evaluated the energy profile of this complementary debromination by DFT. Interestingly, as illustrated in Fig. 4, this reaction not only exhibits an even lower activation energy of 0.54 eV, but also a sizably enhanced reaction energy of −1.20 eV. The latter originates in the markedly increased strength of the second organometallic bond as similarly found by DFT for the bonding of phenyl radicals to Cu adatoms on Cu(111).44 Although this alternative process is energetically favored, it requires the availability of accessible, singly bonded organometallic Ag atoms as well as sufficient mobility of the species to be debrominated. Consequently, it should be less relevant in the early and final stages of the debromination, because initially organometallic Ag sites are sparse, and towards completion of the debromination monomeric or smaller, still mobile entities are already depleted. Albeit the relevance of this alternative debromination pathway remains currently unresolved, its energetic superiority and dependence on boundary conditions nevertheless suggest a higher complexity in the seemingly straightforward debromination. In summary, our DFT calculations of activation energies indicate that debromination reactions activated by Ag adatoms, either freely diffusing or immobilized through preceding debromination events, are energetically preferred over unimolecular debromination reactions on Ag(111) terraces.Discussion and summary
We comparatively studied the thermally activated debromination of 3BPT and 2BPT on Ag(111) by TP-XPS using different temperature profiles. First, we conventionally acquired debromination versus temperature traces with linear ramps. For the simultaneous fitting of both activation energies and pre-exponentials of the rate constant grid searches were employed, which made clear that comparably good fits can be obtained for linear combinations of Ea and ln(A) (Fig. 1(c) and (d)) for an extended range of the fit parameters. In order to independently determine Ea and A in experiments, we carried out TP-XPS experiments with stepped temperature profiles to obtain rate constants for a series of temperatures. Albeit different conversion versus time courses are expected for first- versus second-order reaction kinetics in principal, the fitting curves that were separately obtained for both reaction orders at a given temperature run prohibitively similar for directly inferring the reaction order (ESI, Fig. S7†). Yet, the corresponding Arrhenius plots for first-order kinetics result in surprisingly low Ea that always correlate with low A. The derived activation energies are significantly lower than those calculated by DFT (Fig. 3),2,21–23 but the associated low pre-exponentials could be considered as an experimental signature of a diffusion-controlled reaction that is described by pseudo first-order kinetics.24 By contrast, activation energies closer to the calculated values are obtained by assuming second-order reaction kinetics. Thus, both descriptions with either first- or second-order kinetics consistently indicate, each in its own way, the involvement of a second reaction partner for the debromination on Ag(111).These results prompted us to explore Ag adatom-activated debromination reaction pathways by DFT as the most plausible second-order process, given the metastable organometallic intermediates that are commonly observed on Ag(111).15–18,28 Our calculations indicate approximately 0.3 eV lower activation energies for Ag adatom-activated debromination reactions (with the exception of the first debromination of 3BPT, where the activation energy was 0.2 eV lower), which translates into a three to four orders of magnitude larger Boltzmann factor at the reaction temperature. In addition, DFT suggests the existence of an alternative debromination pathway with even lower activation energy, when the reaction takes place at a molecule-bound organometallic Ag atom. However, discrepancies between experiment and theory remain. DFT suggests a lower effective activation energy for debromination of 2BPT as compared to 3BPT, which is not corroborated by our experiments, where we find essentially similar activation energies for both compounds. Moreover, DFT indicates 0.2–0.3 eV lower activation energies as compared to the experimental values derived from the Arrhenius plots assuming second-order kinetics. The origin of this quantitative mismatch remains presently unclear, but needs to be addressed in future studies (vide infra). It should be emphasized that DFT is an approximate method with respect to the functional used, which also adds a largely unknown error bar to the calculated activation energies. Moreover, the energy profiles for debromination are evaluated with the reactant or intermediate at its optimized adsorption site. However, such a defined scenario seems implausible under reaction conditions where the molecules are mobile and sample different sites. Thus, it cannot be excluded that the remarkable differences in the activation energies for the first versus the second and third debromination of 3BPT are related to the zero temperature conditions imposed by the calculations.
In summary, the low pre-exponentials and activation energies encountered for evaluating the TP-XPS data by assuming first-order reaction kinetics gave rise to the hypothesis that the debromination reactions of 3BPT and 2BPT on Ag(111) involve an additional, non-obvious reactant. This implies a description by second-order reaction kinetics, a hypothesis further supported by DFT calculations indicating significantly lower activation energies for Ag adatom-activated processes. Second-order reaction kinetics, however, imply appreciable concentration changes of both reactants in the course of the reaction. A large stoichiometric excess of one reactant would leave its concentration virtually constant, resulting in a pseudo first-order reaction kinetics. Accordingly, the abundance of Ag adatoms should also not yield the low pre-exponentials in the fits with first-order kinetics that indicate diffusion control. In other words, both the low pre-exponentials derived from the first-order fits and the improved quality of the second-order fits consistently indicate that the concentration of Ag adatoms must decrease significantly during debromination. In this respect, we note that the Ag adatoms become incorporated into the metastable organometallic intermediates upon debromination, and are only liberated again when these are converted into the final covalent products. However, on Ag(111) this conversion takes place at significantly higher temperatures, when the debromination is already completed.10 Accordingly, the role of Ag adatoms is better described as an activator rather than a catalyst in the strict sense, which would require their availability in the original state after the debromination reaction. On the other hand, the replenishment of Ag adatoms must be kinetically limited. Diffusion barriers of Ag adatoms on terraces are comparatively low (<0.1 eV),49 so that sluggish supply from Ag(111) step-edges offers a more plausible explanation. In addition, the organometallic structures formed upon debromination around room temperature often nucleate at step-edges which may also partly deactivate them for adatom supply. Equilibrium concentrations of adatoms on metal surfaces are conjectured to be exceedingly low in the order of parts per billion with respect to surface atoms.46 Exhaustibility of the adatom reservoir is consistent with our previous finding that the type of intermolecular bonds formed between 1,3,5-tris(4′-biphenyl-4′′-carbonitrile)benzene on Cu(111) can depend on the molecule deposition rate: higher deposition rates resulted in supramolecular bonding, while lower deposition rates tipped the balance in favor of metal-coordination bonds with Cu adatoms, because their replenishment can keep up with the arrival rate of molecules.37 So there is experimental evidence that the kinetic availability of metal adatoms on the (111) facets of coinage metals could indeed be limited around room temperature. Since adatoms preferentially evaporate from low-coordinated sites, that is step-edges and kinks, the real structure of the surface with its specific defect density and distribution should also influence the debromination kinetics.
For the simulation of debromination as a function of either temperature or time, from which the activation energies and pre-exponentials were derived, the second-order reaction rate was assumed to be proportional to the square of the concentration of brominated sites for the sake of simplicity and to reduce the number of parameters. For the proposed Ag adatom-activated debromination, however, the reaction rate is proportional to the product of the concentrations of brominated sites and Ag adatoms. Accordingly, the model was further refined to account for the putative nature of the process (ESI, Section 3†). Therefore, the amount of available Ag adatoms relative to the amount of brominated sites at the beginning of the reaction (N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0)) was introduced as a new fit parameter. The model was restricted to the scenario depicted in Fig. 3, where one Ag adatom is consumed for each debromination, while the alternative process shown in Fig. 4 effectively requires only one Ag adatom for the debromination of two sites. Again, the grid searches were performed in a two-dimensional parameter space consisting of N(Ag,0)
N(Br,0)) was introduced as a new fit parameter. The model was restricted to the scenario depicted in Fig. 3, where one Ag adatom is consumed for each debromination, while the alternative process shown in Fig. 4 effectively requires only one Ag adatom for the debromination of two sites. Again, the grid searches were performed in a two-dimensional parameter space consisting of N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) and the pre-exponential A, while keeping the activation energy fixed at Ea = 0.80 eV. To elucidate the influence of variations in Ea, additional grid searches were performed for a range of activation energies (ESI, Fig. S8†). The grid searches and the corresponding simulated traces for both 2BPT and 3BPT are presented in Fig. 5. First of all, the fit quality is further improved as indicated by the lower RMSD values of 0.015 (3BPT) and 0.014 (2BPT) compared to the second-order with identical reactants (ESI, Fig. S11†). For both molecules, the optimal parameters are confined to a more restricted region in this two-dimensional parameter space. Interestingly, the optimization yields almost similar pre-exponentials for both compounds, while a higher N(Ag,0)
N(Br,0) and the pre-exponential A, while keeping the activation energy fixed at Ea = 0.80 eV. To elucidate the influence of variations in Ea, additional grid searches were performed for a range of activation energies (ESI, Fig. S8†). The grid searches and the corresponding simulated traces for both 2BPT and 3BPT are presented in Fig. 5. First of all, the fit quality is further improved as indicated by the lower RMSD values of 0.015 (3BPT) and 0.014 (2BPT) compared to the second-order with identical reactants (ESI, Fig. S11†). For both molecules, the optimal parameters are confined to a more restricted region in this two-dimensional parameter space. Interestingly, the optimization yields almost similar pre-exponentials for both compounds, while a higher N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) of 1.80 is obtained for 2BPT as compared to 1.18 for 3BPT. Remarkably, the products of the optimized value of N(Ag,0)
N(Br,0) of 1.80 is obtained for 2BPT as compared to 1.18 for 3BPT. Remarkably, the products of the optimized value of N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) times the number of brominated sites of the respective compound, which corresponds to the total amount of available Ag adatoms per molecule within this model, are almost identical (compare 1.80 times 2 for 2BPT and 1.18 times 3 for 3BPT).
N(Br,0) times the number of brominated sites of the respective compound, which corresponds to the total amount of available Ag adatoms per molecule within this model, are almost identical (compare 1.80 times 2 for 2BPT and 1.18 times 3 for 3BPT).
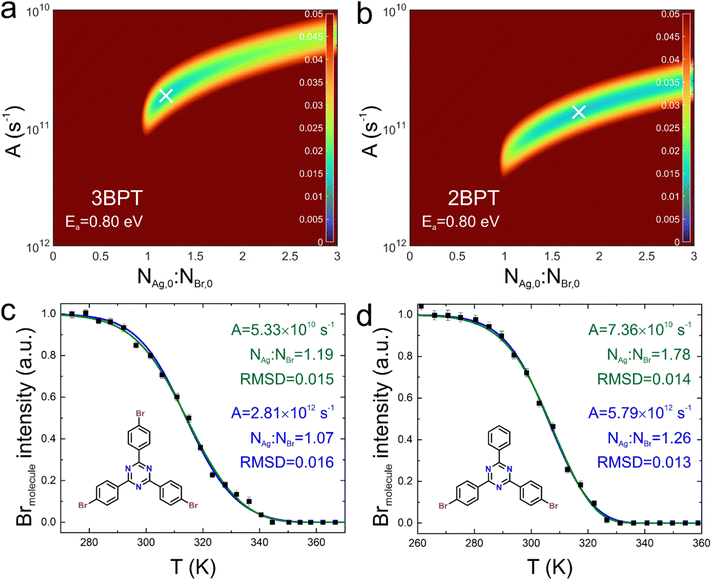 | ||
Fig. 5 Fitting debromination versus temperature with Ag adatom model. Grid searches (400 × 400 points) for optimization of the fitting parameters, that is pre-exponential A and the initial ratio of Ag adatoms to brominated sites N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) for (a) 3BPT and (b) 2BPT. Note that A is plotted on a logarithmic axis. The color coding represents the RMSD between experimental and computed traces. In both grid searches the activation energy was kept fixed at Ea = 0.80 eV. Simulated traces with the optimized fit parameters are shown for (c) 3BPT and (d) 2BPT. Black squares represent experimental data; the olive curves correspond to the optimized parameters found in the grid searches in (a) and (b), while the blue curves correspond to the optimized parameters of a grid search with a different fixed activation energy of Ea = 0.90 eV (ESI, Fig. S6†). The Ag adatom model results in an improved fit as indicated by the lower RMSD. However, the optimized parameters A and N(Ag,0) N(Br,0) for (a) 3BPT and (b) 2BPT. Note that A is plotted on a logarithmic axis. The color coding represents the RMSD between experimental and computed traces. In both grid searches the activation energy was kept fixed at Ea = 0.80 eV. Simulated traces with the optimized fit parameters are shown for (c) 3BPT and (d) 2BPT. Black squares represent experimental data; the olive curves correspond to the optimized parameters found in the grid searches in (a) and (b), while the blue curves correspond to the optimized parameters of a grid search with a different fixed activation energy of Ea = 0.90 eV (ESI, Fig. S6†). The Ag adatom model results in an improved fit as indicated by the lower RMSD. However, the optimized parameters A and N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) obtained for a range of Ea yield similarly good fits. N(Br,0) obtained for a range of Ea yield similarly good fits. | ||
Again, the specific choice of activation energies yields different values for the optimal fit parameters, but with a common trend for both molecules, that is higher activation energies lead to larger pre-exponentials as expected, yet also to lower N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) (ESI, Fig. S8†). In summary, considering the concentration change of Ag adatoms results in a better agreement between simulation and experiment, but does this pleasant fact in itself provide more insight? We are reluctant to express confidence that the high fit quality necessarily indicates an accurate description of the debromination reaction, because relevant aspects are still not included in the model: (1) a possible role of the low activation energy processes shown in Fig. 4, which will also affect the amount of Ag atoms consumed; (2) variations in activation energies that cannot be excluded; (3) the possibility of complete consumption of Ag adatoms with the consequence that the reaction rate is determined by the replenishment of Ag adatoms. On the one hand, it seems to be a coincidence that the optimization yields N(Ag,0)
N(Br,0) (ESI, Fig. S8†). In summary, considering the concentration change of Ag adatoms results in a better agreement between simulation and experiment, but does this pleasant fact in itself provide more insight? We are reluctant to express confidence that the high fit quality necessarily indicates an accurate description of the debromination reaction, because relevant aspects are still not included in the model: (1) a possible role of the low activation energy processes shown in Fig. 4, which will also affect the amount of Ag atoms consumed; (2) variations in activation energies that cannot be excluded; (3) the possibility of complete consumption of Ag adatoms with the consequence that the reaction rate is determined by the replenishment of Ag adatoms. On the one hand, it seems to be a coincidence that the optimization yields N(Ag,0)![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) N(Br,0) close to unity. On the other hand, either a large excess or deficiency of Ag adatoms would result in (pseudo) first-order kinetics. Accordingly, the fitting results can be interpreted as further evidence for a second-order process. However, it is still conceivable that Ag adatoms are completely consumed during the course of the reaction, which would imply a change in the reaction order from about two to either one, if the debromination becomes a unimolecular reaction, or zero, if the debromination rate is entirely determined by the replenishment of Ag adatoms. On the other hand, a change in the reaction mechanism would also imply a notable change in the reaction rate, which has not been observed experimentally. But the simplest model, which explicitly includes Ag adatoms, already gives a near perfect fit. In this respect, we would not consider it useful to extend and refine the model further, since the quality of the fit cannot be improved, and thus validation of competing models by comparison with experimental data is no longer meaningful. A possible solution for future experiments would be to also increase the dimensionality of the data, for example by recording debromination traces for different heating rates.
N(Br,0) close to unity. On the other hand, either a large excess or deficiency of Ag adatoms would result in (pseudo) first-order kinetics. Accordingly, the fitting results can be interpreted as further evidence for a second-order process. However, it is still conceivable that Ag adatoms are completely consumed during the course of the reaction, which would imply a change in the reaction order from about two to either one, if the debromination becomes a unimolecular reaction, or zero, if the debromination rate is entirely determined by the replenishment of Ag adatoms. On the other hand, a change in the reaction mechanism would also imply a notable change in the reaction rate, which has not been observed experimentally. But the simplest model, which explicitly includes Ag adatoms, already gives a near perfect fit. In this respect, we would not consider it useful to extend and refine the model further, since the quality of the fit cannot be improved, and thus validation of competing models by comparison with experimental data is no longer meaningful. A possible solution for future experiments would be to also increase the dimensionality of the data, for example by recording debromination traces for different heating rates.
Finally, with the improved Ag adatom model at hand, we revisited the question of whether the reaction order can be directly inferred from the shape of the debromination versus time traces. To this end, a debromination trace was numerically simulated using the optimized parameters as obtained from the grid search and superimposed with Gaussian white noise (ESI, Fig. S8†). Fitting this more extended trace with first-order reaction kinetics results in a decent fit with R2 = 0.97. Interestingly, the use of second-order reaction kinetics, which should provide a better description of the underlying process, results in only a marginally improved fit with R2 = 0.98. In TP-XPS experiments, however, the acquisition of longer time traces carries the risk of increasing the influence of X-ray induced debromination (beam damage). This could falsify the experimental data, especially if the reaction turnover has already become comparatively low.
Lastly, the remaining specific differences between 2BPT and 3BPT are discussed. In the debromination of 3BPT, the experimental curve indicates a slower debromination in the final stage in the temperature range 330–340 K compared to the simulations, for both second-order (Fig. 5(c) and ESI, Fig. S9†) and first-order kinetics (Fig. 1). This could be an effect of the limited availability of Ag adatoms to complete the debromination, and is more pronounced for 3BPT compared to 2BPT. A possible explanation is the influence of dimensionality: the debromination of 3BPT requires more Ag adatoms, and the tritopic compound also forms reticulated organometallic networks19 in which the accessibility of the brominated sites is more limited compared to the one-dimensional topologies adopted by 2BPT. However, on the basis of the TP-XPS data alone, such interpretations necessarily remain handwaving, and real space observations of the debromination process would be desirable. Overcoming the challenge of tracking reactions with mobile reactants by SPM requires intelligent approaches.
An obvious and worthwhile target for future studies are deiodination reactions on Ag(111). The respective activation energies for deiodination reactions on Ag(111) are sizably lower than for debrominations.2 Accordingly, deiodination proceeds at temperatures below 200 K,50 where the availability and mobility of Ag adatoms becomes noticeably reduced. The key questions are whether this gives rise to a kinetic advantage of unimolecular dehalogenation reactions, and whether an altered reaction mechanism can be inferred as change in reaction order from TP-XPS. Albeit temperature profiles with isothermal segments in principle facilitate the direct determination of activation energies, evaluating the actual experimental error is an important imminent task to obtain a realistic picture of the attainable accuracy, and to also resolve the remaining discrepancies. Given the widespread use of DFT calculated energy profiles for the rationalization of on-surface reactions,44,51–53 benchmarking theoretical energy profiles with highly accurate experimental values is an extremely important task for validating prevalent theoretical approaches. The availability of a trustworthy, sufficiently large database – either from experiment or theory – may eventually facilitate the use of machine learning in surface chemistry, just as it is currently conquering the identification of molecules from their SPM images54 and other areas of chemistry.55
Methods
Sample preparation
The Ag(111) single crystal (Surface Preparation Laboratory) was mounted by Mo clips on a sample holder equipped with two filaments for radiative heating. The temperature was measured by a type K thermocouple in direct contact with the sample surface (in between clips and sample). An additional thermocouple was attached on the cold finger for liquid nitrogen cooling. The Ag(111) surface was prepared by the usual cycles of Ar+ ion sputtering (800 eV, 15 min) and flash annealing (∼450 °C). The absence of contaminations with focus on carbon and oxygen was verified by XPS at photon energies of 390 eV and 650 eV, respectively. 2BPT (150 °C, 20 min) and 3BPT (190 °C, 20 min) were deposited by thermal sublimation from homemade boron nitride crucibles with deposition parameters as indicated and rates monitored by a quartz crystal microbalance. In order to suppress initial debromination upon deposition, the Ag(111) substrate was held at ∼215 K. To avoid the risk of inconsistencies arising from measuring newly prepared samples in different runs, we determined the rate constants at different temperatures in a single experimental run (Fig. 2). Moreover, to reduce an additional potential influence of molecular coverage in our comparative study, we aimed at similar and low coverages of 2BPT and 3BPT. According to C 1s intensity in XPS, and using CVD-grown graphene on a copper foil as reference, the coverages of 2BPT and 3BPT amounted to 35% and 29% for the TP-XPS runs with linear and 37% and 27% for the TP-XPS runs with stepped temperature profiles, respectively (100% coverage corresponds to a full monolayer of the 3BPT derived covalent honeycomb network,18 that is 10.2 carbon atoms per nm2).TP-XPS measurements and data analysis
TP-XPS experiments were carried out at the ALOISA beamline at the Elettra Synchrotron radiation facility (Trieste, Italy).20 XP spectra were acquired at a grazing incidence angle of 4.0° ± 0.05° with the surface oriented transverse to the magnetic field (nearly p-polarization) and near normal emission detection. Photoelectrons were detected with a home-built hemispherical electron analyzer equipped with a high count rate (>4 MHz) two-dimensional delay-line detector developed by Elettra.56 The sample temperature profiles were controlled via a dedicated software suite using a PID algorithm and a heating rate of 0.10 K s−1 was used for the linear temperature profiles. To expedite temperature stabilization, the sample holder was counter-cooled under a constant flow of liquid nitrogen. The debromination was monitored in the Br 3d core levels using a photon energy of 190 eV and a pass energy of 20 eV, corresponding to an overall energy resolution of 210–220 meV. Acquisition of a single XP spectrum took about 45 s. Upon dissociation from the molecule, bromine chemisorbs on the Ag(111) surface, resulting in a ∼1.9 eV chemical shift to lower binding energies.10,15 This shift is conveniently large so that the two Br 3d doublets of molecule- and surface-bound bromine do not overlap (ESI, Fig. S2†). To extract the debromination traces, first a spline background defined by manually chosen fixed points was subtracted from each spectrum. Then the peaks were fitted with Voigt profiles using the fityk software package (version 1.3.1).57 The indicated experimental error corresponds to the standard fitting error as defined in fityk. The amount of bromine covalently bound to the molecule (Brmolecule) was quantified as the area ratio of the high binding energy (i.e. molecule-bound) Br 3d5/2 peak to the sum of both, that is molecule- and surface bound, Br 3d5/2 peaks. This procedure implicitly assumes negligible desorption of bromine from the surface at the reaction temperature, but accounts for variations in the total photoelectron yield. The debromination versus temperature traces shown in Fig. 1 of the main manuscript were additionally normalized to unity prior to debromination. Note that our specific choice of concentration unit (i.e. unity for the unreacted state) also affects the magnitude of the second-order pre-exponential, but not that of the first-order pre-exponential. We refrain from using physical units in molecules per unit area for the concentration due to the limited accuracy of the surface concentration from our XPS calibration. However, this does not affect the fit or the conclusions, as the magnitude of the second order pre-exponential is not discussed further. In the experimental run with 3BPT and the stepped temperature profile (Fig. 2a), a beam dump occurred after finishing the first isothermal segment with a temperature of 15 °C. To save the sample, we immediately cooled back to low enough temperatures to suppress further debromination and resumed our measurement when the beam was recovered and stabilized. Hence, a small offset in reactant concentration occurred between the 15 °C and 20 °C trace.Details of DFT calculations
Periodic DFT calculations were conducted with the VASP code,58 using the projector-augmented wave method to describe ion–core interactions,59 and with plane waves expanded to a kinetic energy cutoff of 400 eV. The van der Waals density functional60 described exchange–correlation effects, with the version by Hamada denoted as rev-vdWDF2.61 This setting has been shown to describe adsorption of molecules on coinage metals accurately.62The Ag(111) surface was represented by a four layered slab. For the calculations of single atoms on the surface, as well as for dehalogenation of single molecules, we used a p(9 × 9) surface unit cell together with a 4 × 4 k-point sampling, while for the combined dehalogenation and coupling mechanism (Fig. 4 of main manuscript) a p(13 × 11) surface unit cell was used together with a 3 × 3 k-point sampling, ensuring a numerically convergence within 10 meV of all reported values. Transitions states were found using a combination of the Climbing Image Nudge Elastic Band63 (CI-NEB) and dimer methods,64 where CI-NEB was used to provide an initial guess of a transition state to be refined by the dimer method. All structures (local minima as well as transition states) were geometrically optimized until the residual forces on all atoms (except the two bottom layers of the Ag(111) slab which were kept fixed) were smaller than 0.01 eV Å−1.
In the reported results, we state electronic enthalpies at 0 K. For debromination calculations, the relative enthalpy of a state Sx was defined with respect to the intact molecule on the surface (state S0) as:
| ΔH(Sx) = H(Sx) − H(S0) + ΔnBrμBr − ΔnAgμAg, | (1) |
| μBr = H(Br@Ag(111)) − H(Ag(111)), | (2) |
| μAg = H(Ag@Ag(111)) − H(Ag(111)), | (3) |
For the debromination calculations with adatoms both 3BPT and 2BPT change their preferred azimuthal orientation with respect to the surface. For 3BPT this happens both for the 2nd and 3rd debromination step, while for 2BPT it happens as a consequence of the 1st debromination. For evaluating the activation energy, we need to decide whether the rotation shall be performed before or after the respective debromination step. In the presented calculations we decided to enforce the rotation before each debromination. The activation energies for 3BPT and 2BPT in Fig. 3 are given with respect to the more stable (already rotated) configuration prior to debromination, as indicated by the arrows in Fig. S8 (ESI†). We have not checked whether the alternative of performing the rotation after the debromination will result in lower activation energies. Accordingly, the calculated activation energies for the Ag adatom-activated 2nd and 3rd debromination for 3BPT and the 2nd debromination for 2BPT should be viewed as upper limits.
Author contributions
M. L., L. G. and W. M. H. conceived and designed the study. A. G. and M. S. synthesized and purified both 2BPT and 3BPT. L. G., G. G., M. H., M. L. and G. C. prepared the samples and carried out the TP-XPS experiments. A. C. and L. F. supervised the TP-XPS experiments and also implemented the feed-back control that allowed the alternative temperature profiles. L. G. analyzed the data and implemented the grid search algorithm. J. B. and J. R. performed the DFT calculations and analyzed the results. M. L. co-wrote the manuscript, with contributions and approval from all authors.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Financial support from Deutsche Forschungsgemeinschaft grant LA 1842/9-1 is gratefully acknowledged. We acknowledge Elettra Sincrotrone Trieste for providing access to its synchrotron radiation facilities. The research leading to this result has been supported by the project CALIPSOplus under grant agreement 730872 from the EU Framework Programme for Research and Innovation HORIZON 2020. J. B. acknowledges funding from the Swedish Research Council and J. R. funding from the Göran Gustafsson Foundation for Research in Natural Sciences and Medicine. Computational resources were allocated at the National Supercomputer Centre, Sweden, and PDC Center for High Performance Computing, both allocated by SNIC.References
- N. A. A. Zwaneveld, R. Pawlak, M. Abel, D. Catalin, D. Gigmes, D. Bertin and L. Porte, Organized Formation of 2D Extended Covalent Organic Frameworks at Surfaces, J. Am. Chem. Soc., 2008, 130, 6678–6679 CrossRef CAS PubMed.
- J. Björk, F. Hanke and S. Stafstrom, Mechanisms of Halogen-Based Covalent Self-Assembly on Metal Surfaces, J. Am. Chem. Soc., 2013, 135, 5768–5775 CrossRef PubMed.
- J. Eichhorn, D. Nieckarz, O. Ochs, D. Samanta, M. Schmittel, P. J. Szabelski and M. Lackinger, On-Surface Ullmann Coupling: The Influence of Kinetic Reaction Parameters on the Morphology and Quality of Covalent Networks, ACS Nano, 2014, 8, 7880–7889 CrossRef CAS PubMed.
- J. Wintterlin, Scanning Tunneling Microscopy Studies of Catalytic Reactions, Adv. Catal., 2000, 45, 131–206 CAS.
- L. L. Patera, F. Bianchini, C. Africh, C. Dri, G. Soldano, M. M. Mariscal, M. Peressi and G. Comelli, Real-Time Imaging of Adatom-Promoted Graphene Growth on Nickel, Science, 2018, 359, 1243–1246 CrossRef CAS PubMed.
- M. Di Giovannantonio, M. Tomellini, J. Lipton-Duffin, G. Galeotti, M. Elrahimi, A. Cossaro, A. Verdini, N. Kharche, V. Meunier, G. Vasseur, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, Mechanistic Picture and Kinetic Analysis of Surface-Confined Ullmann Polymerization, J. Am. Chem. Soc., 2016, 138, 16696–16702 CrossRef CAS PubMed.
- G. Galeotti, M. Di Giovannantonio, J. Lipton-Duffin, M. Ebrahimi, S. Tebi, A. Verdini, L. Floreano, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, The Role of Halogens in on-Surface Ullmann Polymerization, Faraday Discuss., 2017, 204, 453–469 RSC.
- M. Di Giovannantonio, O. Deniz, J. I. Urgel, R. Widmer, T. Dienel, S. Stolz, C. Sanchez-Sanchez, M. Muntwiler, T. Dumslaff, R. Berger, A. Narita, X. L. Feng, K. Müllen, P. Ruffieux and R. Fasel, On-Surface Growth Dynamics of Graphene Nanoribbons: The Role of Halogen Functionalization, ACS Nano, 2018, 12, 74–81 CrossRef CAS PubMed.
- K. A. Simonov, A. V. Generalov, A. S. Vinogradov, G. I. Svirskiy, A. A. Cafolla, C. McGuinness, T. Taketsugu, A. Lyalin, N. Martensson and A. B. Preobrajenski, Synthesis of Armchair Graphene Nanoribbons from the 10,10′-Dibromo-9,9′-Bianthracene Molecules on Ag(111): The Role of Organometallic Intermediates, Sci. Rep., 2018, 8, 3506 CrossRef CAS PubMed.
- M. Fritton, D. A. Duncan, P. S. Deimel, A. Rastgoo-Lahrood, F. Allegretti, J. V. Barth, W. M. Heckl, J. Björk and M. Lackinger, The Role of Kinetics Versus Thermodynamics in Surface-Assisted Ullmann Coupling on Gold and Silver Surfaces, J. Am. Chem. Soc., 2019, 141, 4824–4832 CrossRef CAS PubMed.
- G. Galeotti, M. Di Giovannantonio, A. Cupo, S. Xing, J. Lipton-Duffin, M. Ebrahimi, G. Vasseur, B. Kierren, Y. Fagot-Revurat, D. Tristant, V. Meunier, D. F. Perepichka, F. Rosei and G. Contini, An Unexpected Organometallic Intermediate in Surface-Confined Ullmann Coupling, Nanoscale, 2019, 11, 7682–7689 RSC.
- S. Stolz, M. Di Giovannantonio, J. I. Urgel, Q. Sun, A. Kinikar, G. B. Barin, M. Bommert, R. Fasel and R. Widmer, Reversible Dehalogenation in on-Surface Aryl-Aryl Coupling, Angew. Chem., Int. Ed., 2020, 59, 14106–14110 CrossRef CAS PubMed.
- D. Dettmann, G. Galeotti, O. MacLean, M. Tomellini, M. Di Giovannantonio, J. Lipton-Duffin, A. Verdini, L. Floreano, Y. Fagot-Revurat, D. F. Perepichka, F. Rosei and G. Contini, Identification of Topotactic Surface-Confined Ullmann-Polymerization, Small, 2021, 17, 2103044 CrossRef CAS PubMed.
- S. Stolz, M. Di Giovannantonio, O. Groning and R. Widmer, On-Surface Synthesis: What Happens Behind the Scenes?, Chimia, 2022, 76, 203–211 CrossRef CAS PubMed.
- J. Eichhorn, T. Strunskus, A. Rastgoo-Lahrood, D. Samanta, M. Schmittel and M. Lackinger, On-Surface Ullmann Polymerization Via Intermediate Organometallic Networks on Ag(111), Chem. Commun., 2014, 50, 7680–7682 RSC.
- M. Lackinger, Surface-Assisted Ullmann Coupling, Chem. Commun., 2017, 53, 7872–7885 RSC.
- M. Di Giovannantonio and G. Contini, Reversibility and Intermediate Steps as Key Tools for the Growth of Extended Ordered Polymers Via on-Surface Synthesis, J. Phys.: Condens. Matter, 2018, 30, 093001 CrossRef PubMed.
- M. Lischka, G. S. Michelitsch, N. Martsinovich, J. Eichhorn, A. Rastgoo-Lahrood, T. Strunskus, R. Breuer, K. Reuter, M. Schmittel and M. Lackinger, Remote Functionalization in Surface-Assisted Dehalogenation by Conformational Mechanics: Organometallic Self-Assembly of 3,3′,5,5′-Tetrabromo-2,2′,4,4′,6,6′-Hexafluorobiphenyl on Ag(111), Nanoscale, 2018, 10, 12035–12044 RSC.
- L. Grossmann, D. A. Duncan, S. P. Jarvis, R. G. Jones, S. De, J. Rosen, M. Schmittel, W. M. Heckl, J. Björk and M. Lackinger, Evolution of Adsorption Heights in the on-Surface Synthesis and Decoupling of Covalent Organic Networks on Ag(111) by Normal-Incidence X-Ray Standing Wave, Nanoscale Horiz., 2021, 7, 51–62 RSC.
- L. Floreano, A. Cossaro, R. Gotter, A. Verdini, G. Bavdek, F. Evangelista, A. Ruocco, A. Morgante and D. Cvetko, Periodic Arrays of Cu-Phthalocyanine Chains on Au(110), J. Phys. Chem. C, 2008, 112, 10794–10802 CrossRef CAS.
- B. Cirera, J. Björk, R. Otero, J. M. Gallego, R. Miranda and D. Ecija, Efficient Lanthanide Catalyzed Debromination and Oligomeric Length-Controlled Ullmann Coupling of Aryl Halides, J. Phys. Chem. C, 2017, 121, 8033–8041 CrossRef CAS.
- J. B. Wang, K. F. Niu, C. J. Xu, H. M. Zhu, H. H. Ding, D. Han, Y. J. Zheng, J. H. Xi, S. F. You, C. Deng, H. P. Lin, J. Rosen, J. F. Zhu, J. Bjoerk, Q. Li and L. F. Chi, Influence of Molecular Configurations on the Desulfonylation Reactions on Metal Surfaces, J. Am. Chem. Soc., 2022, 21596–21605 CrossRef CAS PubMed.
- J. Liu, Q. W. Chen, K. Cai, J. Li, Y. R. Li, X. Yang, Y. J. Zhang, Y. F. Wang, H. Tang, D. H. Zhao and K. Wu, Stepwise on-Surface Dissymmetric Reaction to Construct Binodal Organometallic Network, Nat. Commun., 2019, 10, 2545 CrossRef PubMed.
- R. C. Baetzold and G. A. Somorjai, Pre-Exponential Factors in Surface-Reactions, J. Catal., 1976, 45, 94–105 CrossRef CAS.
- Z. W. Zeng, D. Z. Guo, T. Wang, Q. F. Chen, A. Matej, J. M. Huang, D. Han, Q. Xu, A. D. Zhao, P. Jelínek, D. G. de Oteyza, J. S. Mcewen and J. F. Zhu, Chemisorption-Induced Formation of Biphenylene Dimer on Ag(111), J. Am. Chem. Soc., 2022, 144, 723–732 CrossRef CAS PubMed.
- W. Z. Gao, F. M. Kang, X. Qiu, Z. W. Yi, L. N. Shang, M. X. Liu, X. H. Qiu, Y. Luo and W. Xu, On-Surface Debromination of C6br6: C6 Ring Versus C6 Chain, ACS Nano, 2022, 16, 6578–6584 CrossRef CAS PubMed.
- C. X. Wang, J. L. Chen, C. H. Shu, K. J. Shi and P. N. Liu, On-Surface Synthesis of 2D COFs on Cu(111) Via the Formation of Thermodynamically Stable Organometallic Networks as the Template, Phys. Chem. Chem. Phys., 2019, 21, 13222–13229 RSC.
- M. Bieri, S. Blankenburg, M. Kivala, C. A. Pignedoli, P. Ruffieux, K. Müllen and R. Fasel, Surface-Supported 2D Heterotriangulene Polymers, Chem. Commun., 2011, 47, 10239–10241 RSC.
- A. Rastgoo Lahrood, J. Björk, W. M. Heckl and M. Lackinger, 1,3-Diiodobenzene on Cu(111) – an Exceptional Case of on-Surface Ullmann Coupling, Chem. Commun., 2015, 51, 13301–13304 RSC.
- N. Lin, D. Payer, A. Dmitriev, T. Strunskus, C. Woll, J. V. Barth and K. Kern, Two-Dimensional Adatom Gas Bestowing Dynamic Heterogeneity on Surfaces, Angew. Chem., Int. Ed., 2005, 44, 1488–1491 CrossRef CAS PubMed.
- H. B. Shu, X. S. Chen, X. M. Tao and F. Ding, Edge Structural Stability and Kinetics of Graphene Chemical Vapor Deposition Growth, ACS Nano, 2012, 6, 3243–3250 CrossRef CAS PubMed.
- Y. C. Yang, A. Taranovskyy and O. M. Magnussen, Thiolate-Induced Metal Adatom Trapping at Solid-Liquid Interfaces, Angew. Chem., Int. Ed., 2012, 51, 1966–1969 CrossRef CAS PubMed.
- K. F. Niu, H. P. Lin, J. J. Zhang, H. M. Zhang, Y. Y. Li, Q. Li and L. F. Chi, Mechanistic Investigations of the Au Catalysed C-H Bond Activations in on-Surface Synthesis, Phys. Chem. Chem. Phys., 2018, 20, 15901–15906 RSC.
- J. Björk, C. Sánchez-Sánchez, Q. Chen, C. A. Pignedoli, J. Rosen, P. Ruffieux, X. L. Feng, A. Narita, K. Müllen and R. Fasel, The Role of Metal Adatoms in a Surface-Assisted Cyclodehydrogenation Reaction on a Gold Surface, Angew. Chem., Int. Ed., 2022, 61, e202212354 CrossRef PubMed.
- G. Pawin, K. L. Wong, D. Kim, D. Z. Sun, L. Bartels, S. Hong, T. S. Rahman, R. Carp and M. Marsella, A Surface Coordination Network Based on Substrate-Derived Metal Adatoms with Local Charge Excess, Angew. Chem., Int. Ed., 2008, 47, 8442–8445 CrossRef CAS PubMed.
- H. Walch, J. Dienstmaier, G. Eder, R. Gutzler, S. Schlögl, T. Sirtl, K. Das, M. Schmittel and M. Lackinger, Extended Two-Dimensional Metal-Organic Frameworks Based on Thiolate-Copper Coordination Bonds, J. Am. Chem. Soc., 2011, 133, 7909–7915 CrossRef CAS PubMed.
- T. Sirtl, S. Schlögl, A. Rastgoo-Lahrood, J. Jelic, S. Neogi, M. Schmittel, W. M. Heckl, K. Reuter and M. Lackinger, Control of Intermolecular Bonds by Deposition Rates at Room Temperature: Hydrogen Bonds Versus Metal Coordination in Trinitrile Monolayers, J. Am. Chem. Soc., 2013, 135, 691–695 CrossRef CAS PubMed.
- Q. T. Fan, C. C. Wang, Y. Han, J. F. Zhu, J. Kuttner, G. Hilt and J. M. Gottfried, Surface-Assisted Formation, Assembly, and Dynamics of Planar Organometallic Macrocycles and Zigzag Shaped Polymer Chains with C-Cu-C Bonds, ACS Nano, 2014, 8, 709–718 CrossRef CAS PubMed.
- Z. Feng, S. Velari, A. Cossaro, C. Castellarin-Cudia, A. Verdini, E. Vesselli, C. Dri, M. Peressi, A. De Vita and G. Comelli, Trapping of Charged Gold Adatoms by Dimethyl Sulfoxide on a Gold Surface, ACS Nano, 2015, 9, 8697–8709 CrossRef CAS PubMed.
- Q. T. Fan, L. M. Liu, J. Y. Dai, T. Wang, H. X. Ju, J. Zhao, J. Kuttner, G. Hilt, J. M. Gottfried and J. F. Zhu, Surface Adatom Mediated Structural Transformation in Bromoarene Monolayers: Precursor Phases in Surface Ullmann Reaction, ACS Nano, 2018, 12, 2267–2274 CrossRef CAS PubMed.
- C. J. Judd, F. L. Q. Junqueira, S. L. Haddow, N. R. Champness, D. A. Duncan, R. G. Jones and A. Saywell, Structural Characterisation of Molecular Conformation and the Incorporation of Adatoms in an on-Surface Ullmann-Type Reaction, Commun. Chem., 2020, 3, 166 CrossRef CAS PubMed.
- D. Barton, H. Y. Gao, P. A. Held, A. Studer, H. Fuchs, N. L. Doltsinis and J. Neugebauer, Formation of Organometallic Intermediate States in on-Surface Ullmann Couplings, Chem. – Eur. J., 2017, 23, 6190–6197 CrossRef CAS PubMed.
- C. Zhang, E. Kazuma and Y. Kim, Atomic-Scale Visualization of the Stepwise Metal-Mediated Dehalogenative Cycloaddition Reaction Pathways: Competition between Radicals and Organometallic Intermediates, Angew. Chem., Int. Ed., 2019, 58, 17736–17744 CrossRef CAS PubMed.
- Z. Z. Zhang, D. F. Perepichka and R. Z. Khaliullin, Adatoms in the Surface-Confined Ullmann Coupling of Phenyl Groups, J. Phys. Chem. Lett., 2021, 12, 11061–11069 CrossRef CAS PubMed.
- A. Sarasola, A. Barragan and L. Vitali, Cooperative Action for Molecular Debromination Reaction on Cu(110), J. Am. Chem. Soc., 2018, 140, 15631–15634 CrossRef CAS PubMed.
- M. Giesen, Step and Island Dynamics at Solid/Vacuum and Solid/Liquid Interfaces, Prog. Surf. Sci., 2001, 68, 1–153 CrossRef CAS.
- N. Merino-Dez, A. P. Paz, J. C. Li, M. Vilas-Varela, J. Lawrence, M. S. G. Mohammed, A. Berdonces-Layunta, A. Barragn, J. I. Pascual, J. Lobo-Checa, D. Pea and D. G. de Oteyza, Hierarchy in the Halogen Activation During Surface-Promoted Ullmann Coupling, ChemPhysChem, 2019, 20, 2305–2310 CrossRef PubMed.
- H. Lu, E. Wenlong, L. L. Cai, Z. B. Ma, W. Xu and X. M. Yang, Dissymmetric on-Surface Dehalogenation Reaction Steered by Preformed Self-Assembled Structure, J. Phys. Chem. Lett., 2020, 11, 1867–1872 CrossRef CAS PubMed.
- A. Sanchez-Grande, J. I. Urgel, I. Garcia-Benito, J. Santos, K. Biswas, K. Lauwaet, J. M. Gallego, J. Rosen, R. Miranda, J. Björk, N. Martin and D. Ecija, Surface-Assisted Synthesis of N-Containing Pi-Conjugated Polymers, Adv. Sci., 2022, 9, 2200407 CrossRef CAS PubMed.
- M. T. Buelow and A. J. Gellman, The Transition State for Metal-Catalyzed Dehalogenation: C-I Bond Cleavage on Ag(111), J. Am. Chem. Soc., 2001, 123, 1440–1448 CrossRef CAS.
- S. Blankenburg, J. M. Cai, P. Ruffieux, R. Jaafar, D. Passerone, X. L. Feng, K. Müllen, R. Fasel and C. A. Pignedoli, Intraribbon Heterojunction Formation in Ultranarrow Graphene Nanoribbons, ACS Nano, 2012, 6, 2020–2025 CrossRef CAS PubMed.
- M. Bieri, M. T. Nguyen, O. Groning, J. M. Cai, M. Treier, K. Ait-Mansour, P. Ruffieux, C. A. Pignedoli, D. Passerone, M. Kastler, K. Müllen and R. Fasel, Two-Dimensional Polymer Formation on Surfaces: Insight into the Roles of Precursor Mobility and Reactivity, J. Am. Chem. Soc., 2010, 132, 16669–16676 CrossRef CAS PubMed.
- M. Treier, C. A. Pignedoli, T. Laino, R. Rieger, K. Müllen, D. Passerone and R. Fasel, Surface-Assisted Cyclodehydrogenation Provides a Synthetic Route Towards Easily Processable and Chemically Tailored Nanographenes, Nat. Chem., 2011, 3, 61–67 CrossRef CAS PubMed.
- J. Carracedo-Cosme, C. Romero-Muñiz, P. Pou and R. Pérez, Molecular Identification from AFM Images Using the IUPAC Nomenclature and Attribute Multimodal Recurrent Neural Networks, ACS Appl. Mater. Interfaces, 2023, 15, 22692–22704 CrossRef CAS PubMed.
- J. Bures and I. Larrosa, Organic Reaction Mechanism Classification Using Machine Learning, Nature, 2023, 613, 689–695 CrossRef CAS PubMed.
- G. Cautero, R. Sergo, L. Stebel, P. Lacovig, P. Pittana, M. Predonzani and S. Carrato, A Two-Dimensional Detector for Pump-and-Probe and Time Resolved Experiments, Nucl. Instrum. Methods Phys. Res., Sect. A, 2008, 595, 447–459 CrossRef CAS.
- M. Wojdyr, Fityk: A General-Purpose Peak Fitting Program, J. Appl. Crystallogr., 2010, 43, 1126–1128 CrossRef CAS.
- G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- M. Dion, H. Rydberg, E. Schröder, D. C. Langreth and B. I. Lundqvist, Van Der Waals Density Functional for General Geometries, Phys. Rev. Lett., 2004, 92, 246401 CrossRef CAS PubMed.
- I. Hamada, Van Der Waals Density Functional Made Accurate, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 121103 CrossRef.
- J. Björk and S. Stafstrom, Adsorption of Large Hydrocarbons on Coinage Metals: A Van Der Waals Density Functional Study, ChemPhysChem, 2014, 15, 2851–2858 CrossRef PubMed.
- G. Henkelman, B. P. Uberuaga and H. Jonsson, A Climbing Image Nudged Elastic Band Method for Finding Saddle Points and Minimum Energy Paths, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- J. Kaestner and P. Sherwood, Superlinearly Converging Dimer Method for Transition State Search, J. Chem. Phys., 2008, 128, 014106 CrossRef PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Scanning tunneling microscopy images; TP-XPS data; details of the models; additional grid search results; fitting results; evaluation of second-order kinetics; additional DFT results; synthesis and characterization of 2BPT. See DOI: https://doi.org/10.1039/d4nr00468j |
| This journal is © The Royal Society of Chemistry 2024 |