Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Benchmarking break-junction techniques: electric and thermoelectric characterization of naphthalenophanes†
Juan
Hurtado-Gallego‡
 a,
Sebastiaan
van der Poel‡
b,
Matthias
Blaschke‡
a,
Sebastiaan
van der Poel‡
b,
Matthias
Blaschke‡
 c,
Almudena
Gallego
d,
Chunwei
Hsu
c,
Almudena
Gallego
d,
Chunwei
Hsu
 b,
Rubén
López-Nebreda
a,
Marcel
Mayor
b,
Rubén
López-Nebreda
a,
Marcel
Mayor
 *def,
Fabian
Pauly
*def,
Fabian
Pauly
 *c,
Nicolás
Agraït
*c,
Nicolás
Agraït
 *ag and
Herre S. J.
van der Zant
*ag and
Herre S. J.
van der Zant
 *b
*b
aDepartamento de Física de la Materia Condensada, Universidad Autónoma de Madrid, 28049 Madrid, Spain. E-mail: nicolas.agrait@uam.es
bKavli Institute of Nanoscience, Delft University of Technology, Lorentzweg 1, 2628 CJ Delft, The Netherlands. E-mail: H.S.J.vanderZant@tudelft.nl
cInstitute of Physics and Center for Advanced Analytics and Predictive Sciences, University of Augsburg, 86159 Augsburg, Germany. E-mail: fabian.pauly@uni-a.de
dDepartment of Chemistry, University of Basel, St. Johanns-Ring 19, 4056 Basel, Switzerland. E-mail: marcel.mayor@unibas.ch
eInstitute for Nanotechnology, Karlsruhe Institute of Technology (KIT), P. O. Box 3640, 76021 Karlsruhe, Germany
fLehn Institute of Functional Materials, School of Chemistry, Sun Yat-Sen University, Guangzhou 510274, P. R. China
gCondensed Matter Physics Center (IFIMAC) and Instituto Universitario de Ciencia de Materiales ‘Nicolás Cabrera’ (INC), Universidad Autónoma de Madrid, 28049 Madrid, Spain
First published on 15th April 2024
Abstract
Break-junction techniques provide the possibility to study electric and thermoelectric properties of single-molecule junctions in great detail. These techniques rely on the same principle of controllably breaking metallic contacts in order to create single-molecule junctions, whilst keeping track of the junction's conductance. Here, we compare results from mechanically controllable break junction (MCBJ) and scanning tunneling microscope (STM) methods, while characterizing conductance properties of the same novel mechanosensitive para- and meta-connected naphtalenophane compounds. In addition, thermopower measurements are carried out for both compounds using the STM break junction (STM-BJ) technique. For the conductance experiments, the same data processing using a clustering analysis is performed. We obtain to a large extent similar results for both methods, although values of conductance and stretching lengths for the STM-BJ technique are slightly larger in comparison with the MCBJ. STM-BJ thermopower experiments show similar Seebeck coefficients for both compounds. An increase in the Seebeck coefficient is revealed, whilst the conductance decreases, after which it saturates at around 10 μV K−1. This phenomenon is studied theoretically using a tight binding model. It shows that changes of molecule-electrode electronic couplings combined with shifts of the resonance energies explain the correlated behavior of conductance and Seebeck coefficient.
Introduction
The vision of molecular electronics inspired numerous experimental and theoretical studies in the last decades.1,2 A main theme of the field is to explore both the potential and the limitation of single molecules as functional units of electronic circuits such as diodes, switches or thermoelectric nanodevices.3–6 The in-depth analysis of electric and thermoelectric properties of single-molecule junctions is essential for scientific advances.7 Different experimental approaches have been used for the study of single-molecule junctions, with the most popular one being the break-junction (BJ) technique, comprising mechanically controlled break junction (MCBJ) and scanning tunneling microscopy break junction (STM-BJ) methods. Both approaches have in common that the electrode distance can be varied with sub-Ångström resolution during transport experiments, making them particularly appealing for the analysis of mechanosensitive systems. We have investigated the mechanosensitivity of cyclophanes of various dimensions, ranging from compact [2.2]paracyclophanes8–10 to considerably larger porphyrin cyclophanes,11–13 which both displayed a complex interplay between mechanical stimulation and electric transport properties.Here, we report the optimization of compact naphthalenophane model compounds para-NP (Fig. 1a) and meta-NP (Fig. 1b), together with their electric and thermoelectric transport characterization in terms of the two mentioned break-junction techniques: MCBJ14 (Fig. 1c) and STM-BJ15 (Fig. 1d). Using these two techniques yields insights into the interdependent mechanical and electronic behavior of the molecular junctions. The two naphtalenophanes differ in the substitution pattern of the thiol anchor groups and thus enable to investigate correlations between transport and substitution pattern, as well as differences in the operation modes of both experimental set-ups. To compare the measurement methods, the same data analysis technique was applied to the collected data sets. Additionally, Seebeck coefficient measurements using the STM-BJ technique allow us to study not only the electronic transport but also the thermoelectric transport properties of the compounds. In this report, we focus on the electrical and thermoelectrical properties of the compounds, leaving further details and in particular the mechanosensitive properties of these molecules for a subsequent work.
Experimental
Synthesis
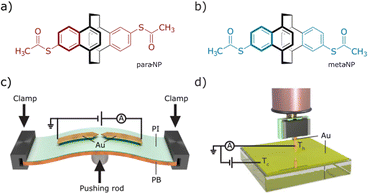
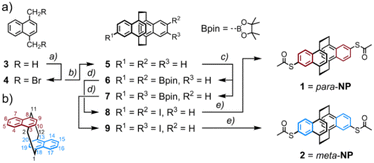
Mechanosensitive [2.2]paracyclophanes (PCPs) that have been investigated so far were decorated with phenyl substituents exposing the anchor group.8,9 Either the torsion angle between both aromatic systems9 or the sp-hybridized carbon atoms of the ethynyl linker8 obstructed the electronic transparency of the structure. With the intention to maximize the electronic coupling of the anchor-group bearing phenyl ring and the mechanosensitive PCP subunit, the naphthalenophane model compounds were designed.The syntheses of the model compounds labeled as para-NP (5,15-bis(acetylthio)-anti-[2.2](1,4)naphthalenophane (see Fig. 1a)) and meta-NP (5,16-bis(acetylthio)-anti-[2.2](1,4)naphthalenophane (see Fig. 1b)) are summarized in Scheme 1a, and the corresponding synthetic protocols and characterization data are provided in the ESI.† The target structures para-NP (1) and meta-NP (2) were obtained by functionalizing the parent structure anti-[2.2](1,4)naphthalenophane (5). Note, the numbering of the positions in the parent structure 5, which is depicted in Scheme 1b. For simplicity we refer to the target structures with trivial names, pointing at the arrangement of the anchor groups in the anti-[2.2](1,4)naphthalenophane core by using para-NP for 1 and meta-NP for 2.
The parent anti-[2.2](1,4)naphthalenophane skeleton was synthesized with a slight modification of a reported protocol.16 Treating commercially available 1,4-dimethylnaphthalene 3 with N-bromosuccinimide (NBS) provided 1,4-bis(bromomethyl)naphthalene 4 in good isolated yields.17 Exposing 4 to samarium(II) diiodide in THF gave the parent anti-[2.2](1,4)naphthalenophane 5 in excellent 89% isolated yield. A C–H activation-based protocol for the borylation of naphthalenes,18 applied to 5, provided the regioisomers 6 and 7, which were isolated as mixture in 77% yield. In several HPLC runs the mixture was separated into the di-borylated regioisomers 6 and 7, which were isolated in 29% and 31% yield, respectively. Hydrolysis of the boronic ester followed by substitution of the boronic acids by iodine gave the regioisomers 8 and 9 in 65% and 77% isolated yields, respectively. With a palladium catalyzed protocol,19 the iodines of 8 and 9 were substituted by acetylsulfanyl groups, giving the target structures 1 (para-NP) and 2 (meta-NP) in 69% and 84% isolated yields, respectively.
The new compounds were fully characterized by 1H- and 13C-NMR spectroscopy and mass spectrometry. The identities of both target structures were corroborated by their analytical data. In addition, single crystals suitable for X-ray analysis were obtained by slow evaporation of the solvent from a solution of 2 (meta-NP) in CHCl3. The solid-state structure, displayed in Fig. 2, confirms the assigned substitution pattern and the identity of 2.
 | ||
| Fig. 2 Solid-state structure of 5,16-bis(acetylthio)-anti-[2.2](1,4)naphthalenophane 2 (meta-NP). Oak Ridge Thermal Ellipsoids (ORTEPs) are plotted on a 50% probability level. Hydrogen atoms and solvent molecules are omitted for clarity. Crystallographic data are deposited under CCDC 2267417.† | ||
Conductance measurements
Single-molecule studies were performed by employing break-junction techniques with two different home-built set-ups: a MCBJ and a STM-BJ, both operating at room temperature under ambient conditions.The MCBJ technique entails the repeated process of breaking and making a thin, initially lithographically defined, gold (Au) nanowire on a layer of polyimide (PI) on top of a flexible phosphorous bronze (PB) substrate (see Fig. 1c). Using a three-point bending mechanism containing two clamps, in which the substrate is placed, and a pushing rod connected to a piezoelectrical element, the gold nanowires can be broken and made repeatedly. Upon breaking the nanowire, two atomically sharp electrodes are formed, and the distance in between them can be manipulated with picometer precision. While bending and ultimately breaking the gold nanowire, we apply a bias voltage (Vbias = 100 mV) across the structure and continuously monitor the current as a function of the electrode separation distance.20 Molecules are deposited by dropcasting a dicholoromethane (DCM) solution of them directly onto the MCBJ sample. The concentration is 5 μM for both molecules. With molecules deposited onto the sample, the breaking of the gold wire results in either the formation of empty (tunneling) junctions or molecular junctions. It is noteworthy that on the gold surface, probably in the presence of traces of water, the acetyl protection groups cleave and covalent sulfur–gold bonds are formed.21 The formation of these rather robust bonds, mounting the molecule at the interface, is of particular importance when mechanical properties of the molecule in the junction are under investigation. After attaining a junction, the electrodes are separated until the current drops below the detection level of the measurement system, i.e., the noise floor. Afterwards, the electrodes are brought into contact again, until a current is measured corresponding to a multiple of G0 in conductance, whereafter the breaking process is repeated. Here, G0 = 2e2/h is the quantum of conductance, where e is the electron charge and h is Planck's constant.
The STM-BJ method creates single-molecule junctions using a homemade STM. The employed STM is a system capable of measuring the tunneling current through a tip and a conductive substrate, both acting as electrodes. Mechanically cut Au wires (0.25 mm diameter, 99.99% purity, Goodfellow) are used as tips. The tip is connected by a tip holder to a piezoelectric tube, which moves the tip vertically and horizontally with a resolution of 10–20 pm. The tip is placed above an Au (111) substrate (11 × 11 mm2, Arrandee; Fig. 1d), where molecules have been deposited by immersion of the pre-annealed substrates for 20 minutes in a 1 mM DCM solution of the respective compound. Subsequent blowing with nitrogen gas eliminates the remaining solvent from the substrate. The tip is approached to the sample until the conductance of the junction is several times G0; hereafter, it is retracted until the current drops below the noise floor of the system. During the retraction process one or several molecules, deposited on the sample, may be trapped between the tip and the sample, forming a molecular junction. The current is recorded during the entire piezo movement, and the breaking process is repeated many times.15
Fig. 3 shows conductance (G) measurements of the para-NP (a and c) and meta-NP (b and d) compounds, using both break-junction methods. All measured traces for both compounds are included in Fig. 3a and b, located in the left (MCBJ) and middle (STM) panels of the two-dimensional conductance vs. displacement histograms. The right panels show the corresponding one-dimensional conductance histograms. The red (MCBJ) and blue (STM) drawn lines represent the main conductance peak with the respective Gaussian distribution fits (dashed lines and colored areas). Differences in the noise saturation level of both compounds emerge from the current amplifiers used for the two measurement techniques, i.e., a logarithmic amplifier for the MCBJ method and a linear one for the STM method. The histograms in Fig. 3c and d are compiled from conductance–distance traces corresponding to molecular junctions of both compounds and methods (with molecular yields between 22–41%), which are selected from the total number of curves using a non-supervised clustering technique based on Matlab's ‘k-means’ function.22,23 Most probable conductance values (Gm) and apparent stretching. Lengths (Ls) are obtained for each compound and method. They are summarized in Table 1 (see the ESI† for further details).
| para-NP | meta-NP | ||||||
|---|---|---|---|---|---|---|---|
| MCBJ | STM-BJ | MCBJ | STM-BJ | ||||
| G m (G0) | L s (nm) | G m (G0) | L s (nm) | G m (G0) | L s (nm) | G m (G0) | L s (nm) |
| (7.9 ± 4.8) × 10−5 | 0.7 ± 0.1 | (1.5 ± 0.9) × 10−4 | 1.2 ± 0.2 | (1.7 ± 0.7) × 10−4 | 0.6 ± 0.1 | (1.6 ± 0.9) × 10−4 | 0.7 ± 0.1 |
| — | S (μV K−1) | — | S (μV K−1) | ||||
| 10.1 ± 0.2 | 10.0 ± 0.2 | ||||||
Similar Gm and Ls values are obtained for the meta-NP compound using the MCBJ and STM-BJ methods, yielding 1.7 × 10−4G0 and 1.6 × 10−4G0 for the conductance and 0.6 nm and 0.7 nm for the stretching lengths, respectively. This indicates good agreement between the two different measurement techniques. For the para-NP compound Gm and Ls values however differ for both measurement methods, yielding mean conductance values of 1.5 × 10−4G0 and 7.9 × 10−5G0, and Ls values of 0.7 nm and 1.2 nm for the MCBJ and STM, respectively. Considering the standard deviations, the conductances of both methods are still compatible with each other. The variations in conductance and stretching length may be due to the different shapes of the electrodes which could lead to varied contact geometries or modified local molecular concentrations in the junctions. Additional MCBJ measurements on para-NP with a higher molecular concentration of 50 μM, presented in the ESI (Fig. S2†), indicate however that changes in the concentration do not play a significant role. The fact that the breaking of the molecular junctions for the MCBJ appears smoother, as can be seen in the individual breaking traces shown in Fig. S4 of the ESI,† suggests that differences in conductance and stretching length obtained in the two setups may also be a consequence of the higher mechanical stability of the MCBJ. Regarding the conductance uncertainties, shown in Table 1, the higher mechanical stability of the MCBJ is indeed reflected in smaller errors for all the high G values.
Applying the same clustering technique to the molecular traces, additional lower conductance plateaus are found in the two-dimensional histograms for all compounds using both experimental methods (see the ESI† for further details). These lower conductance plateaus could indicate the existence of other stable configurations of the molecule inside the junction. Further studies on the origin of the multiple conductance values are required. The current hypothesis is that they arise from different configurations between the molecule and the electrode, which might or might not involve the anchor groups.24
Seebeck coefficient measurements
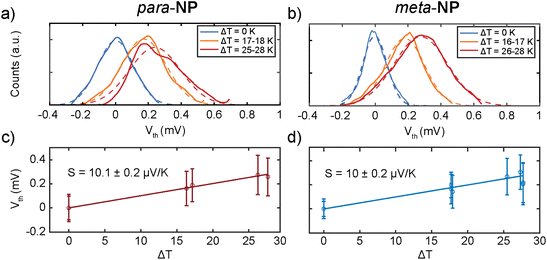
Seebeck coefficient or equivalently thermopower measurements were performed with a temperature difference, ΔT, established between both electrodes using the STM-BJ setup. We heated the tip using a 1 kΩ surface resistor, placed on top of the tip holder, while the substrate remained at room temperature. Voltage ramps of ±10 mV were applied during the formation of molecular junctions, and the resulting current–voltage curves were recorded (as detailed in section S8 of the ESI†). This procedure allows to measure simultaneously the conductance and the thermovoltage, Vth, at different electrode displacements. Here, Vth is defined as the voltage response between the sample and the tip of the STM.Additionally, Vth was measured with different ΔT between 0 and 28 K, as shown in Fig. 4a and b for the para-NP and meta-NP compounds, respectively. Gaussian distributions were fitted to the different ensembles of thermovoltage, yielding for each of them the mean thermovoltage and the standard deviation. As a function of the temperature difference between tip and sample, these are plotted in Fig. 4c and d as empty circles and error bars, respectively. From the thermovoltage of the system (Vth = (S − Slead)ΔT) we extract the Seebeck coefficient of the junction (S), taking into account the thermoelectrical influence of the copper lead (Slead)25 that connects the tip to the rest of the experiment.
The Seebeck coefficient was obtained from the slope of linear fits to the Vthvs. ΔT data points, and the values are displayed in Fig. 4c and d and Table 1. Positive S values indicate hole transport mainly through the HOMO, as reported before for thiol anchoring groups.26,27 Similar S values of around 10 μV K−1 are obtained for both compounds, showing negligible influence of the substitution patterns on the thermoelectric response.
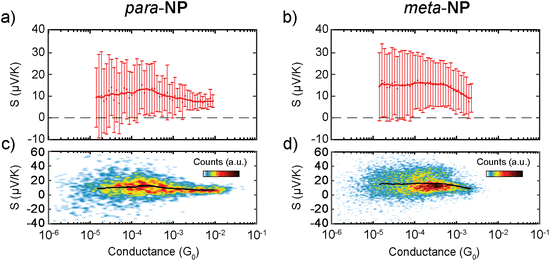
Mean S vs. G traces of each compound are displayed in Fig. 5a and b with their respective standard deviations, and two-dimensional S vs. G histograms of both compounds are shown in Fig. 5c and d, where all the measured Seebeck coefficient points are included. An increase in S as the conductance decreases in the range of 10−2–10−4G0 is followed by a saturation at low G values for both molecules, as shown in Fig. 5a and b. This behavior is also observed in individual S vs. displacement traces. Examples of conductance vs. displacement traces with S measurements along the molecular plateau are shown in Fig. S7,† exhibiting an increase in S followed by a saturation for lower G and larger electrode displacement distances.
Theoretical
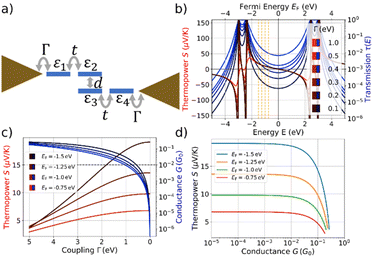
According to Table 1, the overall behavior of para-NP and meta-NP in terms of conductance and thermopower is similar. In this work we do not aim at explaining individual conductance-distance traces or the mechanosensitive response, and an atomistic modeling of the molecular junctions will be presented in a subsequent manuscript. Instead, we study here a generic model that can be applied to both molecules and try, in particular, to understand the general trend of an increasing thermopower for a decreasing conductance, as visible in Fig. 5.For this purpose we explore a four-site tight-binding model for the metal-molecule-metal junctions, where each phenyl ring is represented by a single site. The model is depicted in Fig. 6a. It contains on-site energies, εi, for all four sites i = 1, …4, two distinct hopping parameters, t and d, which describe the couplings inside the naphthalene decks and between them, and a symmetric coupling to left and right electrodes, Γ. The parameters t and d are fitted using DFT calculations28 of the isolated molecule combined with the G0W0 correction.29 Further details can be found in the ESI.†
We model transport properties within the framework of the Landauer-Büttiker scattering theory30 using the wide-band limit approximation.31 From the energy-dependent electronic transmission we compute32–34 the conductance G = G0K0 and the thermopower S = −K1/(eTK0) with 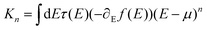 . Here, f(E) is the Fermi function, and μ the electrochemical potential, which we assume to be equal to the Fermi energy, EF. Additional information on the formalism can be found in the ESI.†
. Here, f(E) is the Fermi function, and μ the electrochemical potential, which we assume to be equal to the Fermi energy, EF. Additional information on the formalism can be found in the ESI.†
While stretching a molecular junction, the molecule, trapped between the macroscopic gold metallic electrodes, will adjust its position. During this process the variation of three distinct model parameters seems reasonable: (i) decreasing electronic couplings, Γ, between molecule and electrodes due to a reduced electronic overlap, (ii) variation of the interdeck hopping, d, due to geometric changes inside the molecule, and (iii) shifts of on-site energies, arising from varying charge transfer and screening between molecule and electrodes. We assume that changes in the intradeck hopping terms, t, between both benzene rings of the naphthalene units can be neglected due to strong covalent bonds within both naphthalene subunits.
We explore first, whether the characteristic coupled behavior of increasing S for reduced G can be explained by decreasing molecule-electrode electronic couplings, Γ.35–39 We assume that the electronic couplings to the electrodes are reduced in the stretching process towards the point of rupture, where the molecule is fully erected inside the junction. Fig. 6b displays the transmission and thermopower as a function of energy for different Γ. Note, that for the transmission we plot τ(E) as a function of E (lower x-axis) in Fig. 6b, while S is plotted vs. EF due to the energy integration at finite T = 300 K (upper x-axis). As Γ decreases, broadenings of transmission resonances shrink, resulting in a reduced transmission or conductance at the four indicated Fermi energies inside the HOMO–LUMO gap (vertical dashed orange lines in Fig. 6b). The thermopower reaches its highest absolute values in the vicinity of molecular energy levels for low values of Γ due to the increased slope of τ(E) and decreased value of τ(E).
Thermopower values are shown in Fig. 6c at the marked Fermi energies together with the conductance, both plotted vs. a varying Γ. We find an increase of S from approximately 3.5 μV K−1 for all indicated Fermi energies to 6.8 μV K−1 (EF = −0.75 eV), 9.8 μV K−1 (EF = −1.0 eV) 13.6 μV K−1 (EF = −1.25 eV) and 19.1 μV K−1 (EF = −1.5 eV). Initially, the thermopower rises rather linearly with increasing Γ at the chosen values of EF, but saturates for low values of Γ, while the conductance simultaneously decays to low values.
The correlated behavior can best be perceived by plotting S as a function of G, as shown in Fig. 6d. This panel visualizes the saturated behavior of S in the off-resonant transport regime at low G and the decrease of S for increasing G, when G is plotted on a logarithmic scale.
A comparison of Fig. 6d with the experimental data in Fig. 5 shows a qualitative agreement of a growing S for decreasing G, followed by a subsequent saturation at low G. The experimental mean values for para-NP (meta-NP) start at approximately 5.90 μV K−1 for a conductance of 10−2G0 (4.53 μV K−1 for a conductance of 2 × 10−3G0) and saturate around 15.96 μV K−1 at a conductance of 3 × 10−4G0 (13.33 μV K−1 at a conductance of 3 × 10−4G0), which agrees favorably with the theoretically determined thermopower S especially for Fermi energies EF = −1.25 eV and EF = −1.5 eV. To achieve the variation in S, however, the range of conductance values G in the experimental data is around two orders of magnitude smaller than in the theoretical toy model. Consequently, we assume that the range of reasonable values for electrode-molecule couplings should be restricted to values Γ < 1.0 eV to stay in the experimentally observed window for the conductance, as indicated by the horizontal dashed line in Fig. 6c. For molecule–electrode couplings in the range 0 ≤ Γ ≤ 1.0 eV, unfortunately, the variation of S is significantly smaller than in the experimental data.
We analyze the effect of asymmetric molecule–electrode couplings, which might be realized during the stretching, in the ESI.† Here, a qualitatively similar behavior to the symmetric configuration is observed. The change in Γ (symmetric or asymmetric) qualitatively represents the measured data, yet, for a quantitative agreement, the variation of additional parameters appears to be important.
Similar to previous work on paracyclophanes,8,9 the interdeck coupling, d, between the naphthalene planes is expected to play a crucial role for quantum interference effects, leading to mechanosensitivity. Features from destructive quantum interference in conductance–distance traces occur, however, only at specific stretching distances during the stick-slip motion of the molecules on the gold electrodes.8 Variations in interdeck electronic coupling are thus not expected to be responsible for the global decrease of thermopower S with reduced conductance G, which happens on larger displacement distances than the stick-slip periods. Conductance–distance traces, as presented in the ESI (see especially Fig. S4†), indeed show multiple conductance oscillations, which we assign to destructive quantum interference effects, on a single conductance plateau. A detailed analysis of variations in d in our simple four-site model can be found in the ESI.† If we reduce the coupling, d, between the naphthalene planes (see Fig. 1a and b and Fig. 6a), the thermopower and conductance both decrease, which is in contradiction to the experimental data. Additionally, the relative change in S is rather small for the estimated parameter range. Thus, we conclude that a reduction of the interdeck hopping d is most likely not decisive for the experimentally observed global conductance-thermopower behavior in Fig. 5.
Another degree of freedom are the on-site energies, εi, which can modify the energies, where transmission resonances occur. For sake of simplicity, we restrict ourselves to changes which uniformly shift all resonance energies to orthogonalize the effect to the preceding discussion. Within our modelling, uniform shifts of on-site energies can be translated to changes in the Fermi energy, allowing the effects to be estimated from Fig. 6c and d. We restrict values of the coupling strength to Γ < 1.0 eV to operate in the experimentally realized window of conductance values below 10−2G0. A quantitative agreement of theoretically computed thermopower and conductance with the experimental data is achieved, if the Fermi energy is gradually shifted from EF = −0.75 eV to EF = −1.5 eV, while Γ drops simultaneously. Since EF = 0 means that the Fermi energy is located in the middle of the HOMO–LUMO gap, this corresponds to a decreasing separation of the HOMO level from the electrode Fermi energy during the stretching. To obtain the saturation in the thermopower S for low conductance values, the shift of the molecular orbital energies must also saturate during the stretching. Although the precise mechanism cannot be elucidated due to the simplicity of our model, the thermopower is very sensitive to the alignment of molecular energy levels to the electrodes’ Fermi energy. Such molecular energy level shifts and their influence on the thermopower have been reported in the literature for various molecules and models.35–37,40,41
Overall, the four-site tight-binding model offers a framework for elucidating the significant mechanisms, leading to the global trends of S and G in the experimental results. Based on our analysis, a reduction in Γ during the stretching combined with shifts in orbital energies that bring the HOMO level closer to the Fermi energy are responsible for the observed behavior.
Conclusions
para- and meta-connected naphthalenophane compounds were electrically characterized using two different break-junction techniques, i.e., MCBJ and STM-BJ. The molecules were designed to be more rigid and to have higher electrical conductance than previously measured paracyclophane compounds.8,9 Conductance measurements with both techniques show a good agreement for the para- and meta-connected naphthalenophanes, which exhibit strong similarities in their electrical conductance. The higher mechanical stability of the MCBJ leads to smaller conductance uncertainties for the two compounds. The usage of different current amplifiers is not directly reflected in the conductance values of both molecules but just in the noise saturation level of the measurements. As anticipated, the conductance is higher than that of the previously studied paracyclophane derivatives.8,9 MCBJ has the advantage of a better mechanical stability for the conductance measurements. On the other hand, the higher versatility of the STM makes it easier to implement thermopower measurements. We find similar thermopower values for para- and meta-connected naphthalenophanes of around 10 μV K−1 and a global increase of the thermopower up to around 15 μV K−1 as the conductance decreases to values down to 10−4G0. A tight-binding model suggests that this is related to a decrease of the electronic couplings of the molecule to the electrodes combined with shifts of the molecular orbital energies to become more resonant.Author Contributions
J. H.-G., R. L.-N., and N. A. contributed to the STM experimental part. S. v. d. P., C. H., and H. S. J. v. d. Z. contributed to the MCBJ experimental measurements. M. B. and F. P. performed the theoretical modelling. A. G. and M. M. synthesized the compounds.Conflicts of interest
There are no conflicts to declare.Acknowledgements
J. H.-G., A. G., R. L.-N., M. M., N. A., and H. S. J. v. d. Z. acknowledge funding from the EC H2020 FET Open project grant agreement number 767187 “QuIET”. M. M. acknowledges support by the Swiss National Science Foundation (SNF Grant Number 200020-207744). F. P. is supported through the Collaborative Research Center 1585, Project C02 of the German Research Foundation (Grant Number 492723217). N. A. acknowledges funding from the Comunidad de Madrid NANOMAGCOST-CM (P2018/NMT-4321) and from the Spanish Ministry of Science and Innovation through grants PID2020-114880GB-I00 and the “María de Maeztu” Programme for Units of Excellence in R&D (CEX2018-000805-M). C. H. and H. S. J. v. d. Z. acknowledge support from the Dutch funding agency, NWO.References
- M. Ratner, Nat. Nanotechnol., 2013, 8, 378–381 CrossRef CAS PubMed.
- J. R. Heath, Annu. Rev. Mater. Res., 2009, 39, 1–23 CrossRef CAS.
- A. Harzheim, Mater. Sci. Technol., 2018, 34, 1275–1286 CrossRef CAS.
- J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022 RSC.
- B. Capozzi, J. Xia, O. Adak, E. J. Dell, Z. F. Liu, J. C. Taylor, J. B. Neaton, L. M. Campos and L. Venkataraman, Nat. Nanotechnol., 2015, 10, 522–527 CrossRef CAS.
- M. L. Perrin, E. Galán, R. Eelkema, J. M. Thijssen, F. Grozema and H. S. J. van der Zant, Nanoscale, 2016, 8, 8919–8923 RSC.
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306 RSC.
- D. Stefani, K. J. Weiland, M. Skripnik, C. Hsu, M. L. Perrin, M. Mayor, F. Pauly and H. S. J. van der Zant, Nano Lett., 2018, 18, 5981–5988 CrossRef CAS PubMed.
- K. Reznikova, C. Hsu, W. M. Schosser, A. Gallego, K. Beltako, F. Pauly, H. S. J. van der Zant and M. Mayor, J. Am. Chem. Soc., 2021, 143, 13944–13951 CrossRef CAS.
- M. Blaschke and F. Pauly, J. Chem. Phys., 2023, 159, 024126 CrossRef CAS PubMed.
- P. Zwick, C. Hsu, M. El Abbassi, O. Fuhr, D. Fenske, D. Dulić, H. S. J. van der Zant and M. Mayor, J. Org. Chem., 2020, 85, 15072–15081 CrossRef CAS PubMed.
- W. M. Schosser, C. Hsu, P. Zwick, K. Beltako, D. Dulić, M. Mayor, H. S. J. van der Zant and F. Pauly, Nanoscale, 2022, 14, 984–992 RSC.
- C. Hsu, W. M. Schosser, P. Zwick, D. Dulić, M. Mayor, F. Pauly and H. S. J. van der Zant, Chem. Sci., 2022, 13, 8017–8024 RSC.
- M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 251–254 CrossRef.
- C. Evangeli, K. Gillemot, E. Leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141–2145 CrossRef CAS.
- S. Takahashi and N. Mori, J. Chem. Soc., Perkin Trans. 1, 1991, 1, 2029–2033 RSC.
- V. M. Cangelosi, A. C. Sather, L. N. Zakharov, O. B. Berryman and D. W. Johnson, Inorg. Chem., 2007, 46, 9278–9284 CrossRef CAS PubMed.
- T. Yamamoto, A. Ishibashi, M. Koyanagi, H. Ihara, N. Eichenauer and M. Suginome, Bull. Chem. Soc. Jpn., 2017, 90, 604–606 CrossRef CAS.
- M. Kim, S. Yu, J. G. Kim and S. Lee, Org. Chem. Front., 2018, 5, 2447–2452 RSC.
- C. A. Martin, R. H. M. Smit, R. van Egmond, H. S. J. van der Zant and J. M. van Ruitenbeek, Rev. Sci. Instrum., 2011, 82, 053907 CrossRef.
- E. Leary, A. La Rosa, M. T. González, G. Rubio-Bollinger, N. Agraït and N. Martín, Chem. Soc. Rev., 2015, 44, 920–942 RSC.
- D. Cabosart, M. El Abbassi, D. Stefani, R. Frisenda, M. Calame, H. S. J. van der Zant and M. L. Perrin, Appl. Phys. Lett., 2019, 114, 143102 CrossRef.
- L. A. Zotti, B. Bednarz, J. Hurtado-Gallego, D. Cabosart, G. Rubio-Bollinger, N. Agraït and H. S. J. van der Zant, Biomolecules, 2019, 9, 580 CrossRef CAS PubMed.
- S. T. Schneebeli, M. Kamenetska, Z. Cheng, R. Skouta, R. A. Friesner, L. Venkataraman and R. Breslow, J. Am. Chem. Soc., 2011, 133, 2136–2139 CrossRef CAS PubMed.
- N. Cusack and P. Kendall, Proc. Phys. Soc., 1956, 72, 898 CrossRef.
- L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306 RSC.
- A. Ismael, X. Wang, T. L. R. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Chem. Sci., 2020, 11, 6836–6841 RSC.
- Y. J. Franzke, C. Holzer, J. H. Andersen, T. Begušić, F. Bruder, S. Coriani, F. Della Sala, E. Fabiano, D. A. Fedotov, S. Fürst, S. Gillhuber, R. Grotjahn, M. Kaupp, M. Kehry, M. Krstić, F. Mack, S. Majumdar, B. D. Nguyen, S. M. Parker, F. Pauly, A. Pausch, E. Perlt, G. S. Phun, A. Rajabi, D. Rappoport, B. Samal, T. Schrader, M. Sharma, E. Tapavicza, R. S. Treß, V. Voora, A. Wodyński, J. M. Yu, B. Zerulla, F. Furche, C. Hättig, M. Sierka, D. P. Tew and F. Weigend, J. Chem. Theory Comput., 2023, 19, 6859–6890 CrossRef CAS PubMed.
- M. J. van Setten, F. Weigend and F. Evers, J. Chem. Theory Comput., 2013, 9, 232–246 CrossRef CAS PubMed.
- J. C. Cuevas and E. Scheer, Molecular Electronics: An Introduction to Theory and Experiment, World Scientific Series in Nanoscience and Nanotechnology, 2nd edn, 2017 Search PubMed.
- C. J. O. Verzijl, J. S. Seldenthuis and J. M. Thijssen, J. Chem. Phys., 2013, 138, 094102 CrossRef CAS PubMed.
- U. Sivan and Y. Imry, Phys. Rev. B: Condens. Matter Mater. Phys., 1986, 33, 551–559 CrossRef CAS PubMed.
- K. Esfarjani, M. Zebarjadi and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085406 CrossRef.
- K. H. Müller, J. Chem. Phys., 2008, 129, 044708 CrossRef PubMed.
- S. Park, J. Jang and H. J. Yoon, J. Phys. Chem. C, 2021, 125, 20035–20047 CrossRef CAS.
- A. Torres, R. B. Pontes, A. J. R. da Silva and A. Fazzio, Phys. Chem. Chem. Phys., 2015, 17, 5386–5392 RSC.
- S. Fujii, E. Montes, H. Cho, Y. Yue, M. Koike, T. Nishino, H. Vázquez and M. Kiguchi, Adv. Electron. Mater., 2022, 8, 2200700 CrossRef CAS.
- S. Kobayashi, S. Kaneko, S. Fujii, T. Nishino, K. Tsukagoshi and M. Kiguchi, Phys. Chem. Chem. Phys., 2019, 21, 16910–16913 RSC.
- J. Vacek, J. V. Chocholoušová, I. G. Stará, I. Starý and Y. Dubi, Nanoscale, 2015, 7, 8793–8802 RSC.
- M. A. Popp, A. Erpenbeck and H. B. Weber, Sci. Rep., 2021, 11, 2031 CrossRef CAS PubMed.
- C. Bruot, J. Hihath and N. Tao, Nat. Nanotechnol., 2012, 7, 35–40 CrossRef CAS PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available. CCDC 2267417. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d4nr00704b |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |

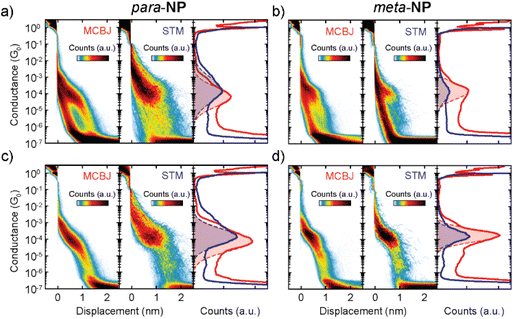
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 and 2200 traces, respectively. The right panel shows the corresponding one-dimensional conductance histograms of MCBJ (red) and STM (blue) measurements. Dashed lines are Gaussian fits of the respective peaks for STM and MCBJ. (b) Same as (a) but for the
000 and 2200 traces, respectively. The right panel shows the corresponding one-dimensional conductance histograms of MCBJ (red) and STM (blue) measurements. Dashed lines are Gaussian fits of the respective peaks for STM and MCBJ. (b) Same as (a) but for the