Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Transport, trapping, triplet fusion: thermally retarded exciton migration in tetracene single crystals†
Dominik
Muth
 a,
Sebastian
Anhäuser
a,
Sebastian
Anhäuser
 b,
Daniel
Bischof
b,
Daniel
Bischof
 b,
Anton
Krüger
b,
Anton
Krüger
 a,
Gregor
Witte
a,
Gregor
Witte
 *b and
Marina
Gerhard
*b and
Marina
Gerhard
 *a
*a
aDepartment of Physics and Material Sciences Center, Semiconductor Spectroscopy Group, Philipps-Universität Marburg, Renthof 7a, 35032 Marburg, Germany. E-mail: marina.gerhard@physik.uni-marburg.de
bDepartment of Physics and Material Sciences Center, Molecular Solids Group, Philipps-Universität Marburg, Renthof 7, 35032 Marburg, Germany. E-mail: gregor.witte@physik.uni-marburg.de
First published on 25th June 2024
Abstract
Efficient exciton migration is crucial for optoelectronic organic devices. While the transport of triplet excitons is generally slow compared to singlet excitons, triplet exciton migration in certain molecular semiconductors with endothermic singlet fission appears to be enhanced by a time-delayed regeneration of the more mobile singlet species via triplet fusion. This combined transport mechanism could be exploited for devices, but the interplay between singlet fission and triplet fusion, as well as the role of trap states is not yet well understood. Here, we study the spatiotemporal exciton dynamics in the singlet fission material tetracene by means of time resolved photoluminescence micro-spectroscopy on crystalline samples of different quality. Varying the temperature allows us to modify the dynamic equilibrium between singlet, triplet and trapped excitons. Supported by a kinetic model, we find that thermally activated dissociation of triplet pairs into free triplet excitons can account for an increase of the diffusion length below room temperature. Moreover, we demonstrate that trapping competes efficiently with exciton migration.
Introduction
Organic semiconductors (OSCs) offer a versatile and abundant platform for the development of optoelectronic devices with tailored properties.1–5 Contrasting with the majority of their inorganic counterparts, the primary photoexcitations in molecular systems are Frenkel excitons with binding energies on the order of several hundreds of millielectronvolts.6–9 This excitonic character imposes special guidelines for the design of organic photovoltaic (OPV) devices, because excitons must reach a site where they separate into free charges or where their energy can be harvested before recombining. Recombination losses can be minimized by manufacturing intimately mixed donor–acceptor systems, so-called bulk heterojunctions, with domain sizes on the order of the exciton diffusion length (typically <10 nm).10,11 Increasing the exciton diffusion length would allow the use of active layers with larger domains, which would be beneficial for the transport of separated charges.To boost the performance of future generation solar cells, it is also considered to exploit the singlet fission (SF) mechanism, which is a spin-allowed process that converts a singlet exciton efficiently into two triplet excitons with half or less than half the energy of the singlet state.12 SF materials could serve as add-layers for solar cells in order to harvest higher-energy photons more efficiently,13–15 provided that the created triplet excitons migrate efficiently into the underlying material. In any of these scenarios, understanding and controlling the excitonic transport properties is crucial for the targeted development of OSC devices.
Beside some exceptions where coherent transport was reported,16,17 the migration of excitons in most OSCs is dominated by incoherent processes based on Förster and Dexter mechanisms.11 While the Förster process is more efficient through long-range dipole interactions, it is spin-forbidden for triplet excitons, which consequently propagate much slower compared to the singlet species.18 Recently, however, for some SF materials, a combined transport mechanism was reported, which is based on time-delayed re-generation of mobile singlet excitons via fusion of two triplets. Since triplet migration is in this case assisted by singlets, this transport mechanism is often termed “cooperative” exciton transport and it is found to contribute significantly to the diffusion length of the photo-generated exciton population in some SF materials.18–23 Presently, however, it is not sufficiently understood how this combined mechanism can be manipulated and how it is affected by extrinsic material parameters such as defects or disorder, which could lead to exciton trapping, as illustrated in Scheme 1.
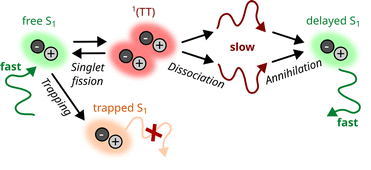 | ||
| Scheme 1 Combined transport mechanism20 based on the interconversion between singlet excitons (S1) and the correlated triplet pair state 1(TT), which may dissociate into free triplets. Beside this mechanism, we also consider the possibility of exciton trapping. | ||
In the present study, we focus on the model system tetracene (TET), a molecular semiconductor with a herringbone packing motif,24 from which van der Waals bound crystals of high quality can be produced.25 The exciton energetics of TET are well understood9,26–29 and also its kinetics have been thoroughly characterized by means of time-resolved photoluminescence (TRPL) and transient absorption (TA) spectroscopy, yielding SF time constants on the order of 100 ps.30–36 Moreover, there is a general consensus about the absence of a large exothermic driving force for SF, giving rise to a dynamic equilibrium between the singlet and the intermediate spin-correlated triplet pair 1(TT) state.22,31,32 However, literature reports differ regarding the actual role of temperature in driving SF and dissociation of the 1(TT) state. TRPL and TA studies suggest that the SF rate is independent of temperature in polycrystalline thin films,30,32,33,35 potentially because defects or structural imperfections accelerate the process. On the other hand, for TET single crystals, TRPL and magnetic field dependent studies indicate that the yield of triplets is lower at low temperatures,35,37,38 which implies that at least for crystalline samples temperature does play a decisive role in shifting the dynamic equilibrium either towards the singlet or the free triplet population. The underlying interplay between singlet fission, triplet fusion and triplet dissociation, the impact of material imperfections and implications for the exciton transport thus need further clarification.
In this work, varying the temperature allows us to modify the underlying exciton kinetics in TET, giving either more weight to the singlet or the triplet population. We study crystals with intentionally varied quality in order to explore the influence of trap states on the transport of excitons. The strongest effect would be expected when comparing an amorphous film with a single crystal. However, as has been shown in previous work,39 amorphous TET films begin to recrystallize at low temperatures, so that they exhibit undefined structural properties in the course of temperature-dependent measurements. Therefore, we compare two TET single crystals of the bulk crystal structure but of different quality. To study the ultrafast photoexcitation dynamics in excitonic materials on a micrometer scale, spatiotemporal techniques such as transient absorption or transient luminescence microscopy have proven powerful methods to extract information about the evolution of an exciton population both spatially and temporally.19,23,40 Here, we utilize a streak camera to probe the spatiotemporal exciton dynamics based on the strong luminescence of TET and the same instrumentation is employed for complementary studies of the spectrally resolved dynamics. We find that in pristine TET crystals with low defect density, exciton transport is enhanced at lower temperatures, which is corroborated by a kinetic model where SF is mediated by the transient 1(TT) state. In contrast, for a defect-rich sample, no increase in the diffusion length is observed at low temperatures, which we attribute to exciton trapping competing efficiently with the dynamic equilibrium between SF and triplet fusion.
Methods
We investigated TET single crystals of different quality, which were prepared from purified tetracene powder (Sigma Aldrich, purity 99.99%) and will be referred to as pristine (“PSC”) and defect rich single crystal (“DSC”) in the following. PSCs were grown by cooling down a hot, saturated toluene solution, similar to the procedure described in ref. 9, yielding large crystals. To remove small crystallites that are formed on the surface upon vaporization of the remaining solvent and to obtain crystals of homogeneous thickness, both surfaces of the PSC crystals were exfoliated using adhesive Viton tape. The DSCs were grown via liquid mediated organic molecular beam deposition (OMBD), where TET was continuously evaporated from a Knudsen cell into a supersaturated solution of vacuum stable silicone oil film (VWR GmbH, 47 V 350 Rhodorsil) that had been spin-coated onto a quartz glass support.41 Corresponding specular X-ray diffraction measurements confirm that both preparation methods yield (001)-oriented TET crystals of the known bulk structure,24 but the DSC crystals show a lower intensity of the higher order (00n) reflections, which indicates a lower crystalline order (see ESI†).Optical micrographs of the samples were obtained with a Nikon Eclipse LV-FMA microscope. Additionally, PL micrographs were acquired by illuminating the sample with UV-light using a SOLA light source (Lumencor) in combination with a fluorescence filter yielding an excitation wavelength of λexc = 360–380 nm. The microscope is further equipped with an OceanOptics QE Pro optical spectrometer (resolution 1.7 nm) via a beam splitter that allows the acquisition of microspot absorption and PL spectra.
To enable temperature dependent PL measurements, the TET crystals were sandwiched between two sheets of quartz glass, which were in turn glued onto the sample holder of the cryostat via rubber cement (Fixogum, Marabu GmbH). The samples were then placed inside a microscopy cryostat (CryoVac), which was evacuated to around 10−5 mbar. The temperature of the samples was adjusted via a temperature controller (CryoVac), which regulates the power of a heating element inside the cryostat and the throughput of a coolant, liquid nitrogen, in the range of 80–290 K. By recording PL spectra in reflection geometry, possible influences from a luminescent substrate can be minimized. For the spatially and temporally resolved experiments we employed a pulsed titanium sapphire laser (Spectra Physics Tsunami) with a repetition rate of 80 MHz and a pulse duration of 100 fs. The wavelength of the laser was tuned to 920 nm and frequency doubled via a Beta Barium Borate (BBO) crystal (TOPAG Lasertechnik GmbH) to 460 nm. The laser beam with an average power of 25 μW was focused onto the sample via a 50× apochromatic microscope objective with a working distance of 20.5 mm, which at the same time served to image the PL profile. Due to the long working distance and the rather thin (1 mm) cryostat window, the impact on image quality was manageable and we estimate a spatial resolution of 1.1 μm (see ESI† for details). The spatial resolution is not as high as in some studies employing a similar methodology19,20,42 and could certainly have been improved with an objective with higher numerical aperture and adjustable glass thickness correction. However, we do not expect this impairment to affect the experimental results, because the effect of the point spread function is cancelled out, when the area of the (Gaussian) PL profile at time zero is subtracted from the PL profile at later times.40 A 490 nm dichroic long pass filter separated the PL from the excitation path and any remaining laser radiation was absorbed by a 495 nm long pass filter. The PL of the excited samples was spectrally resolved by a spectrometer (Bruker, model no. 250-30) and recorded with a UV/VIS streak camera setup (Hamamatsu C6860), with a time resolution of about 40 ps for the employed 2 ns time window.
To present the spectrally resolved data of all PL measurements on an energy scale, the measured intensities were converted using a Jacobian transformation.43 For the exciton diffusion measurements, the PL spot was spatially imaged onto the horizontal entrance slit of the streak camera and the spot size was studied as function of time. The spatial axis of the diffusion measurements was calibrated with a resolution target (Thorlabs, see ESI† for details).
Results and discussion
Free and trapped exciton emission
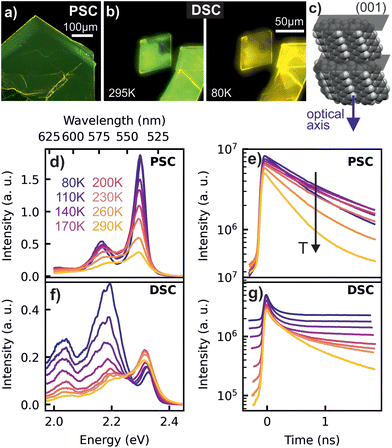
As depicted in Fig. 1a and b, PL micrographs of the differently prepared TET crystals exhibit a green colour at room temperature. Interestingly, the PL of the DSC turns to yellow at low temperatures, which is reversible upon heating, while the PSC does not change its colour. The temperature dependent PL spectra and corresponding transients, presented in Fig. 1d–g provide detailed insights into this behaviour. The PSC reveals the highest energy emission maximum at 2.30 eV (538 nm) and a lower energy replica at 2.17 eV (572 nm). Based on the small Stokes shift between the UV/VIS absorption and PL spectra (see ESI†), the high energy peak is attributed to the zero-phonon line of the free singlet exciton emission. Since the energetic distance to the next lower energy emission (ΔE ≈ 140 meV) is similar to that of vibrational progressions obtained in the absorption spectra, we assign this emission line to a vibronic sideband. The intensity of the zero phonon line emission is significantly enhanced at lower temperatures (cf.Fig. 1d), which is often attributed to the phenomenon of superradiance,8,26,28i.e. an increase of the radiative decay rate connected with an increase of the coherence volume, as disturbing vibrational modes diminish at low temperatures. Considering that singlet fission in TET is a slightly endothermic process,44 the overall increase in PL intensity with decreasing temperature can also be attributed to a decreasing fission and subsequent triplet dissociation. This is consistent with a faster PL decay with increasing temperature seen in the corresponding transients (cf.Fig. 1e).The DSC samples exhibit also a dominating emission around 2.3 eV at room temperature, together with two weaker satellites at lower energies. A closer inspection shows that the zero-phonon emission line in the DSC appears at slightly higher energy than in the PSC (2.33 eV vs. 2.30 eV). This effect has been identified previously as a sample thickness effect,9 which is caused by emission and re-absorption of the exciton lines (see ESI†) and leads to the observed difference in emission energies, since the DSCs are significantly thinner (<1 μm) than the PSCs (>70 μm). In contrast to PSCs the DSCs reveal an increasing intensity of the satellite emission with decreasing temperature, so that the emission of the DSC sample at lower temperatures (cf.Fig. 1f and g) is dominated by a signature peaking at around 2.19 eV (565 nm), giving rise to the yellow color impression at low temperature. As depicted in Fig. 1g, the corresponding transients reveal a largely increased lifetime of the excited states below room temperature. With decreasing temperature, the contribution of the red-shifted 565 nm feature, which we will in the following call ‘yellow emission band’, increases drastically and along with this, the PL dynamics at low temperatures becomes multiexponential.
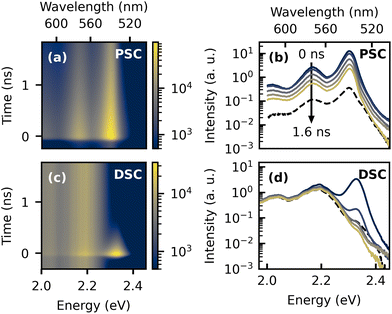
The presence of two distinct emitting species in the TET samples is further highlighted in the two-dimensional plots of the low temperature TRPL data and the time-dependent spectra in Fig. 2. The dashed lines in Fig. 2b and d represent delayed PL spectra extracted from the time range before t = 0, which originate from accumulation effects, because the PL signal does not fully decay between two laser pulses with a time spacing of 12.5 ns. In the highly ordered PSC sample, the spectral shape of the delayed PL is almost identical to the prompt PL, whereas in the DSC sample, the yellow emission band clearly dominates the emission at later times. This is further illustrated by the PL transients extracted from different emission energies, which are shown in the ESI.†
In order to motivate our picture of the underlying exciton species and their dynamics, it appears instructive at this point to give a brief summary about the ongoing discussion about the origin of the yellow emission band. The emission energy observed here agrees well with earlier reports, where the signature was tentatively assigned to a trap state,32,39 potentially originating from excimers31,45,46 or structural defects, which could be related to a low temperature phase transition.30 On the other hand, it was also suggested that the correlated triplet pair state itself could give rise to the red-shifted emission.33 This hypothesis was later supported by a study which combined TRPL with transient absorption (TA) spectroscopy for a broader series of acene derivatives.47 The authors observed red-shifted emission with respect to the free singlet exciton emission with similar properties and found that the emission energy was correlated with the triplet state energies of the studied materials. Moreover, sequential kinetics were observed in TA, with an intermediate species demonstrating very similar dynamics as the red-shifted PL, suggesting the presence of a partially emissive 1(TT) state, which could originate from a Herzberg–Teller coupling mechanism. On the other hand, the low temperature TA signatures of TET were difficult to interpret due to the poor signal-to-noise ratio.47 We note that based on a triplet state energy of 1.25 eV,44 the 1(TT) state of TET should occur at higher energies. Moreover, the model of an emissive 1(TT) state in TET was recently challenged by the observation of delayed luminescence of the original singlet species arising from triplet–triplet annihilation (TTA) after the yellow emission band had decayed, which is incompatible with a sequential model in which an emissive 1(TT) state mediates triplet formation.38
This latter view is consistent with our observation of a strong dependence of the yellow emission band on the preparation method, which actually suggests that the signature is not intrinsic. Notably, a strong variation of the relative intensity of the yellow emission band is also observed among various literature reports.30,32,38,46,48 In addition, our observation of delayed PL from the original singlet species (cf.Fig. 2c), which is likely to originate from TTA, corroborates the perception that the majority of triplet states is not generated via the states, which are giving rise to the yellow emission band. It is also noteworthy that in our study the yellow emission band emerged in freshly prepared crystals at temperatures well above the broad temperature range which was reported for phase transitions (130–200 K),49,50 suggesting that its emergence is not connected with these.
Based on the foregoing discussion, we rather consider structural defects or impurities as the most likely origin for the yellow emission band. While the same starting material of high purity was used for both crystal preparations, the liquid assisted growth in silicone oil appears to be more critical for photo-oxidation, as the oil was also exposed to air and daylight with UV content. Thus, it is conceivable that photo-oxidation could give rise to the formation of keto-defects (i.e. quinones),51,52 especially since the employed silicone oil has a high viscosity, potentially leading to anisotropic crystal growth and the preferred formation of structural imperfections that are susceptible to oxidation.41 In order to narrow down possible reasons for the yellow emission of the DSC sample and to identify the actual cause, we additionally examined the low temperature PL signature of amorphous TET, TET-quinone and quinone doped TET films (see ESI†). These results show that while amorphous TET films reveal a rather similar PL signature as the PSC samples with a dominating green emission, the quinone-doped TET film exhibits a strong suppression of the green emission together with a dominating yellow emission. Therefore, we attribute the yellow emission band to trap states caused by quinone impurities formed upon light exposure. This is further corroborated by the fact that samples exposed several months to air showed yellow PL even at room temperature.
Exciton transport
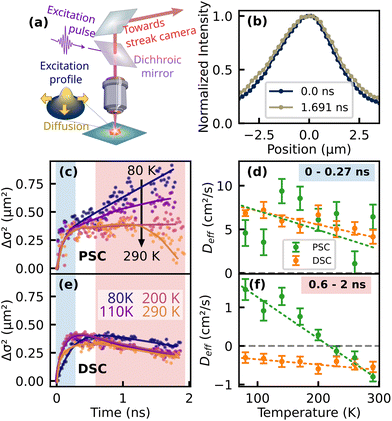
Next, we investigate the exciton migration in both samples by analyzing the spatiotemporal evolution of the luminescence profile. A schematic representation of the technique together with exemplary data of the PL profile of the PSC sample at different times after the excitation pulse is presented in Fig. 3a and b. The spectrally integrated PL profile is imaged onto the entrance slit of the streak camera, which captures a horizontal cross section of the luminescence spot. For further analysis, the spatial PL profile was fitted by a one-dimensional Gaussian function at each time step and the variance was extracted from the fitting parameters. The change in variance, also known as mean squared displacement (MSD) Δσ2(t) = σ2(t) − σ2(0) is presented in Fig. 3c and e for the PSC and the DSC sample, respectively. In general, transport of the photoexcited species can occur through coherent and incoherent processes, with Δσ2 displaying either subdiffusive, normal or ballistic behavior.40 Normal diffusion would be characterized by a linear slope, i.e.| Δσ2(t) = 2Dt | (1) |
Notably, for the PSC sample at temperatures above 200 K, Deff becomes negative at later times (Fig. 3c and f). Such an effective negative diffusion coefficient was reported earlier for TET by Berghuis et al. on a comparable time scale.22 The authors attributed the initial increase and subsequent shrinkage of the luminescence profile to a concerted effect of singlet–singlet annihilation (SSA) causing the initial broadening and delayed luminescence emerging from triplet–triplet annihilation (TTA). The latter originates from triplets with poor mobility and the fusion back to emissive singlet excitons, which is most efficient in the center of the excitation profile with the largest triplet concentration, thus the overall profile of the delayed luminescence was found to be even narrower than the initial excitation profile. With decreasing temperature, Deff extracted from the longer time range increases and changes its sign from negative to positive. This observation is consistent with the hypothesis of thermally activated triplet formation in TET,35,37,38,52 since a higher probability to populate the mobile singlet state at low temperatures should also increase the diffusion coefficient.
Another consequence of the lower triplet yield is the absence of negative effective diffusion in the investigated time window. It is noteworthy that we also carried out the presented experiments for thin polycrystalline films of high quality which were deposited via OMBD (see ESI†) and qualitatively show the same behavior as the PSC, i.e. effective negative diffusion at room temperature and the absence of the yellow emission band at lower temperatures. Interestingly, for the DSC sample, we observe effective negative diffusion in the longer time range (0.60–2 ns) throughout the whole investigated range of temperatures. Here, an intuitive assumption would be that trapping leads to a strong localization of the population and effective negative diffusion could emerge when the relative contribution of the mobile species to the overall PL diminishes with respect to the more localized subset. However, the negative diffusion prevails at longer times of approx. 1 ns, where the free singlet population virtually does not contribute to the overall PL (cf.Fig. 2d) and the emission profile of a localized subset of excitons should then rather remain constant over time. This finding actually suggests that in the DSC sample at low temperatures, TTA remains significant.
Kinetic modeling
Motivated by the preceding discussion, we attempt to comprehend and quantify the above-made statements about the exciton dynamics with a two-dimensional kinetic model proposed by Huang and co-workers.20,23 In addition, as suggested by Wilson et al.,32 we implement the contribution of the yellow emission as a trapping mechanism which competes with SF and contributes significantly to the luminescence profile of the DSC sample at low temperatures. Overall, the following set of coupled rate equations is numerically solved: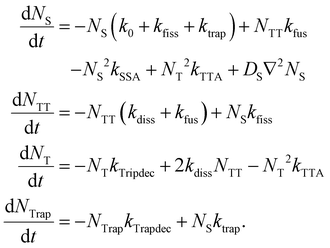 | (2) |
The model comprises four spatiotemporal population distributions: free singlet excitons Ns(x, y, t), correlated triplet pairs NTT(x, y, t), free triplets NT(x, y, t) and trapped singlet excitons NTrap(x, y, t). Possible transitions between these populations are illustrated in the kinetic scheme in Fig. 4a. After photoexcitation, singlet excitons can either recombine with the intrinsic rate k0, they can be trapped with a rate constant ktrap or undergo SF to the 1(TT) state via kfiss, from where they dissociate into free triplets (T + T) or transfer back to the singlet state with rate constants kdiss and kfus, respectively. Non-radiative singlet–singlet annihilation is described by a rate coefficient kSSA. We also consider the possibility of a delayed formation of singlet excitons via a triplet–triplet annihilation coefficient kTTA. Our model comprises two pathways of radiative decay back to the ground state: one originating from free singlet excitons with a rate constant k0 and one originating from trapped singlets via kTrapdec. Beside the interconversion between the populations, we add a diffusion term to the rate equation for NS, where DS denotes the diffusion coefficient of singlet excitons. To keep the model simple, we neglect any migration of triplet excitons or trapped excitons in the observed time window of 2 ns. This is justified by the reported diffusion coefficients for triplet excitons in TET, which are approximately three orders of magnitude smaller than those of the singlet species.19,20,23 Moreover, the TET molecules in the (001)-oriented samples investigated here are upright and thus the transition dipole moments of the lowest exciton states lie in this plane.9 This leads to emission perpendicular to the sample surface, so that we do not consider lateral radiative transport in our modeling. Another simplification in our approach is the assumption that the diffusion coefficient DS is constant over time, while it is actually well established that the effective diffusivity of excited populations in disordered organic systems appears to be time-dependent, especially at longer times.53,54 Therefore, the fitted values of DS should be rather considered as effective values, which depend on the observed time window.
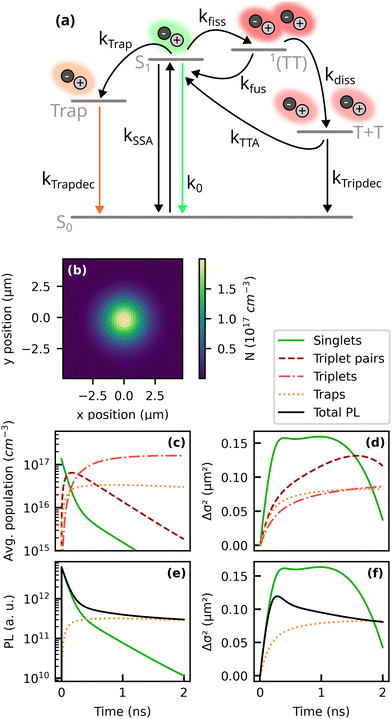 | ||
| Fig. 4 Two-dimensional kinetic model based on ref. 20, 23 and 32. (a) Kinetic scheme and (b) estimated initial profile of the excitation density (see ESI†). The dynamics of the excited populations and the respective change in the variance Δσ2 of their distribution is presented in (c) and (d). Panels (e) and (f) display the resulting PL and MSD of the total PL and the contributions of the sub-populations. As model parameters we used the literature values summarized in Table 1. | ||
Our estimate for the initial population of singlet excitons in the TRPL experiments is presented in Fig. 4b (for details, see ESI†) and yields approximately 2 × 1017 cm−3 in the center of the excitation spot. Based on this initial population density, we can simulate the spatiotemporal evolution of the different exciton species. As a first step, in order to comprehend their different contributions to the spatiotemporal PL dynamics, we used a set of kinetic parameters from the literature, as summarized in Table 1. The resulting dynamics of the exciton populations is presented in Fig. 4c and d.
| Description | Kin. parameter | Literature value | Fitted values |
|---|---|---|---|
| a Ref. 20. b Ref. 32. c Ref. 23. | |||
| Radiative decay of singlets | k 0 | 8 × 107 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
| Singlet fission | k fiss | 8.3 × 109 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
| Fusion from correlated triplet pairs | k fus | 1.0 × 109 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
| Dissociation into free triplets | k diss | 2.0 × 109 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
6.2 × 107…7.2 × 108 s−1 |
| Decay of free triplets | k tripdec | 5.0 × 107 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
| Trapping of singlets | k trap | 2.5 × 109 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
9.0 × 107…3.3 × 1010 s−1 |
| Decay of trapped excitons | k trapdec | 1.6 × 108 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
7.4 × 108…2.4 × 109 s−1 |
| Rel. oscillator strength of trap emission | α | 0.48![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) b b |
0.04…2.83 |
| Singlet–singlet annihilation | k SSA | 2.0 × 10−9 cm3 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
|
| Triplet–triplet-annihilation | k TTA | 1.7 × 10−11 cm3 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
2.0 × 10−8 cm3 s−1 |
| Diffusion of singlets (along fast axis) | D S | 3.1 cm2 s−1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) c c |
13.2…55.0 cm2 s−1 |
Moreover, we calculate the luminescence of free and trapped singlet excitons via PLS = NSk0 and PLTrap = αNTrapkTrapdec. Here, the parameter α denotes the relative oscillator strength of the trap recombination in relation to the free singlet exciton emission. The total PL is the sum of PLS and PLTrap. Qualitatively, the simulated TRPL data in Fig. 4e and f show good agreement with the experimentally observed PL transients and the MSD. The simulation allows us to connect the trends observed in the experimental data with the underlying kinetic processes. Let us first consider a situation without any emission from trapped excitons, i.e. α = 0. The PL transient and the MSD would then originate exclusively from free singlet excitons, as described by the green curves in Fig. 4e and f. Regarding the exciton kinetics, we can identify three distinct time regimes: first, the initial population of free and mobile singlet excitons is rapidly depleted by SF and trapping. This regime is characterized by a fast growth of the MSD caused by diffusion of the prompt free singlet excitons. In the second regime, the initial population of singlet excitons is drained, but delayed singlet excitons are generated via fusion from correlated triplet pairs. This causes a time regime where Δσ2 grows slower or reaches a plateau. Eventually, also the reservoir of correlated triplet pairs is depleted, leaving TTA from free triplets as the only source of emissive singlet excitons. Since the excitons involved in TTA have spent most of their lifetime as triplets, they could not diffuse very far and consequently the PL profile shrinks when delayed luminescence from TTA starts to dominate. These three regimes can also be observed in the experimental results for Δσ2 (Fig. 3c and e).
Our findings of effective negative diffusion are in line with the observations of Berghuis et al. who investigated the temporal evolution of the luminescence profile of TET at room temperature on comparable time scales.22 Due to the higher exciton densities in their work, the initial increase of Δσ2 was mainly attributed to SSA. Here, however, we used lower fluences where the contribution of SSA can be neglected. To assure that the estimated exciton density of approx. 2 × 1017 cm−3 does indeed not lead to significant SSA or to a non-radiative annihilation of singlet and triplet excitons, we performed fluence dependent measurements, which did not reveal remarkably accelerated PL dynamics at higher fluences (see ESI†), from which we conclude that in our experiments the initial slope of Δσ2 is indeed caused by exciton diffusion and not by exciton annihilation effects.
As a next step, the kinetic model is fit to the experimental data. To fully exploit the information provided by the spatiotemporal PL measurements, the model is optimized simultaneously for both the MSD data and the PL transients (see ESI† for details). Parameters that were adapted for the fits are summarized in the last column of Table 1, while for other parameters without an entry in the “fitted values” column the reported literature values were found to give a good approximation to the experimental data for the whole investigated temperature range. Exemplary fits for the PSC and the DSC sample at 290 K and 80 K are presented in Fig. 5. As we will further elaborate in the following, a major difference between the fitting parameters obtained for the PSC and the DSC samples is found in the dissociation rates into free triplet excitons and the higher oscillator strength of the trap state emission of the DSC sample, both contributing to the pronounced differences in the slopes of the MSD at low temperatures.
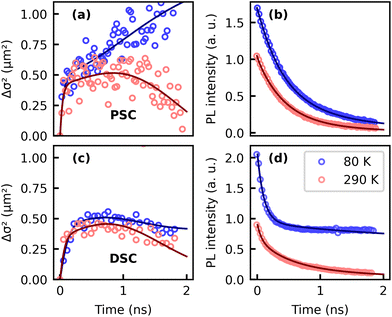 | ||
| Fig. 5 Fits of the proposed model to experimental data. Panels (a) and (b) show the experimentally recorded MSD and the PL transients of the pristine sample as circles, whereas fits are represented as solid curves. For a better readability only every 7th experimental data point was plotted. Results for the DSC are shown in (c) and (d). Data and fits for the full temperature range are presented in the ESI.† | ||
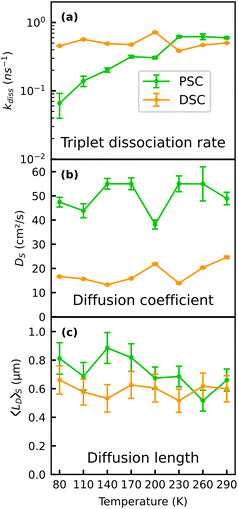
Our experimental data can be well described with a temperature independent SF rate.20 More vividly, a SF rate which is rather independent of temperature is also suggested by the “kink” in the experimentally recorded slopes of the MSD, which we attribute to a draining of the prompt singlet population via SF. This feature appears at similar times in all MSD curves, thus suggesting similar SF time constants for all measured temperatures. On the other hand, the fitted dissociation rate into free triplets kdiss must be thermally activated (cf.Fig. 6a) to reproduce the slope of the MSD of the PSC sample at later times, which clearly changes from negative to positive with decreasing temperature (Fig. 3f). A consequence of suppressed dissociation into free triplets at low temperatures is that photoexcitations spend on average more time as mobile singlets, which in turn results in enhanced diffusion of the population. Thus, our findings support the view that the “endothermic” character of SF in TET actually originates from a thermal barrier for the dissociation of the correlated 1(TT) state rather than from a thermally activated SF rate itself.30,32 Interestingly, such a barrier seems to be absent for the defect rich sample where we find effective negative diffusion originating from TTA even at the lowest temperature of 80 K. Note that a trapped population alone cannot account for negative effective diffusion, as this would rather result in a constant MSD over time (cf.Fig. 4f). This result corroborates an earlier study based on TRPL which concluded that SF is thermally activated in TET single crystals but not in polycrystalline thin films.35 Moreover, the rate of triplet generation in TET was found to be sensitive to grain sizes and the underlying polymorph,36 which could explain the higher triplet yield at low temperatures in the defect rich sample. While these two studies do not make a distinction between singlet fission and dissociation of the 1(TT) state, they essentially agree with our findings about the impact of thermal energy and defects or distortions on the yield of free triplet excitons.
It is noteworthy that two of the model parameters used in the present study are not fully consistent with earlier reports.20,22 First, the negative slopes of the MSD could only be reproduced assuming a higher TTA rate of 2 × 10−8 cm3 s−1. A reason for this discrepancy could be the high repetition rate of the laser with a time spacing of 12.5 ns between two laser pulses, which likely leads to an accumulation of the long-lived triplet excitons. In the simulation, we did not explicitly take such accumulation effects into account, as this would require very precise knowledge of the triplet recombination rate. However, a background population of triplet excitons could lead to enhanced triplet–triplet annihilation, which becomes evident in the higher effective value of kTTA. Second, the fitted diffusion constants of the singlet excitons DS of 20–50 cm2 s−1 are about one order of magnitude higher compared to other reports on singlet exciton diffusion in TET single crystals (see Fig. 6b)20,21 and the discrepancy is even three orders of magnitude compared to ref. 22. We have calibrated the spatial axis of our MSD measurements carefully with a resolution target (see ESI†), thus we do not anticipate discrepancies on this order to originate from a systematic error of the measured PL spot size. In other studies, non-radiative Auger-like processes such as exciton–exciton annihilation were found to increase the slope of the MSD at early times,22 because these nonlinear effects are most prominent in the center of the excitation spot with the highest exciton density, leading to a flattening of the Gaussian distribution of excitons in the center and thus a broader fitted MSD. However, as stated earlier, here we used fluences which should not lead to pronounced annihilation effects.36 It is noteworthy that our approach with the streak camera provides a time resolution of approx. 40 ps and a high signal-to-noise-ratio, allowing for an accurate inspection of the early time range, while other studies rather focus on longer time scales.20,22 Given that our assignment of the early time MSD to exciton diffusion is correct, the finding of temperature-independent Ds in Fig. 6b suggests that thermally activated hopping transport, as often observed for disordered organic semiconductors,11,55 does not govern the early time exciton diffusion in TET, which is apparently rather robust against temperature. A potential origin of the high values of DS could therefore be the high mobility of the initially generated exciton population, which subsequently (after the first few 100 ps) relaxes into more localized sites within the disordered density of states. At early times after photoexcitation, this population has several possibilities to energetically relax into lower lying states via the emission of phonons, resulting in high mobility, which, however, decreases as soon as the population has relaxed into sites from where transport can only occur through thermally activated hopping. The impact of an apparent time-dependent diffusivity on lateral transport measurements was recently also discussed for other disordered systems,42,56 and yields surprisingly high effective diffusion coefficients at early times (first few ns) after excitation through a laser pulse.
Further fitting parameters describing the trapping and the decay of the trapped exciton population are summarized in the ESI.† By comparing the time evolution of the MSD and the PL dynamics, it is noteworthy that without assuming any further contribution e.g. arising from a localized subset of emissive excitons, as implemented in our model, the simulated PL would decay much faster than the experimentally observed transients and delayed PL caused by free singlet excitons created through TTA alone cannot account for this effect (see ESI†). This result contrasts with the perception that the decay of the prompt PL in TET originates exclusively from SF which was earlier exploited in TRPL experiments to estimate SF rates.33,35 Therefore, to explain both the slope of the MSD and the PL dynamics simultaneously, we find it necessary to make a further assumption, i.e. that trapping contributes to the initial PL decay and that the PL at later times is partially caused by a subset of trapped excitons which did not undergo SF. From the time-dependent spectra of the DSC sample in Fig. 2d, it becomes obvious that at low temperatures the yellow emission band gives rise to such long lived delayed PL and consequently we have attributed the underlying mechanism to trapping and slow recombination of trapped excitons. Surprisingly, also the data of the PSC sample which does not show the yellow emission band, can only be fitted with a contribution of a delayed emissive species which lasts longer than what would be assumed based on the SF rate. The relative oscillator strength of this subset of presumably trapped excitons in the PSC sample is much lower than that of the yellow emission band (see ESI†) and according to Fig. 2c, the emission spectra look similar to the emission spectrum of the initially generated singlet excitons. Based on this we hypothesize that the excitons causing the longer-lived PL in the PSC sample are not substantially different from the initially created exciton species.
Instead, we speculate that the underlying picture of a unique SF rate is actually too simplistic. Since the TET crystals are subject to spatial and energetic disorder, it appears feasible that there is also a distribution of SF rates. Following this perception, the SF rate of 8.3 × 109 s−1 would rather represent an upper limit for a certain range of SF rates present in the material. Consequently, the temperature independent rates ktrap and ktrapdec found for the PSC sample summarized in the ESI† could also be interpreted as the population and dissociation of exciton states from where SF occurs more slowly with rate constants of 2 × 109 s−1 (corresponding to decay times of approx. 0.5 ns).
As a final point we discuss the effects of thermally activated dissociation of the 1(TT) state and the trapping of excitons on the diffusion length. While the relatively short time window of 2 ns probed in our experiments does not allow us to make a statement about triplet diffusion, we can estimate the contribution of the singlet species to the overall diffusion length.21 Based on the kinetic model (eqn (2)), we can disentangle the contribution of singlet excitons MSDS(t) to the overall slope of the MSD and their contribution IPL,S(t) to the overall PL intensity. Since the PL of excitons is proportional to the exciton population at a given time interval, we can estimate the average MSD caused by the singlet population by averaging over all MSD values in the probed time range weighted by the PL intensity (i.e. the number of singlet excitons) present at a particular time:
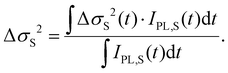 | (3) |
From this, the average diffusion length is calculated via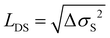 . The results for the diffusion length are presented in Fig. 6c. The room temperature values are on the order of 600 nm, which is higher than a former estimate of approx. 300 nm based on transient absorption microscopy.21 We find an increase of the diffusion length in the pristine sample to approx. 800 nm with decreasing temperature, while the diffusion length of the DSC sample shows no notable temperature dependence. Qualitatively, our results on the temperature-dependent diffusion length in the PSC sample show the same trend as observed in an early study by Vaubel and Bässler,52 who already proposed thermally activated singlet fission as the underlying reason for the observed temperature dependence. They determined diffusion lengths of singlet excitons of approx. 60 nm at low temperatures, which is substantially lower than results originating from recent spatiotemporal probing techniques. This discrepancy likely originates from the fact that they probed exciton transport in the direction of the c-axis, along which exciton diffusion is approximately one order of magnitude lower than in the (a,b)-plane, due to the absence of pronounced overlap of π-orbitals.19 Note that a precise alignment of the crystals to probe exciton transport either along the a- or the b-axis was not possible with the given setup. Therefore, here we did not take a detailed look into the anisotropy of exciton transport within the (a,b)-plane. Previous work found that the diffusion coefficients along the a- and b-direction vary by a factor of approximately 3.20 Notably, our results suggest that the influence of the material quality on the effective diffusion coefficients is actually on the same order. When comparing azimuth-resolved diffusion by polarization resolved experiments one has to also consider anisotropic effects of both Davydov components causing anisotropic phonon-coupling due to the phonon-bottleneck effect.29 Based on the kinetic model, the different temperature dependencies of lD in the PSC and the DSC sample can be rationalized by efficient exciton trapping in the DSC sample, while in the PSC sample a trapping mechanism competing with SF is largely absent. Moreover, dissociation of the correlated triplet pair state is kinetically hampered in the pristine sample at low temperature, leading to a preferred population of the mobile singlet state.
. The results for the diffusion length are presented in Fig. 6c. The room temperature values are on the order of 600 nm, which is higher than a former estimate of approx. 300 nm based on transient absorption microscopy.21 We find an increase of the diffusion length in the pristine sample to approx. 800 nm with decreasing temperature, while the diffusion length of the DSC sample shows no notable temperature dependence. Qualitatively, our results on the temperature-dependent diffusion length in the PSC sample show the same trend as observed in an early study by Vaubel and Bässler,52 who already proposed thermally activated singlet fission as the underlying reason for the observed temperature dependence. They determined diffusion lengths of singlet excitons of approx. 60 nm at low temperatures, which is substantially lower than results originating from recent spatiotemporal probing techniques. This discrepancy likely originates from the fact that they probed exciton transport in the direction of the c-axis, along which exciton diffusion is approximately one order of magnitude lower than in the (a,b)-plane, due to the absence of pronounced overlap of π-orbitals.19 Note that a precise alignment of the crystals to probe exciton transport either along the a- or the b-axis was not possible with the given setup. Therefore, here we did not take a detailed look into the anisotropy of exciton transport within the (a,b)-plane. Previous work found that the diffusion coefficients along the a- and b-direction vary by a factor of approximately 3.20 Notably, our results suggest that the influence of the material quality on the effective diffusion coefficients is actually on the same order. When comparing azimuth-resolved diffusion by polarization resolved experiments one has to also consider anisotropic effects of both Davydov components causing anisotropic phonon-coupling due to the phonon-bottleneck effect.29 Based on the kinetic model, the different temperature dependencies of lD in the PSC and the DSC sample can be rationalized by efficient exciton trapping in the DSC sample, while in the PSC sample a trapping mechanism competing with SF is largely absent. Moreover, dissociation of the correlated triplet pair state is kinetically hampered in the pristine sample at low temperature, leading to a preferred population of the mobile singlet state.
To put our results into a broader context, it is important to stress that luminescence studies only present one side of the coin. While TRPL experiments are only sensitive to the luminescent subset of an exciton population, transient absorption spectroscopy can also access excitons which are not emissive, e.g. because their decay is spin- or momentum forbidden.20 Combining both methods can thus provide more insight into the fate of the triplet population and provide a potentially more balanced picture of the singlet exciton dynamics and diffusion. On the other hand, TRPL experiments are simpler to implement and allow to acquire robust datasets which are less susceptible to noise and artifacts. Importantly, TRPL microscopy is also more sensitive to defects and band tail states, making it an ideal tool to correlate the lateral transport properties with the material quality, as demonstrated here using the example of TET. A topic that certainly deserves more detailed research is the influence of disorder on exciton transport and on the interconversion between singlet and triplet excitons. We have noted that our experimental results are not fully consistent with diffusion measurements at low excitation fluences (see ESI†). This could originate from the dominant role of localized band tail states or excitons trapped at defects, which are not considered in the applied model. Even though our temperature dependent study gives strong evidence that thermally activated dissociation into free triplets is the underlying reason of the observed effective negative diffusion, the phenomenon can in general also originate from other processes, such as the transition from a mobile species dominating the emission at early times into a more localized one within a disordered density of states.42
In general, lateral transport measurements can give further insights into the underlying density of states in disordered systems. Variations in the underlying energy scale of disorder, different probed time regimes as well as the presence of defects, which in our study is likely tetraquinone, can all contribute to discrepancies in reported diffusion coefficients and it is important to take these effects into account in spatiotemporal probing techniques. In particular, we have learned that trapping into tetraquinone-defects can efficiently compete with SF and thus impede combined singlet and triplet exciton transport.
Moreover, it is possible to learn more about the validity of thermal activation laws regarding the transport behavior from spatiotemporal studies. Notably, contrasting with the generally observed trends,57 thermally activated transport of excitons is not observed in our work on TET and this trend can be potentially generalized for a larger number of materials where SF is endothermic. In contrast, the thermal activation of dissociation into slowly moving free triplets could rather be understood as a partial “de-activation” of the fast singlet exciton transport at elevated temperatures, making simple activation laws not applicable here.
For future work it would be intriguing to apply the presented methodology to less well explored molecular systems or to co-crystals where the SF mechanism and its impact on exciton transport are less well understood compared to TET.
Conclusions
In this work, we have studied the temperature dependent spatiotemporal exciton dynamics in TET single crystals on a picosecond time scale. By correlating spectral and spatial dynamics, we have made two key findings with broader implications for exciton transport in OSC devices. First, we have demonstrated how singlet exciton transport can be slowed down in pristine TET crystals with increasing temperature, which is expected due to a higher yield of slowly moving triplet excitons. Apparently, more triplet excitons are generated, because dissociation into free triplets is a thermally activated step. Second, we found a clear correlation between singlet exciton transport and sample quality. A high density of trap states due to tetraquinone impurities, which is associated with the yellow emission band in TET, immobilizes the exciton population within a few 100 ps. The effect becomes particularly pronounced at low temperatures where the yellow emission band gains oscillator strength. Overall, the experimental framework utilized in this study demonstrates how correlating spectrally, spatially and time resolved information yields robust datasets against which kinetic models can be thoroughly tested. Beside model systems like TET, it is of great interest to explore other systems with presumable endothermic SF, but more experimental efforts such as for example complementary transient absorption microscopy measurements are needed to understand the exciton transport at early times with the surprisingly high diffusion coefficients found here.Data availability
Raw data for our manuscript entitled “Transport, Trapping, Triplet Fusion: Thermally Retarded Exciton Migration in Tetracene Single Crystals” are available at figshare via the following link: https://doi.org/10.6084/m9.figshare.26005081.v1Spectrally and spatially resolved streak camera raw data and backgrounds recorded for a pristine and a defect rich tetracene single crystal at different temperatures.
Correction data and Python-based code to analyze the raw data.
Author contributions
D. M.: data curation, investigation, methodology, software, validation, visualization, writing – original draft. S. A.: data curation, investigation, resources, validation, visualization, sample preparation and structural characterization, writing – original draft. D. B.: resources, writing – review & editing. A. K.: investigation, validation. G. W.: conceptualization, funding acquisition, project administration, writing – review & editing. M. G.: conceptualization, funding acquisition, methodology, project administration, resources, supervision, writing – original draft, writing – review & editing.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors acknowledge financial support provided by the German Science Foundation (Deutsche Forschungsgemeinschaft, DFG), project-ID 223848855-SFB 1083 “Structure and Dynamics of Internal Interfaces” within the projects A2 and B10. Moreover, the authors thank Prof. Martin Koch for the possibility to access the streak camera setup.References
- S. Fratini, M. Nikolka, A. Salleo, G. Schweicher and H. Sirringhaus, Nat. Mater., 2020, 19, 491–502 CrossRef CAS PubMed.
- D. N. Congreve, J. Lee, N. J. Thompson, E. Hontz, S. R. Yost, P. D. Reusswig, M. E. Bahlke, S. Reineke, T. Van Voorhis and M. A. Baldo, Science, 2013, 340, 334–337 CrossRef CAS PubMed.
- H. Bronstein, C. B. Nielsen, B. C. Schroeder and I. McCulloch, Nat. Rev. Chem., 2020, 4, 66–77 CrossRef CAS PubMed.
- M. Muccini, Nat. Mater., 2006, 5, 605–613 CrossRef CAS PubMed.
- G. Schweicher, G. Garbay, R. Jouclas, F. Vibert, F. Devaux and Y. H. Geerts, Adv. Mater., 2020, 32, 1905909 CrossRef CAS PubMed.
- R. Kersting, U. Lemmer, M. Deussen, H. Bakker, R. Mahrt, H. Kurz, V. Arkhipov, H. Bässler and E. Göbel, Phys. Rev. Lett., 1994, 73, 1440–1443 CrossRef PubMed.
- M. Knupfer, Appl. Phys. A, 2003, 77, 623–626 CrossRef CAS.
- C. J. Bardeen, Annu. Rev. Phys. Chem., 2014, 65, 127–148 CrossRef CAS PubMed.
- A. M. Valencia, D. Bischof, S. Anhäuser, M. Zeplichal, A. Terfort, G. Witte and C. Cocchi, Electron. Struct., 2023, 5, 033003 CrossRef.
- M. C. Scharber and N. S. Sariciftci, Prog. Polym. Sci., 2013, 38, 1929–1940 CrossRef CAS PubMed.
- O. V. Mikhnenko, P. W. M. Blom and T.-Q. Nguyen, Energy Environ. Sci., 2015, 8, 1867 RSC.
- M. B. Smith and J. Michl, Annu. Rev. Phys. Chem., 2013, 64, 361–386 CrossRef CAS PubMed.
- A. J. Baldacchino, M. I. Collins, M. P. Nielsen, T. W. Schmidt, D. R. McCamey and M. J. Y. Tayebjee, Chem. Phys. Rev., 2022, 3, 021304 CrossRef CAS.
- M. Einzinger, T. Wu, J. F. Kompalla, H. L. Smith, C. F. Perkinson, L. Nienhaus, S. Wieghold, D. N. Congreve, A. Kahn, M. G. Bawendi and M. A. Baldo, Nature, 2019, 571, 90–94 CrossRef CAS PubMed.
- J. Lee, P. Jadhav, P. D. Reusswig, S. R. Yost, N. J. Thompson, D. N. Congreve, E. Hontz, T. Van Voorhis and M. A. Baldo, Acc. Chem. Res., 2013, 46, 1300–1311 CrossRef CAS PubMed.
- A. T. Haedler, K. Kreger, A. Issac, B. Wittmann, M. Kivala, N. Hammer, J. Köhler, H. W. Schmidt and R. Hildner, Nature, 2015, 523, 196–199 CrossRef CAS PubMed.
- A. Sharma, L. Zhang, J. O. Tollerud, M. Dong, Y. Zhu, R. Halbich, T. Vogl, K. Liang, H. T. Nguyen, F. Wang, S. Sanwlani, S. K. Earl, D. Macdonald, P. K. Lam, J. A. Davis and Y. Lu, Light: Sci. Appl., 2020, 9, 2047–7538 Search PubMed.
- T. Zhu and L. Huang, J. Phys. Chem. Lett., 2018, 9, 6502–6510 CrossRef CAS PubMed.
- G. M. Akselrod, P. B. Deotare, N. J. Thompson, J. Lee, W. A. Tisdale, M. A. Baldo, V. M. Menon and V. Bulovic, Nat. Commun., 2014, 5, 3646 CrossRef CAS PubMed.
- Y. Wan, Z. Guo, T. Zhu, S. Yan, J. Johnson and L. Huang, Nat. Chem., 2015, 7, 785–792 CrossRef CAS PubMed.
- T. Zhu, Y. Wan, Z. Guo, J. Johnson and L. Huang, Adv. Mater., 2016, 28, 7539–7547 CrossRef CAS PubMed.
- A. M. Berghuis, T. V. Raziman, A. Halpin, S. Wang, A. G. Curto and J. G. Rivas, J. Phys. Chem. Lett., 2021, 12, 17 Search PubMed.
- T. Zhu, Y. Wan and L. Huang, Acc. Chem. Res., 2017, 50, 1725–1733 CrossRef CAS PubMed.
- D. Holmes, S. Kumaraswamy, A. J. Matzger and K. P. C. Vollhardt, Chem. – Eur. J., 1999, 5, 3399–3412 CrossRef CAS.
- R. W. I. De Boer, T. M. Klapwijk and A. F. Morpurgo, Appl. Phys. Lett., 2003, 83, 4345–4347 CrossRef CAS.
- A. Camposeo, M. Polo, S. Tavazzi, L. Silvestri, P. Spearman, R. Cingolani and D. Pisignano, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 033306 CrossRef.
- H. Yamagata, J. Norton, E. Hontz, Y. Olivier, D. Beljonne, J. L. Brédas, R. J. Silbey and F. C. Spano, J. Chem. Phys., 2011, 134, 204703 CrossRef CAS PubMed.
- S. H. Lim, T. G. Bjorklund, F. C. Spano and C. J. Bardeen, Phys. Rev. Lett., 2004, 92, 107402 CrossRef PubMed.
- J. J. P. Thompson, D. Muth, S. Anhäuser, D. Bischof, M. Gerhard, G. Witte and E. Malic, Nat. Sci., 2023, 3, e20220040 CrossRef CAS.
- J. J. Burdett, D. Gosztola and C. J. Bardeen, J. Chem. Phys., 2011, 135, 214508 CrossRef PubMed.
- J. J. Burdett and C. J. Bardeen, J. Am. Chem. Soc., 2012, 134, 8597 CrossRef CAS PubMed.
- M. W. B. Wilson, A. Rao, K. Johnson, S. Gélinas, R. di Pietro, J. Clark and R. H. Friend, J. Am. Chem. Soc., 2013, 135, 16680–16688 CrossRef CAS PubMed.
- M. J. Y. Tayebjee, R. G. C. R. Clady and T. W. Schmidt, Phys. Chem. Chem. Phys., 2013, 15, 14797–14805 RSC.
- Z. Birech, M. Schwoerer, T. Schmeiler, J. Pflaum and H. Schwoerer, J. Chem. Phys., 2014, 140, 114501 CrossRef PubMed.
- G. B. Piland and C. J. Bardeen, J. Phys. Chem. Lett., 2015, 6, 1841–1846 CrossRef CAS PubMed.
- D. H. Arias, J. L. Ryerson, J. D. Cook, N. H. Damrauer and J. C. Johnson, Chem. Sci., 2016, 7, 1185–1191 RSC.
- N. Geacintov, M. Pope and F. Vogel, Phys. Rev. Lett., 1969, 22, 593–596 CrossRef CAS.
- C. D. Cruz, E. L. Chronister and C. J. Bardeen, J. Chem. Phys., 2020, 153, 234504 CrossRef CAS PubMed.
- H. Müller and H. Bässler, Chem. Phys. Lett., 1975, 36, 312–315 CrossRef.
- N. S. Ginsberg and W. A. Tisdale, Annu. Rev. Phys. Chem., 2020, 71, 1–30 CrossRef CAS PubMed.
- X. Liu, V. Kaiser, M. Wuttig and T. Michely, J. Cryst. Growth, 2004, 269, 542–549 CrossRef CAS.
- J. D. Ziegler, J. Zipfel, B. Meisinger, M. Menahem, X. Zhu, T. Taniguchi, K. Watanabe, O. Yaffe, D. A. Egger and A. Chernikov, Nano Lett., 2020, 20, 6674–6681 CrossRef CAS PubMed.
- J. Mooney and P. Kambhampati, J. Phys. Chem. Lett., 2013, 4, 3316–3318 CrossRef CAS.
- V. K. Thorsmølle, R. D. Averitt, J. Demsar, D. L. Smith, S. Tretiak, R. L. Martin, X. Chi, B. K. Crone, A. P. Ramirez and A. J. Taylor, Phys. Rev. Lett., 2009, 102, 017401 CrossRef PubMed.
- H. Nishimura, T. Yamaoka, A. Matsui, K. Mizuno and G. J. Sloan, J. Phys. Soc. Jpn., 1985, 54, 1627 CrossRef CAS.
- M. Voigt, A. Langner, P. Schouwink, J. M. Lupton, R. F. Mahrt and M. Sokolowski, J. Chem. Phys., 2007, 127, 114705 CrossRef CAS PubMed.
- C. K. Yong, A. J. Musser, S. L. Bayliss, S. Lukman, H. Tamura, O. Bubnova, R. K. Hallani, A. Meneau, R. Resel, M. Maruyama, S. Hotta, L. M. Herz, D. Beljonne, J. E. Anthony, J. Clark and H. Sirringhaus, Nat. Commun., 2017, 8, 15953 CrossRef CAS PubMed.
- G. Peter and H. Bässler, Chem. Phys., 1980, 49, 9–16 CrossRef CAS.
- U. Sondermann, A. Kutoglu and H. Bässler, J. Phys. Chem., 1985, 89, 1735–1741 CrossRef CAS.
- E. Venuti, R. Guido, D. Valle, L. Farina, A. Brillante, M. Masino and A. Girlando, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 104106 CrossRef.
- S. Guha, J. Rice, Y. Yau, C. Martin, M. Chandrasekhar, H. Chandrasekhar, R. Guentner, P. Scanduicci de Freitas and U. Scherf, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 125204 CrossRef.
- G. Vaubel and H. Bässler, Mol. Cryst. Liq. Cryst., 1970, 12, 47–56 CrossRef CAS.
- H. Bässler, Phys. Status Solidi B, 1993, 175, 15–56 CrossRef.
- S. D. Baranovskii, Phys. Status Solidi B, 2014, 251, 487–525 CrossRef CAS.
- J. D. A. Lin, O. V. Mikhnenko, T. S. Van Der Poll, G. C. Bazan and T. Q. Nguyen, Adv. Mater., 2015, 27, 2528–2532 CrossRef CAS PubMed.
- G. Banappanavar, R. Saxena, H. Bässler, A. Köhler and D. Kabra, J. Phys. Chem. Lett., 2024, 15, 3109–3117 CrossRef CAS PubMed.
- I. I. Fishchuk, A. K. Kadashchuk, J. Genoe, V. N. Poroshin and H. Bässler, Mol. Cryst. Liq. Cryst., 2011, 535, 1–9 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4nr01086h |
| This journal is © The Royal Society of Chemistry 2024 |